- Electrical Engineering, Maulana Azad National Institute of Technology, Bhopal, India
As the modern power system continues to grow in size, complexity, and uncertainty, traditional methods may occasionally prove insufficient in addressing the associated challenges. The improper location of distributed generation varies the voltage profile, increases losses and compromises network capacity. Machine learning algorithms predict accurate site positions, and network reconfiguration improves the capacity of the power system. The proposed algorithm is a hybrid of machine learning and deep learning algorithms. It cascades Support Vector Machine as the main model and uses Random Forest and Radial Neural Networks as classification algorithms for accurately predicting DG position. The non-linearity characteristics of the DG problem are directly mapped to the proposed algorithms. The proposed algorithm is employed on familiar test setups like the IEEE 33-bus and 69-bus distribution systems using MATLAB R2017 as simulation software. The R-squared (R2) values for all parameters yield a value of 1, while the MAPE values are minimal for the proposed cascaded algorithm in contrast to other algorithms of LSTM, CNN, RNN and DQL.
1 Introduction
1.1 Background
As electricity demands grow, rather than solely relying on constructing new centralized power plants and transmission infrastructure, it is wise to integrate smaller-scale production units nearer to consumption hubs. Compact yet powerful generating units, commonly known as distributed generation (DG), have garnered increased attention due to their numerous advantages. Improper allocation of DG within the distribution system (DS) can have detrimental effects on the power system rather than providing benefits. To guarantee the best allocation of distributed generation (DG), several optimization investigations have been recorded in scholarly works.
The optimization of distributed generation (DG) is directed towards fortifying the reliability of the power network. The application of distributed generation has several advantages over conventional generation, such as technical, economic, and environmental, for the electric distribution company and the end consumers. Due to the development of emerging technologies, an appropriate allocation involves various factors like reliability, power quality, voltage profile, power loss, and control stability of the electric grid.
Effective approaches for the recognition of power system control challenges have consistently been a focal point. To tackle this issue, machine learning and deep learning methodologies are utilized to predict occurrences, evaluate the multitude of variables and conditions, categorize them, and identify key features when managing power system control challenges across preventive, normal, emergency, and recovery situations. Machine learning methods play a crucial role in discerning patterns and structures within data, enabling the analysis, processing, prediction, and categorization of extensive pertinent to the evaluation of intricate power system issues. Numerous studies have explored machine learning algorithms, and the proposal introduces the cascaded machine learning algorithm (CML) specifically designed to optimize the siting and sizing aspects within distribution systems. Menke et al. (2019).
An approach centered on estimation for assessing the dimensions of DG (Distributed Generation) and its impact on the network, aiming to circumvent the cumbersome and obligatory application of load flow methods. Various machine learning techniques, including linear regression, artificial neural networks, support vector regression, K-nearest neighbours, and decision trees, have been leveraged for these estimations and applied across established test systems. Purlu and Turkay (2021).
1.2 Related work
The progression of distributed generation alongside the utilization of machine learning algorithms and various optimization methods contributes to enhancing the voltage profile with minimized losses within the transmission network. Recently, numerous authors have introduced a variety of algorithms, incorporating machine learning, deep learning, and several meta-heuristic functions, aimed at optimizing the allocation of distributed generation. In Essallah et al. (2019) The goal of the authors is to secure voltage stability amid load variations while simultaneously pinpointing ideal locations for distributed generation (DG) and determining their most suitable power capacities. Employing the PSAT MATLAB toolbox, they utilized this approach on the IEEE evaluation systems, encompassing the 33-bus and 69-bus configurations, revealing the method’s efficacy, reliability, and robust performance. In the initial scenario, there was a noteworthy enhancement in the system’s active power, exceeding its rated value by 50%. Additionally, both the active and reactive power loads saw a substantial increase of 50% in the subsequent scenario. In Sambaiah et al. (2019) the authors employed the Slaps Swarm Algorithm (SSA) for DG allocation. The concept is based on how slaps forage and navigate by swarming together in the water. In Liu et al. (2019) The total power losses are decreased by 90%, the cost is lowered by 21%, and the emissions are decreased by 67% for the 33-bus system.
To ascertain the optimal position and dimensions for DG units, the authors take into account multiple factors including voltage variation, line loss, and energy-saving benefits during the model selection process. This necessitates a comprehensive analysis to ensure accurate decision-making. This thorough evaluation ensures the optimal decision-making process. In Onlam et al. (2019) The authors utilized the Adaptive Shuffled Frog Leaping Algorithm (ASFLA) technique to carry out both network reconfiguration and DG installation. This approach was implemented across seven different scenarios for the electrical systems of IEEE 33-bus configuration and 69-bus configuration. In the most favorable scenario, the 33-bus system achieved loss savings of up to 75.57%, while the 69-bus system experienced an impressive 84.90% reduction in losses. Moreover, the Voltage Stability Index (VSI) increased by approximately 35.45% and 40.82%, respectively, surpassing their base values. In Mohammadpourfard et al. (2019) The contribution generates valuable training data through a scenario generator, along with specific details outlining the Artificial Neural Network (ANN) architecture. The results unequivocally illustrate that the proposed approach effectively addresses the limitations observed in existing ANN methodologies, particularly those that are not suitable for grids with significant Distributed Generation (DG) penetration. In Chege et al. (2019) the authors employ the voltage stability index technique to determine where distributed generation and capacitors should be placed. By employing a hybrid evolutionary programming method, the search for the most suitable sizes of distributed generation and capacitors to be installed at the indicated locations is facilitated. When the placement was carried out using this technique, the lowest voltage values of the network rose from 0.9036 to 0.9400 per unit, while the minimum Voltage Stability Index (VSI) values increased from 0.6690 to 0.7841. In Yin et al. (2019) to determine the feasibility and efficiency of the model, it is essential to carry out a thorough validation process. Therefore, a comparison is made between the results obtained and those achieved through the utilization of genetic algorithms (GA), support vector machines (SVM), and particle swarm algorithms (PSO). The kernel machine learning obtains the results of the capacity choice of the DG that satisfy the target function by training the model. In Shaheen et al. (2019) The authors suggest that the Stochastic Fractal Optimization (SFO) algorithm showcases validity, accuracy, feasibility, and robustness, surpassing alternative simulation methods in addressing the optimum load power flow (OPF) issue. In Arif et al. (2020) the authors suggest the implementation of the Analytical Hybrid Particle Swarm Optimization (AHPSO) algorithm to assist in evenly distributing, progressively dispersing, centrally distributing, and randomly distributing loads. Based on simulation outcomes, the AHPSO algorithm showcases significantly accelerated convergence rates compared to the traditional Particle Swarm Optimization technique. Notably, it demonstrates substantial enhancements in convergence performance across various distribution systems. The achieved enhancements are significant, demonstrating improvements of 32%, 42.59%, 50.91%, and 55.56% for the distribution systems of IEEE 10-bus, IEEE 33-bus, IEEE 69-bus, and KEPCO, respectively. Notably, both the normal PSO and AHPSO algorithms yield similar results for the location and scaling of DG in every scenario. In Hassan et al. (2020) the authors suggest a methodology directed at addressing the concern of siting and determining the dimensions of distributed generation units fueled by sustainable energy sources. Morales et al. (2020) A procedure is described to identify the current flow along the distribution feeder (DF) while integrating distributed generation (DG). This method incorporates decision trees (DT), empirical decomposition (ED), and support vector machines (SVM) to achieve the intended objective, delineating the steps of the methodology. In Ismail et al. (2020) The authors introduce an algorithm designed for power systems utilizing deep learning principles.
This algorithm achieved an exceptional detection rate of 99.3% and demonstrated a minimal false alarm rate of only 0.22% by incorporating specific details related to PV generation, data, and interpretations extracted from SCADA systems. In Farh et al. (2020) an inventive technique, the Crow Search Algorithm-based Auto-Drive Particle Swarm Optimization (CSA-PSO) technique, is employed to optimize the setup, scale, and quantity of [unclear] systems with the goal of minimizing overall expenses and reducing power losses. In Tran et al. (2020) seven different scenarios were used to evaluate the proposed Stochastic Fractal search (SFS) algorithm on 33, 69, 84, 119, and 136 buses distribution networks. When the results from SFS were contrasted with those from other methodologies, it became clear that SFS produced more effective solutions. The SFS algorithm has the potential to search heuristics for solving issues quickly and with high-quality solutions. In Agajie et al. (2020) the application of the development of a Grid-based Multi-Objective Harmony Search Algorithm (GrMHSA) to improve the sizing and placement of Distributed Generation units ensures the enhancement of the overall system performance. In Admasie et al. (2020) the Intelligent Detection Method (IIDM) integrates a sophisticated approach termed Feature-based Wolf-Optimized 113. Artificial Neural Network (GWO-ANN) using an intrinsic mode function (IMF). Through MATLAB simulations, the IIDM’s efficacy is highlighted in achieving high classification accuracy, computational efficiency, and robustness against noise interference in measured voltages. In contrast to directly resolving models under varying operational conditions, this method addresses the volt-VAR optimization (VVO) challenge in unbalanced distribution networks employing an advanced Deep Q-Network (DQN) framework. Its effectiveness is evaluated on IEEE 13-bus and 123-bus networks with imbalanced characteristics. In Haider et al. (2021) the application of the algorithm demonstrated significant efficacy in mitigating voltage fluctuations and reducing power losses within the distribution network. MATLAB software was employed to estimate the efficiency of this technique on the radial distribution network of the IEEE-33 bus system. Through the integration of a hybrid strategy named Enhanced Wolf Optimizer and Particle Swarm Optimization (EGWO-PSO), it became viable to attain optimized placement and sizing, resulting in an overall enhancement of the system’s performance. This heuristic approach, EGWO, draws inspiration from wolf behaviors and presents a hybrid methodology that converges rapidly without being limited by local best practices Venkatesan et al. (2021). In Ogunsina et al. (2021) The authors employed the ant colony optimization (ACO) algorithm identifying the Optimal Positions and quantities for distributed resources within a power network. Bajaj and Singh (2021) The authors introduced a multi-objective method integrating multiple performance index constraints and compared its outcomes with hosting capacity augmentation techniques. The method involves the ENLPCI (Extended Nonlinear Load Position-based APF Current Injection) technique, facilitating the identification of optimal bus locations for Active Power Filter (APF) placement and the determination of required APF quantities.
The algorithm underwent performance evaluation through tests conducted on the IEEE test system with 69-bus. The outcomes highlighted the considerable impact of solar fluctuations on the best positioning and dimensions of Active Power Filters (APF)as part of the Optimal Placement and Sizing (OPAS) approach. Lakum and Mahajan (2021). In Lakum and Mahajan (2019) The authors introduced a novel technique called Non-Linear Load Position-Based Current Injection (NLPCI) aimed at strategically positioning the Active Power Filter (APF). The process involves the identification of suitable bus locations while considering the presence of Distributed Generation (DG) and excluding linear loads. To reduce the APF’s size, the algorithm utilizes a voltage threshold of 5%, employing the Total Harmonic Distortion method. The implementation of this proposed algorithm notably enhanced system performance indices, increasing the Hosting Capacity (HC) across various test systems, including the 59-node Egyptian test system, 135-node Brazilian test distribution network, additionally, the analysis includes the IEEE 33-node and IEEE 69-node test power networks. Moreover, using the NR (Newton-Raphson) and AOA (Artificially Optimized Algorithm) enhanced the HC of the 59-node and 135-node test systems by 38.832% and 72.895%, respectively. Ali et al. (2021) The use of the Meta-heuristic Rider Algorithm (ROA) aids in evaluating the optimal dimensions and positions for Distributed Generation (DG) units, which are driven by sustainable energy resources like biomass-based generation, wind turbines (WT), and photo voltaic (PV) systems within distribution networks. Khasanov et al. (2021) The authors ingeniously employed the coyote technique to efficiently determine the positioning and capacity of distributed generation (DG) within radial networks. This approach demonstrated superior performance compared to other methods like SFO, SSA, and COA in making optimal DG decisions. Pham et al. (2021). The authors assessed their proposed Modified Sequential Switch Opening and Exchange (MSSOE) algorithm using industry-standard distribution systems like IEEE 33-node, IEEE 69-node, and IEEE 119-node. The findings show that MSSOE surpasses existing algorithms, delivering a superior global solution with reduced computational time. Vannak Vai et al. (2021). The study incorporated the Firefly Algorithm (FA), a meta-heuristic technique, within the IEEE 33-bus distribution system as part of its methodologies. This method includes the application of a mixed probabilistic model to manage both output power uncertainty and the system load. Naguib et al. (2021). The research integrates hybrid particle swarm optimization (PSO) algorithms, these methods incorporate chaotic maps and adaptive acceleration coefficients to identify the optimal configuration and dimensions of photovoltaic (PV) systems connected to an electric grid. Belbachir et al. (2021). In Bajaj et al. (2020) A methodology inspired by the Analytical Hierarchy Process (AHP) is introduced for evaluating Power Quality (PQ) in modified distribution power systems undergoing changes. In Kushal et al. (2020) The authors have introduced a decision-making methodology that uses the Analytical Hierarchy Process (AHP) to assess various distributions of Photovoltaic (PV) and Battery Energy Storage Systems (BESS) resources to load buses., considering various scenarios focused on cost and resilience enhancement. The results indicate that this approach offers valuable guidance for planners in making informed investments. Additionally, they introduced a hybrid technique merging clustering with particle swarm optimization to optimize Distributed Generation (DG) allocation. This algorithm clusters buses within the distribution network and selects the most suitable cluster for DG allocation, thereby reducing the number of viable production buses. In the optimal scenarios, the algorithm reduces test feeder losses by 69%, 86%, and 90%, while considering uncertainties in three different scenarios, achieving reductions of 39%, 53%, and 55% respectively Eyübog˘lu and Gül (2021). The revised method for updating control variables of the initial slime algorithm led to the development of a new solution. As a result, the proposed algorithm demonstrates a notable improvement in reducing voltage deviation to 1.4779 Pu and power loss to 78.88%. In contrast, alternative algorithms provided results within the range of 69.10%–78.87% for loss and 1.5759 to 1.4996 Pu for voltage deviation Pham et al. (2022). The authors incorporated wind generation into the distribution system, resulting in enhanced bus voltages and reduced active power losses. Specifically, nodes 19 and 12 experienced voltage increases of 2.2% and 3.26%, respectively. Consequently, in the IEEE-19 bus system, losses reduced from 13.54 kW to 6.36 kW, while in the IEEE-25 bus system, losses decreased from 150 kW to 95.30 kW Routray et al. (2021). The Loss Sensitivity Factor plays a pivotal role in determining the search space for Distributed Generation (DG) sites. Employing an analytical technique, the initial DG sizes are calculated based on a specific interpretation. Selim et al. (2021). In Rathore and Patidar (2021) The authors introduce a deep learning-based algorithm designed for effectively placing and arranging DG units in optimal locations. This algorithm aims to enhance voltage characteristics and minimize losses within the system. In Dheeban and Selvan (2021) The authors utilized the Thevenin Equivalent Impedance method to simulate the distributed generation (DG) source on the high-voltage side of the transformer. The previous sections demonstrate various methods for determining distribution system voltages, including distribution load flow for unbalanced systems, symmetrical components, mesh, and nodal analysis. An enhanced algorithm, incorporated into an adaptive interference controller, was then applied to the proposed PV-UPQC (Photovoltaic - Unified Power Quality Conditioner) system. This advanced fuzzy-model-based controller enhances the system by analyzing system parameters and facilitating the generation of reference current Zhang et al. (2020). Mo and Sansavini (2019) The exploration involves utilizing Optimal Power Flow (OPF) to calculate the suitability of Energy Not Served (ENS) and Operation and Maintenance (O&M) costs for Distributed Generation (DG). This process tends to overestimate unreliability and costs. To address this issue, the simulation results provide guidance for decision-making in managing, maintaining, and planning Distributed Generations. The objective is to mitigate the effects, minimize O&M expenses, and decrease energy loss, ensuring more efficient and reliable systems Zhao et al. (2019). The paper undertakes a comparative analysis between two operational strategies and multiple islanding strategies for coordinating dispersed power and storage devices. The study’s results demonstrate the considerable enhancement in the dependability of the distribution system caused by implementation of the proposed dynamic strategy. This enhancement maintains the steady functioning of vital loads within the system. Furthermore, it deeply explores fault detection and protection techniques employed in distributed networks alongside distributed generation. This paper uniquely contributes by offering a comprehensive understanding of diverse fault detection strategies, emphasizing the operational and communication methodologies of Distributed Generation (DG), different parameters involved, and their respective limitations Nsaif et al. (2021). In Lotfi (2022) The method’s effectiveness is evaluated on both a 95-node and a 136-node test system. The results indicate significant improvements compared to the base standards. In the first system, energy losses reduced by 11%, operational costs by 25.5%, and Energy Not Served (ENS) by 5% through the optimization of the distributed units and shunt capacitors values. Moreover, in the second system, when employing the Time-of-Use mechanism to determine DG units, there was a remarkable decrease of 29% in energy losses, 65% in operational costs, and 7% in ENS compared to the base values. In Bhusal et al. (2022) The method was tested on diverse systems, including the IEEE 123-node distribution setup and an actual 240-node system in the United States. Findings demonstrate that the approach effectively identifies coordinated attacks with remarkable accuracy of up to 99.9%. The research employs different neural networks, encompassing Convolutional Neural Networks (CNN), Residual Neural Networks, and Multi-Layer Perceptrons (MLP) to evaluate the effectiveness of this method. Additionally, the method contributes significantly to precisely detecting the attack type within a DG, distinguishing between additive or deductive attacks. This distinction provides operators with explicit data, enabling them to undertake corrective measures effectively. The Gauss-Seidel (GS) method is applied for load flow analysis, offering a simple iterative approach to solving load flow equations when partial derivatives are not required Alnabi et al. (2022). A completely distributed energy trading system based on machine learning was proposed. Design skeletons for a DC grid energy management system are designed by developing an experimental strategy and assessing the efficacy in comparison to other available options. In Yılmaz et al. (2022) the pyramidal algorithm with wavelet transform is a novel feature extraction strategy used in the proposed hybrid machine learning method (UWT). With an accuracy rate of up to 99.59%, the UWT SGBT approach effectively groups data according to mathematical and real data results. Furthermore, this approach has been extensively tested in noisy environments, and the pyramidal UWT-SGBT method demonstrates superior noise immunity compared to other machine learning methods that utilize wavelet transform (WT)-based techniques. In Gawusu et al. (2022) The study delves into the exploration of patterns and trends in dispersed generation through data mining (DG). While still at an early stage, this research provides valuable insights into ongoing research trends and patterns. These findings would be particularly beneficial and of significant interest to researchers actively engaged in the Distributed Generation field. In Bhadoriya et al. (2022), As the load increases, distribution network losses can cause voltage deviations and compromise stability. In response, the Transmission System Operator (TSO) has developed an optimization solution for the allocation of Distributed Generation (DG) that meets various equality and inequality requirements. The goal is to mitigate reduce voltage fluctuation, decrease active power dissipation and guarantee voltage stability. Significantly, both the IEEE 33-bus and 69-bus distribution systems have experienced considerable decrease in active power dissipation, reaching percentages of 94.29% and 94.71%, respectively. In Pereira et al. (2016), a combined strategy that merges tabu search with genetic algorithms (GA) has been proposed for the incorporation of distributed generation (DG) and capacitor banks into distribution systems (DS) to improve overall system efficiency. In Battapothula et al. (2019), an innovative optimization technique, utilizing a hybrid shuffled frog leap teaching and learning algorithm, has been suggested and implemented to determine the most efficient placement and dimensions of electric vehicle rapid charging stations and distributed generation (DG) units within distribution systems (DS). In Bo et al. (2020), a hybrid load forecasting model has been developed by integrating data preprocessing techniques, forecast algorithms, and weight identification theories. An approach utilizing wavelet decomposition and quadratic gray neural network, in conjunction with the enhanced Dickey-Fuller test, Li et al. (2017), dynamic model selection relying on Q-learning Feng et al. (2020), a method employing boosting-based multiple kernel learning Wu et al. (2020), hybrid method that merges convolutional neural networks (CNN) with long short-term memory (LSTM) for deep learning (DL). Alhussein et al. (2020), a DL method Hong et al. (2020), and a hybrid model clustering with feed forward neural networks (FFNN) Panapakidis et al. (2020) have been proposed for STLF. A proficient forecasting model is introduced, incorporating a feature extraction module that merges variational mode decomposition (VMD) with a variational auto encoder (VAE) Yang et al. (2022). The project entails sharing data, which necessitates disclosing the private information of the participants. To tackle this concern, the authors integrated variational mode decomposition (VMD), the federated k-means clustering algorithm (FK), and SecureBoost into a unified algorithm, named VMD-FK-SecureBoost. Yang et al. (2023).
1.3 Research Gap
A machine learning algorithm was recently employed in several data and flow-oriented applications for prediction and selection. The non-linear machine learning algorithm mapped the objectives and multiple constraints of DG placement and sizing. Machine learning provides several algorithms in the domain specified, such as supervised, unsupervised, and reinforced learning. The reported survey suggests that most authors employed supervised learning-based algorithms such as support vector machine (SVM), K-nearest (KNN), decision tree (DT), extreme learning (ELM), and many more hybrid algorithms. The limitations of feature selection and mapping of machine learning algorithms are overcome with deep learning algorithms.
As evident from the literature review, it is commonly acknowledged that the load is typically presumed to remain constant, and the DG output can be regulated during DG allocation. However, in real-world scenarios, both loads and DG output fluctuate continuously. This variability poses challenges when calculating losses and other parameters using power flow-based algorithms, making the process cumbersome and time-intensive.
Several methodologies focus solely on active power injection, specifically for distributed generation (DG) with a unity power factor. Some techniques are designed for allocating a single DG unit, neglecting environmental considerations. Certain network constraints may go unnoticed, and economic factors are overlooked in certain articles. Furthermore, certain methods exhibit excessively long computational times, and the outcomes derived from certain approaches may not be optimal.
1.4 Paper contributions
The proposed algorithm effectively addresses issues such as voltage imbalance, line loading, and power losses within the distribution system. The frequently employed algorithm for Distributed Generation (DG) allocation is the support vector machine (SVM). Recently, several authors employed convolutional neural networks (CNN) for DG allocation. The proposed algorithm offers a significant advantage by overcoming limitations present in Artificial Neural Networks such as Convolutional Neural Networks (CNN) and Recurrent Neural Networks (RNN), including Long Short-Term Memory (LSTM) and Deep Q-learning (DQL) algorithms, while accumulating various benefits.
The specific contributions of the work proposed are as follows:
1. Estimation of generation unit sizes, power losses within the distribution network, and minimum voltage (without power flow estimation)utilized in the test scenarios of IEEE 33-bus and IEEE 69-bus distribution systems.
2. Evaluation and comparison of RNN, CNN, LSTM, and DQL algorithm performances on similar test systems, utilizing metrics like Mean Absolute Percentage Error (MAPE) and R2.
1.5 Paper organization
The forthcoming sections of this manuscript will follow this structured approach:
Section II: Methodology description detailing DG allocation and sizing.
Section III: Experimental analysis, presenting the results.
Section IV: Comprehensive overview of the entire study.
Section V: Exploration of potential future avenues in this field of research.
2 Methodology
The application of Machine Learning for predicting the optimal locations for distributed generation is explored in this study. The paper delves into four key algorithms: Recurrent Neural Networks (RNN) and Convolutional Neural Networks (CNN) under the Neural Network category, Deep Q-Learning (DQL) as a Reinforcement Learning method, and Long Short-Term Memory (LSTM) representing Supervised Machine Learning.
In a quest to enhance distribution system performance, a novel approach named the cascaded machine learning algorithm is introduced. This algorithm combines Random Forest, Radial Neural Network, and Support Vector Machine (SVM). Its primary goal is to enhance the placement of Distributed Generation (DG)with the intention of minimizing power dissipation within the distribution system. The investigation comprehensively evaluates the impact on various aspects such as Distributed Generation power injection, minimum voltage for, and both active and reactive electrical losses. The study employs test systems based on the IEEE 33-bus and 69-bus configurations. In the method presented, the division of data is random, with a ratio of 80:20 for training and validation.
The process encompasses various key steps, including feature selection (input), training and testing phases, as well as validation. Within this framework, multiple ML models—specifically RNN, CNN, Proposed model, DQL, and LSTM are constructed to facilitate predictions. The validation of the final model is conducted using the method of hours to ensure accurate predictions for both the testing setups of IEEE 33-bus and 69-bus systems. Furthermore, the entire process is elucidated through a flowchart in Figure 1, outlining the comprehensive process.
2.1 Machine learning algorithms applied
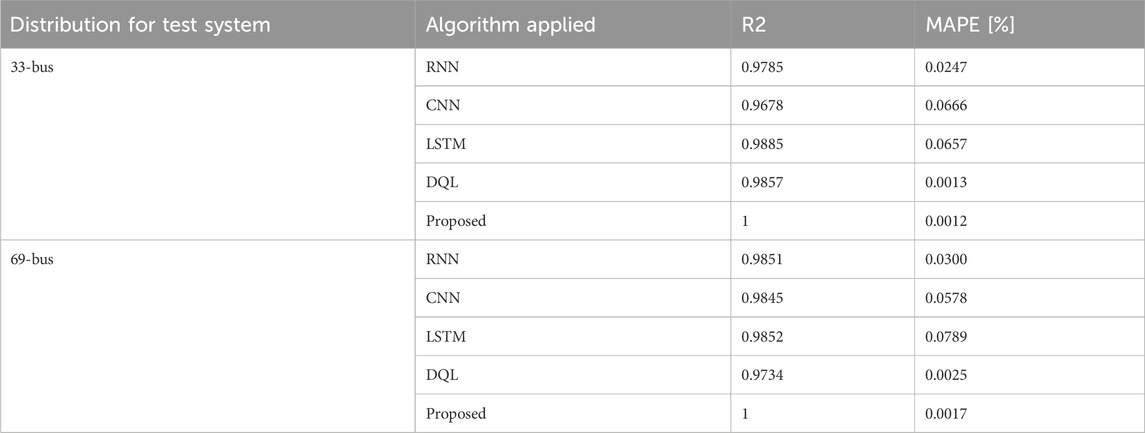
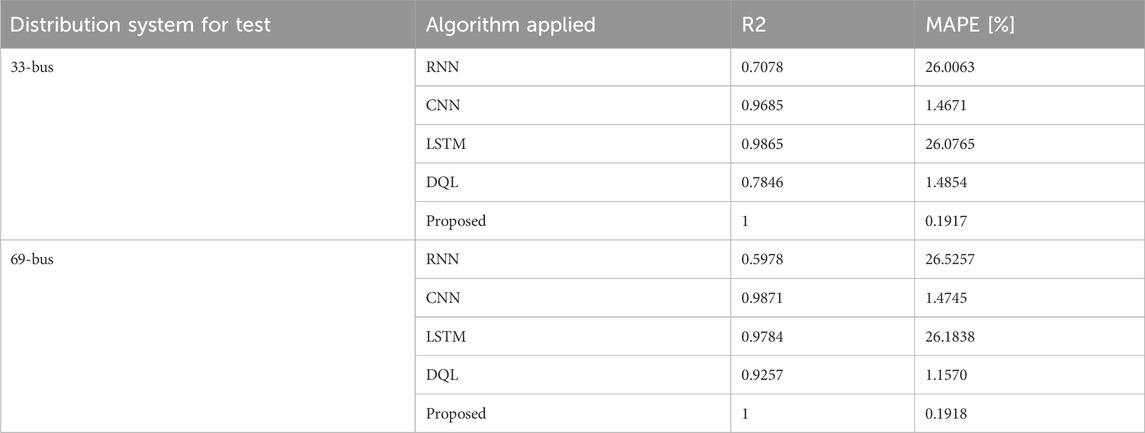
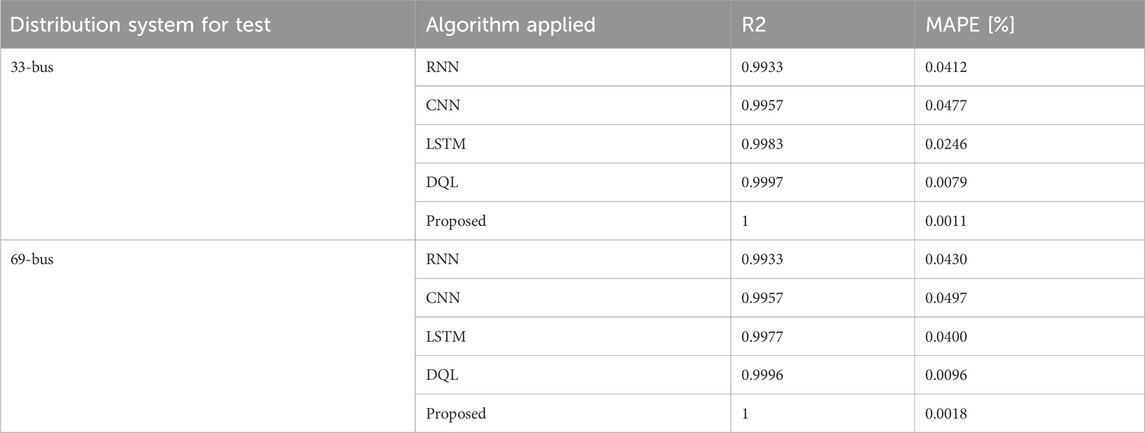
The Machine Learning models were constructed using generated data sets to facilitate training. Regression-based training algorithms, including Support Vector Machine (SVM), CNN, and CML, were utilized. Subsequently, their respective R2 scores and MAPE were computed to predict reactive power losses and minimum busbar voltages. The outcomes of Mean Absolute Percentage Error (MAPE) and R-squared (R2) values for all five models are showcased in Tables 1–4. These models allow the extraction of output parameters for forthcoming input data. The study applied the following machine learning algorithms:
2.1.1 Support vector Machines
Support vector machines (SVM) were created for empirical data as regression models and binary classifiers as prediction models. The operation of a support vector machine maps input data onto a two-dimensional space via a hyperplane. The significance of this hyperplane lies in its ability to classify data into distinct categories. The effectiveness of support vector machines relies heavily on the appropriate choice and maximization of hyperplanes. Optimization enhances the optimal scope of the hyperplane, leading to improved predictions by the support vector machine. The equation for hyperplane is given as Eq. 1
Here data to yi (w.xi + b)≥1-Ti, Ti ≥ 0 for all i
where yi stands in for the class label, which is either +1 or −1, and xi represents the ith example. The issue’s dual form is used to solve it, given in Eq. 2
Where 0 ≤ αi ≤ C for all i, ∑iαiyi
2.1.2 Convolutional neural network (CNN)
A Convolutional Neural Network (CNN) is structured with multiple layers that serve distinct roles in data processing. This architecture comprises input layers, a convolutional layer, a pooling layer, a fully connected layer, and an output layer. The effectiveness of CNN classifiers in data classification and detection is attributed to the diverse capabilities of these layers.
The convolutional layer, through various window sizes, extracts different feature information from the data matrix by employing convolution kernels. Utilizing this convolution operation enables parameter sharing, wherein the same weight and offset are shared across the network. As a result, this parameter-sharing technique substantially diminishes the total number of parameters required by the neural network, thereby amplifying its efficiency.
After the convolutional layer, the pooling layer implements diverse sampling techniques to down sample the feature map, typically using mean or maximum values within specified window regions. This down-sampling process reduces the size of the features, effectively diminishing the impact of redundant information and aids in managing computational complexity.
Consider that the input features of CNN are a map of layer x, Mx (M0 = F)
The convolutional process can be expressed in Eq. 3 as Li et al. (2017); Wu et al. (2020)
Here Wx is the convolutional kernel weight vector of the x layer,
Symbol ⊗ represents convolutional approach,
bi is the offset vector of x layer. F(x) represents the activation function. By employing diverse window values, the convolutional layer extracts varied feature information from the data matrix, utilizing different convolution kernels. Embracing the concept of ‘parameter sharing,’ the convolution operation involves using the same weight and offset for all convolution kernels, thereby significantly reducing the total number of parameters in the neural network. Subsequent to the convolutional layer, the pooling layer typically conducts feature map sampling through various algorithms. The pooling layer can be expressed as follows, where
Mx is the input, and Mx+1 is the output of the pooling layeras given in Eq. 4
The sampling criterion typically involves selecting the mean or maximum value within the window region. The main objective of the pooling layer is to reduce the size of the features, thereby mitigating the impact of redundant features on the model.
2.1.3 Recurrent neural network
The Recurrent Neural Network (RNN) distinguishes itself as a specialized variant of an artificial neural network designed particularly for analyzing sequential time series data. One of its key advantages lies in its ability to process data in a sequential manner through the establishment of signal pathways both forward and backwards. This is accomplished by creating internal loops within the network, enabling connections among hidden components.
RNNs, due to these internal connections, are adept at leveraging information from past data to predict future data points, a capability that becomes particularly useful when exploring temporal correlations among diverse data sets. These networks excel in capturing and understanding sequential patterns within data sequences, making them highly suitable for tasks involving time-dependent data analysis and predictions. Wang et al. (2019) Wang et al. (2020).
2.1.4 Long short-term memory
The inception of Long Short-Term Memory (LSTM) was driven by a specific aim: to address the challenge of vanishing gradients that conventional Recurrent Neural Networks (RNNs) encounter when handling long-term dependencies. Unlike the simple chain-like structure of a regular RNN consisting of a series of recurrent units forming a single layer, the architecture of LSTM’s hidden layers is more intricate and involves a sequence of repeating modules.
LSTM (Long Short-Term Memory) incorporates gate mechanisms and memory cells within each hidden layer, forming a memory block with essential components: an input gate, an output gate, memory cells, and a gate. Each element fulfils specific functions in regulating information flow within the network. The input gate controls which data to preserve in the memory cell, while the output gate determines when to transmit this information to the next layers. The forget gate, on the other hand, aids the network in discarding unnecessary or outdated information, essentially resetting the memory cells.
Crucially, LSTM employs multiplicative gates that facilitate the retention and access of information over longer time intervals. By strategically incorporating these gates, LSTM significantly mitigates the problem of vanishing gradients, ensuring the network can effectively capture and retain relevant information over extended sequences, thereby enhancing its ability to handle long-term dependencies in data. Hu et al. (2020) Qiao et al. (2020).
2.1.5 Deep Q learning
Deep Learning holds significant promise in transforming power load forecasting methodologies. Its impact on the energy sector’s data processing methods is noteworthy. Artificial Neural Networks (ANNs) specifically engineered for this objective include multiple layers positioned among the input and output strata. These layers enable the seamless transmission of information forward across the network through a process known as feed-forward propagation. This architecture enables the ANN to process forecasting data effectively, contributing to the growing acceptance and application of deep neural networks within the energy sector. Eyübog˘lu and Gül (2021).
2.1.6 Proposed Algorithm
The Cascaded Machine Learning algorithm enhances data training and minimizes network errors by integrating three supervised learning algorithms: Random Forest, Radial Neural Network and Support Vector Machine (SVM). Within this context, the Support Vector Machine serves as the central processing model. Meanwhile, the Random Forest and Radial Neural Network serve as classification algorithms. The Random Forest classifier operates for variable feature selection from DG data, whereas the Radial Neural Network is responsible for predicting the optimality of the DGs. This amalgamation enables improved data processing and accurate prediction within the network.
The processing of the cascaded machine-learning algorithm is described in Eq. 5 as
Here Mc (x) is the multiple-stage function of the support vector machine. The processing of multiple stages is carried out on the feature data of DGs on distributed networks. For the optimality of DGs, this employs support vector machine function SVM (fsvm) to separate the hyperplane of optimal and non-optimal data, as given in Eq. 6.
The selection of features data from DGs matrix is given in Eq. 7 as
Here p1,…, pn are the vectors of selected DGs matrix data.
Estimate the entropy of class by variable selector,as mentioned below in Eq. 8
Here E is entropy of variables of DGs matrix.
The training set is derived pairwise (s, [E1,…, Ek])
Where s represent the input variable and [P1,…, Pk] the target variable.
Eq. 9 signifies multiple support vectors. The optimal process of the variable is selected, and then the process pattern on the radial neural network call adjusts the weight factor of the cascading process.
Mc ∈ ejd∼ ← mapping of optimal data in kernel function.
Call kernel function as described in Eq. 10
End if.
3 Simulation and results analysis
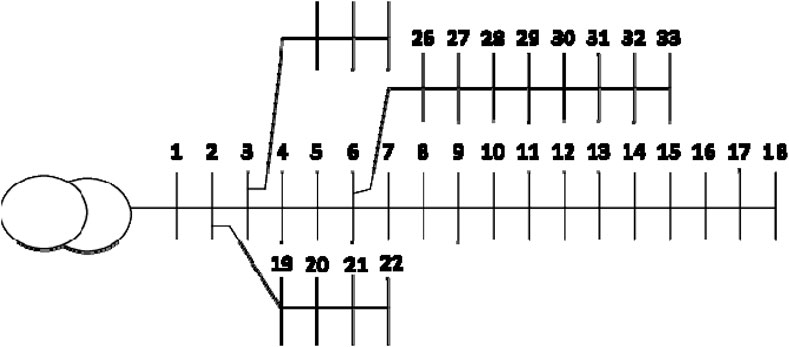
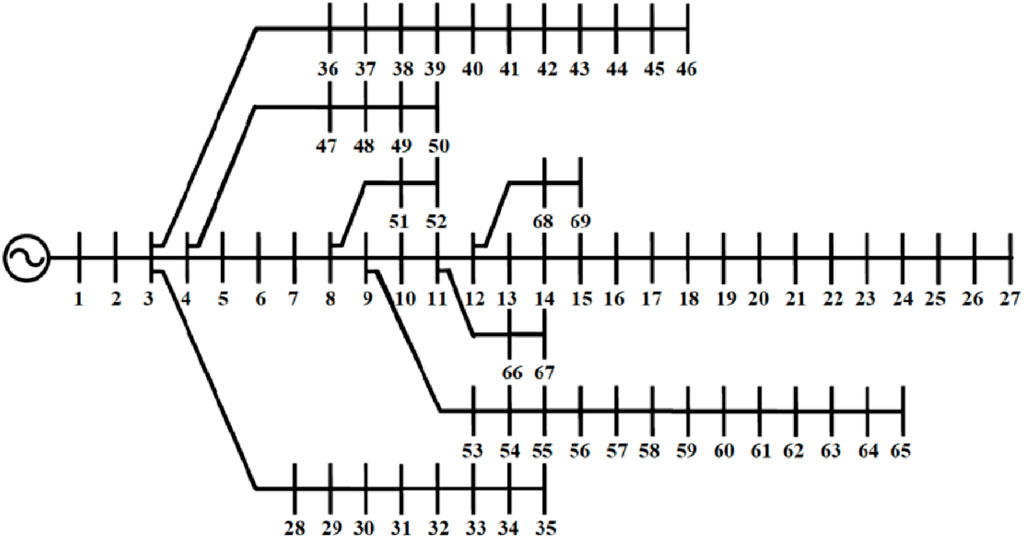
The simulation of the entire process is conducted through MATLAB R2017 software. It includes information regarding DG power injection, bus bar voltages, load variations, as well as both active and reactive power losses. The evaluation of these parameters is conducted using the IEEE 33-bus and IEEE 69-bus distribution networks as case studies. Figure 2 depicts the single-line diagram for the 33-bus distribution system, and Figure 3 illustrates the diagram for the 69-bus distribution system. This simulation methodology enables a comprehensive examination and assessment of the system’s performance across various scenarios and conditions. Arif et al. (2020). The power load data obtained varies based on the time of day and seasonal changes. These data can be found in the GitHub repository Lotfi (2022). The assessment of the algorithms’ performance involves the utilization of MAPE and R-squared indices. The results in the upcoming figures illustrate the distributed generation (DG) power injection, active power losses, reactive power losses, and minimum busbar voltage for both the IEEE 33-bus and 69-bus networks, respectively. The gathered R2 and MAPE values used for prediction are presented in Tables 1–4. Each case is thoroughly explored in the subsequent section, systematically analyzing the results and observations.
3.1 DG power injection
Figures 2, 3 illustrate the single-line diagram of the 33-bus and 69-bus distribution systems, respectively. Distributed generation (DG) sizing is determined through the utilization of normalized load variation (NLV).
PDtt = 2566.1833 x Load Level - 53.5766 for 33-bus distribution system.
PL = 286.3641 x Load Level - 97.0291 for 33-bus distribution system.
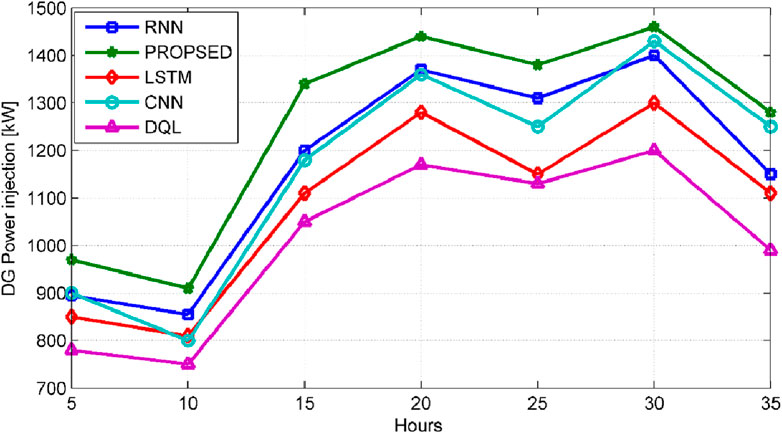
Figure 4 depicts the optimal power injection at different intervals of scheduled working hours. The methodology for power injection prediction encompasses the utilization of diverse deep learning algorithms, including long short-term memory networks (LSTM), convolutional neural networks (CNN), deep Q-learning (DQL), recurrent neural networks (RNN), and the defined algorithm. Comparatively, the sequential algorithm of RNN demonstrates superior performance when compared to the CNN algorithm, leading to a notable 7% enhancement in prediction accuracy. Additionally, the proposed algorithm exhibits superiority over existing algorithms in terms of prediction ratio, which falls within the range of 5%–7%.
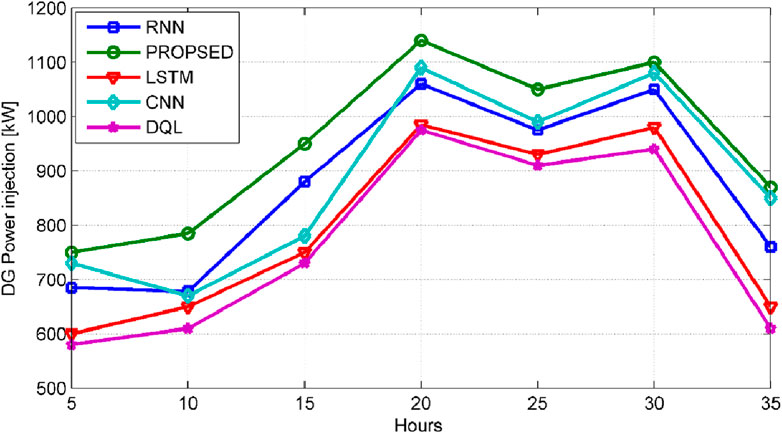
Figure 4. A comparative analysis of distributed generation (DG) sizing predictions for a 33-bus distribution system.
PDtt = 1827.2793 x Load Level - 4.711 for bus 69 distribution system
PL = 318.0325 x Load Level - 108.6808 for bus 69 distribution system.
Figure 5 depicts the optimal power injection at different intervals of scheduled working hours. The 69-bus system exhibits a diverse prediction compared to the 33-bus system. The figure illustrates the deep learning-based approaches employed for the assessment of optimal DG prediction to enhance the distribution systems. The proposed algorithm for DG optimal prediction reached the maximum prediction of the actual value of DG sizing. The proposed algorithm overcomes the limitations of LSTM, RNN, CNN, and DQL. The RNN and LSTM algorithms suffer from training error rates; however, the prediction rate of RNN and LSTM is less than the actual value of prediction. The CNN algorithm is better than RNN and LSTM. The overall improvement in the prediction ratio of DG sizing is 4%–8% compared to existing algorithms.
3.2 Active power loss estimation
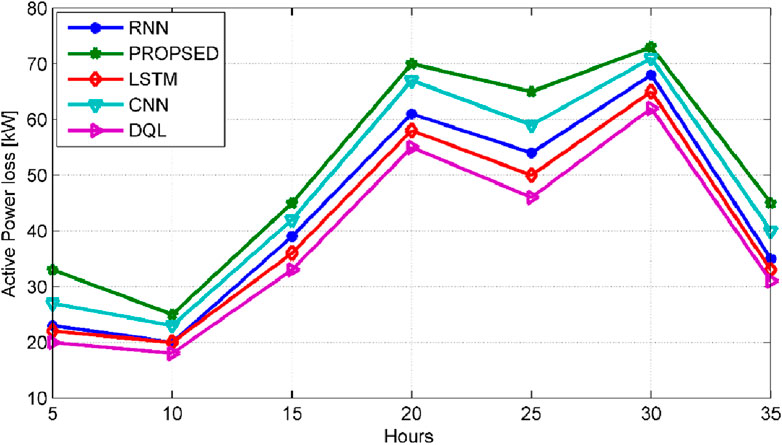
Figure 6 displays the predictions for active power losses in the 33-bus systems based on normalized load variation (NLV). We employed deep learning based algorithms such as RNN, LSTM, CNN, DQL, and the proposed algorithm to predict active power loss. The variation of algorithms employed in deep learning is estimated in different hours of optimal DG sizing. The LSTM algorithm exhibits inferior performance compared to both CNN and RNN algorithms. The LSTM algorithm suffers from the problem of training errors in prediction data. The conventional RNN algorithms are better than LSTM. The cascaded proposed algorithm overcomes the training errors and improves the prediction of active power loss.
Figure 7 illustrates the forecasts for active power loss by utilizing the normalized load variation (NLV) of 69-bus systems. The employed DQL algorithm for deep learning is inferior to other algorithms for prediction. The primary concern lies in the sluggish training rate of Deep Q-Learning (DQL), which adversely affects the prediction rate of active power loss compared to CNN, RNN, and LSTM. To address this limitation, the proposed algorithm is introduced, markedly enhancing the accuracy of active power loss prediction and maximizing accuracy in forecasting actual values. In the context of 69-bus systems, optimal sizing results in a notable 5%–10% improvement in the predictive performance for active power loss.
3.3 Reactive power loss estimation
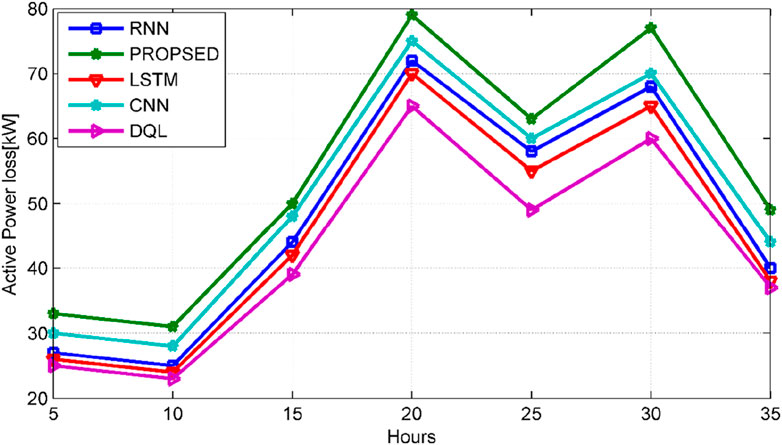
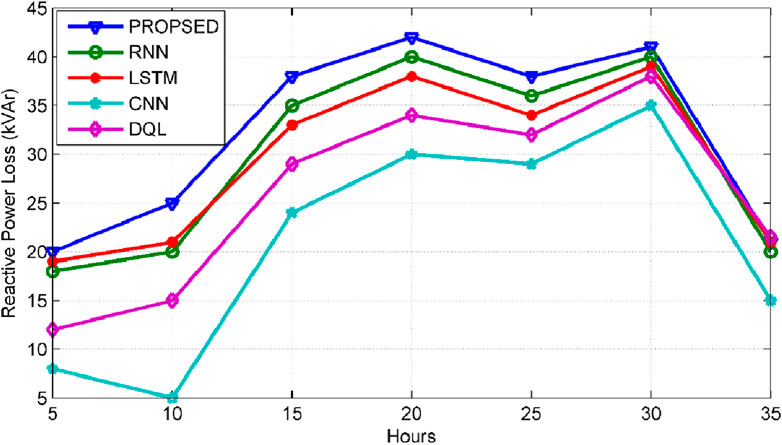
Figure 8 displays the forecasted reactive loss for the 33-bus systems, where the CNN algorithm utilized for deep learning shows inferior performance compared to other deep learning algorithms in prediction accuracy. The challenge primarily arises from the selection of the filter matrix for DG sizing data, resulting in errors and a reduction in active power loss prediction rates when compared to DQL, RNN, and LSTM. However, with the integration of the proposed algorithm, there’s a notable enhancement in active power loss prediction and a substantial improvement in actual value prediction. For the 33-bus systems, achieving optimal sizing results in a notable enhancement of 7%–12% in the prediction ratio of reactive power loss.
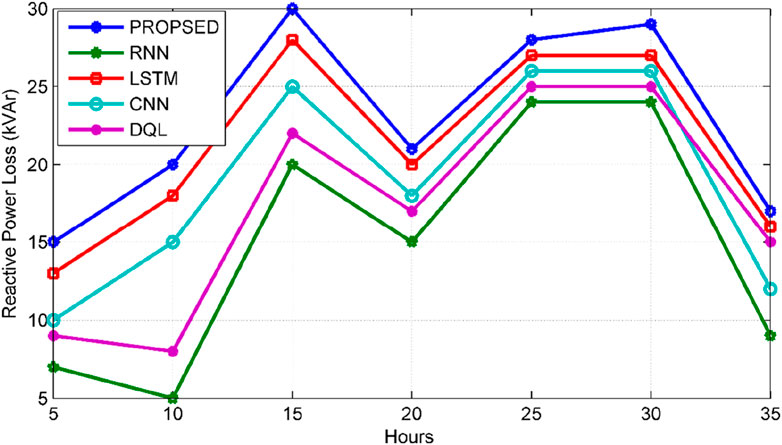
Figure 9 showcases the predictions of reactive power loss based on actual values specifically for the 69-bus system. The predictive analysis utilized various deep learning algorithms, namely, RNN, LSTM, CNN, and DQL. The variance in prediction results stems from the training sequence applied to the DG sizing data, significantly influencing the outcome. The training process significantly shapes and exacerbates errors, consequently affecting the performance of RNN. Moreover, alternative deep learning algorithms like DQL, CNN, and LSTM show divergent predictions for reactive power loss. The implementation of the designated algorithm results in an enhancement of the predictive accuracy for reactive power loss by 2%–8% in comparison to the observed reactive power loss.
3.4 Minimum busbar voltage estimation
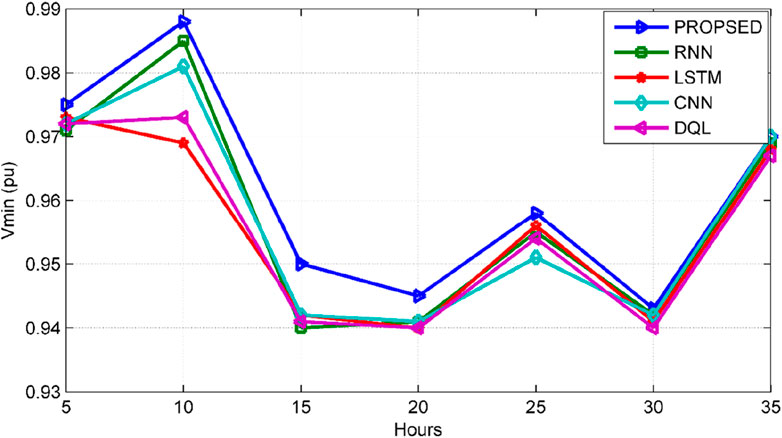
The precise estimation of Minimum Busbar voltages in the 33-node and 69-node distribution systems has been successfully accomplished by deploying the advanced Cascaded Machine Learning model. Figure 10 displays the prediction of minimum busbar voltages specifically related to the 33-bus distribution system. Various deep-learning algorithms of RNN, LSTM, CNN, and DQL were employed for minimum voltage prediction. Since busbar voltage is a time-series data, RNN and LSTM are more suitable for its prediction. However, due to slow training error rates, the LSTM’s prediction rate is relatively lower compared to other deep learning algorithms. The proposed algorithm successfully addresses the issue of slow training error rates and notably enhances the prediction rate, improving the actual prediction rate by 5%.
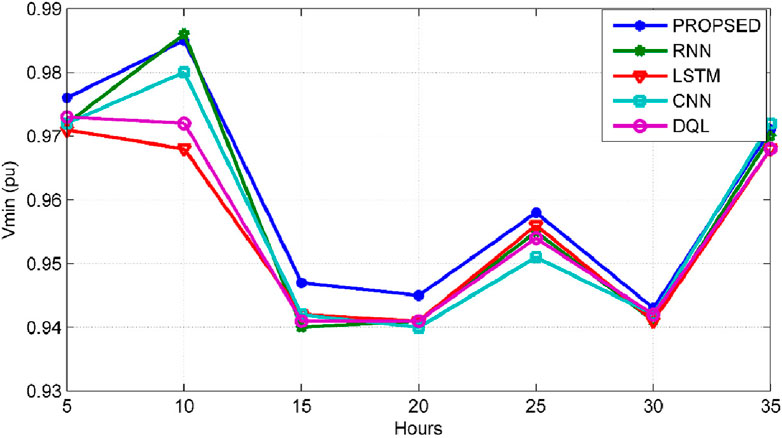
Figure 11 depicts the forecast of minimum busbar voltage focusing on the 69-bus grid system. In this investigation, analogous to the 33-bus system, RNN, LSTM, CNN, and DQL models were employed to perform predictions for minimum voltage. With busbar voltage being a time-series data, RNN and LSTM are considered more effective for prediction. Nevertheless, due to slow training error rates, the DQL’s prediction rate is inferior to other deep learning algorithms. The proposed algorithm effectively overcomes the challenge of slow training error rates, significantly enhancing the prediction rate and improving the actual prediction rate by 7%.
3.5 Performance evaluation metrics
The assessment of the cascaded machine learning algorithm’s performance is conducted using MATLAB software, comparing it with existing algorithms. This evaluation focuses on DG sizing placement, minimum busbar voltage, active power loss, and reactive power loss. The evaluation metrics employed to measure the algorithm’s performance include R-squared/Coefficient of Determination and Mean Absolute Percentage Error (MAPE).
The objective is to assess the effectiveness of the cascaded machine learning algorithm in forecasting DG sizing placement, minimum busbar voltage, as well as both active and reactive power losses. This assessment involves comparing the algorithm’s performance with established methods, utilizing R-squared and MAPE as crucial metrics.
This structured approach highlights the specific focus on evaluating and comparing the strength of the cascaded machine learning algorithm across several parameters against the existing algorithms.
3.5.1 R-squared/coefficient of determination
The evaluation of the model’s performance and reliability involves calculating R-squared error metrics. In this evaluation, real values are utilized to confirm the precision of the model. R-squared (R2), known as the coefficient of determination, acts as a statistical indicator in regression models. It denotes the portion of the variability in the reliant variable clarified by the independent one. R2 gauges how well the data fits the regression model, ranging between 0 and 1.
3.5.2 Mean Absolute Percentage Error (MAPE)
The assessment of forecast accuracy and outcome calculation is performed employing the Mean Absolute Percentage Error (MAPE). MAPE measures the correlation among absolute prediction inaccuracies and the real values. These metrics quantifies the accuracy of predictions relative to the actual data.
Tables 1–4 offer a comprehensive analysis of DG sizing, active power loss, reactive power loss, and minimum voltage estimation.
The results from the proposed model suggest that proposed algorithm surpasses CNN, RNN, LSTM, and DQL by 5.7%, 6.6%, 13.2%, and 14.2%, respectively, in estimating DG sizing within the 33-bus system, thereby enhancing the model’s efficiency. Similarly, in the 69-bus system, the proposed model predicts DG sizing better by 5.6%, 9.3%, 15.8%, and 18.7% for CNN, RNN, LSTM, and DQL, respectively.
Comparing the proposed method with other state-of-the-art methods for active power loss estimation reveals significant performance improvements: 9.1% for CNN, 16.7% for RNN, 24.2% for LSTM, and 28.8% for DQL in the 33-bus test system. Likewise, in the 69-bus system, the proposed algorithm outperforms by 4.6%, 6.1%, 10.7%, and 23% for CNN, RNN, LSTM, and DQL, respectively.
Analyzing reactive power using the proposed method indicates superior performance over RNN, LSTM, DQL, and CNN with 5.3%, 10.5%, 13.2%, and 23.7%, respectively for the 33-bus test system. Similarly, in the 69-bus system, improvements over LSTM, CNN, DQL, and RNN are 3.6%, 7.1%, 10.7%, and 14.3%, respectively.
Predictions for Minimum Busbar voltage in the 33-bus system using LSTM, RNN, DQL, and CNN are less accurate compared to the proposed method by 0.2%, 0.3%, 0.4%, and 0.8%, respectively. Similarly, estimations for the 69-bus test system with the proposed method exhibit superiority by 0.1%, 0.3%, 0.5%, and 0.8%, respectively.
This section begins by analyzing the data relevant to the issue at hand. It then proceeds to compare the results obtained from the newly introduced models with those of the previously utilized ones. The efficacy of the proposed algorithm surpasses that of CNN, RNN, LSTM, and DQL across both the 33-bus and 69-bus systems. The utilization of the proposed algorithm for parameter estimation showcases superior effectiveness compared to relying on CNN, RNN, LSTM, and DQL. MAPE values indicate that the proposed algorithm consistently outperforms other algorithms for all parameters. R2 values exceeding 0.9 for various parameters underscore the effectiveness of the developed model. These findings affirm that the newly proposed model exhibits enhanced performance and can be relied upon to effectively address the challenge of predicting distribution system.
4 Conclusion
The study proposed the utilization of a cascaded machine learning algorithm for distributed generation (DG) allocation within distribution systems. It found that machine learning (ML) delivers impressive results for estimations based on single inputs. The CNN model exhibited significant effectiveness in forecasting different parameters like distributed generation (DG) sizing, system inefficiencies, and minimum voltage levels, especially in systems before incorporating the integration of distributed generation (DG).
The study aimed to assess the electrical distribution system by analyzing diverse factors, such as distributed generation (DG) power injection, active and reactive power losses, and minimum voltage, across both test systems, namely, IEEE 33-bus and IEEE 69-bus. Various machine learning (ML) models, such as CNN, RNN, LSTM, DQL, and Cascaded ML algorithm-based models, were developed and assessed using MAPE and R2 values. Notably, the Cascaded ML model exhibited high R2 values close to 1, indicating its suitability for accurate estimations. Validation with test data confirmed the effectiveness of these models. The findings emphasize the effectiveness of the proposed method in precisely assessing the DG dimension and its consequential impacts on the power distribution network.
5 Future scope
To further enhance forecasting capabilities, the approach can be expanded by integrating additional features like line current or voltage drops during the model’s development. These additional factors can be incorporated as extra inputs (features) in the input-output design to improve predictive accuracy. Moreover, the Machine Learning codes created in this study are versatile and can be adapted for other methods by adjusting the input data and utilizing the modified data to train different Machine Learning models.
However, in cases where there is a nonlinear correlation between input and output data, this model may not be appropriate for estimating DG integration. It is most effective for single-input predictions. Additionally, the suggested algorithm can be utilized to attain the most accurately predicted outcomes, including the distributed generation unit size, system losses, and minimum voltages in systems prior to the integration of DG.
Data availability statement
Publicly available datasets were analyzed in this study. This data can be found here: https://github.com/VasuBalan/RA.
Author contributions
AJ: Writing–review and editing, Writing–original draft, Validation, Software, Resources, Methodology, Investigation, Formal Analysis, Data curation, Conceptualization. SG: Supervision, Formal analysis, Validation, Visualization, Writing–original draft, Writing–review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Admasie, S., Basit, S., Bukhari, A., Gush, T., Haider, R., and Kim, C. H. (2020). Intelligent islanding detection of multi-distributed generation using artificial neural network based on intrinsic mode function feature. J. Mod. Power Syst. Clean Energy 8, 511–520. doi:10.35833/mpce.2019.000255
Agajie, T., Ferede, B., Khan, H., Alhelou, O. P. H., and Mahela, (2020). Optimal expansion planning of distribution system using grid-based multi-objective harmony search algorithm. Comput. Electr. Eng. 87, 106823. doi:10.1016/j.compeleceng.2020.106823
Alhussein, M., Aurangzeb, K., and Haider, S. I. (2020). Hybrid CNN-LSTM model for short-term individual household load forecasting. IEEE Access 8, 180544–180557. doi:10.1109/ACCESS.2020.3028281
Ali, Z. M., Diaaeldin, A. I. M., El-Rafei, H. M., HasanienAleem, A. Y., and Abdelaziz, (2021). A novel distributed generation planning algorithm via graphically-based network reconfiguration and soft open points placement using Archimedes optimization algorithm. Ain Shams Eng. J. 12, 1923–1941. doi:10.1016/j.asej.2020.12.006
Alnabi, L. A., Abbas, K., Dhaher, M. B., and Essa, (2022). Optimal allocation of distributed generation with reconfiguration by genetic algorithm using both Newton raphson and gauss seidel methods for power losses minimizing. Int. J. Intelligent Eng. Syst. 15, 464. doi:10.22266/ijies2022.0228.42
Arif, S., Muhammad, A., Hussain, T., Lie, T., Ahsan, H. A. S. M., and Khan, (2020). Analytical hybrid particle swarm optimization algorithm for optimal siting and sizing of distributed generation in smart grid. J. Mod. Power Syst. Clean Energy 8, 1221–1230. doi:10.35833/mpce.2019.000143
Bajaj, M., and Singh, A. K. (2021). Hosting capacity enhancement of renewable-based distributed generation in harmonically polluted distribution systems using passive harmonic filtering. Sustain. Energy Technol. Assessments 44, 101030. doi:10.1016/j.seta.2021.101030
Bajaj, M., Singh, A. K., Alowaidi, M., Sharma, N. K., Sharma, S. K., and Mishra, S. (2020). Power quality assessment of distorted distribution networks incorporating renewable distributed generation systems based on the analytic hierarchy process. IEEE Access 8, 145 713–145 737. doi:10.1109/access.2020.3014288
Battapothula, G., Yammani, C., and Maheswarapu, S. (2019). Multi-objective optimal planning of FCSs and DGs in distribution system with future EV load enhancement. IET Electr. Syst. Transp. 9, 128–139. doi:10.1049/iet-est.2018.5066
Belbachir, N., Zellagui, M., Lasmari, A., El-Bayeh, C. Z., and Bekkouche, B. (2021). Optimal integration of photovoltaic distributed generation in electrical distribution network using hybrid modified PSO algorithms. Indonesian J. Electr. Eng. Comput. Sci. 24, 50–60. doi:10.11591/ijeecs.v24.i1.pp50-60
Bhadoriya, J., Singh, A. R., and Gupta, (2022). A novel transient search optimization for optimal allocation of multiple distributed generator in the radial electrical distribution network. Int. J. Emerg. Electr. Power Syst. 23, 23–45. doi:10.1515/ijeeps-2021-0001
Bhusal, N., Gautam, M., Shukla, R. M., Benidris, M., and Sengupta, S. (2022). Coordinated data falsification attack detection in the domain of distributed generation using deep learning. Int. J. Electr. Power & Energy Syst. 134, 107345. doi:10.1016/j.ijepes.2021.107345
Bo, H., Nie, Y., and Wang, J. (2020). Electric load forecasting use a novelty hybrid model on the basic of data preprocessing technique and multi-objective optimization algorithm. IEEE Access 8, 13858–13874. doi:10.1109/access.2020.2966641
Chege, S. N., Murage, D. K., and Kihato, P. K. (2019). Optimal placement of distributed generation and capacitors in radial distribution networks using hybrid evolution programming algorithm. Eur. J. Adv. Eng. Technol. 6, 19–31. doi:10.5281/zenodo.10671905
Dheeban, S. S., and Selvan, N. B. M. (2021). ANFIS-based power quality improvement by photovoltaic integrated UPQC at distribution system. IETE J. Res. 69, 1–19.
Essallah, S., Khedher, A., and Bouallegue, A. (2019). Integration of distributed generation in electrical grid: optimal placement and sizing under different load conditions. Comput. Electr. Eng. 79, 106461. doi:10.1016/j.compeleceng.2019.106461
Eyübog˘lu, O., and Gül, Ö. (2021). Optimal allocation of multiple distributed generations including uncertainties in distribution networks by k-means clustering and particle swarm optimization algorithms. Renew. Energy Power Qual. J. 19.
Farh, H., Mh, A. M., Al-Shaalan, A. M., Eltamaly, A. A., and Al-Shamma, (2020). A novel crow search algorithm auto-drive PSO for optimal allocation and sizing of renewable distributed generation. IEEE Access 8, 27807–27820. doi:10.1109/access.2020.2968462
Feng, C., Sun, M., and Zhang, J. (2020). Reinforced deterministic and probabilistic load forecasting via $Q$-learning dynamic model selection. IEEE Trans. Smart Grid 11, 1377–1386. doi:10.1109/TSG.2019.2937338
Gawusu, S., Mensah, R. A., and Das, O. (2022). Exploring distributed energy generation for sustainable development: a data mining approach. J. Energy Storage 48, 104018. doi:10.1016/j.est.2022.104018
Haider, W., Hassan, S. J. U., Mehdi, A., Hussain, A., Adjayeng, G. O. M., and Kim, C.-H. (2021). Voltage profile enhancement and loss minimization using optimal placement and sizing of distributed generation in reconfigured network. Machines 9, 20. doi:10.3390/machines9010020
Hassan, S., Abdurrahman, Y., Sun, Z., and Wang, (2020). Optimization techniques applied for optimal planning and integration of renewable energy sources based on distributed generation: recent trends. Cogent Eng. 7, 1766394. doi:10.1080/23311916.2020.1766394
Hong, Y., Zhou, Y., Li, Q., Xu, W., and Zheng, X. (2020). A deep learning method for short-term residential load forecasting in smart grid. IEEE Access 8, 55785–55797. doi:10.1109/ACCESS.2020.2981817
Hu, H., Wang, L., Peng, L., and Zeng, Y.-R. (2020). Effective energy consumption forecasting using enhanced bagged echo state network. Energy 193, 116778. doi:10.1016/j.energy.2019.116778
Ismail, M., Shaaban, M. F., Naidu, M., and Serpedin, E. (2020). Deep learning detection of electricity theft cyber-attacks in renewable distributed generation. IEEE Trans. Smart Grid 11, 3428–3437. doi:10.1109/tsg.2020.2973681
Khasanov, M., Kamel, S., Rahmann, C., Hany, M., Hasanien, A., and Al-Durra, (2021). Optimal distributed generation and battery energy storage units integration in distribution systems considering power generation uncertainty. IET Generation, Transm. Distribution 15, 3400–3422. doi:10.1049/gtd2.12230
Kushal, T. R., Billah, M. S., and Illindala, (2020). Decision support framework for resilience-oriented cost-effective distributed generation expansion in power systems. IEEE Trans. Industry Appl. 57, 1246–1254. doi:10.1109/tia.2020.3047595
Lakum, A., and Mahajan, V. (2019). Optimal placement and sizing of multiple active power filters in radial distribution system using grey wolf optimizer in presence of nonlinear distributed generation. Electr. Power Syst. Res. 173, 281–290. doi:10.1016/j.epsr.2019.04.001
Lakum, A., and Mahajan, V. (2021). A novel approach for optimal placement and sizing of active power filters in radial distribution system with nonlinear distributed generation using adaptive grey wolf optimizer. Eng. Sci. Technol. Int. J. 24, 911–924. doi:10.1016/j.jestch.2021.01.011
Li, B., Zhang, J., He, Y., and Wang, Y. (2017). Short-term load-forecasting method based on wavelet decomposition with second-order gray neural network model combined with ADF test. IEEE Access 5, 16324–16331. doi:10.1109/access.2017.2738029
Liu, W., Luo, F., Liu, Y., and Ding, W. (2019). Optimal siting and sizing of distributed generation based on improved nondominated sorting genetic algorithm II. Processes 7, 955. doi:10.3390/pr7120955
Lotfi, H. (2022). Optimal sizing of distributed generation units and shunt capacitors in the distribution system considering uncertainty resources by the modified evolutionary algorithm. J. Ambient Intell. Humaniz. Comput. 13, 4739–4758. doi:10.1007/s12652-021-03194-w
Menke, N. J., Hendrik, M., and Bornhorst, B. (2019). Distribution system monitoring for smart power grids with distributed generation using artificial neural networks. Int. J. Electr. Power & Energy Syst. 113, 472–480. doi:10.1016/j.ijepes.2019.05.057
Mo, H., and Sansavini, G. (2019). Impact of aging and performance degradation on the operational costs of distributed generation systems. Renew. energy 143, 426–439. doi:10.1016/j.renene.2019.04.111
Mohammadpourfard, M., Weng, Y., and Tajdinian, M. (2019). Benchmark of machine learning algorithms on capturing future distribution network anomalies. IET Generation, Transm. Distribution 13, 1441–1455. doi:10.1049/iet-gtd.2018.6801
Morales, J., Orduña, E., Villarroel, H., and Quispe, J. C. (2020). High-speed directional protection without voltage sensors for distribution feeders with distributed generation integration based on the correlation of signals and machine learning. Electr. Power Syst. Res. 184, 106295. doi:10.1016/j.epsr.2020.106295
Naguib, M., Mina, W. A., Omran, H., and Talaat, (2021). Performance enhancement of distribution systems via distribution network recon figuration and distributed generator allocation considering uncertain environment. J. Mod. Power Syst. Clean Energy 10, 647–655. doi:10.35833/mpce.2020.000333
Nsaif, Y. M., Lipu, A. M. H., Ayob, Y., Yusof, A., and Hussain, (2021). Fault detection and protection schemes for distributed generation integrated to distribution network: challenges and suggestions. IEEE Access 9, 142693–142717. doi:10.1109/access.2021.3121087
Ogunsina, A., Amos, M., Petinrin, O. O., Petinrin, E. N. O., Offornedo, J., Petinrin, G. O. O., et al. (2021). Optimal distributed generation location and sizing for loss minimization and voltage profile optimization using ant colony algorithm. SN Appl. Sci. 3, 248. doi:10.1007/s42452-021-04226-y
Onlam, A., Yodphet, D., Chatthaworn, R., Surawanitkun, C., Siritaratiwat, A., and Khunkitti, P. (2019). Power loss minimization and voltage stability improvement in electrical distribution system via network re configuration and distributed generation placement using novel adaptive shuffled frogs leaping algorithm. Energies 12, 553. doi:10.3390/en12030553
Panapakidis, I. P., Skiadopoulos, N., and Christoforidis, G. C. (2020). Combined forecasting system for short-term bus load forecasting based on clustering and neural networks. IET Generation, Transm. Distribution 14, 3652–3664. doi:10.1049/iet-gtd.2019.1057
Pereira, B. R., Costa, G. R. M. D., Contreras, J., and Mantovani, J. R. S. (2016). Optimal distributed generation and reactive power allocation in electrical distribution systems. IEEE Trans. Sustain. Energy 7, 975–984. doi:10.1109/tste.2015.2512819
Pham, T., Dinh Nguyen, B. T. T., and Dinh, H. (2021). Find optimal capacity and location of distributed generation units in radial distribution networks by using enhanced coyote optimization algorithm. Neural Comput. Appl. 33, 4343–4371. doi:10.1007/s00521-020-05239-1
Pham, T., Dinh Nguyen, L. C. T. T., and Kien, (2022). Optimal placement of photovoltaic distributed generation units in radial unbalanced distribution systems using MATLAB and OpenDSS-based cosimulation and a proposed metaheuristic algorithm. Int. Trans. Electr. Energy Syst. 2022, 1–21. doi:10.1155/2022/1446479
Purlu, M., and Turkay, B. E. (2021). Estimating the distributed generation unit sizing and its effects on the distribution system by using machine learning methods. Elektron. Elektrotech. 27, 24–32. doi:10.5755/j02.eie.28864
Qiao, W., Lu, H., Zhou, G., Azimi, M., Yang, Q., and Tian, W. (2020). A hybrid algorithm for carbon dioxide emissions forecasting based on improved lion swarm optimizer. J. Clean. Prod. 244, 118612. doi:10.1016/j.jclepro.2019.118612
Rathore, A., and Patidar, N. P. (2021). Optimal sizing and allocation of renewable based distribution generation with gravity energy storage considering stochastic nature using particle swarm optimization in radial distribution network. J. Energy Storage 35, 102282. doi:10.1016/j.est.2021.102282
Routray, A., Mistry, K. D., Arya, S. R., and Chittibabu, B. (2021). “Applied machine learning in wind speed prediction and loss minimization in unbalanced radial distribution system”. in Energy sources, Part A: recovery, utilization, and environmental effects, 1–21.
Sambaiah, K., Sampangi, T., and Jayabarathi, (2019). Optimal allocation of renewable distributed generation and capacitor banks in distribution systems using salp swarm algorithm. Int. J. Renew. energy Res. 9, 96–107. https://doi.org/10.20508/ijrer.v9i1.8581.g75
Selim, A., Kamel, S., Mohamed, A. A., and Elattar, E. E. (2021). Optimal allocation of multiple types of distributed generations in radial distribution systems using a hybrid technique. Sustainability 13, 6644. doi:10.3390/su13126644
Shaheen, M. A., Hany, M., Hasanien, S. F., Mekhamer, H., and Talaat, (2019). Optimal power flow of power systems including distributed generation units using sunflower optimization algorithm. IEEE Access 7, 109289–109300. doi:10.1109/access.2019.2933489
Tran, T., The, K., Truong, D. N. H., and Vo, (2020). Stochastic fractal search algorithm for reconfiguration of distribution networks with distributed generations. Ain Shams Eng. J. 11, 389–407. doi:10.1016/j.asej.2019.08.015
Vai, V., Suk, S., Lorm, R., Chhlonh, C., Eng, S., and Bun, L. (2021). Optimal reconfiguration in distribution systems with distributed generations based on modified sequential switch opening and exchange. Appl. Sci. 11, 2146. doi:10.3390/app11052146
Venkatesan, C., Kannadasan, R., Alsharif, M. H., Kim, M.-K., and Nebhen, J. (2021). A novel multiobjective hybrid technique for siting and sizing of distributed generation and capacitor banks in radial distribution systems. Sustainability 13, 3308. doi:10.3390/su13063308
Wang, H., Lei, Z., Zhang, X., Zhou, B., and Peng, J. (2019). A review of deep learning for renewable energy forecasting. Energy Convers. Manag. 198, 111799. doi:10.1016/j.enconman.2019.111799
Wang, H., Liu, Y., Zhou, B., Li, C., Cao, G., Voropai, N., et al. (2020). Taxonomy research of artificial intelligence for deterministic solar power forecasting. Energy Convers. Manag. 214, 112909. doi:10.1016/j.enconman.2020.112909
Wu, D., Wang, B., Precup, D., and Boulet, B. (2020). Multiple kernel learning-based transfer regression for electric load forecasting. IEEE Trans. Smart Grid 11, 1183–1192. doi:10.1109/TSG.2019.2933413
Yang, Y., Wang, Z., Gao, Y., Wu, J., Zhao, S., and Ding, Z. (2022). An effective dimensionality reduction approach for short-term load forecasting. Electr. Power Syst. Res. 210, 108150. doi:10.1016/j.epsr.2022.108150
Yang, Y., Wang, Z., Zhao, S., and Wu, J. (2023). An integrated federated learning algorithm for short-term load forecasting. Electr. Power Syst. Res. 214, 108830. doi:10.1016/j.epsr.2022.108830
Yılmaz, A., Küçüker, A., and Bayrak, G. (2022). Automated classification of power quality disturbances in a SOFC&PV-based distributed generator using a hybrid machine learning method with high noise immunity. Int. J. Hydrogen Energy 47, 19797–19809. doi:10.1016/j.ijhydene.2022.02.033
Yin, Z., Tu, J., and Xu, Y. (2019). Development of a kernel extreme learning machine model for capacity selection of distributed generation considering the characteristics of electric vehicles. Appl. Sci. 9, 2401. doi:10.3390/app9122401
Zhang, Y., Wang, X., and Wang, J. (2020). Deep reinforcement learning based volt-var optimization in smart distribution systems. IEEE Trans. Smart Grid 12, 361–371. doi:10.1109/tsg.2020.3010130
Keywords: distributed generation (DG), optimal placement, distribution systems, machine learning, artificial neural network
Citation: Jain A and Gupta SC (2024) Optimal placement of distributed generation in power distribution system and evaluating the losses and voltage using machine learning algorithms. Front. Energy Res. 12:1378242. doi: 10.3389/fenrg.2024.1378242
Received: 29 January 2024; Accepted: 05 March 2024;
Published: 04 April 2024.
Edited by:
Jinran Wu, Australian Catholic University, AustraliaCopyright © 2024 Jain and Gupta. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Akanksha Jain, YWthbmtzaGEwOTEwOTFAZ21haWwuY29t
 Akanksha Jain
Akanksha Jain S. C. Gupta
S. C. Gupta