Study on the turbulent Prandtl number model for liquid metal flow and heat transfer in a narrow rectangular channel

In order to improve the core power density of liquid metal reactors, plate-type fuel assemblies are typically used, which have obvious advantages in heat transfer capacity. For the low Prandtl number fluid, the RANS turbulence model-based CFD method needs to be modified by inserting the turbulent Prandtl number model. This paper investigated the turbulent Prandtl number model for the turbulent heat transfer of liquid metal flow in a narrow rectangular channel. First, the existing turbulent Prandtl number models were summarized and classified as the local turbulence Prandtl number model and the global turbulence Prandtl number model. They were evaluated based on the experimental data. The results showed that the prediction results of each model are not ideal. Then, a typical numerical example was used to analyze the temperature field and flow field in the narrow gap of a narrow rectangular channel. It was shown that the entire flow region only includes the near-wall region and the transition region, and the transition region accounts for the main proportion. A semi-empirical local turbulence Prandtl number model was obtained by solving the turbulent transport equation, and the unknown coefficients were determined iteratively with the experimental data. The error was controlled within ±20%. Finally, the applicability of the newly proposed turbulent Prandtl number model was explored, and the results showed that it has good applicability for the different runner sizes and different liquid metal types. This study can provide a reference for the numerical simulation of turbulent heat transfer of metal liquid in the narrow rectangular channel.

1 Introduction

The development of cleaner, more efficient, and safer new nuclear energy systems is of great significance for the sustainable development of nuclear energy, and the performance of nuclear fuels and structural materials, especially their irradiation performance, has always been an important foundation for the development of new nuclear energy systems. The irradiation test capability of the research reactor is mainly determined by the neutron flux level. The higher the flux, the faster the material irradiation test and the shorter the material development cycle. The liquid metal fast reactor is one of the most promising reactor types in the fourth-generation advanced nuclear energy system. At present, there is an extreme lack of data on fast neutron irradiation of reactor materials, as well as a lack of fast neutron research reactors. These issues are one of the important reasons that constrain the development of fast reactors (Rudenko et al., 2017). In the above context, our institute proposed a liquid metal high-flux fast neutron research reactor design, namely, the ultra-high-flux reactor (UFR), to accelerate the development of fast reactor material technology (Zhang et al., 2022a).

To achieve a high neutron flux level, the power density of the core will also be vastly improved, which causes higher requirements for the heat transfer capability of the core. The plate-type fuel assembly was adopted by UFR. Among the typical fuel assembly forms, the plate-type fuel assembly has obvious advantages in heat exchange capacity, which can increase the heat exchange area of the core and take more core heat. Unlike the coolant channel form of rod bundle fuel assemblies, the coolant channel is narrow and rectangular, with a channel gap of only 2–3 mm. There is a significant difference in the characteristics of flow and heat transfer between the narrow rectangular channels and the conventional channels (Zhang et al., 2020). Some flow and heat transfer phenomena that occur in conventional channels will be suppressed in narrow channels, and the influence of some factors will be reflected or amplified. In addition, for liquid metal, which is a low Prandtl number fluid, the thermal boundary layer is much larger than the velocity boundary layer (Pandey, 2021), and its heat transfer characteristics are different from those of conventional fluids.

At present, the experimental research on the flow and heat transfer of liquid metal mostly focuses on rod bundle channels and circular tube channels. There are relatively few experiments on the flow and heat transfer of liquid metal in narrow rectangular channels (Jaeger et al., 2015). In 1949, Sineath (1949) conducted experiments on the flow and heat transfer of Hg in narrow rectangular channels, but the experimental results may have some problems due to oxidation at that time. In 1953, Tidball (1953) carried out experiments on the flow and heat transfer of NaK in a narrow rectangular channel with an aspect ratio of 20, but the experimental years were long, and the experimental points were too few. In 1964, Duchatelle and Vautrey (1964) carried out an experiment to measure the heat transfer coefficient of liquid NaK in a parallel narrow rectangular channel. The Reynolds number range was 2,990–102000, the Prandtl number range was 0.0022–0.01, and the Peclet number range was 70–1,200. In 2002, Crye et al. (2002) of the United States carried out an experiment to measure the heat transfer coefficient of liquid Hg in a narrow rectangular channel, and the Peclet number range was 750–3,000.

Some studies have used high-precision simulation methods to simulate the turbulent heat transfer of liquid metal in channels. Kawamura et al. (1999) studied the turbulent heat transfer in a channel flow by DNS. Bhushan et al. (2022) assessed the low- and high-fidelity turbulence models, including LES and RANS models, for heat transfer predictions in the low Prandtl number flow. However, the DNS and LES methods have limitations in computational resources and are not suitable for engineering applications. Therefore, many scholars have studied the numerical simulation method of low Prandtl number fluid based on the RANS model. The RANS model adopts the Reynolds analogy assumption. Feng et al. (2020) carried out the numerical simulation of liquid metal natural circulation heat transfer by CFX. Li et al. (2020) adopted the SST k-omega model with the modified turbulent Prandtl model to simulate the thermal-hydraulic behaviors of liquid metal in the wire-wrapped assembly. When predicting the turbulent heat transfer of low Prandtl number fluid, the turbulent Prandtl number model needs to be introduced. For the solution of the temperature field in the fluid domain, the turbulent Prandtl number is a very important parameter, which represents the ratio of the turbulent momentum diffusion rate and turbulent heat transfer diffusion rate. In the Reynolds average numerical simulation method RANS, the turbulent viscosity coefficient can be calculated from the velocity field. By the turbulent Prandtl number that has been given before calculation, the turbulent thermal diffusion coefficient can be calculated, and then, the fluid flow and heat transfer can be solved. Aoki (1963) proposed a semi-empirical formula of the turbulent Prandtl number related to Re and Pr. Reynolds (1974) proposed an empirical turbulent Prandtl number model related to Pe and Re. Jischa and Rieke (1979) modeled the turbulent kinetic energy transport equation based on the turbulent heat flux or turbulent momentum flux, deduced a form of turbulent Prandtl number relationship related to Pr and Re through assumptions and simplification, and fitted the experimental data to determine the unknown coefficient. Kays (1994) critically examined the presently available experimental data on turbulent Prandtl numbers for the two-dimensional turbulent boundary layer and fully developed flow in a circular tube or a flat duct. Finally, a relationship related to the local Peclet number (Pe_t=(ε_m/υ)·Pr) is obtained. On the basis of this relation, considering the influence of the near-wall boundary layer, Weigand et al. (1997) proposed a new relation. Cheng and Tak (2006) proposed a new correlation of the turbulent Prandtl number for numerical applications to LBE flows based on the assessment of the existing models and the CFD results for circular tube geometry. Li et al. (2019) proposed a three-zone theory in view of the characteristic that the thermal boundary layer of the lead–bismuth fluid is much thicker than the velocity boundary layer. Referring to Jischa’s method of solving the turbulent kinetic energy transport equation based on the turbulent heat flux or turbulent momentum flux, the lead–bismuth turbulent Prandtl number model was derived, and a turbulent Prandtl number zoning theoretical model suitable for lead–bismuth was established. Based on the existing experimental data, Zhang et al. (2022b) proposed the appropriate turbulent Prandtl number for different Pe in the simulation of liquid metal flow and heat transfer in the narrow rectangular channel. Chen et al. (2013) reviewed and assessed the existing turbulent Prandtl number models and various heat transfer correlations in circular tubes, and they evaluated the applicability of various turbulent Prandtl number models for LBE in the circular tube under boundary conditions of constant heat flux and constant wall temperature. Ge et al. (2017) assessed the applicability of different turbulent Prandtl number models in the bundle flow. The turbulent heat transfer in triangular and square lattices with different pitch-to-diameter ratios are simulated, and different turbulent Prandtl number models are used to solve turbulent heat transport. Based on the results achieved, the turbulent Prandtl number models of Kays and Aoki are recommended.

Through the above research, it is found that although there have been some studies on the turbulent Prandtl number model, the applicability analysis of liquid metal flow and heat transfer in narrow rectangular channels is still lacking. From the theoretical analysis, the turbulent Prandtl number should be related to the local state of the fluid, and the current research trend is gradually moving toward this direction. Therefore, the turbulent Prandtl number model suitable for the turbulent heat transfer of liquid metal in narrow rectangular channels is studied in this paper. The purpose is to establish the model method of turbulent heat transfer of liquid metal in narrow rectangular channels and provide a basis for the research of turbulent heat transfer of liquid metal in narrow rectangular channels.

2 Evaluation of existing turbulent Prandtl number models

2.1 Overview of existing models

According to the survey, the turbulence Prandtl number model is mainly divided into two types: the model related to the wall distance and the model unrelated to the wall distance, which are called the local turbulence Prandtl number model and the global turbulence Prandtl number model in this paper, respectively. The following representative models are selected for subsequent evaluation and analysis.

The global turbulent Prandtl number model mainly includes the following:

Aoki (1963):

${\mathit{Pr}}_t^{-1}=0.014R{e}^{0.45}{\mathit{Pr}}^{0.2}\left[1-\mathit{exp}\left(\frac{-1}{0.014R{e}^{0.45}{\mathit{Pr}}^{0.2}}\right)\right].(1)$

Reynolds (1974):

${\mathit{Pr}}_t=\left(1+100{Pe}^{-1/2}\right)\left(\frac{1}{1+120{Re}^{-1/2}}-0.15\right).(2)$

Jischa and Rieke (1979):

${\mathit{Pr}}_t=0.9+\frac{182.4}{PrR{e}^{0.888}}.(3)$

Cheng and Tak (2006):

${\mathit{Pr}}_t=\left\{\begin{array}{ll}4.12\hfill & forPe⩽1000\\ \frac{0.01Pe}{{\left[0.018P{e}^{0.8}-\left(7.0-A\right)\right]}^{1.25}}& for1000<Pe⩽6000\end{array}\right.=\left\{\begin{array}{c}4.5forPe⩽1000\hfill \\ 5.4-9\times {10}^{-4}Pefor1000<Pe⩽2000\\ 3.6forPe>2000\hfill \end{array}\right..(4)$

The local turbulent Prandtl number model mainly includes the following:

Kays (1994) found that in the logarithmic region, Pr_t seems to be mainly a function of Pe_t. When Pe_t is large, Pr_t generally approaches a constant of 0.85. When Pe_t decreases, Pr_t increases with uncertainty. For liquid metals with low Pr, the Pr_t value is relatively large, and the following calculation formula is proposed. The results are in good agreement with DNS and the experimental data at the center of the pipe.

${\mathit{Pr}}_t=0.85+\frac{0.7}{{Pe}_t},(5)$

${Pe}_t=\frac{{\epsilon }_M}{\upsilon }\mathit{Pr}=\frac{{\epsilon }_M}{\kappa }.(6)$

Weigand et al. (1997) obtained an extended relationship based on the Kays turbulent Pr_t model, and the calculated Nu can be in good agreement with the experimental data on a fully developed and thermally developed pipeline flow. This formula considers the spatial distribution of turbulent Pr_t, that is, the influence of the wall distance, and can express the turbulent Pr_t situation in the entire velocity boundary layer. It is more reasonable to deal with the near wall.

$\frac{1}{{\mathit{Pr}}_t}=\frac{1}{{2\mathit{Pr}}_{t\infty }}+C{Pe}_t\frac{1}{\sqrt{{\mathit{Pr}}_{t\infty }}}-{\left(C{Pe}_t\right)}^2\left[1-\mathit{exp}\left(\frac{-1}{C{Pe}_t\sqrt{{\mathit{Pr}}_{t\infty }}}\right)\right],(7)$

${\mathit{Pr}}_{t\infty }=0.85+\frac{100}{\mathit{Pr}{Re}^{0.888}},C=0.3.(8)$

Li et al. (2019) put forward the three-zone theory, deduced the lead–bismuth Pr_t model, and established the Pr_t zoning theoretical model suitable for lead–bismuth. The first zone (Y+ < 50) adopts Weigand’s Pr_t model, and the second zone (50 $\le$ Y+ $\le$ 500) establishes a new Pr_t model by combining the renormalization group analysis method and turbulent heat transfer equation method and further using the physical property Pr correction. The third zone (Y+ > 500) adopts a Pr_t value of 1, as shown in Table 1.

Table 1

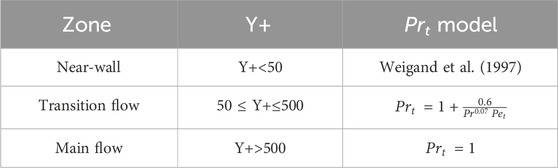
Table 1. Pr_t model of Li et al. (2019).

2.2 Reference object

This study will evaluate the existing turbulent Prandtl number models mentioned above. A set of experimental data with a relatively wide range of operating conditions and representative geometric conditions was selected as a reference, which was an experiment conducted by Crye et al. (2002) in the United States to measure the heat transfer coefficient of liquid Hg in a narrow rectangular channel. Tables 2 and 3 are the specific channel dimensions and operating conditions.

Table 2

Table 2. Characteristics of the test section.

Table 3

Table 3. Operating conditions of the experiment.

2.3 CFD models

A three-dimensional, narrow rectangular channel model is established. The geometric size and boundary conditions fully refer to the above experimental conditions. In previous studies (Zhang et al., 2022b), after comparison and analysis, it was found that the turbulence model that selected the standard k-epsilon model, combined with the enhanced wall treatment model, was more reasonable. After grid independence analysis, the grid division method is as follows: 300 nodes are evenly divided along the flow direction of the channel. A total of 120 segments are divided in the long side direction of the cross section, and densification is performed near the wall. The thickness of the first layer of the grid is 0.0005 mm, with a growth rate of 1.2. The narrow edge of the cross section is divided into a total of 40 segments, with a first-layer grid thickness of 0.0005 mm and a growth rate of 1.1. There are approximately 920 thousand grids in total.

The numerical calculation is based on Fluent 18.0, which is a typical commercial CFD software application. For the solution method, SIMPLE is adopted as the pressure–velocity coupling scheme. The spatial discretization of pressure adopts the second-order format and that of momentum adopts the bounded central differencing format. Using the steady-state calculation method, the residual convergence standard is set to 10⁻⁶. The physical properties of the working fluid Hg in the flow channel are calculated by the following polynomial equations embedded in the software application, which are transformed from nonlinear equations (Jaeger et al., 2015).

Density, kg/m³, is expressed as follows:

$\rho =-9.61751\times {10}^{-7}{T}^3+9.89515\times {10}^{-4}{T}^2-2.84542T+14320.20376.(9)$

Specific heat capacity, J/kg·K, is expressed as follows:

$C_p=-6.11564\times {10}^{-9}{T}^3+8.03019\times {10}^{-5}{T}^2-0.08138T+156.68834.(10)$

Thermal conductivity, W/m·K, is expressed as follows:

$\lambda =-6.378\times {10}^{-8}{T}^2+0.01363T+4.4584.(11)$

Dynamic viscosity, kg/(m·s), is expressed as follows:

$\mu =7.98384\times {10}^{-15}{T}^4-2.54132\times {10}^{-11}{T}^3+3.03574\times {10}^{-8}{T}^2-1.65123\times {10}^{-5}T+0.00431.(12)$

“T" represents the fluid temperature in K. The calculation method of the Nusselt number refers to the calculation method in the experimental data processing process. The temperature at a certain point on the wall is selected as the wall temperature, and the average temperature of the cross section is obtained based on energy conservation of the fluid temperature. In this study, the position in the middle of the heating section along the axial direction was selected as the calculation position.

2.4 Evaluation results

First, the existing global turbulence Prandtl number model was evaluated based on experimental data, as shown in Table 4.

Table 4

Table 4. Evaluation of the existing global turbulence Prandtl number models.

Two sets of typical operating conditions with different Peclet numbers were selected, and the Nusselt numbers calculated using different models were compared. Among them, Nu-cal represents the calculated value of CFD; Nu-exp represents the Nusselt number calculated by the Lubarski and Kaufman relationship, which is highly consistent with the experimental data (Crye et al., 2002); and Nu-J represents the empirical value of the Nusselt number calculated by the relationship of Jaeger et al. (2015). The results show that all four models have certain errors in predicting Nu. The smaller the Pe, the greater the error. Among them, the calculation results of Cheng et al.'s model are closest to the empirical values, but the error is still greater than 20%.

Then, the applicability of three typical local turbulence Prandtl number models was evaluated. The three models were implanted into FLUENT software using the UDF method, and the Nusselt numbers were calculated and compared with the empirical values. The results are shown in Table 5:

Table 5

Table 5. Evaluation of the existing local turbulence Prandtl number models.

The results show that the above three local turbulent Prandtl number models all have significant errors in calculating the heat transfer process of liquid metal flow in narrow rectangular channels, which should be because the fitting data source of the above semi-empirical model formula is mostly circular tubes or rod bundles.

3 A new local turbulent Prandtl number model

In previous work, a global turbulent Prandtl number model suitable for narrow rectangular channels was studied (Zhang et al., 2022b). The DNS calculation results of Kawamura et al. (1999) showed that there is a certain relationship between the turbulent Prandtl number and position, so it is necessary to research local turbulent Prandtl number models. This article will propose a local turbulent Prandtl number model suitable for turbulent heat transfer of liquid metal in narrow rectangular channels based on existing research, providing a numerical model for CFD numerical simulation.

3.1 The process of proposing a new local turbulent Prandtl number model

V. Karman divides the flow field into three parts: a viscous bottom layer (Y+<5), a transition layer (5<Y+<30), and a turbulent wake layer (Y+>30). In the intermediate transition layer, it is assumed that the molecular and turbulent physical quantities are the same. Li et al. (2019) drew inspiration from the idea of V. Karman’s analogy and proposed a partition theory for low Pr fluids. According to the heat transfer mechanism, the entire turbulent region was divided into three parts: (1) in the velocity boundary layer, due to the high thermal conductivity of liquid metal molecules (about 20 times that of water) and the relatively small flow rate in the velocity boundary layer, the molecular thermal conductivity dominates heat transfer compared to the eddy current diffusion rate. (2) The transition zone between the velocity boundary layer and the heat flux boundary layer, where the flow velocity has reached the mainstream velocity, enhances eddy heat transfer, and the molecular viscosity is much smaller than the eddy viscosity. Due to the good thermal conductivity and high thermal diffusion coefficient of liquid metals, it can be assumed that the molecular and turbulent physical quantities in terms of heat transfer are the same. (3) The fully mainstream region outside the heat flow boundary layer, with fully developed velocity and temperature.

Drawing on the above analytical approach, a typical numerical example is used to analyze the temperature field and flow field in the narrow gap of a narrow rectangular channel in this paper. Figure 1 shows the velocity and temperature distribution along the narrow slot direction during the turbulent heat transfer process of a narrow rectangular liquid metal. It can be seen that the velocity boundary layer is very thin, and most areas have reached the mainstream velocity. Due to the good thermal conductivity of the liquid metal, the temperature boundary layer is very thick, and the gap size of the narrow rectangular channel is very small, resulting in the temperature boundary layers of the two heating surfaces overlapping. Therefore, the entire flow region only includes the near-wall region and the transition region.

Figure 1

Figure 1. Velocity and temperature distribution of the narrow gap.

It can be observed that the transition region accounts for the main proportion. Therefore, this article focuses on the turbulent Prandtl number model in the turbulent region. For the near-wall region, based on existing research experience (Li et al., 2019), the model improved by Weigand et al. (1997) is selected. For the transition region that accounts for the majority, the basic form of the model is determined by referring to Jischa’s method for solving turbulent transport equations (Jischa and Rieke, 1979). Based on the experimental data, the unknown coefficients of the semi-empirical model are iteratively solved and finally compared with other experiments to verify the accuracy of the model. The following will introduce the process of establishing the semi-empirical model.

The definition formula of the turbulent Prandtl number is shown in Equation 13.

${\mathit{Pr}}_t=\frac{\overline{u^{\prime }{v}^{\prime }}\frac{\partial T}{\partial y}}{\overline{v^{\prime }{T}^{\prime }}\frac{\partial u}{\partial y}}.(13)$

In the equation, u represents the velocity in the x direction (perpendicular to the heating wall), and v represents the velocity in the y direction (along the direction of flow). In order to obtain the ${\mathit{Pr}}_t$, $\overline{u^{\prime }{v}^{\prime }}$ and $\overline{v^{\prime }{T}^{\prime }}$ need to be derived by solving the transport equation. The following will introduce the derivation steps of Jischa and Rieke (1979).

The work is based on the work of Prandtl, who modeled the transport equation for the turbulent kinetic energy as follows:

$k=\frac{1}{2}\left(\overline{{u^{\prime }}^2}+\overline{{v^{\prime }}^2}\right).(14)$

For Prandtl’s original modeling assumptions:

Turbulent shear stress

$-\overline{u^{\prime }{v}^{\prime }}={\epsilon }_m\frac{\partial u}{\partial y}=C_{\tau }\sqrt{k}L\frac{\partial u}{\partial y}.(15)$

Production is expressed as follows:

$-\overline{u^{\prime }{v}^{\prime }}\frac{\partial u}{\partial y}=C_{\tau }\sqrt{k}L{\left(\frac{\partial u}{\partial y}\right)}^2.(16)$

Dissipation is expressed as follows:

$\epsilon =C_D\frac{k^{3/2}}{L}.(17)$

Diffusion is expressed as follows:

$-\frac{\partial }{\partial y}\left[\dots ..\right]=C\frac{\partial }{\partial y}\left|\sqrt{k}L\frac{\partial k}{\partial y}\right|.(18)$

Here, L is the turbulence length scale. In the following process of derivation, only Eq 15 will be used. The others are given to lead over to the similar modeling of the transport equation.

To obtain $\overline{v^{\prime }{T}^{\prime }}$, one multiplies the equation for the instantaneous value of temperature (T + T′) with the velocity fluctuation ${v_j}^{\prime }$ and adds it to the $x_j$ component of the Navier–Stokes equations multiplied by the temperature fluctuation $T^{\prime }$. j and k represent the x and y directions, respectively:

$v_k\frac{\partial \overline{T^{\prime }{v_j}^{\prime }}}{\partial x_k}=\underset{Production}{\underbrace{-\overline{{v_j}^{\prime }{v_k}^{\prime }}\frac{\partial T}{\partial x_k}-\overline{{v_k}^{\prime }{T}^{\prime }}\frac{\partial v_j}{\partial x_k}+\frac{1}{\rho C_p}\overline{{v_j}^{\prime }{v_k}^{\prime }}\frac{\partial p}{\partial x_k}}}$

$+\underset{Dissipativeterms}{\underbrace{\frac{1}{\rho C_p}\left[\rho \overline{{\epsilon }^{\prime }{v_j}^{\prime }}+\lambda \overline{{v_j}^{\prime }\frac{{\partial }^2{T}^{\prime }}{\partial {x_k}^2}}+C_p\eta \overline{T^{\prime }\frac{{\partial }^2{v_j}^{\prime }}{\partial {x_k}^2}}\right]}}$

$+\underset{Redistributiveterms}{\underbrace{\frac{1}{\rho C_p}\left[{-C}_p\overline{T^{\prime }\frac{\partial p^{\prime }}{\partial x_j}}+\overline{{v_j}^{\prime }\frac{\partial p^{\prime }}{\partial t}}+v_k\overline{{v_j}^{\prime }\frac{\partial p^{\prime }}{\partial x_k}}+\overline{{v_j}^{\prime }{v_k}^{\prime }\frac{\partial p^{\prime }}{\partial x_k}}\right]}}\underset{Diffusion}{-\underbrace{\frac{\partial }{\partial x_k}\left(\overline{T^{\prime }{v_j}^{\prime }{v_k}^{\prime }}\right)}}.(19)$

Eq 19 is expanded and simplified to obtain the following Eq 20.

$\underset{Convection}{\underbrace{u\frac{\partial }{\partial x}\left(\overline{T^{\prime }{v}^{\prime }}\right)+v\frac{\partial }{\partial y}\left(\overline{T^{\prime }{v}^{\prime }}\right)}}+\underset{Production}{\underbrace{v^{\prime 2}\frac{\partial \overline{T}}{\partial y}-\frac{\overline{u^{\prime }{v}^{\prime }}}{\rho C_p}\frac{dp}{dx}}}$

$\underset{Dissipation}{\underbrace{-\frac{1}{C_p}\overline{v^{\prime }\epsilon }+\nu \frac{\mathit{Pr}+1}{\mathit{Pr}}\overline{\frac{\partial v^{\prime }}{\partial x}\frac{\partial T^{\prime }}{\partial x}}}}\underset{Redistribution}{\underbrace{-\frac{p^{\prime }}{\rho }\frac{\partial T^{\prime }}{\partial y}+\dots }}+\underset{Diffusion}{\underbrace{\frac{\partial }{\partial y}\left[\overline{T^{\prime }{v}^{\prime 2}}-\dots \right]}}=0.(20)$

For the research object between the velocity boundary layer and the temperature boundary layer, the velocity of the flow has been fully developed; therefore, the convection term is zero in Eq 20.

In analogy to the modeling of Eq 16, neglecting the pressure gradient production, the production term is transformed as follows:

$v^{\prime 2}\frac{\partial T}{\partial y}=ak{\left(\frac{\partial T}{\partial y}\right)}^2.(21)$

The diffusion term can be neglected in the boundary layer. Usually, all dissipation terms in the transport equations can be neglected to expect the turbulent dissipation $\epsilon$. This is because when the turbulence Reynolds number is high, regardless of isotropic or anisotropic turbulence, the dissipation correlation is zero, which means the redistribution term limits the growth of the Reynolds heat flux. So, the dissipation term and redistribution terms both can be modeled using the same assumption in analogy to Eq 17, as follows:

$\text{Dissipation\hspace{0.17em}and\hspace{0.17em}}/\text{or\hspace{0.17em}redistribution}=K_D\frac{\sqrt{k}}{L}\overline{T^{\prime }{v}^{\prime }}.(22)$

Therefore, the following can be obtained:

$ak\frac{dT}{dy}+K_D\frac{\sqrt{k}}{L}\overline{T^{\prime }{v}^{\prime }}=0,(23)$

$-\overline{T^{\prime }{v}^{\prime }}=\frac{a}{K_D}\sqrt{k}L\frac{dT}{dy},(24)$

${\mathit{Pr}}_t=\frac{C{K}_D}{a}.(25)$

The above derivation ignores the second term of the dissipation, which depends on the molecular Prandtl number. However, when Pr is particularly small, the impact of this term cannot be ignored.

Need to make a new assumption

$\text{Dissipation\hspace{0.17em}and\hspace{0.17em}}/\text{or\hspace{0.17em}redistribution}=\left(K_D+K_p\frac{\mathit{Pr}+1}{\mathit{Pr}}\right)\frac{\sqrt{k}}{L}\overline{T^{\prime }{v}^{\prime }}.(26)$

Then,

$ak\frac{dT}{dy}+\left(K_D+K_p\frac{\mathit{Pr}+1}{\mathit{Pr}}\right)\frac{\sqrt{k}}{L}\overline{T^{\prime }{v}^{\prime }}=0,(27)$

${\mathit{Pr}}_t=\frac{C}{a}\left(K_D+K_p\frac{\mathit{Pr}+1}{\mathit{Pr}}\right)=A+B\frac{\mathit{Pr}+1}{\mathit{Pr}}=E+\frac{B}{\mathit{Pr}}.(28)$

Here, “E" is a constant number. When the $\mathit{Pr}$ is large enough, it can be considered that the fluid has the same characteristics as conventional fluids such water so that “E" can be equal to 1.0. The coefficient “B" seems to be a function of the Reynolds number under the effect of the diffusion term, which was not considered in the previous derivation. After taking it into account, the above equation can be converted into the following equation:

${\mathit{Pr}}_t=1.0+\frac{F}{{Pe}_t}.(\mathrm{28a})$

Finally, based on CFD and using the experimental data as a benchmark for an iterative solution, the value of the constant number "F" is selected to obtain the turbulent Prandtl number model for the transition region, which is expressed as follows:

${\mathit{Pr}}_t=1.0+\frac{8.0}{{Pe}_t}.(29)$

The applicable range of the model for Pe: 1,200–3,000. Figure 2 shows the comparison of the Nu between that calculated by the CFD implanted the new ${\mathit{Pr}}_t$ model with the experimental data by Crye et al. (2002). Figure 3 shows the error between the Nu calculated by the CFD implanted the new ${\mathit{Pr}}_t$ model with that calculated by the Lubarski and Kaufman relationship (Lubarsky and Kaufman, 1956). The error is within the range of ±20% and is acceptable.

Figure 2

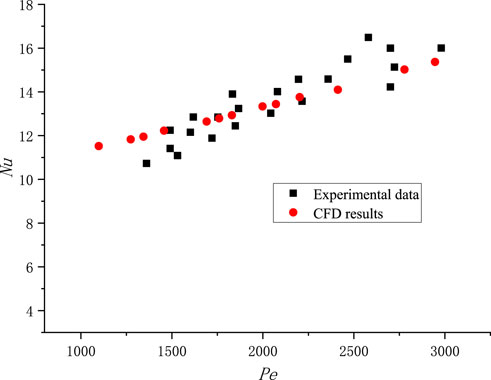
Figure 2. Comparison of Nu between that calculated by the CFD implanted the new ${\mathit{Pr}}_t$ model and the experimental data.

Figure 3

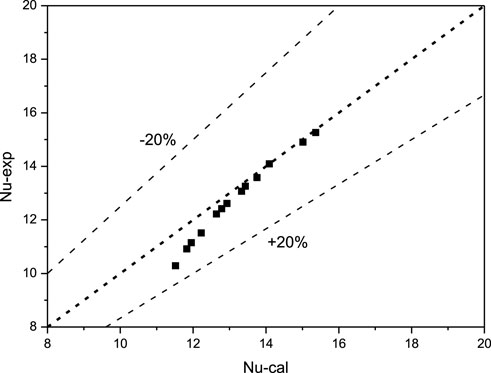
Figure 3. Error comparison between Nu calculated by the CFD implanted the new ${\mathit{Pr}}_t$ model with that calculated by the Lubarski and Kaufman relationship.

3.2 Verification and comparison of the new model

In order to explore the applicability of the newly proposed turbulent Prandtl number model, the obtained model was validated with the experimental data of liquid NaK in parallel narrow rectangular channels measured by Duchatelle and Vautrey (1964) from France. Tables 6 and 7 show the characteristics of the test section and the operating conditions.

Table 6

Table 6. Characteristics of the test section.

Table 7

Table 7. Operating conditions of the experiment.

The working fluid NaK consists of 78% potassium and 22% sodium. The physical properties can be calculated by the following equations.

Density, kg/m³, is expressed as follows:

$\rho =953.8505-0.27T.(30)$

Specific heat capacity, J/kg·K, is expressed as follows:

$C_p=1238.86485-1.5126T+0.002T^2.(31)$

Thermal conductivity, W/m·K, is expressed as follows:

$\lambda =141.16476-0.86103T+0.00156T^2.(32)$

Dynamic viscosity, kg/(m·s), is expressed as follows:

$\mu =0.00267-9.38492\times {10}^{-6}T+9.4\times {10}^{-9}{T}^2.(33)$

When Pe is greater than 200, the experimental data are highly consistent with an empirical relationship:

$Nu=5.58+0.0003417{Pe}^{1.29}.(34)$

Figure 4 shows the comparison of Nu calculated by the proposed local ${\mathit{Pr}}_t$ model with experimental data, empirical values, and the previously proposed global model (Zhang et al., 2022b). The results show that the simulation results are in good agreement with the experimental data within approximately 20% error, and the calculation results of the local ${\mathit{Pr}}_t$ model proposed in this article are closer to the experimental values than those of the previously proposed global ${\mathit{Pr}}_t$ model. This indicates that the local ${\mathit{Pr}}_t$ model has better applicability to different runner sizes and different liquid metal types.

Figure 4

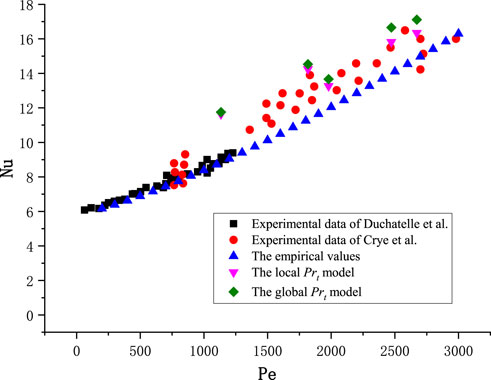
Figure 4. Comparison of the Nu calculated by the proposed local Pr_t model with the experimental data.

4 Conclusion

In this study, the turbulent Prandtl number model for turbulent heat transfer of liquid metal flow in a narrow rectangular channel was studied. The existing turbulent Prandtl number models were summarized, classified, and evaluated. A semi-empirical model of local turbulence Prandtl number was proposed, and its applicability was evaluated. The conclusions gained are as follows:

1) The turbulence Prandtl number model is mainly divided into two types: the local turbulence Prandtl number model and the global turbulence Prandtl number model, respectively. The evaluation results showed that the prediction results of each model for liquid metal flow and heat transfer in narrow rectangular channels are not ideal.

2) The temperature boundary layer is very thick, and the gap size of the narrow rectangular channel is very small, resulting in the temperature boundary layers of the two heating surfaces overlapping. Therefore, the entire flow region only includes the near-wall and transition regions. The transition region accounts for the main proportion.

3) A local turbulent Prandtl number model suitable for turbulent heat transfer of liquid metal in narrow rectangular channels was proposed within the error of ±20%. In addition, it can indicate that the local ${\mathit{Pr}}_t$ model has better applicability to different runner sizes and different liquid metal types than the global ${\mathit{Pr}}_t$ model proposed in previous work.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

ZX: methodology, validation, and writing–original draft. YH: writing–review and editing. DJ: methodology and writing–review and editing. DS: data curation, methodology, and writing–review and editing. WX: formal analysis, resources, and writing–review and editing. FW: formal analysis, software, and writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The authors are grateful for the support of the National Natural Science Foundation of China (grant no: 12305193), the Sichuan Science and Technology Program (grant no: 23NSFSC6149 and 24NSFSC4579), and the China Postdoctoral Science Foundation (grant no: 2022M722996).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aoki, S. (1963). A consideration on the heat transfer in liquid metal. Bull. Tokyo Inst. Tech. 54, 63–73.

Google Scholar

Bhushan, S., Elmellouki, M., Jamal, T., Busco, G., Walters, D. K., Hassan, Y. A., et al. (2022). Assessment of low- and high-fidelity turbulence models for heat transfer predictions in low-prandlt number flows. Nucl. Eng. Des. 388, 111614–115493. doi:10.1016/j.nucengdes.2021.111614

CrossRef Full Text | Google Scholar

Chen, F., Huai, X., Cai, J., Li, X., and Meng, R. (2013). Investigation on the applicability of turbulent-Prandtl-number models for liquid lead-bismuth eutectic. Nucl. Eng. Des. 257 (apr), 128–133. doi:10.1016/j.nucengdes.2013.01.005

CrossRef Full Text | Google Scholar

Cheng, X., and Tak, N. I. (2006). Investigation on turbulent heat transfer to lead-bismuth eutectic flows in circular tubes for nuclear applications. Nucl. Eng. Des. 236 (4), 385–393. doi:10.1016/j.nucengdes.2005.09.006

CrossRef Full Text | Google Scholar

Crye, J. M., Ruggles, A. E., Pointer, W. D., Felde, D. K., Jallouk, P. A., McFee, M. T., et al. Measurement of the heat transfer coefficient for mercury flowing in a narrow channel.J. Heat Transf., 2002, 124(6):págs. 1034–1038. doi:10.1115/1.1518500

CrossRef Full Text | Google Scholar

Duchatelle, L., and Vautrey, L. (1964). Determination des coefficients de convection d'un alliage nak en ecoulement turbulent entre plaques planes paralleles. Int. J. Heat Mass Transf. 7 (9), 1017–1031. doi:10.1016/0017-9310(64)90043-2

CrossRef Full Text | Google Scholar

Feng, X., Zhou, T., Zhang, J., Boya, Z., and Juan, C. (2020). Study on natural circulation heat transfer characteristics of different liquid metals based on factor analysis. Front. Energy Res. 8. doi:10.3389/fenrg.2020.00123

CrossRef Full Text | Google Scholar

Ge, Z., Liu, J., Zhao, P., Nie, X., and Ye, M. (2017). Investigation on the applicability of turbulent-Prandtl-number models in bare rod bundles for heavy liquid metals. Nucl. Eng. Des. 314 (APR), 198–206. doi:10.1016/j.nucengdes.2017.01.032

CrossRef Full Text | Google Scholar

Jaeger, W., Hering, W., Lux, M., and Portes, F. (2015). ICONE23-1101 LIQUID METAL THERMAL HYDRAULICS IN RECTANGULAR DUCTS: REVIEW, PROPOSAL AND VALIDATION OF EMPIRICAL MODELS. Jpn. Soc. Mech. Eng. 2015.23. doi:10.1299/jsmeicone.2015.23._icone23-1_56

CrossRef Full Text | Google Scholar

Jischa, M., and Rieke, H. B. (1979). About the prediction of turbulent Prandtl and schmidt numbers from modeled transport equations. Int. J. Heat Mass Transf. 22, 1547–1555. doi:10.1016/0017-9310(79)90134-0

CrossRef Full Text | Google Scholar

Kawamura, H., Abe, H., and Matsuo, Y. (1999). DNS of turbulent heat transfer in channel flow with respect to Reynolds and Prandtl number effects. Int. J. Heat. Fluid Flow. 20 (3), 196–207. doi:10.1016/s0142-727x(99)00014-4

CrossRef Full Text | Google Scholar

Kays, W. M. (1994). Turbulent Prandtl number—where are we? Asme Trans. J. Heat Transf. 116, 284–295. doi:10.1115/1.2911398

CrossRef Full Text | Google Scholar

Li, J., Fang, D., Guo, C., Wang, M., Deng, J., Tian, W., et al. (2020). Numerical study on the thermal hydraulic characteristics in a wire-wrapped assembly of LFRs. Front. Energy Res. 8. doi:10.3389/fenrg.2020.548065

CrossRef Full Text | Google Scholar

Li, P., Yu, H., Du, S., Yan, M., Yaou, S., et al. (2019). A new turbulent Prandtl number model for forced fully-developed pipe heat transfer of liquid metals. 27rd Int. Conf. Nucl. Engineering(ICONE-27) 2019.27, 1412. doi:10.1299/jsmeicone.2019.27.1412

CrossRef Full Text | Google Scholar

Lubarsky, B., and Kaufman, S. (1956). Review of experimental investigations of liquid-metal heat transfer. Washington D.C: National Advisory Committee for Aeronautics, GPO. Report 1270.

Google Scholar

Pandey, A. (2021). Thermal boundary layer structure in low-Prandtl-number turbulentconvection. J. Fluid Mech., 910. doi:10.1017/jfm.2020.961

CrossRef Full Text | Google Scholar

Reynolds, A. J. (1974). The prediction of turbulent Prandtl and Schmidt numbers. Dept. Mech. Eng. Brunel Univ. Rep. HT74-2. doi:10.1016/0017-9310(75)90223-9

CrossRef Full Text | Google Scholar

Rudenko, V. A., Golovko, M. V., Tomilin, S. A., et al. Project of multi-purpose research nuclear installation on fast neutrons is to ensure the national economy safety. 2017.

Google Scholar

Sineath, H. H. (1949). Heat transfer to mercury (China: University of Tennessee). M.S. thesis.

Tidball, R. A. (1953). Performances of small liquid metal heat exchangers. AIChE J. 49, 43–49.

Google Scholar

Weigand, B., Ferguson, J. R., and Crawford, M. E. (1997). An extended Kays and Crawford turbulent Prandtl number model. Int.j.heat Mass Transf. 40, 4191–4196. doi:10.1016/s0017-9310(97)00084-7

CrossRef Full Text | Google Scholar

Zhang, X., Feng, W., Chen, H., Guo, S., and Ding, W. (2020). Experimental study on flow instability for downward flow in a narrow rectangular channel with flow pattern transition. Int. Commun. Heat Mass Transf. 114C, 104586. doi:10.1016/j.icheatmasstransfer.2020.104586

CrossRef Full Text | Google Scholar

Zhang, X., Yu, H., et al. (2022b). Investigation on the simulation of turbulent heat transfer of liquid metal flow in a narrow rectangular channel. Int. Conf. Nucl. Eng. doi:10.1115/ICONE29-92595

CrossRef Full Text | Google Scholar

Zhang, X., Yu, H., Xia, B., et al. (2022a). Research on Ultra high flux research reactor. Pac. Basin Nucl. Conf. doi:10.1007/978-981-99-1023-6_75

CrossRef Full Text | Google Scholar