Numerical scrutinization of heat transfer subject to physical quantities through bioconvective nanofluid flow via stretching permeable surfaces

1 Introduction

Nanofluids have gained much importance in recent times due to their uses in information technology, especially in modern appliances. In engineering processes, these are utilized as coolants in refrigeration and various forms in other phenomena. Nanofluid was first introduced by Choi and Eastman (1995). Hayat et al. (2017) investigated a 3D stream of Williamson nano-liquid passing via a convectively warmed stretching surface having the Darcy–Forchheimer effect. Kiyani et al., 2021 took into account the dual-directional Williamson nano-liquid passing through a stretching surface using the improved Darcy’s law. Raza et al. (2021) discussed the mechanism of heat transport through a curved stretching medium via the movement of radiative Williamson liquid. Sharif et al. (2022) introduced the theoretical model of mass and heat transfer through a flexible medium. Algehyne and Saeed (2022) conducted a numerical study of the Williamson nano-liquid stream through irregular surfaces, including those with gyrotactic microbes. Hussain et al. (2022a) elaborated on a two-phase stream of Williamson nano-liquid through a stretching sheet and investigated the impacts of electromagnetism and radiation on it.

Thermal radiation, commonly known as heat radiation or infrared radiation, is a form of electromagnetic radiation released by any object having a temperature greater than absolute zero (−273.15°C or 0 K). This type of radiation is caused by the thermal energy held by the atoms and molecules within the item. Khan et al. (2017) analyzed the impacts of thermal radiation and Soret and Dufour effects on the Williamson nano-liquid flow passing via a stretchable surface. Shah et al. (2018) explored the radiative time-dependent Williamson nano-liquid moving through a porous, flexible thin film. Hashim et al. (2019) examined the influences of thermal rays over the stagnation point stream of Williamson nano-liquid via an extendable sheet. Tlili et al. (2020) reported the pseudo-plastic nano-liquid stream, which is chemically charged through a nonlinear medium involving thermal rays. Mangathai (2021) discussed a comparative analysis of time-dependent Casson and Williamson nano-liquids under the influences of viscous dissipation and radiation.

To start a chemical reaction, reactant molecules need to reach a certain energy level, known as the activation energy. The molecules of the reactant can only move on to produce products when they have enough energy to cross the activation energy barrier. The reaction becomes exothermic (releases energy) or endothermic (absorbs energy) once the activation energy has been exceeded, depending on whether the products have a lower or greater amount of energy than the reactants. Jyotshna and Dhanalaxmi (2022) considered the influence of the minimal required amount of energy and thermal sink/source over a tri-directional stream of Williamson nano-liquid passing above a shrinkable surface. Dharmaiah et al. (2023) investigated the heat transfer through Williamson nano-liquid flowing through an exponentially stretched medium. Gadelhak et al. (2023) expressed that the FDM approach is more suitable for evaluating energy transfer through Williamson nano-liquid over a curved extendable medium. The numerical solution of a nonlinear oscillator is acquired by using the Laplace transform and investigating heat transport rate increment by adding motile microorganisms in the suspension [as mentioned in the following studies: Basit et al. (2023a); Basit et al. (2024a); Basit et al. (2024b); Imran et al. (2024)], and response surface methodology is implemented to check the optimality of the mathematical model. Salahuddin et al. (2023) experimented with double stratification and activation energy impacts on the nanofluid stream over a stretchable medium. Taj and Salahuddin (2023) scrutinized the impacts of activation energy and radiation, which are not linear over the 3D flow of Williamson nano-liquid through the stretchable surface. Basit et al. (2023b); Basit et al. (2023c) numerically inspected nanofluid and hybrid nanofluid passing through a porous medium and rotating disk by taking nanoparticles and the base fluid of blood and water, respectively.

A phenomenon known as bioconvection is seen in some biological systems, especially in suspensions of motile microorganisms like specific strains of bacteria, algae, and protozoa. In response to environmental cues like gravity or light gradients, these microorganisms move and organize as a group. Abdal et al. (2022) investigated the impacts of Fourier flux and radiation on thermal transport through a bioconvective Williamson nano-liquid stream via an extending surface. Cui et al. (2022) introduced the influence of the chemical process over forced convective nano-liquid passing through a stretchable medium. Siddique et al. (2022) elaborated on the mechanism of heat transport in bioconvective Maxwell nano-liquid flow through an extendable cylinder. Abdul Basit et al. (2023b) showed the PDE modeling of parabolic surfaces by considering bioconvective Sutterby nano-liquid movement. Farooq et al. (2023) presented the latest modifications in the bioconvective Carreau nano-liquid involving gyrotactic microorganisms passing through a stretchable cylinder that is not linear and subject to activation energy. Ahmad et al. (2023) examined the MHD nanofluid stream flow involving Dufour and Soret effects, multi-slip conditions, and chemical processes. Anjum et al. (2023) investigated a radiative 3D cross nano-liquid stream through a surface subject to activation energy. Çolak et al. (2022) applied an artificial neural network approach to model bioconvective Powell–Eyring nanofluid flow subject to the Darcy–Forchheimer flow. Shafiq et al. (2022a); Shafiq et al. (2022b); Shafiq et al. (2023) enumerated the thixotropic nanofluid flow, magnetized Walter B nanofluid flow, and MHD Williamson nanofluid flow over a variety of geometries. Various studies on nanofluids are reported by Nojoomizadeh and Karimipour (2016); Javadpour et al. (2020); Noreen et al. (2021); Dash et al. (2022); Kumari et al. (2022); Singupuram et al. (2023), subject to distinct physical quantities while keeping in mind the importance of heat and mass transfer. Numerical treatments of nanofluid problems are performed (Rasheed and Anwar, 2018; Ali et al., 2021; Hussain et al., 2021; Hussain et al., 2022b; Anwar et al., 2023a; Anwar, 2023; Anwar et al., 2023b; Anwar et al., 2023c) by fractional approaches, and the impacts of involving parameters are discussed with the graphical representations.

Researchers are motivated to investigate heat and mass transport through stretchable media by involving various physical quantities, like activation energy and thermal radiation. Most importantly, they are motivated to consider the presence of motile microorganisms. Figures 1A, B show the applications of nanomaterials and the physical utilization of nanofluids in various domains of life and engineering. The assumptions are as follows:

• The presence of living organisms increases thermal transport in such mechanisms.

• Activation energy initiates the movement of microorganisms.

• Thermal radiation and physical quantities are considered in the flow problem.

• The outcomes were numerically evaluated using the MATLAB package.

Figure 1

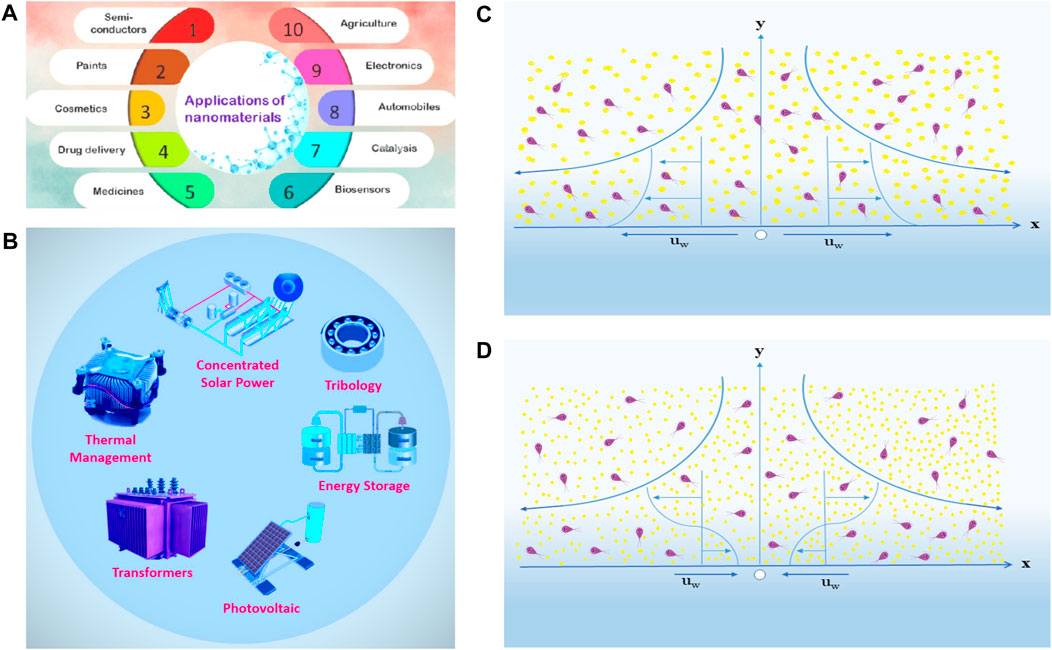
Figure 1. (A) Exploration of the applications of nanomaterials. (B) Physical usage of nanofluid. (C) Geometry (when the surface is stretching). (D) Geometry (when the surface is shrinking).

This work aimed to figure out how thermal radiation, activation energy, and the involvement of motile microorganisms impact nanofluid flow through stretchable surfaces.

2 Mathematical formulation

Consider a time-dependent laminar Williamson nanofluid stream through a porous, shrinkable surface subject to slip boundary constraints and the effects of magnetic field and electric charge on the normal state of the fluid-flowing surface.

The coordinate system has taken the x-axis as a stretching surface and the y-axis as normal to it. u and v are velocity components of the x- and y-axis, respectively. The geometry of the flow is shown in Figures 1C, D from both perspectives when the sheet is stretching and shrinking. $u_w\left(x,t\right)$ and $v_w\left(x,t\right)$ denote the momentum of the shrinking sheet and momentum of mass transfer, respectively, where $x$ is the distance and t is the time. Under the above assumptions, the governing equations (Maiti and Nandy, 2023) are as follows:

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,(1)$

$\begin{array}{l}\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\upsilon \frac{{\partial }^{2}u}{\partial y^2}+\sqrt{2}\upsilon \mathrm{\Gamma }\frac{\partial u}{\partial y}\frac{{\partial }^{2}u}{\partial y^2}-\frac{\sigma B_0^2}{\rho }u\\ +\frac{1}{{\rho }_f}\left[\left(1-C_{\infty }\right)\rho f_{\infty }\beta \left(T-T_{\infty }\right)-\left({\rho }_p-{\rho }_{f_{\infty }}\right)\left(C-C_{\infty }\right)+\left(N-N_{\infty }\right)\left({\rho }_{m_{\infty }}-{\rho }_f\right)\right]g\cos \alpha ,\end{array}(2)$

$\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha \left(1+\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k{k}^{*}}\right)\frac{{\partial }^{2}T}{\partial y^2}+\tau \left[D_B\frac{\partial C}{\partial y}\frac{\partial T}{\partial y}+\frac{D_T}{T_{\infty }}{\left(\frac{\partial T}{\partial y}\right)}^2\right],(3)$

$\frac{\partial C}{\partial t}+u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=D_B\frac{{\partial }^{2}C}{\partial y^2}+\frac{D_T}{T_{\infty }}\frac{{\partial }^{2}T}{\partial y^2}-k_r^2\left(C-C_{\infty }\right){\left(\frac{T}{T_{\infty }}\right)}^e\exp \left(\frac{E_a}{k_{1}T}\right),(4)$

$u\frac{\partial N}{\partial x}+v\frac{\partial N}{\partial y}+b{W}_c\frac{\partial }{\partial y}\left(\frac{n}{\Delta C}\frac{\partial C}{\partial y}\right)=D_m\frac{\partial }{\partial y}\frac{\partial N}{\partial y},(5)$

with B.Cs

$\begin{array}{l}u=u_w\left(x,t\right)+u_{slip}\left(x,t\right),v=v_w\left(x,t\right),T=T_w,C=C_w,N=N_{w}aty=0\\ u\to 0,T\to T_{\infty },C\to C_{\infty },N\to N_{\infty }asy\to \infty ,\end{array}(6)$

where $u_w\left(x,t\right)=-\left(ax\right)/\left(1-\lambda t\right)$, $u_{slip}\left(x,t\right)=N_1\upsilon \left(\partial u/\partial y\right),$ $N_1=N{\left(1-\lambda t\right)}^{1/2}$ is the slip velocity, and N is the initial velocity slip. The mass transport velocity becomes

$v_w\left(x,t\right)=-\sqrt{\frac{a\upsilon }{1-\lambda t}}s.(7)$

In Eq. 7, s is the wall’s mass transport constant. For implementing similarity transform, take $B_0=B/\sqrt{1-\lambda t},$ and the similarity variables are

$\psi =\sqrt{\frac{a\upsilon }{1-\lambda t}}xf\left(\eta \right),\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }},\varphi \left(\eta \right)=\frac{C-C_{\infty }}{C_w-C_{\infty }},\chi \left(\eta \right)=\frac{N-N_{\infty }}{N_w-N_{\infty }},\eta =y\sqrt{\frac{a}{\upsilon \left(1-\lambda t\right)}},(8)$

$\text{where\hspace{0.17em}the\hspace{0.17em}stream\hspace{0.17em}function\hspace{0.17em}is\hspace{0.17em}defined\hspace{0.17em}as\hspace{0.17em}}u=\frac{\partial \psi }{\partial y}\text{\hspace{0.17em}and\hspace{0.17em}}v=-\frac{\partial \psi }{\partial x}.(9)$

Now, implementing the similarity variables defined in Eqs 8, 9 to governing equations along with boundary conditions in Eqs 1–6, we have

$f^{‴}+f{f}^{″}-{f^{\prime }}^2-A\left(f^{\prime }+\frac{\eta }{2}{f}^{″}\right)+\beta f^{″}{f}^{‴}-M{f}^{\prime }+\lambda \left(\theta -Nr\varphi -Rb\chi \right)=0,(10)$

$\frac{1}{\mathrm{Pr}}\left(1+\frac{4}{3}Rd\right){\theta }^{″}+\left(f-A\frac{\eta }{2}\right){\theta }^{\prime }+Nb{\theta }^{\prime }{\varphi }^{\prime }+Nt{{\theta }^{\prime }}^2=0,(11)$

${\varphi }^{″}+Le\left(f-A\frac{\eta }{2}\right){\varphi }^{\prime }+\frac{Nt}{Nb}{\theta }^{″}-Sc*A\varphi {\left(1+\delta \theta \right)}^m\exp \left(\frac{-E}{1+\delta \theta }\right)=0,(12)$

${\chi }^{″}+\frac{1}{2}Scf{\chi }^{\prime }-Pe\left[{\chi }^{\prime }{\varphi }^{\prime }+\left(\chi +1\right){\varphi }^{″}\right]=0,(13)$

with

$\begin{array}{l}f\left(0\right)=s,f^{\prime }\left(0\right)=-1+\delta f^{″}\left(0\right),\theta \left(0\right)=1,\varphi \left(0\right)=1\\ f^{\prime }\left(\infty \right)=0,\theta \left(\infty \right)=0,\varphi \left(\infty \right)=0\end{array}.(14)$

The involving quantities are as follows:

$A=\left(\lambda /a\right)$ is the unsteadiness variable, the Prandtl number is $\mathrm{Pr}=\frac{\upsilon }{a}$, $\beta =\left(\sqrt{2}\mathrm{\Gamma }/{\upsilon }^{1/2}\right)\left(a^{3/2}x\right)/{\left(1-\lambda t\right)}^{3/2}$ shows the Williamson fluid variable, the Brownian motion is $Nb=\left(\tau D_B\left(C_w-C_{\infty }\right)\right)/\upsilon$, $M=\frac{\sigma B^2}{\rho a}$ denotes the Hartmann number, the Lewis number is $Le=\left(\upsilon /D_B\right)$, and $Nt=\left(\tau D_T\left(T_w-T_{\infty }\right)\right)/\left(\upsilon T_{\infty }\right)$ is a thermophoresis variable.

The physical parameters involved in the heat transfer through fluid flow are the local Nusselt number, microorganism density number, local Sherwood number, and local skin friction coefficient, which are given as follows:

$N{u}_x=\frac{x{q}_w}{\alpha \left(T_w-T_{\infty }\right)},N{n}_x=\frac{\mathrm{x}{\mathrm{q}}_{\mathrm{n}}}{{\mathrm{D}}_{\mathrm{m}}\left({\mathrm{N}}_{\mathrm{w}}-{\mathrm{N}}_{\infty }\right)},S{h}_x=\frac{x{q}_m}{D_B\left(C_w-C_{\infty }\right)},C_f=\frac{{\tau }_w}{\rho u_w^2}.(15)$

Here, in Eq. 15$q_w$ is the wall heat flux, ${\tau }_w$ is the shear stress, and $q_m$ is the wall mass flux, and their relations are given as Eq. 16

$q_w=-\alpha {\left(\frac{\partial T}{\partial y}\right)}_{y=0},{\tau }_w=\mu {\left[\frac{\partial u}{\partial y}+\frac{\mathrm{\Gamma }}{2}{\left(\frac{\partial u}{\partial y}\right)}^2\right]}_{y=0},q_m=-D_B{\left(\frac{\partial C}{\partial y}\right)}_{y=0}.(16)$

Hence, implementing the defined variables, we get

$R\sqrt{e_x}{C}_f=f^{″}\left(0\right)\left[1+\frac{\beta }{2\sqrt{2}}{f}^{″}\left(0\right)\right],(17)$

$\frac{R}{\sqrt{e_x}}N{u}_x=-{\theta }^{\prime }\left(0\right),(18)$

$\frac{R}{\sqrt{e_x}}S{h}_x=-{\varphi }^{\prime }\left(0\right),(19)$

$\frac{R}{\sqrt{e_x}}N{n}_x=-{\chi }^{\prime }\left(0\right),(20)$

The physical quantities are described as in Eqs 17–20.

where ${\text{Re}}_x=\left(u_{w}x\right)/\upsilon$ is the local Reynolds number.

3 Numerical algorithm

For the numerical solution, we have to develop a numerical algorithm for the implementation of the numerical approach. After implementing similarity variables, we have nonlinear ODEs with a set of boundary constraints. To tackle the system of ODEs numerically, we use the built-in package of MATLAB called “bvp4c.” This package gives us very fine results compared to other techniques because it has a very low error tolerance (i.e. 10⁻⁶). For this, dummy variables are first introduced for conversion to first-order nonlinear ODEs. Here,

$\begin{array}{l}f={\mathcal{l}}_1,f^{\prime }={\mathcal{l}}_2,f^{″}={\mathcal{l}}_3,f^{‴}={\mathcal{l}}_3^{\prime }\\ \theta ={\mathcal{l}}_4,{\theta }^{\prime }={\mathcal{l}}_5,{\theta }^{″}={\mathcal{l}}_5^{\prime }\\ \varphi ={\mathcal{l}}_6,{\varphi }^{\prime }={\mathcal{l}}_7,{\varphi }^{″}={\mathcal{l}}_7^{\prime }\\ \chi ={\mathcal{l}}_8,{\chi }^{\prime }={\mathcal{l}}_9,{\chi }^{″}={\mathcal{l}}_9^{\prime }\end{array}.$

Then, the system of Eqs 10–14 along with boundary conditions are transformed by using above dummy variables as in Eqs 21–25

${\mathcal{l}}_3^{\prime }=\frac{1}{\left(1+\beta {\mathcal{l}}_3\right)}\left[-{\mathcal{l}}_1{\mathcal{l}}_3+{\mathcal{l}}_2^2+A\left({\mathcal{l}}_2+\frac{\eta }{2}{\mathcal{l}}_3\right)+M{\mathcal{l}}_2-\lambda \left({\mathcal{l}}_4-Nr{\mathcal{l}}_6-Rb{\mathcal{l}}_8\right)\right],(21)$

${\mathcal{l}}_5^{\prime }=-\frac{1}{\frac{1}{\mathrm{Pr}}\left(1+\frac{4}{3}Rd\right)}\left({\mathcal{l}}_1-A\frac{\eta }{2}\right){\mathcal{l}}_5-Nb{\mathcal{l}}_5{\mathcal{l}}_7-Nt{\mathcal{l}}_5^2,(22)$

${\mathcal{l}}_7^{\prime }=-Le\left({\mathcal{l}}_1-A\frac{\eta }{2}\right){\mathcal{l}}_7-\frac{Nt}{Nb}{\mathcal{l}}_5^{\prime }+Sc*A{\mathcal{l}}_6{\left(1+\delta {\mathcal{l}}_4\right)}^m\exp \left(\frac{-E}{1+\delta {\mathcal{l}}_4}\right),(23)$

${\mathcal{l}}_9^{\prime }=Pe\left[{\mathcal{l}}_9{\mathcal{l}}_7+\left({\mathcal{l}}_8+1\right){\mathcal{l}}_7^{\prime }\right]-\frac{1}{2}Sc{\mathcal{l}}_1{\mathcal{l}}_8,(24)$

with

$\begin{array}{l}{\mathcal{l}}_1\left(0\right)=s,{\mathcal{l}}_2\left(0\right)=-1+\delta {\mathcal{l}}_3\left(0\right),{\mathcal{l}}_4\left(0\right)=1,{\mathcal{l}}_6\left(0\right)=1\\ {\mathcal{l}}_2\left(\infty \right)=0,{\mathcal{l}}_4\left(\infty \right)=0,{\mathcal{l}}_6\left(\infty \right)=0\end{array}.(25)$

4 Outcomes and discussion

In this section, we discuss the outcomes obtained through this approach and the effects of involving physical quantities on the bioconvective flow of time-dependent heat transport through the MHD stream of Williamson nano-liquid passing through a shrinking sheet. The velocity, temporal, concentration, and microorganism profiles are visualized and discussed in Figures 2–14, respectively. In Figure 2, the impact of the mixed convection variable over the momentum depiction shows increasing behavior while boosting the values of the parameter. In mixed convection, density changes brought on by temperature differences and external forces (forced convection) can both affect the fluid flow. These two processes’ relative dominance is influenced by a number of variables, including fluid velocity, temperature gradients, fluid characteristics, and the geometrical layout of the system. Figure 3 exhibits the impact of the magnetic field on the fluid flow through a shrinking surface. A magnetic field decreases the nanofluid flow by increasing the values of variables. The MHD phenomenon is associated with the physical importance of the magnetic field in fluid movement. The study of magnetohydrodynamics examines how magnetic fields affect electrically conductive liquids, such as liquid metals, plasmas, and ionized gases. Figure 4 displays the impact of the bioconvection Rayleigh number on the momentum profile. It causes resistance to the flow of fluid and decreases mass and heat transport rates. In bioconvection, environmental conditions frequently impact microorganism migration. The presence of nanoparticles in a nanofluid may result in interactions with microorganisms, and the Rayleigh parameter might influence the strength and type of these interactions. Figure 5 shows the influence of the buoyancy ratio variable on the momentum depiction of the flow problem. The buoyancy ratio variable, which has no dimensions, is used to describe how fluids behave in buoyancy-driven flows, especially when natural convection is present.

Figure 2

Figure 2. Exhibits $\lambda$ over $f^{\prime }$

Figure 3

Figure 3. Exhibits $M$ over $f^{\prime }$.

Figure 4

Figure 4. Exhibits $Nc$ over $f^{\prime }$.

Figure 5

Figure 5. Exhibits $Nr$ over $f^{\prime }$.

The thermal profile of the flow problem is discussed and visualized in Figures 6–9, involving various physical parameters. Figure 6 displays the variation that occurred due to the magnetic field over the thermal profile of the flow problem. The increase in temporal depiction arises because of the increase in the counts of the concerned parameter. Figure 7 shows the significance of the Brownian motion on the temperature articulation of stretching surface nano-liquid flow, which shows an increase in mass and heat transport rates because of the increased count of nanoparticles with random motion. Nanoparticles’ random motion can facilitate their penetration into biological tissues and delivery to particular target locations, thereby boosting the efficiency and efficacy of therapeutic or diagnostic procedures. Figure 8 depicts the breakthrough of thermophoresis variable involvement in the nano-liquid stream and its influence on the transfer rate, as shown in the increased figure rate when the values of the variable were boosted. The interplay of thermophoresis and temperature gradients has the potential to affect nanofluid stability. Nanoparticles’ temperature-induced mobility may have an impact on the overall stability of the dispersion. Figure 9 shows the influence of thermal radiation on temporal depiction. The increment in the flow rate is noticed by inclining the values of the variable. A primary way to transport energy is through thermal radiation. Thermal radiation is produced by objects that are warmer than absolute zero. The electromagnetic waves that make up this radiation carry energy from the item.

Figure 6

Figure 6. Exhibits $M$ over $\theta$.

Figure 7

Figure 7. Exhibits $Nb$ over $\theta$.

Figure 8

Figure 8. Exhibits $Nt$ over $\theta$.

Figure 9

Figure 9. Exhibits $Rd$ over $\theta$.

The concentration profile of the mass and heat transport mechanisms is explored in Figures 10–12. The impacts of modeling variables on the profile are debated in an organized manner. Figure 10 displays the influence on the concentration depiction due to a minimal amount of energy. An increase in the transfer rate is noticed by increasing the counts of parameters. The pace at which a chemical reaction takes place is governed by activation energy. Reactant molecules need more energy to cross the energy barrier and change into products in reactions with higher activation energies. Figure 11 depicts the variation in the Lewis number over the concentration depiction of the flow problem. The increment in the variable shows a fall in the flow rate. The Lewis number is a tool used in heat transfer applications to analyze the relationship between thermal diffusion and heat conduction. When thermal diffusion predominates, it results in higher thermal stratification and slower heat transfer rates, as indicated by a high Lewis number. Figure 12 shows the impact of Brownian motion on the concentration depiction. Scattering in the concentration occurs due to the enhancement of the values of the variable. With regard to nanoparticles and colloidal suspensions, in particular, the Brownian motion is a crucial factor in nanotechnology. It is possible to manage the stability and behavior of nanoscale systems and nanoparticles in a variety of applications, including drug delivery, nanomedicine, and nanocomposites, by comprehending the Brownian motion.

Figure 10

Figure 10. Exhibits $E$ over $\varphi$.

Figure 11

Figure 11. Exhibits $Le$ over $\varphi$.

Figure 12

Figure 12. Exhibits $Nb$ over $\varphi$.

The influence of the number of physical variables on the motile microorganism profile is visualized in Figures 13, 14. Physical quantity effects are very important in the flow of nano-liquids through stretchable media. Figure 13 shows the variation that occurred in the microorganism profile of the thermal transport mechanism due to the Maxwell variable, which minimizes the transport rate. Figure 14 explains the impact of the bioconvection Lewis number over the microorganism depiction, which shows a decrease in the transport of heat and mass through the flow of nano-liquid over a stretchable surface. Specifically, taking into account heat conduction and mass diffusion, the “bioconvection Lewis number” would most likely relate to how the mobility and distribution of microorganisms during bioconvection (i.e., its physical presence) affect the transport processes in the fluid. The movement of the microorganisms may vary or have an impact on the ratio of thermal diffusivity to mass diffusivity, which might potentially alter the overall transport phenomenon.

Figure 13

Figure 13. Exhibits $\lambda$ over $\chi$

Figure 14

Figure 14. Exhibits $Lb$ over $\chi$.

The comparison of our computed outcomes with already reported outcomes is tabulated in Table 1, and the accordance of results shows the smoothness of our results.

Table 1

Table 1. Comparison of recent results with published results for distinct values of $\lambda =0.1,0.2,\text{and\hspace{0.17em}}0.3.$

5 Conclusion

In this study, heat and mass transport through time-dependent bioconvective Williamson nanofluid flow through stretchable surfaces subject to activation energy and thermal radiation are investigated. Additionally, the significance of gyrotactic motile microorganisms in the transport rate is enumerated. The numerical results are discussed and graphically visualized, along with the impacts of physical parameters. The major outcomes of the study are as follows:

❖ With an increase in $\lambda$, the momentum profile increases. On the other hand, by increasing the values of the buoyancy force, magnetic field, and buoyancy ratio variables, the momentum profile shows a decrease in the flow rate.

❖ In the thermal profile, by increasing the counts of the magnetic field, Brownian motion, thermophoresis, and thermal rays, an increment is noticed.

❖ An increase in the values of activation energy shows an increase in the concentration profile, whereas an increase in the counts of the Brownian motion and Lewis number shows a downfall. Physically, by increasing the Lewis number, the concentration of particles decreases.

❖ The microorganism density profile shows a downfall by boosting the values of the mixed convection parameter and bioconvection Lewis number.

❖ Graphical visualization clearly shows that our boundary conditions are asymptotically satisfied.

In the future, this idea may be extended to any other physical problem and also used to scrutinize heat and mass transfer efficiency using hybrid particles.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

SS: writing–review and editing. ZY: investigation, methodology, and writing–review and editing. QW: writing–original draft. FL: formal analysis, software, and writing–review and editing. LJ: writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is supported by the National Natural Science Foundation of China (No. 52106205).

Conflict of interest

Author ZY was employed by Shanghai Aerospace Equipment Manufacturing Co., Ltd. Author FL was employed by Ningbo Radi-Cool Advanced Energy Technologies Co. Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdal, S., Siddique, I., Din, I. S. U., and Hussain, S. (2022). On prescribed thermal distributions of bioconvection Williamson nanofluid transportion due to an extending sheet with non-Fourier flux and radiation. Waves Random Complex Media, 1–20. doi:10.1080/17455030.2022.2136416

CrossRef Full Text | Google Scholar

Abdul Basit, M., Imran, M., Khan, S. A., Alhushaybari, A., Sadat, R., and Ali, M. R. (2023). Partial differential equations modeling of bio-convective sutterby nanofluid flow through paraboloid surface. Sci. Rep. 13 (1), 6152. doi:10.1038/s41598-023-32902-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Ahmad, B., Ahmad, M. O., Farman, M., Akgül, A., and Riaz, M. B. (2023). A significance of multi slip condition for inclined MHD nano-fluid flow with non linear thermal radiations, Dufuor and Sorrot, and chemically reactive bio-convection effect. South Afr. J. Chem. Eng. 43, 135–145. doi:10.1016/j.sajce.2022.10.009

CrossRef Full Text | Google Scholar

Algehyne, E. A., and Saeed, A. (2022). Numerical study of motile microorganism in Williamson MHD nanofluid flow over an elastic slender surface of an irregular thickness. Waves Random Complex Media, 1–16. doi:10.1080/17455030.2022.2108159

CrossRef Full Text | Google Scholar

Ali, I., Rasheed, A., Anwar, M. S., Irfan, M., and Hussain, Z. (2021). Fractional calculus approach for the phase dynamics of Josephson junction. Chaos, Solit. Fractals 143, 110572. doi:10.1016/j.chaos.2020.110572

CrossRef Full Text | Google Scholar

Anjum, N., Khan, W. A., Azam, M., Ali, M., Waqas, M., and Hussain, I. (2023). Significance of bioconvection analysis for thermally stratified 3D Cross nanofluid flow with gyrotactic microorganisms and activation energy aspects. Therm. Sci. Eng. Prog. 38, 101596. doi:10.1016/j.tsep.2022.101596

CrossRef Full Text | Google Scholar

Anwar, M. S. (2023). Heat transfer in MHD convective stagnation point flow over a stretching surface with thermal radiations. Numer. Heat. Transf. Part A Appl., 1–16. doi:10.1080/10407782.2023.2299289

CrossRef Full Text | Google Scholar

Anwar, M. S., Alghamdi, M., Muhammad, T., Hussain, M., and Puneeth, V. (2023b). Analysis of nonlinear convection and diffusion in viscoelastic fluid flow with variable thermal conductivity and thermal radiations. Mod. Phys. Lett. B, 2450146. doi:10.1142/s021798492450146x

CrossRef Full Text | Google Scholar

Anwar, M. S., Hussain, M., Hussain, Z., Puneeth, V., and Irfan, M. (2023a). Clay-based cementitious nanofluid flow subjected to Newtonian heating. Int. J. Mod. Phys. B 37 (14), 2350140. doi:10.1142/s0217979223501400

CrossRef Full Text | Google Scholar

Anwar, M. S., Muhammad, T., Khan, M., and Puneeth, V. (2023c). MHD nanofluid flow through Darcy medium with thermal radiation and heat source. Int. J. Mod. Phys. B, 2450386. doi:10.1142/s0217979224503867

CrossRef Full Text | Google Scholar

Basit, M. A., Farooq, U., Imran, M., Fatima, N., Alhushaybari, A., Noreen, S., et al. (2023c). Comprehensive investigations of (Au-Ag/Blood and Cu-Fe3O4/Blood) hybrid nanofluid over two rotating disks: numerical and computational approach. Alexandria Eng. J. 72, 19–36. doi:10.1016/j.aej.2023.03.077

CrossRef Full Text | Google Scholar

Basit, M. A., Imran, M., Safdar, R., Tahir, M., Ali, M. R., Hendy, A. S., et al. (2024b). Thermally radiative bioconvective nanofluid flow on a wavy cylinder with buongiorno model: a sensitivity analysis using response surface methodology. Case Stud. Therm. Eng. 55, 104178. doi:10.1016/j.csite.2024.104178

CrossRef Full Text | Google Scholar

Basit, M. A., Imran, M., Tahir, M., Eladeb, A., and Kolsi, L. (2024a). Numerical analysis of mathematical model for heat and mass transfer through Bioconvective Maxwell nanofluid flow subject to Darcy-Forcheimer and Lorentz forces. Int. J. Heat Fluid Flow 106, 109322. doi:10.1016/j.ijheatfluidflow.2024.109322

CrossRef Full Text | Google Scholar

Basit, M. A., Tahir, M., Riasat, A., Khan, S. A., Imran, M., and Akgül, A. (2023b). Numerical simulation of bioconvective Casson nanofluid through an exponentially permeable stretching surface. Int. J. Mod. Phys. B 38, 2450128. doi:10.1142/s0217979224501285

CrossRef Full Text | Google Scholar

Basit, M. A., Tahir, M., Shah, N. A., Tag, S. M., and Imran, M. (2023a). An application to formable transform: novel numerical approach to study the nonlinear oscillator. J. Low Freq. Noise, Vib. Act. Control, 14613484231216198. doi:10.1177/14613484231216198

CrossRef Full Text | Google Scholar

Choi, S. U., and Eastman, J. A. (1995). Enhancing thermal conductivity of fluids with nanoparticles (No. ANL/MSD/CP-84938; CONF-951135-29). Argonne, IL (United States): Argonne National Lab.ANL.

Google Scholar

Çolak, A. B., Shafiq, A., and Sindhu, T. N. (2022). Modeling of Darcy–Forchheimer bioconvective Powell Eyring nanofluid with artificial neural network. Chin. J. Phys. 77, 2435–2453. doi:10.1016/j.cjph.2022.04.004

CrossRef Full Text | Google Scholar

Cui, J., Razzaq, R., Farooq, U., Khan, W. A., Farooq, F. B., and Muhammad, T. (2022). Impact of non-similar modeling for forced convection analysis of nano-fluid flow over stretching sheet with chemical reaction and heat generation. Alexandria Eng. J. 61 (6), 4253–4261. doi:10.1016/j.aej.2021.09.045

CrossRef Full Text | Google Scholar

Dash, A. P., Alam, T., Siddiqui, M. I. H., Blecich, P., Kumar, M., Gupta, N. K., et al. (2022). Impact on heat transfer rate due to an extended surface on the passage of microchannel using cylindrical ribs with varying sector angle. Energies 15 (21), 8191. doi:10.3390/en15218191

CrossRef Full Text | Google Scholar

Dharmaiah, G., Balamurugan, K. S., Prasad, J. R., and Chamkha, A. J. (2023). Simulation of Hydromagnetic Williamson nanofluid flow with melting heat transfer and Activation Energy across a porous exponential stretching surface. doi:10.21203/rs.3.rs-2787850/v1

CrossRef Full Text | Google Scholar

Farooq, U., Basit, M. A., Noreen, S., Fatima, N., Alhushaybari, A., El Din, S. M., et al. (2023). Recent progress in Cattaneo-Christov heat and mass fluxes for bioconvectional Carreau nanofluid with motile microorganisms and activation energy passing through a nonlinear stretching cylinder. Ain Shams Eng. J. 15, 102316. doi:10.1016/j.asej.2023.102316

CrossRef Full Text | Google Scholar

Gadelhak, A. A., Mekheimer, K. S., Seddeek, M. A., Abo-Elkhair, R. E., Ali, K. K., and Salem, A. M. (2023). Energy transport of Williamson nano-fluid over a curved stretching surface by means of FDM. BioNanoScience 13, 1116–1125. doi:10.1007/s12668-023-01120-2

CrossRef Full Text | Google Scholar

Hashim, H., Anuar Mohamed, M. K., Ishak, N., Sarif, N. M., and Salleh, M. Z. (2019). Thermal radiation effect on MHD stagnation point flow of Williamson fluid over a stretching surface. J. Phys. Conf. Ser. 1366 (1), 012011. doi:10.1088/1742-6596/1366/1/012011

CrossRef Full Text | Google Scholar

Hayat, T., Aziz, A., Muhammad, T., and Alsaedi, A. (2017). Darcy–Forchheimer three-dimensional flow of Williamson nanofluid over a convectively heated nonlinear stretching surface. Commun. Theor. Phys. 68 (3), 387. doi:10.1088/0253-6102/68/3/387

CrossRef Full Text | Google Scholar

Hussain, M., Ranjha, Q. A., Anwar, M. S., Jahan, S., and Ali, A. (2022b). Eyring-Powell model flow near a convectively heated porous wedge with chemical reaction effects. J. Taiwan Inst. Chem. Eng. 139, 104510. doi:10.1016/j.jtice.2022.104510

CrossRef Full Text | Google Scholar

Hussain, S. M., Jamshed, W., Pasha, A. A., Adil, M., and Akram, M. (2022a). Galerkin finite element solution for electromagnetic radiative impact on viscid Williamson two-phase nanofluid flow via extendable surface. Int. Commun. Heat Mass Transf. 137, 106243. doi:10.1016/j.icheatmasstransfer.2022.106243

CrossRef Full Text | Google Scholar

Hussain, Z., Muhammad, S., and Anwar, M. S. (2021). Effects of first-order chemical reaction and melting heat on hybrid nanoliquid flow over a nonlinear stretched curved surface with shape factors. Adv. Mech. Eng. 13 (4), 168781402199952. doi:10.1177/1687814021999526

CrossRef Full Text | Google Scholar

Ibrahim, W., and Negera, M. (2020). The investigation of MHD Williamson nanofluid over stretching cylinder with the effect of activation energy. Adv. Math. Phys. 2020, 1–16. doi:10.1155/2020/9523630

CrossRef Full Text | Google Scholar

Imran, M., Basit, M. A., Yasmin, S., Khan, S. A., Elagan, S. K., Akgül, A., et al. (2024). A proceeding to numerical study of mathematical model of bioconvective Maxwell nanofluid flow through a porous stretching surface with nield/convective boundary constraints. Sci. Rep. 14 (1), 1873. doi:10.1038/s41598-023-48364-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Javadpour, S. M., Abadi, E. A. J., Akbari, O. A., and Goharimanesh, M. (2020). Optimization of geometry and nano-fluid properties on microchannel performance using Taguchi method and genetic algorithm. Int. Commun. heat mass Transf. 119, 104952. doi:10.1016/j.icheatmasstransfer.2020.104952

CrossRef Full Text | Google Scholar

Jyotshna, M., and Dhanalaxmi, V. (2022). Impact of activation energy and heat source/sink on 3D flow of Williamson nanofluid with Gan nanoparticles over A stretching sheet. Eur. J. Math. Statistics 3 (5), 16–29. doi:10.24018/ejmath.2022.3.5.133

CrossRef Full Text | Google Scholar

Khan, W., Gul, T., Idrees, M., Islam, S., and Khan, I. (2017). Dufour and Soret effect with thermal radiation on the nano film flow of Williamson fluid past over an unsteady stretching sheet. J. Nanofluids 6 (2), 243–253. doi:10.1166/jon.2017.1328

CrossRef Full Text | Google Scholar

Kiyani, M. Z., Hayat, T., Ahmad, I., Waqas, M., and Alsaedi, A. (2021). Bidirectional Williamson nanofluid flow towards stretchable surface with modified Darcy’s law. Surfaces Interfaces 23, 100872. doi:10.1016/j.surfin.2020.100872

CrossRef Full Text | Google Scholar

Kumari, N., Alam, T., Ali, M. A., Yadav, A. S., Gupta, N. K., Siddiqui, M. I. H., et al. (2022). A numerical investigation on hydrothermal performance of micro channel heat sink with periodic spatial modification on sidewalls. Micromachines 13 (11), 1986. doi:10.3390/mi13111986

PubMed Abstract | CrossRef Full Text | Google Scholar

Maiti, H., and Nandy, S. K. (2023). Scrutinization of unsteady magnetohydrodynamics Williamson nanofluid flow and heat transfer past a permeable shrinking sheet. J. Nanofluids 12 (4), 1095–1106. doi:10.1166/jon.2023.1989

CrossRef Full Text | Google Scholar

Malik, M. Y., Bibi, M., Khan, F., and Salahuddin, T. (2016). Numerical solution of Williamson fluid flow past a stretching cylinder and heat transfer with variable thermal conductivity and heat generation/absorption. AIP Adv. 6 (3). doi:10.1063/1.4943398

CrossRef Full Text | Google Scholar

Mangathai, P. (2021). Unsteady MHD Williamson and Casson nano fluid flow in the presence of radiation and viscous dissipation. Turkish J. Comput. Math. Educ. (TURCOMAT) 12 (13), 1036–1051. doi:10.17762/turcomat.v12i13.8592

CrossRef Full Text | Google Scholar

Nojoomizadeh, M., and Karimipour, A. (2016). The effects of porosity and permeability on fluid flow and heat transfer of multi walled carbon nano-tubes suspended in oil (MWCNT/Oil nano-fluid) in a microchannel filled with a porous medium. Phys. E Low-dimensional Syst. Nanostructures 84, 423–433. doi:10.1016/j.physe.2016.07.020

CrossRef Full Text | Google Scholar

Noreen, S., Waheed, S., Lu, D. C., and Hussanan, A. (2021). Entropy generation in electromagnetohydrodynamic water based three Nano fluids via porous asymmetric microchannel. Eur. J. Mechanics-B/Fluids 85, 458–466. doi:10.1016/j.euromechflu.2020.11.002

CrossRef Full Text | Google Scholar

Rasheed, A., and Anwar, M. S. (2018). Numerical computations of fractional nonlinear Hartmann flow with revised heat flux model. Comput. Math. Appl. 76 (10), 2421–2433. doi:10.1016/j.camwa.2018.08.039

CrossRef Full Text | Google Scholar

Raza, R., Mabood, F., Naz, R., and Abdelsalam, S. I. (2021). Thermal transport of radiative Williamson fluid over stretchable curved surface. Therm. Sci. Eng. Prog. 23, 100887. doi:10.1016/j.tsep.2021.100887

CrossRef Full Text | Google Scholar

Salahuddin, T., Maqsood, A., Awais, M., Khan, M., and Altanji, M. (2023). Significance of MHD Cross nanofluid analysis near a stretched surface with double stratification and activation energy. Int. Commun. Heat Mass Transf. 143, 106732. doi:10.1016/j.icheatmasstransfer.2023.106732

CrossRef Full Text | Google Scholar

Shafiq, A., Çolak, A. B., and Sindhu, T. N. (2022a). Significance of bioconvective flow of MHD thixotropic nanofluid passing through a vertical surface by machine learning algorithm. Chin. J. Phys. 80, 427–444. doi:10.1016/j.cjph.2022.08.008

CrossRef Full Text | Google Scholar

Shafiq, A., Çolak, A. B., and Sindhu, T. N. (2022b). Optimization of bioconvective magnetized walter’s B nanofluid flow towards a cylindrical disk with artificial neural networks. Lubricants 10 (9), 209. doi:10.3390/lubricants10090209

CrossRef Full Text | Google Scholar

Shafiq, A., Çolak, A. B., and Sindhu, T. N. (2023). Modeling of Darcy-Forchheimer magnetohydrodynamic Williamson nanofluid flow towards nonlinear radiative stretching surface using artificial neural network. Int. J. Numer. Methods Fluids 95 (9), 1502–1520. doi:10.1002/fld.5216

CrossRef Full Text | Google Scholar

Shah, Z., Bonyah, E., Islam, S., Khan, W., and Ishaq, M. (2018). Radiative MHD thin film flow of Williamson fluid over an unsteady permeable stretching sheet. Heliyon 4 (10), e00825. doi:10.1016/j.heliyon.2018.e00825

PubMed Abstract | CrossRef Full Text | Google Scholar

Sharif, H., Hussain, M., Khadimallah, M. A., Ayed, H., Taj, M., Bhutto, J. K., et al. (2022). Theoretical fabrication of Williamson nanoliquid over a stretchable surface. Adv. Concr. Constr. 14 (2), 103–113. doi:10.12989/acc.2022.14.2.103

CrossRef Full Text | Google Scholar

Siddique, I., Habib, U., Ali, R., Abdal, S., and Salamat, N. (2022). Bioconvection attribution for effective thermal transportation of upper convicted Maxwell nanofluid flow due to an extending cylindrical surface. Int. Commun. Heat Mass Transf. 137, 106239. doi:10.1016/j.icheatmasstransfer.2022.106239

CrossRef Full Text | Google Scholar

Singupuram, R., Alam, T., Ali, M. A., Shaik, S., Gupta, N. K., Akkurt, N., et al. (2023). Numerical analysis of heat transfer and fluid flow in microchannel heat sinks for thermal management. Case Stud. Therm. Eng. 45, 102964. doi:10.1016/j.csite.2023.102964

CrossRef Full Text | Google Scholar

Taj, M., and Salahuddin, T. (2023). Analysis of viscously dissipated three-dimensional flow of Williamson fluid with nonlinear radiation and activation energy. Alexandria Eng. J. 76, 595–607. doi:10.1016/j.aej.2023.06.043

CrossRef Full Text | Google Scholar

Tlili, I., Bilal, M., Qureshi, M. Z. A., and Abdelmalek, Z. (2020). Thermal analysis of magnetized pseudoplastic nano fluid flow over 3D radiating non-linear surface with passive mass flux control and chemically responsive species. J. Mater. Res. Technol. 9 (4), 8125–8135. doi:10.1016/j.jmrt.2020.05.073

CrossRef Full Text | Google Scholar