- 1Hubei Branch of State Power Investment Group Co, Ltd, Wuhan, China
- 2Institute of New Energy, Wuhan, China
- 3School of Automation, China University of Geosciences, Wuhan, China
The intermittent renewable energy in a virtual power plant (VPP) brings generation uncertainties, which prevents the VPP from providing a reliable and user-friendly power supply. To address this issue, this paper proposes a gated recurrent unit proximal policy optimization (GRUPPO)-based optimal VPP economic dispatch method. First, electrical generation, storage, and consumption are established to form a VPP framework by considering the accessibility of VPP state information. The optimal VPP economic dispatch can then be expressed as a partially observable Markov decision process (POMDP) problem. A novel deep reinforcement learning method called GRUPPO is further developed based on VPP time series characteristics. Finally, case studies are conducted over a 24-h period based on the actual historical data. The test results illustrate that the proposed economic dispatch can achieve a maximum operation cost reduction of 6.5% and effectively smooth the supply–demand uncertainties.
1 Introduction
1.1 Background and motivation
With the global energy shortage and environmental deterioration becoming increasingly prominent, distributed renewable energy resources have gained popularity in the power system and developed rapidly (Naveen et al., 2020; Huang et al., 2021; Liu et al., 2023). Although the renewable energy implementation can generally reduce the dependence on fossil generation, the low unit capacity and high fluctuation hinder its reliable supply. As a result of inherent temporal–spatial complementarities, virtual power plants (VPPs) integrated with cooperative and transactive energy management can effectively cope with the core issues and enhance the overall economy (Koraki and Strunz, 2017).
The VPP is defined as an aggregator of distributed supply–demand resources, which would independently perform a transactive behavior with the market or operator (Etherden et al., 2015; Lin et al., 2020; Gough et al., 2022). However, due to its lower capacity and inherent sporadic nature, its integration into the current power system is complicated (Xu et al., 2021). Although VPPs have developed rapidly, the high penetration of renewable energy and the proactive end users make VPPs more uncertain. These uncertainties cause disturbances in the optimal VPP economic dispatch and prevent VPPs from providing a reliable and user-friendly power supply. Therefore, it is essential to design an effective VPP economic dispatch method to enhance economic benefits and smooth the supply–demand uncertainties.
1.2 Literature review
In order to handle the uncertainties in the VPP dispatch, various optimization methods have been proposed, including stochastic optimization and robust optimization. Liu et al. (2018) proposed an interval-deterministic combined optimization method to maximize the deterministic profits and profit intervals of VPPs (Liu et al., 2018). A data-adaptive robust optimization method was proposed by Zhang et al. (2018) to optimize the dispatch scheme with adjustable robustness parameters. A deterministic price-based unit commitment was proposed by Mashhour and Moghaddas-Tafreshi (2010), and a genetic algorithm was used to solve the uncertainties. Chen et al. (2018) presented a fully distributed method for VPP economic dispatch using the alternating direction multiplier method (ADMM) and the consensus algorithm (Chen et al., 2018). Yang et al. (2013) proposed a consensus-based distributed economic dispatch algorithm through the iterative coordination of local agents.
When faced with the supply–demand uncertainties, these traditional optimization-based methods usually rely on accurate system models and a priori knowledge, which are difficult to obtain in practice (Xu et al., 2019). Although robust optimization methods can deal with uncertainties to some extent, these methods are very conservative. Meanwhile, these methods cannot deal with dynamic and random changes, due to which real-time information and interactions with various energy sources may not be able to capture. Traditional optimization-based methods also rely on reliable solvers or heuristic algorithms (Xu et al., 2020), which is time-consuming and cannot meet the real-time requirements of practical VPP problems.
Reinforcement learning has become a highly effective approach for addressing optimization problems in various domains (Książek et al., 2019). Unlike traditional optimization methods that often rely on extensive domain knowledge or problem-specific heuristics, reinforcement learning allows agents to discover effective strategies through trial-and-error processes (Bui et al., 2020). Reinforcement learning is well suited for sequential decision-making. In many optimization problems, decisions must be made in a sequential manner with each decision influencing future decisions. Reinforcement learning algorithms, such as Q-learning and policy gradient methods, explicitly model this sequential aspect of decision-making by updating the agent’s policy based on the outcomes of previous actions. This allows the agent to learn optimal sequences of decisions that lead to desired outcomes (Huang et al., 2021). In many real-world optimization problems, the agent may not have complete information about the state of the system. Reinforcement learning agents learn to make decisions based on partial information, effectively reasoning about the most likely state of the system and taking actions accordingly. This ability to handle incomplete information makes reinforcement learning suitable for a wide range of real-world optimization problems with uncertainties.
Deep reinforcement learning integrates deep learning and reinforcement learning, which has been widely adopted for solving VPP problems in the Internet of Energy (IoE) domain. For instance, Sun et al. (Hua et al., 2019) mainly studied IoE management, and reinforcement learning was adopted to formulate the best operating strategies. Du et al. (2018) studied the IoE architecture design and adopted reinforcement learning to optimize electric vehicle charging. Liu et al. (2018) combined deep learning with reinforcement learning for improving the generating unit tripping strategy. Combining reinforcement learning and deep neural network, Lu et al. (2019) presented a demand response algorithm for the IoE system based on real-time execution. However, the reinforcement learning methods in the above studies are all based on Q-learning or deep Q-learning methods, which are limited to discrete action spaces. To address this problem, Zhao et al. (2022) adopted a proximal policy optimization (PPO)-based reinforcement learning method, which contains both continuous and discrete action spaces. Zhao et al. (2022) proved that the system cost is reduced by 12.17% compared to the Q-learning method.
However, two problems still remain to be addressed in the existing reinforcement learning-based VPP economic dispatch method. The first problem is that the historical VPP information is not considered in the above studies. Actually, the VPP economic dispatch cannot follow the Markov decision process (MDP) since the integration of renewable energy sources makes it a sequential decision process problem. As a type of artificial neural network, the recurrent neural network (RNN) is commonly used to address these ordinal or temporal problems, which can extract the time series information effectively. The gated recurrent unit (GRU), which optimizes the update and reset gates, is another type of the long short-term memory network. Compared to RNN, GRU offers computational efficiency, superior long-term dependency capture, effective vanishing gradient solution, and remarkable generalization capabilities (Canizo et al., 2019). These key advantages make the GRU an excellent choice for various sequential learning tasks, particularly in domains where capturing long-term dependencies is of paramount importance (Thanh et al., 2022).
The second problem is that the above methods all need a central agent to coordinate the VPP supply–demand balance. Actually, the VPP would not be managed with a single operator, and this centralized management would give rise to various disadvantages, including intensive information transmission and low-efficiency operation. It is a foreseeable trend that the VPP would gradually form a distributed manner, which could potentially satisfy geographical end users. Various decomposition techniques, including ADMM (Chen et al., 2018; Xu et al., 2019) and consensus algorithm (Yang et al., 2013), have been successfully applied for decentralized/distributed decision-making. Compared with the central method based on the single agent, the multi-agent optimization method can assign dispatch tasks to multiple agents for processing, which improves the processing capacities and solution efficiency. In addition, even if one agent fails or another agent is added, the entire system can still maintain a stable operation. In other words, the multi-agent approach will be more scalable, adaptive, and robust (Gronauer et al., 2023).
1.3 Contribution
To sum up the above discussion, this paper proposes a gated recurrent unit proximal policy optimization (GRUPPO)-based optimal VPP economic dispatch method. The contributions of this article are as follows:
(1) The PPO-based deep reinforcement learning method is developed to handle both continuous and discrete action spaces. Compared with the traditional method, including the deterministic optimization and robust optimization in Mashhour and Moghaddas-Tafreshi (2010), Yang et al. (2013), Chen et al. (2018), Liu et al. (2018), and Zhang et al. (2018), the proposed approach can better deal with the supply–demand uncertainties and meet the real-time economic dispatch requirement for the VPP.
(2) The GRU network is equipped into the PPO-based deep reinforcement learning method to form the GRUPPO approach. Different from the reinforcement learning approaches in Sun et al. (2017), Du et al. (2018), Liu et al. (2018), and Lu et al. (2019), the proposed GRUPPO scheme can fully consider the historical time series information for economic decision-making, effectively reducing the VPP operation cost.
(3) A multi-agent optimization framework is developed to capture the distributed characteristics in the VPP. The optimization framework adopts centralized training and distributed execution, thereby performing higher flexibility and scalability against complex situations.
The remainder of this paper is organized as follows: in Section 2, the modeling of the VPP economic dispatch is established, and its objective function is designed. In Section 3, the GRUPPO strategy and its multi-agent framework are proposed for the optimal VPP economic dispatch. In Section 4, case studies are conducted based on the actual historical data. Conclusions are drawn in Section 5.
2 VPP economic dispatch
2.1 Framework and assumptions
The VPP leverages advanced information communication technology to aggregate and coordinate multiple distributed energy resources. The core concept of a VPP is aggregation and coordination. The following assumptions and simplifications are considered:
1) The VPP is assumed to have access to real-time data on generation, demand, and grid conditions. These data are necessary for the VPP to make decisions about power generation and distribution.
2) The VPP is assumed to have efficient and reliable control and communication systems to coordinate multiple distributed energy resources.
3) Thermal properties of heating, ventilation, and air-conditioning (HVAC), including heat generation, storage, and transfer, are assumed to happen only in thermal nodes.
Though raising concerns over the inaccuracy issues, reasonable assumptions and simplifications here could render the model a more computationally tractable and more practically meaningful analysis.
2.2 VPP supply–demand model
The VPP components comprise thermal power generation, photovoltaic generation, battery energy storage, the basic load, the power flexible load, and the temperature-adjustable load.
1) Thermal power generation unit
The VPP relies on small-scale thermal power units to maintain the flexibility and stability. The operation of thermal power generation unit in the VPP meets the output constraints and the ramp constraints:
where PTH,t and PTH,t-1 are the thermal power output at moments t and t−1, respectively; PTH,min, PTH,max, RTH,min, and RTH,max are minimum output power, maximum output power, ramp-down power, and ramp-up power of the thermal unit, respectively.
2) Power flexible loads
The power flexible loads, including LED lights with adjustable brightness or electric fans with adjustable speed, can participate in the VPP economic dispatch as a flexible load. In general, these loads can be adjusted within the rated capacity range. Their total power needs to meet the following constraints:
where Ppf,min and Ppf,max are minimum power and maximum power of these loads, respectively; Ppf,exp,t, Ppf,exp,T, and Ppf,exp are total power of the previous moment t, the total power of the whole time period T, and the minimum power to meet user needs, respectively.
3) Temperature flexible loads
Heating loads, including pitch heating, water heating, and HVAC, are taken as temperature-adjustable loads. The common feature of these heating loads is that the operating temperature t can be adjusted according to artificial settings. The working temperature t should be enforced to ensure the safe and reliable operation of the equipment:
where Tmin and Tmax are the lower and upper temperatures, respectively; a1 and a2 are the physical parameters which is jointly calculated via thermal capacities and resistances; THVAC,t-1 is the temperature of the last time moment t−1; Tout,t represents the current outside temperature; PHVAC,heat,t and PHVAC,cool,t denote the heating and cooling power of the air-conditioner, respectively; and aHVAC is the running state of the air-conditioner, where aHVAC = 1 and 0 indicate that the air-conditioner is in a state of heating and cooling, respectively.
4) Battery energy storage
Battery energy storage is an important energy storage, which has the advantages of strong environmental adaptability, short construction period, and convenient small-scale configuration. The charge and discharge states of the battery energy storage system must be limited to a certain range so as to avoid overcharge or discharge:
where SOCt and SOCt-1 are the current charge of the battery energy storage and the charge of the last time t−1, respectively; ηch, ηdis, PSOC,ch,t-1, and PSOC,dis,t-1 are charge efficiency, discharge efficiency, charge power, and discharge power, respectively;
In addition, the operation of the battery energy storage needs to meet the battery capacity limit:
where SOCmin and SOCmax represent the minimum and maximum battery capacities, respectively; PSOC,ch,max and PSOC,dis,max are the maximum charging and discharge power, respectively.
5) Power balance
With the regulation from energy storage and market buying/selling, power generation can be used to fulfill the power demand:
where Pbuy,t, PPV,t, and Psell,t are the purchased electricity power, photovoltaic power, and electricity sold, respectively.
2.3 Objective function
The objective function in the VPP economic dispatch consists of the coal consumption cost, battery degradation cost, air-conditioning discomfort cost, and buying/selling electricity cost.
1) Coal consumption cost
The coal consumption cost function of the thermal power unit can use the quadratic function related to the unit output:
where a, b, and c are the coefficients of the quadratic function; PTH,t is the power of thermal power. Through the linearization of the quadratic function, the cost function of the coal consumption is divided into M parts and denoted by
where Km,t is the slope of section m at time t of the coal consumption function after piecewise linearization; Ct is the coal consumption caused by starting up the thermal power unit and running at the minimum output PTH,min; and PTH,m,t represents the output power of the thermal power unit in the m section at the t period.
2) Battery degradation cost
The battery degradation cost can be represented by
where T,
3) Air-conditioning discomfort cost
While the constraints (Eqs 6–8) enforce the physical operation of air-conditioning, the discomfort level is introduced to measure the degree of satisfaction. The air-conditioning discomfort cost is related to the set temperature and current temperature.
where Tset and THVAC,t are set temperature and current time period temperature, respectively;
4) Buying and selling electricity costs
The buying and selling electricity costs are calculated as follows:
where abuy,t denotes the status of buying and selling electricity in the VPP, where abuy = 1 means that the VPP buys electricity from the market and abuy = 0 means that the VPP sells electricity to the market; λbuy,t and λsell,t are electricity buying price and electricity selling price, respectively.
The objective function is defined as
where λTH, λSOC, λHVAC, and λbuy represent the cost coefficients of the coal consumption, battery degradation, air-conditioning discomfort, and buying and selling electricity, respectively.
3 The GRUPPO-based optimal VPP economic dispatch
In this section, the designed GRUPPO-based optimal VPP economic dispatch will be presented. First, the VPP economic dispatch is expressed as a partially observable Markov decision process (POMDP). Then, a GRUPPO-based deep reinforcement learning approach is introduced to optimize the VPP economic dispatch.
3.1 POMDP for the VPP economic dispatch
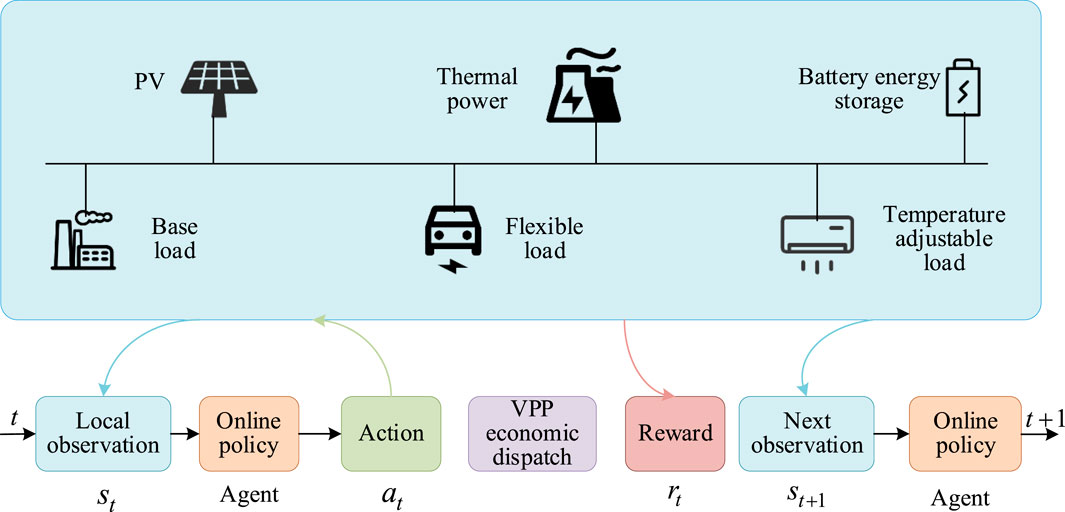
When using the reinforcement learning method to solve problems, MDP is usually used to describe the environment. MDP is characterized by the environment that is completely observable, and the current state can fully represent the process. That is, according to the current state, the next state can be deduced, the current state captures all relevant information from history, and the current state is a sufficient statistic for the future. However, for the VPP economic dispatch problem, the model contains random renewable energy. In the dispatch process, the next state of the VPP is not only completely determined by the current state but also depends on external random factors. The model state is not completely observable, and it is reasonable to express the VPP economic dispatch problem as a POMDP. Its structure diagram is shown in Figure 1. Generally, POMDP can be realized as a 7-tuple model {S, A, s, a, T, R, λ} (Wang et al., 2023).
The VPP model shown in Figure 1 represents the environment, and the agent is a hypothetical entity responsible for the VPP economic dispatch. The agent makes a corresponding decision based on the state of the environment, where the state and decision represent the observations and actions of the agent, respectively. The environment accepts the action of the agent and produces the corresponding change, which depends on the state transfer function T(st, at, χ). The environment gives the corresponding reward according to the agent action, and the reward received by the agent is related to the objective function of the VPP economic dispatch.
1) Environment
Considering the supply–demand uncertainties, the reinforcement learning environment operates according to the individual device models in Chapter 2 and also needs to satisfy their physical constraints in Chapter 2. These devices include thermal power generation, photovoltaic power generation, battery storage, base load, flexible load, and temperature-adjustable load.
2) Agent
The VPP dispatch agent is a deep neural network, which obtains the reward by constantly interacting with the environment and then updates the neural network parameters according to the reward. The interaction process between the agent and environment is to output the VPP dispatch instructions through the neural network and calculate the corresponding objective function value. The construction process of the specific agent will be described in detail in the next section.
3) State and observation
The agent needs to implement the corresponding action according to the environment state, which is the state space. For the VPP economic dispatch, the state observation space st
4) Action space
The action carried out by the agent according to the environment state is the action space. Lower-dimensional actions help the agent learn faster. Since battery charging and discharging cannot take place simultaneously, the charging and discharging of the battery are combined into a single action (instead of positive and negative). The same applies to the air-conditioner. For the economic dispatch task, the action space is expressed as follows:
5) State transition
Based on a policy π(at|st), the agent could calculate and perform an action after its current observation st. Afterward, based on the state transition function st+1 = T(st, at, χ), the environment proceeds to st+1, which is impacted by state st, actions at, and the environmental randomness χt.
Here, χt = [λbuy,t, λsell,t, THVAC,t, PPV,t, Pbase,t] indicates the exogenous states, which are unrelated to the agent’s actions and show model variability. In general, reinforcement learning could cope with such variabilities in a data-driven way. It does not rely on precise probability uncertainty distributions and updates state characteristics from the dataset. The state of χ′t = [PTH,t, SOCt, THVAC,t, Ppf,exp,t] has no association with the external environment but is associated only with the policy π(at|st). The state update is required to satisfy the system constraints.
6) Reward
The reward function is to drive the agent’s decision-making, and reward signals can be of any value (Canizo et al., 2019). The reward function is generally set in the range of 0–1 to enhance and ensure the convergence and optimality. Since the goal is to minimize the dispatch cost, the establishment function of each time step is designed as follows:
7) Objective
Each episode is divided into discrete time nodes t∈{0,1,2, … ,T}. The agent starts from an initial state s0. At each time point t, the agent moves to the next state st+1 based on the observation of the environment state st, action at, and an immediate reward rt. Based on this, the agent creates its trajectories of observations, actions, and rewards: τ = s0, a0, r0, s1, a1, r1 … , rT. In the POMDP, the agent seeks an optimal policy π(at|st) for the maximization of the discounted reward:
where γ∈[0,1] is the discount factor to decide the importance of immediate and future rewards.
3.2 GRUPPO-based deep reinforcement learning
In this subsection, a reinforcement learning method called GRUPPO is used for optimizing the VPP economic dispatch based on the POMDP. The GRUPPO approach includes the following three crucial steps:
1) Update the dispatch policy via a standard PPO algorithm
PPO, as a policy gradient algorithm, has been employed in a multitude of optimization models. Generally, PPO is featured by an actor–critic network and is able to handle high-dimensional continuous spaces. Through the Gaussian distribution, a stochastic policy πθ (at|st) of the actor network could be developed to feature the continuous action spaces in (24). It gives the standard deviation σ and mean μ, sampling the action at on st for all VPP economic dispatch agents. The PPO renews the policy πθ (at|st), maximizing the following clipped surrogate.
where the product of ζt and Ât is the policy gradient; ζt is the probability ratio clipped by clip(.). ε∈[0,1] is used to limit the policy gradient update against its old version, if ζt is beyond [1−ε, 1+ε]. This technique ensures that the policy gradient is updated to a stable area.
ζt in the PPO clipped policy (29) is expressed as follows:
where πθ (at|st) and πθold (at|st) are the current and old policies, respectively. The advantage function
where Vϕ(s) denotes the state-value function approximated by a critic network parameterized by ϕ; γ ∈ [0,1] and λ ∈ [0,1].
2) Introduce GRU into PPO to consider the time characteristics
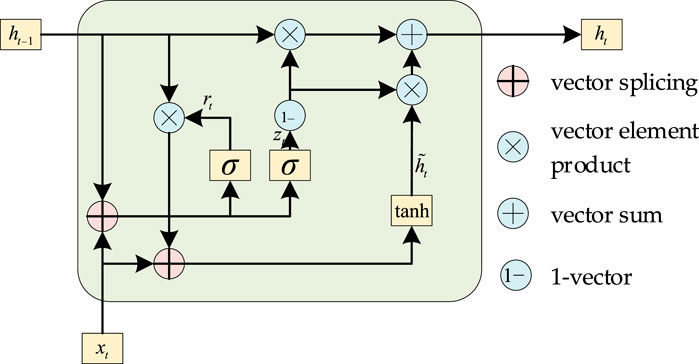
Since the proposed VPP economic dispatch model is partially observable, the Markov property is not valid. Compared with MDP, the next state in a POMDP is not completely determined by the present observations and actions (Ma et al., 2023). Conversely, the complete history of the observation sequences ought to be taken into account. By adding a GRU layer before the multi-layer perceptron (MLP) to concisely capture the history, recursion is introduced to deal with the non-Markovian nature of the POMDP.
GRUs are well suited for capturing and modeling time series characteristics due to their ability to control information flow using gates and adapt to long-term dependencies. GRUs comprise two gates: the reset gate (r) and the update gate (z). The reset gate controls how much of the previous hidden state is passed on to the next time step, while the update gate determines how much of the new input information is incorporated into the updated hidden state. The reset gate effectively “forgets” or disregards part of the previous state, allowing the network to focus on relevant information and adapt to changing patterns in the time series. By using gates to control the flow of information, GRUs can handle long sequences more effectively than traditional RNNs. They are less likely to suffer from exploding or vanishing gradients, which can be a problem for long sequences. GRUs also have fewer parameters than some other RNN variants, making them more efficient and less prone to overfitting. When applied to a time series analysis, GRUs can capture dependencies across time steps and generate meaningful representations of the sequence data. GRUs can also be combined with other techniques, such as attention mechanisms, to further improve their performance in specific tasks.
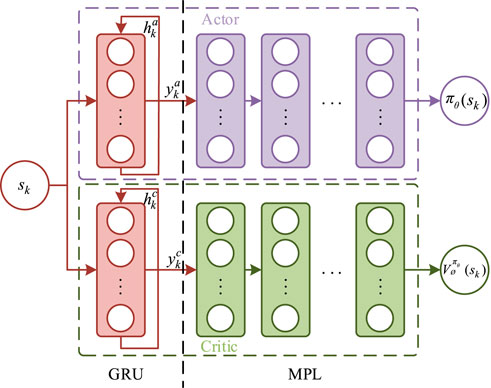
The GRU and actor–critic networks are given in Figures 2, 3.
where rt is the reset gate; zt is the update gate; Wr, Ur, Wz, Uz, Wc, and Uc are neural network weight matrices; σ is the sigmoid activation function; and
The leveraged GRUPPO method is used to apply the PPO algorithm together with the recurrent neural network. The actor and critic networks include GRU and MLP layers. The network structure is regulated via tuning the amounts of network layers and neurons. For the activation function, tanh is chosen in the GRU layer and the output layer of MLP. In other layers of MLP, ReLU is used due to its fast convergence and low computational complexity. However, the phenomenon of gradient disappearance and gradient explosion will occur when the ReLU is used directly in the experiment. In order to solve the problem of gradient disappearance and gradient explosion caused by the ReLU activation function, the layer is standardized to the neural network. In the actual experiment, this operation can effectively alleviate the phenomenon of gradient disappearance and gradient explosion so that the neural network can be trained normally.
The VPP dispatch problem using the PPO algorithm is realized through the neural network. The actor network uses the Gaussian strategy to output mean and variance.
where a represents the action taken in state s; θ represents the policy function parameters; μθ(s) represents the average value of action a in state s; and σθ(s) represents the standard deviation of action a in state s. The real action is randomly sampled according to the mean and standard deviation of the actor network output. The other network is the critic network, which outputs the value of the state according to the current state of the VPP.
3) Construct the safety layer to meet the VPP model constraints
The training reinforcement learning algorithm is an unconstrained optimization algorithm via deep neural networks, which disregards model constraints. Deploying the reinforcement learning actions to the VPP would violate the constraints, and thus a safety layer is introduced. It shows that the calculated reinforcement learning actions would be slightly updated (only when facing system safety).
Safe operation is the premise of VPP economic dispatch tasks. For the VPP economic dispatch, the physical constraints are to ensure the normal operation, while the illegal actions will violate the constraints. In general, there are two ways to ensure the constraint satisfaction of the action output. The first method is to add the penalty terms for the constraint violations to the reward so that the agent can avoid making illegal action. The other method is to set the agent to take action within the allowable range. The first step is to calculate the boundary between the current state and the constraint. The action lower boundary a− and upper boundary a+ are calculated based on the current state st and constraints as follows:
The second step is to cut the action according to the clip function. a is a constant value when the action meets the above range. When action a exceeds the boundary, the clip function is used to limit the action a within its boundary.
For the GRUPPO training process, the agent is equipped with πθ (a|s) to interact with the environment. Then, the trajectory τ is collected and utilized to evaluate the discounted reward
According to the PPO algorithm, the corresponding gradient formula can be derived. Ât can also be computed with the state-value function Vϕ(s) and trajectory τ. The actor network can be trained while maximizing
Accordingly, the critic network of GRUPPO can be trained by minimizing the following loss function of the mean-squared error:
A weighting update for the actor and critic networks is
where αθ and αϕ are the learning rates of actor and critic networks, respectively.
Finally, the pseudo-code of GRUPPO is given in Algorithm 1. First of all, GRUPPO initializes the agent’s policy network and value function network. The agent collects empirical data by interacting with the environment and stores these data for subsequent training. Then, the value function network is used to compute the advantage function of the agent. Finally, the agent’s strategy network is updated until a satisfactory level of performance is reached.
Algorithm 1.GRUPPO for the agent.
1: Initialize θ, ϕ for the actor–critic network
2: Set learning rates αθ, αϕ
3: For episode (i.e., an operating day)
4: Initialize VPP state s0
5: For the VPP agent, create a new trajectory τ = []
6: For each time step (e.g., 1 hour)
7: Chooses PPO action at according to observation st via the policyπθ (a|s)
8: Correct action at values based on the security layer
9: Observes reward rts and the next observation st+1
10: Stores the sample experience into trajectory τ + = [st, ats, rts]
11: Updates observation st → st+1 for the VPP agent
12: End for
13: Approximates discounted reward-to-go
14: Updates the parameters θ, ϕ of networks in (44)–(45)
15: End for
3.3 Multi-agent framework for GRUPPO
When using a single agent for the VPP economic dispatch, the stable operation can be drastically affected by agent failure or a new plug-and-play framework. The motivation behind the multi-agent framework is to harness the power of autonomous agents and enable collaborative problem-solving in VPP systems. By distributing tasks among multiple agents, the multi-agent framework enhances scalability, robustness, adaptability, and coordination. They allow for parallel processing, fault-tolerance, and efficient utilization of resources, making them suitable for various domains and dynamic environments. The multi-agent-based GRUPPO strategy can be developed based on the above GRUPPO approach. In the multi-agent GRUPPO method, each agent is directly responsible for its own device or area, which makes it easy to expand. Here, the detailed implementation method of the multi-agent GRUPPO is given as follows:
where st represents the overall observation value of the agent at time t; si,t represents the observation value of the i agent at time t.
The training steps for the multi-agent framework differ from those of the single-agent framework, specifically in the computation of gradients and rewards. The reward function needs to compute the overall value since multiple agents are included. During training, the actor and critic network update of each agent i is
where ζt, Ât, and Vϕ(s) represent probability ratio, advantage function, and state-value function, respectively; αθ and αϕ denote the learning rates of actor and critic networks of the ith device, respectively.
Finally, the pseudo-code of multi-agent GRUPPO is given in Algorithm 2. First of all, multi-agent GRUPPO initializes the policy network and the value function network of each agent. The agents collect experience data by interacting with the environment and store these data in a shared experience pool so that other agents can access and learn from it. Then, centralized-distributed training is performed, where agents perform training locally but share global information to facilitate better collaborative learning. A value function network is utilized to compute the advantage function for each agent. Finally, the policy network is updated for each agent until a satisfactory level of performance is reached.
Algorithm 2.Multi-agent GRUPPO for agents.
Initialize θi, ϕi for the actor–critic network
Set learning rates αθ, αϕ
For episode (i.e., an operating day)
Initialize both the local observation si,0 and global state s0
For each time step (e.g., 1 hour)
For VPP agents, i = 1 to N
Chooses PPO action ai,t according to observation si,t via the policy πθi (a|s)
Correct action ai,t of all agent values based on the security layer
Observes reward rts and the next observation si,t+1
Stores the sample experience into trajectory τi + = [si,t, ai,ts, rts]
End for
Updates observation si,t → si,t+1 for the VPP agent i
End for
For VPP agents, i = 1 to N
Approximates discounted reward-to-go
Updates the parameters θi, ϕi of networks in (49)–(50)
End for
End for
4 Case studies
In this section, case studies are conducted to show the effectiveness and advantages of the proposed GRUPPO approach for the VPP economic dispatch. The simulation tests are undertaken based on the actual historical data, which are compared with the other two schemes: the PPO scheme and the non-economic dispatch scheme. The detailed parameters of electrical generation, storage, and consumption can be found in Xu et al. (2020), Wang et al. (2023), and Xu et al. (2023).
4.1 Comparison of the convergence and stability performance
In order to compare the stability and convergence, the GRUPPO and PPO algorithms are implemented to optimize the VPP economic dispatch. In order to avoid the randomness of the test results, 10 different random seeds are used to conduct 1,000 rounds. In order to capture the uncertainties of PV power and base load, the Monte Carlo method is implemented to obtain 1,000 scenarios for simulation, where forecasting errors were assumed to follow a normal distribution function. Subsequently, the optimization results of 10 groups of economic dispatch are recorded and depicted in Figure 4. The mean variances of the corresponding 1,000 rounds are also calculated to further explain the differences in stability and convergence performance.
It can be seen in Figure 4 that both methods can achieve almost stable rewards after approximately 30 rounds. However, the reward in the PPO scheme shows a significant increase after 420 rounds in the test, i.e., from approximately −4,600 to −4,900. In contrast, the reward of the proposed GRUPPO still fluctuates up and down near −4,600. Thus, it can be concluded that the GRUPPO approach has better convergence and is more stable to optimize the VPP economic dispatch. These results also illustrate that the introduction of the GRU network into PPO can fully consider the historical time series information and effectively improve the performance of the PPO algorithm.
4.2 Comparison of the VPP economic dispatch
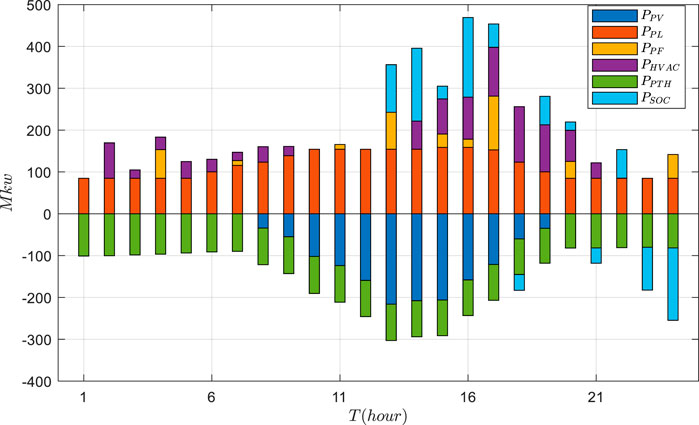
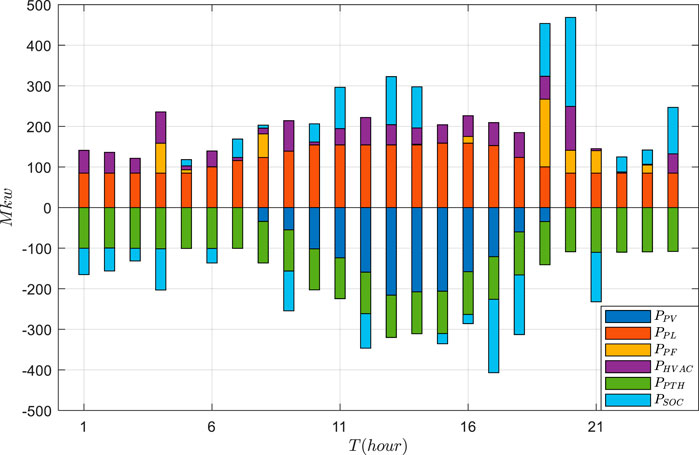
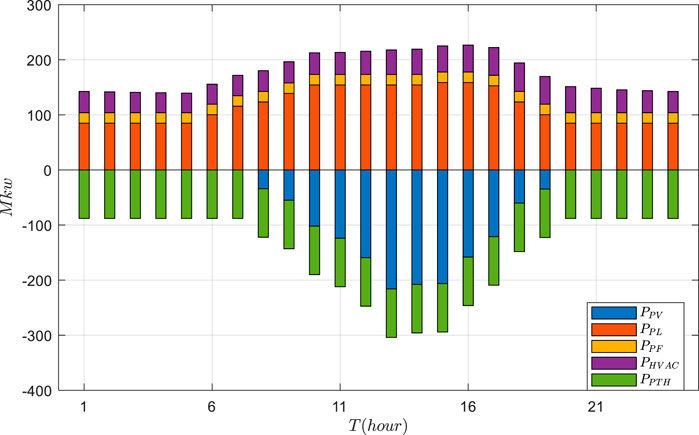
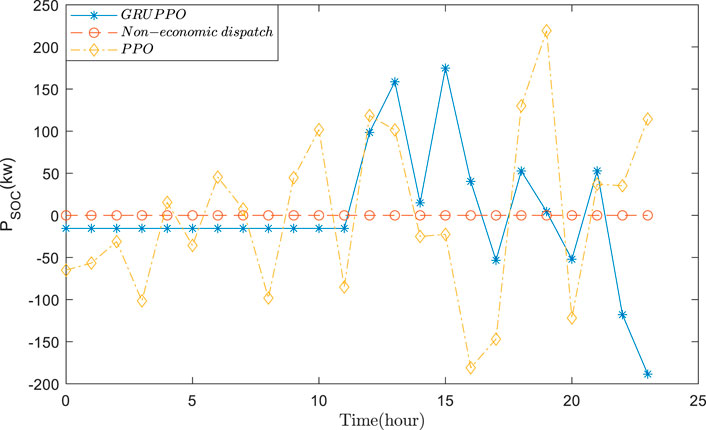
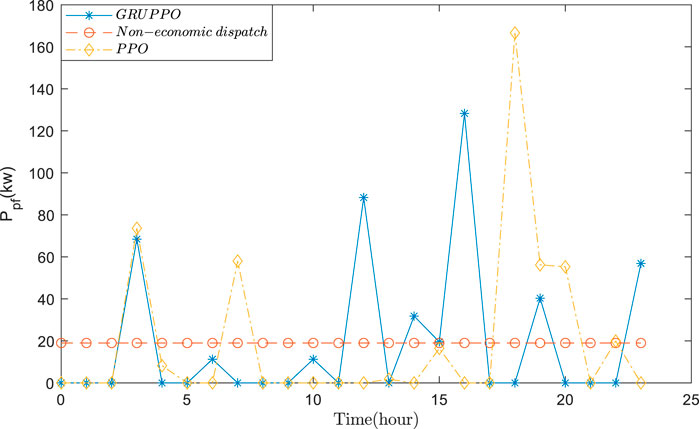
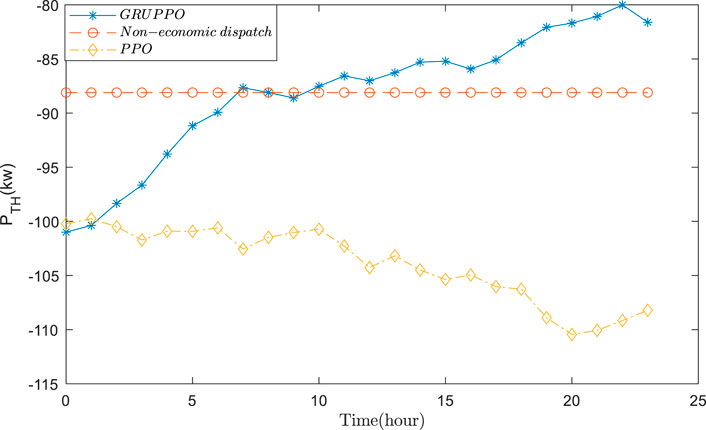
Based on the actual data, the VPP economic dispatch results are tested using GRUPPO and PPO approaches. The general supply–demand results under three schemes are shown in Figures 5–7, and Figures 8–11 depict the detailed operational results of VPP components. Compared with other two schemes, the battery energy storage under the GRUPPO approach can appropriately store the excess photovoltaic power for later release. It can be observed that the flexible load of the VPP can increase its demand as the PV generation increases. In contrast, in the non-economic dispatch scenario, these loads are evenly distributed over the 24-h period. Although the PPO method can also dispatch all components, the flexible loads do not exhibit higher demand during the high PV generation for 10–15 h. This would increase the pressure on the thermal power units and the power purchase cost.
It can be seen in Figure 10 that the power generation of the thermal power units in the GRUPPO method shows more intense fluctuations compared to that in the other two methods. This indicates that the proposed method can better adjust the thermal power generation to follow the changes in PV power, thereby reducing the VPP operating costs. Moreover, it can be observed from Figure 11 that the HVAC power increases with the increase in PV power. In contrast, in the absence of the economic dispatch, the HVAC power changes with the daytime temperature. Although PPO can also dispatch the HVAC power to follow the power fluctuation, its sensitivity is lower than that of the GRUPPO method.
The overall operating costs of three schemes are 4,322$, 4,431$, and 4,620$, respectively. It is evident that the operating cost of the GRUPPO method is the lowest. Specifically, compared to the PPO method and non-economic dispatch scheme, the proposed GRUPPO method reduces the operating costs by 2.4% and 6.5%, respectively. Overall, these results demonstrate the effectiveness and superiority of the proposed GRUPPO method in reducing the VPP economic dispatch costs.
5 Conclusion
This paper proposed a deep reinforcement learning-based VPP economic dispatch framework. The VPP economic dispatch is captured via a POMDP, which is then solved using a novel GRUPPO approach. The findings of this paper are summarized as follows:
(1) Compared with PPO, the proposed GRUPPO approach can make full use of the time series characteristics, improving its convergence and stability performance.
(2) Based on the POMDP, GRUPPO learns to make decisions based on partial information, which is suitable to handle real-world optimization problems with uncertainty.
(3) Both continuous and discrete actions can be effectively handled using the proposed GRUPPO approach, thereby achieving a maximum cost reduction of 6.5%.
(4) The GRUPPO strategy can outperform other methods in higher economy and scalability, exhibiting huge development and application potentialities in the high-renewable modern power system.
Electrical market development has become an inevitable trend under the background of economic globalization and industrial revolution. Further research would focus on strategic offering of the VPP in the electrical market.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
ZG: investigation, project administration, writing–original draft, writing–review and editing, and conceptualization. WK: formal analysis, funding acquisition, methodology, writing–original draft, writing–review and editing, and conceptualization. XC: conceptualization, methodology, visualization, writing–original draft, and writing–review and editing. SG: data curation, methodology, writing–original draft, and writing–review and editing. ZL: conceptualization, formal analysis, investigation, writing–original draft, and writing–review and editing. DH: conceptualization, formal analysis, investigation, methodology, writing–original draft, writing–review and editing, and resources. SS: writing–original draft, writing–review and editing, investigation, methodology, software, validation, and visualization. X-CS: conceptualization, investigation, supervision, writing–original draft, writing–review and editing, and validation.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The authors gratefully acknowledge the support of the Hubei Provincial Natural Science Foundation of China under Grant 2022CFB907.
Conflict of interest
Authors ZG, WK, XC, SG, and ZL were employed by Hubei Branch of State Power Investment Group Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bui, V., Hussain, A., and Kim, H. M. (2020). Double deep $Q$ -Learning-Based distributed operation of battery energy storage system considering uncertainties. IEEE Trans. Smart Grid 11, 457–469. doi:10.1109/TSG.2019.2924025
Canizo, M., Triguero, I., Conde, A., and Onieva, E. (2019). Multi-head CNN–RNN for multi-time series anomaly detection: an industrial case study. Neurocomputing 363, 246–260. doi:10.1016/j.neucom.2019.07.034
Chen, G., and Li, J. (2018). A fully distributed ADMM-based dispatch approach for virtual power plant problems. Appl. Math. Model. 58, 300–312. doi:10.1016/j.apm.2017.06.010
Du, L., Zhang, L., Tian, X., and Lei, J. (2018). Efficient forecasting scheme and optimal delivery approach of energy for the energy Internet. IEEE Access 6, 15026–15038. doi:10.1109/ACCESS.2018.2812211
Etherden, N., Vyatkin, V., and Bollen, M. H. J. (2015). Virtual power plant for grid services using IEC 61850. IEEE Trans. Ind. Inf. 12, 437–447. doi:10.1109/TII.2015.2414354
Gough, M., Santos, S. F., Lotfi, M., Javadi, M. S., Osorio, G. J., Ashraf, P., et al. (2022). Operation of a technical virtual power plant considering diverse distributed energy resources. IEEE Trans. Ind. Appl. 58, 2547–2558. doi:10.1109/TIA.2022.3143479
Gronauer, S., and Diepold, K. (2023). Multi-agent deep reinforcement learning: a survey. Artif. Intell. Rev. 55, 895–943. doi:10.1007/s10462-021-09996-w
Hua, H., Qin, Y., Hao, C., and Cao, J. (2019). Optimal energy management strategies for energy Internet via deep reinforcement learning approach. Appl. Energy. 239, 598–609. doi:10.1016/j.apenergy.2019.01.145
HuangYangZhang, S. M. C., Gao, Y., and Yun, J. (2021). A control strategy based on deep reinforcement learning under the combined wind-solar storage system. IEEE Trans. Ind. Appl. 57, 6547–6558. doi:10.1109/TIA.2021.3105497
Koraki, D., and Strunz, K. (2017). Wind and solar power integration in electricity markets and distribution networks through service-centric virtual power plants. IEEE Trans. Power Syst. 33, 473–485. doi:10.1109/TPWRS.2017.2710481
Książek, W., Abdar, M., Acharya, U. R., and Pławiak, P. (2019). A novel machine learning approach for early detection of hepatocellular carcinoma patients. Cogn. Syst. Res. 54, 116–127. doi:10.1016/j.cogsys.2018.12.001
Lin, L., Guan, X., Peng, Y., Wang, N., Maharjan, S., and Ohtsuki, T. (2020). Deep reinforcement learning for economic dispatch of virtual power plant in internet of energy. IEEE Internet Things J. 7, 6288–6301. doi:10.1109/JIOT.2020.2966232
Liu, L., Xu, D., and Lam, C. S. (2023). Two-layer management of HVAC-based multi-energy buildings under proactive demand response of fast/slow-charging EVs. Energy Convers. Manag. 289, 117208. doi:10.1016/j.enconman.2023.117208
Liu, W., Zhang, D., Wang, X., and Hou, J. (2023). A decision making strategy for generating unit tripping under emergency circumstances based on deep reinforcement learning. Proc. CSEE 38, 109–119. doi:10.13334/j.0258-8013.pcsee.171747
Liu, Y. Y., Li, M., Lian, H., Tang, X., Liu, C., and Jiang, C. (2018). Optimal dispatch of virtual power plant using interval and deterministic combined optimization. Int. J. Electr. Power Energy Syst. 102, 235–244. doi:10.1016/j.ijepes.2018.04.011
Lu, R., and Hong, S. H. (2019). Incentive-based demand response for smart grid with reinforcement learning and deep neural network. Appl. Energy. 236, 937–949. doi:10.1016/j.apenergy.2018.12.061
Ma, Y., Hu, Z., and Song, Y. (2023). A Reinforcement learning based coordinated but differentiated load frequency control method with heterogeneous frequency regulation resources. IEEE Trans. Power Syst. 39, 2239–2250. doi:10.1109/TPWRS.2023.3262543
Mashhour, E., and Moghaddas-Tafreshi, S. M. (2010). Bidding strategy of virtual power plant for participating in energy and spinning reserve markets—Part I: problem formulation. IEEE Trans. Power Syst. 26 (2), 949–956. doi:10.1109/TPWRS.2010.2070884
Naveen, R., Revankar, P. P., and Rajanna, S. (2020). Integration of renewable energy systems for optimal energy needs-a review. Int. J. Energy Res. 10, 727–742. doi:10.20508/ijrer.v10i2.10571.g7944
Thanh, P., Cho, M., Chang, C. L., and Chen, M. J. (2022). Short-term three-phase load prediction with advanced metering infrastructure data in smart solar microgrid based convolution neural network bidirectional gated recurrent unit. IEEE Access 10, 68686–68699. doi:10.1109/ACCESS.2022.3185747
Wang, Y., Qiu, D., Sun, X., Bie, Z., and Strbac, G. (2023). Coordinating multi-energy microgrids for integrated energy system resilience: a multi-task learning approach. IEEE Trans. Sustain. Energy, 1–18. doi:10.1109/TSTE.2023.3317133
Xu, D., Wu, Q., Zhou, B., Bai, L., and Huang, S. (2019). Distributed multi-energy operation of coupled electricity, heating, and natural gas networks. IEEE Trans. Sustain. Energy 11, 2457–2469. doi:10.1109/TSTE.2019.2961432
Xu, D., Zhou, B., Wu, Q., Chung, C. Y., Huang, S., Chen, S., et al. (2020). Integrated modelling and enhanced utilization of power-to-ammonia for high renewable penetrated multi-energy systems. IEEE Trans. Power Syst. 35, 4769–4780. doi:10.1109/TPWRS.2020.2989533
Xu, D., Zhou, B., Liu, N., Wu, Q., Voropai, N., Li, C., et al. (2021). Peer-to-peer multienergy and communication resource trading for interconnected microgrids. IEEE Trans. Ind. Inf. 17, 2522–2533. doi:10.1109/TII.2020.3000906
Xu, D., Zhong, F., Bai, Z., Wu, Z., Yang, X., and Gao, M. (2023). Real-time multi-energy demand response for high-renewable buildings. Energy Build. 281, 112764. doi:10.1016/j.enbuild.2022.112764
Yang, S., Tan, S., and Xu, J. X. (2013). Consensus based approach for economic dispatch problem in a smart grid. IEEE Trans. Power Syst. 28, 4416–4426. doi:10.1109/TPWRS.2013.2271640
Zhang, Y., Ai, X., Wen, J., Fang, J., and He, H. (2018). Data-adaptive robust optimization method for the economic dispatch of active distribution networks. IEEE Trans. Smart Grid 10 (4), 3791–3800. doi:10.1109/TSG.2018.2834952
Keywords: virtual power plant, demand response, deep reinforcement learning, gated recurrent unit, proximal policy optimization
Citation: Gao Z, Kang W, Chen X, Gong S, Liu Z, He D, Shi S and Shangguan X-C (2024) Optimal economic dispatch of a virtual power plant based on gated recurrent unit proximal policy optimization. Front. Energy Res. 12:1357406. doi: 10.3389/fenrg.2024.1357406
Received: 18 December 2023; Accepted: 15 January 2024;
Published: 01 February 2024.
Edited by:
Kaiping Qu, China University of Mining and Technology, ChinaReviewed by:
Weiyu Wang, Changsha University of Science and Technology, ChinaCao Yingping, Hong Kong Polytechnic University, Hong Kong SAR, China
Copyright © 2024 Gao, Kang, Chen, Gong, Liu, He, Shi and Shangguan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xing-Chen Shangguan, c3RhckBjdWcuZWR1LmNu
 Zhiping Gao1
Zhiping Gao1 Shen Shi
Shen Shi Xing-Chen Shangguan
Xing-Chen Shangguan