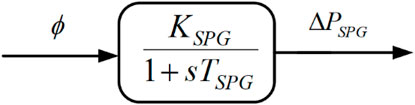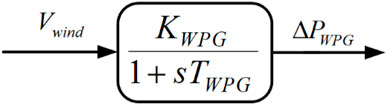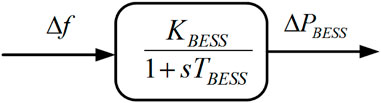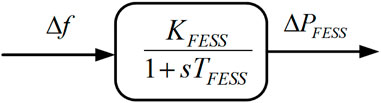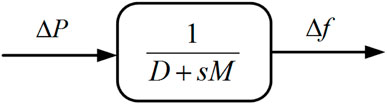Student psychology-based optimization-tuned cascaded controller for frequency regulation of a microgrid

This paper presents a student psychology-based optimization (SPBO)-tuned cascaded control scheme for an interconnected microgrid scenario. Generally, the different distributed energy sources are assembled to form the microgrid architecture, and the majority of the sources are environment-dependent. Furthermore, the intermittent power output from these sources causes a generation–load power mismatch, resulting in power and frequency oscillations. In this regard, the proposed student psychology-based optimization-tuned cascaded controller tackles the power-frequency mismatch issues under an interconnected microgrid scenario. Additionally, an improved power tie-line model is introduced considering the effect of line resistance in the microgrid scenario, as line resistance plays a significant role in power flow between the control areas. In addition, numerous case studies are investigated to examine the effectiveness of the proposed design methodology under the suggested control scheme. Furthermore, a detailed performance analysis is carried out considering the proposed model operation under a 12-node radial distribution network in order to examine the system compatibility in a practical distribution network. The obtained results ensure superior performances in terms of the system’s overall peak over/undershoots, oscillations, and settling time utilizing the proposed controller under the improved microgrid scenario.

1 Introduction

Nowadays, modern power system scenarios utilize distributed energy resources (DERs) extensively. This highly emerging concept of DERs involves various renewable energy sources (RESs) and energy storage systems (ESSs) for seamless power flow in any power system network (Biswas et al., 2023). Accordingly, the utilization of the microgrid is gaining enormous popularity where the load power demand is fulfilled by the aggregated power from different DER units. In practice, the microgrids can operate either in an islanded/isolated mode or grid-connected mode for seamless power distribution amongst the loads (Shiva et al., 2022). In connection with that, it is observed that the output power from solar power generators (SPGs) and wind power generators (WPGs) is intermittent and depends on the environmental conditions. This intermittency further results in a power mismatch between the generated and demanded power. As a consequence, frequency and tie-line power oscillations are very common among DER-based microgrid scenarios. In this context, automatic generation control (AGC) plays a crucial role in regulating the frequency and tie-line power oscillations under DER-based microgrid systems (Mishra et al., 2023). In recent times, diesel engine generators (DEGs), battery energy storage systems (BESSs), and flywheel energy storage systems (FESSs) have been vigorously utilized along with SPGs and WPGs for proper system operations. Here, the roles of BESS and FESS are as ESSs, and these are mostly utilized to accomplish primary frequency control (PFC) operations in power systems. However, these units are less effective in making the system respond to the steady-state values. Furthermore, DEGs are very suitable for secondary frequency control (SFC) operations and help in reaching the tie-line power and frequency parameters to their steady-state value (Ranjan and Shankar, 2022). The transformation of the traditional power system model to unconventional microgrid scenarios motivates the authors to research and examine the effects of various power system elements on system parameter responses.

In the last few decades, several control strategies, including different optimization techniques, have been incorporated to improve the AGC performance under microgrid systems, both in islanded and grid-connected scenarios (Khan et al., 2023). In the following section, various control topologies are discussed, considering the islanded microgrid scenario. Furthermore, the discussion is extended to the interconnected microgrid scenario. The available controller designs for an islanded microgrid scenario are discussed as follows: a quasi-opposition-based harmonic search (QOHS)-optimized, fuzzy logic-based fractional-order proportional–integral derivative (FOPID) control scheme is incorporated to enhance the AGC performance under frequent load perturbations (Mahto et al., 2021). Moth flame optimization (MFO)-based fuzzy proportional–integral derivative (PID) controller is incorporated to enhance system performance (Sanki et al., 2021b). The power system instability due to the continuous frequency fluctuations is addressed by considering the whale optimization algorithm (WOA)-tuned fuzzy cascaded proportional–integral proportional–derivative (PI-PD) controller (Sahu et al., 2022). In this article, the WOA is adopted to evaluate the control parameters. Detailed investigations are carried out considering the effect of the sliding mode controller in the islanded power system scenario to address the AGC issue (Izadkhast et al., 2014; Khooban, 2017). Furthermore, a generalized active disturbance rejection control (GADRC) topology is proposed, considering the effect of communication delay to manage frequency fluctuations (Jain and Hote, 2021). Bevrani et al. (2012) addressed the particle swarm optimization (PSO)-based proportional–integral (PI) control scheme to address the frequency control aspect under a microgrid scenario.

Similar to the islanded microgrid scenario, several control topologies are implemented for the interconnected power system scenarios to perform AGC operations (Francis and Chidambaram, 2015; Hasanien, 2018; Chintu et al., 2022). A non-integer FOPID control is proposed for a two-area power system where the control parameters are estimated using the water cycle algorithm (WCA). In this work, a sensitivity analysis is carried out, considering rigorous load perturbations to the system (Latif et al., 2019b). The PSO-optimized PID-PD control scheme with detailed control system analysis is presented by (Tah and Das, 2016) and an imperialist competitive algorithm (ICA)-tuned cascaded fuzzy fractional-order integral derivative (CF-FOID) is proposed to achieve an improved frequency control scheme for a two-area interconnected power system model (Arya, 2020). A secondary frequency control scheme is proposed where the biogeography-based optimization (BBO) technique is utilized (Rahman et al., 2017). Another article proposes a dragonfly algorithm (DA)-optimized three degree of freedom (3 DOF)-based PID control scheme (Guha et al., 2018) in AGC operation. A robust dual-integral mode control (DL-IMC) topology for a multi-area hybrid power system model is proposed by Sonker et al. (2019). The proposed controller is capable of addressing issues like disturbance rejection and oscillation reduction. A fuzzy-PID with filter (PIDF)-based controller is implemented considering the marine predator algorithm (MPA) technique under an interconnected microgrid scenario to enhance the power system performance (Yakout et al., 2021b). A combined operation of fuzzy FOPID and tilt-integral derivative (TID) controllers is presented under a hybrid multi-area power system model considering the wild horse optimizer (WHO) algorithm (Ali et al., 2022). Furthermore, the virtual generation ecosystem control (VGEC) scheme is proposed for a multi-area power system model to achieve faster AGC under different disturbances. In addition, special attention is given to the implementation of robust control topologies, cost minimization, and achieving a faster convergence rate (Xi et al., 2020). A comparative analysis between PI, PID with filter (PIDN) and proportional fractional-order integral derivative (PFOID) under a multi-area power system is presented to examine the dynamic performance under different power system disturbances. Here, PSO, firefly optimization, WOA, and butterfly optimization algorithm (BOA) are utilized separately to evaluate the controller gain parameters to compare their performance and convergence rate (Latif et al., 2019a). In the earlier research works, several approaches can be observed considering cascaded control schemes. It is noteworthy to mention that the cascaded controller is very efficient in addressing the frequency and power oscillation issues very effectively (Singh and Zaheeruddin, 2021; Zaheeruddin et al., 2022; Singh and Arya, 2023). In most cases, the cascaded control scheme is utilized, considering two loops combined to improve the system’s performance (Ali et al., 2021; Yakout et al., 2021a; Çelik et al., 2021; Choudhary et al., 2022; Singh et al., 2023).

Based on the above discussion, it can be illustrated that, to date, several controllers in the presence of different metaheuristic techniques have been proposed to handle frequency fluctuations and tie-line power deviation in single- and multi-area microgrid systems. Several cascaded control topologies are also adopted to improve performance under different microgrid scenarios. Accordingly, it is noteworthy that the objective function computation time will increase with the incremental gain parameter numbers. Furthermore, several power system configurations have been adopted, so far considering DER-based AGC operations and excluding the effect of line resistance in the power tie-line model. However, it has been observed that the major utilization of microgrids encompasses medium- and low-voltage applications. In such microgrid scenarios, power loss due to line resistance between the control areas cannot be excluded. According to the critical literature review and research gaps, the major contributions of this article are framed and structured as follows:

• An improved two-area microgrid model is proposed considering the effect of R_Ln. Furthermore, this research work explores a DER-integrated microgrid considering a high R_Ln/X_Ln ratio along with a smaller power angle “δ” compared to conventional power system scenarios.

• A stability margin analysis is carried out such that the gain parameter values should lie under the stable system region. Based on the gain parameter value ranges, the initialization process was conducted to find out the minimum objective function.

• A cascaded proportional–integral–proportional derivative (CPIPD) controller (with four tunable parameters and a simplified structure) is proposed in order to achieve the desired dynamic performance of the considered microgrid under different power system scenarios. Furthermore, this work utilizes the student psychology-based optimization (SPBO) technique to tune the gain parameters of the proposed controller, due to its faster convergence than the other state-of-the-art methods in the presence of an improved power tie-line model.

• Numerous simulation case studies are investigated to examine the performance of the proposed controller under various power system scenarios. Additionally, the system performance analysis is carried out with and without considering the effect of R_Ln in order to validate the power tie-line modification.

• Detailed investigations are conducted considering the proposed two-area microgrid model in a 12-node radial distribution network in order to validate its performance under a realistic distribution scenario.

Based on the above discussion, the configuration of the paper is presented as follows: the detailed modeling of the microgrid with various power generators is presented in Section 2. Section 3 presents the tie-line modeling between the interconnecting areas of the considered microgrid. The proposed CPIPD controller design aspects are furnished in Section 4, followed by Section 5, where the various simulation result analyses are illustrated. Finally, the concluding remarks of this proposed work are furnished in Section 6.

2 Modeling of different components of the interconnected microgrid scenario

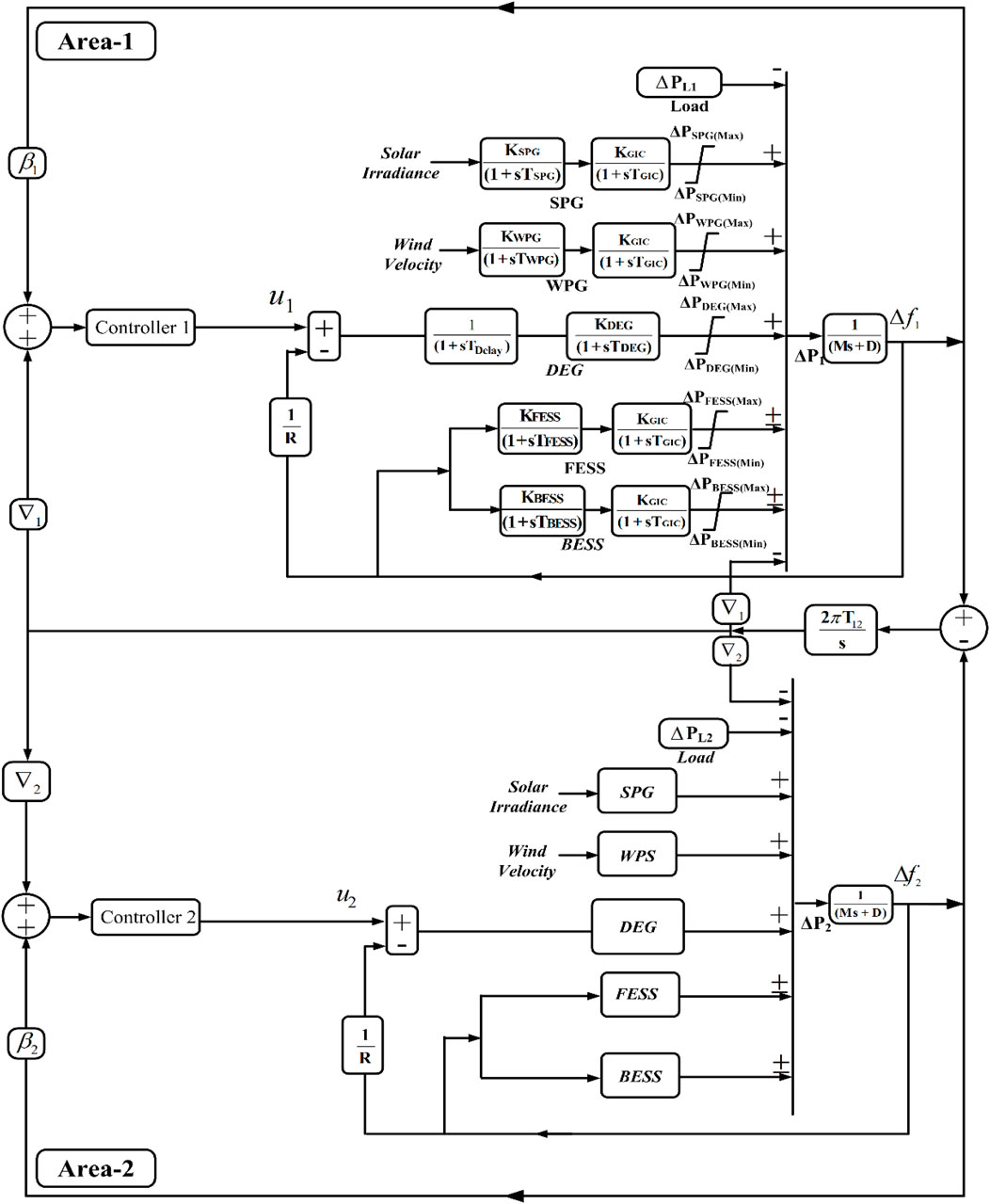
This section illustrates the modeling of a two-area microgrid system comprised of different power generators. In the considered power system, each area consists of an SPG, WPG, DEG, FESS, and BESS. In addition, a first-order transfer function is utilized to resemble grid-integrated connections (GICs). Generally, power electronics converters, line transformers, and interconnected power lines are presented by GICs. The complete schematic presentation of a two-area microgrid scenario is depicted in Figure 1. This power system model is utilized to investigate the detailed system operation. Furthermore, the nominal loading condition is considered 1% step load perturbation (SLP) with 80% loading. First-order transfer function models are utilized to represent the DER units in order to investigate the effect of their dynamics on the overall system performance. The values of each parameter and the time constants are presented in the Appendix. The detailed modeling of the power generators is presented in the following section.

Figure 1

Figure 1. Schematic diagram of the linearized two-area interconnected microgrid model.

2.1 Solar power generator

Among all the types of RESs, SPG is the most common and committed eco-friendly energy resource. In the past few years, rigorous research and development related to SPG units has reduced the per kilowatt/hour generation cost. Furthermore, the extensive capability of SPG units makes them a deserving alternative to traditional power generators. The power generation from SPG highly depends on solar irradiance and ambient temperature (Sanki and Basu, 2018; Sahu et al., 2022). The basic equation of SPG-generated power can be presented as Eq. 1:

$P_{SPG}=\eta \varphi A\left\{1-0.005\left(T_a+25\right)\right\}.(1)$

According to the small-signal stability analysis, control system engineers have the freedom to investigate any system dynamics using the transfer function model. The considered linearized transfer function of SPGs is depicted in Figure 2.

Figure 2

Figure 2. Linearized transfer function model of the SPG unit.

2.2 Wind power generator

WPGs are evolving as one of the most promising clean power producers, along with SPGs. The progressive development of WPGs has already crossed the global utilization threshold of 21%. These DERs convert the kinetic energy from the wind into electrical energy (Tah and Das, 2016; Latif et al., 2019b). The power expression of WPGs can be expressed as shown in Eq. 2.

$P_{WPG}=0.5\rho A_r{C}_p\left({\lambda }_w,\beta \right)V_{wind}^3.(2)$

This work utilizes a linearized transfer function model of the WPG, as shown in Figure 3.

Figure 3

Figure 3. Linearized transfer function model of the WPG unit.

2.3 Diesel engine generator

The last few decades have utilized the extensive applications of DEG units in microgrid scenarios. In addition to renewable energy sources, non-renewable generators like DEGs are very effective in AGC operations (Tah and Das, 2016). The primary objective of the DEG unit is to ensure the frequency deviation is zero at steady-state conditions under any load perturbations. In this regard, a linearized model of DEGs is utilized along with the renewable energy sources, which is expressed in Eq. 3. Accordingly, a schematic diagram is presented in Figure 4. Moreover, a linearized model of a delay unit is utilized along with the DEG unit to represent the overall system performance more realistically.

$∆P_{\mathit{DEG}}=\left(\frac{K_{\mathit{DEG}}}{1+s{T}_{\mathit{DEG}}}\right)\left(\frac{1}{1+s{T}_{Delay}}\right)∆u_{\mathit{DEG}}.(3)$

Figure 4

Figure 4. Linearized transfer function model of the DEG unit with delay.

2.4 Energy storage system

Renewable source-based power plants frequently suffer from a mismatch between the generated power and load demand due to their intermittent nature (Siti et al., 2022). In order to achieve a seamless power balance between the generating units and loads, ESSs can be used as backup power units. Based on the detailed literature reviews, it is observed that in most cases, BESS and FESS units are utilized as ESSs. Therefore, in this work, the BESS and FESS models are taken into consideration. The considered linearized models of BESS and FESS are presented in Figures 5, 6, respectively.

Figure 5

Figure 5. Linearized transfer function model of the BESS unit.

Figure 6

Figure 6. Linearized transfer function model of the FESS unit.

2.5 Power frequency block of the proposed power system

The power fluctuations between generation and power demand directly affect the system’s operating frequency and cause oscillations. Thus, the total generated power should be controlled and matched with the load power demand to avoid such an unwanted situation (Sanki et al., 2021). Furthermore, the mismatch between the generated and demanded power can be expressed as shown in Eq. 4:

$∆P=P_G-P_L.(4)$

Now, the relation between power mismatch and frequency perturbation is presented in Eq. 5.

$∆f=\frac{P_G-P_L}{\kappa }.(5)$

In Eq. 5, for the $P_G<P_L$ condition, $-∆f$ will be considered and for the $P_L<P_G$ condition, $+∆f$ will be considered. Furthermore, a time delay operator is incorporated to represent the relationship between the change in power and frequency. Therefore, the change in frequency with the change in power is presented in Eq. 6.

$G_{PS}=\frac{∆f}{∆P}=\frac{1}{\kappa \left(1+s{T}_{PS}\right)}=\frac{1}{D+sM}.(6)$

The linearized power system model is depicted in Figure 7.

Figure 7

Figure 7. Linearized transfer function model of the power-frequency block.

3 Modeling of the tie-line design for the interconnected microgrid scenario

3.1 Conventional tie-line power design

The tie-lines between the interconnected areas under any power system play a significant role in sustaining synchronism by exchanging power between the control areas during load disturbances. To date, the majority of AGC studies have considered a multi-area power system model without including the effect of line resistance R_Ln (Tah and Das, 2016). Thus, the power flow equations only consist of line reactance X_Ln. Considering the effect of X_Ln, the conventional tie-line power flow P₁₂ is presented in Eqs 7, 8. A typical two-area power system schematic diagram is depicted in Figure 8A.

$P_{12}=\frac{E_{A1}{E}_{A2}}{X_{\mathit{Ln}}}\mathit{sin}\left(\angle {\delta }_1-\angle {\delta }_2\right)=\frac{E_{A1}{E}_{A2}}{X_{\mathit{Ln}}}\mathit{sin}\angle \delta ,(7)$

Figure 8

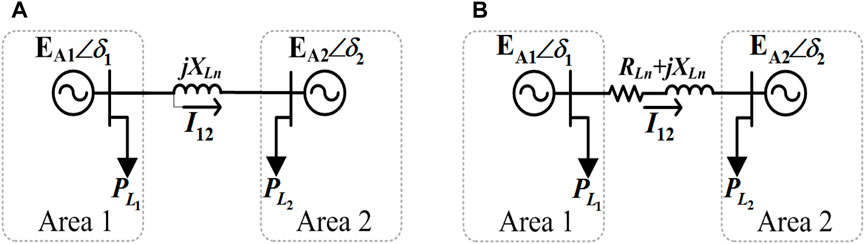
Figure 8. Two-area interconnected power system model, (A) without considering the effect of tie-line R_Ln and (B) considering the effect of tie-line R_Ln.

where,

${\angle \delta =\angle \delta }_1-\angle {\delta }_2.(8)$

This article focuses only on the frequency regulation issue. Therefore, a change in active power causes a change in frequency.

Under small load perturbations, the change in $\delta$ can be considered $∆\delta$. Hence, the power flow equation under small load perturbations becomes (Eq. 9)

$∆P_{12}=T_{12}\left(\angle {\delta }_1-\angle {\delta }_2\right),(9)$

where T₁₂ is the tie-line synchronizing co-efficient, which is presented in Eq. 10.

$T_{12}=\frac{E_{A1}{E}_{A2}}{X_{\mathit{Ln}}}\mathit{cos}\left(\angle {\delta }_1-\angle {\delta }_2\right)=\frac{E_{A1}{E}_{A2}}{X_{\mathit{Ln}}}\mathit{cos}\angle \delta .(10)$

Finally, according to the conventional AGC studies, the frequency deviation due to load perturbation is presented in Eq. 11.

$∆P_{12}\left(s\right)=2\pi T_{12}\int \left(∆f_1-∆f_2\right)dt=\frac{2\pi T_{12}}{s}\left(∆f_1\left(s\right)-∆f_2\left(s\right)\right).(11)$

3.2 Proposed improved power tie-line model

In modern decentralized power systems like microgrids, the exchange of power between the interconnected areas is very frequent, as they consist of intermittent energy resources. In such a scenario, the losses due to R_Ln are essential for power flow calculations. Therefore, modification of traditional power flow equations for such decentralized interconnected systems is highly required. Accordingly, the line impedance Z_Ln is considered to appear in the tie-line, connecting different areas under the microgrid scenario. For example, a schematic diagram of a two-area power system model is considered in Figure 8B. According to Figure 8B, the improved power flow equation $P_{12}$ becomes

$P_{12}=\frac{E_{A1}{E}_{A2}}{Z_{\mathit{Ln}}}\mathit{cos}\angle {\theta }_Z-\frac{E_{A1}{E}_{A2}}{Z_{\mathit{Ln}}}\mathit{cos}\left(\angle \delta +\angle {\theta }_Z\right).(12)$

Here, current expression from bus 1 to 2 is as follows:

${\overrightarrow{I}}_{12}=\frac{E_{A1}\angle {\delta }_1}{Z_{\mathit{Ln}}\angle {\theta }_Z}-\frac{E_{A2}\angle {\delta }_2}{Z_{\mathit{Ln}}\angle {\theta }_Z}.(13)$

Simplifying Eq. 12, 13 by substituting $Z_{\mathit{Ln}}=\sqrt{{\left(R_{\mathit{Ln}}\right)}^2+{\left(X_{\mathit{Ln}}\right)}^2}$, $\mathit{cos}\angle {\theta }_Z=\frac{R_{\mathit{Ln}}}{Z_{\mathit{Ln}}}$, and $\mathit{sin}\angle {\theta }_Z=\frac{X_{\mathit{Ln}}}{Z_{\mathit{Ln}}}$, we get Eq. 14

$P_{12}=\frac{E_{A1}^2{R}_{\mathit{Ln}}}{Z_{\mathit{Ln}}^2}-\frac{\left(E_{A1}{E}_{A2}\right)R_{\mathit{Ln}}}{Z_{\mathit{Ln}}^2}\mathit{cos}\angle \delta +\frac{\left(E_{A1}{E}_{A2}\right)X_{\mathit{Ln}}}{Z_{\mathit{Ln}}^2}\mathit{sin}\angle \delta .(14)$

Under a small load perturbation situation, the governing power flow equation from bus 1 to 2 becomes

$∆P_{12}=\frac{E_{A1}{E}_{A2}}{{\left(R_{\mathit{Ln}}\right)}^2+{\left(X_{\mathit{Ln}}\right)}^2}\left(R_{\mathit{Ln}}\mathit{sin}\left(\angle {\delta }_1-\angle {\delta }_2\right)+X_{\mathit{Ln}}\mathit{cos}\left(\angle {\delta }_1-\angle {\delta }_2\right)\right)\times \left(∆\angle {\delta }_1-∆\angle {\delta }_2\right).(15)$

Similar to Eq. 15, the power flow equation from bus 2 to 1 becomes as follows (Eq. 16).

$∆P_{21}=\frac{E_{A2}{E}_{A1}}{{\left(R_{\mathit{Ln}}\right)}^2+{\left(X_{\mathit{Ln}}\right)}^2}\left(X_{\mathit{Ln}}\mathit{cos}\left(\angle {\delta }_1-\angle {\delta }_2\right)-R_{\mathit{Ln}}\mathit{sin}\left(\angle {\delta }_1-\angle {\delta }_2\right)\right)\times \left(∆\angle {\delta }_1-∆\angle {\delta }_2\right).(16)$

Furthermore, ${{▽}_1=R}_{\mathit{Ln}}\mathit{sin}\left(\angle {\delta }_1-\angle {\delta }_2\right)+X_{\mathit{Ln}}\mathit{cos}\left(\angle {\delta }_1-\angle {\delta }_2\right)$ and ${{▽}_2=X}_{\mathit{Ln}}\mathit{cos}\left(\angle {\delta }_1-\angle {\delta }_2\right)-R_{\mathit{Ln}}\mathit{sin}\left(\angle {\delta }_1-\angle {\delta }_2\right)$, as presented in Figure 1. The power loss during small load perturbation can be presented using Eq. 17.

$∆P_{Loss}=∆P_{12}+∆P_{21}.(17)$

4 Modeling of the controller for the two-area interconnected microgrid

4.1 Controller design

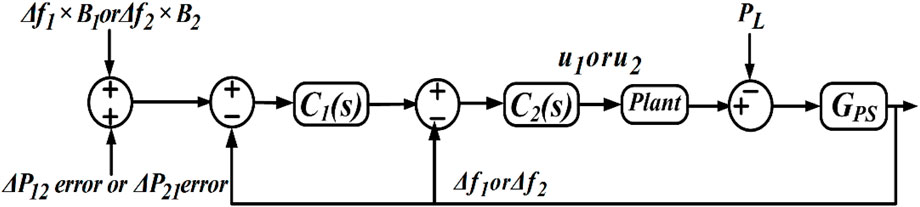
The contribution from the renewable generating components, i.e., SPGs and WPGs, is always non-deterministic in nature. As a result, frequency fluctuations with load perturbations are very frequent phenomena in microgrids. It is essential to incorporate suitable control schemes in order to ensure proper system stability and smooth frequency regulation by maintaining a power balance between generation and load demand. To date, PID or various combinations of PID controllers are extensively used in AGC due to their faster and more flexible operations. Therefore, this paper proposes a CPIPD controller (as depicted in Figure 9) for a two-area microgrid to achieve dynamic frequency regulation by ensuring proper power balance. The PD feedback controller is effective in filtering out unwanted noises due to the available system disturbances, and the forward path PI controller is efficient in providing zero steady-state error of the frequency and tie-line power deviations under load perturbation (Sanki et al., 2021). The proposed CPIPD controller parameters can be represented using Eqs 18, 19, where suffixes 1 and 2 present the forward and feedback paths of the proposed controller, respectively. Suffix “n” presents the specific area of the microgrid.

$C_1\left(s\right)=K_{pi1,n}+\frac{K_{i1,n}}{s}.(18)$

$C_2\left(s\right)=K_{pd2,n}+{sK}_{d2,n}.(19)$

Figure 9

Figure 9. Schematic diagram of the proposed CPIPD controller for the microgrid operation.

According to Figure 9, the frequency error due to any load perturbation is corrected by the PI controller, and noise filtration due to uncertainties is accomplished by the PD controller.

To date, numerous metaheuristic algorithms have been proposed in order to evaluate the optimum controller gain parameters. It is always desired that these metaheuristic algorithms exhibit a faster convergence rate with less computational time to tune the gain parameters. However, the majority of them struggle to satisfy such basic criteria. Recently, the SPBO technique has been proposed to overcome such hardships (Das et al., 2020). In this regard, a detailed discussion of SPBO is presented in the upcoming section.

The controller gain parameter evaluation plays an important role in achieving the desired responses. Generally, metaheuristic algorithms are utilized to obtain suitable controller gain parameters with minimum objective functions. In this scenario, various performance indices like ISE, IAE, ITSE, and ITAE have so far been incorporated in the presence of different optimization techniques to derive the objective functions (Antonopoulos et al., 2020). In this work, different performance indices are adopted to evaluate the suitable controller parameters. The detailed mathematical expressions of the different performance indices are presented in Eqs 20–23.

$J_{ISE}={\displaystyle \underset{0}{\overset{T}{\int }}}\left\{\left({∆f}_i^2\right)+\left({∆P}_{tie,ij}^2\right)dt\right..(20)$

$J_{IAE}={\displaystyle \underset{0}{\overset{T}{\int }}}\left\{\left|{∆f}_i\right|+\left|{∆P}_{tie,ij}\right|\right\}dt.(21)$

$J_{ITSE}={\displaystyle \underset{0}{\overset{T}{\int }}}t\{\left({∆f}_i^2\right)+\left({∆P}_{tie,ij}^2\right)dt.(22)$

$J_{ITAE}={\displaystyle \underset{0}{\overset{T}{\int }}}t\left\{\left|{∆f}_i\right|+\left|{∆P}_{tie,ij}\right|\right\}dt.(23)$

The considered objective functions of this work can be represented as Eqs 24, 25.

$J_{\mathit{min}}={\displaystyle \underset{0}{\overset{T}{\int }}}\left\{\left({∆f}_1^2\right)+\left({∆f}_2^2\right)+\left({∆P}_{tie,12}^2\right)+\left({∆P}_{tie,21}^2\right)\right\},(24)$

where,

$K_{pi,\mathit{min}}<K_{pi}<K_{pi,\mathit{max}},K_{i,\mathit{min}}<K_i<K_{i,\mathit{max}}$

$K_{pd,\mathit{min}}<K_{pd}<K_{pd,\mathit{max}},K_{d,\mathit{min}}<K_d<K_{d,\mathit{max}}.(25)$

4.2 Student psychology-based optimization

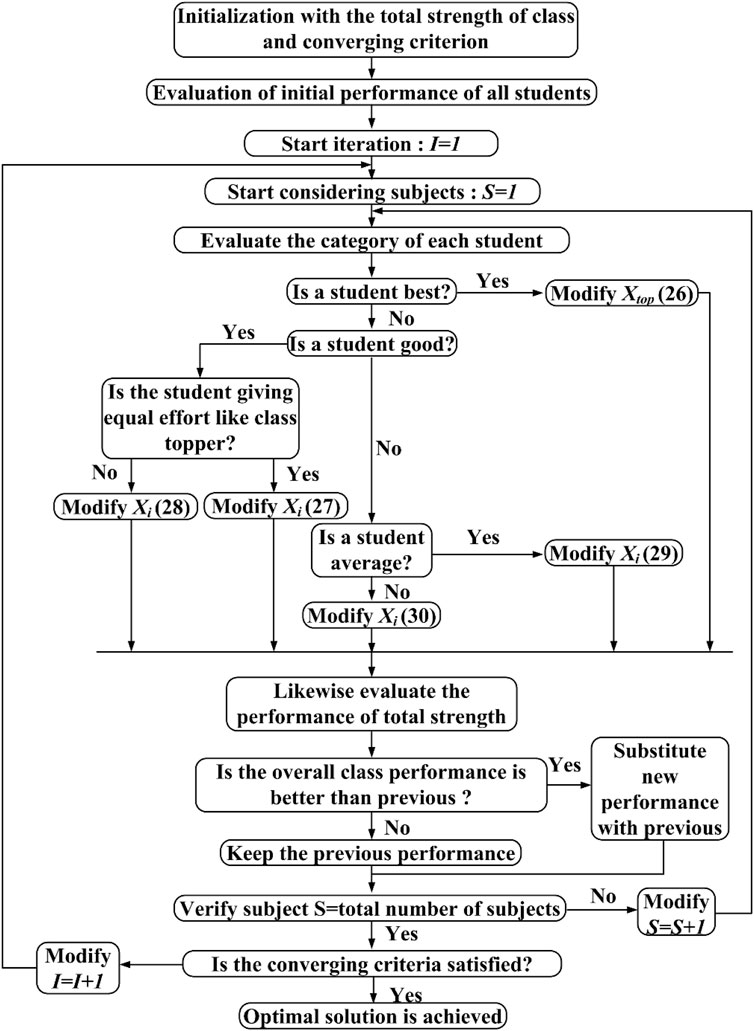
Performance analysis of any student in a particular class during an examination is mostly carried out based on the secured marks. The student who secures the overall highest mark is generally considered the class topper and is appreciated with some reward. Therefore, all students in any class attempt to provide maximum effort for each subject to secure the overall highest mark. The SPBO algorithm works with the same student psychology, where each student in a class tries to score the overall highest mark by improving their performance.

In order to sustain the position of class topper, gradual performance improvement for each subject is required. Therefore, students need to provide equal effort in all subjects to improve their overall scores. However, in reality, the effort of each student does vary based on their merit, efficiency, and subject interest. Additionally, the physiology of each student does differ, and as a result, performance during examinations discriminates against individuals. Some of the students consider the class topper as their reference and accordingly manage their efforts to become a topper. On the other hand, some of them consider both the class topper and the average student to manage their efforts to become a topper. Based on this analysis, the students of a particular class can be categorized into the following sections:

Topper: in an examination, the student who scores the maximum overall marks is generally considered a class topper. In order to sustain the position of the topper, a student must put forth equal effort in all the subjects to secure the overall maximum marks. Now, the improvement in the performance of a topper can be evaluated using Eq. 26.

$X_{top-new}=X_{top}+\left\{{\left(-1\right)}^k\times rnd\times \left(X_{top}-X_i\right)\right\}.(26)$

Good student: the choice of this section of students is a random process as the psychology of individual students differs. The students who manage their effort, considering the class topper as their reference, can be assessed as Eq. 27:

$X_{new,i}=X_i+\left\{rnd\times \left(X_{top}-X_i\right)\right\}.(27)$

However, the students who consider both the class topper and the average student to manage their effort regarding the study can be assessed as Eq. 28:

$X_{new,i}=X_i+\left\{rnd\times \left(X_{top}-X_i\right)\right\}+\left\{rnd\times \left(X_i-X_{mean}\right)\right\}.(28)$

Average student: this section of students can be considered subject-wise average candidates. Effort on any particular subject depends greatly on interest in its topics. Therefore, a student who has less interest in a particular subject tries to focus more on the subjects of their interest for overall improvement. The performance analysis of this category of student can be carried out as Eq. 29:

$X_{new,i}=X_i+\left\{rnd\times \left(X_{mean}-X_i\right)\right\}.(29)$

Students who improve randomly: this category of students randomly puts extra effort into a particular subject of their interest to improve their overall score during examinations. The performance analysis of this category of students can be carried out as Eq. 30:

$X_{new,i}=X_{\mathit{min}}+\left\{rnd\times \left(X_{\mathit{max}}-X_{\mathit{min}}\right)\right\}.(30)$

The detailed flowchart of the SPBO algorithm is presented in Figure 10.

Figure 10

Figure 10. Flowchart of the SPBO algorithm.

5 Simulation results with discussion

This section presents a detailed performance analysis of the proposed system under the suggested control scheme. In this scenario, all the test cases are simulated in the MATLAB/Simulink environment. A detailed discussion of the different test cases is presented in the following sections. A brief overview of the different test cases is represented in Table 1.

Table 1

Table 1. Overview of the simulated test cases.

5.1 Performance analysis of the proposed CPIPD controller with the SPBO algorithm in the proposed microgrid scenario under SLP

This case study is performed in a two-fold process. First, a stability margin analysis of the proposed controller gain parameters is presented in order to ensure proper and stable system operation. Based on the stable gain parameter values, the ranges of the controller gain parameters are decided during the optimization procedure. However, in the earlier research works, the controller gain parameters were randomly selected to find out the minimum objective function. Furthermore, a detailed comparative analysis is presented between the traditional controllers, state-of-the-art control techniques, and the proposed control scheme. The extensive performance analysis is presented in the following sections.

5.1.1 Stability margin analysis of the proposed control schemes

This section presents the stability margin analysis of the proposed controller gain parameters. In the earlier published works, the initialization of the gain parameters was carried out considering some randomly generated numbers within a particular range. However, in this approach, based on the stability margin analysis, the initialization range of gain parameters is decided. In this condition, K_p1 and K_i1 are the outer loop controllers (as shown in Figure 9) and K_p2 and K_d2 are the gain parameters of the inner controller (same as shown in Figure 9). The detailed stability range is presented in Figure 11. The stability margin analysis is carried out considering the individual controller gain parameter range between 0.01 and 15.

Figure 11

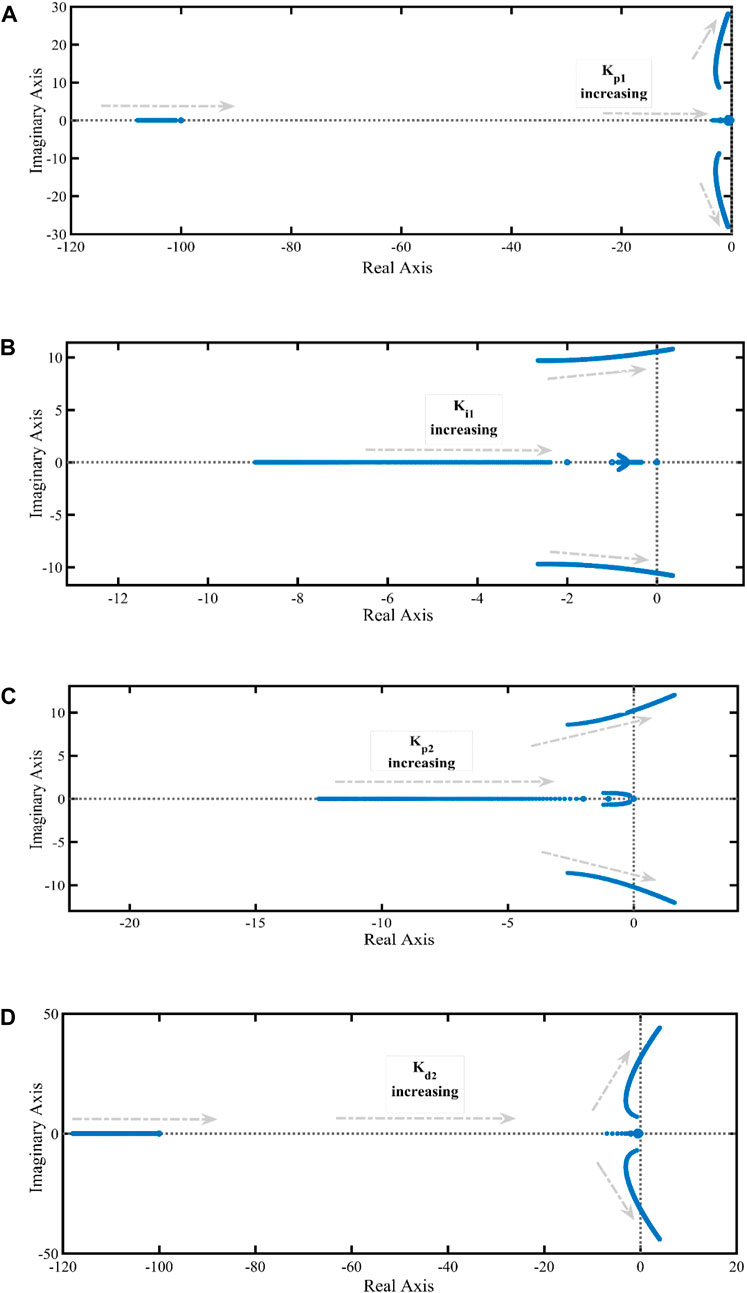
Figure 11. Stability margin analysis of the gain parameters of the proposed controller. (A) With increasing K_{p1}; (B) With increasing K_{i1}, (C) With increasing K_{p2}, (D) With increasing K_{d2}.

5.1.2 Performance analysis under SLP in an improved two-area interconnected microgrid scenario

This section presents a detailed performance analysis of the interconnected microgrid scenario considering the proposed CPIPD controller under 1% SLP at area-1. A comparative analysis is presented between the traditional controller, state-of-the-art controllers, and the proposed SPBO-based CPIPD controller to examine the effectiveness of the suggested control scheme. In this regard, the detailed convergence curve is presented (considering the ISE technique where the best response is obtained) in Figure 12. The obtained results confirm faster convergence of the proposed controller under the suggested metaheuristic technique. The detailed comparative analysis considering different performance indices is presented in Table 2, and the dynamic responses are depicted in Figure 13. Figures 13A, B present the frequency deviations in both areas, and the tie-line power fluctuations are depicted in Figure 13C. The investigation is carried out under 1% SLP at area-1 in the interconnected microgrid scenario under different control schemes. Based on the obtained results, it can be stated that the interconnected microgrid scenario gives the best performance in the presence of the proposed control scheme. The magnified dynamic responses suggest that the system performance is improved under the proposed controller in terms of peak over/undershoots, oscillations, and settling time.

Figure 12

Figure 12. Convergence curve comparisons between various control topologies.

Table 2

Table 2. System parameter comparison under 1% SLP.

Figure 13

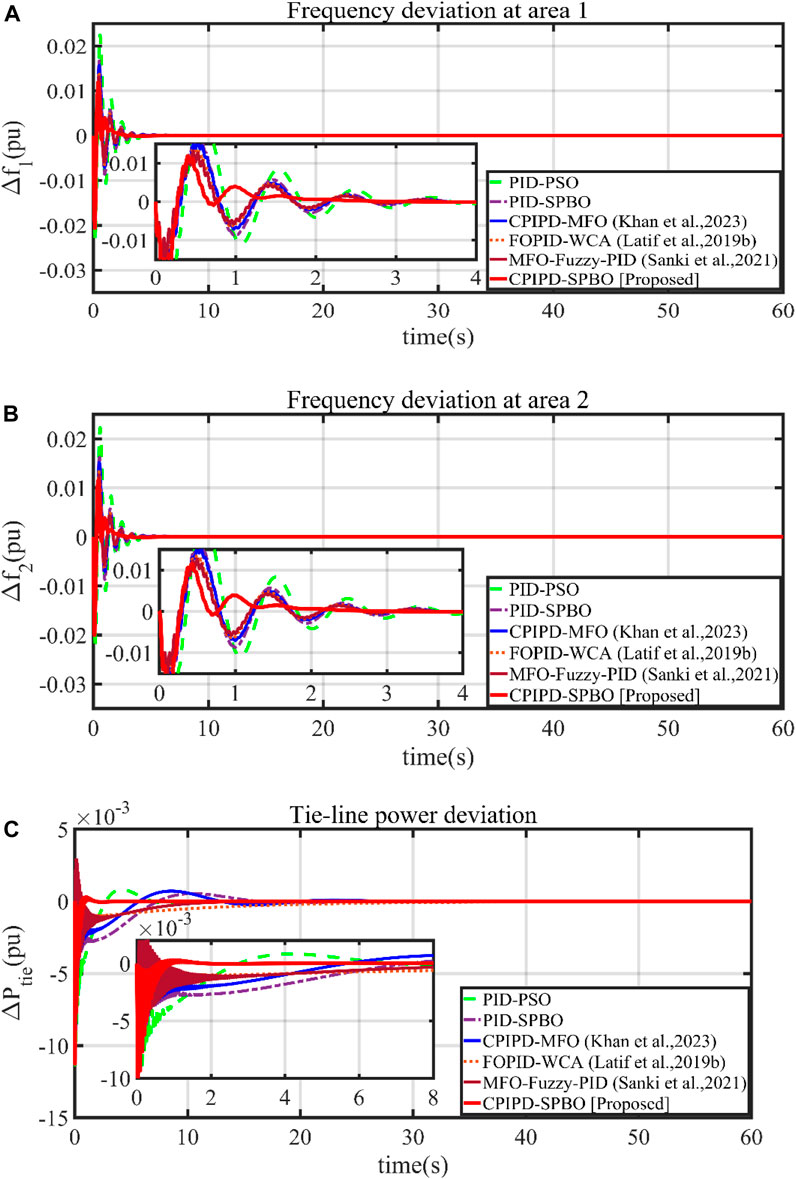
Figure 13. Dynamic responses in microgrid under 1% SLP, (A) frequency deviation of area-1, (B) frequency deviation of area-2, and (C) tie-line power deviation.

Critical observation also suggests that the minimum objective function is achieved under the ISE technique under the proposed control scheme. This validates the efficacy of the proposed control topology. Based on the obtained results, it can be confirmed that the best performance is achieved when the CPIPD controller is accompanied by the SPBO algorithm under the ISE technique.

5.2 Performance analysis of a two-area interconnected microgrid with/without considering the effect of tie-line resistance (R_Ln) under SLP

This section presents a comparative performance analysis of the proposed two-area microgrid with and without considering the effect of R_Ln during SLP. Conventional power systems are extensively utilized for high-voltage and low-current applications. Therefore, the power angle value (δ) is taken considerably high (within the range of 45°), and the tie-line is considered lossless (Tah and Das, 2016). Therefore, in conventional power systems, the effect of R_Ln becomes negligible during system performance evaluation. However, in decentralized multi-area power systems, like microgrids during interconnected mode operation, the above-mentioned parametric values are completely different. In this scenario, the system operates with comparatively low-voltage and high-current ratings. Accordingly, the value of δ is found to be considerably low. Thus, the inclusion of tie-line R_Ln in decentralized power systems becomes essential for power flow calculation. In the previous section, the superior performance of the proposed CPIPD controller over the traditional PID for an improved two-area microgrid model was already established. Thus, in this test case, the proposed CPIPD controller with SPBO is considered for the two-area microgrid to analyze the significance of R_Ln during performance evaluation.

In this section, 1% SLP is considered at area-1 of the proposed microgrid scenario. Like in the previous case, the frequency regulation of area-1, area-2, and the power flow through the tie-line is examined with and without considering the effect of R_Ln. As depicted in Figures 14A–C, the oscillations in frequency and tie-line power signals have reduced much after considering the effect of R_Ln. It should be noted that the power tie-line also acts as a feedback signal in each area. Therefore, the oscillation in the power tie-line is responsible for the oscillations in the frequency signals. Based on the dynamic responses, it is clear that the inclusion of R_Ln has reduced the system oscillations significantly. Hence, the effectiveness of the suitable tie-line design can be established.

Figure 14

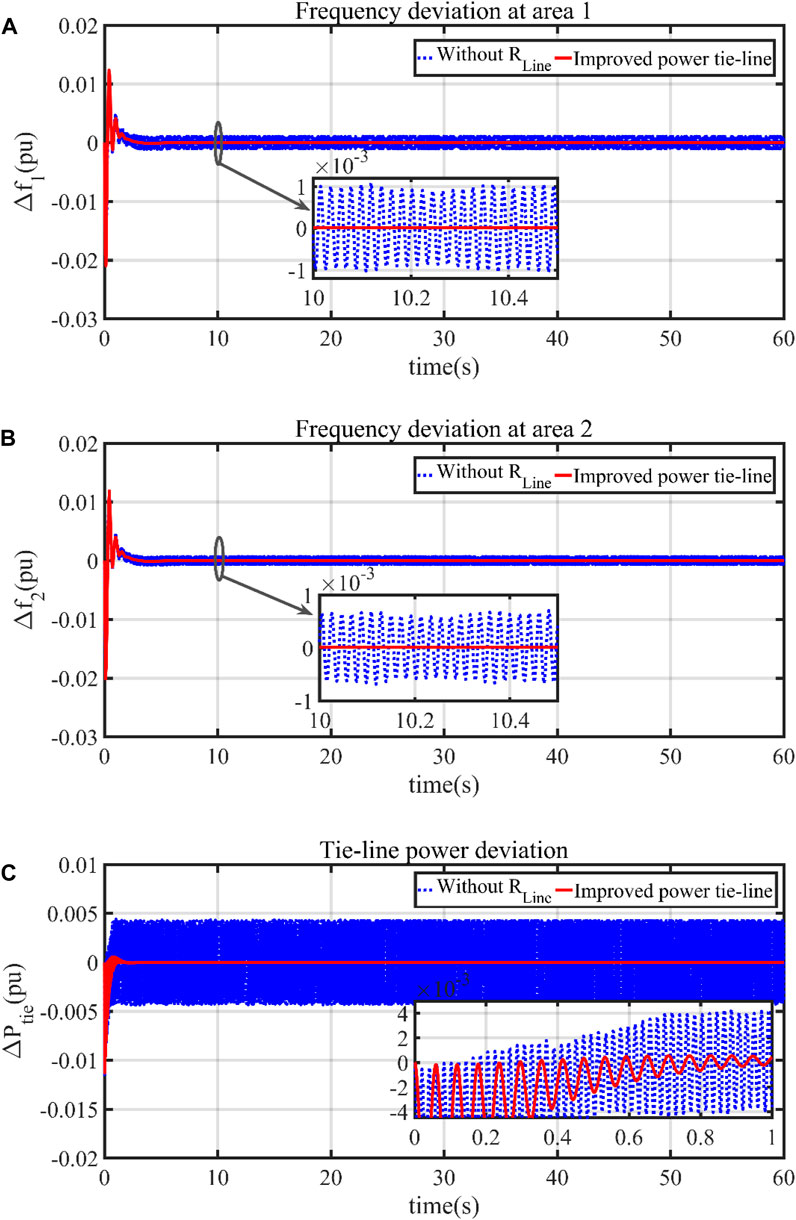
Figure 14. Dynamic responses considering the effect of R_Ln in microgrid, (A) frequency deviation of area-1, (B) frequency deviation of area-2, and (C) tie-line power deviation.

5.3 Performance analysis of the proposed CPIPD controller with the SPBO algorithm in an improved two-area microgrid under RLP with the uncertainty of renewable resources

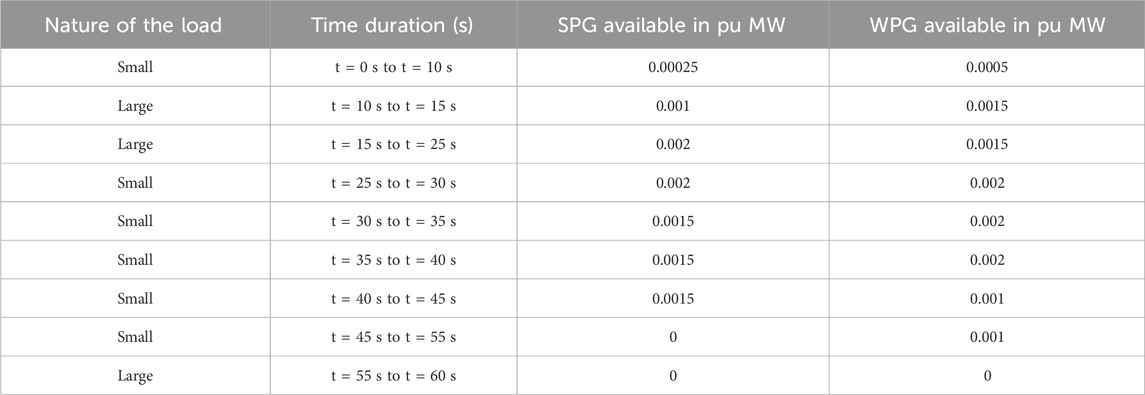
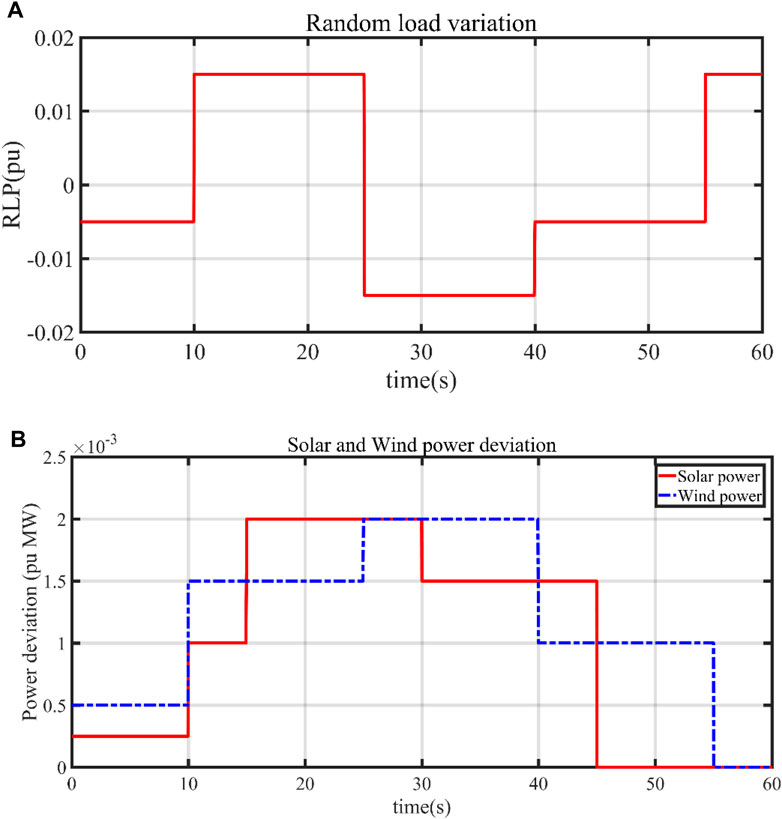
In real-life power systems, the load is always random in nature. Therefore, the performance of the proposed CPIPD controller using SPBO in an improved two-area microgrid is further examined under random load perturbation (RLP) and in the presence of uncertain renewable energy resource generation. The RLP is applied in area-1 to investigate the system performance. The nature of the load (small or large change in magnitude) with its switching instants is presented in Table 3. Furthermore, the available power contributions from SPG and WPG based on their intermittent nature are presented in Table 4. Additionally, the patterns of the RLP and the SPG–WPG units are depicted in Figures 15A, B, respectively.

Table 3

Table 3. Nature of the RLPs with their instant of switching and duration.

Table 4

Table 4. Output power pattern of the SPG and WPG implemented at area-1.

Figure 15

Figure 15. (A) Pattern of the RLP at area-1. (B) Pattern of the SPG and WPG power output.

The detailed dynamic responses are presented in Figure 16. According to the obtained results, it can be stated that the system performance outperforms the other available control schemes in the presence of the proposed control topology in terms of the peak of over/undershoots, oscillations, and setting time. The effectiveness of the proposed control scheme under the improved microgrid scenario can also be validated with the available magnified responses. Therefore, it can be stated that the proposed controller with SPBO is capable of providing improved performance in a multi-area microgrid model during RLP with uncertain power output from SPG–WPG.

Figure 16

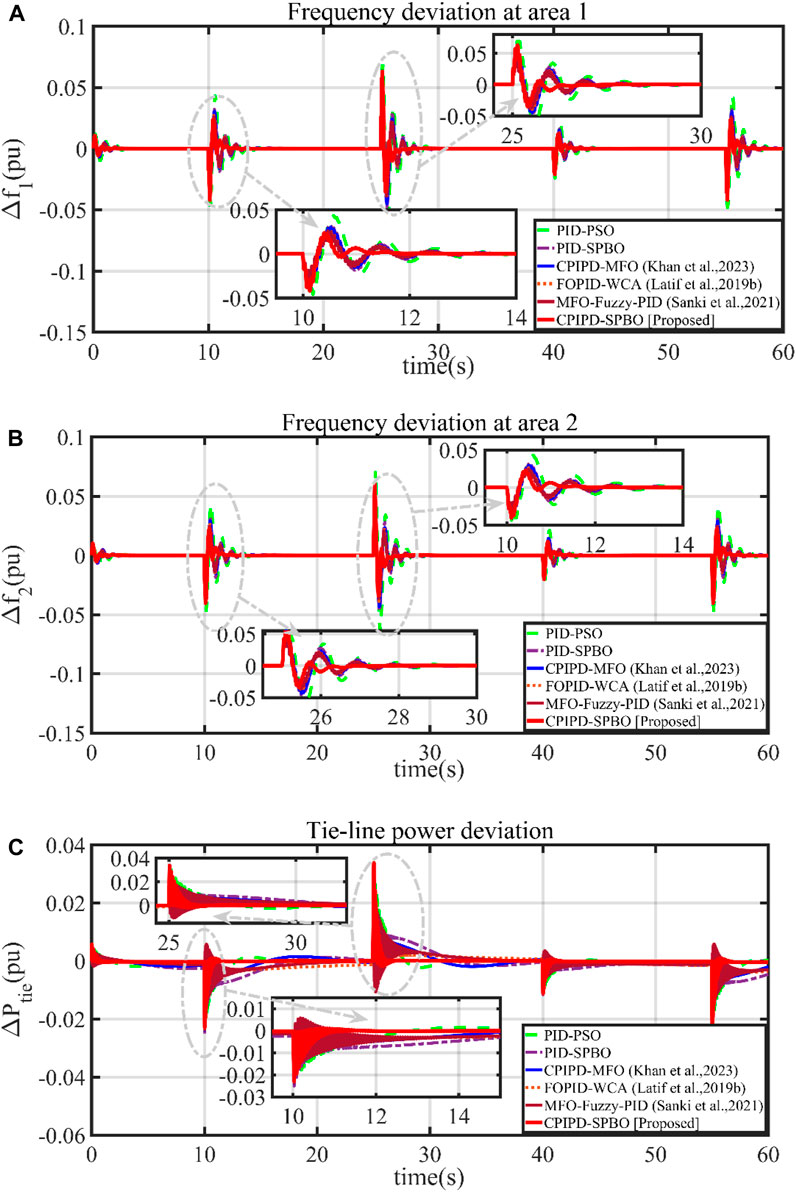
Figure 16. Dynamic responses under the effect of RLP, (A) frequency deviation of area-1, (B) frequency deviation of area-2, and (C) tie-line power deviation.

5.4 Performance analysis of the proposed CPIPD controller with the SPBO algorithm in an improved three-area microgrid under RLP and power uncertainty of renewable resources

The capacity and size of the microgrid will increase in the future with increasing load demand. Accordingly, the integration of renewable source-based energy will increase. Therefore, there will be a requirement for design modifications where the microgrid will increase in size, capacity, and interconnections. This case study presents a detailed performance analysis of a three-area microgrid scenario with an SPBO-optimized CPIPD controller and an improved power tie-line model. In this section, the RLP is considered as the load disturbance. In addition, to examining the controller performance under RLP, the intermittent nature of the SPG and WPG is also considered to create a realistic situation. The nature of RLP and the intermittent nature of SPG–WPG are considered the same, as described in Section 5.3.

The frequency fluctuation of the considered three-area interconnected microgrid scenario and the overall tie-line power deviation are depicted in Figure 17. Based on the obtained results, it can be concluded that the frequency and the tie-line power deviations are efficiently handled by the proposed SPBO-tuned CPIPD controller. Furthermore, the overall power sharing between the areas has taken place seamlessly without abrupt oscillations.

Figure 17

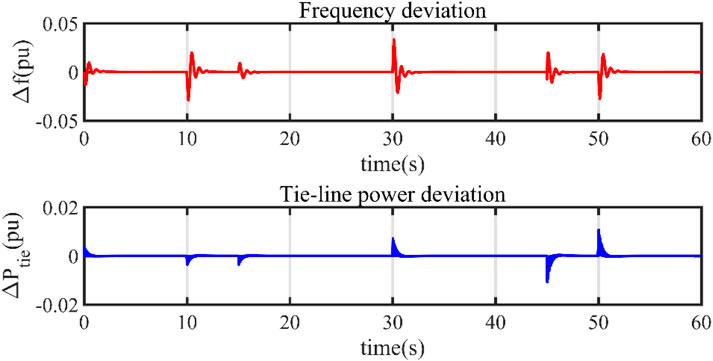
Figure 17. Frequency deviation and tie-line power deviation under the three-area microgrid operation.

5.5 Performance analysis of the improved two-area microgrid under a 12-node radial distribution network

In this section, the performance analysis is presented by considering the improved two-area microgrid integrated with a 12-node radial distribution network, as shown in Figure 18A. The proposed system is connected by bus numbers 9 and 11, respectively. The substation (SS), which is situated far away from the connecting nodes, is considered as the swing bus in the network. In this test case, prior to integration, the voltages of nodes 9 and 11 of the considered distribution network were 0.9895 pu and 0.986 pu, respectively. The corresponding loss of the distribution network was 19.02 kW. However, after integrating the proposed two-area microgrid, the node voltages are improved significantly from 0.9895 pu to 0.9980 pu (for node 9) and from 0.9860 pu to 0.9954 pu (for node 11). In addition to that, a notable power loss reduction takes place (from 19.02 kW to 15.34 kW) accordingly. The simulated responses of the corresponding bus voltages and power losses are presented in Figure 18B. The improved voltage profile and reduction of power loss clearly show the effectiveness of the improved two-area microgrid interconnection in the 12-node distribution network. A critical performance analysis of the improved two-area microgrid under 12-node distribution networks in terms of pu voltage (nodes 9 and 11) and power loss reduction is presented in Table 5. Based on the obtained results, the efficacy of the proposed microgrid model is justified.

Figure 18

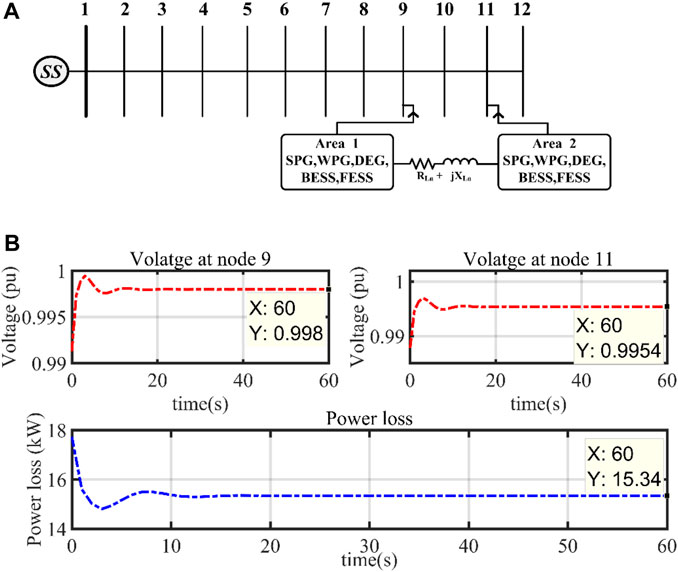
Figure 18. (A) Schematic diagram of the improved two-area interconnected microgrid with a 12-node radial distribution network. (B) Voltage profile at the buses 9 and 11 and overall power loss of the distribution network.

Table 5

Table 5. Performance analysis of the modified two-area hybrid microgrid in a 12-node radial distribution network.

6 Conclusion

This article proposes an SPBO-optimized CPIPD controller for an improved multi-area interconnected microgrid in order to improve the system’s performance. Furthermore, the suggested multi-area microgrid model is critically investigated under numerous test scenarios with different power system configurations. Based on the obtained results, the significant outcomes of the proposed microgrid under the suggested control scheme are discussed as follows:

1. First of all, a two-area interconnected microgrid is presented, considering the effect of line resistance R_Ln. To date, the tie-line power flow model of conventional multi-area power systems has been designed excluding the effect of R_Ln. However, in the case of interconnected microgrid scenarios, R_Ln plays a significant role in power flow between the control areas. Therefore, extensive investigation of the proposed two-area microgrid has been carried out, and the obtained responses confirm that unwanted power oscillations can be damped out, including the effect of R_Ln.

2. A CPIPD controller is incorporated to accomplish the desired dynamic performance under various power system scenarios. Furthermore, for the first time, the stability margin analysis of the gain parameters was carried out, and based on the stable range, the proposed CPIPD controller was tuned utilizing the SBPO technique under the proposed microgrid operation. The proposed controller outperforms the available state-of-the-art control schemes in terms of over/undershoots, oscillations, and settling time.

3. A comparative performance analysis between the traditional controllers, state-of-the-art controllers, and the proposed CPIPD controller is investigated under SLP and RLP conditions in the modified microgrid system. Furthermore, the effect of the intermittent nature of SPGs and WPGs is considered to examine the system’s performance. Under this comparative analysis, the gain parameters of the controllers are optimized using different optimization algorithms. The critical investigation of the system responses ensures that the best response with a minimum objective function is achieved under the proposed CPIPD controller using the SPBO technique in the ISE technique.

4. The performance analysis of the improved two-area system is carried out, considering a 12-node radial distribution network. The obtained results indicate a significant improvement in the voltage profile and a reduction in overall power loss in the tested power distribution network. Therefore, this microgrid model is suitable for future power system modeling and operation.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

SG: conceptualization, data curation, formal analysis, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. SM: conceptualization, data curation, formal analysis, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. AB: conceptualization, data curation, formal analysis, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. PrS: conceptualization, data curation, formal analysis, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. PaS: conceptualization, data curation, formal analysis, investigation, methodology, project administration, resources, software, supervision, visualization, and writing–review and editing. SB: conceptualization, data curation, formal analysis, investigation, methodology, project administration, resources, software, supervision, validation, visualization, and writing–review and editing. BK: conceptualization, data curation, formal analysis, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. AA: conceptualization, formal analysis, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. PB: conceptualization, data curation, formal analysis, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing.

Funding

The authors declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ali, M., Kotb, H., Aboras, K. M., and Abbasy, N. H. (2021). Design of cascaded pi-fractional order PID controller for improving the frequency response of hybrid microgrid system using gorilla troops optimizer. IEEE Access 9, 150715–150732. doi:10.1109/ACCESS.2021.3125317

CrossRef Full Text | Google Scholar

Ali, M., Kotb, H., Kareem AboRas, M., and Nabil Abbasy, H. (2022). Frequency regulation of hybrid multi-area power system using wild horse optimizer based new combined Fuzzy Fractional-Order PI and TID controllers. Alexandria Eng. J. 61, 12187–12210. doi:10.1016/j.aej.2022.06.008

CrossRef Full Text | Google Scholar

Antonopoulos, I., Robu, V., Couraud, B., Kirli, D., Norbu, S., Kiprakis, A., et al. (2020). Artificial intelligence and machine learning approaches to energy demand-side response: a systematic review. Renew. Sustain. Energy Rev. 130, 109899. doi:10.1016/j.rser.2020.109899

CrossRef Full Text | Google Scholar

Arya, Y. (2020). Effect of electric vehicles on load frequency control in interconnected thermal and hydrothermal power systems utilising CF-FOIDF controller. IET Generation, Transm. Distribution 14, 2666–2675. doi:10.1049/iet-gtd.2019.1217

CrossRef Full Text | Google Scholar

Bevrani, H., Habibi, F., Babahajyani, P., Watanabe, M., and Mitani, Y. (2012). Intelligent frequency control in an AC microgrid: online PSO-based fuzzy tuning approach. IEEE Trans. smart grid 3, 1935–1944. doi:10.1109/TSG.2012.2196806

CrossRef Full Text | Google Scholar

Biswas, S., Roy, P. K., and Chatterjee, K. (2023). FACTS-based 3DOF-PID controller for LFC of renewable power system under deregulation using GOA. IETE J. Res. 69, 1486–1499. doi:10.1080/03772063.2020.1870874

CrossRef Full Text | Google Scholar

Çelik, E., Öztürk, N., Arya, Y., and Ocak, C. (2021). (1 + PD)-PID cascade controller design for performance betterment of load frequency control in diverse electric power systems. Neural Comput. Applic 33, 15433–15456. doi:10.1007/s00521-021-06168-3

CrossRef Full Text | Google Scholar

Chintu, J. M. R., Sahu, R. K., and Panda, S. (2022). Adaptive differential evolution tuned hybrid fuzzy PD-PI controller for automatic generation control of power systems. Int. J. Ambient Energy 43, 515–530. doi:10.1080/01430750.2019.1653986

CrossRef Full Text | Google Scholar

Choudhary, R., Rai, J. N., and Arya, Y. (2022). Cascade FOPI-FOPTID controller with energy storage devices for AGC performance advancement of electric power systems. Sustain. Energy Technol. Assessments 53, 102671. doi:10.1016/j.seta.2022.102671

CrossRef Full Text | Google Scholar

Das, B., Mukherjee, V., and Das, D. (2020). Student psychology based optimization algorithm: a new population based optimization algorithm for solving optimization problems. Adv. Eng. Softw. 146, 102804. doi:10.1016/j.advengsoft.2020.102804

CrossRef Full Text | Google Scholar

Francis, R., and Chidambaram, I. A. (2015). Optimized PI+ load–frequency controller using BWNN approach for an interconnected reheat power system with RFB and hydrogen electrolyser units. Int. J. Electr. Power & Energy Syst. 67, 381–392. doi:10.1016/j.ijepes.2014.12.012

CrossRef Full Text | Google Scholar

Guha, D., Roy, P. K., and Banerjee, S. (2018). Optimal tuning of 3 degree-of-freedom proportional-integral-derivative controller for hybrid distributed power system using dragonfly algorithm. Comput. Electr. Eng. 72, 137–153. doi:10.1016/j.compeleceng.2018.09.003

CrossRef Full Text | Google Scholar

Hasanien, H. M. (2018). Whale optimisation algorithm for automatic generation control of interconnected modern power systems including renewable energy sources. IET Generation, Transm. Distribution 12, 607–614. doi:10.1049/iet-gtd.2017.1005

CrossRef Full Text | Google Scholar

Izadkhast, S., Garcia-Gonzalez, P., and Frías, P. (2014). An aggregate model of plug-in electric vehicles for primary frequency control. IEEE Trans. Power Syst. 30, 1475–1482. doi:10.1109/TPWRS.2014.2337373

CrossRef Full Text | Google Scholar

Jain, S., and Hote, Y. V. (2021). Generalized active disturbance rejection controller design: application to hybrid microgrid with communication delay. Int. J. Electr. Power & Energy Syst. 132, 107166. doi:10.1016/j.ijepes.2021.107166

CrossRef Full Text | Google Scholar

Khan, I. A., Mokhlis, H., Mansor, N. N., Illias, H. A., Awalin, L. J., and Wang, L. (2023). New trends and future directions in load frequency control and flexible power system: a comprehensive review. Alexandria Eng. J. 71, 263–308. doi:10.1016/j.aej.2023.03.040

CrossRef Full Text | Google Scholar

Khooban, M.-H. (2017). Secondary load frequency control of time-delay stand-alone microgrids with electric vehicles. IEEE Trans. Industrial Electron. 65, 7416–7422. doi:10.1109/TIE.2017.2784385

CrossRef Full Text | Google Scholar

Latif, A., Das, D. C., Barik, A. K., and Ranjan, S. (2019a). Maiden coordinated load frequency control strategy for ST-AWEC-GEC-BDDG-based independent three-area interconnected microgrid system with the combined effect of diverse energy storage and DC link using BOA-optimised PFOID controller. IET Renew. Power Gener. 13, 2634–2646. doi:10.1049/iet-rpg.2019.0199

CrossRef Full Text | Google Scholar

Latif, A., Das, D. C., Ranjan, S., and Barik, A. K. (2019b). Comparative performance evaluation of WCA-optimised non-integer controller employed with WPG–DSPG–PHEV based isolated two-area interconnected microgrid system. IET Renew. Power Gener. 13, 725–736. doi:10.1049/iet-rpg.2018.5419

CrossRef Full Text | Google Scholar

Mahto, T., Malik, H., Mukherjee, V., Alotaibi, M. A., and Almutairi, A. (2021). Renewable generation based hybrid power system control using fractional order-fuzzy controller. Energy Rep. 7, 641–653. doi:10.1016/j.egyr.2021.01.022

CrossRef Full Text | Google Scholar

Mishra, S., Nayak, P. C., Prusty, R. C., and Panda, S. (2023). Hybrid dragonfly algorithm and pattern search optimized adaptive fuzzy PID controller for frequency regulation of multi microgrid system using Henkel matrix based reduced-order model. Int. J. Numerical Modelling. 36, e3029. doi:10.1002/jnm.3029

CrossRef Full Text | Google Scholar

Rahman, A., Saikia, L. C., and Sinha, N. (2017). Automatic generation control of an interconnected two-area hybrid thermal system considering dish-stirling solar thermal and wind turbine system. Renew. energy 105, 41–54. doi:10.1016/j.renene.2016.12.048

CrossRef Full Text | Google Scholar

Ranjan, M., and Shankar, R. (2022). A literature survey on load frequency control considering renewable energy integration in power system: recent trends and future prospects. J. Energy Storage 45, 103717. doi:10.1016/j.est.2021.103717

CrossRef Full Text | Google Scholar

Sahu, P. C., Prusty, R. C., and Panda, S. (2022). Frequency regulation of an electric vehicle-operated micro-grid under WOA-tuned fuzzy cascade controller. Int. J. Ambient Energy 43, 2900–2911. doi:10.1080/01430750.2020.1783358

CrossRef Full Text | Google Scholar

Sanki, P., and Basu, M. (2018). New approach in two-area interconnected AGC including various renewable energy sources using PSO. Turkish J. Electr. Eng. Comput. Sci. 26, 1491–1504. doi:10.3906/elk-1707-241

CrossRef Full Text | Google Scholar

Sanki, P., Basu, M., Pal, P. S., and Das, D. (2021a). Application of a novel PIPDF controller in an improved plug-in electric vehicle integrated power system for AGC operation. Int. J. Ambient Energy 43, 4767–4781. doi:10.1080/01430750.2021.1920460

CrossRef Full Text | Google Scholar

Sanki, P., Mazumder, S., Basu, M., Pal, P. S., and Das, D. (2021b). Moth flame optimization based fuzzy-PID controller for power–frequency balance of an islanded microgrid. J. Inst. Eng. India Ser. B 102, 997–1006. doi:10.1007/s40031-021-00607-4

CrossRef Full Text | Google Scholar

Shiva, C. K., Vedik, B., Mahapatra, S., Nandi, M., Raj, S., and Mukherjee, V. (2022). Load frequency stabilization of stand-alone hybrid distributed generation system using QOHS algorithm. Int. J. Numerical Modelling. 35, e2998. doi:10.1002/jnm.2998

CrossRef Full Text | Google Scholar

Singh, K.Zaheeruddin (2021). Enhancement of frequency regulation in tidal turbine power plant using virtual inertia from capacitive energy storage system. J. Energy Storage 35, 102332. doi:10.1016/j.est.2021.102332

CrossRef Full Text | Google Scholar

Singh, K., and Arya, Y. (2023). Tidal turbine support in microgrid frequency regulation through novel cascade Fuzzy-FOPID droop in de-loaded region. ISA Trans. 133, 218–232. doi:10.1016/j.isatra.2022.07.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Singh, K., Dahiya, M., Grover, A., Adlakha, R., and Amir, M. (2023). An effective cascade control strategy for frequency regulation of renewable energy based hybrid power system with energy storage system. J. Energy Storage 68, 107804. doi:10.1016/j.est.2023.107804

CrossRef Full Text | Google Scholar

Siti, M. W., Mbungu, N. T., Tungadio, D. H., Banza, B. B., and Ngoma, L. (2022). Application of load frequency control method to a multi-microgrid with energy storage system. J. Energy Storage. 52, 104629. doi:10.1016/j.est.2022.104629

CrossRef Full Text | Google Scholar

Sonker, B., Kumar, D., and Samuel, P. (2019). Dual loop IMC structure for load frequency control issue of multi-area multi-sources power systems. Int. J. Electr. Power & Energy Syst. 112, 476–494. doi:10.1016/j.ijepes.2019.04.042

CrossRef Full Text | Google Scholar

Tah, A., and Das, D. (2016). Operation of small hybrid autonomous power generation system in isolated, interconnected and grid connected modes. Sustain. Energy Technol. Assessments 17, 11–25. doi:10.1016/j.seta.2016.07.001

CrossRef Full Text | Google Scholar

Xi, L., Zhang, L., Liu, J., Li, Y., Chen, X., Yang, L., et al. (2020). A virtual generation ecosystem control strategy for automatic generation control of interconnected microgrids. IEEE Access 8, 94165–94175. doi:10.1109/ACCESS.2020.2995614

CrossRef Full Text | Google Scholar

Yakout, A. H., Attia, M. A., and Kotb, H. (2021a). Marine predator algorithm based cascaded PIDA load frequency controller for electric power systems with wave energy conversion systems. Alexandria Eng. J. 60, 4213–4222. doi:10.1016/j.aej.2021.03.011

CrossRef Full Text | Google Scholar

Yakout, A. H., Kotb, H., Hasanien, H. M., and Aboras, K. M. (2021b). Optimal fuzzy PIDF load frequency controller for hybrid microgrid system using marine predator algorithm. IEEE Access 9, 54220–54232. doi:10.1109/access.2021.3070076

CrossRef Full Text | Google Scholar

Zaheeruddin, , Singh, K., and Amir, M. (2022). Intelligent fuzzy TIDF-II controller for load frequency control in hybrid energy system. IETE Tech. Rev. 39, 1355–1371. doi:10.1080/02564602.2021.1994476

CrossRef Full Text | Google Scholar

Appendix

1 System parameters

K_SPG = 1, T_SPG = 1.5 s, K_WPG = 1, T_WPG = 1.8 s, K_Delay = 1, T_Delay = 1s, K_DEG = 1, T_DEG = 2 s, K_FESS = 1, T_FESS = 0.01 s, K_BESS = 1, T_BESS = 0.01 s, K_GIC = 1, T_GIC = 0.01 s, M = 0.1, D = 0.013, R = 1 Hz/pu MW.

2 Controller parameters

Area-1: K_pi1 = 6.81, K_i1 = 4.23, K_pd2 = 5.21, K_d2 = 2.65.

Area-2: K_pi1 = 5.45, K_i1 = 3.78, K_pd2 = 1.46, K_d2 = 3.08.

Glossary