Quantum model prediction for frequency regulation of novel power systems which includes a high proportion of energy storage

As the proportion of renewable energy generation continues to increase, the participation of new energy stations with high-proportion energy storage in power system frequency regulation is of significant importance for stable and secure operation of the new power system. To address this issue, an energy storage control method based on quantum walks and model predictive control (MPC) has been proposed. First, historical frequency deviation signals and energy storage charge–discharge state signals are collected. Simulation data are generated through amplitude encoding and quantum walks, followed by quantum decoding. Subsequently, the decoded data are inputted into the MPC framework for real-time control, with parameters of the predictive model continuously adjusted through a feedback loop. Finally, a novel power system frequency regulation model with high-proportion new energy storage stations is constructed on the MATLAB/Simulink platform. Simulation verification is conducted with the proportional–integral–derivative (PID) and MPC methods as comparative approaches. Simulation results under step disturbances and random disturbances demonstrate that the proposed method exhibits stronger robustness and better control accuracy.

1 Introduction

With continuous development of the power system toward green and low-carbon goals, the proportion of renewable energy in the power grid is increasing (Shao, B. et al., 2023; Gao, Y. et al., 2021). Global renewable energy capacity additions reached a record high of 315 GW in 2021 (Song, J. Y. et al., 2023). By the end of 2019, more than 60 countries had proposed targets for 100% renewable power systems (Zhang G. H. et al., 2023), and studies have shown that 100% renewable power systems are achievable at global, regional, and national levels by 2050 (Holechek, J. L. et al., 2022). However, the intermittent and random nature of new energy generation causes challenges to frequency stability control of the power grid (Wang, K. et al., 2023). Ensuring safe, stable, and efficient control of active power balance in emerging power systems and enhancing the integration of new energy sources constitute a pivotal research focus and a pressing challenge demanding resolution (Duan, Y. et al., 2023; Lin et al., 2022a; Lin et al., 2022b).

Existing power system frequency stabilization control methods are mainly divided into traditional control methods and intelligent control methods (Shirkhani, M. et al., 2023). Based on the proportional-integral-derivative (PID) and its improved automatic generation control (AGC) method, which is widely used in today’s power system science its simple structure, stability, and effectiveness, it is representative of traditional control methods (Daraz, 2023). For example, Zhang G. Q. et al. (2023) suggest combining fractional order integers with proportional and derivative filters to improve the frequency stability of two-area interconnected power systems containing electric vehicles. However, as the proportion of renewable energy generation continues to increase and the complexity of the system increases, traditional AGC control methods have poor control effects due to fixed strategies. Intelligent control methods represented by Q learning (Liu, G. H., 2021) are gradually replacing traditional control methods. For example, Yin and He (2023) proposed an artificial emotional deep Q-learning method for power system voltage regulation. The designed artificial emotion quantizer can improve Q-learning updates by converting social factors into agent-acceptable function values.

To enable new energy to be connected to the grid and prevent the abandonment of wind and light, new energy stations need to be equipped with energy storage systems (ESSs) (Yu, C. L. et al., 2023). The ESS represented by lithium-ion batteries is often used to assist the power system with frequency regulation because of its fast response, high tracking accuracy, and bidirectional flow of energy (Huang, Z. et al., 2022). For example, Folly and Okafor (2023) provides additional inertial support for power system networks consisting of wind renewable energy and conventional energy through battery energy storage systems.

Most of the existing methods for energy storage participation in frequency modulation are improved methods based on droop control and virtual inertia control (Li S. J. et al., 2023). Despite the improved control of energy storage by droop control and virtual inertia control methods, slower correspondence of droop control to frequency fluctuations and reduced reliability of virtual inertia control, which relies on complex electronic systems, remain (Arani et al., 2019). Therefore, model predictive control (MPC), which is characterized by strong robustness, has been widely used in energy storage control (Fei, M. D. et al., 2024). For instance, Wang et al. (2020) proposed an MPC-based dual-battery energy storage control strategy for solving the wind power fluctuation problem, in which the two batteries are kept in the charging and discharging states separately by MPC, and tracking the scheduling commands alternately. In addition, Huang, C. X. et al. (2024) proposes a distributed MPC method for load frequency control in power systems and solves it using linear quadratic programming. Although the MPC-based energy storage-assisted frequency modulation method is simple and effective, there is relatively less research on energy storage control strategies for situations where data are hard to obtain or data are limited in quantity.

Quantum ideas have been demonstrated to be applicable in power system generation control (Yin and Cao, 2022). New energy stations equipped with energy storage devices can both generate electricity and store it. Uncertainty in energy storage charging and discharging is analogous to quantum states. Inspired by quantum walks, Melnikov, A. et al. (2023) proposes a quantum model predictive control (QMPC) method for frequency control in novel power systems, which includes a high proportion of energy storage new energy stations. Quantum walks are employed to adapt to situations where data are challenging to acquire by statistically processing historical control data, allowing quantum methods to swiftly acquire the target control strategy and, thereby, increasing the data samples. For controlling the target parameter, MPC is used for real-time control, with ongoing adjustments to the predictive model parameters through feedback loops. The simulation of the constructed system validates the effectiveness of the QMPC in mitigating frequency deviations.

2 Energy storage control method based on quantum walks and model predictive control

2.1 Quantum model predictive control

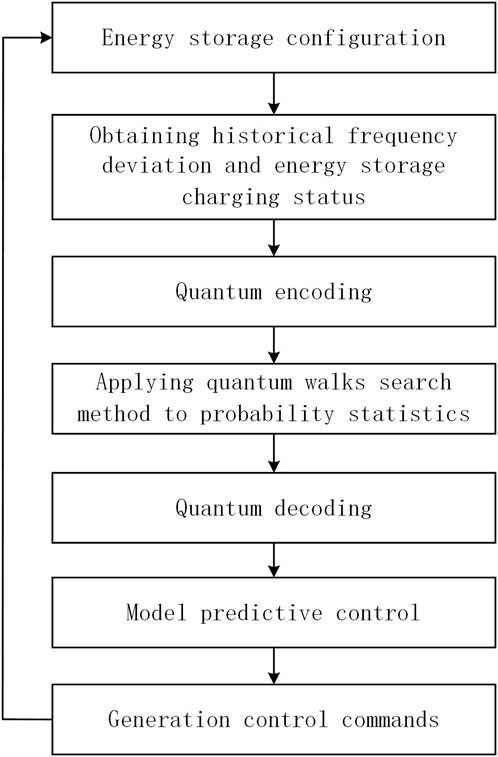
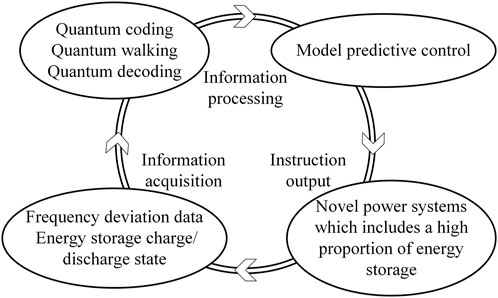
The data in the power system are changing all the time (Li, P. et al., 2022). In the new type of the power system with various new energy sources and emerging loads, the frequency deviation and energy storage charging/discharging state are full of randomness and uncertainty. The manager can foresee a certain range, however, not the exact value, which is similar to the physical state in the quantum field. Inspired by the quantum walks, a quantum model prediction control method has been proposed in this study. The QMPC strategy is mainly composed of three parts: information acquisition, information processing, and instruction output. The overall flowchart of QMPC and the relationship diagram of each part are shown in Figure 1 and Figure 2, respectively.

Figure 1

Figure 1. QMPC flowchart.

Figure 2

Figure 2. Relationship of the QMPC components.

2.2 Quantum walks

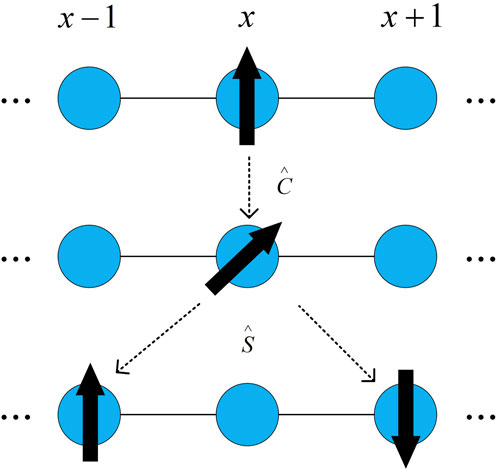
Quantum walks are the correspondence of classical random walks in the quantum world (Li S. et al., 2023; Pan, L. et al., 2024). Quantum walks can enable the walker to traverse all positions at a faster speed under the influence of quantum coherence and entanglement, thereby accelerating the solution of various problems.

In this study, historical frequency deviation $\Delta f\left(i\right)$ values were collected and coded using amplitude. Amplitude code equation is shown in Eq. 1 (Miyamoto and Ueda, 2023):

$\left|\Delta \mathit{f}\left(\mathit{i}\right)\right.⟩=\sqrt{{\mathit{p}}_{\mathit{i}}}\left|\mathbf{0}\right.⟩+\sqrt{\mathbf{1}-{\mathit{p}}_{\mathit{i}}}\left|\mathbf{1}\right.⟩,(1)$

where $\left|\Delta f\left(i\right)\right.⟩$ is the quantum state representation of $\Delta f\left(i\right)$, $p_i$ is the amplitude, and $\left|0\right.⟩$ and $\left|1\right.⟩$ are standard computational basis states.

For the frequency deviation data of the time series, quantum walks in discrete-time one-dimensional position space are chosen for evolution. The system state space of quantum walks is shown in Eq. 2 (Melnikov, A. et al., 2023)

$\mathit{H}={\mathit{H}}_{\mathit{W}}\otimes {\mathit{H}}_{\mathit{C}},(2)$

where $H_W$ is the positional state of the walker, composed of position vectors $\left|x\right.⟩,x\in \mathbb{Z}$; $x$ is the integer represented by the current position; $H_C$ is a coin state consisting of a linear combination of two basis vectors $\left|c\right.⟩,c=0,1$; $\otimes$ is the direct product operation.

The selection and design of coin operators and walking operators can affect the coherence and entanglement of quantum walks. Therefore, coin operators and walking operators play an important role in quantum walks. Each discrete step of the quantum walk can be divided into two parts: flipping a coin and walking. The coin operator $\stackrel{\wedge }{C}$ is a quantum operator used in quantum computing to model the behavior of a classical coin flip. The commonly used coin operator expression for the Hadamard operation is shown in Eq. 3 (Melnikov, A. et al., 2023)

$\stackrel{\wedge }{\mathit{C}}=\frac{\mathbf{1}}{\sqrt{\mathbf{2}}}\left(\begin{array}{c}\begin{array}{cc}\mathbf{1}& \mathbf{1}\end{array}\\ \begin{array}{cc}\mathbf{1}& -\mathbf{1}\end{array}\end{array}\right).(3)$

The walking operator $\stackrel{\wedge }{S}$ is a description of the translational operations performed by the walker according to the coin state it is in and is used to model the movement of quanta through space. The expression form of the walking operator $\stackrel{\wedge }{S}$ is shown in Eq. 4 (Melnikov, A. et al., 2023)

$\stackrel{\wedge }{\mathit{S}}=\left|\mathbf{0}⟩\right.\left.⟨\mathbf{0}\right|\otimes {\displaystyle \sum _{\mathit{x}}}\left|\mathit{x}+\mathbf{1}⟩\right.⟨\mathit{x}\left|+\left|\mathbf{1}⟩\right.\left.⟨\mathbf{1}\right|\otimes \right.{\displaystyle \sum _{\mathit{x}}}\left|\mathit{x}-\mathbf{1}⟩\right.\left.⟨\mathit{x}\right|,(4)$

where $\left.⟨\cdot \right|$ is the conjugate transpose of $\left|\cdot ⟩\right.$.

Therefore, one-step evolution of a discrete quantum walk can be described by the unitary operator $U=\stackrel{\wedge }{S}\stackrel{\wedge }{C}$. At the moment $t$, the unitary operator $U$ acts on the state $\left|\psi (t\right.-\left.1\right)⟩$ to obtain the evolved state $\left|\psi \left(t\right)\right.⟩$. As shown in Figure 3, at time $t-1$, the spin-up coin state $\left|1\right.⟩$ at grid point $x$, represented by an upward solid arrow in Figure 3, undergoes a coin flip first under the action of the coin operator $\stackrel{\wedge }{\mathit{C}}$. Subsequently, combined with the operation of the conditional shift operator $\stackrel{\wedge }{\mathit{S}}$ in Equation 4, the particle at grid point $x$ with coin state $\left|1\right.⟩$ moves one step to the right to grid point $x+1$, while the particle with coin state $\left|0\right.⟩$ moves one step to the left to grid point $x-1$. At this point, a complete step of quantum walk evolution is achieved.

Figure 3

Figure 3. Quantum walks in discrete-time one-dimensional position space.

On repeatedly applying $U$ to the initial state, after walking $N$ steps, the end state of the whole system evolves to $\left|{\psi }_N⟩\right.=U^N\left|{\psi }_0⟩\right.$.

Quantum decoding can be accomplished by measuring the amplitude during evolution. Since measurements of quantum states are usually statistical descriptions of classical information, and the expectation values of quantum operators are statistical descriptions of quantum states, the decoding process involves measuring the expectation values of certain quantum operators in order to extract classical information from quantum states. Considering the correlation with frequency deviation, this study chooses to measure the Pauli-Z operator. The estimated value of the frequency deviation at step $i$ in the quantum state $\Delta f^E\left(i\right)$ can be calculated from the amplitude obtained by decoding (Miyamoto and Ueda, 2023), and the formula is shown in Eq. 5:

$\Delta {\mathit{f}}^{\mathit{E}}\left(\mathit{i}\right)=\mathbf{2}\left(\left.⟨{\mathit{\psi }}_{\mathit{i}}\right|{\mathit{\sigma }}_{\mathit{Z}}\left|{\mathit{\psi }}_{\mathit{i}}⟩\right.\right)-\mathbf{1},(5)$

where $\left|{\psi }_i⟩\right.$ is the quantum state after walking $i$ steps, $\left.⟨{\psi }_i\right|$ is the conjugate transpose of $\left|{\psi }_i⟩\right.$, and ${\sigma }_Z$ is the Pauli-Z operator.

In this study, the quantum walks can be divided into three parts: encoding, quantum state walk, and decoding. Amplitude coding is a commonly used coding method in quantum computing. Through amplitude coding, the frequency deviation data can be reflected to the amplitude of the quantum state to establish the mapping relationship between the classical world and the quantum world. Next, the unitary operator $U$ acting on the quantum state is obtained by setting up the walking operator $\stackrel{\wedge }{S}$ and the coin operator $\stackrel{\wedge }{C}$ to specify the walking law. Finally, the expectation value of the Pauli-Z operator is computed during the quantum decoding process to extract the classical information from the quantum state. The pseudocode for quantum walks is as follows:

2.3 Model predictive control

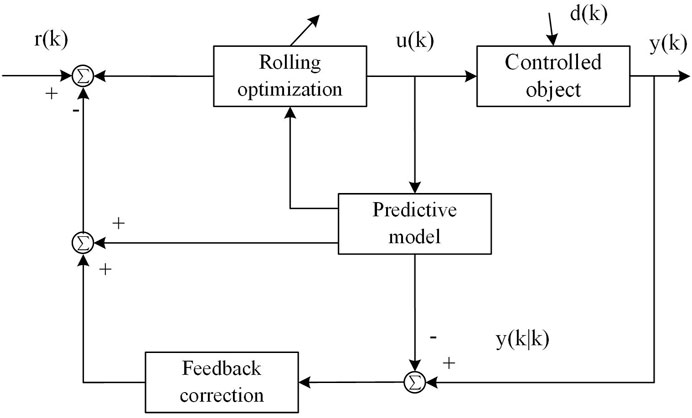
Model predictive control (MPC) is a closed-loop optimization process based on a predictive model, rolling optimization, and feedback correction. Instead of optimizing the entire future time series at once, the model predictive controller reconsiders the best control strategy for a finite period at each time step. Rolling optimization is one of the characteristics of MPC. Over time, the entire optimization window moves forward, continuously updating and adjusting control inputs to adapt to the current state and objectives of the system, ensuring that the controlled system operates more robustly in dynamic environments. The framework of MPC is shown in Figure 4.

Figure 4

Figure 4. MPC framework.

In this study, the system is discretized and the formula of system optimization problem based on model predictive control over a period of time $k$ is shown in Eq. 6 (Hu, J. F. et al., 2021)

$\mathit{J}\left(\mathit{x}\left(\mathit{k}\right),{\mathit{U}}^{*}\right)=\left.{\displaystyle {\sum }_{\mathit{i}=\mathbf{0}}^{\mathit{P}-\mathbf{1}}}\mathit{L}\left(\mathit{x}\left(\mathit{k}+\mathit{i}\right)|\mathit{k}\right),\mathit{u}\left(\mathit{k}+\mathit{i}\left|\mathit{k}\right.\right)\right)+\mathit{V}\left(\mathit{x}\left(\mathit{k}+\mathit{P}\left|\mathit{k}\right.\right)\right),(6)$

where $J\left(\cdot \right)$ is the overall performance metric function and the two variables are the state vector at the current time step $x\left(k\right)$ and the sequence of control inputs $U^{*}$, where $U^{*}=\left[u\left(k\left|k),u(k+1\right|k\right),...,u\left(k+P-1\left|k\right.\right)\right]$; $u\left(k+i|k\right)$ is the predicted value of the system control input at time step $k$ for the future time step $k+i$; $L\left(\cdot \right)$ is time window performance indicator function; $V\left(\cdot \right)$ is the terminal cost function; $P$ is the number of steps corresponding to the predicted time domain.

Solve the control sequence $U^{*}$ of length $P$ to obtain the optimal control sequence $U^{\text{opt}}$, take the first element of $U^{\text{opt}}$ input to the controlled system, and hold the command until the next time step. Finally, the control quantity is compensated according to the target error caused by disturbances and deviations, the future dynamic output behavior is predicted, and feedback correction is performed to improve the robustness and control accuracy of the system.

3 System modeling and analysis

3.1 System frequency characteristics

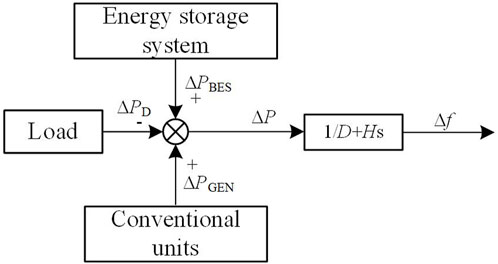
In the event of an imbalance between the active power output of generator units and the power demand, the power system experiences power fluctuations, leading to frequency deviations (Zhang X. et al., 2023). The power system model chosen in this study mainly includes conventional units, load, and ESS. The frequency characteristics of the system are shown in Figure 5.

Figure 5

Figure 5. System frequency characterization.

The frequency deviation $\Delta f$ and power deviation $\Delta P$ can be obtained from Figure 5, the equations are shown in Eqs 7, 8:

$\Delta \mathit{f}=\frac{\Delta \mathit{P}}{\mathit{D}+\mathit{H}\mathit{s}},(7)$

$\Delta \mathit{P}=\Delta {\mathit{P}}_{\mathbf{GEN}}+\Delta {\mathit{P}}_{\mathbf{BES}}-\Delta {\mathit{P}}_{\mathit{D}},(8)$

where $\Delta f$ is frequency deviation; $\Delta P$ is power deviation; and $\Delta P_{\text{GEN}}$, $\Delta P_{\text{BES}}$, and $\Delta P_D$ are the unit output power, energy storage output power, and load disturbance, respectively. $D$ and $H$ are the load-damping factor and the inertia time constant of the grid, respectively.

3.2 Modeling of the novel power system that includes a high proportion of energy storage new energy stations

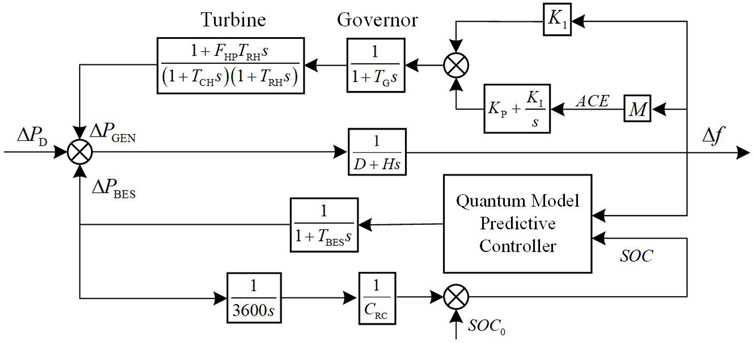
In this study, a single-area power grid equipped with a battery energy storage unit is selected as the research object. The primary frequency modulation unit, the secondary frequency modulation unit, and the storage battery model are expressed in the form of the transfer function, and the power system frequency modulation model is obtained as shown in Figure 6.

Figure 6

Figure 6. Novel power system frequency modulation model.

Battery energy storage (BES) is a common form of the ESS; therefore, BES is chosen for this study. To prevent overcharging and discharging of energy storage batteries, the model takes into account the state of charge of the energy storage battery and inputs it into the quantum model predictive controller through a feedback channel. In practice, the energy storage participates in system frequency regulation with loss and delay in the output power; therefore, the converter and filtering link are replaced by the first-order inertia link equivalent.

In Figure 6, $s$ is the Laplace operator; $M$ is the grid deviation factor; $K_p$ and $K_I$ are the proportional and integral coefficients of the PI controller, respectively; $T_G$ is the governor time constant; $T_{\text{CH}}$, $T_{\text{RH}}$, and $F_{\text{HP}}$ are the turbine time constant, re-heater time constant, and re-heater gain, respectively; $T_{\text{BES}}$ is the charging and discharging time constant of the BES; $C_{\text{RC}}$ is the rated capacity of BES; $SOC$ and $SO{C}_0$ are the actual state of charge and the initial state of charge of BES, respectively.

4 Example analysis

4.1 Parameter pretreatment

To verify the feasibility and effectiveness of the quantum model prediction strategy proposed in this study, the PID and MPC methods, which are commonly used in power systems, are selected as comparison algorithms. The optimal parameters in the operating range are obtained by empirical methods through continuous debugging. A novel power system that includes a high proportion of energy storage new energy stations is established and simulated on the MATLAB/Simulink platform.

The rated capacity of the conventional unit is set to 500 MW. The ESS consists of 10 battery storage units, and each battery storage unit has a power of 1 MW and a capacity of 0.5 MWh. The base frequency of the system is set to 50 Hz. The initial state of charge (SOC) of the ESS is an important parameter (Zhang et al., 2023c), and the initial SOC is set to 0.6 in this study. The simulation time is set to 60 s. The other main relevant parameters are shown in Table 1.

Table 1

Table 1. Main parameters of the model.

4.2 Analysis of step perturbation

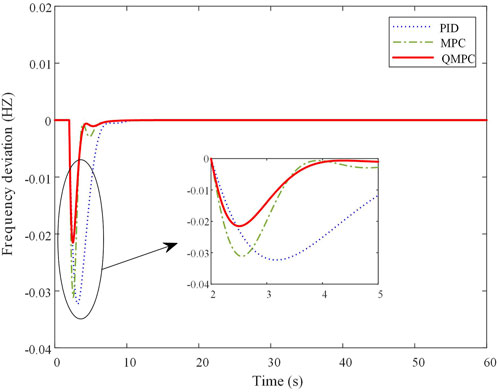
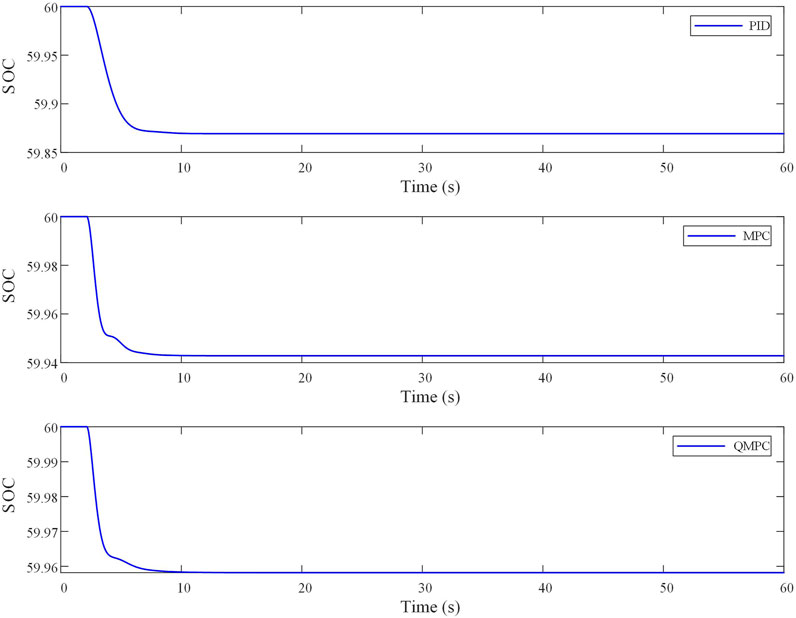
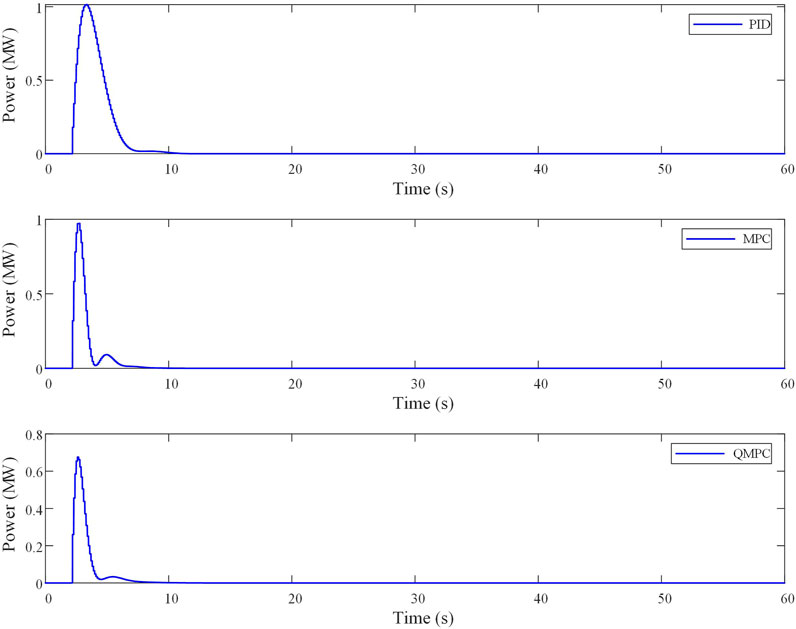
Step perturbation, which is used to model the effects of sudden load changes on the power system in real situations, is a common type of perturbation encountered in power system simulation. By adding a step disturbance at the 2nd second, the frequency deviation curve, SOC curve, and energy storage output curve of QMPC and comparison methods are shown in Figures 7, 8, 9.

Figure 7

Figure 7. Frequency deviation curve comparison under step perturbation.

Figure 8

Figure 8. SOC curve comparison under step perturbation.

Figure 9

Figure 9. BES output power curve comparison under step perturbation.

As shown in Figure 7, Figure 8, and Figure 9, the load is suddenly increased at 2 s, resulting in a deficit in the active power of the system. As can be seen from Table 2, the maximum frequency deviation obtained by the PID controller is −0.032 Hz, with a regulation time of 4.34 s. The MPC approach yields a maximum frequency deviation of −0.031 Hz and a regulation time of 3.36 s. The QMPC proposed in this study has the best control effect, with the maximum frequency deviation and the regulation time being −0.022 Hz and 1.80 s, respectively; the maximum frequency deviation and the regulation time are at least 29.1% and 46.4% smaller than the previous two, respectively. Therefore, the QMPC can more effectively restrain the increase in frequency deviation under step disturbance and more quickly stabilize the system in the target state with better dynamic characteristics. This further illustrates the ability of QMPC to better adapt to a sudden load in the power system.

Table 2

Table 2. Comparison of control performance under step perturbation.

4.3 Analysis of random perturbation

Normally distributed random numbers are generated in MATLAB/Simulink as random perturbations added to the simulation model to simulate load joining with randomness and volatility.

The error integral criterion is commonly used as an evaluation index in the control field. Therefore, in this section, integral absolute error (IAE), integral squared error (ISE), integral time multiple absolute errors (ITAE), and integral time multiple square error (ITSE) are chosen as evaluation indexes. The specific formulas are shown in Eqs 9–12:

$\mathit{I}\mathit{A}\mathit{E}={\displaystyle \underset{\mathbf{0}}{\overset{\mathit{T}}{\int }}}\left|\Delta \mathit{f}\left.\left(\mathit{t}\right)\right|\mathit{d}\mathit{t}\right.,(9)$

$\mathit{I}\mathit{S}\mathit{E}={\displaystyle \underset{\mathbf{0}}{\overset{\mathit{T}}{\int }}}\Delta {\mathit{f}}^{\mathbf{2}}\left(\mathit{t}\right)\mathit{d}\mathit{t},(10)$

$\mathit{I}\mathit{T}\mathit{A}\mathit{E}={\displaystyle \underset{\mathbf{0}}{\overset{\mathit{T}}{\int }}}\mathit{t}|\Delta \mathit{f}\left.\left(\mathit{t}\right)\right|\mathit{d}\mathit{t},(11)$

$\mathit{I}\mathit{T}\mathit{S}\mathit{E}={\displaystyle \underset{\mathbf{0}}{\overset{\mathit{T}}{\int }}}\mathit{t}\Delta {\mathit{f}}^{\mathbf{2}}\left(\mathit{t}\right)\mathit{d}\mathit{t},(12)$

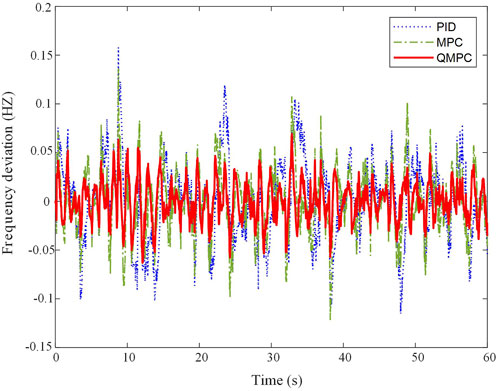
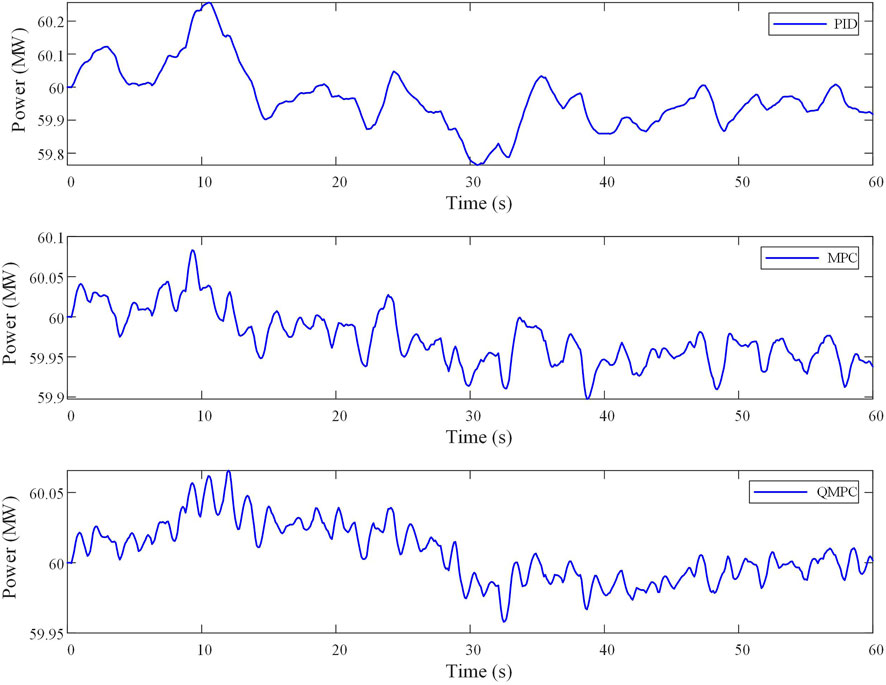
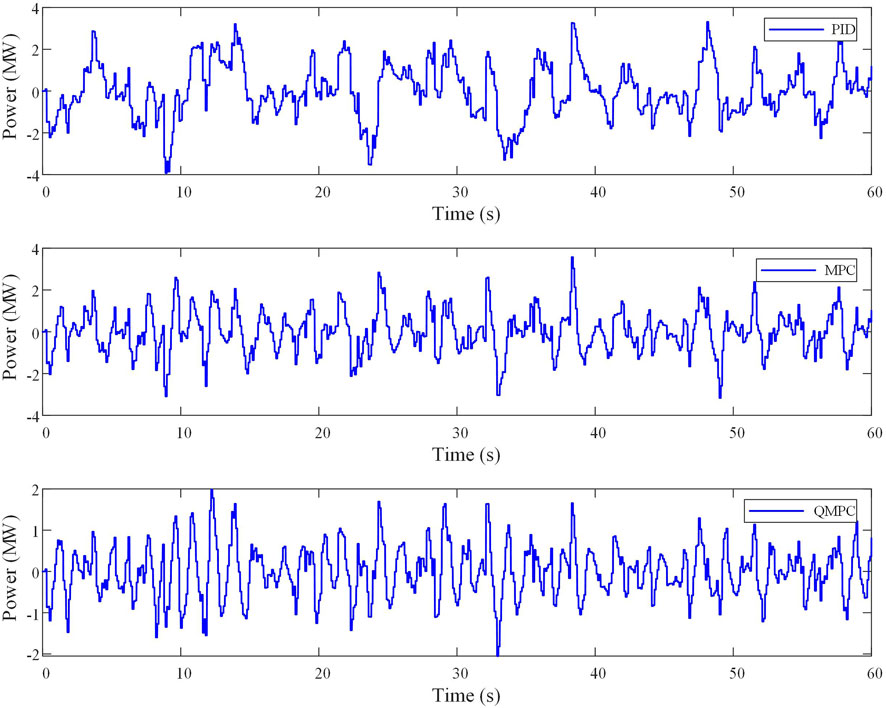
After the random perturbation load is added, the frequency deviation curve, SOC curve, and energy storage output curve of QMPC compared to other comparison methods are shown in Figure 10, Figure 11, and Figure 12, respectively. The error integral indexes, mean absolute error (MAE), and standard deviation (SD) are shown in Table 3.

Figure 10

Figure 10. Frequency deviation curve comparison under random perturbation.

Figure 11

Figure 11. SOC curve comparison under random perturbation.

Figure 12

Figure 12. BES output power curve comparison under random perturbation.

Table 3

Table 3. Comparison of indicators.

It can be concluded from Figure 10, Figure 11, Figure 12, and Table 4 that under random perturbation, the maximum frequency deviation obtained by PID, MPC, and QMPC is 0.157 Hz, 0.136 Hz, and 0.069 Hz, respectively, and the average frequency deviation of the absolute values obtained is 0.032 Hz, 0.025 Hz, and 0.016 Hz, respectively. The maximum frequency deviation and average frequency deviation of the absolute values in the proposed method are at least 49.26% and 36.00% smaller than those in the comparison method, respectively. As shown in Table 3, the four integration error indexes of the proposed algorithm have minimum values, with reductions of at least 34.92%, 60.78%, 36.96%, and 63.63%, respectively. The mean absolute error and standard deviation of the proposed method are the minimum values of various algorithms. The data above indicate that the proposed method exhibits stronger overall anti-interference ability and stability. It has excellent control performance and robustness under random disturbance. Therefore, the QMPC is more adaptable to complex operating environments than conventional control methods.

Table 4

Table 4. Comparison of control performance under random perturbation.

5 Conclusion

In response to the frequency modulation problem of a novel power system that includes a high proportion of energy storage new energy stations, this study established a frequency regulation model for power systems equipped with battery energy storage and proposed the QMPC method. Through simulation analysis, the following conclusions are obtained:

(1) This study expands the raw data by encoding historical frequency deviation time series with quantum walks and decoding operations to provide more information for model predictive control and improve the controller’s understanding of the system dynamics.

(2) Compared with the comparison method, the proposed method obtains the minimum frequency deviation, regulation time, and integral control error indexes under two different types of perturbation simulations, and it has a stronger control performance.

However, the proposed method has high computational resource requirements, which increases the time complexity (Zhang et al., 2023d). Compared with real-world simulation, the types of perturbations simulated by the simulation are too idealized, which may be more complicated in real engineering. In addition, when the system parameters change, the parameters of QMPC should be adjusted accordingly. Therefore, further research work can focus on optimizing the algorithm structure to improve computational efficiency, increasing the types of new energy and power electronic devices in the system to enrich the power system structure, and introducing online learning and optimization techniques in quantum walks to cope with the change in system parameters.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

WL: writing–original draft. YX: writing–original draft. WD: writing–original draft. SW: writing–original draft. ZF: writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Yangjiang Power Supply Bureau of Guangdong Power Grid Co., Ltd (Research on Online Monitoring and Coordinated Control Technology for Primary Frequency Modulation of New Energy Field Station, 031700KC23040009). The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication

Acknowledgments

The authors thank the Yangjiang Power Supply Bureau of Guangdong Power Grid Co., Ltd. for their support.

Conflict of interest

Authors WL, YX, and SW were employed by Yangjiang Power Supply Bureau of Guangdong Power Grid Co., Ltd.

Author WD was employed by Electric Power Science Research Institute of Guangdong Power Grid Co., Ltd.

Author ZF was employed by Shenzhen Huagong Energy Technology Co., Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2024.1354262/full#supplementary-material

References

Arani, A. A. K., Gharehpetian, G. B., and Abedi, M. (2019). Review on energy storage systems control methods in microgrids. Int. J. Electr. power and energy Syst. 107, 745–757. doi:10.1016/j.ijepes.2018.12.040

CrossRef Full Text | Google Scholar

Daraz, A. (2023). Optimized cascaded controller for frequency stabilization of marine microgrid system. Appl. Energy 350, 121774. doi:10.1016/j.apenergy.2023.121774

CrossRef Full Text | Google Scholar

Duan, Y., Zhao, Y., and Hu, J. (2023). An initialization-free distributed algorithm for dynamic economic dispatch problems in microgrid: modeling, optimization and analysis. Sustain. Energy, Grids Netw. 34, 101004. doi:10.1016/j.segan.2023.101004

CrossRef Full Text | Google Scholar

Fei, M. D., Zhang, Z. Y., Zhao, W. B., Zhang, P., and Xing, X. L. (2024). Optimal power distribution control in modular power architecture using hydraulic free piston engines. Appl. Energy 358, 122540. doi:10.1016/j.apenergy.2023.122540

CrossRef Full Text | Google Scholar

Folly, K. A., and Okafor, C. E. (2023). “Provision of additional inertia support for a power system network using battery energy storage system,” in IEEE access (IEEE), 74936–74952. doi:10.1109/access.2023.3295333

CrossRef Full Text | Google Scholar

Gao, Y., Doppelbauer, M., Ou, J., and Qu, R. (2021). Design of a double-side flux modulation permanent magnet machine for servo application. IEEE J. Emerg. Sel. Top. Power Electron. 10 (2), 1671–1682. doi:10.1109/JESTPE.2021.3105557

CrossRef Full Text | Google Scholar

Holechek, J. L., Geli, H. M. E., Sawalhah, M. N., and Valdez, R. (2022). A global assessment: can renewable energy replace fossil fuels by 2050? Sustainability 14 (8), 4792. doi:10.3390/su14084792

CrossRef Full Text | Google Scholar

Hu, J. F., Shan, Y. H., Guerrero, J. M., Ioinovici, A., Chan, K. W., and Rodriguez, J. (2021). Model predictive control of microgrids–An overview. Renew. Sustain. Energy Rev. 136, 110422. doi:10.1016/j.rser.2020.110422

CrossRef Full Text | Google Scholar

Huang, C. X., Yang, M. T., Ge, H., Deng, S., and Chen, C. Y. (2024). DMPC-based load frequency control of multi-area power systems with heterogeneous energy storage system considering SOC consensus. Electr. Power Syst. Res. 228, 110064. doi:10.1016/j.epsr.2023.110064

CrossRef Full Text | Google Scholar

Huang, Z., Luo, P. F., Jia, S. K., Zheng, H. H., and Lu, Z. C. (2022). A sulfur-doped carbon-enhanced Na3V2 (PO4) 3 nanocomposite for sodium-ion storage. J. Phys. Chem. Solids 167, 110746. doi:10.1016/j.jpcs.2022.110746

CrossRef Full Text | Google Scholar

Li, P., Hu, J., Qiu, L., Zhao, Y., and Ghosh, B. K. (2022). A distributed economic dispatch strategy for power–water networks. IEEE Trans. Control Netw. Syst. 9 (1), 356–366. doi:10.1109/TCNS.2021.3104103

CrossRef Full Text | Google Scholar

Li, S., Wang, F., Ouyang, L., Chen, X., Yang, Z., Rozga, P., et al. (2023b). “Differential low-temperature AC breakdown between synthetic ester and mineral oils: insights from both molecular dynamics and quantum mechanics,” in IEEE transactions on dielectrics and electrical insulation (IEEE). doi:10.1109/TDEI.2023.3345299

CrossRef Full Text | Google Scholar

Li, S. J., Xu, Q. S., and Huang, J. Y. (2023a). Research on the integrated application of battery energy storage systems in grid peak and frequency regulation. J. Energy Storage 59, 106459. doi:10.1016/j.est.2022.106459

CrossRef Full Text | Google Scholar

Lin, X., Liu, Y., Yu, J., Yu, R., Zhang, J., and Wen, H. (2022a). Stability analysis of Three-phase Grid-Connected inverter under the weak grids with asymmetrical grid impedance by LTP theory in time domain. Int. J. Electr. Power and Energy Syst. 142, 108244. doi:10.1016/j.ijepes.2022.108244

CrossRef Full Text | Google Scholar

Lin, X., Wen, Y., Yu, R., Yu, J., and Wen, H. (2022b). Improved weak grids synchronization unit for passivity enhancement of grid-connected inverter. IEEE J. Emerg. Sel. Top. Power Electron. 10 (6), 7084–7097. doi:10.1109/JESTPE.2022.3168655

CrossRef Full Text | Google Scholar

Liu, G. H. (2021). Data collection in MI-assisted wireless powered underground sensor networks: directions, recent advances, and challenges. IEEE Commun. Mag. 59 (4), 132–138. doi:10.1109/MCOM.001.2000921

CrossRef Full Text | Google Scholar

Melnikov, A., Kordzanganeh, M., Alodjants, A., and Lee, R.-K. (2023). Quantum machine learning: from physics to software engineering. Adv. Phys. X 8 (1), 2165452. doi:10.1080/23746149.2023.2165452

CrossRef Full Text | Google Scholar

Miyamoto, K., and Ueda, H. (2023). Extracting a function encoded in amplitudes of a quantum state by tensor network and orthogonal function expansion. Quantum Inf. Process. 22 (6), 239. doi:10.1007/s11128-023-03937-y

CrossRef Full Text | Google Scholar

Pan, L., Wang, F., He, Y., Sun, X., Du, G., Zhou, Q., et al. (2024). “Reassessing self-healing in metallized film capacitors: a focus on safety and damage analysis,” in IEEE transactions on dielectrics and electrical insulation (IEEE). doi:10.1109/TDEI.2024.3357441

CrossRef Full Text | Google Scholar

Shao, B., Xiao, Q., Xiong, L., Wang, L., Yang, Y., Chen, Z., et al. (2023). Power coupling analysis and improved decoupling control for the VSC connected to a weak AC grid. Int. J. Electr. Power and Energy Syst. 145, 108645. doi:10.1016/j.ijepes.2022.108645

CrossRef Full Text | Google Scholar

Shirkhani, M., Tavoosi, J., Danyali, S., Sarvenoee, A. K., Abdali, A., Mohammadzadeh, A., et al. (2023). A review on microgrid decentralized energy/voltage control structures and methods. Energy Rep. 10, 368–380. doi:10.1016/j.egyr.2023.06.022

CrossRef Full Text | Google Scholar

Song, J. Y., Zhou, X. H., Zhou, Z. Q., Wang, Y., Wang, Y. F., and Wang, X. T. (2023). Review of low inertia in power systems caused by high proportion of renewable energy grid integration. Energies 16 (16), 6042. doi:10.3390/en16166042

CrossRef Full Text | Google Scholar

Wang, B., Cai, G. W., and Yang, D. Y. (2020). Dispatching of a wind farm incorporated with dual-battery energy storage system using model predictive control. IEEE Access 8, 144442–144452. doi:10.1109/access.2020.3014214

CrossRef Full Text | Google Scholar

Wang, K., Xie, Y. F., Zhang, W. M., Cai, H., Liang, F., and Li, Y. (2023). Research on optimal dispatch of distributed energy considering new energy consumption. Energy Rep. 10, 1888–1898. doi:10.1016/j.egyr.2023.08.040

CrossRef Full Text | Google Scholar

Yin, L. F., and Cao, X. H. (2022). Inspired lightweight robust quantum Q-learning for smart generation control of power systems. Appl. Soft Comput. 131, 109804. doi:10.1016/j.asoc.2022.109804

CrossRef Full Text | Google Scholar

Yin, L. F., and He, X. Y. (2023). Artificial emotional deep Q learning for real-time smart voltage control of cyber-physical social power systems. Energy 273, 127232. doi:10.1016/j.energy.2023.127232

CrossRef Full Text | Google Scholar

Yu, C. L., Zhang, S., Shen, J. H., Li, W. W., Ji, Y. C., and Wang, J. Q. (2023). Research on the optimal capacity configuration method of park-type wind-photovoltaic storage complementary power generation system. J. Phys. Conf. Ser. IOP Publ. 2503 (1), 012042. doi:10.1088/1742-6596/2503/1/012042

CrossRef Full Text | Google Scholar

Zhang, G. H., Ren, J. Z., Zeng, Y., Liu, F., Wang, S. B., and Jia, H. J. (2023a). Security assessment method for inertia and frequency stability of high proportional renewable energy system. Int. J. Electr. Power and Energy Syst. 153, 109309. doi:10.1016/j.ijepes.2023.109309

CrossRef Full Text | Google Scholar

Zhang, G. Q., Daraz, A., Khan, I. A., Ullah, M., and Basit, A. (2023b). Driver training based optimized fractional order PI-pdf controller for frequency stabilization of diverse hybrid power system. Fractal Fract. 7 (4), 315. doi:10.3390/fractalfract7040315

CrossRef Full Text | Google Scholar

Zhang, L., Sun, C., Cai, G., and Koh, L. H. (2023c). Charging and discharging optimization strategy for electric vehicles considering elasticity demand response. eTransportation 18, 100262. doi:10.1016/j.etran.2023.100262

CrossRef Full Text | Google Scholar

Zhang, L., Yin, Q., Zhu, W., Lyu, L., Jiang, L., Koh, L. H., et al. (2023d). “Research on the orderly charging and discharging mechanism of electric vehicles considering travel characteristics and carbon quota,” in IEEE transactions on transportation electrification (IEEE). doi:10.1109/TTE.2023.3296964

CrossRef Full Text | Google Scholar

Zhang, X., Gong, L., Zhao, X., Li, R., Yang, L., and Wang, B. (2023e). Voltage and frequency stabilization control strategy of virtual synchronous generator based on small signal model. Energy Rep. 9, 583–590. doi:10.1016/j.egyr.2023.03.071

CrossRef Full Text | Google Scholar