A data-driven early warning method for thermal runaway of energy storage batteries and its application in retired lithium batteries

The safety of battery energy storage systems (BES) is of paramount importance for societal development and the wellbeing of the people. This is particularly true for retired batteries, as their performance degradation increases the likelihood of thermal runaway occurrences. Existing early warning methods for BES thermal runaway face two main challenges: mechanism-based research methods only consider a single operating state, making their application and promotion difficult; while data-driven methods based on supervised learning struggle with limited sample sizes. To address these issues, this paper proposes a data-driven early warning method for BES thermal runaway. The method utilizes unsupervised learning to create a framework that measures BES differences through reconstruction errors, enabling effective handling of limited samples. Additionally, ensemble learning is employed to enhance the method’s stability and quantify the probability of BES experiencing thermal runaway. To accurately capture the time-varying behaviors of BES, such as voltage, temperature, current, and state of charge (SOC), and detect performance differences in BES before and after thermal runaway, a bidirectional long short-term memory (Bi-LSTM) network with an attention mechanism is utilized. This approach effectively extracts features from training data. Subsequently, a Case study was conducted using the actual operation data of retired lithium batteries to verify the effectiveness of the proposed method.

1 Introduction

Currently, lithium battery are primarily used in electric vehicles and energy storage stations. With the large-scale promotion of electric vehicles and energy storage stations, as well as the secondary use of retired lithium batteries, incidents of combustion and explosions caused by thermal runaway of lithium battery are not uncommon. According to incomplete statistics, there have been 32 fire and explosion incidents caused by thermal runaway in energy storage stations globally over the past decade. The combustion or explosion of lithium battery in energy systems poses a significant threat to the national economy and people’s lives. The National Renewable Energy Lab (Doughty, 2012; Wang et al., 2012) considers early warning of lithium-ion battery thermal runaway as an important measure to safeguard people’s lives and property. Retired batteries have a shorter lifespan compared to operating batteries. As cascading or reusing retired lithium battery is an important measure to improve the full life cycle utilization rate of lithium battery, retired batteries are more likely to approach the end of thermal runaway. Therefore, early warning of thermal runaway in retired batteries can ensure the personal safety of users.

The causes of lithium-ion battery thermal runaway can be divided into three categories: mechanical failure, electrical failure (Wen et al., 2012; Spotnitz et al., 2003), and thermal failure, with a common factor being internal short circuit (Zheng et al., 2013). The development time scale of internal short circuits in lithium battery, including retired batteries, can be as long as several hundred hours (Feng et al., 2014; Barnett, 2014). Initial symptoms may not be apparent, while the final stage can potentially lead to combustion and explosions within a short period of time. Therefore, the issue of thermal runaway prevention and control warning is of great significance. To solve the problem of thermal runaway prevention and control warning, the mainstream methods in academia are divided into three categories: experimental-based, model-based, and data-driven. Experimental-based methods can determine the temperature safety boundaries of batteries and guide battery system design. However, the accuracy of the experimental method depends on a large number of experiments (Feng et al., 2018), which can be unsafe and costly, making it difficult to promote and apply. Model-based methods mainly indirectly warn of thermal runaway by estimating the temperature rise, voltage change, or temperature distribution of the battery (Shah et al., 2016; Chalise et al., 2017; Ren et al., 2018). The advantage of this method is that the physical meaning is clear, but the disadvantage is that it is more suitable for a relatively simple working condition and may not be applicable to complex and variable real-world conditions (Chen et al., 2011; Ping et al., 2014).

The data-driven approach is one of the emerging research hotspots in this field. By using historical data, data models can be established to analyze the relationship between lithium battery voltage, temperature, current, SOC, and its thermal runaway. Its advantage is that it can reflect the real working conditions of the battery and avoid the study of the complex electrochemical mechanism inside the lithium battery. Currently, data-driven methods are mostly supervised methods, and the research idea is to obtain thermal runaway lithium battery data under specific working conditions through experimental methods, and use it as a label to train neural network models to distinguish the thermal runaway situation of lithium batteries (Fang et al., 2012; Hussein and Chehade, 2020). However, the above-mentioned supervised methods have the following problems: although there is a large amount of operational data for lithium batteries, the proportion of thermal runaway battery data is small, resulting in a small sample problem and low model accuracy. Literature (Ding et al., 2021) have used similarity theory to construct more thermal runaway data, which has alleviated the problem of small samples to some extent. However, the thermally runaway data constructed by theory differs from the actual data, which affects the accuracy of the model. Therefore, supervised methods have limitations in this problem.

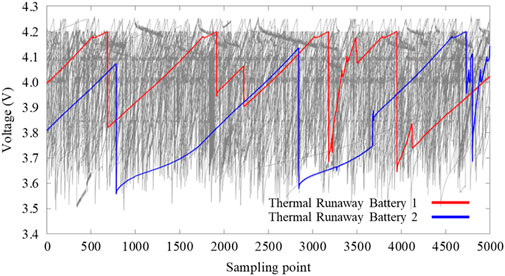
Unsupervised methods can learn from unlabeled data sets and are insensitive to imbalanced data. This method is suitable for the problem of abnormal judgment of lithium batteries containing a large number of normal samples. In literature (Yi and Xu, 2021), unsupervised methods were used for battery fault diagnosis, mainly by classifying batteries based on feature distances. However, the differences between lithium batteries in the mid to pre-thermal runaway stages and normal batteries are very small, as shown in Figures 1, 2. In the figures, thermal runaway battery data is labeled in red and blue, while normal battery data is labeled in gray. Using a simple distance calculation method for unsupervised clustering makes it difficult to distinguish thermal runaway lithium batteries. The current challenge is how to effectively extract the temporal characteristics (this paper regards the time-varying data information of potential thermal runaway batteries running for a long-time scale as temporal characteristics) of lithium battery voltage, temperature, SOC and other data during the thermal runaway process, and efficiently excavate the differences in features between thermal runaway lithium batteries and normal batteries, in order to improve model accuracy. The time series modeling of LSTM has been applied in the field of predicting the lifespan of automotive batteries, but it has not addressed the issue of thermal runaway of retired batteries (Ma et al., 2023a; Ma et al., 2023b). The concept of reconstruction error has made progress in other fields of anomaly detection (Hundman et al., 2018; Sakurada and Yairi, 2014).

FIGURE 1

FIGURE 1. Battery voltage versus time curve.

FIGURE 2

FIGURE 2. Battery temperature versus time curve.

This paper proposes a data-driven lithium battery thermal runaway early warning method based on reconstruction error calculation to address the aforementioned problems. Firstly, an unsupervised and ensemble learning-based framework for data-driven electrochemical lithium battery thermal runaway early warning is established, and the accuracy of this framework depends on the feature extraction ability of the basic model. To this end, a lithium battery data features extraction method based on Bi-LSTM and attention mechanism is proposed. The method aims to identify potential thermally unstable lithium batteries under long-term real working conditions, and has a wider range of applications compared to traditional mechanism-based methods (such as repeated charge and discharge) for identifying thermally unstable batteries under single working conditions. In essence, supervised learning methods require a typical form of data pattern, but the mechanism of thermal runaway in decommissioned batteries is complex, and there is no uniform trend in the abnormal performance of multidimensional data. However, normal batteries do not lack training samples. The unsupervised learning method proposed in this article is to train a large number of normal battery data to form a model, and the cumulative amount of reconstruction error calculated by the model for thermal runaway batteries is significantly increased. Therefore, the method proposed in this article has a good early warning effect on the thermal runaway problem of decommissioned batteries. The effectiveness of the proposed method is verified by the real operating data of electric vehicle lithium batteries. The proposed method in this paper is also applicable to the thermal runaway early warning of retired lithium batteries. The main contributions of this article are as follows:

1) Establish a lithium battery thermal runaway early warning framework based on unsupervised and ensemble learning, which can effectively deal with the problem of small sample size. Firstly, the reconstruction error of lithium battery time series data is used to define the degree of difference between batteries, and the idea of using small reconstruction error for normal data and large reconstruction error for abnormal data is used to construct a reconstruction error-based basic model. Furthermore, an unsupervised learning-based electrochemical lithium battery thermal runaway early warning ensemble framework is established to quantify the probability of lithium battery thermal runaway, enhance model stability, and enable the basic model to accurately select thermally unstable lithium batteries in different validation sets.

2) Propose a lithium battery data feature extraction method based on Bi-LSTM and attention mechanism. Firstly, a lithium battery parameter time series feature extraction method based on Bi-LSTM is proposed, which effectively extracts the time-varying characteristics of lithium battery voltage, temperature, SOC, and other data during the thermal runaway process. Based on this, an attention mechanism-based data mining algorithm is proposed to solve the problem of different importance of each dimension data at different times, realize the differentiated weight learning of various lithium battery data at different times, and further reduce the missed diagnosis and misdiagnosis of the basic model for thermally unstable lithium batteries.

2 A basic model for theramal runaway failure warning of retired batteries based on reconstruction error calculation

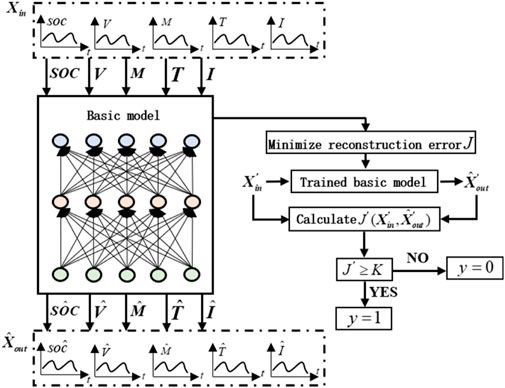
The core idea of unsupervised learning is to mine potential rules in unlabeled data sets, so as to classify data. The reconstruction error is an important classification basis of unsupervised learning method. The reconstruction error is obtained by calculating the difference between the original data and the reconstructed data (Figure 3). This paper uses unsupervised learning to measure the risk of thermal runaway failure of retired batteries. Its ideas are as follows: First, use the operating data of normal batteries to train the basic model; Subsequently, the operating status of the battery is determined by measuring the reconstruction error of the data to be determined. During the abnormal detection process of the battery to be tested, due to the difference between the thermal runaway failed battery data and the normal data used for training, the reconstruction error of the detection is relatively large; The normal battery data is close to the training samples, and the test reconstruction error is relatively small. Therefore, the reconstruction error of the battery data to be tested can serve as a criterion for determining whether the battery has thermal runaway failure.

FIGURE 3

FIGURE 3. Basic model for thermal runaway early warning of BES.

The operating status of retired batteries can be described by variables such as battery voltage (V), current (I), state of charge (SOC), temperature (T), etc. These variables can be monitored in real-time through the Battery Management System (BMS). Due to the different dimensions and significant numerical differences of these variables, in order to ensure the training accuracy of the basic reconstruction model, it is necessary to first standardize the data of the energy storage battery samples. Due to the influence of changes in battery physical state on retired batteries, there may be some extreme data that deviates from the sample mean, and the z-score standardization method utilizes the overall information of the sample, which is less affected by extreme data. Therefore, this article chooses the z-score standardization method. The z-score standardization method utilizes sample mean and standard deviation for data preprocessing, as shown in Equation 1:

$x^{*}=\frac{x-x_{\mu }}{x_{\sigma }}(1)$

where $x$ is the sample value to be normalized, $x^{*}$ represents the normalized sample value, $x_{\mu }$ represents the mean of the sample, $x_{\sigma }$ represents the standard deviation of the sample, This thesis uses standardized variables as input feature vectors for the basic model.

The input vector of the basic model for thermal runaway failure warning of retired batteries can be recorded as ${\mathit{X}}_{\mathit{i}\mathit{n}}=\left[\mathit{V},\mathit{S}\mathit{O}\mathit{C},\mathit{I},\mathit{T},\mathit{M}\right]$, where ${\mathit{X}}_{\mathit{i}\mathit{n}}$ is the input data, This data contains the voltage vector $\mathit{V}$, battery pack state of charge vector $\mathit{S}\mathit{O}\mathit{C}$, total current vector $\mathit{I}$, temperature vector $\mathit{T}$, and statistical variables of energy storage battery cells $\mathit{M}$. Each vector contains a time series, taking the total voltage as an example, $\mathit{V}=\left[V_1,...V_t,...V_N\right]$, where $V_t$ represents the total voltage value at time t in the time series, and N represents the total duration. Due to the fact that a set of retired batteries usually contains multiple battery cells, this article uses statistical methods to characterize the voltage characteristics of the cells, that is, $\mathit{M}$ contains statistical variables such as voltage variance, mean, maximum, and minimum values of all cells in a set of battery data. The output is the reconstructed data of the input features, which can be written as ${\widehat{\mathit{X}}}_{\mathit{o}\mathit{u}\mathit{t}}=\left[\widehat{\mathit{V}},\mathit{S}\widehat{\mathit{O}}\mathit{C},\widehat{\mathit{I}},\widehat{\mathit{T}},\widehat{\mathit{M}}\right]$, The dimensions of the input and output variables are equal. The optimization objective of the model training process is to minimize the reconstruction error of input and output data, as shown in Equation 2:

$\min J\left({\mathit{X}}_{\mathit{i}\mathit{n}},{\widehat{\mathit{X}}}_{\mathit{o}\mathit{u}\mathit{t}}\right)=\frac{1}{m}{\displaystyle \sum _{t=1}^N}{\displaystyle \sum _{i=1}^m}{\left(x_{in,i,t}-x_{out,i,t}\right)}^2(2)$

where $J$ is the reconstruction error between input data ${\mathit{X}}_{\mathit{i}\mathit{n}}$ and output data ${\mathit{X}}_{\mathit{o}\mathit{u}\mathit{t}}$, m is the number of dimensions for ${\mathit{X}}_{\mathit{i}\mathit{n}}$ and ${\mathit{X}}_{\mathit{o}\mathit{u}\mathit{t}}$, $x_{in,i,t}$ are the element value at time t of the ith dimension in ${\mathit{X}}_{\mathit{i}\mathit{n}}$, $x_{out,i,t}$ is the element value at time t of the ith dimension in ${\mathit{X}}_{\mathit{o}\mathit{u}\mathit{t}}$. After the above basic model training is completed, it can be used to determine the thermal runaway failure of the energy storage battery to be detected. The reconstruction error of the energy storage battery to be tested is obtained through basic model calculation, and the discrimination rule is shown in Equation 3:

$y=\left\{\begin{array}{l}1,J^{\prime }\left({\mathit{X}}_{\mathit{i}\mathit{n}}^{\prime },{\widehat{\mathit{X}}}_{\mathit{o}\mathit{u}\mathit{t}}^{\prime }\right)\ge K\\ 0,J^{\prime }\left({\mathit{X}}_{\mathit{i}\mathit{n}}^{\prime },{\widehat{\mathit{X}}}_{\mathit{o}\mathit{u}\mathit{t}}^{\prime }\right)<K\end{array}\right.(3)$

Where ${\mathit{X}}_{\mathit{i}\mathit{n}}^{\prime }$ represents the input of a certain energy storage battery to be judged; ${\widehat{\mathit{X}}}_{\mathit{o}\mathit{u}\mathit{t}}^{\prime }$ represents the output of a certain energy storage battery to be judged; y represents the judgment result of the basic model on the energy storage battery to be judged; K represents the threshold for determining whether thermal runaway failure has occurred; $J^{\prime }$ represents the reconstruction error of the sample to be judged calculated from the basic model. If the reconstruction error $J^{\prime }$ is greater than or equal to the set threshold K, the energy storage battery is judged as thermal runaway failure and assigned a value of 1; If the reconstruction error $J^{\prime }$ is less than the set threshold K, the energy storage battery is judged as normal and assigned a value of 0. This article obtains the corresponding reconstruction error set by training different normal battery samples, and calculates the average value and standard deviation of this set. Generally, the reconstruction error at three standard deviations greater than the average value should be selected as the threshold. However, the safety of retired batteries is particularly important, as high threshold values can easily lead to thermal runaway failure of retired batteries; If the reconstruction error value at one standard deviation greater than the average value is used as the threshold K, it will cause too many normal retired batteries to be judged as abnormal. In summary, this article selects the reconstruction error value at exactly two standard deviations greater than the average value as the threshold K.

To illustrate the importance of various characteristic parameters of self-initiated thermal runaway failure, a basic model was used and the reconstruction errors of known thermal runaway failure battery voltage (V), current (I), state of charge (SOC), temperature (T), and statistical variables (M) were calculated using Equations 4–8:

$J_V^{\prime }\left({\mathit{V}}_{\mathit{i}\mathit{n}}^{\prime },{\widehat{\mathit{V}}}_{\mathit{o}\mathit{u}\mathit{t}}^{\prime }\right)={\displaystyle \sum _{t=1}^N}{\left(v_{in,t}^{\prime }-v_{out,t}^{\prime }\right)}^2(4)$

$y=J_{SOC}^{\prime }\left(\mathit{S}\mathit{O}{\mathit{C}}_{\mathit{i}\mathit{n}}^{\prime },\mathit{S}\widehat{\mathit{O}}{\mathit{C}}_{\mathit{o}\mathit{u}\mathit{t}}^{\prime }\right)={\displaystyle \sum _{t=1}^N}{\left(so{c}_{in,t}^{\prime }-so{c}_{out,t}^{\prime }\right)}^2(5)$

$J_I^{\prime }\left({\mathit{I}}_{\mathit{i}\mathit{n}}^{\prime },{\widehat{\mathit{I}}}_{\mathit{o}\mathit{u}\mathit{t}}^{\prime }\right)={\displaystyle \sum _{t=1}^N}{\left(i_{in,i}^{\prime }-i_{out,t}^{\prime }\right)}^2(6)$

$J_T^{\prime }\left({\mathit{T}}_{\mathit{i}\mathit{n}}^{\prime },{\widehat{\mathit{T}}}_{\mathit{o}\mathit{u}\mathit{t}}^{\prime }\right)={\displaystyle \sum _{t=1}^N}{\left(T_{in,t}^{\prime }-T_{out,t}^{\prime }\right)}^2(7)$

$J_M^{\prime }\left({\mathit{M}}_{\mathit{i}\mathit{n}}^{\prime },{\widehat{\mathit{M}}}_{\mathit{o}\mathit{u}\mathit{t}}^{\prime }\right)={\displaystyle \sum _{t=1}^N}{\left(m_{in,t}^{\prime }-m_{out,t}^{\prime }\right)}^2(8)$

Taking Equation 4 as an example: $v_{in,t}^{\prime }$ is the element value at time t in ${\mathit{V}}_{\mathit{i}\mathit{n}}^{\prime }$; $v_{out,t}^{\prime }$ is the element value at time t in ${\widehat{\mathit{V}}}_{\mathit{o}\mathit{u}\mathit{t}}^{\prime }$. Sum the above reconstruction errors to obtain the reconstruction error of the battery, as shown in Equation 9.

$J_X^{\prime }=J_V^{\prime }+J_{SOC}^{\prime }+J_I^{\prime }+J_T^{\prime }+J_M^{\prime }(9)$

Calculate the ratio of the reconstruction error of each feature to the total reconstruction error $J_X^{\prime }$ of the battery to obtain the distribution proportion of the reconstruction error. Taking the proportion of voltage reconstruction error as an example, as shown in Equation 10:

${\alpha }_V=J_V^{\prime }/J_X^{\prime }(10)$

Where ${\alpha }_V$ is the proportion of voltage reconstruction error. Due to the normalization of the reconstruction errors in the calculation of various characteristic parameters of the battery, the proportion of reconstruction errors in each feature can to some extent reflect the cause of thermal runaway failure of the battery.

3 A thermal runaway failure warning method for energy storage battery based on Bi-LSTM and attention mechanism

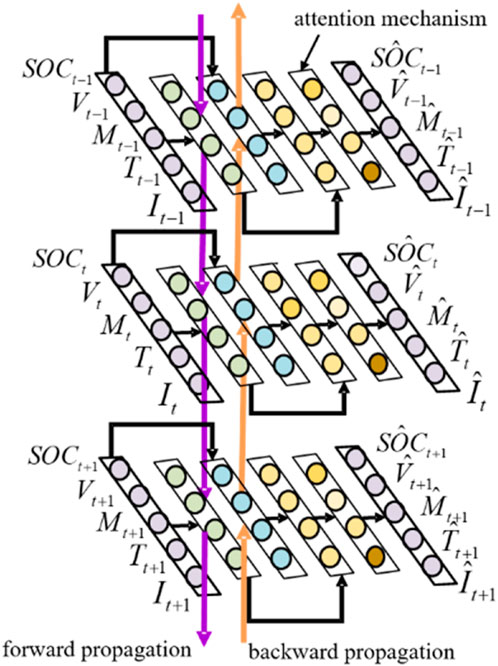
To effectively enhance the feature extraction capability of the basic model, this section proposes an energy storage battery thermal runaway failure warning method based on Bidirectional Long Short-Term Memory (Bi-LSTM) and attention mechanism. The thermal runaway failure process of retired batteries often involves a time span of several hundred hours. Therefore, during the process of data reconstruction, the basic model needs to have the ability to handle long-term span information (Graves, 2012). Bi-LSTM (Cong et al., 2018) can effectively capture the features of long-term-span information, so this paper uses Bi-LSTM as the basic model. Its structure is shown in Figure 4 and is obtained by combining two layers of long short-term memory (LSTM) (Hochreiter and Schmidhuber, 1997) networks. The output of the hidden layer at time t can be calculated by Equations 11–13.

$h_t=LSTM\left(V_t,I_t,SO{C}_t,T_t,M_t,h_{t-1}\right)(11)$

$h_i=LSTM\left(V_t,I_t,SO{C}_t,T_t,M_t,h_{i-1}\right)(12)$

$h_t^{\prime }=a_t{h}_t+b_t{h}_i+c_t(13)$

FIGURE 4

FIGURE 4. Basic model of BES feature extraction based on Bi-LSTM.

Where $LSTM\left(\cdot \right)$ represents the operation process of the LSTM network, and $h_t$ represents the forward hidden layer output at time t calculated using the input variables $V_t$, $I_t$, $SO{C}_t$ $T_t$ $M_t$ and the previous hidden layer output $h_{t-1}$. The calculation of the forward hidden layer output takes into consideration the influence of past hidden layer outputs on the current hidden layer output, as indicated by the blue circle in Figure 4. $h_i$ represents the backward hidden layer output at time t calculated using the input variables $V_t$, $I_t$, $SO{C}_t$ $T_t$ $M_t$ and the next backward hidden layer output $h_{i-1}$. The calculation considers the influence of future hidden layer outputs on the current hidden layer output, as indicated by the red circle in Figure 4. Bi-LSTM uses the reconstruction error in Equation 2 as the loss function and updates the network’s hidden layer output $h_t^{\prime }$ using Equation 13, represented by the yellow circle in Figure 4.

When calculating the accumulated reconstruction error of energy storage battery data during a specific period N, the relative importance of each input variable in the reconstruction error at the current time can differ. Directly adding up the reconstruction error of the multi-dimensional time series of retired batteries as if it were single variable time series data can result in inaccurate anomaly detection. Thus, it is necessary to assign dynamic weights to the Bi-LSTM hidden layer concerning changing times. The attention mechanism can learn differences in the weight of features at different time points in time-series data (Kuo and Huang, 2018; Feng et al., 2020). Therefore, this section adds an attention mechanism layer to the Bi-LSTM-based reconstruction model, represented by the colorful circles in Figure 4, which assigns different weight coefficients to feature vectors after passing through the attention mechanism layer. The input features of each time point in the basic model for thermal runaway failure warning of retired batteries undergo weight distribution using the attention mechanism. The resulting hidden layer output is updated and represents new inputs, $h_t^{″}$ which use Equation 14.

$h_t^{″}=A_t{h}_t^{\prime }(14)$

Where $A_t$ represents the weight matrix of the attention mechanism layer, and the elements ${{\alpha }_i}_{,j}$ in $A_t$ are calculated using the similarity formula in Equation 15:

${\alpha }_{i,j}=\frac{\exp \left(h_{i,t}^{\prime }{h}_{j,t}^{\prime }\right)}{{\displaystyle \sum _{j=1}^l}\exp \left(h_{i,t}^{\prime }{h}_{j,t}^{\prime }\right)}(15)$

Where $h_{i,t}^{\prime }$ and $h_{j,t}^{\prime }$ represent the ith and jth elements of the Bi-LSTM hidden layer output $h_t^{\prime }$ at time t, and l is the dimension of the hidden layer output. Finally, the outputs ${\widehat{V}}_t$, ${\widehat{I}}_t$, $S\widehat{O}{C}_t$, ${\widehat{T}}_t$, ${\widehat{M}}_t$ are obtained through a fully connected layer, which are represented by the top green circle in Figure 4.

In summary, to effectively extract the data features of energy storage battery group, including voltage (V), current (I), state of charge (SOC), temperature (T), and battery cell voltage variance, mean, maximum, and minimum values, this study comprehensively considers the time-series characteristics of energy storage battery operating data and the differentiation in feature weights. This expands the difference between the reconstruction errors of normal energy storage battery data and those experiencing thermal runaway and failure while calculating reconstruction error, further improving the accuracy of thermal runaway warning.

4 A thermal runaway failure warning method of retired batteries based on ensemble learning

The stability of the basic model for thermal runaway failure warning of retired batteries is defined as whether the model can accurately select the batteries that have experienced thermal runaway and failure in different test datasets. Due to the significant influence of the input sample set on the basic model parameters described in Section 3, it is challenging to ensure the stability of the basic model. As the basic model will be used multiple times in the thermal runaway failure warning of retired batteries, its insufficient stability would increase the probability of misjudgment and omission during certain warning processes (Shi and Zhang, 2019). Ensemble learning (Bahdanau et al., 2014) uses the judgment results of multiple basic models to evaluate thermal runaway failure, which can enhance the stability of the model. Therefore, to ensure the stability of the basic model, this section further establishes an ensemble learning model for thermal runaway failure warning of retired batteries based on bagging algorithm. In ensemble learning, a multi-model training strategy is usually adopted to solve specific problems, which combines multiple basic models to construct a more precise and robust ensemble model while retaining their respective advantages. The core assumption of this strategy is that when combining basic models reasonably, the overall performance of the model can be further improved while retaining their strengths. The bagging algorithm in the ensemble model typically trains basic models independently and in parallel, and combine them by some deterministic averaging process. This is shown in Figure 5. By integrating the discriminant results of multiple basic models trained from different normal energy storage battery sample sets, the probability of thermal runaway failure P can be obtained as shown in Equation 16.

$P={\displaystyle \sum _{k=1}^n}{y}_k/n(16)$

FIGURE 5

FIGURE 5. Ensemble learning model for thermal runaway warning of energy storage battery based on bagging algorithm.

Where P represents the probability of the energy storage battery being identified as experiencing thermal runaway and failure; $y_k$ is the judgment result of the kth basic model for the energy storage battery, which can be calculated using Equation 3; and n is the total number of basic models. The architecture of the basic models in the ensemble model shown in Figure 5 is the same, and they are trained on different normal energy storage battery data sets, with a total of n sample sets.

The ensemble stability mentioned in this paper can be described by the variance of the probability P calculated by the ensemble model (Friedman et al., 2021), denoted by ${\sigma }_E$, as shown in Equation 17:

${\sigma }_E=Var\left({\displaystyle \sum _{k=1}^n}{y}_k/n\right)=\rho {\sigma }^2+\left(1-\rho \right){\sigma }^2/n(17)$

Where the average correlation between the basic models can be set to $\rho$, the variance of the discriminant results of each basic model is ${\sigma }^2$, and the variance of the ensemble model’s discriminant result is negatively correlated with n, such that a larger n leads to smaller variance and greater stability of the model. In practice, due to limited sample data, the value of n in this study is determined based on the actual situation of the sample set.

The energy storage battery thermal runaway failure warning model based on the bagging algorithm uses the idea of ensemble learning to train a corresponding number of thermal runaway failure warning ensemble models by synthesizing multiple normal energy storage battery data of the same type, and calculates the thermal runaway failure warning probability using Equation 16. Therefore, the accuracy of energy storage battery safety warning depends on the accuracy of the ensemble model. However, the above method cannot determine the optimal ensemble model, as there is no standard for selecting the basic models that make up the ensemble model. To determine the best ensemble model, we need to first understand the relationship between the accuracy of the basic models, the diversity of the basic models and the accuracy of the ensemble model. The error-divergence theory provides a theoretical basis for selecting the best ensemble model by describing the relationship between the accuracy of the ensemble model and the basic models. Specifically, using n basic models $h_1,...,h_i,...,h_n$ to form an ensemble model, the output is obtained through weighted averaging, as shown in Equation 18:

$H\left(x\right)={\displaystyle \sum _{i=1}^T}{w}_i{h}_i\left(x\right)(18)$

Where $w_i$ represents the weight of basic model $h_i$, subject to constraints $w_i\ge 0$ and ${\displaystyle \sum _{i=1}^n}{w}_i=1$. Given a sample x, the divergence of the ith basic model can be defined as:

$A\left(h_i|x\right)={\left(h_i\left(x\right)-H\left(x\right)\right)}^2(19)$

Where $H\left(x\right)$ represents the output of the ensemble model.

The divergence of the ensemble model can be defined as the weighted average of the divergences of the basic models:

$\overline{A}\left(h|x\right)={\displaystyle \sum _{i=1}^n}{w}_i{\left(h_i\left(x\right)-H\left(x\right)\right)}^2(20)$

Clearly, differences define the variation of the base model on the sample. While there are multiple definitions of error, this paper measures the error of the base model using mean squared error. Assuming that the true discrimination result of sample x is $f\left(x\right)$, the errors of the base model $h_i\left(x\right)$ and ensemble model $H\left(x\right)$ can be expressed as follows:

$E\left(h_i|x\right)={\left(f\left(x\right)-h_i\left(x\right)\right)}^2(21)$

$E\left(H|x\right)={\left(f\left(x\right)-H\left(x\right)\right)}^2(22)$

The weighted average error of all the base models on the overall sample can be represented as follows:

$\overline{E}\left(h|x\right)={\displaystyle \sum _{i=1}^n}{w}_i{\left(f\left(x\right)-h_i\left(x\right)\right)}^2(23)$

By rearranging Equation 20:

$\begin{array}{l}\overline{A}\left(h|x\right)={\displaystyle \sum _{i=1}^n}{w}_i{\left(h_i\left(x\right)-H\left(x\right)\right)}^2\\ ={\displaystyle \sum _{i=1}^n}{w}_i{\left(h_i\left(x\right)-f\left(x\right)+f\left(x\right)-H\left(x\right)\right)}^2\\ ={\displaystyle \sum _{i=1}^n}{w}_i{\left(h_i\left(x\right)-f\left(x\right)\right)}^2+{\displaystyle \sum _{i=1}^n}{w}_i{\left(f\left(x\right)-H\left(x\right)\right)}^2+\\ 2{\displaystyle \sum _{i=1}^n}{w}_i\left(h_i\left(x\right)f\left(x\right)-h_i\left(x\right)H\left(x\right)+f\left(x\right)H\left(x\right)-{\left(f\left(x\right)\right)}^2\right)\end{array}(24)$

Combining Equations 18–22 and constraint ${\displaystyle \sum _{i=1}^n}{w}_i=1$, Equation 24 can be further transformed to:

$\begin{array}{l}{\displaystyle \sum _{i=1}^n}{w}_i{\left(h_i\left(x\right)-f\left(x\right)\right)}^2+{\displaystyle \sum _{i=1}^n}{w}_i{\left(f\left(x\right)-H\left(x\right)\right)}^2+\\ 2{\displaystyle \sum _{i=1}^n}{w}_i{h}_i\left(x\right)\left(f\left(x\right)-H\left(x\right)\right)+2f\left(x\right)\left(H\left(x\right)-f\left(x\right)\right)\\ =\overline{E}\left(h|x\right)-E\left(H|x\right)\end{array}(25)$

Simplifying the above equation results in:

$E\left(H|x\right)=\overline{E}\left(h|x\right)-\overline{A}\left(h|x\right)(26)$

According to Equation 26, the error of the ensemble model is determined by the weighted average of all the base models on the overall sample and the weighted average of the divergence of the base model. The second item on the right-hand side of the equation is positive and subtracted from the first item, which theoretically ensures that the error after integration is lower than the weighted average error of the base model. Moreover, the higher the accuracy of each base model, and the greater their differences, the higher the accuracy of the integrated model. Therefore, to further optimize the warning model for thermal runaway failure of retired batteries based on the bagging algorithm, this subsection adopts the integrated model optimization method proposed in [70] based on the conclusion obtained from Equation 26. Given M basic models and m battery samples waiting for discrimination, the discrimination results are recorded in matrix P, and the element $P_{ij}$ in the ith row and jth column of P is shown as Equation 27:

$P_{ij}=\left\{\begin{array}{l}\begin{array}{l}0,\text{basical} \text{model} \text{Correct} \text{judgment} \text{of} j\\ \text{on} \text{energy} \text{storage} \text{battery} \text{sample} i\end{array}\\ \begin{array}{l}1,\text{basical} \text{model} \text{Wrong} \text{judgment} \text{of} j\\ \text{on} \text{energy} \text{storage} \text{battery} \text{sample} i\end{array}\end{array}\right.(27)$

Let $U=P^{T}P$, then the diagonal elements $U_{ii}$ of $U$ represent the number of times the base model $U_{ii}$ makes an incorrect judgment, reflecting the weighted average error of all the base models on the overall sample, while the off-diagonal elements $U_{ij,i\ne j}$ represent the number of times both the base models $h_i$ and $h_j$ make a mistake simultaneously, reflecting the divergence of the ensemble model. Therefore, $U$ contains the errors of each base model as well as their divergence, enabling effective measurement of the error of the integrated model. Normalize the elements in $U$ using Equation 28. According to the definition of the integrated model error in Equation 26, the integrated model performs best when each element in $\stackrel{\sim }{U}$ is minimized.

${\stackrel{\sim }{U}}_{ij}=\left\{\begin{array}{l}\frac{U_{ii}}{m},i=j\\ \frac{1}{2}\left(\frac{U_{ij}}{U_{ii}}+\frac{U_{ij}}{U_{jj}}\right),i\ne j\end{array}\right.(28)$

Where m is the number of samples to be discriminated. The optimization problem of the integrated model can be transformed into the following quadratic integer programming problem:

$\underset{x}{\min }F=x^T\stackrel{\sim }{U}x(29)$

$s.t.{\displaystyle \sum _{i=1}^M}{x}_i=s(30)$

$x_i=\left\{0,1\right\}(31)$

Where the binary scalar $x_i$ indicates whether the ith base model is selected for the integrated model, and parameter s denotes the optimized size of the integrated model. Thus, based on the theoretical foundation of determining the optimal integrated model using equation 26, a quadratic integer programming model can be established by Equations 27–31 to find the optimal warning model for thermal runaway failure of retired batteries with a given integrated model size.

In summary, this section proposes a thermal runaway warning method for retired batteries based on ensemble learning. Firstly, the probability of thermal runaway and failure of batteries is quantified using ensemble learning, and a thermal runaway failure warning method for retired batteries based on the bagging algorithm is proposed to ensure the stability of the algorithm. Then, a warning method for thermal runaway failure of retired batteries is proposed based on ensemble optimization, which can select the optimal integrated model to further improve the warning accuracy under the premise of reducing the size of the integrated model.

5 Warning process for thermal runaway failure of retired batteries

This paper proposes a data-driven thermal runaway warning method for retired batteries. The overall flowchart is shown in Figure 6, and the specific steps are described as follows:

FIGURE 6

FIGURE 6. Data-driven thermal runaway early warning algorithm process of BES.

Step 1:. Data preprocessing

Firstly, to eliminate the impact of different units on the calculation of reconstruction errors, normalization is performed on different dimensional features $x3$ using Equation 1 to obtain $x^{*}$. Then, multi-dimensional time-series feature vectors ${\mathit{X}}_{\mathit{i}\mathit{n}}$ are constructed using the method in Section 2. Finally, n normal battery data sets in the data set are used as n training sets, and the remaining battery data set is used as the test set.

Step 2:. Model training

Firstly, based on the feature mining method for energy storage battery data using Bi-LSTM and attention mechanism, a basic model is constructed including Equations 2, 3 and Equations 11–15. Then, n basic models are sequentially trained based on n training sets obtained in Step 1. The reconstruction error set is obtained, and the reconstruction error threshold K is calculated from the reconstruction error set. Finally, an ensemble model is formed by combining the n basic models according to the method in Section 4.

Step 3:. Model optimization

Firstly, the optimization objective of the ensemble model is designed according to Equations 27–29. Then, given the optimized size of the ensemble model, the optimal combination of the ensemble model with a given size s is determined using the branch and bound method based on the quadratic integer programming model in Section 4.

Step 4:. Calculation of the samples to be judged

A given energy storage battery sample to be judged is input into the ensemble model. Eq. 2 is used to calculate the reconstruction error $J^{\prime }$ of the sample, and it is compared with the given reconstruction error threshold K. The output $K$ (0/1) of each basic model is determined, and the warning probability P is calculated using Equation 16. The warning probability threshold can be set as a variable for different industrial requirements and can be selected based on different safety/economic considerations. This paper regards retired batteries with a warning probability threshold exceeding 70% as potentially thermally runaway-failed batteries.

6 Example analysis

Due to a significant proportion of retired batteries being present in the thermal runaway batteries, this study employs retired lithium battery for the numerical simulation tests. This paper collected actual retired batteries data from a domestic company, involving 48 batteries in total, including voltage, current, state of charge, temperature, and other data for each group of batteries. The time span is about half a year for all data sets, with a sampling frequency of 0.1 Hz. Two groups of retired batteries caused combustion due to thermal runaway failure. All simulation examples in this chapter were tested on hardware with an Intel(R) Core (TM) i7-9750H CPU @2.60GHz and 24 GB RAM.

This paper will compare the following methods (M0-M5), as shown in Table 1. M1 is the basic model of this paper’s proposed unsupervised learning energy storage battery thermal runaway warning model based on reconstruction error calculation. The model uses Bi-LSTM, with 2 hidden layers, and 32 neurons per layer. The initial learning rate is set to 0.001, and the optimizer used is Adaptive Moment Estimation (ADAM). M2-M4 are the proposed ensemble models without optimization, and M5 is this paper’s proposed energy storage battery thermal runaway failure warning method based on ensemble optimization.

TABLE 1

TABLE 1. Comparison of multiple warning methods for thermal runaway failure of retired batteries.

M0: Unsupervised clustering method based on K-means;

M1: Energy storage battery thermal runaway failure warning model based on reconstruction error calculation (as the basic model). The model uses Bi-LSTM with 2 hidden layers, 32 neurons per layer, an initial learning rate of 0.001, and the ADAM optimizer (Kingma and Ba, 2014);

M2: The basic model is M1, and an ensemble learning framework is further adopted to form the ensemble model;

M3: The ensemble model framework is the same as M2, but the basic model uses a fully connected neural network with 2 hidden layers, 32 neurons per layer, an initial learning rate of 0.001, and the ADAM optimizer;

M4: The same as M2, but the basic model is a Bi-LSTM network with an added attention mechanism;

M5: The same as M4, but after optimization of the basic model selection in the ensemble model through a quadratic integer programming model.

This paper evaluates the algorithm performance using commonly used industrial metrics, as shown in Equations 32–35:

$ACC=\left(TP+TN\right)/\left(TP+TN+FP+FN\right)(32)$

$PRE=TP/\left(TP+FP\right)(33)$

$REC=TP/\left(TP+FN\right)(34)$

$F1=2\times PRE\times REC/\left(PRE+REC\right)(35)$

Where TP represents the number of samples where the true value is considered positive, while the model considers it positive, FN represents the number of samples whose true values are considered positive, while the model considers them negative, FP represents the number of samples considered negative by the true value, while the model considers positive by the model, TN represents the number of samples whose true value is considered negative, while the model considers negative, TP/TN represents the number of positive samples predicted correctly or negative samples predicted correctly, and FP/FN represents the number of negative samples predicted as positive or positive samples predicted as negative. ACC is accuracy; PRE is precision; REC is recall; F1 is the harmonic mean of precision and recall, which can simultaneously consider the precision and recall of the classification model. All of these indices have a better model classification performance when the values are larger. In addition, this paper sets up the sorting index for battery thermal runaway failure warning, which calculates the warning probability of all batteries in the same test set, sorts the probability values in descending order, records the probability rank values of the two known thermal runaway failure batteries, and the smaller the rank value of the thermal runaway failure battery, the better the model performance.

6.1 Validation of effectiveness for thermal runaway failure warning of retired batteries

To compare the effects of the basic model for the thermal runaway failure warning of retired batteries based on unsupervised learning and the unsupervised clustering method based on distance calculation, M0 and M1 were compared. The following example was set: M1 randomly selected 20 sets of normal energy storage battery samples out of 48 groups of battery data as the training set and used the remaining 28 sets of energy storage battery data (including two sets of thermal runaway failure batteries) as the test set. M0 used the same test set data values as M1 and conducted direct clustering analysis on the test set, and the results are shown in Table 2.

TABLE 2

TABLE 2. Comparison of warning effects for thermal runaway failure between M0 and M1.

The accuracy of the M1 method was 14.3% higher than that of the M0 method, and the recall rate of the M1 method reached 100%, which means no true thermal runaway failure energy storage battery was missed. The recall rate of M0 was 0%, and all true thermal runaway failure retired batteries were missed. These results indicate that there is a weak difference between the data of retired batteries in the early and middle stages of thermal runaway failure and normal batteries, and it is difficult to distinguish thermal runaway failure retired batteries using only a simple distance calculation method for unsupervised clustering. This also validates the effectiveness of the proposed basic model M1 in this paper.

6.2 Validation of effectiveness for ensemble models of thermal runaway failure warning of retired batteries based on bagging algorithm

Ensemble models can improve the stability of basic models. In order to illustrate the stability performance of the ensemble model, this section compared the warning indicators of M1 and M2. The training set and test set of M1 were the same as those in Section 1, while the training set and test set of M2 were the same as those in M1, except that M2 used each set of normal battery data to train a basic model, resulting in 20 basic models in total. M1 and M2 were tested three times each with different 20 sets of normal battery data randomly selected as the training set, and the remaining 28 batteries (including two sets of thermal runaway failure batteries) were used as the test set. The training set and test set of M2 were consistent with those of M1 in each test.

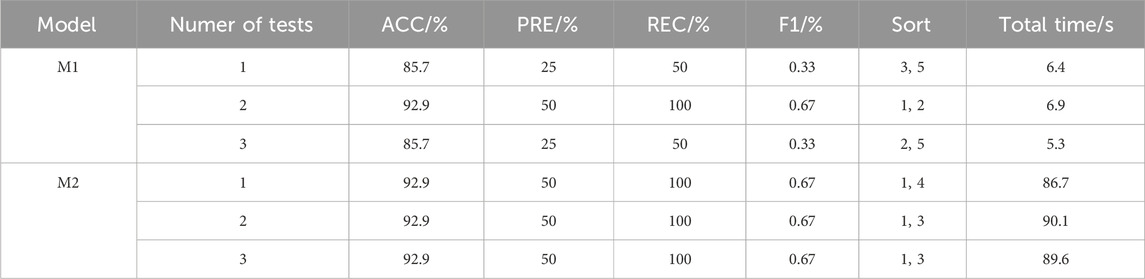
According to Table 3, for the basic model M1, the evaluation indicators varied greatly in the three tests, and the accuracy was low in the first and third evaluations while high in the second evaluation. In contrast, the evaluation indicators of the ensemble model M2 were consistently high in all three tests, and except for a slight fluctuation in the warning ranking value of thermal runaway failure batteries, other indicators remained unchanged. These results demonstrate that the ensemble model for the thermal runaway failure warning of retired batteries has higher stability compared to the basic model. Although the total time required for training and testing for M2 is longer than that for M1, the time spent at the hundred-second level does not significantly influence the thermal runaway failure warning compared to the long-term use of batteries. Thus, this section verifies the stability advantage of the ensemble model over the basic model.

TABLE 3

TABLE 3. Comparison of warning effects for thermal runaway failure between M1 and M2.

6.3 Validation of the effectiveness of thermal runaway failure warning method for energy

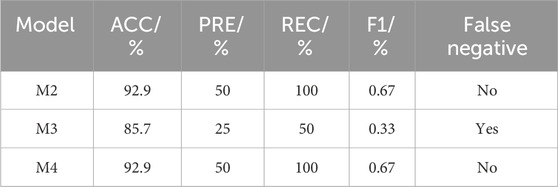
Storage Batteries Based on Bi-LSTM and Attention Mechanism The accurate feature mining method for energy storage battery data aims to improve the accuracy of each basic model in the integrated model. In order to demonstrate the improvement in model accuracy of this method, the following experiment was conducted: M2 randomly selected 20 sets of normal energy storage battery samples out of 48 groups of battery data as the training set and used the remaining 28 sets of energy storage battery data (including two sets of thermal runaway failure batteries) as the test set. The training set and test sets of M3 and M4 were the same as those of M2. The results are shown in Tables 4, 5, and Figure 7.

TABLE 4

TABLE 4. Performance comparison of integration models based on different learning strategies.

TABLE 5

TABLE 5. Early warning probability and sequencing of thermal runaway energy storage battery.

FIGURE 7

FIGURE 7. The top 10 early warning probability values of early warning probability.

According to Table 4, since M2 and M4 considered the temporal features of data, there was no missing detection of thermal runaway failure retired batteries, and the classification accuracy, precision, and recall rates increased by 7.2%, 25%, and 50%, respectively, compared to M3. To further explain the advantage of the method proposed in this paper, M4 was analyzed for warning probability and sorting index for thermal runaway failure retired batteries. According to Table 5, for thermal runaway failure retired batteries, M3 had a warning probability of only 45% and 70% for the two groups of thermal runaway failure retired batteries, and the above two groups were ranked only 8 and 4 in terms of thermal runaway failure probability among 28 retired batteries. Compared with M3, M2 and M4 significantly improved the warning probability of the two groups of thermal runaway failure retired batteries to 75%, 85%, and 80%, 90%, respectively. Further comparison between M2 and M4 shows that the attention mechanism set in M4 effectively improved the model accuracy.

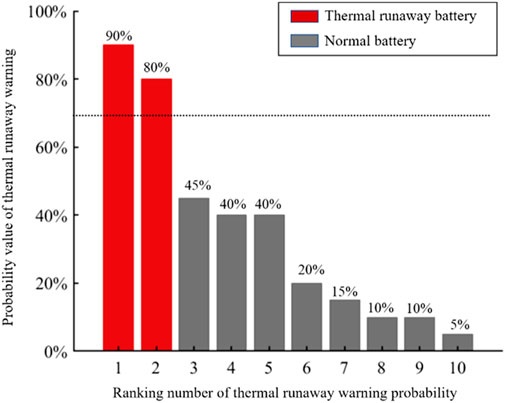
To further illustrate the difference in warning probability between thermal runaway failure and normal batteries in the prediction results of M4, the warning probability values for the top 10 ranked cases in the test set were compared and shown in Figure 7. The red bars with warning probability values higher than represent thermal runaway failure batteries, while the blue bars with warning probability values lower than represent normal batteries. According to Figure 7, there was a significant difference in warning probability values between the third-ranked normal energy storage battery and the thermal runaway failure battery. This result demonstrates the effectiveness of M4.

6.4 Validation of the effectiveness of thermal runaway failure warning method for retired batteries based on ensemble optimization

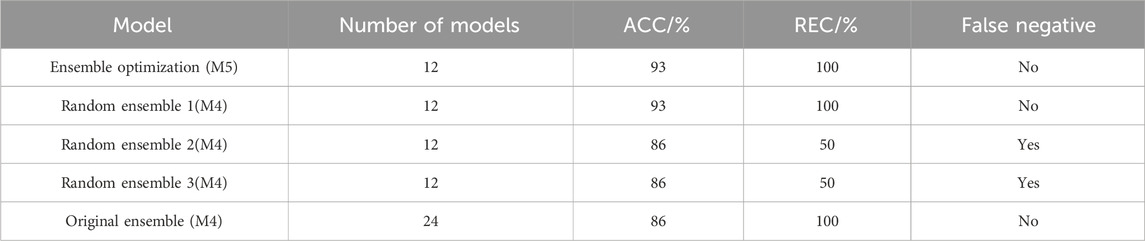
The ensemble optimization-based thermal runaway failure warning method proposed in this chapter aims to provide the optimal ensemble model based on error-divergence theory, given a fixed ensemble model size. In order to demonstrate the improvement in prediction accuracy of the ensemble model using this method, the following experiment was conducted: M4 randomly selected 24 sets of normal energy storage battery samples out of 48 groups of battery data as the training set (the original ensemble model), and used the remaining 24 sets of energy storage battery data (including two sets of thermal runaway failure batteries) as the test set. The optimized ensemble model size was set to 12, and as a control group, three models with a size of 12 were randomly selected from the 24 training sets for combination, with the test set unchanged. The results are shown in Table 6 and Figure 8.

TABLE 6

TABLE 6. Performance comparison of integrated models before and after optimization.

FIGURE 8

FIGURE 8. Effect comparison of thermal runaway warning models before and after optimization.

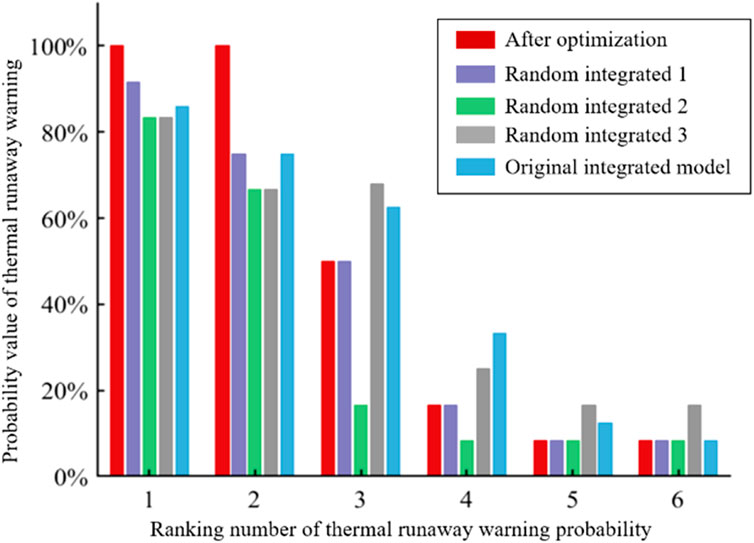
According to Table 6, compared with the original ensemble model (M4), the ensemble optimization method (M5) achieved higher accuracy with the same number of ensemble models. It performed better than random ensemble 2 and 3, without any missed detection of thermal runaway failure batteries, and had higher accuracy and recall rates. To further illustrate the effectiveness of the optimized model, the warning probability values of batteries with high warning probabilities in different models were compared in Figure 8. Batteries labeled 1 and 2 are real thermal runaway failure batteries, and batteries labeled 3, 4, 5, and 6 have high warning probabilities and are normal batteries. As shown in Figure 8, both real thermal runaway failure batteries were calculated to have a thermal runaway failure warning probability value of 100% by the optimized model, which is significantly higher than that of the original model and random ensemble models with the same size. In summary, ensemble optimization improved the accuracy of the original model and performed even better than random ensemble models.

6.5 Importance analysis of various features of thermal runaway failure batteries

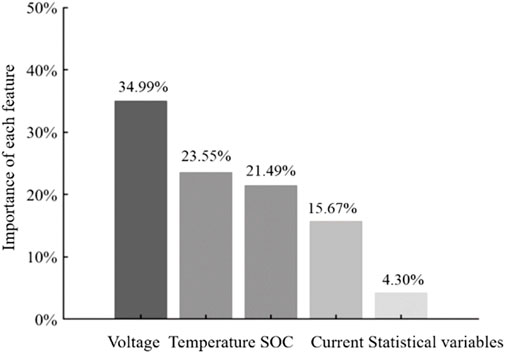
Using M5, the reconstruction errors and percentages of each feature were calculated for two sets of thermal runaway failure batteries according to Equations 4–10, as shown in Figures 9, 10. The darker the color in the figure, the larger the percentage. From the figures, it can be seen that the reconstruction errors of the two sets of thermal runaway failure batteries are mainly distributed among three factors: voltage, temperature, and SOC. In particular, voltage has the largest impact on the overall reconstruction error, accounting for 34.99% and 42.87% respectively for the two sets, indicating that voltage is the most important factor.

FIGURE 9

FIGURE 9. Reconstruction error distribution of No. 1 thermal runaway battery.

FIGURE 10

FIGURE 10. Reconstruction error distribution of No. 2 thermal runaway battery.

6.6 Conclusion

To address the issue of ineffective warning for thermal runaway failure of retired batteries, this paper proposes a data-driven thermal runaway failure warning method for retired batteries and validates the effectiveness of the proposed method using real operational data from a company’s retired batteries. First, the paper establishes a basic model for thermal runaway failure warning of retired batteries based on reconstruction error calculation, which defines the degree of difference between batteries using their reconstruction errors and forms a discriminant model. By comparing the basic model with K-means clustering method, the study demonstrates that the reconstructed basic model is effective in identifying thermal runaway failure batteries. Second, the paper proposes a thermal runaway failure warning method for retired batteries based on Bi-LSTM and attention mechanism, which effectively extracts dynamic features of voltage, temperature, SOC, etc., during the thermal runaway failure process, and uses attention mechanism to improve the basic model by learning differentiated weights of various parameters at different time intervals, thereby reducing false negatives and false positives of the ensemble model for thermal runaway failure batteries. Furthermore, the paper proposes an ensemble learning-based thermal runaway failure warning method for retired batteries, which quantifies the probability of thermal runaway failure and reduces the variance of the ensemble model while ensuring its accuracy, compared with the basic model. Finally, the study proposes an ensemble optimization-based thermal runaway failure warning method for retired batteries, which optimizes the original model given a fixed ensemble model size and achieves higher accuracy than random ensemble models. This paper proposes a precise warning method for thermal runaway failure of retired batteries, which helps ensure the safe and reliable operation of energy storage battery systems at the safety level. The proposed method is applicable to thermal runaway warning of lithium batteries, including retired batteries. From the perspective of data requirements, the method can utilize time-series data from batteries under various operating conditions such as charging, discharging, and storage in any combination. This makes it easier to generalize and apply compared to mechanism research methods.

This article studies the precise warning method for the thermal runaway problem of energy storage batteries, which has certain practical significance. From the perspective of data requirements, the time-series data of energy storage batteries required by this method can be arbitrarily combined with various working conditions (charging, discharging, static, etc.), making it more easy to expand compared with mechanistic research methods. In addition, for the accurate description of the time and degree of thermal runaway in thermal runaway warning problems, this article will continue to explore in subsequent studies.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

FC: Data curation, Project administration, Resources, Supervision, Writing–review and editing. XC: Data curation, Formal Analysis, Funding acquisition, Investigation, Writing–review and editing. JJ: Data curation, Validation, Writing–review and editing. YQ: Data curation, Validation, Writing–review and editing. YC: Investigation, Methodology, Software, Validation, Writing–original draft, Writing–review and editing, Conceptualization, Supervision.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported in part by the Postdoctoral Merit Funding of Zhejiang Province of China (ZJ2022052).

Conflict of interest

Authors FC, XC, JJ, and YQ were employed by PowerChina Huadong Engineering Co. Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bahdanau, D., Cho, K., and Bengio, Y. (2014). Neural machine translation by jointly learning to align and translate. Comput. Sci.

Google Scholar

Barnett, B. (2014). “Technologies for detection and intervention of internal short circuits in Li-ion batteries,” in Proceedings of the 5th Annual Battery Safety, Washington D.C., USA, November 2014.

Google Scholar

Chalise, D., Shah, K., Halama, T., Komsiyska, L., and Jain, A. (2017). An experimentally validated method for temperature prediction during cyclic operation of a Li-ion cell. Int. J. Heat. Mass Transf. 112, 89–96. doi:10.1016/j.ijheatmasstransfer.2017.04.115

CrossRef Full Text | Google Scholar

Chen, Z., Qin, Y., Ren, Y., Lu, W., Orendorff, C., Roth, E. P., et al. (2011). Multi-scale study of thermal stability of lithiated graphite. Energy Environ. Sci. 4, 4023. doi:10.1039/c1ee01786a

CrossRef Full Text | Google Scholar

Cong, Q., Feng, Z., Li, F., Xiang, Y., Rao, G., and Tao, C. (2018). “X-A-BiLSTM: a deep learning approach for depression detection in imbalanced data,” in In Proceedings of the 2018 IEEE International Conference on Bioinformatics and Biomedicine, Madrid, Spain, December 2018.

CrossRef Full Text | Google Scholar

Ding, S., Dong, C., Zhao, T., Koh, L., Bai, X., and Luo, J. (2021). A meta-learning based multimodal neural network for multistep ahead battery thermal runaway forecasting. IEEE Trans. Ind. Inf. 17, 4503–4511. doi:10.1109/tii.2020.3015555

CrossRef Full Text | Google Scholar

Doughty, D. H. (2012). Vehicle battery safety roadmap guidance. Golden, CO (United States): National Renewable Energy Lab. No. NREL/SR-5400-54404.

Google Scholar

Fang, K., Mu, D., Shi, C., Wu, B., and Wu, F. (2012). A prediction model based on artificial neural network for surface temperature simulation of nickel–metal hydride battery during charging. J. Power Sources 208, 378–382. doi:10.1016/j.jpowsour.2012.02.059

CrossRef Full Text | Google Scholar

Feng, B., Zhang, Y., Tang, X., Guo, C., Wang, J., and Yang, Q. (2020). Power equipment defect text mining based on bilstm attention neural network. Proc. CSEE 40, 1–10. doi:10.1016/j.jpowsour.2014.01.005

CrossRef Full Text | Google Scholar

Feng, X., Fang, M., He, X., Ouyang, M., Lu, L., Wang, H., et al. (2014). Thermal runaway features of large format prismatic lithiumion battery using extended volume accelerating rate calorimetry. J. Power Sources 255, 294–301. doi:10.1016/j.jpowsour.2014.01.005

CrossRef Full Text | Google Scholar

Feng, X., Ouyang, M., Liu, X., Lu, L., Xia, Y., and He, X. (2018). Thermal runaway mechanism of lithiumion battery for electric vehicles: a review. Energy Storage Mater 10, 246–267. doi:10.1016/j.ensm.2017.05.013

CrossRef Full Text | Google Scholar

Friedman, J. H. T., Tibshirani, R., Friedman, J., Hastie, T., Tibshirani, R., Kuo, P.-H., et al. (2021). A solution manual and notes for the text: the elements of statistical learning.

Google Scholar

Graves, A. (2012). Supervised sequence labelling with recurrent neural networks. Stud. Comput. Intell. 385. doi:10.1007/978-3-642-24797-2

CrossRef Full Text | Google Scholar

Hochreiter, S., and Schmidhuber, J. (1997). Long short-term memory. Neural comput. 9, 1735–1780. doi:10.1162/neco.1997.9.8.1735

PubMed Abstract | CrossRef Full Text | Google Scholar

Hundman, K., Constantinou, V., and Laporte, C. (2018). “Detecting spacecraft anomalies using lstms and nonparametric dynamic thresholding,” in Proceedings of the 24th ACM SIGKDD international conference on knowledge discovery and data mining, New York, NY, July 2018, 387–395.

CrossRef Full Text | Google Scholar

Hussein, A., and Chehade, A. (2020). Robust artificial neural network-based models for accurate surface temperature estimation of batteries. IEEE Trans. Ind. Appl. 56, 5269–5278. doi:10.1109/tia.2020.3001256

CrossRef Full Text | Google Scholar

Kingma, D., and Ba, J. (2014). Adam: a method for stochastic optimization. Comput. Sci. doi:10.48550/arXiv.1412.6980

CrossRef Full Text | Google Scholar

Kuo, P., and Huang, C. (2018). A high precision artificial neural networks model for short-term energy load forecasting. Energies 11, 213–226. doi:10.3390/en11010213

CrossRef Full Text | Google Scholar

Ma, B., Yu, H. Q., Wang, W. T., Yang, X. B., Zhang, L. S., Xie, H. C., et al. (2023b). State of health and remaining useful life prediction for lithium-ion batteries based on differential thermal voltammetry and a long and short memory neural network. Rare Met. 42 (3), 885–901. doi:10.1007/s12598-022-02156-1

CrossRef Full Text | Google Scholar

Ma, B., Yu, H. Q., Yang, L. H., Liu, Q., Xie, H. C., Chen, S. Y., et al. (2023a). Toward a function realization of multi-scale modeling for lithium-ion battery based on CHAIN framework. Rare Met. 42 (2), 368–386. doi:10.1007/s12598-022-02138-3

CrossRef Full Text | Google Scholar

Ping, P., Wang, Q., Huang, P., Sun, J., and Chen, C. (2014). Thermal behaviour analysis of lithium-ion battery at elevated temperature using deconvolution method. Appl. Energy 129, 261–273. doi:10.1016/j.apenergy.2014.04.092

CrossRef Full Text | Google Scholar

Ren, D., Xiang, L., Feng, X., Lu, L., Ouyang, M., Li, J., et al. (2018). Model-based thermal runaway prediction of lithium-ion batteries from kinetics analysis of cell components. Appl. Energy 228, 633–644. doi:10.1016/j.apenergy.2018.06.126

CrossRef Full Text | Google Scholar

Sakurada, M., and Yairi, T. (2014). “Anomaly detection using autoencoders with nonlinear dimensionality reduction,” in Proceedings of the MLSDA 2014 2nd workshop on machine learning for sensory data analysis, New York, NY, December 2014, 4–11.

CrossRef Full Text | Google Scholar

Shah, K., Chalise, D., and Jain, A. (2016). Experimental and theoretical analysis of a method to predict thermal runaway in Li-ion cells. J. Power Sources 330, 167–174. doi:10.1016/j.jpowsour.2016.08.133

CrossRef Full Text | Google Scholar

Shi, J., and Zhang, J. (2019). Load forecasting method based on multi model fusion stacking integrated learning. Proc. CSEE 39, 4032–4042.

Google Scholar

Spotnitz, R., Franklin, J., Wen, J., Yu, Y., and Chen, C. (2003). Abuse behavior of high-power, lithium-ion cells. J. Power Sources 113, 81–100. doi:10.1016/s0378-7753(02)00488-3

CrossRef Full Text | Google Scholar

Wang, Q., Ping, P., Zhao, X., Chu, G., Sun, J., and Chen, C. (2012). Thermal runaway caused fire and explosion of lithiumion battery. Cheminform 208, 210–224. doi:10.1016/j.jpowsour.2012.02.038

CrossRef Full Text | Google Scholar

Wen, J., Yu, Y., and Chen, C. (2012). A review on lithium-ion batteries safety issues: existing problems and possible solutions. Mater. Express 2, 197–212. doi:10.1166/mex.2012.1075

CrossRef Full Text | Google Scholar

Yi, L., and Xu, H. (2021). Fault diagnosis method of lithiumion battery based on vibration signal. Power Syst. Technol. 22, 71–75.

Google Scholar

Zheng, Y., Han, X., Lu, L., Li, J., and Ouyang, M. (2013). Lithiumion battery pack power fade fault identification based on Shannon entropy in electric vehicles. J. Power Sources 223, 136–146. doi:10.1016/j.jpowsour.2012.09.015

CrossRef Full Text | Google Scholar