
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 29 December 2023
Sec. Energy Storage
Volume 11 - 2023 | https://doi.org/10.3389/fenrg.2023.1333147
This article presents a DOD-SOH equalization method for a DRB system based on the Deep DQN algorithm. The proposed method utilizes DQN to learn the operational processes of the system. By integrating the advantages of DRB with SOH equalization theory and the DQN algorithm from the perspective of DOD, our method significantly improve battery performance and ensure cell balancing. To begin with, we present a dynamic reconfigurable battery system with a simple topological structure and outline its switching control process. Additionly, we provide an analysis of the SOH balancing principle and elaborate on the control process of DQN algorithm. Finally, subsequent simulations are carried out, and the simulation results demonstrate outstanding performances in reducing the variance of SOHs, which indicates an enhancement in the level of SOH balancing as well.
The development of energy storage science and technology has greatly propelled the advancement of various intelligent electrical devices in recent years (Lawder et al., 2014; Li et al., 2021; Abomazid et al., 2022). With ongoing technological advancements and breakthroughs in battery materials, battery management, and battery systems, the development of battery energy storage has become increasingly significant. Under traditional methods, battery system configurations often employ fixed series and parallel connections, resulting in inevitable differences among individual battery cells. Consequently, battery systems are prone to the “barrel effect,” wherein cells with lower capacity discharge first, and cells with poorer health degrade faster. This imbalance leads to premature failure of the battery system, causing issues such as capacity loss, reduced energy efficiency, and shorter cycle life.
In order to overcome the challenges posed by differences among individual battery cells, the concept of a dynamic reconfigurable battery system has been proposed (Kim and Shin, 2009; Ci et al., 2012; Ci et al., 2016). This system involves high-speed MOSFETs connected in series and parallel to each individual battery cell, controlling the opening and closing of switches based on the real-time state of the battery to achieve SOH equilibrium. In recent years, there has been a growing body of research in the field of DRB, with much of the focus on circuit topology design and control. (Morstyn et al., 2016),critically, they have summarized the existing hardware topologies, and compared their functionalities and losses. Another study by (Gunlu et al., 2017) proposed a dynamically reconfigurable independent cellular switch circuit to facilitate the necessary battery connections, significantly improving circuit efficiency. Additionally, (Kim et al., 2012), introduced a novel battery switch topology circuit and high-performance battery management system to enhance battery energy conversion efficiency.
The dynamic reconfigurable battery system has proven effective in overcoming the “weakest link” issue and achieving balance among individual battery cells. SOH represents the battery’s health status in terms of the remaining charge capacity, and is often used to quantitatively measure differences among batteries. Accurately measuring SOH is not a simple task, but it is an essential step before implementing SOH balance control. Existing methods for measuring SOH typically involve model-based and data-driven approaches. Model-based methods entail constructing electrochemical and equivalent circuit models, utilizing Kalman filtering (Duan et al., 2023; Zhao et al., 2018; Chen et al., 2022) and Gaussian filtering (Wang et al., 2023; Cui et al., 2022; Fan et al., 2023) to estimate SOH. Data-driven methods primarily rely on machine learning (Shu et al., 2021; Buchicchio et al., 2023; Raoofi and Yildiz, 2023) and deep learning (Wang et al., 2022; Khalid and Sarwat, 2021b; Xu et al., 2023). These methods require feature extraction, establishing the mapping between features and SOH for predictive purposes.
For a battery pack, smaller differences in SOH at the end of discharge significantly improve the pack’s lifespan. A study by (Ma et al., 2020) proposed a hierarchical SOH balancing control method by combining passive (Khalid et al., 2021a) or active battery balancing circuits (Ren et al., 2018) with battery pack SOH balancing schemes. Similarly, (Li et al., 2018), introduced a relative SOH balancing method by indirectly balancing SOH through power redistribution among sub-modules.
While the aforementioned methods for SOH balancing have shown promising results, they often require detailed modeling of the battery system or the design of complex balancing circuit topologies. Typically, these battery models necessitate rich experience and intricate parameters. In situations where the system is highly complex, reliance on model-based methods might even be challenging to implement.
Contrary to model-based approaches, artificial intelligence methods do not require the establishment of a system model. Instead, they learn control strategies from vast amounts of historical system data. By integrating deep reinforcement learning methods (Mnih et al., 2015), it's possible to continuously generate training data while the system is operating, continually adjusting the model’s parameters. This approach has garnered attention from researchers in recent years (Mocanu et al., 2019; Wan et al., 2019). In a groundbreaking move, (Yang et al., 2022), for the first time introduced deep reinforcement learning algorithms into dynamic reconfigurable battery systems and obtain excellent performance in battery balance.
Up to this point, there hasn't been a paper that introduces artificial intelligence algorithms into the study of SOH balancing in a DRB system. Traditional methods often rely on sorting algorithms or expert systems to achieve specific objectives for simpler tasks. However, for systems with complex features and tasks, solving them using traditional empirical and model-based approaches can be challenging. Deep reinforcement learning, on the other hand, can continuously attempt different actions based on various types of state values in a battery system. By combining these attempts with reward values to update network model parameters, even when dealing with high-dimensional data inputs, it can still achieve relatively good results for complex tasks.
Therefore, this paper introduces the deep reinforcement learning algorithm into the dynamic reconfigurable battery system to address the issue of SOH balancing. Firstly, we proposes a simple dynamic reconfigurable battery topology and analyzes the process of battery insertion and removal. Subsequently, leveraging the principle of achieving SOH balance and combining it with the DQN algorithm, the paper constructs a simulation model of the battery system in the Gym environment and conducts simulation experiments. Finally, the paper evaluates the simulation training, analyzes and compares the testing process. The simulation results indicate that the proposed method, in contrast to traditional approaches, exhibits a significant advantage in reducing the disparity in SOH between batteries.
The DRBS depicted in the diagram consists of multiple battery cells connected in series to form a particular branch of the system. Due to differences in the initial capacity, health status, internal resistance, and other factors among the batteries, variability among the batteries is a common issue. Figure 1 illustrates a diagram of DRB system, focusing on a series-connected branch. This series branch is formed by N batteries connected in series via reconfigurable switches. Assuming an external load requires connection to a specified number of batteries, denoted as K, the system achieves a reconfiguration through a selection of K out of N batteries. In order to achieve SOH balance among multiple batteries, the system typically operates with a discharge principle: batteries with higher SOH should receive more opportunities for discharge, while those with lower SOH receive fewer discharge opportunities.
Figure 2 displays the internal structure of the reconfigurable switch, typically composed of two N-type MOSFETs, S11 and S11′, which jointly control the connection and disconnection of the battery. When S11 is conducting and S11 is off, the battery is engaged for use. Conversely, when S11 is off and S11’ is conducting, the battery is bypassed. This dual-MOSFET switch structure is simple in design and offers flexible and convenient control.
For an entire series branch within the circuit, Figure 3 illustrates the detailed switching process of two batteries in the circuit, reflecting changes in the system’s topology. In the configuration depicted in Figure 3, initially, battery B11 is connected to the circuit, while battery B12 remains disconnected. When a battery switch is required in the circuit, the process begins by closing the main branch switch, Sm2, and opening the main branch switch, Sm11. Subsequently, the sequence involves opening S11 and S12′, closing S11′ and S12 to connect battery B12 into the branch. Finally, the branch’s main switch, Sm12, is opened, and the main branch switch, Sm11, is closed.
Sm11 and Sm12 employ MOSFET switches to prevent arcing. The role of the branch diode Dm1 is to prevent localized loop currents caused by transient voltage fluctuations during the insertion or removal process of a battery within a particular branch.
The batteries within the battery pack exhibit varying capacities among individual cells. Some battery cells may possess higher capacities, while others have lower capacities. This disparity leads to certain battery cells depleting or charging more quickly during the discharge and charge processes, ultimately shortening the overall lifespan of the entire battery pack.
Depth of Discharge, often referred to DOD, is typically considered a key factor influencing the number of cycles a battery can undergo. As DOD increases, the rate of change in SOH also accelerates. In a study by (Li et al., 2018), a method for relative SOH balancing is proposed. By employing different DOD levels among battery packs within the system, the SOH curves of different battery packs gradually converge, optimizing the overall system’s output capacity and lifespan.
To provide a more comprehensive description of the relationship between DOD, SOH, and cycle life, Figure 4 illustrates the theoretical situation of SOH changes concerning DOD and the number of cycles. If the SOC is controlled to be the same as traditional methods, the DODs among different battery packs will be identical, leading to the SOH of the weaker batteries deteriorating first to retirement levels, as depicted in Figure 4A. Adopting the proposed SOH balancing method, the better (poorer) batteries are subjected to higher (lower) DOD levels initially. As their SOH levels align, their DODs are then regulated to be the same. This process results in a uniform decline in the SOH of all battery packs, as shown in Figure 4B.
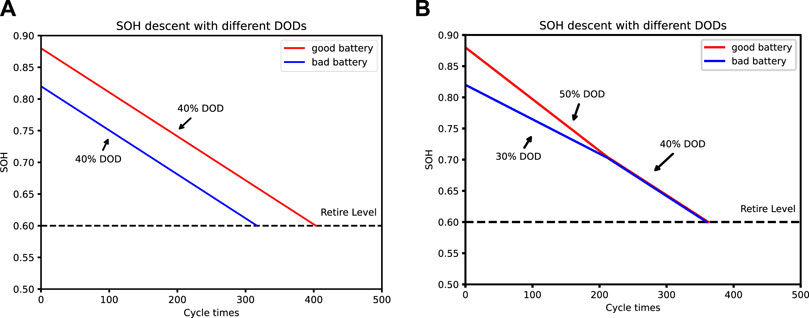
FIGURE 4. SOH variation profiles with (A) SOC balancing control strategy and (B) proposed SOH balancing method.
In order to simplify our research focus, our work primarily concentrates on a single serial branch of the dynamic reconfigurable battery system. Let us define a serial branch with N batteries, where the voltage at the two ends of the branch is denoted as
For a typical series-connected battery energy storage system, it is easier for the batteries within the battery pack to reach retirement levels with similar SOH when the differences in SOH between batteries are smaller. Therefore, addressing the issue of SOH balance should be the primary concern. When battery packs already have batteries with approximately similar SOH, maintaining a close proximity of SOC among them can significantly enhance the overall lifespan of the battery pack.
Here, we first need to introduce a metric to quantify the SOH disparity within a particular serial branch of the dynamic reconfigurable system at time t, denoted as δ.
Here,
The control objective of the dynamic reconfigurable battery system is to minimize the δ value in Eq. 1 during the SOH balancing phase.
In typical situations, SOH can be defined based on the degradation of battery maximum capacity and the increase in internal resistance. SOH based on capacity degradation can be defined Eq. 1:
In the paper (Wang and Hong, 2018), the authors propose a SOH definition based on cycle life, expressed as in Eq. 4:
Here,
Building upon prior research, this paper defines and analyzes SOH from the perspective of cycle life (Wang and Hong, 2018) proposes a method for calculating battery cycle life without considering temperature. The relationship between total cycle life and DOD can be expressed in a simplified form by the following Eq. 5.
where a and b are parameters that vary for different types of batteries. To better describe the relationship between SOH, DOD, and in the subsequent sections, this paper’s case study is proposed with constant values of a = 694 and b = 0.795 for a typical lithium-ion batteries (Li et al., 2018; Dallinger et al., 2013)
Where DOD can be expressed in terms of SOC of the battery:
Subsequently, based on Eqs 5, 6, the relationship between the battery’s cycle life, discharge depth, and SOH can be derived.
It can be observed in Eq. 7 that with an increase in discharge depth, the rate of change of SOH also accelerates. In theory, by applying different DODs to batteries with varying health states, the SOH of different batteries will eventually converge to a single curve.
In order to achieve the goal of SOH balance, we consider the SOH states of two batteries, denoted as i and j. Let’s assume these two batteries have different initial SOH values. Their instantaneous SOH can be represented as:
From Figure 5 and Eq. 8, it can be observed that with specific cycle numbers and the application of varying DODs to different batteries, when certain conditions for DOD application are met, the SOH levels among the batteries tend to converge.
The subsequent algorithms, while ensuring final SOH balance, essentially coordinate the simultaneous achievement of a particular SOH equilibrium level by each battery, as will be detailed in the following sections.
The control framework of this article is depicted in Figure 6. It consists of two neural networks with an identical structure and an experience replay module, commonly referred to as the agent. The experience replay area generally stores data collected from the environment, where each data entry includes a tuple of state, action, reward, and the next action. Data sampled from the experience replay is usually shuffled randomly to disrupt the correlations between the data. Due to the efficient access characteristics of experience replay, the DQN algorithm does not need to rely on real-time generated data every time, which reduces the demands on computational resources.
In addition, The two neural networks are known as the evaluation neural network and the target neural network. The evaluation neural network updates its parameters through loss gradient descent and backpropagation after each decision by the agent. Meanwhile, the parameters of the target neural network are copied from the evaluation network every C steps. The evaluation neural network chooses the next action based on its maximum value at each decision of the agent. This action is then fed back into the environment for further decisions.
The entire system forms a closed-loop control, allowing the agent not only to learn an existing control strategy from historical data offline but also to update the control strategy parameters through interaction with the environment. The algorithmic steps used in training the intelligent agent are summarized in Algorithm 1.
The proposed agent’s state space consists of thirty state values, which include the SOC, SOH, and switch state for each of the ten batteries. These values are represented as:
Behavior of individual battery
It is worth noting that here, in Eq. 9 “ai” serves as both the set of actions that each switch can take and can also be stored as a state value in the state space. The previously mentioned SS1, SS2,
The smaller the difference in SOH among the batteries, the better the balance performance. During the SOH balance phase, let us define the reward at time t as
A total reward R for one episode is defined as in Eq. 11:
T represents the number of switch actions taken in one episode.
The experience replay memory stores environmental state information collected from the environment. During the training process of the neural network, a batch of data is sampled from the experience replay buffer. The current state value‘s' and action value ‘a' are passed to the evaluation neural network, and the resulting next state value after taking the current action is passed to the target neural network for forward propagation. The evaluation neural network calculates the loss gradient based on the Q-values and rewards from the target neural network and performs backpropagation to update network parameters, gradually seeking the optimal policy. The number of input neurons in the neural network corresponds to the quantity of elements in the state space. The configuration of hidden neurons is typically predetermined and can be adjusted based on experimental results. The number of output neurons corresponds to the number of possible actions, and the output values represent Q-values, indicating the maximum value of the current action.
The loss function is defined as follows in Eq. 12:
The gradient value for gradient descent is in Eq. 13:
The update of the network parameters is
where in Eq. 14, α is the learning rate, generally in the range between 0 and 1.
The target neural network does not undergo backpropagation; its weight parameters are periodically copied from the evaluation neural network every few training steps.
Based on the neural network training in the learning process, there are typically many possible actions for the current state. However, taking different actions leads to different output values from the neural network. The agent selects the action with the highest Q-value output and applies it to the environment for the environment to make control decisions.
Algorithm 1.DQN Algorithm.
: 1 Initalize Experience Replay memory D to capacity N;
: 2 Initialize behavior network with random parameter W=
: 3 Initialize target network with parameter
: 4 for episode = 1,M do
: 5 Initialize sequence
: 6 for t =1,T do
: 7 With probability ε select a random action
: 8 otherwise, select
: 9 Execute action
: 10 observe reward
: 11 Store transition (
: 12 Experience Replay
: 13 Sample a batch of (S,A,R,S_) randomly from D;
: 14 Set
: 15 Perform a gradient descent step on
: 16 Calculate the update parameter
: 17 Update the behavior network parameter
: 18 Update of target network
: 19 Replace
: 20 End for
: 21 End for
In a DRB system, the battery state is taken as the observation state, and the switch control sequence is taken as the control target. Reward value
During the training process, the goal of DQN is to minimize the error between the estimated Q-values and the target Q-values, gradually learning a more accurate action-value function. This enables the agent to make wiser decisions to maximize the cumulative reward. While in the testing phase, the trained DQN is used to make decisions in the environment. During testing, the agent employs its learned Q-values to choose actions in different states.
In concrete terms, if the state values of the DRB system at a specific moment are transmitted to the DQN agent, we can obtain the optimal switch control strategy for the system at that particular state.
Furthermore, to better leverage the advantages of the DQN algorithm and achieve a higher level of SOH balance, we have introduced an additional evaluation criterion into the testing results of DQN. When the system meets the specified criterion, we consider that the balance of SOH has achieved satisfactory results. This condition is also permissible for practical system deployment.
Here, we define a new indicator ε, where ε can be calculated in Eq. 15 as follows:
ε reflects the degree of difference between the SOH of each battery at a specific moment and its mean. A smaller ε indicates that the SOH balance has reached a higher level at that moment.
Meanwhile, the criterion for considering that the SOH has achieved a good balance is as follows in Eq. 16:
In the actual simulation scenarios, We can set a 5% deviation band, and theoretically, during the interval from the first entry to the first exit of ε into this deviation band, we can randomly choose a termination time for the algorithm. Furthermore, if we select the minimum value of ε as the termination criterion, it will result in the best SOH balancing effect.
The simulation experiments were conducted in the Gym environment developed by OpenAI (OpenAI, 2023). Here, Gym is a toolkit tailored for reinforcement learning algorithms, aiming to furnish researchers and developers with a standardized interface, facilitating the seamless design, implementation, and evaluation of diverse reinforcement learning algorithms.
Initially, a battery discharge model was set up in the configured environment. Then, using the reinforcement learning DQN algorithm, appropriate simulation parameters were set to facilitate the training and testing processes. The neural network parameters and hyperparameters during the training process are shown in Tables 1, 2. In order to better demonstrate the effectiveness of the DQN algorithm, Table 3 provides the initial values of the battery state information during the algorithm’s testing phase.
Due to the computational demands of the DQN algorithm in solving optimal control strategies, a certain amount of computing resources, typically GPUs, is needed to accelerate the training process, especially for complex tasks. However, in the simulated experiments conducted in this study, the training process is not aimed at achieving an exceptionally fast training speed. The simulations are run on a personal Huawei laptop equipped with an AMD Ryzen 7 3700U processor.
In this section, we evaluated the proposed control framework based on simulation experiments. We compared the proposed control method with traditional methods by analyzing battery discharge curves under the proposed method and assessed the performance advantages.
According to Eq. 7, it can be observed that the decay of SOH for individual batteries is related to the number of cycles and the depth of discharge. If a specific number of cycles is set, such as 300 cycles in this simulation, the DQN algorithm will eventually converge to a certain SOH level. As shown in Figure 7 and Figure 8, to achieve better practical simulation results, we selected the process from the initial value to the 40th step based on the changes in values of Ɛ as our control strategy according to the 5% criteria.
In the task of SOH balancing, the main objective of the control strategy is to achieve the desired DOD for each battery within a predetermined number of cycles. The reduction curve of SOC within a single cycle, as shown in Figure 9, also reflects the switching control process to achieve this control goal. Figure 10 displays the state changes of the 10 switches in achieving the expected DOD. A state value of 1 indicates that the switch controls the insertion of the corresponding battery, while a state value of 0 indicates the removal of the corresponding battery at that time. The corresponding insertion and removal principles and processes are illustrated in Figures 2, 3.
Once a control strategy for a cycle is determined, theoretically, in the real DRB system, this strategy will be repeated for a set of numbers to achieve the balance of SOH.
Figure 11 shows the change in episode rewards during our training process. Figures 11A, B represent the changes in reward values and reward variance values, respectively. The reward values gradually converge to a relatively stable value as the training episodes increase. The variance of rewards is initially large at the beginning of an episode but gradually decreases to a smaller level. When the reward values stabilize, the variance of rewards also stabilizes at a smaller level, indicating that the training process has reached a good level of performance at this point. Figure 11 also reflects, from a certain perspective, the learning process of the agent: in the initial stages of learning, the agent may be completely unfamiliar with the environment and undergo exploratory actions. Over time, the intelligent agent gradually learns the patterns of the environment, the strategy becomes stable, and both the reward and its variance decrease, ultimately reaching stability.
To better illustrate the advantages of the DQN algorithm combined with SOH balancing theory, we conducted a simulation comparison between the SOH balancing under the DQN algorithm and the traditional fixed series-parallel configuration (Li et al., 2018).
As shown in Figure 12A, the initial variance and range of SOH correspondingly match the variance and range at cycle times = 300, being 13.43% and 12%, respectively. This indicates that the traditional fixed series-parallel topology is not effective in addressing the issue of SOH balance. Batteries with lower SOH will reach retirement levels prematurely, thereby reducing the cycle life of the battery system.
In contrast, as shown in Figure 12B, our approach, utilizing DQN and the principle of SOH balance as features, is capable of reducing the initial SOH variance from 13.43 to 0.21 and decreasing the SOH range from 12% to 1.56%. This significantly reduces the variability among batteries when reaching or approaching a certain ideal DOD level. For example, in this case, the SOH imbalance, represented by the variance, is reduced by 87%. Consequently, by reducing this variability among batteries, our method plays a crucial role in enhancing the overall cycle life of the entire DRB system, contributing significantly to energy efficiency.
While our method has indeed achieved outstanding results in achieving the goal of SOH balance, Figure 9 indicates that this balance obtained at the expense of sacrificing SOC balance, posing a challenging and difficult-to-reconcile issue. Our future work will attempt to comprehensively address the balance between SOC and SOH from alternative perspectives. Meanwhile, We will fully consider the challenges presented in achieving a balance between SOC and SOH, and focus on deploying the DQN algorithm in a real DRB system.
This paper introduces a DOD-SOH balancing method for DRB system based on the DQN algorithm in deep reinforcement learning. The proposed intelligent agent progresses from initially having no knowledge of the system’s environmental features to gaining a profound understanding of the system’s operational procedures. First of all, we presents a simple dynamic reconfigurable battery topology, and analyzes the process of battery insertion and removal. Subsequently, by utilizing the principles of SOH for equilibrium, our work combines the balancing process with the advantages of the DQN algorithm in seeking the optimal decision sequence. Finally, Simulation results indicate that our method exhibits a significant advantage over traditional methods in reducing the disparity in SOH among batteries. Future work will be geared toward the deployment of the proposed method in practical systems, aiming to bridge the gap between the theoretical framework and real-world application.
The original contributions presented in the study are included in the article/supplementary materials. Further inquiries can be directed to the corresponding author.
XY: Investigation, Methodology, Validation, Visualization, Writing–original draft. PL: Conceptualization, Methodology, Software, Validation, Writing–original draft. FL: Conceptualization, Funding acquisition, Methodology, Project administration, Writing–original draft. ZL: Data curation, Methodology, Writing–original draft. DW: Formal Analysis, Project administration, Writing–review and editing. JZ: Funding acquisition, Project administration, Supervision, Writing–review and editing. TW: Funding acquisition, Project administration, Supervision, Writing–review and editing.
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported in part by the Joint Fund of the Chinese Academy of Sciences and Shandong Energy Research Institute under Grant SEI U202310, in part by the Institute of Electrical Engineering, CAS under Grant E155610301 and 480E155610201.
This is a brief acknowledgement of the contributions of individual colleagues, institutions, or agencies that assisted the writers’ efforts in the writing of this article.
Author FL was employed by Wuhan Huayuan Electric Power Design Institute Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
DOD, Depth of discharge; SOH, State of health; SOC, State of charge; DRB, Dynamic reconfigurable battery; DQN, Deep Q-network; DRL, Deep reinforcement learning; OCV, Open circuit voltage; Gym, Toolkit tailored for reinforcement learning algorithms developed by OpenAI.
Abomazid, A. M., El-Taweel, N. A., and Farag, H. E. Z. (2022). Optimal energy management of hydrogen energy facility using integrated battery energy storage and solar photovoltaic systems. IEEE Trans. Sustain. Energy 13 (3), 1457–1468. doi:10.1109/TSTE.2022.3161891
Buchicchio, E., De Angelis, A., Santoni, F., Carbone, P., Bianconi, F., and Smeraldi, F. (2023). Battery SOC estimation from EIS data based on machine learning and equivalent circuit model. Energy 283, 128461. doi:10.1016/j.energy.2023.128461
Chen, L., Wu, X., Lopes, A. M., Yin, L., and Li, P. (2022). Adaptive state-of-charge estimation of lithium-ion batteries based on square-root unscented Kalman filter. Energy 252, 123972. doi:10.1016/j.energy.2022.123972
Ci, S., Lin, N., and Wu, D. (2016). Reconfigurable battery techniques and systems: a survey. IEEE Access 4, 1175–1189. doi:10.1109/ACCESS.2016.2545338
Ci, S., Zhang, J., Sharif, H., and Alahmad, M. (2012). “Dynamic reconfigurable multi-cell battery: a novel approach to improve battery performance,” in Proceedings of the 2012 27th Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, February 2012, 439–442. doi:10.1109/APEC.2012.6165857
Cui, Z., Hu, W., Zhang, G., Zhang, Z., and Chen, Z. (2022). An extended Kalman filter based SOC estimation method for Li-ion battery. Energy Rep. 8 (Suppl. 5), 81–87. doi:10.1016/j.egyr.2022.02.116
Dallinger, D. (2013). Plug-in electric vehicles: integrating fluctuating renewable electricity. Kassel, Germany: Kassel Univ. Press.
Duan, L., Zhang, X., Jiang, Z., Gong, Q., Wang, Y., and Ao, X. (2023). State of charge estimation of lithium-ion batteries based on second-order adaptive extended Kalman filter with correspondence analysis. Energy 280, 128159. doi:10.1016/j.energy.2023.128159
Fan, K., Wan, Y., Wang, Z., and Jiang, K. (2023). Time-efficient identification of lithium-ion battery temperature-dependent OCV-SOC curve using multi-output Gaussian process. Energy 268, 126724. doi:10.1016/j.energy.2023.126724
Gunlu, G. (2017). Dynamically reconfigurable independent cellular switching circuits for managing battery modules. IEEE Trans. Energy Convers. 32 (1), 194–201. doi:10.1109/TEC.2016.2616190
Khalid, A., and Sarwat, A. I. (2021b). Unified univariate-neural network models for lithium-ion battery state-of-charge forecasting using minimized akaike information criterion algorithm. IEEE Access 9, 39154–39170. doi:10.1109/ACCESS.2021.3061478
Khalid, A., Stevenson, A., and Sarwat, A. I. (2021a). Performance analysis of commercial passive balancing battery management system operation using a hardware-in-the-loop testbed. Energies 14, 8037. doi:10.3390/en14238037
Kim, H., and Shin, K. G. (2009). “On dynamic reconfiguration of a large-scale battery system,” in Proceedings of the 2009 15th IEEE Real-Time and Embedded Technology and Applications Symposium, San Francisco, CA, USA, April 2009, 87–96. doi:10.1109/RTAS.2009.13
Kim, T., Qiao, W., and Qu, L. (2012). Power electronics-enabled self-X multicell batteries: a design toward smart batteries. IEEE Trans. Power Electron. 27 (11), 4723–4733. doi:10.1109/TPEL.2012.2183618
Lawder, M. T., Suthar, B., Northrop, P. W. C., De, S., Hoff, C. M., Leitermann, O., et al. (2014). Battery energy storage system (BESS) and battery management system (BMS) for grid-scale applications. Proc. IEEE 102 (6), 1014–1030. doi:10.1109/JPROC.2014.2317451
Li, N., Gao, F., Hao, T., Ma, Z., and Zhang, C. (2018). SOH balancing control method for the MMC battery energy storage system. IEEE Trans. Industrial Electron. 65 (8), 6581–6591. doi:10.1109/TIE.2017.2733462
Li, X., Wang, L., Yan, N., and Ma, R. (2021). Cooperative dispatch of distributed energy storage in distribution network with PV generation systems. IEEE Trans. Appl. Supercond. 31 (8), 1–4. doi:10.1109/TASC.2021.3117750
Ma, Z., Gao, F., Gu, X., Li, N., Wu, Q., Wang, X., et al. (2020). Multilayer SOH equalization scheme for MMC battery energy storage system. IEEE Trans. Power Electron. 35 (12), 13514–13527. doi:10.1109/TPEL.2020.2991879
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness, J., Bellemare, M. G., et al. (2015). Human-level control through deep reinforcement learning. Nature 518, 529–533. doi:10.1038/nature14236
Mocanu, E., Mocanu, D. C., Nguyen, P. H., Liotta, A., Webber, M. E., Gibescu, M., et al. (2019). On-line building energy optimization using deep reinforcement learning. IEEE Trans. Smart Grid 10 (4), 3698–3708. doi:10.1109/TSG.2018.2834219
Morstyn, T., Momayyezan, M., Hredzak, B., and Agelidis, V. G. (2016). Distributed control for state-of-charge balancing between the modules of a reconfigurable battery energy storage system. IEEE Trans. Power Electron. 31 (11), 7986–7995. doi:10.1109/TPEL.2015.2513777
OpenAI (2023). OpenAI Gym. Available at: https://gym.openai.com/.
Raoofi, T., and Yildiz, M. (2023). Comprehensive review of battery state estimation strategies using machine learning for battery Management Systems of Aircraft Propulsion Batteries. J. Energy Storage 59, 106486. doi:10.1016/j.est.2022.106486
Ren, H., Zhao, Y., Chen, S., and Wang, T. (2018). Design and implementation of a battery management system with active charge balance based on the SOC and SOH online estimation. Energy 166, 908–917. doi:10.1016/j.energy.2018.10.133
Shu, X., Shen, S., Shen, J., Zhang, Y., Li, G., Chen, Z., et al. (2021). State of health prediction of lithium-ion batteries based on machine learning: advances and perspectives. iScience 24 (11), 103265. doi:10.1016/j.isci.2021.103265
Wan, Z., Li, H., He, H., and Prokhorov, D. (2019). Model-free real-time EV charging scheduling based on deep reinforcement learning. IEEE Trans. Smart Grid 10 (5), 5246–5257. doi:10.1109/TSG.2018.2879572
Wang, S., Takyi-Aninakwa, P., Jin, S., Yu, C., Fernandez, C., and Stroe, D.-I. (2022). An improved feedforward-long short-term memory modeling method for the whole-life-cycle state of charge prediction of lithium-ion batteries considering current-voltage-temperature variation. Energy 254, 124224. doi:10.1016/j.energy.2022.124224
Wang, S., Wu, F., Takyi-Aninakwa, P., Fernandez, C., Stroe, D.-I., and Huang, Q. (2023). Improved singular filtering-Gaussian process regression-long short-term memory model for whole-life-cycle remaining capacity estimation of lithium-ion batteries adaptive to fast aging and multi-current variations. Energy 284, 128677. doi:10.1016/j.energy.2023.128677
Wang, T.-H., and Hong, Y.-W. P. (2018). “Learning-based energy management policy with battery depth-of-discharge considerations,” in Proceedings of the 2015 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Orlando, FL, USA, December 2015, 992–996. doi:10.1109/GlobalSIP.2015.7418346
Xu, H., Wu, L., Xiong, S., Li, W., Garg, A., and Gao, L. (2023). An improved CNN-LSTM model-based state-of-health estimation approach for lithium-ion batteries. Energy 276, 127585. doi:10.1016/j.energy.2023.127585
Yang, F., Gao, F., Liu, B., and Ci, S. (2022). An adaptive control framework for dynamically reconfigurable battery systems based on deep reinforcement learning. IEEE Trans. Industrial Electron. 69 (12), 12980–12987. doi:10.1109/TIE.2022.3142406
Keywords: state of health, state of charge, deep reinforcement learning, deep Q-network, dynamic reconfigurable battery, battery imbalance
Citation: Yang X, Liu P, Liu F, Liu Z, Wang D, Zhu J and Wei T (2023) A DOD-SOH balancing control method for dynamic reconfigurable battery systems based on DQN algorithm. Front. Energy Res. 11:1333147. doi: 10.3389/fenrg.2023.1333147
Received: 04 November 2023; Accepted: 11 December 2023;
Published: 29 December 2023.
Edited by:
Sandip K. Saha, Indian Institute of Technology Bombay, IndiaReviewed by:
Shunli Wang, Southwest University of Science and Technology, ChinaCopyright © 2023 Yang, Liu, Liu, Liu, Wang, Zhu and Wei. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fang Liu, bGYuZHEwNjA1QDE2My5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.