- 1Department of Electrical Engineering, Tsinghua University, Beijing, China
- 2College of Electrical Engineering and Control Science, Nanjing Tech University, Nanjing, China
Pumped-storage hydropower plant (PSHP) is a type of valuable energy storage system and a flexible resource to the modern power system with increasing renewable energy integration. As independent market participants, a PSHP can participate in both the energy market and frequency regulation market to maximize its revenue and contribution to the secure and economic operation of the power system. In some PSHPs, both fixed-speed and variable-speed units are installed to improve the flexibility, especially when operating in the pumping mode. However, it’s difficult to deal with the nonlinear relationships among power, flow, and water head in pumping and generating modes. This paper proposes iterative solution methods for scheduling the PSHP by considering the relationship between power and flow at different water heads for different types of units. The scheduling problem is established as a scenario-based optimization formulation by considering PSHP’s participation in both the energy market and frequency regulation market. In each iteration, the optimal dispatch model is formulated as a Mixed Integer Linear Programming (MILP) problem. Case studies are performed and simulation results validate the effectiveness of the model and the iterative solution methods.
1 Introduction
The large-scale development of renewable energy, such as wind and solar, is very important to achieve the targets of carbon neutrality (Outlook, 2020; Stančin et al., 2020). However, the volatile and intermittent characteristic of renewable energy generation brings great challenges to power balance of power systems (Cai et al., 2019). Energy storage systems, especially pumped storage hydropower plants (PSHP), will play a key role in the future power systems with very high penetration of renewable power generation.
Currently, pumped-storage hydropower units can be divided into fixed-speed units and variable-speed units. Compared to variable-speed units, fixed-speed units are mature and used in most pumped storage hydropower plants worldwide (Yang and Yang, 2019; Vasudevan et al., 2021). Meanwhile, with the development of AC excitation technology, power can be adjusted for variable speed units in pumping mode. In addition, variable-speed units can generate a lower percentage of the rated power in comparison to fixed-speed units, which means that variable-speed units have a stronger power regulation capability to cope with future large-scale renewable energy output fluctuations and renewable energy consumption.
In the US and some regions in Europe, PSHPs can participate in the local electricity market as independent players. The PSHPs can pump water to store energy when the electricity tariff is low, while generating to get profits during periods with high electricity price (Kim et al., 2021; Liu et al., 2021). Therefore, the PSHP declares its generating and pumping curve in the day-ahead market according to the forecast electricity price and receives the revenue as a price-taker. In Emmanuel and Denholm (2022), a modified price-taker model with a market feedback function is established to simulate the impact of increased storage including PSHP. A market participation strategy and schedule for a PSHP with hydraulic short-circuit technology are proposed using a price-taker model presented in Kwon et al. (2021). However, with the development of pumped storage unit technology and the improvement of the electricity market, pumped storage power plants can participate not only in the energy market, but also in the regulation and reserve market (Chazarra et al., 2017). In Chazarra et al. (2017), a scheduling model is established for a closed-loop PSHP participating in both the energy and secondary regulation market. Besides, using variable-speed units also makes it possible to get profits from the regulation market, when units operate in pumping mode (Rayati et al., 2022). By establishing an accurate model for PSHPs, PSHPs can be dispatched effectively, contributing to improving the overall benefits of PSHPs.
In the previous research, studies related to the optimal scheduling of PSHPs were mostly based on the constant head model, which means PSHPs were considered to maintain a constant head in operation. With this assumption, power shows a linear relationship with the flow in pumping and generating modes. In Bruninx et al. (2015); Moradi et al. (2017); Li et al. (2018); Abdelshafy et al. (2020); He et al. (2020), different coefficients are used to describe the linear relationship between the power and flow in pumping mode and generating mode. The pumping and generating constraints with corresponding coefficients are included in the optimization model. In fact, many PSHPs are head-sensitive plants, meaning the actual pumping and generating power of the pumped storage units is influenced by the combination of the head and flow. In order to dispatch PSHPs more effectively, it is necessary to establish an optimal dispatch model for PSHPs reflecting the nonlinear relationship of “power-flow-water head” for both fixed-speed and variable-speed units in pumping and generating modes.
Some researchers proposed linearized methods to accurately demonstrate the relationship between the flow and power under different hydraulic heads (Su et al., 2019; Toubeau et al., 2019; Wang et al., 2021; Yuan et al., 2021). In Toubeau et al. (2019), nonlinear pump/turbine head-dependent curves are modeled and linearized to decrease the endogenous uncertainties in the models. In Su et al. (2019); Wang et al. (2021), the MILP formulation is used to model the hydropower plants, which can give an approximate model to demonstrate the model of plants with nonlinear and non-convex features. However, it takes a long time or cannot get the optimal solution, when the PSHP contains multiple units or too many linearized constraints with a large number of binary variables included in the model to give a better approximation. Besides, the different operating characteristics of variable-speed and fixed-speed units make it difficult to optimize the scheduling of pumped storage power plants with multi-type of units.
Two major contributions have been made in this paper. One of the contributions is to propose an optimal day-ahead dispatch method for a PSHP containing multi-type of units considering the effect of hydraulic heads. The optimization objective is to maximize the revenue of PSHPs in the energy market and the regulation market. Nonlinear characteristics among the “power-flow-water head” of fixed-speed and variable-speed units are considered to establish a more realistic model for the PSHP. The other contribution is to propose an iterative method for solving the optimal scheduling model of the PSHP considering the influence of hydraulic effects. A heuristic-based acceleration method is proposed to improve the effectiveness of the computational results. The proposed method significantly shortens the solution time compared to directly solving complicated linearized models and gives a better approximation solution for the model. Therefore, it is more practical for the proposed algorithm to be used in engineering.
The remaining of this paper is organized as follows. Section 2 establishes the day-ahead dispatch model to maximize the revenues for the PSHP in the energy market and regulation market. Section 3 introduces the mathematical formulation of the fixed-speed and variable-speed units in both pumping and generating states. Section 4 describes the iteration strategy for optimal scheduling. Several cases are conducted in Section 5 to validate the correctness and effectiveness of the method of the proposed methods. Finally, conclusions are drawn in Section 6.
2 Basic day-ahead dispatch model for a PSHP containing multi-type units
In contrast to a fixed-speed unit, the pumping power of a variable-speed unit can be changed in the pumping mode. Therefore, a PSHP containing multi-type of units can participate in energy and frequency regulation with higher flexibility. By optimizing the generating and pumping power of units, it is possible for the PSHP’s operator to get more revenue by fully making use of the multiple units. Considering the participation of PSHP in both energy and frequency regulation markets, we construct the basic day-ahead self-scheduling model for a PSHP to maximize the expected total revenue in this section.
In the model, the PSHP is regarded as a price-taker of the electricity markets, and the uncertainties of demand for frequency regulation are also considered. The nonlinear characteristics of “power-flow-water head” for the fixed-speed and variable-speed units in the PSHP are modeled and elaborated in the next section.
2.1 Objective function
The objective function includes the revenues of PSHP trading in energy market
Eq. 2 represents the revenues of PSHP with fixed-speed and variable units in the energy market. Eq. 3 depicts the revenues of the PSHP from the regulation market. The payment of regulation services consists of a capacity payment and a performance-based payment. The former payment indicates the opportunity costs of enabled capacities, while the latter reflects the contribution to the frequency regulation. As uncertainties exist in the Automatic Generation Control (AGC) signal, a scenario-based optimization objective function is established to consider the uncertainty of the AGC signals. Eq. 4 shows the total startup and shutdown cost of the PSHP at time t.
2.2 Constraints
Constraints (5–7) show the number of units in the pump state in operation. Constraints (8, 9) limit the number of times that units can switch between the pump state and the generation state. Constraint (10) guarantees that the PSHP cannot pump and generate at the same time. The number of units in operation should be less than the total number of units by constraints (11–14). Besides, units are not allowed to change from pump state to generation state between adjacent dispatch periods according to constraints (15–16).
Constraints (17–26) show the pumping and generating power constraints for fixed-speed and variable-speed units in the PSHP. The pumping and generating power for each unit should be within the feasible operating region. As the PSHP participates in the regulation market, the expected pump and generation power is limited by constraints (18, 21, 24). The operating power is the sum of the pump and generation power participating in the day-ahead market and the actual power participating in the regulation market.
The volume constraints of the upper and the lower reservoirs are shown in constraints (30–34). Constraints (30, 31) represent the volume balance of the PSHP between dispatch periods. In operation, the amount of water stored in the reservoir should not exceed the reservoir capacity. Besides, the daily volume change should be limited by constraint (34) to guarantee the reservoir’s starting volume of the next day.
3 An improved model for the nonlinear “power-flow-water head” characteristics of PSHP
In Section 2, a general day-ahead scheduling model is established for PSHP. However, the model does not include detailed constraints to describe the relationship between the water flow and the power for the fixed-speed and variable-speed units. In this section, an improved mathematical model for the units are established considering the nonlinear relationship among power, flow, and water head.
3.1 Overview of the traditional constant water head (CWH) model
This is the most commonly used model in the previous studies, but it has an obvious error as the hydraulic effects on the power and flow are not considered. Under the constant water head hypothesis, the power is approximately proportional to the flow.
Equations (35) and (36) indicate the linear relationship between the water flow and the generating/pumping power of the PSHP. The water head is assumed to maintain as
3.2 An improved linearized model based on a cluster of typical water heads (ACTWH)
In operation, the variation of the water head influences the flow and the pumping/generating power. Usually, the detailed parameters can be obtained through experiments before the unit is put into operation.
Figure 1 shows the nonlinear relationship among water head, flow, and power for a variable-speed unit in generating/pumping mode, separately. In order to maintain the operating life of the unit up to the design life, there are restrictions on the operating zone of the unit in generating/pumping modes. Without loss of generality, this section constructs a pumping and generating model for the units considering the water head effects according to references (Wood et al., 2013; Mousavi et al., 2019; Alvarez, 2020). The data used can be found at https://pan.baidu.com/s/14QUJkkbEkAr10JZ7XhvUFA?pwd=1111. In real application, the model parameters can be replaced based on experimental data during the optimization.
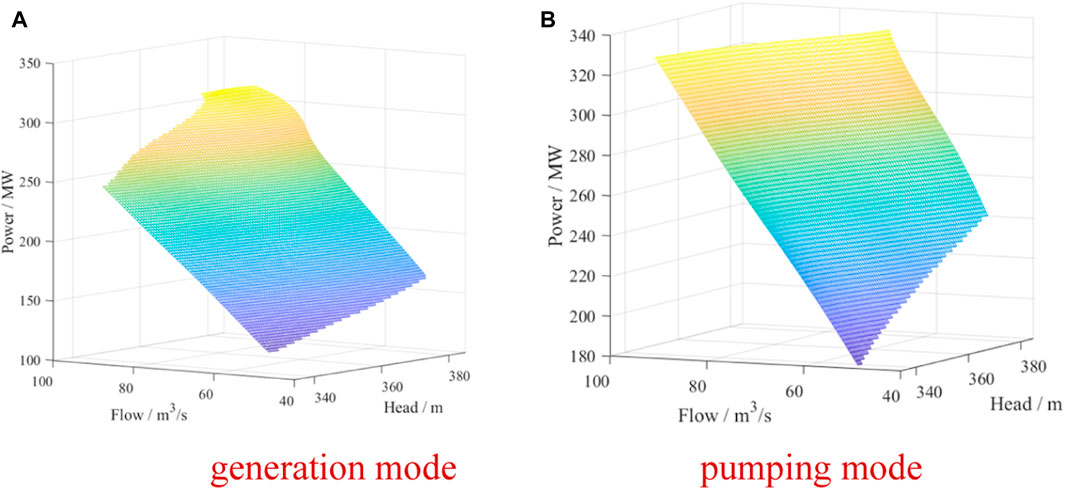
FIGURE 1. Nonlinear relationship among water head, flow and power for a variable-speed unit. (A) generation mode, (B) pumping mode.
For the fixed-speed units in generation mode and variable-speed units in generating/pumping mode, the power is approximately proportional to the flow at the same water head. A series of linear functions reflecting the relationship between power and flow can be established by choosing a cluster of water heads at equal distances as shown in Figure 2.
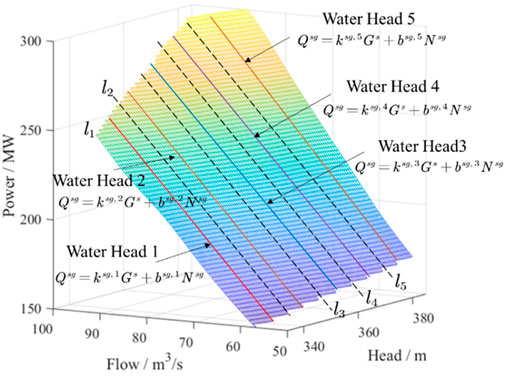
FIGURE 2. Typical water heads and the corresponding function for fixed-speed units in generating mode.
The function of the power varying with flow at any water head can be represented by the linear function at the nearest typical water heads. For example, when the water head is between l1 and l2 in Figure 2, the relationship between power and flow can be represented by the line named Water Head 1. Assuming that the water head is close to the jth typical water head at time k under scenario
Equations (37)–(40) show the linearized function of flow varying with power at typical water head j in hour t under scenario
4 Customized iterative solution method for the ACTWH based PSHP
The optimal scheduling model for a PSHP with multi-type of units is established based on the ACTWH idea in Sections 2, 3. The objective function of the model is (1), and the constraints of the model are composed of (5)-(34) and (37)-(47). In this model, the indices of the water heads at each hour in (37)-(47) are hyper-parameters, which influences the choice of the solution method.
One solution method is to reformulate the ACTWH-based model as an MILP problem by the Big M technique. In this case, the model can be directly solved by commercial solvers, and details are given in the Appendix. However, there is a dilemma when using the Big M technique based direct solution method (DSM): 1) increasing the typical water heads introduce many auxiliary binary variables and relevant constraints, which significantly increases the complexity and solution time of the model; 2) a small number of typical water heads are unable to precisely reflect the nonlinear relationship between power and flow at different water heads.
4.1 Design of the customized iterative solution method (CISM)
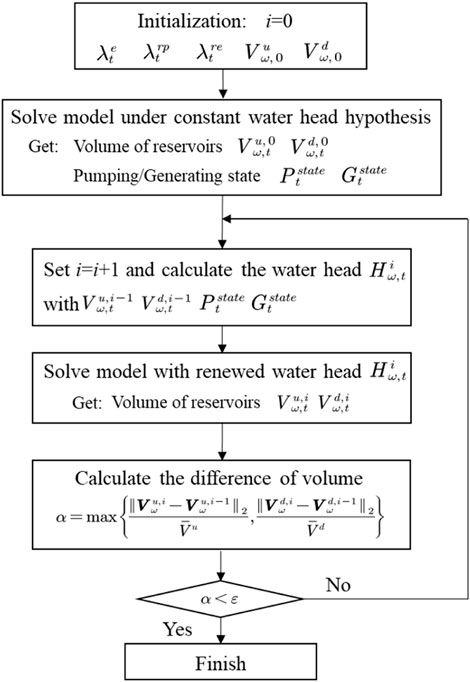
To relieve the bottleneck of DSM, CISM is designed in this section to shorten the solution time and improve the practicability of the ACTWH-based model for PSHPs. The procedures are detailed below and illustrated by Figure 3.
Firstly, the volume of reservoirs (i.e.,
In the ith iteration, according to
Finally, the results of the last iteration are the optimal dispatch strategy considering the effects of the water heads.
With CISM, the renewal of water heads is decoupled with the optimization of the ACTWH-based model, and the auxiliary binary variables and constraints in DSM are all eliminated, which reduce the complexity and solution time.
4.2 Proof of CISM by deduction from the fixed-point view
The iteration of CISM can be described by the interaction between the Hω, Φω and Vω presented in Figure 4. Each box in Figure 4 represents some key state variables, and links between boxes stand for the corresponding decision processes formulated above, which constitute one closed directed loop.
For such interacted models, the optimal solutions should make them reach optimality simultaneously, which is not guaranteed. Hence, we adopt the fixed-point theory to analyze whether the solutions exist or not.
First, we define some mappings according to the logic in Figure 4:
• {Φω} = MWH({Hω}): According to the proposed ACTWH idea, with the water head Hω given, mapping MWH determines the parameters of the linear function at the typical water heads, which are denoted by {Φω}. It is illustrated by Figure 2 that MWH is constructed by a mapping function instead of an optimization process, so its feasibility is ensured. Besides, the mapping in Figure 2 is obviously continuous because the variation of {Hω} falling in the domain cannot cause step changes in {Φω}.
• {Vω} = MDM({Φω}): Mapping MDM represents the optimal dispatch model of a PSHP participating in energy and frequency regulation markets, which is an optimal power flow problem. MDM can also be seen as continuous because: 1) Φω is regard as constant parameters instead of optimization variables; 2) Vω is not composed of the dual variables of the binding constraints in the optimal dispatch model, so there are no step changes in Vω with respect to the variation of Φω.
• {Hω} = MVH({Vω}): Once the volumes of water in the upper and the lower reservoirs Vω are known, the corresponding water levels of the two reservoirs can be easily derived. The difference between the two water levels is the value of the water head Hω, so the mapping between Vω and Hω (i.e., MVH) is obviously a continuous function, whose feasibility is also ensured like MWH.
Then the loop in Figure 4 can be described by mapping Mwhole defined as follows:
With the water head space A defined as
it can be seen that Mwhole is a self-mapping A→A. Since the mappings MWH, MDM, and MVH are continuous, composite mapping Mwhole is also continuous.
Due to the continuity, convexity and compactness of A, the fixed point is proved to exist in A according to the Brouwer fixed point theorem (Kellogg et al., 1976), which is the solution to the interacted optimization problem shown in Figure 4. Such fixed-point problem can be commonly solved by the iterative method, which we have given in Figure 4.
5 Case studies
5.1 Simulation settings and parameters
A PSHP with 7 fixed-speed units and 2 variable-speed units is used to perform the case study, with the goal of maximizing its total revenue. The rated power of the fixed-speed units is 300 MW, while the counterpart of variable-speed units is 330 MW. The operation characteristics of the units are shown in Figure 1. Bath County PSHP is chosen to carry out the case studies, and the relationship between the volume and the water head is proportionally scaled by referring to Shisanling PSHP, China. The basic parameters of Bath County PSHP given in (Cao et al., 2021) are used.
The interval between two adjacent typical water heads is 10 m, while the counterpart for a cluster of water heads is 2 m. At each chosen water head, the power approximately shows a linear relationship to the flow. Therefore, the discretized model of the “power-flow-water head” for units can be used to optimize the operation of PSHP. The time interval is 15 min in daily operation, while the bidding power in the regulation market remains the same in an hour.
The forecast prices for energy and regulation are from (Kazempour et al., 2009). The RegA-type regulation signals of PJM market for a whole year are used to establish the energy demand for frequency regulation (Zhang et al., 2018; Cheng et al., 2023; Zhou et al., 2024). The energy demand for frequency regulation are calculated by averaging regulation signals in every 15 min, and the k-means clustering method is used to generate 10 scenarios to represent the potential frequency regulation requirements. The probability of scenarios ranges between 0.8% and 47.1%. Besides, according to historical statistical data, the average regulation mileage is 2.75 (Xia et al., 2016).
The models are solved by using GUROBI 9.1.0 solver and CVX toolbox in MATLAB environment (Grant and Boyd, 2014). Besides, numerical simulations are performed on a laptop containing an Intel Core i7-4700MQ CPU with 2.4 GHz and 16 GB of RAM.
5.2 Simulation results
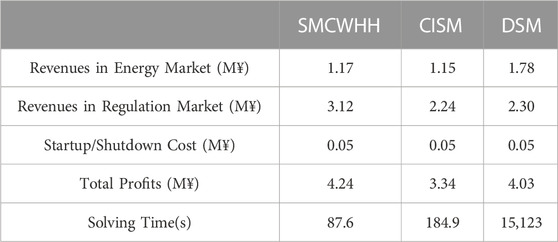
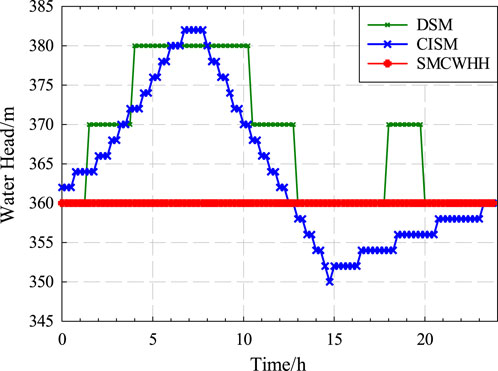
The objective of the model is to maximize the profits of the PSHP with multi-type of units. According to the simulation results, the solution time of DSM is significantly longer than that of the other methods. This subsection compares the optimization results solved by three solution methods, including Solution Method under CWH Hypothesis (SMCWHH), DSM and CISM.
Table 1 shows the operational results of PSHP under different solution methods. According to the results, the PSHP can get more profits from the regulation market than the energy market. SMCWHH is the fastest solution method, and the total profit is also the largest. In fact, since the water head increases in pump mode, more energy needs to be cost. Besides, the actual generation power declines with the decrease of water head, which further leads to a decrease in revenue. Therefore, more profit is expected to be gotten for SMCWHH, which is an error for the solution method.
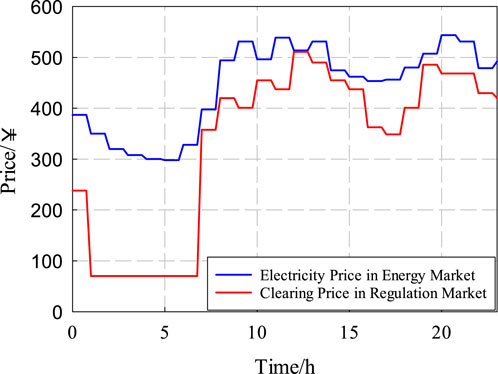
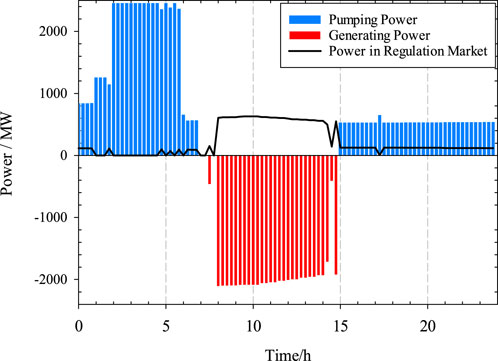
Figure 5 demonstrates the clearing price in the energy and regulation market (Kazempour et al., 2009). According to Figure 5, the electricity price is low between 0:00 and 7:00. The total pumping and generating power of PSHP with CISM under scenario 5 is shown in Figure 6. The units pump when the electricity is low, while generating when the electricity is high. For the fixed-speed units, the units can only participate in the regulation market in generation mode. When the PSHP generates power, more power can participate in the regulation market to get more profits.
Figure 7 shows the water head profiles calculated by different solution methods. In daily operation, the water heads with the volume of water stored in the reservoirs. Besides, the change in water heads has an effect on the power and flow. For the constant water head model, the water heads remain the same in daily operations, causing errors to some extent. Since the relationship between power and flow at different heads can be better approximated, the model solved by CISM can give the closest solution to the actual operation.
5.3 Discussions
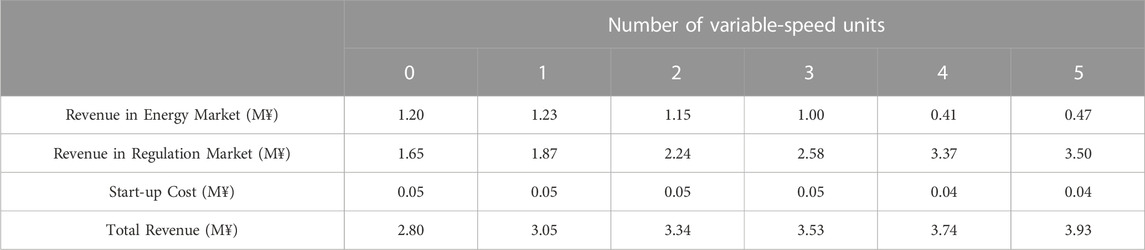
Sensitivity analyses are performed by setting the different number of variable-speed units in the subsection. Besides, this part also shows the change of revenue of PSHP, when the PSHP is working in the hydraulic short-circuit mode.
5.3.1 Impact of the number of variable-speed units on simulation results
Assuming the total number of units is 9 in the PSHP, Table 2 compares the effect of different variable-speed units on the profits of the PSHP by setting the number of variable-speed units from 0 to 5. According to Table 2, the revenue of the PSHP is mainly from the regulation market. As the generating power of variable-speed units can change in a wider range at the same water head compared to the fixed-speed units and its pumping power can also be changed in pumping mode, a PSHP with more variable-speed units can gain more revenue from the regulation market.
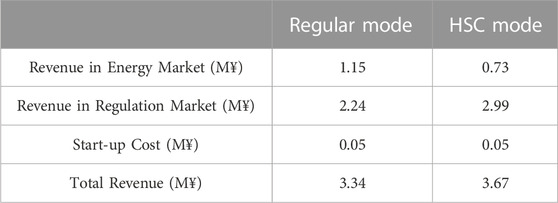
5.3.2 Impact of hydraulic short-circuit (HSC) mode for PSHP
In HSC mode, PSHP can pump and generate simultaneously. Although the efficiency of the HSC mode is less than the regular mode, the power of PSHP can be regulated within a wider range under the HSC mode. Table 3 demonstrates the operation results of PSHP in the regular and HSC mode. When the PSHP works in HSC mode, it loses 0.42 M¥ in the energy market. However, working in HSC mode also makes the PSHP gain 0.75 M¥ more in the regulation market than the PSHP working in the regular mode. According to Table 3, the PSHP can gain more profits from the regulation market in HSC mode.
6 Conclusion
This paper proposes an optimal scheduling method for the PSHP with variable-speed and fixed-speed units considering variable head effects. The objective is to maximize the profits of the PSHP by participating in the energy and regulation markets. The nonlinear relationship of power and flow for the variable-speed and fixed-speed units is established in detail by considering the water head effects. Besides, two iteration solution methods for revising the water head are proposed to optimize the operation of multi-type of units in PSHP. The numerical results show that the scheduling results are closer to the actual operation than the results under the assumption of constant water head. The iteration solution method considering a cluster of water heads can give the most practical solution with less time. Moreover, the PSHP can get more profits by installing more variable-speed units or by operating in short-circuit mode. Besides, PSHP is expected to participate in the intra-day market to further improve the flexibility of the power systems, so its two-stage dispatch model considering the water head effects is among our future work.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
MC: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Validation, Visualization, Writing–original draft. ZH: Conceptualization, Investigation, Software, Writing–review and editing. JC: Conceptualization, Formal Analysis, Supervision, Writing–original draft, Writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported in part by the National Natural Science Foundation of China under Grant 52107105.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abdelshafy, A. M., Jurasz, J., Hassan, H., and Mohamed, A. M. (2020). Optimized energy management strategy for grid connected double storage (pumped storage-battery) system powered by renewable energy resources. Energy 192, 116615. doi:10.1016/j.energy.2019.116615
Alvarez, G. E. (2020). Operation of pumped storage hydropower plants through optimization for power systems. Energy 202, 117797. doi:10.1016/j.energy.2020.117797
Bruninx, K., Dvorkin, Y., Delarue, E., Pandžić, H., D’haeseleer, W., and Kirschen, D. S. (2015). Coupling pumped hydro energy storage with unit commitment. IEEE Trans. Sustain. Energy 7 (2), 786–796. doi:10.1109/tste.2015.2498555
Cai, J., Xu, Q., Cao, M., and Yang, B. (2019). A novel importance sampling method of power system reliability assessment considering multi-state units and correlation between wind speed and load. Int. J. Electr. Power & Energy Syst. 109, 217–226. doi:10.1016/j.ijepes.2019.02.019
Cao, M., Hu, Z., Meng, Y., Cai, F., and Duan, X. (2021). Day-ahead optimal dispatching strategy for flexible HVDC transmission system including pumped storage hydro plant and renewable energy generation. Automation Electr. Power Syst. 45 (15), 36–44. doi:10.7500/AEPS20330331010
Chazarra, M., Pérez-Díaz, J. I., and García-González, J. (2017). Optimal joint energy and secondary regulation reserve hourly scheduling of variable speed pumped storage hydropower plants. IEEE Trans. Power Syst. 33 (1), 103–115. doi:10.1109/tpwrs.2017.2699920
Cheng, L., Zang, H., Wei, Z., and Sun, G. (2023). Secure multi-party household load scheduling framework for real-time demand-side management. IEEE Trans. Sustain. Energy 14 (1), 602–612. doi:10.1109/tste.2022.3221081
Emmanuel, M. I., and Denholm, P. (2022). A market feedback framework for improved estimates of the arbitrage value of energy storage using price-taker models. Appl. Energy 310, 118250. doi:10.1016/j.apenergy.2021.118250
Grant, M., and Boyd, S. (2014). CVX: matlab software for disciplined convex programming, version 2.1.
He, J., Sun, B., Jia, Q., Xu, F., Liu, L., and Gao, B. (2020). “Research on intraday rolling optimal dispatch including pumped storage power station,” in 2020 International Conference on Intelligent Computing, Automation and Systems (ICICAS), Chongqing, China, December 29-31, 2022 (IEEE), 261–265.
Kazempour, S. J., Hosseinpour, M., and Moghaddam, M. P. (2009). “Self-scheduling of a joint hydro and pumped-storage plants in energy, spinning reserve and regulation markets,” in 2009 IEEE Power & Energy Society General Meeting, Calgary, Alberta, Canada, 26-30 July 2009 (IEEE), 1–8.
Kellogg, R. B., Li, T.-Y., and Yorke, J. (1976). A constructive proof of the brouwer fixed-point theorem and computational results. SIAM J. Numer. Anal. 13 (4), 473–483. doi:10.1137/0713041
Kim, H. J., Sioshansi, R., and Conejo, A. J. (2021). Benefits of stochastic optimization for scheduling energy storage in wholesale electricity markets. J. Mod. Power Syst. Clean Energy 9 (1), 181–189. doi:10.35833/mpce.2019.000238
Kwon, J., Levin, T., and Koritarov, V. (2021). “Optimal market participation of pumped storage hydropower plants considering hydraulic short-circuit operation,” in 2020 52nd North American Power Symposium (NAPS), Tempe, Arizona, USA, 11-13 April 2021 (IEEE), 1–6.
Li, J., Wang, S., Liu, Y., and Fang, J. (2018). A coordinated dispatch method with pumped-storage and battery-storage for compensating the variation of wind power. Prot. control Mod. power Syst. 3, 1–14. doi:10.1186/s41601-017-0074-9
Liu, Y., Wu, L., Yang, Y., Chen, Y., and Bo, R. (2021). Secured reserve scheduling of pumped-storage hydropower plants in ISO day-ahead market. IEEE Trans. Power Syst. 36 (6), 5722–5733. doi:10.1109/tpwrs.2021.3077588
Moradi, J., Shahinzadeh, H., and Khandan, A. (2017). A cooperative dispatch model for the coordination of the wind and pumped-storage generating companies in the day-ahead electricity market. Int. J. Renew. Energy Res. 7 (4), 2057–2067. doi:10.20508/ijrer.v7i4
Mousavi, N., Kothapalli, G., Habibi, D., Khiadani, M., and Das, C. K. (2019). An improved mathematical model for a pumped hydro storage system considering electrical, mechanical, and hydraulic losses. Appl. energy 247, 228–236. doi:10.1016/j.apenergy.2019.03.015
Outlook, I. G. R. (2020). Energy transformation 2050. Masdar City, United Arab Emirates: International Renewable Energy Agency IRENA.
Rayati, M., Sheikhi, A., Ranjbar, A. M., and Sun, W. (2022). Optimal equilibrium selection of price-maker agents in performance-based regulation market. J. Mod. Power Syst. Clean Energy 10 (1), 204–212. doi:10.35833/mpce.2019.000559
Stančin, H., Mikulčić, H., Wang, X., and Duić, N. (2020). A review on alternative fuels in future energy system. Renew. Sustain. Energy Rev. 128, 109927. doi:10.1016/j.rser.2020.109927
Su, C., Cheng, C., Wang, P., Shen, J., and Wu, X. (2019). Optimization model for long-distance integrated transmission of wind farms and pumped-storage hydropower plants. Appl. Energy 242, 285–293. doi:10.1016/j.apenergy.2019.03.080
Toubeau, J., Grève, Z. D., Goderniaux, P., Vallée, F., and Bruninx, K. (2019). Chance-constrained scheduling of underground pumped hydro energy storage in presence of model uncertainties. IEEE Trans. Sustain. Energy 11 (3), 1516–1527. doi:10.1109/tste.2019.2929687
Vasudevan, K. R., Ramachandaramurthy, V. K., Venugopal, G., Ekanayake, J. B., and Tiong, S. K. (2021). Variable speed pumped hydro storage: a review of converters, controls and energy management strategies. Renew. Sustain. Energy Rev. 135, 110156. doi:10.1016/j.rser.2020.110156
Wang, S., Liu, J., Chen, H., Bo, R., and Chen, Y. (2021). Modeling state transition and head-dependent efficiency curve for pumped storage hydro in look-ahead dispatch. IEEE Trans. Power Syst. 36 (6), 5396–5407. doi:10.1109/tpwrs.2021.3084909
Wood, A. J., Wollenberg, B. F., and Sheble, G. B. (2013). Power generation, operation, and control. New Jersey, United States: John Wiley & Sons.
Xia, R., Hu, Z., Wu, L., and Liu, H. (2016). Joint operation optimization of wind-storage union with energy storage participating frequency regulation. Power Syst. Technol. 40 (8), 2251–2257. doi:10.13335/j.1000-3673.pst.2016.08.001
Yang, W., and Yang, J. (2019). Advantage of variable-speed pumped storage plants for mitigating wind power variations: integrated modelling and performance assessment. Appl. Energy 237, 720–732. doi:10.1016/j.apenergy.2018.12.090
Yuan, W., Wang, X., Su, C., Cheng, C., and Wu, Z. (2021). Stochastic optimization model for the short-term joint operation of photovoltaic power and hydropower plants based on chance-constrained programming. Energy 222, 119996. doi:10.1016/j.energy.2021.119996
Zhang, H., Hu, Z., Munsing, E., Moura, S. J., and Song, Y. (2018). Data-driven chance-constrained regulation capacity offering for distributed energy resources. IEEE Trans. Smart Grid 10 (3), 2713–2725. doi:10.1109/tsg.2018.2809046
Zhou, Y., Li, X., Han, H., Wei, Z., Zang, H., Sun, G., et al. (2024). Resilience-oriented planning of integrated electricity and heat systems: a stochastic distributionally robust optimization approach. Appl. Energy 353, 122053. doi:10.1016/j.apenergy.2023.122053
Nomenclature
Appendix: Direct Soution Method (DSM) under Typical Water Head
The dispatch model based on ACTWH proposed in Section II and III can be reformulated as an MILP model as follows.
Firstly, to ensure that the water head at any hour is represented by only one typical water head, we add an equality constraint (48).
where all
Then, with the introduction of
where a large number M called Big M is introduced to coordinate a series of exclusive constraints at different typical water heads. When
Constraints (A12)-(A13) are supplementary volume constraints for the upper reservoir in operation. As the volume of reservoir is equally divided by the typical water heads, the actual volume at each moment can only be in one of these intervals. When
According to the reformulation above, the model solved by the direct method is constructed as:
1) The objective function is shown as (1);
2) The constraints consist of Constraints (5)–(34) and (A1)–(A13). In theory, such an MILP problem can be directly solved by commercial solvers, which is not elaborated here.
Keywords: pumped-storage hydropower plant, water head effects, scenario-based optimization, fixed-speed units, variable-speed units
Citation: Cao M, Hu Z and Cai J (2023) Optimal scheduling of pumped storage hydropower plants with multi-type of units in day-ahead electricity market considering water head effects. Front. Energy Res. 11:1326068. doi: 10.3389/fenrg.2023.1326068
Received: 22 October 2023; Accepted: 07 November 2023;
Published: 22 November 2023.
Edited by:
Shuai Yao, Cardiff University, United KingdomReviewed by:
Wei Liu, Nanjing University of Science and Technology, ChinaShuxin Tian, Shanghai University of Electric Power, China
Copyright © 2023 Cao, Hu and Cai. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Minjian Cao, dHljbWpfc2Nob2xhckAxNjMuY29t
 Minjian Cao
Minjian Cao Zechun Hu
Zechun Hu Jilin Cai
Jilin Cai