Integration method of large-scale photovoltaic system in distribution network based on improved multi-objective TLBO algorithm

The increasing integration of distributed generations brings great challenges to the power grid. In this paper, a distributed photovoltaic (PV) integration methodology in distribution network is established for large-scale PV penetration. Firstly, a PV integration model was formulated with the aim of maximizing PV integration capacity and enhancing the voltage profile. Specially, the PV large-scale integration model for county-wide promotion is proposed by considering various typical integration scenarios. Additionally, a novel improved multi-objective Teaching-Learning based optimization (TLBO) algorithm, namely, IM-TLBO, was proposed to seek an optimal Pareto front of the PV integration model. The IM-TLBO algorithm innovatively incorporates the elite reverse learning search strategy to enhance exploration in the solution space. Moreover, the differentiated teaching guided by optimal individual and central location is employed to improve the efficiency of the “teaching” process. Meanwhile, a cyclic crowded sort deletion based on crowding distance is developed to enhance the diversity of elite individuals and the distribution characteristics of the Pareto Frontier. Finally, the performance of IM-TLBO is tested in benchmark functions. Also, a simulation case in IEEE 33 bus system is performed to verify the proposed PV integration method. It is observed that the proposed method in this paper can not only realize the overall optimal integration of roof distributed PV, but also improve voltage profile. The results of IM-TLBO are compared to other classical algorithms, and it is shown that IM-TLBO outperformed them in terms of convergence, distribution and diversity.

1 Introduction

Energy conservation and pollutant emission reduction have gained global attention in recent years (Du and Lu, 2011; Wang et al., 2021). It is of great practical significance to vigorously promote the development of renewable energy generation technology (Painuly, 2001; Tahvonen and Salo 2001). Among various forms of distributed power generation, such as wind power and photovoltaic (PV) generation, the latter has received significant attention as a crucial research topic due to its environmental friendliness. In particular, China, with its expansive territory and abundant PV resources, considers PV generation as a primary and significant source of renewable energy (Zhang et al., 2020; Yan et al., 2014). However, the increasing PV integration scale and uncertain generation nature pose enormous challenges to the security of distribution network (Liu et al., 2022; Zhao et al., 2015). In order to integrate resources, reduce power peak load and optimize distribution network investment, the Chinese government began to officially promote PV integration to the grid in a whole county. Improper large-scale PV integration raises the risk of system instability. It is urgent to solve the problem of large-scale PV integration in the whole county.

The subject of optimum integration of PV system has received considerable attention in the literature (Shah et al., 2015). In (Paatero and Lund, 2007), the authors conducted an analysis on the impact of high PV penetration in medium-voltage distribution networks. They investigated the PV integration effect on voltage drop, network losses and grid benefits. In Ref. (Yong et al., 2022), a continuous time scenario-based optimal configuration method was proposed for PV and energy storage systems. The authors adopted a collaborative approach involving source-network-load coordination to address uncertainty related to sources and loads. In Ref. (Zhang et al., 2020), a dual-layer planning method for distribution networks incorporating distributed PV and energy storage was introduced. The upper layer aimed to minimize the life cycle cost by determining the capacities of PV and energy storage systems. Meanwhile, the lower layer considered the influences of PV and load uncertainty to regulate energy storage. In (Xiaorong et al., 2021), a robust optimal allocation model for energy storage in distribution networks was proposed, considering the flexibility of both generation and load sides. This model specifically addressed the sharp fluctuations in load caused by distributed PV generation. The current approach of renewable energy network planning often lacks a comprehensive optimization plan for large-scale integration throughout the entire county. Specifically, the planning for large-scale PV integration in counties should take into account the distinct access requirements associated with different scenarios. Also, the majority of existing research in the field of PV integration has primarily focused on maximizing PV integration capacity. However, there has been limited consideration given to the joint optimization planning, including economic, technical, and other related aspects. Economic and technical optimization objectives of integration schemes often have conflicts. Most studies only transform the multi-objective problem into a single-objective model through a linear combination of different objectives based on a weighted sum.

The optimal integration of PV system in the distribution networks is a complex non-linear optimization problem. Numerous heuristic methods and approaches have been rendered for PV integration problems. In (Song et al., 2009), the authors present a sigmoid function-based PV system allocation methodology using multi-valued discrete particle swarm optimization. This approach aims to enhance the quality of solutions obtained. In (Tan et al., 2019), in order to reduce power loss and voltage deviation, a multi-objective PV allocation methodology based on an artificial fish swarm algorithm (AFSA) is proposed. In (Varaprasad and Radha, 2022), a novel optimization algorithm called Archimedes Optimization Algorithm (AOA) was proposed. Inspired by physical principles, this algorithm addresses PV configuration in electrical distribution networks with the goal of minimizing emissions and reducing network dependence as much as possible. In Ref. (Zhang et al., 2023), a PV hosting capacity depiction model based on information gap decision theory optimization was proposed. This model offers insights into determining the maximum PV hosting capacity in a distribution network. In (Can and Yong, 2018), the methodology for distributed hybrid solar-wind-battery system capacity planning is proposed based on Grey Wolf Optimization (GWO). In (Kornelakis and Marinakis, 2010), PSO (particle swarm optimization) algorithm is used to locate the optimal number of system devices and the optimal values of the PV module installation in PV grid-connected systems. In (Merei et al., 2013), GA (genetic algorithm) is adopted to optimize off-grid hybrid PV-wind-diesel system with different battery. In (Mahmoud and Ahmed, 2016), an optimization method of a PV fed water pumping system without storage based on teaching-learning-based optimization algorithm is developed. The above-mentioned traditional algorithms frequently encounter problems. GWO also has the disadvantages of poor population diversity, slow convergence rate in late stage, and easy to fall into local optimization. AFSA has the shortcomings of high initial value requirement and slow convergence. AOA has some problems such as weak global exploration ability, slow convergence speed and low solving accuracy when solving optimization problems. Simple GA and PSO get local optimal solution too easily and converge slowly. Classical TLBO algorithm has high convergence speed, but lacks of diversity when attempting to solve multi-objective optimization problems in large-scale renewable energy integration models. Consequently, these methods are plagued with low solving efficiency and suboptimal accuracy.

Motivated by the above concerns, this paper proposed a large-scale distributed PV integration method for a whole county territory. The contributions of this paper are organized as follows.

1) To begin with, this study conducts a comprehensive analysis of the distinct PV integration requirements across four typical scenarios within the entire county territory. Subsequently, a PV integration model for county-wide promotion is formulated, where the objective functions are defined as maximizing the access capacity while minimizing voltage deviations in the distribution network.

2) The TLBO algorithm, originally designed for single-objective optimization, often suffers from shortcomings such as a lack of diversity and a tendency to converge to local optima. To address these limitations and enhance the algorithm’s searching capability, this study proposes an improved multi-objective TLBO algorithm, namely, IM-TLBO. The IM-TLBO algorithm innovatively incorporates elite reverse learning, differentiated teaching and learning, elite individual preservation, and cyclic crowded sort deletion. These enhancements aim to promote diversity and prevent premature convergence, thereby improving the overall performance of the algorithm.

3) The multi-objective benchmark functions are employed to verify the performance of IM-TLBO. To demonstrate the effectiveness of proposed PV integration method, the IEEE33-bus system is employed to simulate the power grid of the county territory. A comparative analysis is performed with other existing methods to evaluate the performance of the solutions. The experimental results unequivocally support the rationality and superiority of the improved multi-objective TLBO algorithm method.

The reminder of this paper is structured as follows. Section 2 presents the formulation of a distributed PV integration model within the county territory. The following section provides a detailed explanation of the IM-TLBO algorithm and subsequently presents the model solving using the IM-TLBO approach. The numerical simulation study on benchmark functions and IEEE-33 bus system are then presented in Section 4 and Section 5, respectively. Finally, conclusions are shown in Section 6.

2 Problem formulation

To develop an effective large-scale PV integration strategy for the entire county, this study considers the installation requirements for four typical scenarios. The PV integration model is established as follows.

2.1 Objective functions

In pursuit of carbon emission reduction and the advancement of renewable energy, maximizing the utilization of PV holds paramount importance in the research on county roof distributed PV integration. The first objective function of this research f₁:

$\begin{array}{l}{f}_1=\max \left(C_1+C_2+C_3+C_4\right)\\ =\max \left({\displaystyle \sum _{i=1}^{N_{\text{pv}}}}{P}_{\text{pv},i}\right)\end{array}(1)$

where C₁, C₂, C₃, C₄ are the total distributed PV access capacity on roofs of party and government organs, public buildings, industry and commerce, and rural residents in the whole county, respectively; N_pv represents the total number of PV; $P_{\text{pv},i}$ represents the PV access capacity of i_th node.

The integration of renewable energy into the distribution network will result in changes to the voltage quality. The second objective function, denoted as voltage deviation (f₂), is expressed as follows:

$f_2=\min {\displaystyle \sum _{i=1}^{N_{\text{bus}}}}{\left(\frac{U_i-U_{\mathrm{i}}^{\exp }}{∆U_{\mathrm{i}}^{\max }}\right)}^2(2)$

Where N_bus is the bus number of power system; U_i is the voltage of i_th nod; $U_i^{\exp }$ is the expected voltage of i_th node; $∆U_i^{\max }$ is the maximum allowable voltage deviation of i_th node.

2.2 Constraints

1) PV integration constraints

When planning the large-scale integration of PV systems on county roofs, it is crucial to consider the diverse requirements associated with different types of PV scenarios.

Party and government building roof constraints:

$50\%\le P\left({\text{AR}}_1\right)\le 100\%(3)$

Roofs of public buildings such as schools and hospitals constraints:

$40\%\le P\left({\text{AR}}_2\right)\le 100\%(4)$

Commercial roof constraints:

$30\%\le P\left({\text{AR}}_3\right)\le 100\%(5)$

Residential roof constraints:

$20\%\le P\left({\text{AR}}_4\right)\le 100\%(6)$

where $P\left({\text{AR}}_1\right)$, $P\left({\text{AR}}_2\right)$, $P\left({\text{AR}}_3\right)$ and $P\left({\text{AR}}_4\right)$ represents the proportion of the actual installed capacity of rooftop PV to the maximum installed capacity of Party and government organs, public buildings, industry and commerce, residential, respectively.

PV installed capacity constraint:

$P_{\text{pv},i}\le P_{i,\max }(7)$

where $P_{\text{pv},i}$ represents i_th installed PV power capacity and $P_{i,\max }$ represents i_th allowed max installed PV power capacity.

The integration of large-scale PV systems has an impact on the security and stability of the power system. Along with this, there are several other constraints that need to be considered in the distributed PV access model. These constraints can be summarized as follows:

2) Power flow balance constraints (Cheng et al., 2017b).

$\left\{\begin{array}{l}{P}_{\mathrm{G}i}+P_{{\text{DG}}_i}-P_{{\mathrm{L}}_i}-U_i{\sum }_{j=1}^{N_{\text{bus}}}{U}_j\left(G_{ij}\cos {\theta }_{ij}+B_{ij}\sin {\theta }_{ij}\right)=0\\ Q_{\mathrm{G}i}+Q_{{\text{DG}}_i}-Q_{{\mathrm{L}}_i}-U_i{\sum }_{j=1}^{N_{\text{bus}}}{U}_j\left(G_{ij}\sin {\theta }_{ij}+B_{ij}\cos {\theta }_{ij}\right)=0\end{array}\right.(8)$

where N_bus is the number of the nodes; P_Gi, P_Dgi and P_Li are traditional generation active power output, DG (distributed generation) active power output and load active power demand of i_th node, respectively; Q_Gi、Q_Dgi and Q_Li are traditional generation reactive power output, DG reactive power output and load reactive power demand of ith node, respectively; U_i is the voltage of i_th node; G_k (i,j) and B_ij represents conductance and susceptance between i_th node and j_th node; θ_ij is the phase difference between nodes i and j.

3) Node voltage constraints (Cheng et al., 2018).

When implementing rooftop distributed PV integration, it is crucial to consider the voltage impact on the distribution network, particularly the voltage deviation. For instance, the integration of large-scale PV systems can lead to reverse power flow, resulting in an elevated terminal voltage. As the PV integration ratio continues to rise, the issue of overvoltage becomes more severe. Hence, it is imperative to enforce deterministic voltage constraints. Given that the power flow within the system is influenced by the integration of distributed PV, the system voltage deviation is constrained, and the node voltage deviation can be expressed as follows:

$∆u\%=\frac{U-U_{\exp }}{U_{\exp }}\times 100\%(9)$

where U_i is the voltage of i_th nod; $U_{\exp }$ represents the expected voltage.

4) Power flow constraint of distribution network lines.

$P_{\text{line},i}\le P{}_{\text{capacity}}\left(i=1,.......,{\text{NO}}_{bra}\right)(10)$

where i stands for the branch number of distribution network; ${\text{NO}}_{bra}$ is the number of branches; $P_{l\text{ine},i}$ is the active power flow of i_th branch; $P_{\text{capacity}}$ is active power capacity of line.

5) Transmission line constraints.

$S_{i,\min }\le S_i\le S_{i,\max }(11)$

where i stands for the branch number of distribution network; $S_{l\text{ine},i}$ is the power flow of i_th branch; $S_{\text{capacity}}$ is power capacity of line.

3 IM-TLBO based model solving

3.1 Basic TLBO

The TLBO algorithm is an emerging artificial intelligence optimization technique that draws inspiration from the teaching and learning process. TLBO offers a multitude of advantages, including the elimination of parameter adjustment, a simple algorithm structure, and rapid convergence speed (Rao et al., 2011; Rao and Patel, 2013).

1) Teaching process

In this stage, a teacher is chosen from the group, often identified as the most proficient individual. The teacher x_teacher endeavors to maximize the performance of the entire group by employing their utmost capabilities and expertise.

$\text{di}\_{\mathrm{m}}_{\mathrm{i}}=r_3\left(x_{\text{teacher}}-\text{TF}\cdot \mathrm{M}\right)(12)$

${x_{\text{new},}}_i=x_i+\text{di}\_{\mathrm{m}}_i(13)$

Where r₃ is the random number between [0,1]; TF is learning factor; M is the central location of the class.

2) Learning process

In this stage, the students enhance their scores through effective communication with one another. Each individual, denoted as x_i, updates their location by learning from another individual, x_j. In the context of a minimizing problem, the learning process can be expressed as follows:

$x_{new,i}=\left\{\begin{array}{l}{x}_i+r_4\left(x_i-x_j\right),f\left(x_i\right)<f\left(x_j\right)\\ x_i+r_5\left(x_j-x_i\right),\text{other}\end{array}\right.(14)$

Where r₄ and r₅ are random number between [0,1], f (x_i) and f (x_j) are objective function values of x_i and x_j, respectively.

3.2 IM-TLBO algorithm

In this paper, an improved multi-objective TLBO algorithm, named IM-TLBO, is developed. The primary improvements are listed as follows.

3.2.1 Elite reverse learning based teaching strategy

In the conventional TLBO approach, the valuable information concerning the global convergence of elite individuals within the group is not effectively utilized in the teaching and learning processes. Hence, in this paper, reverse learning strategies based on elite individuals is proposed to address the drawbacks of the traditional TLBO search strategy, which often leads to local optima and reduced solution accuracy. This approach enables us to fully leverage the effective information possessed by elite individuals, thereby enhancing both search efficiency and the algorithm’s local exploration ability.

If there is a real number x between [L,U], its inverse number is defined as: $x^{\prime }=L+U-x$ (15)

For $x=\left(x_1,x_2,\cdot \cdot \cdot ,x_n\right)$, $x_i\in \left[L_i,U_i\right]$, $i=\mathrm{1,2},...,d$, the reverse number of x is $x^{\prime }=\left(x_1^{\prime },x_2^{\prime },\cdot \cdot \cdot ,x_n^{\prime }\right)$

$x_i^{\prime }=k\left(L_i+U_i\right)-x_i(16)$

Where k is the random number between [0,1].

Based on optimization of elite reverse solutions, an improved teaching process is developed. For original individual x_teacher and $x_{\text{teacher}}^{\prime }$:

If $f\left(x_{\text{teacher}}^{\prime }\right)<f\left(x_{\text{teacher}}\right)$, $x_{\text{teacher}}^{\prime }$ replace x_teacher.

For multi-objective optimization problem, multi-objective individual comparison strategy for x_teacher individual selection will be introduced in latter chapter.

3.2.2 Differentiated teaching and learning strategy

In the traditional TLBO algorithm, the central position of the group is typically guided by the optimal individual x_teacher, without considering the variations among individuals. To address this limitation, this paper introduces a differentiated teaching and learning strategy based on the principle of “teaching students according to their aptitude”. In this strategy, parts of individuals continue to be guided by x_teacher, playing the role of outstanding individuals. Meanwhile, the other individuals tempt to approach the average score (central position). This strategy helps expedite the overall improvement of these specific individuals and prevents their scores from falling significantly below the group average. The individuals of the population are sorted according to fitness in ascending order in the minimization problem. The differentiate teaching and learning strategy can be expressed as follows.

$\left\{\begin{array}{l}\text{di}\_{\mathrm{m}}_i=r_{3-1}\left(x_{\text{teacher}}-T\cdot M\right),\left(i=\mathrm{1,2},\cdot \cdot \cdot \cdot \cdot \cdot \cdot ,N_1\right)\\ \text{di}\_{\mathrm{m}}_i=r_{3-2}\left(T\cdot M-x_i\right),\left(i=N_1+1,N_1+2,\cdot \cdot \cdot \cdot \cdot \cdot \cdot ,N\right)\end{array}\right.(17)$

${x_{\text{new},}}_i=x_i+\text{di}\_{\mathrm{m}}_i(18)$

where r_3-1, r_3-2 are the random numbers between [0,1]; TF is learning factor; M is the central location of the class; N is the size of the population.

3.2.3 Elite archive set reduction strategy

In the multi-objective optimization process, the elite archive plays a crucial role in preserving non-dominated solutions. The selection of x_teacher individuals is of significant importance. The ultimate objective is to achieve a final Pareto solution set that closely approximates the true Pareto solution set while promoting an equitable distribution of solutions. To address this objective, the CCSD (cyclic crowded sort deletion) strategy is presented in multi-objective TLBO when the number of elite individuals exceeds the maximum threshold. This strategy aims to enhance the algorithm’s performance by effectively managing the crowdedness of solutions in the elite archive. By incorporating the CCSD strategy, the algorithm strives to improve the quality and diversity of the final Pareto solution set, leading to more accurate and well-distributed solutions (Chenga et al., 2017).

The Euclidean crowding distance of x_i and x_j is defined:

$\text{Cr}\left(x_i,x_j\right)=\sqrt{{\displaystyle \sum _{k=1}^{\text{obj}}}{\left(f_k\left(x_i\right)-f_k\left(x_j\right)\right)}^2}(19)$

Where obj is the number of objective functions; f is the fitness function of the individual.

The steps of elite archive set reduction strategy are outlined as follows:

Step 1. The distances between each individual in the archive are computed by measuring the average Euclidean distance to its two nearest neighbors. This calculation yields the crowding distance for each individual, providing a measure of their proximity within the file set. Subsequently, the individuals are sorted based on their crowding distances.

Step 2. The archive is then pruned by removing the most crowded individuals, which are identified as having the least crowding distance. Afterward, the crowding distances of the remaining individuals in the archive are recalculated to reflect the new configuration.

Step 3. Step 2 is iteratively repeated until the expected number of individuals in the archive is attained, ensuring the optimization process aligns with the predefined objectives.

3.2.4 Comparing strategy of multi-objective individuals

In the original TLBO algorithm, the elite x_teacher serves as a guiding force for the population’s center. During the learning process, random individuals are selected to learn from each other. The comparing strategy becomes essential in determining the fitness values during the stages of elite individual reverse learning and learning. In this paper, a comparing strategy is developed to select both the elite individual and the learned individual. Suppose the two individuals x_i and x_j, and their minimizing objective functions are $f_i\left(x_1\right)$ and $f_i\left(x_2\right)$, respectively.

1) If all $f_i\left(x_1\right)\le f_i\left(x_2\right)\left(i=\mathrm{1,2},...,n\right)$, i.e., $x_1\prec x_2$, then the individual $x_1$ is selected as the better individual.

2) If all $f_i\left(x_2\right)\le f_i\left(x_1\right)\left(i=\mathrm{1,2},...,n\right)$, i.e., $x_2\prec x_1$, then the individual $x_2$ is selected as the better individual.

3) Other situations, x₁ and x₂ are non-dominated with each other, x₁ or x₂ is randomly selected as the better individual.

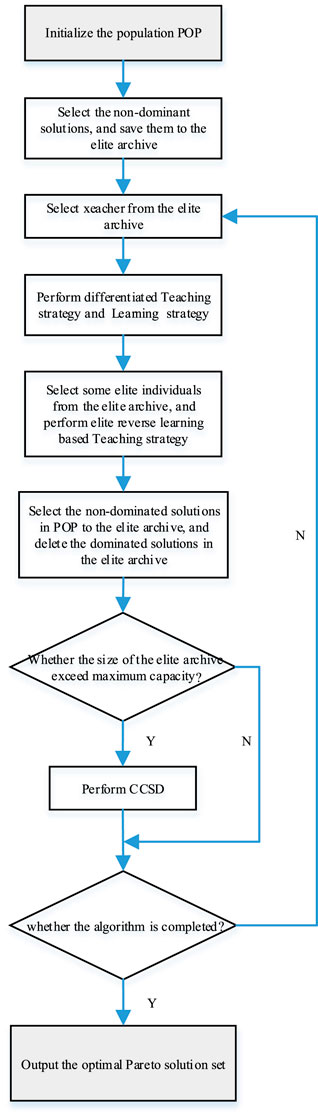
Based on above elite reverse learning, differentiated teaching and learning strategy, CCSD and comparing strategy, the improved multi-objective TLBO, i.e., IM-TLBO algorithm is proposed in Figure 1.

FIGURE 1

FIGURE 1. The outline of IM-TLBO algorithm.

3.3 IM-TLBO based model solving

The approach for solving the county roof PV access model using the IM-TLBO algorithm is presented in detail below.

Step 1. Model Initialization

To begin, the model is initialized by obtaining the parameters of the distribution network and investigating the available area for distributed PV installation on different types of rooftops. Furthermore, the parameters of the IM-TLBO algorithm are assigned.

Step 2. Algorithm Initialization

In this step, the algorithm is initialized by setting the PV installing capacity as control variables x and initializing the location of the population. Additionally, the values of the fitness functions f₁ and f₂ based on equations 1 and (2) are calculated.

Step 3. Population Iteration

During this phase, the population undergoes iteration by updating their locations based on the proposed IM-TLBO algorithm. Non-dominated individuals are saved in an elite archive. The x_teacher is selected to execute the elite reverse learning process. If individual constraints are not satisfied, penalty functions are added to the fitness functions. Random and dynamic selection methods are employed to select x_teacher individuals from the elite archive. When the number of individuals in the archive exceeds its maximum capacity, the cyclic crowded sort deletion CCSD strategy is utilized to remove individuals.

Step 4. Termination Condition Evaluation

At this stage, the optimization solution is evaluated to determine if it meets the termination condition specified during the model initialization. If the termination condition is satisfied, the non-dominated solution is outputted as the final optimized result. Otherwise, the process returns to Step 3 for further iteration.

By following this systematic procedure, the county roof PV access model can be effectively solved using the improved IM-TLBO algorithm.

4 Benchmark functions test

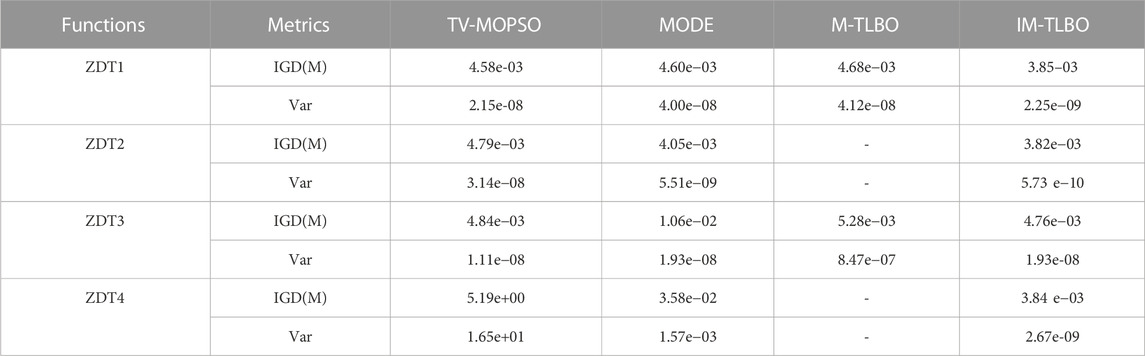
To evaluate the effectiveness of the IM-TLBO algorithm in addressing multi-objective optimization problems, a series of tests are conducted using ZDT1-ZDT4 benchmark functions (Deb et al., 2002; Cheng et al., 2017a; Tripathi et al., 2017) in Table 1. The simulation tests are performed in matlab 2017 software under core i7 windows 10. The optimization results are presented in Figure 2. Furthermore, the performance of the IM-TLBO algorithm is compared with the widely used TV-MOPSO, MODE, and M-TLBO algorithms, and the comparative results are summarized in Table 2.

TABLE 1

TABLE 1. Benchmark functions.

FIGURE 2

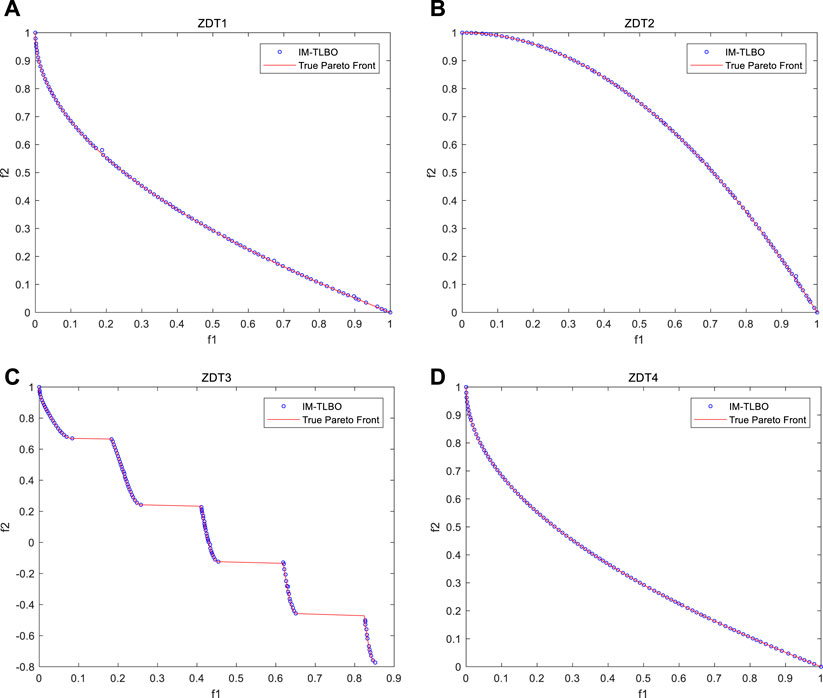
FIGURE 2. Pareto fronts of ZDT1-ZDT4 by IM-TLBO. (A): Pareto front of ZDT1. (B): Pareto front of ZDT2. (C): Pareto front of ZDT3. (D): Pareto front of ZDT4.

TABLE 2

TABLE 2. Comparison results in ZDT1-ZDT4 of different algorithms.

It is demonstrated in Figure 2 that the IM-TLBO algorithm is highly effective in optimizing the ZDT1-ZDT4 benchmark functions. The generated Pareto front accurately converges to the true Pareto Frontier, indicating good convergence. Moreover, the Pareto Frontier solutions obtained by the IM-TLBO algorithm are uniformly distributed, signifying its superior diversity and solution distribution. A comprehensive comparison of IM-TLBO with other classical algorithms is presented in Table 2, where the performance characteristics of convergence and diversity are analyzed using the IGD index. The results indicate that the IM-TLBO algorithm outperforms other classical algorithms in terms of convergence and diversity. Hence, proposed IM-TLBO algorithm has good performance in both convergence and diversity.

5 Case study

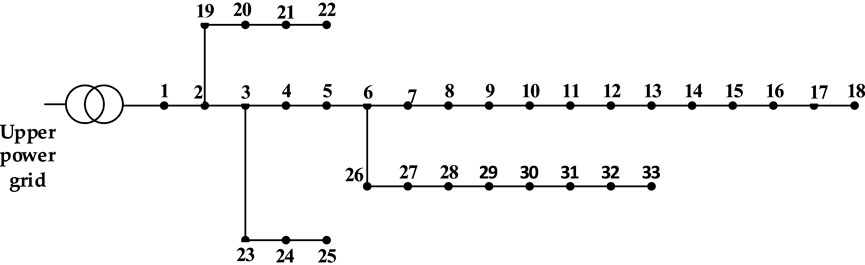
5.1 Case introduction

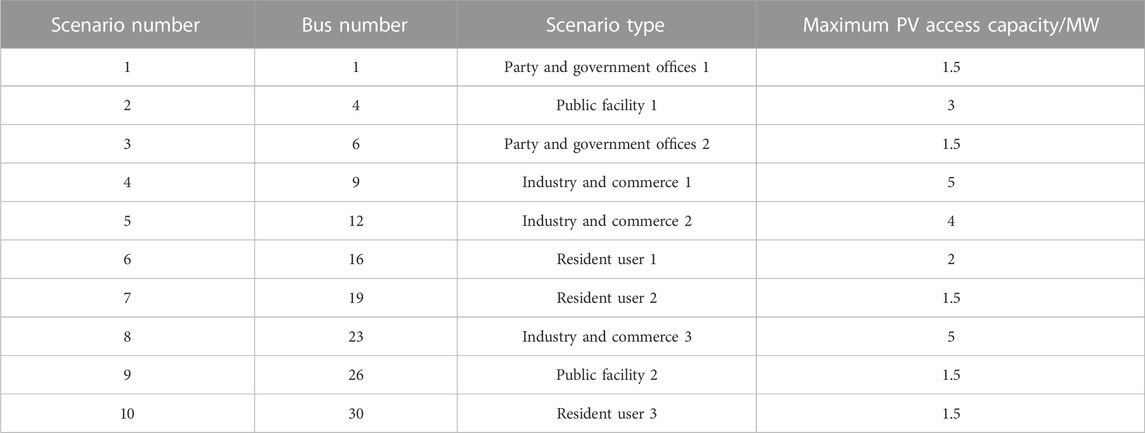
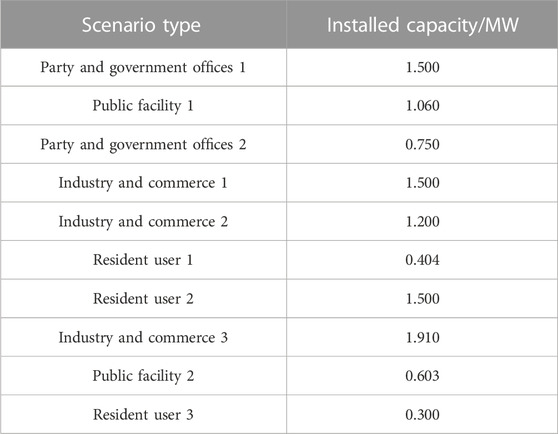
In order to demonstrate the effectiveness of proposed PV integration method of the whole county, IEEE 33 BUS system in Figure 3 is adopted to simulate distribution network. In test system, the total PV installed capacity f₁ in Eq. 1 and voltage deviation f₂ in Eq. 2 are multi-objective fitness functions of optimization algorithms. The basic reference voltage grade of the system is 12.66 kV. Bus 1 is the balance bus which is connected with upper power grid. The roof PV integration scenarios setting are shown Table 3.

FIGURE 3

FIGURE 3. IEEE33bus system.

TABLE 3

TABLE 3. Roof PV integration scenarios setting.

5.2 PV integration solutions analysis

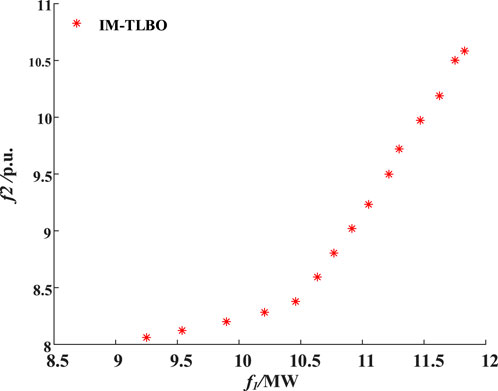
The obtained non-dominated Pareto solutions for PV access using the proposed IM-TLBO algorithm are presented in Figure 4. It is evident from the results that the method proposed in this paper effectively addresses the PV integration problem for the entire county by simultaneously maximizing the installed capacity and minimizing voltage deviation. The IM-TLBO algorithm successfully yields a well-distributed Pareto front, showcasing its ability to handle conflicting objective functions. The distributed PV integration method introduced in this study takes into account both the access capacity and its impact on the system voltage index. These results offer decision-makers a range of PV integration schemes to choose from, catering to different economic and technical preferences.

FIGURE 4

FIGURE 4. Pareto solutions of large-scale PV access based on IM-TLBO.

To further validate the superiority of the proposed PV integration method, four different cases are compared. Four cases are no PV system installed case (Case 1), full PV integration case (Case 2), minimum ratio for the entire county case (Case 3), and PV optimal access case (Case 4). The comparative results are presented in Table 4. It is revealed in Table 4 that Case 1, representing the original IEEE-33 node system, renders certain nodes below the lower voltage limit. Consequently, this case fails to meet the necessary conditions for secure, stable operation, making it infeasible. Similarly, Case 2, characterized by full PV access, demonstrates an excessive access ratio leading to an overvoltage phenomenon. Consequently, this case is also deemed impractical. Case 3 satisfies the minimum installation ratio requirement of the whole county, ensuring that the system’s power flow adheres to the conditions necessary for secure and stable operation. However, Case 4, which employs the proposed PV optimal integration method not only fulfills the system’s requirements for safe and stable operation but also outperforms Case 3 in terms of optimal total PV capacity and voltage deviation indexes. In conclusion, these results affirm the effectiveness of the proposed PV optimal integration method by guaranteeing the system’s safety and stability while simultaneously improving the overall PV capacity and decrease voltage deviation.

TABLE 4

TABLE 4. Comparison of PV integration results of different case.

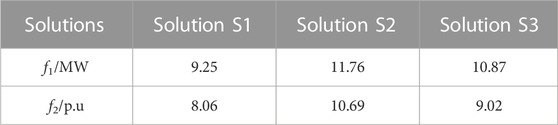
5.3 PV integration schemes analysis

The selected optimal solutions from Figure 4, namely, the representative optimal voltage deviation scheme (S1), optimal PV capacity scheme (S2), and compromise scheme (S3), are presented in Table 5, showcasing their respective maximum integration capacity and minimum voltage deviation. These results serve as valuable references for decision-makers involved in distribution network planning, offering multiple perspectives for economic and technical decision supports.

TABLE 5

TABLE 5. Result of Rooftop PV integration.

Table 6 demonstrates the distributed photovoltaic capacity installation scheme for the compromise solution S3. A detailed analysis of the planning results in Table 6 reveals that the installation solution effectively satisfies the installation ratio requirements across various scenarios for large-scale photovoltaic access within the county. It is worth noting that due to the imposed voltage limit, the installation capacity ratio decreases as the node moves further away from the balance bus.

TABLE 6

TABLE 6. Compromise solution S3 of roof PV access.

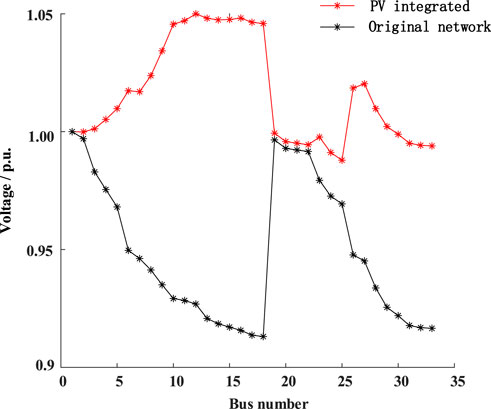
Figure 5 illustrates the bus voltages of the compromise solution S3 in the distribution network. Prior to the installation of rooftop distributed PV systems, the voltages of all buses in the original IEEE33 bus distribution network are generally below 1 p.u. Notably, the voltage quality of nodes located near the end of the line falls below the normal range, measuring below 0.95 p.u. However, when the rooftop distributed PV systems integrated, the bus voltage profile of the distribution network undergoes a significant improvement. The roof distributed PV integration method proposed in this paper effectively enhances the voltage quality to bring the voltage value near the end of the line back into the normal range. These results demonstrate that the proposed method not only maximizes the actual intergation capacity, but also enhances the node voltage profile.

FIGURE 5

FIGURE 5. Impact of roof PV on bus voltage in compromise solution S3.

5.4 Algorithms comparison analysis

In order to evaluate the performance of the strategies utilized in the proposed IM-TLBO algorithm, a comparison was made with the multi-objective TLBO algorithm without elite reverse search strategy and differentiated teaching learning strategy (M-TLBO) and the classic TV-MOPSO and MODE algorithm, as presented in Figure 6. It is evident that all algorithms were able to effectively address the multi-objective programming problem of PV large-scale integration presented in this study. The optimal Pareto solutions obtained in Figure 6 validate the effectiveness of each algorithm.

FIGURE 6

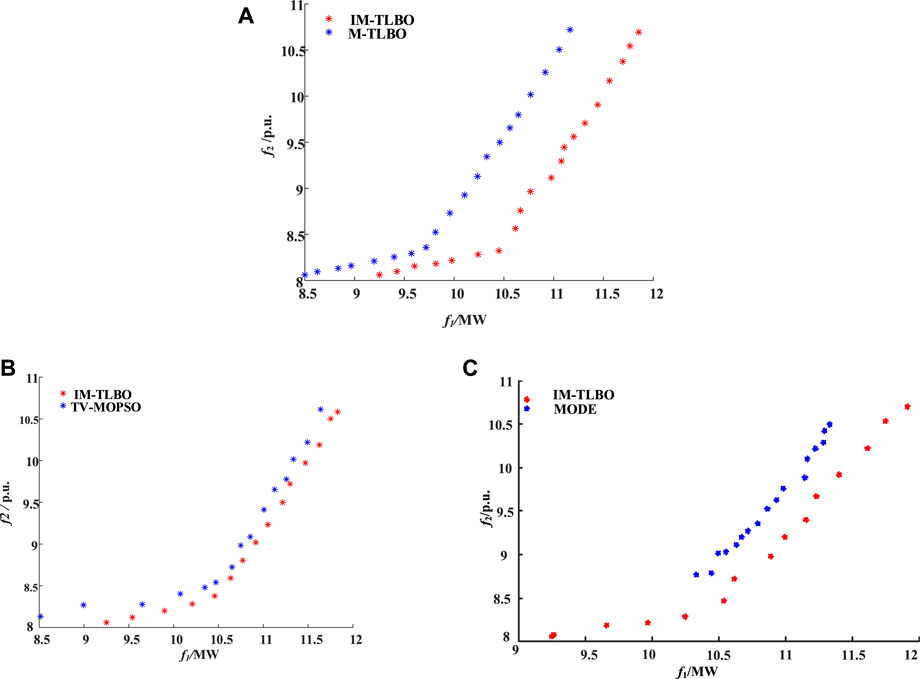
FIGURE 6. Comparing results of PV access schemes between different algorithms. (A): Comparison results of IM-TLBO and M-TLBO. (B): Comparison results of IM-TLBO and TV-MOPSO. (C): Comparison results of IM-TLBO and MODE.

A closer comparing of the optimization results obtained from the comparison reveals that the Pareto Frontier obtained by the IM-TLBO algorithm, as depicted in Figure 6A, is situated on the lower right when compared to the M-TLBO Frontier as a whole. This indicates that the convergence of the IM-TLBO algorithm is superior to that of the M-TLBO algorithm. The improved strategy employed in the IM-TLBO algorithm thus enhances its search ability.

Furthermore, it can be inferred from the results illustrated in Figure 6B that the convergence of the IM-TLBO algorithm surpasses that of the TV-MOPSO algorithm. Additionally, the Pareto Frontier solutions achieved by the IM-TLBO algorithm in Figure 6B are more uniformly distributed, indicating that IM-TLBO displays better diversity than TV-MOPSO. Therefore, it can be concluded that the CCSD proposed in this study effectively improves the diversity of individuals as well as the uniformity of their distribution. Comparing the results depicted in Figure 6C, it is shown that the convergence of the Pareto Frontier solutions achieved by the MODE algorithm is notably inferior to that of the IM-TLBO algorithm. Additionally, the distribution characteristics of the MODE Pareto Frontier are also poorer.

In summary, the comparison analyses conducted in this research demonstrate the superior performance of the strategies utilized in the proposed IM-TLBO algorithm when compared to the M-TLBO algorithm, the classic TV-MOPSO and MODE algorithms.

6 Conclusion

This paper focuses on the method for large-scale distributed PV integration in an entire county. To begin with, a roof PV integration model is developed to maximize roof PV access capacity and minimize voltage deviation within the distribution network system, taking into account the requirements of large-scale integration scenarios across the county. The model ensures the maximization of photovoltaic access capacity in different scenarios while maintaining the safe and stable operation of the distribution network. Furthermore, it considers the impact of photovoltaic access on power flow within the distribution network.

In order to solve the PV large-scale planning integration model efficiently, an improved IM-TLBO is proposed. This algorithm enhances the optimization process and the quality of solutions. Simulation experiments are conducted using the IEEE33 bus system to validate the performance of the enhanced multi-objective TLBO algorithm in PV access planning. The analysis reveals that the proposed method successfully addresses the maximum photovoltaic access capacity challenge and significantly improves the voltage quality at each node of the system after installing the rooftop distributed photovoltaic systems.

Moving forward, future research on roof distributed PV systems will explore the integration of energy storage systems to achieve peak shaving and load shifting functions during the scheduling process.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

SL: Writing–review & editing, Funding acquisition and Methodology. FY: Conceptualization, Funding acquisition. JL: Methodology and Investigation. ZC: Validation and Data curation. TZ: Writing–review & editing. TC: Writing–original draft, Writing–review and editing. YG: Formal Analysis.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was founded by the State Grid Anhui Electric Power Co., Ltd. Economic Research Institute Project (B6120921000R), the Fundamental Research Funds for the Central Universities (No. JZ2022HGTA0320).

Conflict of interest

Authors SL, FY, and JL were employed by State Grid Anhui Electric Power Co., Ltd. Economic Research Institute. Authors ZC and TZ were employed by State Grid Anhui Electric Power Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Can, Y., and Yong, W. (2018). Optimal method for distributed hybrid solar-wind-battery system based on Grey Wolf optimization. Microcomput. Appl. 34 (12), 11–14.

Google Scholar

Cheng, T., Chen, M., Wang, Y., Li, B., Hassan, M. A. S., Chen, T., et al. (2018). Adaptive robust method for dynamic economic emission dispatch incorporating renewable energy and energy storage. Complexity 2018, 1–13. doi:10.1155/2018/2517987

CrossRef Full Text | Google Scholar

Chenga, T., Chena, M., Flemingb, P. J., Yang, Z., and Gan, S. (2017). A novel hybrid teaching learning based multi-objective particle swarm optimization. Neurocomputing 222, 11–25. doi:10.1016/j.neucom.2016.10.001

CrossRef Full Text | Google Scholar

Cheng, T., Chen, M., Fleming, P. J., Yang, Z., and Gan, S. (2017a). A novel hybrid teaching learning based multi-objective particle swarm optimization. Neurocomputing 222, 11–25. doi:10.1016/j.neucom.2016.10.001

CrossRef Full Text | Google Scholar

Cheng, T., Chen, M., and Luo, H. (2017b). Multi-objective allocation of energy storage in distribution network penetrated with renewable energy generation. Power Syst. Technol. 41 (9), 2808–2815. doi:10.13335/j.1000-3673.pst.2017.0095

CrossRef Full Text | Google Scholar

Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002). A fast and elitist multiobjective genetic algorithm:nsga-ii. IEEE Trans. Evol. Comput. 6 (2), 182–197. doi:10.1109/4235.996017

CrossRef Full Text | Google Scholar

Du, Y., and Lu, D. C. (2011). Battery-integrated boost converter utilizing distributed MPPT configuration for photovoltaic systems. Sol. Energy 85 (9), 1992–2002. doi:10.1016/j.solener.2011.05.008

CrossRef Full Text | Google Scholar

Kornelakis, A., and Marinakis, Y. (2010). Contribution for optimal sizing of grid-connected PV-systems using PSO. Renew. Energy 35 (6), 1333–1341. doi:10.1016/j.renene.2009.10.014

CrossRef Full Text | Google Scholar

Liu, R., Wu, K., Feng, L., Liang, R., Wang, X., and Yang, S. (2022). Voltage partition coordinated optimization control of active distribution network of high penetration distributed pvs. acta energiae solaris sin. 43 (2), 189–197.

Google Scholar

Mahmoud, M. E., and Ahmed, F. (2016). Optimization of a PV fed water pumping system without storage based on teaching-learning-based optimization algorithm and artificial neural network. Sol. Energy 139, 199–212. doi:10.1016/j.solener.2016.09.022

CrossRef Full Text | Google Scholar

Merei, G., Berger, C., and Sauer, D. U. (2013). Optimization of an off-grid hybrid PV-Wind-Diesel system with different battery technologies using genetic algorithm. Sol. Energy 97, 460–473. doi:10.1016/j.solener.2013.08.016

CrossRef Full Text | Google Scholar

Paatero, J. V., and Lund, P. D. (2007). Effects of large-scale photovoltaic power integration on electricity distribution networks. Renew. Energy 32 (2), 216–234. doi:10.1016/j.renene.2006.01.005

CrossRef Full Text | Google Scholar

Painuly, J. P. (2001). Barriers to renewable energy penetration; a framework for analysis. Renew. Energy 24 (1), 73–89. doi:10.1016/s0960-1481(00)00186-5

CrossRef Full Text | Google Scholar

Rao, R. V., Savsani, V. J., and Vakharia, D. P. (2011). Teaching–learning-based optimization: a novel method for constrained mechanical design optimization problems. Comput. Aided Des. 43 (3), 303–315. doi:10.1016/j.cad.2010.12.015

CrossRef Full Text | Google Scholar

Rao, R. V., and Patel, V. (2013). An improved teaching-learning-based optimization algorithm for solving unconstrained optimization problems. Sci. Iran. 20 (3), 710–720. doi:10.1016/j.scient.2012.12.005

CrossRef Full Text | Google Scholar

Shah, R., MithulananthanBansa, N. R. C., and Ramachandaramurthy, V. K. (2015). A review of key power system stability challenges for large-scale PV integration. Renew. Sustain. Energy Rev. 41 (41), 1423–1436. doi:10.1016/j.rser.2014.09.027

CrossRef Full Text | Google Scholar

Song, H., Diolata, R., and Joo, Y. H. (2009). Photovoltaic system allocation using discrete particle swarm optimization with multi-level quantization. J. Electr. Eng. Technol. 4 (2), 185–193. doi:10.5370/jeet.2009.4.2.185

CrossRef Full Text | Google Scholar

Tahvonen, O., and Salo, S. (2001). Economic growth and transitions between renewable and nonrenewable energy resources. Eur. Econ. Rev. 45, 1379–1398. doi:10.1016/s0014-2921(00)00062-3

CrossRef Full Text | Google Scholar

Tan, X. C., Wang, W. J., Lu, G. B., Li, Z. X., and Huang, N. T. (2019). Multi-objective distributed photovoltaic generation allocation using artificial fish swarm algorithm. Power Syst. Clean Energy 35 (1), 84–90.

Google Scholar

Tripathi, P. K., Bandyopadhyay, S., and Pal, K. (2017). Multi-objective particle swarm optimization with time variant inertia and acceleration coefficients. Inf. Sci. 177 (22), 5033–5049. doi:10.1016/j.ins.2007.06.018

CrossRef Full Text | Google Scholar

Varaprasad, J., and Radha, R. K. (2022). Optimal allocation of solar photovoltaic distributed generation in electrical distribution networks using Archimedes optimization algorithm. Clean. Energy 2, 271–287.

Google Scholar

Wang, Y., Guo, C. H., Chen, X. J., Jia, L. Q., Guo, X. N., Chen, R. S., et al. (2021). Carbon peak and carbon neutrality in China: goals, implementation path and prospects. China Geol. 4 (4), 720–746.

CrossRef Full Text | Google Scholar

Xiaorong, Z. H. U., Guowei, L. U., and Wanying, X. I. E. (2021). Robust planning of energy storage in distribution network considering source-network-load flexible resources. Electr. Power Autom. Equip. 41 (8), 8–16. doi:10.16081/j.epae.202104004

CrossRef Full Text | Google Scholar

Yan, H., Pan, D., and Yao, H. (2014). Method of photovoltaic arry maximum power point tracking based on golden section search. J. Hefei Univ. teahnology 37 (4), 416–419.

Google Scholar

Yong, L., Tianyu, Y., Xuebo, Q., Juanxia, X., and Yijia, C. (2022). Optimal configuration of distributed photovoltaic and energy storage system based on joint sequential scenario and source-network-load coordination. Trans. CHINA Electrotech. Soc. 37 (13), 3289–3303.

Google Scholar

Zhang, Y., Zhang, S., Liu, S., and Yi, Y. (2020). Dual planning of a distribution transformer considering the impact of distributedphotovoltaics and energy storage access. Power Syst. Prot. Control 48 (24), 9–15. doi:10.19783/j.cnki.pspc.200128

CrossRef Full Text | Google Scholar

Zhang, S., Ge, S., Liu, H., Li, J., and Wang, C. (2023). Model and observation of the feasible region for PV integration capacity considering Wasserstein-distance-based distributionally robust chance constraints. Appl. Energy 347, 121312. doi:10.1016/j.apenergy.2023.121312

CrossRef Full Text | Google Scholar

Zhao, S., Wang, M., Hu, Y., et al. (2015). Research on the prediction of PV output based on uncertainty theory. Trans. China Electrotech. Soc. 30 (16), 213–220.

Google Scholar