A novel solution for the optimal reactive power dispatch problem using an artificial neural network integrated with the firefly optimization algorithm

This article applies a novel intelligence technique to solve power system issues faced daily. Compensation for reactive power is a significant issue faced by power system operators in research. The solution can be obtained by handling a multi-objective task and multiconstraints by reducing the active power loss and minimizing the voltage deviation at the load end. The novelty of the research focuses on integrating artificial neural network techniques with the firefly algorithm, a novel optimization algorithm for attaining an objective function. The Levenberg–Marquardt back-propagation algorithm is most suited for proper tuning of the control variables. The objective of this research can be attained by appropriately tuning the control variables connected with the IEEE test bus systems, which helps to maximally improve the voltage profile. Existing research studies have focused on reactive power management, which is attained by solving optimal reactive power flow problems employing nature-inspired approach techniques such as the symbiotic organism search algorithm, the cuckoo search algorithm, the black hole algorithm, the krill herd algorithm, and whale optimization. The evolving strategy, the firefly algorithm (FFA), minimizes the multiconstraint functions more competently and effectively than any conventional algorithm. To showcase the strength of the firefly algorithm incorporating AI, it is examined on standard IEEE test bus systems, namely, the 14-, 30-, and 58-bus networks. The obtained results quantify the effectiveness of the proposed methodology, that is, the artificial intelligence technique implementing the firefly algorithm gives better results than conventional methods.

1 Introduction

In the past decade, the environment has been subjected to repercussions from power plants that use traditional fossil fuels to generate power. The non-renewable energy resources are having a devastating impact on the ecosystem and are soon going to run out. Conventional grid plants cannot meet ever-increasing energy requirements. At the same time, the complexities of electric power distribution are expanding daily, and outdated planning methodologies need to be improved due to increased demand. Therefore, distributed generation (DG), in which electric power is generated close to load centers, has emerged as a feasible alternative in this area. Reactive power management or compensation has been highly explored. It has emerged in the drive to enhance safety, and various power system issues, including voltage profile concerns, abundant power loss across extremely loaded lines, voltage instabilities, and issues related to reliability and power quality, must be addressed to create a complete furnished infrastructure in the intelligent grid network.

The power requirement has substantially increased, which increases the load needed by consumers and results in inadequate distribution of power. The electrical hazards could result in a grid collapse. Active power loss has become an emerging challenge for power system operators to estimate and schedule accurate power demand. Inadequate volts-amps-reactive (VAR) accessibility in the power network or non-optimized VAR flow in the power grid results in extremely overcrowded conditions. Truncating voltages across the power lines minimizes power losses, thereby enhancing grid stability. The power losses across the grid network can be reduced with the help of optimal VAR injectors, resulting in improved system performance.

The reduction in the amount of actual power loss results in the improved stability of the system, which further helps to improve the enhancement of the voltage profile in the electric grid. An enormous quantity of VAR requirements in the network clearly shows the considerable drop of active power. The dynamic power loss minimization confirms the power system network’s steady reactive power flow. An optimization tool based upon the bio-geographical feature (BBO) is applied to solve multiple objective in a multiconstraint problem (Roy et al., 2012). Power flow has been optimized through a gravitational search algorithm (Duman et al., 2012). Optimization of VAR by minimizing the active power drop (PD) has extended an attempt to enhance the voltage profile (Rabiee et al., 2012). The Power Grid Corporation of India has utilized various flexible AC transmission system (FACTS) devices to maintain a steady power flow by controlling the voltage. Various attempts have been made to determine appropriate solutions for assuring the grid network safety by ensuring voltage stability.

A healthy electrical grid network has several desirable characteristics, including minimized active PD and improved voltage profile across the grid. In recent years, the genetic algorithm has been essential for addressing a variety of complexities, such as differential evolution (DE) (Varadarajan and Swarup, 2008), that are amenable to resolution. The solution for optimal power flow has employed an artificial bee colony (ABC) algorithm (KursatAyan and Kılıç, 2012), implementation of D-particle swarm optimization (D-PSO) for maintaining VAR to an optimum level (Badar et al., 2012), and stabilization of voltage across the grid with multiconstraint functions for the optimal reactive power dispatch (ORPD) problem (Amit and Ashish, 2012). The global harmony search algorithm has been implemented for the optimal power flow problem (Sirjani et al., 2012). Optimal control of VAR via minimizing the active PD and voltage profile has been done for optimal VAR planning through an annealing technique. The PSO is implemented with power system constraints to deal with the security constraints and obtain the linear power flow. An identical set of objective functions is used to solve multiconstraint and multi-objective hybrid PSO algorithms (Esmin et al., 2005). A genetic algorithm has been implemented to attain the objective by optimizing the objective function. The hybrid evolutionary programming approach uses functional optimization to achieve the optimal reactive power flow (Mallipeddi et al., 2012).

The implementation of novel computational techniques has paved the way for solving the power system problem, as discussed in Nguyen and Truong (2015) and VC (2018). The power system constraints are handled by applying swarm and evolutionary computation techniques (VC and T., 2018). The network in a novel distribution system can be reconfigured to obtain maximum power flow in power lines using the symbiotic organism search algorithm (Olabode et al., 2023). The gravitational search algorithm has been implemented to solve power system complexities and obtain the objective function (Duman et al., 2010). The big bang–big crunch algorithm has been used to determine an optimal reactive power dispatch solution that is essential for power system operations (Erol and Eksin, 2006; Verma, 2012). A bacterial foraging algorithm was implemented to optimize the active power loss in the power distribution network (Kumar and Jayabarathi, 2012). The dynamic power loss has been minimized in DG using a firework algorithm (Imran and Kowsalya, 2014) and a cuckoo search algorithm (Nguyen and Truong, 2015). The ant lion optimization algorithm was employed for handling power system problems that can be solved by optimal sizing of generators and implementing renewable energy resources (VC, 2018). Various power system problems can be solved in real time by implementing the firefly optimization technique (VC and T., 2018; Olabode et al., 2023). The proposed firefly algorithm is effective in minimizing the objective functions while considering the power system constraints and obtains the optimal reactive power dispatch solution (Balachennaiah et al., 2018; Jun et al., 2021). The gray wolf algorithm that has been implemented to solve the power loss problem in a radial distribution system is also attractive, as given in astronomical models (RoutrayMistry and Raj Arya, 2020). The VAR supply is done by relocating the generators to regulate the voltage across the photovoltaic (PV) bus and switchable static SVCs to supply the reactive power and transformer taps in the grid network (Biswas et al., 2018; Singh and Agrawal, 2018).

Voltage stability in the grid network denotes the capability to conserve or optimize VAR, which makes the system load demand manageable across the power markets by connecting the FACTS devices to maintain the voltage profile while considering the real power losses (Iqbal et al., 2018; Dash et al., 2019). The voltage profile of the system is both focused on the active power loss minimization and reflects on power system stability, which can be done by implementing the shuffled frog leap algorithm (Onlam et al., 2019).

The latest advancements in the power system are the implementation of artificial intelligence techniques with optimization techniques to attain voltage control. This topology has been implemented with PSO to solve the optimal reactive power dispatch problem (Kanata et al., 2018). The constraints involved in implementing the bio-inspired optimization technique with the artificial neural network technique are presented by discussing the system conditions of the grid (Kumar et al., 2021a). The renewable energy-based hybrid grid system is being designed with the integration of artificial intelligence techniques to attain the objective function (Kumar et al., 2021b).

Lotfi H has presented distributed generation units (DGUs) that can serve as supplementary power supplies and effectively contribute to satisfying the load requirements of the distribution network. DGUs offer the potential to reduce power loss and enhance voltage levels, resulting in good outcomes. Furthermore, capacitors used for reactive power compensation yield beneficial outcomes that are comparable to DGUs in distribution networks. This study proposes the concept of combining DGUs and shunt capacitors with a demand response program (DRP) in order to maximize the advantages of its deployment. The time of use (TOU) technique is employed as a DRP to modify the consumption pattern of subscribers and enhance the efficiency of the distribution system. Objective functions encompass the minimizing of energy loss, functional expense, and energy not supplied (ENS). Typically, the issue of selecting the most efficient capacity of DGUs and storage capacities is intricate because of the fluctuation in demand. In addition, taking into account the impact of unclear sources adds complexity to the optimization problem. Therefore, a proposed solution to address the intricacies of this problem is the modified shuffled frog leaping algorithm (MSFLA).

Lotfi H and Ghazi R have suggested that feeder reconfiguration is a crucial operations procedure in electricity distribution grids to improve system efficiency by effectively controlling the switching. The operating challenges of the distributed system in smart distribution networks are primarily influenced by the fluctuations in energy cost and load trends. These challenges are highly time-dependent and involve intricate complexities. In order to address these temporal dependencies, it is crucial to expand the scope of the challenge to encompass various time intervals. The approach takes into account distributed generators, energy storage systems, and solar photovoltaic units and considers different time intervals. DRP encourages energy consumers to reconsider their energy consumption patterns through incentive and punishment policies. The feeder reconfiguration problem often focuses on minimizing power loss and voltage variation, which are crucial targets for conventional distributed systems. However, less emphasis has been placed on ensuring voltage security in distribution networks. The objective is to achieve operational and voltage security objectives by considering factors such as operating cost, energy loss, and the voltage stability index. The dynamic feeder reconfiguration problem is a challenging integer nonlinear program that requires the use of suitable optimization methods to achieve convergence towards the global optima or approximate global optima. Moreover, a fuzzy decision-maker is utilized to choose the optimal compromise option from the set of non-dominated solutions.

Lotfi et al. (2020) has demonstrated that as renewable energy sources and energy storage (ES) units become more prevalent in the power supply structure, it is critical to investigate their impact on the functioning of the strategy and reliability. The voltage stability index is specified as a function of interest in the present research, and improving it through energy management in the distribution network is a critical challenge. Given the existence of distributed generators, solar PV panels, Energy Storage (ES) units, and capacitors, the dynamic distribution feeder reconfiguration (DDFR) is introduced as an efficient approach for energy management in the distribution network, taking energy loss, reliability of voltage index, and operational expenditure as its primary functions. The requirement response program, which includes interruptible/curtailable service, is designed to allow energy consumers to reconsider their energy usage habits in light of inducement and punishment measures. A modified PSO approach is used to tackle the optimization problem under consideration. The proposed method is tested on a 95-node test system, and its superiority is demonstrated through comparison with other evolutionary algorithms.

The novelty involved in this study has been elucidated by incorporating the artificial neural network technique with optimization algorithms to improve the voltage profile by minimizing real power losses and bus voltage deviations at the load level. This proposed methodology of integrating the firefly optimization technique with the artificial neural network technique is feasible for attaining an optimal reactive power dispatch solution.

The article is structured as follows: Section 2 formulates the problem, which relates to the multi-objective functions. Section 3 discusses the firefly algorithm. Section 4 explains the role of artificial intelligence, that is, an artificial neural network. Implementation of the firefly algorithm with ANN is shown in Section 5. Results and discussion are presented in Section 6. Section 7 presents the conclusion.

2 Problem formulation

A multiconstraint function is adopted to manage the VAR requirement by reducing the real PD and computing voltage deviation (V_D) across the PQ buses. The constraints involved while solving optimal reactive power dispatch are explained in the following subsections.

2.1 Objective function

The equation adopted for solving a multi-objective problem with multiconstraints is given as follows:

$\mathrm{f}=\min \left\{{\text{wP}}_{\mathrm{D}}+\left(1-\mathrm{w}\right)\text{VD}\right\}.(1)$

In the aforementioned equation, f is the stated objective function of the research, and w is the weighing factor for attaining the objective. P_D represents the actual power loss or active power drop/loss; V_D is voltage deviation.

2.1.1 Active/real power drop minimization (P_D)

The active PD in the system can be computed using the following expression:

${\mathrm{P}}_{\text{drop}}={\displaystyle {\sum }_{\mathrm{K}=1}^{{\mathrm{N}}_{\mathrm{L}}}}{\mathrm{G}}_{\mathrm{k}}\left[{{\mathrm{V}}_{\mathrm{i}}^2+\mathrm{V}}_{\mathrm{j}}^2-2\left|{\mathrm{V}}_{\mathrm{i}}\right|\left|{\mathrm{V}}_{\mathrm{j}}\right|\cos {\mathrm{\delta }}_{\mathrm{i}}-{\mathrm{\delta }}_{\mathrm{j}}\right],(2)$

where G_k is the conductance, N_L represents the number of transmission lines, and Vi and Vj represent the sending end and receiving voltages with angles as ${\mathrm{\delta }}_{\mathrm{i}}\text{\hspace{0.17em}and\hspace{0.17em}}{\mathrm{\delta }}_{\mathrm{j}}$.

2.1.2 Voltage deviation minimization (V_D)

The voltage deviation across the system can be minimized by the following equation:

${\mathrm{V}}_{\mathrm{D}}={\displaystyle {\sum }_{\mathrm{k}=1}^{{\mathrm{N}}_{\text{PQ}}}}\left|\left.\left({\mathrm{V}}_{\mathrm{i}}-{\mathrm{V}}_{\text{ref}}\right)\right|\right.(3)$

2.2 Constraints

The limitation of solving multi-objective functions can be dealt with by considering parity and non-parity constraints.

2.2.1 Equality constraints

2.2.1.1 Power flow constraints

The set of system parity constraints can be represented for the ith bus as follows:

${\mathrm{P}}_{\text{gi}}-{\mathrm{P}}_{\text{Di}}={\displaystyle {\sum }_{\mathrm{j}=1}^{\text{NB}}}{\mathrm{V}}_{\mathrm{i}}{\mathrm{V}}_{\mathrm{j}}{\mathrm{Y}}_{\text{ij}}\cos \left({\mathrm{\delta }}_{\text{ij}}+{\mathrm{\gamma }}_{\mathrm{j}}-{\mathrm{\gamma }}_{\mathrm{i}}\right),(4)$

${\mathrm{Q}}_{\text{gi}}-{\mathrm{Q}}_{\text{Di}}={\displaystyle {\sum }_{\mathrm{j}=1}^{\text{NB}}}{\mathrm{V}}_{\mathrm{i}}{\mathrm{V}}_{\mathrm{j}}{\mathrm{Y}}_{\text{ij}}\sin \left({\mathrm{\delta }}_{\text{ij}}+{\mathrm{\gamma }}_{\mathrm{i}}-{\mathrm{\gamma }}_{\mathrm{j}}\right).(5)$

2.2.2 Inequality constraints

2.2.2.1 Generator constraints

The total amounts of VAR requirement and voltage supplied by the generator bus are specified as follows:

${\mathrm{V}}_{\text{gbi}}^{\min }\le {\mathrm{V}}_{\text{gbi}}\le {\mathrm{V}}_{\text{gbi}}^{\max }\hspace{1em}\mathrm{i}=\mathrm{1,2},\dots .{\mathrm{N}}_{\mathrm{G}},(6)$

${\mathrm{Q}}_{\text{gb}1}^{\min }\le {\mathrm{Q}}_{\text{gb}1}\le {\mathrm{Q}}_{\text{gb}1}^{\max }\hspace{1em}\mathrm{i}=\mathrm{1,2},\dots .{\mathrm{N}}_{\mathrm{G}}.(7)$

2.2.2.2 Load bus constraints

${\mathrm{V}}_{\mathrm{L}1}^{\min }\le {\mathrm{V}}_{\mathrm{L}1}\le {\mathrm{V}}_{\mathrm{L}1}^{\max }\hspace{1em}\mathrm{i}=\mathrm{1,2},\dots .{\mathrm{N}}_{\mathrm{L}}(8)$

Here, ${\mathrm{V}}_{\mathrm{L}1}^{\min }$ and ${\mathrm{V}}_{\mathrm{L}1}^{\max }$ will be the voltage levels at the upper and lower limits, respectively.

2.2.2.3 Power line constraints

${\mathrm{S}}_{\mathrm{L}1}\le {\mathrm{S}}_{\mathrm{L}1}^{\max }\hspace{1em}\mathrm{i}=\mathrm{1,2},\dots ,{\mathrm{N}}_{\text{TL}}(9)$

Here, S_L1 represents the net or total power in the line, and ${\mathrm{S}}_{\mathrm{L}1}^{\max }$ is the max range of total power flow at the ith line.

2.2.2.4 Transformers tap setting constraints

The operating range of the tap-changing transformer is specified as follows:

${\mathrm{T}}_{\mathrm{i}}^{\max }\le {\mathrm{T}}_{\mathrm{i}}\le {\mathrm{T}}_{\mathrm{i}}^{\min }\hspace{1em}\mathrm{i}=\mathrm{1,2},\dots ,{\mathrm{N}}_{\mathrm{T}}.(10)$

Here, ${\mathrm{T}}_{\mathrm{i}}^{\max }$ and ${\mathrm{T}}_{\mathrm{i}}^{\min }$ are the operating ranges at the ith bus.

2.2.2.5 Shunt compensator constraints

The limitations involved for operating the shunt VAR compensating device are given as follows:

${\mathrm{Q}}_{{\mathrm{C}}_1}^{\min }\le {\mathrm{Q}}_{{\mathrm{C}}_1}\le {\mathrm{Q}}_{{\mathrm{C}}_1}^{\max }\hspace{1em}\mathrm{i}=\mathrm{1,2}\dots .,{\mathrm{N}}_{\mathrm{C}}.(11)$

Here, ${\mathrm{Q}}_{{\mathrm{C}}_1}^{\max }$ and ${\mathrm{Q}}_{{\mathrm{C}}_1}^{\min }$ will be the max and min limits of reactive power at the ith device, respectively.

3 Firefly algorithm

Nature has been a significant inspiration in creating a broad spectrum of new algorithms over the previous two decades. The significant benefit of evolved algorithms that require specific characteristics to be optimized is the solution of real-time issues with decreased computation time and fewer complications. Transnational methods for the optimization of a function are commonly employed. Firefly is an algorithm inspired by fireflies’ spawning or flashing activity (VC and T., 2018). Compared with conventional algorithms like PSO, ABC, and ACO, this approach is more accessible, understandable, and implementable. Fireflies are lightning bugs that emit light energy to attract a partner or prey using a unique frequency (Olabode et al., 2023). The luminosity (I) and the radius (R) of the light emitted by the insects are negatively proportionate. Fireflies may interact over a range of more than a thousand meters. The flickering lights develop a network that can be improved in conjunction with desired functions. Some criteria apply while implementing the firefly algorithm (Jun et al., 2021).

• Fireflies, irrespective of gender, will attract each other.

• Attraction is directly related to their luminosity and inversely proportionate to their distance.

• The objective function landscape will evaluate the amount of luminosity the firefly emits.

The functioning concept that explains the algorithm’s effectiveness is stated as follows.

The most simple form of luminous flux f(r) changes depending on the inverse square law.

$\mathrm{F}\left(\mathrm{r}\right)=\frac{{\mathrm{f}}_{\mathrm{s}}}{{\mathrm{r}}^2}.(12)$

Here, f(r) is the luminous flux emitted from the source, where fs is the object’s source and r is the distance between the object and the source.

3.1 Attractiveness and light intensity

An adjacent firefly can identify the attractiveness and luminous intensity of nearby firefly, and the attractiveness of the firefly can be portrayed as $\propto$:

$\propto ={\propto }_0{\mathrm{e}}^{-\mathrm{x}{\mathrm{r}}^2}(13)$

to determine the distance of the firefly from the source r = 0.

3.2 Distance

A simple equation can evaluate the distance between the two adjacent fireflies:

${\mathrm{Q}}_{\text{ij}}=‖{\mathrm{d}}_{\mathrm{i}}-{\mathrm{d}}_{\mathrm{j}}‖(14)$

Here, the variables i and j represent the movement of the firefly from the ith position to the jth position. The information used by the firefly algorithm comprises three main terms:

• The firefly’s current position

• Comparing the attractiveness of the firefly with the adjacent firefly

• The random walk of the firefly

4 Artificial neural network–artificial intelligence

Artificial neural networks are an essential component of artificial intelligence techniques. Artificial intelligence systems are used to fine-tune the optimization parameters involved in the objectives of the power system. A synthetic intelligence strategy based on ANN deals with nonlinear computation. It can generate outputs of linear as well as nonlinear complex functions. The term “artificial neural network” refers to a system that operates in a manner entirely inspired by the operation of the central nervous system. The ANN system comprises a cluster of multiple nodes collectively referred to as neurons that are connected to one another. The representation of neurons in the human brain serves as a model. The framework of an artificial neural network typically consists of many operating units linked in parallel to one another and feeding information forward to solve various power system issues by interconnecting the different layers. The adoption of ANNs has significantly increased in recent developments in electrical engineering because of the precise and rapid computing that can be performed across the many levels of neural networks compared to other methods. The processed output from the firefly algorithm is fed as input to an ANN. Then, the standards are tweaked using the ANN’s hidden layer, the feedforward network for the middle layer. After completing the analysis at the hidden layer, the results are shown as output across the third layer.

Figure 1A shows the general representation of the ANN structure, which comprises an input layer that collects the input signal. Inputs are processed in the hidden layer, and the processed data are displayed in the output layer.

FIGURE 1

FIGURE 1. (A) Structure of ANN. (B) Feedforward network with three layers. (C) Process flow-bio-inspired technique with ANN.

4.1 Training process in ANN

The training process is a significant element of an ANN model when the execution of ANNs mainly relies on completing the training process and the training algorithm. The objective of the training phase is to lessen a cost function stated as a mean squared error (MSE) or a sum of squared error (SSE) within its real and target outputs through the adjustment of weights and biases. Two special issues are important in the ANN training process.

1. Avoiding the local minimum

2. Attaining quick convergence

Therefore, submitting an acceptable and effective training algorithm has always been a challenging task. Different algorithms have been adopted to train ANNs, including back-propagation algorithms and heuristic algorithms. One technique employed in the training phase is the back-propagation (BP) algorithm, including the standard BP and the enhanced BP. Researchers have evidence that the BP algorithm—a gradient-based algorithm—has merits. Its shortfalls incorporate the tendency to become trapped in local minima. Heuristic algorithms are known for their capability to generate optimal or adjacent optimal solutions for optimization issues. Numerous research studies have exhibited that any continuous function can be approximated with only one hidden layer in a feedforward neural network (FNN). Hence, FNN is an interesting technique. Figure 1B illustrates a multilayer perceptron (MLP) with one hidden layer.

In Figure 2,

FIGURE 2

FIGURE 2. (A) Structure of an IEEE 14-bus system network. (B) Convergence graph of FFA with an IEEE 14-bus system. (C) Voltage profile enhancement at load buses across an IEEE 14-bus system.

I, H, and O are the numbers of input, hidden neurons, and output, respectively;

iw and hw are the input and hidden weight matrices, respectively;

hb and ob are the bias vectors of the hidden and output layers, respectively;

x is the input vector of the network; ho is the output vector of the hidden layer; and

y is the output vector of the network.

The neural network in Figure 1 can be stated by the subsequent Eqs 15, 16:

${ho}_i=f\left({\displaystyle {\sum }_{j=1}^R}{iw}_{ji}.x_j-{hb}_i\right)\text{for}i=1,\dots \dots ..N,(15)$

$yi=f\left({\displaystyle {\sum }_{k=1}^N}{hw}_{ko}.{ho}_k-{ob}_i\right)\text{for}i=1,\dots \dots ..S,(16)$

where

f is the activation function,

iw_ij is the connection weight from the jth node in the input layer to the ith node in the hidden layer, and hw_ik is the connection weight from the kth node in the hidden layer to the ith node in the output layer.

It is mandatory to find the structure with respect to the number of layers and number of neurons in the layers. The fitness function in the training process is stated in Eqs 17, 18:

$SSE={\displaystyle {\sum }_{k=1}^Q}{E}_k,(17)$

$E_k={\displaystyle {\sum }_{i=1}^S}{\left(y_i^k-d_i^k\right)}^2,(18)$

where

Q is the number of training samples,

${\mathrm{y}}_{\mathrm{i}}^{\mathrm{k}}$ is the actual output of the ith input when the kth training sample is employed, and

${\mathrm{d}}_{\mathrm{i}}^{\mathrm{k}}$ is the desired output of the ith input when the kth training sample is employed.

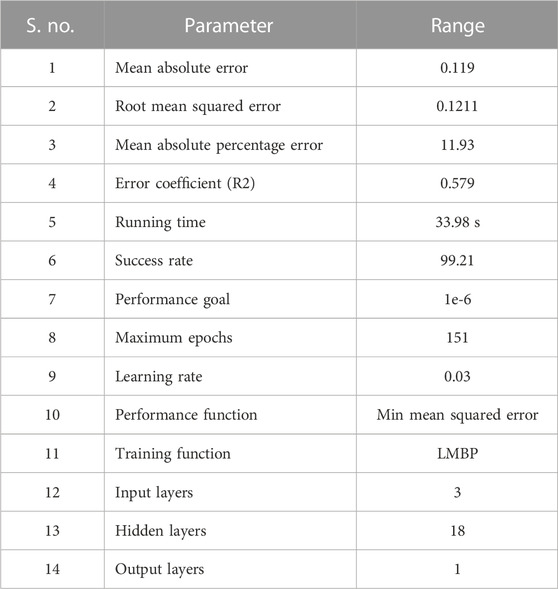
The best fitness function values of the training ANN parameters are listed in Table 1.

TABLE 1

TABLE 1. ANN training parameters with best fitness values.

4.2 Strategy employed in training ANN

A direct learning strategy was employed for training the artificial neural network. The weight of the neural network is updated by the Levenberg–Marquardt back-propagation (LMBP) algorithm. The parameters obtained from optimization algorithms are treated as input for ANN. The LMBP trains the entire system because of its accuracy and dynamic response. The ANN outputs are employed to improve the system’s voltage profile ratings. Optimization algorithms have been integrated with an ANN to improve optimal reactive power control and reactive power compensation parameters in the power system. The LMBP algorithm is suited for all the power system constraints, including various loading conditions. The LMBP algorithm is framed with two combinations: the gradient descent method and the Gauss–Newton method. The LMBP method is vital in increasing the entire universal conveyance property. The only disadvantage in neural network training is data overtraining, which can be avoided by following a bidirectional recursive neural network. A bidirectional recursive neural network is applied to adjust the system’s weight throughout the process, as shown in Figure 1C.

Step 1:. The input control pulse (y) with different time intervals is trained with the network with the available information.

Step 2:. The target errors $\mathrm{y}\left(1\right),\mathrm{y}\left(2\right)\dots \mathrm{y}\left(\mathrm{n}\right)$ can be determined by using the following equation.

${LMBP}_{error}^n={\mathrm{y}\left(\mathrm{n}\right)}^{\text{NN}\left(\text{target}\right)}-{\mathrm{y}\left(\mathrm{n}\right)}^{\text{NN}\left(\text{out}\right)}(19)$

Step 3:. Network outputs are determined by the following formula:

${\mathrm{y}\left(\mathrm{n}\right)}^{\text{NN}\left(\text{out}\right)}={\mathrm{q}}_{\mathrm{n}}+{\displaystyle {\sum }_{n=1}^N}{X}_{1n}{y\left(n\right)}^{NN\left(k\right)}(20)$

The node bias function q varies from $\mathrm{1,2},\dots \mathrm{n}$.

Step 4:. The neuron weight for each strand can be computed by

${\mathrm{j}}_{\text{new}}={\mathrm{j}}_{\text{old}}+∆\mathrm{j},(21)$

${\mathrm{y}\left(\mathrm{n}\right)}^{\text{NN}\left(\mathrm{k}\right)}=\frac{1}{1+\exp \left(-j_{nn}z\left(n\right)-j_{1n}z\left(1\right)\right)}.(22)$

Step 5:. The change in weight can be calculated by

${∆j}_n=T_{r}y\left(n\right).{LMBP}_{error}^n.(23)$

Step 6:. The aforementioned steps can be repeated to minimize the LMBP errors and the number of epochs. The coefficient of determination (R2), mean absolute error (MAE), root mean square error (RMSE), and mean absolute percentage error (MAPE) are evaluated to determine the performance of ANN.

$\mathrm{R}2=1-\frac{{\displaystyle {\sum }_{i=1}^n}{\left(x_n-y_n\right)}^2}{{\displaystyle {\sum }_{i=1}^n}{\left(y_n\right)}^2},(24)$

$\text{MAE}=\frac{{\displaystyle {\sum }_{i=1}^n}{\left|S_{pre,i}-S_i\right|}^2}{n},(25)$

$\text{RMSE}=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^n}{S}_{pre,i}-S_i}{n}},(26)$

$\text{MAPE}=\frac{1}{n}{\displaystyle {\sum }_{i=1}^n}\left|\frac{y_n-x_n}{y_n}\right|.(27)$

4.3 Implementation of FFA for an ORPD problem with ANN

1. Generator bus voltage (VG_B)

2. Transformer tap setting (T_T)

3. Megavolt ampere of reactive power (MVAR) by the static compensator (QSVC: Reactive power generated by static var compensator)

Table 2 shows the control parameter limits used for the firefly algorithm with three IEEE bus systems.

TABLE 2

TABLE 2. Control variables and their limits.

Table 2 shows the training parameter range for the artificial neural network to control the variables of the firefly optimization algorithm (Kumar et al., 2021a). The listed ANN training parameters effectively configure the objective of the proposed research.

Step 1:. Initialize the population size by randomly selecting each variable’s luminous intensity and generations.

Step 2:. Every firefly insect is characterized by the control variables within their respective limits.

Step 3:. Each firefly’s total luminous intensity and luminaries are calculated using Newton Raphson power flow analysis.

Step 4:. Compute luminous intensity and luminaries for each adjacent firefly and evaluate each firefly’s fitness function.

Step 5:. The evaluation of the fitness function will be repeated from Step 2 until the optimal luminous intensity and luminaries are attained.

Step 6:. Execute the same procedure and implement the ANN technique to regulate the parameters for better voltage profile ratings.

5 Results and discussion

Standard IEEE 14-, 30-, and 57-bus systems are employed to determine the robustness of the proposed firefly optimization algorithm. The optimal reactive power dispatch objective can be obtained by optimizing voltage deviation and active PD in the power network. The research objective is well structured with different constraints to meet the required reactive power requirements of the grid system. The ORPD problem has been analyzed using three IEEE bus system networks for three solutions.

5.1 Case 1: IEEE 14-bus system

In this case, a standard IEEE 14-bus system has been implemented to attain the objective function. Here, the network comprises buses connected with generators at 1, 2, 3, 6, and 8. Transformer tap settings are connected at three locations across the entire network. Figure 2A depicts the structure of the IEEE 14-bus system network.

5.2 Minimization of the objective function

The scope of the research focuses on reducing the amount of active power loss and variations in bus voltage as much as possible. The reduction of the objective function leads to an improvement in the voltage profile of the power network, which significantly impacts the grid stability of the system. The minimization of objective functions using the IEEE 14-bus system is shown in Table 3.

TABLE 3

TABLE 3. Minimization of the objective function in Case 1.

Figure 2B represents the total iteration carried over to attain the steady fitness value to obtain a better voltage profile while solving the ORPD problem.

The bar chart shown in Figure 2C depicts the enhanced voltage profile attained by implementing an artificial neural network with a firefly algorithm. This figure shows an ideal situation where the voltage across most PQ buses remains the same, that is, approximately 1.0 p.u.

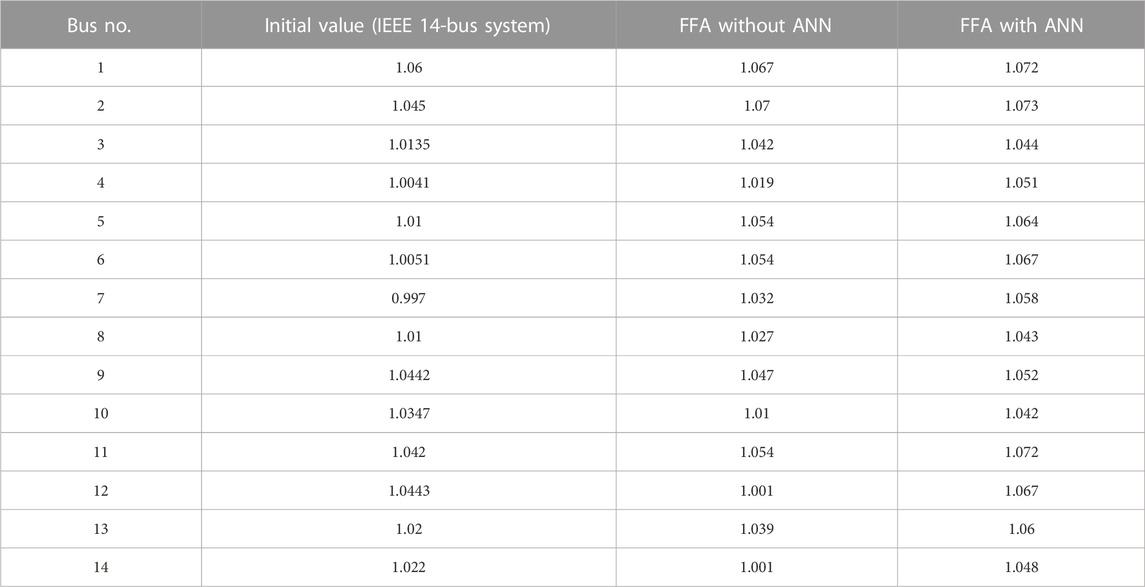
The comparative study of the voltage profile achieved while operating the test bus system is shown in Table 4. The data presented in the table demonstrate that incorporating an artificial neural network with the firefly algorithm into a plan will positively impact the voltage profile of an IEEE 14-bus system.

TABLE 4

TABLE 4. Voltage profile values of Case 1.

Table 5 shows the average value of the voltage profile attained from operating the firefly optimization technique with and without incorporating ANN on an IEEE 14-bus system network.

TABLE 5

TABLE 5. Average value of the voltage profile in an IEEE 14-bus system network.

Table 6 shows the effect of using the firefly optimization technique with and without ANN on the testing and training of data sets applied to the IEEE 14-bus system network.

TABLE 6

TABLE 6. Testing and training an ANN with the firefly algorithm in an IEEE 14-bus system.

5.3 Case II: IEEE 30 bus system

In this case, the IEEE 30-bus system is employed to achieve the objective function. This system comprises six generators linked across the 1st, 2nd, 5th, 8th, 11th, and 13th buses. Shunt connections are used to couple the reactive power compensation devices between the 10th and 24th buses, and 41 transmission lines connect the various parts of the system. Figure 3A shows the single-line structure of the IEEE 14-bus system network.

FIGURE 3

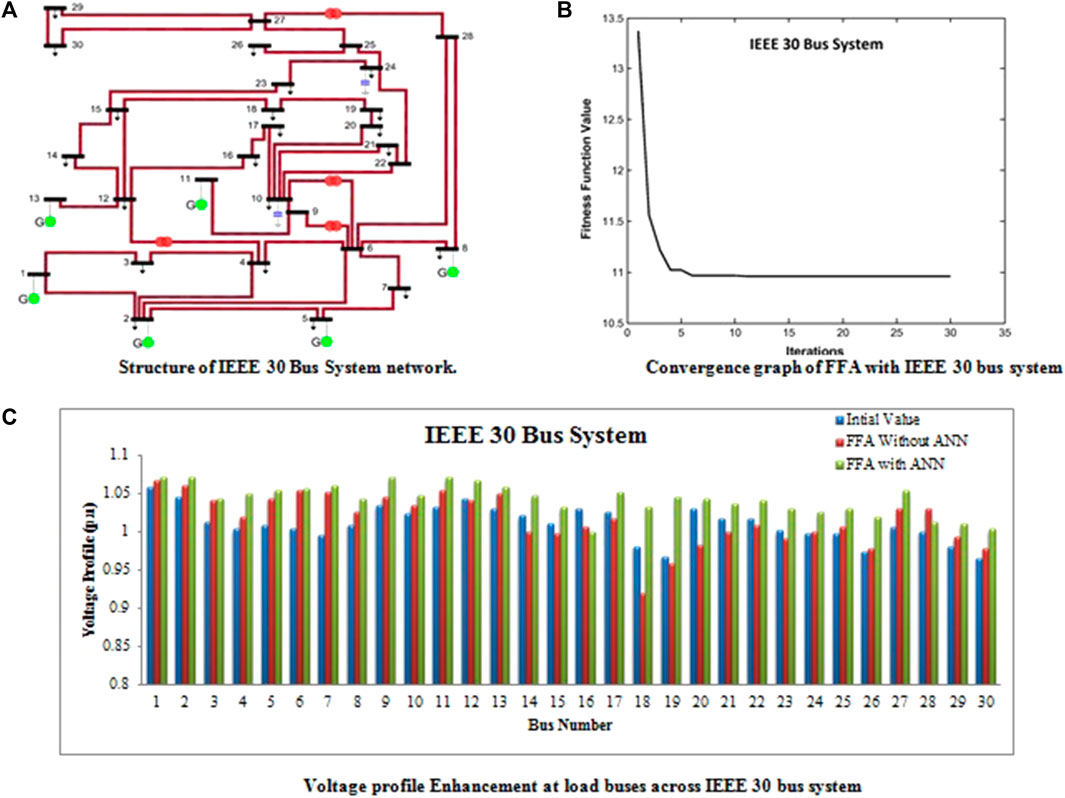
FIGURE 3. (A) Structure of an IEEE 30-bus system network. (B) Convergence graph of FFA with an IEEE 30-bus system. (C) Voltage profile enhancement at load buses across an IEEE 30-bus system.

5.4 Minimization of the objective function

One of the most critical parameters to consider when solving an optimal reactive power flow problem is minimizing bus voltage deviation and active power loss. Table 7 displays the minimization of objective terms for Case 2 using the firefly algorithm.

TABLE 7

TABLE 7. Minimization of the objective function for Case 2.

Figure 3B shows the convergence graph obtained while running the NR power flow model. The total number of iterations required to attain the ideal fitness value for obtaining a better voltage profile while solving the ORPD problem is presented in the figure.

In Figure 3C, the bar chart shows the enhanced voltage profile attained by implementing an artificial neural network with a firefly algorithm. From this figure, the voltage profile across all 30 buses is encouraging, and the profile ratings are more than 1.0 p.u.

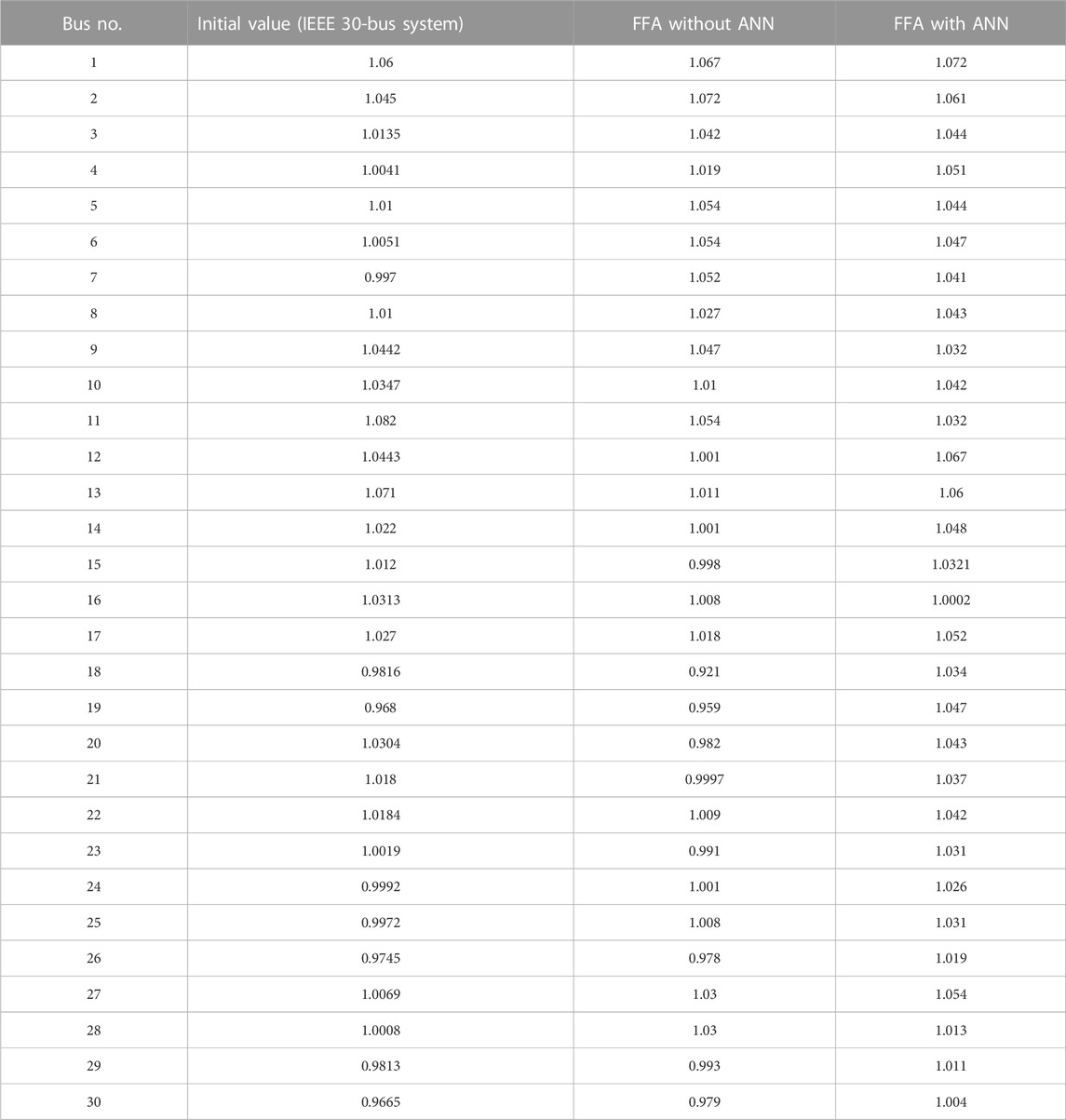
Below, Table 8 displays a comparative analysis of the voltage profile attained while running the test bus system. The table shows that implementing an ANN with the firefly algorithm improves the voltage profile of the IEEE 30-bus system.

TABLE 8

TABLE 8. Voltage profile values of Case 2.

Table 9 presents the results of utilizing the firefly optimization method with and without ANN while working with the IEEE 30-bus system network. The results are presented as a mean value of the obtained voltage profile.

TABLE 9

TABLE 9. Average value of the voltage profile in an IEEE 30-bus system network.

Table 10 gives a clear idea about the testing and training of data sets with the effect of artificial intelligence on the firefly optimization technique applied to the IEEE 30-bus system network.

TABLE 10

TABLE 10. Testing and training an ANN with the firefly algorithm in an IEEE 30-bus system.

5.5 Case III: IEEE 57 bus system

The IEEE 57-bus system is chosen to test the objective function obtained to solve the objective. The test bus system comprises seven generators connected across the 1st, 2nd, 3rd, 6th, 8th, 9th, and 12th buses. Figure 4A shows the structural diagram of the IEEE 57 bus system.

FIGURE 4

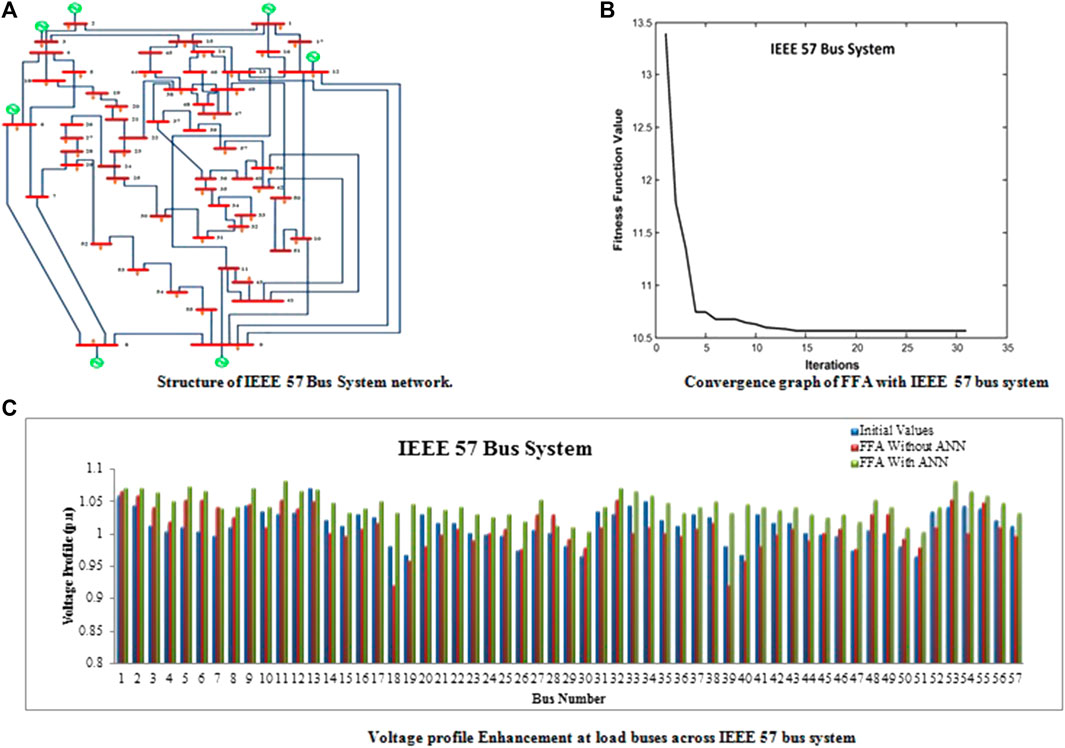
FIGURE 4. (A) Structure of an IEEE 57-bus system network. (B) Convergence graph of FFA with an IEEE 57-bus system. (C) Voltage profile enhancement at load buses across an IEEE 57-bus system.

5.6 Minimization of the objective function

The minimization objective, that is, minimizing bus voltage deviation and active power loss across the test IEEE 57-bus system, is explained in Table 11. The quantified results mentioned in the table show that the proposed algorithm is more effective than conventional algorithms.

TABLE 11

TABLE 11. Minimization of the objective function.

Figure 4B shows the convergence graph obtained while running the Newton–Raphson (NR) power flow pattern. The graph shows the total number of iterations required to attain the fitness value for a better voltage profile.

The following bar chart, Figure 4C, clearly shows the enhanced voltage profile values after implementing ANN with the firefly algorithm on the IEEE 57-bus system network. This indicates that all the load buses have attained a maximum voltage profile of 1.05 p.u.

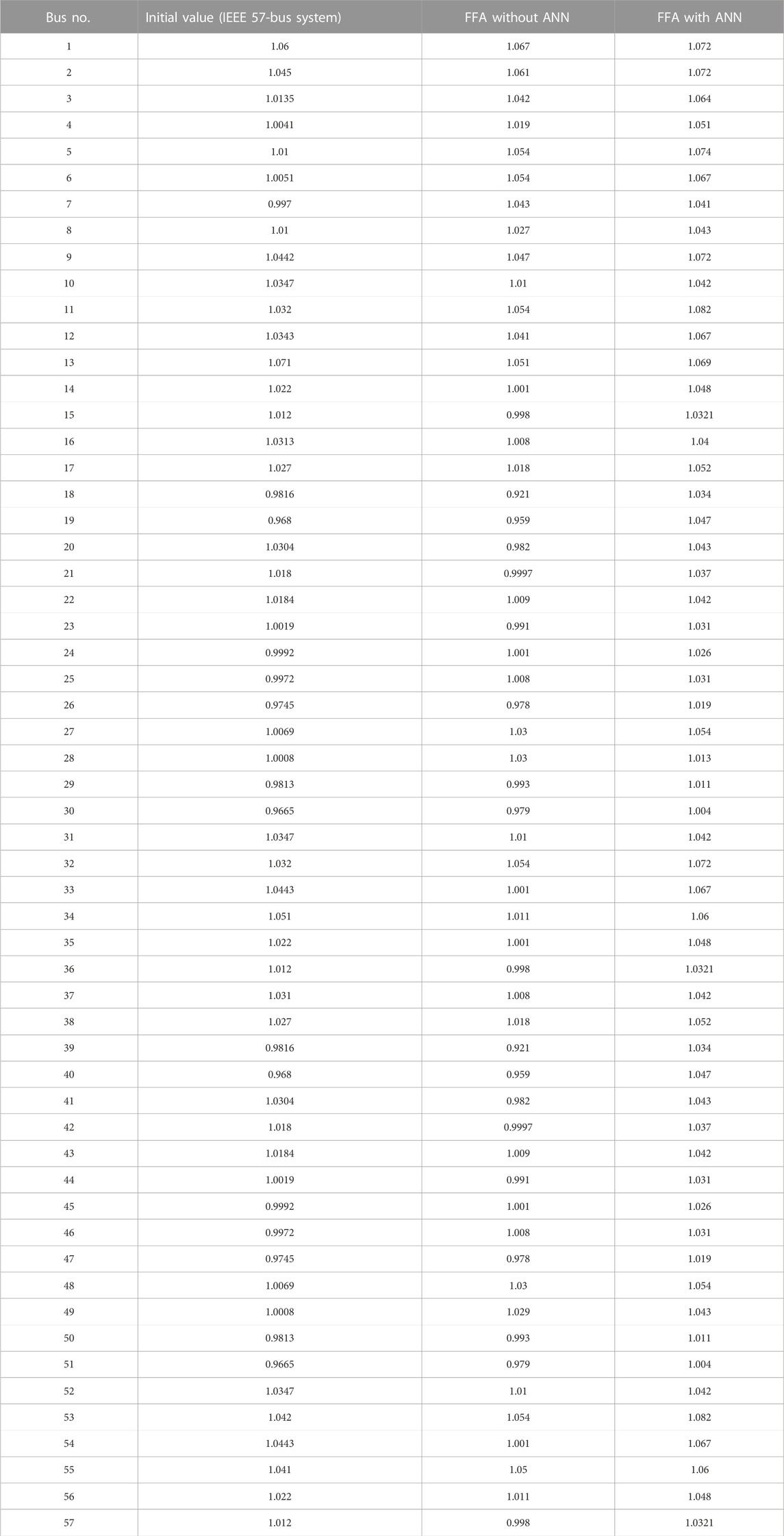
The following Table 12 displays the comparative investigation of the voltage profile attained while running an ANN with the firefly algorithm. The obtained voltage profile ratings are encouraging, and the results are tabulated.

TABLE 12

TABLE 12. Voltage profile values of Case 3.

Table 13 presents the results of utilizing the firefly iterative algorithm with and without the implementation of an artificial neural network while working with the IEEE 57-bus system network to determine the mean value of the voltage profile of the IEEE 57-bus system network.

TABLE 13

TABLE 13. Average value of the voltage profile in an IEEE 57-bus system network.

The following Table 14 gives a clear idea about the testing and training of data sets using artificial intelligence and the firefly optimization technique applied to the IEEE 57-bus system network.

TABLE 14

TABLE 14. Testing and training an ANN with the firefly algorithm in an IEEE 57-bus system.

6 Conclusion

The prime objective of this research is to enhance the voltage profile across the load buses, which can be done by minimizing the real power losses and voltage deviations at the load buses. A novel strategy of integrating an ANN technique with the firefly optimization algorithm is employed to attain the objective function. The results are tested on three different sets of IEEE benchmark systems, namely, an IEEE 14-bus system, a 30-bus system and a 57-bus system. The objective results produced by the firefly algorithm are compared with well-known optimization algorithms, namely, the big bang–big crunch algorithm (BB-BC), the gravitational search algorithm (GSA), the bacterial foraging algorithm (BFA), the biogeography-based optimization (BBO), and PSO. The results produced by this firefly optimization algorithm are quite encouraging when compared with these methods. Integrating the ANN technique with the firefly optimization algorithm plays a vital role in enhancing the voltage profile of the system. Implementing this novel approach enhanced the system’s voltage profile from 1.048 to 1.082 on the IEEE 14-bus system, from 1.032 to 1.089 while running the algorithm with the IEEE 30-bus system, and from 1.027 to 1.091 in the IEEE 57-bus system. From this research, it is clear that implementing an ANN with the firefly algorithm is more effective than conventional methods in solving the optimal reactive power dispatch problem and enhancing the voltage profile across the system.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

SJ: writing–original draft, writing–review and editing. KP: conceptualization, investigation, and writing–review and editing. CK: data curation, software, supervision, and writing–review and editing. ML: methodology and writing–review and editing. AbA: formal analysis, project administration, and writing–review and editing. AJ: funding acquisition, validation, and writing–review and editing. AyA: funding acquisition and writing–review and editing. AM: resources, visualization, and writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Amit, S., and Ashish, S. (2012). Multi-objective optimal reactive power dispatch considering voltage stability in power systems using HFMOEA. Eng. Appl. Artif. Intell. 26, 390–404. doi:10.1016/j.engappai.2012.06.008

CrossRef Full Text | Google Scholar

Badar, A. Q. H., Umre, B. S., and Junghare, A. S. (2012). Reactive power control using dynamic Particle Swarm Optimization for real power loss minimization. Electr. Power & Energy Syst. 41 (1), 133–136. doi:10.1016/j.ijepes.2012.03.030

CrossRef Full Text | Google Scholar

Balachennaiah, P., Suryakalavathi, M., and Nagendra, P. (2018). Firefly algorithm based solution to minimize the real power loss in a power system. Shams Eng. J. 9 (1), 89–100. doi:10.1016/j.asej.2015.10.005

CrossRef Full Text | Google Scholar

Biswas, P. P., Suganthan, P. N., and Amaratunga, G. A. J. (2018). “Distribution network reconfiguration together with distributed generator and shunt capacitor allocation for loss minimization,” in 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, July, 2018, 1–7.

CrossRef Full Text | Google Scholar

Dash, S. P., Subhashini, K. R., and Satapathy, J. K. (2019). Optimal location and parametric settings of FACTS devices based on JAYA blended moth flame optimization for transmission loss minimization in power systems. Microsyst. Technol. 26, 1543–1552. doi:10.1007/s0054.2-019-04692-w

CrossRef Full Text | Google Scholar

Duman, S., Guvenc, U., and Yorukeren, N. (2010). Gravitational search algorithm for economic dispatch with valve-point effects. Int. Rev. Electr. Eng. 5 (6), 2890–2895.

Google Scholar

Duman, S., Guvenc, U., Yusuf, S., and Yorukeren, N. (2012). Optimal power flow using gravitational search algorithm. Energy Convers. Manag. 59, 86–95. doi:10.1016/j.enconman.2012.02.024

CrossRef Full Text | Google Scholar

Erol, O. K., and Eksin, I. (2006). A new optimization method: Big bang–big Crunch. Adv. Eng. Softw. 37 (2), 106–111. doi:10.1016/j.advengsoft.2005.04.005

CrossRef Full Text | Google Scholar

Esmin, A. A. A., Lambert-Torres, G., and de Souza, A. C. Z. (2005). A hybrid particle swarm optimization applied to loss power minimization. IEEE Trans. Power Syst. 20 (2), 859–866. doi:10.1109/tpwrs.2005.846049

CrossRef Full Text | Google Scholar

Imran, A. M., and Kowsalya, M. (2014). A new power system reconfiguration scheme for power loss minimization and voltage profile enhancement using fireworks algorithm. Int. J. Electr. Power & Energy Syst. 62, 312–322. doi:10.1016/j.ijepes.2014.04.034

CrossRef Full Text | Google Scholar

Iqbal, F., Khan, M. T., and Siddiqui, A. S. (2018). Optimal placement of DG and DSTATCOM for loss reduction and voltage profile improvement. Alexandria Eng. J. 57 (2), 755–765. doi:10.1016/j.aej.2017.03.002

CrossRef Full Text | Google Scholar

Jun, C. S., Abd Halim, S., Mohd Rosli, H., and Mohamed Kamari, N. A. (2021). Power loss minimization using optimal power flow based on firefly algorithm. Firefly Algorithm” Int. J. Adv. Comput. Sci. Appl. (IJACSA) 12 (9), 1–14. doi:10.14569/ijacsa.2021.0120940

CrossRef Full Text | Google Scholar

Kanata, S., Gibson, H., Sianipar, M., and Maulidevi, N. U. (2018). “Optimization of reactive power and voltage control in power system using hybrid artificial neural network and particle swarm optimization,” in 2nd International Conference on Applied Electromagnetic Technology (AEMT), Lombok, Indonesia, April, 2018, 67–72.

CrossRef Full Text | Google Scholar

Kumar, C., Jaisiva, S., Clement Raj, A., and Logeshwari, V. (2021b). “Hybrid renewable energy based smart grid system for reactive power management and voltage profile enhancement using artificial neural network” Taylor and Francis - energy Sources. Part A Recovery, Util. Environ. Eff. 43 (19), 2419–2442. doi:10.1080/15567036.2021.1902430

CrossRef Full Text | Google Scholar

Kumar, C., Jaisiva, S., Xavier, F. J., and Prabaakaran, K. (2021a). “Artificial neural network integrated with bio-inspired approach for optimal VAr management and voltage profile enhancement in grid system” Taylor and Francis - energy Sources. Part A Recovery, Util. Environ. Eff. 43 (21), 2838–2859. doi:10.1080/15567036.2021.1919790

CrossRef Full Text | Google Scholar

Kumar, K. S., and Jayabarathi, T. (2012). Power system reconfiguration and loss minimization for an distribution systems using bacterial foraging optimization algorithm. Int. J. Electr. Power & Energy Syst. 36 (1), 13–17. doi:10.1016/j.ijepes.2011.10.016

CrossRef Full Text | Google Scholar

KursatAyan, U., and Kılıç, U. (2012). Artificial bee Colony algorithm solution for optimal reactive power flow. Appl. Soft Comput. 12 (5), 1477–1482. doi:10.1016/j.asoc.2012.01.006

CrossRef Full Text | Google Scholar

Lotfi, H. (2020). Multi-objective energy management approach in distribution grid integrated with energy storage units considering the demand response program. Int. J. Energy Res. 44, 10662–10681. doi:10.1002/er.5709

CrossRef Full Text | Google Scholar

Lotfi, H. (2022). Optimal sizing of distributed generation units and shunt capacitors in the distribution system considering uncertainty resources by the modified evolutionary algorithm. J. Ambient Intell. Humaniz. Comput. 13, 4739–4758. doi:10.1007/s12652-021-03194-w

CrossRef Full Text | Google Scholar

Lotfi, H., and Ghazi, R. (2021). Optimal participation of demand response aggregators in reconfigurable distribution system considering photovoltaic and storage units. J. Ambient Intell. Humaniz. Comput. 12, 2233–2255. doi:10.1007/s12652-020-02322-2

CrossRef Full Text | Google Scholar

Mallipeddi, R., Jeyadevi, S., Suganthan, P. N., and Baskar, S. (2012). Efficient constraint handling for optimal reactive power dispatch problems. Swarm Evol. Comput. 5, 28–36. doi:10.1016/j.swevo.2012.03.001

CrossRef Full Text | Google Scholar

Nguyen, T. T., and Truong, A. V. (2015). Distribution network reconfiguration for power loss minimization and voltage profile improvement using cuckoo search algorithm. Int. J. Electr. Power & Energy Syst. 68, 233–242. doi:10.1016/j.ijepes.2014.12.075

CrossRef Full Text | Google Scholar

Olabode, E. o., AjewoleT, o., OkakwuI, k, and Ade-Ikuesan, O. o. (2023). Optimal sitting and sizing of shunt capacitor for real power loss reduction on radial distribution system using firefly algorithm: a case study of Nigerian system. Energy Sources, Part A Recovery, Util. Environ. Eff. 45 (2), 5776–5788. doi:10.1080/15567036.2019.1673507

CrossRef Full Text | Google Scholar

Onlam, A., Yodphet, D., Chatthaworn, R., Surawanitkun, C., Siritaratiwat, A., and Khunkitti, P. (2019). Power loss minimization and voltage stability improvement in electrical distribution system via network reconfiguration and distributed generation placement using novel adaptive shuffled frogs leaping algorithm. J. Energies 12 (3), 553. doi:10.3390/en12030553

CrossRef Full Text | Google Scholar

Rabiee, A., Vanouni, M., and Parniani, M. (2012). Optimal reactive power dispatch for improving voltage stability margin using a local voltage stability index. Energy Convers. Manag. 59, 66–73. doi:10.1016/j.enconman.2012.02.017

CrossRef Full Text | Google Scholar

RoutrayMistry, A. K. D., and Raj Arya, S. (2020). Power loss minimization in radial distribution systems with obstructed solar astronomical model and temperature effect using grey wolf optimization technique. Energy Sources, Part A Recovery, Util. Environ. Eff., 1–20. doi:10.1080/15567036.2020.1756539

CrossRef Full Text | Google Scholar

Roy, P. K., Ghoshal, S. P., and Thakur, S. S. (2012). Optimal VAR control for improvements in voltage profiles and for real power loss minimization using Biogeography Based Optimization. Electr. Power Energy Syst. 43 (1), 830–838. doi:10.1016/j.ijepes.2012.05.032

CrossRef Full Text | Google Scholar

Singh, B., and Agrawal, G. (2018). Enhancement of voltage profile by incorporation of SVC in power system networks by using optimal load flow method in MATLAB/Simulink environments. Energy Rep. 4 (3), 418–434. doi:10.1016/j.egyr.2018.07.004

CrossRef Full Text | Google Scholar

Sirjani, R., Mohamed, A., and Hussain, S. (2012). Optimal allocation of shunt var compensators in power systems using a novel global Harmony search algorithm. Electr. Power & Energy Syst. 43 (1), 562–572. doi:10.1016/j.ijepes.2012.05.068

CrossRef Full Text | Google Scholar

Varadarajan, M., and Swarup, K. S. (2008). Differential evolutionary algorithm for optimal reactive power dispatch. Electr. Power & Energy Syst. 30 (8), 435–441. doi:10.1016/j.ijepes.2008.03.003

CrossRef Full Text | Google Scholar

Vc, V. R. (2018). Ant Lion optimization algorithm for optimal sizing of renewable energy resources for loss reduction in distribution systems. J. Electr. Syst. Inf. Technol. 5 (3), 663-680.

Google Scholar

Vc, V. R., and T., G. M. (2018). Optimal renewable resources placement in distribution networks by combined power loss index and whale optimization algorithms. J. Electr. Syst. Inf. Technol. 5 (2), 175–191. doi:10.1016/j.jesit.2017.05.006

CrossRef Full Text | Google Scholar

Verma, Dr. H. K. (2012). Yogesh manekar, “Big Bang Big Crunch optimization for determination of worst case loading margin”. Int. J. Eng. Res. Appl. 2 (4), 421–426.

Google Scholar