Hybrid bilevel optimization-based interaction between the distribution grid and PV microgrids with differentiated demand response

Demand response plays an important role in improving the balance of power generation and consumption between the distribution grid and photovoltaic (PV) microgrids. However, due to the uncertainty and volatility of PV output, as well as the different operation goals of PV microgrids, a conventional single-tier optimization approach is infeasible to realize the coordinated interaction between the distribution grid and PV microgrids. To address these challenges, we propose a second-order cone and improved consensus algorithm-based hybrid bilevel optimization algorithm for the interaction between the distribution grid and PV microgrids. First, we construct price-based and incentive-based differentiated demand response models to deal with various supply and demand dynamics of the distribution grid and PV microgrids. Building upon this foundation, we construct a hybrid bilevel optimization model. In the lower level, distributed optimization is adopted, and an improved consensus algorithm is used to optimize power output of PV microgrids to maximize the revenue based on output power of upper-level generator sets. In the upper level, centralized optimization is adopted, and second-order cone programming is employed to minimize the grid loss in the distribution grid based on the power output of lower-level PV microgrids. Hybrid bilevel optimization is iterated until the convergence condition is satisfied. Simulation results verify the proposed algorithm for achieving a coordinated interaction between the distribution grid and PV microgrids.

1 Introduction

With the gradual integration of renewable energy sources such as solar energy and wind energy, as well as distributed energy resources, the distribution grid is facing unprecedented challenges and opportunities Byun et al. (2011); Cui et al. (2022). In order to improve the penetration rate of renewable energy in the distribution grid and optimize the energy structure, multiple photovoltaic (PV) microgrids can be connected to the distribution grid to become backup energy (Hui et al., 2022; Guan et al., 2022; Liao et al., 2023). Price-based and incentive-based differentiated demand responses are further employed to coordinate the interaction between the distribution grid and PV microgrid and improve the balance between energy generation and consumption. However, the goals of a microgrid and distribution grid participating in differentiated demand response are different. The distribution grid needs to ensure operation stability, while the PV microgrid expects to maximize its benefit. The difference between optimization objectives makes the conventional single-tier optimization approach infeasible (Liu et al., 2017; Chanda and Srivastava, 2016; Li et al., 2023d). Therefore, it is urgent to explore new optimization methods to realize more flexible and intelligent interactions between the distribution grid and PV microgrids.

The bilevel optimization based interaction between the distribution grid and PV microgrids has been proven to be a feasible solution due to its flexibility and scalability (Yu et al., 2015; Zhang J. et al., 2023; Zhou et al., 2020). This method models the PV microgrids and distribution grid systems separately and applies different optimization methods based on their respective objectives, aiming to maximize benefits for both sides. However, the bilevel optimization-based interaction between the distribution grid and PV microgrids still faces some challenges Zhai et al. (2022). First, bilevel optimization involves both centralized optimization on the distribution grid side and distributed optimization on the PV microgrid side. The interaction between the distribution grid and PV microgrids is very complex. The existing methods ignore the hybrid bilevel optimization of centralized dispatching of the distribution grid and distributed dispatching of PV microgrids, resulting in high grid loss and dispatching cost. Second, due to the influence of the construction scale and geographical factors, the output and energy storage characteristics of PV microgrids are quite different. The existing consensus optimization methods do not incorporate differentiated characteristics of PV microgrids such as power generation capacity, microgrid load demand, and PV energy storage in the consensus iteration process to design communication weights, resulting in slow response speed.

There have been studies on the bilevel optimization-based interaction between the distribution grid and PV microgrids. Kou and Park (2023) designed a centralized demand response energy interaction management system, which verified the feasibility of distributed energy coordination in the operation of intelligent parks. Zhang et al. (2021) proposed a two-layer structure for coordinated optimization of the distribution grid, considering the bidding demand response model of different stakeholders. Liu et al. (2023) proposed a two-stage bilevel optimization model, which integrates renewable energy and energy storage systems, effectively controls energy sharing between multiple microgrids participating in demand response services, and minimizes operational costs. However, the aforementioned studies fail to consider the hybrid bilevel optimization of centralized dispatching of the distribution grid and distributed dispatching of PV microgrids, resulting in poor dispatching performance, including large voltage deviations, high network loss of the distribution grid, and low selling revenue of the PV microgrids.

There have been studies on distributed dispatching of PV microgrids. Li H. et al. (2023) designed a net-zero emission operation strategy to realize the optimal planning of the island dual-zero microgrid, and balanced the environmental and economic problems in the planning. Li et al. (2022) proposed a non-cooperative game-based planning method for the microgrid, considering the interconnection between developing and developed privately owned clustered microgrids on an island. Consensus algorithm plays a crucial role in distributed dispatching by enabling nodes to reach an agreement on a shared value or state. The consensus algorithm ensures coordination and consistency among the participating nodes. There have been studies on distributed dispatching using the consensus algorithm. Zhu et al. (2018) proposed a consensus algorithm based on the charging and discharging characteristics of electric vehicles, which solved the difficulty of microgrid distributed dispatching caused by the integration of intermittent power supply and electric vehicles. Hua et al. (2022) proposed an optimal distribution grid distributed dispatching model, considering the two-layer interaction of the energy storage system, and used the consensus algorithm to minimize the dispatching cost. Hu et al. (2020) improved the consensus algorithm based on the segmented voltage-power droop control of the key node to mitigate the voltage violation problems using the distributed energy storage unit. Li et al. (2021) proposed a distributed optimal dispatching method based on the consensus algorithm to solve the convex optimization model about the AC/DC hybrid microgrid, and the results of an example prove the feasibility of the presented distributed optimal dispatching method. Chen et al. (2021) proposed that each node only needs to exchange part of the information according to the communication topology and adopts the consensus algorithm to complete the iterative calculation so that the consensus variable of each energy supply equipment in the system tends to be consistent, and the distributed optimization of the system is realized. However, the aforementioned study ignores the impact of differentiated output and energy storage operating characteristics of PV microgrids on their distributed dispatching, resulting in higher operational costs and slower response speed for demand response participation.

Faced by these challenges, we propose a second-order cone and improved consensus algorithm-based hybrid bilevel optimization algorithm for the interaction between the distribution grid and PV microgrids. First, we model the PV microgrid, and construct price-based and incentive-based demand response models. Second, we determine the hybrid bilevel optimization problem and optimization objective. The upper level minimizes grid loss, considering the power balance, power output, and power ramp rate constraints of the generator sets, while the lower level maximizes electricity sales revenue of PV microgrids, considering the energy storage constraints, power output constraints, and incentive-based demand response subsidies of the PV microgrids. Finally, we achieve hybrid bilevel optimization based on the interaction of two levels. The contributions of this method can be summarized as follows:

Hybrid bilevel optimization for the interaction between the distribution grid and PV microgrids with centralized-distributed coordination: Based on the output power of the upper-level generator sets, PV microgrids perform distributed optimization of output power based on the improved consensus algorithm and send the output power of them to the upper-level distribution grid. Based on the injected power from the PV microgrids, the distribution grid performs centralized optimization of output power of generator sets. The aforementioned iteration process is repeated until the output power of the PV microgrids and the active power of the generator sets meet the termination conditions. Hybrid bilevel optimization for the interaction between the distribution grid and PV microgrids with centralized-distributed coordination effectively mitigates voltage deviations, reduces grid loss of the distribution grid, and maximizes the selling revenue of the PV microgrids.

Differentiated characteristic-based improved consensus algorithm for PV microgrid dispatch: During the process of distributed dispatch of PV microgrids, the differentiated characteristic of PV microgrids, such as power generation capacity, microgrid load demand, and PV energy storage, are fully considered. Based on the differentiated characteristics of PV microgrids mentioned previously, different consensus iteration weights are designed for each PV microgrids. With this approach, the distributed dispatch of PV microgrids can effectively reduce the number of iterations and improve the convergence speed of the optimization process. It effectively improves the revenue of PV microgrids from selling electricity and reduces the operational cost.

The rest of the paper is organized as follows: Section 2 introduces the system model; Section 3 introduces the hybrid bilevel optimization problem formulation; Section 4, a second-order cone and improved consensus algorithm-based hybrid bilevel optimization algorithm for the interaction between the distribution grid and PV microgrids is proposed; Section 5 gives the simulation results; Section 6 concludes the paper.

2 System model

Considering the intermittent and random characteristics of PV microgrids’ power output, this paper constructs a system model, as shown in Figure 1. The distribution grid is divided into upper and lower levels. A total of I PV microgrids are considered in the lower level, and a total of N_bus generator sets are considered in the upper level. The overall time is divided into T time slots with equal intervals Δt. In the upper level, generator sets generate electricity to meet the power demand of the distribution grid, and the distribution grid purchases electricity from PV microgrids when power consumption peaks. In the lower level, the PV microgrid can sell electricity to the distribution grid on the premise of meeting its own needs. In addition, this paper considers price-based and incentive-based demand responses and models them separately according to their differences. The price-based demand response guides the user’s electricity consumption by changing the electricity price, and the incentive-based demand response guides the PV microgrid to sell electricity through incentive subsidies.

FIGURE 1

FIGURE 1. System model.

2.1 Lower-level PV microgrid model

The PV microgrid comprises the PV panel cluster, PV energy storage units, and PV microgrid loads Wang et al. (2023). It represents a type of small-scale generation-distribution-utilization system. Through effective dispatch strategies, it can achieve a high degree of autonomy and facilitate a seamless connection with the distribution grid, promoting grid-friendly integration Abu-elzait and Parkin (2019); Zhao and Xu (2017); Zhou et al. (2017).

2.1.1 PV microgrid output model

The PV microgrid converts solar energy into electrical energy through a cluster of PV panels. The total output power of the PV panel cluster for the PV microgrid i at the t-th time slot can be expressed as follows (Yan and Li, 2020; Li et al., 2020):

$P_i^{\mathrm{p}\mathrm{v},\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}\left(t\right)=r_i^{\mathrm{p}\mathrm{v}}\left(t\right){\zeta }_i^{\mathrm{p}\mathrm{v}}\left(t\right)A_i^{\mathrm{p}\mathrm{v}}\left(t\right),(1)$

where $r_i^{\mathrm{p}\mathrm{v}}(t)$, $A_i^{\mathrm{p}\mathrm{v}}(t)$, and ${\zeta }_i^{\mathrm{p}\mathrm{v}}(t)$represent the solar irradiance, PV panel cluster area, and PV conversion efficiency of the PV microgrid i at time slot t, respectively. Higher solar irradiance, larger PV panel cluster area, and greater PV conversion efficiency lead to a higher total output power of the PV panel cluster.

The output power of the PV microgrid i at the t-th time slot, i.e., the power supplied to the distribution grid while meeting its own demands, can be expressed as

$P_i^{\text{pv}}\left(t\right)=P_i^{\text{pv,total}}\left(t\right)-P_i^{\text{pv,load}}\left(t\right)+P_i^{\text{pv,es}}\left(t\right),(2)$

where $P_i^{\text{pv,es}}(t)$ represents the output power of the PV energy storage system in the PV microgrid i. $P_i^{\text{pv,load}}(t)$ represents the operating load of the PV microgrid i, which is the load that must be met to ensure the normal operation of the PV microgrid. $P_i^{\text{pv,es}}(t)>0$ indicates that the PV energy storage system is discharging, while $P_i^{\text{pv,es}}(t)<0$ indicates that the PV energy storage system is charging.

The power output of the PV microgrid is influenced by the total output power of the PV panel cluster, the operational load of the PV microgrid, and the charging/discharging of the PV energy storage system. The upper and lower limits of the power output for the PV microgrid i at the t-th time slot can be expressed as

$\left\{\begin{array}{c}{P}_i^{\text{pv,max}}\left(t\right)=P_i^{\text{pv,total}}\left(t\right)-P_i^{\text{pv,load}}\left(t\right)+\frac{\left[S_i\left(t\right)-S_i^{\text{min}}\right]E_i^{\text{max}}}{\mathrm{\Delta }t},\hfill \\ P_i^{\text{pv,min}}\left(t\right)=P_i^{\text{pv,total}}\left(t\right)-P_i^{\text{pv,load}}\left(t\right)-\frac{\left[S_i^{\text{max}}-S_i\left(t\right)\right]E_i^{\text{max}}}{\mathrm{\Delta }t},\hfill \end{array}\right.(3)$

where S_i(t), $S_i^{\text{max}}$, $S_i^{\text{min}}$, and $E_i^{\text{max}}$ represent the state of charge (SoC), upper SoC limit, lower SoC limit, and capacity of the PV energy storage system within the PV microgrid i, respectively. Δt represents the time slot duration.

2.1.2 Operational cost model of the PV microgrid

The operational cost of the PV microgrid consists of the operational cost of the PV panel cluster and the dispatch cost of the PV energy storage system (Xiao et al., 2017; Zhang X. et al., 2023). When optimizing the PV microgrid, it is necessary to consider the factors such as the power generation of the PV panel cluster and the charging and discharging of the energy storage system. These factors increase losses in both PV panel clusters and energy storage systems, resulting in operational costs for PV microgrids.

The operational cost of the PV panel cluster can be expressed as

$g_i^{\text{pvp}}\left(t\right)={\alpha }_i^{\text{pvp}}{\left(P_i^{\text{pv}}\left(t\right)\right)}^2+{\beta }_i^{\text{pvp}}{P}_i^{\text{pv}}\left(t\right)+{\gamma }_i^{\text{pvp}},(4)$

where ${\alpha }_i^{\text{pvp}}$, ${\beta }_i^{\text{pvp}}$, and ${\gamma }_i^{\text{pvp}}$ represent the cost coefficients associated with the operation of the PV panel cluster.

The dispatch cost of the PV energy storage system can be expressed as

$g_i^{\text{pv,es}}\left(t\right)={\delta }_i^{\text{pv,es}}{\left(P_i^{\text{pv,es}}\left(t\right)\right)}^2,(5)$

where ${\delta }_i^{\text{pv,es}}$ represents the dispatch cost coefficient of the PV energy storage system in the PV microgrid i.

In summary, the operational cost of the PV microgrid can be expressed as

$g_i^{\text{pv}}\left(t\right)=g_i^{\text{pvp}}\left(t\right)+g_i^{\text{pv,es}}\left(t\right).(6)$

2.2 Differentiated demand response

The distribution grid and PV microgrid are different stakeholders and have different purposes in power grid dispatching. The distribution grid needs to achieve a balance between supply and demand, and the PV microgrid aims to obtain maximum benefits. Differentiated demand response is a complementary relationship, which is more suitable for the current complex grid dispatching environment than single demand response. When the power demand of the distribution grid is large and the user’s load reduction reaches saturation, the power generation cannot meet the power demand. Therefore, the incentive-based demand response is needed to supplement the power, and the incentive subsidy is issued to the PV microgrid to encourage electricity selling so as to meet the balance of supply and demand of the distribution grid. This paper considers price-based demand response and incentive-based demand response, which are described in the following paragraphs.

2.2.1 Price-based demand response

Price-based demand response is a controllable load adjustment resource primarily achieved by implementing time-of-use electricity pricing to guide users in altering their electricity consumption patterns, thereby redistributing the load distribution. Price-based demand response optimizes users’ electricity consumption behavior, thus mitigating electricity shortages during peak periods and increasing electricity demand during off-peak periods, with the goal of peak load reduction and low load increase (Si et al., 2022; Pawakul and Srirattanawichaikul, 2020; Li et al., 2023c).

In practical situations, there are basic load and saturated load in the electricity consumption of users. Saturated load refers to the maximum electricity consumption that users can reach, while basic load is the minimum electricity consumption level. Therefore, price-based demand response has upper and lower limits on load variations, which can be expressed as

$\left\{\begin{array}{c}{P}^{+}\left(t\right)=P_{\max }\left(t\right)-P_0\left(t\right),\hfill \\ P^{-}\left(t\right)=P_{\min }\left(t\right)-P_0\left(t\right),\hfill \end{array}\right.(7)$

where P⁺(t) and P⁻(t) represent the upper and lower limits of the grid’s total load variation at the t-th time slot, respectively. P_max(t) and P_min(t) represent the saturated load and basic load, respectively. P₀(t) represents the initial load of the grid at the t-th time slot.

Demand price elasticity represents the sensitivity of load demand to price changes during different time slots. In practical situations, the effect of load demand adjustment is more pronounced when electricity prices vary within a certain normal range. However, when the price variation becomes very significant, the effectiveness of load adjustment through price changes diminishes. Therefore, constructing an exponential relationship between load demand and electricity price is a way to model self-elastic response to price changes, which can be expressed as

$\left\{\begin{array}{c}\mathrm{\Delta }H\left(t\right)=H_{\text{PDR}}\left(t\right)-H_0\left(t\right),\hfill \\ \mathrm{\Delta }{P}_t\left(t\right)=\left\{\begin{array}{c}{P}^{-}\left(t\right)\left(1-e^{-{\mu }_{t,t}\mathrm{\Delta }H\left(t\right)}\right),\mathrm{\Delta }H\left(t\right)\ge 0,\hfill \\ P^{+}\left(t\right)\left(1-e^{{\mu }_{t,t}\mathrm{\Delta }H\left(t\right)}\right),\mathrm{\Delta }H\left(t\right)<0,\hfill \end{array}\right.\hfill \end{array}\right.(8)$

where H₀(t) represents the initial electricity price at the t-th time slot. H_PDR(t) represents the time-of-use electricity price for the grid at the t-th time slot, considering price-based demand response. ΔH(t) is the price variation at the t-th time slot. μ_t,t represents the self-elasticity coefficient of load variation at the t-th time slot caused by changes in the electricity price. ΔP_t(t) represents the self-elastic load variation at the t-th time slot caused by changes in electricity price. According to Eq. 8, when ΔH(t) ≥ 0, the electricity price at the time slot t increases. When ΔP_t(t) ≤ 0, the grid’s load during that time slot decreases. Conversely, when ΔH(t) < 0, the electricity price at the time slot t decreases. When ΔP_t(t) > 0, the grid’s load during that time slot increases. In addition, the exponential relationship between load demand and electricity price limits ΔP_t(t) to a certain range, i.e., P⁻(t) < ΔP_t(t) < P⁺(t).

In practical situations, the load during the t-th time slot is not only influenced by the current time slot’s electricity price but also affected by past time slot prices. Therefore, constructing an exponential cross-elasticity response relationship between load demand and electricity price is necessary, which can be expressed as

$\mathrm{\Delta }{P}_x\left(t\right)=\left\{\begin{array}{c}{P}^{-}\left(t\right)\left(1-e^{-{\mu }_{t,x}\mathrm{\Delta }H\left(t\right)}\right),\mathrm{\Delta }H\left(t\right)\ge 0,\hfill \\ P^{+}\left(t\right)\left(1-e^{{\mu }_{t,x}\mathrm{\Delta }H\left(t\right)}\right),\mathrm{\Delta }H\left(t\right)<0,\hfill \end{array}\right.(9)$

where t and x are two different time slots, with x < t. μ_t,x represents the cross-elasticity coefficient of load variation in time slot t caused by changes in the electricity price in time slot x. ΔP_x(t) represents the cross-elastic load variation in time slot t caused by changes in the electricity price in time slot x.

Considering that the response of load to electricity price changes varies across different time slots, this paper constructs an elasticity matrix O composed of self-elasticity coefficients and cross-elasticity coefficients, which can be represented as

$\mathbf{O}=\left[\begin{array}{cccc}\hfill {\mu }_{\mathrm{1,1}}\hfill & \hfill \hfill & \hfill \hfill & \hfill 0\hfill \\ \hfill {\mu }_{\mathrm{2,1}}\hfill & \hfill {\mu }_{\mathrm{2,2}}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill \\ \hfill {\mu }_{T,1}\hfill & \hfill {\mu }_{T,2}\hfill & \hfill \cdots \hfill & \hfill {\mu }_{T,T}\hfill \end{array}\right],(10)$

where T represents the number of time slots. The main diagonal elements of the matrix are the self-elasticity coefficients corresponding to each respective time slot, while the off-diagonal elements represent the cross-elasticity coefficients between the two corresponding time slots.

Combining Eqs 8–10, the total load at the t-th time slot considering the price-based demand response, P_PDR(t), can be expressed as

$\left\{\begin{array}{c}{\kappa }_t\left(t\right)=\frac{1}{{\displaystyle \sum _{x^{\prime }=1}^t}{e}^{x^{\prime }-t}},\hfill \\ {\kappa }_x\left(t\right)=\frac{e^{x-t}}{{\displaystyle \sum _{x^{\prime }=1}^t}{e}^{x^{\prime }-t}},\hfill \\ P_{\text{PDR}}\left(t\right)=P_0\left(t\right)+{\kappa }_t\left(t\right)\mathrm{\Delta }{P}_t\left(t\right)+{\displaystyle \sum _{x=1}^{t-1}}{\kappa }_x\left(t\right)\mathrm{\Delta }{P}_x\left(t\right),\hfill \end{array}\right.(11)$

where κ_t(t) represents the self-elastic weighted coefficient of ΔP_t(t) and κ_x(t) represents the cross-elastic weighted coefficient of ΔP_x(t). According to Eq. 11, the self-elastic weighted coefficient is larger than all the cross-elastic weighted coefficients. The normalization of the coefficient can ensure that the total load P_PDR(t) meets the upper and lower load constraints shown in Eq. 7. In addition, the increase of the interval between the time slot x and time slot t will lead to the decrease in the cross-elastic weighted coefficient κ_x(t).

2.2.2 Incentive-based demand response

Incentive-based demand response primarily stimulates the participation of the PV microgrid in demand response and adjusts their power output through incentive subsidies. The grid dispatch center sets a minimum incentive subsidy threshold and provides subsidies to the portion of the PV microgrid’s output that exceeds this threshold (Eslaminia and Mashhadi, 2022; Li et al., 2023b; Ma et al., 2022). The incentive subsidy power, which represents the portion of the PV microgrid’s output that receives subsidy, can be expressed as

$P_i^{\text{rew}}\left(t\right)=P_i^{\text{pv}}\left(t\right)-P_{\text{low}},(12)$

where P_low represents the incentive subsidy threshold.

Based on the magnitude of the incentive subsidy power, this paper constructs an incentive response mechanism for the PV microgrid, which can be expressed as

$\begin{array}{l}\hfill g_i^{\mathrm{d}\mathrm{r}}\left(t\right)=\left\{\begin{array}{c}\begin{array}{c}0,P_i^{\mathrm{r}\mathrm{e}\mathrm{w}}\left(t\right)\le 0,\hfill \\ c_1{P}_i^{\mathrm{r}\mathrm{e}\mathrm{w}}\left(t\right),0<P_i^{\mathrm{r}\mathrm{e}\mathrm{w}}\left(t\right)\le D_1,\hfill \end{array}\hfill \\ {\displaystyle \sum _{l=1}^{k_i\left(t\right)-1}}{c}_l{D}_l+c_{k_i\left(t\right)}\left(P_i^{\mathrm{r}\mathrm{e}\mathrm{w}}\left(t\right)-{\displaystyle \sum _{l=1}^{k_i\left(t\right)-1}}{D}_l\right),\text{if\hspace{0.17em}}{\displaystyle \sum _{l=1}^{k_i\left(t\right)-1}}{D}_l<P_i^{\mathrm{r}\mathrm{e}\mathrm{w}}\left(t\right)\le {\displaystyle \sum _{l=1}^{k_i\left(t\right)}}{D}_l,\hfill \end{array}\right.\end{array}(13)$

where $g_i^{\text{dr}}(t)$ represents the incentive subsidy provided by the grid dispatch center to the PV microgrid i at the t-th time slot based on incentive-based demand response. k_i(t) represents the tiered pricing level corresponding to $P_i^{\text{pv}}(t)$, where k_i(t) ∈ {1, 2, … , K} and K is the maximum tiered pricing level. c_l is the unit power incentive subsidy corresponding to the l-th tier, and D_l is the power interval of the l-th tier incentive subsidy.

3 Hybrid bilevel optimization problem formulation

This paper models and optimizes the upper-level distribution grid and lower-level PV microgrids as separate stakeholders. The optimization and dispatching of both levels are both independent and interconnected, and the optimization problem is solved based on the hybrid bilevel optimization. The lower-level PV microgrids adopt a distributed optimization approach, utilizing the power output transmitted from the upper level’s generator sets as decoupling variables for optimization. On the other hand, the upper-level distribution grid adopts a centralized optimization approach, utilizing the power output transmitted from the lower-level PV microgrids as decoupling variables for optimization. Hybrid bilevel optimization is iteratively performed until the convergence condition is met.

3.1 Lower-level PV microgrid optimization problem

To maximize the revenue from selling electricity and minimize operational cost, lower-level optimization aims to maximize the difference between electricity sales revenue and operational cost. The optimization problem of the lower-level PV microgrids is constructed as

$\begin{array}{ll}\hfill \mathbf{P}\mathbf{1}:f_{\mathit{sub}}\left(t\right)& =\underset{\left\{P_i^{\text{pv}}\left(t\right)\right\}}{\max }{\displaystyle \sum _{i=1}^I}\left[g_i^{\text{ep}}\left(t\right)+g_i^{\text{dr}}\left(t\right)-g_i^{\text{pv}}\left(t\right)\right],\hfill \\ \hfill \text{s.t.}{C}_1:P_{\text{PDR}}\left(t\right)& ={\displaystyle \sum _{i=1}^I}{P}_i^{\text{pv}}\left(t\right)+{\displaystyle \sum _{n=1}^{N_{\text{bus}}}}{P}_{\text{G,n}}\left(t\right),\hfill \\ C_2:\frac{\left[S_i\left(t\right)-S_i^{\mathrm{m}\mathrm{a}\mathrm{x}}\right]E_i^{\mathrm{m}\mathrm{a}\mathrm{x}}}{\mathrm{\Delta }t}\hfill & \le P_i^{\mathrm{p}\mathrm{v},\mathrm{e}\mathrm{s}}\left(t\right)\hfill \\ \hfill & \le \frac{\left[S_i\left(t\right)-S_i^{\mathrm{m}\mathrm{i}\mathrm{n}}\right]E_i^{\mathrm{m}\mathrm{a}\mathrm{x}}}{\mathrm{\Delta }t},\hfill \\ C_3:P_i^{\text{pv,min}}\left(t\right)\hfill & \le P_i^{\text{pv}}\left(t\right)\le P_i^{\text{pv,max}}\left(t\right),\hfill \end{array}(14)$

where I represents the number of PV microgrids. $\{P_i^{\text{pv}}(t)\}$ is the set of optimization variables, i.e., the output power of each PV microgrid. $g_i^{\text{dr}}(t)$ represents the incentive subsidy received by the PV microgrid i for participating in incentive-based demand response at time slot t. $g_i^{\text{pv}}(t)$ represents the operational cost of the PV microgrid i at time slot t. $P_i^{\text{pv,max}}(t)$ and $P_i^{\text{pv,min}}(t)$ represent the upper and lower limits of the output power of the PV microgrid i at the t-th time slot, respectively. $g_i^{\text{ep}}(t)$ represents the revenue obtained by the PV microgrid i from selling electricity to the distribution grid at time slot t, and it can be expressed as

$g_i^{\text{ep}}\left(t\right)=\sigma P_i^{\text{pv}}\left(t\right),(15)$

where σ represents the unit electricity selling price.

3.2 Upper-level distribution grid optimization problem

The upper-level distribution grid meets its load demand by using the output from generator sets and purchasing electrical energy from the lower-level PV microgrids. However, in some cases, the integration of intermittent and highly variable renewable energy sources like PVs can increase grid loss and introduce voltage deviation in the distribution grid.

Assuming that the total number of nodes in the upper-level distribution grid is N_bus, the grid loss of the distribution grid, P_loss(t), can be expressed as

$\begin{array}{ll}\hfill P_{\text{loss}}\left(t\right)& ={\displaystyle \sum _{\left(n,m\right)\in \mathbf{W},n\ne m}}{G}_{nm}\left(t\right)\left[U_n^2\left(t\right)+U_m^2\left(t\right)\right.\hfill \\ \hfill & \left.-2U_n\left(t\right)U_m\left(t\right)\cos {\theta }_{nm}\left(t\right)\right],\hfill \end{array}(16)$

where n and m are grid nodes and W is the set of grid branch. U_n(t) and U_m(t) are the voltage magnitudes at nodes n and m. θ_nm(t) is the voltage phase difference between nodes n and m. G_nm(t) is the admittance of the branch connecting nodes n and m.

The voltage deviation in the distribution grid, ΔU(t), can be expressed as

$\mathrm{\Delta }U\left(t\right)={\displaystyle \sum _{n=1}^{N_{\text{bus}}}}{\left[\frac{U_n\left(t\right)-U_n^{\exp }\left(t\right)}{\mathrm{\Delta }{U}_n^{\max }\left(t\right)}\right]}^2,(17)$

where $U_n^{\exp }(t)$ is the expected voltage magnitude at node n at the t-th time slot and $\mathrm{\Delta }{U}_n^{\max }(t)$ is the maximum voltage deviation set considering equipment safety.

In order to minimize the adverse effects of the randomness and variability of PV output on the distribution grid, the upper-level distribution grid uses the active power output and reactive power output of generator sets as optimization variables. The optimization objective is to minimize the weighted sum of grid loss P_loss(t) and voltage deviation ΔU(t) in the distribution grid. The optimization problem of the upper-level distribution grid is constructed as

$\begin{array}{ll}\hfill & \mathbf{P}\mathbf{2}:f_{\text{up}}\left(t\right)=\underset{\left\{P_{\text{G},n}\left(t\right)\right\},\left\{Q_{\text{G},n}\left(t\right)\right\}}{\min }\left[P_{\text{loss}}\left(t\right)+\xi \times \left(\mathrm{\Delta }U\left(t\right)\right)\right],\hfill \\ \hfill \text{s.t.}& C_1:P_{\text{G},n}\left(t\right)+P_{\text{pur},n}\left(t\right)-P_{\text{L},n}\left(t\right)\hfill \\ \hfill & =U_n\left(t\right){\displaystyle \sum _{m=1,m\ne n}^{N_{\text{bus}}}}{U}_m\left(t\right)\left[G_{nm}\left(t\right)\cos {\theta }_{nm}\left(t\right)\right.\hfill \\ \hfill & \left.+B_{nm}\left(t\right)\sin {\theta }_{nm}\left(t\right)\right],\hfill \\ \hfill & C_2:Q_{\text{G},n}\left(t\right)+Q_{\text{pur},n}\left(t\right)-Q_{\text{L},n}\left(t\right)\hfill \\ \hfill & =U_n\left(t\right){\displaystyle \sum _{m=1,m\ne n}^{N_{\text{bus}}}}{U}_m\left(t\right)\left[G_{nm}\left(t\right)\sin {\theta }_{nm}\left(t\right)\right.\hfill \\ \hfill & \left.-B_{nm}\left(t\right)\cos {\theta }_{nm}\left(t\right)\right],\hfill \\ \hfill & C_3:\left\{\begin{array}{c}{P}_{\text{G},n}^{\min }\left(t\right)\le P_{\text{G},n}\left(t\right)\le P_{\text{G},n}^{\max }\left(t\right),\hfill \\ Q_{\text{G},n}^{\min }\left(t\right)\le Q_{\text{G},n}\left(t\right)\le Q_{\text{G},n}^{\max }\left(t\right),\hfill \end{array}\right.\hfill \\ \hfill & C_4:U_n^{\min }\left(t\right)\le U_n\left(t\right)\le U_n^{\max }\left(t\right),\hfill \\ \hfill & C_5:C_{G,n}^{\min }\left(t\right)\le \left|\frac{P_{G,n}\left(t\right)-P_{G,n}\left(t-1\right)}{\mathrm{\Delta }t}\right|\le C_{G,n}^{\max }\left(t\right),\hfill \end{array}(18)$

where ξ is the scaling factor. C₁ and C₂ represent active and reactive power flow balance constraints in the distribution grid, respectively. P_G,n(t) and Q_G,n(t) are the active power output and reactive power output of the generator set at node n at the t-th time slot. P_L,n(t) and Q_L,n(t) represent the active and reactive power consumption of node n at the t-th time slot. G_nm(t) and B_nm(t) represent the real and imaginary parts of the admittance matrix element at row n and column m at the t-th time slot. $P_{\text{G},n}^{\min }(t)$ and $P_{\text{G},n}^{\max }(t)$ represent the lower and upper bounds of the active power output of generator set at node n at the t-th time slot, respectively. $Q_{\text{G},n}^{\min }(t)$ and $Q_{\text{G},n}^{\max }(t)$ represent the lower and upper bounds of the reactive power output of the generator set at node n at the t-th time slot, respectively. $U_n^{\min }(t)$ and $U_n^{\max }(t)$ represent the lower and upper voltage limits of node n at the t-th time slot, respectively. $C_{G,n}^{\min }(t)$ and $C_{G,n}^{\max }(t)$ represent the lower and upper bounds of the ramp rate for the generator set at node n, respectively. P_pur,n(t) and Q_pur,n(t) represent the active and reactive power injected into node n from the PV microgrid at the t-th time slot, satisfying

$\begin{array}{ll}\hfill & P_{\text{pur},n}\left(t\right)=\left\{\begin{array}{c}{P}_i^{\text{pv}}\left(t\right),\text{node\hspace{0.17em}}n\text{\hspace{0.17em}is\hspace{0.17em}directly\hspace{0.17em}connected\hspace{0.17em}to\hspace{0.17em}the\hspace{0.17em}PV\hspace{0.17em}microgrid\hspace{0.17em}}i,\hfill \\ 0,\text{node\hspace{0.17em}}n\text{\hspace{0.17em}is\hspace{0.17em}not\hspace{0.17em}directly\hspace{0.17em}connected\hspace{0.17em}to\hspace{0.17em}any\hspace{0.17em}PV\hspace{0.17em}microgrid},\hfill \end{array}\right.\hfill \\ \hfill & G_{\text{pur},n}\left(t\right)=\left\{\begin{array}{c}\mathit{tan}{\varphi }_i\left(t\right)P_i^{\text{pv}}\left(t\right),\text{node\hspace{0.17em}}n\text{\hspace{0.17em}is\hspace{0.17em}directly\hspace{0.17em}connected\hspace{0.17em}to\hspace{0.17em}the\hspace{0.17em}PV\hspace{0.17em}microgrid\hspace{0.17em}}i,\hfill \\ 0,\text{node\hspace{0.17em}}n\text{\hspace{0.17em}is\hspace{0.17em}not\hspace{0.17em}directly\hspace{0.17em}connected\hspace{0.17em}to\hspace{0.17em}any\hspace{0.17em}PV\hspace{0.17em}microgrid}.\hfill \end{array}\right.\hfill \end{array}(19)$

If node n is directly connected to the PV microgrid i, then $P_{\text{pur},n}(t)=P_i^{\text{pv}}(t)$ and $G_{\text{pur},n}(t)=\mathit{tan}{\varphi }_i(t)P_i^{\text{pv}}(t)$, where ϕ_i(t) is the power factor angle of the PV microgrid i at the t-th time slot. If node n is not directly connected to the PV microgrid, then P_pur,n(t) = Q_pur,n(t) = 0.

4 Second-order cone and improved consensus algorithm-based hybrid bilevel optimization algorithm for the interaction between the distribution grid and PV microgrids

The differentiated demand response makes the coupling relationship between the distribution grid and PV microgrid complex. The hybrid bilevel optimization between the distribution grid and PV microgrids needs frequent interaction. Specifically, the PV microgrids in the lower level are optimized by using the power output of generator sets transmitted from the upper level. At the same time, the distribution grid in the upper level is optimized by using the power output of the PV microgrids transmitted from the lower level. The hybrid bilevel optimization for the interaction between the distribution grid and PV microgrids is shown in Algorithm 1 and carried out as follows.

Algorithm 1. Second-order cone and improved consensus algorithm-based hybrid bilevel optimization algorithm for the interaction between the distribution grid and PV microgrids

1: Step 1: Improved consensus algorithm-based distributed dispatching of PV microgrids.

2: Input the total active output power of the upper-level generator sets $P_{\text{G},n}^{\vartheta -1}(t)$.

3: Calculate the consensus variables η_i(t) based on Eq. 21.

4: Calculate the improved adjacency matrix Z = (z_i,j(t)) and the target deviation variable Δd based on Eqs 22, 23.

5: Do

6:  Carry out the consensus iteration based on Eq. 24.

7:  Calculate the output power and energy storage device power of each PV microgrid after the consensus variables are updated based on Eq. 25.

8:  If: the output power of PV microgrid does not satisfy the constraints in Eq. 14.

9:   Modify the energy storage device power and output power based on Eqs 26, 27.

10:  End if

11:  Update the consensus variables based on Eq. 27.

12: Until: satisfy convergence condition Eq. 28.

13: The active output power of the PV microgrid $P_i^{\text{pv},\vartheta }(t)$ is calculated based on Eq. 25.

14: Step 2: Second-order cone-based centralized dispatching of the distribution grid

15: Input the active output power of each lower-level PV microgrid.

16: Calculate the active output power and reactive output power of the PV microgrid injected into node n based on Eq. 19.

17: Construct the upper-level optimization model based on Eq. 18.

18: Employ second-order cone techniques to transform the upper-level optimization model into a convex feasible region second-order cone programming model based on Eqs 29–32.

19: The Gurobi solver is used to complete the upper-level optimization, and the active power $P_{\text{G},n}^{\vartheta }(t)$ and reactive power output $G_{\text{G},n}^{\vartheta }(t)$ of the generator set are obtained.

20: Step 3: Bilevel interaction

21:  If: the active output power of PV $P_i^{\text{pv},\vartheta }(t)$ or the generator set $P_{\text{G},n}^{\vartheta }(t)$ does not satisfy the convergence conditions in Eq. 33.

22:   ϑ = ϑ + 1 and return to Step 1 for next iteration.

23:  End if

24: Complete the hybrid bilevel optimization.

4.1 Improved consensus algorithm-based distributed dispatching of PV microgrids

Consensus algorithm allows the PV microgrid to realize distributed dispatching through the interaction of information and has the advantages of simple dispatching and easy implementation. However, the traditional consensus algorithm ignores the differentiated output, energy storage, and other characteristics of PV microgrids, and regards each PV microgrid as the same individual for dispatching, resulting in a slow response speed and poor dispatching effect. To solve the aforementioned problems, this paper fully considers the differentiated output, energy storage, and other characteristics of the PV microgrid, and designs the differentiated consensus iteration coefficient based on the differentiated characteristics of PV microgrids to effectively improve the distributed dispatching response speed of the PV microgrids.

First, we construct the Lagrangian function, denoted as L, which can be expressed as

$\begin{array}{ll}\hfill L\left(t\right)& ={\displaystyle \sum _{i=1}^I}\left[g_i^{\text{ep}}\left(t\right)+g_i^{\text{dr}}\left(t\right)-g_i^{\text{pv}}\left(t\right)\right]\hfill \\ \hfill & +\lambda \left(P_{\text{PDR}}\left(t\right)-{\displaystyle \sum _{n=1}^{N_{\text{bus}}}}{P}_{\text{G,n}}\left(t\right)-{\displaystyle \sum _{i=1}^I}{P}_i^{\text{pv}}\left(t\right)\right),\hfill \end{array}(20)$

where λ is the Lagrange multiplier.

We take the partial derivative of the Lagrangian function L(t) with respect to the PV microgrid output $P_i^{\text{pv}}(t)$ to obtain the consensus variable, which can be expressed as

$\begin{array}{ll}\hfill {\eta }_i\left(t\right)& =\frac{\partial L}{\partial P_i^{\mathrm{p}\mathrm{v}}\left(t\right)}\hfill \\ \hfill & =\sigma +c_{k_i\left(t\right)}-\left(2{\delta }_i^{\mathrm{p}\mathrm{v},\mathrm{e}\mathrm{s}}+2{\alpha }_i^{\mathrm{p}\mathrm{v}\mathrm{p}}+{\beta }_i^{\mathrm{p}\mathrm{v}\mathrm{p}}\right)P_i^{\mathrm{p}\mathrm{v}}\left(t\right),\hfill \end{array}(21)$

where η_i(t) represents the consensus variable for PV microgrid i at time slot t.

After obtaining the consensus variable, the consensus algorithm needs to construct a communication iteration matrix, with matrix elements serving as iteration coefficients to determine whether entities are adjacent. In the general consensus algorithm, the communication iteration matrix typically has matrix elements set to 1 for adjacent entities. However, in cases where the convergence precision remains unchanged, variations in the matrix elements do not affect the final convergence results. Given the differences in PV generation capacity, internal load demands, and PV energy storage capacity among different PV microgrids, the efficiency of convergence can be improved by setting the weight proportion of adjacent PV microgrid’s power output capacity as the matrix element. Therefore, the communication iteration matrix is denoted as $\mathbf{Z}={(z_{i,j}(t))}_{I\times I}$, and its elements are defined as

$z_{i,j}\left(t\right)=\left\{\begin{array}{c}\frac{\omega \left[P_i^{\mathrm{p}\mathrm{v},\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}\left(t\right)-P_i^{\mathrm{p}\mathrm{v},\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}\left(t\right)\right]+\chi P_i^{\mathrm{p}\mathrm{v},\mathrm{e}\mathrm{s}}\left(t\right)}{\omega \left[P_j^{\mathrm{p}\mathrm{v},\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}\left(t\right)-P_j^{\mathrm{p}\mathrm{v},\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}\left(t\right)\right]+\chi P_j^{\mathrm{p}\mathrm{v},\mathrm{e}\mathrm{s}}\left(t\right)},\left(v_i,v_j\right)\in E,\hfill \\ 0,\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{s},\hfill \end{array}\right.(22)$

where z_i,j(t) represents the communication weight for the iteration between the PV microgrids i and j. ω and χ are weight coefficients. $\left(v_i,v_j\right)\in E$ denotes the existence of an edge in the directed graph between two points, indicating that PV microgrids i and j are neighbors.

According to Eq. 14, the power balance constraint for the lower-level microgrid group optimization is considered. The deviation between the current state of the microgrid and the target state is calculated to obtain the target deviation variable Δd. This provides the basis for the step size of the lower-level consensus algorithm iteration in this round. Δd is calculated as

$\mathrm{\Delta }d=P_{\text{PDR}}\left(t\right)-{\displaystyle \sum _{n=1}^{N_{\text{bus}}}}{P}_{\text{G,n}}\left(t\right)-{\displaystyle \sum _{i=1}^I}{P}_i^{\mathrm{p}\mathrm{v}}\left(t\right).(23)$

The consensus variables of the PV microgrids are updated as

${\eta }_i^{ite+1}\left(t\right)={\eta }_i^{\mathit{ite}}\left(t\right)+{\epsilon }_i\mathrm{\Delta }d+{\displaystyle \sum _{j=1,i\ne j}^I}{z}_{i,j}\left(t\right)\left({\eta }_i^{\mathit{ite}}\left(t\right)-{\eta }_j^{\mathit{ite}}\left(t\right)\right),(24)$

where ite represents the number of consensus iterations. z_ij(t) is the element in the i-th row and j-th column of the communication matrix Z. Δd is the target deviation variable. ɛ_i is the step size correction coefficient for the PV microgrid i.

For each updated consensus variable ${\eta }_i^{ite+1}(t)$, the corresponding power of the PV microgrid may not meet the constraints in Eq. 14, so the consensus variable ${\eta }_i^{ite+1}(t)$ needs to be corrected as follows.

First, we calculate the output power of each PV microgrid and the output power of the energy storage devices in the PV microgrids as

$\begin{array}{l}\hfill \begin{array}{cc}{P}_i^{\text{pv}}\left(t\right)\hfill & =\frac{\sigma +c_{k_i\left(t\right)}-{\eta }_i^{ite+1}\left(t\right)}{2{\delta }_i^{\mathrm{p}\mathrm{v},\mathrm{e}\mathrm{s}}+2{\alpha }_i^{\mathrm{p}\mathrm{v}\mathrm{p}}+{\beta }_i^{\text{pvp}}},\hfill \\ P_i^{\text{pv,es}}\left(t\right)\hfill & =P_i^{\mathrm{p}\mathrm{v}}\left(t\right)-P_i^{\text{pv,total}}\left(t\right)+P_i^{\text{pv,load}}\left(t\right).\hfill \end{array}\end{array}(25)$

$P_i^{\text{pv,es}}(t)>0$ indicates that the PV energy storage system is discharging, while $P_i^{\text{pv,es}}(t)<0$ indicates that the PV energy storage system is charging.

Then, we consider the power constraints of each PV microgrid’s energy storage system based on Eq. 14. If the power exceeds the constraint boundaries, we adjust it to the nearest boundary and update the corresponding PV microgrid’s output power as

$\begin{array}{ll}{P}_i^{\text{pv,es}}\left(t\right)\hfill & =\left\{\begin{array}{c}\frac{\left[S_i\left(t\right)-S_i^{\mathrm{m}\mathrm{i}\mathrm{n}}\right]E_i^{\mathrm{m}\mathrm{a}\mathrm{x}}}{\mathrm{\Delta }t},P_i^{\text{pv,es}}\left(t\right)>\frac{\left[S_i\left(t\right)-S_i^{\mathrm{m}\mathrm{i}\mathrm{n}}\right]E_i^{\mathrm{m}\mathrm{a}\mathrm{x}}}{\mathrm{\Delta }t},\hfill \\ \frac{\left[S_i\left(t\right)-S_i^{\mathrm{m}\mathrm{a}\mathrm{x}}\right]E_i^{\mathrm{m}\mathrm{a}\mathrm{x}}}{\mathrm{\Delta }t},P_i^{\text{pv,es}}\left(t\right)<\frac{\left[S_i\left(t\right)-S_i^{\mathrm{m}\mathrm{a}\mathrm{x}}\right]E_i^{\mathrm{m}\mathrm{a}\mathrm{x}}}{\mathrm{\Delta }t},\hfill \\ P_i^{\text{pv,es}}\left(t\right),\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{s},\hfill \end{array}\right.\hfill \\ P_i^{\text{pv}}\left(t\right)\hfill & =P_i^{\text{pv,total}}\left(t\right)-P_i^{\text{pv,load}}\left(t\right)+P_i^{\text{pv,es}}\left(t\right).\hfill \end{array}(26)$

Finally, we take into account the output power constraints of PV microgrids based on Eq. 14. If the power exceeds the constraint boundaries, we adjust it to the nearest boundary and update the consensus variables as

$\begin{array}{ll}{P}_i^{\text{pv}}\left(t\right)\hfill & =\left\{\begin{array}{c}{P}_i^{\mathrm{p}\mathrm{v},\mathrm{m}\mathrm{a}\mathrm{x}}\left(t\right),P_i^{\text{pv}}\left(t\right)>P_i^{\mathrm{p}\mathrm{v},\mathrm{m}\mathrm{a}\mathrm{x}}\left(t\right),\hfill \\ P_i^{\mathrm{p}\mathrm{v},\min }\left(t\right),P_i^{\text{pv}}\left(t\right)<P_i^{\mathrm{p}\mathrm{v},\min }\left(t\right),\hfill \\ P_i^{\text{pv}}\left(t\right),\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{s},\hfill \end{array}\right.\hfill \\ {\eta }_i^{ite+1}\left(t\right)\hfill & =\sigma +c_{k_i\left(t\right)}-\left(2{\delta }_i^{\mathrm{p}\mathrm{v},\mathrm{e}\mathrm{s}}+2{\alpha }_i^{\mathrm{p}\mathrm{v}\mathrm{p}}+{\beta }_i^{\mathrm{p}\mathrm{v}\mathrm{p}}\right)P_i^{\text{pv}}\left(t\right).\hfill \end{array}(27)$

After updating all consensus variables, we update the target deviation variable Δd according to Eq. 23. Then, we check whether the consensus variables have converged. The convergence condition is given by

$\left\{\begin{array}{c}\frac{{\displaystyle \sum _{i=1}^I}{‖{\eta }_i^{ite+1}\left(t\right)-{\eta }_i^{\mathit{ite}}\left(t\right)‖}_2^2}{I}\le {\phi }_1,\hfill \\ \left|\mathrm{\Delta }d\right|\le {\phi }_2,\hfill \end{array}\right.(28)$

where the first term indicates the need for convergence of PV microgrid consensus variables and the second term indicates that the total output power of the PV microgrids can meet the power demand of the grid. φ₁ and φ₂ are convergence precisions of the consensus algorithm.

If the consensus variables converge, the active power output of each PV microgrid is obtained according to Eq. 25 and sent to the upper level for grid loss optimization. Otherwise, the consensus iterations continue until convergence is achieved.

The proposed algorithm does not depend on the form of PV cost function, which is scalable and can be applied to other non-convex cost functions. For all forms, we only need to take the partial derivative of the Lagrange function L(t) with respect to the PV microgrid output $P_i^{\text{pv}}(t)$ to obtain the consensus variable. The consensus variables derived from different forms of cost functions are different, but as long as there is a one-to-one correspondence between the consensus variables and the PV microgrid output, consensus optimization can be performed.

4.2 Second-order cone-based centralized dispatching of the distribution grid

The upper-level distribution grid model aims to minimize the weighted sum of grid loss and voltage deviation. The output power of each PV microgrid obtained from the lower-level optimization is incorporated into the upper-level optimal power flow model. This allows us to solve for the generator set outputs in the distribution grid that satisfy the power flow constraints. The solution steps for the upper-level distribution grid model are as follows.

1) The output power of each PV microgrid, obtained from the lower-level optimization, is substituted into the line parameters of the distribution grid.

2) The power balance constraints in Eq. 18 lead to non-convex non-linearity in the upper-level model. We employ second-order cone techniques to transform the upper-level optimization model into a convex feasible region second-order cone programming model.

First, there exists

$\left\{\begin{array}{c}{e}_n\left(t\right)e_m\left(t\right)+w_n\left(t\right)w_m\left(t\right)=\left|U_n\left(t\right)\right|\left|U_m\left(t\right)\right|\cos {\theta }_{nm}\left(t\right),\hfill \\ e_n\left(t\right)w_m\left(t\right)-e_m\left(t\right)w_n\left(t\right)=\left|U_n\left(t\right)\right|\left|U_m\left(t\right)\right|\sin {\theta }_{nm}\left(t\right),\hfill \\ {\left|U_n\left(t\right)\right|}^2=e_n^2\left(t\right)+w_n^2\left(t\right),\hfill \end{array}\right.(29)$

where e_n(t) and w_n(t) represent the real and imaginary parts of the voltage vector at node n. e_m(t) and w_m(t) represent the real and imaginary parts of the voltage vector at node m.

Then, we define intermediate variables s_nm, y_nn, and y_nm, which satisfy

$\left\{\begin{array}{c}{s}_{nm}\left(t\right)=e_n\left(t\right)w_m\left(t\right)-e_m\left(t\right)w_n\left(t\right),\hfill \\ y_{nn}\left(t\right)=e_n^2\left(t\right)+w_n^2\left(t\right),\hfill \\ y_{nm}\left(t\right)=e_n\left(t\right)e_m\left(t\right)+w_n\left(t\right)w_m\left(t\right),\hfill \\ y_{nm}^2\left(t\right)+s_{nm}^2\left(t\right)=y_{nn}\left(t\right)y_{nm}\left(t\right).\hfill \end{array}\right.(30)$

The active and reactive power flow balance constraints of the upper-level distribution grid can be transformed into

$\left\{\begin{array}{c}{P}_{\text{G},n}\left(t\right)+P_{\text{pur},n}\left(t\right)-P_{\text{L},n}\left(t\right)=\hfill \\ G_{nn}\left(t\right)y_{nn}\left(t\right)+{\displaystyle \sum _{m=1,m\ne n}^{N_{\text{bus}}}}\left[G_{nm}\left(t\right)y_{nm}\left(t\right)-B_{nm}\left(t\right)s_{nm}\left(t\right)\right],\hfill \\ Q_{\text{G},n}\left(t\right)+Q_{\text{pur},n}\left(t\right)-Q_{\text{L},n}\left(t\right)=\hfill \\ -B_{nn}\left(t\right)y_{nn}\left(t\right)+{\displaystyle \sum _{m=1,m\ne n}^{N_{\text{bus}}}}\left[-B_{nm}\left(t\right)y_{nm}\left(t\right)-G_{nm}\left(t\right)s_{nm}\left(t\right)\right],\hfill \end{array}\right.(31)$

simultaneously satisfying

$\left\{\begin{array}{c}{y}_{nm}\left(t\right)=y_{mn}\left(t\right),\hfill \\ s_{nm}\left(t\right)=-s_{mn}\left(t\right),\hfill \\ {U_n^{\min }}^2\left(t\right)\le y_{nn}\left(t\right)\le {U_n^{\max }}^2\left(t\right),\hfill \\ y_{nm}^2\left(t\right)+s_{nm}^2\left(t\right)=y_{nn}\left(t\right)y_{mm}\left(t\right),\hfill \\ y_{nm}^2\left(t\right)+s_{nm}^2\left(t\right)+{\left[\frac{y_{nn}\left(t\right)-s_{mm}\left(t\right)}{2}\right]}^2\le {\left[\frac{y_{nn}\left(t\right)+s_{mm}\left(t\right)}{2}\right]}^2.\hfill \end{array}\right.(32)$

3) We utilize the Gurobi solver to solve the upper-level optimization model and obtain the active power and reactive power outputs of the upper-level generator sets.

4.3 The iterative interaction process between the distribution grid and PV microgrid

Step 1. Based on the (ϑ − 1)-th iteration of the upper-level generator active power output $P_{\text{G},n}^{\vartheta -1}(t)$, the improved consensus algorithm is utilized to realize the distributed dispatching of PV microgrids. Then, output the active power output of the PV microgrid as $P_i^{\text{pv},\vartheta }(t)$.

Step 2. Based on the obtained active power output of the PV microgrid $P_i^{\text{pv},\vartheta }(t)$, the distribution grid utilizes the Gurobi solver to solve the optimization objective. It then outputs the active power output $P_{\text{G},n}^{\vartheta }(t)$ and reactive power output $G_{\text{G},n}^{\vartheta }(t)$ of the upper-level generator set.

Step 3. Steps 1, 2 constitute one iteration of the optimization process. After completing one iteration, check whether the power output of each PV microgrid and the active power output of each generator set in adjacent iterations satisfy the termination conditions, as shown as follows. If they do, the iteration process ends, and the power output $P_i^{\vartheta ,\mathrm{p}\mathrm{v}}(t)$ of the PV microgrid at this point is the final power output. At the same time, the active power output $P_{\text{G},n}^{\vartheta }(t)$ of the upper-level generator set corresponds to the optimal active power output for minimum grid loss. If not, we set ϑ = ϑ + 1 and return to Step 1 for the next iteration.

$\left\{\begin{array}{c}\frac{{\displaystyle \sum _{n=1}^{N_{\text{bus}}}}{‖P_{\text{G},n}^{\vartheta }\left(t\right)-P_{\text{G},n}^{\vartheta -1}\left(t\right)‖}_2^2}{N_{\text{bus}}}\le {\phi }_3,\hfill \\ \frac{{\displaystyle \sum _{i=1}^I}{‖P_i^{\text{pv},\vartheta }\left(t\right)-P_i^{\text{pv},\vartheta -1}\left(t\right)‖}_2^2}{I}\le {\phi }_4,\hfill \end{array}\right.(33)$

where φ₃ and φ₄ represent the precision criteria for terminating the iteration between the distribution grid and PV microgrids.

5 Case results and analysis

To validate the feasibility of the proposed model and solution algorithm in this paper, a simulation study is conducted using the modified IEEE-33 node distribution grid system shown in Figure 2 as the research case (Fu et al., 2020; Ni and Zheng, 2021).

FIGURE 2

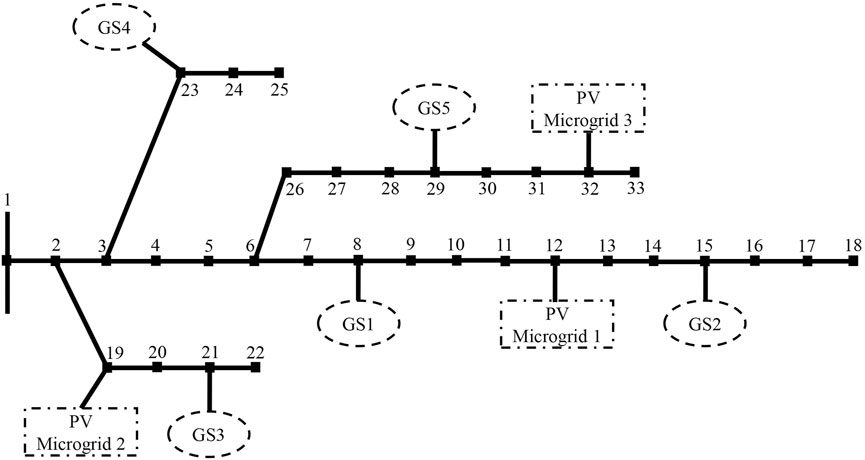
FIGURE 2. Simulation scenario of the proposed algorithm based on the IEEE-33 node distribution grid system.

As shown in Figure 2, the distribution grid consists of a total of five generator sets, namely, GS1–GS5, connected to nodes 8, 15, 21, 23, and 29, respectively. Additionally, there are three PV microgrids, designated as PV Microgrid 1–PV Microgrid 3, connected to this distribution grid with corresponding nodes 12, 19, and 23.

5.1 The parameter settings for simulation

This paper defines one time slot as 1 h, and the price-based demand response load shifting occurs over a total of T = 24 time slots. For example, the 3rd time slot corresponds to 3:00–4:00. The load consumption is divided into three periods: peak, off-peak, and valley. The peak period includes time slots 11–12 and 16–21, the off-peak period includes time slots 8–10 and 13–15, and the valley period includes time slots 1–7 and 22–24. Based on this, the sets of time slots for each period are defined as follows: peak time slots set V₁ = {11, 12, 16, 17, 18, 19, 20, 21}, off-peak time slots set V₂ = {8, 9, 10, 13, 14, 15}, and valley time slots set V₃ = {1, 2, 3, 4, 5, 6, 7, 22, 23, 24}. The price-based demand response price elasticity coefficients are given in Table 1, and the cross-price elasticity coefficients are presented in Table 2 (Shailendra and Bhim, 2019).

TABLE 1

TABLE 1. Self-elasticity coefficients.

TABLE 2

TABLE 2. Cross-elasticity coefficients.

In this paper, the PV microgrids and distribution grid are considered an interconnected system capable of directly achieving energy mutual assistance. The capacity and parameters of each PV microgrid are shown in Table 3 (Valibeygi Amri and de, 2021).

TABLE 3

TABLE 3. Capacity and parameters of the PV microgrids.

5.2 Simulation result

Taking the PV microgrid consensus iteration at a certain moment as an example, Figure 3 reflects the consensus iteration error of the PV microgrid versus the consensus iteration number. η^ave represents the consensus iteration error, defined as the average norm of the difference between adjacent iterations of all consensus variables in the PV microgrid. η^ave is calculated as

${\eta }^{\text{ave}}=\frac{{\displaystyle \sum _{i=1}^I}{‖{\eta }_i^{ite+1}\left(t\right)-{\eta }_i^{\mathit{ite}}\left(t\right)‖}_2^2}{I}.(34)$

FIGURE 3

FIGURE 3. Consensus iteration error of the PV microgrid.

According to Eq. 28, the consensus iteration terminates only when both the consensus iteration error η^ave and the target deviation variable Δd satisfy the convergence accuracy of the consensus algorithm. From the figure, it can be observed that Δd and η^ave satisfy the convergence accuracy of the consensus algorithm in the 8th and 13th iterations, respectively. Therefore, the consensus iteration terminates in the 13th iteration.

Figures 4, 5 show the output power of the PV microgrid versus the consensus iteration number for the proposed algorithm and traditional consensus algorithm, respectively. From the figure, it can be observed that the output power of the PV microgrid for the proposed algorithm and traditional consensus algorithm reaches convergence in the 13th and 19th consensus iteration numbers, respectively. It effectively proves the effectiveness of the proposed algorithm in accelerating consensus convergence.

FIGURE 4

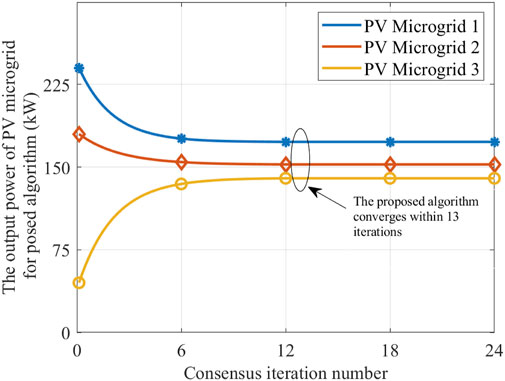
FIGURE 4. Output power of the PV microgrid versus the consensus iteration number of the proposed algorithm.

FIGURE 5

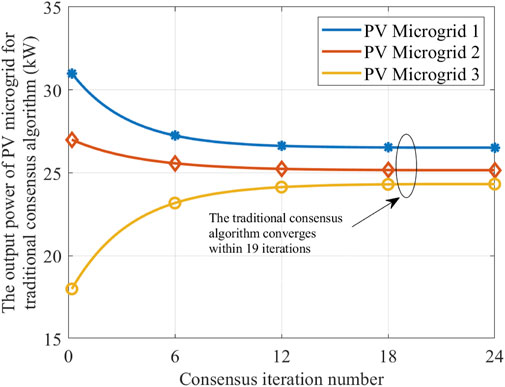
FIGURE 5. Output power of the PV microgrid versus the consensus iteration number of the traditional consensus algorithm.

Figure 6 reflects the iteration error of bilevel optimization versus the iteration number of bilevel optimization ϑ. $P_{\text{G}}^{\vartheta ,\mathrm{a}\mathrm{v}\mathrm{e}}$ represents the upper-level iteration error of the active power outputs of the generator sets, defined as the average norm of the difference between adjacent iterations of the active power outputs of all generator sets. P^pv,ϑ,ave represents the lower-level iteration error of the outputs of the PV microgrids, defined as the average norm of the difference between adjacent iterations of the outputs of all PV microgrids. $P_{\text{G}}^{\vartheta ,\mathrm{a}\mathrm{v}\mathrm{e}}$ and P^pv,ϑ,ave are calculated as

$\left\{\begin{array}{c}{P}_{\text{G}}^{\vartheta ,\mathrm{a}\mathrm{v}\mathrm{e}}=\frac{{\displaystyle \sum _{n=1}^{N_{\text{bus}}}}{‖P_{\text{G},n}^{\vartheta }\left(t\right)-P_{\text{G},n}^{\vartheta -1}\left(t\right)‖}_2^2}{N_{\text{bus}}},\hfill \\ P^{\text{pv},\vartheta ,\mathrm{a}\mathrm{v}\mathrm{e}}=\frac{{\displaystyle \sum _{i=1}^I}{‖P_i^{\text{pv},\vartheta }\left(t\right)-P_i^{\text{pv},\vartheta -1}\left(t\right)‖}_2^2}{I}.\hfill \end{array}\right.(35)$

FIGURE 6

FIGURE 6. Iteration error of bilevel optimization.

According to Eq. 35, the iteration between the distribution grid and the PV microgrids terminates only when both the iteration error of the active power output of the generator set $P_{\text{G}}^{\vartheta ,\mathrm{a}\mathrm{v}\mathrm{e}}$ and the iteration error of the output of the PV microgrid P^pv,ϑ,ave satisfy the termination condition accuracy. From the figure, it can be observed that the iteration optimization between the distribution grid and the PV microgrid satisfies the termination condition in the 22nd interaction.

Figures 7A, B show the voltage of the IEEE-33 node distribution grid system before and after bilevel optimization, respectively. From the figures, it can be observed that the voltage fluctuations of each node are smaller after optimization compared to before optimization. This is because the proposed algorithm solves the distribution grid optimization problem by minimizing the weighted sum of grid loss and voltage deviation as the objective. It effectively reduces the voltage fluctuations at the node.

FIGURE 7

FIGURE 7. Voltage fluctuation: (A) before bilevel optimization and (B) after bilevel optimization.

Figure 8 shows the voltage deviation and grid loss versus the scaling factor for the proposed algorithm. As the scaling factor increases, the voltage deviation gradually decreases and the grid loss gradually increases. For example, the grid loss increases by 18.33% and the voltage deviation decreases by 10.21% when the scaling factor increases from 4 to 6. This is because the larger the scaling factor, the more attention the proposed algorithm pays in optimizing the voltage deviation, thus ignoring the grid loss.

FIGURE 8

FIGURE 8. Voltage deviation and grid loss versus the scaling factor of the proposed algorithm.

5.3 Algorithm comparison

To better validate the effectiveness of the proposed second-order cone and improved consensus algorithm-based hybrid bilevel optimization algorithm for the interaction between the distribution grid and PV microgrids, two comparative algorithms are designed for verification in this paper: 1) iterative interaction optimization algorithm between the distribution grid and PV microgrid based on particle swarm optimization-Gurobi (IIOA-PSOG) (Silva de Souza et al., 2017; Li et al., 2016) and 2) iterative interaction optimization algorithm between the distribution grid and PV microgrid based on traditional consensus-Gurobi (IIOA-TCG) Fan et al. (2020); Burgos-Mellado et al. (2020).

When the two comparative algorithms are applied to the bilevel optimization between the distribution grid and PV microgrid, the upper-level distribution grid optimization problem is solved using the same approach as the proposed algorithm, utilizing the Gurobi solver. The lower-level problem, on the other hand, is solved using particle swarm optimization (PSO) and traditional consensus algorithms, respectively, to find the optimal power output of the PV microgrid.

Taking 4:00–5:00 as an example, Figure 9A shows the weighted sum of grid loss and voltage deviation versus the iteration number for the three algorithms. From the figure, it can be observed that the proposed algorithm converges the fastest. When convergence is achieved, the optimization results of the proposed algorithm are 19.23% and 8.71% lower compared to IIOA-PSOG and IIOA-TCG algorithms, respectively. This is because the proposed algorithm incorporates a target deviation variable in the consensus optimization process, which measures the deviation between the sum of the generator and PV microgrid outputs and the grid demand at the current time. Additionally, the proposed algorithm takes into account the differentiated characteristics of PV microgrids during the lower-level consensus iteration process, effectively reducing the convergence time of the consensus iteration, thereby accelerating the iteration efficiency of hybrid bilevel optimization. This effectively improves the efficiency of the iteration optimization, mitigates voltage deviations between nodes, and consequently reduces the grid loss in the distribution grid.

FIGURE 9

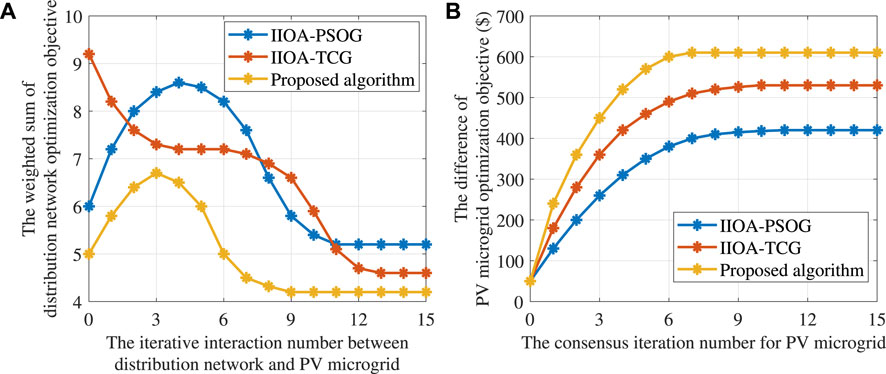
FIGURE 9. (A) Weighted sum of grid loss and voltage deviation versus the iteration number and (B) difference between electricity sale revenue and dispatching cost versus the consensus iteration number.

Taking 8:00-9:00 as an example, Figure 9B shows the difference between electricity sale revenue and dispatching cost versus the consensus iteration number for the three algorithms. From the figure, it can be observed that the proposed algorithm converges the fastest. When convergence is achieved, the optimization results of the proposed algorithm increase by 45.24% and 15.09% compared to IIOA-PSOG and IIOA-TCG algorithms, respectively. This is because the proposed algorithm incorporates communication weights between adjacent PV microgrids based on their output capabilities, which effectively accelerates the convergence speed of the consensus iteration. Additionally, the proposed algorithm introduces a target deviation variable in the consensus optimization process, effectively exploiting the potential of PV microgrids to participate in grid demand response. As a result, the revenue from electricity sales of the PV microgrids is enhanced.

Figure 10 shows the weighted sum of grid loss and voltage deviation versus the time slot for the three algorithms. From the figure, it can be observed that during the low load period, all three algorithms yield lower numerical results in terms of the weighted sum. Conversely, during the high load period, the numerical results for the weighted sum are significantly improved. This observation aligns with the actual operation of the grid. Furthermore, the proposed algorithm consistently yields the lowest numerical results for the weighted sum of grid loss and voltage deviation in the context of hybrid bilevel optimization. Taking 12:00–13:00 as an example, the proposed algorithm reduces numerical results for the weighted sum of grid loss and voltage deviation by 23.03% and 13.01% compared to IIOA-PSOG and IIOA-TCG, respectively, thereby validating the effectiveness of applying the proposed algorithm to the hybrid bilevel optimization based interaction between the distribution grid and PV microgrids.

FIGURE 10

FIGURE 10. Weighted sum of grid loss and voltage deviation versus the time slot.

Figure 11 shows the difference between electricity sale revenue and dispatching cost versus the time slot for the three algorithms. Under the influence of PV output, the three algorithms show a trend of first increasing and then decreasing. From the figure, it can be observed that the proposed algorithm consistently yields the highest numerical results for the difference between electricity sale revenue and dispatching cost. Taking 12:00-13:00 as an example, the proposed algorithm improves numerical results for the difference between electricity sale revenue and dispatching cost by 49.17% and 12.58% compared to IIOA-PSOG and IIOA-TCG, respectively, thereby validating the effectiveness of applying the proposed algorithm to the hybrid bilevel optimization-based interaction between the distribution grid and PV microgrids. It demonstrates that the proposed algorithm can effectively enhance the revenue from the participation of the PV microgrid in demand response.

FIGURE 11

FIGURE 11. Difference between electricity sale revenue and dispatching cost versus the time slot.

Figure 12 shows the algorithm runtime versus the time slot for the three algorithms. From the figure, it can be observed that the proposed algorithm consistently yields the lowest numerical results for the algorithm runtime. Taking 12:00-13:00 as an example, the proposed algorithm reduces numerical results for the algorithm runtime by 31.82% and 24.66% compared to IIOA-PSOG and IIOA-TCG, respectively.

FIGURE 12

FIGURE 12. Algorithm runtime versus the time slot.

6 Conclusion

In this paper, we proposed a second-order cone and improved consensus algorithm-based hybrid bilevel optimization algorithm for the interaction between the distribution grid and PV microgrids. In the lower level, considering the differentiated characteristics of PV microgrids, the communication weights between the adjacent PV microgrids are determined based on the ratio of their output capabilities in the consensus iteration process. The PV microgrids perform distributed optimization based on an improved consensus algorithm for utilizing the active power output of the generator set, and the output power of each PV microgrid is determined and injected into the upper-level distribution grid. In the upper level, the injected power from the PV microgrids is used as inputs for the centralized optimization objective, which is solved using the Gurobi solver. The outputs include the active power and reactive power of the generating units. Simulation results show that the proposed algorithm can achieve the hybrid bilevel optimization-based interaction between the distribution grid and PV microgrids with differentiated demand response, and effectively reduce the dispatching cost of PV microgrids and speed up the convergence of consensus iteration. Compared with IIOA-PSOG and IIOA-TCG, the difference between electricity sale revenue and dispatching cost of the proposed algorithm is increased by 45.24% and 15.09%, respectively, and the weighted sum of grid loss and voltage deviation is reduced by 23.03% and 13.01%, respectively. In the future, we will further study the interaction optimization of the PV microgrids and distribution grid considering energy storage sharing of PV microgrids.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

ZS: conceptualization, data curation, formal analysis, investigation, methodology, writing – original draft, and writing – review and editing. CL: conceptualization, methodology, writing – original draft, and writing – review and editing. RY, CW, LL, ZL, YL, and ZZ: writing – review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Science and Technology Project of State Grid Shandong Electric Power Company (Key Technical Research and Application of Real-time Data Sharing Capability Construction for Large-scale Power Grid Nodes, 520608230007).

Conflict of interest

Author ZS was employed by State Grid Shandong Electric Power Company. CL, CW, LL, YL, and ZZ were employed by State Grid Shandong Dezhou Power Supply Company. RY was employed by State Grid Shandong Pingyuan County Power Supply Company. ZL was employed by State Grid Shandong Yucheng Power Supply Company.

The authors declare that this study received funding from Science and Technology Project of State Grid Shandong Electric Power Company. The funder had the following involvement in the study: study design, collection, analysis, interpretation of data, the writing of this article, and the decision to submit it for publication.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abu-elzait, S., and Parkin, R. (2019). “The effect of dispatch strategy on maintaining the economic viability of PV-based microgrids,” in 2019 IEEE 46th photovoltaic specialists conference (PVSC), 1203–1205. doi:10.1109/PVSC40753.2019.8980548

CrossRef Full Text | Google Scholar

Burgos-Mellado, C., Llanos, J. J., Cárdenas, R., Sáez, D., Olivares, D. E., Sumner, M., et al. (2020). Distributed control strategy based on a consensus algorithm and on the conservative power theory for imbalance and harmonic sharing in 4-wire microgrids. IEEE Trans. Smart Grid 11, 1604–1619. doi:10.1109/TSG.2019.2941117

CrossRef Full Text | Google Scholar

Byun, J., Hong, I., Kang, B., and Park, S. (2011). A smart energy distribution and management system for renewable energy distribution and context-aware services based on user patterns and load forecasting. IEEE Trans. Consumer Electron. 57, 436–444. doi:10.1109/TCE.2011.5955177

CrossRef Full Text | Google Scholar

Chanda, S., and Srivastava, A. K. (2016). Defining and enabling resiliency of electric distribution systems with multiple microgrids. IEEE Trans. Smart Grid 7, 2859–2868. doi:10.1109/TSG.2016.2561303

CrossRef Full Text | Google Scholar

Chen, J., Li, K., Wang, H., Yan, Y., Jiang, C., and Zhang, C. (2021). “Distributed collaborative optimization operation of micro energy grid based on consensus theory,” in 2021 IEEE/IAS industrial and commercial power system asia (I&CPS asia), 299–304. doi:10.1109/ICPSAsia52756.2021.9621438

CrossRef Full Text | Google Scholar

Cui, L., Wang, C., Li, Y., Li, F., and Guo, X. (2022). “Assessment research on accommodation capacity of renewable energy in distribution network,” in 2022 37th youth academic annual conference of Chinese association of automation (YAC), 341–345. doi:10.1109/YAC57282.2022.10023587

CrossRef Full Text | Google Scholar

Eslaminia, N., and Mashhadi, H. R. (2022). “Incentive-based demand response economic model for peak shaving considering load serving entity profit maximization,” in 2022 30th international conference on electrical engineering (ICEE), 144–149. doi:10.1109/ICEE55646.2022.9827315

CrossRef Full Text | Google Scholar

Fan, B., Guo, S., Peng, J., Yang, Q., Liu, W., and Liu, L. (2020). A consensus-based algorithm for power sharing and voltage regulation in DC microgrids. IEEE Trans. Industrial Inf. 16, 3987–3996. doi:10.1109/TII.2019.2941268

CrossRef Full Text | Google Scholar

Fu, J., Lin, L., Li, Y., Pan, J., and Yang, B. (2020). “Distribution robust active and reactive power optimization in distribution network with PV and energy storage system,” in 2020 international conference on smart grids and energy systems (SGES), 579–583. doi:10.1109/SGES51519.2020.00108

CrossRef Full Text | Google Scholar

Guan, Y., Wei, B., Guerrero, J. M., Vasquez, J. C., and Gui, Y. (2022). An overview of the operation architectures and energy management system for multiple microgrid clusters. iEnergy 1, 306–314. doi:10.23919/IEN.2022.0035

CrossRef Full Text | Google Scholar

Hu, J., Zhang, K., Wang, G., Gen, X., Jia, Z., Lei, S., et al. (2020). “Power proportional sharing and SoC equalization strategy for distributed energy storage units based on distributed consensus algorithm,” in 2020 13th international conference on intelligent computation Technology and automation (ICICTA), 712–716. doi:10.1109/ICICTA51737.2020.00156

CrossRef Full Text | Google Scholar

Hua, X., Hou, B., Zheng, Z., Yu, Y., Zheng, H., He, P., et al. (2022). “Optimal scheduling of energy storage systems considering the two-layer interaction of distribution networks,” in 2022 IEEE symposium series on computational intelligence (SSCI), 1380–1385.

CrossRef Full Text | Google Scholar

Hui, H., Bao, M., Ding, Y., and Song, Y. (2022). Exploring the integrated flexible region of distributed multi-energy systems with process industry. Appl. Energy 311.

CrossRef Full Text | Google Scholar

Kou, W., and Park, S.-Y. (2023). A distributed energy management approach for smart campus demand response. IEEE J. Emerg. Sel. Top. Industrial Electron. 4, 339–347. doi:10.1109/JESTIE.2022.3225755

CrossRef Full Text | Google Scholar

Li, H., Ren, Z., Trivedi, A., Srinivasan, D., and Liu, P. (2023a). Optimal planning of dual-zero microgrid on an island towards net-zero carbon emission. IEEE Trans. Smart Grid 1–1. doi:10.1109/TSG.2023.3299639

CrossRef Full Text | Google Scholar

Li, H., Ren, Z., Trivedi, A., Verma, P. P., Srinivasan, D., and Li, W. (2022). A noncooperative game-based approach for microgrid planning considering existing interconnected and clustered microgrids on an island. IEEE Trans. Sustain. Energy 13, 2064–2078. doi:10.1109/TSTE.20223180842

CrossRef Full Text | Google Scholar

Li, L., Bai, X., Guo, Y., Zhang, J., Chen, C., Yi, Y., et al. (2021). “Distributed optimal dispatching of AC/DC hybrid microgrid based on consensus algorithm,” in 2021 6th asia conference on power and electrical engineering (ACPEE), 1398–1402. doi:10.1109/ACPEE51499.2021.9436903

CrossRef Full Text | Google Scholar

Li, P., Xu, D., Zhou, Z., Lee, W.-J., and Zhao, B. (2016). Stochastic optimal operation of microgrid based on chaotic binary particle swarm optimization. IEEE Trans. Smart Grid 7, 66–73. doi:10.1109/TSG.2015.2431072

CrossRef Full Text | Google Scholar

Li, Z., Wu, L., Xu, Y., Wang, L., and Yang, N. (2023b). Distributed tri-layer risk-averse stochastic game approach for energy trading among multi-energy microgrids. Appl. Energy 331, 120282. doi:10.1016/j.apenergy.2022.120282

CrossRef Full Text | Google Scholar

Li, Z., Xu, Y., Fang, S., Zheng, X., and Feng, X. (2020). Robust coordination of a hybrid AC/DC multi-energy ship microgrid with flexible voyage and thermal loads. IEEE Trans. Smart Grid 11, 2782–2793. doi:10.1109/TSG.2020.2964831

CrossRef Full Text | Google Scholar

Li, Z., Xu, Y., Wang, P., and Xiao, G. (2023c). Coordinated preparation and recovery of a post-disaster multi-energy distribution system considering thermal inertia and diverse uncertainties. Appl. Energy 336, 120736. doi:10.1016/j.apenergy.2023.120736

CrossRef Full Text | Google Scholar

Li, Z., Xu, Y., Wang, P., and Xiao, G. (2023d). Restoration of multi energy distribution systems with joint district network recon figuration by a distributed stochastic programming approach. IEEE Trans. Smart Grid. 1–1. doi:10.1109/TSG.2023.3317780

CrossRef Full Text | Google Scholar

Liao, H., Zhou, Z., Jia, Z., Shu, Y., Tariq, M., Rodriguez, J., et al. (2023). Ultra-low AoI digital twin-assisted resource allocation for multi-mode power IoT in distribution grid energy management. IEEE J. Sel. Areas Commun. 1–1. doi:10.1109/JSAC.2023.3310101

CrossRef Full Text | Google Scholar

Liu, J., Yu, S. S., Hu, H., Zhao, J., and Trinh, H. M. (2023). Demand-side regulation provision of virtual power plants consisting of interconnected microgrids through double-stage double-layer optimization. IEEE Trans. Smart Grid 14, 1946–1957. doi:10.1109/TSG.2022.3203466

CrossRef Full Text | Google Scholar

Liu, Y., Guo, L., Wang, C., and Li, X. (2017). “Strategic bidding optimization of microgrids in electricity distribution market,” in 2017 IEEE power & energy society general meeting, 1–5. doi:10.1109/PESGM.2017.8273800

CrossRef Full Text | Google Scholar

Ma, S., Liu, H., Wang, N., Xie, H., Huang, L., and Li, H. (2022). “Deep reinforcement learning for an incentive-based demand response model,” in 2022 IEEE 6th conference on energy internet and energy system integration (EI2), 246–250. doi:10.1109/EI256261.2022.10117409

CrossRef Full Text | Google Scholar

Ni, S., and Zheng, J. (2021). “Generator-grid-load-storage coordinated optimal dispatch considering CO2 emission in active distribution network,” in 2021 IEEE 5th conference on energy internet and energy system integration (EI2), 1838–1843. doi:10.1109/EI252483.2021.9713594

CrossRef Full Text | Google Scholar

Pawakul, S., and Srirattanawichaikul, W. (2020). “Price-based demand response strategy for coordinated PV distributed generation and demand side management in distribution network,” in 2020 2nd international conference on smart power & internet energy systems (SPIES), 492–497. doi:10.1109/SPIES48661.2020.9243154

CrossRef Full Text | Google Scholar

Shailendra, K., and Bhim, S. (2019). Self-normalized-estimator-based control for power management in residential grid synchronized PV-BES microgrid. IEEE Trans. Industrial Inf. 15, 4764–4774. doi:10.1109/TII.2019.2907750

CrossRef Full Text | Google Scholar

Si, J., Bao, G., Liu, H., Sun, M., Zhou, L., Tan, M., et al. (2022). “A bi-level optimization model for independent system operator considering price-based demand response,” in 2022 IEEE/IAS industrial and commercial power system asia (I&CPS Asia), 451–457. doi:10.1109/ICPSAsia55496.2022.9949669

CrossRef Full Text | Google Scholar

Silva de Souza, J., Percy Molina, Y., Silva de Araujo, C., Pereira de Farias, W., and Santos de Araujo, I. (2017). Modified particle swarm optimization algorithm for sizing photovoltaic system. IEEE Lat. Am. Trans. 15, 283–289. doi:10.1109/TLA.2017.7854624

CrossRef Full Text | Google Scholar

Valibeygi Amri, K. S. A. R., and de, C. R. (2021). Predictive hierarchical control of power flow in large-scale PV microgrids with energy storage. IEEE Trans. Sustain. Energy 12, 412–419. doi:10.1109/TSTE.2020.3001260

CrossRef Full Text | Google Scholar

Wang, S., Hui, H., Ding, Y., Ye, C., and Zheng, M. (2023). Operational reliability evaluation of urban multi-energy systems with equivalent energy storage. IEEE Trans. Industry Appl. 59, 2186–2201.

CrossRef Full Text | Google Scholar

Xiao, S., Shadmand, M. B., and Balog, R. S. (2017). “Model predictive control of multi-string PV systems with battery back-up in a community dc microgrid,” in 2017 IEEE applied power electronics conference and exposition (APEC), 1284–1290. doi:10.1109/APEC.2017.7930861

CrossRef Full Text | Google Scholar

Yan, X., and Li, R. (2020). Flexible coordination optimization scheduling of active distribution network with smart load. IEEE Access 8, 59145–59157. doi:10.1109/ACCESS.2020.2982692

CrossRef Full Text | Google Scholar

Yu, J., Jiao, Y., Wang, X., and Ni, M. (2015). “Bi-level distributed optimal dispatch of micro gird clusters based on mutual communication,” in 2015 5th international conference on electric utility deregulation and restructuring and power technologies (DRPT), 2480–2485. doi:10.1109/DRPT.2015.7432663

CrossRef Full Text | Google Scholar

Zhai, J., Wang, S., Guo, L., Jiang, Y., Kang, Z., and Jones, C. N. (2022). Data-driven distributionally robust joint chance-constrained energy management for multi-energy microgrid. Appl. Energy 326, 119939.

CrossRef Full Text | Google Scholar

Zhang, H., Yue, D., Dou, C., Li, K., and Xie, X. (2021). Event-triggered multiagent optimization for two-layered model of hybrid energy system with price bidding-based demand response. IEEE Trans. Cybern. 51, 2068–2079. doi:10.1109/TCYB.2019.2931706

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, J., Yang, J., Xiao, Q., Wang, J., Li, D., Jin, X., et al. (2023a). “Bi-level energy management strategy for microgrid cluster considering multi-agent game with incomplete information and source-load uncertainty,” in 2023 8th asia conference on power and electrical engineering (ACPEE), 1791–1796. doi:10.1109/ACPEE56931.2023.10135843

CrossRef Full Text | Google Scholar

Zhang, X., Wang, Z., Liao, H., Zhou, Z., Ma, X., Yin, X., et al. (2023b). Optimal capacity planning and operation of shared energy storage system for large-scale photovoltaic integrated 5G base stations. Int. J. Electr. POWER & ENERGY Syst. 147. doi:10.1016/j.ijepes.2022.108816

CrossRef Full Text | Google Scholar

Zhao, J., and Xu, Z. (2017). Ramp-limited optimal dispatch strategy for PV-embedded microgrid. IEEE Trans. Power Syst. 32, 4155–4157. doi:10.1109/TPWRS.2017.2670920

CrossRef Full Text | Google Scholar

Zhou, Z., Sun, C., Shi, R., Chang, Z., Zhou, S., and Li, Y. (2017). Robust energy scheduling in vehicle-to-grid networks. IEEE Netw. 31, 30–37. doi:10.1109/MNET.2017.1600220NM

CrossRef Full Text | Google Scholar

Zhou, Z., Wang, B., Dong, M., and Ota, K. (2020). Secure and efficient vehicle-to-grid energy trading in cyber physical systems: integration of blockchain and edge computing. IEEE Trans. Syst. Man, Cybern. Syst. 50, 43–57. doi:10.1109/TSMC.2019.2896323

CrossRef Full Text | Google Scholar

Zhu, X., Han, H., Gao, S., Shi, Q., Cui, H., and Zu, G. (2018). A multi-stage optimization approach for active distribution network scheduling considering coordinated electrical vehicle charging strategy. IEEE Access 6, 50117–50130.

CrossRef Full Text | Google Scholar