Recent advances in the applications of machine learning methods for heat exchanger modeling—a review

1 Introduction

A heat exchanger is a device that facilitates heat transfer between fluids at different temperatures. It is widely employed in applications such as air-conditioning, refrigeration, power plants, oil refineries, petrochemical plants, natural-gas processing, chemical plants, sewage treatment, and many others (Hall, 2012; Singh et al., 2022). Theoretical analysis, analytical models, experimental methods, and numerical methods were conventionally applied to study the heat transfer and fluid flow processes within the heat exchangers (Du et al., 2023). The analytical models generally involve several assumptions in the derivation of relevant equations and formulae. The process of heat transfer can be evaluated through classical methods, such as the logarithmic mean enthalpy difference (LMHD), the logarithmic mean temperature difference (LMTD), ε–NTU, etc. (Hassan et al., 2016). However, these techniques are generally based on certain assumptions and conditions, such as constant physical properties, steady-state operation, negligible wall heat conduction, uniform distribution of flow properties, and a consistent air fluid temperature along the fin height.

For numerical modeling of heat exchangers, discretization of the refrigerant flow field and of the governing equations is required (Prithiviraj and Andrews, 1998). To achieve detailed analysis in computational solutions, one might consider employing advanced numerical techniques such as the Finite Volume Method (FVM) or the Finite Element Method (FEM). It is essential to achieve a balance of heat and mass in each cell (Moukalled et al., 2016). Computational Fluid Dynamics (CFD) can be a useful tool in designing, troubleshooting, and optimizing heat exchanger systems (Bhutta et al., 2012). It transforms the integral and differential terms in the governing fluid mechanics equations into discrete algebraic forms, thereby generating a system of algebraic equations. These discrete equations are then solved via a computer to obtain numerical solutions at specific time/space points. Nonetheless, numerical methods like CFD often require significant computational resources (Thibault and Grandjean, 1991; Yang, 2008).

In bridging the gap between computational efficiency and accuracy, several studies on machine learning methods for heat exchanger analysis have been developed to predict the performance of heat exchangers. Some representative machine learning methods recently used to analyze heat exchangers include Artificial Neural Networks (ANN), Support Vector Machine (SVM), Tree models, etc., which were shown to generate satisfactory results (Patil et al., 2017; Zhang et al., 2019; Ahmadi et al., 2021; Wang and Wang, 2021; Ewim et al., 2021; Fawaz et al., 2022). An analysis of the number of papers in this field clearly shows a significantly growing trend in recent years, as illustrated in Figure 1.

FIGURE 1

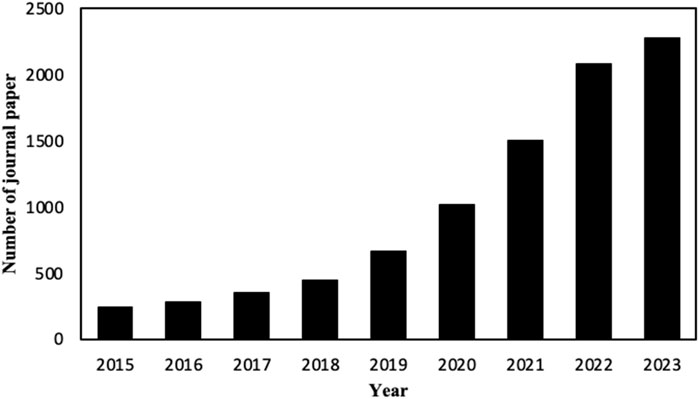
FIGURE 1. Numbers of publications associated with heat exchangers and machine learning from 2015 till September 2023 (based on data from ScienceDirect).

In this review, we mainly focus on the review of machine learning models for air-cooled heat exchangers (finned tube heat exchangers, microchannel heat exchangers, etc.) in the field of refrigeration and air-conditioning. The three main objectives of this paper are: 1) to summarize the studies on machine learning methods related to heat exchanger thermal analysis over the last 8 years; 2) to compare different machine learning methods employed in heat exchanger thermal analysis 3) to point out the limitations and emerging applications of machine learning in heat exchanger thermal analysis. The organization of this paper consists of the following five sections: Section 2 summarizes and classifies the machine learning methods. Section 3 summarizes applications of machine learning methods for modeling heat exchangers in recent years. Sections 4, 5 discuss the limitations of ANN modeling for heat exchanger analysis and future trends in this area, respectively.

2 Introduction to machine learning models

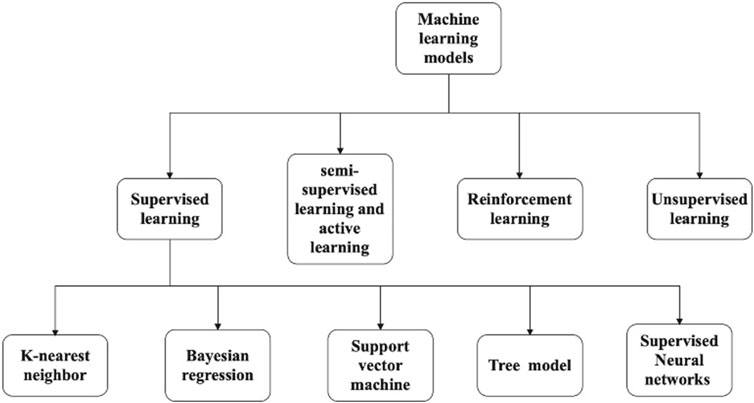
As illustrated in Figure 2, the machine learning approaches to modeling heat exchangers reviewed in this paper include Random Vector Functional Link Network (RVFL), Support Vector Machine (SVM), K-Nearest Neighbor (KNN), Gaussian Process Regression (GPR), Sequential Minimal Optimization (SMO), Radial Basis Function (RBF), Hybrid Radial Basis Function (HRBF), Least Square Fitting Method (LSFM), Artificial Neural Networks (ANN), Random Forest, AdaBoost, Extreme Gradient Boosting (XGBoost), LightGBM, Gradient Boosting Tree (GBT) and Correlated-Informed Neural Networks (CoINN). The following section of the paper focuses on the classifications of the various methods.

FIGURE 2

FIGURE 2. The classification of machine learning models.

2.1 Classification of machine learning methods

Machine learning methods were introduced to predict or regress the performance indicators of heat exchangers, such as the Nusselt number ($Nu$), the Heat Transfer Coefficient ($HTC$), the pressure drop ($\Delta P$), etc. Based on the learning approaches, machine learning categories generally include supervised learning, unsupervised learning, and reinforcement learning. Semi-supervised learning and active learning were also employed in studies as a machine learning category, as shown in Figure 2.

In heat exchanger applications, machine learning techniques primarily use supervised learning, which involves developing predictive models using labeled data. Labeled data establishes a connection between input and output, enabling the prediction model to generate corresponding outputs for specific inputs. The essence of supervised learning lies in understanding the statistical principles that govern the mapping of inputs to outputs (Cunningham et al., 2008). Unsupervised learning is a machine learning approach in which predictive models are developed without relying on labeled data or a clear purpose (Celebi and Aydin, 2016).

Reinforcement learning refers to learning optimal behavior strategies by an intelligent system in continuous interaction with the environment (Wiering and Van Otterlo, 2012). For instance, Keramati, Hamdullahpur, and Barzegari introduced deep reinforcement learning for heat exchanger shape optimization (Keramati, Hamdullahpur, and Barzegari 2022).

Semi-supervised learning refers to the learning prediction considering both labeled data sets and unlabeled data (Zhu and Goldberg, 2009). There is typically a small amount of labeled data and a large amount of unlabeled data because constructing labeled data often requires labor and high cost, and the collection of unlabeled data does not require much cost. This approach aims to use the information in unlabeled data to assist in labeling data for supervised learning and achieve enhanced learning results at a lower cost (Zhu, 2005). Active learning refers to a specialized training approach where the model actively selects the data it wants to learn from. Unlike traditional machine learning methods where all training data is provided upfront, active learning allows the model to selectively acquire new labeled data during its learning process. As a result, semi-supervised learning and active learning are closer to supervised learning. The differences between active learning and semi-supervised learning are: In active learning, the algorithm selectively picks the most informative instances for manual annotation, aiming to enhance model accuracy while minimizing labeling workload. In contrast, in semi-supervised learning, the emphasis is not on actively selecting instances. Instead, it leverages a combination of labeled and unlabeled data to enhance model generalization and performance through the integration of these data sources. Chen et al. (Chen et al., 2021) introduced a hybrid modeling method combining the mechanism with semi-supervised learning for temperature prediction in a roller hearth kiln, which implies the possibility of being employed in heat transfer.

2.2 Introduction of the various machine learning methods

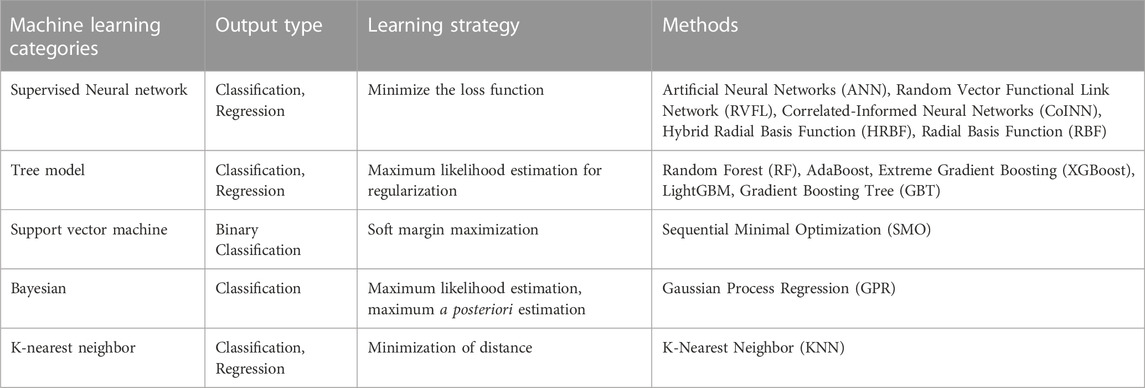
As shown in Table 1, the classification of the machine learning methods considered here is the following:

• Neural networks refer to a series of methods that simulate the human brain in the hierarchical structure of neurons to recognize the relationships among specified data (Mahesh, 2018). Supervised neural network refers to a network consisting of many neurons connected by weighted links, which was first introduced by Hopfield in 1982 in biological research (Hopfield, 1982; Mahesh, 2018). In the literature, the methods presented for heat exchangers, such as ANN or RVFL, are distinctive due to the structure of their network.

• A tree model in machine learning is a type of predictive modeling tool, transitioning from observed attributes of an entity, symbolized by the branches, to deductions about the entity’s target value, encapsulated in the leaves (Clark and Pregibon, 2017). This model employs a hierarchical structure to parse the data, whereby each internal node corresponds to a specific attribute, each branch signifies a decision rule, and each leaf node represents an outcome or a prediction. The process initiates from the root node and progressively branches out based on defined decision rules, effectively segmenting the data space into non-overlapping regions (Rattan et al., 2022). The tree model defines how to get a prediction score. It can be employed for classification and regression, such as Random Forest, AdaBoost, XGBoost, LightGBM, GBT, etc.

• A Support Vector Machine (SVM) is a widely used supervised learning model in machine learning. It is used for both classification and regression tasks (Mahesh, 2018). However, it is primarily used in classification problems. The basic idea behind SVM is to find a hyperplane in $N$-dimensional space (where $N$ is the number of features) that distinctly classifies the data points. The chosen hyperplane is systematically optimized to maximize the “margin,” which is defined as the distance to the nearest data points across different classes. This maximization strategy is intended to minimize the model’s generalization error, thus enhancing its predictive accuracy for classifying new instances. In the domain of SVM, Sequential Minimal Optimization (SMO) serves as an efficient algorithm for training. SMO can be optimized as a heuristic algorithm whose basic idea is to optimize only two variables at one iteration while fixing the remaining variables (Sun et al., 2008).

• Bayesian regression is a statistical method that uses the principles of Bayesian statistics to estimate the parameters of a regression model. It is an alternative to traditional regression models like linear regression, and it takes a fundamentally different approach to model the relationship between the dependent and independent variables (Sun et al., 2008). In Bayesian statistics, probabilities are treated as a measure of belief or uncertainty, which can be updated based on new data. This is especially useful for modeling systems where uncertainty is inherent, providing a flexible framework that allows for iterative refinement as new data is incorporated. Thus, Bayesian regression offers an alternative but robust way of tackling regression problems

• K-nearest neighbor can solve the classification and regression issues related to heat exchangers. A similarity metric is established within the data space, enabling the prediction of data labels by utilizing the nearest neighbors in the data space for reference (Kramer, 2013). In the K-nearest neighbor (KNN) algorithm, when one seeks to predict the label of an unobserved data point, the algorithm specifically identifies ‘K’ instances from the training set that are in closest proximity to the given point. The determination of “proximity” is generally quantified using a distance metric, with the Euclidean distance being the most commonly employed metric in numerous applications. For illustrative purposes, if we set K to 3, the KNN procedure will focus on the three most proximate training data instances relative to the unobserved point to facilitate the prediction. In the realm of classification, the predominant label amongst these three neighbors is then allocated to the unobserved data point. In the context of regression analysis, the algorithm might predict the label by computing the mean value from the labels of the three nearest neighbors.

TABLE 1

TABLE 1. The primary classification of machine learning.

3 Machine learning models applied for heat exchanger modeling

Traditional physics-based models may encounter difficulties when dealing with complex and non-linear problems, requiring extensive specialist knowledge and experience. In this context, machine learning methods have been introduced to the field of heat exchangers. Machine learning models built upon experimental or numerical data can improve state-of-the-art simulation methodologies. Machine learning can reduce calculation time, increase prediction accuracy, and handle complex and non-linear issues. In recent years, there have been notable advances in the application of machine learning methods in the field of heat exchangers, such as using machine learning to predict heat transfer coefficients (Section 3.2.1), pressure drop (Section 3.2.2), and heat exchanger performance (Section 3.2.3) performing real-time analysis of complex experimental data, and optimizing large-scale thermal systems.

This section reviews the recent advances in applications of machine learning methods for heat exchanger modeling in the following categories: (Section 3.2.1) Modeling of Heat Transfer Coefficient (HTC), (Section 3.2.2) Modeling of pressure drops, (Section 3.2.3) Modeling of heat exchanger performance (Section 3.3) Fouling factors, (Section 3.4) Refrigerant thermodynamic properties, and (Section 3.5) Flow pattern recognition based on machine learning methods.

3.1 Heat exchangers

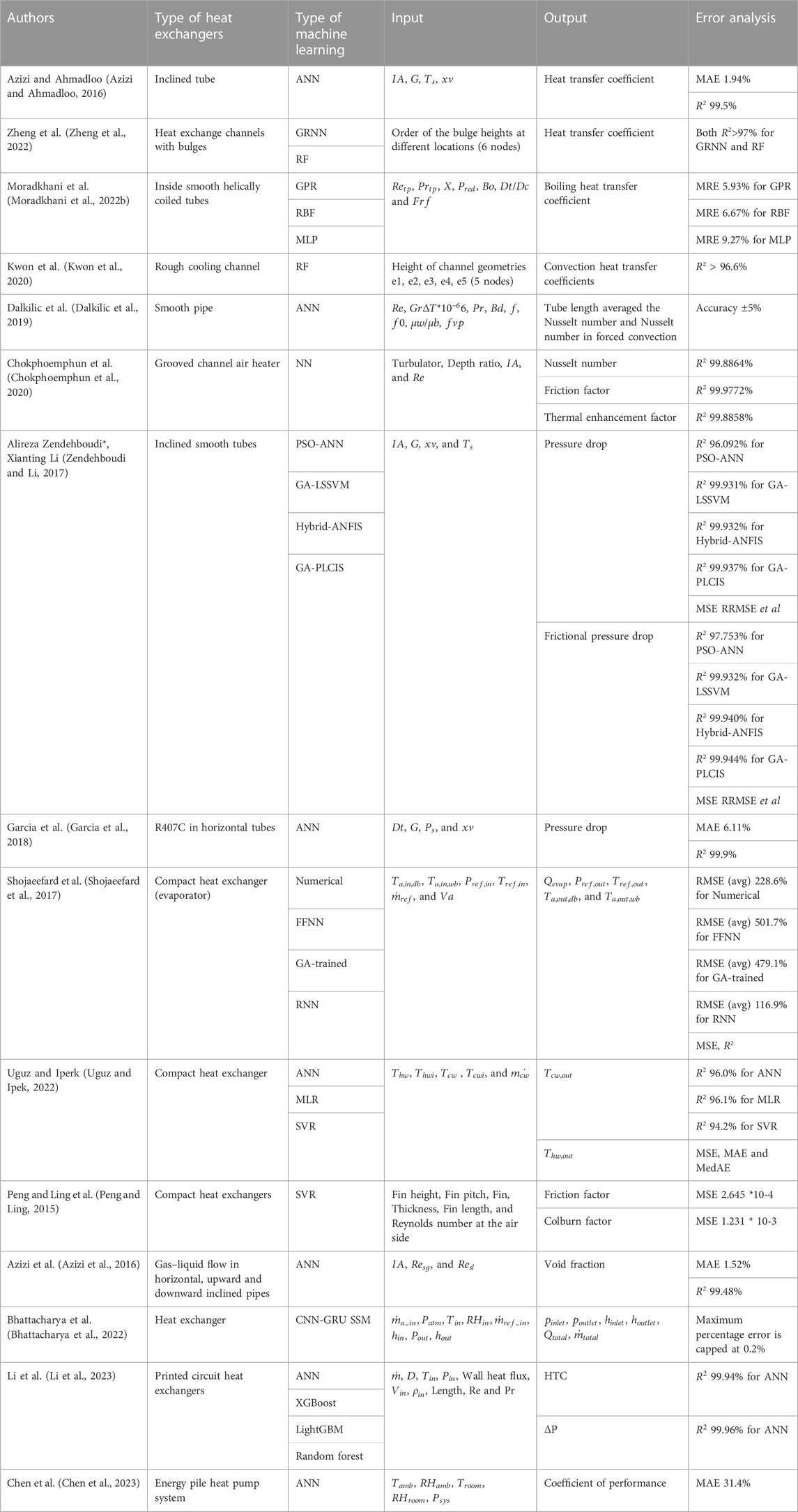
For the heat exchanger reviewed in this section, as shown in Figure 3A, microchannel heat exchangers consist of small-scale finned channels etched in silicon wafers and a manifold system that forces a liquid flow between fins (Harpole and Eninger, 1991). As shown in Figure 3B, the shell and tube heat exchangers are devices consisting of a vessel containing either a bundle of multiple tubes or a single tube bent several times, with the wall of the tube bundle enclosed in the shell being the heat transfer surface. This design has the advantages of simple structure, low cost, and wide flow cross-section (Mirzaei et al., 2017). As shown in Figure 3C, a plate heat exchanger is more compact than the shell and tube heat exchanger design because of its smaller volume and larger surface area and because its modular design can increase or reduce the number of required plates to satisfy different requirements, retaining excellent heat transfer characteristics (Abu-Khader, 2012). As shown in Figure 3D, Tube-Fin Heat Exchangers (TFHXs) are important components in heat pump and air conditioning systems, which consists of a bundle of finned tubes (Li et al., 2019).

FIGURE 3

FIGURE 3. (A) Microchannel heat exchangers. (B) Shell and tube heat exchangers adapted from (Foley, 2013). (C) Plate heat exchangers. (D) Tube-fin heat exchangers.

3.2 Parameters modeling of heat exchangers

This subsection summarizes the use of machine learning in modeling heat exchangers, with each subsubsection describing different parameters predicted in the research, providing a comprehensive summary of the classifications. The different types of heat exchangers are shown in Tables 2–6. Tables 2–6 delineate specific literature references pertaining to each unique type of heat exchanger. Each table incorporates specific references correlating to a distinct type of heat exchanger. This systematic organization of information aims to streamline the process to effectively locate and review pertinent literature based on the unique type of heat exchanger they are researching.

TABLE 2

TABLE 2. Machine learning applications for modeling microchannel heat exchangers.

TABLE 3

TABLE 3. Machine learning applications for modeling plate heat exchangers.

TABLE 4

TABLE 4. Machine learning applications for modeling tube-fin heat exchanger.

TABLE 5

TABLE 5. Machine learning applications for modeling shell and tube heat exchanger.

TABLE 6

TABLE 6. Machine learning applications for modeling other heat exchangers.

To conduct a robust, quantitative assessment of the models introduced in this research, we have incorporated a range of error metrics, as cataloged in Tables 2–9. These metrics not only facilitate an empirical evaluation of model performance but also provide prospective users with a criteria-based framework for model selection relative to specific applications. We delineate the mathematical equations that form the basis for each type of error metric employed as shown in the following equations.

Mean Relative Error (MRE) is a metric that quantifies the relative size of the prediction errors with respect to the actual observed values. The formula for MRE is:

$MRE=\frac{1}{n}\sum _{i=1}^n\frac{\mid X_{predict}-X_{real}\mid }{X_{real}}(1)$

Mean Absolute Error (MAE) is a popular metric for regression. It measures the average absolute difference between observed and predicted values. The formula is:

$MAE=\frac{1}{n}\sum _{i=1}^n\mid X_{predict}-X_{real}\mid (2)$

Root Mean Squared Error (RMSE) is another commonly used regression metric. It first calculates the square of the difference between each observed value and its predicted value, averages these, and then takes the square root. Its formula is:

$RMSE=\frac{1}{n}\sqrt{\sum _{i=1}^n{\left(X_{predict}-X_{real}\right)}^2}(3)$

Median Absolute Error (MedAE) is similar to MAE, but instead of using the mean of the absolute errors, it uses the median. The formula is:

$MedAE=\frac{1}{n}\sum _{i=1}^n\mid X_{predict}-X_{median}\mid (4)$

R-squared, also known as the coefficient of determination, is used to measure how well the model explains the variability among the observed values. It ranges between 0 and 1, with values closer to 1 indicating a better fit. Its formula is:

$R^2=1-\frac{\sum _{i=1}^n{\left(X_{predict}-X_{real}\right)}^2}{\sum _{i=1}^n{\left(X_{predict}-X_{average}\right)}^2}(5)$

3.2.1 Modeling of Heat Transfer Coefficient

The Heat Transfer Coefficient (HTC) plays a pivotal role in the design and optimization of heat exchangers. It is a key parameter that describes the rate of heat transfer per unit area, per unit of temperature difference. In fluid dynamics and heat transfer studies, the Nusselt number is often introduced as a dimensionless parameter delineating the relative significance of convective heat transfer to conductive heat transfer across a defined boundary. It essentially offers a normalized representation of the Heat Transfer Coefficient (HTC). Accurate prediction of HTC can lead to more efficient design and optimization of heat exchangers, resulting in improved performance and reduced energy consumption (Zhu et al., 2021). This subsection summarizes and categorizes studies related to the prediction of the Heat Transfer Coefficient (HTC) presented in recent literature. The classification is primarily based on the types of input parameters used, with a particular focus on distinguishing between dimensionless parameters and structural parameters. Additionally, a separate classification is conducted based on the different sources of data used, including historical literature, experimental data, and Computational Fluid Dynamics (CFD) simulations.

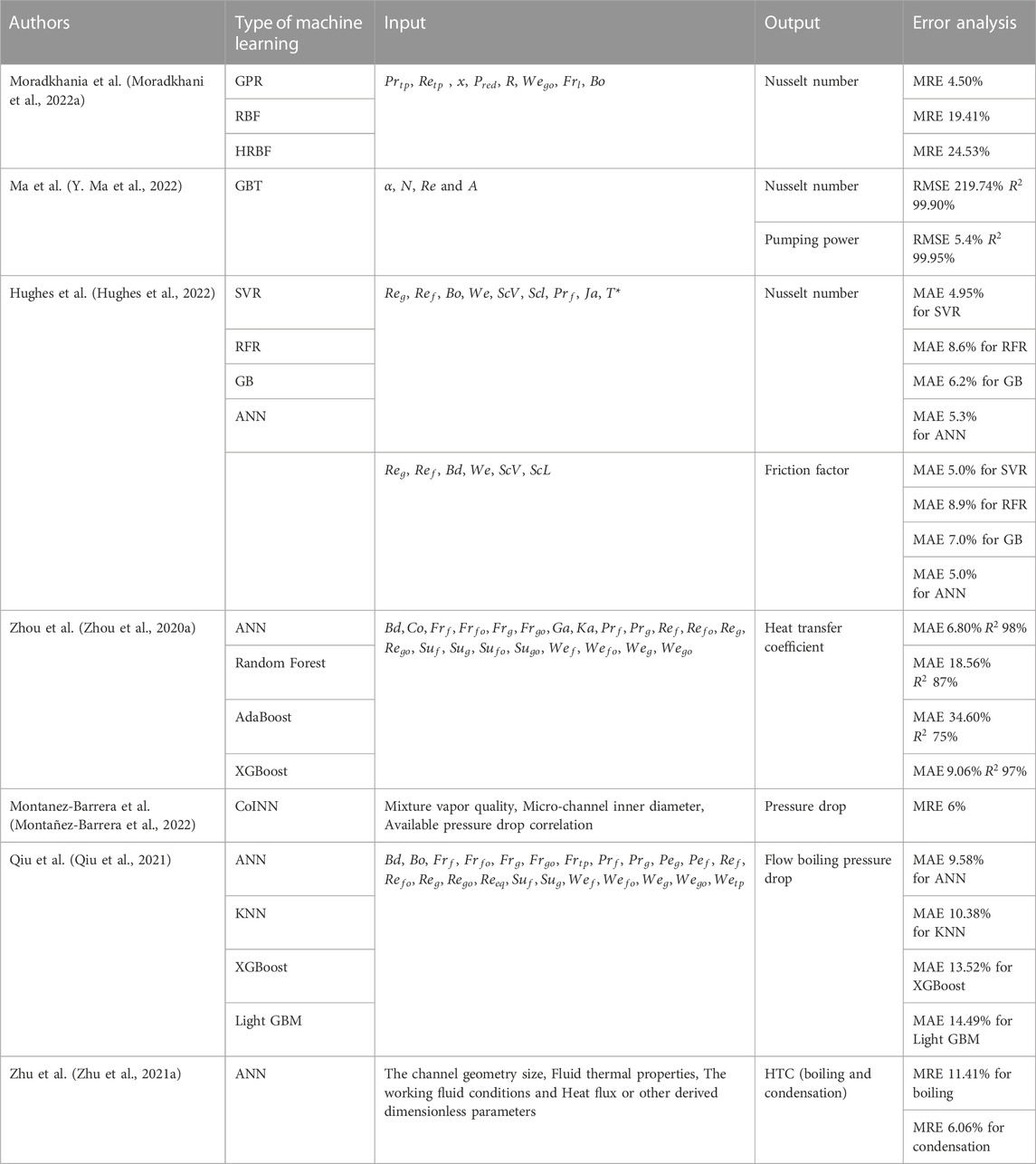
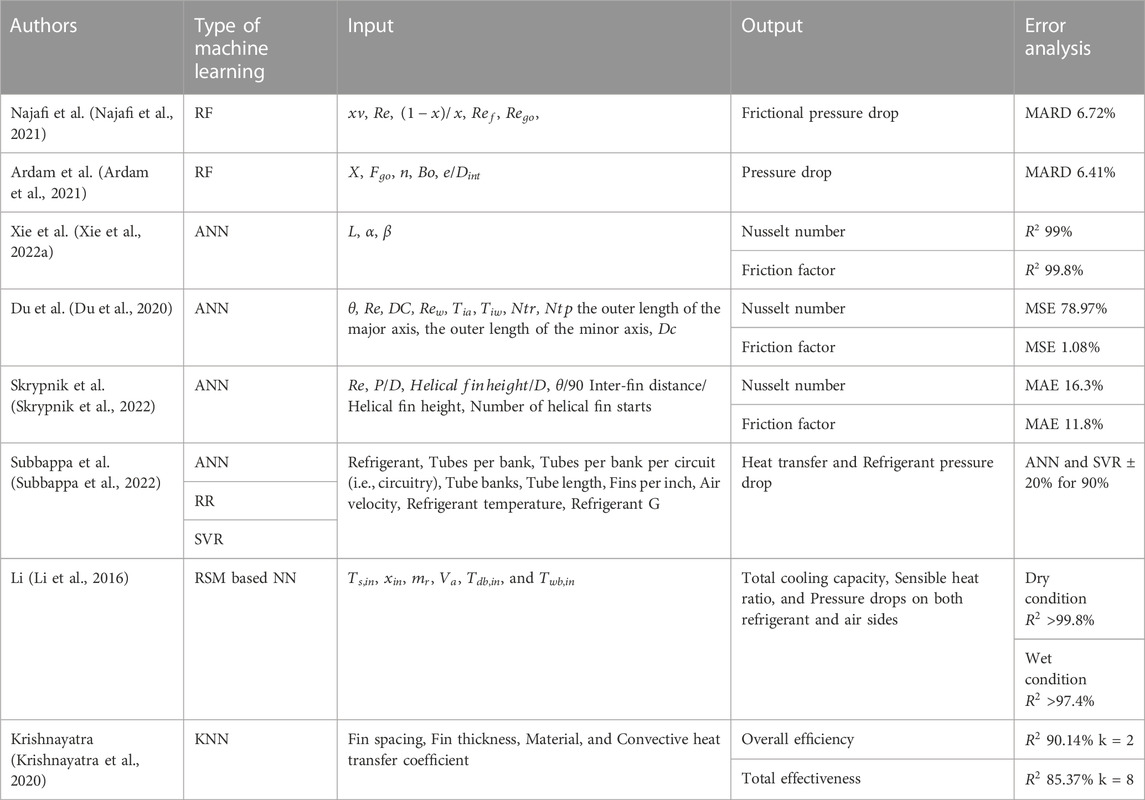
A plethora of research efforts has been methodically invested in the predictive modeling of the Heat Transfer Coefficient (HTC), focusing primarily on the influence of structural parameters to construct effective machine learning training datasets. For instance, Zheng et al. (Zheng et al., 2022) introduced General Regression Neural Network (GRNN) and RF algorithms to predict HTC in heat exchange channels with bulges with the inputs of each bulge height at different locations. Other works by Moradkhani et al. (Moradkhani et al., 2022a) and Kwon et al. (Kwon et al., 2020) have delved into the specifics of boiling and convection heat transfer coefficients, respectively. In these works, the effect of surface roughness on HTC has not been sufficiently explored, and the amount of measurement data on the topic is insufficient to include the impact of surface roughness in predictive models. Therefore, the empirical model that incorporates the effects of surface roughness into the HTC prediction model needs further research.

For a predictive model, the exclusive reliance on structural parameters may prove insufficient. Some studies in the literature have indeed embraced models where the database inputs consist of dimensionless numbers or physical properties, which can standardize data, enhance the stability and performance of the model, and make the model’s output easier to understand and interpret. For instance, Longo et al. (Longo et al., 2020b) developed ANN to estimate the boiling heat transfer coefficients of refrigerants in Brazed Plate Heat Exchangers (BPHEs), where the inputs are the corrugation enlargement ratio ($\mathrm{\Phi }$), the reduced inclination angle ($\beta /\beta \mathit{max}$), the liquid Prandtl number (${\mathit{Pr}}_f,$), the equivalent Reynolds number (${Re}_{eq}$), the boiling number ($Bo$), and the reduced pressure ($P/P_{cr}$).

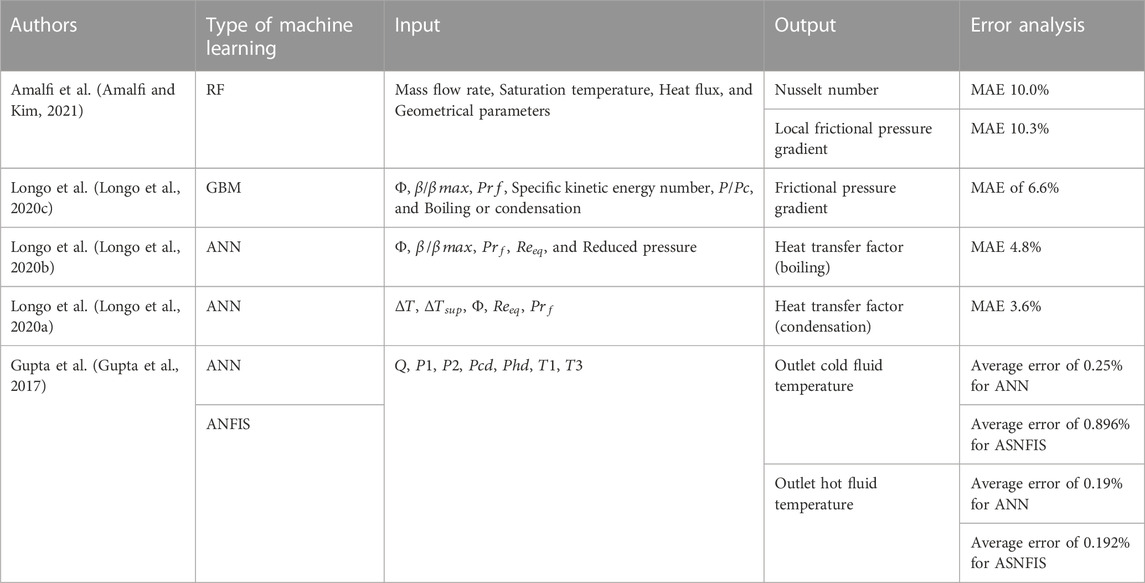
In understanding the various methodologies applied in machine learning modeling, a clear distinction arises from the source of databases utilized in various research. A portion of these investigations derives data from pre-existing literature, while some data are procured from Computational Fluid Dynamics (CFD). Amalfi and Kim (Amalfi and Kim, 2021) introduced the randomized decision trees to predict the Nu. The consolidated experimental database was collected from Amalfi et al. (Amalfi et al., 2016a). The results showed that it could significantly improve the prediction of the thermal performance of two-phase cooling systems compared to the study of Amalfi et al. (Amalfi et al., 2016b), which used physics-based modeling methods. Differently, Ma et al. (Ma et al., 2022) constructed a GBT tree model based on the output of CFD simulations of microchannel refrigerant flow to predict the Nusselt number and the pumping power ($WPP$). This study demonstrates that the most influential parameters are $A$, $N$, and $\alpha$, while Nu shows an insensitivity to the Reynolds number of the inlet flow.

3.2.2 Modeling of pressure drops

Pressure drop or pressure differential refers to the decrease in pressure that a fluid experiences as it flows through a conduit, valve, bend, heat exchanger, or other equipment. This decrease in pressure is due to factors such as frictional resistance, local resistance, or thermal effects (Ardhapurkar and Atrey, 2015). It is imperative to minimize the pressure drop across a heat exchanger (HX) because a reduced pressure drop directly translates to decreased pumping power and a subsequent reduction in the energy input required for the system in which the HX operates. This section summarizes and categorizes historical literature related to the prediction of pressure drop. The categorization is primarily based on the type of machine learning method used, including predictions based on neural networks, random forest algorithms, predictions support vector regression, and other methods. Additionally, some studies specifically focus on predicting frictional pressure drop.

In literature, ANN can be considered one of the most common machine learning models used for pressure drop prediction. Montanez-Barrera et al. (Montañez-Barrera et al., 2022) and Qiu et al. (Qiu et al., 2021) employed ANN or Correlated-informed neural networks to predict pressure drops. In addition, Qiu et al. (Qiu et al., 2021) also explored other techniques, including XGBoost and GBM. Subbappa et al. (Subbappa et al., 2022) employed three different methods, Ridge Regression (RR), Support Vector Regression (SVR), and ANN. In this work, it is reported that the radiator, condenser, and evaporator baseline models are developed with a different database. The inputs involve the refrigerant properties, the number of tubes per bank, the number of tubes per bank per circuit (i.e., circuitry), the tube banks, the tube length, the number of fins per inch, the air velocity, the refrigerant temperature, and the refrigerant mass flux. It is concluded that ANN and SVR can avoid the expensive simulations with a reasonable error of ±20% for the testing data used in the study. However, the validation of this study needs to be verified using high-fidelity models, which refer to models that are highly accurate and detailed. It closely represents or mirrors the real-world system or situation that is being modeled. High-fidelity models aim to capture the intricacies and complexity of the actual system to the maximum extent possible (Jagielski et al., 2020). The machine learning models that have been trained substantially expedite the investigation of the design space, leading to a considerable reduction in engineering time required to reach designs that are nearly optimal.

Despite the highlighted prominence of ANN in the realm of machine learning models, various other computational approaches are also employed as evidenced in the literature. Ardam et al. (Ardam et al., 2021) developed the prediction of pressure drop based on the Random Forest algorithm in micro-finned tubes with evaporating R134a flow. It employed five features ($X$, $f_{go}$, $n$, $Bo$, $e/Dint$) selected among 19 features, which showed the highest prediction accuracy through parametric optimization. The results showed that the proposed methodology is better than the physical model used to respresent the same data (Shannak, 2008). In addition, Zendehboudi and Li (Zendehboudi and Li, 2017) predicted $\Delta P$ and the frictional pressure drop in inclined smooth tubes based on different models, such as PSO-ANN, GA-LSSVM, Hybrid-ANFIS, and GA-PLCIS. The two databases are collected from the experimental study of Adelaja et al. (Adelaja et al., 2017).

In the context of pressure drop predictions discussed thus far, it is of considerable importance to recognize the frictional pressure drop as a major component contributing to the overall pressure losses. Some studies have focused on investigating the frictional pressure drop in heat exchangers, such as Najafi et al. (Najafi et al., 2021), Xie et al. (Xie et al., 2022), Skrypnik et al. (Skrypnik et al., 2022), Peng and Ling et al. (Peng and Xiang, 2015) and Du et al. (X. Du et al., 2020), introduced the estimation model of the friction factor using different machine learning methods. Najafi et al. (Najafi et al., 2021) demonstrated that data-driven estimation of frictional pressure drop provides greater prediction accuracy compared to theoretical physical models (Chisholm, 1967) for two-phase adiabatic air-water flow in micro-finned tubes using the Random Forest model. Their research focused on five dimensionless features ($xv$, $Re$, $\left(1-x\right)/x$, ${Re}_f$, ${Re}_{go}$) selected from 23 features which are slightly different features compared to selection of Ardam et al. (Ardam et al., 2021). Their research estimates the two-phase gas multiplier in two-phase adiabatic air-water flow in micro-finned tubes based on Random Forest model.

3.2.3 Modeling of heat exchanger performance

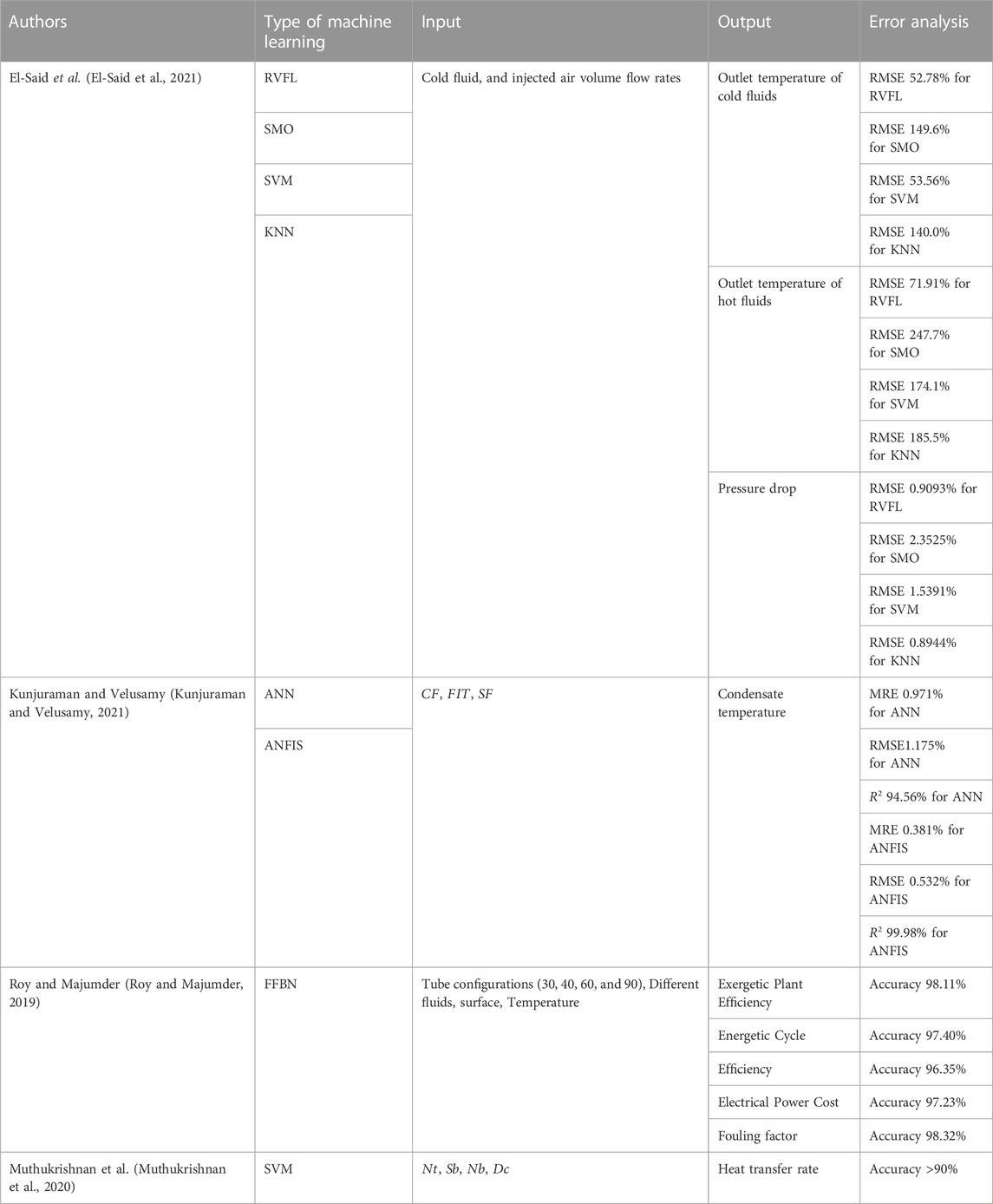
The overall performance of a heat exchanger is typically measured by the overall heating or cooling heat transfer rate capacity, which will be dependent on the dimensions of the heat exchanger, or heat exchanger effectiveness or efficiency, which are dimension-independent. Various research studies have applied different machine learning methods to distinct aspects of heat exchanger performance prediction. Both the work of Li et al. (Li et al., 2016) and Shojaeefard et al. (Shojaeefard et al., 2017) focused on the prediction of cooling capacity in heat exchangers. While Li et al. employed a Response Surface Methodology (RSM)-based Neural Network (NN) model, Shojaeefard et al. evaluated different Artificial Neural Network (ANN) structures in their model. On the other hand, Krishnayatra et al. (Krishnayatra et al., 2020) and Roy and Majumder (Roy and Majumder, 2019) investigate the prediction of performance parameters in shell and tube heat exchangers, including exergetic plant efficiency, energetic cycle efficiency, electric power, fouling factor, and cost, utilizing the FFBN algorithm with tube configurations, fluid type, surface area, and temperatures as input parameters. Furthermore, Muthukrishnan et al. (Muthukrishnan et al., 2020) developed a Support Vector Machine (SVM) in shell and tube heat exchangers to predict the heat transfer rate, with results showing the superior prediction accuracy of SVM over mathematical models. The consolidated database is from the experiments conducted by Wang et al. (Wang et al., 2006). The main differences between these studies lie in the focus of the research (such as cooling capacity, efficiency, heat transfer rate, etc.), the prediction model used (such as RSM-based NN, ANN, FFBN, SVM, etc.), and the type of heat exchanger studied.

Turning our attention to predicting coefficient of performance of heat exchanger systems, it is also clear that this segment has been at the forefront of integrating innovative machine learning approaches in research. Bhattacharya et al. (Bhattacharya et al., 2022) developed and validated a model that combines Convolutional Neural Networks (CNN) with Gated Recurrent Units in a State Space Model framework. Their work aimed to predict the intricate dynamics of heat exchangers observed in vapor compression cycles in heat exchanger. The model processed inputs like ${\dot{m}}_{a\_in}$, $P_{atm}$, $T_{in}$, $R{H}_{in}$, ${\dot{m}}_{ref\_in}$, $h_{in}$, $P_{out}$, $h_{out}$ and produced predictions for $p_{inlet}$, $p_{outlet}$, $h_{inlet}$, $h_{outlet}$, $Q_{total}$, ${\dot{m}}_{total}$.Their research demonstrated remarkable accuracy, with the maximum percentage error being limited to 0.2%. In addition, Chen et al. (Chen et al., 2023) constructed two-year field tests based on an energy pile heat pump system, where in situ results were used as sample points, and the measured ambient temperature and humidity, room temperature and humidity, and hourly power consumption were used as input parameters to predicted coefficient of performance. The results showed that the accuracy was higher than that of the empirical regression models. Moreover, Zhu et al. (Zhu et al., 2021a) investigated the boiling and condensation heat transfer of R134a refrigerant within microchannels under various conditions. Data collected from these experiments were utilized to train machine learning-based artificial neural network models for predicting heat transfer performance. The models effectively forecasted the heat transfer coefficients for both boiling and condensation processes. Further, Li et al. (Li et al., 2023) employed four machine learning methods to anticipate the thermal performance of supercritical methane flow in a Printed Circuit Heat Exchanger. The ANN proved to be highly precise in forecasting the local heat transfer coefficient and unit pressure drop following hyperparameter optimization.

3.2.4 Conclusion of heat exchangers modeling

Upon the review of the recent studies using machine learning to predict various performance indicators for different types of heat exchangers, several key themes and opportunities for enhancement emerge. Regarding the interaction of various factors within the models, it is critical to understand that the reliability and precision of machine learning predictions depend on a comprehensive understanding of the interactions between model parameters. In many of the reviewed studies, parameters such as the Reynolds number, Weber number, and the Froude number were utilized, yet the dynamic interactions between these parameters were not explicitly elucidated. For example, the interplay between Reynolds number and Froude number could potentially influence the prediction of pumping power significantly. A deeper investigation into these correlations could lead to more refined and precise predictions and ultimately, more effective heat exchanger designs. Employing methods such as feature importance analysis or sensitivity analysis could provide more tangible insights into these interactions.

When scrutinizing the model’s training and validation procedures, it becomes imperative to thoroughly outline each stage of the process. Regrettably, the comprehensive explanation of this process, encompassing critical aspects such as the selection of training and validation datasets, hyperparameter tuning, and overfitting prevention, is commonly absent in the studies reviewed. This lack of essential information hampers both reproducibility and potential model enhancement. Therefore, advancing in this field is reliant on a more transparent and detailed presentation of these steps.

On this basis, the role of data transparency and reproducibility cannot be overstated in ensuring the credibility and utility of these models. Some studies, however, fall short by failing to explicitly state their data sources or by not providing clear definitions of model parameters. These omissions could obstruct other researchers’ understanding and reproduction of the models. Hence, by improving data openness and providing a more transparent presentation of model parameters, the field could experience significant advancements, facilitating replication and model improvement.

Lastly, when we turn our attention to the exploration of emerging techniques, it is clear that traditional machine learning methods such as Artificial Neural Networks (ANN), Gradient Boosting Machines (GBM), and Ridge Regression have been well documented. However, a noticeable gap exists in the exploration and application of more recent machine learning methodologies. Techniques like deep learning and reinforcement learning, which have shown promise in various other disciplines, could potentially enhance predictive capabilities and robustness in heat exchanger performance prediction. This untapped potential area is, thus, deserving of further, in-depth investigation.

3.3 Fouling factor

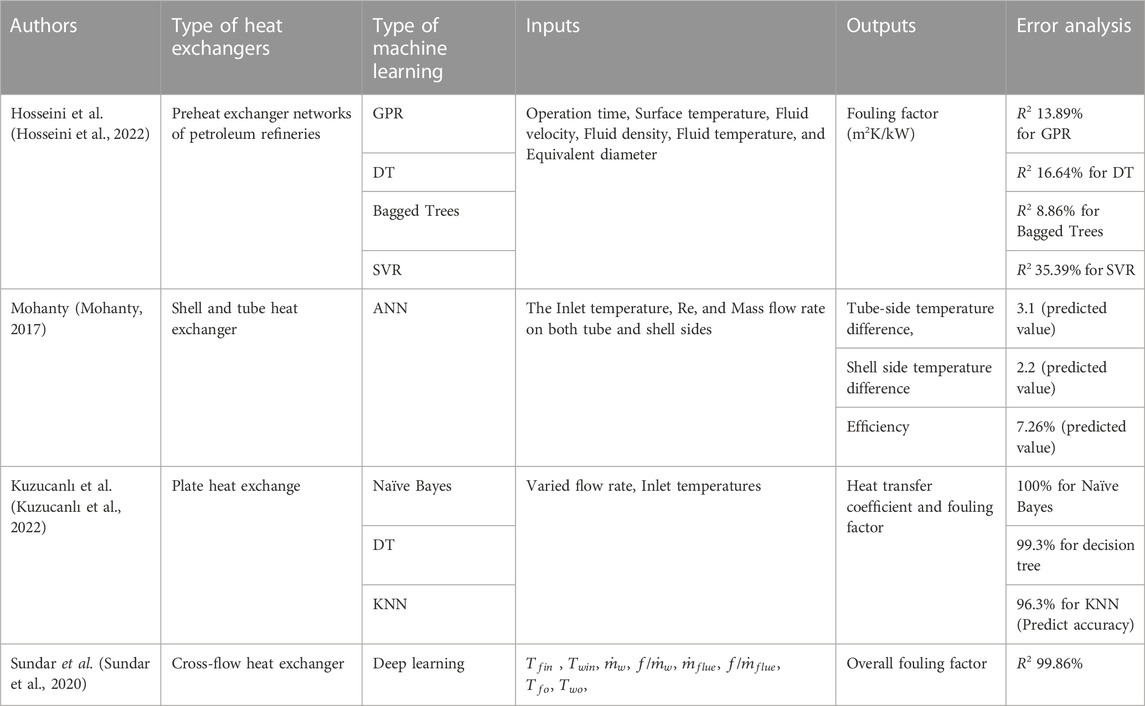
The fouling factor is an index that measures the unit thermal resistance of solid sediments deposited on heat exchange surfaces and reduces the overall heat transfer coefficient of the heat exchanger (Müller-Steinhagen, 1999). Fouling deposits that clog the channels of compact heat exchangers will increase pressure drops and reduce flow rates, resulting into poor heat transfer and fluid flow performance (Asadi et al., 2013). Table 7 lists the details of the literature dealing with fouling factors of heat exchangers. A summary of these investigations is discussed in this subsection. For predicting the fouling factor, Hosseini et al. (Hosseini et al., 2022) estimated the fouling factor through four machine learning methods: Gaussian Process Regression (GPR), Decision Trees (DT), Bagged Trees, and Support Vector Regression (SVR). The database was collected from experiments, and the model inputs were the operation time, the surface temperature, the fluid velocity, the fluid density, the fluid temperature, and the equivalent diameter, selected based on Pearson’s correlation analysis. Mohanty (Mohanty, 2017) estimated the temperature difference on the tube and shell sides of a shell-and-tube heat exchanger, as well as the heat exchanger efficiency as the outputs of a fouling factor-based ANN with network structure 6-5-4-2.

TABLE 7

TABLE 7. Prediction of the fouling factor for heat exchangers based on machine learning methods.

For estimating the fouling factor, Kuzucanlı et al. (Kuzucanlı et al., 2022) predicted the behavior of the overall heat transfer coefficient and of the in plate heat exchangers. It is noteworthy that this work introduced the classification solution. The dataset was collected from the experiment with variable flow rates and inlet temperatures as input parameters. In a similar work, Sundar et al. (Sundar et al., 2020) predicted the fouling factor based on deep learning. A total of 15,600 samples were collected in a database, using the inlet fluid temperatures, the ratio of fouled fluid flow rates to flow rates under clean circumstances, and the outlet temperatures (gas and fluid) as inputs.

Machine learning methods have proven effective in modeling and predicting the fouling factor in heat exchangers, a measure that significantly impacts thermal performance. Techniques such as Gaussian Process Regression, Decision Trees, Bagged Trees, and Support Vector Regression have been used, leveraging operational parameters like operation time, surface temperature, fluid velocity, and more. These methods have shown acceptable prediction accuracy, demonstrating machine learning’s effectiveness in this field. Additionally, machine learning has been effective in predicting fouling’s impact on other parameters, like temperature difference and heat exchanger efficiency. While existing algorithms have been primarily used, there’s potential for new machine learning algorithms to further improve fouling factor prediction.

3.4 Refrigerant thermodynamic properties

The conventional prediction of the refrigerant thermodynamic properties is usually carried out by means of empirical, theoretical, and numerical models. Although these methods have been successfully applied in many cases, their numerical modeling still suffers from computational issues in dealing with the complex molecular structure of refrigerants (Meghdadi Isfahani et al., 2017; Alizadeh et al., 2021a). Table 8 lists several machine learning prediction models of the thermodynamic properties of refrigerants available in the literature, which are briefly described in this subsection.

TABLE 8

TABLE 8. Prediction of the thermodynamic properties for refrigerants based on machine learning methods.

In literature, neural network models have been widely employed by many researchers for the prediction of refrigerant properties. For example, Gao et al. (Gao et al., 2019), Wang et al. (Wang et al., 2020), Zolfaghari and Yousefi (Zolfaghari and Yousefi, 2017), Nabipour (Nabipour, 2018) employed ANN to predict the thermodynamic properties, such as, $P_{red}$, $1-T_r$, $\omega$, $Pc/Pcr$, etc. They employed different parameters to investigate the prediction performance, for instance, Wang et al. (Wang et al., 2020) introduced ANNs to estimate the viscosity and the thermal conductivity, using the reduced pressure ($P_{red}$), the reduced temperature ($T_r$), the molar mass ($M$), and the acentric factor ($\omega$) as inputs. Similarly, Zolfaghari and Yousefi (Zolfaghari and Yousefi, 2017) developed an ANN to predict the density of sixteen lubricant/refrigerant mixtures, considering a total of 3,961 data points from the literature. In this study, the temperature ($T$), the pressure ($P$), the molar fraction ($x$), the total molecular weight ($M_w$), and the average boiling temperature ($T_b$) of pure refrigerants were considered as input parameters.

Shifting away from the singular prediction model approach, numerous studies have adopted a more extensive analysis by examining multiple prediction models. Several studies have embraced a more comprehensive analysis by investigating more than one prediction model; for example, Zhi et al. (Zhi et al., 2018) developed three prediction models of viscosity based on ANFIS, RBFNN, and BPNN for six pure refrigerants, specifically R1234ze(E), R1234yf, R32, R152a, R161, and R245fa in the saturated liquid state. It is reported that a total of 1,089 data points were collected from the literature, of which 80% were allocated to training and 20% to testing, while the algorithm inputs were temperature, pressure, and liquid density. Results demonstrate that the ANFIS algorithm shows the highest prediction accuracy.

Upon reviewing the impressive statistics presented in Table 8, it is evident that machine learning has proven to be an invaluable tool for predicting the thermodynamic properties of refrigerants. A common thread across the studies indicates that factors such as temperature, pressure, and density often serve as inputs for these predictive models. However, we observe variations in the algorithms used and the specific properties predicted. This could be attributed to the unique characteristics of the refrigerants studied and the specific objectives of each study. While these models demonstrate impressive prediction accuracy, it is crucial to acknowledge that model performance varies depending on the refrigerant and property in question. A broader observation reveals a notable trend toward using machine learning in refrigerant property prediction, which presents opportunities for further exploration. Future work could include comprehensive comparative studies of these different machine learning algorithms, considering their strengths and weaknesses in various scenarios. There is also potential for integrating these machine learning models with other computational tools for more robust and accurate predictions. Furthermore, as the field continues to evolve, there may be scope to explore new machine-learning techniques and develop novel approaches for predicting the thermodynamic properties of refrigerants.

3.5 Flow patterns

Two-phase flow is critical in many chemical processes, heat transfer, and energy conversion technologies. The flow pattern in two-phase flow has a critical role in heat transfer coefficient and pressure drop, because the physics governing the pressure drop and the heat transfer is intrinsically linked to the local distribution of the liquid and vapor phases (Cheng et al., 2008). Recently, the prediction of flow patterns based on machine learning has received growing attention. Table 9 summarizes the studies about flow pattern recognition based on machine learning reported in the present work. Identifying flow patterns is crucial in fluid mechanics, employing various methods. High-speed cameras offer direct visual insight but are limited to transparent media. Gamma rays can analyze opaque fluids but raise safety concerns. Pressure sensors can infer flow patterns from pressure changes, albeit with interpretational challenges. The Continuous Wave Doppler technique measures particle velocities using frequency shifts but requires particles or bubbles for measurement. The appropriate method hinges on factors like flow type, fluid transparency, piping material, safety, and the depth of analysis required.

TABLE 9

TABLE 9. Prediction of flow regime based on machine learning methods.

Some studies identified the flow regimes using the high-speed cameras, Shen et al. (Shen et al., 2020) Ahmad et al. (Ahmad et al., 2022), Giri Nandagopal et al. (Giri Nandagopal and Selvaraju, 2016) and Giri Nandagopal et al. (Nandagopal et al., 2017) investigate the flow pattern recognition through high-speed cameras. For instance, Giri Nandagopal et al. (Nandagopal et al., 2017) investigated the same liquid-liquid system in a circular microchannels of 600 μm diameter as the confluence angle of the two fluids was varied in the range 10–170 degrees, in order to predict the flow pattern maps using the confluence angle and the superficial velocities of the two liquids as input. The algorithms considered could identify slug flow, bubble flow, deformed flow, elongated slug flow, deformed flow, and stratified flow. The results showed that GRNN gives the best prediction accuracy again.

Instead of using a high-speed camera to record the flow regimes included in the datasets, some studies used gamma rays to construct the database. For example, Roshani et al. (Roshani et al., 2017) identified the flow regimes by means of the multi-beam gamma ray attenuation technique. In this study, the outputs of two detectors are introduced as input parameters into the RBF models in order to predict the flow regimes. Similarly, Hanus et al. (Hanus et al., 2018) used the gamma-ray attenuation technology to identify flow regimes and generate input data for the algorithm. In particular, nine features obtained from the signal analysis were selected as inputs and applied to six different machine-learning methods. The results showed a promising accuracy for all the methods considered.

In contrast to those described above, some studies employed other methods, such as pressure sensors, ultrasound, and a new concept (take-off ratio). For example, Godfrey Nnabuife et al. (Godfrey et al., 2021) used Deep Neural Networks (DNNs) operating on features extracted from Continuous Wave Doppler Ultrasound (CWDU) to recognize the flow regimes of an unknown gas-liquid flow in an S-shaped riser. A Twin-window Feature Extraction algorithm generates the vectors that contain all the information used as input of the Deep NN, reducing the amount of input data and eliminating the noise. The identified flow regimes are annular, churn, slug, and bubbly flow. The results show the highest prediction accuracy, which is better in comparison with that of four conventional machine learning methods: AdaBoost, Bagging, Extra Trees, and DT. Khan et al. (Khan et al., 2022) developed CNN to identify the flow regimes in air-water flow in a horizontal pipe with a 5 cm inner diameter, using the scalograms obtained from pressure detectors as input database. Differently from the described above, Giannetti et al. (Giannetti et al., 2020) introduced the concept of take-off ratio to develop an ANN to predict the two-phase flow distribution in microchannel heat exchangers based on a limited amount of input information. The concept of take-off ratio is based on Prigogine’s theorem of minimum entropy generation (Onsager, 1931; Prigogine and Van Rysselberghe, 1963). As a result, the 4-3-3-3-1 architecture achieves the highest prediction accuracy reported.

Machine learning has increasingly been applied to predict and understand flow patterns in two-phase flow systems, a topic of substantial significance across various fields, from chemical processes to energy conversion technologies. The range and diversity of research in this domain underline the complex interplay between the physical parameters governing the pressure drop and heat transfer, which are intricately related to the local distribution of liquid and vapor phases. Key to this research is the use of machine learning to identify and distinguish different flow patterns accurately. This has been addressed using diverse techniques, such as CNNs, DL, and various types of ANNs, including the PNN, GRNN, and ANFIS. These methods have demonstrated high degrees of prediction accuracy in their respective applications, offering promising advancements in the field. The generation of input data for these machine learning models has employed an array of innovative methodologies, such as high-speed camera image capturing and the use of the multi-beam gamma ray attenuation technique. Some studies have further expanded upon this by introducing novel concepts, such as the take-off ratio, which applies Prigogine’s theorem of minimum entropy generation to predict two-phase flow distribution. Other research has veered towards the use of Deep Neural Networks (DNNs) to identify flow regimes based on Continuous Wave Doppler Ultrasound (CWDU) information, exhibiting high prediction accuracy rates. This move toward the use of DNNs and similar methods demonstrates the field’s continuous evolution and the trend toward more sophisticated, precise prediction models.

3.6 Structured approach to model selection in machine learning: A guide

The selection and evaluation of machine learning algorithms necessitates a comprehensive and multi-faceted approach, involving numerous interdependent steps and considerations. This section delineates a systematic methodology devised to aid practitioners in judiciously selecting the pertinent machine learning algorithm tailored for a specific problem domain.

1. Problem Definition: The preliminary step involves a comprehensive understanding of the problem landscape. This encompasses identifying the nature of the problem—be it a classification, regression, clustering, or another variant.

2. Exploratory Data Analysis: Exploratory Data Analysis is the initial phase of understanding data, aiming to summarize its main characteristics, often visually. This phase includes assessing feature distributions through histograms or boxplots to spot skewness, understanding data sparsity with matrix visualizations, detecting outliers via scatter plots or Interquartile Range methods, and discerning missing value patterns with heatmaps or bar charts. Correlation matrices and pair plots can reveal relationships between variables. Dimensionality reduction techniques, such as Principal Component Analysis or t-distributed Stochastic Neighbor Embedding, provide a compressed visual perspective on multi-dimensional data.

3. Data Pre-processing: Based on Exploratory Data Analysis findings, data pre-processing refines the dataset for modeling. Feature engineering may involve creating polynomial features, encoding categorical variables, or extracting time-based metrics. Outliers could be capped, transformed, or removed entirely. Standard practices also include scaling features using methods like Minimum-Maximum or z-score normalization. Categorical data often require encoding techniques such as one-hot or ordinal. Finally, data may be split into training, validation, and test sets to evaluate the model’s performance effectively.

4. Evaluation Metric Selection: The choice of an evaluation metric should align closely with both the problem definition and organizational objectives. For instance, in classification problems, metrics like accuracy, MAE, MRE, etc. may be considered.

5. Comparative Model Assessment: Employing techniques like cross-validation, the performance of multiple candidate algorithms should be rigorously compared to ascertain the most effective model based on the validation dataset.

6. Hyperparameter Optimization: Subsequent to model selection, hyperparameter tuning is conducted to further refine the performance of the selected models.

7. Validation and Testing: Final performance evaluation is conducted using an independent test set to ascertain the generalizability of the model and to mitigate the risk of overfitting.

4 Limitations and potential solutions

Despite the remarkable potential and superior performance of machine learning techniques compared to traditional computational methods, their unique features, such as a tendency towards overfitting and interpretability can present hurdles in their application within heat exchanger systems. The ensuing discussion will delve into the primary issues in deploying machine learning strategies in the process of modeling heat exchangers, alongside exploring possible solutions.

4.1 Overfitting

Like most probabilistic models, the issues of overfitting and under-fitting are unavoidable in machine learning models (Dobbelaere et al., 2021). Overfitting refers to the prediction accuracy being extremely high in the training dataset, while the performance on the testing dataset is unsatisfactory (Dietterich, 1995). There are multiple potential explanations of the phenomenon, such as noise over-learning on the training set (Paris et al., 2003), hypothesis complexity (Paris et al., 2003), and multiple comparison procedures (Jensen and Cohen, 2000).

In order to mitigate overfitting problems, it is recommended to introduce the following strategies: a) Early stopping (Jabbar and Khan, 2015), which requires defining the criteria of stopping functions, for instance, monitoring the performance of the model on a validation set during the training process. The training is stopped when the error on the validation set starts to increase, which is a sign of overfitting. The validation set is a small portion of the training data set aside to check the model’s performance during training. b) Network structure optimization (Dietterich, 1995), which involves tuning the architecture of the neural network to find the most efficient structure. For example, one could experiment with different numbers of layers or different numbers of neurons per layer. Additionally, pruning methods can be used to reduce the complexity of decision trees or neural networks by eliminating unnecessary nodes. c) Regularization (Jabbar and Khan, 2015), similar to penalty methods, is used to reduce the influence of noise. This term discourages the model from assigning too much importance to any one feature, reducing the risk of overfitting. In conclusion, while several studies in Tables 1–8 have incorporated the early stopping and network structure optimization techniques, it is unclear if they significantly reduced overfitting. Further evaluation of these methods’ effectiveness in the studies mentioned might offer more insights. Regularization, however, seems to be less frequently employed, based on our review.

4.2 Interpretability

Machine learning methods are essentially black box models, where data analysis can be understood as a pattern recognition process (Dobbelaere et al., 2021). According to Vellido (Vellido et al., 2012), interpretability refers to the ability to assess and explain the reasoning behind machine learning model decisions, which is one of the most significant qualities machine learning methods should achieve in practice. Model hyperparameters, such as node optimization in artificial neural networks, are key elements in constructing an effective model. The selection and tuning of these hyperparameters typically have a significant impact on the performance of the model. However, for these types of models, the analysis usually focuses on prediction accuracy rather than the interpretability of the model (Feurer and Hutter, 2019). To implement interpretability, dimensionality reduction can be introduced for supervised and unsupervised (Azencott, 2018) problems through feature selection and feature extraction (Dy et al., 2000; Guyon and Elisseeff, 2003; Guyon et al., 2008). In addition, Vellido (Alcacena et al., 2011) stated that information visualization is a feasible solution to interpret the machine learning models such as Partial Dependency Plots (PDP) (Greenwell, 2017) and Shapley Additive explanation (SHAP) (Mangalathu et al., 2020). It is important to build models that can self-learn to recognize patterns and self-evaluate.

In the latest study, Xie et al. (Xie et al., 2022) introduced a mechanistic data-driven approach called dimensionless learning. It identifies key dimensionless figures and governing principles from limited data sets. This physics-based method simplifies high-dimensional spaces into forms with a few interpretable parameters, streamlining complex system design and optimization. It also states that the processes could find very useful application in heat exchanger modeling and heat exchanger experimental data characterization. This method unveils scientific knowledge from data through two processes. The first process embeds the principle of dimensionless invariance (i.e., physical laws being independent of the fundamental units of measurement) into a two-tier machine learning framework. It discovers the dominating dimensionless numbers and scaling laws from noisy experimental data of complex physical systems. The subjects of investigation include Rayleigh–Bénard convection, vapor-compression dynamics in the process of laser melting metals, and pore formation in 3D printing. The second process combines dimensionless learning with a sparsity-promoting technique to identify dimensionless homogeneous differential equations and dimensionless numbers from data. This method can enhance the physical interpretability of machine learning models.

4.3 Data quality and quantity

The prediction of parameters based on machine learning can provide a reference for scientific research and practical applications to both researchers and engineers However, it is worth mentioning that dealing with a database containing too many outsider data points can generate system errors. Compared with an extensive database, machine learning is more sensitive to a small database, which can influence machine learning models (Pourkiaei et al., 2016).

It is possible to increase the number of data points (Dietterich, 1995), delete the outsider data points, and use algorithms for anomaly detection, such as the principal component analysis (PCA) algorithm (Thombre et al., 2020) and LSTM (Zhang et al., 2019). In addition, it is also possible to carefully examine the data for stable, reliable, and repeatable data (Zhou et al., 2020). Although decades of modeling, simulations, and experiments have produced several datasets about heat exchangers, they are often archived in research laboratories or companies and are not open access.

Lindqvist et al. (Lindqvist et al., 2018) introduced the employment of structured and adaptive sampling methodologies. Structured sampling techniques, such as Latin Hypercube Sampling, systematically distribute sample points throughout the design space, thereby providing a robust approach to experimental design. Conversely, adaptive sampling dynamically modifies the location of sample points contingent on the predictive outcomes of the model, thereby optimizing model performance.

4.4 Model generalization

Model generalization refers to the ability of a machine learning model to adapt properly to new, unseen data drawn from the same distribution as the one used to train the model (Bishop and Nasrabadi, 2006). It is a critical aspect of machine learning models, particularly in complex fields such as fluid dynamics and heat transfer, where phenomena can be influenced by a multitude of factors. A model’s generalization capability determines its utility and applicability in real-world scenarios beyond the confines of the training data. However, achieving good generalization is a significant challenge and often requires careful model design and validation strategies. When applying machine learning methods outside the scope of the database, outputs will be unreasonable. A limited training dataset determines the scope of the application.

When assessing unknown data points via a predictive model, users must ensure that these data points lie within the model’s operational domain. “Unknown data points” typically represent data not previously encountered during the model’s training process. As they are excluded from the training dataset, the model extrapolates its learned patterns to generate predictions for these data points. These unknown data points are instrumental in evaluating the model’s generalization capabilities. However, should these data points fall outside the model’s operational domain, the reliability of the resultant predictions could be undermined. To maintain the trustworthiness of computations under such circumstances, it is recommended to either augment the training database to encompass a broader data spectrum or cross-validate the predicted values employing alternative credible methodologies (Azencott, 2018).

5 Emerging applications

Here, the emerging heat exchanger applications involving machine learning will be discussed, including the novel nanofluid mixture modeling, heat exchanger design, and topology optimization.

5.1 Nanofluid

Nanofluids are widely used in solar collectors, heat exchangers, heat pipes, and other energy systems (Ramezanizadeh et al., 2019). The presence of nanoparticles within the fluid can enhance the thermophysical properties of the fluid to benefit the heat transfer behavior within the system. Currently, several machine learning models have been introduced to predict the thermodynamic properties of hybrid nanofluids (Maleki et al., 2021). According to the Web of Science database, about 3% of nanofluid research papers published in 2019 involved machine learning, with an increasing trend (T. Ma et al., 2021).

In the literature, several machine-learning models have been applied to heat exchangers containing nanofluids (Naphon et al., 2019; Ahmadi et al., 2020; Gholizadeh et al., 2020; Hojjat, 2020; Kumar and Rajappa, 2020; Alimoradi et al., 2022). Nanofluids involve complex physical, chemical, and fluid dynamic phenomena, and traditional modeling and analysis methods may face challenges. However, machine learning, as a data-driven approach, can help address the complex problems in nanofluid research by learning and discovering patterns and correlations in the data (Ma et al., 2021). For instance, Cao et al. (Cao et al., 2022) employed machine learning to simulate the electrical performance of photovoltaic/thermal (PV/T) systems cooled by water-based nanofluids. Alizadeh et al. (Alizadeh et al., 2021a) proposed a novel machine learning approach for predicting transport behaviors in multiphysics systems, including heat transfer in a hybrid nanofluid flow in porous media. Another study by Alizadeh et al. (Alizadeh et al., 2021b) used an artificial neural network for predictive analysis of heat convection and entropy generation in a hybrid nanofluid flowing around a cylinder embedded in porous media. Machine learning also can assist in analyzing large amounts of experimental data to extract useful information and trends, accelerating research progress. For example, machine learning algorithms can be used to predict and optimize the surface properties, dispersibility, and flow behavior of nanoparticles (El-Amin et al., 2023). Moreover, machine learning can be used for simulating and optimizing the design and performance of the system containing nanofluid providing more efficient solutions (T. Ma et al., 2021).

At the nanoscale, the conventional principles of fluid mechanics and heat transfer may not hold true, thus necessitating innovative theories to decode the behavior of nanofluids. While machine learning could reveal unseen patterns and correlations within data, it does not guarantee the applicability of these trends under nanoscale constraints. Nanofluidic research, given its complex nature, requires experimental verification for the predictions formulated by machine learning models. However, this verification process often demands sophisticated instrumentation, advanced methodologies, and considerable financial resources, which may pose significant challenges and potentially exceed the capabilities of numerous research groups. Nanofluid systems are marked by a high degree of complexity due to the interaction among various components such as fluids, nanoparticles, and interfaces, thereby rendering the prediction process through machine learning models extremely challenging. Moreover, nanofluid research is data-intensive, and procuring the requisite amount of data can often be problematic.

5.2 Heat exchangers design and optimization

Machine learning algorithms can analyze large amounts of data, identify patterns, and make predictions or decisions without being explicitly programmed to perform the task. This ability to learn from data makes machine learning particularly useful in optimization problems, where the goal is to find the best solution among a set of possible solutions. It indicates that it can be a powerful tool for dealing with various engineering issues. It is reported that machine learning can potentially optimize the topology structure of heat exchangers. According to Fawaz (Fawaz et al., 2022), machine learning algorithms can be combined with a density-based topology algorithm, which is mainly aimed at structural design at the present stage (Sosnovik and Oseledets, 2019; Abueidda et al., 2020; Chandrasekhar and Suresh, 2021; Chi et al., 2021). Moreover, few studies are coupled with ML and Topology (TO) for HXs, which may be related to the complexity of coupled heat transfer (particularly the fluid flow part) and the complexity of HXs structure (Fawaz et al., 2022). Michalski (Michalski and Kaufman, 2006) introduced the Learnable Evolution Model (LEM), containing the hypothesis generation and instantiation to create new designs based on machine learning methods, which can automatically search for the highest capacity heat exchangers under given technical and environmental constraints. LEM has a wide range of potential applications, especially in complex domains, optimization, or search problems (Michalski, 2000). The results of the methods have been highly promising, producing solutions exceeding the performance of the best human designs (Michalski and Kaufman, 2006).

Although machine learning holds significant promise for the design and optimization of heat exchangers, however, it is crucial to acknowledge that the application of these techniques in this field is still in its infancy. The intricate physical phenomena and interactions involved in heat exchanger systems present a significant challenge for machine learning models. Despite the potential, there are substantial hurdles to overcome. Future work in this field should concentrate on enhancing the interpretability of machine learning models, as previously mentioned. Additionally, efforts should be made to develop methods for generating novel design concepts and to create high-quality datasets for training these models. By addressing these challenges, we can better harness the power of machine learning in the design and optimization of heat exchangers.

6 Conclusion

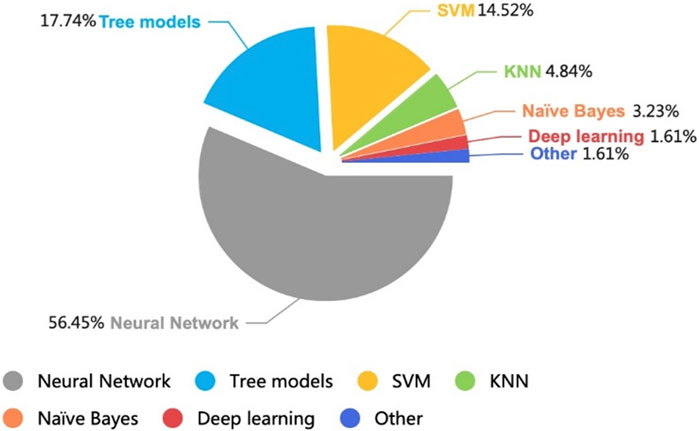
This paper provides a comprehensive review of heat exchanger modeling based on machine learning methods, drawing on literature published over the past 8 years. The review evidences a clear expansion of this field, with a significant publication growth rate observed after 2018. As shown in Figure 4, neural networks have been widely implemented, accounting for about 56% of the literature. This is attributed to their high prediction accuracy and powerful parallel and distributed processing capabilities. The paper systematically explores the entire gamut of heat exchanger modeling based on machine learning methods, focusing on types of algorithms, input parameters, output parameters, and error analysis. These insights can guide researchers in selecting appropriate machine learning models for various heat exchangers, predicting fouling factors, and thermodynamic properties of refrigerants, tailored to their specific objectives.

FIGURE 4

FIGURE 4. The proportion of publications on various machine learning methods.

Despite the promising performance of machine learning methods under the right database conditions, several limitations exist, including data overfitting, anomaly processing, limited scope, and low interpretability. Accordingly, feasible schemes have been introduced to mitigate these limitations. The paper also emphasizes the potential of Dimensionless Learning as discussed in Section 3. Specifically, incorporating the interplay between dimensionless numbers such as Re, We, and Fr numbers could provide a more generalizable and physically intuitive understanding of heat exchanger performance and fluid flow behavior. Furthermore, an area that is conspicuously underrepresented in the current literature is the modeling of surface roughness using machine learning methods, presenting a clear opportunity for future research.

Finally, two emerging areas, nanofluids in new energy applications and heat exchanger design optimization, are also discussed. The data-driven approach to machine learning offers new possibilities for thermal analysis of fluids, cycles, and heat exchangers with faster calculation and higher prediction accuracy. The information provided in this paper will greatly benefit researchers who aim to utilize machine learning methods in the field of heat exchangers and thermo-fluid systems in general.

Author contributions

JZ: Writing–original draft, Writing–review and editing, Investigation, Project administration. TH: Writing–review and editing, Methodology. JA: Writing–review and editing, Visualization. LH: Writing–review and editing, Conceptualization, Funding acquisition, Methodology, Project administration, Supervision. JC: Writing–review and editing, Conceptualization, Methodology, Supervision.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Natural Science Foundation of the Higher Education Institutions of Jiangsu Province, China (Grant No. 21KJB470011), State Key Laboratory of Air-conditioning Equipment and System Energy Conservation Open Project (Project No. ACSKL2021KT01) and the Research Development Fund (RDF 20-01-16) of Xi’an Jiaotong-Liverpool University. For the purpose of open access, the authors have applied a Creative Commons Attribution (CC-BY) licence to any Author Accepted Manuscript version arising from this submission.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abueidda, D. W., Koric, S., and Sobh, N. A. (2020). Topology optimization of 2D structures with nonlinearities using deep learning. Comput. Struct. 237, 106283. doi:10.1016/j.compstruc.2020.106283

CrossRef Full Text | Google Scholar

Abu-Khader, (2012). Plate heat exchangers: recent advances. Renew. Sustain. Energy Rev. 16, 1883–1891. doi:10.1016/j.rser.2012.01.009

CrossRef Full Text | Google Scholar

Adelaja, A. O., Dirker, J., and Meyer, J. P. (2017). Experimental study of the pressure drop during condensation in an inclined smooth tube at different saturation temperatures. Int. J. Heat Mass Transf. 105, 237–251. doi:10.1016/j.ijheatmasstransfer.2016.09.098

CrossRef Full Text | Google Scholar

Ahmad, H., Kim, S. K., Park, J. H., and Sung, Y. J. (2022). Development of two-phase flow regime map for thermally stimulated flows using deep learning and image segmentation technique. Int. J. Multiph. Flow 146, 103869. doi:10.1016/j.ijmultiphaseflow.2021.103869

CrossRef Full Text | Google Scholar

Ahmadi, M. H., Kumar, R., Mamdouh El Haj Assad, , and Phuong Thao Thi Ngo, (2021). Applications of machine learning methods in modeling various types of heat pipes: a review. J. Therm. Analysis Calorim. 146, 2333–2341. Springer Science and Business Media B.V. doi:10.1007/s10973-021-10603-x

CrossRef Full Text | Google Scholar

Ahmadi, M. H., Mohseni-Gharyehsafa, B., Ghazvini, M., Goodarzi, M., Jilte, R. D., and Kumar, R. (2020). Comparing various machine learning approaches in modeling the dynamic viscosity of CuO/water nanofluid. J. Therm. Analysis Calorim. 139 (4), 2585–2599. doi:10.1007/s10973-019-08762-z

CrossRef Full Text | Google Scholar

Alcacena, V., Alfredo, J. D. M., Rossi, F., and Lisboa, P. J. G. (2011). “Seeing is believing: the importance of visualization in real-world machine learning applications,” in Proceedings: 19th European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, ESANN 2011, Bruges, Belgium, April 27-28-29, 2011, 219–226.

Google Scholar

Alimoradi, H., Eskandari, E., Pourbagian, M., and Shams, M. (2022). A parametric study of subcooled flow boiling of Al2O3/water nanofluid using numerical simulation and artificial neural networks. Nanoscale Microscale Thermophys. Eng. 26 (2–3), 129–159. doi:10.1080/15567265.2022.2108949

CrossRef Full Text | Google Scholar

Alizadeh, R., Abad, J. M. N., Ameri, A., Mohebbi, M. R., Mehdizadeh, A., Zhao, D., et al. (2021a). A machine learning approach to the prediction of transport and thermodynamic processes in multiphysics systems - heat transfer in a hybrid nanofluid flow in porous media. J. Taiwan Inst. Chem. Eng. 124, 290–306. doi:10.1016/j.jtice.2021.03.043

CrossRef Full Text | Google Scholar

Alizadeh, R., Javad Mohebbi Najm Abad, , Fattahi, A., Mohebbi, M. R., Hossein Doranehgard, M., Larry, K. B. Li, et al. (2021b). A machine learning approach to predicting the heat convection and thermodynamics of an external flow of hybrid nanofluid. J. Energy Resour. Technol. 143 (7). doi:10.1115/1.4049454

CrossRef Full Text | Google Scholar

Amalfi, R. L., and Kim., J. (2021). “Machine learning-based prediction methods for flow boiling in Plate Heat exchangers,” in InterSociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems, ITHERM, San Diego, California, June-2021 (IEEE Computer Society), 1131–1139. doi:10.1109/ITherm51669.2021.9503302

CrossRef Full Text | Google Scholar

Amalfi, R. L., Vakili-Farahani, F., and Thome, J. R. (2016a). Flow boiling and frictional pressure gradients in Plate Heat exchangers. Part 1: review and experimental database. Int. J. Refrig. 61, 166–184. doi:10.1016/j.ijrefrig.2015.07.010

CrossRef Full Text | Google Scholar

Amalfi, R. L., Vakili-Farahani, F., and Thome, J. R. (2016b). Flow boiling and frictional pressure gradients in Plate Heat exchangers. Part 2: comparison of literature methods to database and new prediction methods. Int. J. Refrig. 61, 185–203. doi:10.1016/j.ijrefrig.2015.07.009

CrossRef Full Text | Google Scholar

Ardam, K., Najafi, B., Lucchini, A., and Rinaldi, F.Luigi Pietro Maria Colombo (2021). Machine learning based pressure drop estimation of evaporating R134a flow in micro-fin tubes: investigation of the optimal dimensionless feature set. Int. J. Refrig. 131, 20–32. November. doi:10.1016/j.ijrefrig.2021.07.018

CrossRef Full Text | Google Scholar

Ardhapurkar, P. M., and Atrey, M. D. (2015). “Prediction of two-phase pressure drop in heat exchanger for mixed refrigerant joule-thomson cryocooler,” in IOP Conference Series: Materials Science and Engineering, China, 3-6 August 2015 (IOP Publishing). 101:012111. doi:10.1088/1757-899X/101/1/012111

CrossRef Full Text | Google Scholar

Asadi, M., Ramin, Dr, and Khoshkhoo, H. (2013). Investigation into fouling factor in compact heat exchanger. Int. J. Innovation Appl. Stud. 2.

Google Scholar

Azencott, C.-A. (2018). Machine learning and genomics: precision medicine versus patient privacy. Philosophical Trans. R. Soc. A Math. Phys. Eng. Sci. 376 (2128), 20170350. doi:10.1098/rsta.2017.0350

PubMed Abstract | CrossRef Full Text | Google Scholar

Azizi, S., and Ahmadloo, E. (2016). Prediction of heat transfer coefficient during condensation of R134a in inclined tubes using artificial neural network. Appl. Therm. Eng. 106, 203–210. August. doi:10.1016/j.applthermaleng.2016.05.189

CrossRef Full Text | Google Scholar

Azizi, S., Ahmadloo, E., and Mohamed, M. A. (2016). Prediction of void fraction for gas–liquid flow in horizontal, upward and downward inclined pipes using artificial neural network. Int. J. Multiph. Flow 87, 35–44. doi:10.1016/j.ijmultiphaseflow.2016.08.004

CrossRef Full Text | Google Scholar

Bhattacharya, C., Chakrabarty, A., Laughman, C., and Qiao, H. (2022). Modeling nonlinear heat exchanger dynamics with convolutional recurrent networks. IFAC-PapersOnLine 55 (37), 99–106. doi:10.1016/j.ifacol.2022.11.168

CrossRef Full Text | Google Scholar

Bhutta, M. M. A., Hayat, N., Bashir, M. H., Khan, A. R., Ahmad, K. N., and Khan, S. (2012). “CFD applications in various heat exchangers design: a review.” applied thermal engineering. Amsterdam, Netherlands: Elsevier Ltd. doi:10.1016/j.applthermaleng.2011.09.001

CrossRef Full Text | Google Scholar

Bishop, C. M., and Nasrabadi, N. M. (2006). Pattern recognition and machine learning. Vol. 4. Cham: Springer.

Google Scholar

Cao, Y., Kamrani, E., Mirzaei, S., Khandakar, A., and Vaferi, B. (2022). Electrical efficiency of the photovoltaic/thermal collectors cooled by nanofluids: machine learning simulation and optimization by evolutionary algorithm. Energy Rep. 8, 24–36. doi:10.1016/j.egyr.2021.11.252

CrossRef Full Text | Google Scholar

Celebi, M. E., and Aydin, K. (2016). Unsupervised learning algorithms. Cham: Springer.

Google Scholar

Chandrasekhar, A., and Krishnan, S. (2021). TOuNN: topology optimization using neural networks. Struct. Multidiscip. Optim. 63 (3), 1135–1149. doi:10.1007/s00158-020-02748-4

CrossRef Full Text | Google Scholar

Chen, J., Gui, W., Dai, J., Jiang, Z., Chen, N., and Xu, Li (2021). A hybrid model combining mechanism with semi-supervised learning and its application for temperature prediction in roller hearth kiln. J. Process Control 98, 18–29. February. doi:10.1016/j.jprocont.2020.11.012

CrossRef Full Text | Google Scholar

Chen, Yu, Kong, G., Xu, X., Hu, S., and Yang, Q. (2023). Machine-learning-based performance prediction of the energy pile heat pump system. J. Build. Eng. 77, 107442. doi:10.1016/j.jobe.2023.107442

CrossRef Full Text | Google Scholar

Cheng, L., Ribatski, G., and Thome, J. R. (2008). Two-phase flow patterns and flow-pattern maps: fundamentals and applications. Appl. Mech. Rev. 61 (5). doi:10.1115/1.2955990

CrossRef Full Text | Google Scholar

Chi, H., Zhang, Y., Tsz Ling Elaine Tang, , Mirabella, L., Dalloro, L., Song, Le, et al. (2021). Universal machine learning for topology optimization. Comput. Methods Appl. Mech. Eng. 375, 112739. doi:10.1016/j.cma.2019.112739

CrossRef Full Text | Google Scholar

Chisholm, D. (1967). A theoretical basis for the lockhart-martinelli correlation for two-phase flow. Int. J. Heat Mass Transf. 10 (12), 1767–1778. doi:10.1016/0017-9310(67)90047-6

CrossRef Full Text | Google Scholar

Chokphoemphun, S., Somporn, H., Thongdaeng, S., and Chokphoemphun, S. (2020). Experimental study and neural networks prediction on thermal performance assessment of grooved channel air heater. Int. J. Heat Mass Transf. 163, 120397. December. doi:10.1016/j.ijheatmasstransfer.2020.120397

CrossRef Full Text | Google Scholar

Clark, L. A., and Pregibon, D. (2017). “Tree-based models,” in Statistical models in S (England, UK: Routledge), 377–419.

CrossRef Full Text | Google Scholar

Cunningham, P., Cord, M., and Jane Delany, S. (2008). “Supervised learning,” in Machine learning techniques for multimedia (Cham: Springer), 21–49. doi:10.1007/978-3-540-75171-7_2

CrossRef Full Text | Google Scholar

Dalkilic, A. S., Çebi, A., and Celen, A. (2019). Numerical analyses on the prediction of Nusselt numbers for upward and downward flows of water in a smooth pipe: effects of buoyancy and property variations. J. Therm. Eng. 5, 166–180. Yildiz Technical University Press. doi:10.18186/thermal.540367

CrossRef Full Text | Google Scholar

Dietterich, T. (1995). Overfitting and undercomputing in machine learning. ACM Comput. Surv. (CSUR) 27 (3), 326–327. doi:10.1145/212094.212114

CrossRef Full Text | Google Scholar

Dobbelaere, M. R., Plehiers, P. P., Van de Vijver, R., Stevens, C. V., and Van Geem, K. M. (2021). Machine learning in chemical engineering: strengths, weaknesses, opportunities, and threats. Engineering 7 (9), 1201–1211. doi:10.1016/j.eng.2021.03.019

CrossRef Full Text | Google Scholar

Du, R., Zou, J., An, J., and Huang, L. (2023). A regression-based approach for the explicit modeling of simultaneous heat and mass transfer of air-to-refrigerant microchannel heat exchangers. Appl. Therm. Eng. 235, 121366. Available at SSRN 4436121. doi:10.1016/j.applthermaleng.2023.121366

CrossRef Full Text | Google Scholar

Du, X., Chen, Z., Qi, M., and Song, Y. (2020). Experimental analysis and ANN prediction on performances of finned oval-tube heat exchanger under different air inlet angles with limited experimental data. Open Phys. 18 (1), 968–980. doi:10.1515/phys-2020-0212

CrossRef Full Text | Google Scholar

Dy, J. G., and Brodley, C. E. (2000). “Feature subset selection and order identification for unsupervised learning,” in Icml (Citeseer), 247–254.

Google Scholar

El-Amin, M. F., Alwated, B., and Hoteit, H. A. (2023). Machine learning prediction of nanoparticle transport with two-phase flow in porous media. Energies 16 (2), 678. doi:10.3390/en16020678

CrossRef Full Text | Google Scholar

El-Said, E. M., Abd Elaziz, M., and Elsheikh, A. H. (2021). Machine learning algorithms for improving the prediction of air injection effect on the thermohydraulic performance of shell and tube heat exchanger. Appl. Therm. Eng. 185, 116471. February. doi:10.1016/j.applthermaleng.2020.116471

CrossRef Full Text | Google Scholar

Ewim, D. R. E., Okwu, M. O., Onyiriuka, E. J., Abiodun, A. S., Abolarin, S. M., and Kaood, A. (2021). A quick review of the applications of artificial neural networks (ANN) in the modelling of thermal systems. Eng. Appl. Sci. Res. Paulus Editora. doi:10.14456/easr.2022.45

CrossRef Full Text | Google Scholar

Fawaz, A., Hua, Y., Le Corre, S., Fan, Y., and Luo, L. (2022). Topology optimization of heat exchangers: a review. Energy 252, 124053. doi:10.1016/j.energy.2022.124053

CrossRef Full Text | Google Scholar

Feurer, M., and Hutter, F. (2019). Hyperparameter optimization. Autom. Mach. Learn. Methods, Syst. Challenges, 3–33. doi:10.1007/978-3-030-05318-5_1

CrossRef Full Text | Google Scholar

Foley, A. (2013). How to model a shell and tube heat exchanger. COMSOL Blog. September 11, 2013.

Google Scholar

Gao, N., Wang, X., Xuan, Y., and Chen, G. (2019). An artificial neural network for the residual isobaric heat capacity of liquid HFC and HFO refrigerants. Int. J. Refrig. 98, 381–387. February. doi:10.1016/j.ijrefrig.2018.10.016

CrossRef Full Text | Google Scholar

Garcia, J. J., Garcia, F., Bermúdez, J., and Machado, L. (2018). Prediction of pressure drop during evaporation of R407C in horizontal tubes using artificial neural networks. Int. J. Refrig. 85, 292–302. January. doi:10.1016/j.ijrefrig.2017.10.007

CrossRef Full Text | Google Scholar

Gholizadeh, M., Jamei, M., Ahmadianfar, I., and Pourrajab, R. (2020). Prediction of nanofluids viscosity using random forest (RF) approach. Chemom. Intelligent Laboratory Syst. 201, 104010. doi:10.1016/j.chemolab.2020.104010

CrossRef Full Text | Google Scholar

Giannetti, N., Redo, M. A., Jeong, J., Yamaguchi, S., Saito, K., Kim, H., et al. (2020). Prediction of two-phase flow distribution in microchannel heat exchangers using artificial neural network. Int. J. Refrig. 111, 53–62. doi:10.1016/j.ijrefrig.2019.11.028

CrossRef Full Text | Google Scholar

Giri Nandagopal, M. S., Abraham, E., and Selvaraju, N. (2017). Advanced neural network prediction and system identification of liquid-liquid flow patterns in circular microchannels with varying angle of confluence. Chem. Eng. J. 309, 850–865. doi:10.1016/j.cej.2016.10.106

CrossRef Full Text | Google Scholar

Giri Nandagopal, M. S., and Selvaraju, N. (2016). Prediction of liquid–liquid flow patterns in a Y-junction circular microchannel using advanced neural network techniques. Industrial Eng. Chem. Res. 55 (43), 11346–11362. doi:10.1021/acs.iecr.6b02438

CrossRef Full Text | Google Scholar

Godfrey, N., Somtochukwu, B. K., Whidborne, J. F., and Rana, Z. (2021). Non-intrusive classification of gas-liquid flow regimes in an S-shaped pipeline riser using a Doppler ultrasonic sensor and deep neural networks. Chem. Eng. J. 403, 126401. doi:10.1016/j.cej.2020.126401

CrossRef Full Text | Google Scholar

Greenwell, B. M. (2017). Pdp: an R package for constructing partial dependence plots. R. J. 9 (1), 421. doi:10.32614/rj-2017-016

CrossRef Full Text | Google Scholar

Gupta, A. K., Kumar, P., Sahoo, R. K., Sahu, A. K., and Sarangi, S. K. (2017). Performance measurement of plate fin heat exchanger by exploration: ANN, ANFIS, ga, and sa. J. Comput. Des. Eng. 4 (1), 60–68. doi:10.1016/j.jcde.2016.07.002

CrossRef Full Text | Google Scholar

Guyon, I., and Elisseeff, A. (2003). An introduction to variable and feature selection andré elisseeff. J. Mach. Learn. Res. 3, 1157–1182. doi:10.1162/153244303322753616

CrossRef Full Text | Google Scholar

Guyon, I., Gunn, S., Nikravesh, M., and Zadeh, L. A. (2008). Feature extraction: foundations and applications. Vol. 207. Cham: Springer.

Google Scholar

Hall, S. (2012). “2 - heat exchangers,” in Branan’s rules of thumb for chemical engineers. Editor Stephen Hall. 5 (Oxford: Butterworth-Heinemann), 27–57. doi:10.1016/B978-0-12-387785-7.00002-5

CrossRef Full Text | Google Scholar

Hanus, R., Zych, M., Kusy, M., Jaszczur, M., and Petryka, L. (2018). Identification of liquid-gas flow regime in a pipeline using gamma-ray absorption technique and computational intelligence methods. Flow Meas. Instrum. 60, 17–23. doi:10.1016/j.flowmeasinst.2018.02.008

CrossRef Full Text | Google Scholar

Harpole, G. M., and Eninger, J. E. (1991). “Micro-Channel heat exchanger optimization,” in Proceedings - IEEE Semiconductor Thermal and Temperature Measurement Symposium, Phoenix, AZ, USA, 12-14 February 1991 (Publ by IEEE), 59–63. doi:10.1109/stherm.1991.152913

CrossRef Full Text | Google Scholar

Hassan, H., Abdelrahman, S.M.-B., and Gonzálvez-Maciá, J. (2016). Two-dimensional numerical modeling for the air-side of minichannel evaporators accounting for partial dehumidification scenarios and tube-to-tube heat conduction. Int. J. Refrig. 67, 90–101. July. doi:10.1016/j.ijrefrig.2016.04.003

CrossRef Full Text | Google Scholar

Hojjat, M. (2020). Nanofluids as coolant in a shell and tube heat exchanger: ANN modeling and multi-objective optimization. Appl. Math. Comput. 365, 124710. doi:10.1016/j.amc.2019.124710

CrossRef Full Text | Google Scholar

Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. U. S. A. 79, 2554–2558. doi:10.1073/pnas.79.8.2554

PubMed Abstract | CrossRef Full Text | Google Scholar

Hosseini, S., Khandakar, A., Chowdhury, M. E., Ayari, M. A., Rahman, T., Chowdhury, M. H., et al. (2022). Novel and robust machine learning approach for estimating the fouling factor in heat exchangers. Energy Rep. 8, 8767–8776. November. doi:10.1016/j.egyr.2022.06.123

CrossRef Full Text | Google Scholar

Hughes, M. T., Chen, S. M., and Garimella, S. (2022). Machine-learning-based heat transfer and pressure drop model for internal flow condensation of binary mixtures. Int. J. Heat Mass Transf. 194, 123109. September. doi:10.1016/j.ijheatmasstransfer.2022.123109

CrossRef Full Text | Google Scholar

Jabbar, H., and Khan, R. Z. (2015). Methods to avoid over-fitting and under-fitting in supervised machine learning (comparative study). Comput. Sci. Commun. Instrum. Devices 70. doi:10.3850/978-981-09-5247-1_017

CrossRef Full Text | Google Scholar

Jagielski, M., Carlini, N., Berthelot, D., Kurakin, A., and Papernot, N. (2020). “High accuracy and high fidelity extraction of neural networks,” in Proceedings of the 29th USENIX conference on security symposium, 1345–1362.

Google Scholar

Jensen, D. D., and Cohen, P. R. (2000). Multiple comparisons in induction algorithms. Mach. Learn. 38 (3), 309–338. doi:10.1023/A:1007631014630

CrossRef Full Text | Google Scholar

Khan, U., Pao, W., Sallih, N., and Hassan, F. (2022). Flow regime identification in gas-liquid two-phase flow in horizontal pipe by deep learning. J. Adv. Res. Appl. Sci. Eng. Technol. 27 (1), 86–91. doi:10.37934/araset.27.1.8691

CrossRef Full Text | Google Scholar

Kramer, O. (2013). Dimensionality reduction with unsupervised nearest neighbors 123. Intell. Syst. Ref. Libr. 51. doi:10.1007/978-3-642-38652-7

CrossRef Full Text | Google Scholar

Krishnayatra, G., Tokas, S., and Kumar, R. (2020). Numerical heat transfer analysis and predicting thermal performance of fins for a novel heat exchanger using machine learning. Case Stud. Therm. Eng. 21, 100706. October. doi:10.1016/j.csite.2020.100706

CrossRef Full Text | Google Scholar

Kumar, P. C. M., and Rajappa, B. (2020). A review on prediction of thermo physical properties of heat transfer nanofluids using intelligent techniques. Mater. Today Proc. 21, 415–418. doi:10.1016/j.matpr.2019.06.379

CrossRef Full Text | Google Scholar

Kunjuraman, S., and Velusamy, B. (2021). Performance evaluation of shell and tube heat exchanger through ANN and ANFIS model for dye recovery from textile effluents. Energy Sources, Part A Recovery, Util. Environ. Eff. 43 (13), 1600–1619. doi:10.1080/15567036.2020.1832627

CrossRef Full Text | Google Scholar

Kuzucanlı, S. A., Vatansever, C., Yaşar, A. E., and Karadeniz, Z. H. (2022). Assessment of fouling in Plate Heat exchangers using classification machine learning algorithms. doi:10.34641/clima.2022.127

CrossRef Full Text | Google Scholar

Kwon, B., Ejaz, F., and LeslieHwang, K. (2020). Machine learning for heat transfer correlations. Int. Commun. Heat Mass Transf. 116, 104694. July. doi:10.1016/j.icheatmasstransfer.2020.104694

CrossRef Full Text | Google Scholar

Li, Q., Qi, Z., Yu, S., Sun, J., and Cai, W. (2023). Study on thermal-hydraulic performance of printed circuit heat exchangers with supercritical methane based on machine learning methods. Energy 282, 128711. doi:10.1016/j.energy.2023.128711

CrossRef Full Text | Google Scholar

Li, Z., Aute, V., and Ling, J. (2019). Tube-fin heat exchanger circuitry optimization using integer permutation based genetic algorithm. Int. J. Refrig. 103, 135–144. doi:10.1016/j.ijrefrig.2019.04.006

CrossRef Full Text | Google Scholar

Li, Ze Yu, Shao, L. L., and Zhang, C.Lu (2016). Modeling of finned-tube evaporator using neural network and Response surface methodology. J. Heat Transf. 138 (5). doi:10.1115/1.4032358

CrossRef Full Text | Google Scholar

Lindqvist, K., Wilson, Z. T., Næss, E., and Sahinidis, N. V. (2018). A machine learning approach to correlation development applied to fin-tube bundle heat exchangers. Energies 11 (12), 3450. doi:10.3390/en11123450

CrossRef Full Text | Google Scholar

Longo, G. A., Giulia, R., Claudio, Z., Ludovico, O., Mauro, Z., and Brown, J. S. (2020c). “Application of an artificial neural network (ANN) for predicting low-GWP refrigerant condensation heat transfer inside herringbone-type brazed Plate Heat exchangers (BPHE)”. Int. J. Heat Mass Transf. 156, 119824. August. doi:10.1016/j.ijheatmasstransfer.2020.119824

CrossRef Full Text | Google Scholar

Longo, G. A., Simone, M., Giulia, R., Claudio, Z., Ludovico, O., and Mauro, Z. (2020b). Application of an artificial neural network (ANN) for predicting low-GWP refrigerant boiling heat transfer inside brazed Plate Heat exchangers (BPHE). Int. J. Heat Mass Transf. 160, 120204. October. doi:10.1016/j.ijheatmasstransfer.2020.120204

CrossRef Full Text | Google Scholar

Longo, G. A., Mancin, S., Righetti, G., Zilio, C., Ceccato, R., and Salmaso, L. (2020a). Machine learning approach for predicting refrigerant two-phase pressure drop inside brazed Plate Heat exchangers (BPHE). Int. J. Heat Mass Transf. 163, 120450. December. doi:10.1016/j.ijheatmasstransfer.2020.120450

CrossRef Full Text | Google Scholar

Ma, T., Guo, Z., Lin, M., and Wang, Q. (2021). Recent trends on nanofluid heat transfer machine learning research applied to renewable energy. Renew. Sustain. Energy Rev. 138, 110494. doi:10.1016/j.rser.2020.110494

CrossRef Full Text | Google Scholar

Ma, Y., Liu, C., Jiaqiang, E., Mao, X., and Yu, Z. (2022). Research on modeling and parameter sensitivity of flow and heat transfer process in typical rectangular microchannels: from a data-driven perspective. Int. J. Therm. Sci. 172, 107356. February. doi:10.1016/j.ijthermalsci.2021.107356

CrossRef Full Text | Google Scholar

Mahesh, B. (2018). Machine learning algorithms-A review machine learning algorithms-A review view Project self flowing generator view Project batta Mahesh independent researcher machine learning algorithms-A review. Int. J. Sci. Res. doi:10.21275/ART20203995

CrossRef Full Text | Google Scholar

Maleki, A., Haghighi, A, and Mahariq, I. (2021). Machine learning-based approaches for modeling thermophysical properties of hybrid nanofluids: a comprehensive review. J. Mol. Liq. 322, 114843. doi:10.1016/j.molliq.2020.114843

CrossRef Full Text | Google Scholar

Mangalathu, S., Hwang, S. H., and Jeon, J. S. (2020). Failure mode and effects analysis of RC members based on machine-learning-based SHapley additive ExPlanations (SHAP) approach. Eng. Struct. 219, 110927. doi:10.1016/j.engstruct.2020.110927

CrossRef Full Text | Google Scholar

Meghdadi Isfahani, A. H., Reiszadeh, M., Yaghoubi Koupaye, S., and Honarmand, M. (2017). Empirical correlations and an artificial neural network approach to estimate saturated vapor pressure of refrigerants. Phys. Chem. Res. 5 (2), 281–292. doi:10.22036/pcr.2017.41111

CrossRef Full Text | Google Scholar

Michalski, R. S. (2000). Learnable evolution model: evolutionary processes guided by machine learning. Mach. Learn. 38 (1), 9–40. doi:10.1023/A:1007677805582

CrossRef Full Text | Google Scholar

Michalski, R. S., and Kaufman, K. A. (2006). Intelligent evolutionary design: a new approach to optimizing complex engineering systems and its application to designing heat exchangers. Int. J. Intelligent Syst. 21 (12), 1217–1248. doi:10.1002/int.20182

CrossRef Full Text | Google Scholar

Mirzaei, M., Hassan, H., and Fadakar, H. (2017). Multi-objective optimization of shell-and-tube heat exchanger by constructal theory. Appl. Therm. Eng. 125, 9–19. doi:10.1016/j.applthermaleng.2017.06.137

CrossRef Full Text | Google Scholar

Mohanty, D. K. (2017). Application of neural network model for predicting fouling behaviour of a shell and tube heat exchanger. Int. J. Industrial Syst. Eng. 26, 228. doi:10.1504/IJISE.2017.083674

CrossRef Full Text | Google Scholar

Montañez-Barrera, J. A., Barroso-Maldonado, J. M., Bedoya-Santacruz, A. F., and Mota-Babiloni, A. (2022). Correlated-informed neural networks: a new machine learning framework to predict pressure drop in micro-channels. Int. J. Heat Mass Transf. 194, 123017. September. doi:10.1016/j.ijheatmasstransfer.2022.123017

CrossRef Full Text | Google Scholar

Moradkhani, M. A., Hosseini, S. H., and Karami, M. (2022a). Forecasting of saturated boiling heat transfer inside smooth helically coiled tubes using conventional and machine learning techniques. Int. J. Refrig. 143, 78–93. November. doi:10.1016/j.ijrefrig.2022.06.036

CrossRef Full Text | Google Scholar

Moradkhani, M. A., Hosseini, S. H., and Song, M. (2022b). Robust and general predictive models for condensation heat transfer inside conventional and mini/micro channel heat exchangers. Appl. Therm. Eng. 201, 117737. January. doi:10.1016/j.applthermaleng.2021.117737

CrossRef Full Text | Google Scholar

Moukalled, F., Mangani, L., and Darwish, M. (2016). Fluid mechanics and its applications the finite volume method in computational fluid dynamics. Cham: Springer. Available at: http://www.springer.com/series/5980.

Google Scholar

Müller-Steinhagen, H. (1999). “Cooling-water fouling in heat exchangers,” in Advances in heat transfer. Editors P. H. James, T. F. Irvine, Y. I. Cho, and G. A. Greene (Amsterdam, Netherlands: Elsevier), 33, 415–496. doi:10.1016/S0065-2717(08)70307-1

CrossRef Full Text | Google Scholar

Muthukrishnan, S., Krishnaswamy, H., Thanikodi, S., Sundaresan, D., and Venkatraman, V. (2020). Support vector machine for modelling and simulation of heat exchangers. Therm. Sci. 24, 499–503. 1PartB. doi:10.2298/TSCI190419398M

CrossRef Full Text | Google Scholar

Nabipour, M. (2018). Prediction of surface tension of binary refrigerant mixtures using artificial neural networks. Fluid Phase Equilibria 456, 151–160. January. doi:10.1016/j.fluid.2017.10.020

CrossRef Full Text | Google Scholar

Najafi, B., Ardam, K., Hanušovský, A., Rinaldi, F., and Luigi Pietro Maria Colombo, (2021). Machine learning based models for pressure drop estimation of two-phase adiabatic air-water flow in micro-finned tubes: determination of the most promising dimensionless feature set. Chem. Eng. Res. Des. 167, 252–267. March. doi:10.1016/j.cherd.2021.01.002

CrossRef Full Text | Google Scholar

Naphon, P., Wiriyasart, S., Arisariyawong, T., and Nakharintr, L. (2019). ANN, numerical and experimental analysis on the jet impingement nanofluids flow and heat transfer characteristics in the micro-channel heat sink. Int. J. Heat Mass Transf. 131, 329–340. doi:10.1016/j.ijheatmasstransfer.2018.11.073

CrossRef Full Text | Google Scholar

Onsager, L. (1931). Reciprocal relations in irreversible processes. I. Phys. Rev. 37 (4), 405–426. doi:10.1103/PhysRev.37.405

CrossRef Full Text | Google Scholar

Paris, G., Robilliard, D., and Fonlupt, C. (2003). “Exploring overfitting in genetic programming,” in International conference on artificial evolution (evolution artificielle) (Cham: Springer), 267–277. doi:10.1007/978-3-540-24621-3_22

CrossRef Full Text | Google Scholar

Patil, M. S., and Seo, J. H.Moo Yeon Lee (2017). “Heat transfer characteristics of the heat exchangers for refrigeration,” in Air conditioning and heap pump systems under frosting, defrosting and dry/wet conditions—a review.” applied thermal engineering (Amsterdam, Netherlands: Elsevier Ltd). doi:10.1016/j.applthermaleng.2016.11.107

CrossRef Full Text | Google Scholar

Peng, H., and Xiang, L. (2015). Predicting thermal-hydraulic performances in compact heat exchangers by support vector regression. Int. J. Heat Mass Transf. 84, 203–213. doi:10.1016/j.ijheatmasstransfer.2015.01.017

CrossRef Full Text | Google Scholar

Pourkiaei, S. M., Hossein Ahmadi, M., and Mahmoud Hasheminejad, S. (2016). Modeling and experimental verification of a 25W fabricated PEM fuel cell by parametric and GMDH-type neural network. Mech. Industry 17 (1), 105. doi:10.1051/meca/2015050

CrossRef Full Text | Google Scholar

Prigogine, I., and Van Rysselberghe, P. (1963). Introduction to thermodynamics of irreversible processes. J. Electrochem. Soc. 110 (4), 97C. doi:10.1149/1.2425756

CrossRef Full Text | Google Scholar

Prithiviraj, M., and Andrews, M. J. (1998). Three dimensional numerical simulation of shell-and-tube heat exchangers. Part I: foundation and fluid mechanics. Numer. Heat. Transf. Part A Appl. 33 (8), 799–816. doi:10.1080/10407789808913967

CrossRef Full Text | Google Scholar

Qiu, Y., Garg, D., Sung, M. K., Mudawar, I., and ChiragKharangate, R. (2021). Machine learning algorithms to predict flow boiling pressure drop in mini/micro-channels based on universal consolidated data. Int. J. Heat Mass Transf. 178, 121607. October. doi:10.1016/j.ijheatmasstransfer.2021.121607

CrossRef Full Text | Google Scholar

Ramezanizadeh, M., Hossein Ahmadi, M., Alhuyi Nazari, M., Sadeghzadeh, M., and Chen, L. (2019). “A review on the utilized machine learning approaches for modeling the dynamic viscosity of nanofluids,” in Renewable and sustainable energy reviews (Amsterdam, Netherlands: Elsevier Ltd). doi:10.1016/j.rser.2019.109345

CrossRef Full Text | Google Scholar

Rattan, P., Penrice, D. D., and Simonetto, D. A. (2022). Artificial intelligence and machine learning: what you always wanted to know but were afraid to ask. Gastro Hep Adv. 1 (1), 70–78. doi:10.1016/j.gastha.2021.11.001

CrossRef Full Text | Google Scholar

Roshani, G. H., Nazemi, E., and Roshani, M. M. (2017). A novel method for flow pattern identification in unstable operational conditions using gamma ray and radial basis function. Appl. Radiat. Isotopes 123, 60–68. doi:10.1016/j.apradiso.2017.02.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Roy, U., and Majumder, M. (2019). Evaluating heat transfer analysis in heat exchanger using NN with IGWO algorithm. Vacuum 161, 186–193. March. doi:10.1016/j.vacuum.2018.12.042

CrossRef Full Text | Google Scholar

Shannak, B. A. (2008). Frictional pressure drop of gas liquid two-phase flow in pipes. Nucl. Eng. Des. 238 (12), 3277–3284. doi:10.1016/j.nucengdes.2008.08.015

CrossRef Full Text | Google Scholar

Shen, C., Zheng, Q., Shang, M., Zha, Li, and Su, Y. (2020). Using deep learning to recognize liquid–liquid flow patterns in microchannels. AIChE J. 66 (8), e16260. doi:10.1002/aic.16260

CrossRef Full Text | Google Scholar

Shojaeefard, M. H., Zare, J., Tabatabaei, A., and Mohammadbeigi, H. (2017). Evaluating different types of artificial neural network structures for performance prediction of compact heat exchanger. Neural Comput. Appl. 28 (12), 3953–3965. doi:10.1007/s00521-016-2302-z

CrossRef Full Text | Google Scholar

Singh, A., Sahu, D., and Verma, Om P. (2022). Study on performance of working model of heat exchangers. Mater. Today Proc. Sept. doi:10.1016/j.matpr.2022.09.373

CrossRef Full Text | Google Scholar

Skrypnik, A. N., Shchelchkov, A. V., Gortyshov, Yu F., and Popov, I. A. (2022). Artificial neural networks application on friction factor and heat transfer coefficients prediction in tubes with inner helical-finning. Appl. Therm. Eng. 206, 118049. April. doi:10.1016/j.applthermaleng.2022.118049

CrossRef Full Text | Google Scholar

Sosnovik, I., and Oseledets, I. (2019). Neural networks for topology optimization. Russ. J. Numer. Analysis Math. Model. 34 (4), 215–223. doi:10.1515/rnam-2019-0018

CrossRef Full Text | Google Scholar

Subbappa, R., Aute, V., and Ling, J. (2022). Development and comparative evaluation of machine learning algorithms for performance approximation of air-to-refrigerant heat exchangers.

Google Scholar

Sun, L., Zhang, Y., Zheng, X., Yang, S., and Qin, Y. (2008). “Research on the fouling prediction of heat exchanger based on support vector machine,” in Proceedings - International Conference on Intelligent Computation Technology and Automation, ICICTA 2008, Changsha, Hunan, 20-22 October 2008, 240–244. 1. doi:10.1109/ICICTA.2008.156

CrossRef Full Text | Google Scholar

Sundar, S., Rajagopal, M. C., Zhao, H., Kuntumalla, G., Meng, Y., Chang, Ho C., et al. (2020). Fouling modeling and prediction approach for heat exchangers using deep learning. Int. J. Heat Mass Transf. 159, 120112. October. doi:10.1016/j.ijheatmasstransfer.2020.120112

CrossRef Full Text | Google Scholar

Thibault, J., and Grandjean, B. P. A. (1991). A neural network methodology for heat transfer data analysis. Int. J. Heat Mass Transf. 34, 2063–2070. doi:10.1016/0017-9310(91)90217-3

CrossRef Full Text | Google Scholar

Thombre, M., Mdoe, Z., and Johannes, J. (2020). Data-driven robust optimal operation of thermal energy storage in industrial clusters. Processes 8 (2), 194. doi:10.3390/pr8020194

CrossRef Full Text | Google Scholar

Uguz, S., and Osman, I. (2022). Prediction of the parameters affecting the performance of compact heat exchangers with an innovative design using machine learning techniques. J. Intelligent Manuf. 33 (5), 1393–1417. doi:10.1007/s10845-020-01729-0

CrossRef Full Text | Google Scholar

Vellido, A., José David Martín-Guerrero, , and Lisboa, P. J. G. (2012). “Making machine learning models interpretable,” in ESANN, 12 (Belgium: Bruges), 163–172.

Google Scholar

Wang, Bo, and Wang, J. (2021). “Application of artificial intelligence in computational fluid dynamics.” industrial and engineering chemistry research. Washington, United States: American Chemical Society. doi:10.1021/acs.iecr.0c05045

CrossRef Full Text | Google Scholar

Wang, Q., Xie, G., Zeng, M., and Luo, L. (2006). Prediction of heat transfer rates for shell-and-tube heat exchangers by artificial neural networks approach. J. Therm. Sci 15, 257–262. doi:10.1007/s11630-006-0257-6

CrossRef Full Text | Google Scholar

Wang, X., Li, Y., Yan, Y., Wright, E., Gao, N., and Chen, G. (2020). Prediction on the viscosity and thermal conductivity of hfc/hfo refrigerants with artificial neural network models. Int. J. Refrig. 119, 316–325. November. doi:10.1016/j.ijrefrig.2020.07.006

CrossRef Full Text | Google Scholar

Wiering, M. A., and Van Otterlo, M. (2012). Reinforcement learning. Adapt. Learn. Optim. 12 (3), 729. doi:10.1007/978-3-642-27645-3

CrossRef Full Text | Google Scholar

Xie, C., Yan, G., Ma, Q., Elmasry, Y., Singh, P. K., Algelany, A. M., et al. (2022a). Flow and heat transfer optimization of a fin-tube heat exchanger with vortex generators using Response surface methodology and artificial neural network. Case Stud. Therm. Eng. 39, 102445. November. doi:10.1016/j.csite.2022.102445

CrossRef Full Text | Google Scholar

Xie, X., Samaei, A., Guo, J., Liu, W. K., and Gan, Z. (2022b). Data-driven discovery of dimensionless numbers and governing laws from scarce measurements. Nat. Commun. 13 (1), 7562. doi:10.1038/s41467-022-35084-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, K. T. (2008). Artificial neural networks (ANNs): a new paradigm for thermal science and engineering. J. Heat Transf. 130 (9). doi:10.1115/1.2944238

CrossRef Full Text | Google Scholar

Zendehboudi, A., and Li, X. (2017). A robust predictive technique for the pressure drop during condensation in inclined smooth tubes. Int. Commun. Heat Mass Transf. 86, 166–173. August. doi:10.1016/j.icheatmasstransfer.2017.05.030

CrossRef Full Text | Google Scholar

Zhang, G., Wang, B., Li, X., Shi, W., and Cao, Y. (2019a). Review of experimentation and modeling of heat and mass transfer performance of fin-and-tube heat exchangers with dehumidification. Appl. Therm. Eng 146, 701–717. Elsevier Ltd. doi:10.1016/j.applthermaleng.2018.10.032

CrossRef Full Text | Google Scholar

Zhang, Xu, Zou, Y., Li, S., and Xu, S. 2019b. “A weighted auto regressive LSTM based approach for chemical processes modeling.” Neurocomputing 367: 64–74. doi:10.1016/j.neucom.2019.08.006

CrossRef Full Text | Google Scholar

Zheng, X., Yang, R., Wang, Q., Yan, Y., Zhang, Yu, Fu, J., et al. (2022). Comparison of GRNN and RF algorithms for predicting heat transfer coefficient in heat exchange channels with bulges. Appl. Therm. Eng. 217, 119263. November. doi:10.1016/j.applthermaleng.2022.119263

CrossRef Full Text | Google Scholar

Zhi, L. H., Hu, P., Chen, L. X., and Zhao, G. (2018). Viscosity prediction for six pure refrigerants using different artificial neural networks. Int. J. Refrig. 88, 432–440. doi:10.1016/j.ijrefrig.2018.02.011

CrossRef Full Text | Google Scholar

Zhou, L., Garg, D., Qiu, Y., Sung, M. K., Mudawar, I., and Chirag Kharangate, R. (2020a). Machine learning algorithms to predict flow condensation heat transfer coefficient in mini/micro-channel utilizing universal data. Int. J. Heat Mass Transf. 162, 120351. December. doi:10.1016/j.ijheatmasstransfer.2020.120351

CrossRef Full Text | Google Scholar

Zhou, X., Hu, Y., Liang, W., Ma, J., and Jin, Q. (2020b). Variational LSTM enhanced anomaly detection for industrial big data. IEEE Trans. Industrial Inf. 17 (5), 3469–3477. doi:10.1109/TII.2020.3022432

CrossRef Full Text | Google Scholar

Zhu, G., Wen, T., and Zhang, D. (2021a). Machine learning based approach for the prediction of flow boiling/condensation heat transfer performance in mini channels with serrated fins. Int. J. Heat Mass Transf. 166, 120783. doi:10.1016/j.ijheatmasstransfer.2020.120783

CrossRef Full Text | Google Scholar

Zhu, X., and Goldberg, A. B. (2009). Introduction to semi-supervised learning. Synthesis Lect. Artif. Intell. Mach. Learn. 3 (1), 1–130. doi:10.1007/978-3-031-01548-9

CrossRef Full Text | Google Scholar

Zhu, X. J. (2005). Semi-supervised learning literature survey. Available at: http://digital.library.wisc.edu/1793/60444.

Google Scholar

Zhu, Z., Li, J., Peng, H., and Liu, D. (2021b). Nature-inspired structures applied in heat transfer enhancement and drag reduction. Micromachines 12 (6), 656. doi:10.3390/mi12060656

PubMed Abstract | CrossRef Full Text | Google Scholar

Zolfaghari, H., and Yousefi, F. (2017). Thermodynamic properties of lubricant/refrigerant mixtures using statistical mechanics and artificial intelligence. Int. J. Refrig. 80, 130–144. August. doi:10.1016/j.ijrefrig.2017.04.025

CrossRef Full Text | Google Scholar

Nomenclature