- Economic and Technical Research Institute of State Grid Shanxi Electric Power Company, Taiyuan, China
Introduction: The urban distribution system plays a crucial role in efficient power distribution within urban areas. The increasing frequency and intensity of extreme events in recent years pose significant challenges to the reliable operation of urban distribution systems. While extensive research focuses on emergency frequency control strategies for large-scale power grids, there is a need for targeted attention to address the emergency frequency control challenges arising when the urban distribution system becomes isolated from the superior power grid due to extreme events.
Methods: This paper aims to enhance the system's resilience to extreme events by investigating the coordinated regulation of various resources within the urban distribution system. The studied resources include synchronous generators, wind farms, battery energy storage systems, temperature control loads, and conventional load resources. A reduced-order model for the multi-resource system’s frequency response is established. Analytical expressions for key parameters, including the lowest system frequency, lowest point time, and quasi-steady state frequency, are derived.
Results: To address the challenge of multi-resource coordinated regulation, an emergency frequency control strategy is proposed. This strategy takes into account the system safety frequency constraint, resource control amount constraint, and line power flow constraint. Simulations are conducted using the MATLAB/Simulink platform, considering IEEE 13 bus and IEEE 33 bus distribution systems as test cases.
Discussion: Simulation results demonstrate the effectiveness of the proposed method in regulating the distribution system's resources, ensuring that the lowest frequency remains within the safety threshold of 49.8 Hz. Moreover, the proposed method minimizes control costs and limits load shedding, thereby fully leveraging the capabilities of diverse resources in the urban distribution system. This research contributes valuable insights into addressing emergency frequency control challenges in urban distribution systems during extreme events.
1 Introduction
With the development of the national economy and society, the scale of the power grid is expanding. As the core link of the urban power system, the urban distribution system plays a vital role in the reliable and reasonable distribution of power to users (Sarma et al., 2017). In recent years, the frequency and intensity of extreme events have increased, bringing challenges to the safe operation of the urban distribution system. Large cities have essential political, economic, and social functions and many significant loads (Bevrani et al., 2021; Nga. et al., 2021). Once their distribution system gets impacted, it will significantly affect the city’s energy transmission and distribution and result in substantial societal losses (Prakash et al., 2022a). Severe natural disasters, deliberate attacks, and other extreme events can cause two main extreme scenarios: First, the critical transmission lines to the distribution system are destroyed, and the distribution system will be passively disconnected from the superior power grid; the second is the continuous fault of the superior power grid, which leads to the global or regional blackout accident of the urban distribution system. In order to protect itself, the distribution system can choose to disconnect from the superior power grid. The frequency drops because there will be a large power shortage after the distribution system is disconnected from the superior power grid. Therefore, it is necessary to have corresponding emergency control strategies to avoid frequency safety accidents. This strategy can ensure that the distribution system can switch to island operation, maintain an uninterrupted power supply of important loads, and improve the reliability and flexibility of the power system. However, existing research primarily focuses on the large power grid’s frequency response model modeling and emergency frequency control strategy formulation, with little research on emergency frequency control after the distribution system is disconnected from the superior (Dreidy et al., 2017; Ju et al., 2021; Qinglei. et al., 2023).
In the research of system frequency response (SFR) model of large power grid, Zhongda. et al. (2020), Prakash et al. (2022b) and Zhang et al. (2022) studies the frequency response model of wind turbine system and the control method of frequency regulation using wind turbine. Obaid et al. (2020), Alcaide-Godinez et al. (2022), Huang and Yang (2022) and Tang et al. (2022) models and controls multiple battery energy storage systems (BESS) to provide frequency response. Considering the response of storage units, an improved reduced-order SFR power system model is proposed in Li et al. (2021) and Yahong et al. (2022). Alhelou et al. (2020) and Yuan et al. (2021) proposed a frequency response model using electric vehicles as virtual power plants (VPPS) on the demand side to improve the frequency response capability of the whole system. Mohamed et al. (2022) proposed a frequency response model of a hybrid energy storage system, which is composed of a photovoltaic (PV), synchronous generator (SG), energy storage system, and load.
In the research of emergency frequency control strategy (EFC) in large power grid, Alhelou et al. (2018) and Zeyad et al. (2019) summarizes the methods of emergency frequency control in large power grid by using synchronous machines, energy storage systems, electric vehicles, HVDC support, and load, respectively. Liu et al. (2022) uses the central air conditioning load to participate in emergency frequency control after a sudden large power shortage of the receiving power grid, such as an HVDC blocking fault. Fang et al. (2017), Choi et al. (2019) and Xuekuan et al. (2021) proposed an adaptive emergency frequency control strategy for battery energy storage systems. Shi et al. (2021) and Wei et al. (2023) uses wind farms to support emergency frequency control of power systems. Changgang et al. (2020) studies the method of adaptive load shedding in emergency frequency control.
The urban distribution system contains rich source-load-storage resources (Patel et al., 2019; Das et al., 2023). The emergency frequency control strategy can quickly allocate controllable resources to ensure frequency stability. However, there is little research on the coordinated regulation of various sources, loads, and storage resources. So, it is necessary to fully consider the coordination of various resources when formulating an emergency frequency control strategy. “Source” refers to synchronous machines and wind farms, “load” refers to conventional loads and temperature control loads, and “storage” refers to battery energy storage resources. Among them, the urban distribution system has many electric water heater loads with energy storage characteristics. Because its short-time switching or adjusting the set temperature has little impact on user comfort and has thermal inertia, it can be used as a demand response resource (DR) (Khan et al., 2015; Wu and Tang, 2019; Gasca et al., 2022; Xiang et al., 2022). A large number of electric water heater loads can be aggregated into aggregated temperature control loads (ATL) to enhance the system inertia (Ruisheng et al., 2012). Because of its advantages of fast response, low cost, and zero pollution, it has gradually become an important frequency modulation resource. Nevertheless, at present, the research on the control and scheduling of this kind of temperature control load is less. Through reasonable coordination of source load storage resources, the resilience of the urban distribution system to cope with disturbances can be improved, and a robust local power grid in the city can be built.
In the realm of traditional emergency frequency control strategies, the primary method of ensuring frequency stability revolves around the inherent frequency modulation capacity of synchronous machines. In certain scenarios, these strategies may involve the coordinated participation of synchronous machines, wind farms, and energy storage systems in frequency regulation. However, the potential shortfall in the system’s ability to modulate frequency can necessitate load-shedding, a practice that, when employed in distribution systems, can notably degrade the end-user experience. Of even greater concern is the significant societal impact that arises from the disconnection of critical loads. In light of these challenges, our proposed strategy introduces a noteworthy innovation by incorporating temperature control loads and orchestrating the rational coordination of diverse power sources within the distribution system. This innovative approach amalgamates these resources into a unified system, substantially amplifying the system’s frequency modulation capabilities and, as a result, significantly reducing or even eliminating the need for load-shedding. This pivotal advancement promises substantial benefits to the entire distribution system and its users.
The difficulty of the current research is that the response characteristics of various resources are different, and the problem of how to aggregate and coordinate multi-resource needs to be solved. Based on the aggregation of multi-resource, this paper will quantitatively calculate the lowest point of the system frequency, the lowest point time, and the quasi-steady state frequency of the system through the derivation of an analytical formula so as to support the implementation of the emergency frequency control strategy. In order to solve the emergency frequency control problem of the distribution system with multi-resource coordinated regulation, the work done in this paper is as follows:
1. The frequency response characteristics of each resource are analyzed, and a multi-resource SFR model is established, including synchronous machines, wind farms, battery energy storage systems, temperature control loads, and conventional loads.
2. According to the reduced order model of SFR, the analytical expressions of the lowest point of frequency, the time of the lowest point, and the quasi-steady state frequency of the analytical system are derived.
3. An EFC decision-making strategy for multi-resource coordinated control is proposed, considering system security frequency constraints, resource control constraints, and line power flow constraints. The power of controllable resources in emergency frequency control is obtained by optimizing decisions.
The rest of this paper is arranged as follows: In the first section, the system frequency response model of multi-resources, including synchronous machines, wind farms, battery energy storage systems, temperature control loads, and conventional loads, will be derived and reduced. In the second section, the analytical expressions of the lowest point of the system frequency and the quasi-steady state frequency will be derived. The third section puts forward the emergency frequency control strategy. In the fourth section, the effectiveness of the proposed strategy will be verified by simulation. The fifth section summarizes the work done in this paper.
2 System frequency response model
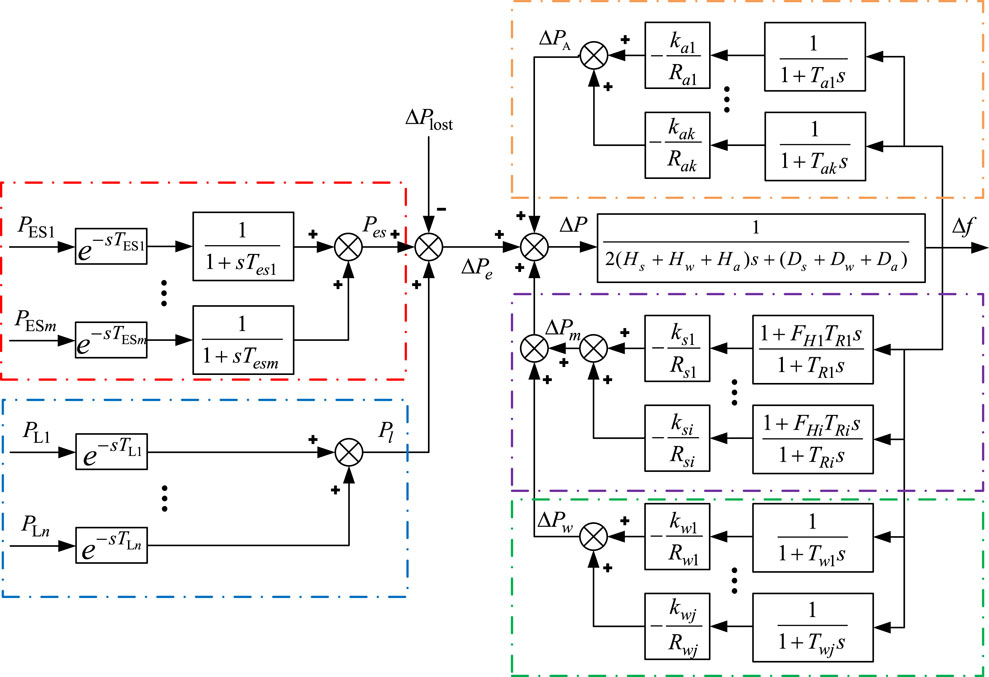
In this section, we construct a reduced-order SFR model that includes SG, WF, BESS, ATL, and load resources. In a system with a high penetration of renewable energy, the reduction of system inertia may affect the accuracy of the SFR model.
2.1 Synchronous generator
When a disturbance occurs, SG will respond according to the rotor motion equation under the action of unbalanced torque (Anderson and Mirheydar, 1990):
In the formula,
The generator governor will respond to power imbalance, and its characteristics can be described as follows:
In the formula,
In the frequency response model of multi-SG system, the capacity difference between units makes the disturbance power shared between units different, which will change at different speeds, and the influence weight on the system is expressed by the proportion coefficient
In the formula,
2.2 Wind farm
When the disturbance occurs, the wind turbine will respond according to the rotor motion equation under the action of unbalanced torque (Sudipta et al., 2016; Huang et al., 2022):
In the formula,
The governor dynamic description is as follows:
In the formula,
Similarly, in the frequency response model of the multi-WF system, the influence weight of wind farms with different capacities on the system is expressed as a proportion coefficient
In the formula,
2.3 Aggregated temperature control load
The key to temperature control loads participating in system frequency regulation is to respond to the change in system frequency through its power consumption (Conte et al., 2021).
The temperature control load used in this paper is a typical temperature-controlled household electric water heater, and the electric heating wire is a pure resistive electric load. The purpose of frequency control can be achieved by changing the load power. When a disturbance causes the system’s frequency to fluctuate, the power consumption is adjusted by using the linear relationship between the target temperature change value and the frequency deviation. As a result, the adaptive load regulation of an electric water heater contributes to frequency response.
In the formula,
In the formula,
The larger the
The way temperature control load aggregation participates in the primary frequency regulation of the power grid is frequency droop control. The demand response aggregator acts as a virtual generator to respond to the frequency modulation demand, and responds according to the rotor motion equation under unbalanced torque:
In the formula,
Here, the governor of the first-order inertia link is considered, so the equivalent transfer function of temperature control load participating in primary frequency regulation can be expressed as:
In the formula,
Similarly, in the frequency response model of multi ATL system, the influence weight of polymerization units with different capacities on the system is represented by the proportion coefficient
In the formula,
2.4 Battery energy storage system and load shedding
BESS can achieve millisecond response, and the time scale of primary frequency regulation is typically seconds, so the frequency response function of BESS can be expressed by a delay function and a first-order inertial link:
In the formula,
The control function of the load can be expressed by a delay function with time constant
In the formula,
2.5 Frequency response reduced-order model of multi-resource system
They are considering the frequency response characteristics of various resources, including synchronous machines, wind farms, battery energy storage systems, temperature control loads, and conventional loads. The multi-resource SFR model is established, as shown in Figure 1. The frequency variation in the power grid can usually be regarded as the unity of the whole system, so the inertia of each unit of SG, WF, and ATL can be superimposed according to the unified standard during synchronous operation, which is equivalent to one unit providing the overall inertia of the system, and the response time constant is very small, which is simplified after ignoring. The parameters of the reduced order model are as follows:
In the formula,
Since the response time of BESS and load is fast, it is assumed that the time constant can be ignored. The parameters of the reduced model are as follows:
In the formula,
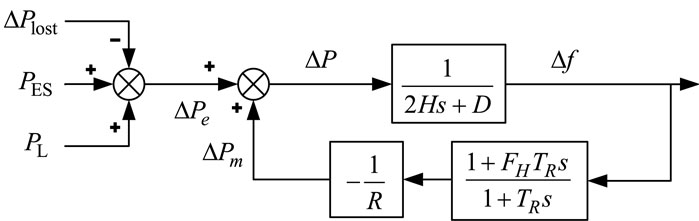
In summary, the reduced-order model is shown in Figure 2.
3 Analytical expression of frequency
Based on the reduced-order system frequency response model, the analytical expressions of frequency nadir and quasi-steady state frequency can be derived (Liu. et al., 2020).
3.1 Frequency nadir
The change of the power shortage of the system can be expressed as:
In the formula,
According to the transfer function in Figure 2, the expression of
Considering that the step type disturbance in the power system is the most common and has the greatest impact, such as generator cut-off, sudden load increase, et cetera, assume that
The expression of frequency change
Where
According to the superposition principle of linear system, the frequency deviation
Combined with Formulas (16–20), the analytical formulas of the frequency nadir
In the formula,
3.2 Quasi-steady state frequency
After the frequency of the system passes through the lowest frequency point, the primary frequency regulation makes the system return to the quasi-steady state frequency. The expression of quasi-steady state frequency is:
In the formula,
4 Emergency frequency control strategy
In this section, an EFC decision-making strategy for multi-resource coordinated control is proposed, considering system security frequency constraints, resource control constraints, and line power flow constraints. The coordinated regulation and control of multi-resource such as synchronous machines, wind farms, battery energy storage systems, temperature control loads, and conventional loads ensures the system frequency safety under fault. The basic framework is shown in Figure 3. The decision variables of the proposed decision-making strategy are controllable electric energy storage system output
4.1 System frequency constraints
The analytical expressions of frequency minima and quasi-steady state frequencies have a linear relationship with the decision variables. Frequency constraints include frequency minima and quasi-steady state frequency constraints.
In the formula,
During regular operation, the system frequency deviation is required to be controlled at ±0.2 Hz to set an appropriate constraint boundary.
4.2 Control amount constraints of multi-resource
To prevent the control amount of each resource exceeding its own limits, it is necessary to constrain the control amount of each resource.
In the formula,
4.3 The power flow constraints on transmission lines
The power flow constraints are set on all transmission lines to ensure the power flow on transmission lines does not exceed their limits, which are as follows:
In the formula,
4.4 The emergency frequency control strategy
The EFC decision optimization aims at the minimum control cost, which is a mixed integer linear programming (MILP) problem considering frequency constraints. The decision variables are controllable electric energy storage output power
In the formula,
The weight coefficient is related to the priority of the control resources, and the resources with smaller weight coefficients are scheduled preferentially. Dispatchers can set the weight coefficients of different resources according to the control requirements of the system. In the actual power system, the control cost of BESS is usually low, and the cost of load shedding is the highest.
5 Simulation results
Through simulation examples, we aim to validate our approach’s emphasis on maximizing the system’s inherent frequency modulation capabilities and resorting to load-shedding only when deemed absolutely necessary, thus presenting clear and unique advantages compared to traditional control strategies.
This chapter will set up two simulation examples in IEEE 13 bus distribution system and IEEE 33 bus distribution system to verify the applicability of the emergency frequency control strategy.
5.1 Accuracy analysis
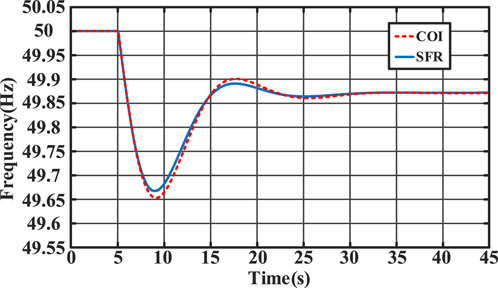
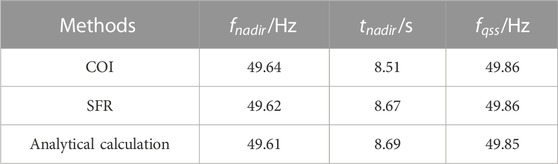
This section initiates the verification of the accuracy of the frequency response reduction model and conducts a frequency analysis of the multi-resource system through simulation. To facilitate this verification, a three-machine nine-node system, as depicted in Figure 4, is employed as the simulation framework. The system’s initial state is configured to be in normal operation, and a disturbance, in the form of a 0.1 per unit (p.u.) active power deficiency, is introduced at 5 s. The center of inertia (COI) frequency is employed as the representative metric for the system’s frequency behavior during time-domain simulations. The simulation results, presented in Figure 5, provide a visual representation of the system’s response to the introduced disturbance.
Analysis of the obtained results, as illustrated in Figure 5 and summarized in Table 1, reveals a notable congruence between the COI frequency curve derived from time-domain simulations and the frequency curve predicted by the SFR transfer function model developed in this study. Additionally, the results computed using the frequency analytical formula align closely with the outcomes of the time-domain simulations. This consistency underscores the accuracy and precision of both the SFR transfer function model introduced in this paper and the associated frequency analytical formula. These modeling approaches, in conjunction with the time-domain simulation, exhibit minimal discrepancies, thus affirming their reliability and robustness.
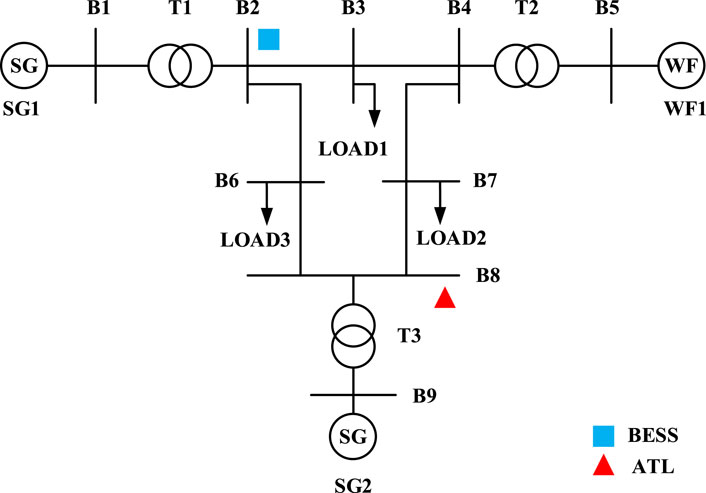
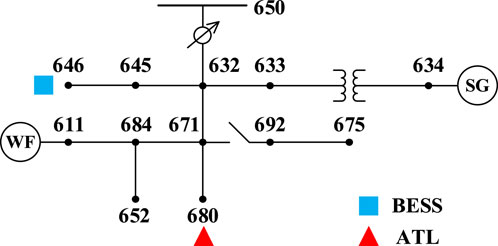
5.2 IEEE 13 bus distribution system
The modified IEEE 13 bus distribution system is adopted for the test, and the structure is shown in Figure 6. SG, WF, BESS, and ATL are set, respectively. The system’s initial state is set to operate normally, and then the power distribution system is disconnected from the superior power grid due to the accident, resulting in the disturbance of active power shortage. In order to illustrate the feasibility and effectiveness of the EFC strategy, the influence of the EFC strategy decision on the primary frequency regulation of the system will be compared.
Two test scenarios will be set: (1) Set the total capacity of BESS participating in frequency modulation to 0.03p.u. and the total capacity of removable load to 0.05p.u. The system initially operates normally. At 10 s, the active power shortage of 0.12p.u. occurs suddenly in the stable system. (2) Set the total capacity of BESS participating in frequency modulation as 0.05p.u. and the total capacity of removable load to 0.05p.u. The system initially operates normally. At 10 s, the active power shortage of 0.1p.u. occurs suddenly in the stable system.
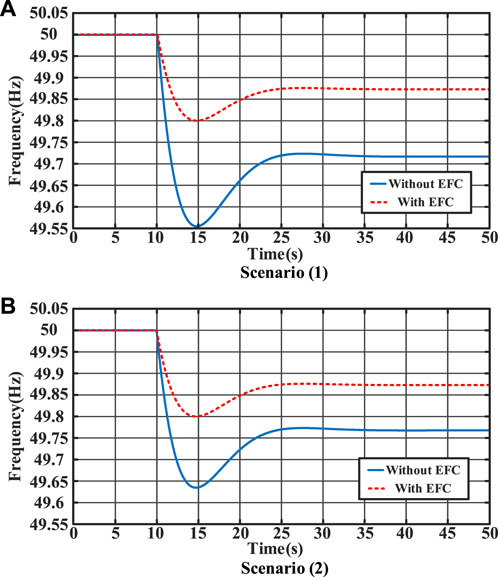
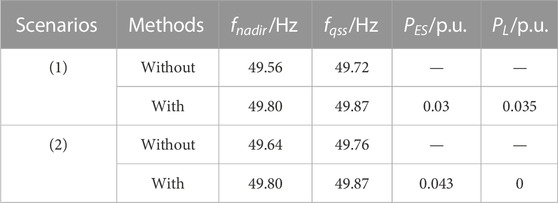
Figure 7 and Table 2 provide a clear representation of the system’s frequency transient change process. Without the application of the EFC strategy, the system’s lowest frequency exhibits a significant decline to 49.56 Hz, with the quasi-steady state frequency stabilizing at 49.72 Hz.
In Scenario (1), the EFC strategy is implemented, resulting in an initial energy storage system output of 0.03 p.u. This prioritization of the energy storage system leads to the utilization of its entire output capacity. However, due to the limited energy storage system capacity, this output alone is insufficient to restore the system frequency to a safe operating level. Consequently, a load shedding of 0.035 p.u. becomes necessary. Subsequently, the lowest system frequency rises to 49.80 Hz, and the quasi-steady state frequency increases to 49.87 Hz. In contrast, in Scenario (2) with the EFC strategy, the energy storage system exhibits an output of 0.043 p.u. Since this output remains within the energy storage system’s operational limits, no load shedding is required. Consequently, the lowest system frequency is restored to 49.80 Hz, with the quasi-steady state frequency reaching 49.87 Hz.
The test results confirm the EFC strategy’s effectiveness in raising both the lowest and quasi-steady state frequencies to levels within the defined safety thresholds. Furthermore, it successfully allocates the output of controllable resources in an efficient manner. This empirical validation underscores the feasibility and efficacy of the proposed EFC strategy.
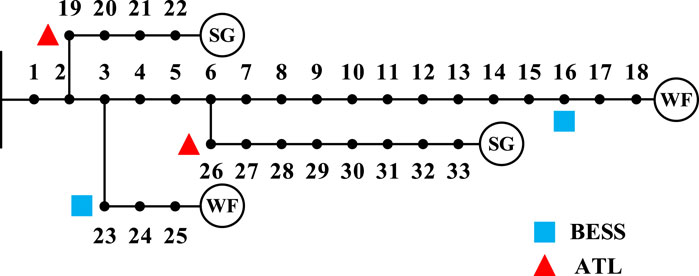
5.3 IEEE 33 bus distribution system
Our approach to emergency frequency control aims to address the limitations of traditional methods that predominantly rely on the frequency modulation capability of synchronous machines or involve various combinations of synchronous machines, wind farms, and energy storage systems. These conventional strategies, while effective to a certain extent, may result in load-shedding if the system’s frequency modulation ability falls short of requirements. In the context of distribution systems, load-shedding can lead to an unsatisfactory user experience and have significant societal implications, especially when essential loads are disconnected. In our proposed method, we have introduced an innovative approach by incorporating temperature control loads and optimizing the coordination of multiple power sources within the distribution system. This innovation allows us to aggregate these resources effectively, thereby enhancing the system’s frequency regulation capabilities. The ultimate goal is to minimize or eliminate load-shedding, which is advantageous for both the distribution system’s overall performance and the satisfaction of its users.
The modified IEEE 33 bus distribution system is adopted for the test, and the structure is shown in Figure 8. SG, WF, BESS, and ATL are set at two places, respectively. The system initially operates normally. Then, the distribution system is disconnected from the superior power grid due to the accident, resulting in the disturbance of active power shortage. In order to illustrate the feasibility and effectiveness of multi-resource regulation, the effect of EFC strategy with or without multi-resource regulation on the primary frequency regulation of the system will be compared.
The system initially operates normally. However, at 10 s, the active power shortage occurs suddenly in the stable system. To assess the impact of frequency modulation by different resource combinations, we establish the following test scenarios:
Scenario 1. A sudden active power shortage of 0.1 p.u. occurs at 10 s in the stable system. We evaluate the frequency modulation effects using the following combinations:
Case 1. SG only
Case 2. SG and WF
Case 3. SG, WF, and ATL
Case 4. SG, WF, ATL, BESS, and load
Scenario 2. A sudden active power shortage of 0.5 p.u. occurs at 10 s in the stable system. We assess the frequency modulation effects with the same combinations as in Scenario 1.
These scenarios enable a comprehensive examination of the frequency modulation capabilities of the specified resource combinations under varying degrees of active power shortage in the power system.
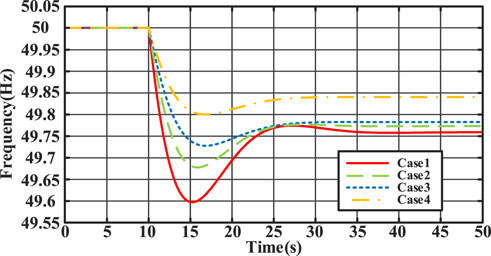
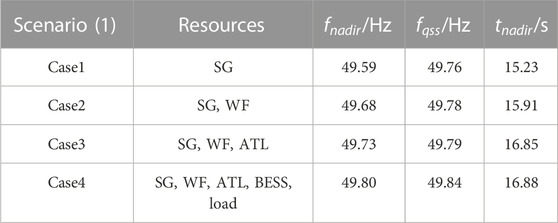
Analysis of the system’s primary frequency response, as depicted in Figure 9 and summarized in Table 3, reveals the impact of various resource combinations on system frequency during disturbance scenarios. In scenario (1), where only the SG is engaged in frequency modulation, the system’s lowest frequency is observed at 49.59 Hz, with a quasi-steady state frequency of 49.76 Hz. This initial assessment underscores the limitation of relying solely on a single resource for maintaining frequency stability within the distribution system during disturbances. Upon introducing WF in conjunction with SG for frequency modulation, we observe an improvement in the system’s primary frequency response. The lowest frequency in this case is 49.68 Hz, with a quasi-steady state frequency of 49.77 Hz, demonstrating the beneficial impact of combining resources. Expanding the resource pool further to include ATL alongside SG and WF for frequency modulation results in a more robust primary frequency modulation capability. The system’s lowest frequency in this configuration is measured at 49.73 Hz, with a quasi-steady state frequency of 49.78 Hz. However, it is still not enough to ensure that the system frequency is within the safety threshold until SG, WF, ATL, BESS, and load-shedding participation in frequency modulation. The lowest frequency observed in this comprehensive scenario is 49.80 Hz, with a quasi-steady state frequency of 49.84 Hz.
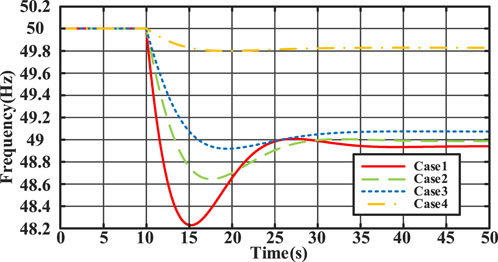
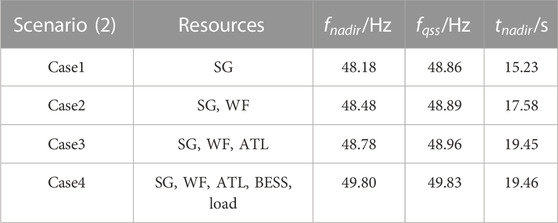
Analysis of the system’s primary frequency response, as depicted in Figure 10 and summarized in Table 4. In scenario (2), where only the SG is engaged in frequency modulation, the system’s lowest frequency is observed at 48.18 Hz, with a quasi-steady state frequency of 48.86 Hz. Upon introducing WF alongside SG for frequency modulation, the lowest system frequency increases to 48.48 Hz, with a quasi-steady state frequency of 48.89 Hz. Furthermore, the addition of ATL to frequency modulation raises the lowest frequency to 48.78 Hz, with the quasi-steady state frequency reaching 48.96 Hz. Subsequently, the involvement of BESS and load-shedding participation in frequency modulation further enhances the system’s frequency stability. In this configuration, where SG, WF, ATL, BESS, and load-shedding collectively engage in frequency modulation, the lowest system frequency significantly improves, measuring 49.80 Hz, while the quasi-steady state frequency closely follows at 49.83 Hz.
The test results have indeed conducted a comparative analysis of various resource combinations, including those found in existing methods, show that the regulation of multi-resource in the distribution system can improve the primary frequency regulation ability of the distribution system in response to disturbances. Moreover, the EFC strategy can improve the system’s lowest frequency and quasi-steady state frequency within the safety threshold, ensuring the safe and stable operation of the distribution system in the event of an accident. These results unequivocally demonstrate that our proposed strategy outperforms the alternatives, delivering superior outcomes in terms of system frequency regulation during emergency scenarios.
6 Conclusion
In this paper, we have introduced an innovative decision-making strategy for emergency frequency control to orchestrate and regulate multiple resources within urban distribution systems, addressing the critical issue of frequency safety during extreme events. Our research emphasizes a comprehensive analysis of the frequency response characteristics of a diverse set of resources, including synchronous generators, wind farms, battery energy storage systems, aggregated temperature control loads, and conventional load resources. We have successfully developed a reduced-order system frequency response model to capture the dynamic behavior of these resources under emergency conditions. Subsequently, we derived and thoroughly analyzed key metrics, including the lowest point of the system frequency, the lowest point time, and the quasi-steady state frequency. To ensure the practicality and viability of our EFC strategy, we incorporated multiple constraints into our decision model, resulting in a coherent and effective multi-resource control strategy.
To validate the efficacy of the proposed strategy, we implemented simulations using the MATLAB/Simulink platform, considering IEEE 13 bus and IEEE 33 bus distribution systems as representative test cases. The simulation outcomes unequivocally affirm the capability of the proposed strategy to maintain the system frequency within prescribed safety thresholds. Furthermore, the strategy exhibits a notable capability to optimize the utilization of diverse resources within the distribution system while significantly mitigating the necessity for load-shedding. In comparison to conventional load-shedding methods employed for emergency frequency control, the proposed strategy displays a distinct advantage. It actively orchestrates and regulates multiple resources, leading to reduced frequency deviations and minimized load-shedding requirements, thereby culminating in enhanced operational performance and stability.
The significance of this research extends beyond academic curiosity, as it directly impacts the energy industry and the wider community. By offering a robust solution to emergency frequency control in urban distribution systems, our work contributes to the stability and resilience of energy supply, ultimately enhancing the quality of life for residents and supporting the sustainability of urban infrastructure. Building on the insights gained from this research, future research can focus on several promising directions. These include the implementation of our EFC strategy in real-world distribution systems, the development of advanced control algorithms to optimize resource utilization, and the exploration of additional constraints and operational scenarios. Furthermore, it provides a foundation for the integration of renewable energy sources and advanced energy storage technologies, paving the way for a more sustainable and efficient energy ecosystem.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
ZS: Conceptualization, Methodology, Writing–original draft. CW: Writing–original draft. YW: Validation, Writing–review and editing. HZ: Supervision, Validation, Writing–review and editing. ZW: Supervision, Validation, Writing–review and editing. EH: Writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The authors declare that this research was funded by the Technology Project of State Grid Shanxi Electric Power Company (520533220007). The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.
Conflict of interest
Authors ZS, CW, YW, HZ, ZW, and EH are employed by the Economic and Technical Research Institute of State Grid Shanxi Electric Power Company.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alcaide-Godinez, I., Bai, F., Saha, T. K., and Castellanos, R. (2022). Contingency reserve estimation of fast frequency response for battery energy storage system. Int. J. Electr. Power and Energy Syst. 143, 108428. doi:10.1016/j.ijepes.2022.108428
Alhelou, H. H., Hamedani-Golshan, M., Zamani, R., Heydarian-Forushani, E., and Siano, P. (2018). Challenges and opportunities of load frequency control in conventional, modern and future smart power systems: a comprehensive review. Energies 11 (10), 2497. doi:10.3390/en11102497
Alhelou, H. H., Siano, P., Tipaldi, M., Iervolino, R., and Mahfoud, F. (2020). Primary frequency response improvement in interconnected power systems using electric vehicle virtual power plants. World Electr. Veh. J. 11 (2), 40. doi:10.3390/wevj11020040
Anderson, P. M., and Mirheydar, M. (1990). A low-order system frequency response model. IEEE Trans. Power Syst. 5 (3), 720–729. doi:10.1109/59.65898
Bevrani, H., Golpîra, H., Messina, A. R., Hatziargyriou, N., Milano, F., and Ise, T. (2021). Power system frequency control: an updated review of current solutions and new challenges. Electr. Power Syst. Res. 194, 107114. doi:10.1016/j.epsr.2021.107114
Changgang, Li, Yue, Wu, Yanli, S., Hengxu, Z., Yutian, L., Yilu, L., et al. (2020). Continuous under-frequency load shedding scheme for power system adaptive frequency control. IEEE Trans. Power Syst. 35 (2), 950–961. doi:10.1109/TPWRS.2019.2943150
Choi, W. Y., Kook, K. S., and Yu, G. R. (2019). Control strategy of BESS for providing both virtual inertia and primary frequency response in the Korean power system. Energies 12 (21), 4060. doi:10.3390/en12214060
Conte, F., Crosa Di Vergagni, M., Massucco, S., Silvestro, F., Ciapessoni, E., and Cirio, D. (2021). Performance analysis of frequency regulation services provided by aggregates of domestic thermostatically controlled loads. Int. J. Electr. Power and Energy Syst. 131, 107050. doi:10.1016/j.ijepes.2021.107050
Das, N., Haque, A., Zaman, H., Morsalin, S., and Islam, S. (2023). Domestic load management with coordinated photovoltaics, battery storage and electric vehicle operation. IEEE Access 11, 12075–12087. doi:10.1109/ACCESS.2023.3241244
Dreidy, M., Mokhlis, H., and Mekhilef, S. (2017). Inertia response and frequency control techniques for renewable energy sources: a review. Renew. Sustain. Energy Rev. 69, 144–155. doi:10.1016/j.rser.2016.11.170
Fang, Z., Zechun, Hu, Xu, X., Jing, Z., and Yonghua, S. (2017). Assessment of the effectiveness of energy storage resources in the frequency regulation of a single-area power system. IEEE Trans. Power Syst. 32 (5), 3373–3380. doi:10.1109/TPWRS.2017.2649579
Gasca, M. V., Ibáñez, F., and Pozo, D. (2022). Flexibility quantification of thermostatically controlled loads for demand response applications. Electr. Power Syst. Res. 202, 107592. doi:10.1016/j.epsr.2021.107592
Huang, H., Ju, P., Jin, Y., Yuan, X., Qin, C., Pan, X., et al. (2020). Generic system frequency response model for power grids with different generations. IEEE Access 8, 14314–14321. doi:10.1109/ACCESS.2020.2965591
Huang, J., and Yang, D. (2022). Improved system frequency regulation capability of a battery energy storage system. Front. Energy Res. 10. doi:10.3389/fenrg.2022.904430
Huang, J., Yang, Z., Yu, J., Xiong, L., and Xu, Y. (2022). Frequency dynamics-constrained parameter design for fast frequency controller of wind turbine. IEEE Trans. Sustain. Energy 13 (1), 31–43. doi:10.1109/TSTE.2021.3102611
Ju, P., Jiang, T., Chung, C. Y., Gong, Y., and Zhou, H. (2021). Incorporating demand response in two-stage frequency emergency control. Int. J. Electr. Power and Energy Syst. 131, 107122. doi:10.1016/j.ijepes.2021.107122
Khan, A. H., Islam, A., Islam, M. S., Pial, H. H., and Rahman, M. S. (2015). “Consumer is producer - a novel model for electricity generation,” in 2015 3rd International Conference on Green Energy and Technology (ICGET), Dhaka, Bangladesh, September, 2015, 1–5.
Li, C., Zhang, Z., Li, J., Ma, Y., and Zou, J. (2021). Design of control strategy and effect evaluation for primary frequency regulation of wind storage system. Front. Energy Res. 9. doi:10.3389/fenrg.2021.739439
Liu, L., Weidong, Li, Yu, Ba, Jiakai, S., Cuicui, J., and Kerui, W. (2020). An analytical model for frequency nadir prediction following a major disturbance. IEEE Trans. Power Syst. 35 (4), 2527–2536. doi:10.1109/TPWRS.2019.2963706
Liu, M., Tian, Y., Cheng, D., Zhang, Y., and Ding, L. (2022). Modelling and control of central air-conditioning loads for power system emergency frequency control. IET Generation, Transm. Distribution 16 (20), 4054–4067. doi:10.1049/gtd2.12571
Mohamed, M. M., El Zoghby, H. M., Sharaf, S. M., and Mosa, M. A. (2022). Optimal virtual synchronous generator control of battery/supercapacitor hybrid energy storage system for frequency response enhancement of photovoltaic/diesel microgrid. J. Energy Storage 51, 104317. doi:10.1016/j.est.2022.104317
Nga, N., Dilip, P., Riley, Q., and Joydeep, M. (2021). Frequency response in the presence of renewable generation: challenges and opportunities. IEEE Open Access J. Power Energy 8, 543–556. doi:10.1109/OAJPE.2021.3118393
Obaid, Z. A., Cipcigan, L. M., Muhssin, M. T., and Sami, S. S. (2020). Control of a population of battery energy storage systems for frequency response. Int. J. Electr. Power and Energy Syst. 115, 105463. doi:10.1016/j.ijepes.2019.105463
Patel, K., Das, N., and Khan, M. M. K. (2019). “Optimization of hybrid solar, wind and diesel energy systems from economic point of view,” in 2019 29th Australasian Universities Power Engineering Conference (AUPEC), Nadi, Fiji, November, 2019, 1–6.
Prakash, K., Ali, M., Siddique, M. N. I., Chand, A. A., Kumar, N. M., Dong, D., et al. (2022a). A review of battery energy storage systems for ancillary services in distribution grids: current status, challenges and future directions. Front. Energy Res. 10. doi:10.3389/fenrg.2022.971704
Prakash, V., Kushwaha, P., Chand Sharma, K., and Bhakar, R. (2022b). Frequency response support assessment from uncertain wind generation. Int. J. Electr. Power and Energy Syst. 134, 107465. doi:10.1016/j.ijepes.2021.107465
Qinglei, Z., Jiaming, W., Gean, C., Qi, D., and Tong, W. (2023). “Self-adaptive emergency control strategy of wind farm-level energy storage for improving frequency stability of wind power grid-connected system,” in 2023 IEEE 6th International Electrical and Energy Conference (CIEEC), Hefei, China, May, 2023, 2290–2295.
Ruisheng, D., Shuai, Lu, Marcelo, E., Ebony, M., Yu, Z., and Nader, S. (2012). “Electric water heater modeling and control strategies for demand response,” in 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, July, 2012, 1–8.
Sarma, S. S., Reddy, D. G., Kumar, C. S. K. B. P., and Devdass, P. (2017). “Large scale synchronization of hybrid distributed generation sources to the low voltage grids,” in 2017 International Conference on Energy, Communication, Data Analytics and Soft Computing (ICECDS), Chennai, India, August, 2017, 443–448.
Shi, Q., Liu, L., Wang, Y., Lu, Y., Zou, Q., Zhang, Q., et al. (2021). Cooperative synthetic inertia control for wind farms considering frequency regulation capability. Front. Energy Res. 9. doi:10.3389/fenrg.2021.738857
Sudipta, G., Sukumar, K., Nilanjan, S., and Johan, E. (2016). Doubly fed induction generator (DFIG)-Based wind farm control framework for primary frequency and inertial response application. IEEE Trans. Power Syst. 31 (3), 1861–1871. doi:10.1109/TPWRS.2015.2438861
Tang, Y., Yang, C., Yan, Z., Xue, Y., and He, Y. (2022). Coordinated control of a wind turbine and battery storage system in providing fast-frequency regulation and extending the cycle life of battery. Front. Energy Res. 10. doi:10.3389/fenrg.2022.927453
Wei, Yu, Bo, C., Chen, Z., Chenxing, J., Xiaoxia, J., Silei, Y., et al. (2023). “Wind farm power support based transient stability collaborative emergency control strategy,” in 2023 IEEE 6th International Electrical and Energy Conference (CIEEC), Hefei, China, May, 2023, 3114–3118.
Wu, Y., and Tang, K. (2019). Frequency support by demand response – review and analysis. Energy Procedia 156, 327–331. doi:10.1016/j.egypro.2018.11.150
Xiang, S., Yang, H., and Cao, B. (2022). An evaluation of domestic electric water heaters for frequency control. Front. Energy Res. 10. doi:10.3389/fenrg.2022.962361
Xuekuan, X., Yuchen, Z., Ke, M., Zhao, Y. D., and Liu, J. (2021). Emergency control strategy for power systems with renewables considering a utility-scale energy storage transient. CSEE J. Power Energy Syst. 7 (5), 986–995. doi:10.17775/CSEEJPES.2019.02320
Yahong, C., Wei, Xu, Yi, L., Rashad, E. M., Zhen, B., Juncai, J., et al. (2022). Reduced-order system frequency response modeling for the power grid integrated with the type-II doubly-fed variable speed pumped storage units. IEEE Trans. Power Electron. 37 (9), 10994–11006. doi:10.1109/TPEL.2022.3166567
Yuan, Z., Xu, D., Jin, L., and Wang, H. (2021). Delay-dependent stability analysis of load frequency control for power system with EV aggregator. Front. Energy Res. 9. doi:10.3389/fenrg.2021.771465
Zeyad, A. O., Liana, M. C., Lahieb, A., and Mazin, T. M. (2019). Frequency control of future power systems: reviewing and evaluating challenges and new control methods. J. Mod. Power Syst. Clean Energy 7 (1), 9–25. doi:10.1007/s40565-018-0441-1
Zhang, J., Ma, Q., Shan, R., Zhou, G., Wang, L., Li, B., et al. (2022). Short-term frequency regulation of power systems based on DFIG wind generation. Front. Energy Res. 10. doi:10.3389/fenrg.2022.948185
Keywords: emergency frequency control, multi-resource regulation, frequency response model, urban distribution system, temperature control load
Citation: Shen Z, Wang C, Wang Y, Zhao H, Wu Z and Hu E (2023) Emergency frequency control strategy of distribution system based on the coordination of multi-resource. Front. Energy Res. 11:1290450. doi: 10.3389/fenrg.2023.1290450
Received: 07 September 2023; Accepted: 17 November 2023;
Published: 01 December 2023.
Edited by:
Rakibuzzaman Shah, Federation University Australia, AustraliaReviewed by:
Narottam Das, Central Queensland University, AustraliaUsman Bashir Tayab, RMIT University, Australia
Copyright © 2023 Shen, Wang, Wang, Zhao, Wu and Hu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zeyuan Shen, c3p5MzM1MTlAMTYzLmNvbQ==
 Zeyuan Shen
Zeyuan Shen Chao Wang
Chao Wang