Experimental study on helical tubes heat transfer characteristics considering corrosion products

1 Introduction

Helical-coiled One-Through Steam Steam generator (H-OTSG) has been widely used in small modular reactors because of its compact structure and high thermal efficiency (Xu et al., 2021; Liu et al., 2022). The reactor primary coolant flows through the outside of the H-OTSG helical tube and exchanges heat with the secondary loop, the coolant inside the tube is heated and generates superheated steam. Compared with straight tube, the helical tube could enhance turbulent mixing, thus obtaining higher thermal efficiency (Awais and Bhuiyan, 2019). The stronger turbulent mixing might accelerate the deposition of corrosion products (Xie and Zhang, 2016; Manacorda et al., 2020), and the heat transfer characteristics of helical tube will be affected (Xiao et al., 2018).

The flow and heat transfer mechanisms of water within the helical tube structure include two-phase flow, asymmetric phase distribution and local dry-out, which have been studied by researchers (Shah, 2019; Zhu et al., 2019; Breitenmoser et al., 2021). Void et al. (2014) used high-temperature sodium as the primary side heat source to heat low-temperature water on the secondary side of the H-OTSG. They obtained heat transfer characteristics of the secondary-side water under normal operating conditions of a sodium-cooled reactor and demonstrated that the H-OTSG had an 8.3% heat transfer area margin at an electric heating power of 5.5MWt. Chung et al. (2014) studied the heat transfer characteristics of H-OTSG secondary-side water at different pressures (1–6 MPa) and mass flow rates (0.02–0.06 kg/s) and found that steam pressure had a significant effect on subcooled nucleate boiling and steam superheat degree. Under typical nuclear reactor operating conditions (pressure 2–6 MPa, mass flow rate 200–800 kg/(m²∙s), power density 40–230 kW/m²), Santini et al. (2016) conducted thermal-hydraulic experiment on a single helical heat transfer tube and proposed empirical correlation for helical tube flow heat transfer based on 1,575 sets of experimental data. Statham and Novog (2017) investigated the subcooled nucleate boiling characteristics and dry-out characteristics of water in a helical tube structure through experiments, and the results indicated that the dry-out point distribution along the length of the helical tube was essentially the same when the void fraction exceeded 0.65.

The growth of fouling on the secondary side of the steam generator involves thermal-chemical coupling mechanisms. Mu et al. (2022) simulated the growth of fouling on the heat transfer tubes of a steam generator under natural circulation conditions in a nuclear reactor. Their calculations showed that fouling within one cycle could reduce the overall heat transfer capability of the steam generator by 9%. Lister and Cussac (2009) proposed that the deposition of corrosion products on the steam generator heat transfer tube surfaces involves mechanisms such as transport, deposition, removal, and solidification. Calculations based on a thermal-chemical model showed that subcooled nucleate boiling contributed to over 80% of corrosion product deposition (Basset et al., 2000; Lister and Cussac, 2009). Prusek et al. (2013) simulated the distribution of corrosion products on the heat transfer tubes of the steam generator and their impact on tube blockage, with a discrepancy between the simulated tube blockage rate and the measured data in a nuclear reactor ranging from 3% to 11.1%. Forster et al. (1999) developed a model to simulate the growth of fouling on the heat transfer tube surfaces of an H-OTSG and assessed the influence of flow-induced vibrations on fouling stability, revealing that fouling would undergo significant spalling when the coolant flow velocity exceeded 0.5 m/s.

Because of the different thermal hydraulic characteristics of OTSG and UTSG, it is necessary to clarify the corrosion products effect on OTSG heat transfer characteristics. Currently, there is limited research on the experimental investigation of heat transfer characteristics considering corrosion products in helical tubes. To reveal the mechanism of how corrosion products affect the heat transfer characteristics of helical tubes, this study conducted dynamic water heat transfer experiments inside fouled helical tubes under simulated conditions of a small modular reactor. By establishing models for the influence of bulk coolant temperature, wall temperature and thermal equilibrium void fraction on helical tube heat transfer performance, and by measuring the fouling thickness and thermal resistance distribution, the impact of corrosion products on the heat transfer characteristics of helical tubes was revealed. The research results provide reference for the optimization of thermal-hydraulic performance in H-OTSGs of nuclear reactors.

2 Methodology

2.1 Experimental facility

2.1.1 Experimental sample

The experimental sample, as shown in Figure 1, is fabricated by bending Inconel 600 alloy into Φ25 × 3 mm tubes. The heating section has a height of 4.5 m and is flattened to a length of approximately 50 m. Pressure measurement points are strategically positioned at locations with higher curvature in the helical tube to avoid excessive pressure. Due to the small inner diameter of the helical tube, temperature measurement points are arranged on the outer wall surface. Thermocouples are used as temperature sensors and are secured to the outer wall surface with insulating material. Eight symmetric measurement points are placed on the same cross-section to measure the temperature of the bulk coolant and the outer wall surface temperature of the helical tube.

FIGURE 1

FIGURE 1. Schematic diagram of experimental sample and measurement position.

The real H-OTSG has multiple parallel helical-coiled tubes. Because the corrosion products deposit on the inside of helical-coiled tubes, the current experimental sample is representative to the real H-OTSG heat transfer tubes.

2.1.2 Heat transfer circulation loop

Figure 2 illustrates the schematic diagram of the experimental loop (China Nuclear Power Technology Research Institute Co., Ltd. et al., 2022), which consists of the following main components to simulate and study the effects of corrosion products on the heat transfer characteristics of the helical tube during reactor operation: electrodes, used to apply an electric current to the iron plate, simulating corrosion during the operation of the helical tube; iron plate, generates simulated corrosion products similar to those found on the inner surface of the helical tube; water tank, provides coolant for the circulation loop; pressure relief valve, assists in controlling the pressure within the circulation loop to prevent it from becoming excessively high; filter, removes impurities from coolant; water pump, provides the power necessary to maintain stable coolant flow within the circulation loop; pre-heater, raises the temperature of the coolant at the inlet of the experimental sample to the target value; valves, regulates the flow rate of the coolant entering the experimental sample; electric heater, simulates the heat generated on the primary side during reactor operation. Changing the medium from water to liquid metal, the heat transfer process of liquid metal reactors also could be simulated; power controller, adjusts the heater’s power output according to the requirements of the experiment; heating chamber, simulates the heat transfer process from the primary side to the secondary side; temperature meter, measures the temperature within the circulation loop; pressure meter, measures the pressure within the circulation loop; heat exchanger, controls the total power of the circulation loop based on data obtained from temperature meter and pressure meter.

FIGURE 2

FIGURE 2. Schematic diagram of heat transfer circulation loop.

The design parameters of the experimental facility are presented in Table 1, which can characterize the thermal-hydraulic performance under typical operating conditions of a nuclear reactors. The artificial fouling experiment conducted under these operating condition parameters involves the following main steps:

1) Start the water pump and pre-heater. Monitor the secondary side coolant temperature and pressure using temperature meters and pressure meters. Adjust the bulk coolant temperature and pressure on the secondary side to a range similar to the operating conditions.

2) Start the water pump, electric heater and power controller on the primary side. Continuously heat the medium on the primary side using the heating chamber.

3) Start the power controller and heat exchanger on the secondary side. Adjust the inlet subcooling degree and outlet superheat degree on the secondary side of the experimental sample to a range similar to the operating conditions.

4) Continuously apply electric current to the iron plate with the electrodes to simulate the continuous release of corrosion products into the coolant on the secondary side of the H-OTSG.

5) Monitor the bulk coolant temperature and wall temperature continuously throughout the experimental cycle. During the heat transfer experiment period, shutdown the electric current of iron plate to avoid the influence of corrosion products on heat transfer characteristics.

6) After the experiment concludes, stop the heating on both the primary and secondary sides. Open the pressure relief valve to rapidly drain the coolant on the secondary side. This helps reduce the dissolution of fouling into the coolant during the cooling phase, ensuring that the extracted sample accurately represents the fouling characteristics during operation.

7) Retrieve the experimental sample and slice it axially and radially. Analyze the thickness of fouling in various regions using equipment such as scanning electron microscopes and X-ray photoelectron spectroscopy.

TABLE 1

TABLE 1. Design parameters of the experimental facility.

2.2 Analytical methods

2.2.1 Deposition of corrosion products

Currently, there is limited data available for the analysis of fouling in helical tubes under the operating conditions of nuclear reactors. According to theoretical derivation, the main factors influencing the formation of fouling are water chemistry parameters and thermal-hydraulic parameters. The general formula for fouling deposition rate is as follows (Meng et al., 2022):

$w_i=\frac{k_i{\dot{m}}_e}{k_i+k_{m,i}}{C}_i+\frac{k_i{k}_{m,i}}{k_i+k_{m,i}}\left(C_i-C_{0,i}\right)(1)$

Where $w_i$ represents the deposition rate, unit in g/(cm²∙s); ${\dot{m}}_e$ represents the rate of subcooled nucleate boiling, unit in g/(cm²∙s); k_i and k_m,i represent mass transfer coefficient, unit in g/(cm²∙s); C_i and C_0,i represent the saturation solubility of corrosion products in the bulk coolant and on the fuel surface, respectively, unit in g/g; i represents various metal elements.

Equation 1 is derived from the mechanistic study of the corrosion product deposition process in the primary circuit of a pressurized water reactor. Differences in water chemistry parameters and thermal-hydraulic parameters between the primary and secondary circuits will affect the numerical values of k_i, k_m,i, C_i and C_0,i. However, the form of the fouling deposition rate formula remains unchanged. Therefore, this formula is applicable for characterizing the growth process of fouling on the inner surface of helical tubes.

In this experiment, the characterization of artificial fouling with respect to real fouling is achieved by controlling the water chemistry parameters in the experimental facility. Specific limit values are presented in Table 2. While ensuring that water chemistry parameters and thermal-hydraulic parameters are similar to actual operating conditions, reference is made to the experience of artificial corrosion products experiments in the primary circuit of pressurized water reactors (Xue et al., 2023). This is accomplished by adjusting the concentration of iron solution injected into the circulation loop to simulate the deposition process of corrosion products on the inner surface of the helical tube. The analysis of artificial fouling is carried out using X-ray photoelectron spectroscopy and scanning electron microscopy to determine the distribution pattern of fouling thickness in different regions of the helical tube.

TABLE 2

TABLE 2. Specific limit values of water chemistry parameters.

2.2.2 Coolant temperature and wall temperature

As shown in Figure 3, the heat transfer between the inner and outer sides of the helical tube can be visualized as a heat conduction process through the cylindrical wall. Considering a differential element within the helical tube and applying the principle of energy conservation, the general equation for the heat conduction differential equation is as follows (Incropera et al., 2007):

$\rho c\frac{\partial t}{\partial \tau }=\frac{1}{r}\cdot \frac{\partial }{\partial r}\left(\lambda r\frac{\partial t}{\partial r}\right)+\frac{1}{r^2}\cdot \frac{\partial }{\partial \phi }\left(\lambda \frac{\partial t}{\partial \phi }\right)+\frac{\partial }{\partial z}\left(\lambda \frac{\partial t}{\partial z}\right)+\dot{\varphi }(2)$

FIGURE 3

FIGURE 3. Schematic diagram of helical tube differential element.

Where $\rho$ represents the density of the differential element, unit in g/cm³; $c$ represents the specific heat capacity of the differential element, unit in J/(kg∙K); $\lambda$ represents the thermal conductivity, unit in W/(m∙K); $\dot{\varphi }$ represents the internal heat source per unit volume, unit in W/cm³; t represents the temperature difference of the differential element, unit in K.

Assumingthat the differential element is always in thermal equilibrium, with constant temperatures on both sides of the heat transfer tube and no internal heat source within the cylindrical wall, the heat conduction differential equation can be simplified as follows:

$\frac{d}{dr}\left(r\frac{dt}{dr}\right)=0(3)$

By performing a second integration of equation (3), the general solution for the temperature distribution along the radial direction of the cylindrical tube could be obtained:

$t=c_1\ln r+c_2(4)$

Where r represents the radius of the differential element from the center of the cylinder, unit in m; $c_1$ and $c_2$ represent integration constants.

As shown in Figure 4A, the boundary conditions for Eq. 4 are:

$r=r_{in},t=t_{bulk}(5)$

$r=r_{out},t=t_{wall}(6)$

FIGURE 4

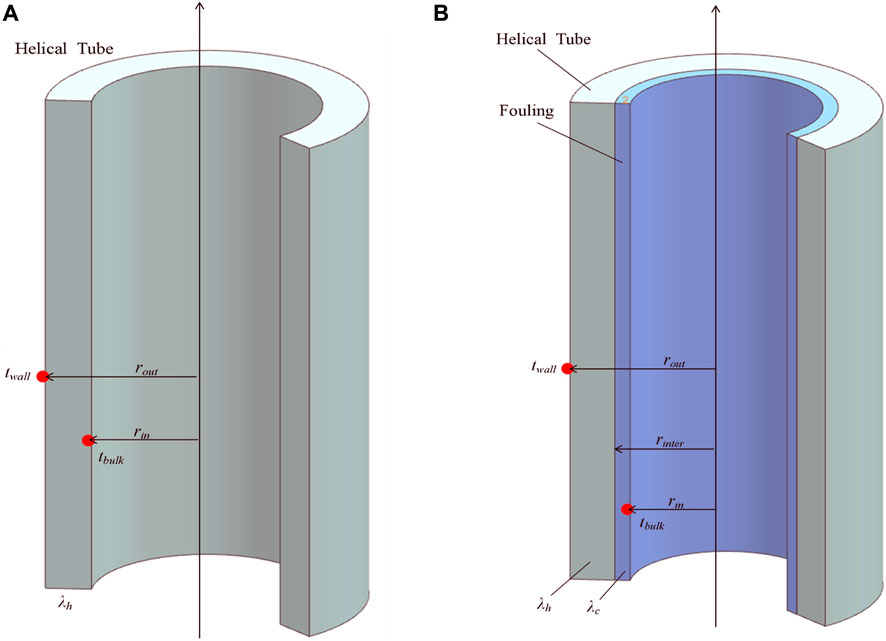
FIGURE 4. Schematic diagram of heat transfer process of helical tube: (A) Clean surface. (B) Fouled surface.

Where r_in and r_out represent the inner and outer diameter of helical tube, respectively, unit in m.

Combining Eqs 4–6, the formula for the radial temperature distribution of the cylindrical tube could be derived:

$t=t_{bulk}+\frac{t_{wall}-t_{bulk}}{\ln \left(r_{out}/r_{in}\right)}\cdot \ln \left(r/r_{in}\right)(7)$

Considering that the total heat across the entire cylindrical wall remains constant, taking derivatives of both ends of Eq. 7 and applying Fourier’s law (Incropera et al., 2007; Short et al., 2013), the formula for the radial heat flux density q could be obtained:

$q=\frac{2\pi \lambda l\left(t_{wall}-t_{bulk}\right)}{\ln \left(r_{out}/r_{in}\right)}(8)$

The thermal resistance is defined as the ratio of temperature difference across the cylindrical wall to the heat flux density. When fouling forms on the inner side of the helical tube, as shown in Figure 4B, the calculation formula for the heat flux density q_c is modified using the principle of serial thermal resistance stacking:

$q_c=\frac{2\pi l\left(t_{wall}-t_{bulk}\right)}{\ln \left(r_{\mathrm{int}er}/r_{in}\right)/{\lambda }_c+\ln \left(r_{out}/r_{\mathrm{int}er}\right)/{\lambda }_h}(9)$

Where l represents the total length of the helical tube, unit in m; $r_{\mathrm{int}er}$ represents the radius from the center of the cylinder to the interface between fouling and the heat transfer surface, unit in m; ${\lambda }_c$ and ${\lambda }_h$ represent thermal conductivity of fouling and clean surfaces, respectively, unit in W/(m∙K).

From Eq. 9, it can be observed that during the experiment, by controlling the heat flux density and maintaining the bulk coolant temperature constant, the impact of corrosion products on the heat transfer performance of the helical tube can be quantified by monitoring the change in the outer wall temperature t_wall of the heat transfer tube.

2.2.3 Thermal equilibrium void fraction

When the vapor-liquid two-phase system is in a thermodynamic equilibrium state, the degree of superheat of the fluid can be represented by the thermal equilibrium vapor quality x, defined by the formula:

$x=\frac{h-h_s}{h_g}(10)$

Where h and h_s represent the enthalpy of two-phase fluid and saturated liquid phase, respectively, unit in kJ/kg; h_g represents the latent heat of vaporization of the fluid, unit in kJ/kg.

The experiments conducted in this study involve uniform heating, and the enthalpy values of the fluid along the length of the helical tube follow a linear distribution. Using the starting point of the effective heating section as a reference, the enthalpy value h_fd of the fluid at the position d along the helical tube is given by:

$h_{fd}=h_{in}+\Delta h\frac{d}{l}(11)$

Where h_in represents the enthalpy of fluid at the inlet of the experimental sample, unit in kJ/kg; $\Delta h$ represents the total enthalpy rise of the fluid flowing through the effective heating section, unit in kJ/kg.

When the bulk coolant reaches its saturation temperature, the fluid enters the saturated boiling heat transfer stage and subsequently undergoes nucleate boiling, forced convection evaporation in the liquid film, and dry-out regions (Xiao et al., 2018; Xu et al., 2021; Rui et al., 2023). The point of nucleate boiling initiation is the boundary between the subcooled and saturated boiling segments of the fluid, and its theoretical thermal equilibrium void fraction is zero. According to the principle of energy conservation, the calculation formula for the position do of the nucleate boiling initiation point is derived as follows:

$d_o=\frac{m{C}_p{r}_{in}\left(t_{sat}-t_{in}\right)}{4q}(12)$

Where m represents the mass flow rate of the coolant, unit in kg/s; C_p represents the specific heat capacity of subcooled liquid, unit in J/(kg∙K); t_sat and t_in represent the saturation temperature of the coolant and the inlet temperature of heating section, respectively, unit in K.

Under the same conditions of heat flux density, coolant flow rate, and inlet temperature of the heating section, a nucleate boiling initiation point closer to the inlet of the heating section indicates a higher heat transfer capability of the coolant and a higher thermal equilibrium void fraction. Equations 10, 12 demonstrate that by controlling the heat flux density and maintaining the inlet temperature of the heating section relatively constant, the impact of corrosion product deposition on the heat transfer performance of the helical tube can be reflected by measuring the thermal equilibrium void fraction at various measurement points along the heating section.

3 Results and discussion

3.1 Corrosion products

Following the nominal operating conditions parameters provided in Table 1 and controlling the limits of water chemistry parameters in the circulation loop as specified in Table 2, an experiment on the impact of corrosion products on the heat transfer performance of helical tube was conducted, lasting for 120 days.

Figure 5 illustrates the trend of heat flux density during the experimental period. The calculations for heating efficiency and heat flux density are as follows:

$\eta =\frac{\left(h_{out}-h_{in}\right)}{\sqrt{3}UI}(13)$

$q=\frac{\sqrt{3}\eta UI}{A}(14)$

FIGURE 5

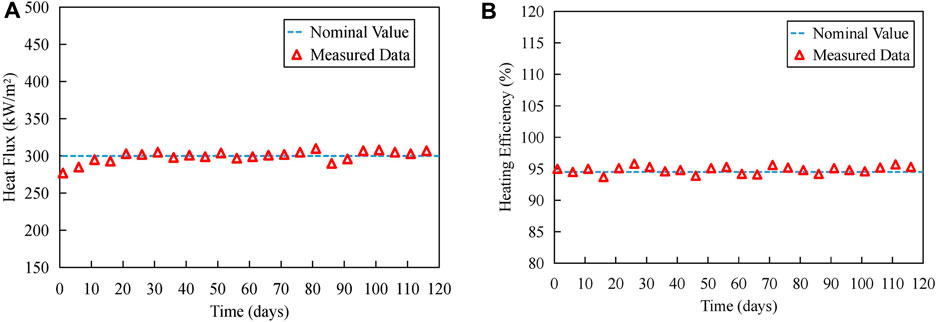
FIGURE 5. Trend of heat flux density during experiment period: (A) Heat flux density. (B) Heating efficiency.

Where η represents the heating efficiency; h_out represents the enthalpy of fluid at the outlet of the experimental sample, unit in kJ/kg; U and I represent the voltage and current of the electric heater, respectively, units in V(volts) and A(amperes); q represents heat flux density, unit in kW/m²; A represents the surface area of effective heating section, unit in m².

Figure 6 provides the measured data of the thickness distribution of fouling along the length of helical tube after the experiment concluded. The average fouling thickness over the entire effective heating section is calculated with the following weighted formula:

$\overline{\delta }={\displaystyle \sum _1^{i+1}}\left(\frac{d_{i+1}-d_i}{l}{\delta }_{i+1}\right)(15)$

FIGURE 6

FIGURE 6. Measured data of fouling thickness distribution.

Where ${\delta }_{i+1}$ represents the fouling thickness at the i+1st measurement point, unit in μm; $d_{i+1}$ and $d_i$ represent the lengths from the i+1st measurement point to the ith measurement point and from the heating section inlet, respectively, unit in m.

Based on the experimental results, it can be concluded that:

1) The heat flux density remained relatively constant throughout the experimental period, indicating the stable and long-term operation of the experimental platform in dissipating heat.

2) Corrosion products predominantly deposited near the nucleate boiling initiation point, with a maximum thickness of approximately 50 μm.

3) In other regions, the deposition of corrosion products was relatively minimal, with an average deposit thickness of around 3 μm.

3.2 Wall temperature and void fraction

Throughout the experimental process, the heat flux density remained relatively constant. Therefore, the temperature difference between the wall surface and the bulk coolant temperature can directly reflect changes in the heat transfer coefficient of the helical tube. Figure 7 provides the distribution of the outer wall temperature of the helical tube on different days of the experimental period, and it can be observed that:

1) Along the length of the helical tube, the wall temperatures in the liquid phase and vapor phase regions showed a linear increase with respect to the bulk coolant temperature, while in the two-phase region, they remained relatively constant.

2) After the deposition of corrosion products, the wall temperature near the nucleate boiling initiation point (x = 0) and the dry-out point (x = 1) significantly increased, with the maximum wall surface temperature near the nucleate boiling initiation point reaching approximately 773 K.

3) Considering the distribution of corrosion products, it can be inferred that the main factor causing an increase in wall temperature near the nucleate boiling initiation point is the deposition of corrosion products, while the increase in wall temperature near the dry-out point is due to the reduced heat transfer capability of the vapor-phase coolant.

FIGURE 7

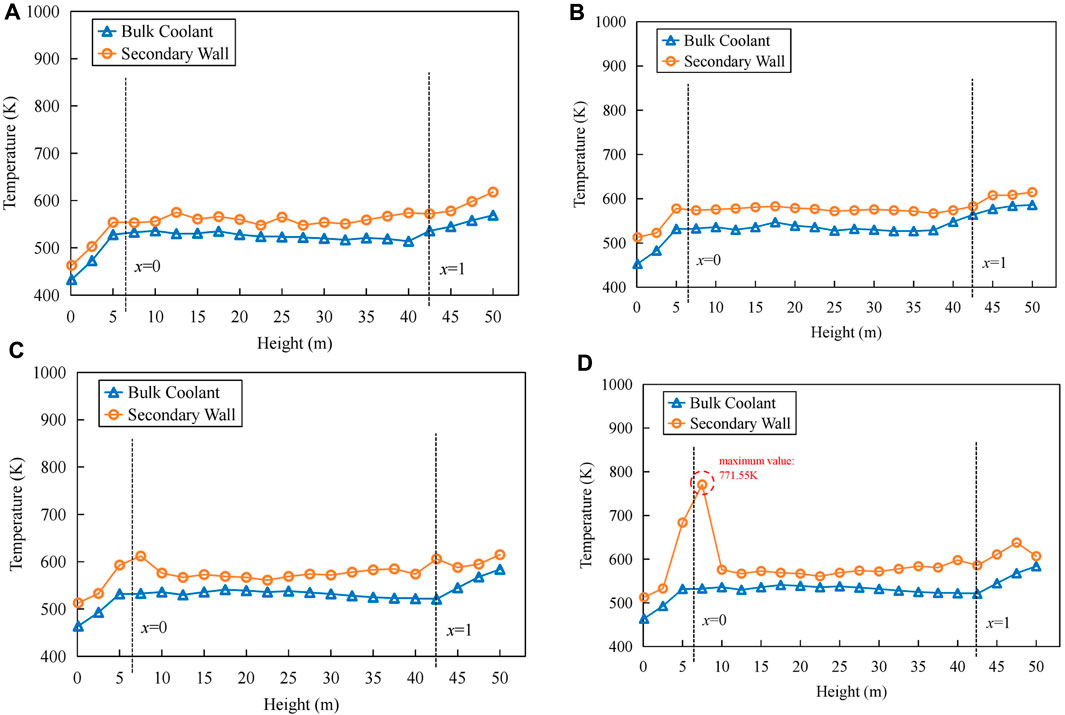
FIGURE 7. Trend of wall temperature changes in the helical tube: (A) 10 days. (B) 40 days. (C) 90 days. (D) 120 days.

Figure 8 presents the distribution of the saturated boiling initiation point and dry-out point of the coolant inside the helical tube, and it can be observed that:

1) The positions of the saturated boiling initiation point and dry-out point remained relatively unchanged.

2) Due to the uniform heating of experimental sample, the fluid enthalpy values along the length of the helical tube showed a linear increasing trend.

FIGURE 8

FIGURE 8. Trend of void fraction changes along the length of helical tube.

3.3 Thermal resistance

By measuring the bulk coolant temperature (t_bulk) and the wall temperature (t_wall), the overall thermal resistance and fouling resistance of the helical heat transfer tube can be calculated using Equation 9.

Figure 9 illustrates the trends in heat resistance in different flow regimes, and it can be observed that:

1) In the subcooling and superheating regions, the thermal resistance of helical tube remains almost constant, indicating that there is little fouling formation in these two regions.

2) In the region between the end of the subcooling section and the nucleate boiling initiation point, the thermal resistance of helical tube shows periodic fluctuations. It is inferred that this periodic variation is caused by increased mixing at the interface due to the transition of coolant from liquid to vapor, leading to periodic deposition and removal of fouling.

3) Near the nucleate boiling initiation point, the thermal resistance of helical tube remains relatively constant in the first 10 days but then exhibits a rapid increase. This suggests that during the initial 10 days of the experiment, corrosion products deposited in other areas of the circulation loop. Subsequently, as the deposition rate in the heating section continues to increase, fouling begins to accumulate near the nucleate boiling initiation point.

4) In the two-phase region, the thermal resistance of helical tube shows a linear increasing trend over the course of the experiment. The farther the measurement point is from the entrance of the heating section, the lower the heat transfer efficiency of the helical tube. Near the dry-out point, heat transfer efficiency reaches its lowest value, at which point the thermal equilibrium void fraction approaches 1, and almost all of the coolant vaporizes.

5) Near the dry-out point, the thermal resistance of helical tube has significantly increased after 10 days of the experiment and then exhibits periodic fluctuations. It is suggested that in this region, fouling undergoes a deposition-removal-redeposition process under the influence of high-speed vapor-phase coolant flushing.

FIGURE 9

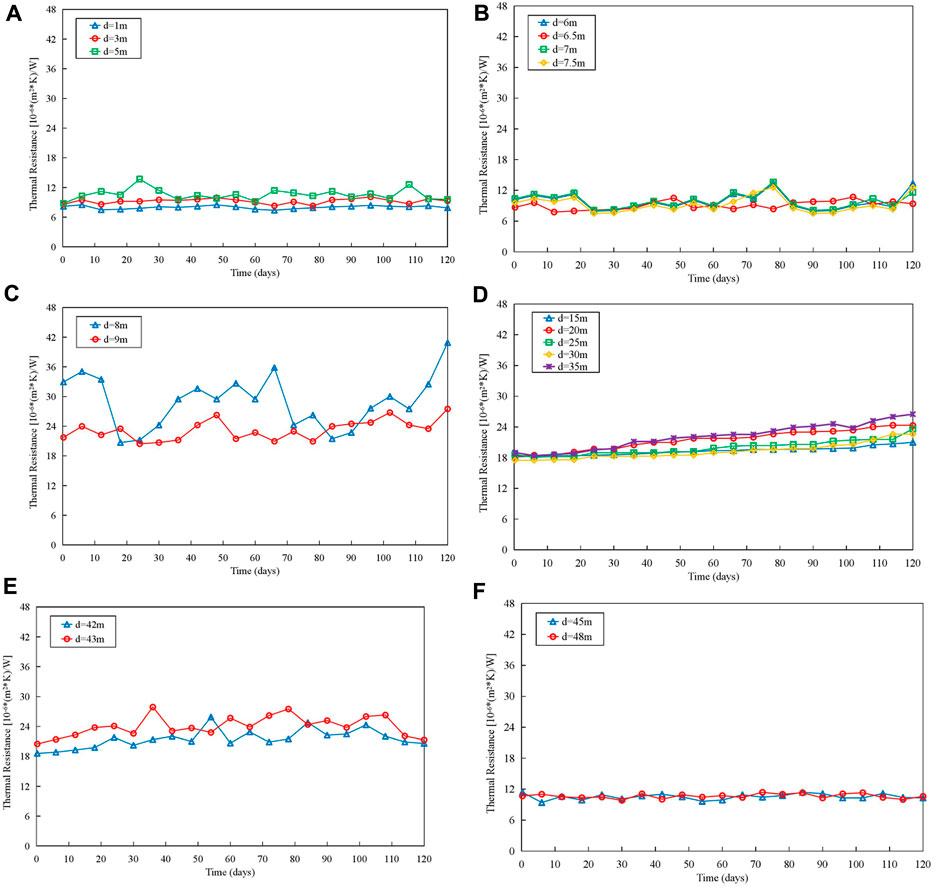
FIGURE 9. Trend of thermal resistance changes of helical tube: (A) Subcooling region. (B) Region between the end of the subcooling section and the nucleate boiling initiation point. (C) Region near the nucleate boiling initiation point. (D) Two-phase region. (E) Region near the dry-out point. (F) superheating region.

The experimental results regarding helical tube thermal resistance indicate that corrosion products mainly affect the heat transfer characteristics near the nucleate boiling initiation point, two-phase region and the region near dry-out point. Furthermore, by using Eq. 9 to analyze the fouling thermal resistance in these three regions, the fouling contributes about 70% thermal resistance of helical tubes, and the processed data is shown in Figure 10.

FIGURE 10

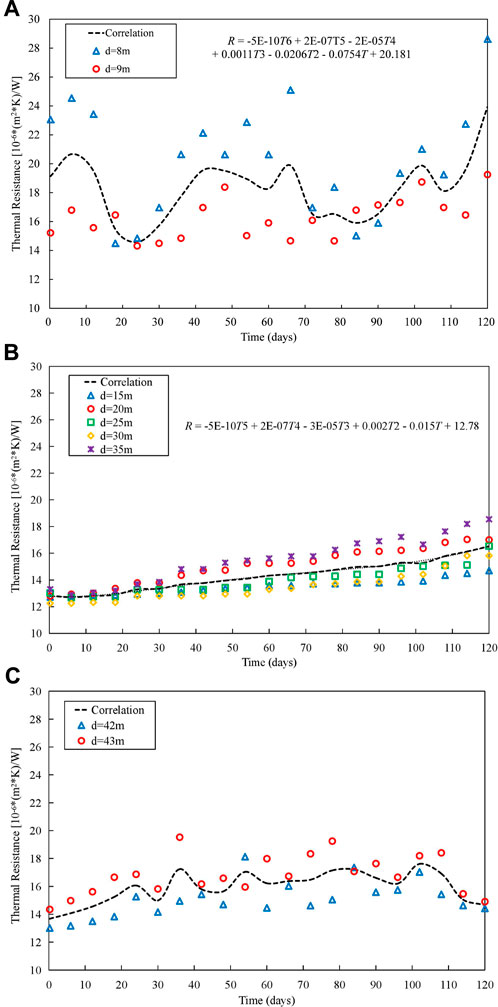
FIGURE 10. Trend of Fouling thermal resistance changes: (A) Region near the nucleate boiling initiation point. (B) Two-phase region. (C) Region near the dry-out point.

Based on the experimental data from Figures 9, 10, and following the recommended method from National Association of Corrosion Engineers guidelines(Liao et al., 2022), the fouling thermal resistance of helical tube is fitted into an empirical relationship correlated with operational time:

$R=\left\{\begin{array}{cc}\begin{array}{l}12.5,\\ -5\times {10}^{-7}{T}^6+2\times {10}^{-7}{T}^5-2\times {10}^{-5}{T}^4\\ +1.1\times {10}^{-3}{T}^3-2.1\times {10}^{-2}{T}^2-7.6\times {10}^{-2}T+20.2,\\ -5\times {10}^{-10}{T}^5+2\times {10}^{-7}{T}^4-3\times {10}^{-5}{T}^3\\ +2\times {10}^{-3}{T}^2-1.5\times {10}^{-2}T+12.8,\\ -4\times {10}^{-7}{T}^4+8\times {10}^{-5}{T}^3-6.6\times {10}^{-3}{T}^2\\ +0.23T+14.1,\\ 13.2,\end{array}& \begin{array}{l}0\le d<5\\ 5\le d<11\\ 11\le d<35\\ 35\le d<42\\ d\ge 42\end{array}\end{array}\right.(16)$

Where R represents fouling thermal resistance, unit in (m²∙K∙10⁻⁶)/W; T represents operational time, unit in hours; d represents the distance of the fouling region from the entrance of the helical tube’s effective heating section, unit in m.

4 Conclusion

This study utilized experimental methods to investigate the distribution patterns of corrosion products on the inner surface of helical tubes and their impact on heat transfer performance under simulated operating conditions in the secondary loop of a small modular reactor. Furthermore, empirical relationships were derived from the experimental data to correlate helical tube fouling thermal resistance with operational time. The main conclusions of this study are as follows:

1) Corrosion products tend to accumulate near the nucleate boiling initiation point on the inner surface of the helical tube, leading to an increase in wall temperature in that region. However, the location of nucleate boiling initiation point is minimally affected by fouling.

2) In two-phase region, both helical tube’s thermal resistance and thermal equilibrium void fraction exhibit linear growth trends over the course of the experiment. Near dry-out point, fouling in the helical tube reaches the lowest heat transfer efficiency.

3) In superheating region of the inner helical tube, fouling undergoes a continuous cycle of deposition-removal-redeposition due to the flushing of high-speed vapor-phase coolant. This leads to periodic fluctuations in both the helical tube’s thermal resistance and fouling thermal resistance in this region.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

MY: Conceptualization, Writing–review and editing. MS: Conceptualization, Writing–review and editing. LX: Methodology, Writing–original draft, Writing–review and editing. JD: Methodology, Writing–original draft. WX: Data curation, Formal Analysis, Writing–original draft, Writing–review and editing. LK: Data curation, Formal Analysis, Writing–original draft. HYi: Writing–original draft. HYo: Writing–review and editing, Methodology. RM: Writing–review and editing, Supervision.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was funded by the National Natural Science Foundation of China (Grant Numbers U20B0211 and 52171085).

Conflict of interest

Authors MY, MS, LX, JD, WX, LK, HYi, HYo, and RM were employed by China Guangdong Nuclear Research Institute Co., Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Awais, M., and Bhuiyan, A. (2019). Recent advancements in impedance of fouling resistance and particulate depositions in heat exchangers. Int. J. Heat Mass Transf. 141, 580–603. doi:10.1016/j.ijheatmasstransfer.2019.07.011

CrossRef Full Text | Google Scholar

Basset, M., Mcinerney, J., Arbeau, N., and Lister, D. (2000). The fouling of alloy-800 heat exchange surfaces by magnetite particles. Can. J. Chem. Eng. 778, 40–52. doi:10.1002/cjce.5450780108

CrossRef Full Text | Google Scholar

Breitenmoser, D., Manera, A., Prasser, H. M., Adams, R., and Petrov, V. (2021). High-resolution high-speed void fraction measurements in helically coiled tubes using X-ray radiography. Nucl. Eng. Des. 373, 110888. doi:10.1016/j.nucengdes.2020.110888

CrossRef Full Text | Google Scholar

China Nuclear Power Technology Research Institute Co Ltd (2022). Facility and experimental for simulating corrosion products deposition in OTSG secondary side heat transfer tube. China: China General Nuclear Power Group Co., Ltd., China General Nuclear Power Co. China Ltd.

Google Scholar

Chung, Y. J., Bae, K. H., Kim, K. K., and Lee, W. J. (2014). Boiling heat transfer and dryout in helically coiled tubes under different pressure conditions. Ann. Nucl. Energy 71, 298–303. doi:10.1016/j.anucene.2014.04.015

CrossRef Full Text | Google Scholar

Forster, M., Augustin, W., and Bohnet, M. (1999). Influence of the adhesion force crystal: heat exchanger surface on fouling mitigation. Chem. Eng. Process. 38, 449–461. doi:10.1016/S0255-2701(99)00042-2

CrossRef Full Text | Google Scholar

Incropera, F. P., DeWitt, D. P., Bergman, T. L., and Lavine, A. S. (2007). Fundamentals of heat and mass transfer. Indiana, USA: University of Notre Dame. Notre Dame.

Google Scholar

Liao, J., Hu, Y., Li, J., Jin, D., Meng, S., Ruan, T., et al. (2022). Corrosion release behavior of alloy 690 and its application in high-temperature water with Zn injection. Nucl. Eng. Technol. 54 (3), 984–990. doi:10.1016/j.net.2021.09.009

CrossRef Full Text | Google Scholar

Lister, D., and Cussac, F. (2009). Modeling of particulate fouling on heat exchanger surfaces: influence of bubbles on iron oxide deposition. Heat. Transf. Eng. 30 (10-11), 840–850. doi:10.1080/01457630902751528

CrossRef Full Text | Google Scholar

Liu, L., Hu, B., Liu, S., Wang, K., and Gu, H. (2022). Recognition of gas-liquid flow regimes in helically coiled tube using wire-mesh sensor and KNN algorithm. Int. J. Multiph. Flow 154, 104144. doi:10.1016/j.ijmultiphaseflow.2022.104144

CrossRef Full Text | Google Scholar

Manacorda, A., Schehr, G., and Zamponi, F. (2020). Numerical solution of the dynamical mean field theory of infinite-dimensional equilibrium liquids. J. Chem. Phys. 152 (16), 164506. doi:10.1063/5.0007036

PubMed Abstract | CrossRef Full Text | Google Scholar

Meng, S., Yan, Y., Hu, Y., Hu, Y., and Ruan, T. (2022). Research of thermal hydraulic conditions effect on PWR CIPS risk. Front. Energy Res. 10, 823872. doi:10.3389/fenrg.2022.823872

CrossRef Full Text | Google Scholar

Mu, D., Wang, M., Zhang, J., Tian, W., Qiu, S., and Su, G. H. (2022). Migration-deposition coupling characteristics and influence of corrosion products on heat transfer in steam generators. Appl. Therm. Eng. 211, 118507. doi:10.1016/j.applthermaleng.2022.118507

CrossRef Full Text | Google Scholar

Prusek, T., Moleiro, E., Oukacine, F., Adobes, A., Jaeger, M., and Grandotto, M. (2013). Deposit models for tube support plate flow blockage in Steam Generators. Nucl. Eng. Des. 262, 418–428. doi:10.1016/j.nucengdes.2013.05.017

CrossRef Full Text | Google Scholar

Rui, M., Chen, T., Zhou, M., Zheng, X., Hu, Y., Jin, D., et al. (2023). Study on physical prediction model of liquid film development and dry out point in helical tube. Front. Energy Res. 11, 1224006. doi:10.3389/fenrg.2023.1224006

CrossRef Full Text | Google Scholar

Santini, L., Cioncolini, A., Butel, M. T., and Ricotti, M. E. (2016). Flow boiling heat transfer in a helically coiled steam generator for nuclear power applications. Int. J. Heat Mass Transf. 92, 91–99. doi:10.1016/j.ijheatmasstransfer.2015.08.012

CrossRef Full Text | Google Scholar

Shah, M. M. (2019). Prediction of heat transfer during saturated boiling in helical coils. J. Therm. Sci. Eng. Appl. 11 (3), 031013. doi:10.1115/1.4042354

CrossRef Full Text | Google Scholar

Short, M. P., Hussey, D., Kendrick, B. K., Besmann, T. M., Stanek, C. R., and Yip, S. (2013). Multiphysics modeling of porous crud deposits in nuclear reactors. J. Nucl. Mater. 443 (1-3), 579–587. doi:10.1016/j.jnucmat.2013.08.014

CrossRef Full Text | Google Scholar

Statham, B. A., and Novog, D. R. (2017). The effects of transient conditions on the onset of intermittent dryout during blowdown. Nucl. Eng. Des. 317, 118–132. doi:10.1016/j.nucengdes.2017.02.025

CrossRef Full Text | Google Scholar

Void, V., Sivakumar, L. S., Suresh Kumar, V. A., Noushad, I. B., Padmakumar, G., and Rajan, K. K. (2014). Experimental evaluation of the heat transfer performance of sodium heated once through steam generator. Nucl. Eng. Des. 273, 412–420. doi:10.1016/j.nucengdes.2014.03.034

CrossRef Full Text | Google Scholar

Xiao, Y., Hu, Z., Chen, S., and Gu, H. (2018). Experimental study of two-phase frictional pressure drop of steam-water in helically coiled tubes with small coil diameters at high pressure. Appl. Therm. Eng. 132, 18–29. doi:10.1016/j.applthermaleng.2017.12.074

CrossRef Full Text | Google Scholar

Xie, Y., and Zhang, J. (2016). Corrosion and deposition on the secondary circuit of steam generators. J. Nucl. Sci. Technol. 53 (10), 1455–1466. doi:10.1080/00223131.2016.1152923

CrossRef Full Text | Google Scholar

Xu, Z., Liu, M., Xiao, Y., and Gu, H. (2021). Development of a RELAP5 model for the thermo-hydraulic characteristics simulation of the helically coiled tubes. Ann. Nucl. Energy 153, 108032. doi:10.1016/j.anucene.2020.108032

CrossRef Full Text | Google Scholar

Xue, C., Zhang, Z., Tan, J., Wu, X., Han, E. H., and Ke, W. (2023). Effects of Zn injection on corrosion behavior and crud deposition of FeCrAl fuel cladding under subcooled nuclear boiling condition in high-temperature pressurized water. Corros. Sci. 211, 110909. doi:10.1016/j.corsci.2022.110909

CrossRef Full Text | Google Scholar

Zhu, G., Yang, X., Jiang, S., and Zhu, H. (2019). Intermittent gas-liquid two-phase flow in helically coiled tubes. Int. J. Multiph. Flow 116, 113–124. doi:10.1016/j.ijmultiphaseflow.2019.04.013

CrossRef Full Text | Google Scholar