Effect of mechanical vibration on heat and mass transfer performance of pool boiling process in porous media: a literature review

Pool boiling in porous media has been applied in various thermal management systems by using latent heat and increasing the heat transfer area and thermal conduction path to improve the heat transfer performance. In mechanical equipment, vibration is an inevitable problem due to reasons such as engine operation and high-speed relative motion between transmission system components, which causes the system components to be affected by vibration forces or vibration accelerations. This study focuses on a review of published articles about the effects of mechanical vibration on the characteristics of boiling process in porous media by two aspects: heat transfer performance and bubble dynamics. Heat transfer coefficient (HTC) and critical heat flux are two main parameters used to measure the boiling heat transfer characteristics of porous media. For bubble dynamics investigations, properties such as migration, fragment, coalescence, departure diameter and frequency are the focus of research attention. Different mechanical vibration parameters, i.e., direction, frequency, and amplitude, will have different effects on the above characteristics. It is worth mentioning that the greatest influence occurs under resonance conditions, and this has been verified through experimental and simulation calculations. This review highlights the importance of considering mechanical vibrations in the design and optimization of porous media systems for efficient heat transfer applications. Further research is warranted to explore the detailed mechanisms and optimize the vibration parameters for enhanced heat transfer performance in thermal management systems using porous media.

1 Introduction

Thermal management system plays an important role in various fields such as solar collectors, smart phones, electric vehicle power batteries, high-power LEDs, notebook computers, etc. Compared with single phase heat transfer on smooth surfaces, pool boiling in porous material increases the heat transfer area and uses the latent heat of working fluid, thereby greatly improving the heat transfer performance, which is mainly reflected in the increase of the heat transfer coefficient (HTC), the enhancement of the critical heat flux (CHF), and the reduction of wall superheat (Habibishandiz and Saghir, 2022). The enhancement relevant studies mainly include the enhanced heat transfer effect of different porous structures and parameters (Zhou et al., 2022), the pressure drop characteristics and boiling heat transfer ability of two-phase flow (Zhang et al., 2021), and the distribution law of two-phase inside the porous structure (Liao et al., 2021). During the pool boiling process, the timely detachment and removal of bubbles from the heating surface are important conditions to ensure the normal operation of the system. Porous materials rely on the pores to generate capillary forces that drive the circulation of working fluid, allowing liquid to flow to the heating zone to replenish the gasified working medium. Increasing the capillary forces allows liquid to return more quickly, while reducing the flow resistance enables the bubbles to detach and be expelled as soon as possible. Therefore, in the study of pool boiling in porous media, one key problem is to reduce pore sizes while minimizing the flow resistance as much as possible.

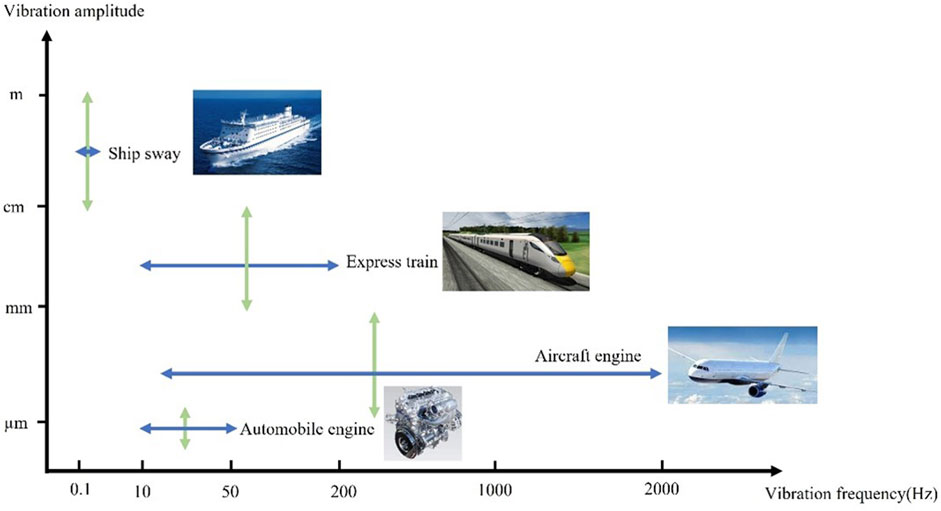
Mechanical vibration is a common phenomenon in many industrial applications, such as vehicle radiator (Li et al., 2020), chemical battery (Joshy et al., 2020; Zuo et al., 2022), high-voltage overhead transmission (Meng et al., 2018), and aircraft engine (ElSaid et al., 2018). Based on related reference (Energy Institute Great Britain, 2008; Haym et al., 2022-09; Stewart and Shaw, 2015), we have summarized several mechanical vibrations in different engineering applications, as shown in Figure 1. Excessive vibration can reduce the performance and shorten the lifespan of mechanical and electronic equipment. Therefore, the adaptability to vibration environment is often considered as one of the important factors for the mechanical performance and is commonly used in the design and research of anti-vibration systems. Vibrations also subject system components to additional vibration forces, resulting in certain vibration displacements and accelerations. This has a significant impact on the heat transfer mechanisms of boiling processes in porous media, thus affecting the operating characteristics of the entire thermal management system.

FIGURE 1

FIGURE 1. Several vibration situations in different mechanical engineering applications.

Some studies showed that vibration could destroy the flow and heat transfer boundary layer under certain conditions (Majeed Mohammed et al., 2021), increase the convective heat transfer coefficient (Hosseinian et al., 2018), and enhance the heat transfer effect. Vibration may cause the separation, backflow, and vortex formation of fluid layers, thereby altering the flow pattern and velocity distribution of fluid, which affects the heat transfer efficiency. In boiling processes, vibration can induce changes in the shape, merging, or separation of bubbles, influencing the morphology, motion, and distribution of bubbles and consequently impacting the boiling heat transfer characteristics.

The main objective of this review is to summarize and analyze the existing literature about effect of mechanical vibration on pool boiling process in porous media in two aspects: 1) heat transfer performance and 2) bubble dynamics; specifically focusing on the reported progress about HTC, onset of thermo-vibrational convection, resonant effect, and bubble dynamics under mechanical vibration. Firstly, the review of published studies with respect to boiling performance under mechanical vibration is reported, covering boiling curve, non-resonant effect, resonant effect, and thermo-vibrational convection mechanisms. Then, published studies on the bubble behaviors in porous media are reviewed, including stable state and unstable state. Finally, conclusions and research focuses are given. This review can provide a systematic reference for the design of thermal management system in the future.

2 Effect of vibration on the heat transfer performance

2.1 Pool boiling in porous media

Porous materials currently used in thermal management systems mainly include sintered metal powder, screen/wire mesh and metal foam, as shown in Figure 2. With the maturation of porous structure preparation technology, to meet the needs of different heat exchangers, porous media are made into different structural forms such as porous coating surfaces (Starodubtseva et al., 2021), porous channels (He et al., 2023), porous fins (Jain et al., 2023), porous membrane (Li et al., 2023) and so on. With the increase of heating power, the formation process of vapor in porous media can be roughly divided into four stages: conduction-convection stage, liquid layer recession stage, nucleate boiling stage, and film boiling stage, which ultimately leads to the occurrence of dry out (Weibel et al., 2010a). CHF determines the maximum heat dissipation capacity of the system, which mainly depends on the liquid reflux in the heating zone. The reflux process is largely affected by the resistance of vapor-liquid flow inside the porous structure (Liang et al., 2020).

FIGURE 2

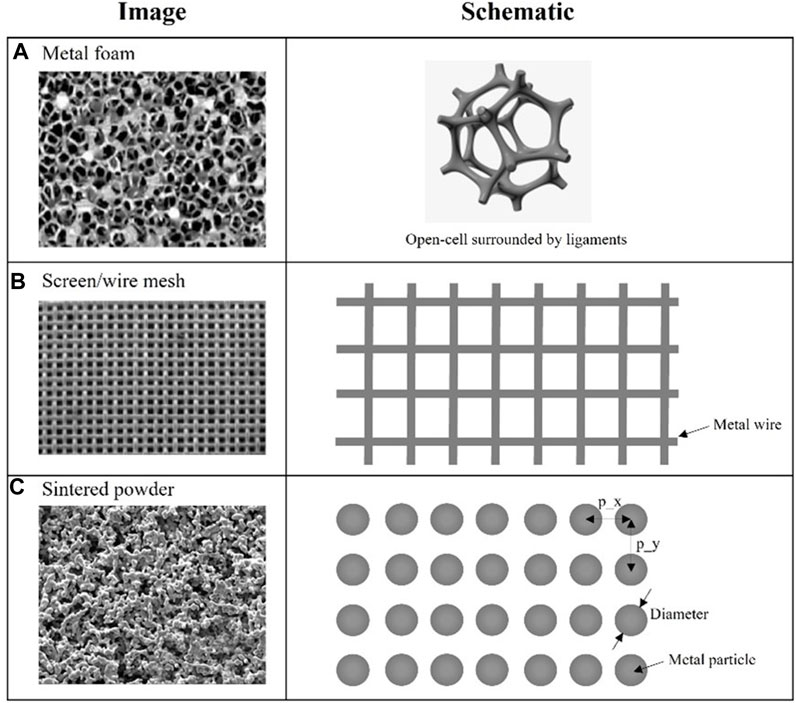
FIGURE 2. Actual image and schematic diagram of (A) Metal foam, (B) Screen/wire mesh, and (C) Sintered power.

Particularly, in electronic devices, as the structures become increasingly compact, various ultra-thin heat dissipation devices, such as flat heat pipe or vapor chamber in Figure 3 (Weibel and Garimella, 2013), have become a hot research topic. Because of the size difference, boiling in ultra-thin porous media, also called capillary-fed boiling (Weibel et al., 2010b), is quite different from the submerged pool boiling. Figure 4 shows the primary differences in heat transfer regimes between capillary-fed and pool boiling (Weibel and Garimella, 2013). In the submerged pool boiling, when the heat flux was low, heat was initially transported by natural convection, followed by nucleate boiling until reaching CHF. However, in the ultra-thin porous media, there was a liquid-vapor free surface boundary at the top layer, and heat transport first occurred in an evaporation regime prior to boiling incipience.

FIGURE 3

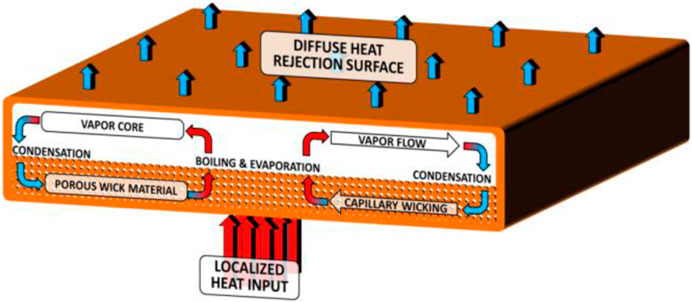
FIGURE 3. Schematic diagram of the operation and form factor of a flat heat pipe or vapor chamber heat spreader (scale in the thickness direction magnified to show details of operation) (Weibel and Garimella, 2013).

FIGURE 4

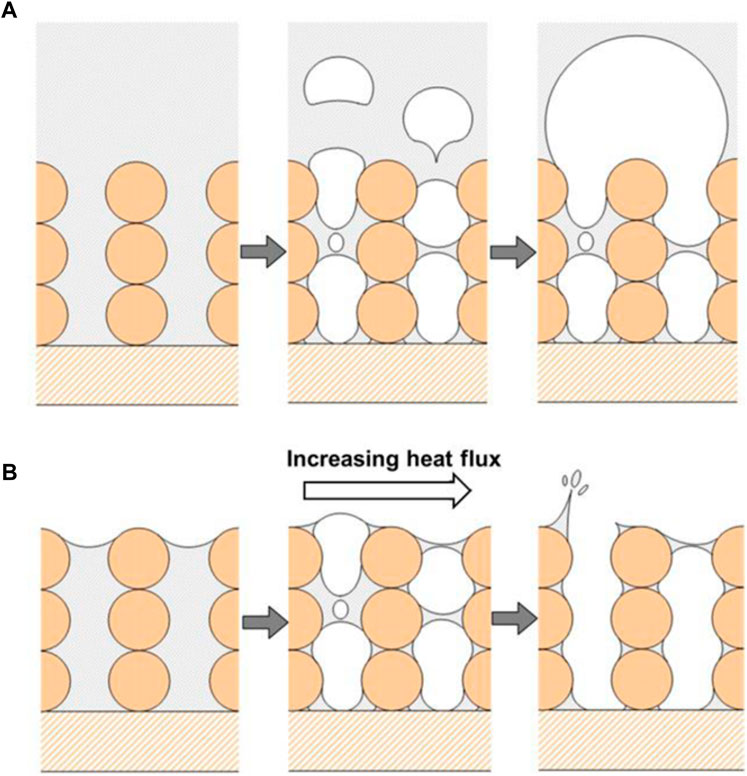
FIGURE 4. Schematic representation of the vapor formation characteristics for (A) submerged pool boiling and (B) capillary-fed boiling conditions (Weibel and Garimella, 2013).

In the research of Justin A. Weibel and Suresh V. Garimella (Weibel and Garimella, 2012), capillary-fed boiling of water from porous sintered powder wicks with thickness of 1 mm was investigated and the boiling curve comparison between porous surface and carbon nanotube (CNT) coating was obtained, as shown in Figure 5. With the increase of heating power, the curves were divided into four regions: regime 1—evaporation, regime 2—localized nucleate boiling, regime 3—uniform nucleate boiling and regime 4—receded boiling. Compared with the bare porous surface, addition of a CNT-coating caused transition to a localized nucleate boiling regime and the occurrence of CHF at lower heat fluxes.

FIGURE 5

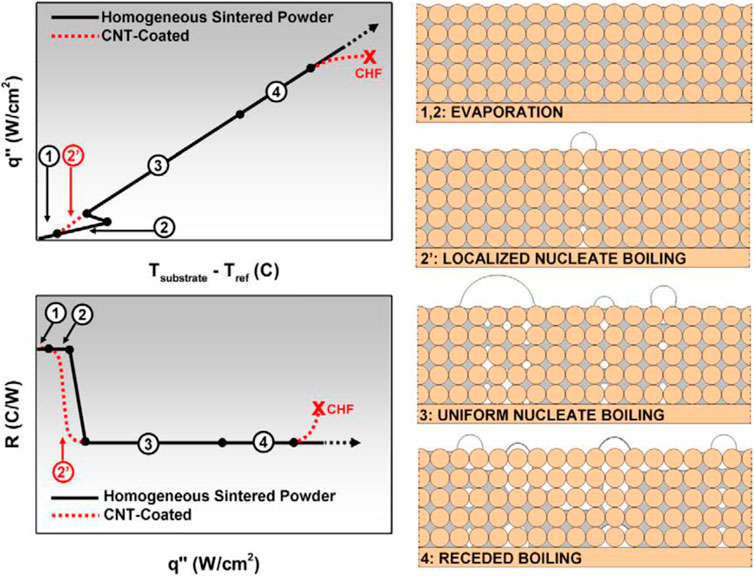
FIGURE 5. Schematic diagram of typical vapor formation regimes along the boiling curve for homogeneous sintered powder wicks. Expected modifications to the curve and regimes induced by CNT-coating are shown as dashed lines (Weibel and Garimella, 2012).

Yousaf Shah et al. (Shah et al., 2023) conducted pool boiling experiment using multistage cross-flow porous structure (MCPS) and saturated FC-72 as the working fluid. Figure 6 gives the boiling curves comparison between MCPS and plane surface. It was clear that HTC and CHF were significantly increased for the MCPS at all directions. At low heat flux, the performance of MCPS was almost identical. However, with the increase of heat flux, due to boiling mechanism in different orientations, this enhancement performance gradually became different.

FIGURE 6

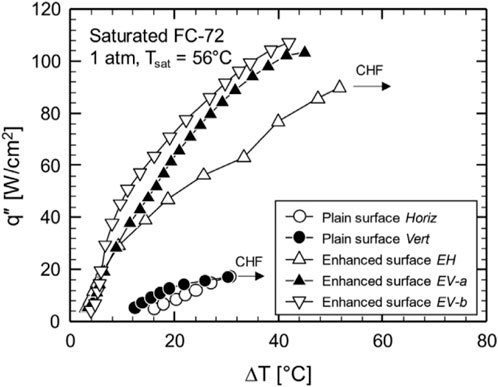
FIGURE 6. Boiling curves for MCPS and plain surface at horizontal and vertical orientations (Shah et al., 2023).

Porous media has found extensive applications in the field of heat transfer. Previous research regarding the utilization of porous mesh on the surface for heat dissipation has demonstrated numerous advantages such as efficient heat transfer mechanisms (Yang et al., 2022), an abundance of active nucleation sites (Krittacom et al., 2022), fragmentation of large vapor bubbles (Waramit et al., 2021), and the segregation of vapor and liquid pathways to improve the replenishment of the surface (Khatri et al., 2020). Wong et al. (Wong and Leong, 2018) conducted experimental research of pool boiling heat transfer of saturated FC-72 for porous lattice structures fabricated using the Selective Laser Melting (SLM) technique. The best performing substrate with the 3-mm unit cell size and 5-mm structure height had an average nucleate boiling heat transfer coefficient of 1.35 W/cm²⋅K, which was 2.81 times that of the plain surface at 0.48 W/cm²⋅K. In the study of Jiang et al. (Jiang et al., 2022), two types of microporous coating surfaces, including sintered spherical copper powder and wire mesh microporous surfaces, were fabricated. Results showed that the wire mesh surface demonstrated the best performance which presented an outstanding CHF of 48.95 W/cm² with a corresponding HTC of 2.2 W/cm²⋅K, increasing by up to 81.50% and 144.44% compared to the polished copper surface, respectively.

Recently, porous foam has attracted much attention due to its lightweight and heat transfer enhancement (Tao et al., 2023). Yuan et al. (Yuan et al., 2023) investigated a unique design of copper foam with a wettability gradient for pool boiling enhancement. They found that the super-hydrophilic top with superhydrophobic bottom copper foam structure and super-hydrophobic top with super-hydrophilic bottom copper foam structure could achieve the CHF of 113.3 and 108.3 W/cm², corresponding to the maximum HTC of 5.93 and 5.28 W/cm²⋅K, respectively. In the research of Lv et al. (Lv et al., 2023), metalized diamond was added in copper porous structures to increase the structure thermal conductivity, and good pool boiling performance was observed, with an increasement by 25% compared with the tablets without treatment.

2.2 Non-resonant effect

The current research on the impact of mechanical vibrations on heat transfer in porous media primarily focuses on convective heat transfer, while studies on the influence of vibrations on boiling are limited. We can draw references from studies on the effects of mechanical vibrations on other modes of heat transfer to understand their potential impact.

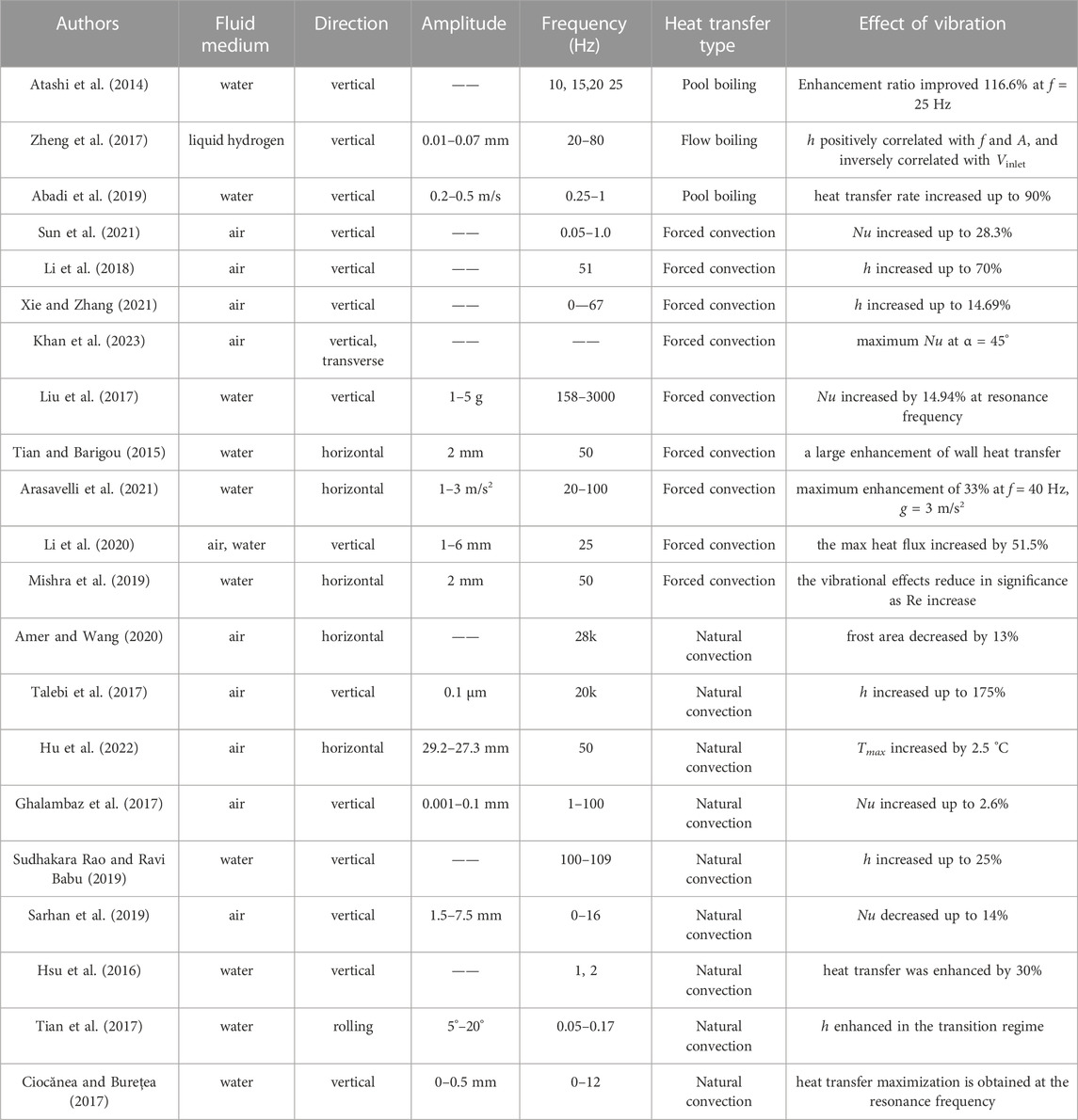
Mechanical vibration can induce alterations in the flow boundary layer and thermal boundary layer near the wall, resulting in the formation of vortices that can impact the overall fluid dynamics of the working medium and, in turn, influence the heat transfer process. We can divide the vibration into three categories: wall vibration (Leal et al., 2013), local vibration in the tube (Sun et al., 2019), and overall vibration (Arasavelli et al., 2021). Scholars have carried out relevant research about the influence of vibration parameters (frequency, amplitude, direction) on different heat exchangers [metallic line (Lemlich, 1955), pipe (Liu et al., 2017), plate (Blankenship and Clark, 1964), microgrooves (Guo et al., 2013)] and different heat transfer methods [natural convection (EshghyArpaciClark and Clark, 1965), forced convection (Takahashi and Endoh, 1990)]. It is found that in most cases the heat transfer process can be enhanced by vibration, but there are also a few cases where the vibration has no effect (Sreenivasan and Ramachandran, 1961) or even weakens the heat transfer process (Klaczak, 1997). We have summarized the relevant literature on the effect of vibration on heat transfer in the past decade, as shown in Table 1. The literature is sorted according to the heat transfer type such as pool boiling, flow boiling, forced convection and natural convection.

TABLE 1

TABLE 1. The effect of vibration on different heat transfer types.

It should be mentioned that the mechanical vibration generated by the engine or the transmission of mechanical components are passive vibrations for the thermal management systems. Since vibration can greatly improve the heat transfer performance, it is gradually utilized as an active heat transfer enhancement method. Acoustic wave generated by high frequency oscillations of a membrane is one of the main techniques and it attracted research interests at the early 1960s. According to ultrasound is defined as acoustic waves whose frequency exceeds the highest threshold that the human can hear by 16 or 20 kHz. For boiling process under acoustic vibration, configurations such as wall superheat, HTC and CHF, are reviewed in the study of Legay et al. (Legay et al., 2011) and L Léal et al. (Léal et al., 2013), where readers can find further details and analysis.

2.3 Resonant effect

The resonance problem in mechanical vibration refers to the situation where the self-vibration of a system or structure at a specific frequency is the same as or close to the external excitation frequency, leading to a sharp increase in amplitude. In general, resonance is harmful and can cause significant deformation and dynamic stress in mechanical and structural systems, even leading to destructive accidents.

Some resonance phenomena have been observed in the study of heat transfer process under vibration conditions (Paolucci and Chenoweth, 1989; Ishida et al., 2010). Compared with the situation without vibration, HTC was increased 50% when the vibration frequency was close to the resonant natural frequency (Forbes et al., 1970; Gershuni and Zhukhovitskii, 1986). Yurkov (Yurkov, 1981a; Yurkov, 1981b) studied a 2D square cavity with different wall temperatures and linear temperature distribution on top and bottom surfaces, under vertical vibrations. He calculated the average Nusselt number over a frequency range including the resonant region, and found that heat transfer rates increased significantly in the resonant region. In a similar study of Fu and Shieh (Fu and Shieh, 1992), vibration was set to be parallel to gravity in the form of g(t) = g + bωsin (ωt). In deriving the relationship for the resonant frequency, the inertial terms were comparable to the buoyancy terms, or

$\frac{dv}{dt}\sim b{\omega }^2\beta \Delta T\sin \omega t+g\beta \Delta T(1)$

They thought that the resonant frequency was only slightly affected by the static gravitational term and ignored the second term on the right side of the formula. At resonant state, the flow frequency is equal to the vibration frequency. Then the resonant vibration frequency ω_r is obtained:

${\omega }_r=\sqrt{\left(2Gr\right)\cdot \mathit{Pr}}(2)$

Where Gr is the vibration Grashof number and Pr is the Prandtl number of the fluid. Ferguson and Lilleleht (Ferguson and Lilleleht, 1996) confirmed this method and furtherly modified the predictive model equation by including the effect of the static gravitational component, which meant the second term on the right side of Eq. 1 was considered. The predicted resonant frequency was:

${\omega }_r=\frac{\sqrt{2G{r}_{v}P{r}^2}+\sqrt{2G{r}_{v}P{r}^2+2{\pi }^{2}RaPr}}{2}(3)$

With this solution, the numerical resonant frequency value was closer to the experimental value when Ra and Gr were roughly comparable in magnitude.

It is worth mentioning that currently there is relatively little analysis and experimentation regarding the mechanism of the impact of on the pool boiling process in porous media under the condition of mechanical resonance. In future designs of thermal management systems, attention should be paid to research in this aspect.

2.4 Thermo-vibrational convection in porous media

Mechanical vibration, recognized as a source of pattern generating mechanism on the surface of a liquid-filled container by Faraday in 1831, was firstly investigated to increase the stability threshold of thermos-fluid system. Then the thermo-vibrational convection was gradually developed, mainly concerning the form of a mean flow in a confined cavity filled with a fluid presenting temperature non-homogeneities (Pedramrazi et al., 2008). The study of thermo-vibrational convection in porous media can be divided into two groups: porous media saturated by a pure fluid (Kolchanova, 2020) or by a binary-mixture (Elhajjar et al., 2009a). Since the main background of this article is mechanical vibration, we mainly focus on high-frequency and small-amplitude vibration.

2.4.1 Pure fluid

For thermo-vibrational convection of pure fluid in porous media, the linear stability analysis is the primary focus. The most common geometric model is a closed square cavity. Then the study extends to different shapes, such as wavy walls (Misirlioglu et al., 2005), square enclosure (Basak et al., 2006), Γ-shape cavity (Dehnavi and Rezvani, 2012), L-shape cavity (Mohebbi and Rashidi, 2017), triangular cavity (Triveni and Panua, 2016), rectangular form (Al-Farhany and Turan, 2012), and even τ-shaped channel (Ma et al., 2019). Figure 7 shows the schematic diagram of two common structures in the study of thermo-vibrational convection of in porous media, namely, closed cavity and infinite horizontal plate, where a layer of pure fluid is on top of a layer of porous material. The fluid can be heated from below or above. H is the height and L is the length of the cavity. The direction of vibration is defined as:

$\mathbf{e}=\cos \left(\mathrm{\alpha }\right)\mathbf{i}+\sin \left(\mathrm{\alpha }\right)\mathbf{j}(4)$

Where α is the angle between the vibration direction and the horizontal direction. Vertical vibration is obtained with α = π/2 and horizontal vibration is obtained with α = 0.

FIGURE 7

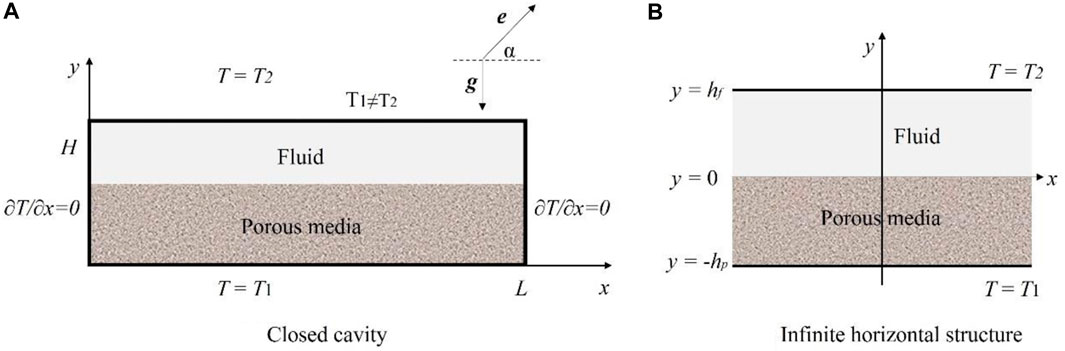
FIGURE 7. Two common structures in the study of thermo-vibrational convection in porous media: (A) Closed cavity; (B) Infinite horizontal structure.

Research has found that when a fluid layer superposed on a porous layer is heated from below, the linear stability theory predicts that there is a critical depth ratio, the ratio of the thickness of the fluid layer to that of the porous layer. For depth ratios less than the critical value, onset of thermal convection is in the form of large convection cells in the porous layer with wavelength comparable to the depth of the porous layer. For depth ratios larger than the critical value, the onset of thermal convection is confined within the fluid layer. At the critical depth ratio there is a dramatic increase in the critical wave number by one order of magnitude (CHEN and CHEN, 1992). A decrease in the fluid layer thickness leads to an increase of the critical Rayleigh number (Sun, 1973). Here we define two parameters, Ra_T as the thermal Rayleigh number, Ra_v as the vibrational Rayleigh number. By this method, the amplitude and frequency of vibrations are combined into a non-dimensional parameter referred to as the Ra_v.

$R{a}_T=\frac{Kg{\beta }_T\Delta TH}{v{a}^{*}}(5)$

$R{a}_v=R^{2}R{a}_T^2=\frac{\epsilon v{a}^{*}}{2K}{\left(\frac{b\omega }{gH}\right)}^{2}R{a}_T^2(6)$

To investigate the onset of convection, the Darcy model (Zen’kovskaya, 1992) is used in the momentum equation. There are two approaches of stability analysis, namely, the time-averaged method and the direct method (Pedramrazi et al., 2002).

In the time-averaged method, two different time scales are adopted to subdivide the temperature, velocity, and pressure fields into two different parts: one varying lowly with time and the other one varying rapidly with period τ = 2π/ω. The scale analysis method (Bejan, 2000) is used to resolve the closure problem lying in establishing relations between oscillatory velocity and temperature fields in terms of the averaged ones. Then two coupled systems of equations are obtained, one for the mean flow and the other one for oscillatory flow. The mechanical stability can be achieved when the direction of vibration is parallel to gravitational acceleration, which means the vibration should be vertical (Zen’Kovskaya and Rogovenko, 1999). It should be mentioned that the time-averaged method can be used only when the vibration frequency is high enough so that the vibration period is smaller than the response time of fluid. Otherwise, the full transient equations must be solved.

In the direct formulation method, the field variables are infinitesimally perturbed around the motionless equilibrium state. The perturbed equations are similar to a mechanical pendulum with oscillation support. We define B as the transient coefficient and ω^∗ as the dimensionless pulsation. When Bω^∗ <<1, with the presence of vibration, the stability depends on the position of heating section: if it is above the porous layer, the system will be stable; if it is below the porous media, vibration has no effect on stability threshold. When Bω∗ >>1, there are two modes of convection onset, namely, harmonic and sub-harmonic. For heating from below, vibration has a stabilizing effect on harmonic mode and a destabilizing effect on sub-harmonic mode. The thermal Rayleigh number Ra_T in the two modes also performs oppositely (Aniss et al., 2000). For the vertical vibration, vibration has a stabilizing effect; it increases the critical value of Ra_T for the onset of convection. For the horizontal vibration, with the increase of Ra_T, the gravitational effect gets more important than the vibrational effect.

2.4.2 Binary mixture

The effect of transversal vibration on the convection instability of a mixture layer was first studied in 1981 (Zen’kovskaya, 1981). Then, thermal diffusion is considered together with the longitudinal vibration in the research of stability mechanical quasi-equilibrium or mechanical equilibrium of a binary mixture horizontal layer subjected to a vertical temperature gradient (Gershuni et al., 1997; Gershuni et al., 1999).

For the study of thermo-vibrational problem in porous media filled with a binary mixture, the interaction between Soret-driven convection and thermo-vibrational convection is considered (Mojtabi et al., 2004). Under the Soret effect, a concentration gradient is formed because of the temperature gradient. The following expression is used to elaborate the equation for concentration taking into account the Soret effect:

$\mathbf{j}=-\overline{\rho }D\left(\nabla C+\alpha \nabla T\right)(7)$

Where D is the diffusion coefficient and α is the thermos-diffusional ratio (α > 0 and α < 0 correspond to the anomalous and normal Soret effect respectively).

Some interesting instability mechanisms and pattern generating phenomena have been observed in the research of binary mixture. In the research of Bilal Elhajjar et al. (Elhajjar et al., 2009b), a cavity filled with porous media and a binary mixture (90%-water and 10%-isopropanol) was utilized for the simulation. The gravitational field g is replaced by g + bω²sin (ωt)e to simulate the oscillating system. Results in Figure 8 were the comparison of streamlines and isoconcentrations without and with vibration. It is very clear that vibrations modify the structure of the flow from multicellular to monocellular, leading to the stratification of the concentration field and the separation of the binary mixture components. This means the vertical vibration can be utilized for the species separation.

FIGURE 8

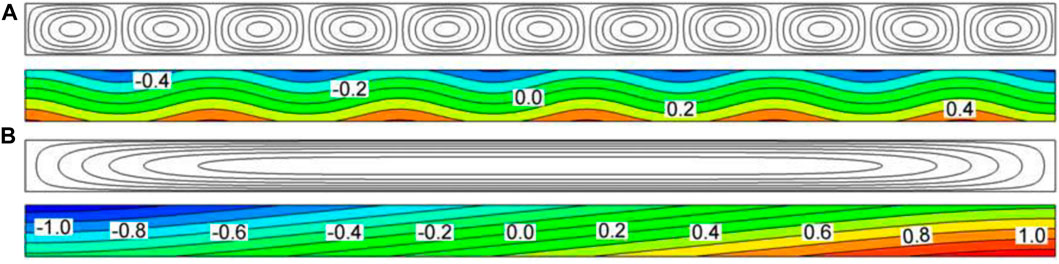
FIGURE 8. Streamlines and isoconcentrations for Le = 30, Ra_T = 13.5 (A) Ra_v = 0 (without vibration) (B) Ra_v = 10. A multicellular flow is obtained at the transition from the equilibrium solution for Ra_v = 0, whereas a monocellular flow is obtained for Ra_v = 10 (Elhajjar et al., 2009b).

Ouadhani et al. (Ouadhani et al., 2017) conducted an investigation on the effect of vibration on the separation of a binary mixture saturating a porous cavity by both direct numerical simulation and analytical model. The direction of the vibration was vertical. In their mathematical model, the density of the binary fluid was set to depend linearly on the local temperature and mass fraction:

$\rho ={\rho }_r\left[1-{\beta }_T\left(T^{\prime }-T_r\right)-{\beta }_C\left(C^{\prime }-C_r\right)\right](8)$

where ρ_r is the fluid mixture density at temperature Tr and mass fraction Cr. β_T and β_C are the thermal and concentration expansion coefficients respectively. In the numerical results, they also found that vibration modified the structure of the flow from multicellular to unicellular. But unicellular flow could lose its stability via oscillatory bifurcation. In another of their research (Ouadhani et al., 2018), the porous layer was subjected to a vertical heat flux and vertical vibrations. They found that the vibrations had no effect on the critical Rayleigh number Ra_c and critical wavenumber (k_c = 0) when φ > −1/(1 + Le). But the vibrations had an effect on the Hopf bifurcation threshold (positive Ra_c and φ < −1/(1+Le)) and on the steady bifurcation when Ra_c < 0 and φ < −1/(1 + Le).

In the research of Kumar et al. (Kumar et al., 2023), they investigated Darcy-Brinkman thermal convection in the stratified porous saturated suspension of active particles subjected to vertical oscillation. They found that the layer became unstable due to the thermal-oscillational connection of the thermal vibration parameter and porosity had a destabilizing effect that considerably lessened the ability of vertical vibration to stabilize. This conclusion was different from that of Lyubimova et al. (Lyubimova and Kolchanova, 2018), where vibration significantly stabilized the fluid equilibrium state and led to an increase in the wavelength of its perturbations. Different from the mechanical vibration, in the study of Srivastava et al. (Srivastava et al., 2018), the gravity modulation was adopted to investigate the effect on temperature dependent viscous fluid. The amplitude and of gravity modulation was found significant and more effective for the low values of frequency of modulation.

It is worth mentioning that in the above studies, only the convective process is involved (Kushwaha et al., 2021), without considering the phase transition process. It is well known that the study of heat transfer performance in mixed fluids is a focal point, such as water and ethanol (Hu et al., 2018), 2-propanol aqueous mixtures and alcohol (Sakashita et al., 2010), FC-72 and FC-75 (Yokouchi et al., 1987), Novec 7300 and 1-butanol (Chen et al., 2020), HFE-7100 and HFE-7200 (Arik and Bar-Cohen, 2002). In the follow-up studies, it is suggested that the phase change model be considered to explore whether the binary mixture in the porous media will also produce separation phenomenon during the boiling process under mechanical vibration. At the same time, it is important to focus on studying the variations of CHF and HTC during boiling processes under vibration conditions.

3 Effect of vibration on bubble dynamic characteristics

In addition to the impact on heat transfer performance, mechanical vibrations can also significantly affect the of bubble behaviors within the porous media. These bubbles can have a significant impact on the heat transfer process, as they can act as barriers to fluid flow and reduce the effective heat transfer area. The flow of bubbles within porous media is a typical vapor-liquid two-phase flow problem at the pore scale, which is a nonlinear and unstable dynamic process (SHI et al., 2019). Under the influence of mechanical vibrations, the behavior of these bubbles can become even more complex. Vibration can cause the bubbles to move and merge with others, leading to changes in their size, shape, and position within the porous media.

3.1 Stable state

During the pool boiling process, there is relative flow between liquid and vapor. Therefore, due to the influence of liquid turbulence, bubbles will also be subjected to transverse turbulent drag and the shear lift forces caused by the difference in velocity between the vapor-liquid two-phase flow (Nahra and Kamotani, 2000; Bai and Thomas, 2001; Nahra and Kamotani, 2003; Liu et al., 2010). Liquid turbulence makes bubbles more easily detach from the wall and makes bubbles more dispersed and less likely to coalesce. Zhou et al. (Zhou et al., 2018) pointed out that for cases where there was an external heat source, the Marangoni effect should be considered. The bubbles were drawn towards the heated surface due to the temperature gradient of the superheated liquid layer near the heated surface.

3.1.1 Experiments

Experiments for observing the dynamic characteristics of bubbles in porous media can be divided into two-dimensional and three-dimensional ones. Due to the complexity of the porous media structure, sophisticated instruments, such as CT scan (Minde et al., 2018) and nuclear magnetic resonance (Liu et al., 2018), are required for three-dimensional experiments to clearly measure macroscopic physical parameters and to provide a clear depiction of the micro-fluid characteristics. In comparison, it is easier to observe the motion characteristics of the fluid through two-dimensional experiments, in which glass beads (Di Federico et al., 2017) are one of the best choices due to the easy availability, high transparency, good chemical stability, and corrosion resistance. In the experiment of Liu et al. (Liu et al., 2019), transparent glass beads with the diameter of 4 mm were chosen and fixed on a test bench that can change the tilt angle. Dynamic performance of bubbles was observed, as illustrated in Figure 9. The coalescence and fragment of single bubble occurred frequently. Decreases of inclination angles and porosities of the glass beads porous media could result in the decrease of buoyancy and increase of flow resistance, increasing of volume of trapped bubbles.

FIGURE 9

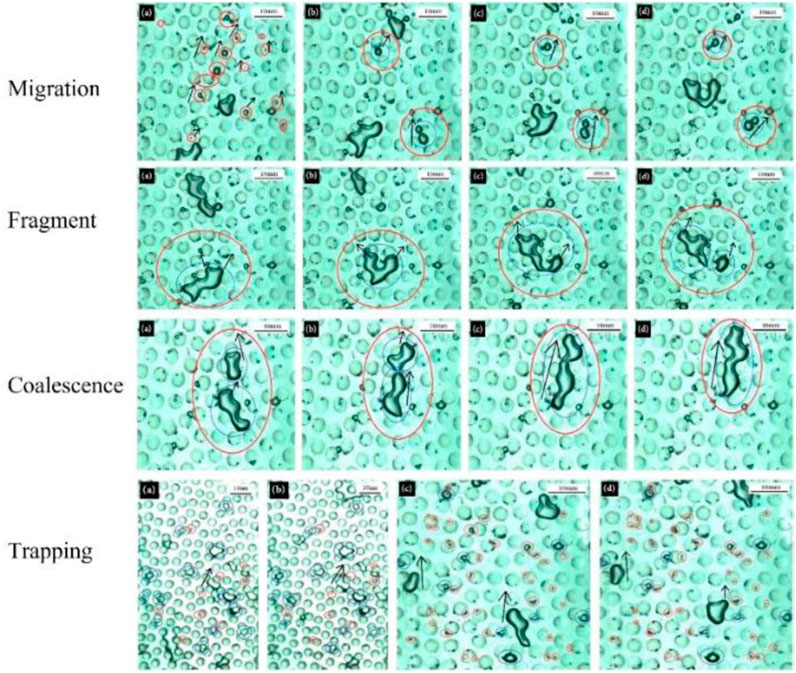
FIGURE 9. Bubble migration, fragment, coalescence, and trapping mechanism in porous media (Liu et al., 2019).

Through the study of flow boiling phenomena and bubble behavior in microscale two-dimensional porous media channels (Hu et al., 2021), it has been found that under the combined action of capillary force, viscous force, and inertial force, there were phenomena such as local bubble blockage, coalescence, liquid film evaporation, and rewetting, which were different from those in straight channels. Then, Huang et al. (Huang et al., 2018) used gradient foam metals to study the bubble behaviors in pool boiling. They observed two common types of bubble escape, as shown in Figure 10. In “A-type bubble,” the metal skeletons resisted the escaping bubble but eventually the bubble shifted to the upper side of the metal skeleton without cracking. In “B-type bubble,” a bubble was separated into two smaller bubbles and then departed from the skeletons due to a strong shear force formation between the upper and lower parts of the copper foam.

FIGURE 10

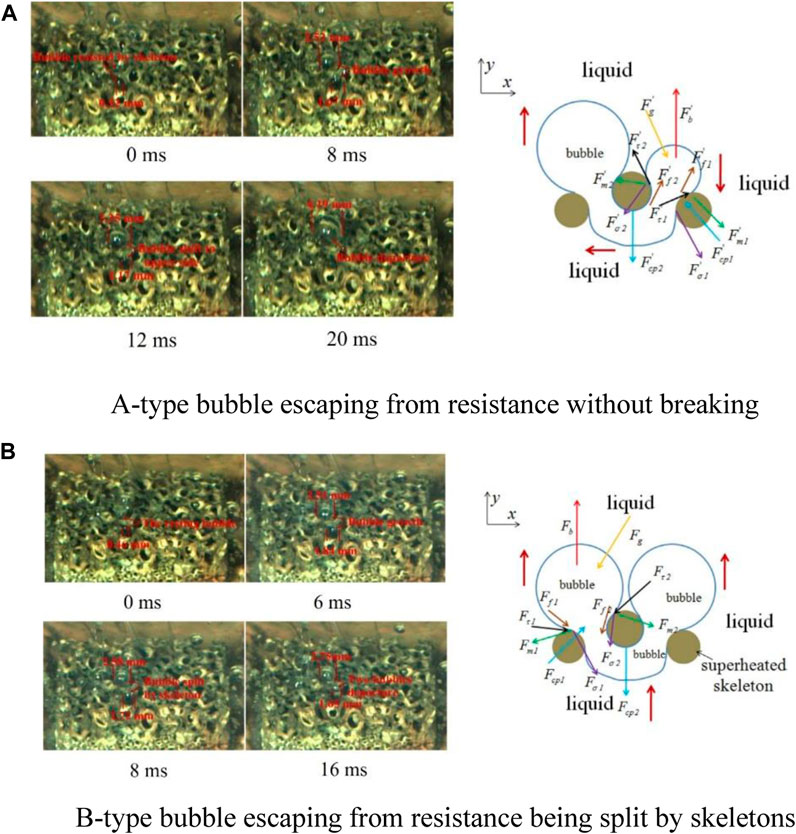
FIGURE 10. Bubble escaping types in porous media (Huang et al., 2018). (A) A-type bubble escaping from resistance without breaking. (B) B-type bubble escaping from resistance being split by skeletons.

3.1.2 Numerical simulations

Due to the opacity of porous media, it is difficult to directly observe the movement of bubbles inside through experiments. The method of numerical simulation is a good choice to solve this problem. The complexity of the solid structure leads to highly irregular phase interfaces within the porous media, making boundary treatment issues very difficult. To avoid this problem, the method of representative elementary volume (REV) is adopted in many numerical studies (Yuki et al., 2008; Lu and Zhao, 2009; Li and Leong, 2011), averaging the fluid parameters around a certain point inside the porous media at a macroscopic level, and using the averaged values over a certain range to replace the local true values. The local thermal equilibrium (LTE) (Bénard et al., 2005) and the local thermal non-equilibrium (LTNE) (Xin et al., 2014) are also considered when dealing with the problem of fluid-solid temperature difference.

The development of Lattice Boltzmann method (LBM) (Fang et al., 2017; Zhou et al., 2019) makes it possible to investigate the pore-scale boiling phenomena, with the pseudopotential model being the most commonly employed multiphase model. In 1993, Shan and Chen (Shan and Chen, 1993) developed a model to simulate flows containing multiple phases and components. Then, Hazi and Markus (Hazi and Markus, 2009) extended the model and studied the bubble departure diameter and release frequency of heterogeneous boiling on a horizontal plate in stagnant and slowly flowing fluid. Furtherly, Gong and Cheng (Gong and Cheng, 2013; Gong and Cheng, 2015a; Gong and Cheng, 2015b) improved this method and proposed a liquid-vapor phase change LB model with a new source term, where the bubble nucleation process, surface wettability effect and boiling curves were investigated. Gong and Cheng’s model was adopted by Xu et al. (Yue and Xu, 2023) to investigate the pore-scale boiling mechanism with complex geometry such as uniform and gradient (Qin et al., 2018) and the V-shaped grooved (Xu et al., 2022) porous structures, as shown in Figure 11.

FIGURE 11

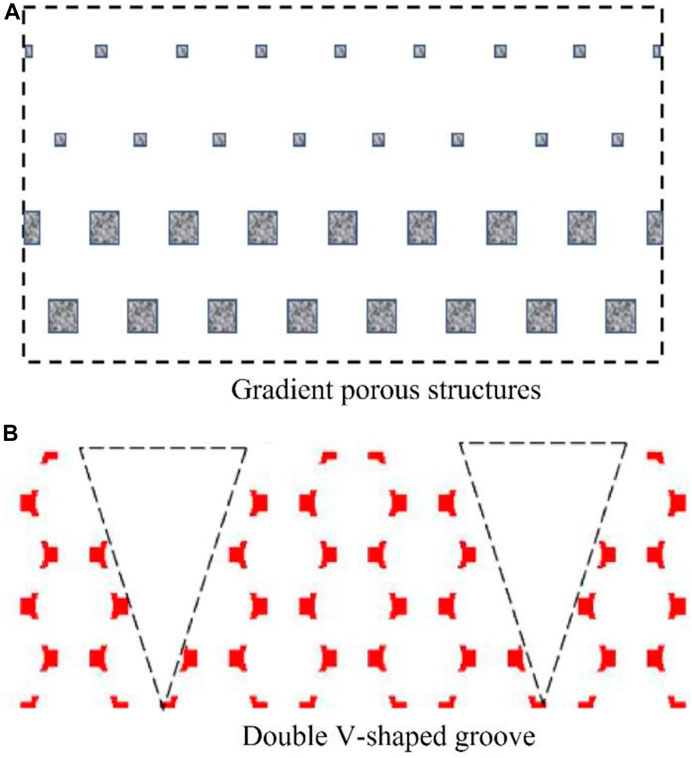
FIGURE 11. Porous metal models with (A) gradient (Qin et al., 2018) and (B) V-shaped groove (Xu et al., 2022) structures.

Bubble growth is affected by many factors, such as liquid wettability (Allred et al., 2019; Cha et al., 2023), surface properties (Godinez et al., 2019; Zakšek et al., 2019) and working conditions (Collini and MatthewJackson, 2022). The effect of horizontal wettability on bubble behaviors with gradient contact angle of 65° (in the central zone) and 105° (in the lateral zones) is shown in Figure 12. Due to the promoting effect of hydrophobic surface on the nucleation and departure of bubbles, the bubbles on lateral zones nucleated before the middle bubbles. The growth rate of the middle bubbles also slowed down, and the two nucleation sites on the heating substrate outside the detached bubbles were activated.

FIGURE 12

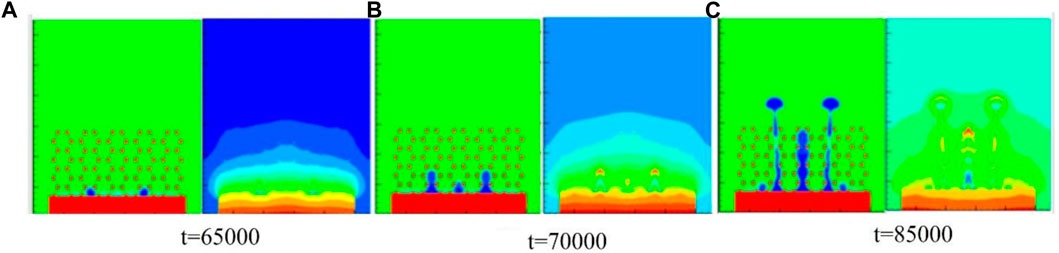
FIGURE 12. Horizontal wettability effect on bubble behaviors at contact angle = 105°-65°-105°: (A) t = 65000; (B) t = 70000; (C) t = 85000.

3.2 Unstable state

Due to external mechanical vibrations, the geometric shape and dynamic characteristics of bubbles are inevitably influenced by the driving effect of vibration forces. The influence of vibration frequency (Zhou et al., 2005), vibration direction and vibration amplitude on the bubble size and rising velocity (Mawatari et al., 2002) is mainly investigated. In the research of Zhang et al. (Zhang et al., 2022), the vibration energy effectively decreased the size and number of bubbles with the vibration frequency of 20 Hz and an amplitude of 2 mm.

In the chemical industry for carrying out liquid phase reactions, vibration can be utilized as a bubble controlling method, in which single bubble can be held stationary in the column when the downward force due to vibrations balances the buoyancy force (Ellenberger and Krishna, 2007). In the study of O’Hern et al. (O’Hern et al., 2012), experiments were performed in a thin, quasi-two-dimensional rectangular acrylic test cell subjected to sinusoidal vertical vibrations, as shown in Figure 13A. The liquid was polydimethylsiloxane (PDMS) silicone oil, and the gas was air. The vertical vibration caused violent fluctuations in the liquid surface, generating many small liquid droplets and bubbles. The small bubbles moved downward against the direction of buoyancy, and eventually merged into a larger bubble, which remained stable under the liquid-vapor interface, as shown in Figure 13B.

FIGURE 13

FIGURE 13. (A) Experiment (B) Gas cavity stably levitated by vibration. Free-surface breakup generates small bubbles that descend and coalesce to form the gas cavity, which then rises to reach position of stable levitation. Liquid is 20-cSt PDMS silicone oil; gas is air. Vibration conditions are 280 Hz, 15-g peak acceleration, and 94-μm peak-to-peak displacement (O’Hern et al., 2012).

Furtherly, a much higher vibration frequency, up to 10k Hz, was achieved by Dongjun Kim et al. (Kim et al., 2013). Similarly, liquid jets were also observed in the bubble surface, which had a critical effect on the bubble departure. The nonlinear growth of surface waves generated by parametric instability led to the jet formation. As the amplitude increased, the surface of the bubble oscillated more violently, as shown in Figure 14.

FIGURE 14

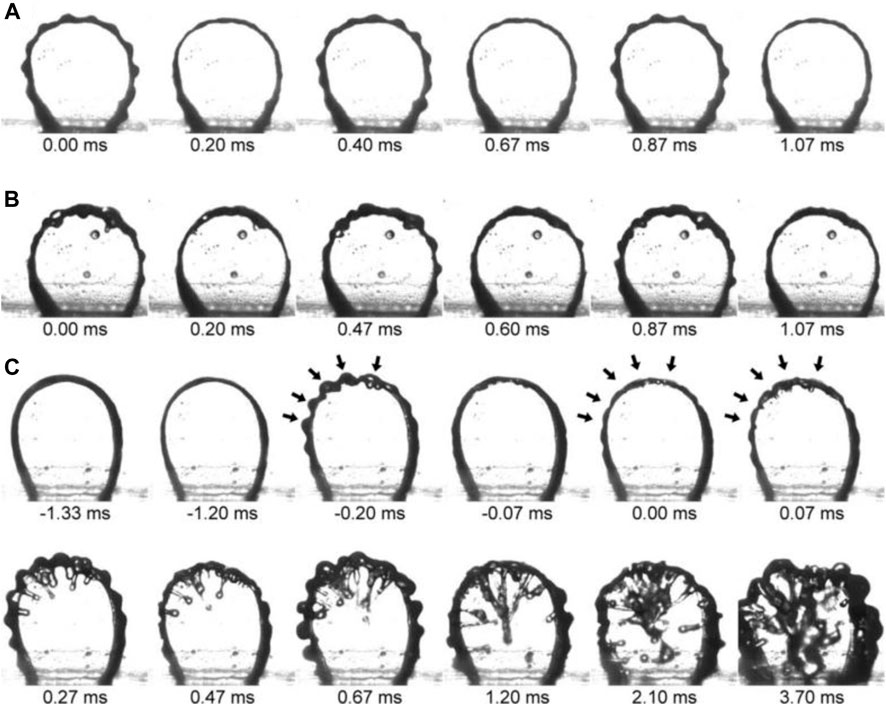
FIGURE 14. Observation of a 10-μL bubble surface oscillation and the inner part of it. The amplitude of the vibrating chamber is increased from (A) to (C) at 2,400 Hz. (A) Regular shape mode oscillation stage. (B) Chaotic oscillation stage. (C) Jet and chaotic oscillation stage. The bubble was placed in a 1.5-mm gap between two vertical acrylic sheets. Arrows indicate locations of jet generation where curvatures collapse after the surface began to bulge due to the growth of instability. The moment at which jets start to penetrate was designated as 0 s. Vibrating accelerations of (A–C) are 480 m/s², 765 m/s², and 1795 m/s², respectively (Kim et al., 2013).

Based on the research above, vibration causes pressure fluctuation, generating gas or vapor bubbles in the liquid. In recent years, equations specifically developed for the application of studying bubbles in porous media have been utilized to estimate the gas content and size of bubbles (Cheng et al., 2023). Kim et al. (Kim et al., 2012) effectively explained the impact of gas bubbles on the attenuation and compressibility of a medium. By understanding this phenomenon, it became possible to calculate the gas void fraction within the medium. They also presented a non-linear acoustic method that utilized a piezoelectric transducer to determine the gas void fraction. This method involved generating pressure signals at different frequencies and amplitudes, specifically 58 kPa at 28 kHz and 53 kPa at 33 kHz. By analyzing the resulting signals, the gas void fraction of the porous medium could be accurately determined.

Different from the visual observation technology, in the research of Lehmann et al. (Lehmann et al., 2019), the capacitance probe measurement technique was utilized. If particles pass the field lines of a capacitor in air, the dielectric constant K_e, and thereby the capacitance, will be affected. They found that vibration led to significant increase in bed expansion and a reduction of bubble volume fraction, leading to the conclusion that gas which would in the non-vibrated case be part of the bubble phase was forced into the suspension phase by mechanical vibration.

Mechanical vibrations in porous media can trigger convective instabilities. The concept of modulated force plays a crucial role in various domains, including petroleum fabrication, solidification of molten alloys, and space research laboratories. In the research of Purusothaman et al. (Purusothamana et al., 2019), a study of thermos-vibrational convective instability in a porous module was investigated, focusing on the small amplitude mechanical vibration. Results showed that in the case of isotropic and mechanically anisotropic, raising the parameters Γ and ξ favored the convective instability, thereby influencing the system to destabilize and hence dynamically activate the heat flow.

Under static conditions on the ground, Fritz (Fritz and Ende, 1935) used the principle of fluid static equilibrium to suggest that the buoyancy force acting on a bubble at the moment of detachment from a heating surface was equal to the surface tension. However, the bubble growth and detachment are not a static state but a dynamic process, with upward motion and radial expansion due to volume expansion. The rate of bubble expansion depends on the resonant frequency, which is determined by factors such as the shape, size, wall properties, surrounding medium, and amplitude and frequency of external vibrations (Lyubimov et al., 2021; Sojahrood et al., 2021). Generally, when the frequency of external vibration gets close to the natural frequency of the bubble, the resonant effect of the bubble is most significant, and the wave formed on the surface of the bubble is also the largest (Wu et al., 2019; Haghi and MichaelKolios, 2022), leading to generation of instability. Therefore, when the frequency of vibration matches the natural frequency of the bubble, the rate of expansion of the bubble may increase significantly.

Currently, through visualization experiments without vibration, it has been observed that in the initial stage of boiling, when the superheat was small, small bubbles that were generated adhered to the pores of the porous structure and did not detach (Zu et al., 2021). Only when the degree of superheat increases, the amount of steam generated and the volume of bubbles increase, causing an increase in buoyancy, will the bubbles detach from the solid structure. However, based on the existing research about vibration, we can predict that the vapor-liquid interface inside a porous medium will also experience severe fluctuations and fragmentation under the influence of mechanical vibration. The additional force from vibration can act as a driving force on small bubbles in the appropriate direction, causing them to detach from the skeleton even at low degrees of superheat, thereby affecting liquid backflow and the heat transfer characteristics of the system.

Based on the relevant research about bubble behaviors in porous medina under vibrations, it can be concluded that: 1) Mechanical vibrations can help overcome the surface tension force, leading to easier detachment of bubbles from the heated surface. This can result in more frequent bubble formation and a higher HTC. 2) The vibrations can promote bubble growth by assisting in the removal of vapor from the heated surface. Additionally, when the vibrations stop or change direction, the collapsing bubbles create micro-jets and induce fluid motion within the porous media, enhancing overall heat transfer. 3) Mechanical vibrations can induce motion in the liquid within the porous media, causing bubbles to move and distribute more evenly. This can prevent bubble coalescence and improve liquid replenishment on the heated surface, enhancing heat transfer efficiency.

4 Conclusion

In thermal management systems, compared with single-phase heat transfer on smooth surfaces, pool boiling on porous structured surfaces can greatly improve the heat transfer efficiency. Mechanical vibrations cannot be avoided in engineering applications, which have a significant impact on the boiling heat transfer characteristics and bubble behavior in porous media. The literature review has shown that mechanical vibrations can enhance heat transfer in some cases, but also have a detrimental effect in others. The effects of vibrations on HTC have been found to be influenced by various factors, such as the amplitude, frequency, and direction of vibration. The maximum effect of vibrations is observed under resonance conditions. Based on the analysis of this review, the main conclusions are drawn as follows:

1) In most cases, such as natural convection, forced convection and boiling, HTC can be increased to varying degrees under different mechanical vibration conditions. But there are also a few cases where the vibration has no effect or even weakens the heat transfer process. It is necessary to conduct in-depth research on the impact of different vibration parameters within the range of system vibrations on heat transfer, in order to improve structural design (such as increasing or reducing anti-vibration measures) and achieve optimal heat transfer efficiency.

2) Based on existing research, although resonance is not desirable from the perspective of mechanical strength stability of the system, it significantly improves the heat transfer efficiency when resonance occurs. However, there is currently limited analysis and experimentation on the mechanism of the impact of mechanical resonance on the pool boiling process in porous media. Therefore, in future designs of thermal management systems, it is important to focus on research in this aspect, aiming to find the optimal range of mechanical vibration that achieves both efficient heat transfer and mechanical stability.

3) In the thermo-vibrational convection study, binary mixture can be separated by mechanical vibration. But only the convective process is involved in the investigations, and the phase transition process is not considered. In follow-up studies, it is suggested that the phase change model be added to the calculation equation to explore whether the mixed working fluid in the porous medium will also produce separation phenomenon during the boiling process under mechanical vibration.

4) The behavior of bubbles in porous media is complex and nonlinear, and is affected by the interfacial forces, flow resistance, and pore structure. Mechanical vibrations can cause the bubbles to move and merge with other bubbles, leading to changes in their size, shape, and position within the porous media.

Author contributions

YZ: Funding acquisition, Investigation, Writing–original draft. HW: Writing–review and editing. CD: Conceptualization, Writing–review and editing.

Funding

The authors declare financial support was received for the research, authorship, and/or publication of this article.Support of the Natural Science Foundation of Shandong Province under Grant No. ZR2020QE195 and the program of China Scholarship Council (CSC) (No.202008370051) is gratefully acknowledged.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abadi, S. M. A. N. R., Ahmadpour, A., and Meyer, J. P. (2019). Effects of vibration on pool boiling heat transfer from a vertically aligned array of heated tubes. Int. J. Multiph. Flow 118, 97–112. doi:10.1016/j.ijmultiphaseflow.2019.06.006

CrossRef Full Text | Google Scholar

Al-Farhany, K., and Turan, A. (2012). Numerical study of double diffusive natural convective heat and mass transfer in an inclined rectangular cavity filled with porous medium. Int. Commun. Heat Mass Transf. 39 (2), 174–181. doi:10.1016/j.icheatmasstransfer.2011.11.014

CrossRef Full Text | Google Scholar

Allred, T. P., Weibel, J. A., and Garimella, S. V. (2019). The petal effect of parahydrophobic surfaces offers low receding contact angles that promote effective boiling. Int. J. Heat Mass Transf. 135, 403–412. doi:10.1016/j.ijheatmasstransfer.2019.02.002

CrossRef Full Text | Google Scholar

Amer, M., and Wang, C.-C. (2020). Experimental investigation on defrosting of a cold flat plate via ultrasonic vibration under natural convection. Appl. Therm. Eng. 179, 115729. doi:10.1016/j.applthermaleng.2020.115729

CrossRef Full Text | Google Scholar

Aniss, S., Souhar, M., and Belhaq, M. (2000). Asymptotic study of the convective parametric instability in Hele-Shaw cell. Phys. Fluids 12 (2), 262–268. doi:10.1063/1.870304

CrossRef Full Text | Google Scholar

Arasavelli, S. S., Konijeti, R., and Budda, G. R. (2021). Influence of transverse vibrations on convective heat transfer in parallel flow tube-in-tube heat exchanger. Heat. Transf. 50 (3), 1985–2006. doi:10.1002/htj.21965

CrossRef Full Text | Google Scholar

Arik, M., and Bar-Cohen, A. (2002). Ebullient cooling of integrated circuits by Novec fluids. GE Global Research. Technical Report No. GRC027.

Google Scholar

Atashi, H., Alaei, A., Kafshgari, M. H., Aeinehvand, R., and Rahimi, S. K. (2014). New pool boiling heat transfer in the presence of low-frequency vibrations into a vertical cylindrical heat source. Exp. Heat. Transf. 27 (5), 428–437. doi:10.1080/08916152.2013.797940

CrossRef Full Text | Google Scholar

Bai, H., and Thomas, B. G. (2001). Bubble formation during horizontal gas injection into downward-flowing liquid. Metallurgical Mater. Trans. B 32, 1143–1159. doi:10.1007/s11663-001-0102-y

CrossRef Full Text | Google Scholar

Basak, T., Roy, S., Paul, T., and Pop, I. (2006). Natural convection in a square cavity filled with a porous medium: effects of various thermal boundary conditions. Int. J. Heat Mass Transf. 49 (7-8), 1430–1441. doi:10.1016/j.ijheatmasstransfer.2005.09.018

CrossRef Full Text | Google Scholar

Bejan, A. (2000). Shape and structure, from engineering to nature. Cambridge: Cambridge University Press.

Google Scholar

Bénard, J., Eymard, R., and Nicolas, X. (2005). Boiling in porous media: model and simulations. Transp. Porous Media 60, 1–31. doi:10.1007/s11242-004-2594-9

CrossRef Full Text | Google Scholar

Blankenship, V. D., and Clark, J. A. (1964). Experimental effects of transverse oscillations on free convection of a vertical, finite plate. J. heat Mass Transf. 86, 159–165. doi:10.1115/1.3687088

CrossRef Full Text | Google Scholar

Cha, L., Feng, Q., Wang, S., Xu, S., and Xie, C. (2023). Pore-scale modeling of immiscible displacement in porous media: the effects of dual wettability. SPE J. 28, 239–250. doi:10.2118/210589-pa

CrossRef Full Text | Google Scholar

Chen, FALIN, and Chen, C. F. C. (1992). Convection in superposed fluid and porous layers. J. Fluid Mech. 234, 97–119. doi:10.1017/s0022112092000715

CrossRef Full Text | Google Scholar

Chen, P., Harmand, S., and Ouenzerfi, S. (2020). Immersion cooling effect of dielectric liquid and self-rewetting fluid on smooth and porous surface. Appl. Therm. Eng. 180, 115862. doi:10.1016/j.applthermaleng.2020.115862

CrossRef Full Text | Google Scholar

Cheng, X., Al-Khafaji, S. H., Hashemian, M., Ahmed, M., Ali Eftekhari, S., Ihsan Alanssari, A., et al. (2023). Statistical analysis and Neural Network Modeling of functionally graded porous nanobeams vibration in an elastic medium by considering the surface effects. Eng. Appl. Artif. Intell. 123, 106313. Part B. doi:10.1016/j.engappai.2023.106313

CrossRef Full Text | Google Scholar

Ciocănea, A., and Burețea, D. L. (2017). The influence of flow tube vibrations over the efficiency of solar water heating collectors. Energy Procedia 112, 330–335. doi:10.1016/j.egypro.2017.03.1059

CrossRef Full Text | Google Scholar

Collini, H., and MatthewJackson, D. (2022). Relationship between zeta potential and wettability in porous media: insights from a simple bundle of capillary tubes model. J. Colloid Interface Sci. 608, 605–621. doi:10.1016/j.jcis.2021.09.100

PubMed Abstract | CrossRef Full Text | Google Scholar

Dehnavi, R., and Rezvani, A. (2012). Numerical investigation of natural convection heat transfer of nanofluids in a Γ shaped cavity. Superlattices Microstruct. 52 (2), 312–325. doi:10.1016/j.spmi.2012.05.006

CrossRef Full Text | Google Scholar

Di Federico, V., Longo, S., King, S., Chiapponi, L., Petrolo, D., and Ciriello, V. (2017). Gravity-driven flow of Herschel–Bulkley fluid in a fracture and in a 2D porous medium. J. Fluid Mech. 821, 59–84. doi:10.1017/jfm.2017.234

CrossRef Full Text | Google Scholar

Elhajjar, B., Mojtabi, A., and Charrier Mojtabi, M. C. (2009a). Influence of vertical vibrations on the separation of a binary mixture in a horizontal porous layer heated from below. Int. J. Heat Mass Transf. 52, 165–172. doi:10.1016/j.ijheatmasstransfer.2008.05.033

CrossRef Full Text | Google Scholar

Elhajjar, B., Mojtabi, A., and Charrier-Mojtabi, M.-C. (2009b). Influence of vertical vibrations on the separation of a binary mixture in a horizontal porous layer heated from below. Int. J. Heat Mass Transf. 52, 165–172. doi:10.1016/j.ijheatmasstransfer.2008.05.033

CrossRef Full Text | Google Scholar

Ellenberger, J., and Krishna, R. (2007). Levitation of air bubbles in liquid under low frequency vibration excitement. Chem. Eng. Sci. 62, 5669–5673. doi:10.1016/j.ces.2006.12.043

CrossRef Full Text | Google Scholar

ElSaid, A. E. R., El Jamiy, F., Higgins, J., Wild, B., and Desell, T. (2018). Optimizing long short-term memory recurrent neural networks using ant colony optimization to predict turbine engine vibration. Appl. Soft Comput. 73, 969–991. doi:10.1016/j.asoc.2018.09.013

CrossRef Full Text | Google Scholar

Energy Institute (Great Britain) (2008). Guidelines for the avoidance of vibration induced fatigue failure in process pipework. Energy Institute.

Google Scholar

EshghyArpaciClark, S. V. S. J. A., and Clark, J. A. (1965). The effect of longitudinal oscillations on free convection from vertical surfaces. J. Appl. Mech. 87, 183–191. doi:10.1115/1.3625716

CrossRef Full Text | Google Scholar

Fang, W. Z., Chen, L., and Kang, Q. J. (2017). Lattice Boltzmann modeling of pool boiling with large liquid-gas density ratio. Int. J. Therm. Sci. 114, 172–183. doi:10.1016/j.ijthermalsci.2016.12.017

CrossRef Full Text | Google Scholar

Ferguson, F. T., and Lilleleht, L. U. (1996). Thermovibrational convection in a vertical cylinder. Int. J. Heat Mass Transf. 39, 2895–2906. doi:10.1016/0017-9310(95)00384-3

CrossRef Full Text | Google Scholar

Forbes, R. E., Carley, C. T., and Bell, C. J. (1970). Vibration effects on convective heat transfer in enclosures. ASME J. Heat Mass Transf. 92 (3), 429–437. doi:10.1115/1.3449681

CrossRef Full Text | Google Scholar

Fritz, W., and Ende, W. (1935). Berechnung des maximalvolumens von dampfslasen. Phys. Zeitschr 36, 379–384.

Google Scholar

Fu, W. S., and Shieh, W. J. (1992). A study of thermal convection in an enclosure induced simultaneously by gravity and vibration. Int. J. heat mass Transf. 35 (7), 1695–1710. doi:10.1016/0017-9310(92)90140-n

CrossRef Full Text | Google Scholar

Gershuni, G. Z., Kolesnikov, A. K., Legros, J. C., and Myznikova, B. (1999). On the convective instability of a horizontal binary mixture layer with Soret effect under transversal high frequency vibration. Int. J. heat mass Transf. 42 (3), 547–553. doi:10.1016/s0017-9310(98)00154-9

CrossRef Full Text | Google Scholar

Gershuni, G. Z., Kolesnikov, A. K., Legros, J. C., and Myznikova, B. I. (1997). On the vibrational convective instability of a horizontal, binary-mixture layer with Soret effect. J. Fluid Mech. 330, 251–269. doi:10.1017/s002211209600376x

CrossRef Full Text | Google Scholar

Gershuni, G. Z., and Zhukhovitskii, E. M. (1986). Vibrational thermal convection in zero gravity. Fluid Mech. Sov. Res. 15, 63–84.

Google Scholar

Ghalambaz, M., Jamesahar, E., Ismael, M. A., and Chamkha, A. J. (2017). Fluid-structure interaction study of natural convection heat transfer over a flexible oscillating fin in a square cavity. Int. J. Therm. Sci. 111, 256–273. doi:10.1016/j.ijthermalsci.2016.09.001

CrossRef Full Text | Google Scholar

Godinez, J. C., Fadda, D., and Lee, J. (2019). Enhancement of pool boiling heat transfer in water on aluminum surface with high temperature conductive microporous coating. Int. J. Heat Mass Transf. 132, 772–781. doi:10.1016/j.ijheatmasstransfer.2018.11.166

CrossRef Full Text | Google Scholar

Gong, S., and Cheng, P. (2013). Lattice Boltzmann simulation of periodic bubble nucleation, growth and departure from a heated surface in pool boiling. Int. J. Heat Mass Transf. 64, 122–132. doi:10.1016/j.ijheatmasstransfer.2013.03.058

CrossRef Full Text | Google Scholar

Gong, S., and Cheng, P. (2015a). Numerical simulation of pool boiling heat transfer on smooth surfaces with mixed wettability by lattice Boltzmann method. Int. J. Heat Mass Transf. 80, 206–216. doi:10.1016/j.ijheatmasstransfer.2014.08.092

CrossRef Full Text | Google Scholar

Gong, S., and Cheng, P. (2015b). Lattice Boltzmann simulations for surface wettability effects in saturated pool boiling heat transfer. Int. J. Heat Mass Transf. 85, 635–646. doi:10.1016/j.ijheatmasstransfer.2015.02.008

CrossRef Full Text | Google Scholar

Guo, C., Hu, X., Cao, W., Yu, D., and Tang, D. (2013). Effect of mechanical vibration on flow and heat transfer characteristics in rectangular microgrooves. Appl. Therm. Eng. 52 (2), 385–393. doi:10.1016/j.applthermaleng.2012.12.010

CrossRef Full Text | Google Scholar

Habibishandiz, M., and Saghir, M. Z. (2022). A critical review of heat transfer enhancement methods in the presence of porous media, nanofluids, and microorganisms. Therm. Sci. Eng. Prog. 30, 101267. doi:10.1016/j.tsep.2022.101267

CrossRef Full Text | Google Scholar

Haghi, H., and MichaelKolios, C. (2022). The role of primary and secondary delays in the effective resonance frequency of acoustically interacting microbubbles. Ultrason. Sonochemistry 86, 106033. doi:10.1016/j.ultsonch.2022.106033

CrossRef Full Text | Google Scholar

Haym, B., Mark, N., and Mi, S. H. (2022). Mechanical vibration: theory and application. Rutgers University Press.

Google Scholar

Hazi, G., and Markus, A. (2009). On the bubble departure diameter and release frequency based on numerical simulation results. Int. J. Heat Mass Transf. 52 (5-6), 1472–1480. doi:10.1016/j.ijheatmasstransfer.2008.09.003

CrossRef Full Text | Google Scholar

He, B., Luo, X., Fan, Yu, Li, T., Wang, L., Zhou, J., et al. (2023). Effects of inlet subcooling on the flow boiling heat transfer performance of bi-porous mini-channels. Appl. Therm. Eng. 229, 120577. doi:10.1016/j.applthermaleng.2023.120577

CrossRef Full Text | Google Scholar

Hosseinian, A., Meghdadi Isfahani, A. H., and Shirani, E. (2018). Experimental investigation of surface vibration effects on increasing the stability and heat transfer coeffcient of MWCNTs-water nanofluid in a flexible double pipe heat exchanger. Exp. Therm. Fluid Sci. 90, 275–285. doi:10.1016/j.expthermflusci.2017.09.018

CrossRef Full Text | Google Scholar

Hsu, H. J., Huang, Y. H., and Liu, Y. H. (2016). Natural convection in an oscillating cylindrical enclosure with pin fins. Int. J. Heat Mass Transf. 93, 720–728. doi:10.1016/j.ijheatmasstransfer.2015.10.057

CrossRef Full Text | Google Scholar

Hu, H., Xu, R., and Jiang, P. (2021). Experimental investigation of flow boiling in porous media with micromodels. J. Eng. Thermophys. 42, 424–429.

Google Scholar

Hu, J., Wang, K., Xie, L., Min, C., and Rao, Z. (2022). Effects of electromagnetic-vibration fan with folding blades on convective heat transfer. Appl. Therm. Eng. 213, 118651. doi:10.1016/j.applthermaleng.2022.118651

CrossRef Full Text | Google Scholar

Hu, Y., Chen, S., Huang, J., and Song, M. (2018). Marangoni effect on pool boiling heat transfer enhancement of self-rewetting fluid. Int. J. Heat Mass Transf. 127, 1263–1270. doi:10.1016/j.ijheatmasstransfer.2018.08.003

CrossRef Full Text | Google Scholar

Huang, R. L., Zhao, C. Y., and Xu, Z. G. (2018). Investigation of bubble behavior in gradient porous media under pool boiling conditions. Int. J. Multiph. Flow 103, 85–93. doi:10.1016/j.ijmultiphaseflow.2018.02.005

CrossRef Full Text | Google Scholar

Ishida, H., Takagi, Y., Kin, N., Yoshimura, H., and Kawahara, G. (2010). Resonant thermal convections in a square cavity induced by heat-flux vibration on the bottom wall. Numer. Heat. Transf. Part A Appl. 58 (1), 20–40. doi:10.1080/10407782.2010.490445

CrossRef Full Text | Google Scholar

Jain, A., Abbas, M. M., and Torabi, M. (2023). Steady state thermal analysis of a porous fin with radially outwards fluid flow. Int. J. Heat Mass Transf. 209, 124109. doi:10.1016/j.ijheatmasstransfer.2023.124109

CrossRef Full Text | Google Scholar

Jiang, Y., Zhou, G., Zhou, J., Zhou, F., and Huai, X. (2022). Saturated pool boiling heat transfer of HFE-7100 on sintered copper powder and wire mesh microporous surfaces: a comparison study. Appl. Therm. Eng. 216, 119067. doi:10.1016/j.applthermaleng.2022.119067

CrossRef Full Text | Google Scholar

Joshy, N., Hajiyan, M., Siddique, A. R. M., Tasnim, S., Simha, H., and Mahmud, S. (2020). Experimental investigation of the effect of vibration on phase change material (PCM) based battery thermal management system. J. Power Sources 450, 227717. doi:10.1016/j.jpowsour.2020.227717

CrossRef Full Text | Google Scholar

Khan, M. A., Masood, S., Fahad Anwer, S., Khan, S. A., and Arif, M. R. (2023). Vortex induced vibration for mixed convective flow past a square cylinder. Int. J. Heat Mass Transf. 202, 123722. doi:10.1016/j.ijheatmasstransfer.2022.123722

CrossRef Full Text | Google Scholar

Khatri, R., Goswami, S., Anas, M., Sharma, S., Agarwal, S., and Aggarwal, S. (2020). Performance evaluation of an arched plate solar air heater with porous aluminum wire mesh cylindrical fins. Energy Rep. 6 (Suppl. 9), 627–633. doi:10.1016/j.egyr.2020.11.177

CrossRef Full Text | Google Scholar

Kim, B. N., Yoon, S. W., Choi, B. K., and Jung, S. K. (2012). Gas void fraction estimation in gas-bubble-contained sands with difference frequency waves. Jpn. J. Appl. Phys. 51–7. Issue2. doi:10.1143/JJAP.51.07GD02

CrossRef Full Text | Google Scholar

Kim, D., Park, J. K., Kang, S., and Kang, K. H. (2013). Mechanism of bubble detachment from vibrating walls. Phys. Fluids 25, 112108. doi:10.1063/1.4829895

CrossRef Full Text | Google Scholar

Klaczak, A. (1997). Report from experiments on heat transfer by forced vibrations of exchangers. Heat Mass Transf. 32 (6), 477–480. doi:10.1007/s002310050148

CrossRef Full Text | Google Scholar

Kolchanova, E. A. (2020). Onset of thermal convection in a superposed fluid-porous layer subjected to high-frequency longitudinal vibration in weightlessness. Int. J. Heat Mass Transf. 159, 120123. doi:10.1016/j.ijheatmasstransfer.2020.120123

CrossRef Full Text | Google Scholar

Krittacom, B., Bunchan, S., and Luampon, R. (2022). Heat transfer enhancement of solar collector by placing wire mesh stainless porous material on the solar absorber plate of indirect forced convection solar dryer. Therm. Sci. Eng. Prog. 32, 101304. doi:10.1016/j.tsep.2022.101304

CrossRef Full Text | Google Scholar

Kumar, V., Srikanth, K., and Grover, D. (2023). Darcy–Brinkman analysis of thermo-vibrational convection in gyrotactic swimmers: an overstability theory. J. Therm. Analysis Calorim. 148, 10189–10201. doi:10.1007/s10973-023-12383-y

CrossRef Full Text | Google Scholar

Kushwaha, A. K., Sharma, Y. D., and Saini, S. (2021). Impact of vertical vibration and gyrotactic microorganisms on stability of thermo-bioconvection. Mech. Res. Commun. 116, 103769. doi:10.1016/j.mechrescom.2021.103769

CrossRef Full Text | Google Scholar

Leal, L., Lavieille, P., Miscevic, M., Pigache, F., and Tadrist, L. (2013). Control of pool boiling incipience in confined space: dynamic morphing of the wall effect. Appl. Therm. Eng. 51 (1-2), 451–458. doi:10.1016/j.applthermaleng.2012.09.031

CrossRef Full Text | Google Scholar

Léal, L., Miscevic, M., Lavieille, P., Amokrane, M., Pigache, F., Topin, F., et al. (2013). An overview of heat transfer enhancement methods and new perspectives: focus on active methods using electroactive materials. Int. J. heat mass Transf. 61, 505–524. doi:10.1016/j.ijheatmasstransfer.2013.01.083

CrossRef Full Text | Google Scholar

Legay, M., Gondrexon, N., Le Person, S., Boldo, P., and Bontemps, A. (2011). Enhancement of heat transfer by ultrasound: review and recent advances. Int. J. Chem. Eng. 2011, 1–17. doi:10.1155/2011/670108

CrossRef Full Text | Google Scholar

Lehmann, S. E., Hartge, E.-U., Jongsma, A., deLeeuw, I.-M., Innings, F., and Heinrich, S. (2019). Fluidization characteristics of cohesive powders in vibrated fluidized bed drying at low vibration frequencies. Powder Technol. 357, 54–63. doi:10.1016/j.powtec.2019.08.105

CrossRef Full Text | Google Scholar

Lemlich, R. (1955). Effect of vibration on natural convective heat transfer. Industrial Eng. Chem. 47 (6), 1175–1180. doi:10.1021/ie50546a024

CrossRef Full Text | Google Scholar

Li, D., Yang, X., Wang, S., Duan, D., Wan, Z., Xia, G., et al. (2020). Experimental research on vibration-enhanced heat transfer of fin-tube vehicle radiator. Appl. Therm. Eng. 180, 115836. doi:10.1016/j.applthermaleng.2020.115836

CrossRef Full Text | Google Scholar

Li, H. Y., and Leong, K. C. (2011). Experimental and numerical study of single and two-phase flow and heat transfer in aluminum foams. Int. J. Heat Mass Transf. 54 (23-24), 4904–4912. doi:10.1016/j.ijheatmasstransfer.2011.07.002

CrossRef Full Text | Google Scholar

Li, M., Cheng, X., Wei, J., and Tao, W. (2023). Lattice Boltzmann simulation of condensation on self-cleaning porous membrane. Int. Commun. Heat Mass Transf. 141, 106595. doi:10.1016/j.icheatmasstransfer.2022.106595

CrossRef Full Text | Google Scholar

Li, X.-J., Zhang, J.-zhou, and Tan, X.-ming (2018). An investigation on convective heat transfer performance around piezoelectric fan vibration envelope in a forced channel flow. Int. J. Heat Mass Transf. 126, 48–65. doi:10.1016/j.ijheatmasstransfer.2018.06.021

CrossRef Full Text | Google Scholar

Liang, G., Chen, Y., Han, Y., Li, D., and Shen, S. (2020). Nucleate boiling heat transfer and critical heat flux (CHF) from micro-pit surfaces. Int. J. Heat Mass Transf. 152, 119510. doi:10.1016/j.ijheatmasstransfer.2020.119510

CrossRef Full Text | Google Scholar

Liao, X., Jian, Q., Zu, S., Li, D., and Huang, Z. (2021). Visualization study and analysis on the heat transfer performance of an ultra-thin flat-plate heat pipe. Int. Commun. Heat Mass Transf. 126, 105464. doi:10.1016/j.icheatmasstransfer.2021.105464

CrossRef Full Text | Google Scholar

Liu, N., Ju, B., Chen, X., Thompson Brantson, E., Mu, S., Yang, Y., et al. (2019). Experimental study of the dynamic mechanism on gas bubbles migration, fragment, coalescence and trapping in a porous media. J. Petroleum Sci. Eng. 181, 106192. doi:10.1016/j.petrol.2019.106192

CrossRef Full Text | Google Scholar

Liu, W., Yang, Z., Zhang, B., and Lv, P. (2017). Experimental study on the effects of mechanical vibration on the heat transfer characteristics of tubular laminar flow. Int. J. Heat Mass Transf. 115, 169–179. doi:10.1016/j.ijheatmasstransfer.2017.07.025

CrossRef Full Text | Google Scholar

Liu, Z., Liu, D., Cai, Y., and Pan, Z. (2018). The impacts of flow velocity on permeability and porosity of coals by core flooding and nuclear magnetic resonance: implications for coalbed methane production. J. Petroleum Sci. Eng. 171, 938–950. doi:10.1016/j.petrol.2018.08.037

CrossRef Full Text | Google Scholar

Liu, C., Liang, B., Tang, S., Zhang, H., and Min, E. (2010). A theoretical model for the size prediction of single bubbles formed under liquid cross-flow. Chin. J. Chem. Eng. 18 (5), 770–776. doi:10.1016/s1004-9541(09)60128-2

CrossRef Full Text | Google Scholar

Lu, W., and Zhao, C. Y. (2009). Numerical modelling of flow boiling heat transfer in horizontal metal-foam tubes. Adv. Eng. Mater. 11 (10), 832–836. doi:10.1002/adem.200900139

CrossRef Full Text | Google Scholar

Lv, Z., Yi, An, and Huang, C. (2023). Enhanced pool boiling heat transfer by adding metalized diamond in copper porous materials. Appl. Therm. Eng. 226, 120288. doi:10.1016/j.applthermaleng.2023.120288

CrossRef Full Text | Google Scholar

Lyubimov, D., Lyubimova, T., and Cherepanov, A. (2021). Resonance oscillations of a drop (bubble) in a vibrating fluid. J. Fluid Mech. 909, A18. doi:10.1017/jfm.2020.949

CrossRef Full Text | Google Scholar

Lyubimova, T. P., and Kolchanova, E. A. (2018). The onset of double-diffusive convection in a superposed fluid and porous layer under high-frequency and small-amplitude vibrations. Transp. Porous Media 122, 97–124. doi:10.1007/s11242-017-0991-0

CrossRef Full Text | Google Scholar

Ma, Y., Mohebbi, R., Rashidi, M. M., and Yang, Z. (2019). MHD forced convection of MWCNT–Fe₃O₄/water hybrid nanofluid in a partially heated τ-shaped channel using LBM. J. Therm. Analysis Calorim. 136, 1723–1735. doi:10.1007/s10973-018-7788-4

CrossRef Full Text | Google Scholar

Majeed Mohammed, A., Kapan, S., Sen, M., and Celik, N. (2021). Effect of vibration on heat transfer and pressure drop in a heat exchanger with turbulator. Case Stud. Therm. Eng. 28, 101680. doi:10.1016/j.csite.2021.101680

CrossRef Full Text | Google Scholar

Mawatari, Y., Akune, T., Tatemoto, Y., and Noda, K. (2002). Bubbling and bed expansion behavior under vibration in a gas-solid fluidized bed. Chem. Eng. Technol. 25, 1095–1100. doi:10.1002/1521-4125(20021105)25:11<1095::aid-ceat1095>3.0.co;2-8

CrossRef Full Text | Google Scholar

Meng, Z., Xu, J., Zhao, G., and Hao, G. (2018). Enhanced heat transfer characteristics and ampacity analysis of a high-voltage overhead transmission line under aeolian vibration. IET Generation, Transm. Distribution 12 (12), 2918–2925. doi:10.1049/iet-gtd.2017.1764

CrossRef Full Text | Google Scholar

Minde, M. W., Wang, W., Madland, M. V., Zimmermann, U., Korsnes, R. I., Bertolino, S. R. A., et al. (2018). Temperature effects on rock engineering properties and rock-fluid chemistry in opal-CT-bearing chalk. J. Petroleum Sci. Eng. 169, 454–470. doi:10.1016/j.petrol.2018.05.072

CrossRef Full Text | Google Scholar

Mishra, S. K., Chandra, H., and Arora, A. (2019). Effects on heat transfer and radial temperature profile of non-isoviscous vibrational flow with varying Reynolds number. J. Appl. Fluid Mech. 12 (1), 135–144. doi:10.29252/jafm.75.253.28952

CrossRef Full Text | Google Scholar

Misirlioglu, A., Baytas, A. C., and Pop, I. (2005). Free convection in a wavy cavity filled with a porous medium. Int. J. heat mass Transf. 48 (9), 1840–1850. doi:10.1016/j.ijheatmasstransfer.2004.12.005

CrossRef Full Text | Google Scholar

Mohebbi, R., and Rashidi, M. M. (2017). Numerical simulation of natural convection heat transfer of a nanofluid in an L-shaped enclosure with a heating obstacle. J. Taiwan Inst. Chem. Eng. 72, 70–84. doi:10.1016/j.jtice.2017.01.006

CrossRef Full Text | Google Scholar

Mojtabi, M. C., Razi, Y. P., Maliwan, K., and Mojtabi, A. (2004). Influence of vibration on Soret-driven convection in porous media. Numer. Heat. Transf. Part A 46 (10), 981–993. doi:10.1080/10407780490517638

CrossRef Full Text | Google Scholar

Nahra, H. K., and Kamotani, Y. (2000). Bubble formation from wall orifice in liquid cross-flow under low gravity. Chem. Eng. Sci. 55 (20), 4653–4665. doi:10.1016/s0009-2509(00)00102-0

CrossRef Full Text | Google Scholar

Nahra, H. K., and Kamotani, Y. (2003). Prediction of bubble diameter at detachment from a wall orifice in liquid cross-flow under reduced and normal gravity conditions. Chem. Eng. Sci. 58 (1), 55–69. doi:10.1016/s0009-2509(02)00516-x

CrossRef Full Text | Google Scholar

O’Hern, T. J., Shelden, B., Torczynski, J. R., and LouisRomero, A. (2012). Bubble oscillations and motion under vibration. Phys. Fluids 24, 091108. doi:10.1063/1.4747165

CrossRef Full Text | Google Scholar

Ouadhani, S., Ali, A., and Mojtabi, A. (2017). Analytical and numerical stability analysis of Soret-driven convection in a horizontal porous layer: the effect of vertical vibrations. Eur. Phys. J. E 40, 38. doi:10.1140/epje/i2017-11527-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Ouadhani, S., Ali, A., Mojtabi, A., and Bergeon, A. (2018). Influence of vertical vibrations on the stability of a binary mixture in a horizontal porous layer subjected to a vertical heat flux. Transp. Porous Media 124, 203–220. doi:10.1007/s11242-018-1059-5

CrossRef Full Text | Google Scholar

Paolucci, S., and Chenoweth, D. (1989). Transition to chaos in a differentially heated vertical cavity. J. Fluid Mech. 201, 379–410. doi:10.1017/s0022112089000984

CrossRef Full Text | Google Scholar

Pedramrazi, Y., Charrier-Mojtabi, M. C., and Mojtabi, A. (2008). “Thermal vibrational convection in a porous medium saturated by a pure or binary fluid,” in Emerging topics in heat and mass transfer in porous media: from bioengineering and microelectronics to nanotechnology, 149–179.

Google Scholar

Pedramrazi, Y., Maliwan, K., and Mojtabi, A. (2002). “Two different approaches for studying the stability of the Horton–Rogers–Lapwood problem under the effect of vertical vibration,” in Proceedings of the first international conference in applications of porous media Jerba, Tunisia, 489–497.

Google Scholar

Purusothamana, A., Chandra Guru Sekarb, R., and Murugesan, K. (2019). Magnetic field and vibration effects on the onset of thermal convection in a grade fluid permeated anisotropic porous module. Therm. Sci. Eng. Prog. 10, 138–146. doi:10.1016/j.tsep.2019.01.012

CrossRef Full Text | Google Scholar

Qin, J., Zhou, X., Zhao, C. Y., and Xu, Z. G. (2018). Numerical investigation on boiling mechanism in porous metals by LBM at pore scale level. Int. J. Therm. Sci. 130, 298–312. doi:10.1016/j.ijthermalsci.2018.05.004

CrossRef Full Text | Google Scholar

Sakashita, H., Ono, A., and Nakabayashi, Y. (2010). Measurements of critical heat flux and liquid–vapor structure near the heating surface in pool boiling of 2-propanol/water mixtures. Int. J. heat mass Transf. 53 (7-8), 1554–1562. doi:10.1016/j.ijheatmasstransfer.2009.11.028

CrossRef Full Text | Google Scholar

Sarhan, A. R., Karim, M. R., Kadhim, Z. K., and Naser, J. (2019). Experimental investigation on the effect of vertical vibration on thermal performances of rectangular flat plate. Exp. Therm. Fluid Sci. 101, 231–240. doi:10.1016/j.expthermflusci.2018.10.024

CrossRef Full Text | Google Scholar

Shah, Y., Kim, H. G., Choi, W. W., and Kim, S. M. (2023). Experimental pool boiling study on novel multistage cross-flow porous structure using FC-72 for high-heat-flux electronic applications. Int. J. Heat Mass Transf. 213, 124270. doi:10.1016/j.ijheatmasstransfer.2023.124270

CrossRef Full Text | Google Scholar

Shan, X., and Chen, H. (1993). Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E 47 (3), 1815–1819. doi:10.1103/physreve.47.1815

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, J., Ma, Q., and Chen, Z. (2019). Numerical study on bubble motion in pore structure under microgravity using the Lattice Boltzmann Method. Microgravity Sci. Technol. 31 (2), 207–222. doi:10.1007/s12217-019-9681-6

CrossRef Full Text | Google Scholar

Sojahrood, A. J., Earl, R., and Haghi, H. (2021). Nonlinear dynamics of acoustic bubbles excited by their pressure-dependent subharmonic resonance frequency: influence of the pressure amplitude, frequency, encapsulation and multiple bubble interactions on oversaturation and enhancement of the subharmonic signal. Nonlinear Dyn. 103, 429–466. doi:10.1007/s11071-020-06163-8

CrossRef Full Text | Google Scholar

Sreenivasan, K., and Ramachandran, A. (1961). Effect of vibration on heat transfer from a horizontal cylinder to a normal air stream. Int. J. Heat Mass Transf. 3 (1), 60–67. doi:10.1016/0017-9310(61)90006-0

CrossRef Full Text | Google Scholar

Srivastava, A., Bhadauria, B. S., and Singh, A. K. (2018). Study of heat and mass transport in bénard-Darcy convection with G-jitter and variable viscosity liquids in a porous layer with internal heat source. J. Appl. Fluid Mech. 11 (5), 1217–1229. doi:10.29252/jafm.11.05.28459

CrossRef Full Text | Google Scholar

Starodubtseva, I. P., Kuznetsov, D. V., and Pavlenko, A. N. (2021). Experiments and modeling on cryogenic quenching enhancement by the structured capillary-porous coatings of surface. Int. J. Heat Mass Transf. 176, 121388. doi:10.1016/j.ijheatmasstransfer.2021.121388

CrossRef Full Text | Google Scholar

Stewart, R. A., and Shaw, J. M. (2015). A dynamic pressure view cell for acoustic stimulation of fluids--Micro-bubble generation and fluid movement in porous media. Rev. Sci. Instrum. 86, 095101. doi:10.1063/1.4929460

PubMed Abstract | CrossRef Full Text | Google Scholar

Sudhakara Rao, B., and Ravi Babu, S. (2019). Experimental investigation on natural convection heat transfer augmentation with vibration effect. Int. Res. J. Eng. Technol. 6 (8), 1496–1501.

Google Scholar

Sun, W. J. (1973). Convective instability in superposed porous and free layers. Minneapolis: University of Minnesota. Ph.D. thesis.

Google Scholar

Sun, Xu, Li, S., Lin, G.-G., and Zhang, J.-Z. (2021). Effects of flow-induced vibration on forced convection heat transfer from two tandem circular cylinders in laminar flow. Int. J. Mech. Sci. 195, 106238. doi:10.1016/j.ijmecsci.2020.106238

CrossRef Full Text | Google Scholar

Sun, X., Ye, Z., Li, J., Wen, K., and Tian, H. (2019). Forced convection heat transfer from a circular cylinder with a flexible fin. Int. J. Heat Mass Transf. 128, 319–334. doi:10.1016/j.ijheatmasstransfer.2018.08.123

CrossRef Full Text | Google Scholar

Takahashi, K., and Endoh, K. (1990). A new correlation method for the effect of vibration on forced-convection heat transfer. J. Chem. Eng. Jpn. 23 (1), 45–50. doi:10.1252/jcej.23.45

CrossRef Full Text | Google Scholar

Talebi, M., Setareh, M., Saffar-Avval, M., and Hosseini Abardeh, R. (2017). Numerical investigation of natural convection heat transfer in a cylindrical enclosure due to ultrasonic vibrations. Ultrasonics 76, 52–62. doi:10.1016/j.ultras.2016.12.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Tao, X., Sun, K., Chen, R., Suo, M., Liu, H., Che, Z., et al. (2023). Two-phase flow in porous metal foam flow fields of PEM fuel cells. Chem. Eng. Sci. 282, 119270. doi:10.1016/j.ces.2023.119270

CrossRef Full Text | Google Scholar

Tian, S., and Barigou, M. (2015). An improved vibration technique for enhancing temperature uniformity and heat transfer in viscous fluid flow. Chem. Eng. Sci. 123, 609–619. doi:10.1016/j.ces.2014.11.029

CrossRef Full Text | Google Scholar

Tian, W., Cao, X., Yan, C., and Wu, Z. (2017). Experimental study of single-phase natural circulation heat transfer in a narrow, vertical, rectangular channel under rolling motion conditions. Int. J. Heat Mass Transf. 107, 592–606. doi:10.1016/j.ijheatmasstransfer.2016.10.094

CrossRef Full Text | Google Scholar

Triveni, M. K., and Panua, R. (2016). Numerical simulation of natural convection in a triangular enclosure with caterpillar (C)-curve shape hot wall. Int. J. Heat Mass Transf. 96, 535–547. doi:10.1016/j.ijheatmasstransfer.2016.02.002

CrossRef Full Text | Google Scholar

Waramit, P., Chanmak, P., Peamsuwan, R., and Krittacom, B. (2021). Forced convection enhancement of air flowing inside circular pipe with varying the pitch (P) of wire-mesh porous media. Energy Rep. 7 (Suppl. 5), 70–82. doi:10.1016/j.egyr.2021.09.046

CrossRef Full Text | Google Scholar

Weibel, J. A., and Garimella, S. V. (2012). Visualization of vapor formation regimes during capillary-fed boiling in sintered-powder heat pipe wicks. Int. J. Heat Mass Transf. 55 (13-14), 3498–3510. doi:10.1016/j.ijheatmasstransfer.2012.03.021

CrossRef Full Text | Google Scholar

Weibel, J. A., and Garimella, S. V. (2013). Recent advances in vapor chamber transport characterization for high-heat-flux applications. Adv. Heat Transf. 45, 209–301. doi:10.1016/B978-0-12-407819-2.00004-9

CrossRef Full Text | Google Scholar

Weibel, J. A., Garimella, S. V., and North, M. T. (2010a). Characterization of evaporation and boiling from sintered powder wicks fed by capillary action. Int. J. Heat Mass Transf. 53, 4204–4215. doi:10.1016/j.ijheatmasstransfer.2010.05.043

CrossRef Full Text | Google Scholar

Weibel, J. A., Garimella, S. V., and North, M. T. (2010b). Characterization of evaporation and boiling from sintered powder wicks fed by capillary action. Int. J. Heat Mass Transf. 53 (19-20), 4204–4215. doi:10.1016/j.ijheatmasstransfer.2010.05.043

CrossRef Full Text | Google Scholar

Wong, K. K., and Leong, K. C. (2018). Saturated pool boiling enhancement using porous lattice structures produced by Selective Laser Melting. Int. J. Heat Mass Transf. 121, 46–63. doi:10.1016/j.ijheatmasstransfer.2017.12.148

CrossRef Full Text | Google Scholar

Wu, H., Zhou, C., Pu, Z., Yu, H., and Li, D. (2019). Effect of low-frequency ultrasonic field at different power on the dynamics of a single bubble near a rigid wall. Ultrason. Sonochemistry 58, 104704. doi:10.1016/j.ultsonch.2019.104704

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, P., and Zhang, X. (2021). Study of laminar convection heat transfer in single-side-heating small-scale cooling channel with vibration cylinder. Int. Commun. Heat Mass Transf. 120, 105030. doi:10.1016/j.icheatmasstransfer.2020.105030

CrossRef Full Text | Google Scholar

Xin, C., Rao, Z., and You, X. (2014). Numerical investigation of vapor–liquid heat and mass transfer in porous media. Energy Convers. Manag. 78, 1–7. doi:10.1016/j.enconman.2013.10.047

CrossRef Full Text | Google Scholar

Xu, Z. G., Qin, J., and Qu, G. M. (2022). Numerical and experimental study of pool boiling heat transfer mechanisms in V-shaped grooved porous metals. Int. J. Therm. Sci. 173, 107393. doi:10.1016/j.ijthermalsci.2021.107393

CrossRef Full Text | Google Scholar

Yang, G., Xu, R., Wang, Ye, Zhu, Y., Ren, F., Li, C., et al. (2022). Pore-scale numerical simulations of flow and convective heat transfer in a porous woven metal mesh. Chem. Eng. Sci. 256, 117696. doi:10.1016/j.ces.2022.117696

CrossRef Full Text | Google Scholar

Yokouchi, K., Kamehara, N., and Niwa, K. (1987). Immersion cooling for high-density packaging. IEEE Trans. Components, Hybrids, Manuf. Technol. 10 (4), 643–646. doi:10.1109/tchmt.1987.1134778

CrossRef Full Text | Google Scholar

Yuan, X., Du, Y., and Wang, C. (2023). Experimental study on pool boiling enhancement by unique designing of porous media with a wettability gradient. Appl. Therm. Eng. 231, 120893. doi:10.1016/j.applthermaleng.2023.120893

CrossRef Full Text | Google Scholar

Yue, S. J., and Xu, Z. G. (2023). Numerical simulation on pore-scale pool boiling mechanisms of horizontal gradient porous metals. Int. Commun. Heat Mass Transf. 142, 106640. doi:10.1016/j.icheatmasstransfer.2023.106640

CrossRef Full Text | Google Scholar

Yuki, K., Abei, J., and Hashizume, H. (2008). Numerical investigation of thermofluid flow characteristics with phase change against high heat flux in porous media. J. heat Transf. 130 (1). doi:10.1115/1.2780175

CrossRef Full Text | Google Scholar

Yurkov, Yu. S. (1981a). “Vibration-induced thermal convection in a square cavity in weightlessness at arbitrary frequencies,” in II Vseso.vuznvve seminor po gidromekhanike i teplomassoobmenu V nevesomosti [Tezisy dokladov] Perm, 36–37.

Google Scholar

Yurkov, Yu. S. (1981b). “Vibration-induced thermal convection in a square cavity in weightlessness (finite frequencies),” in Konvektivnyye techeniya (Perm: Convective Perm Teachers’ Institute), 98–103.

Google Scholar

Zakšek, P., Zupančič, M., Gregorčič, P., and Golobič, I. (2019). Investigation of nucleate pool boiling of saturated pure liquids and ethanol-water mixtures on smooth and laser-textured surfaces. Nanoscale Microscale Thermophys. Eng. 24 (1), 29–42. doi:10.1080/15567265.2019.1689590

CrossRef Full Text | Google Scholar

Zen’kovskaya, S. M. (1981). “Effect of vibrations on emergence of convection in a binary mixture,” in Deposited in VINITI 04.10.81 (Rostov-on-Don: Rostov University), 1570–1581.

Google Scholar

Zen’kovskaya, S. M. (1992). Effect of high-frequency vibration on filtration convection. J. Appl. Mech. Tech. Phys. 33, 691–695. doi:10.1007/BF00852201

CrossRef Full Text | Google Scholar

Zen’Kovskaya, S. M., and Rogovenko, T. N. (1999). Filtration convection in a high-frequency vibration field. J. Appl. Mech. Tech. Phys. 40 (3), 379–385. doi:10.1007/bf02468390

CrossRef Full Text | Google Scholar

Zhang, Y., Huang, L., Yuan, J., Zhao, Y., Duan, C., Yang, X., et al. (2022). Study on the suppression of bubble behavior by the synergistic effect of vibration and airflow based on pressure and particle collision signals. Powder Technol. 410, 117840. doi:10.1016/j.powtec.2022.117840

CrossRef Full Text | Google Scholar

Zhang, Y., Tao, L., Jiang, H., and Liu, J. (2021). Visualization study on start-up characteristics of a loop heat pipe with a carbon fiber capillary wick. Int. J. Heat Mass Transf. 169, 120940. doi:10.1016/j.ijheatmasstransfer.2021.120940

CrossRef Full Text | Google Scholar

Zheng, Y., Chen, J., Shang, Y., Chang, H., Chen, H., and Shu, S. (2017). Numerical analysis of the influence of wall vibration on heat transfer with liquid hydrogen boiling flow in a horizontal tube. Int. J. Hydrogen Energy 42 (52), 30804–30812. doi:10.1016/j.ijhydene.2017.10.149

CrossRef Full Text | Google Scholar

Zhou, J., Liu, L., Yang, X., Zhang, Y., and Wei, J. (2022). Visualization research on influencing factors of flat heat pipes. Appl. Therm. Eng. 207, 118193. doi:10.1016/j.applthermaleng.2022.118193

CrossRef Full Text | Google Scholar

Zhou, J., Zhang, Y., and Wei, J. (2018). A modified bubble dynamics model for predicting bubble departure diameter on micro-pin-finned surfaces under microgravity. Appl. Therm. Eng. 132, 450–462. doi:10.1016/j.applthermaleng.2017.12.113

CrossRef Full Text | Google Scholar

Zhou, P., Liu, W., and Liu, Z. (2019). Lattice Boltzmann simulation of nucleate boiling in micro-pillar structured surface. Int. J. Heat Mass Transf. 131, 1–10. doi:10.1016/j.ijheatmasstransfer.2018.11.038

CrossRef Full Text | Google Scholar

Zhou, T., Kage, H., and Li, H. (2005). Bubble characteristics in a two-dimensional vertically vibro-fluidized bed. China Particuology 3, 224–228. doi:10.1016/s1672-2515(07)60191-2

CrossRef Full Text | Google Scholar

Zu, S., Liao, X., Huang, Z., Li, D., and Jian, Q. (2021). Visualization study on boiling heat transfer of ultra-thin flat heat pipe with single layer wire mesh wick. Int. J. Heat Mass Transf. 173, 121239. doi:10.1016/j.ijheatmasstransfer.2021.121239

CrossRef Full Text | Google Scholar

Zuo, S., Chen, S., and Yin, B. (2022). Performance analysis and improvement of lithium-ion battery thermal management system using mini-channel cold plate under vibration environment. Int. J. Heat Mass Transf. 193, 122956. doi:10.1016/j.ijheatmasstransfer.2022.122956

CrossRef Full Text | Google Scholar