A sustainable NEV manufacturer-retailer system under the Nash bargaining framework: considering the impact of the COVID-19 epidemic under the CVaR criterion

Suppose a new energy vehicle (NEV) manufacturer-retailer system where the wholesale price and the order quantity are determined through a negotiation procedure. Considering the impact of the COVID-19 epidemic, the manufacturer and the retailer are both assumed to be risk averse with Conditional Value-at-Risk (CVaR) as their performance measure. With the uniform distribution assumption, we derive the equilibrium solutions as well as the players’ profit shares in the Stackelberg game and Nash bargaining framework. We quantitatively address the impacts of the players’ confidence levels and government subsidy on the equilibrium order quantity, wholesale price and profit allocation in both negotiation frameworks. We find that, in both negotiation frameworks and considering the impact of the COVID-19 epidemic, a more risk-averse (i.e., with lower confidence level in CVaR model) manufacturer or retailer tends to occupy a higher profit share. On the other hand, a higher government subsidy aiming at offsetting the epidemic’s impact leads to a higher profit share for the manufacturer and a lower one for the retailer. A quantitive comparison of the equilibriums in the two negotiation frameworks indicates that more NEVs are ordered by the retailer and a higher system profit is generated in the Nash bargaining framework than the Stackelberg game. Thus, we analytically prove that the Nash bargaining framework is superior to the Stackelberg game for the NEV manufacturer-retailer system in terms of both quantity and profit with consideration of the epidemic impact. In addition, a series of numerical experiments is carried out to illustrate the effects of some significant parameters on the equilibrium order quantity and the system profit allocation in different negotiation frameworks. These numerical experiments also further demonstrate the superiority of the Nash bargaining framework for either NEV player—no matter how the epidemic trend and the government subsidy vary—and provide a quantitative scope for the retailer’s bargaining power to sustainably maintain the win-win cooperation between the NEV manufacturer and retailer in the superior Nash bargaining framework within the epidemic environment. From the perspective of policy, the government should increase subsidy within the epidemic environment to offset the negative effect and can degenerate subsidy when the epidemic dissipates. Furthermore, as the subsidy degenerates, both model results and numerical experiments show that the manufacturer suffers a more unfavorable effect, so the government can preferentially support the manufacturer by adjusting the subsidy to a higher level to alter players’ relative powers and profit shares.

1 Introduction

Automobile exhaust is considered one of the main sources of carbon dioxide (CO₂) contributing to the greenhouse effect (Achtnicht, 2012). According to the report by the European Environment Agency (EEA), CO₂ generated by the transport sector has increased from 1990 to 2006 and accounted for 23% of the total CO₂ in the air in 2006 (European Environment Agency EEA, 2009; China Association of Automobile Manufactures CAAM, 2018). On the other hand, the incredible increase of automobile consumption meanwhile has resulted in a petroleum shortage. The desire to promote the sustainable development of society, energy conservation, and emission reduction has attracted a great deal of attention from governments all around the world. As an industry emerging to cope with environmental deterioration and energy challenges, new energy vehicles (NEVs) have obtained substantial support from many countries. In China, the sustainable development of NEVs is extremely meaningful for improving air quality and adjusting the energy structure as well as for promoting the reform and transformation of the automotive industry.

Benefiting from the government’s policy and the technology research and development, the NEV production and sales have experienced a rapid increase in recent years. However, at present, most NEV managerial studies consist in qualitative research on policies or empirical research on consumers’ purchase intentions. Although supply chain management has been a hot issue for many years and some researchers have focused on supply chain issues in different situations (see Das Roy and Sana, 2021; Sana, 2022a; Sana et al., 2018 for example,), the NEV supply chain has its peculiarities, and quantitative research on it is rare. On the other hand, we know that the negotiation mechanism is commonly used between manufacturers and retailers to determine contract parameters such as price and quantity. The issue on how to sustainably maintain an NEV manufacturer-retailer system under a favorable negotiation mechanism is a research gap. Supposing an NEV manufacturer-retailer system (hereafter we use he/his to stand for manufacturer/manufacturers and she/her for retailer/retailers), we aim to explore the negotiation mechanism between the two players with full consideration of the peculiarities of the NEV industry, such as the extremely high production cost and the inclusion of the government subsidy. We assume that the manufacturer offers the retailer a wholesale price contract based on subsidy sharing (SS-WP); thus, the two players negotiate with each other about the wholesale price and the order quantity. The negotiation mechanism is modeled on the Stackelberg game and the Nash bargaining framework (NBF); in the following, a comparison between them is provided to identify the superior framework.

Usually, research on the negotiation mechanism considers players as risk neutral. However, that is not very practical in the context of NEV commerce. With the marketization process of NEVs, consumers’ diversified demands are increasing. Meanwhile, government policies relating to NEVs are constantly adjusted; for example, the subsidy is decreasing continuously nowadays. In addition, because it is an emerging industry, NEV market demand is very uncertain. As the player directly facing consumers and market demand, the retailer needs to bear great risk when making decisions on order quantity. Therefore, the NEV retailer tends to behave as a risk-averse decision maker rather than a risk-neutral one. On the other hand, the profit of a manufacturer in general industries only depends on the retailer’s order quantity and has nothing to do with the uncertain demand. Accordingly, we can assume these manufacturers are risk neutral. However, some empirical studies have indicated that some manufacturers also tend to be risk averse rather than risk neutral, for example, Fisher and Raman (1996) and Katok and Wu (2009). In the NEV industry, since the government subsidy is based on the realized sales quantity, the subsidy amount the NEV manufacturer obtains is also related to the uncertain demand. In other words, the NEV manufacturer shares the demand risk, and his risk attitude, in turn, affects the negotiation results. Consequently, we assume the NEV manufacturer also behaves in a risk-averse manner. Moreover, considering the shock of the COVID-19 epidemic, the NEV manufacturer or retailer could be more risk averse, which is reflected in a higher degree of risk aversion.

Several studies, such as Eeckhoudt et al. (1995), Agrawal and Seshadri (2000), Chen et al. (2007), and Shen et al. (2016), have involved the risk-averse decision maker using the newsvendor model by the traditional expected-utility method. All these studies imply that the optimal order (or production) quantity is reduced by risk aversion and decreases proportionally to degree of risk aversion without considering shortage penalty. Besides the expected-utility method, three other major approaches have been widely used in operations management to characterize risk aversion: mean-variance (MV) analysis (Markowitz, 1959), Value-at-Risk (VaR) (Jorion, 1997), and Conditional Value-at-Risk (CVaR; see Rockafellar and Uryasev, 2000; Rockafellar and Uryasev, 2002). Mean-variance analysis is an approach to model risk aversion that satisfies a class of decision makers with the concave quadratic utility function (see Buzacott et al., 2011; Chen et al., 2001 for reviews). However, Ma et al. (2012) explained that the MV approach is inadequate because it equally quantifies desirable upside outcomes and undesirable downside outcomes. In the VaR evaluation, the decision maker is allowed to specify a confidence level (say, $\eta$ with $\eta \in$) for attaining a certain level of wealth, and we need to maximize the $\eta$-quantile of the profit function (Jorion, 1997). Because the VaR measure also has some limitations, such as non-subadditivity and nonconvexity, Rockafellar and Uryasev (2000), Rockafellar and Uryasev (2002) defined a new measure of risk, CVaR. The CVaR criterion, which measures the average profit falling below the $\eta$-quantile level (or VaR), has better computational characteristics than VaR (Artz et al., 1999). Hence, recently more studies have investigated the risk-averse newsvendor problem in the CVaR framework (e.g., Ahmed et al. (2007); Gotoh and Takano (2007); Choi and Ruszczyński (2008); Chen et al. (2009). Due to the desirable mathematical characteristics of CVaR, we have adopted CVaR as the risk-averse decision makers’ performance measurement in our model.

In this paper, we investigated the negotiation mechanism in an NEV manufacturer-retailer system where both players are risk averse considering the impact of the COVID-19 epidemic. It was presupposed that the two players negotiate regarding the wholesale price and the order quantity with the objective of maximizing their risky performances, as measured by the CVaR criterion, in the Stackelberg game or the NBF framework. With the uniform distribution assumption, we derived the equilibrium solutions as well as the two players’ profit shares in the two negotiation frameworks. We found that, in both negotiation frameworks, the two players’ risk attitudes play a similar role in affecting the players’ profit shares. The manufacturer or the retailer tends to obtain a higher profit share when he/she becomes more risk averse. The effect of the government subsidy is also similar in both negotiation frameworks. As the subsidy increases to offset the impact of the COVID-19 epidemic, the retailer’s profit share decreases while the manufacturer’s increases. Besides, in the NBF framework, the bargaining power contrast also markedly affects the players’ profit shares. Greater bargaining power always leads to a higher profit share and a higher absolute profit for either player. By comparing the Stackelberg game with the NBF framework, we analytically proved that the NBF equilibrium brings about a larger NEV order quantity and a higher system profit. Thus, we concluded that the NBF framework is superior to the Stackelberg game for the NEV manufacturer-retailer system in terms of both quantity and profit. Comparing the effects of some significant parameters in the two negotiation frameworks through numerical experiments further testified to the superiority of the NBF framework for either NEV player no matter how the epidemic trend and the government subsidy vary. It provides a necessary condition for the bargaining power contrast to sustainably maintain the NEV manufacturer-retailer system in the superior NBF framework. Our proposed model enriches research on the negotiation mechanism between the NEV manufacturer and retailer by incorporating the risk aversion effect with the CVaR approach considering the COVID-19 epidemic effect and quantitatively analyze the impacts of the players’ confidence levels and government subsidy on the equilibrium order quantity, wholesale price and profit allocation. By a quantitive comparison of the equilibrium order quantity and profit allocation in the two negotiation frameworks, we analytically prove that the NBF framework is effective, feasible, and superior in promoting NEV sales and enhancing each player’s profit when compared to the Stackelberg game. In addition, both model results and numerical experiments show that the manufacturer suffers a more unfavorable effect from the subsidy degeneration, so the government can preferentially support the manufacturer by adjusting the subsidy to a higher level to alter players’ relative powers and profit shares. The findings may provide guiding principles for the sustainable win-win cooperation between the NEV manufacturer and retailer, which can be beneficial to promote the sustainable development of NEV commerce against the backdrop of the epidemic effect.

The rest of this paper is organized as follows. We review literature related to our work in Section 2. Section 3 solves the Stackelberg model with the manufacturer as the leader and analyzes the players’ profit shares in this case. In Section 4, we derive the equilibrium solutions and the players’ profit shares in the NBF framework and compare the results to those in the Stackelberg game. We carry out numerical experiments and report additional observations and implications in Section 5. In Section 6, we conclude this paper and present some managerial insights according to the findings.

2 Literature review

As an essential issue in the operations management field, the newsvendor model is the foundation of our study (see Khouja (1999) and Qin et al. (2011) for reviews). The newsvendor model has recently been adopted in different scenes to deal with some modern problems (see Sana, 2020; Sana, 2022b; Sana, 2022c for examples) and is also regarded as a common method to characterize the risk aversion effect in supply chain management. Among the studies on the risk-averse newsvendor model, those using the CVaR criterion are more closely related to our work. For example, two early studies by Gotoh and Takano (2007) and Chen et al. (2009) investigated the risk-averse newsvendor problem under the CVaR criterion with the objective of minimizing CVaR in regard to loss and maximizing CVaR in regard to profit; both studies demonstrated that risk aversion can reduce the newsvendor’s order quantity. Due to the desirable mathematical characteristics of CVaR, many researchers have adopted it to model complex problems regarding risk-averse newsvendors. The related literature includes (Cheng et al., 2009; Xu, 2010; Xu and Li, 2010; Wu et al., 2014; Luo et al., 2015; Xue et al., 2015; Xu et al., 2016), and others. For example, Xu (2010) has used CVaR to investigate the effects of parameter changes, Wu et al. (2014) employed it to characterize the optimal quantity and pricing decisions of a risk-averse newsvendor under both quantity and price competition, and Xu et al. (2016) utilized it to formulate a risk-averse newsvendor’s opportunity loss. The appearance of a vast amount of literature on the application of CVaR in the inventory problem indicates the accuracy and effectiveness of the CVaR approach. Even though the above-named studies focused on different problems, all of them have verified that a risk-averse newsvendor’s order quantity is reduced by risk aversion and decreases with respect to the degree of risk aversion. These studies incorporating risk aversion with CVaR in different settings further make up the basis for analyzing the negotiation mechanism in a supply chain containing risk-averse players within the COVID-19 epidemic environment.

The previously mentioned literature only focused on the retailer’s risk aversion effect and considered the manufacturer to be risk neutral. However, empirical studies have indicated that the manufacturer also tends to be risk averse rather than risk neutral. For example, Fisher and Raman (1996) found that the manager of a ski-wear factory usually decides to produce less than the theoretical quantity in the risk-neutral case. Katok and Wu (2009) conducted experimental research on supply chain contracts and showed that the wholesale price set by the manufacturer systematically deviates from the theoretical value with the risk-neutral assumption. To our best knowledge, very few studies have addressed the negotiation problem considering both players as risk averse. Gang et al. (2011) considered the supplier and the manufacturer as risk-averse decision makers to investigate the quality investment and price decision in a supply chain. They showed that, compared to a risk-neutral supply chain, a risk-averse supply chain may have lower, same, and higher product quality, depending on the supply chain strategy. For an NEV manufacturer-retailer system in which the manufacturer also undertakes some of the demand risk, it is more practical to involve the effect of the manufacturer’s risk attitude. In this paper, considering the COVID-19 epidemic effect, both the NEV manufacturer and retailer have been characterized as risk-averse players to explore the effects of their risk attitudes on the negotiation mechanism.

Negotiation is a common mechanism to determine the contract parameters in a supply chain. Mieghem (1999), one of the first researchers to consider the bargaining problem in supply chains, investigated negotiations on incomplete contracts, where some of the contract parameters are left unspecified ex-ante and the surplus is divided based on the players’ ex-post bargaining power. Some other researchers have analyzed the bargaining problem in a supply chain under different model assumptions. For example, Ertogral and Wu (2001) proposed bargaining models in one-buyer/one-supplier and one-buyer/multiple-suppliers cases and studied the contract negotiation process. Nagarajan and Sosic (2008) surveyed papers on applications of cooperative bargaining models to supply chain management and provided some future research directions. Plambeck et al. (2007a), Plambeck and Taylor (2007b) addressed the effects of renegotiation on contracts in different settings. Song and Gao (2018) established a game model for a green supply chain with a revenue-sharing contract and determined that the bargaining revenue-sharing contract can make the supply chain’s total profit higher than the retailer-led revenue-sharing contract. These studies showed the equilibrium solutions and supply chain profit allocations or the players’ preferences with different negotiation mechanisms under different contracts.

As respective representatives of noncooperative and cooperative games, the Stackelberg game and NBF framework are more frequently used in the supply chain area. The Stackelberg model is considered a classic noncooperative game, and related literature includes (Bernstein and Marx, 2006; Chen et al., 2012; Wu, 2013; Hua et al., 2017), among others. Bernstein and Marx (2006) adopted the Stackelberg game to address the effect of a retailer’s bargaining power, modeled using the ability to set reservation profit levels, on the supply chain profit allocation. Chen et al. (2012) examined the manufacturer’s pricing strategies and the coordination schemes in a dual-channel supply chain under the Stackelberg game with the manufacturer as the leader. Wu (2013) analyzed the effects of buyback policy on retail price, order quantity, and wholesale price in a duopoly competing supply chain under two channel policies: vertical integration and manufacturer’s Stackelberg. Hua et al. (2017) established a Stackelberg game model to identify the optimal pricing and advertising strategies for both players in a two-echelon reverse supply chain of household unwanted medications.

As a representative of cooperative game models, the NBF problem also has attracted much attention. Hua et al. (2006) investigated the negotiation mechanism between a manufacturer and a retailer and provided the NBF equilibrium regarding the wholesale price and order quantity. Gurnani and Shi (2006) derived the NBF solution in the supply chain where the supplier is unreliable in delivery and discussed the effect of using a down-payment or nondelivery penalty in the contract for the two cases of buyer overtrust or undertrust. Nagarajan and Bassok (2008) used the NBF framework to model the multilateral negotiations between an assembler and various suppliers and examined the profit allocation in the supply chain. Ye et al. (2018) examined a mixed contract with an asymmetric NBF model and proved that such a contract is feasible to achieve an efficient biofuel supply chain. Although these studies have provided optimization approaches under the Stackelberg game or the NBF framework for various supply chains, all of them held to the risk-neutral assumption rather than considering the risk aversion effect.

Recently, some research studies incorporating risk aversion in the supply chain bargaining model have arisen. Ma et al. (2012) extended the study by Hua et al. (2006) and showed that a NBF equilibrium also exists in the two-echelon supply chain when the retailer is risk averse and tries to maximize her CVaR about profit. Li et al. (2014) explored a NBF problem in a dual-channel supply chain where the risk-neutral manufacturer and the risk-averse retailer negotiate with each other and explored the effect of the retailer’s risk aversion degree on the retail price and the profit allocation. He et al. (2017) considered a supply chain consisting of one risk-neutral manufacturer and one risk-averse supplier with CVaR measurement and proposed a risk diversification contract that has a Pareto improvement and can allocate supply chain profit appropriately under the NBF framework. However, most papers with risk-averse assumptions considered only one of the players as risk averse. As mentioned previously, it is not appropriate to ignore the risk aversion effect of either player in an NEV manufacturer-retailer system, especially considering the COVID-19 epidemic effect.

As an emerging industry, NEVs garner much attention from many governments. Research on NEVs has focused on battery technology and has also emphasized marketing and consumer behavior. Bapna et al. (2002) suggested that governments should improve charging facilities to decrease NEV usage costs for consumers; Wang et al. (2017) used a multiple linear regression method to identify four key factors that promote NEV sales; Zhang and Bai (2017) proposed a policy-dependency mapping method to analyze 175 NEV government policies at various levels with multiple purposes. These qualitative studies have shown that several policies can promote the advancement of NEV commerce, such as strengthening research and development, establishing specific subsidies and tax policies, improving charging facilities, and so on. Some quantitative studies have addressed the NEV supply chain or NEV commerce. For example, Luo et al. (2014) quantitatively investigated the NEV supply chain under a government’s price-discount incentive scheme that involves a price discount rate and a subsidy ceiling. They derived the most effective discount rate and subsidy ceiling that maximizes NEV sales as well as most effectively improves the manufacturer’s incentive for NEV production. Liu et al. (2017) built an evolutionary game model between auto manufacturers and governments and discovered that the evolutionary game presents as stable when governments implement a dynamic taxation strategy or a dynamic subsidy strategy. The simulation of China’s NEV industry indicates that a policy of dynamic taxations and static subsidies is effective for NEV industry development. Shao et al. (2017) addressed the NEV market under two different structures (monopoly and duopoly) and formulated a utility model composed of consumers who make utility-maximizing choices and manufacturers who set optimal pricing. They showed that the government prefers to implement a subsidy incentive scheme rather than a price discount incentive scheme, and, under the subsidy incentive scheme, the NEV market in the monopoly setting has a smaller environmental impact than that in the duopoly setting. In particular, two other papers have included in their considerations a behavioral element, loss aversion, to explore the NEV optimal production strategy under risk. Zhang (2014) considered both consumer trade-offs and government subsidies together with decision makers’ loss aversion to evaluate relevant influences on the NEV optimal production strategy and indicated that subsidies can help to increase the production quantity and offset the loss aversion effect. Gu et al. (2017) investigated a loss-averse NEV manufacturer’s optimal production decision considering battery recycling and proved that battery recycling can offset the negative effects of loss aversion on the optimal production quantity and expected utility. Concerning another behavioral element, risk aversion, Han and Xu (2018) designed a sales rebate/penalty contract based on subsidy sharing (SS-SRP) to coordinate a two-echelon NEV supply chain consisting of a risk-neutral manufacturer and a risk-averse retailer and evaluated the coordination efficiency. However, studies on NEV supply chains considering risk aversion are still quite scarce. Furthermore, the bargaining problem in an NEV manufacturer-retailer system considering the risk aversion effect has not yet been investigated.

The COVID-19 epidemic (National Health Commission, 2022) has had a tremendous impact on all walks of life and the overall national economy. Although the current situation of the epidemic in China continues to improve, due to the complex and severe situation of the overseas epidemic, the epidemic impact may persist for a long time. Since the outbreak of the COVID-19 epidemic, each national government put forward a series of policies to resist the epidemic impact, and many scholars investigated the effectiveness of these policies. For example, Ahmed et al. (2023) and Khan et al. (2021) adopted ARDL approach or the PMG-ARDL model to analyze the government policy response to COVID-19 epidemic and indicated that government economic support, debt/contract relief, stringency, and health and containment measures play a significant role in the fight against COVID-19 epidemic. In China, some scholars conducted researches on the impact of the COVID-19 epidemic on China’s national economy and social production and life, such as Xue and Sha (2020), Li (2020), Zheng et al. (2020). Huang (2020) analyzed the impact of the epidemic on the automobile industry, while (Chen, 2020; Wang, 2020a; Wang, 2020b; Liu, 2020) and others paid attention to the impact the NEV industry in particular suffered. Regarding the epidemic impact on the NEV industry, the above studies mostly briefly analyzed from a qualitative perspective. There are almost no relevant quantitative analyses and model research approaches, and, in particular, research on the impact of the epidemic from the perspective of behavioral theory is mostly lacking.

Deviating from the previously mentioned studies, we consider the COVID-19 epidemic effect and risk aversion with the CVaR criterion, propose quantitative models with the Stackelberg game and the NBF framework, and focus on the profit allocation between the NEV manufacturer and retailer with full consideration of the peculiarities of NEV commerce. We adopted a quantitative approach to deal with the supply chain issue in NEV industry, assuming both the NEV manufacturer and retailer are risk-averse agents, considering the COVID-19 epidemic effect with the CVaR criterion, comparing different negotiation frameworks and providing a superior mechanism, these are the main contributions of this article. By exploring the negotiation mechanism under different frameworks, we hope to provide some insights into implications for the sustainable win-win cooperation between the NEV manufacturer and retailer under the superior NBF framework, which may help to promote NEV marketization within the COVID-19 epidemic environment.

3 Stackelberg game

For a two-echelon NEV supply chain, coordination is an ideal state (see Han and Xu, 2018). Although it meets the incentive compatibility constraint of the slave party, it does not necessarily meet the participation constraint of the master party and the slave party. In this case, each player in the supply chain usually determines the contract parameters and profit allocation through a specific negotiation mechanism. Suppose an NEV manufacturer-retailer system that faces a stochastic market demand $x$ with a probability density function (p.d.f.) of $f\left(x\right)$ and a cumulative distribution function (c.d.f.) of $F\left(x\right)$. The NEV manufacturer and retailer are both risk averse with CVaR as their risk performance measurement. The manufacturer’s and retailer’s confidence levels are denoted as ${\eta }_m$ and ${\eta }_r$, respectively. The lower ${\eta }_m$ and ${\eta }_r$ are, the more risk averse the manufacturer and retailer are. The epidemic effect is involved in the risk aversion degree. When the epidemic situation is severe/optimistic, the manufacturer’s and retailer’s respective risk aversion degrees are higher/lower, i.e., the confidence levels are lower/higher. Moreover, as the retailer faces the market demand directly and bears the inventory risk, we assume that $0<{\eta }_r<{\eta }_m\le 1$.

Referring to the model by Zhang (2014), suppose NEVs are produced at a unit cost of $c$ and sold to consumers at an exogenous price $p$. At the end of the selling season, the unsatisfied demand will be lost, and the leftover inventory will be disposed of at a unit salvage value $s$. Assume that $c>p>s$. Such an assumption conforms to the practice in the NEV industry because the NEV production cost is extremely high (especially the battery cost), even higher than the retail price. Since the NEV manufacturer and retailer cannot afford the high production cost independently, NEVs are subsidized by both national and local governments. We denoted the per-unit government subsidy as $Y$ and assumed that $+Y>c$ , which ensures that the NEV manufacturer-retailer system can obtain positive profit from the perspective of the system with the government’s financial support. In addition, according to common practice in NEV commerce, we assumed that $Y$ is shared by the manufacturer and the retailer by the proportion $\beta :\left(1-\beta \right)$ ($0\le \beta \le 1$).

We assumed that the manufacturer offers an SS-WP contract to the retailer (see Han and Xu, 2018) and that the two players negotiate with each other about the order quantity $q$ and the wholesale price $w$. Denote $q_i^{*}$ and $w_i^{*}$, where $i=s,n$, as the equilibrium optimal order quantity and wholesale price, respectively, under the Stackelberg game and the NBF framework. With the CVaR as the objective functions, we used the calculus method to derive optimal solutions under the Stackelberg game and the NBF framework respectively, used a partial derivative approach to conduct a factor analysis, used comparative analysis to identify the superior negotiation framework, and then employed numerical experiments to extend and clarify the mathematical results. We started our analysis with the CVaR formulations of the retailer and the manufacturer.

3.1 The CVaR expressions of the retailer and the manufacturer

The retailer’s and manufacturer’s profits, denoted as ${\pi }_r\left(q,w\right)$ and ${\pi }_m\left(q,w\right)$, can be expressed, respectively, as follows.

$\begin{array}{l}{\pi }_r\left(q,w\right)=\left[p+\left(1-\beta \right)Y\right]\min \left(q,x\right)-wq+s{\left(q-x\right)}^{+}\\ =\left[p+\left(1-\beta \right)Y-w\right]\min \left(q,x\right)-\left(w-s\right){\left(q-x\right)}^{+}\\ =\left[p+\left(1-\beta \right)Y-w\right]\left[q-{\left(q-x\right)}^{+}\right]-\left(w-s\right){\left(q-x\right)}^{+}\\ =\left[p+\left(1-\beta \right)Y-w\right]q-\left[p+\left(1-\beta \right)Y-s\right]{\left(q-x\right)}^{+}\end{array}(3.1)$

${\pi }_m\left(q,w\right)=\left(w-c\right)q+\beta Y⌊q-{\left(q-x\right)}^{+}⌋=\left(w+\beta Y-c\right)q-\beta Y{\left(q-x\right)}^{+}(3.2)$

For calculation convenience, we have adopted the definition of CVaR by Rockafellar and Uryasev (2000), Rockafellar and Uryasev (2002) and referred to the risk-averse newsvendor model under CVaR criterion proposed by Chen et al. (2009), and the CVaR expressions for the retailer and the manufacturer, denoted as $CVaR\left({\pi }_r\left(q,w\right)\right)$ and $CVaR\left({\pi }_m\left(q,w\right)\right)$, are provided as follows, respectively.

$CVaR\left({\pi }_r\left(q,w\right)\right)=\underset{v_r\in R}{\max }\rightleftharpoons \left\{v_r+\frac{1}{{\eta }_r}E\left[\min \left({\pi }_r\left(q,w\right)-v_r,0\right)\right]\right\}=\underset{v_r\in R}{\max }\rightleftharpoons \left\{v_r-\frac{1}{{\eta }_r}E{\left[v_r-{\pi }_r\left(q,w\right)\right]}^{+}\right\}(3.3)$

$CVaR\left({\pi }_m\left(q,w\right)\right)=\underset{v_m\in R}{\max }\rightleftharpoons \left\{v_m+\frac{1}{{\eta }_m}E\left[\min \left({\pi }_m\left(q,w\right)-v_m,0\right)\right]\right\}=\underset{v_m\in R}{\max }\rightleftharpoons \left\{v_m-\frac{1}{{\eta }_m}E{\left[v_m-{\pi }_m\left(q,w\right)\right]}^{+}\right\}(3.4)$

where $E$ is the expectation operator, ${\left(\cdot \right)}^{+}=\max \left\{\cdot ,0\right\}$, and $v_r$ and $v_m$ are profit thresholds denoted in the real number set $R$ (Chen et al., 2009). Based on these definitions and results, we provide the following theorem to show the CVaR expressions for the retailer and the manufacturer.

Theorem 3.1. The CVaR expressions for the retailer and the manufacturer can be formulated, respectively, as follows.

$CVaR\left({\pi }_r\left(q,w\right)\right)=\left\{\begin{array}{cc}\left[p+\left(1-\beta \right)Y-w\right]q-\frac{p+\left(1-\beta \right)Y-s}{{\eta }_r}{\int }_0^{q}F\left(x\right)dx& q\le F^{-1}\left({\eta }_r\right)\\ \left[p+\left(1-\beta \right)Y-s\right]F^{-1}\left({\eta }_r\right)-\left(w-s\right)q-\frac{p+\left(1-\beta \right)Y-s}{{\eta }_r}{\int }_0^{F^{-1}\left({\eta }_r\right)}F\left(x\right)dx& q>F^{-1}\left({\eta }_r\right)\end{array}\right.(3.5)$

$CVaR\left({\pi }_m\left(q,w\right)\right)=\left\{\begin{array}{cc}\left(w+\beta Y-c\right)q-\frac{\beta Y}{{\eta }_m}{\int }_0^{q}F\left(x\right)dx& q\le F^{-1}\left({\eta }_m\right)\\ \left(w-c\right)q+\beta Y{F}^{-1}\left({\eta }_m\right)-\frac{\beta Y}{{\eta }_m}{\int }_0^{F^{-1}\left({\eta }_m\right)}F\left(x\right)dx& q>F^{-1}\left({\eta }_m\right)\end{array}\right.(3.6)$

Proof. Refer to Supplementary Appendix SA1.

Theorem 3.1 explicitly provides the CVaR expressions for the risk-averse NEV retailer and manufacturer under the SS-WP contract. With all variables given, if the retailer’s ordering quantity is $q$ and the wholesale price is $w$, the retailer’s and manufacturer’s risky performances measured by CVaR can be calculated using Eq. 3.5 and Eq. 3.6, respectively.

The NEV retailer’s CVaR measurement just extends the expression shown by Chen et al. (2009) by introducing the government subsidy $Y$ with the assumption that the retail price $p$ is exogenous. In regard to the NEV manufacturer’s CVaR measurement shown by Eq. 3.6, we can see that $CVaR\left({\pi }_m\left(q,w\right)\right)$ is calculated by the retailer’s payment $wq$ minus the production cost $-cq$ and plus the profit obtained from the government subsidy $Y$. The portion $\left(w-c\right)q$ is a riskless part that depends only on the wholesale price and the retailer’s order quantity while having nothing to do with the realized demand or the manufacturer’s risk attitude. The payoff related to the government subsidy is influenced by the realized demand and thus is considered a risky part. Such a risky payoff is affected by the manufacturer’s risk attitude. When $q\le F^{-1}\left({\eta }_m\right)$, i.e., ${\eta }_m\ge F\left(q\right)$, indicating that the manufacturer’s risk aversion degree is low, the risky payoff can be expressed as $\beta Yq-\frac{\beta Y}{{\eta }_m}{\displaystyle {\int }_0^q}F\left(x\right)dx$, which is decided by the manufacturer’s risk attitude as well as the retailer’s order quantity. When $q>F^{-1}\left({\eta }_m\right)$, i.e., ${\eta }_m<F\left(q\right)$, indicating that the manufacturer’s risk aversion degree is high, the risky payoff can be expressed as $\beta Y{F}^{-1}\left({\eta }_m\right)-\frac{\beta Y}{{\eta }_m}{\displaystyle {\int }_0^{F^{-1}\left({\eta }_m\right)}}F\left(x\right)dx$, which depends only on the manufacturer’s risk attitude while having no relation to the retailer’s order quantity.

3.2 Stackelberg equilibrium

Under the Stackelberg game with the manufacturer as the leader, given the SS-WP contract, the retailer firstly decides her optimal order quantity with the objective of maximizing her CVaR. In anticipation of the retailer’s order quantity, the manufacturer then decides the optimal wholesale price for himself to maximize his CVaR. For calculating convenience, we assumed that the demand is subject to a uniform distribution on $\left[0,B\right]$. According to the CVaR expressions given in Theorem 3.1, we derived the Stackelberg equilibrium, shown in the following theorem.

Theorem 3.2. The Stackelberg equilibrium between the NEV manufacturer and retailer is $\left(q_s^{*},w_s^{*}\right)$, where

$q_s^{*}=\frac{B{\eta }_r{\eta }_m\left(p+Y-c\right)}{2{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y}(3.7)$

$w_s^{*}=\frac{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]\left[p+\left(1-2\beta \right)Y+c\right]+{\eta }_r\beta Y\left[p+\left(1-\beta \right)Y\right]}{2{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y}(3.8)$

Proof. Recall Eq. 3.5, when $q\le F^{-1}\left({\eta }_r\right)$, and take the first-order derivative of $CVaR\left({\pi }_r\left(q,w\right)\right)$ with respect to $q$:

$\frac{\partial CVaR\left({\pi }_r\left(q,w\right)\right)}{\partial q}=\left[p+\left(1-\beta \right)Y-w\right]-\frac{p+\left(1-\beta \right)Y-s}{{\eta }_r}F\left(q\right)$

Then, taking the second-order derivative of $CVaR\left({\pi }_r\left(q,w\right)\right)$ with respect to q, we obtain

$\frac{{\partial }^{2}CVaR\left({\pi }_r\left(q,w\right)\right)}{\partial q^2}=-\frac{p+\left(1-\beta \right)Y-s}{{\eta }_r}f\left(q\right)<0$

This means that $CVaR\left({\pi }_r\left(q,w\right)\right)$ is concave with respect to $q$; so, let $\frac{\partial CVaR\left({\pi }_r\left(q,w\right)\right)}{\partial q}=0$, and we obtain

$q_s^{*}=F^{-1}\left(\frac{{\eta }_r\left[p+\left(1-\beta \right)Y-w\right]}{p+\left(1-\beta \right)Y-s}\right)=\frac{B{\eta }_r\left[p+\left(1-\beta \right)Y-w\right]}{p+\left(1-\beta \right)Y-s}(3.9)$

When $q>F^{-1}\left({\eta }_r\right)$, take the first-order derivative of $CVaR\left({\pi }_r\left(q,w\right)\right)$ with respect to $q$, and we obtain

$\frac{\partial CVaR\left({\pi }_r\left(q,w\right)\right)}{\partial q}=-\left(w-s\right)<0$

So $CVaR\left({\pi }_r\left(q,w\right)\right)$ is decreasing with respect to $q$ when $q>F^{-1}\left({\eta }_r\right)$.

Combining the above two cases, a unique optimal order quantity $q_s^{*}\in$ exists, shown by Eq. 3.9.

Predicting the retailer’s order quantity $q_s^{*}$, the manufacturer intends to determine an optimal wholesale price with the objective of maximizing his CVaR.

Note that $q_s^{*}\le F^{-1}\left({\eta }_r\right)<F^{-1}\left({\eta }_m\right)$, according to Eq. 3.6; so there is

$CVaR\left({\pi }_m\left(q_s^{*},w\right)\right)=\left(w+\beta Y-c\right)q_s^{*}-\frac{\beta Y}{{\eta }_m}{\int }_0^{q_s^{*}}F\left(x\right)dx$

Take the first-order derivative of $CVaR\left({\pi }_m\left(q_s^{*},w\right)\right)$ with respect to $w$:

$\begin{array}{l}\frac{\partial CVaR\left({\pi }_m\left(q_s^{*},w\right)\right)}{\partial w}=q_s^{*}+\left(w+\beta Y-c\right)\frac{\partial q_s^{*}}{\partial w}-\frac{\beta Y}{{\eta }_m}\frac{\partial q_s^{*}}{\partial w}F\left(q_s^{*}\right)\\ =\frac{B{\eta }_r\left[p+\left(1-\beta \right)Y-w\right]}{p+\left(1-\beta \right)Y-s}-\left(w+\beta Y-c\right)\frac{B{\eta }_r}{\left[p+\left(1-\beta \right)Y-s\right]}+\frac{\beta Y}{{\eta }_m}\frac{B{\eta }_r}{\left[p+\left(1-\beta \right)Y-s\right]}\frac{{\eta }_r\left[p+\left(1-\beta \right)Y-w\right]}{p+\left(1-\beta \right)Y-s}\\ =\frac{B{\eta }_r}{p+\left(1-\beta \right)Y-s}\left\{\left[p+\left(1-2\beta \right)Y-2w+c\right]+\frac{{\eta }_r\beta Y\left[p+\left(1-\beta \right)Y-w\right]}{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]}\right\}\end{array}$

Then take the second-order derivative of $CVaR\left({\pi }_m\left(q_s^{*},w\right)\right)$ with respect to $w$, and we obtain

$\frac{{\partial }^{2}CVaR\left({\pi }_m\left(q_s^{*},w\right)\right)}{\partial w^2}=\frac{B{\eta }_r}{p+\left(1-\beta \right)Y-s}\left\{-2-\frac{{\eta }_r\beta Y}{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]}\right\}<0$

This means that $CVaR\left({\pi }_m\left(q_s^{*},w\right)\right)$ is concave with respect to $w$; so let $\frac{\partial CVaR\left({\pi }_m\left(q_s^{*},w\right)\right)}{\partial w}=0$, and we obtain the optimal wholesale price for the manufacturer $w_s^{*}$, shown by Eq. 3.8. Substitute Eq. 3.8 into Eq. 3.9, and the equilibrium optimal order quantity is obtained and expressed as Eq. 3.7.

In the NEV manufacturer-retailer system, when the manufacturer and the retailer are both risk averse with the CVaR criterion and negotiate with each other under the Stackelberg game, the equilibrium consists in the retailer ordering $q_s^{*}$ NEVs at a wholesale price $w_s^{*}$. Under such an equilibrium, the subsidy-sharing proportion between the manufacturer and the retailer decides the system profit allocation by markedly affecting the equilibrium wholesale price $w_s^{*}$. And we can prove that the Stackelberg game can always achieve a situation where both players obtain positive profit no matter how much the manufacturer’s subsidy-sharing proportion $\beta$ is.

Corollary 3.1. Under the Stackelberg game, both the manufacturer and the retailer can always obtain positive profit no matter how the government subsidy is shared.

Proof. In order to ensure that both the manufacturer and the retailer can obtain positive profit under the Stackelberg equilibrium, the necessary condition is $c-\beta Y<w_s^{*}<p+\left(1-\beta \right)Y$. Recalling Eq. 3.8 there is

$\begin{array}{l}c-\beta Y<\frac{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]\left[p+\left(1-2\beta \right)Y+c\right]+{\eta }_r\beta Y\left[p+\left(1-\beta \right)Y\right]}{2{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y}<p+\left(1-\beta \right)Y\\ \Rightarrow \left\{\begin{array}{l}\left(c-\beta Y\right)\left\{2{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}<{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]\left[p+\left(1-2\beta \right)Y+c\right]+{\eta }_r\beta Y\left[p+\left(1-\beta \right)Y\right]\\ {\eta }_m\left[p+\left(1-\beta \right)Y-s\right]\left[p+\left(1-2\beta \right)Y+c\right]+{\eta }_r\beta Y\left[p+\left(1-\beta \right)Y\right]<\left[p+\left(1-\beta \right)Y\right]\left\{2{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}\end{array}\right.\\ \Rightarrow \left\{\begin{array}{l}{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y>0\\ p+Y-c>0\end{array}\right.\end{array}$

It is easily found that the above inequalities hold unconditionally for arbitrary $\beta$ on $\left[\mathrm{0,1}\right]$.

Corollary 3.1 shows the availability of the Stackelberg game. No matter how the manufacturer and the retailer share the government subsidy, the equilibrium can guarantee that both players will obtain at least a positive profit and further remain motivated to participate in the business. The subsidy-sharing proportion between the two players directly affects the system profit allocation. We further analyzed this issue in the next subsection.

By observing Eq. 3.7 and Eq. 3.8, we can see that, with the assumption $0<{\eta }_r<{\eta }_m\le 1$, the Stackelberg equilibrium is influenced by both players’ risk attitudes. The reason is that the manufacturer decides the equilibrium wholesale price based on the retailer’s order decision, which is related to the retailer’s risk attitude and his own risk attitude as well. The effects of two players’ confidence levels on the Stackelberg equilibrium are provided in the following proposition.

Proposition 3.1. Under the Stackelberg game, the equilibrium order quantity increases with respect to either the manufacturer’s or retailer’s confidence level; the equilibrium wholesale price increases in connection with the retailer’s confidence level yet decreases in connection with the manufacturer’s.

Proof. Recalling Eq. 3.7, we convert the expression of $q_s^{*}$ as follows.

$q_s^{*}=\frac{B{\eta }_r{\eta }_m\left(p+Y-c\right)}{2{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y}=\frac{B{\eta }_m\left(p+Y-c\right)}{2{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]/{\eta }_r+\beta Y}=\frac{B{\eta }_r\left(p+Y-c\right)}{2\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y/{\eta }_m}$

We can easily find that $q_s^{*}$ increases in ${\eta }_r$ or ${\eta }_m$.

According to Eq. 3.8, taking the first-order derivative of $w_s^{*}$ with respect to ${\eta }_r$, we obtain

$\begin{array}{l}\frac{\partial w_s^{*}}{\partial {\eta }_r}=\frac{\beta Y\left[p+\left(1-\beta \right)Y\right]\left\{2{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}-\beta Y\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]\left[p+\left(1-2\beta \right)Y+c\right]+{\eta }_r\beta Y\left[p+\left(1-\beta \right)Y\right]\right\}}{{\left\{2{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}}^2}\\ =\frac{{\eta }_m\beta Y\left(p+Y-c\right)\left[p+\left(1-\beta \right)Y-s\right]}{{\left\{2{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}}^2}>0\end{array}$

Therefore, $w_s^{*}$ increases in ${\eta }_r$.

Then take the first-order derivative of $w_s^{*}$ with respect to ${\eta }_m$, and we obtain

$\begin{array}{l}\frac{\partial w_s^{*}}{\partial {\eta }_m}=\frac{\left[p+\left(1-\beta \right)Y-s\right]\left[p+\left(1-2\beta \right)Y+c\right]\left\{2{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}-2\left[p+\left(1-\beta \right)Y-s\right]\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]\left[p+\left(1-2\beta \right)Y+c\right]+{\eta }_r\beta Y\left[p+\left(1-\beta \right)Y\right]\right\}}{{\left\{2{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}}^2}\\ =-\frac{{\eta }_r\beta Y\left[p+\left(1-\beta \right)Y-s\right]\left(p+Y-c\right)}{{\left\{2{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}}^2}<0\end{array}$

Therefore, $w_s^{*}$ decreases in ${\eta }_m$.

A lower confidence level indicates a higher risk aversion degree. Proposition 3.1 reveals that, under the Stackelberg game, the equilibrium order quantity decreases in connection with the either the manufacturer’s or the retailer’s risk aversion degree. Previous literature has concluded that a more risk-averse retailer tends to order less when the manufacturer is assumed to be risk neutral. When the NEV manufacturer is also considered a risk-averse decision maker, the Stackelberg equilibrium order quantity is further reduced as the manufacturer or the retailer becomes more risk averse. On the other hand, the equilibrium wholesale price decreases in connection with the retailer’s risk aversion degree yet increases in connection with the manufacturer’s. When the retailer/manufacturer becomes more risk averse, the wholesale price should be adjusted to attract the more conservative retailer/manufacturer to participate in the business. The epidemic exacerbates the retailer’s risk aversion degree and thus decreases the equilibrium order quantity as well as the equilibrium wholesale price; simultaneously, it heightens the manufacturer’s risk aversion degree and thus decreases the equilibrium order quantity and increases the equilibrium wholesale price.

3.3 Profit allocation under the Stackelberg game

The previous subsection provides the equilibrium under the Stackelberg game and the impacts of players’ risk attitudes. However, we are more interested in the system profit allocation and what elements it is related to. To investigate this, we first defined the retailer’s profit share as

${\rho }_r=\frac{E{\pi }_r\left(q,w\right)}{E\pi \left(q,w\right)}=\frac{E{\pi }_r\left(q,w\right)}{E{\pi }_r\left(q,w\right)+E{\pi }_m\left(q,w\right)}(3.10)$

where $E{\pi }_r\left(q,w\right)$, $E{\pi }_m\left(q,w\right)$, and $E\pi \left(q,w\right)$ stand for the expected profits of the retailer, the manufacturer, and the entire system, respectively. Thus, the retailer’s profit share under the Stackelberg game ${\rho }_{rs}$ can be obtained, as shown in the following theorem.

Theorem 3.3. Under the Stackelberg equilibrium, the retailer’s profit share is:

${\rho }_{rs}=\frac{\left(2-{\eta }_r\right){\eta }_m\left[p+\left(1-\beta \right)Y-s\right]}{4{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+2{\eta }_r\beta Y-{\eta }_r{\eta }_m\left(p+Y-s\right)}(3.11)$

Proof. Under the Stackelberg equilibrium, $\left(q_s^{*},w_s^{*}\right)$, $E{\pi }_r\left(q_s^{*},w_s^{*}\right)$, and $E{\pi }_m\left(q_s^{*},w_s^{*}\right)$ can be obtained by ordering ${\eta }_r=1$ and ${\eta }_m=1$ in the expressions of $CVaR\left({\pi }_r\left(q_s^{*},w_s^{*}\right)\right)$ and $CVaR\left({\pi }_m\left(q_s^{*},w_s^{*}\right)\right)$. Therefore, we have

$\begin{array}{l}E{\pi }_r\left(q_s^{*},w_s^{*}\right)=\left[p+\left(1-\beta \right)Y-w_s^{*}\right]q_s^{*}-\left[p+\left(1-\beta \right)Y-s\right]{\int }_0^{q_s^{*}}F\left(x\right)dx\\ =\left[p+\left(1-\beta \right)Y-w_s^{*}\right]q_s^{*}-\frac{p+\left(1-\beta \right)Y-s}{2B}{q_s^{*}}^2\end{array}(3.12)$

$E{\pi }_m\left(q_s^{*},w_s^{*}\right)=\left(w_s^{*}+\beta Y-c\right)q_s^{*}-\beta Y{\int }_0^{q_s^{*}}F\left(x\right)dx=\left(w_s^{*}+\beta Y-c\right)q_s^{*}-\frac{\beta Y}{2B}{q_s^{*}}^2(3.13)$

Moreover, the supply chain’s total expected profit can be obtained.

$\begin{array}{l}E\pi \left(q_s^{*},w_s^{*}\right)=E{\pi }_r\left(q_s^{*},w_s^{*}\right)+E{\pi }_m\left(q_s^{*},w_s^{*}\right)\\ =\left(p+Y-c\right)q_s^{*}-\left(p+Y-s\right){\int }_0^{q_s^{*}}F\left(x\right)dx\\ =\left(p+Y-c\right)q_s^{*}-\frac{p+Y-s}{2B}{q_s^{*}}^2\end{array}(3.14)$

Recalling Eq. 3.7 and Eq. 3.8, we obtain

$\begin{array}{l}E\pi \left(q_s^{*},w_s^{*}\right)=\left(p+Y-c\right)q_s^{*}-\frac{p+Y-s}{2B}{q_s^{*}}^2\\ =\left(p+Y-c\right)q_s^{*}-\frac{p+Y-s}{2B}\frac{B{\eta }_r{\eta }_m\left(p+Y-c\right)}{2{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y}{q}_s^{*}\\ =\left(p+Y-c\right)q_s^{*}-\frac{{\eta }_r{\eta }_m\left(p+Y-c\right)\left(p+Y-s\right)}{4{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+2{\eta }_r\beta Y}{q}_s^{*}\end{array}$

$\begin{array}{l}E{\pi }_r\left(q_s^{*},w_s^{*}\right)=\left[p+\left(1-\beta \right)Y-w_s^{*}\right]q_s^{*}-\frac{p+\left(1-\beta \right)Y-s}{2B}{q_s^{*}}^2\\ =\left[p+\left(1-\beta \right)Y-w_s^{*}\right]q_s^{*}-\frac{{\eta }_r\left[p+\left(1-\beta \right)Y-w_s^{*}\right]}{2}{q}_s^{*}\\ =\left[p+\left(1-\beta \right)Y-w_s^{*}\right]\left(1-\frac{{\eta }_r}{2}\right)q_s^{*}\\ =\frac{\left(2-{\eta }_r\right){\eta }_m\left[p+\left(1-\beta \right)Y-s\right]\left(p+Y-c\right)}{4{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+2{\eta }_r\beta Y}{q}_s^{*}\end{array}$

Finally, ${\rho }_{rs}$ can be calculated through Eq. 3.10.

$\begin{array}{l}{\rho }_{rs}=\frac{E{\pi }_r\left(q_s^{*},w_s^{*}\right)}{E\pi \left(q_s^{*},w_s^{*}\right)}\\ =\frac{\frac{\left(2-{\eta }_r\right){\eta }_m\left[p+\left(1-\beta \right)Y-s\right]\left(p+Y-c\right)}{4{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+2{\eta }_r\beta Y}{q}_s^{*}}{\left(p+Y-c\right)q_s^{*}-\frac{{\eta }_r{\eta }_m\left(p+Y-c\right)\left(p+Y-s\right)}{4{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+2{\eta }_r\beta Y}{q}_s^{*}}\\ =\frac{\left(2-{\eta }_r\right){\eta }_m\left[p+\left(1-\beta \right)Y-s\right]}{4{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+2{\eta }_r\beta Y-{\eta }_r{\eta }_m\left(p+Y-s\right)}\end{array}$

Under the Stackelberg equilibrium with the manufacturer as the leader, the retailer and the manufacturer share the system profit by the proportion ${\rho }_{rs}:\left(1-{\rho }_{rs}\right)$, where ${\rho }_{rs}$ is given by Eq. 3.11. We can find in Eq. 3.11 that ${\rho }_{rs}$ depends on both the manufacturer’s and the retailer’s confidence levels when other variables are determined. That is to say, the players’ profit shares are affected by both players’ risk attitudes. The following proposition focuses on this issue.

Proposition 3.2. Under the Stackelberg equilibrium, the retailer’s profit share decreases in relation to her confidence level and increases in relation to the manufacturer’s.

Proof. Recalling Eq. 3.11, we take the first-order derivative of ${\rho }_{rs}$ with respect to ${\eta }_r$ and obtain

$\begin{array}{l}\frac{\partial {\rho }_{rs}}{\partial {\eta }_r}=\frac{-4{\eta }_m{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]\left[p+\left(1-\beta \right)Y-s\right]-2{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]\left[2\beta Y-{\eta }_m\left(p+Y-s\right)\right]}{{\left\{4{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+2{\eta }_r\beta Y-{\eta }_r{\eta }_m\left(p+Y-s\right)\right\}}^2}\\ =-\frac{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]\left[4\beta Y\left(1-{\eta }_m\right)+2{\eta }_m\left(p+Y-s\right)\right]}{{\left\{4{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+2{\eta }_r\beta Y-{\eta }_r{\eta }_m\left(p+Y-s\right)\right\}}^2}<0\end{array}$

Therefore, ${\rho }_{rs}$ decreases in ${\eta }_r$.

We convert the expression of ${\rho }_{rs}$ as follows.

$\begin{array}{l}{\rho }_{rs}=\frac{\left(2-{\eta }_r\right){\eta }_m\left[p+\left(1-\beta \right)Y-s\right]}{4{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+2{\eta }_r\beta Y-{\eta }_r{\eta }_m\left(p+Y-s\right)}\\ =\frac{\left(2-{\eta }_r\right)\left[p+\left(1-\beta \right)Y-s\right]}{4\left[p+\left(1-\beta \right)Y-s\right]+2{\eta }_r\beta Y/{\eta }_m-{\eta }_r\left(p+Y-s\right)}\end{array}$

We can easily find that ${\rho }_{rs}$ increases in ${\eta }_m$.

Proposition 3.2 explains how the manufacturer’s and retailer’s respective risk attitudes affect the players’ profit shares under the Stackelberg equilibrium. The retailer obtains a larger profit share when she becomes more risk averse or when the manufacturer becomes less risk averse. Such a conclusion is also symmetrically applicable for the manufacturer. In other words, a more risk-averse player tends to occupy a larger profit share. The risk aversion degree of the player who is more sensitive to the epidemic could be enlarged more and thus achieve a larger profit share increase. However, a more risk-averse player results in a lower order quantity and further a lower profit for the entire system. Therefore, the effect of the risk aversion degree on a player’s absolute profit is not very clear, and we further addressed this issue later by numerical experiments.

As one of the peculiarities in NEV commerce, the government subsidy is another point we should pay close attention to. The impact of the subsidy on the players’ profit shares in the NEV manufacturer-retailer system under the Stackelberg equilibrium is provided as follows.

Proposition 3.3. Under the Stackelberg equilibrium, the retailer’s profit share decreases in relation to the government subsidy.

Proof. Recalling Eq. 3.11, we convert the expression of ${\rho }_{rs}$ as follows.

${\rho }_{rs}=\frac{\left(2-{\eta }_r\right){\eta }_m\left[p+\left(1-\beta \right)Y-s\right]}{4{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+2{\eta }_r\beta Y-{\eta }_r{\eta }_m\left(p+Y-s\right)}=\frac{\left(2-{\eta }_r\right){\eta }_m}{4{\eta }_m+\frac{2{\eta }_r\beta Y-{\eta }_r{\eta }_m\left(p+Y-s\right)}{p+\left(1-\beta \right)Y-s}}$

Denote

$P=\frac{2{\eta }_r\beta Y-{\eta }_r{\eta }_m\left(p+Y-s\right)}{p+\left(1-\beta \right)Y-s}$

Take the first-order derivative of $P$ with respect to $Y$, and we obtain

$\begin{array}{l}\frac{\partial P}{\partial Y}=\frac{\left(2{\eta }_r\beta -{\eta }_r{\eta }_m\right)\left[p+\left(1-\beta \right)Y-s\right]-\left(1-\beta \right)\left[2{\eta }_r\beta Y-{\eta }_r{\eta }_m\left(p+Y-s\right)\right]}{{\left[p+\left(1-\beta \right)Y-s\right]}^2}\\ =\frac{{\eta }_r\beta \left(2-{\eta }_m\right)\left(p-s\right)}{{\left[p+\left(1-\beta \right)Y-s\right]}^2}>0\end{array}$

Therefore, $P$ increases in $Y$ and ${\rho }_{rs}=\left(2-{\eta }_r\right){\eta }_m/\left(4{\eta }_m+P\right)$ decreases in $Y$.

Besides affecting the two players’ risk attitudes, the government subsidy also has a noticeable impact on the players’ profit shares in the NEV manufacturer-retailer system. When the government subsidy is augmented, the retailer’s profit share is reduced while the manufacturer’s is enlarged. Since the change in the subsidy amount can alter the players’ profit shares, the government can choose to support the NEV manufacturer/retailer more by adjusting the subsidy amount. However, a larger government subsidy always leads to a higher profit for the entire system. Therefore, the effect of the government subsidy on a player’s absolute profit also needs further discussion by numerical experiments.

4 Nash bargaining

In the NBF framework, the manufacturer and the retailer negotiate with each other about the order quantity and the wholesale price in order to enlarge the payoff pie and split it according to the bargaining power contrast between the two players. Suppose that the retailer’s bargaining power is $\omega$ ($0\le \omega \le 1$). Then $\left(1-\omega \right)$ represents the manufacturer’s bargaining power. Other notations are the same as for the Stackelberg model. In addition, we assumed that the manufacturer’s and retailer’s respective reserved payoffs measured by CVaR are deterministic and set as zero for calculating convenience. Rockafellar and Uryasev (2002) explained why this assumption is reasonable and indicated that this setting does not change the equilibrium qualitative properties. Thus, the NBF problem can be formulated as follows.

$\underset{q>0,c-\beta Y<w<p+\left(1-\beta \right)Y}{\max }CVaR{\left({\pi }_r\left(q,w\right)\right)}^{\omega }\cdot CVaR{\left({\pi }_m\left(q,w\right)\right)}^{1-\omega }(4.1)$

4.1 Nash bargaining equilibrium

According to the CVaR expressions given in Theorem 3.1, we can derive the NBF equilibrium in an NEV manufacturer-retailer system by solving Eq. 4.1. The results are provided in the following theorem.

Theorem 4.1. The NBF equilibrium between the NEV manufacturer and retailer is $\left(q_n^{*},w_n^{*}\right)$, where

$q_n^{*}=F^{-1}\left(\frac{{\eta }_r{\eta }_m\left(p+Y-c\right)}{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y}\right)(4.2)$

$w_n^{*}=\left[\left(1-\omega \right)p+\left(1-\beta -\omega \right)Y+\omega c\right]-\frac{\left\{\left(1-\omega \right){\eta }_m\left[p+\left(1-\beta \right)Y-s\right]-\omega {\eta }_r\beta Y\right\}{\int }_0^{q_n^{*}}F\left(x\right)dx}{{\eta }_r{\eta }_m{q}_n^{*}}(4.3)$

Proof. Recalling Eq. 3.5, take the first-order derivatives of $CVaR\left({\pi }_r\left(q,w\right)\right)$ with respect to $q$ and $w$, respectively:

$\frac{\partial CVaR\left({\pi }_r\left(q,w\right)\right)}{\partial q}=\left\{\begin{array}{cc}\left[p+\left(1-\beta \right)Y-w\right]-\frac{p+\left(1-\beta \right)Y-s}{{\eta }_r}F\left(q\right)& q\le F^{-1}\left({\eta }_r\right)\\ -\left(w-s\right)& q>F^{-1}\left({\eta }_r\right)\end{array}\right.$

$\frac{\partial CVaR\left({\pi }_r\left(q,w\right)\right)}{\partial w}=-q$

Similarly, recalling Eq. 3.6, take the first-order derivatives of $CVaR\left({\pi }_m\left(q,w\right)\right)$ with respect to $q$ and $w$, respectively:

$\frac{\partial CVaR\left({\pi }_m\left(q,w\right)\right)}{\partial q}=\left\{\begin{array}{cc}\left(w+\beta Y-c\right)-\frac{\beta Y}{{\eta }_m}F\left(q\right)& q\le F^{-1}\left({\eta }_m\right)\\ \left(w-c\right)& q>F^{-1}\left({\eta }_m\right)\end{array}\right.$

$\frac{\partial CVaR\left({\pi }_m\left(q,w\right)\right)}{\partial w}=q$

To solve Eq. 4.1, the necessary conditions are:

$\left\{\begin{array}{c}\omega \frac{\partial CVaR\left({\pi }_r\left(q,w\right)\right)}{\partial q}CVaR\left({\pi }_m\left(q,w\right)\right)+\left(1-\omega \right)\frac{\partial CVaR\left({\pi }_m\left(q,w\right)\right)}{\partial q}CVaR\left({\pi }_r\left(q,w\right)\right)=0\\ \omega \frac{\partial CVaR\left({\pi }_r\left(q,w\right)\right)}{\partial w}CVaR\left({\pi }_m\left(q,w\right)\right)+\left(1-\omega \right)\frac{\partial CVaR\left({\pi }_m\left(q,w\right)\right)}{\partial w}CVaR\left({\pi }_r\left(q,w\right)\right)=0\end{array}\right.(4.4)$

According to the scale of $q$, noting the assumption ${\eta }_r<{\eta }_m$, we have three cases for further discussion.

(1) When $q\le F^{-1}\left({\eta }_r\right)<F^{-1}\left({\eta }_m\right)$, Eq. 4.4 can be converted to:

$\left\{\begin{array}{l}\begin{array}{l}\omega \left\{\left[p+\left(1-\beta \right)Y-w\right]-\frac{p+\left(1-\beta \right)Y-s}{{\eta }_r}F\left(q\right)\right\}\left\{\left(w+\beta Y-c\right)q-\frac{\beta Y}{{\eta }_m}{\int }_0^{q}F\left(x\right)dx\right\}\\ +\left(1-\omega \right)\left\{\left(w+\beta Y-c\right)-\frac{\beta Y}{{\eta }_m}F\left(q\right)\right\}\left\{\left[p+\left(1-\beta \right)Y-w\right]q-\frac{p+\left(1-\beta \right)Y-s}{{\eta }_r}{\int }_0^{q}F\left(x\right)dx\right\}=0\end{array}\\ -q\omega \left\{\left(w+\beta Y-c\right)q-\frac{\beta Y}{{\eta }_m}{\int }_0^{q}F\left(x\right)dx\right\}+q\left(1-\omega \right)\left\{\left[p+\left(1-\beta \right)Y-w\right]q-\frac{p+\left(1-\beta \right)Y-s}{{\eta }_r}{\int }_0^{q}F\left(x\right)dx\right\}=0\end{array}\right.$

It can be further simplified:

$\left\{\begin{array}{l}\left(p+Y-c\right)-\left[\frac{p+\left(1-\beta \right)Y-s}{{\eta }_r}+\frac{\beta Y}{{\eta }_m}\right]F\left(q_r\right)=0\\ \left\{\left[p+\left(1-\beta \right)Y-w\right]-\omega \left(p+Y-c\right)\right\}{q}_r-\left\{\frac{\left(1-\omega \right)\left[p+\left(1-\beta \right)Y-s\right]}{{\eta }_r}-\frac{\omega \beta Y}{{\eta }_m}\right\}{\int }_0^{q_r}F\left(x\right)dx=0\end{array}\right.$

By solving this equation set, we can obtain the NBF equilibrium $\left(q_n^{*},w_n^{*}\right)$ where $q_n^{*}$ and $w_n^{*}$ are given by Eq. 4.2 and Eq. 4.3. At the equilibrium point, we can testify that the Hessian Matrix of the objective function in Eq. 4.1 is negative definite, thus $\left(q_n^{*},w_n^{*}\right)$ is a stable equilibrium.

(2) When $F^{-1}\left({\eta }_r\right)<q<F^{-1}\left({\eta }_m\right)$, Eq. 4.4 can be converted to:

$\left\{\begin{array}{l}\begin{array}{l}-\omega \left(w-s\right)\left\{\left(w+\beta Y-c\right)q-\frac{\beta Y}{{\eta }_m}{\int }_0^{q}F\left(x\right)dx\right\}\\ +\left(1-\omega \right)\left\{\left(w+\beta Y-c\right)-\frac{\beta Y}{{\eta }_m}F\left(q\right)\right\}\left\{\left[p+\left(1-\beta \right)Y-s\right]F^{-1}\left({\eta }_r\right)-\left(w-s\right)q-\frac{p+\left(1-\beta \right)Y-s}{{\eta }_r}{\int }_0^{F^{-1}\left({\eta }_r\right)}F\left(x\right)dx\right\}=0\end{array}\\ -q\omega \left\{\left(w+\beta Y-c\right)q-\frac{\beta Y}{{\eta }_m}{\int }_0^{q}F\left(x\right)dx\right\}+q\left(1-\omega \right)\left\{\left[p+\left(1-\beta \right)Y-s\right]F^{-1}\left({\eta }_r\right)-\left(w-s\right)q-\frac{p+\left(1-\beta \right)Y-s}{{\eta }_r}{\int }_0^{F^{-1}\left({\eta }_r\right)}F\left(x\right)dx\right\}=0\end{array}\right.$

It can be further simplified:

$\left\{\begin{array}{ll}\left(\beta Y-c+s\right)-\frac{\beta Y}{{\eta }_m}F\left(q\right)=0& a\\ \left[p+\left(1-\beta \right)Y-s\right]F^{-1}\left({\eta }_r\right)-\left(2w+\beta Y-c-s\right)q-\frac{p+\left(1-\beta \right)Y-s}{{\eta }_r}{\int }_0^{F^{-1}\left({\eta }_r\right)}F\left(x\right)dx+\frac{\beta Y}{{\eta }_m}{\int }_0^{q}F\left(x\right)dx=0& b\end{array}\right.(4.5)$

Take the first-order derivatives of two sides in Eq. 4.5 with respect to $q$, respectively:

$-\left(2w+\beta Y-c-s\right)+\frac{\beta Y}{{\eta }_m}F\left(q\right)=0(4.6)$

Combining Eq. 4.6 and Eq. 4.5, we obtain $w=s$. That is obviously contradictory to the model assumption. Thus, there is no equilibrium in this case.

(3) When $q\ge F^{-1}\left({\eta }_m\right)>F^{-1}\left({\eta }_n\right)$, the equilibrium also does not exist. The proof is similar to the second case and thus omitted here.

In the NEV manufacturer-retailer system, when the manufacturer and the retailer are both risk averse with the CVaR criterion and negotiate with each other under the NBF framework, the equilibrium consists in the retailer ordering $q_n^{*}$ NEVs at a wholesale price $w_n^{*}$. From Eq. 4.2 and Eq. 4.3, we can observe that the equilibrium order quantity depends on the two players’ risk attitudes while having nothing to do with the bargaining power contrast between them. The equilibrium wholesale price is related to the two players’ risk attitudes as well as the bargaining power contrast. In order to further analyze the effects of both players’ risk attitudes and bargaining power, we considered the special case with a uniform distribution assumption. Consistent with the Stackelberg model, suppose that the demand is subject to a uniform distribution on $\left[0,B\right]$. Then $q_n^{*}$ and $w_n^{*}$ can be expressed as follows.

$q_n^{*}=F^{-1}\left(\frac{{\eta }_r{\eta }_m\left(p+Y-c\right)}{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y}\right)=\frac{B{\eta }_r{\eta }_m\left(p+Y-c\right)}{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y}(4.7)$

$\begin{array}{l}{w}_n^{*}=\left[\left(1-\omega \right)p+\left(1-\beta -\omega \right)Y+\omega c\right]-\frac{\left\{\left(1-\omega \right){\eta }_m\left[p+\left(1-\beta \right)Y-s\right]-\omega {\eta }_r\beta Y\right\}{\int }_0^{q_n^{*}}F\left(x\right)dx}{{\eta }_r{\eta }_m{q}_n^{*}}\\ =\left[\left(1-\omega \right)p+\left(1-\beta -\omega \right)Y+\omega c\right]-\frac{\left(p+Y-c\right)\left\{\left(1-\omega \right){\eta }_m\left[p+\left(1-\beta \right)Y-s\right]-\omega {\eta }_r\beta Y\right\}}{2\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}}\end{array}(4.8)$

Based on the above results, we provide the following proposition to explain the relationships between the NBF equilibrium and the two players’ confidence levels.

Proposition 4.1. Under the NBF framework, the equilibrium order quantity increases in connection with either the manufacturer’s or retailer’s confidence level; the equilibrium wholesale price increases in relation to the retailer’s confidence level yet decreases in relation to the manufacturer’s.

Proof. Recalling Eq. 4.2, we convert the expression of $q_n^{*}$ as follows.

$q_n^{*}=\frac{B{\eta }_r{\eta }_m\left(p+Y-c\right)}{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y}=\frac{B{\eta }_m\left(p+Y-c\right)}{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]/{\eta }_r+\beta Y}=\frac{B{\eta }_r\left(p+Y-c\right)}{\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y/{\eta }_m}$

We can easily find that $q_n^{*}$ increases in ${\eta }_r$ or ${\eta }_m$.

According to Eq.(4.3), taking the first-order derivative of $w_n^{*}$ with respect to ${\eta }_r$, we obtain

$\begin{array}{l}\frac{\partial w_n^{*}}{\partial {\eta }_r}=-\frac{-2\omega \beta Y\left(p+Y-c\right)\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}-2\beta Y\left(p+Y-c\right)\left\{\left(1-\omega \right){\eta }_m\left[p+\left(1-\beta \right)Y-s\right]-\omega {\eta }_r\beta Y\right\}}{4{\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}}^2}\\ =\frac{{\eta }_m\beta Y\left(p+Y-c\right)\left[p+\left(1-\beta \right)Y-s\right]}{2{\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}}^2}>0\end{array}$

Therefore, $w_n^{*}$ increases in ${\eta }_r$.

Then take the first-order derivative of $w_n^{*}$ with respect to ${\eta }_m$, and we obtain

$\begin{array}{l}\frac{\partial w_n^{*}}{\partial {\eta }_m}=-\frac{2\left(1-\omega \right)\left(p+Y-c\right)\left[p+\left(1-\beta \right)Y-s\right]\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}-2\left[p+\left(1-\beta \right)Y-s\right]\left(p+Y-c\right)\left\{\left(1-\omega \right){\eta }_m\left[p+\left(1-\beta \right)Y-s\right]-\omega {\eta }_r\beta Y\right\}}{4{\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}}^2}\\ =-\frac{{\eta }_r\beta Y\left(p+Y-c\right)\left[p+\left(1-\beta \right)Y-s\right]}{2{\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}}^2}<0\end{array}$

Therefore, $w_n^{*}$ decreases in ${\eta }_m$.

As mentioned previously, a lower confidence level indicates a higher risk aversion degree. Proposition 4.1 reveals that the effects of the two players’ risk attitudes and the epidemic on the equilibrium under the NBF framework are similar to those under the Stackelberg game. The NBF equilibrium order quantity also decreases in connection with either the manufacturer’s or the retailer’s risk aversion degree. When both the NEV manufacturer and retailer are considered risk-averse decision makers, the NBF equilibrium order quantity is doubly reduced and decreases as the manufacturer or the retailer become more risk averse. The NBF equilibrium wholesale price also decreases in connection with the retailer’s risk aversion degree while increasing in relation to the manufacturer’s. The reason is the same as that under the Stackelberg game: when the retailer/manufacturer becomes more risk averse, the wholesale price should be increased/decreased to attract the more conservative retailer/manufacturer to participate in the business.

Under the cooperative NBF framework, the manufacturer and the retailer have a joint aim to increase the supply chain’s total payoff. Consequently, the equilibrium order quantity is derived by maximizing the objective function in Eq. 4.1 and is not related to the bargaining power contrast. The other equilibrium solution, the wholesale price, depends on the two players’ bargaining powers.

Proposition 4.2. Under the NBF framework, the equilibrium wholesale price decreases in connection with the retailer’s bargaining power.

Proof. According to Eq. 4.3, taking the first-order derivative of $w_n^{*}$ with respect to $\omega$, we obtain

$\frac{\partial w_n^{*}}{\partial \omega }=-\left(p+Y-c\right)-\frac{\left(p+Y-c\right)\left\{-{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]-{\eta }_r\beta Y\right\}}{2\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}}=-\frac{p+Y-c}{2}<0$

Therefore, $w_n^{*}$ decreases in $\omega$.

This result is intuitive, because the retailer will have a more advantageous position in the bargaining procedure and ask for a lower wholesale price to strive for a higher profit if her bargaining power increases. Similarly, when the retailer’s bargaining power is lowered, meaning the manufacturer’s bargaining power increases, the equilibrium wholesale price will be higher, and the manufacturer will profit from that. That is why an NEV player always tries his/her best to increase his/her bargaining power by promoting his/her competitiveness in the aspects of scale, effectiveness, reputation, market shares, and so on.

4.2 Profit allocation under the Nash bargaining framework

Similar to the Stackelberg case, we attempted to examine the effects of the players’ risk attitudes, the government subsidy, and the bargaining power contrast on the players’ profit shares in the NEV manufacturer-retailer system under the NBF framework. To this end, we first calculated the retailer’s profit share under the NBF equilibrium ${\rho }_{rn}$ according to Eq. 3.10, shown in the following theorem.

Theorem 4.2. Under the NBF equilibrium, the retailer’s profit share is:

${\rho }_{rn}=\frac{\left(1+\omega -{\eta }_r\right){\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+\omega {\eta }_r\beta Y}{2\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}-{\eta }_r{\eta }_m\left(p+Y-s\right)}(4.9)$

Proof. Under the NBF equilibrium $\left(q_n^{*},w_n^{*}\right)$, the expected profits for the retailer, the manufacturer, and the entire system, respectively, denoted as $E{\pi }_r\left(q_n^{*},w_n^{*}\right)$, $E{\pi }_m\left(q_n^{*},w_n^{*}\right)$, and $E\pi \left(q_n^{*},w_n^{*}\right)$, can be obtained by replacing $\left(q_s^{*},w_s^{*}\right)$ with $\left(q_n^{*},w_n^{*}\right)$ in Eq. 3.12, Eq. 3.13, and Eq. 3.14. Therefore, we have

$E{\pi }_r\left(q_n^{*},w_n^{*}\right)=\left[p+\left(1-\beta \right)Y-w_n^{*}\right]q_n^{*}-\frac{p+\left(1-\beta \right)Y-s}{2B}{q_n^{*}}^2(4.10)$

$E{\pi }_m\left(q_n^{*},w_n^{*}\right)=\left(w_n^{*}+\beta Y-c\right)q_n^{*}-\frac{\beta Y}{2B}{q_n^{*}}^2(4.11)$

$E\pi \left(q_n^{*},w_n^{*}\right)=\left(p+Y-c\right)q_n^{*}-\frac{p+Y-s}{2B}{q_n^{*}}^2(4.12)$

Recalling Eq. 4.7 and Eq. 4.8, we obtain

$\begin{array}{l}E\pi \left(q_n^{*},w_n^{*}\right)=\left(p+Y-c\right)q_n^{*}-\frac{p+Y-s}{2B}{q_n^{*}}^2\\ =\left(p+Y-c\right)q_n^{*}-\frac{p+Y-s}{2B}\frac{B{\eta }_r{\eta }_m\left(p+Y-c\right)}{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y}{q}_n^{*}\\ =\left(p+Y-c\right)q_n^{*}-\frac{{\eta }_r{\eta }_m\left(p+Y-c\right)\left(p+Y-s\right)}{2\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}}{q}_n^{*}\end{array}$

$\begin{array}{l}E{\pi }_r\left(q_n^{*},w_n^{*}\right)=\left[p+\left(1-\beta \right)Y-w_n^{*}\right]q_n^{*}-\frac{p+\left(1-\beta \right)Y-s}{2B}{q_n^{*}}^2\\ =\left[\omega \left(p+Y-c\right)+\frac{\left(p+Y-c\right)\left\{\left(1-\omega \right){\eta }_m\left[p+\left(1-\beta \right)Y-s\right]-\omega \beta {\eta }_{r}Y\right\}}{2\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}}-\frac{{\eta }_r{\eta }_m\left(p+Y-c\right)\left[p+\left(1-\beta \right)Y-s\right]}{2\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}}\right]q_n^{*}\\ =\frac{\left(p+Y-c\right)\left\{\left(1+\omega -{\eta }_r\right){\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+\omega {\eta }_r\beta Y\right\}}{2\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}}{q}_n^{*}\end{array}$

Finally, ${\rho }_{rn}$ can be calculated with Eq. 3.10.

$\begin{array}{l}{\rho }_{rn}=\frac{E{\pi }_r\left(q_n^{*},w_n^{*}\right)}{E\pi \left(q_n^{*},w_n^{*}\right)}\\ =\frac{\frac{\left(p+Y-c\right)\left\{\left(1+\omega -{\eta }_r\right){\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+\omega {\eta }_r\beta Y\right\}}{2\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}}{q}_n^{*}}{\left(p+Y-c\right)q_n^{*}-\frac{{\eta }_r{\eta }_m\left(p+Y-c\right)\left(p+Y-s\right)}{2\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}}{q}_n^{*}}\\ =\frac{\left(1+\omega -{\eta }_r\right){\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+\omega {\eta }_r\beta Y}{2\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}-{\eta }_r{\eta }_m\left(p+Y-s\right)}\end{array}$

Under the NBF equilibrium, the retailer takes over ${\rho }_{rn}$ proportion of the system profit, while the remaining $\left(1-{\rho }_{rn}\right)$ proportion belongs to the manufacturer, where ${\rho }_{rn}$ is given by Theorem 4.2. Similar to the Stackelberg model, Eq. 4.9 shows that, under the NBF framework, the players’ profit shares are also influenced by both players’ confidence levels when other variables are determined. We provide the following proposition to address this issue.

Proposition 4.3. Under the NBF equilibrium, the retailer’s profit share decreases in connection with her confidence level and increases in connection with the manufacturer’s.

Proof. Recalling Eq. 4.9, take the first-order derivative of ${\rho }_{rn}$ with respect to ${\eta }_r$, and we obtain

$\begin{array}{l}\frac{\partial {\rho }_{rn}}{\partial {\eta }_r}=\frac{\begin{array}{l}\left\{-{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+\omega \beta Y\right\}\left\{2\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}-{\eta }_r{\eta }_m\left(p+Y-s\right)\right\}\\ -\left\{\left(1+\omega -{\eta }_r\right){\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+\omega {\eta }_r\beta Y\right\}\left\{2\beta Y-{\eta }_m\left(p+Y-s\right)\right\}\end{array}}{{\left\{2\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}-{\eta }_r{\eta }_m\left(p+Y-s\right)\right\}}^2}\\ =\frac{-2\beta Y{\eta }_m\left(1-{\eta }_m\right)\left[p+\left(1-\beta \right)Y-s\right]-{\eta }_m^2\left(1-\omega \right)\left(p+Y-s\right)\left[p+\left(1-\beta \right)Y-s\right]}{{\left\{2\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}-{\eta }_r{\eta }_m\left(p+Y-s\right)\right\}}^2}<0\end{array}$

Therefore, ${\rho }_{rn}$ decreases in ${\eta }_r$.

Similarly, take the first-order derivative of ${\rho }_{rn}$ with respect to ${\eta }_m$, and we obtain

$\begin{array}{l}\frac{\partial {\rho }_{rn}}{\partial {\eta }_m}=\frac{\begin{array}{l}\left(1+\omega -{\eta }_r\right)\left[p+\left(1-\beta \right)Y-s\right]\left\{2\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}-{\eta }_r{\eta }_m\left(p+Y-s\right)\right\}\\ -\left\{\left(1+\omega -{\eta }_r\right){\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+\omega {\eta }_r\beta Y\right\}\left\{2\left[p+\left(1-\beta \right)Y-s\right]-{\eta }_r\left(p+Y-s\right)\right\}\end{array}}{{\left\{2\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}-{\eta }_r{\eta }_m\left(p+Y-s\right)\right\}}^2}\\ =\frac{2{\eta }_r\beta Y\left(1-{\eta }_r\right)\left[p+\left(1-\beta \right)Y-s\right]+\omega {\eta }_r^2\beta Y\left(p+Y-s\right)}{{\left\{2\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}-{\eta }_r{\eta }_m\left(p+Y-s\right)\right\}}^2}>0\end{array}$

Therefore, ${\rho }_{rn}$ increases in ${\eta }_m$.

The conclusion about the effects of the two players’ risk attitudes and the epidemic on the players’ shares is the same as that under the Stackelberg game: under the NBF equilibrium, the retailer’s profit share increases in connection with her risk aversion degree yet decreases in connection with the manufacturer’s. Such a conclusion is also symmetrically applicable for the manufacturer; the epidemic also heightens either player’s risk aversion degree and, thus, increases his/her profit share. We can conclude that, whether the two risk-averse players participate in the Stackelberg game or the NBF procedure, a more risk-averse player always occupies a larger profit share. Also, we further conducted numerical experiments to clarify the effect of the risk aversion degree on a player’s absolute profit under the NBF framework—to be discussed at a later point.

Similar to Proposition 3.3, we also examined the effect of the government subsidy on the players’ profit shares under the NBF framework. The relationship between the subsidy and the retailer’s profit share under the NBF equilibrium is provided as follows.

Proposition 4.4. Under the NBF equilibrium, the retailer’s profit share decreases in connection with the government subsidy.

Proof. Recalling Eq. 4.9, take the first-order derivative of ${\rho }_{rn}$ with respect to $Y$, and we obtain

$\begin{array}{l}\frac{\partial {\rho }_{rn}}{\partial Y}=\frac{\begin{array}{l}\left\{\left(1+\omega -{\eta }_r\right){\eta }_m\left(1-\beta \right)+\omega {\eta }_r\beta \right\}\left\{2\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}-{\eta }_r{\eta }_m\left(p+Y-s\right)\right\}\\ -\left\{\left(1+\omega -{\eta }_r\right){\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+\omega {\eta }_r\beta Y\right\}\left\{2\left\{{\eta }_m\left(1-\beta \right)+{\eta }_r\beta \right\}-{\eta }_r{\eta }_m\right\}\end{array}}{{\left\{2\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}-{\eta }_r{\eta }_m\left(p+Y-s\right)\right\}}^2}\\ =\frac{\beta {\eta }_r{\eta }_m\left(p-s\right)\left[-\left(2-{\eta }_m\right)\left(1-{\eta }_r\right)+\left({\eta }_m-{\eta }_r\right)\omega \right]}{{\left\{2\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}-{\eta }_r{\eta }_m\left(p+Y-s\right)\right\}}^2}\end{array}$

Note that when $0<{\eta }_r<{\eta }_m\le 1$ and $\omega \le 1$, there is

$-\left(2-{\eta }_m\right)\left(1-{\eta }_r\right)+\left({\eta }_m-{\eta }_r\right)\omega \le -\left(2-{\eta }_m\right)\left(1-{\eta }_r\right)+\left({\eta }_m-{\eta }_r\right)=-\left(1-{\eta }_m\right)\left(2-{\eta }_r\right)\le 0$

Therefore, $\partial {\rho }_{rn}/\partial Y<0$ and ${\rho }_{rn}$ decreases in $Y$.

Proposition 4.4 shows that the effect of the government subsidy on the players’ profit shares is also the same as that under the Stackelberg game: under the NBF equilibrium, a higher subsidy also increases the retailer’s profit share yet decreases the manufacturer’s. We therefore conclude that the government subsidy can alter the players’ profit shares under either the Stackelberg game or the NBF framework. The government can choose to preferentially support the NEV manufacturer/retailer by offering a higher/lower subsidy. Also, we further analyzed the effect of the government subsidy on a player’s absolute profit under the NBF framework through numerical experiments.

Besides the players’ risk attitudes and the government subsidy, the bargaining power contrast also affects the players’ profit shares under the NBF framework. The following proposition focuses on this issue.

Proposition 4.5. Under the NBF equilibrium, the retailer’s profit share increases with respect to her bargaining power.

Proof. Recalling Eq. 4.9, take the first-order derivative of ${\rho }_{rn}$ with respect to $\omega$, and we obtain

$\frac{\partial {\rho }_{rn}}{\partial \omega }=\frac{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y}{2\left\{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y\right\}-{\eta }_r{\eta }_m\left(p+Y-s\right)}>0$

Therefore, ${\rho }_{rn}$ increases in $\omega$.

A player with a higher bargaining power will have a more advantageous position in the bargaining procedure and obtain a larger profit share. According to Eq. 4.7 and Eq. 4.12, the bargaining power contrast does not affect the equilibrium order quantity nor the supply chain’s total profit. Thus, the bargaining power contrast can change the players’ profit shares by altering the equilibrium wholesale price. Moreover, a larger profit share indicates a higher profit since the system profit keeps constant with respect to the bargaining power contrast.

Additionally, it is worth emphasizing that $\omega =1/2$ is a special case indicating that the retailer and the manufacturer have equal bargaining power. In this case, the above results hold unconditionally.

4.3 A comparison between Stackelberg game and Nash bargaining

We have derived the equilibrium solutions about the order quantity and the wholesale price under both the Stackelberg game and the NBF framework. This subsection compares the results of these two models.

Theorem 4.3. Under the NBF equilibrium, the equilibrium order quantity and the supply chain’s total profit dominate those under the Stackelberg game, i.e., $q_n^{*}>q_s^{*}$ and $E\pi \left(q_n^{*},w_n^{*}\right)>E\pi \left(q_s^{*},w_s^{*}\right)$.

Proof. According to Eq. 3.7 and Eq. 4.7, we can easily find that

$q_n^{*}=\frac{B{\eta }_r{\eta }_m\left(p+Y-c\right)}{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y}>\frac{B{\eta }_r{\eta }_m\left(p+Y-c\right)}{2{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y}=q_s^{*}$

The integrated supply chain’s centralized optimal order quantity is

$q^{*}=\frac{B\left(p+Y-c\right)}{\left(p+Y-s\right)}$

According to Proposition 4.1, $q_n^{*}$ increases in ${\eta }_r$ or ${\eta }_m$; so, we have

$q^{*}=\frac{B\left(p+Y-c\right)}{\left(p+Y-s\right)}\ge \frac{B{\eta }_r{\eta }_m\left(p+Y-c\right)}{{\eta }_m\left[p+\left(1-\beta \right)Y-s\right]+{\eta }_r\beta Y}=q_n^{*}>q_s^{*}$

Though the supply chain’s total profit $E\pi \left(q,w\right)$ increases in $q$ on, $\left(0\right.,\left.q^{*}\right]$ it has nothing to do with the wholesale price. Therefore, we obtain $E\pi \left(q_n^{*},w_n^{*}\right)>E\pi \left(q_s^{*},w_s^{*}\right)$.

Compared to the Stackelberg game, the NBF framework brings about a larger order quantity as well as a higher system profit. Under the cooperative NBF framework, the retailer and the manufacturer collaborate to achieve equilibrium to maximize the supply chain’s total payoff and then split it according to their bargaining powers. Under the uncooperative Stackelberg game, the two players respectively make decisions to maximize their individual payoffs without consideration of the supply chain’s total payoff. The manufacturer and the retailer negotiate about the equilibrium by competing with each other, which is unbeneficial for the entire system. Consequently, with systematic consideration, the NEV manufacturer and retailer should participate in the NBF procedure rather than the Stackelberg game. Within the epidemic environment, both players are considered risk averse; therefore, the NBF framework is advantageous for promoting NEV production/sale quantity and enhancing the supply chain’s overall profit. We provide further analysis later by numerical experiments to show how to ensure both players’ profits higher so that both prefer the NBF framework.

5 Numerical experiments

So far, we have derived the equilibriums as well as the corresponding profit shares under the Stackelberg game and the NBF framework and analyzed the effects of some relevant elements, such as players’ risk attitudes, the government subsidy, and the bargaining power. In this section, we have carried out numerical experiments to further clarify the effects of these significant elements on the equilibrium order quantity and the profit allocation under different negotiation frameworks. Comparisons of the results under the two negotiation frameworks illustrate the superiority of the NBF model more intuitively. These findings may provide guidelines for sustainably maintaining the NEV manufacturer-retailer system by balancing the profit allocation between the retailer and the manufacturer under different negotiation frameworks.

Related parameters are theoretically assumed as follows: the NEV market demand is subject to a uniform distribution on $\left[\mathrm{0,1000}\right]$, the per-unit retail price is $p=80000$, the per-unit production cost is $c=100000$, the per-unit salvage value is $s=40000$, and the manufacturer’s subsidy-sharing proportion is $\beta =0.2$.

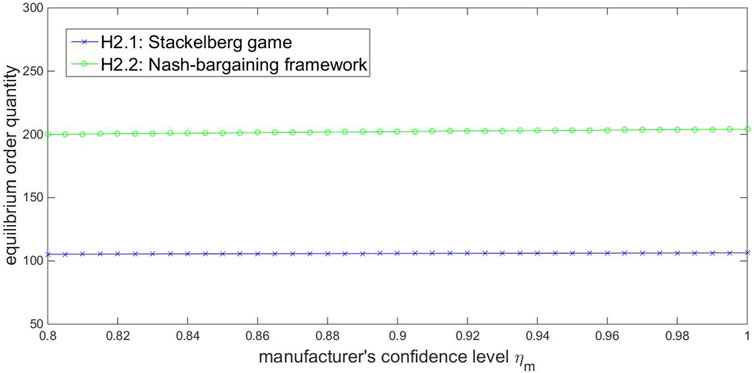
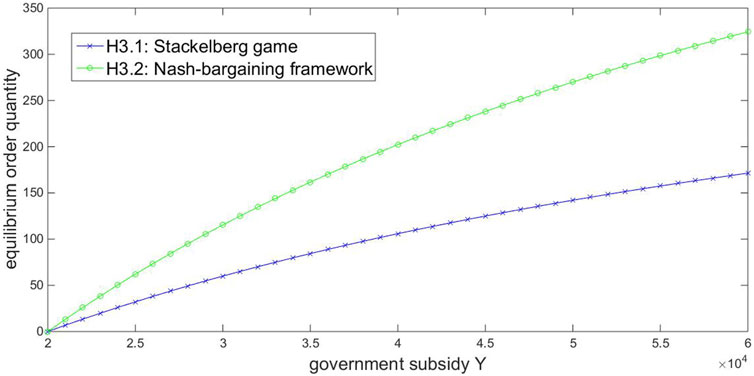
Based on the above numerical assumptions, we first illustrated the effects of some parameters on the equilibrium order quantities under the Stackelberg game and the NBF framework. Given $Y=40000$ and ${\eta }_m=0.9$, Figure 1 describes that the equilibrium order quantities under both negotiation frameworks increase according to the retailer’s confidence level ${\eta }_r$. Given $Y=40000$ and ${\eta }_r=0.8$, Figure 2 displays that the equilibrium order quantities under both negotiation frameworks slightly increase according to the manufacturer’s confidence level ${\eta }_m$. The confidence level of either the NEV manufacturer or retailer goes lower considering the impact of the COVID-19 epidemic, thus the equilibrium order quantities under both negotiation frameworks are reduced and the retailer’s risk attitude brings about a lager influence. Given ${\eta }_r=0.8$ and ${\eta }_m=0.9$, Figure 3 shows that the equilibrium order quantities under both negotiation frameworks increase according to the government subsidy $Y$. It is indicated that the government subsidy increasing can improve the equilibrium order quantities under both negotiation frameworks so as to offset the negative impact raised by the COVID-19 epidemic. In addition, these three figures all demonstrate that the equilibrium order quantity under the NBF framework is always larger than that under the Stackelberg game. Thus, it is verified that the superior NBF framework can promote NEV sales no matter how the relevant parameters vary. Moreover, we can also observe that the promoting effect of the NBF framework compared to the Stackelberg game is augmented when the government subsidy increases or when either player becomes less risk averse. We can conclude that when the COVID-19 epidemic eliminates or the government subsidy degeneration is delayed, the superiority of the NBF framework is extended compared to the Stackelberg game.

FIGURE 1

FIGURE 1. Impact of ${\eta }_r$ on the order quantity ($Y=40000$; ${\eta }_m=0.9$).

FIGURE 2

FIGURE 2. Impact of ${\eta }_m$ on the order quantity ($Y=40000$; ${\eta }_r=0.8$).

FIGURE 3

FIGURE 3. Impact of $Y$ on the order quantity (${\eta }_r=0.8$; ${\eta }_m=0.9$).

As mentioned before, since players’ risk attitudes, the epidemic, and the government subsidy affect the equilibrium order quantity and further affect the supply chain’s total profit, the players’ profit shares cannot directly reflect the system profit allocation. Next, we conducted numerical experiments to address the effects of some significant parameters on the profit allocation under the Stackelberg game and the NBF framework respectively. Under the Stackelberg equilibrium provided in Theorem 3.2, the profits of the retailer, the manufacturer, and the entire system can be calculated by Eq. 3. 12, Eq. 3.13, and Eq. 3.14, respectively. The profits of the retailer, the manufacturer, and the entire system under the NBF equilibrium provided in Theorem 4.1 can be calculated by Eq. 4.10, Eq. 4.11, and Eq. 4.12, respectively.

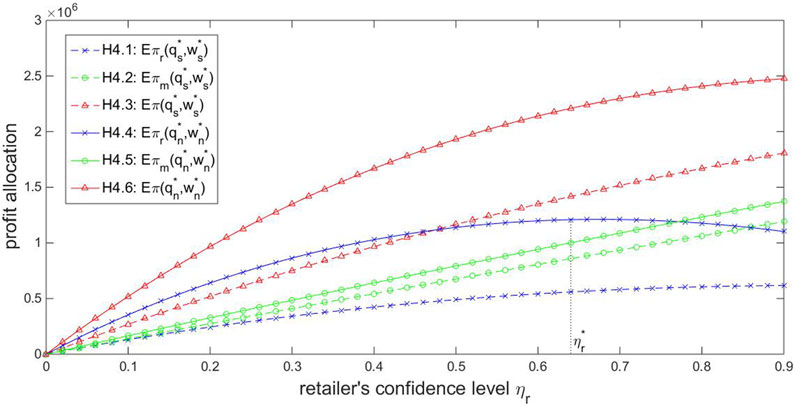
Based on these results, we next tried to compare the effect of the retailer’s risk attitude on the system profit allocation under different negotiation frameworks. Given $Y=40000$, ${\eta }_m=0.9$, and $\omega =0.4$, we can see in Figure 4 that the profits of the retailer, the manufacturer, and the entire system under the Stackelberg game all increase according to the retailer’s confidence level ${\eta }_r$. Recalling Proposition 3.1, a retailer’s higher confidence level enlarges the equilibrium order quantity and further leads to a higher profit for the entire system, according to the proof of Theorem 4.3. Proposition 3.2 indicates that a higher ${\eta }_r$ reduces the retailer’s profit share while increasing the manufacturer’s. Thus, as ${\eta }_r$ increases, the manufacturer’s profit will be augmented because both the supply chain’s total profit and the manufacturer’s profit share increase simultaneously. For the retailer, when ${\eta }_r$ increases, although her profit share is reduced, she gains more from the system profit increase. Thus, the retailer’s profit also increases in ${\eta }_r$, but the growth rate is lower than the manufacturer’s. Figure 4 also shows that both the manufacturer’s and the entire system’s profits under the NBF framework increase in connection with the retailer’s confidence level ${\eta }_r$. Recalling Proposition 4.1, a retailer’s higher confidence level enlarges the equilibrium order quantity and further leads to a higher profit for the entire system according to the proof of Theorem 4.3. Proposition 4.3 indicates that a higher ${\eta }_r$ reduces the retailer’s profit share while increasing the manufacturer’s. Thus, as ${\eta }_r$ increases, the manufacturer’s profit will be enhanced because both the supply chain’s total profit and the manufacturer’s profit share increase simultaneously. For the retailer, the effect of ${\eta }_r$ under the NBF framework is very different from that under the Stackelberg game. Under the NBF equilibrium, if the manufacturer’s confidence level is determined, an optimal confidence level exists for the retailer to maximize her profit (${\eta }_r^{*}$ marked in Figure 4). If ${\eta }_r<{\eta }_r^{*}$, when ${\eta }_r$ increases, although the retailer’s profit share is reduced, she benefits more from the system profit increase and her profit also increases. If ${\eta }_r>{\eta }_r^{*}$, when ${\eta }_r$ increases, the retailer’s profit share is reduced, and she cannot gain sufficiently from the system profit increase, and therefore her profit decreases.

FIGURE 4

FIGURE 4. Impact of ${\eta }_r$ on the profit allocation ($Y=40000$; ${\eta }_m=0.9$; $\omega =0.4$).

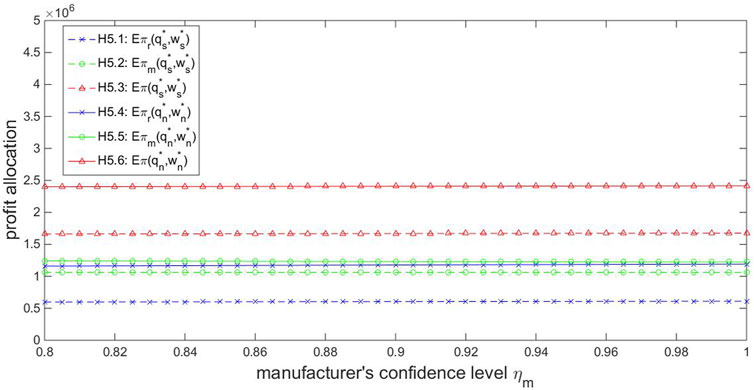
Then we paid attention to the effect of the manufacturer’s risk attitude. Given $Y=40000$, ${\eta }_r=0.8$, and $\omega =0.4$, Figure 5 shows how the profits of the retailer, the manufacturer, and the entire system vary in connection with the manufacturer’s confidence level ${\eta }_m$ under different negotiation frameworks. We can observe that the change of ${\eta }_m$ brings about a very slight influence on the profit allocation under either the Stackelberg game or the NBF framework. Recalling the reasonable model assumption $0<{\eta }_r<{\eta }_m\le 1$, note that the manufacturer’s confidence level is usually so high that each player’s profit under either negotiation framework is almost unaffected.

FIGURE 5

FIGURE 5. Impact of ${\eta }_m$ on the profit allocation ($Y=40000$; ${\eta }_r=0.8$; $\omega =0.4$).

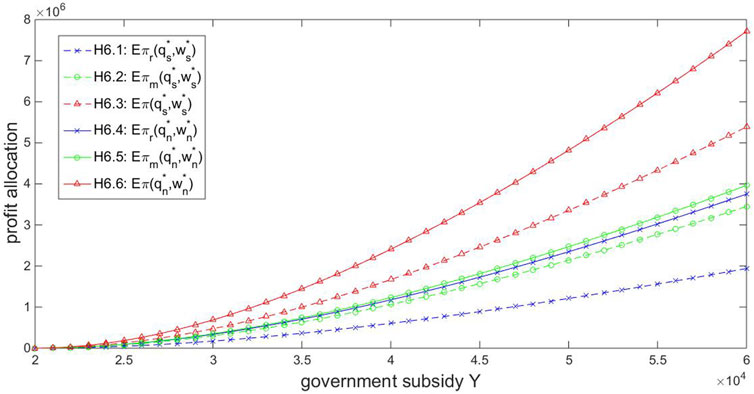
As a major characteristic of the NEV industry, the government subsidy plays an important role in the system profit allocation. Given ${\eta }_r=0.8$, ${\eta }_m=0.9$, and $\omega =0.4$, Figure 6 shows the effect of $Y$ on the profit allocation under the Stackelberg game and the NBF framework. We can see that the effects of $Y$ on the profit allocation under the different negotiation frameworks are almost identical. An increase of $Y$ enhances the profits of the retailer, the manufacturer, and the entire system simultaneously. As a profit source outside the supply chain, the government subsidy always benefits both players and the entire system. Proposition 3.3 and Proposition 4.4 indicate that a higher $Y$ reduces the retailer’s profit share while increasing the manufacturer’s under both negotiation frameworks. Thus, as $Y$ increases, the manufacturer’s profit will be augmented because the supply chain’s total profit and the manufacturer’s profit share increase simultaneously. For the retailer, when $Y$ increases, although her profit share is reduced, she benefits more from the system profit increase. Thus, the retailer’s profit also increases in $Y$, but the growth rate is lower than the manufacturer’s.

FIGURE 6

FIGURE 6. Impact of $Y$ on the profit allocation (${\eta }_r=0.8$; ${\eta }_m=0.9$; $\omega =0.4$).

In practice, the government subsidy is decreasing continuously nowadays. Figure 6 shows that both players’ profits will be reduced as the subsidy diminishes. Since a lower $Y$ reduces the manufacturer’s profit share while increasing the retailer’s, we can know that the manufacturer will suffer more from the decreasing subsidy. We summarize such a conclusion as follows.

Observation 6.1. As the government subsidy decreases, both the manufacturer’s and the retailer’s profits are reduced. However, the manufacturer is more severely affected by the decreasing subsidy.

The diminishing subsidy shocks the manufacturer more seriously, and the epidemic further exacerbates this negative effect. Within the epidemic environment, China has delayed the NEV subsidy decrease, which has been more beneficial for the manufacturer. In addition, the government could support the NEV manufacturer in other aspects to enhance his bargaining power, or the manufacturer could share more of the subsidy, consequently, to help the manufacturer offset the subsidy decrease and the epidemic effect.

We can observe two important common points in Figures 4–6. One is that, under the Stackelberg equilibrium, the manufacturer always obtains a higher profit than the retailer. This is because the manufacturer acts as a leader while the retailer is a follower in the Stackelberg game. Based on the expectation about the retailer’s order quantity, the manufacturer can make the final decision about the wholesale price to maximize his CVaR performance. Thus, the manufacturer has an advantageous position and occupies a larger part of the system profit. The other common point in Figures 4–6 is that the retailer’s, the manufacturer’s and the entire system’s profits under the NBF framework are all higher than those under the Stackelberg game no matter how the relevant parameters vary. Thus, the superiority of the NBF framework for both NEV players is further verified. The noncooperative competition between the manufacturer and the retailer in the Stackelberg game is unbeneficial for their own profits and the entire system, while the cooperative NBF framework benefits both players as well as the entire system.

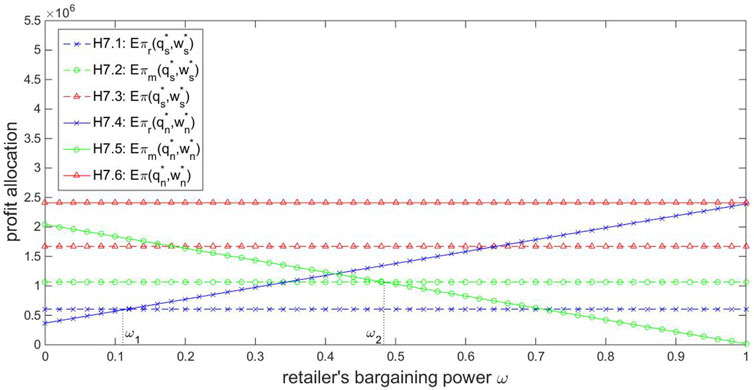
In regard to the effect of the bargaining power on the profit allocation under the NBF framework, Proposition 4.5 and related discussions pointed out that the players’ bargaining power contrast decides their profits obtained by affecting their profit shares. For further analysis, given $Y=40000$, ${\eta }_r=0.8$, and ${\eta }_m=0.9$, we provide Figure 7 to illustrate how the retailer’s, the manufacturer’s, and the entire system’s profits vary in connection with the retailer’s bargaining power $\omega$. As the comparison object, the profit allocation under the Stackelberg game, which has nothing to do with $\omega$, is also involved. We can observe in Figure 7 that, under the NBF framework, with the increase of $\omega$, the retailer’s profit is enlarged while the manufacturer’s profit is reduced, and the total profit of the supply chain stays invariant. Obviously, a higher degree of bargaining power brings about a higher profit for either player. However, if $\omega$ is lower than a certain level ${\omega }_1$ (marked in Figure 7), the retailer will obtain a lower profit under the NBF framework than the Stackelberg game and thus prefer to participate in the Stackelberg game. On the other hand, if $\omega$ exceeds a certain level ${\omega }_2$ (also marked in Figure 7), the manufacturer will obtain a lower profit under the NBF framework than the Stackelberg game and thus prefer to participate in the Stackelberg game. In other words, $\omega$ should fall within a certain scope $\left({\omega }_1,{\omega }_2\right)$ to ensure both players obtain higher profits under the NBF framework than the Stackelberg game and therefore choose to participate in the NBF procedure. Otherwise, either the manufacturer or the retailer will choose to participate in the Stackelberg game, which hurts the other player’s and the entire system’s profits. We summarized such an observation as follows, offering a principle on the bargaining power contrast between the two players to sustainably maintain the NEV manufacturer-retailer system under the superior NBF framework.

FIGURE 7

FIGURE 7. Impact of $\omega$ on the profit allocation ($Y=40000$; ${\eta }_r=0.8$; ${\eta }_m=0.9$).

Observation 6.2. In order to sustainably maintain the NEV manufacturer-retailer system under the superior NBF framework, the retailer’s bargaining power should fall within the scope $\left({\omega }_1,{\omega }_2\right)$.

6 Concluding remarks

In this paper, we investigated the negotiation problem in an NEV manufacturer-retailer system with the Stackelberg model and the NBF framework. Considering the impact of the COVID-19 epidemic, supposing that the NEV manufacturer and retailer are both risk-averse decision makers with the CVaR criterion, we derived the respective equilibriums about the order quantity and the wholesale price under different negotiation frameworks. We then evaluated the two players’ profit shares and identified some elements affecting the profit allocation. With numerical experiments, we further compared the effects of these elements on the equilibrium order quantity and the system profit allocation under the two negotiation frameworks.

Under the Stackelberg equilibrium with the manufacturer as the leader, for either player, the increase of his/her risk aversion degree can lead to a higher profit share for him/her. That means the players’ risk attitudes can change their relative powers. With the consideration of the epidemic, a more sensitive player’s risk aversion degree is enlarged more, which, in turn, leads to a larger profit share increase for that player. However, because the decrease of either player’s risk aversion degree creates a higher profit for the entire system, the corresponding numerical experiments showed that both players can finally obtain higher profits when either of them becomes less risk averse (the effect of the manufacturer’s risk aversion degree is very slight). As an outside element, the government subsidy ensures that both players obtain positive profits no matter how it is shared between the players. Moreover, the subsidy can also affect the players’ relative powers. A subsidy increase results in a higher profit share for the manufacturer and a lower share for the retailer. However, since the subsidy increase brings about a higher profit for the entire system, the corresponding numerical experiment shows that both players can benefit from the subsidy increase.

Under the NBF equilibrium, just like in the Stackelberg case, the increase of a player’s risk aversion degree can lead to a higher profit share for him/her. The players’ risk attitudes can also change their relative powers under the NBF framework, while the effect of the epidemic remains the same as in the Stackelberg game. However, because the increase of either player’s risk aversion degree results in a lower profit for the entire system, a more risk-averse player perhaps cannot obtain a higher profit even though his/her profit share is enhanced. Actually, the corresponding numerical experiment demonstrated that when the manufacturer’s confidence level is determined, an optimal confidence level exists for the retailer to maximize her profit. When the retailer’s confidence level is determined, the manufacturer’s risk attitude plays an insignificant role in affecting the profit allocation. When both players’ risk attitudes are determined, the profit allocation depends on the bargaining power contrast between them. Greater bargaining power signifies a higher profit share and a larger profit for either player. The effect of the government subsidy on the profit allocation under the NBF equilibrium is the same as that under the Stackelberg case. The increase of the subsidy results in a higher profit share and a larger profit for the manufacturer. The retailer can also benefit from the subsidy increase, though her profit share is reduced. Considering the role of the government subsidy in the system profit allocation, the government can preferentially support the manufacturer/retailer by adjusting the subsidy to a higher/lower level to alter players’ relative powers and profit shares. Within the epidemic environment, the manufacturer will suffer a more unfavorable effect from the subsidy degeneration that is happening nowadays and needs more government support.

Comparing the equilibrium solutions under the Stackelberg game and the NBF framework, we find that the retailer will order more NEVs and the manufacturer-retailer system will obtain a higher profit in the NBF case. With the overall consideration of the system, no matter how relevant parameters and the epidemic situation vary, the NBF framework is always beneficial for promoting NEV sales and enhancing system profit. Thus, we can conclude that the NBF framework is superior to the Stackelberg game for the NEV manufacturer-retailer system in terms of both quantity of sales and profit. Numerical experiments further demonstrated that the NBF framework is superior for either NEV player no matter how the players’ risk attitudes and the government subsidy vary. The corresponding numerical experiment indicated that, only if the bargaining power contrast between players is restricted in a certain scope, both players can obtain higher profits under the NBF framework compared to the Stackelberg game. The findings may provide guidelines to maintain the sustainability of the NEV manufacturer-retailer system under the superior NBF framework within the epidemic environment.

By incorporating the risk aversion effect with the CVaR criterion, our investigation enriches the research on the negotiation mechanism in an NEV manufacturer-retailer system. By exploring the effects of some significant elements on the equilibrium order quantity and the system profit allocation under different negotiation frameworks, we have proved the superiority of the NBF framework and offered some guiding principles for the NEV win-win cooperation between the manufacturer and the retailer, which may help to promote the sustainable development of NEV commerce within the epidemic environment.

From the perspective of the NEV industry practice, the following policy suggestions or countermeasures are put forward. ①The risk aversion degree of either the NEV manufacturer or retailer has been increased by the shock of the COVID-19 epidemic, thus the government subsidy degeneration should be appropriately delayed and the policy stability should be maintained. ②The subsidy degeneration can be continued when the COVID-19 epidemic dissipates, but subsidy policies should be adapted to local conditions, and local government subsidy can be used to improve the market vitality in certain areas which are severely affected by the COVID-19 epidemic. ③The subsidy sharing proportion should be appropriately tilted to the manufacturer, which helps to alleviate the larger pressure on the manufacturer raised by the subsidy degeneration and the COVID-19 epidemic and stimulate the vitality of the entire NEV market, but at the same time, the overall balance of the manufacturer-retailer system must be taken into account.

Although the COVID-19 epidemic has gradually subsided, the proposed NEV negotiation model under the CVaR criterion and corresponding results still have reference significance for the equilibrium and profit allocation between the risk-averse NEV retailer and manufacturer under special situations in the future. However, many questions remain unanswered. For example, we use the confidence level in the CVaR model to explain the epidemic effect, which yielded that the epidemic effect is not very conspicuous. In future work, our research direction is to involve an epidemic correction factor and extend the model to a case in which the market demand is influenced by an endogenous price or the retailer’s sales effort. Additionally, based on the investigation on the NEV single-channel supply chain in this paper, we are also interested in the negotiation mechanism of an NEV dual-channel supply chain (traditional retail channel and online channel). China’s NEV market has developed rapidly in recent years, but after the subsidy decline, the negotiation equilibrium and profit allocation between the NEV retailer and manufacturer will change accordingly, which is also worth further exploration.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

SH: Formal Analysis, Funding acquisition, Investigation, Methodology, Writing–original draft. YC: Data curation, Software, Validation, Writing–review and editing.

Funding

The authors declare financial support was received for the research, authorship, and/or publication of this article. This study is supported by the Social Science Foundation of Fujian Province (FJ2021C076), the Natural Science Foundation of Fujian Province (2022J05255), the Science and Technology Planning Project of Putian City (2021R4001ptxy11), and the Talent Introduction Project of Putian University (2020007 and 2019018).

Acknowledgments

The authors thank the reviewers and the editors for their helpful comments.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2023.1286381/full#supplementary-material

References

Achtnicht, M. (2012). German car buyers’ willingness to pay to reduce CO2 emissions. Clim. Change 113, 679–697. doi:10.1007/s10584-011-0362-8

CrossRef Full Text | Google Scholar

Agrawal, V., and Seshadri, S. (2000). Impact of uncertainty and risk aversion on price and order quantity in the newsvendor problem. Manuf. Serv. Operations Manag. 2 (4), 410–423. doi:10.1287/msom.2.4.410.12339

CrossRef Full Text | Google Scholar

Ahmed, N., Khan, D., Oláh, J., and Popp, J. (2023). A comparative study of the policy response to COVID-19 in the ASEAN region: a dynamic simulated ARDL approach. PLoS ONE 18 (1), e0276973. doi:10.1371/journal.pone.0276973

PubMed Abstract | CrossRef Full Text | Google Scholar

Ahmed, S., Cakmak, U., and Shapiro, A. (2007). Coherent risk measures in inventory problems. Eur. J. Operational Res. 182, 226–238. doi:10.1016/j.ejor.2006.07.016

CrossRef Full Text | Google Scholar

Artzner, P., Delbaen, F., Eber, J. M., and Heath, D. (1999). Coherent measures of risk. Math. Finance 9 (3), 203–228. doi:10.1111/1467-9965.00068

CrossRef Full Text | Google Scholar

Bapna, R., Thakur, L. S., and Nair, S. K. (2002). Infrastructure development for conversion to environmentally friendly fuel. Eur. J. Operational Res. 142 (3), 480–496. doi:10.1016/s0377-2217(01)00309-5

CrossRef Full Text | Google Scholar

Bernstein, F., and Marx, L. M. (2006). Reservation profit levels and the division of supply chain profit. Working paper.

Google Scholar

Buzacott, J., Yan, H., and Zhang, H. (2011). Risk analysis of commitment-option contracts with forecast updates. IIE Trans. 43 (6), 415–431. doi:10.1080/0740817x.2010.532851

CrossRef Full Text | Google Scholar

Chen, F., and Federgruen, A. (2001). Mean-variance analysis of basic inventory models. Working paper. New York: Graduate School of Business, Columbia University.

Google Scholar

Chen, F., Xu, M., and Zhang, G. (2009). Technical note—a risk-averse newsvendor model under the CVaR criterion. Operations Res. 57, 1040–1044. doi:10.1287/opre.1080.0603

CrossRef Full Text | Google Scholar

Chen, J., Zhang, H., and Sun, Y. (2012). Implementing coordination contracts in a manufacturer Stackelberg dual-channel supply chain. Omega 40 (5), 571–583. doi:10.1016/j.omega.2011.11.005

CrossRef Full Text | Google Scholar

Chen, Q. (2020). Short-term downturn, severe throughout the year, the new energy vehicle market is a “ground covered with chicken feathers”? (in Chinese). Automobile & Parts, 44. 06.

Google Scholar

Chen, X., Sim, M., Simchi-Levi, D., and Peng, S. (2007). Risk aversion in inventory management. Operations Res. 55, 828–842. doi:10.1287/opre.1070.0429

CrossRef Full Text | Google Scholar

Cheng, L., Wan, Z. P., and Wang, G. M. (2009). Bilevel newsvendor models considering retailer with CVaR objective. Comput. Industrial Eng. 57, 310–318. doi:10.1016/j.cie.2008.12.002

CrossRef Full Text | Google Scholar

China Association of Automobile Manufactures (CAAM) (2018). The economic operation of the automobile industry in 2017. Putrajaya, Malaysia: CAAM.

Google Scholar

Choi, S., and Ruszczyński, A. (2008). A risk-averse newsvendor with law invariant coherent measures of risk. Operations Res. Lett. 36, 77–82. doi:10.1016/j.orl.2007.04.008

CrossRef Full Text | Google Scholar

Das Roy, M., and Sana, S. S. (2021). Multi-echelon green supply chain model with random defectives, remanufacturing and rework under setup cost reduction and variable transportation cost. Sadhana Acad. Proc. Eng. Sci. 46 (4), 211–218. doi:10.1007/s12046-021-01716-y

CrossRef Full Text | Google Scholar

Eeckhoudt, L., Gollier, C., and Schlesinger, H. (1995). The risk-averse (and prudent) newsboy. Manag. Sci. 41, 786–794. doi:10.1287/mnsc.41.5.786

CrossRef Full Text | Google Scholar

Ertogral, K., and Wu, S. D. (2001). A bargaining game for supply chain contracting. Preprint Available at: https://engineering.lehigh.edu/sites/engineering.lehigh.edu/files/_DEPARTMENTS/ise/pdf/tech-papers/01/01t_002.pdf.

Google Scholar

European Environment Agency (EEA) (2009). Annual European Community greenhouse gas inventory 1990-2007 and inventory report. European Union: EEA.

Google Scholar

Fisher, M., and Raman, A. (1996). Reducing the cost of demand uncertainty through accurate response to early sales. Operations Res. 44 (1), 87–99. doi:10.1287/opre.44.1.87

CrossRef Full Text | Google Scholar

Gang, X., Wang, S., and Lai, K. K. (2011). Quality investment and price decision in a risk-averse supply chain. Eur. J. Operational Res. 214 (2), 403–410. doi:10.1016/j.ejor.2011.04.036

CrossRef Full Text | Google Scholar

Gotoh, J., and Takano, Y. (2007). Newsvendor solutions via conditional Value-at-Risk minimization. Eur. J. Operational Res. 179, 80–96. doi:10.1016/j.ejor.2006.03.022

CrossRef Full Text | Google Scholar

Gu, H., Liu, Z., and Qing, Q. (2017). Optimal electric vehicle production strategy under subsidy and battery recycling. Energy Policy 109, 579–589. doi:10.1016/j.enpol.2017.07.043

CrossRef Full Text | Google Scholar

Gurnani, H., and Shi, M. (2006). A bargaining model for a first-time interaction under asymmetric beliefs of supply reliability. Manag. Sci. 52 (6), 865–880. doi:10.1287/mnsc.1050.0498

CrossRef Full Text | Google Scholar

Han, S., and Xu, X. (2018). NEV supply chain coordination and sustainability considering sales effort and risk aversion under the CVaR criterion. PLoS ONE 13 (6), e0199005. doi:10.1371/journal.pone.0199005

PubMed Abstract | CrossRef Full Text | Google Scholar

He, J., Ma, C., and Pan, K. (2017). Capacity investment in supply chain with risk-averse supplier under risk diversification contract. Transp. Res. Part E Logist. Transp. Rev. 106, 255–275. doi:10.1016/j.tre.2017.08.005

CrossRef Full Text | Google Scholar

Hua, M., Tang, H., and Lai, I. K. W. (2017). Game theoretic analysis of pricing and cooperative advertising in a reverse supply chain for unwanted medications in households. Sustainability 9 (10), 1902. doi:10.3390/su9101902

CrossRef Full Text | Google Scholar

Hua, Z., Li, S., and Liang, L. (2006). Impact of demand uncertainty on supply chain cooperation of single-period products. Int. J. Prod. Econ. 100 (2), 268–284. doi:10.1016/j.ijpe.2004.11.007

CrossRef Full Text | Google Scholar

Huang, Z. (2020). Impact and Forecast on the Auto Industry under the Epidemic (in Chinese). Auto Time (03), 20–21.

Google Scholar

Jorion, P. (1997). Value at Risk. vol. xiii. Chicago: Irwin.

Google Scholar

Katok, E., and Wu, D. Y. (2009). Contracting in supply chains: a laboratory investigation. Manag. Sci. 55 (12), 1953–1968. doi:10.1287/mnsc.1090.1089

CrossRef Full Text | Google Scholar

Khan, D., Ahmed, N., Mehmed, B., and Haq, I. u. (2021). Assessing the impact of policy measures in reducing the COVID-19 pandemic: a case study of south asia. Sustainability 13, 11315. doi:10.3390/su132011315

CrossRef Full Text | Google Scholar

Khouja, M. (1999). The single-period (news-vendor) problem: literature review and suggestions for future research. Omega 27 (5), 537–553. doi:10.1016/s0305-0483(99)00017-1

CrossRef Full Text | Google Scholar

Li, B., Chen, P., Li, Q., and Wang, W. (2014). Dual-channel supply chain pricing decisions with a risk-averse retailer. Int. J. Prod. Res. 52 (23), 7132–7147. doi:10.1080/00207543.2014.939235

CrossRef Full Text | Google Scholar

Li, Q. (2020). Economic development and reaction under the background of COVID-19 epidemic situation: based on the theory of economic resilience (in Chinese). Finance Econ. (04), 70–79.

Google Scholar

Liu, C., Huang, W., and Yang, C. (2017). The evolutionary dynamics of China’s electric vehicle industry-taxes vs. subsidies. Comput. Industrial Eng. 113, 103–122. doi:10.1016/j.cie.2017.08.026

CrossRef Full Text | Google Scholar

Liu, H. (2020). The impact of the slump in crude oil prices on the reform of new energy vehicles (in Chinese). People's Transp. (04), 34–37.

Google Scholar

Luo, C., Leng, M., Huang, J., and Liang, L. (2014). Supply chain analysis under a price-discount incentive scheme for electric vehicles. Eur. J. Operational Res. 235 (1), 329–333. doi:10.1016/j.ejor.2013.11.021

CrossRef Full Text | Google Scholar

Luo, Z., Wang, J., and Chen, W. (2015). A risk-averse newsvendor model with limited capacity and outsourcing under the CVaR criterion. J. Syst. Sci. Syst. Eng. 24 (1), 49–67. doi:10.1007/s11518-015-5263-3

CrossRef Full Text | Google Scholar

Ma, L., Liu, F. M., Li, S. J., and Yan, H. (2012). Channel bargaining with risk-averse retailer. Int. J. Prod. Econ. 139, 155–167. doi:10.1016/j.ijpe.2010.08.016

CrossRef Full Text | Google Scholar

Markowitz, H. (1959). “Portfolio selection: efficient diversification of investment,” in Cowles foundation monograph 16 (New Haven, Connecticut: Yale University Press).

Google Scholar

Mieghem, J. A. V. (1999). Coordinating investment, production, and subcontracting. Manag. Sci. 45 (7), 954–971. doi:10.1287/mnsc.45.7.954

CrossRef Full Text | Google Scholar

Nagarajan, M., and Bassok, Y. (2008). A bargaining framework in supply chains: the assembly problem. Manag. Sci. 54 (8), 1482–1496. doi:10.1287/mnsc.1080.0880

CrossRef Full Text | Google Scholar

Nagarajan, M., and Sosic, G. (2008). Game-theoretic analysis of cooperation among supply chain agents: review and extensions. Eur. J. Operational Res. 187 (3), 719–745. doi:10.1016/j.ejor.2006.05.045

CrossRef Full Text | Google Scholar

National Health Commission (2022). Novel coronavirus diagnosis and treatment protocol for pneumonia (trial version 9) (in Chinese). Beijing: Office of the National Health Commission.

Google Scholar

Plambeck, E. L., and Taylor, T. A. (2007a). Implications of breach remedy and renegotiation design for innovation and capacity. Manag. Sci. 53 (12), 1859–1871. doi:10.1287/mnsc.1070.0730

CrossRef Full Text | Google Scholar

Plambeck, E. L., and Taylor, T. A. (2007b). Implications of renegotiation for optimal contract flexibility and investment. Manag. Sci. 53 (12), 1872–1886. doi:10.1287/mnsc.1070.0731

CrossRef Full Text | Google Scholar

Qin, Y., Wang, R. X., Vakharia, A. J., Chen, Y. W., and Seref, M. M. H. (2011). The newsvendor problem: review and directions for future research. Eur. J. Operational Res. 213 (2), 361–374. doi:10.1016/j.ejor.2010.11.024

CrossRef Full Text | Google Scholar

Rockafellar, R. T., and Uryasev, S. (2000). Optimization of conditional value-at-risk. J. Risk 2, 21–41. doi:10.21314/jor.2000.038

CrossRef Full Text | Google Scholar

Rockafellar, R. T., and Uryasev, S. (2002). Conditional value-at-risk for general loss distributions. J. Bank. Finance 26 (7), 1443–1471. doi:10.1016/s0378-4266(02)00271-6

CrossRef Full Text | Google Scholar

Sana, S. S. (2020). Price competition between green and non green products under corporate social responsible firm. J. Retail. Consumer Serv. 55, 102118. doi:10.1016/j.jretconser.2020.102118

CrossRef Full Text | Google Scholar

Sana, S. S. (2022a). A structural mathematical model on two echelon supply chain system. Ann. Operations Res. 315 (2), 1997–2025. doi:10.1007/s10479-020-03895-z

CrossRef Full Text | Google Scholar

Sana, S. S. (2022b). Sale through dual channel retailing system - a mathematical approach. Sustain. Anal. Model. 2, 100008. doi:10.1016/j.samod.2022.100008

CrossRef Full Text | Google Scholar

Sana, S. S. (2022c). Optimum buffer stock during preventive maintenance in an imperfect production system. Math. Methods Appl. Sci. 45 (15), 8928–8939. doi:10.1002/mma.8246

CrossRef Full Text | Google Scholar

Sana, S. S., Jose, F. C., Andres, Q., and Amaya, R. (2018). A system dynamics model of financial flow in supply chains: a case study. Rairo Operations Res. 52 (1), 187–204. doi:10.1051/ro/2017025

CrossRef Full Text | Google Scholar

Shao, L., Yang, J., and Zhang, M. (2017). Subsidy scheme or price discount scheme? Mass adoption of electric vehicles under different market structures. Eur. J. Operational Res. 262 (3), 1181–1195. doi:10.1016/j.ejor.2017.04.030

CrossRef Full Text | Google Scholar

Shen, Y. W., Xie, J. X., and Li, T. T. (2016). The risk-averse newsvendor game with competition on demand. J. Industrial Manag. Optim. 12 (3), 931–947. doi:10.3934/jimo.2016.12.931

CrossRef Full Text | Google Scholar

Song, H., and Gao, X. (2018). Green supply chain game model and analysis under revenue-sharing contract. J. Clean. Prod. 170, 183–192. doi:10.1016/j.jclepro.2017.09.138

CrossRef Full Text | Google Scholar

Wang, H. (2020a). Analysis of the impact of the COVID-19 epidemic on shanghai's new energy and smart vehicles (in Chinese). Auto. Time (04), 41–42.

Google Scholar

Wang, N., Pan, H., and Zheng, W. (2017). Assessment of the incentives on electric vehicle promotion in China. Transp. Res. Part A Policy & Pract. 101, 177–189. doi:10.1016/j.tra.2017.04.037

CrossRef Full Text | Google Scholar

Wang, Y. (2020b). Impact of COVID-19 epidemic on China's oil industry from a global perspective (in Chinese). Sino-Global Energy. 25 (03), 1–5.

Google Scholar

Wu, D. (2013). Coordination of competing supply chains with news-vendor and buyback contract. Int. J. Prod. Econ. 144 (1), 1–13. doi:10.1016/j.ijpe.2011.11.032

CrossRef Full Text | Google Scholar

Wu, M., Zhu, S. X., and Teunter, R. H. (2014). A risk-averse competitive newsvendor problem under the CVaR criterion. Int. J. Prod. Econ. 156, 13–23. doi:10.1016/j.ijpe.2014.05.009

CrossRef Full Text | Google Scholar

Xu, M. H. (2010). A price-setting newsvendor model under CVaR decision criterion with emergency procurement. J. Syst. Sci. Syst. Eng. 19 (1), 85–104. doi:10.1007/s11518-010-5129-7

CrossRef Full Text | Google Scholar

Xu, M. H., and Li, J. B. (2010). Optimal decisions when balancing expected profit and conditional value-at-risk in newsvendor models. J. Syst. Sci. Complex. 23 (6), 1054–1070. doi:10.1007/s11424-010-7116-y

CrossRef Full Text | Google Scholar

Xu, X., Meng, Z., Ji, P., Dang, C., and Wang, H. (2016). On the newsvendor model with conditional Value-at-Risk of opportunity loss. Int. J. Prod. Res. 54 (8), 2449–2458. doi:10.1080/00207543.2015.1100765

CrossRef Full Text | Google Scholar

Xue, M., and Sha, X. (2020). The impact of COVID-19 on China’s economy and its response (in Chinese). China Econ. Trade Guide (04), 4–5.

Google Scholar

Xue, W., Ma, L., and Shen, H. (2015). Optimal inventory and hedging decisions with CVaR consideration. Int. J. Prod. Econ. 162, 70–82. doi:10.1016/j.ijpe.2015.01.011

CrossRef Full Text | Google Scholar

Ye, F., Li, Y., and Yang, Q. (2018). Designing coordination contract for biofuel supply chain in China. Resour. Conservation Recycl. 128, 306–314. doi:10.1016/j.resconrec.2016.11.023

CrossRef Full Text | Google Scholar

Zhang, X. (2014). Reference-dependent electric vehicle production strategy considering subsidies and consumer trade-offs. Energy Policy 67 (2), 422–430. doi:10.1016/j.enpol.2013.12.028

CrossRef Full Text | Google Scholar

Zhang, X., and Bai, X. (2017). Incentive policies from 2006 to 2016 and new energy vehicle adoption in 2010–2020 in China. Renew. Sustain. Energy Rev. 70, 24–43. doi:10.1016/j.rser.2016.11.211

CrossRef Full Text | Google Scholar

Zheng, J., Fu, Y., and Tao, J. (2020). Impact of the COVID-19 epidemic on consumption economy and countermeasures analysis (in Chinese). Consum. Econ. 36 (2), 3–9.

Google Scholar

Nomenclature

For the readers’ convenience, we provide a nomenclature to show the notations throughout this paper.