Research on optimal configuration of park-level multi-energy complementary system with multiple evaluation indexes

At present, energy shortages are becoming increasingly severe, and the concept of park level multi energy complementary systems (MECS) has provided direction for sustainable energy development. In recent years, how to improve the economy and reliability of multi energy complementary systems has become a research hotspot in this field. In this paper, a two-layer optimal scheduling strategy is proposed to allocate the capacity of various energy equipment in the park, considering the comprehensive energy self-sufficiency rate, comprehensive energy utilization rate and energy shortage expectation. The proposed capacity allocation scheme can effectively improve the economy of MECS in the park. Finally, the effectiveness and practicability of the algorithm are verified by simulation analysis.

1 Introduction

In recent years, there has been a significant shift in the global energy landscape towards renewable and sustainable energy, which has given rise to the concept of a MECS that integrates various renewable energy, storage technologies, and energy management strategies to improve the efficiency and reliability of the overall system (Zheng et al., 2019; Deng et al., 2021; Weizhen et al., 2021; Qian et al., 2022). As the deployment of such systems expands, optimizing their configuration becomes crucial for maximizing their benefits. A key challenge in optimizing MECS is to evaluate their performance using multiple metrics. Traditional single indicator optimization methods often fail to capture the complex interdependence between various system components and their impact on different evaluation criteria (Liu et al., 2020a; Miguel and Ren, 2021; Liu et al., 2022a; Yang et al., 2022). Therefore, it is imperative to develop a comprehensive optimization method that considers multiple evaluation indicators simultaneously (Xu et al., 2020a; Zhang et al., 2021a; Liu et al., 2021).

In recent years, many scholars have conducted research on the optimization scheduling problem of park level MECS. In reference (Wang et al., 2021a), a coordinated optimization framework for the world’s largest multi energy complementary base and MECS in the upper reaches of the Yellow River was proposed, which combines a long-term optimal operation model with a short-term optimal operation model to determine the proportion of multiple energies and optimize the maximum peak shaving capacity; Using the large-scale system decomposition and coordination method to solve the proposed two-level operational model. In reference (Yin et al., 2021), a risk constrained stochastic scheduling model was proposed to utilize the potential scheduling capabilities of multi energy systems, while maintaining the level of system operational risk, to seek solutions for economic operation in response to uncertain renewable energy generation. In reference (Mao et al., 2021), a cooperative operation framework model for a wind solar combined cycle multi energy system was studied. Describing the optimal operation scheduling problem of multi energy systems as a Nash bargaining optimization problem, rather than traditional non cooperative solution based methods, and solving it through the alternating direction multiplier method. In reference (Wang et al., 2020), in order to obtain the minimum operating cost, an operational optimization model was established and the moth flame optimization algorithm was used to optimize the schedule of each unit in the hybrid energy system. In reference (Xu et al., 2020b), an iterative solution was developed to arrange multiple energy conversion and storage devices within the hub to efficiently utilize available hybrid solar wind renewable energy. In reference (Wang et al., 2021b), an optimal scheduling model was proposed for wind power, photovoltaic, hydropower, thermal power, and outsourced power generation systems, with the minimum economic cost of thermal power generation as the objective function, including a complementary system of wind power, photovoltaic, hydropower, and thermal outsourced power. In reference (Zhang et al., 2023a), an energy hub (EH) model including energy storage systems and integrated electric vehicles (EVs) was established. Based on this model, the impact of the pollutant trading market on total operating costs was analyzed, and further optimization scheduling strategies were proposed to achieve the minimum purchase cost and emission tax cost of MES. In reference (Zhang et al., 2023a), a multi product optimal scheduling algorithm considering the complementarity of different hydrogen products is proposed to optimize the scheduling factors of the energy hub system and achieve Profit maximization within the limited resource range. In reference (An et al., 2020), an optimization scheduling model was established with the goal of minimizing output power fluctuations, considering multiple power supply constraints. In order to solve the problem of premature and slow convergence in the second half of Particle swarm optimization (PSO), a niche Particle swarm optimization method is proposed to determine the optimal solution of the model combined with the niche technology in evolution.

However, most of the references mentioned above only consider economic and carbon emission costs, without considering issues such as comprehensive energy utilization and self-sufficiency (Liu et al., 2020b; Zhang et al., 2020; Chen et al., 2021; Liu et al., 2022b; Ororbia and Warn, 2022; Zhang et al., 2022; Li et al., 2023). This study aims to address this urgent need and propose an innovative method for optimizing the configuration of park level MECS that considers multiple evaluation indicators. By doing so, we seek to identify the most effective and sustainable configurations that align with the overall goals of energy security, cost-effectiveness, environmental sustainability, and operational reliability (Yu-Kai et al., 2013; Liu and Mancarella, 2016; Qinglai et al., 2017; Du et al., 2020; Du and Li, 2020; Zhang et al., 2021b; Cai and Ying, 2021).

In order to achieve our research objectives, we will adopt a holistic perspective and consider the interaction of different energy, storage technologies, and energy management strategies within the framework of a multi energy park. This study will utilize advanced modeling and simulation techniques to analyze the dynamic behavior and interactions of different system components (Zhang et al., 2021c; Wang et al., 2022; Xue et al., 2022; Liu et al., 2023a; Liu et al., 2023b; Zhang et al., 2023b; Yang et al., 2023). On the basis of existing literature, this paper takes into account various needs such as economy, energy sustainability, efficiency, and reliability. Among them, economy and energy sustainability are represented by the comprehensive energy self-sufficiency rate, efficiency is represented by the comprehensive energy utilization rate, and reliability is represented by reliability indicators. By examining multiple indicators simultaneously, we can gain a more comprehensive understanding of system performance and determine the optimal configuration to achieve a balance between different evaluation criteria. The results of this study will provide valuable insights for policymakers, energy planners, and system operators to design and deploy future MECS at the park level. The research findings will help promote sustainable energy solutions and facilitate the transition to a low-carbon and resilient energy future.

In the following chapters, the specific arrangement is as follows: In Chapter 2, the overall architecture and equipment model of the park level MECS are introduced; In Chapter 3, three evaluation indicators and their mathematical models are introduced; In Chapter 4, the two-layer optimization model and algorithm used in this paper are introduced; In Chapters 5 and 6, corresponding conclusions were obtained through simulation analysis, proving the accuracy and practicality of the algorithm proposed in this paper.

2 Modeling of park level MECS

2.1 Structure of park level MECS

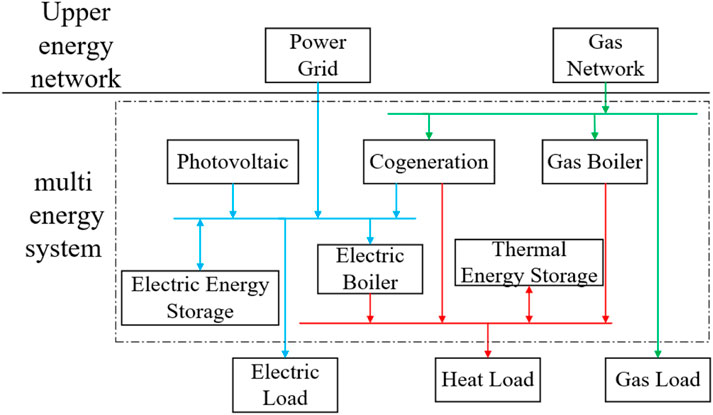
The park level MECS includes links such as energy production, conversion, and storage. This paper uses an energy hub model to describe the energy flow coupling relationship of the park’s comprehensive energy new system, and constructs a typical park level MECS structure as shown in Figure 1.

FIGURE 1

FIGURE 1. Structure of the Park’s MECS.

2.2 Model of energy equipment

2.2.1 Renewable energy power generation equipment model

Photovoltaic power generation is related to light intensity, and its output model is described as follows:

$P_{PV,t}=\left\{\begin{array}{c}\hfill {\alpha }_t{P}_{PV,N}/{\alpha }_{N}0\le {\alpha }_t<{\alpha }_N\hfill \\ \hfill P_{PV,N}{\alpha }_t\ge {\alpha }_N\hfill \end{array}\right.(1)$

where, P_PV,t represents the actual photovoltaic power during time t, P_PV,N represents the rated photovoltaic power, α_t represents the actual light intensity during time t, and α_N represents the rated light intensity.

2.2.2 Energy conversion equipment model

2.2.2.1 Cogeneration model

$P_{\mathit{CHP,t}}^e={\eta }_{\mathit{CHP}}^e{P}_{\mathit{CHP,t}}^g(2)$

$P_{CHP,t}^h={\eta }_{CHP}^h{P}_{CHP,t}^g(3)$

where, $P_{CHP,t}^e$ and $P_{CHP,t}^h$ respectively represent the electric power and thermal power generated by Cogeneration in period t, $P_{CHP,t}^g$ represents the natural gas power absorbed by Cogeneration in period t, and ${\eta }_{CHP}^e$ and ${\eta }_{CHP}^h$ respectively represent the power generation efficiency and heat generation efficiency of cogeneration.

2.2.2.2 Gas boiler model

$P_{GB,t}^h={\eta }_{GB}{P}_{GB,t}^g(4)$

where, $P_{GB,t}^h$ is the heat generation power of the gas boiler, η_GB is the heat generation efficiency of the gas boiler, and $P_{GB,t}^g$ is the natural gas consumption power of the gas boiler during time t.

2.2.2.3 Electric boiler model

$P_{EB,t}^h={\eta }_{EB}{P}_{EB,t}^e(5)$

where, $P_{EB,t}^h$ is the heat generation power of the electric boiler at time t, η_EB is the heat generation efficiency of the electric boiler, and $P_{EB,t}^e$ is the electrical power consumed by the electric boiler at time t.

2.2.3 Energy storage equipment model

2.2.3.1 Electric energy storage model

For electric energy storage equipment, the energy storage ratio during time t is related to the charging and discharging power during that time period and the energy storage state of charge during time t-1, specifically expressed as:

$S_{ES,t}=S_{ES,t-1}+P_{ES,t}^{+}{\eta }_{ES}^{+}\mathrm{\Delta }t-\frac{P_{ES,t}^{-}\mathrm{\Delta }t}{{\eta }_{ES}^{-}}(6)$

where, Δt is the optimized time interval, S_ES,t is the energy of electric energy storage equipment in t period, $P_{ES,t}^{+}$ and $P_{ES,t}^{-}$ are respectively the charging and discharging power of electric energy storage equipment in t period, and ${\eta }_{ES}^{+}$ and ${\eta }_{ES}^{-}$ are respectively the charging and discharging efficiency of electric energy storage equipment.

2.2.3.2 Thermal energy storage model

For thermal energy storage equipment, the energy storage ratio during time t is related to the storage and heat release power during that time period and the energy storage ratio during time t-1, specifically expressed as:

$S_{HS,t}=S_{HS,t-1}+P_{HS,t}^{+}{\eta }_{HS}^{+}\mathrm{\Delta }t-\frac{P_{HS,t}^{-}\mathrm{\Delta }t}{{\eta }_{HS}^{-}}(7)$

where, S_HS,t is the energy of thermal energy storage equipment in period t, and $P_{HS,t}^{+}\cdot$ and $\cdot P_{HS,t}^{-}$ are respectively the charging and discharging power of thermal energy storage equipment in period t, and ${\eta }_{HS}^{+}\cdot$ and $\cdot {\eta }_{HS}^{-}$ are respectively the charging and discharging efficiency of thermal energy storage equipment.

2.2.3.3 Photovoltaic system model

The output of photovoltaic power generation is related to light intensity, and its output model is specifically described as:

$P_{PV,t}=\left\{\begin{array}{c}\hfill P_{PV}^{\text{rated\hspace{0.17em}}}\frac{{\alpha }_t}{{\alpha }^{\text{rated\hspace{0.17em}}}}0\le {\alpha }_t\le {\alpha }^{\text{rated\hspace{0.17em}}}\hfill \\ \hfill P_{PV}^{\text{rated\hspace{0.17em}}}{\alpha }_t>{\alpha }^{\text{rated\hspace{0.17em}}}\hfill \end{array}\right.(8)$

where, P_PV,t is the actual power of the PV during period t, $P_{PV}^{\text{rated\hspace{0.17em}}}$ is the rated power of the PV, is the actual light intensity during period t, and α^rated is the rated light intensity.

3 Evaluation indicators for park level MECS

This article suggests evaluation indicators to assess the sustainability, efficiency, and reliability of the park’s MECS. The proposed indicators include the comprehensive energy self-sufficiency rate, comprehensive energy utilization rate, and energy shortage expectation.

3.1 Comprehensive energy self-sufficiency rate

The comprehensive energy self-sufficiency rate represents the proportion of renewable energy generated by the park’s MECS compared to the energy demanded by its users. A higher comprehensive energy self-sufficiency rate signifies a larger share of renewable energy utilized by the park’s MECS, leading to increased energy sustainability. This rate can be quantified as follows:

${\mu }_{CESR}=\frac{E_{\text{res}}}{E_e+\frac{E_h}{v_K}+v_{LHV}{E}_g}(9)$

where, μ_CESR represents the comprehensive energy self-sufficiency rate, E_e, E_h, and E_g represent the e electricity, heat, and natural gas output f from the MECS in the park, v_LHV representing the low calorific value of natural gas combustion, v_K represents the unit conversion coefficient of electricity and heat energy, and E_res represents the electricity produced by renewable energy equipment.

3.2 Comprehensive energy utilization rate

The comprehensive energy utilization rate serves as a crucial metric for assessing the operational efficiency of the park-level MECS. A higher comprehensive energy utilization rate implies reduced energy loss and improved operational efficiency of the system. This rate can be expressed as follows:

${\mu }_{\text{CEUR\hspace{0.17em}}}=\frac{E_{\mathrm{e}}+E_h/v_k+v_{Llv}{E}_g+E_e^s}{E_{\text{res\hspace{0.17em}}}+E_e^b+v_{LHV}{E}_g^b}(10)$

where, μ_CEUR is the comprehensive energy utilization rate, $E_e^b$ is the electricity purchased by the park level MECS from the superior power grid, $E_e^s$ is the electricity sold by the park level MECS from the superior power grid, and $E_{\mathrm{g}}^b$ is the natural gas purchased by the park level MECS from the superior natural gas grid.

3.3 Energy shortage expectations

The energy shortage expectation of Class β energy refers to the expected value of Class β energy shortage in the park energy internet, taking into account the probability of component failure in the event of N-1 failure of energy equipment. The energy shortage expectation of Class β energy is an important indicator to measure the reliability of the Internet supply of Class β energy in the park. The smaller the energy shortage expectation of Class β energy, the smaller the load of Class β energy that needs to be cut off in case of N-1 failure of energy equipment, and the higher the reliability of the Internet supply of Class β energy in the park.

4 Double layer optimization configuration model

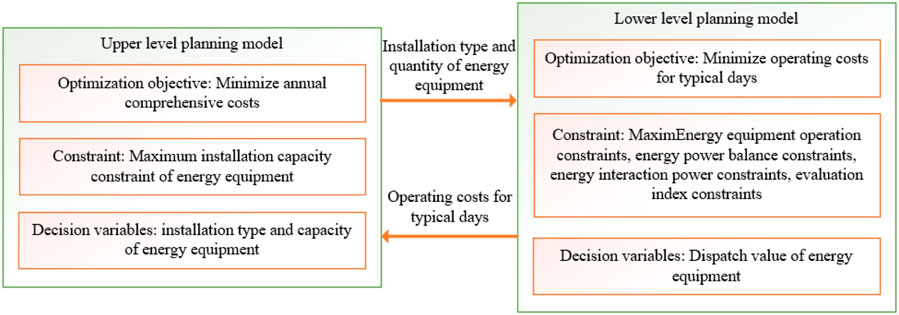
This paper takes into account the above evaluation indicators and constructs a two-layer optimization configuration model for the park level multi energy complementary system, as shown in Figure 2.

FIGURE 2

FIGURE 2. Dual layer optimization configuration model for park level MECS.

The upper level planning model takes minimizing the annual comprehensive cost as the optimization objective, and the decision variables are the installation type and quantity of energy equipment; the lower level planning model takes the minimization of typical daily operating costs as the optimization objective under specific types and quantities of energy equipment installation. The decision variable is the scheduling situation of energy equipment, and the operating costs are transmitted to the upper level to calculate the upper level objective function value.

4.1 Upper level planning model

The objective function of the upper level planning model is the annual comprehensive cost, expressed as

$\min C=C_{iwv}+365{\displaystyle \sum _{\mathrm{s}=1}^S}{p}_{\mathrm{s}}{C}_{op}(11)$

where, C is the annual comprehensive cost, C_inv is the equivalent annual investment cost of all equipment, p_s is the probability of the occurrence of typical day s, S is the total number of selected typical days, and C_op is the operating cost of the system under typical day s.

$C_{inv}={\displaystyle \sum _{\tau }}{\displaystyle \sum _k}{I}_{\tau k}{C}_{\tau }^{inv}{\eta }_{\tau }^{crf}(12)$

where, I_τk is the 0–1 logical variable indicating the installation status of the k τ class of energy equipment (including class i energy conversion equipment, class j energy storage equipment, and class 1 renewable energy equipment). When installing this equipment, I_τk = 1, otherwise $I_{\text{kk}}=0,C_{\tau }^{\text{inv\hspace{0.17em}}}$ are the investment cost of class energy equipment, and ${\eta }_{\tau }^{\text{crf\hspace{0.17em}}}$ is the equivalent annual fund recovery rate of class τ energy equipment. The specific description is as follows

${\eta }_{\mathrm{r}}^{crf}=\frac{r{\left(r+1\right)}^{y_r}}{{\left(r+1\right)}^{y_r}-1}(13)$

where, r is the discount factor, and y_r is the service life of Class τ energy equipment.

C_op specifically includes operation and maintenance costs C₁, fuel costs C₂, electricity trading costs C₃, carbon emissions tax C₄, and energy deficiency penalty costs C₅.

The specific description is as follows

$C_{op}=C_1+C_2+C_3+C_4+C_5(14)$

$\begin{array}{cc}\hfill C_1& ={\displaystyle \sum _i}{\displaystyle \sum _k}{\displaystyle \sum _t}{o}_i^{EC}{P}_{ik,t}^{in}+{\displaystyle \sum _j}{\displaystyle \sum _k}{\displaystyle \sum _t}{o}_j^{ES}\left(P_{jk,t}^{\mathit{dis}}+P_{jk,t}^{ch}\right)\hfill \\ \hfill & +{\displaystyle \sum _l}{\displaystyle \sum _k}{\displaystyle \sum _t}{o}_k^{\mathit{RES}}{P}_{lk,t}\hfill \end{array}(15)$

$C_2={\displaystyle \sum _t}{c}_t^{b,e}{P}_t^{b,e}\mathrm{\Delta }t-{\displaystyle \sum _t}{c}_t^{s,e}{P}_t^{s,e}\mathrm{\Delta }t(16)$

$C_4={\displaystyle \sum _t}{c}_c{a}_e{P}_t^{b,e}\mathrm{\Delta }t+{\displaystyle \sum _t}{c}_c{a}_g{P}_t^{b,g}\mathrm{\Delta }t(17)$

$C_5={\lambda }_e{E}_{EES}^e+{\lambda }_h{E}_{EES}^h(18)$

where, $P_{ik,t}^{in}$ is the input power of the kth i-class energy conversion device during the t period; $P_{jk,t}^{ch}$ and $P_{jk,t}^{dis}$ are the charging and discharging power of the kth class j energy storage equipment during the t period, respectively; P_lk,t s the output power of the kth Class 1 renewable energy equipment during the t period; $o_i^{EC},o_l^{RES}$ and are the operating and maintenance costs of Class I energy conversion equipment, Class J energy storage equipment, and Class I renewable energy equipment, respectively; $P_t^{b,e}\cdot P_t^{s,e}$ and $c_t^{b,e},c_t^{s,e}$ respectively represent the purchase/sale power and purchase/sale electricity price of the park’s energy internet and power grid during time $t;P_t^{b,g}$ is the gas purchasing power of the park’s energy internet during time t; c_fiel is the price of natural gas; a_e and a_g are the carbon emission coefficients of electricity and natural gas, respectively; c_c is the carbon tax price; λ_e and λ_h are the penalty costs for electrical and thermal load interruptions, respectively; $E_{EES}^e$ and $E_{EES}^h$ represent the expected shortfall in electrical and thermal energy, respectively.

4.2 Lower level planning model

The lower level planning model aims to minimize the operating cost of a typical daily park level MECS, specifically represented as

$\min C_{op}(19)$

In addition to meeting the operational constraints of the park level MECS, this paper also takes into account the constraints of the comprehensive energy self-sufficiency rate, utilization rate, and shortage expectations, which are as follows:

4.2.1 Energy and power balance constraints

The operation of a park level MECS requires maintaining a balance of energy power among electricity, heat, and natural gas, expressed as:

$\begin{array}{cc}\hfill & P_t^{b,e}-P_t^{s,e}+{\displaystyle \sum _l}{\displaystyle \sum _k}{P}_{lk,t}+{\displaystyle \sum _i}{\displaystyle \sum _k}{P}_{ik,t}^{out,e}\hfill \\ \hfill & ={\displaystyle \sum _i}{\displaystyle \sum _k}{P}_{ik,t}^{n,e}+{\displaystyle \sum _j}{\displaystyle \sum _k}{P}_{jk,t}^{chm,e}-{\displaystyle \sum _j}{\displaystyle \sum _k}{P}_{jk,t}^{dis,e}+P_t^{L,e}\hfill \end{array}(20)$

${\displaystyle \sum _i}{\displaystyle \sum _k}{P}_{ik,t}^{out,h}={\displaystyle \sum _j}{\displaystyle \sum _k}{P}_{jk,t}^{ch,h}-{\displaystyle \sum _j}{\displaystyle \sum _k}{P}_{jk,t}^{dis,h}+P_t^{L,h}(21)$

$P_t^{b,g}=P_t^{L,g}+{\displaystyle \sum _i}{\displaystyle \sum _k}{P}_{ik,t}^{in,g}(22)$

where, $P_{ik,t}^{\text{in,e\hspace{0.17em}}},P_{ik,t}^{in,g}$, and $P_{ik,t}^{\text{out,\hspace{0.17em}e},},P_{ik,t}^{\text{out\hspace{0.17em}},h}$ respectively represent the input power, natural gas power, output power, and thermal power of the kth class i energy conversion equipment during the t period; $P_{jk,t}^{dis,e}.P_{jk}^{ch,e},P_{jk,t}^{dis,g}$, and $P_{jk}^{ch,g}$ are the charging and discharging, and charging and discharging heat powers of the kth jth class energy storage equipment during the t period, respectively; $P_t^{L,e}.P_t^{L,h}$ and $P_t^{L,g}$ are the electricity, heat, and natural gas loads during time t.

4.2.2 Operational constraints of energy storage equipment

Energy storage equipment includes electrical energy storage equipment and thermal energy storage equipment. Energy storage devices can only supplement or release energy during the same period, and the power of charging and discharging energy is limited by the maximum power of charging and discharging energy and the current remaining capacity. The constraints it needs to meet are specifically expressed as:

$0\le P_{jk,t}^{ch}\le u_{jk,t}{P}_j^{\max }(23)$

$0\le P_{jk,t}^{dis}\le P_j^{\max }-u_{jk,t}{P}_j^{\max }(24)$

$S_{jk,0}=S_{jk,T}(25)$

$S_{jk}^{\min }\le S_{jk,t}\le S_{jk}^{\max }(26)$

where, $P_j^{\max }$ is the maximum charging and discharging energy power of the j-type energy storage device, S_jk,0 and S_jk,T are the energy stored by the kth j-type energy storage device during the initial and end optimization periods, respectively; $S_{jk}^{\max }$ and $S_{jk}^{\min }$ are the upper and lower limits of the energy stored by the kth j-type energy storage device, respectively; u_jk,t is a binary variable that represents the charging state of the kth j-type class energy storage device during the time period t. The charging state is u_jk,t = 1, otherwise u_jk,t = 0.

4.2.3 Operational constraints of energy conversion equipment

Energy conversion equipment includes cogeneration, gas boiler and electric bioler. The output of energy conversion equipment is limited by its own installed capacity, and the operation of energy conversion equipment is also constrained by climbing, specifically represented as:

$0\le P_{ik,t}^{in}\le I_{ik}{P}_i^{\text{rated\hspace{0.17em}}}(27)$

$-r_i\mathrm{\Delta }t\le P_{ik,t}^{in}-P_{ik,t-1}^{in}\le r_i\mathrm{\Delta }t(28)$

where, $P_i^{\text{rated\hspace{0.17em}}}$ is the Nameplate capacity of class i energy konversion equipment; r_i is the maximum climbing rate of Class I energy conversion equipment.

4.2.4 Energy reserve constraints

The backup constraints of energy conversion equipment are expressed as:

$\left\{\begin{array}{c}\hfill R_{ik,t}^{\beta }\le I_{ik}{P}_i^{\text{rated\hspace{0.17em}},\beta }-P_{ik,t}^{\beta }\hfill \\ \hfill 0\le R_{ik,t}^{\beta }\le I_{ik}{r}_i^{\beta }\hfill \end{array}\right.(29)$

where, $P_{ik,t}^{\beta }$ and $R_{ik,t}^{\beta }$ are the output power and backup power of the kth class i energy conversion equipment class energy during the t period, respectively; $P_i^{\text{rated,\hspace{0.17em}},\beta }$ provides the rated power of Class I energy conversion equipment for Class β energy.

The backup constraints of energy storage devices are expressed as:

$\left\{\begin{array}{c}\hfill R_{jk,t}\le I_{jk}{P}_j^{\max }{\eta }_j^{dis}+P_{jk}^{ch}-P_{jk}^{dis}\hfill \\ \hfill 0\le R_{jk,t}\le S_{jk,t}{\eta }_j^{dis}-S_{jk}^{\min }{\eta }_j^{dis}\hfill \end{array}\right.(30)$

where, $r_i^{\beta }$ is the maximum climbing rate of Class I energy conversion equipment providing Class I energy; ${\eta }_j^{\text{dis\hspace{0.17em}}}$ is the energy release efficiency of Class J energy storage equipment; R_jk,t is the backup power of the kth class j energy storage device during the t period.

4.2.5 Energy interaction power constraints

The interaction power between the park level MECS and the superior power grid, natural gas network, needs to meet certain constraints, and the interaction power during the same time period is unidirectional, specifically represented as:

$0\le P_t^{b,e}\le u_t^{b,e}{P}_{\max }^{b,e}(31)$

$0\le P_t^{s,e}\le P_{\max }^{s,e}-u_t^{b,e}{P}_{\max }^{s,e}(32)$

$0\le P_t^{b,g}\le P_{\max }^{b,g}(33)$

where, $P_{\max }^{b,g},P_{\max }^{b,e}$ and $P_{\max }^{s,e}$ respectively represent the maximum purchasing power rate of the energy internet in the park, the maximum purchasing and selling power with the upper power grid; The state variable of the park’s energy internet electricity purchase $u_t^{b,e}=1$ is the state variable of the park’s energy internet electricity purchase $u_t^{b,e}=0$

4.2.6 Constraints on comprehensive energy self-sufficiency rate

In order to meet the energy sustainability requirements of the park level MECS, the corresponding constraints are expressed as:

${\omega }_{CESR}\ge {\omega }_{CESR}^{\min }(34)$

where, ${\omega }_{CESR}^{\min }$ is the lower limit of the comprehensive energy self-sufficiency rate.

4.2.7 Constraints on comprehensive energy utilization rate

In order to achieve the required efficiency of the park level MECS, the corresponding constraints are expressed as:

${\omega }_{CEUR}\ge {\omega }_{CEUR}^{\min }(35)$

where, ${\omega }_{CEUR}^{\min }$ is the lower limit of the comprehensive energy utilization rate.

4.2.8 Energy deficiency expectation constraint

This paper considers the N-1 failure of energy equipment, and the probability of only energy equipment failure is

$p_{\gamma }^{\beta }=I_{\gamma }{p}_{\gamma }^{FR}\underset{{\gamma }^{\prime }\ne \gamma }{\mathrm{\Pi }}\left(1-I_{{\gamma }^{\prime }}{p}_{{\gamma }^{\prime }}^{FR}\right)\approx I_{\gamma }{p}_{\gamma }^{FR}(36)$

where, $p_{{\gamma }^{\prime }}^{FR}$ is the failure rate of the energy equipment γ′ (including the failed energy equipment); I_γ and I_γ′ are 0–1 logical variables that indicate the installation status of energy equipment and energy equipment E that have failed, respectively.

Introduce the binary logical variable ${\phi }_{\gamma ,t}^{\beta }$ to indicate whether there is an energy like power shortage. If there is a Class β energy power shortage, then ${\phi }_{\gamma ,t}^{\beta }=1$, otherwise ${\phi }_{\gamma ,t}^{\beta }=0$. ${\phi }_{\gamma ,t}^{\beta }$ satisfies the following constraints:

${\widehat{P}}_{\gamma ,t}^{\beta }=\left\{\begin{array}{cc}{P}_{\gamma ,t}^{\beta }-{\sum }_{{\gamma }^{\prime }\ne \gamma }{R}_{{\gamma }^{\prime },t}^{\beta }>0\hfill & {\phi }_{\gamma ,t}^{\beta }=1\hfill \\ P_{\gamma ,t}^{\beta }-{\sum }_{{\gamma }^{\prime }\ne \gamma }{R}_{{\gamma }^{\prime },t}^{\beta }\le 0\hfill & {\phi }_{\gamma ,t}^{\beta }=0\hfill \end{array}\right.(37)$

where, ${\widehat{P}}_{\gamma ,t}^{\beta }$ is the difference between the power provided by energy equipment β during time t when it interrupts to provide Class γ energy and the total backup power provided by all non faulty energy equipment for Class β energy; $P_{\gamma ,t}^{\beta }$ refers to the power of Class γ′ energy provided by the energy equipment F during the t period when it is interrupted; γ provides backup power for Class β energy for energy equipment H during time t.

When only energy equipment γ fails, the power shortage ${\widehat{P}}_{\gamma ,t}^{L,\beta }$ of Class β energy during time t is:

${\widehat{P}}_{\gamma ,t}^{L,\beta }={\phi }_{\gamma ,t}^{\beta }{\widehat{P}}_{\gamma ,t}^{\beta }(38)$

Considering

$-{\displaystyle \sum _{{\gamma }^{\prime }}}{P}_{{\gamma }^{\prime }}^{\text{rated\hspace{0.17em}},\beta }\le {\widehat{P}}_{\gamma ,t}^{\beta }\le {\displaystyle \sum _{{\gamma }^{\prime }}}{P}_{{\gamma }^{\prime }}^{\text{rated\hspace{0.17em}},\beta }(39)$

where, $P_{{\gamma }^{\prime }}^{\text{rated,\hspace{0.17em}}\beta }$ is the rated power of Class β energy provided by energy equipment γ′.

${\phi }_{\gamma ,t}^{\beta }$ satisfies the following constraints:

$\frac{{\widehat{P}}_{\gamma ,t}^{\beta }}{{\sum }_{{\gamma }^{\prime }}{P}_{{\gamma }^{\prime }}^{\text{rated\hspace{0.17em}},\beta }}\le {\phi }_{\gamma ,t}^{\beta }\le \frac{{\widehat{P}}_{\gamma ,t}^{\beta }+{\sum }_{{\gamma }^{\prime }}{P}_{{\gamma }^{\prime }}^{\text{rated\hspace{0.17em}},\beta }}{{\sum }_{{\gamma }^{\prime }}{P}_{{\gamma }^{\prime }}^{\text{rated\hspace{0.17em}},\beta }}(40)$

Furthermore, ${\widehat{P}}_{\gamma ,t}^{\beta }$ can be simplified as:

$\begin{array}{cc}\hfill {\widehat{P}}_{\gamma ,t}^{\beta }& =P_{\gamma ,t}^{\beta }-{\displaystyle \sum _{{\gamma }^{\prime }\ne \gamma }^{\mathrm{\Sigma }}}{R}_{{\gamma }^{\prime },t}^{\beta }\hfill \\ \hfill & =P_{\gamma ,t}^{\beta }+R_{\gamma ,t}^{\beta }-{\mathrm{\Sigma }}_{\gamma }{R}_{{\gamma }^{\prime },t}^{\beta }=P_{\gamma ,t}^{\beta }+R_{\gamma ,t}^{\beta }-R_t^{\beta }\hfill \end{array}(41)$

where, $R_{\gamma ,t}^{\beta }$ is the backup power of the energy equipment providing class energy during period t, and $R_t^{\beta }$ is the total backup power of class energy during period t, expressed as

$R_t^{\beta }={\displaystyle \sum _{{\gamma }^{\prime }}}{R}_{{\gamma }^{\prime },t}^{\beta }(42)$

Considering the probability of failure of energy equipment, the expected energy shortage for Class β energy is expressed as:

$E_{EES}^{\beta }={\displaystyle \sum _{\gamma }}{\displaystyle \sum _t}{p}_{\gamma }^{\beta }{\widehat{P}}_{\gamma ,t}^{L,\beta }\mathrm{\Delta }t(43)$

The simultaneous equation yields

$E_{ESS}^{\beta }={\displaystyle \sum _{\gamma }}{\displaystyle \sum _t}{I}_{\gamma }{p}_{\gamma }^{FR}{\phi }_{\gamma ,t}^{\beta }\left(P_{\gamma ,t}^{\beta }+R_{\gamma ,t}^{\beta }-R_t^{\beta }\right)(44)$

Remark 1: This equation is a nonlinear equation, making the lower level programming model a nonlinear model. In order to get a mixed certificate Linear programming (MILP) model that is easy to solve, this paper uses equivalent transformation method to linearize it.

Proof: Equivalent Transformation Linearization Method

Introduce two new variables for equivalent replacement:

$\left\{\begin{array}{c}\hfill {\mu }_{\gamma ,t}^{\beta }=I_{\gamma }{\phi }_{\gamma ,t}^{\beta }\hfill \\ \hfill v_{\gamma ,t}^{\beta }=p_{\gamma }^{FR}\left(P_{\gamma ,T}^{\beta }+R_{\gamma ,t}^{\beta }-R_t^{\beta }\right)\hfill \end{array}\right.(45)$

where, ${\mu }_{\gamma ,t}^{\beta }$ is a binary variable and $v_{\gamma ,t}^{\beta }$ is a continuous variable, meeting the following constraints:

$\left\{\begin{array}{c}\hfill 0\le {\mu }_{\gamma ,t}^{\beta }\le I_{\gamma }\hfill \\ \hfill I_{\gamma }+{\phi }_{\gamma ,t}^{\beta }-1\le {\mu }_{\gamma ,t}^{\beta }\le {\phi }_{\gamma ,t}^{\beta }\hfill \end{array}\right.(46)$

For the convenience of description, it is simplified as:

${\pi }_{\gamma ,t}^{\beta }=I_{\gamma }{p}_{\gamma }^{FR}{\phi }_{\gamma ,t}^{\beta }\left(P_{\gamma ,t}^{\beta }+R_{\gamma ,t}^{\beta }-R_t^{\beta }\right)={\mu }_{\gamma ,t}^{\beta }\times v_{\gamma ,t}^{\beta }(47)$

In order to linearize the above equation, it can be described as:

$\left\{\begin{array}{c}\hfill {\mu }_{\gamma ,t}^{\beta }\times {\underline{v}}_{\gamma t}^{\beta }\le {\pi }_{\gamma ,t}^{\beta }\le {\mu }_{\gamma ,t}^{\beta }\times {\bar{v}}_{\gamma ,t}^{\beta }\hfill \\ \hfill v_{\gamma ,t}^{\beta }-{\bar{v}}_{\gamma ,t}^{\beta }\times \left(1-{\mu }_{\gamma ,t}^{\beta }\right)\le {\pi }_{\gamma ,t}^{\beta }\hfill \\ \hfill \le v_{\gamma ,t}^{\beta }-{\underline{v}}_{\gamma ,t}^{\beta }\times \left(1-{\mu }_{\gamma ,t}^{\beta }\right)\hfill \end{array}\right.(48)$

where, ${\bar{\nu }}_{\gamma ,t}^{\beta }$ and ${\underline{v}}_{\gamma ,t}^{\beta }$ are the upper and lower limits of ${\nu }_{\gamma ,t}^{\beta }$, denoted as:

$\left\{\begin{array}{c}\hfill {\bar{v}}_{\gamma ,t}^{\beta }=p_{\gamma }^{FR}\times P_{\gamma }^{\text{rated\hspace{0.17em}},\beta }\hfill \\ \hfill {\underline{v}}_{\gamma ,t}^{\beta }=-p_{\gamma }^{FR}\times {\mathrm{\Sigma }}_{{\gamma }^{\prime }}{P}_{{\gamma }^{\prime }}^{\text{rated\hspace{0.17em}},\beta }\hfill \end{array}\right.(49)$

The simultaneous equation yields

$\left\{\begin{array}{c}\hfill {\mu }_{\gamma ,t}^{\beta }\times p_{\gamma }^{FR}\times \left(-{\sum }_{{\gamma }^{\prime }}{P}_{{\gamma }^{\prime }}^{rated,\beta }\right)\hfill \\ \hfill \le {\pi }_{\gamma ,t}^{\beta }\le {\mu }_{\gamma ,t}^{\beta }\times p_{\gamma }^{FR}\times P_{\gamma }^{rated,\beta }\hfill \\ \hfill v_{\gamma ,t}^{\beta }-p_{\gamma }^{FR}\times P_{\gamma }^{\text{rated},\beta }\times \left(1-{\mu }_{\gamma ,t}^{\beta }\right)\le {\pi }_{\gamma ,t}^{\beta }\hfill \\ \hfill \le v_{\gamma ,t}^{\beta }-p_{\gamma }^{FR}\times \left(-{\sum }_{{\gamma }^{\prime }}{P}_{{\gamma }^{\prime }}^{\text{rared},\beta }\right)\times \left(1-{\mu }_{\gamma ,t}^{\beta }\right)\hfill \end{array}\right.(50)$

From this, ${\pi }_{\gamma ,t}^{\beta }$ can be transformed into a linear model through the above equation, and $E_{EES}^{\beta }$ can be represented as:

$E_{EES}^{\beta }={\displaystyle \sum _{\gamma }}{\displaystyle \sum _t}{\pi }_{\gamma ,t}^{\beta }\mathrm{\Delta }t(51)$

The corresponding energy deficiency expectation constraint is:

$E_{EES}^{\beta }\le {\bar{E}}_{EES}^{\beta }(52)$

where, ${\bar{E}}_{EES}^{\beta }$ is the expected upper limit of energy shortage for Class β energy.

4.3 Catastrophic Genetic Algorithm-CPLEX hybrid strategy

In the above park level MECS planning model, the upper level planning model transfers the energy equipment configuration plan to the lower level. The lower level planning model optimizes the coordinated operation of the park level MECS based on the energy equipment configuration plan, and returns the operating cost to the upper level. The upper level then calculates the comprehensive cost based on the operating cost returned by the lower level, Optimize the installation type and quantity of energy equipment in the park level MECS.

Cataclysmic genetic algorithm (CGA) is based on genetic algorithm and introduces a mutation operator to avoid the population falling into local optima. It has advantages such as wide applicability, strong optimization ability, and good convergence. This article uses it to solve the configuration problem of energy equipment in the upper planning layer. If there is no new optimal solution every 10 generations and 4 consecutive generations, a mutation operation is carried out to retain the optimal individual and randomly generate other individuals. CPLEX is suitable for solving MILP, with advantages such as fast solving speed and strong robustness. In this paper, it is used to solve the optimization problem of the energy internet in the park in the lower running layer. A lower running layer model is constructed on the software, and the CPLEX solver is called to easily achieve the solution. The solution process for the hybrid strategy is as follows:

Algorithm: Catastrophic Genetic Algorithm - CPLEX Hybrid Strategy

• Data initialization: Input data on photovoltaic lighting and electrical, thermal, and gas loads.

1. Make the population algebra g = 0 to generate the initial population;

2. Determine whether the catastrophic conditions are met. If so, perform a population catastrophic operation and perform CPLEX to solve the lower level programming model; If not, proceed directly to CPLEX to solve the lower level programming model.

3. Calculate the objective function value and fitness value of the upper level planning;

4. Determine whether it converges or reaches the maximum algebraic value, and if so, obtain the optimal configuration plan; If not, perform population selection, crossover, and mutation operations until g = g+1, and then return to step 2.

Remark 2: The steps for CPLEX to solve the lower level planning model include: inputting the capacity of energy devices, constructing a park level MECS operation optimization model, and calling the CPLEX solver to solve.

5 Example analysis

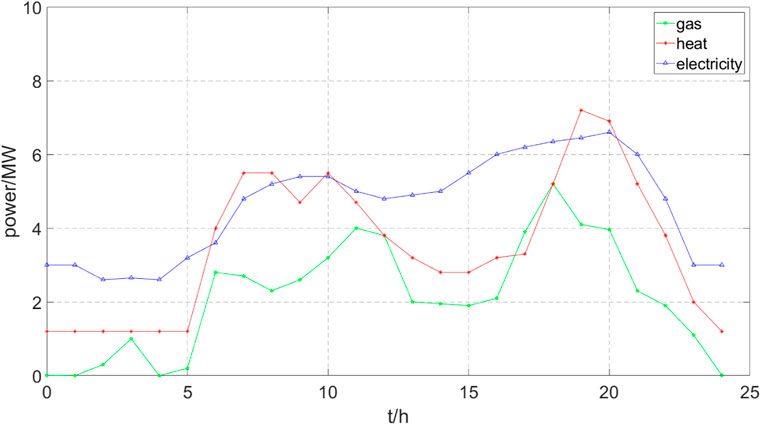
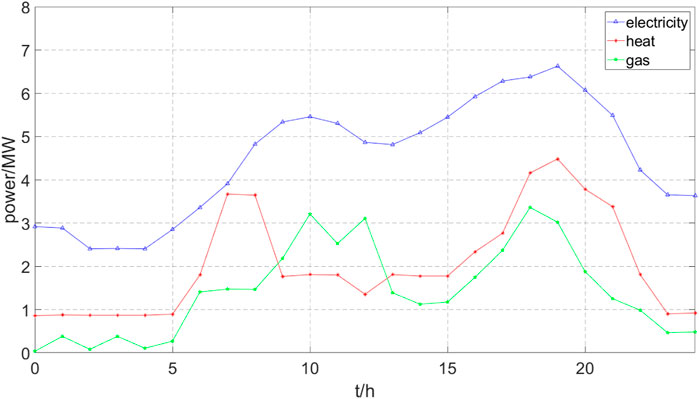
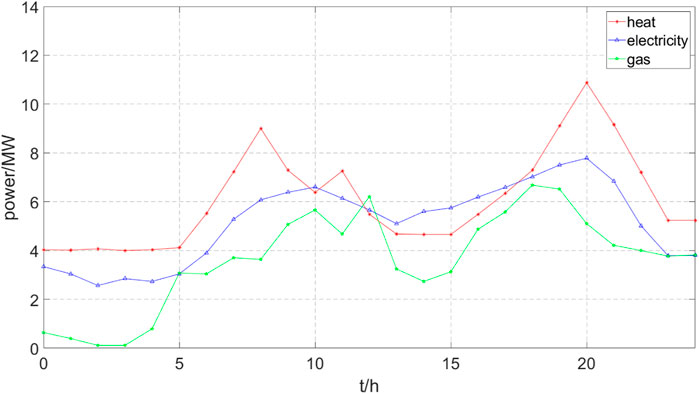
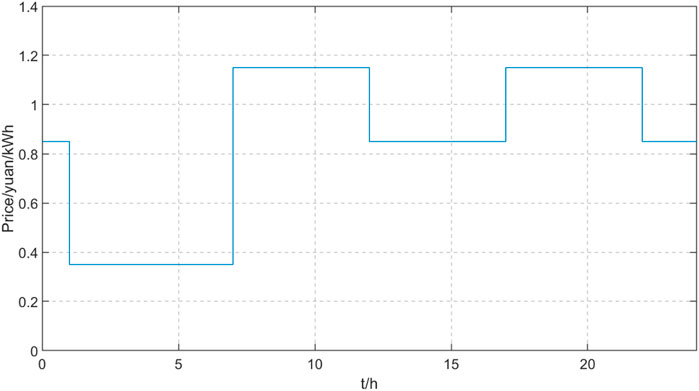
This paper takes a typical park level MECS as the research object, and its structure is shown in Figure 1. The typical daily load curve is shown in Figures 3–5. Among them, the probability of typical days appearing in spring and autumn is 45%, and the probability of typical days appearing in summer and winter is both 20%. This paper adopts a three stage electricity price from peak to flat to valley, with a peak hour electricity price of 1.15 CNY/(kW⋅h), a regular electricity price of 0.85 CNY/(kW⋅h), and a valley hour electricity price of 0.35 CNY/(kW⋅h). The electricity price curve is shown in Figure 6.

FIGURE 3

FIGURE 3. Typical daily energy load curve in spring and autumn.

FIGURE 4

FIGURE 4. Typical daily energy load curve in summer.

FIGURE 5

FIGURE 5. Typical daily energy load curve in winter.

FIGURE 6

FIGURE 6. Electricity price curve.

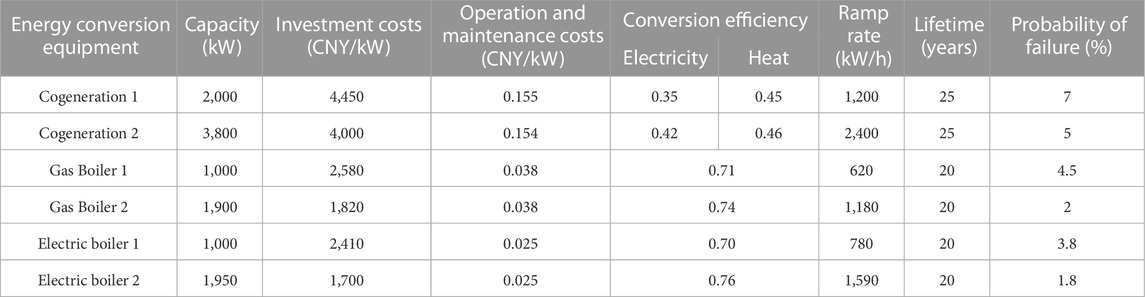
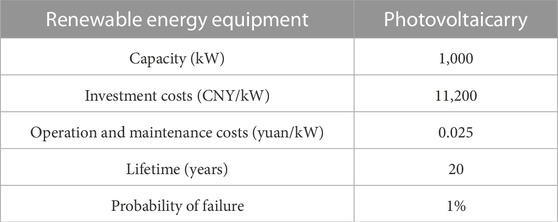
The price of natural gas is 3.25 CNY/m³. The CO² emission coefficients of natural gas and traditional power plants are 1.88 kg/m³ and 0.82 kg/(kW⋅h), respectively, with a carbon tax price of 0.3 CNY/kg. The optional energy equipment parameters are shown in Tables 1–3. Optimization interval is 0.05 s.

TABLE 1

TABLE 1. Energy conversion equipment parameters.

TABLE 2

TABLE 2. Energy storage equipment parameters.

TABLE 3

TABLE 3. Renewable energy equipment parameters.

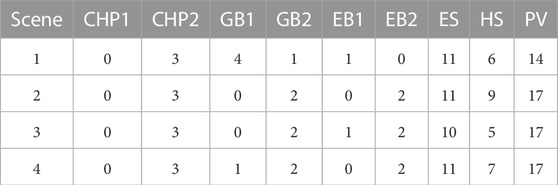
The three indicators in this article are in a progressive relationship, which requires considering the comprehensive energy utilization rate and reliability indicators on the basis of meeting the comprehensive energy self-sufficiency rate. Therefore, this article only considers four application scenarios, as shown in Table 4. Through simulation verification, the configuration quantity of energy equipment in different scenarios is shown in Table 5, and the optimization results in different scenarios are shown in Table 6. The optimization configuration model in Scenario 1 does not consider any constraints of evaluation indicators. The heat load is jointly supplied by CHP, GB, and EB; The electrical load is mainly supplied jointly by CHP and PV. Meanwhile, the EB capacity of the park’s energy internet configuration is smaller than that of CHP and GB, because the cost of configuring EB and using electricity for heating is higher than that of configuring CHP or GB and using natural gas for heating.

TABLE 4

TABLE 4. Comparison of four optimization Configuration scenarios.

TABLE 5

TABLE 5. Configuration quantity of energy equipment in different scenarios.

TABLE 6

TABLE 6. Optimization results under different scenarios.

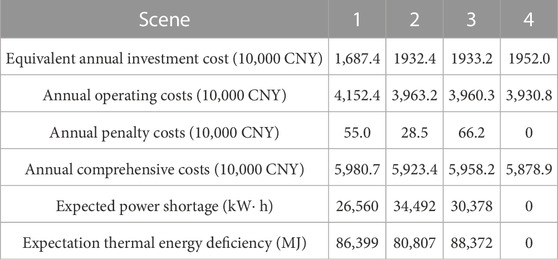
Compared to Scenario 1 and Scenario 2, Scenario 2 is equipped with 3 more PVs to meet the requirements of comprehensive energy self-sufficiency rate. Additionally, one more EB2 device is configured to absorb the surplus electricity generated during daytime PV power generation peaks, while reducing the capacity of GB and increasing the capacity of HS to meet thermal load balance. The equivalent annual investment cost of Scenario 2 is greater than Scenario 1, but the PV installation capacity of Scenario 2 is larger. The energy input of the park level MECS from the superior energy network under Scenario 2 is smaller, so the annual operating cost of Scenario 2 is smaller than Scenario 1. Overall, the annual comprehensive cost of Scenario 2 is greater than Scenario 1.

Comparing Scenario 2 and Scenario 3, in order to meet the requirements of comprehensive energy utilization, the system reduces the configuration and use of ES and HS, thereby reducing energy loss during the charging and discharging process. At the same time, increasing the configuration of EB capacity to directly consume the electricity generated by photovoltaic production reduces the losses in the ES energy storage process. Due to increased constraints on comprehensive energy utilization, the annual comprehensive cost of scenario 3 is greater than that of scenario 2.

Compared to Scenario 3 and Scenario 4, the expected electrical and thermal energy deficits for Scenario 3 are 30378 kW⋅h and 88372 MJ, respectively, while the expected electrical and thermal energy deficits for Scenario 4 are both 0. After considering the reliability indicators, the system has added 1 ES, 2 HS, and 1 GB to provide sufficient backup and reduce the penalty cost of cutting off the load in the event of N-1 faults in energy equipment. At the same time, reduce the configuration of one EB to meet the balance of thermal load. It can be seen that after considering the reliability indicators, the equivalent annual investment cost of the system has increased, but the annual operating cost and annual penalty cost have both decreased, overall reducing the overall cost.

In summary, after considering the evaluation indicators of comprehensive energy self-sufficiency rate and comprehensive energy utilization rate, the energy sustainability and efficiency of the system can meet the requirements, but correspondingly reduce the economic efficiency of the system; After considering the evaluation indicators of energy deficiency expectations, the reliability of the system can meet the requirements while also improving its economy. It can be seen that the proposed two-layer optimization configuration model, which takes into account multiple evaluation indicators, can pursue the economy of system configuration while meeting the requirements of energy sustainability, efficiency, and reliability.

6 Conclusion

This paper constructs a multi indicator evaluation system for park level MECS, taking into account various constraints, and establishes a two-layer optimization configuration model for park level MECS. Through simulation analysis, the following conclusions are drawn: the proposed park level MECS optimization configuration model can fully consider the impact of system operating costs on energy equipment configuration, and the configuration plan is more reasonable; On the other hand, considering the constraints of comprehensive energy self-sufficiency rate, comprehensive energy utilization rate, and expected energy shortage indicators, the configuration plan takes into account various needs such as economy and energy sustainability. Different degrees of indicator constraints have different economic impacts on the configuration results. The stricter the constraints, the greater the annual comprehensive cost of the system. Therefore, in the context of energy marketization, the construction and operation of park level MECS can be guided by economy, and government departments can constrain and guide them by formulating different evaluation indicators.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

YW: Writing–original draft. JC: Writing–original draft. XZ: Writing–original draft. KH: Writing–original draft. LJ: Writing–original draft.

Funding

The authors declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

Authors YW, JC, XZ, and LJ were employed by State Grid Ningbo Electric Supply Company Ningbo. Author KH was employed by Glory Property Branch of Ningbo Power Transmission and Transformation Construction Co., Ltd. Ningbo.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

An, Y., Zhao, Z., and Wang, S. (2020). Coordinative optimization of hydro-photovoltaic-wind-battery complementary power stations. CSEE J. Power Energy Syst. 6 (2), 410–418. doi:10.17775/CSEEJPES.2019.00330

CrossRef Full Text | Google Scholar

Cai, S., and Ying, L. (2021). Incentive policy for battery energy storage systems based on economic evaluation considering flexibility and reliability benefits. Front. Energy Res. 9. doi:10.3389/fenrg.2021.634912

CrossRef Full Text | Google Scholar

Chen, G., Ma, F., Bai, R., Magleby, S. P., and Howell, L. L. (2021). An energy based framework for nonlinear kinetostatic modeling of compliant mechanisms utilizing beam flexures. J. Comput. Inf. Sci. Eng. 21 (6), 064501–064518. doi:10.1115/1.4050472

CrossRef Full Text | Google Scholar

Deng, X., Huang, Y., Chen, Y., Chen, C., Yang, L., Gao, Q., et al. (2021). Multi-scenario physical energy storage planning of integrated energy systems considering dynamic characteristics of heating network and demand response. Front. Energy Res. 9. doi:10.3389/fenrg.2021.783588

CrossRef Full Text | Google Scholar

Du, Y., and Li, F. (2020). A hierarchical real-time balancing market considering multi-microgrids with distributed sustainable resources. IEEE Trans. Sustain. Energy 11 (1), 72–83. doi:10.1109/tste.2018.2884223

CrossRef Full Text | Google Scholar

Du, Y., Wu, J., Li, S., Long, C., and Onori, S. (2020). Hierarchical coordination of two-time scale microgrids with supply-demand imbalance. IEEE Trans. Smart Grid 11 (5), 3726–3736. doi:10.1109/tsg.2020.2980873

CrossRef Full Text | Google Scholar

Li, Z., Xu, Y., Wang, P., and Xiao, G. (2023). Coordinated preparation and recovery of a post-disaster Multi-energy distribution system considering thermal inertia and diverse uncertainties. Appl. Energy 336, 120736. doi:10.1016/j.apenergy.2023.120736

CrossRef Full Text | Google Scholar

Liu, J., Wang, A., Song, C., Tao, R., and Wang, X. (2020a). Cooperative operation for integrated multi-energy system considering transmission losses. IEEE Access 8, 96934–96945. doi:10.1109/access.2020.2996913

CrossRef Full Text | Google Scholar

Liu, S., Xie, S., and Zhang, Q. (2021). Multi-energy synergistic optimization in steelmaking process based on energy hub concept. Int. J. Minerals Metallurgy Mater. 28 (8), 1378–1386. doi:10.1007/s12613-021-2281-7

CrossRef Full Text | Google Scholar

Liu, X., and Mancarella, P. (2016). Modelling, assessment and Sankey diagrams of integrated electricity-heat-gas networks in multi-vector district energy systems. Appl. Energy 167, 336–352. doi:10.1016/j.apenergy.2015.08.089

CrossRef Full Text | Google Scholar

Liu, Y., Jiang, Z., Lichao, H., Xing, Z., Chen, M., and Zhang, P. (2023b). Data-driven robust value iteration control with application to wind turbine pitch control. Optim. Control Appl. Methods 44 (2), 637–646. doi:10.1002/oca.2834

CrossRef Full Text | Google Scholar

Liu, Y., Jiang, Z., Xing, Z., Hao, L., and Qu, B. (2022b). Economic and low-carbon island operation scheduling strategy for microgrid with renewable energy. Energy Rep. 8, 196–204. doi:10.1016/j.egyr.2022.10.099

CrossRef Full Text | Google Scholar

Liu, Y., Xing, Z., Chen, Z., and Xu, J. (2023a). Data-based robust optimal control of discrete-time systems with uncertainties via adaptive dynamic programming. Optim. Control Appl. Methods 44 (3), 1290–1304. doi:10.1002/oca.2775

CrossRef Full Text | Google Scholar

Liu, Y., Xing, Z., Xu, J., Li, Y., and Wang, H. (2020b). control for a class of discrete-time systems via data-based policy iteration with application to wind turbine control. IEEE Access 8, 14565–14572. doi:10.1109/access.2019.2962583

CrossRef Full Text | Google Scholar

Liu, Y., Chen, H., and Li, L. (2022a). Applications and challenges of porous carbon with different dimensions in supercapacitors-a mini review. Front. Energy Res. 10, 10. doi:10.3389/fenrg.2022.951701

CrossRef Full Text | Google Scholar

Mao, Y., Wu, J., Cai, Z., Wang, R., Zhang, R., Chen, L., et al. (2021). Cooperative operation framework for a wind-solar-CCHP multi-energy system based on. Nash Bargain. Solut. 9, 119987–120000. doi:10.1109/ACCESS.2021.3107156

CrossRef Full Text | Google Scholar

Miguel, H., and Ren, Z. (2021). Multi-energy microgrid planning considering heat flow dynamics. IEEE Trans. Energy Convers. 36 (3), 1962–1971. doi:10.1109/tec.2020.3041572

CrossRef Full Text | Google Scholar

Ororbia, M. E., and Warn, G. P. (2022). Design synthesis through a markov decision process and reinforcement learning framework. J. Comput. Inf. Sci. Eng. 22 (2), 021002. doi:10.1115/1.4051598

CrossRef Full Text | Google Scholar

Qian, H., Yun, T., and Chen, Z. (2022). A multi-energy system cluster operation optimization method based on nanocomposite electrode materials energy storage equipment. J. Nanoelectron. Optoelectron. 16 (12), 1931–1941. doi:10.1166/jno.2021.3159

CrossRef Full Text | Google Scholar

Qinglai, W., Shi, G., Song, R., and Liu, Y. (2017). Adaptive dynamic programming-based optimal control scheme for energy storage systems with solar renewable energy. IEEE Trans. Industrial Electron. 64 (7), 5468–5478. doi:10.1109/tie.2017.2674581

CrossRef Full Text | Google Scholar

Wang, D., Peng, D., Huang, D., Ren, L., Yang, M., and Zhao, H. (2021b). Research on short-term and mid-long term optimal dispatch of multi-energy complementary power generation system. IET Renew. Power Gener. 16 (7), 1354–1367. doi:10.1049/rpg2.12366

CrossRef Full Text | Google Scholar

Wang, S., Jia, R., Shi, X., An, Y., Huang, Q., Guo, P., et al. (2021a). Hybrid time-scale optimal scheduling considering multi-energy complementary characteristic. IEEE Access 9, 94087–94098. doi:10.1109/access.2021.3093906

CrossRef Full Text | Google Scholar

Wang, Y., Li, F., Yu, H., Wang, Y., Qi, C., Yang, J., Song, F., et al. (2020). Optimal operation of microgrid with multi-energy complementary based on moth flame optimization algorithm. Energy Sources Part A-Recovery Util. Environ. Eff. 42 (7), 785–806. doi:10.1080/15567036.2019.1587067

CrossRef Full Text | Google Scholar

Wang, Z., Wang, D., Ren, Z., Chen, Y., and Li, X. (2022). Modeling and simulation of fault propagation of combined heat and electricity energy systems under extreme cold disaster based on Markov process. Energy Rep. 8 (1), 619–626. doi:10.1016/j.egyr.2021.11.176

CrossRef Full Text | Google Scholar

Weizhen, Y., Wang, J., Lu, Z., Yang, F., Zhang, Z., Wei, J., et al. (2021). Day-ahead dispatch of multi-energy system considering operating conditions of multi-energy coupling equipment. Energy Rep. 7, 100–110. doi:10.1016/j.egyr.2021.02.016

CrossRef Full Text | Google Scholar

Xu, D., Wu, Q., Zhou, B., Li, C., Bai, L., and Huang, S. (2020a). Distributed multi-energy operation of coupled electricity, heating, and natural gas networks. IEEE Transaction Sustain. Energy 11 (4), 2457–2469. doi:10.1109/tste.2019.2961432

CrossRef Full Text | Google Scholar

Xu, D., Zhou, B., Wu, Q., Chung, C. Y., Li, C., Huang, S., et al. (2020b). Integrated modelling and enhanced utilization of power-to-ammonia for high renewable penetrated multi-energy systems. IEEE Transaction Power Syst. 35 (6), 4769–4780. doi:10.1109/tpwrs.2020.2989533

CrossRef Full Text | Google Scholar

Xue, X., Ai, X., Fang, J., Cui, S., Jiang, Y., Yao, W., et al. (2022). Real time schedule of microgrid for maximizing battery energy storage utilization. IEEE Trans. Sustain. Energy 13 (3), 1356–1369. doi:10.1109/tste.2022.3153609

CrossRef Full Text | Google Scholar

Yang, L., Sun, Q., Zhang, N., and Li, Y. (2022). Indirect multi-energy transactions of energy internet with deep reinforcement learning approach. IEEE Trans. Power Syst. 37 (5), 4067–4077. doi:10.1109/tpwrs.2022.3142969

CrossRef Full Text | Google Scholar

Yang, Y., Li, Z., Mandapaka Pradeep, V., and Lo, E. Y. (2023). Risk-averse restoration of coupled power and water systems with small pumped-hydro storage and stochastic rooftop renewables. Appl. Energy 339, 120953. doi:10.1016/j.apenergy.2023.120953

CrossRef Full Text | Google Scholar

Yin, Y., Liu, T., Wu, L., He, C., Liu, Y., et al. (2021). Day-ahead risk-constrained stochastic scheduling of multi-energy system. J. Mod. Power Syst. Clean Energy 9 (4), 720–733. doi:10.35833/mpce.2020.000375

CrossRef Full Text | Google Scholar

Yu-Kai, C., Wu, Y.-C., Chau-Chung, S., Chen-Yu, Y., et al. (2013). Design and implementation of energy management system with fuzzy control for DC microgrid systems. IEEE Transaction Power Electron. 28 (4), 1563–1570. doi:10.1109/tpel.2012.2210446

CrossRef Full Text | Google Scholar

Zhang, G., Yuan, J., Zhong, L., Yu, S. S., Chen, S. Z., Trinh, H., et al. (2020). Forming a reliable hybrid microgrid using electric spring coupled with non-sensitive loads and ESS. IEEE Trans. Smart Grid 11 (4), 2867–2879. doi:10.1109/tsg.2020.2970486

CrossRef Full Text | Google Scholar

Zhang, J., Sun, K., Li, C., Liu, H., Huang, W., Zhou, B., et al. (2023a). Economic scheduling of gaseous-liquid hydrogen generation and storage plants considering complementarity of multiple products. J. Mod. Power Syst. Clean Energy 11 (1), 223–233. doi:10.35833/mpce.2021.000260

CrossRef Full Text | Google Scholar

Zhang, S., Gu, W., Lu, S., Yao, S., Zhou, S., and Chen, X. (2021c). Dynamic security control in heat and electricity integrated energy system with an equivalent heating network model. IEEE Transaction Smart Grid 12 (6), 4788–4798. doi:10.1109/tsg.2021.3102057

CrossRef Full Text | Google Scholar

Zhang, S., Gu, W., Wang, J., Zhang, X. P., Meng, X., Lu, S., et al. (2023b). Steady-state security region of integrated energy system considering thermal dynamics. IEEE Trans. Power Syst., 1–15. doi:10.1109/TPWRS.2023.3296080

CrossRef Full Text | Google Scholar

Zhang, S., Gu, W., Zhang, X. P., Lu, H., Lu, S., Yu, R., et al. (2022). Fully analytical model of heating networks for integrated energy systems. Appl. Energy 327, 120081. doi:10.1016/j.apenergy.2022.120081

CrossRef Full Text | Google Scholar

Zhang, Y., Hou, H., Huang, J., Zhang, Q., Tang, A., and Zhu, S. (2021a). An optimal subsidy scheduling strategy for electric vehicles in multi-energy systems. Energy Rep. 7, 44–49. doi:10.1016/j.egyr.2021.02.025

CrossRef Full Text | Google Scholar

Zhang, Z., Wang, Z., Wang, H., Zhang, H., Yang, W., and Cao, R. (2021b). Research on Bi-level optimized operation strategy of microgrid cluster based on IABC algorithm. IEEE Access 9, 15520–15529. doi:10.1109/access.2021.3053122

CrossRef Full Text | Google Scholar

Zheng, T., Dai, Z., Yao, J., Yang, Y., and Cao, J. (2019). Economic dispatch of multi-energy system considering load replaceability. Process 7 (9), 570. doi:10.3390/pr7090570

CrossRef Full Text | Google Scholar