- State Grid Shangdong Electric Power Company Economic and Technical Research Institute, Jinan, China
Introduction: The emerging “net-zero carbon” police will accelerate the large-scale penetration of renewable energies in the power grid, which would bring strong random disturbances due to the unpredictable power output. It would affect the coordinated control performance of the distributed grids.
Method: From the quadratic frequency modulation perspective, this paper proposes a fast Q-learning-based automatic generation control (AGC) algorithm, which combines full sampling with full expectation for multi-area coordination. A parameter σ is used to balance the state between the full sampling update and only the expectation update so as to improve the convergence accuracy. Meanwhile, fast Q-learning is incorporated by replacing the historical estimation function with the current state estimation function to accelerate the convergence speed.
Results: Simulations on the IEEE two-region load frequency control model and Hubei power grid model in China have been performed to validate that the proposed algorithm can achieve optimal multi-area coordination and improve the control performance of frequency deviations caused by the strong random disturbances.
Discussion: The proposed Q-learning-based AGC method outperforms the convergence accuracy, speed, and control performance compared with other reinforcement learning algorithms.
1 Introduction
With the rapid development of renewable resources (Xu et al., 2023), distributed energies (Patel et al., 2019; Chen et al., 2022) are being integrated into power grids in large scale. However, their intermittency, randomness, and unpredictability would severely jeopardize the stability and safety of the power systems. The conventional centralized automatic generation control (AGC) (Yu et al., 2011; Wang et al., 2014; Li et al., 2021a; Li et al., 2021b; Xie et al., 2022) aimed to only minimize the area control error (ACE) to output the total regulation power demands, which cannot achieve fast inter-area coordination in such a new type of power systems. Hence, centralized AGC cannot deal with the continuous declination in the control performance standards (CPS), such as system frequency and ACE, due to strong random disturbances. Distributed AGC with multi-area coordination is, thus, developed to regulate the output of the renewable grid.
In recent years, many scholars have aimed at the research on distributed AGC control methods and proposed a series of distributed AGC algorithms by introducing numerical computing methods, reinforcement learning (Yin et al., 2017), deep learning (Li et al., 2023), and neural network (Bhongade et al., 2010). Among them, numerical computation methods have been intensively studied by scholars due to their well-established deployment models. Based on the distributed model prediction algorithm, Yang et al. (2023) proposes a load frequency control (LFC) strategy suitable for the LFC system of new energy with high permeability. Huang (2023) proposed a synovial disturbance observer applied to a flexible LFC system and showed that this scheme has evident advantages in dealing with delayed attacks. However, numerical methods require in-depth analysis and optimization of the model, which is not conducive for applications in complex dynamical systems. Therefore, control algorithms based on heterogeneous multi-agent reinforcement learning are widely applicable in distributed AGC modalities, which have strong advantages in decision making, self-learning, and self-optimization.
Heterogeneous multi-agent reinforcement learning is capable of continuously interacting with the environment, accumulating experience, analyzing, and obtaining the optimal strategies during exploration, which has more advantages in distributed AGC. Li et al. (2022) pointed out the deficiencies of single-agent reinforcement learning in the optimization space and used multi-agent reinforcement learning to improve the adaptability of the AGC system. Zhang et al. (2016) introduced the wolf pack algorithm with competitive strategies among the agents in different areas to obtain the optimal solution, thereby achieving fast convergence to the Nash equilibrium. Xi et al. (2015) proposed an intelligent generation control method for the microgrids based on multi-agent correlated equilibrium reinforcement learning, which can effectively enhance the adaptability of islanded microgrids. In order to remove the lookup table method of traditional Q-learning, Tang et al. (2017) used the neural network (Fu et al., 2023) to approximate the value function. Simulation results confirmed that it can obtain accurate AGC generation commands under renewable energy disturbances. Furthermore, Xi et al. (2020) proposed a decentralized multi-agent algorithm to solve the time credence allocation problem caused by the large time delays of the units, i.e., thermal power plants.
However, the aforementioned reinforcement learning methods are derived from traditional Q-learning, i.e., off-policy reinforcement learning. They generally suffer from strategic bias because their learning goals are inconsistent with the sampling behavior strategies, such that these methods cannot quickly restore the stability under severe random disturbances. On-policy reinforcement learning that applies the unified policy can learn online in different environments and gradually improve, but it is easy to remain in a local optimal policy, and the learning process is relatively slow. Combined with the advantages of off-policy and on-policy, Wang et al. (2014) proposed the Q(σ) algorithm to balance full sampling and only the expectation update to address the bias and local optimal problems. However, the convergence speed of this proposed algorithm hardly meets the requirements of the AGC real-time control.
As for the convergence speed of reinforcement learning, Leed and Powell (2012) proposed a bias-corrected Q-learning algorithm based on the bias correction policy, but it can only be applied when the number of the action values is large. Kamanchi et al. (2019) introduced the relaxation factor ω to target when the agent falls into self-cycling such scenarios. Zhang and Liu (2008) proposed a proving Q-learning algorithm based on the idea of a taboo search which can balance the relationship between exploration and exploitation so as to improve the convergence speed. However, the method requires resetting the length of the taboo table and the aspiration criterion in different environments, which limits its applicability. Furthermore, Azar et al. (2011) proposed speedy Q-learning (SQL), which can replace the historical estimation function with the current function so as to accelerate the convergence. It can be perfectly combined with Q(σ) to improve its convergence speed.
Hence, this paper proposes a novel and efficient multi-agent coordinated AGC algorithm, called SQ(σ), with the combination of Q(σ) and SQL. The proposed algorithm not only has a fast convergence but also solves the local optimality and strategic bias problems by balanced full sampling. Therefore, the AGC controller based on SQ(σ) can meet the real-time control requirements of AGC and has strong robustness in the face of a strong random load disturbance. Simulation experiments on the improved IEEE two-region load-frequency control model and the multi-area interconnected Hubei power grid model in China are used to validate the effectiveness of the proposed algorithm.
The remainder of the paper is organized as follows: the SQ(σ) algorithm is described in Section II. Section III presents the proposed AGC system based on SQ(σ) in detail. Simulation experiments on the improved IEEE two-area load frequency control model and the four-region model of the Hubei power grid are performed from various aspects with comparison analysis in Section IV. Conclusion is provided in Section V.
2 SQ(σ) algorithm
The proposed multi-agent coordinated algorithm SQ(σ) based on Q(σ) and SQL is discussed in detail.
2.1 Q(σ)
Q(σ) combines the on-policy state-action-reward-state-action (SARSA) (Richard, 1988) based on temporal difference (TD) (Engel et al., 2005) and the off-policy Expected SARSA (Van Seijen et al., 2009) by introducing a parameter σ as the sampling step. When σ is 1, it becomes SARSA (full sampling), and when σ is 0, it becomes Expected SARSA (only-expectation). Hence, the parameter σ is used to balance between the full sampling and only-expectation updates to improve the convergence accuracy.
SARSA is a basic on-policy TD algorithm where the action function is used to replace the state function as the estimated value. The characteristic of the on-policy methods is to estimate the optimal Q-value based on the current behavior policy and the all state-action estimates. The update of the on-policy TD algorithm is written as follows:
where α is the learning rate of the agent, γ is the reward discount factor, and kS is TD of SARSA.
Although formally similar to SARSA, Expected SARSA is an off-policy learning algorithm whose target update is the expected Q-value. It can generalize Q-learning to arbitrary target policies via the next state-action values to estimate the expected Q-values as follows:
where kES is TD of Expected SARSA. Although Expected SARSA is more computationally complex than that of SARSA, it can eliminate the variance caused by next action selection with higher performance under the same exploration experience.
Q(σ) can perform a linear weighting between the full sampling and only-expectation updates via the mixed sampling parameter σ, updated as follows:
2.2 The proposed SQ(σ) algorithm
As a derived algorithm of Q-learning, the update criteria with greater exploration weights are applied in SQL, thereby improving the convergence speed of the agent. The Q-table update policy utilizes the estimation function of the previous Q-values to replace the current Q-value estimation function so as to accelerate the convergence of Q-learning. The Q-matrix update is as follows:
where Mk (s’, a’) = maxa’ Qk (s’, a’) and Mk-1 (s’, a’) is the maximum Q-value when the action state (s, a) is transformed to the (s’, a’) state.
With the obtained σ, SQ(σ) can be rewritten as follows:
3 SQ(σ)-based AGC design
3.1 SQ(σ)-based control framework
The interconnected AGC system can fully perceive the operating information on each regional grid and achieve information sharing, that is, when the operating status of one region changes, it will also cause dynamic changes in other regions. This paper adopts CPS (Jaleeli and VanSlyck, 1999) [CPS include CPS1 and CPS2 indicators, and the specific formula can be found in Jaleeli and VanSlyck (1999)] proposed by the North American Electric Reliability Corporation, ACE, and the system frequency deviation (Δf) to evaluate the control performance of the SQ(σ) controller. Without loss of generality, SQ(σ) controllers are designed to incorporate the key elements of reinforcement learning: state, reward (shown in Section 2.2), and action. In keeping with the traditional PI controller design, this paper considers ACE as the state, and the state set S has 13 intervals, S = [|ACE|<1 MW, 1 MW < ACE≤10 MW, 10 MW < ACE≤20 MW, 20 MW < ACE≤30 MW, 30 MW < ACE≤40MW, 40 MW < ACE≤50 MW, ACE>50 MW, −10 MW < ACE ≤ −1 MW, −20 MW < ACE ≤ −10 MW, −30 MW < ACE ≤ −20 MW, −40 MW < ACE ≤ −30MW, −50 MW < ACE ≤ −40 MW, and ACE < −50 MW]. We consider regulating power as action, power is limited to [-50 and 50] MW, and the action set A = [−50, −40, −30, −20, −10, 0, 10, 20, 30, 40, and 50] MW.
The agents within each region can perceive ACE and Δf in real-time, while the historical data can be stored and shared among the agents in different regions for online learning. Thus, the state values of the “real-time monitoring system and long-term historical database” can be used as the inputs to SQ(σ) controllers to calculate the reward values. Meanwhile, the next optimal control strategy can be executed by the controllers with the shared information, eventually obtaining the optimal total regulation power demand ΔPord-k.
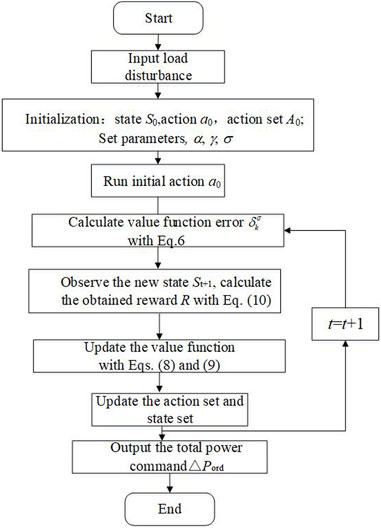
The flowchart of the SQ(σ)-based AGC system is shown in Figure 1.
3.2 Reward function (objective function)
The power balance is the foundation to maintain stable and reliable grid operation. Thus, frequency deviation Δf is the indicator of whether the power is in balance via the control of “power difference.” In pursuit of optimal solution, the reward function is designed to stabilize the output power and maximize the long-term benefits of CPS. Therefore, this paper considers Δf and ACE as the comprehensive target rewards of the SQ(σ) controller. It not only considers the smooth output power but also focuses on the long-term benefits of CPS, thus maximizing the overall performance of the system. In order to deal with the different dimensions of ACE and Δf, the two indexes in reward function are normalized and linearly weighted. Here, the reward function of each regional grid is formed as
where |Δf(i)| and ACE(i) are the instantaneous absolute value of the Δf and ACE value at i moment, respectively; 1-η and η are the weight factors of Δf and ACE, respectively. Here, η is set as 0.5.
3.3 Constraints
1) Regulation capacity constraint: The regulation power input of each regulation resource should be limited within its lower and upper bounds as
where ΔPiin(k)denotes the regulation power input of the ith AGC unit at the kth control interval. ΔPimin and ΔPimax are the minimum and maximum regulation capacities of the ith AGC unit, respectively.
2) GRC: The regulation power output of each AGC unit should satisfy GRC as
where ΔPirate is the maximum ramp rate of the ith AGC unit; ΔT is the time cycle of the AGC dispatch; ΔPiout (k) is the regulation power output of the ith AGC unit at the kth control interval.
3) Regulation direction constraint: To avoid reverse power regulation, the regulation direction of each regulation resource should be consistent with that of the total power regulation command as
where ΔPC is the total power regulation command.
3.4 Parameter setting
During the design of the SQ(σ)-based AGC controller, three parameters α, γ, and σ of SQ(σ) should be set carefully to follow the following principles so as to obtain better control performance.
1) The learning factor α (0<α < 1) is used to determine the trust rank in SQ(σ) for the iterative updates. When α is close to 1, it will speed up the convergence, while a smaller α would enhance the convergence stability.
2) The discount factor γ (0<γ < 1) is used to measure the importance of future rewards and immediate rewards. When γ is close to 1, the agent cares more about the long-term rewards, and when γ approaches 0, the agent cares more about the instant rewards. Hence, γ should be taken a value close to 1 for the long-term rewards.
3) The hybrid sampling parameter σ (0≤σ ≤ 1) is used to combine the on-policy and off-policy. Different values of σ lead to different linear weights between the full sampling SARSA algorithm (σ = 1) updates and the Expected SARSA algorithm (σ = 0) updates. The smaller the σ, the more biased toward full sampling in the policy optimization process and vice versa.
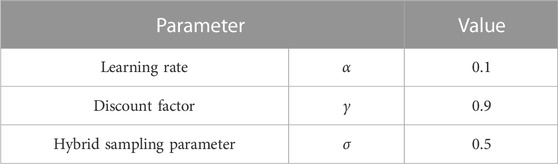
Through extensive simulation experiments, the involved parameters are selected and listed in Table 1.
4 Simulation experiments and result analysis
4.1 LFC model of the improved IEEE standard two-area interconnected system
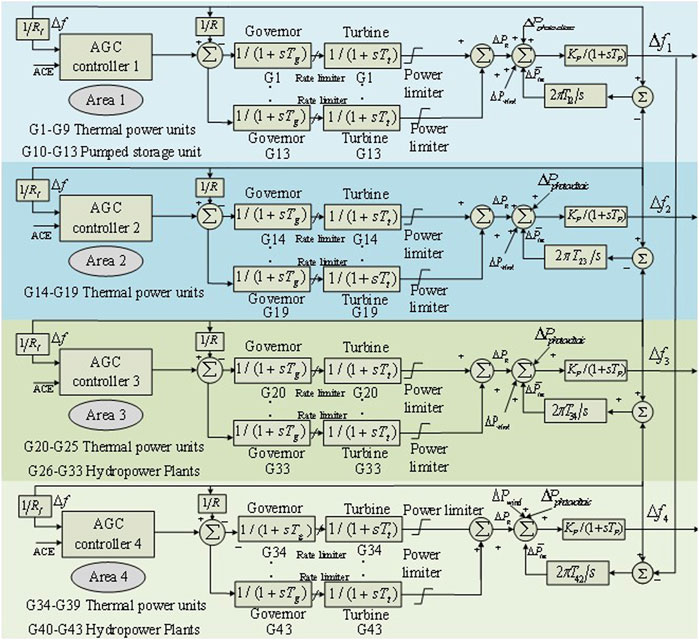
In order to simulate the random disturbances caused by the integration of wind, solar, and other renewable energy sources into the interconnected power grid, small hydro, wind power (Fu and Zhou, 2023), electric vehicles (Shen et al., 2021), photovoltaics (Fu, 2022), biomass energy, and flywheel energy storage are incorporated into Area A of the IEEE standard two-area load frequency control model. The established two-area integrated LFC energy system model is shown in Figure 2. In this model, Tg is the time constant of the generator unit, Tt is the time constant of the turbine unit, and Kp/(1+sTp) represents the time constant of the AC frequency response, and Tg = 0.08 s, Tt = 0.3 s, T12 = 3.42 s, Tp = 0.08 s, and Kp = 0.00012 Hz.
4.1.1 Pre-learning
A large amount of pre-learning is required to obtain the optimal decision-making strategy before the AGC controller is formally put into practice. A sinusoidal load disturbance (period 1,200 s, amplitude 1,000 MW, duration 10,000 s) is used to pre-train SQ(σ) and make it converge to the optimal strategy. Figure 3 shows the various control indicators of the SQ(σ) controller during the pre-learning phase under load disturbances. Figure 3A shows the outputs of areas A and B can track the load disturbance curves in a short period of time. Figure 3B shows the variation curves of the average ACE in areas A and B during the learning process. During the initial stage, when the algorithm control has not fully converged, ACE has a downward fluctuation, but it can gradually converge and remain within a stable range after complete autonomous learning. Figure 3C shows the frequency variation curves during pre-learning, and the |Δfmax| (maximum frequency deviation) values of the two areas are 0.073 and 0.069 Hz, far lower than the practical engineering requirement of 0.2 Hz, indicating that the controller shows higher control performance. Therefore, the SQ(σ) controller can be put into operation after pre-learning.
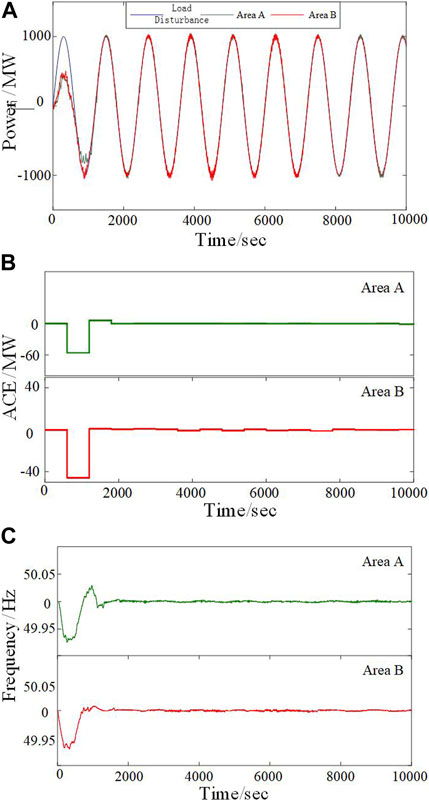
FIGURE 3. Pre-learning of SQ(s) in areas A and B. (A) Controller output in the two areas. (B) ACE values in the two areas. (C) Frequency variation curves in the two areas.
4.1.2 The continuous step disturbance and random square wave disturbance
During the online operation, continuous step load perturbations (amplitude of 500, 1,000, and 1,500 MW) are introduced into the two-area system to simulate the sudden increase in the loads. Using a load disturbance with a duration of 10,000 s as an evaluation period, the performance of SQ(σ), DDQN-AD (Tang et al., 2017), PDWOLF-PHC (Xi et al., 2018), Q(σ), SQL, and Q controllers is analyzed. The control performance indicators of various algorithms in Area A are shown in Figure 4. Figure 4A shows that under each load increase situation, the CPS1 values of the SQ(σ) controller change more smoothly. Although DDQN-AD performs better in CPS1 under a load mutation at 4,000 s, it exhibits larger fluctuations in the later stages, making SQ(σ) possessing the overall superiority. Figure 4B demonstrates that the SQ(σ) controller has smaller ACE values after being disturbed. Figure 4C shows the frequency response curves under the control of the six algorithms, with the maximum frequency deviations of SQ(σ), DDQN-AD, PDWOLF-PHC, Q(σ), SQL, and Q controllers being 0.019, 0.021, 0.025, 0.030, 0.051, and 0.076 Hz, respectively. Thus, it can be seen that after continuous step load perturbations, SQ(σ) exhibits better recovery capability and dynamic control performance, reduced frequency deviation, and improved system stability.
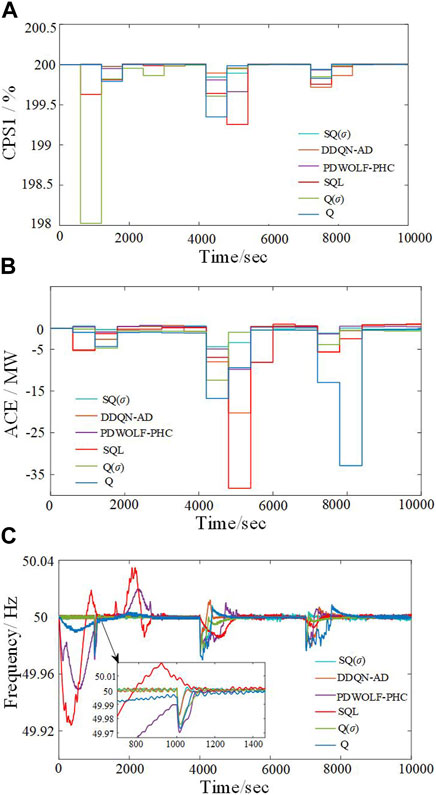
FIGURE 4. Control performance of the six algorithms under continuous step load perturbation. (A) CPS1 with different control algorithms. (B) ACEs with different control algorithms. (C) Frequency variation curves with different control algorithms.
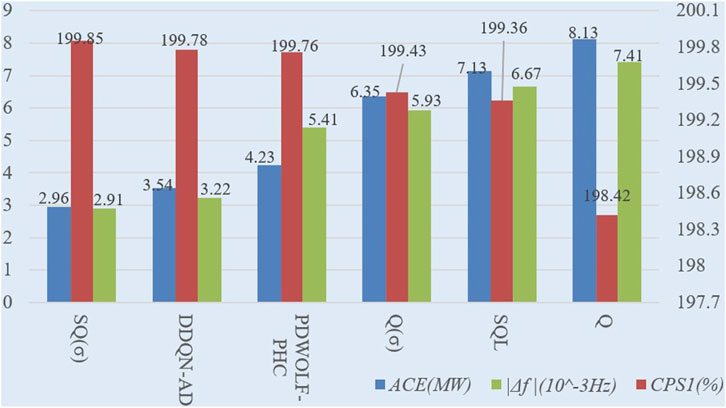
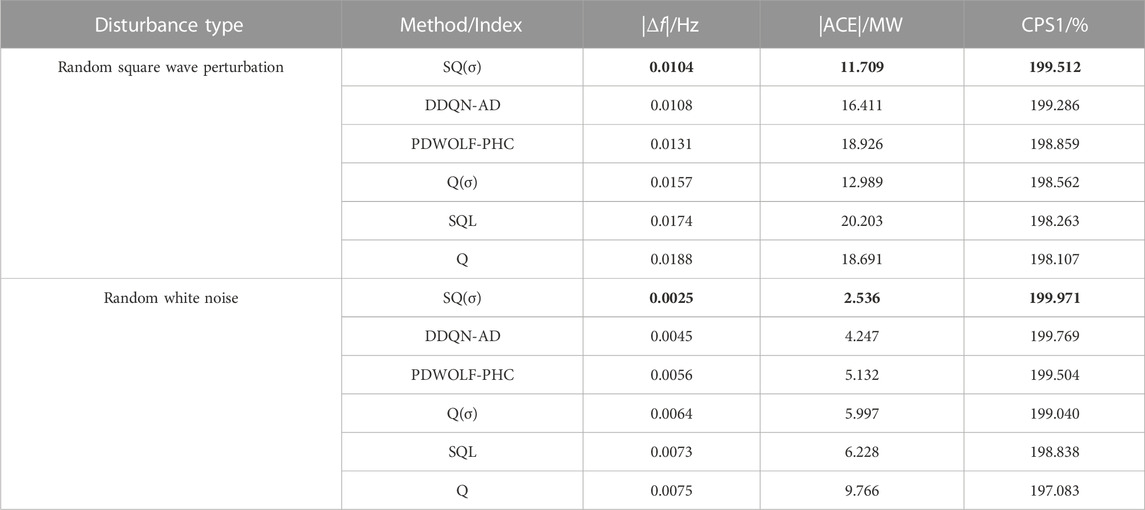
To further verify the control performance of the proposed algorithm under more realistic operating conditions, random square wave perturbations (with an amplitude not exceeding 1,000 MW) are introduced to simulate the random load disturbances caused by the integration of unknown distributed renewable energy sources. The control performance of the six controllers is tested and shown in Figure 5. Compared to the other five algorithms, SQ(σ) can reduce ACE values by 16.38%–63.59%, increase CPS1 by 0.03%–0.72%, and decrease |Δf| by 9.62%–60.72% under random square wave perturbations with stronger robustness and dynamic optimization capabilities.
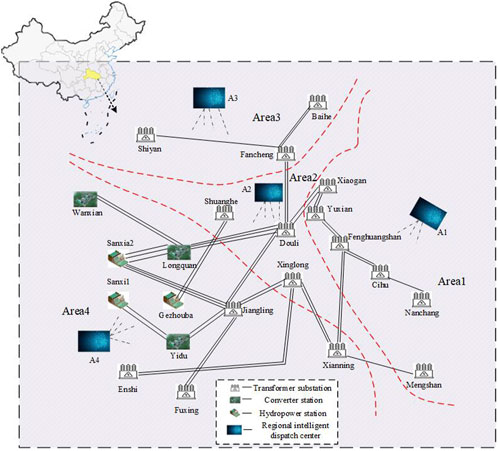
4.2 Four-region model of the Hubei power grid
Based on the interconnected network structure diagram of the Hubei power grid shown in Figure 6 (Xi et al., 2022), a four-region AGC model of the Hubei interconnected power grid is configured with the integration of wind, solar, and other distributed energy sources to verify the practical engineering application of SQ(σ). The configured four-region AGC model is shown in Figure 7, including thermal power plants, hydropower plants, and pumped storage power plants, as well as wind and photovoltaic power generation. In this model, ΔPg represents the output of the prime motor, and Tp = 20 s, T12,23,34,42 = 15.9, 7.96, 15.9, 7.96 s, and Kp = 0.0029 HZ. The distributed energy sources, such as wind power, photovoltaic power, and electric vehicles, are considered the disturbance loads with their typical daily output power, which do not participate in LFC.
In order to simulate the regular sudden increase and decrease of load in a strong stochastic environment and the uncertainty of the power system under the strong random disturbance, the random square waves and random white noise disturbances are introduced into the four-region AGC model through the designed experiments to evaluate the control performance of Q(σ), DDQN-AD, PDWOLF-PHC, Q(σ), Q, and SQL algorithms.
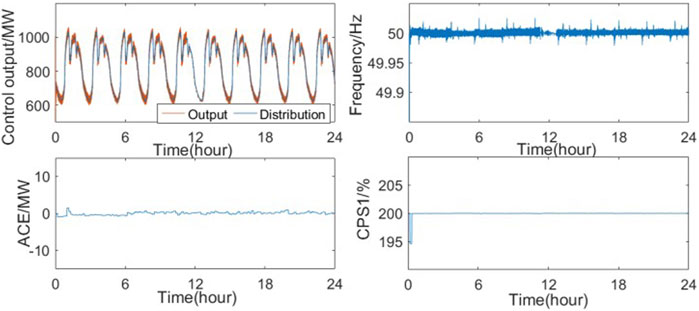
The control performance of the SQ(σ) controller under white noise disturbances is shown in Figure 8. It can be observed that under irregular load variations, the proposed controller can always track the load disturbances well, and the relevant control performance indicators remain within the accepted range.
Compared to the other algorithms, it can be seen from Table 2 that |Δf| is reduced by 3.70%–44.68%, ACE by 9.85%–42.04%, and CPS1 is increased by 0.11%–0.71% via the SQ(σ) algorithm under random square wave perturbations. |Δf| and ACE can be reduced by 44.44%–66.67% and by 38.65% via SQ (σ) under random white noise disturbances.
5 Conclusion
To target the increasingly strong random disturbances due to the large-scale integration of renewable energy sources in the power grid, this paper proposes an SQ(σ) algorithm with the combination of full sampling and full expectation updates from the perspective of distributed AGC. A parameter σ is introduced to balance the full sampling and expectation updates to deal with the issues of convergence difficulty and low convergence accuracy in the off-policy algorithms. Simulation experiments have been performed under various operating conditions, identifying that the proposed algorithm can achieve multi-region optimal and rapid coordination with higher convergence accuracy, faster convergence speed, and lower ACE and frequency deviation. Further on-going research would focus on the application of RL with imitation learning to facilitate the transition from off-line pre-learning to on-line learning.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
SZ: conceptualization, formal analysis, methodology, project administration, supervision, validation, visualization, writing–original draft, and writing–review and editing. FL: conceptualization, formal analysis, methodology, and writing–original draft. BX: validation, visualization, and writing–original draft. QC: visualization and writing–original draft. XQ: supervision and writing–original draft.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was funded by the State Grid Corporation of China Headquarters Management Technology Project (No. 5200-202216099A-1-1-ZN). The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.
Conflict of interest
Authors SZ, FL, BX, QC, and XQ were employed by the State Grid Shangdong Electric Power Company Economic and Technical Research Institute.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Azar, G., Munos, R., and Ghavamzadaeh, M. (2011). Speedy Q-learning. Adv. Neural Inf. Process. Syst., 2411–2419.
Bhongade, S., Gupta, H. O., and Tyagi, B. (2010). “Artificial neural network based automatic generation control scheme for deregulated electricity market [A],” in 2010 conference proceedings IPEC [C] (Singapore: IEEE), 1158–1163.
Chen, M., Shen, Z., Wang, L., and Zhang, G. (2022). Intelligent energy scheduling in renewable integrated microgrid with bidirectional electricity-to-hydrogen conversion. IEEE Trans. Netw. Sci. Eng. 9 (4), 2212–2223. doi:10.1109/tnse.2022.3158988
Engel, Y., Mannor, S., and Meir, R. (2005). “Reinforcement learning with Gaussian processes,” in Proceedings of the 22nd international conference on Machine learning, 201–208.
Fu, W., Jiang, X., Li, B., Tan, C., Chen, B., and Chen, X. (2023). Rolling bearing fault diagnosis based on 2D time-frequency images and data augmentation technique. Meas. Sci. Technol. 34 (4), 045005. doi:10.1088/1361-6501/acabdb
Fu, X. (2022). Statistical machine learning model for capacitor planning considering uncertainties in photovoltaic power. Prot. Control Mod. Power Syst. V (1), 5–63. doi:10.1186/s41601-022-00228-z
Fu, X., and Zhou, Y. (2023). Collaborative optimization of PV greenhouses and clean energy systems in rural areas. IEEE Trans. Sustain. Energy 14 (1), 642–656. doi:10.1109/TSTE.2022.3223684
Huang, D. (2023). Delay-independent load frequency control scheme based on sliding mode perturbation observer. Electron. Des. Eng. 31 (15), 140–144. (in chinese). doi:10.14022/j.issn1674-6236.2023.15.029
Jaleeli, N., and VanSlyck, L. S. (1999). NERC's new control performance standards. IEEE Trans. Power Syst. 14 (3), 1092–1099. doi:10.1109/59.780932
Kamanchi, C., Diddigi, R. B., and Bhatnagar, S. (2019). Successive over-relaxation ${Q}$ -learning. IEEE Control Syst. Lett. 4 (1), 55–60. doi:10.1109/lcsys.2019.2921158
Leed, D., and Powell, W. B. (2012). “An intelligent battery controller using Bias-corrected Q-learning,” in Twenty-sixth AAAI conference on artificial intelligence (AAAI Press), 316–322.
Li, J., Yu, T., and Zhang, X. (2021b). AGC power generation command allocation method based on improved deep deterministic policy gradient algorithm. Proc. CSEE 41 (21), 7198–7212. in Chinese. doi:10.13334/j.0258-8013.pcsee.201253
Li, J., Yu, T., Zhang, X., Li, F., Lin, D., and Zhu, H. (2021a). Efficient experience replay based deep deterministic policy gradient for AGC dispatch in integrated energy system. Appl. Energy 285, 116386. doi:10.1016/j.apenergy.2020.116386
Li, J. W., Yu, T., and Zhang, X. S. (2022). Coordinated load frequency control of multi-area integrated energy system using multi-agent deep reinforcement learning. Appl. ENERGY 306, 117900. JAN 15 2022, Art. no. 117900. doi:10.1016/j.apenergy.2021.117900
Li, J. W., Zhou, T., and Cui, H. Y. (2023). “Brain-inspired deep meta-reinforcement learning for active coordinated fault-tolerant load frequency control of multi-area grids,” in IEEE transactions on automation science and engineering. Early Access, April 26 2023.
Patel, R., Li, C., Meegahapola, L., McGrath, B., and Yu, X. (2019). Enhancing optimal automatic generation control in a multi-area power system with diverse energy resources. IEEE Trans. Power Syst. 34 (5), 3465–3475. doi:10.1109/tpwrs.2019.2907614
Richard, S. (1988). Learning to predict by the methods of temporal differences. Mach. Learn. 3 (1), 9–44. doi:10.1007/bf00115009
Shen, Z., Wu, C., Wang, L., and Zhang, G. (2021). Real-time energy management for microgrid with EV station and CHP generation. IEEE Trans. Netw. Sci. Eng. 8 (2), 1492–1501. doi:10.1109/tnse.2021.3062846
Tang, J., Zhang, Z., and Cheng, L. (2017). Smart generation control for micro-grids based on correlated equilibrium Q(λ) learning algorithm. Electr. Meas. Instrum. 54 (01), 39–45. in Chinese.
Van Seijen, H., Van Hasselt, H., Whiteson, S., et al. (2009). A theoretical and empirical analysis of Expected Sarsa. IEEE symposium Adapt. Dyn. Program. Reinf. Learn., 177–184.
Wang, H., Yu, T., and Tang, J. (2014). Automatic generation control for interconnected power grids based on multi-agent correlated equilibrium learning system. Proc. CSEE 34 (04), 620–635. in Chinese. doi:10.1109/TCYB.2013.2263382
Xi, L., Chen, J., Huang, Y., Xu, Y., Liu, L., Zhou, Y., et al. (2018). Smart generation control based on multi-agent reinforcement learning with the idea of the time tunnel. Energy 153, 977–987. doi:10.1016/j.energy.2018.04.042
Xi, L., Yu, T., Yang, B., and Zhang, X. (2015). A novel multi-agent decentralized win or learn fast policy hill-climbing with eligibility trace algorithm for smart generation control of interconnected complex power grids. Energy Convers. Manag. 103, 82–93. doi:10.1016/j.enconman.2015.06.030
Xi, L., Li, H., Zhu, J., Li, Y., and Wang, S. (2022). A novel automatic generation control method based on the large-scale electric vehicles and wind power integration into the grid. IEEE Trans. Neural Netw. Learn. Syst., 1–11. [Online]. doi:10.1109/TNNLS.2022.3194247
Xi, L., Yu, L., Xu, Y., Wang, S., and Chen, X. (2020). A novel multi-agent DDQN-AD method-based distributed strategy for automatic generation control of integrated energy systems. IEEE Trans. Sustain. Energy 11 (4), 2417–2426. doi:10.1109/tste.2019.2958361
Xie, L., Wu, J., Li, Y., Sun, Q., and Li, X. (2022). Automatic generation control strategy for integrated energy system based on ubiquitous power internet of things. IEEE Internet Things J. 10, 7645–7654. [Online]. doi:10.1109/JIOT.2022.3209792
Xu, P., Fu, W., Lu, Q., Zhang, S., Wang, R., and Meng, J. (2023). Stability analysis of hydro-turbine governing system with sloping ceiling tailrace tunnel and upstream surge tank considering nonlinear hydro-turbine characteristics. Renew. Energy 210, 556–574. doi:10.1016/j.renene.2023.04.028
Yang, D., Zhu, J., and Jiang, C. (2023). High proportion wind power system multi-source collaborate load frequency control strategy based on distributed model prediction [J/OL]. Power Syst. Technol. 1-14. [2023-08-31] (in Chinese). doi:10.13335/j.1000-3673.pst.2023.0889
Yin, L., Yu, T., Zhou, L., Huang, L., Zhang, X., and Zheng, B. (2017). Artificial emotional reinforcement learning for automatic generation control of large-scale interconnected power grids. IET Generation, Transm. Distribution 11 (9), 2305–2313. doi:10.1049/iet-gtd.2016.1734
Yu, T., Zhou, B., Chan, K. W., Chen, L., and Yang, B. (2011). Stochastic optimal relaxed automatic generation control in non-markov environment based on multi-step $Q(\lambda)$ learning. IEEE Trans. Power Syst. 26 (3), 1272–1282. doi:10.1109/tpwrs.2010.2102372
Zhang, X., Yu, T., and Tang, J. (2016). Dynamic optimal allocation algorithm for control performance standard order of interconnected power grids using synergetic learning of multi-agent CEQ(λ). Trans. China Electrotech. Soc. 31 (08), 125–133. in Chinese. doi:10.19595/j.cnki.1000-6753.tces.2016.08.016
Keywords: automation generation control, hybrid sampling, renewable energy, reinforcement learning, artificial intelligence
Citation: Zhang S, Lan F, Xue B, Chen Q and Qiu X (2023) A novel automatic generation control method with hybrid sampling for multi-area interconnected girds. Front. Energy Res. 11:1280724. doi: 10.3389/fenrg.2023.1280724
Received: 21 August 2023; Accepted: 04 October 2023;
Published: 09 November 2023.
Edited by:
Wenlong Fu, China Three Gorges University, ChinaReviewed by:
Jiawen Li, Shanghai University of Electric Power, ChinaXiaomeng Ai, Huazhong University of Science and Technology, China
Qian Zhang, Chongqing University, China
Copyright © 2023 Zhang, Lan, Xue, Chen and Qiu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shengxi Zhang, enN4MTk5M0AxMjYuY29t
 Shengxi Zhang
Shengxi Zhang Feng Lan
Feng Lan