Two-stage robust optimal capacity configuration of a wind, photovoltaic, hydropower, and pumped storage hybrid energy system

The hybrid energy system of hydro-powers, pumped storages and renewable energies has become a new topic direction in modern power system developments. Consequently, it is essential to realize a rational and efficient allocation of different energy source capacities. Nevertheless, there is still a gap between the available studies and the requirement for further hybrid energy system development. This paper focuses on the optimal capacity configuration of a wind, photovoltaic, hydropower, and pumped storage power system. In this direction, a bi-level programming model for the optimal capacity configuration of wind, photovoltaic, hydropower, pumped storage power system is derived. To model the operating mode of a pumped storage power station, two 0-1 variables are introduced. To handle the nonlinear and nonconvex lower level programing problem caused by the two 0-1 variables, it is proposed that the 0-1 variables are treated as some uncertain parameters. Also, by treating the 0-1 variables as some uncertain parameters, a two-stage robust optimization problem to decompose the original bi-level programing one into a master problem and a subproblem is finally introduced. The Karush-Kuhn-Tucker (KKT) conditions are then applied to simplify and linearize the min-max problem and nonlinear terms in the master problem. This results in both the master problem and the subproblem being formulated as mixed integer linear programming (MILP) problems. By utilizing the powerful Column-and-Constraint Generation (C&CG) algorithm, the two-stage robust optimization model is decomposed into an iterative procedure of solving the master problem and the subproblem sequentially. This approach eliminates the need for intricate optimization algorithms as commonly used in existing bi-level planning problems in hybrid energy systems. Finally, the effectiveness and advantages of the proposed model is verified by the numerical results on a case study.

1 Introduction

Developing sustainable energies, particularly promoting the integration of clean energy sources into grid, is a crucial means to address the environmental pollution, the climate change, and the scarcity of fossil fuels (Huang et al., 2009). Consequently, in response to the global energy transition and the increasing prominence of environmental issues, the green energy sources such as photovoltaic and wind powers are receiving more and more attentions. For example, the wind power and photovoltaic installations in China have, respectively, reached 280 GW and 250 GW in year 2020 (Li et al., 2018). However, the intermittent and the fluctuating nature of the renewable energy sources, together with their high degree of uncertainty, lead to a deviation between the renewable energy generation capacity and the energy demand (Bao et al., 2021; Aien et al., 2014; Y et al., 2021). This intermittency, volatility, and anti-peak-shaving characteristics of the renewable energy sources can adversely affect the safe operation of the grid (Pothiya et al., 2008).

Pumped storage power plants, as energy storage facilities, operating on pumping and discharging modes, can be employed to effectively regulate the anti-peak-shaving characteristics of renewable energy sources, thus achieving de-peaking and valley-compensating functions (Zou et al., 2015; Liu et al., 2017). Moreover, hydropower plants possess flexible regulation capabilities (Wen et al., 2021). Obviously, both pumped storage power and hydropower plants are beneficial for mitigating the uncertainty of the renewable energy generation and facilitating the consumption of the renewable energy sources (Abdeltawab and Mohamed, 2017). Consequently, the hybrid energy system of hydropower, pumped storage, and renewable energy has become a new topic direction in modern power system developments.

In order to achieve a maximum economic benefit of the hybrid energy system throughout the duty cycle and ensure its competitiveness in the electricity market, it is essential to realize a rational and efficient allocation of different energy source capacities (Xu et al., 2020). In this direction, numerous efforts have been devoted to the operation and capacity allocation of hybrid energy systems incorporating pumped storage power stations. In the studies of (Baniasad and Ameri, 2012; Wang and Cui, 2014; Zhang et al., 2020), the authors have primarily focused on the economic and environmental issues of the hybrid energy system. The goal of these studies is to minimize the wind power curtailment, the generation cost, the penalties associated with pollutant emissions, and the penalties resulting from renewable energy power curtailments. The models for optimizing the schedule of hybrid energy systems incorporating pumped storage power plants are developed therein. In (Zhang et al., 2020), the authors have considered the integration of wind, photovoltaic, hydropower, thermal power, and other energy sources at a system level for the purpose of optimization their scheduling. In (Wang and Cui, 2014), the authors have investigated the optimal operation of pumped storage power plants in the context of photovoltaic integrations. In (Baniasad and Ameri, 2012), the authors have proposed a joint operation strategy for wind, photovoltaic and pumped storage hydro energy, taking into account the multiple performance benefits. However, a common limitation of these studies is that the capacity allocation of the energy storage systems, and the optimization of their operation and scheduling are considered relatively independently, without establishing a coupling between the two procedures and achieving their coordination.

To address the aforementioned deficiencies of the previously mentioned methodologies in hybrid energy system studies, in recent years, the bi-level programming has been widely applied in system optimizations involving the new energy system optimization. In (Zhao et al., 2014), the authors have used the upper-level procedure to minimize the annual total cost, while the lower-level to minimize the scenario-based distribution network operation cost. The upper-level procedure is used for planning, while the lower-level one performs optimization and simulation based on the upper-level planning. In (Zeng et al., 2017), the authors have employed the upper-level optimization to minimize the total investment cost, and the lower-level one to minimize the operating input. Particle swarm optimization algorithm and the interior point method are respectively used to solve the upper and lower-level optimization problems. Subsequently, most of the solution methodologies for such studies involve the use of complex optimization algorithms to separately solve the upper and lower level optimization problems. In (Luo et al., 2020), the authors have chosen a heuristic algorithm for the upper-level system planning problem, while a sequential quadratic programming algorithm for the lower-level one. In (Chen et al., 2021), the authors have improved a grey wolf algorithm based on tent mapping chaos optimization to solve the optimal capacity configuration of hybrid energy systems.

It should be pointed out that the aforementioned studies have mainly concentrated on a hybrid energy system where the thermal power occupies a large proportion of the system. As explained previously, with the global energy transformation and the concerns on environmental issues, the proportion of the thermal power in a hybrid energy system will be gradually decreased, and a zero-carbon hybrid energy system without any thermal power will emerge. Moreover, the solution approaches for the bi-level model of hybrid energy systems have predominantly been constrained to the application of intricate optimization algorithms for optimizations of the upper and lower-level functions. To bridge the gap between the available studies and the requirement for further hybrid energy system, this paper focuses on the optimal capacity configuration of wind, photovoltaic, hydropower, and pumped storage power system. In this direction, a bi-level programming model for the optimal capacity configuration of wind, photovoltaic, hydropower, and pumped storage power system is derived. To model the operating mode of a pumped storage power station, two 0-1 variables are introduced. To handle the nonconvex lower level programing problem caused by the two 0-1 variables, it is proposed that the 0-1 variables are treated as some uncertain parameters. Also, by treating the 0-1 variables as some uncertain parameters, a two-stage robust optimization procedure to decompose the original problem into a master problem and a subproblem is finally proposed. Moreover, by transforming the min-max form of the master problem using KKT conditions, both the master problem and the subproblem become MILP problems, and can be solved efficiently. Finally, the effectiveness and advantages of the proposed model is verified by solving a case study using the C&CG algorithm.

2 Bi-level model of the proposed hybrid energy systems

The hybrid energy system studied in this paper is consisted of pumped storages, hydro-powers, wind and photovoltaic powers. It uses the flexible regulation capabilities of hydropower and the energy storage capabilities of the pumped storage to mitigate the uncertainty of the renewable energy generation and to facilitate the consumption of the renewable energy sources. To optimize the capacity allocation of hydropower, pumped storage, and renewable energy of a hybrid energy system considering the coupling of different energy sources, a bi-level two-stage robust mathematical programming model is developed.

A bi-level programming, also known as a dual-layer optimization problem, is different from a conventional optimization one in its characteristics of hierarchy, independence, conflict, priority, and autonomy. It is typically mathematically expressed as:

$\left\{\begin{array}{l}\underset{x}{\min }F\left(x,y\right)s.t.\left\{f_1\left(x,y\right)\le 0,\cdots ,f_n\left(x,y\right)\le 0\right\}\\ \underset{y}{\min }G\left(x,y\right)s.t.\left\{g_1\left(x,y\right)\le 0,\cdots ,g_n\left(x,y\right)\le 0\right\}\end{array}\right.(1)$

where, x and y represent the decision variables in the upper and lower-level respectively, F (x, y) and G (x, y) are the objective functions in the upper and lower-level optimizations respectively, f_n and g_n are the corresponding constraint conditions.

In the proposed bi-level optimization model, the upper-level minimizes the investment, while the lower-level optimize the operational plan based on optimized results in the upper-level, in order to achieve maximum economic benefits of the hybrid energy system. The upper-level allocates the capacity to the lower level under the condition that its own constraints are satisfied, and the lower-level designs the optimal power distribution under this capacity and transmits the results to the upper level, thereby influencing the upper level’s decision-making (Boloukat and Foroud, 2018). It can be seen that there is a game relationship between the capacity, the power distribution, and the operation mode in the entire hybrid energy system; and this paper attempts to find a balance between the capacity and the power distribution in order to obtain the maximum economic benefits. The schematic diagram of the proposed bi-level programming model is shown in Figure 1.

FIGURE 1

FIGURE 1. Schematic diagram of a bi-level programming.

2.1 Upper-level optimization model

2.1.1 The objective function

The goal of the upper-level optimization is to minimize the total investment of the whole hybrid energy system by determining the capacity allocation of the pumped storage and the small hydropower in the system. The total investment is composed of three parts: the construction investment, the operation and maintenance investment, and the replacement investment. Consequently, the mathematical expression of the upper-level model is given as:

$\min \left(NPC\right)=\min \left(NP{C}_{\text{pump}}+NP{C}_{HS}\right)(2)$

where, NPC represents the total investment cost, NPC_pump represents the total cost of the pumped storage, and NPC_HS represents the total cost of the small hydropower. The formulas for calculating these costs are:

$NP{C}_{pump}=C_{pump}{P}_{pump\_\max }+{\displaystyle \sum _{n=1}^{T_a}}\frac{C_{OP}{P}_{pump\_\max }}{{\left(1+r\right)}^n}+\frac{C_{rep\_pump}{P}_{pump\_\max }}{{\left(1+r\right)}^{T_{rep\_pump}}}(3)$

where, P_{pump_max} represents the planned installed capacity of the pumped storage unit, C_pump refers to the unit price of the installed capacity per kilowatt, C_OP represents the operation and maintenance costs of the reversible pumped storage unit, T_a signifies the whole duty cycle, r denotes the discount rate, C_{rep_pump} represents the replacement cost of the pumped storage unit, T_{rep_pump} represents the lifespan of the pumped storage unit,

$NP{C}_{\text{HS}}=C_{HS}{P}_{HS\_\max }+{\displaystyle \sum _{n=1}^{T_a}}\frac{C_{OH}{P}_{HS\_\max }}{{\left(1+r\right)}^n}+\frac{C_{rep\_HS}{P}_{HS\_\max }}{{\left(1+r\right)}^{T_{rep\_\text{HS}}}}(4)$

where, P_{HS_max} represents the planned installed capacity of the hydropower unit, C_HS refers to the unit price of the installed capacity per kilowatt, C_OH represents the operating and maintenance costs of the hydropower unit, C_{rep_HS} represents the replacement cost of the hydropower unit, T_{rep_HS} represents the lifespan of the hydropower unit.

2.1.2 The constraints

1) Pumped storage unit constraint

The capacity of a pumped storage unit needs to satisfy the following constraint condition:

$0\le P_{pump\_\max }\le P_{pump\_power\max }(5)$

where P_{pump_powermax} represents the maximum value of the installed capacity of the reversible pumped storage unit.

2) Hydropower unit constraint

The capacity of the hydropower unit needs to satisfy the following constraint condition:

$0\le P_{HS\_\max }\le P_{HS\_power\max }(6)$

where P_{HS_powermax} represents the maximum value of the installed capacity of the hydropower unit.

3) Minimum power constraint

In the entire hybrid energy system, stabilizing the uncertainty of new energy outputs is proposed to be jointly accomplished by the pumped storage and the small hydropower regulations. In addition, there is no any thermal power generation in the system to bear the base load. Consequently, the sum of the installed capacities of the aforementioned two power plants should be not less than the total of the curtailed wind and photovoltaic power at any given time instant. Moreover, the total energy production should also satisfy the load demand with an enough surplus. Therefore, the minimum power constraints on the two energy productions should satisfy the following constrains:

$P_{HS\_\max }+P_{pump\_\max }\ge 2\max \left\{P_{w-q}\left(t\right)+P_{pv-q}\left(t\right),L\left(t\right)-P_W\left(t\right)-P_{PV}\left(t\right)\right\}(7)$

where, P_w-q (t) represents the curtailed wind power, P_pv-q (t) represents the curtailed photovoltaic power, L (t) represents the load, P_W (t) represents the wind power output, and P_PV (t) represents the photovoltaic power output, at time t.

2.2 Lower-level optimization model

2.2.1 The objective function

The goal in the proposed lower-level programing is to maximize the economic benefits of the hybrid energy system by optimizing its operational mode, given the capacity allocation from the upper-level procedure. Mathematically, the lower-level problem is formulated as:

$\max \left(I\right)=\max \left\{{\displaystyle \sum _{t=1}^T}EP\left(t\right)\cdot [P_{PV}\left(t\right)+P_W\left(t\right)+P_{HS}\left(t\right)+P_{pump}\left(t\right)]\right\}(8)$

where, EP (t) represents the time-of-use electricity price, P_HS(t) represents the electricity sold by a small hydropower power plant at time t, P_pump (t) represents the electricity sold by a pumped storage power station at time t, T represents the number of time periods, I represents the total revenue obtained from optimizing the operation.

The electricity sold by a pumped storage power station is calculated from:

$P_{pump}\left(t\right)=\left\{\begin{array}{l}-1.1\times \frac{P_{ch}\left(t\right)}{{\eta }_{ch}}\\ {\eta }_{dis}{P}_{dis}\left(t\right)\end{array}\right.(9)$

where, P_ch (t) represents the power consumed when the pumped storage power station operates in the pumping mode, so the electricity sold is negative as it requires purchasing electricity; P_dis (t) represents the power generated when the pumped storage power station operates in the discharging mode, so the electricity sold is positive. η_ch and η_dis represent the efficiencies of the pumping and discharging processes, respectively.

2.2.2 The constraints

1) Operation constraints of the pumped storage power station

In the operation of a pumped storage power station, different factors such as the maximum power of the units and the upstream reservoir capacity should be considered. Consequently, the following constraints are applied.

(a) Power constraint

The constraints applied to the power include:

$\left\{\begin{array}{l}0\le P_{dis}\left(t\right)\le \min \left(P_{pump\_\max },E_{pump\_\max }/h\right)\\ 0\le P_{ch}\left(t\right)\le \min \left(P_{pump\_\max },E_{pump\_\max }/h\right)\end{array}\right.(10)$

where, E_{pump_max} represents the electricity generation corresponding to the maximum capacity of the upstream reservoir of the pumped storage power plant. It limits the maximum power in the operation of the pumped storage plant to be smaller than the minimum value between the maximum installed capacity of the units and the maximum electricity generation capacity based on the reservoir storage capacity.

(b) Reservoir capacity constraint

The constrains applied to the reservoir capacity are:

$0\le {\displaystyle \sum _{t=1}^{N_k}}{P}_{pump}\left(t\right)\cdot \Delta t+0.5E_{pump\_\max }\le E_{pump\_\max }(11)$

This constraint assumes that the initial reservoir capacity of the upstream reservoir is half of its maximum capacity. N_k represents the kth time period, Δt represents the length of the time periods, ensuring that the upstream reservoir capacity at each time is not smaller than zero and does not exceed its maximum capacity.

(c) Water inflow and outflow constraint

The constraint for the water inflow and the outflow is:

${\displaystyle \sum _{t=1}^T}{P}_{pump}\left(t\right)\cdot \Delta t=0(12)$

This constraint is used to ensure that the consumed electricity and generated electricity of the pumped storage power station remain consistent within a day, guaranteeing that the proposed model can still be applicable after 1 day.

2) Operation constraints of the small hydropower station

Similar to a pumped storage power station, a small hydropower station also needs to meet the following three constraints in operation.

(a) Power constraint

$0\le P_{HS}\left(t\right)\le \min \left(P_{HS\_\max },E_{HS\_\max }/h\right)(13)$

where E_{HS_max} represents the electricity generation corresponding to the maximum capacity of the upstream reservoir of the hydropower plant.

(b) Reservoir capacity constraint

$0\le {\displaystyle \sum _{t=1}^{N_k}}{P}_{HS}\left(t\right)\cdot \Delta t+0.5E_{HS\_\max }\le E_{HS\_\max }(14)$

(c) Water inflow and outflow constraint

${\displaystyle \sum _{t=1}^T}\left[P_{HSK}\left(t\right)\cdot \Delta t-P_{HS}\left(t\right)\cdot \Delta t\right]=0(15)$

where P_HSK(t) represents the corresponding electricity generation capacity for the inflow volume of the water from the upstream at time t.

3 Linearization and solution strategy

3.1 0-1 Variables and a two-stage robust optimization model

A pumped storage power station can not work simultaneously on the pumping and discharging modes. To model this phenomena, two 0-1 variables are introduced in Eq. 10. The two variables respectively indicate that the unit operates on pumping or discharging mode. Moreover, 0 represents that the unit does not operate in the mode in question, while 1 represents that the unit operates in the mode in question. By introducing these two 0-1 variables, the summation of the two variables at a time instant t should not exceed 1 to prevent the occurrence of the two working states simultaneously. Moreover,

$\left\{\begin{array}{l}0\le P_{dis}\left(t\right)\le Z_{dis}\left(t\right)\cdot \min \left(P_{pump\_\max },E_{pump\_\max }/h\right)\\ 0\le P_{ch}\left(t\right)\le Z_{ch}\left(t\right)\cdot \min \left(P_{pump\_\max },E_{pump\_\max }/h\right)\\ Z_{dis}\left(t\right)+Z_{ch}\left(t\right)\le 1Z_{dis}\left(t\right),Z_{ch}\left(t\right)\in \left\{\mathrm{0,1}\right\}\end{array}\right.(16)$

After the introduction of the aforementioned two 0-1 variables, the corresponding lower lever optimization problem becomes a nonlinear and nonconvex one, giving rise to difficulties in developing an efficient and accurate solution methodology. On the other hand, the minimization of the investment cost is only related to the capacities of the pumped storage power station and the small hydropower station, and is independent of the two 0-1 variables. In this point of view, the capacity planning and operation optimizing can be solved separately, and implemented in two consecutive phases. More specially, in the first phase, the decision on the capacity allocation is made, and are then transferred to the second phase. To transform the nonconvex lower level problem to a convex one, it is proposed that the 0-1 variables are treated as some uncertain parameters related to the second-stage decision variables, and are characterized by an uncertain set. As a result, a two-stage robust optimization problem is developed for the lower–level programming, and mathematically formulated as (Zeng and Zhao, 2013):

$\left\{\begin{array}{l}\underset{y}{\min }{c}^{T}y+\underset{z\in Z}{\max }\underset{x\in F\left(y,z\right)}{\max }{b}^{T}x\\ s.t.Ay\ge d,Gx\ge h-Ey-Mz\end{array}\right.(17)$

where, x represents the decision variables for the optimal operation of the pumped storage and the small hydropower; y represents the decision variables for the capacity allocation; c, b, d, h, A, G, E, and M represent the deterministic parameters related to the decision variables; z represents the 0-1 variables, and the uncertain set composed of all possible values of z is denoted by Z; F (y,z) represents the feasible domain of the inner level in the second stage, where the first stage decision variables y and uncertain parameter z are both fixed values at this phase. The corresponding robust “max max” problem in Eq. 17 is readily to be solved by any existing technique. Moreover, in Eq. 17, c^Ty corresponds to the upper-level model in Eq. 2, while b^Tx corresponds to the lower-level model in Eq. 8; z represents the 0-1 variables mentioned in Eq. 16. The constraints here include all the constraints of Eqs 5–7; Eqs 10–15.

After the aforementioned manipulations, the proposed optimization model is no longer a nonconvex optimization problem with 0-1 variables, but rather transformed into a convex two-stage robust optimization problem. It is readily to solve the corresponding problem by using a robust optimizer.

3.2 C&CG algorithm

To simplify the solution methodologies, the C&CG algorithm is used to solve the proposed two-stage robust optimization problems and its fundamental procedure is explained as: initially, only the decision variables and constraints of the first stage are considered, which is equivalent to taking a relaxed version of the original problem. The optimized decision variables of the first stage are then fixed, and the corresponding subproblem of the second stage is solved to find a possible worst-case scenario. The decision variables and constraints corresponding to this scenario are added to the master problem. As the number of variables and constraints in the main problem increases, the objective function values obtained from solving the master problem and subproblem gradually approaches each other until the algorithm converges.

The general form of the master problem is:

$\left\{\begin{array}{l}\underset{y}{\min }{c}^{T}y+\eta \\ s.t.Ay\ge d,G{x}^l\ge h-Ey-M{z}^l\\ \eta \ge b^T{x}^l\end{array}\right.(18)$

where, η represents the objective function of the second stage, x^l and u^l denote the decision variables and uncertain parameter values identified under the recognized scenario l.

The general form of the subproblem is:

$\left\{\begin{array}{l}\underset{z\in Z,x\in F\left(z,y\right)}{\max }{b}^{T}x\\ s.t.Gx\ge h-Ey-Mz\end{array}\right.(19)$

The lower bound of this subproblem determined by solving the master problem, while the solution of the subproblem provides an upper bound for the original problem. The upper and lower bounds are continuously updated by iterations, and their expressions are as follows:

$\left\{\begin{array}{l}LB=\max \left\{c^T{y}_k^{*}+{\eta }_k^{*},LB\right\}\\ UB=\min \left\{b^T{x}_k^{*},UB\right\}\end{array}\right.(20)$

where, y* k represents the value of the decision variables in the first stage in the kth iteration, x* k represents the value of the decision variables in the second stage in the kth iteration, η* k represents the objective value in the second stage in the kth iteration, UB and LB represent the upper and lower bound. When the condition |UB-LB|≤ɛ is satisfied, the iteration is stopped. To facilitate the numerical implementations of the proposed methodology, its flowchart is intuitively shown in Figure 2.

FIGURE 2

FIGURE 2. Flow chart of C&CG algorithm.

3.3 KKT equivalence

The Karush-Kuhn-Tucker (KKT) condition is usually used to simplify and linearize the double-layer structure and nonlinear terms existing in optimization models.

When solving the master problem, there exists a min-max problem that cannot be solved directly. However, for the inner level function in the second stage, the decision variables and uncertain parameters in the first stage are fixed, so the subproblem becomes a continuous linear optimization problem. KKT conditions can be used for reasonable equivalence (Korani and Eydi, 2021), that is, the lower-level objective function and constraint conditions are equivalent to KKT conditions, and then these KKT conditions are added to the upper-level model to form a complementary mathematical programming problem.

4 Case study

To validate the effectiveness and the applicability of the proposed model and methodology for the optimal capacity allocation of a hybrid energy system, the numerical results on a case study are given.

4.1 Prototype hybrid energy system

A typical daily scene in the southwestern part of China is selected as the scenario for optimizing and scheduling the hybrid energy system. The system is equipped with a total installed capacity of 207.5 MW wind power units, a total installed capacity of 1000 MW photovoltaic units, and a yet-to-be-optimized installed capacity of small hydropower and pumped storage.

In this study, the time-of-use electricity prices from an industrial park electricity trading in China are used for the system operation optimization in the lower-level planning model (Huang et al., 2022). The fluctuation trend of electricity prices is shown in Figure 3, indicating the presence of peak-valley fluctuations. Prices are higher during periods of higher electricity load, such as from 11:00 to 14:00 and 18:00 to 22:00, and lower during the night when electricity load is lower. This reflects that electricity prices are determined by the market.

FIGURE 3

FIGURE 3. Electricity price variation in 1 day.

The predicted loads, photovoltaic, and wind power outputs from an industrial park for the typical day in summer are shown in Figures 4–6, respectively. The technical and economic parameters of pumped storage and small hydropower units are given in Table 1, 2. From Figures 4–6, it can be observed that the typical daily loads exhibit two peaks before and after 13:00 and 18:00, with low wind power output and high photovoltaic output. However, the photovoltaic output shows significant fluctuations. The photovoltaic output roughly corresponds to the typical daily loads and demonstrates strong load tracking capabilities with peak-shaving characteristics.

FIGURE 4

FIGURE 4. Typical daily load variations.

FIGURE 5

FIGURE 5. Typical daily photovoltaic output characteristics.

FIGURE 6

FIGURE 6. Typical daily wind power output characteristics.

TABLE 1

TABLE 1. Technical and economic parameters of the pumped storage units.

TABLE 2

TABLE 2. Technical and economic parameters of the small hydro units.

4.2 Numerical results

In the numerical implementations of the proposed methodology, the optimization period for the typical day is T = 24 h, with a time scale of Δt = 1 h. In order to analyse the impact of different energy storage modes in a hybrid energy system on the operational strategies of various power stations and the economic benefits throughout the duty cycle, and to verify the feasibility of optimizing the capacity allocation of the hybrid energy system using the proposed bi-level planning model, two different cases, the hybrid energy systems with and without electricity storages, are considered.

Using the model parameters and cost parameters set in Section 4.1, the planning model proposed in the paper is solved by the C&CG algorithm. According to the typical daily loads and renewable energy output, it is determined that the total installed capacity of the small hydropower and pumped storage needs to reach 1200 MW. The optimized capacity allocation scheme for the hybrid energy system with an energy storage is 500 MW for a pumped storage and 700 MW for a small hydropower. On the other hand, without any energy storage, the installed capacity of hydropower is 1200 MW. Obviously, with and without an electricity storage in the hybrid energy system will significantly affect the capacity allocation of the power plants and therefore influence the economic efficiency of the capacity allocation scheme over the entire duty cycle, as detailed in the proceeding sections. The model parameters and constraints can be abstracted from Table 1, 2.

The following will investigate the optimal capacity configuration of the system obtained through the planning model from the perspectives of the operation mode and the economic benefits of the hybrid energy system. This analysis aims to verify the effectiveness of the planning model in solving the capacity optimization configuration problem of the hybrid energy system.

4.2.1 Operation mode of the system

The optimal operation results of the small hydropower plant with electricity storages is shown in Figure 7 (regardless of the dead water level). From the figure, it can be observed that the small hydropower plant adopts the following operational strategies based on the market electricity price: during the highest electricity price periods 11:00–14:00 and 18:00–22:00, the plant releases waters to generate electricity to maximize economic benefits while meeting all operational constraints. During the lowest electricity price period from 4:00 to 7:00 and the relatively lower electricity price period from 16:00 to 18:00, the water is stored by upstream inflow into the reservoir, so as to have sufficient water volumes for power generations during a high electricity price period.

FIGURE 7

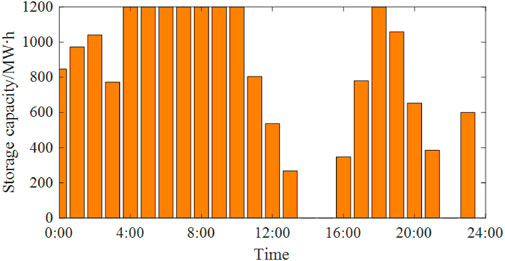
FIGURE 7. Optimized operation results of the hydropower station in the system with electricity storages.

In a system without any electricity storage, the operation results of the small hydropower plant is to continuously release waters through water turbine to generate electricity and sell it to the grid based on the natural flow rate. In this mode, only a small portion of the water flow exceeding the planned turbine capacity can be stored and sold in the peak electricity price periods. As a result, the annual revenue from electricity sales is relatively low, which is also reflected in Table 3.

TABLE 3

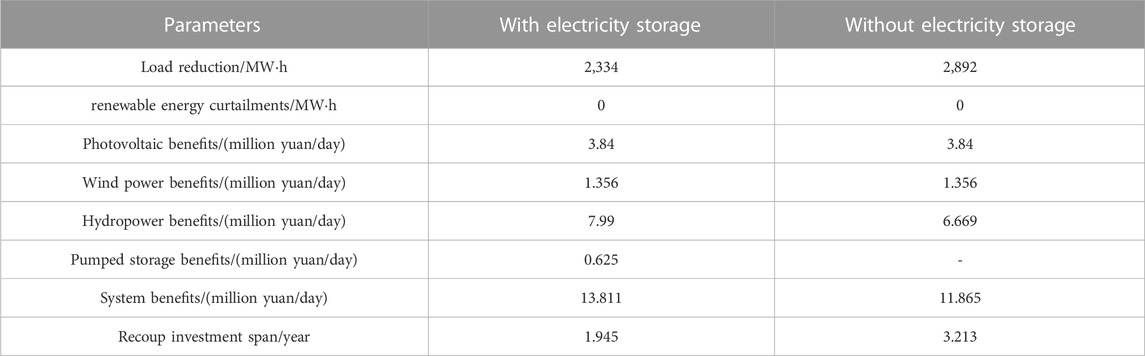
TABLE 3. Comparison of operation results of the hybrid energy system with/without electricity storages.

The hourly pumping and discharge volumes of the reversible pump-turbine in the hybrid energy system with electricity storages are shown in Figure 8. In the lower-level planning model optimization operation mode, the pumped storage power station can receive powers generated by other power plants during the off-peak period (22:00 to 7:00), as well as purchase power from the grid. In the high electricity price periods (12:00 and 21:00), the power station releases water to generate electricity, thus ensuring profitable power sales for the system. By incorporating pumped storage power stations, the hybrid energy system enriches the power supply options and greatly affects the increase in the annual revenue from electricity sales.

FIGURE 8

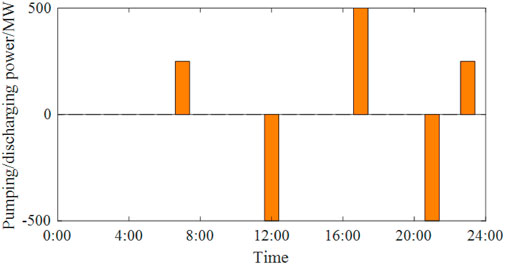
FIGURE 8. Optimized operation results of the pumped storage power station in the system with electricity storages.

4.2.2 Economic benefits of the system

The optimal operation results of the hybrid energy system are shown in Figure 9, and the comparisons of the operational outcomes with and without electricity storages according to various parameters are tabulated in Table 3.

FIGURE 9

FIGURE 9. Optimized operation results of the hybrid energy system.

The recoup investment span for the hybrid energy system with an electricity storage is 1.945 years, compared to 3.213 years in the system without any electricity storage. This indicates that, under the precondition of meeting the optimized operational mode of the hybrid energy system, the system with an energy storage has a higher recoup investment rate compared to that of the system without any energy storage, other thing being equal.

Furthermore, the hybrid energy system with an electricity storage also reduces load reduction to a certain extent.

In addition to the recoup investment span of the hybrid energy system, the benefits obtained during its operation are also important indicators to measure the economy of the system. As shown in Table 3, the hybrid energy system with an energy storage generates a daily revenue of 13.811 million Chinese yuan from electricity sales, which is 1.16 times higher than that in the system without any energy storage.

The above results indicate that the hybrid energy system with an electricity storage can bring significant economic benefits throughout the project cycle, playing a crucial role in the development and investment of renewable energy generation companies.

5 Conclusion

This paper explores the capacity configuration and operational scheduling optimization of the pumped storage and small hydropower plants for a hybrid energy system of wind power, photovoltaic, small hydropower, and pumped storage power plants. In this respect, a two-stage robust optimization model and the corresponding solution methodology are proposed. The numerical results on a case study have demonstrated that integrating the energy storage in hybrid energy systems enhances the consumption capability of renewable energy while ensuring economic benefits, validating that the presented work effectively achieves the coordinated development between the energy storage and the new energy sources.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

HZ: Supervision, Conceptualization, Project administration, Resources, Writing–review and editing. LL: Writing–original draft, Investigation, Conceptualization. LS: Writing–original draft, Formal Analysis, Software, Resources. PZ: Data curation, Resources, Validation, Writing–review and editing. YW: Methodology, Conceptualization, Investigation, Writing–original draft. HJ: Methodology, Investigation, Validation, Writing–review and editing, Writing–original draft, Software. SY: Investigation, Writing–review and editing, Supervision, Funding acquisition.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

Authors HZ, LL, LS, PZ and YW were employed by Southwest Branch of SGCC.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdeltawab, H. H., and Mohamed, A. R. I. (2017). Mobile energy storage scheduling and operation in active distribution systems. IEEE Trans. Industrial Electron. 64 (9), 6828–6840. doi:10.1109/tie.2017.2682779

CrossRef Full Text | Google Scholar

Aien, M., Fotuhi-firuzabad, M., and Rashidinejad, M. (2014). Probabilistic optimal power flow in correlated hybrid wind-photovoltaic power systems. IEEE Trans. Smart Grid 5 (1), 130–138. doi:10.1109/tsg.2013.2293352

CrossRef Full Text | Google Scholar

Baniasad, A. I., and Ameri, M. (2012). Techno-economic feasibility analysis of stand-alone renewable energy systems (PV/bat, wind/bat and hybrid PV/wind/bat) in Kerman, Iran. Energy Sources Part B Econ. Plan. Policy 7 (1), 45–60. doi:10.1080/15567240903330384

CrossRef Full Text | Google Scholar

Bao, Y., Zhang, J., Xu, T., et al. (2021). Online transient stability risk assessment method considering the uncertainty of wind power output. South. Power Syst. Technol. 15 (11), 42–48. doi:10.13648/j.cnki.issn1674-0629.2021.11.005

CrossRef Full Text | Google Scholar

Boloukat, M. H. S., and Foroud, A. A. (2018). Multiperiod planning of distribution networks under competitive electricity market with penetration of several microgrids part-I: modeling and solution methodology. IEEE Trans. Industrial Inf. 4 (11), 4884–4894. doi:10.1109/tii.2018.2807396

CrossRef Full Text | Google Scholar

Chen, M., Tang, Y., Shang, W., et al. (2021). Optimal capacity configuration of pumped-storage power station in wind-pv-fire-pump storage system. Electr. Power Constr. 42 (11), 72–81. doi:10.12204/j.issn.1000-7229.2021.11.008

CrossRef Full Text | Google Scholar

Huang, C., Liu, H., Ma, B., et al. (2022). Research on optimal operation of shared energy-storage power station applying nash negotiation. Electr. Power Constr. 43 (02), 1–9.

Google Scholar

Huang, D., Shu, Y., Ruan, J., and Yi Hu, (2009). Ultra high voltage transmission in China: developments, current status and future prospects. Proc. IEEE 97 (3), 555–583. doi:10.1109/jproc.2009.2013613

CrossRef Full Text | Google Scholar

Korani, E., and Eydi, A. (2021). Bi-level programming model and KKT penalty function solution approach for reliable hub location problem. Expert Syst. Appl. 184, 115505. doi:10.1016/j.eswa.2021.115505

CrossRef Full Text | Google Scholar

Li, J., Liu, G., and Zhang, S. (2018). Smoothing ramp events in wind farm based on dynamic programming in energy internet. Front. Energy 12 (4), 550–559. doi:10.1007/s11708-018-0593-8

CrossRef Full Text | Google Scholar

Liu, Y., Tan, S., and Jiang, C. (2017). Interval optimal scheduling of hydro-PV-wind hybrid system considering firm generation coordination. IET Renew. Power Gener. 11 (1), 63–72. doi:10.1049/iet-rpg.2016.0152

CrossRef Full Text | Google Scholar

Luo, S., Hu, W., Huang, Q., et al. (2020). Optimization of photovoltaic/small hydropower/pumped storage power station system sizing under the market mechanism. Trans. China Electrotech. Soc. 35 (13), 2792–2804. doi:10.19595/j.cnki.1000-6753.tces.191843

CrossRef Full Text | Google Scholar

Pothiya, S., Ngamroo, I., and Kongprawechnon, W. (2008). Application of multiple tabu search algorithm to solve dynamic economic dispatch considering generator constraints. Energy Convers. Manage 49 (4), 506–516. doi:10.1016/j.enconman.2007.08.012

CrossRef Full Text | Google Scholar

Wang, H., and Cui, J. (2014). Optimal operation of pumped hydro energy storage in power system with large integration of photovoltaic generation. Power Syst. Technol. 38 (8), 2095–2101. doi:10.13335/j.1000-3673.pst.2014.08.012

CrossRef Full Text | Google Scholar

Wen, J., Liu, J., Wen, Z., et al. (2021). Capacity allocation method for wind-solar-hydro-storage complementary system considering time and spatial transfer characteristics of load. Electr. Power 54 (02), 66–77+97. doi:10.11930/j.issn.1004-9649.202002151

CrossRef Full Text | Google Scholar

Xu, X., Hu, W., Cao, D., Huang, Q., Chen, C., and Chen, Z. (2020). Optimized sizing of a standalone PV-wind-hydropower station with pumped-storage installation hybrid energy system. Renew. Energy 147, 1418–1431. doi:10.1016/j.renene.2019.09.099

CrossRef Full Text | Google Scholar

Yang, X., Ding, L., Li, Y., et al. (2021). Study on optimal allocation of hybrid energy storage system considering wind power uncertainty. Power Dsm 23 (06), 69–74. doi:10.3969/j.issn.1009-1831.2021.06.014

CrossRef Full Text | Google Scholar

Zeng, B., and Zhao, L. (2013). Solving two-stage robust optimization problems using a column-and-constraint generation method. Operations Res. Lett. 41 (5), 457–461. doi:10.1016/j.orl.2013.05.003

CrossRef Full Text | Google Scholar

Zeng, Q., Zhang, B., Fang, J., and Chen, Z. (2017). A bi-level programming for multistage co-expansion planning of the integrated gas and electricity system. Appl. Energy 200, 192–203. doi:10.1016/j.apenergy.2017.05.022

CrossRef Full Text | Google Scholar

Zhang, G., Chen, Y., Zhang, J., et al. (2020). Research on optimization of day-ahead dispatching of wind power-photovoltaic-hydropower-thermal power-pumped storage combined power generation system. Acta Energiae Solaris Sin. 41 (8), 79–85. doi:10.19912/j.0254-0096.2020.08.011

CrossRef Full Text | Google Scholar

Zhao, Y., An, Y., and Ai, Q. (2014). Research on size and location of distributed generation with vulnerable node identification in the active distribution network. Transm. Distribution 8 (11), 1801–1809. doi:10.1049/iet-gtd.2013.0887

CrossRef Full Text | Google Scholar

Zou, J., Lai, X., and Wang, N. (2015). Mitigation of wind curtailment by coordinating with pumped storage. Proc. CSEE 39 (9), 2472–2477. doi:10.13335/j.1000-3673.pst.2015.09.015

CrossRef Full Text | Google Scholar