- College of Intelligent Systems Science and Engineering, Hubei Minzu University, Enshi, China
Combined economic/emission dispatch (CEED) is generally studied using analytical objective functions. However, for large-scale, high-dimension power systems, CEED problems are transformed into computationally expensive CEED (CECEED) problems, for which existing approaches are time-consuming and may not obtain satisfactory solutions. To overcome this problem, a novel data-driven surrogate-assisted method is introduced firstly. The fuel cost and emission objective functions are replaced by improved Kriging-based surrogate models. A new infilling sampling strategy for updating Kriging-based surrogate models online is proposed, which improves their fitting accuracy. Through this way, the evaluation time of the objective functions is significantly reduced. Secondly, the optimization of CECEED is executed by an improved non-dominated sorting genetic algorithm-II (NSGA-II). The above infilling sampling strategy is also used to reduce the number of evaluations for original mathematic fitness functions. To improve their local convergence ability and global search abilities, the individuals that exhibit excellent performance in a single objective are cloned and mutated. Finally, information about the Pareto front is used to guide individuals to search for better solutions. The effectiveness of this optimization method is demonstrated through simulations of IEEE 118-bus test system and IEEE 300-bus test system.
1 Introduction
In power systems, combined economic/emission dispatch (CEED) problem involves the minimizations of cost and emission while meeting load demand and satisfying operation constraints (Xu et al., 2022). It is an optimization problem with strongly real-time requirements (Li et al., 2020). Mathematical methods for solving it include nonlinear and linear programming methods (Lai et al., 2022). Meta-heuristic algorithms are employed to solve it. For example, multi-objective hybrid bat algorithm (MHBA) (Liang et al., 2018), non-dominated sorting genetic algorithm (NSGA) (Deb et al., 2002), and the improved non-dominated sorting genetic algorithms (Muthuswamy et al., 2015), etc.
However, the above approaches are better suitable to solve CEED problems in low-dimension, small-scale power systems. Along with the expansion of the power grid, the complexity of a power system is greatly increased (Wang et al., 2023), which increases the decision-making dimension of CEED problems (Qu et al., 2023). Unfortunately, existing methods become inefficient when applied to computationally expensive combined economic/emission dispatch (CECEED) problems (Zhang and Yu, 2023). Existing methods are often time-consuming for real-time dispatching, and their solutions generally have low accuracies or may not even converge (Li and Xu, 2018). Therefore, for large-scale, high-dimension power systems, traditional CEED problems are transformed into CECEED problems (Li et al., 2022). New method that is suitable for solving CECEED problems is urgently required.
Data-driven surrogate-assisted schemes are widely applied for solving computationally expensive problems by employing surrogate models (Yu et al., 2022). Accurate surrogate model is indispensable in data-driven optimization (Gao et al., 2023). Many kinds of surrogate models are applied in industrial community including support vector regression (SVR) models, artificial neural network (ANN), linear regression models, etc. In Ref. (Lin et al., 2023), SVR-based NSGA was applied for solving dispatching problems. Objective functions were replaced by SVR models while reducing the computing time. However, it was powerless for solving high-dimension dispatching problems. In Ref. (Pang et al., 2023), a data-driven bat algorithm was proposed for solving economic dispatch (ED) problems. It allowed the ED problems to be solved, but the computing time was spent still relatively long. Ref. (Linka et al., 2021). proposed a data-driven ANN. Few data were used to build ANN with good performance. Though it reduced computing time, the accuracy was low. Based on the above analysis, the data-driven surrogate-assisted method shows its feasibility and superior performance in solving complex scheduling problems.
Effective meta-heuristic algorithms are also the keys to reducing the execution time. For example, a dynamic crowding distance was added to NSGA-II (Muthuswamy et al., 2015), and prohibited operating zones (POZs) were considered for improving the accuracy. However, it did not incorporate sufficient guidance for searching, and the computing time remained a problem. MHBA (Liang et al., 2018) searched each single dimension for excellent solutions in CEED problems. To reduce computation time, parallel computing was used. However, MHBA could only deal with the CEED problem in terms of improving the performance of the algorithm, and does not take into account the time-consuming objective function of CEED model. Thus, it is important to build a meta-heuristic algorithm for fast and accurate convergence in CECEED problems.
Based on the above analyses, CECEED problems need to be solved at two levels. The first level involves employing accurate surrogate models to replace computationally expensive objective functions. The second level involves enhancing convergence and search ability of a meta-heuristic algorithm. In this paper, a novel data-driven surrogate-assisted NSGA-II is proposed for solving CECEED problems. The approach combines a Kriging surrogate model and an enhanced NSGA-II to reduce the execution time. Firstly, an online data-driven Kriging-based surrogate model is introduced for replacing objective functions. Secondly, the original NSGA-II is improved to enhance its performance and to determine what data points should be used for updating Kriging model. The major outcomes of this paper are.
(i) An improved online Kriging surrogate model is proposed. Mathematic fuel cost and emission functions in CECEED problems are replaced by online Kriging-based surrogate models to reduce evaluation time. Specifically, initial Kriging surrogate model is constructed by considering random candidate solutions. As the optimization proceeds, additional sampling points, selected from the Pareto front, are added into the initial data set which is utilized for updating Kriging surrogate models. By this way, evaluation time, accuracy, and stability of the proposed surrogate model are improved.
(ii) Two improved strategies are applied to enhance convergence and uniformity of Pareto front. Furthermore, more accurate dispatching decisions of CECEED problems can be obtained. Convergence and uniformity of the Pareto front are intuitively reflected in the Euclidean distance between individuals. The convergence is improved by reducing the distance between individuals far from the Pareto front and individuals on the Pareto front. The uniformity is then improved by increasing the Euclidean distance between individuals that are too close to each other.
(iii) Two novel methods for enhancing the global and local search capabilities of NSGA-II are proposed. Furthermore, more diverse dispatching decisions of CECEED problems can be obtained. Firstly, a cloned edge particles search approach is proposed to improve both capabilities. Secondly, because the search performance can be visualized in terms of Pareto front extensibility, a linear combination method based on the position relationship between current population extreme values and Pareto front extreme values is proposed for improving the extensibility.
The remainder of this paper is organized as follows. Section 2 describes traditional CEED problem and CECEED problems. Section 3 describes an online Kriging-based data-driven surrogate model and Kriging-based NSGA-II (K-NSGA-II). Section 4 presents simulation results from the proposed method and existing approaches on IEEE 118-bus and 300-bus test systems. Section 5 summarizes this paper by showcasing its contributions and suggests some research directions for future work.
2 Problems description
This section describes CEED problems and CECEED problems. It is also important to build data-driven surrogate models for CECEED problems (Li et al., 2021). The objective functions and constraints are given as follows.
2.1 Objective functions and constraints
The objective functions (Sheng et al., 2023) of fuel cost and pollutant emission are described as follows. The first objective is minimizing the total cost:
where
The second objective is minimizing the emission which is caused by fuel burning. Atmospheric pollutants such as sulfur oxides (SOx) and nitrogen oxides (NOx) produced by units can be simulated separately. However, for comparison purposes, the total emission of these pollutants (a comprehensive pollution emission model) is the sum of the quadratic and exponential functions (the exponential function provides more accurate representation):
where
The constraints are described as follows.
(1) Active/reactive power constraints
where
where
(2) Power balance constraints and load flow calculation
The power balance can be satisfied with load flow calculation:
where
where
(3) Voltage constraints
where
(4) Line flow constraints
where
(5) Ramp rate constraints
where
(6) Prohibited operating zones (POZs) constraints
where
2.2 Descriptions of CECEED problems
Computationally expensive optimization problem refers to a class of optimization problems that require expensive or even unaffordable costs when evaluating alternative solutions. This class of problems exists widely in many importantly practical application scenarios. On one hand, “computationally expensive” means that the evaluation itself needs to consume a lot of time or other expensive costs. On the other hand, it also includes some problems can be transferred to computationally expensive optimization problem within a time-sensitive scene.
As to CECEED problems, on one hand, the computationally expensive challenge is caused by the high-dimension decision variables. On the other hand, due to the time-sensitive dispatching cycle, the CEED problems become computationally expensive. Thus, it is urgent to find a suitable method for solving CECEED problems quickly and accurately.
To reduce execution time of CECEED problems, surrogate-assisted technology can be employed. Original objective functions are replaced by trained surrogate models. The replacements of objective functions reduce evaluation time.
3 Description of Kriging-assisted optimization approach
This section describes the Kriging-assisted optimization approach for CECEED problems. Kriging models are constructed for replacing objective functions. To enhance accuracy of surrogate model, a novel infilling sampling strategy is proposed to update Kriging-based model online. The proposed K-NSGA-II method is employed to execute the optimization of CECEED. As the iterations proceed, the selected candidate solutions from the Pareto front are used not only for the actual evaluation, but also for the updating of the Kriging-based surrogate model.
3.1 Kriging-based surrogate model
3.1.1 Modeling of surrogate model
Existing approaches for solving CECEED problems usually require long time (Sharifian and Abdi, 2023), which is too long for scheduling cycle. Some methods suffer from “curse of dimensionality”, which results in non-convergence. To overcome this drawback, Kriging model is improved for replacing original objective functions with short evaluation time (Li et al., 2022).
The input data of Kriging surrogate model is a certain candidate solution (
where
where
where
where
Compared with original objective functions, Kriging-based surrogate models significantly reduce the evaluation time. Different original objective functions (fuel cost function without valve point effect, fuel cost function with valve point effect, and emission function) for the CECEED in IEEE 118-bus test system are chosen for verifying the effectiveness of Kriging-based surrogate models. Total runtimes (sum of 50 runtimes) of original functions are 0.001982 s, 0.001878 s, and 0.003166 s, respectively. Total runtimes (sum of 50 runtimes) of surrogate models are 0.000792 s, 0.000458 s, and 0.002062 s, respectively. The Kriging model reduce the evaluation time of three objective functions by 60.04%, 59.64%, and 34.87%, respectively. This demonstrates that Kriging model greatly reduces the evaluation time of objectives.
3.1.2 Update of Kriging-based surrogate model
Due to the remarkable fluctuation of data, the accuracy of the Kriging model might not be sufficient (Qian et al., 2023). Kriging model is established on the principle that expected value is similar to that of nearby points. This principle leads to inaccurate predictions of volatile points by the Kriging-based surrogate model. To overcome this drawback, a novel infilling sampling strategy is proposed. The schematic diagram of the proposed infilling sampling strategy is shown as Figure 1A. As the iteration goes on, Pareto front is constantly updated. Some points (circular marks in Figure 1A) with better convergence and diversity occur. However, these points are not included in the data set of the trained Kriging surrogate model. This results in a decrease in the accuracy of the trained surrogate model (The fitting accuracy near the circular marks is lower than that near the fork marks). Thus, these points with circular marks can be added to the data set for updating the Kriging surrogate model.
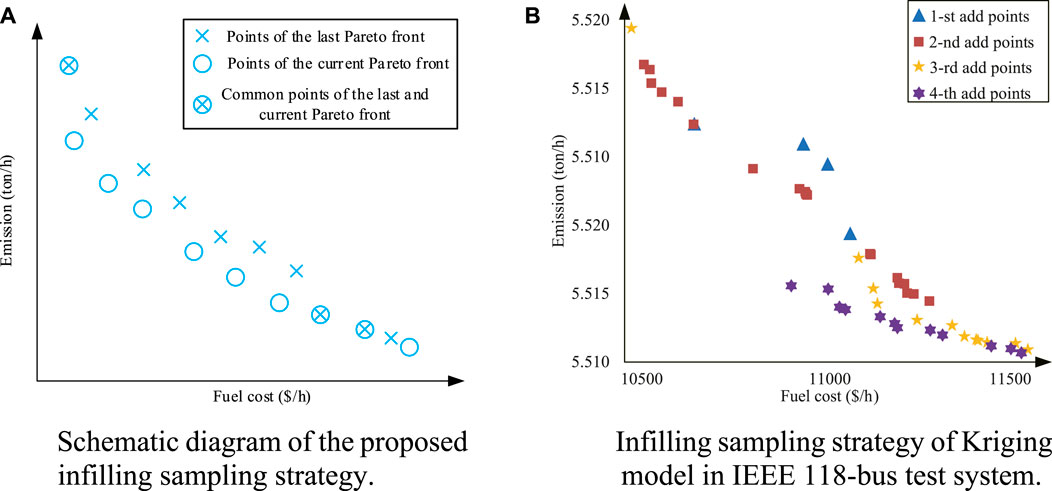
FIGURE 1. The proposed infilling sampling strategy. (A) Schematic diagram of the proposed infilling sampling strategy. (B) Infilling sampling strategy of Kriging model in IEEE 118-bus test system.
Figure 1A Schematic diagram of the proposed Figure 1B. Infilling sampling strategy of Kriging infilling sampling strategy. model in IEEE 118-bus test system.
To further illustrate the effectiveness of the proposed infilling sampling strategy, a CECEED optimization of IEEE 118-bus system is taken as an example. The process of adding points in this strategy is shown in Figure 1B. This strategy enhances the accuracy degree of Kriging model. The inspiration comes from changes in the Pareto front. As the iteration proceed, Pareto front is continuously updated. Assume that there are 100 iterations, and the current Pareto front is recorded every 20 iterations. Candidate solutions, which are inconsistent with the last recorded Pareto front, are selected from the current Pareto front. They are then computed by the original objective functions. This means that the real fitness values are generated, representing the latest optimization information (sampling). The selected points are added to update Kriging-based surrogate models (infilling).
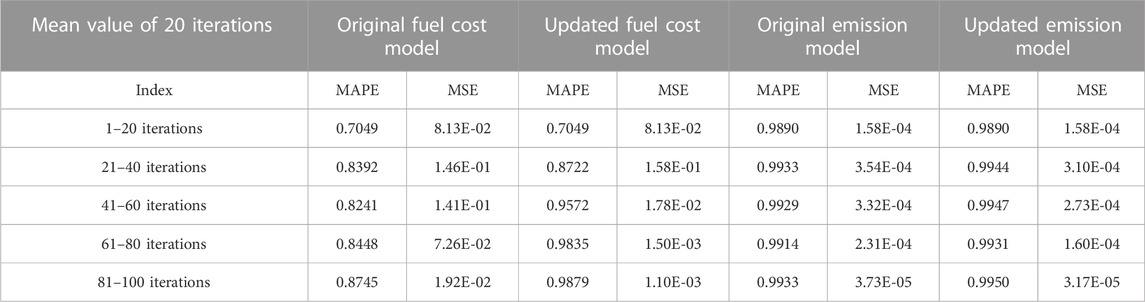
The infilling sampling strategy is executed four times during the optimization process, with 4, 19, 12, and 12 new data points added, respectively. Generally, the added points have a higher degree of convergence than the existing ones. This means that the current Pareto front is closer to the real one. The principle of Kriging models is that things that are closer to each other are more similar than things that are farther away from each other. Thus, the principle and proposed strategy are essentially consistent. More importantly, the infilling sampling strategy guides direction of optimization, as shown in Figure 1A. The accuracy of Kriging model is guaranteed. Figures 2A–D compare Kriging-based surrogate models with or without updating in terms of the mean absolute percentage error (MAPE) and mean square error (MSE). The number of iterations is 100 and the results are averaged over 50 independent tests. Because update strategy is executed every 20 iterations, average MAPE and MSE of 20 generations are selected for comparison and shown in Table 1.
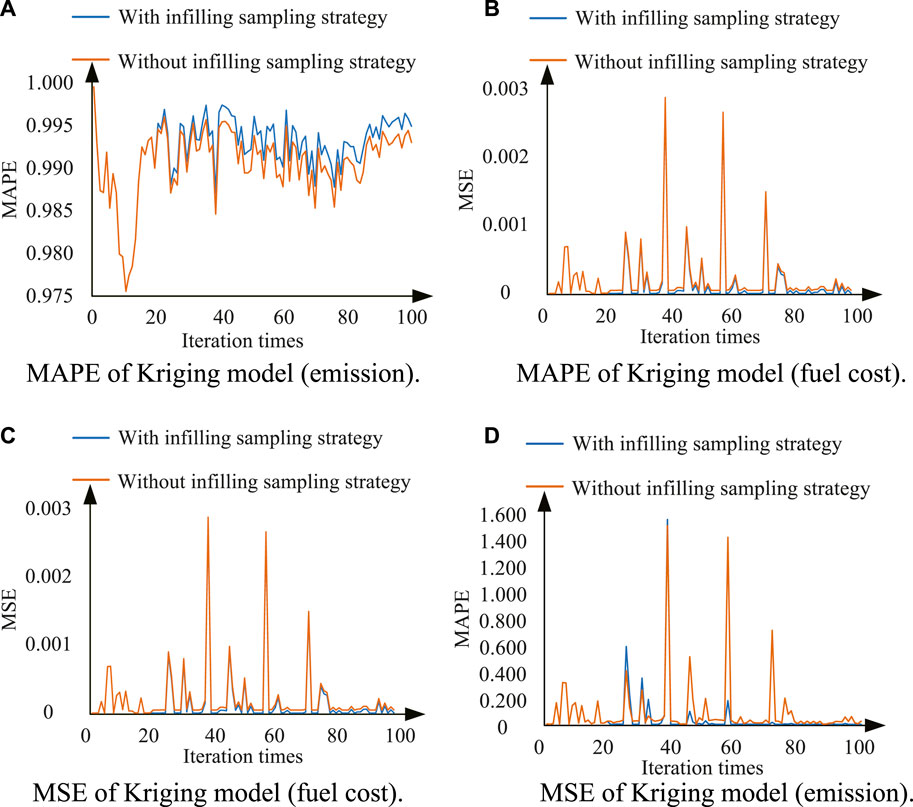
FIGURE 2. Accuracy comparison of Kriging model. (A) MAPE of Kriging model (emission). (B) MAPE of Kriging model (fuel cost). (C) MSE of Kriging model (fuel cost). (D) MSE of Kriging model (emission).
Figure 2A MAPE of Kriging model (emission). Figure 2B. MAPE of Kriging model (fuel cost). Figure 2C. MSE of Kriging model (fuel cost). Figure 2D. MSE of Kriging model (emission).
For the updated Kriging-based surrogate model, there are two levels of improvement. The four updates improve the MAPE by 23.73%, 9.75%, 2.75%, and 0.45%, respectively. This illustrates that the accuracy of Kriging-based surrogate model improves after each update and that the infilling sampling strategy is effective. Compared with the original model (Kriging-based surrogate model without updating), the improvements in the MAPE are 3.93%, 16.15%, 16.42%, and 12.97% in the four updates, respectively. This illustrates that the infilling sampling strategy contributes to better model accuracy.
As for emission function, the situation is similar. The four updates improve the MAPE by 0.55%, 0.03%, −0.16%, and 0.19%, respectively. Although there is a slight decline in accuracy at the third update, the other updates improve the accuracy. Compared with original model, the MAPE improves by 3.93%, 16.15%, 16.42%, and 12.97% over the four updates, respectively. Thus, this strategy enhances the performance of Kriging-based surrogate model.
3.2 Introduction of K-NSGA-II
To solve CECEED problems, NSGA-II suffers from poor convergence (Wei et al., 2022), uniformity, search ability, and extensibility (Chen et al., 2023). To overcome these drawbacks, optimization strategies are applied to Pareto front and search pattern to enhance performance. The convergence, uniformity, extensibility, and search ability of proposed K-NSGA-II are enhanced through the proposed optimization strategies. Additionally, the usage of Kriging surrogate models reduces evaluation time. The flow tree of K-NSGA-II process is described in Figure 3. It can be seen that original NSGA-II flowchart is shown in the black solid frame and the improvements of K-NSGA-II are shown in red dashed box. The evaluations of objective functions are replaced by the evaluations of Kriging surrogate functions. Two kinds of optimization strategies are added to original NSGA-II. The optimization of Pareto front, the improvement of search ability, and the simulation results are described in Section 3.2.1, Section 3.2.2, and Section 3.2.3, respectively.
3.2.1 Enhanced convergence and uniformity
The application of NSGA-II to CECEED problems would result in insufficient convergence and uniformity (Li et al., 2022). The variant operators in NSGA-II are liable to produce precocious genes in early stages. Furthermore, these genes may constitute a high proportion. This leads to some decreases in the convergence and uniformity. To overcome these drawbacks, two optimal strategies are applied to enhance convergence and uniformity, respectively.
3.2.1.1 Strategy to improve convergence
S1: For each individual
S2: For each
S3: The distances
S4: The average
S5: If
where
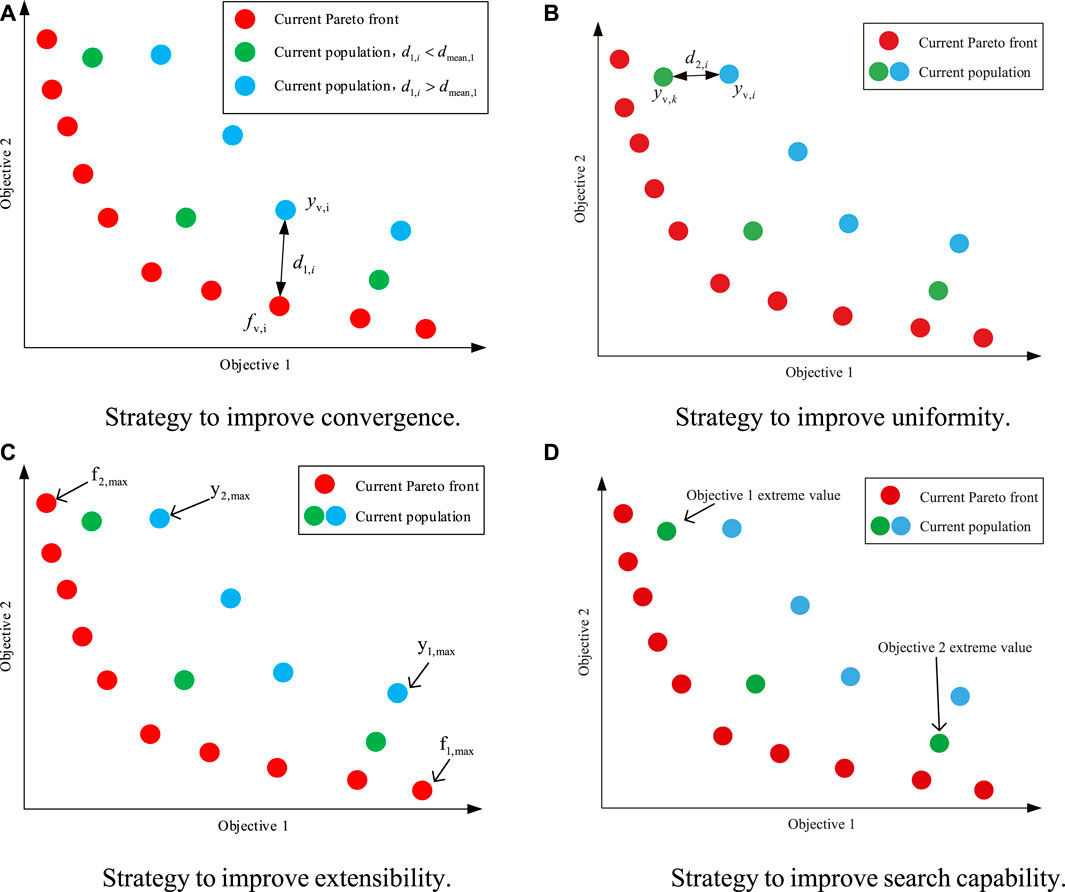
FIGURE 4. Optimization strategies for improving NSGA-II. (A) Strategy to improve convergence. (B) Strategy to improve uniformity. (C) Strategy to improve extensibility. (D) Strategy to improve search capability.
3.2.1.2 Strategy to improve uniformity
S1: For each individual
S2: For each
S3: The distances
S4: The average value
S5: If
where
3.2.2 Improving the search ability of NSGA-II
NSGA-II easily become trapped around a local optimal solution (Yadav et al., 2022). Search directions toward better values are retained with high probability, and search directions toward poor values are retained with a lower probability. In the case of a local optimal value, the probability that NSGA-II will move in other directions is extremely low, so the premature convergence appears. To overcome this drawback, two optimization strategies are applied to improve the search ability of NSGA-II.
Figure 4A Strategy to improve convergence. Figure 4B. Strategy to improve uniformity. Figure 4C Strategy to improve extensibility. Figure 4D. Strategy to improve search capability.
3.2.2.1 Strategy to improve uniformity
The search ability can be visualized in terms of Pareto front extensibility. Thus, a linear combination method based on positional relationship between the current population extremes and current Pareto front extremes is used to enhance extensibility. The method is shown as Figure 4C and described as follows:
S1: For each individual
S2: For the fitness value of each objective function, the maximum value is
S3: For the fitness value of the current
S4: For every
where
3.2.2.2 Mutation strategy to improve search ability
As stated above, NSGA-II is prone to become trapped around local optimal solutions. As another means of overcoming this drawback, a new local and global optimization method based on cloned individuals is proposed. In K-NSGA-II, genes that represent extreme values for a single objective are cloned. A schematic diagram is shown in Figure 4D. Two variation distribution indices are used. The first enables genes to jump away from local optima, and the second is used to improve convergence. The K-NSGA-II with this strategy has stronger ability to jump out of local optimum and enhance global search ability.
3.2.3 Testing of benchmark functions
Three benchmark test functions (ZDT1, 2, and 3) are utilized for illustrating the improvements of K-NSGA-II. The population is set to 40, the number of iterations is 200, cross-distribution index is 20, variation distribution index is 100, and mutation probability is 1/30; benchmark functions are 30- dimensional. For the cloning strategy, variation distribution index for global and local search are 30 and 180, respectively. The results are shown in Figures 5A–C. Performance statistics from the original and improved algorithms are compared in Table 2.
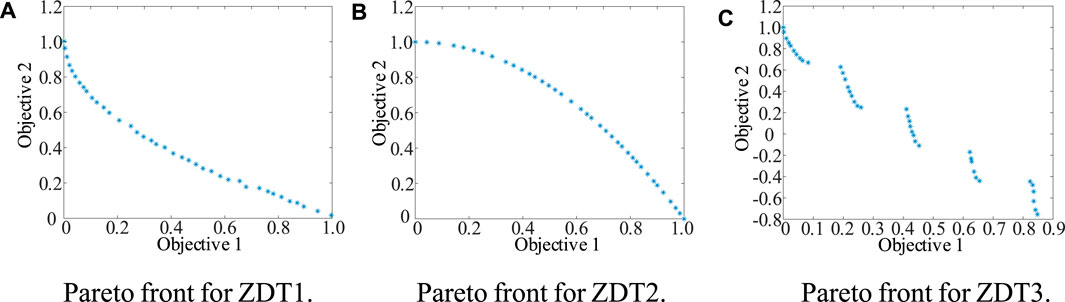
FIGURE 5. Pareto fronts for ZDT1, 2, and 3. (A) Pareto front for ZDT1. (B) Pareto front for ZDT2. (C) Pareto front for ZDT3.
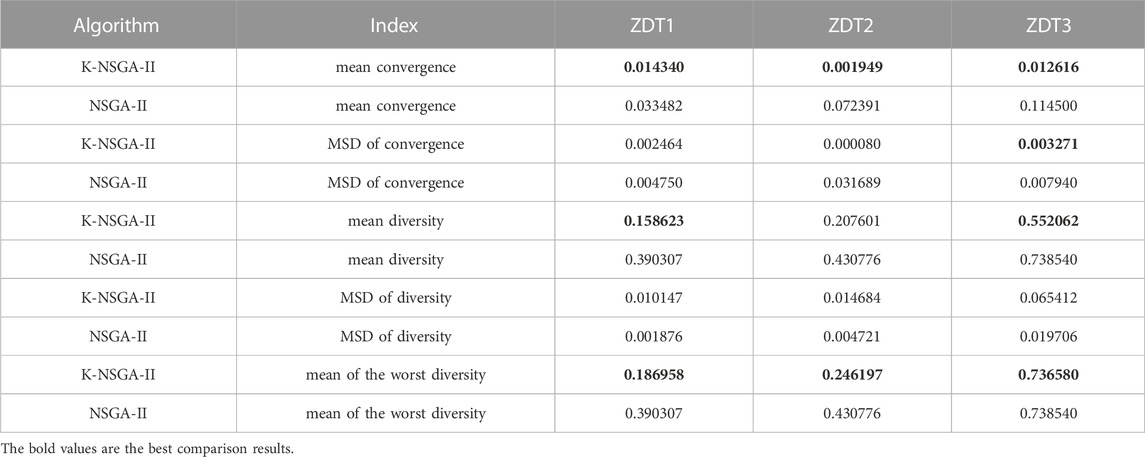
Compared with NSGA-II, the mean convergence of K-NSGA-II on the three benchmark functions improves by 57.17%, 97.31%, and 88.98%, respectively. The mean square deviations (MSD) are improved by 48.13%, 99.75%, and 58.80%, respectively. These improvements illustrate that K-NSGA-II performs much better than NSGA-II of convergence and stability. The mean diversity of K-NSGA-II on benchmark functions has improved by 59.36%, 81.81%, and 25.25%, respectively. It indicates that K-NSGA-II outperforms NSGA-II of diversity.
Although the mean square deviation of diversity is less than that for NSGA-II, the worst diversity over the 20 tests is better than that of NSGA-II, as presented in Table 2. Compared with NSGA-II, the worst diversity score for each benchmark function improves by 52.10%, 42.85%, and 2.65%, respectively. Overall, K-NSGA-II is able to execute multi-objective optimization effectively.
Figure 5A Pareto front for ZDT1. Figure 5B. Pareto front for ZDT2. Figure 5C. Pareto front for ZDT3.
4 Examples and results
In this section, three simulation cases using IEEE 118-bus and IEEE 300-bus systems are considered to illustrate the effectiveness of the proposed method. For emission, cost, power, and time, the units in following tables are ton/h, $/h, MW, and s, respectively. The population number of K-NSGA-II is 50, the number of repetitions is 20, cross-distribution index is 20, variance distribution index is 100, and variation rate is the reciprocal of the units. The given execution time in the following tables contains the update and evolution time of Kriging surrogate models. Additionally, modified NSGA-II (M-NSGA-II) (Muthuswamy et al., 2015), MHBA (Liang et al., 2018), NSGA-II (Deb et al., 2002), and real coded genetic algorithm (RCGA) (Muthuswamy et al., 2015) are chosen for comparison.
4.1 Case 1: IEEE 118-bus test system
Total load demand is set as 3668 MW. The parameters of fuel cost and emission come from reference (Paul et al., 2022). The simulations of this test system are split into two different simulation cases according to the restrictions applied: (a) All constraints mentioned above are included, although valve point effects and POZs are neglected. (b) All constraints are considered.
4.1.1 Case 1.1: Without POZs and valve point
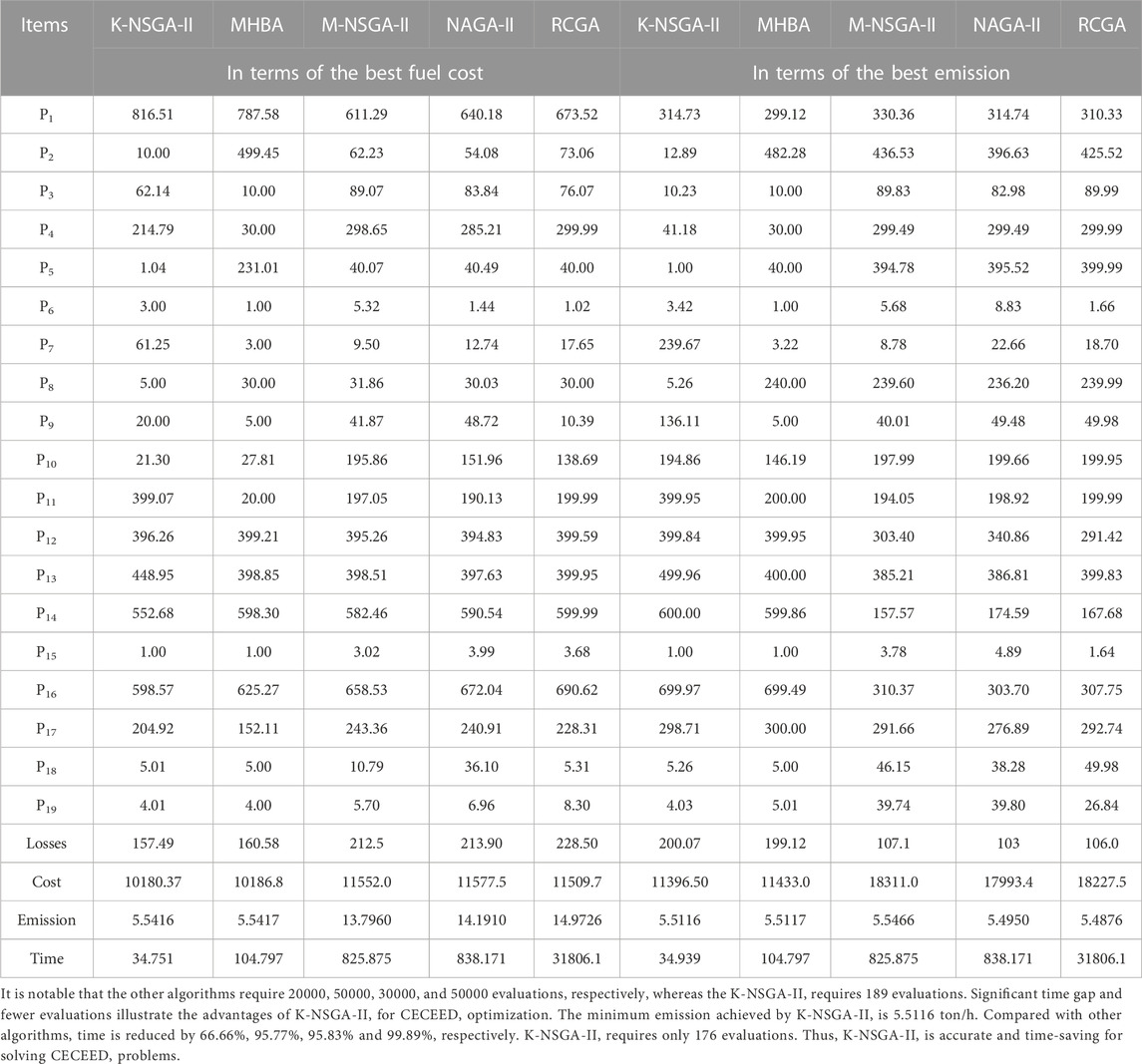
Total 20 solutions are produced on the Pareto front, and they are given in Figures 6A, B. When minimizing fuel cost, the solution (fuel cost, emission) is (10180.37, 5.5416), and when minimizing emission, the solution is (11396.50, 5.5116). Comparisons with other algorithms are shown in Table 3. The minimum value of cost is 10180.37 $/h, and it is less than the fuel costs given by other four algorithms. The runtime of K-NSGA-II is significantly lower than that of the other algorithms. Compared with other four algorithms, the runtime is reduced by 66.84%, 95.81%, 95.85%, and 99.89%, respectively. Further, let us focus on the saved time for evolutions of objective functions. In the optimization process (in terms of the best cost), the surrogate-based evolutions are executed 5,000 (50 × 100 = 5,000) times. For executing two strategies in 3.2.1.1 and 3.2.1.2, due to the number of additional evolutions (based on Kriging surrogate model) is uncertain, the total number of additional evolutions is 9,857. For executing the strategy in 3.2.2.1, the number of additional evolutions is 40000 (400 × 100 = 40000). As for the strategy in 3.2.2.2, the number of additional evolutions is also 40000 (400 × 100 = 40000). Then, the total saved time of evolutions can be computed (94857×(0.001982–0.000792)/50)+94857×(0.003166–0.002062)/50) = 4.35 s). The saved time accounts for 12.52% of the total running time. When obtaining the best emission, the saved time is 4.21 s. It accounts for 12.05% of the total running time. Thus, the proposed Kriging-based surrogate model is time-saving and effective.
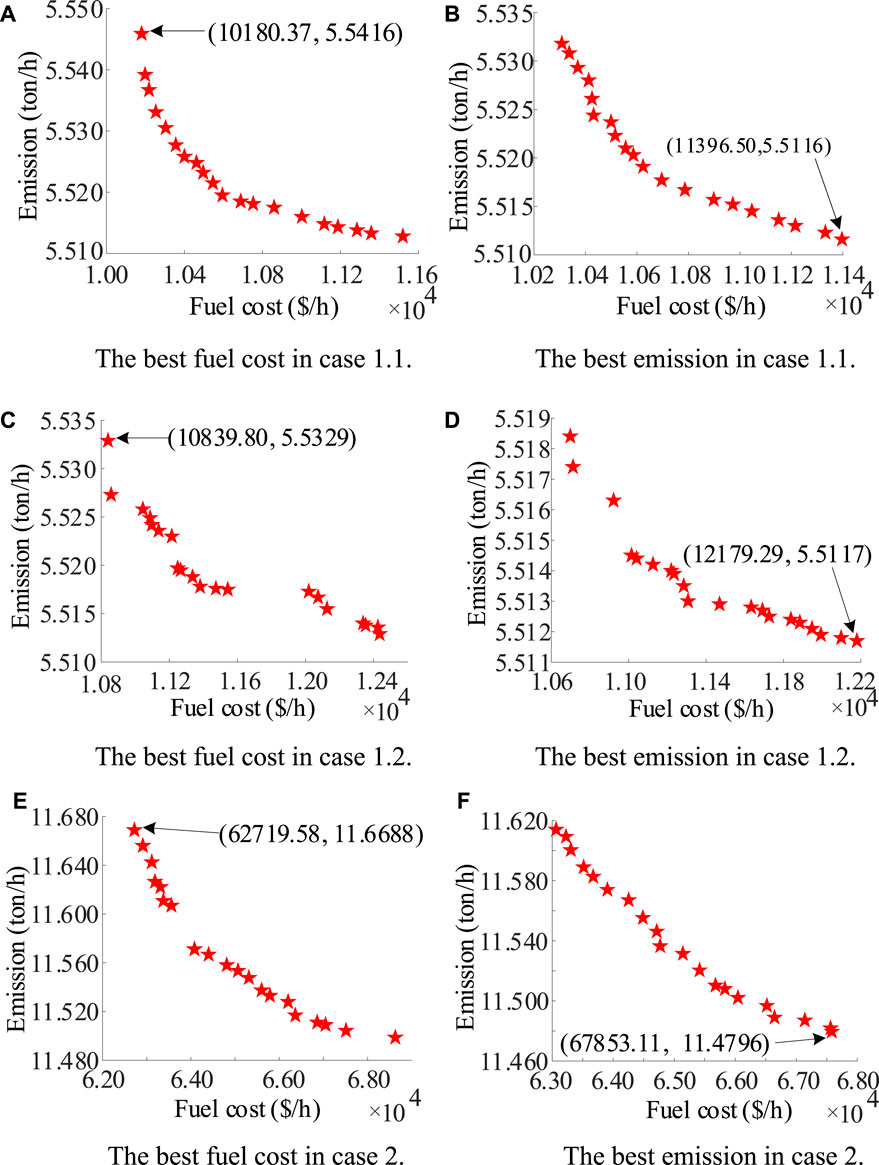
FIGURE 6. Simulation results (Pareto fronts) simulation cases. (A) The best fuel cost in case 1.1. (B) The best emission in case 1.1. (C) The best fuel cost in case 1.2. (D) The best emission in case 1.2. (E) The best fuel cost in case 2. (F) The best emission in case 2.
Figure 6A. The best fuel cost in case 1.1. Figure 6B. The best emission in case 1.1. Figure 6C. The best fuel cost in case 1.2. Figure 6D. The best emission in case 1.2. Figure 6E. The best fuel cost in case 2. Figure 6F. The best emission in case 2.
Let us see what performance the proposed K-NSGA-II can obtain. Firstly, better convergence and diversity are obtained. Thanks to the K-NSGA-II, better diversity is the reason of more powerful search ability. Secondly, excellent decisions are obtained because of promotion of convergence and uniformity in K-NSGA-II. Finally, runtime is reduced. This is due to the utilization of Kriging-based surrogate model. K-NSGA-II is effective and time-saving to solve CECEED problems.
4.1.2 Case 1.2: All proposed constraints
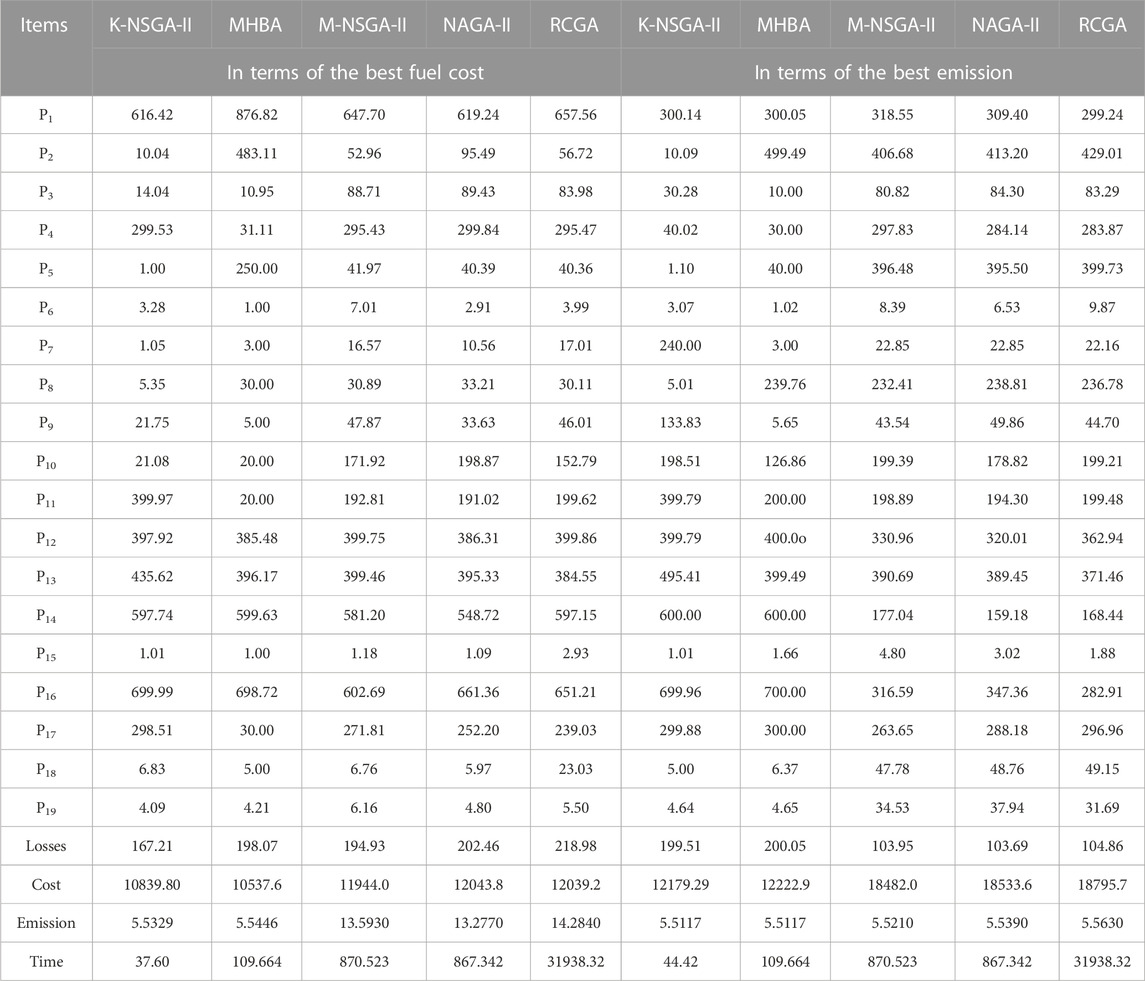
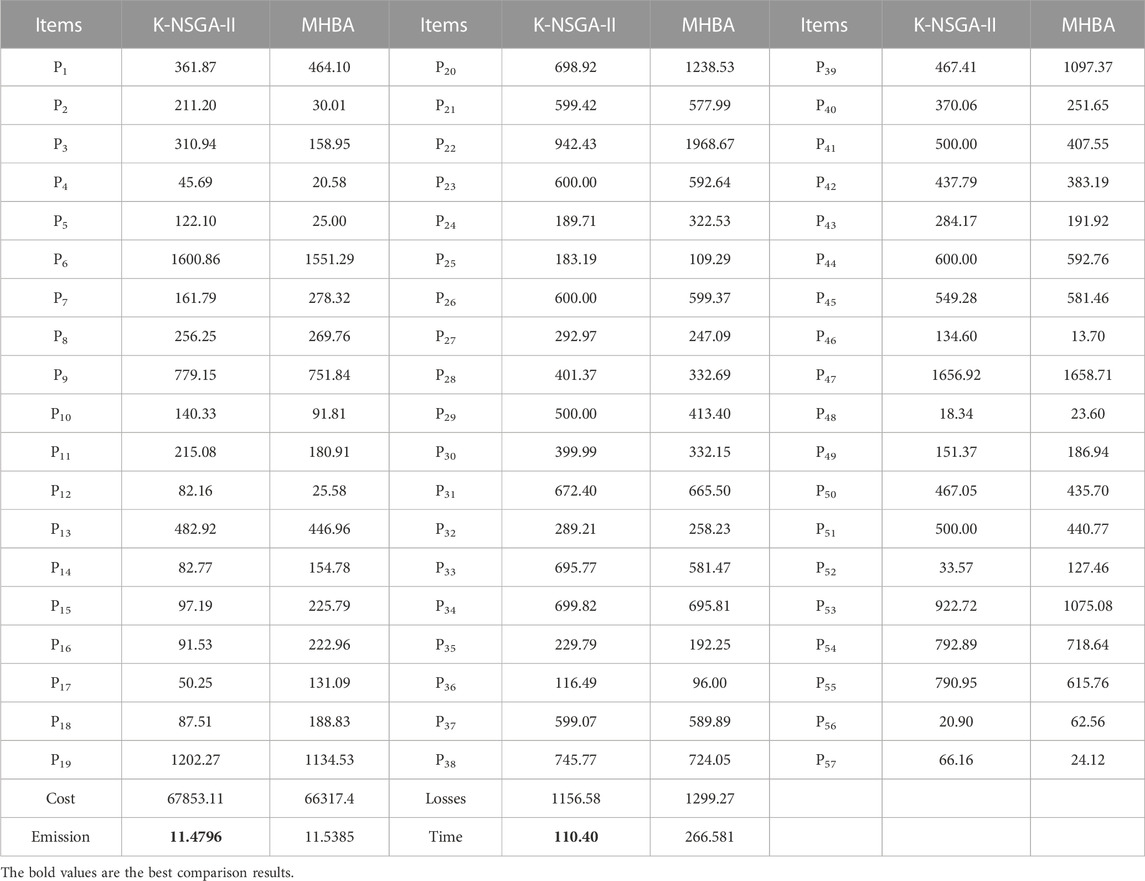
In this case, total 20 solutions are produced on the Pareto front in Figures 6C, D. These solutions when minimizing the fuel cost and emission are (10839.80, 5.53285) and (12179.29, 5.5117), respectively. Comparisons with the other algorithms are presented in Table 4. The minimum fuel cost is only 10839.80 $/h, and it is less than the best results of three other algorithms, i.e., M-NSGA-II, NSGA-II, and RCGA. Again, the runtime is significantly lower than for the other algorithms. Compared with other methods, the runtime is reduced by 65.71%, 95.68%, 95.66%, and 99.88%, respectively. The number of evaluations required by these algorithms are 20000, 50000, 30000, and 50000, respectively, whereas K-NSGA-II requires only 233 evaluations. The time gap and the fewer iterations further illustrate the advantages of K-NSGA-II for CECEED. Table 4 indicates that the minimum emission achieved by the proposed method is 5.5117 ton/h. Compared with four algorithms, runtime is reduced by 59.49%, 94.90%, 94.88%, and 99.86%, respectively. K-NSGA-II requires only 296 evaluations.
In the optimization process (in terms of the best fuel cost), the surrogate-based evolutions are executed 5,000 times. For executing two strategies in 3.2.1.1 and 3.2.1.2, the total number of additional evolutions is 9,765. For executing the strategy in 3.2.2.1, the number of additional evolutions is 40000. As for the strategy in 3.2.2.2, the number of additional evolutions is also 40000. Then, the total saved time of evolutions is 4.78 s. The saved time accounts for 12.72% of the total running time in this case. When obtaining the best emission, the saved time is 4.81 s. It accounts for 10.83% of the total running time. This further demonstrates that the proposed method is time-saving and effective.
Let us see what performance the proposed data-driven surrogate-based method can obtain. In this case, more complex constraints are involved. Proposed method also obtains excellent Pareto fronts for making dispatching decisions in CEED problems. On one hand, the K-NSGA-II is effective to solve optimization problems with complicated constraints. On the other hand, more importantly, the execution time is still very short. This illustrates the Kriging-based surrogate model is capable for replacing original objective functions with complicated constraints. In a word, this data-driven surrogate-assisted algorithm is effective and time-saving for solving CECEED problems with complex constraints.
4.2 Case 2: IEEE 300-bus test system
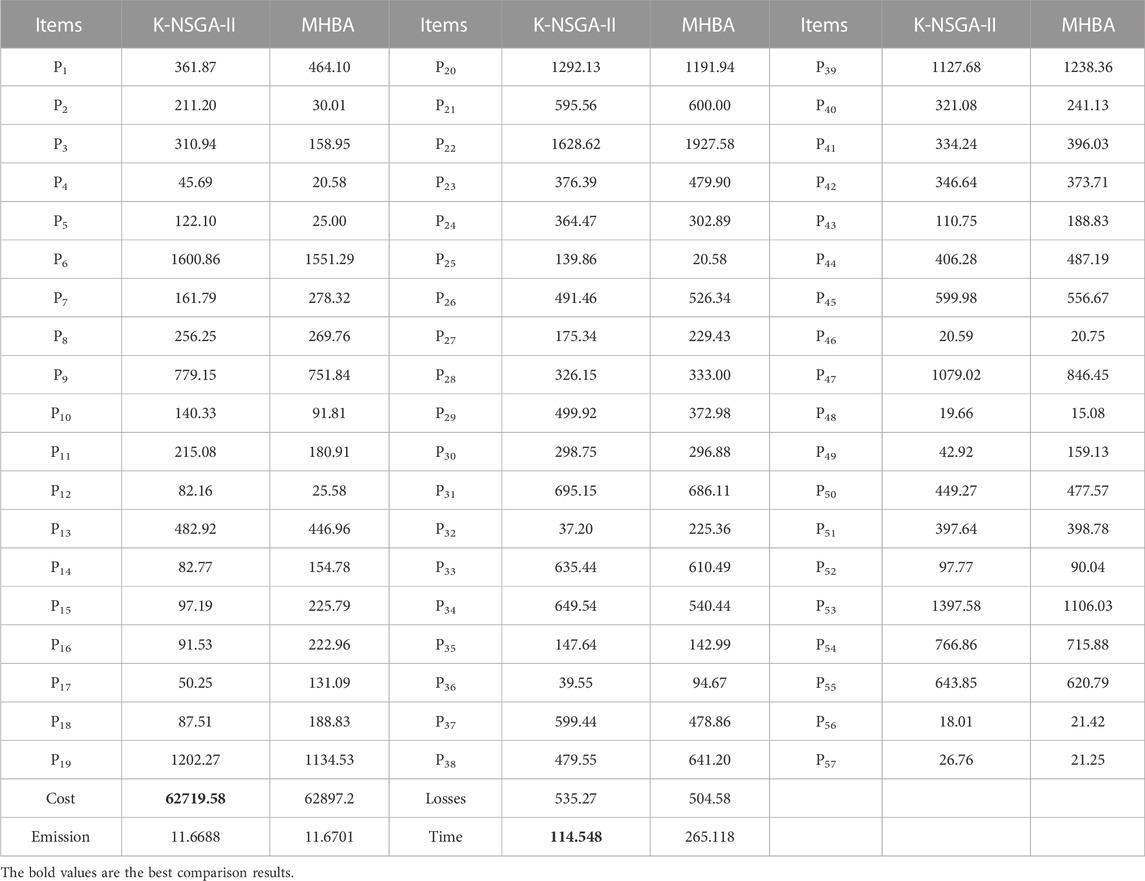
Total load demand is 23525.85 MW (Paul et al., 2022). In this case, total 20 solutions are produced in Figures 6E, F. Solutions given by K-NSGA-II when minimizing the fuel cost and emission are (62719.58, 11.6688) and (67853.11, 11.4796), respectively. Comparison results given by MHBA are presented in Tables 5, 6. The best cost given by K-NSGA-II is 62719.58 $/h, and it is better than that of MHBA. Runtime of K-NSGA-II is lower, by 56.79%, than that of MHBA. MHBA requires 20000 evaluations, compared with just 304 for K-NSGA-II. This time gap and reduced number of evaluations further illustrate the advantages of K-NSGA-II for CECEED. In Table 5, minimum emission is 11.4796 ton/h. Compared with MHBA, runtime is reduced by 58.59% and 20000 evaluations of MHBA is reduced to 288. Thus, K-NSGA-II has strong potential to be applied in CECEED problems. In this case, the number of iterations is set as 100. Total runtimes (sum of 50 runtimes) of fuel cost and emission function are 0.009092 s and 0.012639 s, respectively. Total runtimes (sum of 50 runtimes) of surrogate models are 0.001631 s and 0.004326 s, respectively. In terms of the best cost, the saved time of evolutions is 29.39 s (the number of surrogate-based evaluations is 93165). The saved time accounts for 25.66% of the total running time. In terms of the best emission, the saved time of evolutions is 29.80 s (the number of surrogate-based evaluations is 94447). The saved time accounts for 26.99% of the total running time. This further demonstrates the advantages of the proposed surrogate-based method in solving high-dimension CECEED problems.
Let us see what performance the proposed data-driven method can obtain. In this case, a power grid with more units is used to verify the effectiveness of the proposed Kriging-based optimization method. The proposed method obtains excellent Pareto fronts of CECEED problems. On one hand, the K-NSGA-II is effective for solving CECEED problems. On the other hand, execution time is dramatically reduced in a CECEED problem. This illustrates the Kriging surrogate model is effective to replace original high-dimension objective functions. In a word, the proposed method is effective and time-saving to solve CECEED problems with a high dimension.
4.3 Comparative results with Cplex and Guribo solvers
The comparative results with Cplex (Huo et al., 2022) and Guribo (Ma et al., 2021) solvers for solving the case 1.1, case 1.2, and case 2 are displayed in this section. Mathematical programming and precise algorithms are preferred in most of the real-world applications. However mathematical methods (by using Cplex and Guribo solvers) are usually powerless to solve multi-objective optimization problems. To use the two mathematical solvers, original multi-objective CECEED problems are transferred to single-objective optimization problems by weight sum method (Zuo et al., 2014):
where
where
where
As shown in Table 7, for case 1.1, compared with Cplex solver and Guribo solver, the best fuel cost obtained by the proposed method is reduced by 0.76% and 0.66%, respectively. As for the execution time, it is reduced by 32.33% and 28.14%, respectively. In terms of pollutant emission, the best emission is reduced by 0.56% and 0.56%, respectively. As for the execution time, it is reduced by 32.83% and 29.17%, respectively. In case 1.2, the improved degrees are similar to the comparative results in case 1.1. In case 2, a large-scale system with more dimensions, compared with Cplex and Guribo solvers, the best fuel cost obtained by the proposed method is reduced by 5.47% and 4.43%, respectively. As for the execution time, it is reduced by 79.30% and 39.91%, respectively. In terms of the best emission in case 2, the best emission is reduced by 0.15% and 0.15%, respectively. As for the execution time, it is reduced by 78.82% and 40.18%, respectively. Compared with the test system with 118 buses, the proposed surrogate-assisted method has a stronger advantage. In other words, it is effective for handling the CECEED problems with more dimensions and larger scale.
5 Concluding remarks
This paper proposes a novel data-driven Kriging-assisted method for solving CECEED problems. The optimization process includes two aspects. Kriging-based surrogate models are used to replace the original computationally expensive objective functions, reducing the evaluation time. Additionally, the NSGA-II method is improved to enhance its ability to handle high-dimensional optimization problems. A new infilling sampling strategy is proposed to update the Kriging-based surrogate models, thus enhancing the accuracy of these models. Novel optimization strategies were added to improve NSGA-II, focusing on convergence, uniformity, extensibility, and search ability, respectively. The effectiveness of this method has been illustrated by conducting simulations of the IEEE 118-bus and 300-bus systems. The results indicate that this data-driven Kriging-assisted method is suitable for solving CECEED problems. Note that time-consuming unit commitment problems could be solved by such a surrogate-assisted approach and left as future research.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
CL: Investigation, Software, Validation, Writing–original draft. HL: Conceptualization, Formal Analysis, Funding acquisition, Project administration, Resources, Supervision, Writing–review and editing. AP: Data curation, Writing–review and editing. JZ: Visualization, Writing–review and editing.
Funding
The authors declare financial support was received for the research, authorship, and/or publication of this article. Project Supported by National Natural Science Foundation of China (NSFC) (NO. 62163013).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Chen, C., Wang, L., and Niu, M. (2023). Research on the application of improved nsga-ii in the structure design of wind turbine blade spar cap. Front. Energy Res. 11, 1160423. doi:10.3389/fenrg.2023.1160423
Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002). A fast and elitist multiobjective genetic algorithm: nsga-ii. IEEE Trans. Evol. Comput. 6, 182–197. doi:10.1109/4235.996017
Gao, Y., Kang, B., Xiao, H., Wang, Z., Ding, G., Xu, Z., et al. (2023). A model for identifying the feeder-transformer relationship in distribution grids using a data-driven machine-learning algorithm. Front. Energy Res. 11, 1225407. doi:10.3389/fenrg.2023.1225407
Huo, X., Wu, X., Fan, Y., and Ding, C. (2022). A mixed-integer program (mip) for one-way multiple-type shared electric vehicles allocation with uncertain demand. IEEE Trans. Intelligent Transp. Syst. 23, 8972–8984. doi:10.1109/TITS.2021.3088858
Lai, W., Zheng, X., Song, Q., Hu, F., Tao, Q., and Chen, H. (2022). Multi-objective membrane search algorithm: A new solution for economic emission dispatch. Appl. Energy 326, 119969. doi:10.1016/j.apenergy.2022.119969
Li, J., Zuo, W., E, J., Zhang, Y., Li, Q., Sun, K., et al. (2022a). Multi-objective optimization of mini u-channel cold plate with sio2 nanofluid by rsm and nsga-ii. Energy 242, 123039. doi:10.1016/j.energy.2021.123039
Li, L. L., Liu, Z. F., Tseng, M. L., Zheng, S. J., and Lim, M. K. (2021). Improved tunicate swarm algorithm: solving the dynamic economic emission dispatch problems. Appl. Soft Comput. 108, 107504. doi:10.1016/j.asoc.2021.107504
Li, Q., Liu, Z., Xiao, Y., Zhao, P., Zhao, Y., Yang, T., et al. (2022b). An intelligent optimization method for preliminary design of lead-bismuth reactor core based on kriging surrogate model. Front. Energy Res. 10, 849229. doi:10.3389/fenrg.2022.849229
Li, Z., Wu, L., Xu, Y., Moazeni, S., and Tang, Z. (2022c). Multi-stage real-time operation of a multi-energy microgrid with electrical and thermal energy storage assets: A data-driven mpc-adp approach. IEEE Trans. Smart Grid 13, 213–226. doi:10.1109/TSG.2021.3119972
Li, Z., Xu, Y., Fang, S., Wang, Y., and Zheng, X. (2020). Multiobjective coordinated energy dispatch and voyage scheduling for a multienergy ship microgrid. IEEE Trans. Industry Appl. 56, 989–999. doi:10.1109/TIA.2019.2956720
Li, Z., and Xu, Y. (2018). Optimal coordinated energy dispatch of a multi-energy microgrid in gridconnected and islanded modes. Appl. Energy 210, 974–986. doi:10.1016/j.apenergy.2017.08.197
Liang, H., Liu, Y., Li, F., and Shen, Y. (2018). A multiobjective hybrid bat algorithm for combined economic/emission dispatch. Int. J. Electr. Power and Energy Syst. 101, 103–115. doi:10.1016/j.ijepes.2018.03.019
Lin, C., Liang, H., and Pang, A. (2023). A fast data-driven optimization method of multi-area combined economic emission dispatch. Appl. Energy 337, 120884. doi:10.1016/j.apenergy.2023.120884
Linka, K., Hillgärtner, M., Abdolazizi, K. P., Aydin, R. C., Itskov, M., and Cyron, C. J. (2021). Constitutive artificial neural networks: A fast and general approach to predictive data-driven constitutive modeling by deep learning. J. Comput. Phys. 429, 110010. doi:10.1016/j.jcp.2020.110010
Liu, Y., Wang, M., Zhang, X., Duan, J., Gao, H., and Liu, J. (2022). Kriging surrogate model enabled heuristic algorithm for coordinated volt/var management in active distribution networks. Electr. Power Syst. Res. 210, 108089. doi:10.1016/j.epsr.2022.108089
Ma, Z., Zhong, H., Cheng, T., Pi, J., and Meng, F. (2021). Redundant and nonbinding transmission constraints identification method combining physical and economic insights of unit commitment. IEEE Trans. Power Syst. 36, 3487–3495. doi:10.1109/TPWRS.2020.3049001
Muthuswamy, R., Krishnan, M., Subramanian, K., and Subramanian, B. (2015). Environmental and economic power dispatch of thermal generators using modified nsga-ii algorithm. Int. Trans. Electr. Energy Syst. 25, 1552–1569. doi:10.1002/etep.1918
Pang, A., Liang, H., Lin, C., and Yao, L. (2023). A surrogate-assisted adaptive bat algorithm for large-scale economic dispatch. Energies 16, 1011. doi:10.3390/en16021011
Paul, K., Sinha, P., Mobayen, S., El-Sousy, F. F., and Fekih, A. (2022). A novel improved crow search algorithm to alleviate congestion in power system transmission lines. Energy Rep. 8, 11456–11465. doi:10.1016/j.egyr.2022.08.267
Qian, H. M., Wei, J., and Huang, H. Z. (2023). Structural fatigue reliability analysis based on active learning kriging model. Int. J. Fatigue 172, 107639. doi:10.1016/j.ijfatigue.2023.107639
Qu, K., Zheng, X., and Yu, T. (2023). Environmental-economic unit commitment with robust diffusion control of gas pollutants. IEEE Trans. Power Syst. 38, 818–834. doi:10.1109/TPWRS.2022.3166264
Sharifian, Y., and Abdi, H. (2023). Solving multi-area economic dispatch problem using hybrid exchange market algorithm with grasshopper optimization algorithm. Energy 267, 126550. doi:10.1016/j.energy.2022.126550
Sheng, W., Li, R., Yan, T., Tseng, M. L., Lou, J., and Li, L. (2023). A hybrid dynamic economics emissions dispatch model: distributed renewable power systems based on improved coot optimization algorithm. Renew. Energy 204, 493–506. doi:10.1016/j.renene.2023.01.010
Wang, R., Wen, X., Wang, X., Fu, Y., and Zhao, Y. (2023). Low-carbon economic dispatch of regional integrated energy system based on carbon-oxygen cycle. Front. Energy Res. 11, 1206242. doi:10.3389/fenrg.2023.1206242
Wei, H., Zhang, Y., Wang, Y., Hua, W., Jing, R., and Zhou, Y. (2022). Planning integrated energy systems coupling v2g as a flexible storage. Energy 239, 122215. doi:10.1016/j.energy.2021.122215
Wu, F., and Dong, M. (2023). Eco-routing problem for the delivery of perishable products. Comput. Operations Res. 154, 106198. doi:10.1016/j.cor.2023.106198
Xu, L., Wei, W., Cai, X., Liu, C., Jiang, X., and Yang, J. (2022). Day-ahead economic dispatch strategy for distribution network considering total cost price-based demand response. Front. Energy Res. 10, 870893. doi:10.3389/fenrg.2022.870893
Yadav, A., Mishra, S., and Sairam, A. S. (2022). A multi-objective worker selection scheme in crowdsourced platforms using nsga-ii. Expert Syst. Appl. 201, 116991. doi:10.1016/j.eswa.2022.116991
Yu, F., Gong, W., and Zhen, H. (2022). A data-driven evolutionary algorithm with multi-evolutionary sampling strategy for expensive optimization. Knowledge-Based Syst. 242, 108436. doi:10.1016/j.knosys.2022.108436
Zhang, R., and Yu, J. (2023). New urban power grid flexible load dispatching architecture and key technologies. Front. Energy Res. 11, 1168768. doi:10.3389/fenrg.2023.1168768
Keywords: combined economic/emission dispatch, data-driven, genetic algorithm, surrogate model, computationally expensive optimization problems
Citation: Lin C, Liang H, Pang A and Zhong J (2023) Data-driven method of solving computationally expensive combined economic/emission dispatch problems in large-scale power systems: an improved kriging-assisted optimization approach. Front. Energy Res. 11:1273760. doi: 10.3389/fenrg.2023.1273760
Received: 07 August 2023; Accepted: 23 August 2023;
Published: 06 September 2023.
Edited by:
Zhengmao Li, Aalto University, FinlandReviewed by:
Yikui Liu, Stevens Institute of Technology, United StatesXiaodong Zheng, Southern Methodist University, United States
Copyright © 2023 Lin, Liang, Pang and Zhong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Huijun Liang, bGhqQGhibXp1LmVkdS5jbg==
 Chenhao Lin
Chenhao Lin Huijun Liang
Huijun Liang Aokang Pang
Aokang Pang Jianwei Zhong
Jianwei Zhong