A molecular dynamics investigation on CO2–H2O–CH4 surface tension and CO2–CH4–H2O–graphite sheet contact angles

Introduction: We perform molecular dynamics (MD) simulations of nanoscopic liquid water drops on a graphite substrate mimicking the carbon-rich pore surface in the presence of CH₄/CO₂ mixtures at temperatures in the range 300 K–473 K.

Methods: The surface tension in MD simulation is calculated via virial expression, and the water droplet contact angle is obtained through a cylindric binning procedure.

Results: Our results for the interfacial tension between water and methane as a function of pressure and for the interfacial tension between water and CH₄/CO₂ mixtures as a function of their composition agree well with the experimental and computational literature.

Discussion: The modified Young’s equation has been proven to bridge the macroscopic contact angle and microscopic contact with the experimental literature. The water droplet on both the artificially textured surface and randomly generated surface exhibits a transition between the Wenzel and Cassie–Baxter states with increased roughness height, indicating that surface roughness enhances the hydrophobicity of the solid surface.

1 Introduction

Wettability, namely, interfacial tension and contact angle, is a mesoscale property of liquid–liquid–solid combination that depends on intermolecular forces. It is highly relevant to a wide range of industrial applications, such as designing water-resistant fabrics using wettability control in textile industries (Xue et al., 2014), contact lens evaluation and design in medical discipline (Menzies and Jones, 2010), enhanced oil/gas recovery, and carbon geo-sequestration (CGS) in petroleum industries (Zhou et al., 2016). For organic matter-rich unconventional formation, such as coal bed methane and shale formation, the interactions between (connate) water/methane and organic-rich matter (carbon) control multiphase transport that has direct impact on gas recovery.

Methane, as the main constituent of gas resources in unconventional reservoirs, is generally stored in nanoscale organic matter-rich pores (Curtis, 2002; Louk et al., 2017). The gas recovery of unconventional formation is much lower than that of other conventional formation. CO₂ injection has proven to be an efficient conduction method to enhance the gas recovery (Busch et al., 2008; Edwards et al., 2015; Arif et al., 2017; Xu et al., 2017), which also helps reduce the CO₂ atmosphere emission by storing CO₂ in unconventional reservoirs. This is attributed to CO₂ adsorption trapping (CO₂ is adsorbed over the organic surface) (Eshkalak et al., 2014; Xu et al., 2017) and/or CO₂ structural trapping (CO₂ trapped beneath a tight/seal layer under non-CO₂ wetting conditions) (Naylor et al., 2011) in reservoirs after injection. Both the gas recovery and CO₂ geo-storage efficiency are affected by wettability as it controls the pore-scale fluid configuration (Zhou et al., 2016), trapping (Pentland et al., 2011; Roshan et al., 2016), and adsorption processes (Jho et al., 1978). As a result, a better understanding of interactions of the various components (water–carbon dioxide/methane–carbon) and associated transport process at the pore scale is of great importance.

It is well-known that CH₄ and CO₂ have different molecular properties, and thus, their interactions with water–rock are discrepant (Iglauer, 2017). Although the surface tension between water and CH₄/CO₂ mixture under a wide range of pressure–temperature conditions has been studied extensively through laboratory measurements (Jho et al., 1978; Sachs and Meyn, 1995; Ren et al., 2000; Kashefi et al., 2016), numerical simulation (Biscay et al., 2009; Sakamaki et al., 2011; Yang et al., 2017), and theoretical analysis (Schmidt et al., 2007; Miqueu et al., 2011), very limited effort has been put to analyze CO₂/CH₄/H₂O interfacial phenomena from a molecular scale and how CO₂/CH₄ mixture influences the contact angle defined at the organic solid and water triple contact line.

It is challenging to realistically replicate the conditions in nanoscale organic matter-rich pores using experimental methodology. The nanoscopic length scales make direct visualization of pore-scale processes virtually impossible, specifically at the high temperatures and pressures. Given the length scales we are interested in, molecular dynamics (MD) simulations are an appropriate tool for nano pore-scale process investigation. There is extensive literature relevant to surface phenomena and wetting behavior. For example, the contact angle of a water–CO₂–solid (quartz) system has been well-studied using MD simulation (Iglauer et al., 2012); Liu et al. (2010) studied the pressure dependence of the water contact angle over both hydrophobic and hydrophilic surfaces in the CO₂/water/solid (quartz) system. These results show that the presence of CO₂ changes the system wettability, leading to an increase in the water contact angle. The efficiency of CO₂ displacing methane in carbon channels (Wu et al., 2015) and the methane adsorption mechanism in shale pores represented by graphite sheets (Mosher et al., 2013) have also been investigated through MD simulations. It is noteworthy that the solid surface in these CO₂ and methane-related wetting studies has usually been treated as the smooth surface, while the effect of surface roughness on wetting behavior is still lacking.

The aim of this paper is first to simulate the surface tension of H₂O/CH₄ and H₂O/CH₄/CO₂ under a wide range of temperatures and pressures. Then, we quantify wettability of water on graphite sheets, mimicking the carbon-rich reservoirs in the presence of methane and carbon dioxide. There is a vast literature relating to stacks of graphite sheets that accurately mimic actual organic-rich pores for a wide range of temperatures and pressures in MD simulations. For example, these studies on water contact angle simulation over organic surface (Werder et al., 2003) and methane flow transport in organic shale pores (Kazemi and Takbiri-Borujeni, 2016) treating the organic-rich pores as graphite sheets and their results show a good agreement with both simulation results and experimental data. The effect of artificial and random surface roughness on nano water wetting behavior has been discussed.

The remaining sections of this paper are organized in the following manner. In the next section, we summarize the simulation methodology and the force field parameters used. The model system, simulation methodology, and the force field models used in the MD simulations are described. We then explain the surface roughness creation approach and how simulation data have been collected and analyzed. The Results section consists of two main parts. In the first part, we study—through MD—the surface tension of water against methane and against methane/carbon dioxide mixtures, and we compare our results with the experimental and computational literature in order to build confidence in our simulation approach. In the second part, we report on simulations of the water contact angle on graphite in a CH₄/CO₂ environment over a range of droplet sizes. Then, we reveal the surface roughness effect on the water contact angle. The final section reiterates the main conclusions of our work.

2 Model and methodology

2.1 Model system

Most of our simulation systems consist of a water droplet at the middle of a graphite surface in the presence of a CO₂–CH₄ mixture, as shown in Figure 1. The graphite substrate is represented by two graphene sheets at a distance of 3.35 Å. For surface tension simulation, the carbon atoms in graphite sheets have been removed and a typical symmetric system is shown in Figure 2.

FIGURE 1

FIGURE 1. Front view of configuration of a H₂O–CH₄–CO₂–carbon system at T = 300 K and P = 5 MPa. Blue and green represent C and O in CO₂, respectively, orange and olive represent C and H in methane, respectively, red and white represent O and H in water, respectively, and yellow represents C in graphite sheets.

FIGURE 2

FIGURE 2. Snapshot of CO₂−H₂O molecular distribution at equilibrium (CO₂ mole fraction X_CO2 = 100%), at T = 311 K and at pressure that equals to 14.5 MPa.

The combination of the Lennard–Jones potential and the electrostatic (“Coulombic”) potential is used for pairwise interactions:

$U\left(r_{ij}\right)=4{\epsilon }_{ij}\left[{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^6\right]+\frac{q^i{q}^j}{4\pi {\epsilon }_0{r}_{ij}},(1)$

with ${\epsilon }_{ij}$ and ${\sigma }_{ij}$ being the strength and the length scale of the LJ interaction, respectively, $q^i$ and $q^j$ represent the charges of sites i and j, respectively, and ${\epsilon }_0$ represents the dielectric permittivity of the vacuum. Each atom type $\alpha$ has been given its own size ${\sigma }_{\alpha }$ and strength ${\epsilon }_{\alpha }$. The cross interaction LJ parameters between atoms of different types ($\alpha$ and $\beta$) are deduced from the Lorentz−Berthelot mixing rules (Hudson and McCoubrey, 1960): ${\sigma }_{\alpha \beta }=\left({\sigma }_{\alpha }+{\sigma }_{\beta }\right)/2$ and ${\epsilon }_{\alpha \beta }=\sqrt{{\epsilon }_{\alpha }{\epsilon }_{\beta }}$. The LJ interaction potential has been truncated at 12 Å in all present simulations, and the long-range Coulombic interactions were computed using the particle–particle–particle–mesh (PPPM) method with a relative error of 10⁻⁵ (Darden et al., 1993).

For the intramolecular interactions, we have been using the SPC/E model for water (Wu et al., 2006), Cygan model for CO₂ (Cygan et al., 2012), and OPLS model for CH₄ (Aimoli et al., 2014). The force field for graphene is taken as reported in Stuart et al. (2000). These force fields have been extensively used and validated in a wide body of MD studies. For example, their results about thermodynamic properties and flow transport characteristics have been reported with reasonable accuracy (Aimoli et al., 2014). The velocity Verlet algorithm (Swope et al., 1982) is performed to achieve position and velocity update, with a time step of 2 fs. The carbon atoms in graphite sheets have fixed locations (Yong et al., 2020), and all MD simulations were performed with the open-source molecular dynamic simulation code LAMMPS (Plimpton, 1995), under periodic boundary conditions.

2.2 Surface roughness creation

A randomly rough surface is characterized by its roughness height and correlation length. The correlation length describes lateral dimensions and sometime is called surface spatial wavelengths or roughness length scale. The root-mean-squared (RMS) height ${\sigma }_H$ is usually used to represent the roughness height, as shown in Figure 3, which is given by

${\sigma }_H=\sqrt{\frac{h_1^2+h_2^2+h_3^2+\dots +h_{n.}^2}{n}}.(2)$

FIGURE 3

FIGURE 3. Schematic representation of a rough surface to determine its RMS height.

The random Gaussian surfaces are generated by a (N, M) matrix of rough amplitudes [Z_ij] having Gaussian distribution of heights and by a given (n, m) autocorrelation function (ACF) using linear transformations on the random matrix. For a simple method to generate surface roughness (Patir, 1978), a simple ACF is used, which will result in a constant coefficient matrix. This simple ACF does not require the solution of a system of non-linear equations.

Consider a family of ACFs of the form

$R\left({\lambda }_x,{\lambda }_y\right)=\left\{\begin{array}{l}{\sigma }^2\left(1-\frac{\left|{\lambda }_x\right|}{{\lambda }_x^{*}}\right)\left(1-\frac{\left|{\lambda }_y\right|}{{\lambda }_y^{*}}\right)\\ 0\end{array}\right.\left.\begin{array}{l}\left|{\lambda }_x\right|\le {\lambda }_x^{*}\\ \left|{\lambda }_y\right|\le {\lambda }_y^{*}\\ otherwise\end{array}\right\},(3)$

where ${\lambda }_x^{*}$ and ${\lambda }_y^{*}$ are defined as the correlation lengths of x and y profiles, respectively (i.e., the length at which the profile correlation function becomes zero). Its discrete form is

$R_{pq}={\sigma }^2\left(1-\frac{p}{n}\right)\left(1-\frac{q}{m}\right)\begin{array}{l}p\le n\\ q\le m\end{array},(4)$

where $R_{pq}$ = 0 if $p\ge n$ or $q\ge m$, and $\begin{array}{l}{\lambda }_x^{*}=n\Delta x\\ {\lambda }_y^{*}=m\Delta y\end{array}$. $\Delta x$ and $\Delta y$ are sampling intervals in x and y directions on the generated surface, respectively.

The components of a (N + n, M + m) matrix [η_ij] first generated are independent, and identically distributed Gaussian random numbers with a mean value equal to zero and unit standard deviation. The generation of a Gaussian surface having an ACF of form (4) is accomplished by the linear transformation

$z_{ij}=\frac{\sigma }{{\left(nm\right)}^{1/2}}{\displaystyle \sum _{k=1}^n}{\displaystyle \sum _{l=1}^m}{\eta }_{i+k,j+l}\begin{array}{l}i=\mathrm{1,2},...N\\ j=\mathrm{1,2},...M\end{array}.(5)$

2.3 Data post-processing

For determining surface tension, a planar interface with its normal in the Z-direction was created in a fully periodic domain. After equilibration, surface tension $\gamma$ was determined according to Nielsen et al. (2012):

$\gamma =\frac{L_z}{2}\left[p_{zz}-\frac{1}{2}\left(p_{xx}+p_{yy}\right)\right],(6)$

where $p_{xx}$, $p_{yy}$, and $p_{zz}$ are the diagonal components of the pressure tensor and $L_z,$ the domain length in the z-direction. The pressure tensor $p_{\alpha \beta }$ is given by the following virial expression (Iglauer et al., 2012):

$p_{\alpha \beta }V=〈{\displaystyle \sum _{i=1}^N}{m}_i{\mathrm{v}}_{\alpha ,i}{\mathrm{v}}_{\beta ,i}+{\displaystyle \sum _{i=1}^{N-1}}{\displaystyle \sum _{j>1}^N}{r}_{\alpha ,ij}{f}_{\beta ,ij}〉,(7)$

with V being the volume of the simulation domain, N the total number of atoms, ${\mathrm{v}}_{\alpha ,i}$ the velocity component in the $\alpha$ direction of atom i, and $r_{\alpha ,ij}$ and $f_{\alpha ,ij}$ the $\alpha$ components of vectors ${\mathbf{r}}_{\text{ij}}$ and ${\mathbf{f}}_{\text{ij}}$, respectively. The angled brackets stand for ensemble averaging. The pressure p is the average of the three diagonal pressure tensor components: $p=\left(p_{xx}+p_{yy}+p_{zz}\right)/3$.

For contact angle estimation, a water droplet is placed on a graphite substrate and allowed to equilibrate for 1 ns until it reaches a well-defined droplet shape. The sessile droplet is then used to estimate the contact angle. An example of extracting the contact angle is given in Figure 4. It presents a 2-ns time-averaged axisymmetric average concentration field obtained through a cylindric binning procedure (De Ruijter et al., 1999). Then, a best circular fit through the points of the field that have a water concentration of 0.02 (1/ų), a half of bulk density, is extrapolated to the top graphite sheet where the contact angle θ is measured as 112.55° in this figure.

FIGURE 4

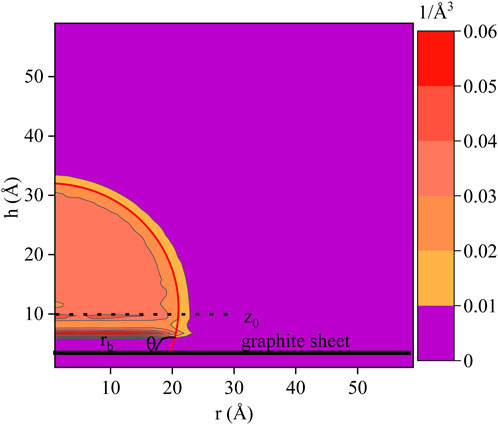
FIGURE 4. Example to extract the contact angle from a radial time-averaged water droplet concentration profile. The points above Z₀ = 10 A are used in the circular fit process.

The dependence of the contact angle on the droplet size is studied through the modified Young’s equation (Pethica, 1997), which allows bridging the macroscopic and microscopic contact angle through the surface tension γ and the line tension τ:

${\gamma }_{SV}={\gamma }_{SL}+{\gamma }_{LV}\cos \theta +\frac{\tau }{r_B},(8)$

where ${\gamma }_{SV}$, ${\gamma }_{SL}$, and ${\gamma }_{LV}$ denote solid–vapor, solid–liquid, and liquid–vapor phase surface tension, respectively. It is noteworthy that when $1/r_B\to 0$, the macroscopic contact ${\theta }_{\infty }$ can be deduced from the definition as $\cos {\theta }_{\infty }=\left({\gamma }_{SL}-{\gamma }_{SL}\right)/{\gamma }_{LV}$. Substituting this into Eq 8 results in the following equation:

$\cos \theta =\cos {\theta }_{\infty }-\frac{\tau }{{\gamma }_{LV}}\frac{1}{r_B}.(9)$

Eq 9 can be used to determine ${\theta }_{\infty }$ through extrapolation of data for $\theta$ as a function of $r_B$.

3 Results and discussion

3.1 Surface tension

3.1.1 CH₄–H₂O surface tension

We first validate our simulation methodology by comparing the surface tension between CH₄ and water with literature data from numerical simulations (Yang et al., 2017) and experiments (Jennings Jr and Newman, 1971; Tian et al., 1997; Shariat, 2014; Kashefi et al., 2016). The simulation domain is an orthogonal box with a size of 40 Å by 40 Å in X and Y directions and a size in the Z-direction that is used to control pressure under periodic boundary conditions. The domain contains 512 CH₄ molecules and 2048 H₂O molecules. Temperature has been fixed at 373 K. The pressure has been varied in the range 0–85 MPa by adjusting the domain length in the Z-direction. The simulations were run for 4 ns in the NPT ensemble to reach the desired pressure and then continued for 2 ns in the NVT ensemble to collect data for surface tension calculation. Surface tension has been calculated using Eq 6. We estimate uncertainties in surface tension and pressure by calculating their standard deviation based on the series of values obtained over 100 ps time intervals.

As shown in Figure 5, our results of surface tension versus pressure are compared to literature data. Our simulations follow the overall trend, as found in previous studies: a decrease in surface tension with increasing pressure until the pressure reaches a value of the order of 30 MPa where surface tension has reduced by approximately 30%. Beyond that pressure, surface tension only weakly depends on pressure. For the lower pressures—below 30 MPa—our results are within the range of variation in the experimental data. Beyond 30 MPa, our surface tension is generally on the high side compared to measured data. It is interesting to note that the same is true for the simulation data set provided in Yang et al. (2017). The results in Figure 5 provide a baseline data set and proper starting point for studying the effects of mixing CO₂ with CH₄ on surface tension.

FIGURE 5

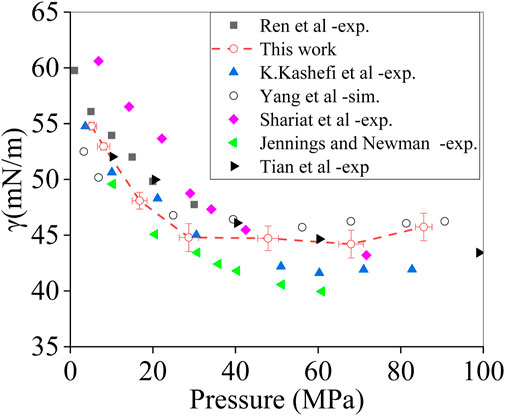
FIGURE 5. Surface tension of the methane–water interface as a function of pressure at T = 373 K. Our simulation data compared to experimental and computational data from the literature, as indicated.

The same procedure has been replicated by varying temperature at another three temperatures T = 311K, 423K, and 473 K. Figure 6 shows a decrease in CH₄–H₂O surface tension with increasing temperature. However, the surface tension versus pressure has a similar trend, as described in Figure 5 at T = 373 K.

FIGURE 6

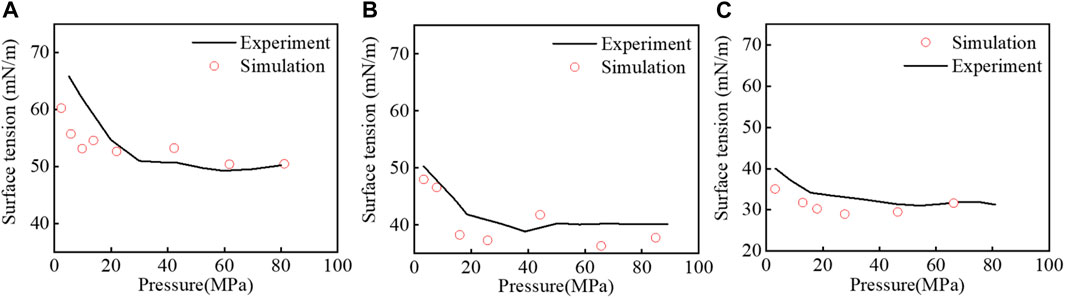
FIGURE 6. Pressure series of IFT for the CH4−H2O systems. The experimental data (black lines) correspond to Kashefi et al. (2016): (A) 311, (B) 423, and (C) 473 K.

3.1.2 CO₂–CH₄–H₂O surface tension

We now turn to surface tension between water and CH₄/CO₂ mixtures. This is conducted at a constant pressure of 15 MPa and at three temperatures, viz., 311 K, 353 K, and 398 K, based on availability of literature data (Ren et al., 2000; Yang et al., 2017). As previously shown, we have 2048 water molecules. The total number of CH₄ plus CO₂ molecules is 512. The number fraction of CO₂ molecules out of these 512 is denoted as $X_{{\text{CO}}_2}$.

Figure 7 shows surface tension as a function of $X_{{\text{CO}}_2}$. Surface tension decreases with increasing temperature and with increasing CO₂ fraction. For the two lower temperatures (311 K and 353 K), we see good agreement with experimental datasets due to Ren et al. (2000). There is also a fair agreement with the simulation results of Yang et al. (2017).

FIGURE 7

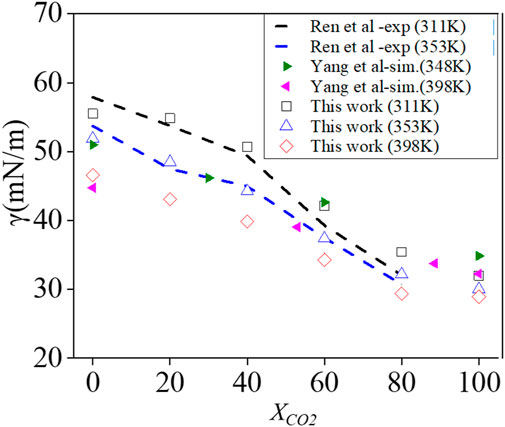
FIGURE 7. Influence of the CO₂ mole fraction on the surface tension of a CH₄/CO₂ mixture against water at p = 15 MPa at three temperatures, as indicated. Comparison with literature data.

The simulation results illustrate that there is a reduction of surface tension when adding CO₂ to a CH₄–water system by adding X_CO2 = 0–100%. This can be understood by the species concentration profiles over the interface that show a stronger interaction between CO₂ and water than that between CH₄ and water with CO₂ partially dissolving in water in Figure 8. Such observations are in line with Miguez et al. (2014); Yang et al. (2017).

FIGURE 8

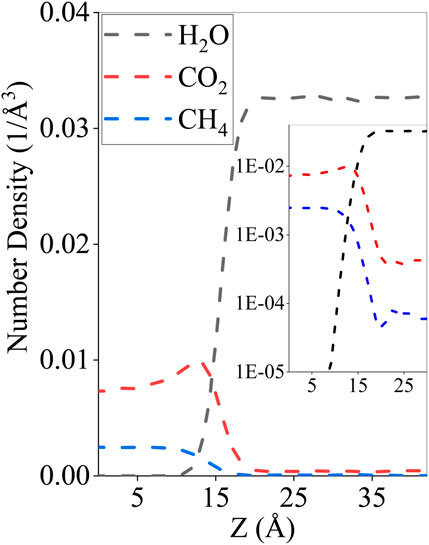
FIGURE 8. Equilibrium molecular number density profile of CO₂, CH₄, and H₂O at T = 311 K and p = 15 MPa. Inset: an enlarged figure of CO2/CH4 number density across the water interface.

3.2 Contact angle

3.2.1 Macroscopic contact angle

Given the modified Young’s equation Eq 9, the water droplets simulated in the current study (that are of nanoscopic size) can be related to the contact angle at the macroscale. The number of water molecules is given as 530, 995, 2015, 3981, and 5000 at fixed temperature 300 K for all three situations:(1) water-only system; (2) water droplet in a CH₄ environment with 3249 CH₄ molecules accounting to 3.0 MPa; (3) water droplet in a CO₂ environment with 3249 CO₂ molecules accounting to 3.5 MPa. The simulation domain has been set to 120 × 120 × 120ų.

As shown in Figure 9, the macroscopic contact angles estimated from modified Young’s equation of the three systems are 79.54° ± 1.15°, 99.56° ± 1.86°, and 112.80° ± 2.14°. The extrapolated macroscopic θ of water sitting on graphite sheets is in line with that from the experimental measurements of 79.3° for the water contact angle on chemically pure graphene (Li et al., 2013). Our simulated ${\theta }_{\infty }$ in CO₂ environment simulation also agrees well with Siemons et al. (2006) on the CO₂–H₂O–coal system, in which a value of 116.95° is reported at p = 3.5 MPa and T = 318 K.

FIGURE 9

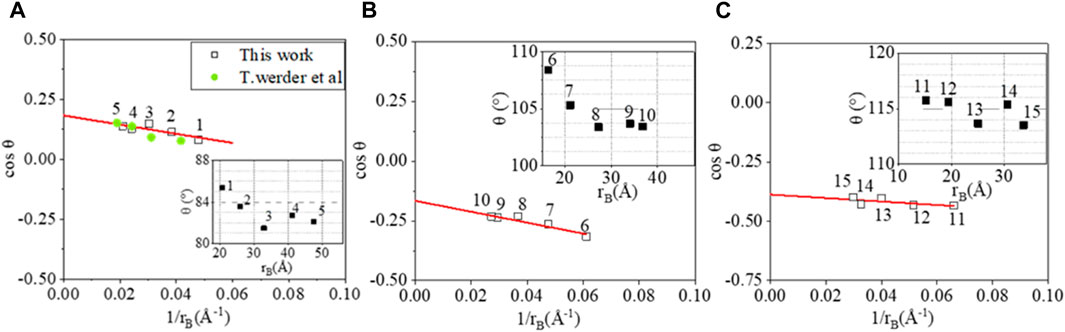
FIGURE 9. cosθ presented as a function of the droplet base curvature ${1/r}_B$. (A) Left: only water droplet sitting on the graphite surface; (B) middle: CH₄–water–carbon system; (C) right: CO₂–water–carbon system. Cases 1, 6, and 11; 2, 7, and 12; 3, 8, and 13; 4, 9, and 14; and 5, 10, and 15 represent 530, 995, 2015, 3981, and 5000 water molecules, respectively. Filled green squares—a simulation study performed by Werder et al. (2003). All insets: contact angle dependence on the radius of a droplet base.

3.2.2 The surface roughness effect on the contact angle

We compare the contact angle results on artificially textured and randomly generated rough surfaces in this section. For the artificial surface, the near-square lattice pillar arrangement has been used with an example of schematic representation of one pillar layer surface shown in Figure 10. There are all five artificial surface-related water contact angle simulations that have been performed from the number of pillar layer(s) that equals to 1 to 5, representing the increased roughness height. For random roughness, four surfaces with random roughness have been generated by changing the standard deviation of the roughness height ${\sigma }_H$ from 1 to 4 Å. An example of the surface with RMS height that equals to 3 has been shown in Figure 11. Both artificially and randomly generated rough surfaces have the same lateral size of 123 * 128 Å and the same correlation length in the X direction with 5.5 Å.

FIGURE 10

FIGURE 10. Perspective view of one-layer pillar substrates used in water contact angle simulations. Quadrangular pillars with a lateral size of 12.3 * 12.8 Å were arranged with a spacing of 12.3/12.8 Å between them in the X/Y direction. The rough layer is at 3.35 Å away from the top of the two-layer graphite sheets.

FIGURE 11

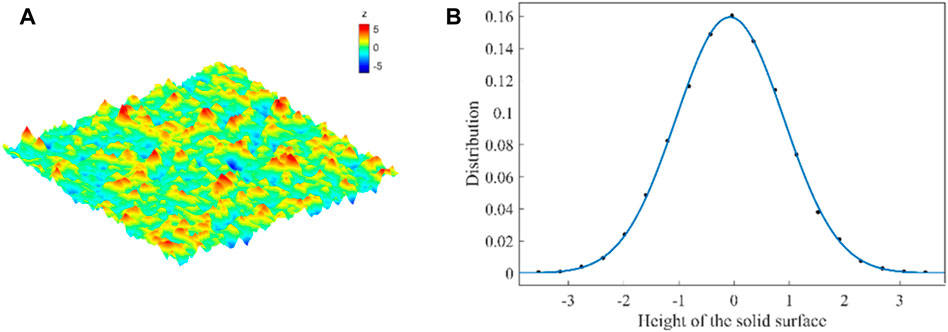
FIGURE 11. (A) Profile of a randomly generated surface with the standard deviation of the roughness height ${\sigma }_H$ = 3 Å and (B) mean statistical distribution of the roughness generated on the solid surface.

Wenzel and Cassie–Baxter models (Koishi et al., 2009) are common among the theories that allow describing the water-wetting behaviors of rough substrates. For the Wenzel model, water molecules completely fill the grooves of the rough surface. In a Cassie–Baxter state, nanodroplets form on rough substrates and the water molecules do not fill the grooves completely. Figure 12 presents the water contact angle results with its interactions with two aforementioned surfaces. It shows that roughness enhances the hydrophobicity of the solid surface, for both artificial and random surfaces, leading a wetting transition between the Wenzel and Cassie–Baxter states with increased root-mean-squared (RMS) height of the surface. Our findings are in agreement with other studies (Park et al., 2011; Khan and Singh, 2014).

FIGURE 12

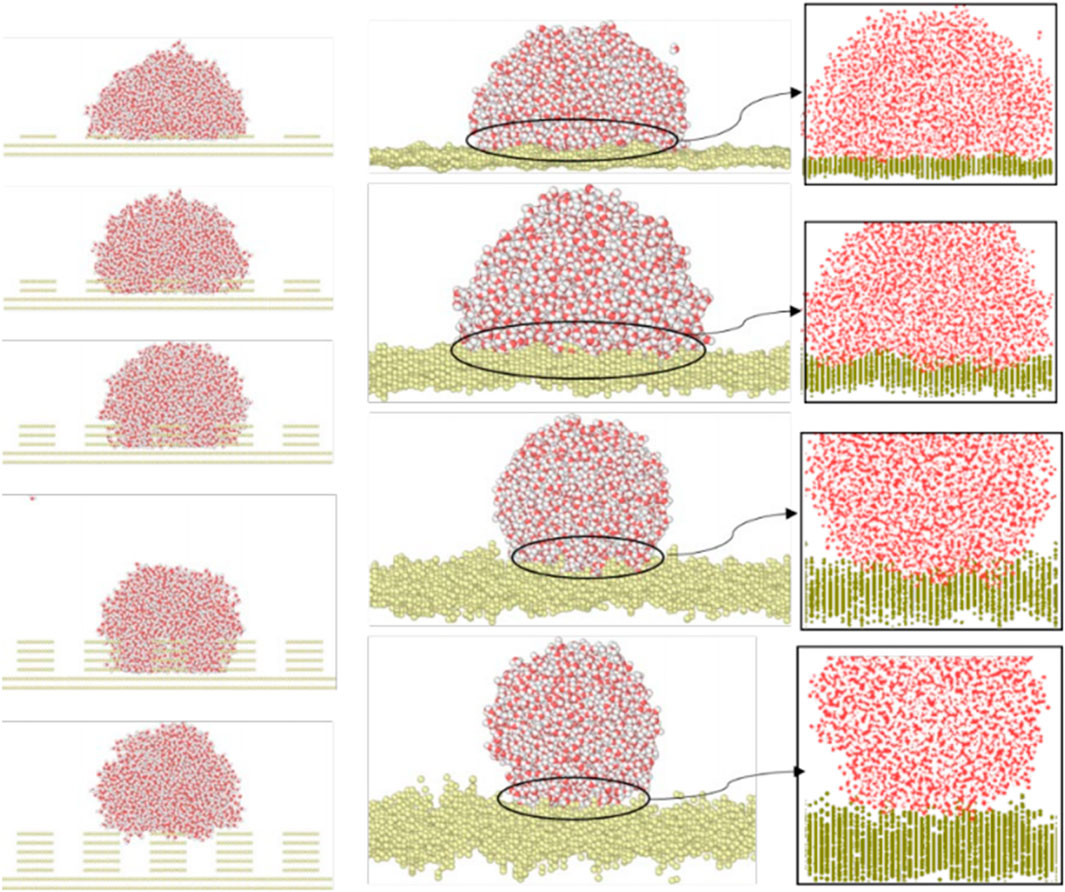
FIGURE 12. Effects of surface roughness on the contact angle. Left column: water droplet on the artificial quadrangular pillars with increased roughness height; right column: drop on the Gaussian random rough surface with RMS amplitude equals to 1, 2, 3, and 4 Å, respectively, together with their corresponding enlarged views.

4 Summary and conclusion

In this work, we have presented a molecular-scale study of the CO₂/CH₄/H₂O surface tension over a range of pressures, compositions, and temperatures and of the dependence of the water droplet contact angle on CH₄ and CO₂ with MD simulations based on a full-atom approach. The effect of surface roughness on the water contact angle is also considered in this study, and our results validate the hydrophobicity of the increasing surface roughness height on the water contact angle. The conclusions of our simulation are as follows:

• Consistent with available data from the literature, we find a decrease in CH₄–H₂O surface tension with increasing pressure until the pressure reaches a value of the order of 30 MPa where surface tension has reduced by approximately 30% at T = 373 K. Beyond that pressure, surface tension only weakly depends on pressure. The surface tension shows a decreasing trend with temperature.

• For CO₂–CH₄–H₂O surface tension, it decreases with increasing temperature and with increasing CO₂ fraction. Approximately 40% decrease was observed when adding CO₂ to the CH₄–water system by adding X_CO2 = 0–100%. This is attributed to a stronger interaction between CO₂ and water than that between CH₄ and water with CO₂ partially dissolving in water.

• The droplet size effect on the contact angle recovered from MD simulations has been analyzed. Our results justify the use of modified Young’s equation that can be used to extrapolate our findings at the nanoscale to macroscopic contact angles that are amenable to experimental validation.

• Roughness enhances the hydrophobicity of the solid surface, leading to a wetting transition between the Wenzel state and Cassie–Baxter state with an increased RMS height of the surface.

In this paper, we have been studying water static wettability in shale nanopores. In future, we will be working on water dynamics wettability under a constant pressure-driven environment to account for more complicated situation.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

WY: writing–original draft, writing-review and editing. Z-jW: Supervision. Y-yL: Data curation. D-qW: software and writing–review and editing. Y-zC: Conceptualization and Investigation.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Independent Prospective Basic Project of State Key Laboratory of Offshore Oil Exploitation in 2023 and the National Natural Science Foundation of China (52074347).

Conflict of interest

Authors WY, Z-jW, Y-yL, D-qW, and Y-zC were employed by CNOOC Research Institute Co., Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aimoli, C. G., Maginn, E. J., and Abreu, C. R. (2014). Transport properties of carbon dioxide and methane from molecular dynamics simulations. J. Chem. Phys. 141, 134101. doi:10.1063/1.4896538

PubMed Abstract | CrossRef Full Text | Google Scholar

Arif, M., Lebedev, M., Barifcani, A., and Iglauer, S. (2017). Influence of shale-total organic content on CO2 geo-storage potential. Geophys. Res. Lett. 44, 8769–8775. doi:10.1002/2017gl073532

CrossRef Full Text | Google Scholar

Biscay, F., Ghoufi, A., Lachet, V., and Malfreyt, P. (2009). Monte Carlo calculation of the methane-water interfacial tension at high pressures. J. Chem. Phys. 131, 124707. doi:10.1063/1.3236390

PubMed Abstract | CrossRef Full Text | Google Scholar

Busch, A., Alles, S., Gensterblum, Y., Prinz, D., Dewhurst, D. N., Raven, M. D., et al. (2008). Carbon dioxide storage potential of shales. Int. J. Greenh. gas control 2, 297–308. doi:10.1016/j.ijggc.2008.03.003

CrossRef Full Text | Google Scholar

Curtis, J. B. (2002). Fractured shale-gas systems. AAPG Bull. 86, 1921–1938. doi:10.1306/61EEDDBE-173E-11D7-8645000102C1865D

CrossRef Full Text | Google Scholar

Cygan, R. T., Romanov, V. N., and Myshakin, E. M. (2012). Molecular simulation of carbon dioxide capture by montmorillonite using an accurate and flexible force field. J. Phys. Chem. C 116, 13079–13091. doi:10.1021/jp3007574

CrossRef Full Text | Google Scholar

Darden, T., York, D., and Pedersen, L. (1993). Particle mesh Ewald: an N⋅ log (N) method for Ewald sums in large systems. J. Chem. Phys. 98, 10089–10092. doi:10.1063/1.464397

CrossRef Full Text | Google Scholar

De Ruijter, M. J., Blake, T. D., and De Coninck, J. (1999). Dynamic wetting studied by molecular modeling simulations of droplet spreading. Langmuir 15, 7836–7847. doi:10.1021/la990171l

CrossRef Full Text | Google Scholar

Edwards, R. W., Celia, M. A., Bandilla, K. W., Doster, F., and Kanno, C. M. (2015). A model to estimate carbon dioxide injectivity and storage capacity for geological sequestration in shale gas wells. Environ. Sci. Technol. 49, 9222–9229. doi:10.1021/acs.est.5b01982

PubMed Abstract | CrossRef Full Text | Google Scholar

Eshkalak, M. O., Al-shalabi, E. W., Sanaei, A., Aybar, U., and Sepehrnoori, K. (2014). Enhanced gas recovery by CO2 sequestration versus re-fracturing treatment in unconventional shale gas reservoirs.

Google Scholar

Hudson, G. H., and McCoubrey, J. C. (1960). Intermolecular forces between unlike molecules. A more complete form of the combining rules. Trans. Faraday Soc. 56, 761–766. doi:10.1039/tf9605600761

CrossRef Full Text | Google Scholar

Iglauer, S. (2017). CO2–water–rock wettability: variability, influencing factors, and implications for CO2 geostorage. Accounts Chem. Res. 50, 1134–1142. doi:10.1021/acs.accounts.6b00602

CrossRef Full Text | Google Scholar

Iglauer, S., Mathew, M. S., and Bresme, F. (2012). Molecular dynamics computations of brine–CO2 interfacial tensions and brine–CO2–quartz contact angles and their effects on structural and residual trapping mechanisms in carbon geo-sequestration. J. colloid interface Sci. 386, 405–414. doi:10.1016/j.jcis.2012.06.052

PubMed Abstract | CrossRef Full Text | Google Scholar

Jennings, H. Y., and Newman, G. H. (1971). The effect of temperature and pressure on the interfacial tension of water against methane-normal decane mixtures. Soc. petroleum Eng. J. 11, 171–175. doi:10.2118/3071-pa

CrossRef Full Text | Google Scholar

Jho, C., Nealon, D., Shogbola, S., and King, A. D. (1978). Effect of pressure on the surface tension of water: adsorption of hydrocarbon gases and carbon dioxide on water at temperatures between 0 and 50 C. J. colloid interface Sci. 65, 141–154. doi:10.1016/0021-9797(78)90266-7

CrossRef Full Text | Google Scholar

Kashefi, K., Pereira, L. M., Chapoy, A., Burgass, R., and Tohidi, B. (2016). Measurement and modelling of interfacial tension in methane/water and methane/brine systems at reservoir conditions. Fluid Phase Equilibria 409, 301–311. doi:10.1016/j.fluid.2015.09.050

CrossRef Full Text | Google Scholar

Kazemi, M., and Takbiri-Borujeni, A. (2016). Flow of gases in organic nanoscale channels: a boundary-driven molecular simulation study. Energy fuels. 30, 8156–8163. doi:10.1021/acs.energyfuels.6b01456

CrossRef Full Text | Google Scholar

Khan, S., and Singh, J. K. (2014). Wetting transition of nanodroplets of water on textured surfaces: a molecular dynamics study. Mol. Simul. 40, 458–468. doi:10.1080/08927022.2013.819578

CrossRef Full Text | Google Scholar

Koishi, T., Yasuoka, K., Fujikawa, S., Ebisuzaki, T., and Zeng, X. C. (2009). Coexistence and transition between Cassie and Wenzel state on pillared hydrophobic surface. PNAS 106, 8435–8440. doi:10.1073/pnas.0902027106

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Z., Wang, Y., Kozbial, A., Shenoy, G., Zhou, F., McGinley, R., et al. (2013). Effect of airborne contaminants on the wettability of supported graphene and graphite. Nat. Mater. 12, 925–931. doi:10.1038/nmat3709

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, S., Yang, X., and Qin, Y. (2010). Molecular dynamics simulation of wetting behavior at CO 2/water/solid interfaces. Chin. Sci. Bull. 55, 2252–2257. doi:10.1007/s11434-010-3287-0

CrossRef Full Text | Google Scholar

Louk, K., Ripepi, N., Luxbacher, K., Gilliland, E., Tang, X., Keles, C., et al. (2017). Monitoring CO2 storage and enhanced gas recovery in unconventional shale reservoirs: results from the Morgan County, Tennessee injection test. J. Nat. Gas Sci. Eng. 45, 11–25. doi:10.1016/j.jngse.2017.03.025

CrossRef Full Text | Google Scholar

Menzies, K. L., and Jones, L. (2010). The impact of contact angle on the biocompatibility of biomaterials. Optometry Vis. Sci. 87, 387–399. official publication of the American Academy of Optometry. doi:10.1097/opx.0b013e3181da863e

PubMed Abstract | CrossRef Full Text | Google Scholar

Miguez, J. M., Garrido, J. M., Blas, F. J., Segura, H., Mejía, A., and Pineiro, M. M. (2014). Comprehensive Characterization of Interfacial Behavior for the Mixture CO₂ + H₂O + CH₄: comparison between Atomistic and Coarse Grained Molecular Simulation Models and Density Gradient Theory. J. Phys. Chem. C 118, 24504–24519. doi:10.1021/jp507107a

CrossRef Full Text | Google Scholar

Miqueu, C., Míguez, J. M., Pineiro, M. M., Lafitte, T., and Mendiboure, B. (2011). Simultaneous application of the gradient theory and Monte Carlo molecular simulation for the investigation of methane/water interfacial properties. J. Phys. Chem. B 115, 9618–9625. doi:10.1021/jp202276k

PubMed Abstract | CrossRef Full Text | Google Scholar

Mosher, K., He, J., Liu, Y., Rupp, E., and Wilcox, J. (2013). Molecular simulation of methane adsorption in micro-and mesoporous carbons with applications to coal and gas shale systems. Int. J. Coal Geol. 109, 36–44. doi:10.1016/j.coal.2013.01.001

CrossRef Full Text | Google Scholar

Naylor, M., Wilkinson, M., and Haszeldine, R. S. (2011). Calculation of CO2 column heights in depleted gas fields from known pre-production gas column heights. Mar. Petroleum Geol. 28, 1083–1093. doi:10.1016/j.marpetgeo.2010.10.005

CrossRef Full Text | Google Scholar

Nielsen, L. C., Bourg, I. C., and Sposito, G. (2012). Predicting CO2–water interfacial tension under pressure and temperature conditions of geologic CO2 storage. Geochimica Cosmochimica Acta 81, 28–38. doi:10.1016/j.gca.2011.12.018

CrossRef Full Text | Google Scholar

Park, J., Ha, M., Choi, H., Hong, S., and Yoon, H. (2011). A study on the contact angles of a water droplet on smooth and rough solid surfaces. J. Mech. Sci. Technol. 25, 323–332. doi:10.1007/s12206-010-1218-2

CrossRef Full Text | Google Scholar

Patir, N. (1978). A numerical procedure for random generation of rough surfaces. Wear 47, 263–277. doi:10.1016/0043-1648(78)90157-6

CrossRef Full Text | Google Scholar

Pentland, C. H., El-Maghraby, R., Iglauer, S., and Blunt, M. J. (2011). Measurements of the capillary trapping of super-critical carbon dioxide in Berea sandstone. Geophys. Res. Lett. 38. doi:10.1029/2011gl046683

CrossRef Full Text | Google Scholar

Pethica, B. A. (1977). The contact angle equilibrium. J. Colloid Interface Sci. 62, 567–569. doi:10.1016/0021-9797(77)90110-2

CrossRef Full Text | Google Scholar

Plimpton, S. (1995). Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19. doi:10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

Ren, Q., Chen, G., Yan, W., and Guo, T. (2000). Interfacial Tension of (CO₂ + CH₄) + Water from 298 K to 373 K and Pressures up to 30 MPa. J. Chem. Eng. Data 45, 610–612. doi:10.1021/je990301s

CrossRef Full Text | Google Scholar

Roshan, H., Al-Yaseri, A. Z., Sarmadivaleh, M., and Iglauer, S. (2016). On wettability of shale rocks. J. colloid interface Sci. 475, 104–111. doi:10.1016/j.jcis.2016.04.041

PubMed Abstract | CrossRef Full Text | Google Scholar

Sachs, W., and Meyn, V. (1995). Pressure and temperature dependence of the surface tension in the system natural gas/water principles of investigation and the first precise experimental data for pure methane/water at 25 C up to 46.8 MPa. Colloids Surfaces A Physicochem. Eng. Aspects 94, 291–301. doi:10.1016/0927-7757(94)03008-1

CrossRef Full Text | Google Scholar

Sakamaki, R., Sum, A. K., Narumi, T., Ohmura, R., and Yasuoka, K. (2011). Thermodynamic properties of methane/water interface predicted by molecular dynamics simulations. J. Chem. Phys. 134, 144702. doi:10.1063/1.3579480

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmidt, K. A., Folas, G. K., and Kvamme, B. (2007). Calculation of the interfacial tension of the methane–water system with the linear gradient theory. Fluid Phase Equilibria 261, 230–237. doi:10.1016/j.fluid.2007.07.045

CrossRef Full Text | Google Scholar

Shariat, A. (2014). Measurement and modeling gas-water interfacial tension at high pressure/high temperature conditions.

Google Scholar

Siemons, N., Bruining, H., Castelijns, H., and Wolf, K. (2006). Pressure dependence of the contact angle in a CO2–H2O–coal system. J. colloid interface Sci. 297, 755–761. doi:10.1016/j.jcis.2005.11.047

PubMed Abstract | CrossRef Full Text | Google Scholar

Stuart, S. J., Tutein, A. B., and Harrison, J. A. (2000). A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 112, 6472–6486. doi:10.1063/1.481208

CrossRef Full Text | Google Scholar

Swope, W. C., Andersen, H. C., Berens, P. H., and Wilson, K. R. (1982). A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules: application to small water clusters. J. Chem. Phys. 76, 637–649. doi:10.1063/1.442716

CrossRef Full Text | Google Scholar

Tian, Y., Xiao, Y., Zhu, H., Dong, X., Ren, X., and Zhang, F. (1997). Interfacial tensions between water and non-polar fluids at high pressures and high temperatures. Acta Physico-Chimica Sin. 13, 89–95. doi:10.3866/pku.whxb19970120

CrossRef Full Text | Google Scholar

Werder, T., Walther, J. H., Jaffe, R. L., Halicioglu, T., and Koumoutsakos, P. (2003). On the water− carbon interaction for use in molecular dynamics simulations of graphite and carbon nanotubes. J. Phys. Chem. B 107, 1345–1352. doi:10.1021/jp0268112

CrossRef Full Text | Google Scholar

Wu, H., Chen, J., and Liu, H. (2015). Molecular dynamics simulations about adsorption and displacement of methane in carbon nanochannels. J. Phys. Chem. C 119, 13652–13657. doi:10.1021/acs.jpcc.5b02436

CrossRef Full Text | Google Scholar

Wu, Y., Tepper, H. L., and Voth, G. A. (2006). Flexible simple point-charge water model with improved liquid-state properties. J. Chem. Phys. 124, 024503. doi:10.1063/1.2136877

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, R., Zeng, K., Zhang, C., and Jiang, P. (2017). Assessing the feasibility and CO2 storage capacity of CO2 enhanced shale gas recovery using Triple-Porosity reservoir model. Appl. Therm. Eng. 115, 1306–1314. doi:10.1016/j.applthermaleng.2017.01.062

CrossRef Full Text | Google Scholar

Xue, C., Li, Y., Zhang, P., Ma, J., and Jia, S. (2014). Washable and wear-resistant superhydrophobic surfaces with self-cleaning property by chemical etching of fibers and hydrophobization. ACS Appl. Mater. interfaces 6, 10153–10161. doi:10.1021/am501371b

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Y., Narayanan Nair, A. K., and Sun, S. (2017). Molecular dynamics simulation study of carbon dioxide, methane, and their mixture in the presence of brine. J. Phys. Chem. B 121, 9688–9698. doi:10.1021/acs.jpcb.7b08118

PubMed Abstract | CrossRef Full Text | Google Scholar

Yong, W., Derksen, J., and Zhou, Y. (2020). The influence of CO2 and CH4 mixture on water wettability in organic rich shale nanopore. J. Nat. Gas. Sci. Eng. 87, 103746. doi:10.1016/j.jngse.2020.103746

CrossRef Full Text | Google Scholar

Zhou, Y., Helland, J. O., and Hatzignatiou, D. G. (2016). Computation of three-phase capillary pressure curves and fluid configurations at mixed-wet conditions in 2D rock images. SPE J. 21, 152–169. doi:10.2118/170883-pa

CrossRef Full Text | Google Scholar