- 1State Grid Hunan Electric Power Company Limited Economic and Technical Research Institute, Changsha, China
- 2Hunan Key Laboratory of Energy Internet Supply-demand and Operation, Changsha, China
This paper presents a method to investigate the impact of centralized and distributed renewable energy on the power grid system, aiming to discern their differences. First, we derived the coupling relationship between renewable energy permeability and access point voltage under a simplified model. Second, we proposed a holomorphic embedding model designed for non-global variation, enabling the construction of the bus state trajectory index. This index is employed to analyze the influence of centralized and distributed renewable energy access on power grid stability and voltage under low-permeability conditions. Furthermore, under high permeability, we determined the limit permeability of centralized and distributed renewable energy. Last, we provided renewable energy configuration recommendations to enhance the system’s receptive capacity.
1 Introduction
Under the global objective of reducing carbon emissions, the share of renewable energy sources in the power system is steadily increasing. However, a significant challenge arises concerning voltage issues when a high proportion of renewable energy is integrated into the power grid. Hence, it becomes crucial to thoroughly analyze the voltage impact when connecting renewable energy units to the power system. Additionally, the integration of renewable energy can take two forms: centralized and distributed. Ensuring stable operation of the multi-form renewable energy feed system raises an urgent need to address the problem of enhancing the system’s capacity to accommodate renewable energy allocation. Consequently, constructing a method to explore the differences in the impact of centralized and distributed renewable energy on the system holds great significance.
Currently, there exists extensive research on the influence of renewable energy grid connections on system voltage stability (Yi et al., 2020; Liu et al., 2022; Qi et al., 2023; Sun et al., 2023). Sun et al. (2023) accounted for the interaction among the feed branches of the renewable energy grid-connected system, utilizing the short-circuit ratio (SCR) to characterize the voltage support strength of the renewable energy grid-connected system. Subsequently, we established a quantitative analysis model of voltage support strength under steady-state voltage security constraints after a fault occurs. Qi et al. (2023) delves into the reactive power regulation characteristics of renewable energy and traditional units, studying the impact of replacing traditional units with a large number of renewable energy sources on stability margin. It also analyzes the uncertainty of the renewable energy output and its influence on the distribution range of stability margin by establishing a source load uncertainty model to generate typical scenarios. An online probability evaluation method of stability margin is presented. In the work of Liu et al. (2022), the impact of photovoltaic permeability and access points on the static voltage stability of grid-connected systems is discussed. To characterize the influence of access points on static voltage stability, two quantitative indexes, namely, the reactive power support coefficient and voltage-active power sensitivity, are proposed. Yi et al. (2020) investigated the critical permeability of renewable energy, constrained by static voltage stability, and proposed a practical engineering method for calculating this critical permeability based on static voltage stability constraints. This method provides an essential basis for determining the maximum consumption of renewable energy power generation and planning regional renewable energy projects. Although the research background mentioned previously primarily focuses on the influence of the renewable energy grid connection mode on power grid stability, there is limited exploration of the differences between centralized and distributed renewable energy grid connections.
The discussion on the uncertain factors of renewable energy is reflected in the literature (Fang et al., 2022; Yang et al., 2022a). In the work of Yang et al. (2022b), to improve the effective planning of electricity-gas integrated energy systems (EGIESs) among various stakeholders with distinct interests, a multi-agent game-based joint long-term planning approach considering wind power uncertainty is proposed. In the work of Fang et al. (2022), to further promote the prediction accuracy of short-term wind speed and maintain the prediction stability, an innovation composite architecture is developed incorporating three modules: data preprocessing, several individual predictors, and Volterra multi-model fusion with enhanced multi-objective optimization algorithm.
The unit commitment (UC) problem is an important theoretical basis for power market decision making and generation planning. A reasonable security-constrained unit commitment (SCUC) decision-making scheme can improve the stability of power system and improve the economy at the same time. In the work of Nan et al. (2018), the stochastic SCUC is modeled and solved at the same time under the constraint of AC power flow. Yang et al.’s (2021) study is a pioneer study for SCUC problems that proposes an expanded sequence-to-sequence (E-Seq2Seq)-based data-driven SCUC expert system for dynamic multiple-sequence mapping samples; it can accommodate the mapping samples of SCUC and consider the various input factors that affect SCUC decision making, possessing strong generality, high solution accuracy, and efficiency over traditional methods. Yang et al. (2022c) summarized the existing research results of SCUC questions based on artificial intelligence technology and data-driven approaches and analyzed the characteristics, advantages, and disadvantages of different types of methods. Finally, the paper puts forward some thoughts on the future research direction of data-driven SCUC. Yang et al. (2022a) proposed an intelligent deep learning (DL)-based approach for Data-Driven Security-Constrained Unit Commitment (DD-SCUC) decision making. The proposed approach includes data preprocessing and a two-stage decision-making process. Li et al. (2023) discussed a tri-layer non-cooperative energy trading approach among multiple grid-tied multi-energy microgrids (MEMGs) in the restructured integrated energy market. The heterogeneous uncertainties from renewable energy, market prices, and electric energy loads are also considered via the risk-averse stochastic programming (SP) approach.
The holomorphic-embedded tidal current method was initially proposed by scholar Trias (2012). As a non-iterative calculation method, this technique finds wide application in power flow calculations of power systems. Given its significant characteristics in handling non-convergence of power flow and its unique determination of initial values, the holomorphic embedding method has seen various improvements and widespread use in power system analysis (Liu et al., 2017; Du et al., 2021; Zhu et al., 2021; Liu et al., 2022). Zhu et al. (2021) introduced a new semi-invariant method based on the holomorphic embedding approach for probabilistic power flow calculations in electric-thermal joint networks. In the work of Du et al. (2021), the holomorphic embedding method is utilized to predict the critical point of static voltage stability, demonstrating better convergence and calculation accuracy compared to the traditional Newton–Raphson method. In the work of Liu et al. (2017), a high-dimensional holomorphic-embedded power flow model is developed to address AC power flow analysis challenges. Liu et al. (2022) established a power system decoupling model based on the holomorphic embedding method to identify voltage-weak buses.
The safe and stable operation of smart grid is also significant. In the work of Fu et al. (2023), in rolling bearing fault diagnosis, a two-dimensional time–frequency diagram is generated by continuous wavelet transform, and data are enhanced based on the generating countermeasure network (GAN). Finally, a convolution neural network (CNN) is used for fault classification. In the work of Xu et al. (2023), the hydraulic turbine governing system is modeled and the stability is analyzed at the same time. In the work of Zhang et al. (2023a), the optimal network attack strategy for economic scheduling of the integrated energy system uses a distributed double consistency algorithm and considers FDI attack and DoS attack. Zhang et al. (2023b) proposed a secondary frequency control strategy for multi-terminal systems considering DoS attacks. In the work of Zhu et al. (2023), a family of bipolar high step-up zeta–buck–boost converters based on the “coat circuit” is proposed, which can be used to connect a low-voltage dc source and a bipolar dc bus.
The centralized and distributed renewable energy grid-connected difference analysis method proposed in this paper is based on the holomorphic embedding model with non-global changes, and the bus state trajectory index is constructed by the holomorphic embedding model.
Under low permeability, the index is used to analyze the influence of centralized and distributed renewable energy access on power grid stability and voltage. Under high permeability, the limit permeability of centralized and distributed renewable energy is solved. Finally, the renewable energy configuration suggestions to improve the receptive capacity of the system are given.
2 Influence of renewable energy grid connection on the system
2.1 Influence of grid connection of renewable energy on voltage
Centralized and distributed renewable energy sources are mainly different in the access voltage level and access capacity, but these two factors do not affect us to simplify them to a unified grid-connected structure as shown in Figure 1A. In Figure 1A, the external electromotive force of the traditional unit is E, the line impedance is R + jX, the voltage at the load bus is U, the load power is equal to Pld + jQld, the renewable energy injection power is equal to Pre + jQre, and the traditional unit injection power to the load bus is equal to Pg + jQg:
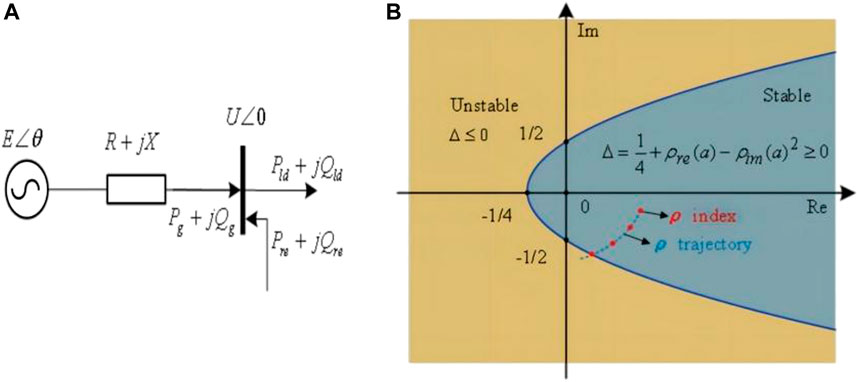
FIGURE 1. (A) Renewable energy access to the grid-simplified structure and (B) schematic diagram of the system instability boundary.
The power injected by traditional units into the load bus is expressed as follows:
The expressions of injected active power and injected reactive power are obtained by separating the imaginary part and the real part of the injected power as follows:
The power balance equation for the load bus can be obtained as follows:
If the load and the renewable energy power factor are constant, then Qld = λ1Pld and Qre = λ2Pre are defined. Substituting formula 2 in (3) gives
In formula 4, η1 = Pld−ηSld and η2 = λ1Pld−λ2ηSld.
After the square of formula 4, the phase angle is eliminated, and the quartic equation about U is obtained as follows:
In formula 5, the ratio of the active power injected into the renewable energy by η to the total load of the system can characterize the permeability of the renewable energy, and the total load of the system is expressed as
In order to simplify the analysis process, the renewable energy power factor is equal to the load power factor, that is, λ1 = λ2. Then, the expression of the square of the voltage amplitude at the renewable energy access point is as follows:
In the range of
According to Eq. 7, it can be judged that the square of the voltage amplitude at the renewable energy access point roughly shows a linear increasing trend with the increase of renewable energy permeability.
The abovementioned analysis determines that the connection of the renewable energy unit to the system will lead to the increase of the voltage at the access point, and the voltage amplitude at the access point is positively correlated with the renewable energy permeability.
In order to better illustrate the relationship of voltage permeability, we provide the following simulation: for a distribution network system whose voltage level is 12.66kV, the voltage amplitude of the traditional unit is 1.05, the line reactance is X = 0.05, the load active power is PLD = 1, and the ratio of reactive power to active power injected into the distributed power supply is λ2 = 0.1. Considering that different line impedance ratio and distributed power factor may affect the voltage amplitude at the access point, the following two scenarios are set:
1) When the line impedance ratio is changed, the ratio of the load active power to reactive power is 1:0.6, and other parameters remain unchanged
By consulting the distribution network design manual, the line impedance ratio of the distribution network is set to change in the range of 1.5–4.
2) The power factor of distributed power supply is supplied, line impedance ratio R/X = 2, and other parameters remain unchanged
The ratio of active power to reactive power of the distributed power varies from 0.3 to 0.8. Figure 2A shows that the voltage amplitude of the access point varies with the DG permeability and impedance ratio. It can be seen that the system with a higher line impedance ratio has lower voltage amplitude at low permeability and higher voltage amplitude at high permeability.
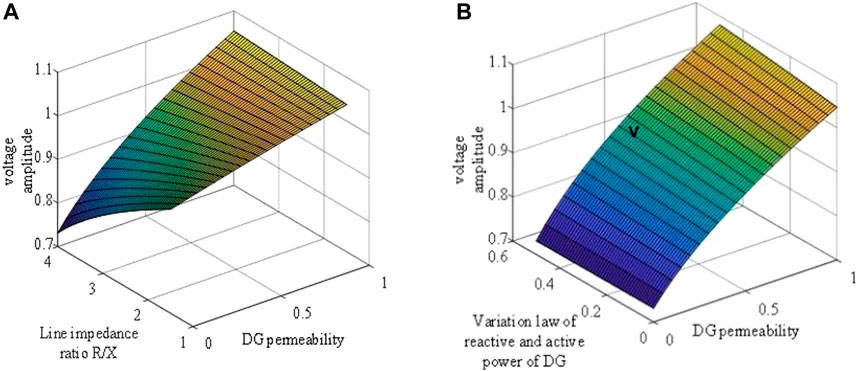
FIGURE 2. (A) Variation law of voltage amplitude, permeability, and impedance ratio of the access point and (B) voltage amplitude permeability of the access point and variation law of the reactive and active power of DG.
The reason is that when the line reactance is certain, the greater the impedance ratio, the greater the line impedance. When the permeability is low, the voltage drop of the system line with a large impedance ratio is large, so it presents lower voltage amplitude. When the permeability is high, the power flow is reversed, and the “voltage rise” of the system line with a large impedance ratio is larger, so it presents higher voltage amplitude. Figure 2B shows the variation of the voltage amplitude of the access point with DG permeability and DG reactive power ratio. It can be seen that under the same permeability, the higher the ratio of reactive power to active power injected by the distributed power, the higher the voltage amplitude of the access point. The reason is that at low permeability, the power generated by the distributed power supply is used to balance the load power, reducing the transmission power of the line and reducing the voltage drop of the line at the same time. At high permeability, the reactive power generated by the distributed power source balances the load reactive power and injects it into the system at the same time, and the capacitive reactive power will increase the local voltage, so the system with a high proportion of reactive power always maintains higher voltage amplitude.
3 Difference analysis method based on the HE method
In the initial section, the analysis of the relationship between renewable energy permeability and voltage amplitude fails to directly elucidate the influence of renewable energy on the static stability of the system, let alone differentiate between the impacts of centralized and distributed renewable energy on system stability. As a result, this paper introduces the bus state trajectory index based on the HE to address these limitations and accomplish the aforementioned objectives.
3.1 Improved HE model
For the desired variables V and Q embedded variable ε in the power flow equation, for different bus types, the traditional holomorphic embedding model can be described as follows:
Among them, Yiksh is the element of the transmission admittance matrix, Yitr is the diagonal element of the parallel admittance matrix, Ω is the set of different types of buses, and Visp represents the initial voltage amplitude of bus i.
The embedded voltage function V(ε) and reactive power function Qg(ε) are holomorphic functions about ε, which can be expanded into a Maclaurin form according to the properties of holomorphic functions.
Considering that the traditional HE only has physical meaning when ε = 1, the scope of application is very limited. In order to expand the scope of the model, we defined the following improved HE model:
In formula 11, ΔPli and ΔQli are the reference data of load active power and reactive power change of bus i, respectively, and ΔQgi is the reference of active power output change of generator bus i.
It is convenient to explain the process of solving the model; the reciprocal function Λ(ε) of voltage is defined, and the relationship between them satisfies V(ε)∙Λ(ε) = 1. The recursive equations of the improved holomorphic embedding model are as follows:
The abovementioned recursive equations all need to satisfy the condition n ≥ 1. Vi [0], Λi [0], and Qgi [0] can be obtained by solving the traditional holomorphic embedding model with the condition ε = 1. According to Eq. 12, the higher-order coefficients can always be calculated from the low-order coefficients; thus, the coefficients corresponding to the orders that meet the requirements of calculation accuracy can be obtained.
3.2 Bus state trajectory index based on HE
TRIAS (2014) defined an index to describe the stability characteristics of buses based on the traditional HE model, which can be used to judge whether the bus is in a stable state by its position, but this index is pointed out by TRIAS (2018) that it cannot effectively represent the margin. A schematic diagram of the system instability boundary is shown in Figure 1B.
In a brief review of this index, it is derived from the current balance equation of the two buses, which is defined as follows:
Among them, Zeq is the equivalent impedance of the two-bus system, S is the bus injection power, Vslack is the balanced bus voltage, and ρ is the bus stable state index, and its definition is similar to the SCR.
The simplified formula can be obtained by substituting ρ back into the two-bus current equation as follows:
U=V/Vslack, which represents the normalized bus voltage. The expression of U can be obtained by solving the quadratic equation shown in formula 14.
In order to ensure that the binary first-order equation has a solution, the following constraints must be satisfied:
In formula 16, ρre and ρim denote the real and imaginary parts of ρ, respectively. Δ can be described as a parabola symmetrical along the real axis and opening to the right on the ρ plane. If index ρ is inside the parabola, the bus is in a stable state; otherwise, it is unstable.
Considering the defect that the ρ index cannot quantify the stability margin, Liu et al. (2022) embedded ε into the ρ index to form a ρ(ε) function. The bus stability margin is quantified by the size of εi’ corresponding to the ρ(ε) function when the parabola intersects. The larger the value, the higher the static stability margin of the bus. Although the detailed process of solving the coefficient of ρ(ε) function is given in the literature, the solving process is tedious and only suitable for a certain kind of the HE model. Because the value of arbitrary order V [n] is known after the solution of the HE model, according to the relationship between normalized voltage and ρ index, any ρ[n] can be obtained by simple calculation:
According to formula 17, the coefficient ρ[n] is solved and the analytical expression of ρ ε) function is obtained. εi’ can be quickly found through functional relations or the method of depicting the trajectory of ρ index. Based on the analysis method of ρ index trajectory, this paper will discuss the difference of the influence of centralized and distributed renewable energy on the static stability of the system.
4 Analysis of the difference between centralized and distributed renewable energy
4.1 Overview of centralized renewable energy and distributed renewable energy features
Large-scale centralized renewable energy (CRE) is usually located at the remote end of the power grid, with a certain reactive power regulation capacity, usually through long-distance lines into the main network, and the resistance is difficult to ignore. Distributed renewable energy (DRE) is usually dispersed into the load center, with a high degree of matching with the load, mostly with small capacity and operating under a unit power factor. If connected through a multi-stage transformer, the transformer impedance is large and the electrical distance is farther than the centralized grid connected.
4.2 Simulation analysis of the influence of CRE and DRE on stability
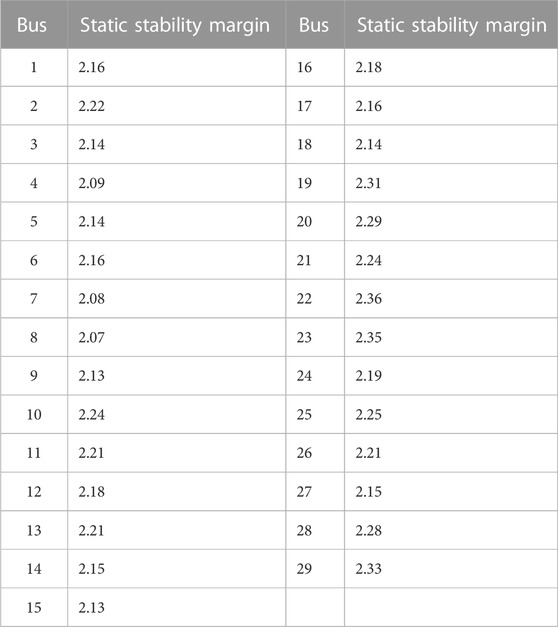
Based on the standard example of the IEEE-39 bus system, the detailed parameters of the IEEE-39 bus system can be found in the MATPOWER toolkit. First, the static stability margin of each bus is given by the abovementioned ρ index trajectory, the solid and weak buses of the system are identified, and the subsequent CRE and DRE access positions are determined.
Through ρ index trajectory in the third section, the specific value of the static stability margin obtained by using the index trajectory in Table 1. Since 30–39 buses are generator PV buses, the calculation of this index has no practical significance, so only bus 1–bus 29 are listed in Table 1.
4.2.1 Low-permeability scenario of renewable energy
For the renewable energy centralized access scenario, a CRE bus is connected by the weak No. 8 bus of the system. Because CRE has a certain reactive power regulation capability, the initial bus is the PV type, and when its reactive power exceeds the limit, it is converted to the PQ type. For the renewable energy distributed access scenario, six DRE buses are set to be accessed by the weak 3, 4, 7, 8, 9, and 15 buses of the system, and the CRE bus is set to the PQ type.
The location where CRE and DRE are connected in IEEE-39 bus simulation is shown in Figure 3A.
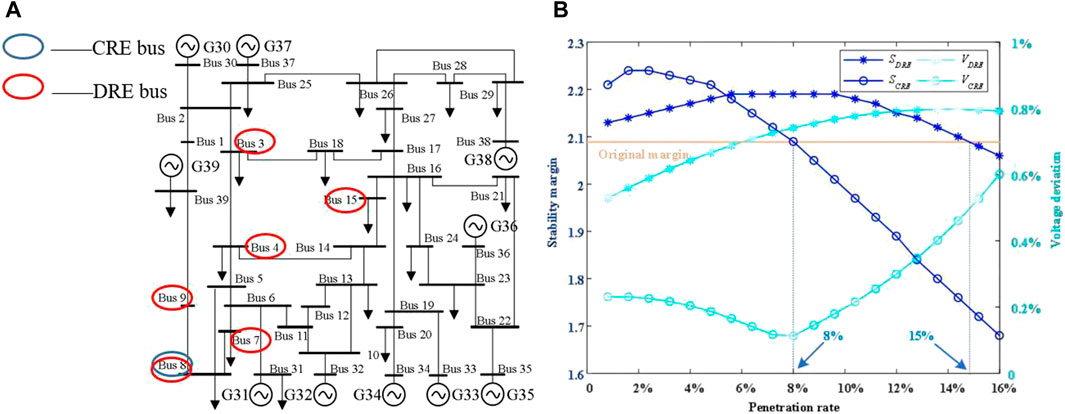
FIGURE 3. (A) Location where CRE and DRE are connected in IEEE-39 bus simulation and (B) effect of CRE and DRE on the system under different permeabilities.
With the increase of the renewable energy capacity of the system, the static stability margin of the system changes, as shown in Figure 3B.
It can be seen that for the original system, the static stability margin is 2.09. For CRE, the static stability of the system decreases rapidly when the permeability is higher than 8%. For DRE, when the permeability is higher than 15%, its access begins to have a negative impact on the system. However, on the whole, both CRE and DRE will improve the static stability margin of the system when the permeability is low, and whether it is positive or negative, the influence of CRE is more significant than DRE. The changing trend of the curve in Figure 3B is that a small amount of renewable energy can be used as active power support, and a large amount of renewable energy leads to a decrease in the stability of the reverse power flow.
In addition, due to the difference between the grid-connected impedance parameters of the two renewable energy sources, it can be concluded that DRE has a greater impact on the overall voltage level of the system than CRE, which is due to the larger voltage deviation caused by the larger impedance of DRE grid-connected lines.
4.2.2 High-permeability scenario of renewable energy
When the system needs to access a high proportion of renewable energy, the renewable energy bus may gradually evolve into a weak bus of the system, so in order to explore the limit of renewable energy acceptance of the system, this paper selects the buses with strong stability of the original system to access CRE and DRE.
The simulation settings are as follows: Scenario 1: renewable energy centralized access is adopted, and a CRE is accessed by 22 buses with the strongest stability. Scenario 2: using renewable energy distributed access, six DREs are connected by stable buses 19, 20, 22, 23, 28, and 29.
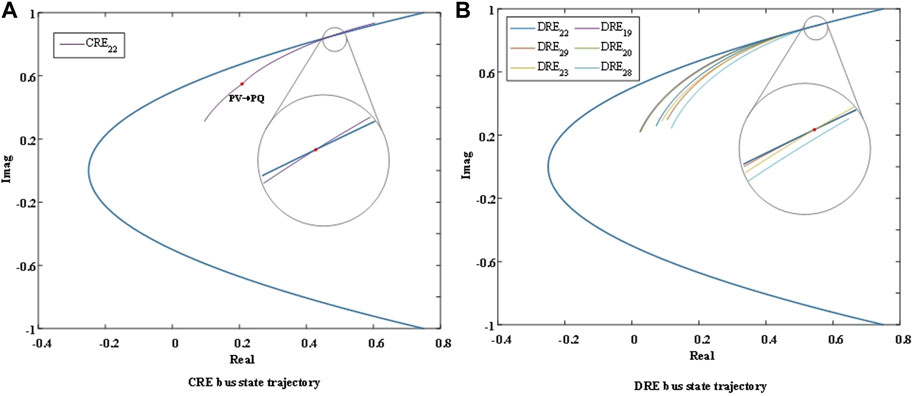
The simulation results show that the limit permeability of CRE in scenario 1 is 28.3%. The point on the trajectory in Figure 4A represents the transformation of the CRE bus type from PV to PQ, the CRE access bus is the first unstable bus in the system. The distributed renewable energy limit permeability in scenario 2 is 57.56%. As shown in Figure 4B, the DRE bus accessed from bus 23 is the first unstable bus in the system. From the abovementioned simulation, it is concluded that the acceptance ability of the system to DRE is significantly higher than that of CRE. The reasons are as follows: in the process of the gradual growth of DRE, the renewable energy power is first used to balance the nearby load. Because the position of DREs is scattered, the trend of power reversal is slower than that of CRE so that more total capacity can be accessed before a certain line of the system reaches the maximum transmission power.
Considering that CRE has certain reactive power regulation ability and can improve the static stability of the access point under small access capacity, we try to use hybrid access to improve the limited permeability of renewable energy. A simulation scenario 3 is set up: using renewable energy hybrid access, one CRE is connected from 23 buses, and five DREs are accessed from 19, 20, 22, 28, and 29 buses with strong stability. Since bus 23 is the first unstable bus in scenario 2, an appropriate capacity of CRE is added to the bus to improve its stability strength. For scenario 3, the simulated limit permeability of renewable energy can reach 71.15%, and the first unstable bus of the system becomes a DRE bus connected by bus 28.
From the simulation results of scenario 3, it can be seen that the reasonable arrangement of CREs and DREs connected to the power grid can improve the limited capacity of the system to accept renewable energy under static stability constraints. Scenario 3 of this paper is used only to verify the feasibility of improving the reception capacity of the renewable energy hybrid access mode. As for how to configure the access location and capacity of the two renewable energy sources to obtain the maximum limit permeability, this is an optimization problem. Follow-up work will be carried out in this area.
5 Conclusion
In this paper, a bus state trajectory index based on the holomorphic embedding method is proposed to explore the impact of CRE and DRE on the system. The main work is summarized as follows. The main results are as follows:
1) The mechanism of the effect of renewable energy on the voltage of the access point is deduced, and the relationship between permeability and voltage amplitude is explained.
2) Based on the traditional HE model, an improved HE model with non-global variation is constructed and the bus state trajectory index and its solving process are further deduced.
3) The effects of CRE and DRE on static stability and bus voltage in a low-permeability scenario are explored, and the limit permeability of renewable energy under the two access modes is calculated. From the simulation results of scenario 3, it can be seen that the reasonable arrangement of CREs and DREs connected to the power grid can improve the limit capacity of the system to accept renewable energy under static stability constraints.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
CX: conceptualization, data curation, investigation, methodology, project administration, software, supervision, validation, and writing–original draft. SH: data curation, formal analysis, methodology, and writing–review and editing. LW: data curation, investigation, methodology, project administration, software, supervision, and writing–review and editing. HY: formal analysis, methodology, and writing–review and editing.
Funding
This work was supported by the Science and Technology Project of State Grid Hunan Electric Power Company Limited No.5216A221001H and the Major science and technology project of Hunan Province No. 2020GK1010. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.
Conflict of interest
CX, SH, LW, and HY were employed by the State Grid Hunan Electric Power Company Limited Economic and Technical Research Institute.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Du, N., Tang, F., Liao, Q., et al. (2021). Static voltage stability based on holomorphic embedding method. Smart Power 49 (9), 8–15+69.
Fang, P., Fu, W., Wang, K., Xiong, D., and Zhang, K. (2022). A compositive architecture coupling outlier correction, ewt, nonlinear volterra multi-model fusion with multi-objective optimization for short-term wind speed forecasting. Appl. Energy 307, 118191. doi:10.1016/j.apenergy.2021.118191
Fu, W., Jiang, X., Li, B., Tan, C., Chen, B., and Chen, X. (2023). Rolling bearing fault diagnosis based on 2D time-frequency images and data augmentation technique. Meas. Sci. Technol. 34 (4), 045005. doi:10.1088/1361-6501/acabdb
Liu, C., Lai, Q., Yao, L., Hökkä, H., Peltoniemi, M., and Hölttä, T. (2022b). Power system decoupling model based on holomorphic embedding method: weak bus identification. Proc. CSEE 42 (5), 1736–1749. doi:10.1093/treephys/tpac037
Liu, C., Wang, B., Xu, X., Sun, K., Shi, D., and Bak, C. L. (2017). A multi-dimensional holomorphic embedding method to solve AC power flows. IEEE Access 5, 25270–25285. doi:10.1109/access.2017.2768958
Liu, Y., Yao, L., Liao, S., et al. (2022a). Study on the impact of photovoltaic penetration on power system static voltage stability. Proc. CSEE 42 (15), 5484–5497.
Li, Z., Wu, L., Xu, Y., Wang, L., and Yang, N. (2023). Distributed tri-layer risk-averse stochastic game approach for energy trading among multi-energy microgrids. Appl. Energy 331, 120282. doi:10.1016/j.apenergy.2022.120282
Nan, Y., Di, Y., Zheng, Z., Jiazhan, C., Daojun, C., and Xiaoming, W. (2018). Research on modelling and solution of stochastic scuc under ac power flow constraints. IET Generation Transm. Distribution 12 (15), 3618–3625. doi:10.1049/iet-gtd.2017.1845
Qi, J., Yao, L., Liao, S., et al. (2023). Online probabilistic assessment of static voltage stability margin for power systems with a high proportion of renewable energy. Power Syst. Prot. Control 51 (5), 47–57.
Sun, H., Yu, L., and Zhao, B. (2023). Quantitative analysis method for system strength of renewable energy generation grid-connected system based on post-fault steady-state voltage security constraint. Proc. CSEE 43 (9), 3322–3332.
Trias, A. (2018). Helm: the holomorphic embedding load-flow method. Foundations and implementations. Found. Trends® Electr. Energy Syst. 3 (3-4), 140–370. doi:10.1561/3100000015
Trias, A. (2014). Sigma algebraic approximants as a diagnostic tool in power networks. US, 20140156094.
Trias, A. (July 2012) . The holomorphic embedding load flow method Proc. IEEE Power Energy Soc. General Meet., San Diego, CA, USA, 1–8.
Xu, P., Fu, W., Lu, Q., Zhang, S., Wang, R., and Meng, J. (2023). Stability analysis of hydro-turbine governing system with sloping ceiling tailrace tunnel and upstream surge tank considering nonlinear hydro-turbine characteristics. Renew. Energy 210, 556–574. doi:10.1016/j.renene.2023.04.028
Yang, N., Yang, C., Wu, L., Shen, X., and Liu, S. (2021). Intelligent data-driven decision-making method for dynamic multi-sequence: an e-seq2seq based scuc expert system. IEEE Trans. Industrial Inf. (99), 1.
Yang, N., Dong, Z., Wu, L., Zhang, L., Shen, X., Chen, D., et al. (2022a). A comprehensive review of security-constrained unit commitment. J. Mod. Power Syst. Clean Energy 10 (3), 562–576. doi:10.35833/mpce.2021.000255
Yang, N., Qin, T., Wu, L., Huang, Y., Huang, Y., Xing, C., et al. (2022b). A multi-agent game based joint planning approach for electricity-gas integrated energy systems considering wind power uncertainty. Electr. Power Syst. Res. 204, 107673. doi:10.1016/j.epsr.2021.107673
Yang, N., Yang, C., Xing, C., Ye, D., Jia, J., Chen, D., et al. (2022c). Deep learning-based scuc decision-making: an intelligent data-driven approach with self-learning capabilities. IET generation, Transm. distribution 16 (4), 629–640. doi:10.1049/gtd2.12315
Yi, J., Lin, W., Yu, F., et al. (2020). Calculation method of critical penetration of renewable energy constrained by StaticVoltage stability. Power Syst. Technol. 44 (08), 2906–2912.
Zhang, Y., Wei, L., Fu, W., Chen, X., and Hu, S. (2023b). Secondary frequency control strategy considering DoS attacks for MTDC system. Electr. Power Syst. Res. 214, 108888. doi:10.1016/j.epsr.2022.108888
Zhang, Y., Xie, X., Fu, W., Chen, X., Hu, S., Zhang, L., et al. (2023a). An optimal combining attack strategy against economic dispatch of integrated energy system. IEEE Trans. Circuits Syst. II Express Briefs 70 (1), 246–250. doi:10.1109/tcsii.2022.3196931
Zhu, B., Liu, Y., Zhi, S., Wang, K., and Liu, J. (2023). A family of bipolar high step-up zeta–buck–boost converter based on “coat circuit”. IEEE Trans. Power Electron. 38 (3), 3328–3339. doi:10.1109/tpel.2022.3221781
Keywords: holomorphic embedding method, static stability, renewable energy, receptive capacity, bus state trajectory
Citation: Xu C, He S, Wang L and Yu H (2023) Difference analysis method of grid connection influence between CRE and DRE based on bus state trajectory. Front. Energy Res. 11:1266252. doi: 10.3389/fenrg.2023.1266252
Received: 24 July 2023; Accepted: 30 August 2023;
Published: 22 September 2023.
Edited by:
Nan Yang, China Three Gorges University, ChinaReviewed by:
Lipeng Zhu, Hunan University, ChinaYunyun Xie, Nanjing University of Science and Technology, China
Copyright © 2023 Xu, He, Wang and Yu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lu Wang, MTgzMTY4OTE0QHFxLmNvbQ==
 Chao Xu1,2
Chao Xu1,2 Lu Wang
Lu Wang