Modified experimental method to investigate micro transport in the shale matrix for shale gas production

Matrix permeability is the primary transport property for shale gas recovery, due to the special production process of gas from matrix to wellbore. With the micro pore size of shale matrix, it is necessary to consider micro transport mechanisms for the obtained permeability from macro experimental techniques. In this study, the macro experimental permeability was investigated in micro way, by the analyzation of pressure drop curves of shale matrix at high- and low-pressure experimental conditions, with modified numerical model containing micro transport mechanisms. As selected parameters, porosity, pore radius and tortuosity were regressed to obtain apparent permeabilities of three samples. The analysis shows that, tortuosity is much higher than macro one, and has been proved to be necessary and reasonable. The Knudsen diffusion and slippage effect control the micro transport of shale matrix at low and high pressure, separately, which is the main difference of macro and micro transports. Slippage flow weight factor helps to increase of slippage flow proportion with pressure. Higher pore radius and tortuosity both could weaken the effect of Knudsen diffusion, and slippage flow appears positive relationship with pore size at high pressure. This research provides an inspiration to shale transport study and a micro perspective theoretical guidance for the macro recovery of in-site shale gas reservoir.

1 Introduction

Shale gas is the vital unconventional hydrocarbon resource for world energy resource development, due to its abundant reserves and strategic role among countries. The recovery of shale gas involves various technologies in different fields, from exploration and exploitation underground to well-productive performances. Each technology should not ignore the properties of the shale matrix, which is the source of gas storage and production (Zhou et al., 2020; Huang et al., 2021). The investigation on gas transport in the shale matrix ensures the effective recovery of the shale gas reservoir.

Hydraulic fracturing is the most common measure to stimulate the shale gas reservoir, due to the highly tight lithology of the shale gas reservoir (Zhao et al., 2015; Clarkson et al., 2016; Cheng et al., 2018; Mohagheghian et al., 2020). Shale gas production is comprehensively affected by hydraulic fractures and the matrix (Cipolla et al., 2009; Jia et al., 2020). These fractures connect the matrix and the wellbore as a stable hydrocarbon production channel (Meng et al., 2021), which has been well-studied by experimental and theoretical methods for shale gas recovery (Berawala et al., 2019; Rubin et al., 2019). Comparatively, the studies of production increasing at the shale matrix level were less focused on. It has been proven that gas transport in the shale matrix affects the accuracy of productivity prediction (Shi et al., 2013) and well performance investigation (Wang and Marongiu-Porcu, 2015). By neglecting transport mechanisms in the shale matrix, we observe an 11% deviation in shale gas recovery for Marcellus Shale (Rubin et al., 2019).

Permeability is the typical characteristic parameter for the hydrocarbon transport ability, which is necessary for experimental, numerical, and analytical research studies or in-field exploitation of the shale gas reservoir. The shale pore structure has a great connection with the gas transport property (Mi et al., 2014) and determines the intrinsic permeability of the shale matrix (Wang and Marongiu-Porcu, 2015). In the shale matrix, nanopores are well developed, leading to gas transport with complex micro-mechanisms (Yang X. et al., 2020; Wu et al., 2022). Compared with the Darcy flow, the non-Darcy flow with a slippage effect and Knudsen diffusion is more appropriate for gas transport in the shale matrix (Shi et al., 2013). Without Knudsen diffusion, shale matrix permeability could be applied only to near wellbore areas with larger pores (Berawala et al., 2019). In addition, the permeability has a complex relationship with productive pressure (McKernan et al., 2014). In the shale gas recovery process, the depletion of reservoir pressure is beneficial to the increase of shale matrix permeability. On the contrary, shale matrix permeability also causes pressure variations by changing the gas transport ability. Thus, in the shale matrix, permeability and pressure show coordinated variation, which deserves a special study with special technologies.

A series of experimental technologies have been developed to measure shale matrix permeability. Owing to the ultra-low permeability of the shale matrix, a massive amount of time is required for the steady-state method (Sinha et al., 2013), while unsteady-state methods are more acceptable due to their time-saving advantage (Cui et al., 2010). The unsteady-state method is a technology used to obtain the permeability by analyzing the pressure variation curve by exerting a pressure pulse on the shale sample. The samples in the unsteady-state method could be divided into two categories; they are the shale core plug and shale particles. The shale core plug was believed to contain abundant fractures, and its permeability could not represent the shale matrix (Heller et al., 2014). Shale particles with appropriate sizes would dramatically reduce the existence of fractures and shale matrix permeability could be well obtained (Luffel et al., 1993; Cui et al., 2010; Fathi et al., 2012; Civan, 2019; Wang and Yu, 2020), whereas for analytical and numerical models to analyze pressure drop curves from the shale matrix particle (Fathi et al., 2012; Tinni et al., 2012; Heller et al., 2014; Cui et al., 2018; Civan, 2019; Wang and Yu, 2020; Wu et al., 2021), gas transport was regarded as the macro one, and the obtained permeability did not include micro transport mechanisms, e.g., Knudsen diffusion. The theoretical model of micro transport permeability, called apparent permeability, was well developed (Wu et al., 2017; Yang Z. et al., 2020; Nan et al., 2020) and has not been applied in shale matrix permeability measuring. It may be related to the barrier of the trans-scale. The apparent transport is in the micro-scale, while the experiments about shale gas recovery are in the macro-scale (Wang et al., 2020).

To acquire the micro transport mechanisms of the real shale matrix, it is necessary to modify the technology of shale matrix permeability measuring, by solving multi-scale problems and finding a corresponding way to investigate shale matrix transport. Based on the gas transport experiment of the real shale matrix, pressure drop curves were recorded. By applying apparent permeability to a numerical model, a novel data analysis model was constructed. The nanopore structure parameters were selected as target fitting parameters, and the micro transport property was further obtained. For the discrepancy of macro and micro transports, the coordinated variation of pressure and apparent permeability and the effects of the nanopore structure on micro transport were discussed in detail. This research provides micro-perspective theoretical guidance for the macro production of the on-site shale gas reservoir.

2 Dynamic transport experiment

2.1 Experimental samples

To avoid the disturbance of fractures to the apparent permeability of matrix nanopores, three samples from the Wufeng–Longmaxi Formation were selected for experimental research, i.e., samples 1–3. The samples should be crushed into particles, in a 20–30 mesh range, to avoid the interference of a microfracture to gas transport in the shale matrix (Luffel et al., 1993). Particles are easier to be filled in the sample chamber (SC) with less void space, as shown in Figure 1, and each particle could be considered as being homogeneous and spherical with various nanopores (marked with blue parallel lines in Figure 1). With water removal and measuring, the density, total volume, external space volume, total surface area, and filling degree of each particle sample in the SC are obtained (Wu et al., 2021), which are also presented in Table A1 of Appendix A.

FIGURE 1

FIGURE 1. Sample chamber filled with the particle sample.

2.2 Experimental method

For an accurate investigation of dynamic gas transport in the real shale matrix, the experimental device should be specially designed. The SC, reference chamber (RC), pressure sensor, and valve were connected with the gas line in the way shown in Figure 2. In the front end and back end, the gas supply and gas vacuumizing and emissions were set up. To avoid the negative influences of the low filling degree and low experimental pressure, an automatic gas supplement and pressurization (AGSP) system is added in the front end. With the AGSP system, the low filling degree could be ignored and a high experimental pressure could be ensured. Herein, the experimental method was introduced succinctly, and the details can be found in the pilot study (Wu et al., 2021).

FIGURE 2

FIGURE 2. Experimental device for dynamic gas transport investigation.

With the designed experimental device, the dynamic transport experiment of the gas in the shale matrix could be conducted. First, the RC and SC with the connected lines were vacuumized. With the valve closed, the RC was filled with helium up to the pressure, p_ini. Then, after the opening of the valve, the gas would expend from the RC to the SC. Sensing the pressure drop, the AGSP system starts instantly, to supply gas to the RC and SC, and stops with the recovery of pressure up to the p_ini value. At this moment, the gas would expend to the pores of the shale matrix particle from the void space of the SC, resulting in a gradual drop of pressure with time, which was recorded using a pressure sensor.

Helium gas was utilized in this experiment due to its smallest molecule diameter and inertia. A smaller molecule could enter the nanopore in an easier way, to reflect a more detailed pore structure and gas transport property in the shale matrix. With the designed experimental device and selected experimental gas, the entry of the gas in the shale matrix could be accurately reflected by the pressure drop, providing a reference for CO₂ injection to the shale matrix and bottom hole flowing pressure determination for a better recovery of shale gas.

2.3 Dynamic transport data interpretation

To analyze the experimental data, a numerical model should be applied. The radius of each particle R denoted the summation of m-piece regions with a uniform thickness Δr. Then, from the center, r₁, to the surface of the particle, r_m, in the radial direction, there were m number of points. The parameter r_i utilized here refers to the i-th position in the particle. The time was also divided with the uniform time quantum, Δt. The parameter n refers to the n-th time quantum. Based on the law of the conservation of mass, the numerical model for experimental data can be constructed (Wu et al., 2021). The numerical control model for the gas entering the spherical particle can be given as follows:

$p_i^{n+1}=\frac{Z_i^n\Delta t}{\varphi {\left(i\Delta r\right)}^2}\left[\begin{array}{l}{\left(i+\frac{1}{2}\right)}^2\frac{k_{i+\frac{1}{2}}^n}{{\mu }_{i+\frac{1}{2}}^n{C_{\mathrm{g}}}_{i+\frac{1}{2}}^n}\left({\left(\frac{p}{Z}\right)}_{i+1}^n-{\left(\frac{p}{Z}\right)}_i^n\right)-\\ {\left(i-\frac{1}{2}\right)}^2\frac{k_{i-\frac{1}{2}}^n}{{\mu }_{i-\frac{1}{2}}^n{C_{\mathrm{g}}}_{i-\frac{1}{2}}^n}\left({\left(\frac{p}{Z}\right)}_i^n-{\left(\frac{p}{Z}\right)}_{i-1}^n\right)\end{array}\right]+p_i^n,(1)$

where p is the gas pressure, Z is the deviation factor, $\varphi$ is the porosity of the particle, k is the permeability of the matrix, and μ and Cg are the viscosity and compressibility factor of the gas, respectively. The subscript i + 1/2 refers to the center of position i and i + 1, and i − 1/2 refers to the center of position i − 1 and i. The values of the parameters with subscript i + 1/2 or i − 1/2, could be obtained via the harmonic average.

To correspond to the law of the conservation of mass better, Eq. 1 could be rewritten as follows:

${\rho }_i^{n+1}=\frac{\Delta t}{\varphi {\left(i\Delta r\right)}^2}\left[\begin{array}{l}{\left(i+\frac{1}{2}\right)}^2\frac{k_{i+\frac{1}{2}}^n}{{\mu }_{i+\frac{1}{2}}^n{C_{\mathrm{g}}}_{i+\frac{1}{2}}^n}\left({\rho }_{i+1}^n-{\rho }_i^n\right)-\\ {\left(i-\frac{1}{2}\right)}^2\frac{k_{i-\frac{1}{2}}^n}{{\mu }_{i-\frac{1}{2}}^n{C_{\mathrm{g}}}_{i-\frac{1}{2}}^n}\left({\rho }_i^n-{\rho }_{i-1}^n\right)\end{array}\right]+{\rho }_i^n,(2)$

where ρ is the in situ density. The pressure at the (n + 1)-th time step could be calculated by the density at the same time step with the equation shown as follows:

$p_i^{n+1}=\frac{{\rho }_i^{n+1}{Z}_i^n\mathrm{R}T}{M},(3)$

where M is the molar mass, R is the universal gas constant, and T is the temperature.

At the initial condition, the gas around the particle is prepared to enter the vacuum particle. Therefore, the initial condition could be expressed as follows:

$\left\{\begin{array}{l}\begin{array}{cc}{p}_i^1=0& \left(1\le i<\left(m-1\right)\right)\end{array}\\ \begin{array}{cc}{p}_m^1=p_{\text{out}-m}& \left(i=m\right)\end{array}\end{array}\right..(4)$

Based on the law of conservation of mass, the inner and outer border equations could be given as follows:

$\left\{\begin{array}{l}{p}_1^n=p_2^n\\ V_{\mathrm{t}}\frac{{\rho }_{\text{out}-m}^n-{\rho }_{\text{out}-m}^{n+1}}{\Delta t}=S_{\mathrm{t}}{\left(\frac{k}{\mu C_{\mathrm{g}}}\right)}_m^n\frac{{\rho }_m^n-{\rho }_{m-1}^n}{\Delta r}\end{array}\right..(5)$

In the traditional experimental research, the transport of helium in a rock is a macro process with the slippage effect (Tinni et al., 2012; Civan et al., 2013; Yang et al., 2021). The permeability for the macro-transport process could be expressed as follows:

$k=k_{\mathrm{int}}\left(1+\frac{b}{p}\right),(6)$

where k_int is the intrinsic permeability and b is the slippage coefficient.

Equation 6 could be substituted into Eq. 2 to analyze the experimental data from a macro perspective. However, in the shale matrix, the well-developed nanopores contribute the most of the specific surface area to the whole shale particle. Due to the nanoscale pore, the gas enters the particle in a gradual process. Considering the confinement effect of nanopores (Chai et al., 2019), in the transport process of helium entering the shale matrix particle by the nanopore, in addition to the slippage flow, Knudsen diffusion should be included (Wu et al., 2014). Herein, slippage transport refers to macro transport with the slippage effect, while slippage flow refers to a transport form in micro transport. Considering the transport with micro-mechanisms, experimental data could be analyzed more accurately from a micro perspective.

As shown in Figure 3, the helium molecules (brown ball) enter the shale matrix with nanopores, driven by the pressure differential. In the nanopore with non-uniform pressure, the helium molecules collide with each other to transport in the slippage flow form marked by collision A in Figure 3. Moreover, the helium molecules collide with the wall to transport in the Knudsen diffusion form, marked by collision B. In the theory study of micro transport, the pressure, tortuosity, and pore size have been given in advance. However, for gas transport in the real shale matrix at the experimental condition, the pressure and pore constructure at any position and time is dynamic and unknown, leading to the dynamic and non-determinacy of gas transport. Therefore, collisions A and B in a nanopore are both inconstant. The corresponding slippage flow and the Knudsen diffusion flow should be regarded as unsteady flows, instead of steady flows in the theory study (Fink et al., 2017; Wu et al., 2017; Sheng et al., 2019; Yang Z. et al., 2020).

FIGURE 3

FIGURE 3. Diagrammatic sketch of the gas entering the shale matrix nanopore.

To express dynamic transport, referring to the traditional apparent theory (Wu et al., 2015), the dynamic apparent flux could be written as follows:

$J_{\mathrm{a}-\mathrm{d}}={\omega }_{\mathrm{s}-\mathrm{d}}{J}_{\mathrm{s}-\mathrm{d}}+{\omega }_{\mathrm{k}-\mathrm{d}}{J}_{\mathrm{k}-\mathrm{d}},(7)$

where, J_a-d, J_s-d, and J_k-d are the bulk transport, slippage flow, and Knudsen diffusion dynamic fluxes, respectively; ω_s-d and ω_k-d are the weight factors. Based on Eq. 7, the apparent permeability of the gas entering the nanopore of the particle could be derived as follows (Coppens and Dammers, 2006; Wu et al., 2014):

$k_{\mathrm{a}-\mathrm{d}}=k_{\mathrm{s}-\mathrm{d}}{\omega }_{\mathrm{s}-\mathrm{d}}+k_{\mathrm{k}-\mathrm{d}}{\omega }_{\mathrm{k}-\mathrm{d}},(8)$

where k_a-d, k_s-d, and k_k-d are the bulk transport, slippage flow, and Knudsen diffusion dynamic permeabilities, respectively. k_s-d and k_k-d could be given as follows:

$k_{\mathrm{s}-\mathrm{d}}=\frac{\varphi r_{\mathrm{t}}^2}{8{\tau }^2}\left(1+\frac{4k_{\mathrm{n}}}{1-b_{\mathrm{c}}{k}_{\mathrm{n}}}\right),(9)$

$k_{\mathrm{k}-\mathrm{d}}=\frac{2\mu C_{\mathrm{g}}\varphi r_{\mathrm{t}}}{3{\tau }^2}{\delta }^{{\mathrm{D}}_{\mathrm{f}}-2}{\left(\frac{8ZRT}{\pi M}\right)}^{0.5},(10)$

where r_t is the radius of the transport channel, k_n is the Knudsen number, b_c is the gas slippage constant for apparent transport, τ is the tortuosity of the shale matrix, and D_f is the surface roughness. The expressions or values of k_n, b_c, and D_f refer to the previous research directly (Wu et al., 2016).

Therefore, the numerical control model for micro transport is given as follows:

${\rho }_i^{n+1}=\frac{\Delta t}{\varphi {\left(i\Delta r\right)}^2}\left[\begin{array}{l}{\left(i+\frac{1}{2}\right)}^2\frac{{k_{\mathrm{a}-\mathrm{d}}}_{i+\frac{1}{2}}^n}{{\mu }_{i+\frac{1}{2}}^n{C_{\mathrm{g}}}_{i+\frac{1}{2}}^n}\left({\rho }_{i+1}^n-{\rho }_i^n\right)-\\ {\left(i-\frac{1}{2}\right)}^2\frac{{k_{\mathrm{a}-\mathrm{d}}}_{i-\frac{1}{2}}^n}{{\mu }_{i-\frac{1}{2}}^n{C_{\mathrm{g}}}_{i-\frac{1}{2}}^n}\left({\rho }_i^n-{\rho }_{i-1}^n\right)\end{array}\right]+{\rho }_i^n.(11)$

With the constructed numerical model, the gradual experimental pressure drop caused by the gas entering the shale matrix particle could be fitted on a microscopic scale with apparent permeability, i.e., Eq. 8. In the pilot study (Wu et al., 2021), the experimental pressure drop was fitted on a macroscopic scale with slippage permeability, i.e., Eq. 2, and unknown parameters $\varphi$, k_int, and b could be obtained. Similarly, $\varphi$, r_t, and τ are unknowns of apparent transport and should be obtained by curve fitting. Based on these three parameters, nanoscale transport properties could be derived and studied.

3 Discussion

3.1 Experimental fitting and analysis

At the experimental temperature of 303.15°C, the gradual pressure drop curves of samples 1–3 at 3 MPa, 4 MPa, 8 MPa, and 9 MPa pressure conditions were recorded. The micro transport properties were obtained indirectly by curve fitting, with the achievements of $\varphi$, r_t, and τ for each shale sample.

Figures 4A,C,E show that r_t and τ were adjusted with the apparent numerical model to fit the experimental curves at high pressure, 9 MPa, and low pressure, 3 MPa. In this research, high and low pressures represent the experimental pressures. The value of parameter $\varphi$ referred to the fitting results of the slippage numerical model (Table A1). The regressed intrinsic permeabilities and slippage coefficients for slippage permeability are given in Table A1. The curve fitting results were further verified by experimental curves at 4 MPa and 8 MPa, shown in Figures 4B,D,F. In Figure 4, p_L and p_H represent low and high pressures.

FIGURE 4

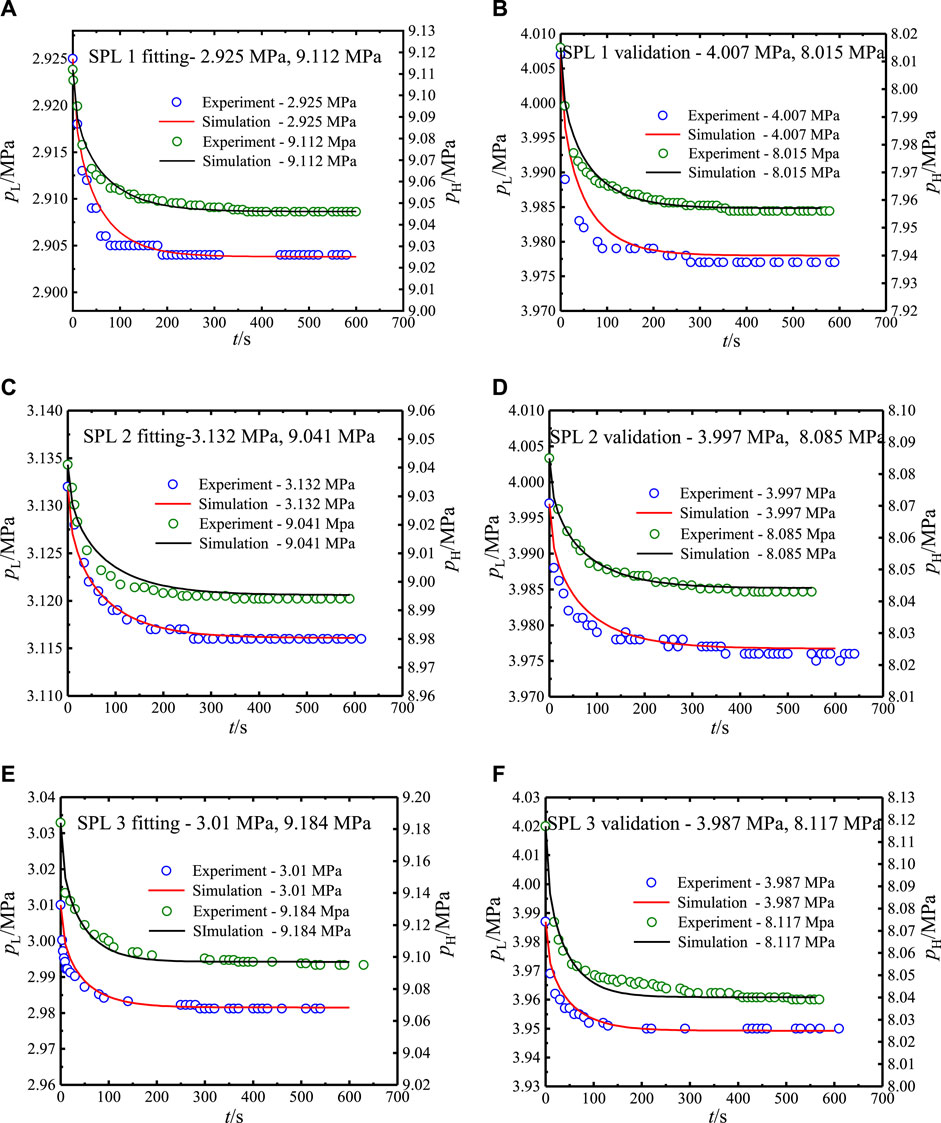
FIGURE 4. Curve fittings of apparent transport for 3 MPa and 9 MPa of samples 1 (A), 2 (C), and 3 (E) and validations of samples 1 (B), 2 (D), and 3 (F) at 4 MPa and 8 MPa (303.15 K).

For curve fitting, the results are given in Table 1. The porosities of samples 1–3 were in the 0.02–0.04 range, indicating the appropriate capacities for gas storage and transport. The pore radii of samples 1–3 were 1.2 nm, 1 nm, and 1.5 nm, separately. As a result, the average pore sizes of the matrix for gas transport are 2.4 nm, 2 nm, and 3 nm, which are just larger than nanopores in the mesopore size range of 2–50 nm (Firouzi et al., 2014). In the gas macro transport studies of the experimental cylindrical core or on-site shale gas reservoir, the values of tortuosity are smaller than 10 (Naraghi and Javadpour, 2015; Feng et al., 2019). Herein, the values of tortuosity for micro transport are approximately 40. In a previous shale matrix transport research, the obtained tortuosities were also much larger than 10 (Hu et al., 2015; Liu et al., 2016; Sun et al., 2018). Considering a much smaller permeability of the shale matrix than bulk shale with fractures, it is consistent with the theory that tortuosity is negatively related to permeability (Yang et al., 2021). With regressed ϕ, r_t, and τ values, apparent permeabilities of samples 1–3 can be calculated by Eq. 8.

TABLE 1

TABLE 1. Regressed parameters of apparent transport for Wufeng–Longmaxi samples.

3.2 Applicability of slippage transport and apparent transport to recovery improvement

Slippage permeability and apparent permeability represent the properties of macro-slippage transport and micro-apparent transport. Based on the regressed results from the same sample, slippage permeability and apparent permeability could be compared effectively for shale gas recovery improvement.

The slippage permeability and apparent permeability values were given for the same pressure drop curve of sample 3, at 303.15 K, shown in Figure 5. Slippage permeability varies with pressure due to the slippage effect, while apparent permeability varies due to the multi-mechanism, slippage effect and Knudsen diffusion. With the increase in pressure, slippage permeability and apparent permeability both decrease gradually, and the decreasing rate reduces with the pressure, too. At a low pressure (<3 MPa), apparent permeability is much higher than slippage permeability. It indicates that, at low pressure, Knudsen diffusion plays a more important role than the slippage effect, resulting in the main difference between slippage permeability and apparent permeability. It is consistent with the finding that shale matrix permeability was not dominated by the slippage effect at an experimental pressure lower than 3.45 MPa (Tinni et al., 2012). At high pressure, apparent permeability is a little smaller than slippage permeability, implicating the dominant role of the slippage effect.

FIGURE 5

FIGURE 5. Comparison of slippage and apparent permeabilities at 303.15 K.

Without the AGSP system, there is a limitation of the experiment device for shale matrix transport at high pressure (Fan et al., 2018). Slippage permeability is not recommended for the shale matrix transport experiment study, due to the great deviation at an ultra-low pressure, while micro transport permeability is suitable for all pressure ranges. Considering the existences of low-reservoir pressure regions around the wellbore and in the shallow shale gas reservoir, apparent permeability is more applicable to the recovery improvement of shale gas.

3.3 Apparent transport in the real shale matrix

During the exploitation of the shale gas reservoir, the reservoir pressure varies dynamically with the production of the gas. Here, high- and low-reservoir pressure regions both exist. The gas transport ability determines the rate of pressure variation. On the contrary, the reservoir pressure also governs the gas transport ability at the same position. Gas transport permeability is the function of pressure. The Knudsen number, deviation factor, viscosity, and compressibility factor of the gas all vary with the reservoir pressure, which determine the value of apparent permeability by Eqs 8–10. Reflected by apparent permeability, the gas transport ability is controlled by the reservoir pressure. Enormous amount of research effort goes into the gas transport property at a constant-pressure condition (Yu et al., 2019; Yu et al., 2020), while dynamic transport was less studied. Thereby, it is necessary to study the dynamic characteristics of pressure and gas transport, comprehensively. With the determined dynamic transport property in the real shale gas reservoir, accurate measures could be provided to improve shale gas production. Taking gas transport in sample 3, with the shale matrix at 9 MPa and 303.15 K as a case study, dynamic gas transport with varying pressure conditions could be investigated.

With the gas entering the shale matrix, the pressure at each region rose and got balanced at 450 s, shown in Figure 6A. The abscissas in Figure 6 and the following similar figures represent the distance of a certain position to the particle center. At 50 s, the Knudsen number at each region is lower than 10 and is still in the 0.1–10 range after 50 s. It represents gas transport in the shale matrix particle in the transition flow form (Michalis et al., 2010). Matching with the pressure distributions of 25 s and 50 s (Figure 6A), the closer the position to the particle center is, the higher the total apparent permeability would be, shown in Figure 6B. The apparent permeability, k_a-d, appears similar to the distribution characteristic and value with the weighted Knudsen diffusion permeability, k_k-d × ω_k-d. It reveals that Knudsen diffusion transport is in control of apparent transport at experimental conditions. It is the reason that the permeability is inconsistent with the slippage property at a low-pressure condition in the study (Tinni et al., 2012). The weighted slippage transport permeability, k_s-d × ω_s-d, appears to be in a positive relationship with pressure, shown in Figure 6B. Increasing the slippage flow, represented by the weighted slippage transport permeability, weakens the dominance of the Knudsen diffusion flow, leading to a larger disparity at a higher pressure between weighted-slippage transport permeability and apparent permeability. Due to the slippage effect, slippage permeability decreases with the increase in pressure (Wang S. et al., 2019), shown in Figure 7. Moreover, the slippage flow weight factor increases positively with the pressure. Considering the positive relationship of k_s-d × ω_s-d with pressure, the slippage flow is dominated by the weight factor instead of slippage permeability. Consequently, the slippage weight factor is the primary adjusted factor used to improve shale gas recovery.

FIGURE 6

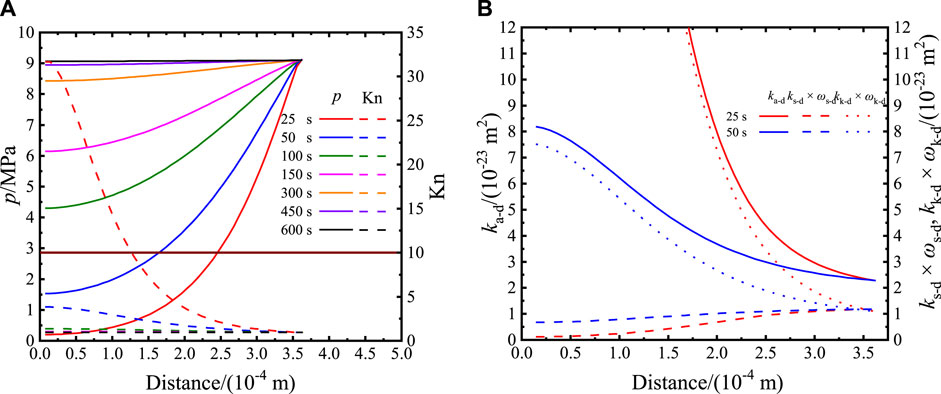
FIGURE 6. Distributions of pressure and Knudsen number (A) and permeability (B) in the matrix particle.

FIGURE 7

FIGURE 7. Distributions of slippage flow permeability and weight factor.

As shown in Figure 8, taking the center and the 1/2R positions as an example, the variations of pressure and permeability with time could be analyzed to investigate the dynamic gas transport in the shale matrix. With the gas entering the shale matrix particle, the pressure at each region increases gradually, leading to the gradual decrease in permeability. Pressure and permeability both turn out to be stable at the late-time stage. It is constant with cognition that the late-time method is suggested for shale matrix transport experimental data analyzation rather than the early time method (Cui et al., 2010). For early-time and late-time methods, the permeability seemed to be a constant value. Due to Knudsen diffusion, the tested permeability at an ultra-low pressure would be much larger.

FIGURE 8

FIGURE 8. Variations of pressure and permeability with time.

3.4 Effects of pore structure on apparent transport

The regressed parameters, r_t and τ, are critical features of the shale pore structure. It is necessary to investigate the effects of the pore structure on gas transport, with different values of r_t and τ. The simulation conditions were the same as given in Section 4.3. An accurate pore structure is beneficial in recognizing shale gas migration and storage, and the stimulation measures for shale gas recovery could be well implemented.

Setting the pore radius as 2 nm, 4 nm, and 6 nm, the variations of permeability with pressure for different pore sizes were simulated, shown in Figure 9. At different pore sizes, the permeability decreases sharply, caused by the dominance of Knudsen diffusion. For 4 nm and 6 nm pore radius values, the decrease in permeabilities is stronger, which could explain the phenomenon that the permeability would decrease significantly with the increase in pore size (Yu et al., 2020). At a high-pressure region, the permeability varies positively with pore size, owing to the stronger slippage effect.

FIGURE 9

FIGURE 9. Variations of permeability with pressure for different pore sizes.

Selecting the permeability distributions at 10 s and 4 s, for 4 nm and 10 nm pore radii, respectively, the transport property in the shale matrix could be studied, as shown in Figure 10, showing the gas transport from the particle surface to the center, following the tendency of pressure conduction. Close to the surface, the apparent permeability is affected mainly by the slippage effect. With the gas entering the shale matrix particle, and with the pressure getting lower, the apparent permeability increases and tends to be dominated by Knudsen diffusion. It is beneficial for frontal gas transport. Comparing 4 nm (Figure 10A) and 10 nm (Figure 10B) of pore radii, this phenomenon is more notable at a larger pore size.

FIGURE 10

FIGURE 10. Distributions of permeability with 4 nm (A), and 10 nm (B) pore radii.

Based on the apparent transport numerical model, the permeability variation with pressure and distribution in the shale matrix could be obtained for different tortuosities, shown in Figure 11. With a higher tortuosity, the apparent permeability decreases more intensely (Figure 11A). Moreover, the permeability is negatively related to tortuosity at the same pressure condition. Accordingly, a higher tortuosity assists the transformation of the dominant role in transport from Knudsen diffusion to the slippage effect, during the pressure increase process.

FIGURE 11

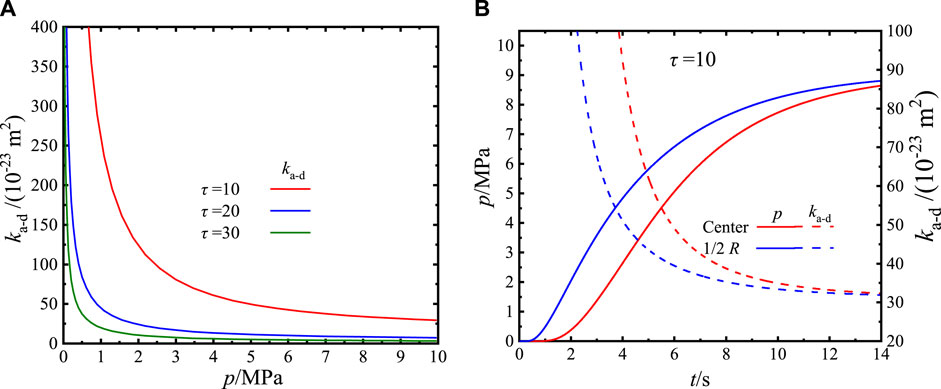
FIGURE 11. Distributions of permeabilities for different tortuosities (A) and the variations of pressure and permeability with time (B).

With the tortuosity value being 10, the pressures at the center and 1/2R positions of the shale matrix particle both rose to 8 MPa, in less than 14 s, as shown in Figure 11B. In Figure 8, with the regressed tortuosity of sample 3 being 37, it would take approximately 300 s for the pressures to rise to 8 MPa. As a result, with the frequently used tortuosity value (<10) in the macro-transport study (Wang et al., 2018; Wang D. et al., 2019), the pressure of the shale matrix particle would be stable in less than 20 s, which could not be detected effectively using a pressure sensor. The apparent permeabilities of this research are in the same order with the initial shale matrix transport study (Luffel et al., 1993; Sinha et al., 2012), proving that tortuosity with an approximate value of 40 rather than the macro transport value of tortuosity (<10) is more suitable for the micro transport shale matrix. With the macro transport value of tortuosity, the production of shale gas would be misled due to an unsuitable matrix permeability.

4 Conclusion

In this paper, the modified technology of shale matrix permeability determination was provided to obtain the typical transport and pore structure parameters and the transport properties in the shale matrix were also analyzed. The conclusions are presented as follows:

(1) The apparent permeability model was well applied to the numerical data analyzing method for a shale matrix transport experiment. Porosity, pore radius, and tortuosity were selected as regressed parameters, and the apparent permeabilities of three samples were further obtained. The pore radii of the shale matrix are all in the mesopore range and were a little larger than the nanopore size, 2 nm. The tortuosities of the matrix are all approximately 40 and are much larger than the macro ones, due to the nanopore size.

(2) At low pressure, Knudsen diffusion brings the great difference between macro and micro transports, due to its dominant role. At high pressure, apparent permeability is a little smaller than slippage permeability, indicating the stronger impact of the slippage effect compared to Knudsen diffusion. With the increase in pressure, the slippage flow appears to be higher in proportion than the Knudsen diffusion flow in the total apparent flow, owing to the increasing slippage flow weight factor.

(3) A higher pore radius and tortuosity both could weaken the effect of Knudsen diffusion, and matrix permeability would decrease more sharply with pressure. With the pressure increasing to a certain degree, the slippage flow takes control of micro transport, showing a positive relationship between permeability and pore size. For the accuracy of real shale matrix permeability, a high tortuosity is necessary and should not be ignored.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

ZH: investigation, writing–original draft, and writing–review and editing. YD: investigation and writing–original draft. JL: data curation, investigation, and writing–original draft. XW: investigation, writing–original draft, and validation. JB: investigation, writing–review and editing, and validation. JT: writing–review and editing.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (grant no. 52004038).

Conflict of interest

Author YD was employed by PetroChina Coalbed Methane Company Limited.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Berawala, D. S., Andersen, P. Ø., and Ursin, J. R. (2019). Controlling parameters during continuum flow in shale-gas production: A fracture/matrix-modeling approach. SPE J. 24, 1378–1394. doi:10.2118/190843-pa

CrossRef Full Text | Google Scholar

Chai, D., Yang, G., Fan, Z., and Li, X. (2019). Gas transport in shale matrix coupling multilayer adsorption and pore confinement effect. Chem. Eng. J. 370, 1534–1549. doi:10.1016/j.cej.2019.03.276

CrossRef Full Text | Google Scholar

Cheng, Z., Wang, Q., Ning, Z., Li, M., Lyu, C., Huang, L., et al. (2018). Experimental investigation of countercurrent spontaneous imbibition in tight sandstone using nuclear magnetic resonance. Energy & Fuels 32, 6507–6517. doi:10.1021/acs.energyfuels.8b00394

CrossRef Full Text | Google Scholar

Cipolla, C. L., Lolon, E., Erdle, J., and Tathed, V. (2009). “Modeling well performance in shale-gas reservoirs,” in SPE Reservoir Characterisation and Simulation Conference and Exhibition?: SPE, Abu Dhabi, UAE, October 2009. SPE-125532-MS.

CrossRef Full Text | Google Scholar

Civan, F. (2019). Can gas permeability of fractured shale be determined accurately by testing core plugs, drill cuttings, and crushed samples? SPE J. 24, 720–732. doi:10.2118/194502-pa

CrossRef Full Text | Google Scholar

Civan, F., Devegowda, D., and Sigal, R. F. (2013). “Critical evaluation and improvement of methods for determination of matrix permeability of shale,” in SPE annual technical conference and exhibition: Society of Petroleum Engineers, Louisiana, USA, September 2013.

CrossRef Full Text | Google Scholar

Clarkson, C., Haghshenas, B., Ghanizadeh, A., Qanbari, F., Williams-Kovacs, J., Riazi, N., et al. (2016). Nanopores to megafractures: current challenges and methods for shale gas reservoir and hydraulic fracture characterization. J. Nat. Gas Sci. Eng. 31, 612–657. doi:10.1016/j.jngse.2016.01.041

CrossRef Full Text | Google Scholar

Coppens, M.-O., and Dammers, A. J. (2006). Effects of heterogeneity on diffusion in nanopores—From inorganic materials to protein crystals and ion channels. Fluid phase equilibria 241, 308–316. doi:10.1016/j.fluid.2005.12.039

CrossRef Full Text | Google Scholar

Cui, G., Liu, J., Wei, M., Shi, R., and Elsworth, D. (2018). Why shale permeability changes under variable effective stresses: new insights. Fuel 213, 55–71. doi:10.1016/j.fuel.2017.10.068

CrossRef Full Text | Google Scholar

Cui, X., Bustin, A. M. M., and Bustin, R. M. (2010). Measurements of gas permeability and diffusivity of tight reservoir rocks: different approaches and their applications. Geofluids 9, 208–223. doi:10.1111/j.1468-8123.2009.00244.x

CrossRef Full Text | Google Scholar

Fan, K., Dong, M., Elsworth, D., Li, Y., Yin, C., and Li, Y. (2018). A dynamic-pulse pseudo-pressure method to determine shale matrix permeability at representative reservoir conditions. Int. J. Coal Geol. 193, 61–72. doi:10.1016/j.coal.2018.04.011

CrossRef Full Text | Google Scholar

Fathi, E., Tinni, A., and Akkutlu, I. Y. (2012). “Shale gas correction to Klinkenberg slip theory,” in SPE Americas Unconventional Resources Conference: Society of Petroleum Engineers, Pittsburgh, Pennsylvania, USA, 5-7 June 2012.

CrossRef Full Text | Google Scholar

Feng, Q., Xu, S., Wang, S., Li, Y., Gao, F., and Xu, Y. (2019). Apparent permeability model for shale oil with multiple mechanisms. J. Petroleum Sci. Eng. 175, 814–827. doi:10.1016/j.petrol.2019.01.038

CrossRef Full Text | Google Scholar

Fink, R., Krooss, B. M., Gensterblum, Y., and Amann-Hildenbrand, A. (2017). Apparent permeability of gas shales–Superposition of fluid-dynamic and poro-elastic effects. Fuel 199, 532–550. doi:10.1016/j.fuel.2017.02.086

CrossRef Full Text | Google Scholar

Firouzi, M., Rupp, E. C., Liu, C. W., and Wilcox, J. (2014). Molecular simulation and experimental characterization of the nanoporous structures of coal and gas shale. Int. J. Coal Geol. 121, 123–128. doi:10.1016/j.coal.2013.11.003

CrossRef Full Text | Google Scholar

Heller, R., Vermylen, J., and Zoback, M. (2014). Experimental investigation of matrix permeability of gas shales. AAPG Bull. 98, 975–995. doi:10.1306/09231313023

CrossRef Full Text | Google Scholar

Hu, Q., Ewing, R. P., and Rowe, H. D. (2015). Low nanopore connectivity limits gas production in Barnett formation. J. Geophys. Res. Solid Earth 120, 8073–8087. doi:10.1002/2015jb012103

CrossRef Full Text | Google Scholar

Huang, L., Zhou, W., Xu, H., Wang, L., Zou, J., and Zhou, Q. (2021). Dynamic fluid states in organic-inorganic nanocomposite: implications for shale gas recovery and co2 sequestration. Chem. Eng. J. 411, 128423. doi:10.1016/j.cej.2021.128423

CrossRef Full Text | Google Scholar

Jia, B., Tsau, J.-S., and Barati, R. (2020). Investigation of shale-gas-production behavior: evaluation of the effects of multiple physics on the matrix. SPE Reserv. Eval. Eng. 23, 068–080. doi:10.2118/197069-pa

CrossRef Full Text | Google Scholar

Liu, J., Wang, J., Gao, F., Ju, Y., Zhang, X., and Zhang, L.-C. (2016). Flow consistency between non-Darcy flow in fracture network and nonlinear diffusion in matrix to gas production rate in fractured shale gas reservoirs. Transp. Porous Media 111, 97–121. doi:10.1007/s11242-015-0583-9

CrossRef Full Text | Google Scholar

Luffel, D., Hopkins, C., and Schettler, P. (1993). “Matrix permeability measurement of gas productive shales,” in SPE annual technical conference and exhibition: Society of Petroleum Engineers, Houston, Texas, 3-6 October 1993.

CrossRef Full Text | Google Scholar

Mckernan, R., Rutter, E., Mecklenburgh, J., Taylor, K., and Covey-Crump, S. (2014). “Influence of effective pressure on mudstone matrix permeability: implications for shale gas production,” in SPE/EAGE European Unconventional Resources Conference and Exhibition: OnePetro, Vienna, Austria, February 2014.

CrossRef Full Text | Google Scholar

Meng, F., He, D., Yan, H., Zhao, H., Zhang, H., and Li, C. (2021). Production performance analysis for slanted well in multilayer commingled carbonate gas reservoir. J. Petroleum Sci. Eng. 204, 108769. doi:10.1016/j.petrol.2021.108769

CrossRef Full Text | Google Scholar

Mi, L., Jiang, H., and Li, J. (2014). The impact of diffusion type on multiscale discrete fracture model numerical simulation for shale gas. J. Nat. Gas Sci. Eng. 20, 74–81. doi:10.1016/j.jngse.2014.06.013

CrossRef Full Text | Google Scholar

Michalis, V. K., Kalarakis, A. N., Skouras, E. D., and Burganos, V. N. (2010). Rarefaction effects on gas viscosity in the Knudsen transition regime. Microfluid. nanofluidics 9, 847–853. doi:10.1007/s10404-010-0606-3

CrossRef Full Text | Google Scholar

Mohagheghian, E., Hassanzadeh, H., and Chen, Z. (2020). Matrix-fracture transfer shape factor for modeling multimechanisitc multicomponent shale gas flow. Int. J. Heat Mass Transf. 158, 120022. doi:10.1016/j.ijheatmasstransfer.2020.120022

CrossRef Full Text | Google Scholar

Nan, Y., Li, W., and Jin, Z. J. F. (2020). Slip length of methane flow under shale reservoir conditions: effect of pore size and pressure. Fuel 259, 116237. doi:10.1016/j.fuel.2019.116237

CrossRef Full Text | Google Scholar

Naraghi, M. E., and Javadpour, F. (2015). A stochastic permeability model for the shale-gas systems. Int. J. Coal Geol. 140, 111–124. doi:10.1016/j.coal.2015.02.004

CrossRef Full Text | Google Scholar

Rubin, C., Zamirian, M., Takbiri-Borujeni, A., and Gu, M. (2019). Investigation of gas slippage effect and matrix compaction effect on shale gas production evaluation and hydraulic fracturing design based on experiment and reservoir simulation. Fuel 241, 12–24. doi:10.1016/j.fuel.2018.12.015

CrossRef Full Text | Google Scholar

Sheng, G., Javadpour, F., and Su, Y. (2019). Dynamic porosity and apparent permeability in porous organic matter of shale gas reservoirs. Fuel 251, 341–351. doi:10.1016/j.fuel.2019.04.044

CrossRef Full Text | Google Scholar

Shi, J., Zhang, L., Li, Y., Yu, W., He, X., Liu, N., et al. (2013). “Diffusion and flow mechanisms of shale gas through matrix pores and gas production forecasting,” in SPE unconventional resources conference Canada: OnePetro, Alberta, Canada, November 2013.

CrossRef Full Text | Google Scholar

Sinha, S., Braun, E., Determan, M., Passey, Q., Leonardi, S., Boros, J., et al. (2013). “Steady-state permeability measurements on intact shale samples at reservoir conditions-effect of stress, temperature, pressure, and type of gas,” in SPE Middle East oil and gas show and conference: Society of Petroleum Engineers, Manama, Bahrain, March 2015.

CrossRef Full Text | Google Scholar

Sinha, S., Braun, E. M., Passey, Q. R., Leonardi, S. A., Wood, A. C., Zirkle, T., et al. (2012). “Advances in measurement standards and flow properties measurements for tight rocks such as shales,” in SPE/EAGE European Unconventional Resources Conference & Exhibition-From Potential to Production, Vienna, Austria, March 2012.

CrossRef Full Text | Google Scholar

Sun, M., Yu, B., Hu, Q., Yang, R., Zhang, Y., Li, B., et al. (2018). Pore structure characterization of organic-rich niutitang shale from China: small angle neutron scattering (sans) study. Int. J. Coal Geol. 186, 115–125. doi:10.1016/j.coal.2017.12.006

CrossRef Full Text | Google Scholar

Tinni, A., Fathi, E., Agarwal, R., Sondergeld, C. H., Akkutlu, I. Y., and Rai, C. S. (2012). “Shale permeability measurements on plugs and crushed samples,” in SPE Canadian Unconventional Resources Conference: Society of Petroleum Engineers, Calgary, Alberta, October - 1 November 2012.

CrossRef Full Text | Google Scholar

Wang, D., Yao, J., Chen, Z., Song, W., and Sun, H. (2019a). Image-based core-scale real gas apparent permeability from pore-scale experimental data in shale reservoirs. Fuel 254, 115596. doi:10.1016/j.fuel.2019.06.004

CrossRef Full Text | Google Scholar

Wang, H., Chen, L., Qu, Z., Yin, Y., Kang, Q., Yu, B., et al. (2020). Modeling of multi-scale transport phenomena in shale gas production—A critical review. Appl. Energy 262, 114575. doi:10.1016/j.apenergy.2020.114575

CrossRef Full Text | Google Scholar

Wang, H., and Marongiu-Porcu, M. (2015). Impact of shale-gas apparent permeability on production: combined effects of non-darcy flow/gas slippage, desorption, and geomechanics. SPE Reserv. Eval. Eng. 18, 495–507. doi:10.2118/173196-pa

CrossRef Full Text | Google Scholar

Wang, M., and Yu, Q. (2020). Comparing the permeability of dry and moisturized crushed shales determined by the dynamic process data of methane adsorption. J. Hydrology 590, 125375. doi:10.1016/j.jhydrol.2020.125375

CrossRef Full Text | Google Scholar

Wang, S., Lukyanov, A. A., and Wu, Y.-S. (2019b). Second-order gas slippage model for the Klinkenberg effect of multicomponent gas at finite Knudsen numbers up to 1. Fuel 235, 1275–1286. doi:10.1016/j.fuel.2018.08.113

CrossRef Full Text | Google Scholar

Wang, Y., Liu, S., and Zhao, Y. (2018). Modeling of permeability for ultra-tight coal and shale matrix: A multi-mechanistic flow approach. Fuel 232, 60–70. doi:10.1016/j.fuel.2018.05.128

CrossRef Full Text | Google Scholar

Wu, K., Chen, Z., Li, X., Guo, C., and Wei, M. (2016). A model for multiple transport mechanisms through nanopores of shale gas reservoirs with real gas effect–adsorption-mechanic coupling. Int. J. Heat Mass Transf. 93, 408–426. doi:10.1016/j.ijheatmasstransfer.2015.10.003

CrossRef Full Text | Google Scholar

Wu, K., Chen, Z., Li, X., Xu, J., Li, J., Wang, K., et al. (2017). Flow behavior of gas confined in nanoporous shale at high pressure: real gas effect. Fuel 205, 173–183. doi:10.1016/j.fuel.2017.05.055

CrossRef Full Text | Google Scholar

Wu, K., Li, X., Wang, C., Chen, Z., and Yu, W. (2014). “Apparent permeability for gas flow in shale reservoirs coupling effects of gas diffusion and desorption,” in Unconventional Resources Technology Conference Society of Exploration Geophysicists, American Association of Petroleum, Denver, Colorado, 25-27 August 2014, 2328–2345.

CrossRef Full Text | Google Scholar

Wu, K., Li, X., Wang, C., Yu, W., and Chen, Z. (2015). Model for surface diffusion of adsorbed gas in nanopores of shale gas reservoirs. Industrial Eng. Chem. Res. 54, 3225–3236. doi:10.1021/ie504030v

CrossRef Full Text | Google Scholar

Wu, X., He, Y., Ning, Z., Lyu, F., Dou, X., and Wu, B. (2022). Mechanistic insights into confined methane adsorption in carbon nanopores at the molecular level. Chem. Eng. Sci. 250, 117374. doi:10.1016/j.ces.2021.117374

CrossRef Full Text | Google Scholar

Wu, X. J., Wang, Q., Lyu, F. T., Ning, Z. F., and Ren, Z. X. (2021). Experimental study on gas transport in shale matrix with real gas and Klinkenberg effects. Geofluids 2021, 1–14. doi:10.1155/2021/5579307

CrossRef Full Text | Google Scholar

Yang, F., Zheng, H., Lyu, B., Wang, F., Guo, Q., and Xu, H. (2021). Experimental investigation about gas transport in tight shales: an improved relationship between gas slippage and petrophysical properties. Energy & Fuels 35, 3937–3950. doi:10.1021/acs.energyfuels.0c04086

CrossRef Full Text | Google Scholar

Yang, X., Zhou, W., Liu, X., and Yan, Y. (2020a). A multiscale approach for simulation of shale gas transport in organic nanopores. Energy 210, 118547. doi:10.1016/j.energy.2020.118547

CrossRef Full Text | Google Scholar

Yang, Z., Bryant, S., and Dong, M. (2020b). A method of determining adsorptive-gas permeability in shale cores with considering effect of dynamic adsorption on flow. Fuel 268, 117340. doi:10.1016/j.fuel.2020.117340

CrossRef Full Text | Google Scholar

Yu, H., Fan, J., Xia, J., Liu, H., and Wu, H. (2020). Multiscale gas transport behavior in heterogeneous shale matrix consisting of organic and inorganic nanopores. J. Nat. Gas Sci. Eng. 75, 103139. doi:10.1016/j.jngse.2019.103139

CrossRef Full Text | Google Scholar

Yu, H., Zhu, Y., Jin, X., Liu, H., and Wu, H. (2019). Multiscale simulations of shale gas transport in micro/nano-porous shale matrix considering pore structure influence. J. Nat. Gas Sci. Eng. 64, 28–40. doi:10.1016/j.jngse.2019.01.016

CrossRef Full Text | Google Scholar

Zhao, X., Rui, Z., Liao, X., and Zhang, R. (2015). The qualitative and quantitative fracture evaluation methodology in shale gas reservoir. J. Nat. gas Sci. Eng. 27, 486–495. doi:10.1016/j.jngse.2015.08.009

CrossRef Full Text | Google Scholar

Zhou, J., Jin, Z., and Luo, K. H. (2020). Insights into recovery of multi-component shale gas by CO2 injection: A molecular perspective. Fuel 267, 117247. doi:10.1016/j.fuel.2020.117247

CrossRef Full Text | Google Scholar

Appendix A

The parameters for shale samples 1–3 are given in Table A1.

TABLE A1

TABLE A1. Parameters for Wufeng–Longmaxi samples (Wu et al., 2021).