A novel approach for utilizing waste heat resources in the steel industry

The efficient utilization of waste heat resources plays a pivotal role in enhancing energy efficiency and curbing carbon emissions. To address this, effective planning for waste heat recovery (WHR) utilization becomes imperative, guiding consumers in device installation and capacity allocation. This paper introduces a novel approach to WHR utilization planning, tailored specifically for steel factories, with the goal of achieving optimal WHR solutions. The approach automates device selection, capacity allocation, and operational strategies while considering their impact on the regular manufacturing processes of the factories to maximize overall benefits. Unlike existing methods, this approach introduces discrete capacity selection modeling, considering the constraints of the limited product range during device selection. A numerical study illustrates the effectiveness of the proposed model in delivering optimal WHR device selection, capacity allocation, and operational strategies under various economic conditions. These enhancements contribute to the increased practicality and realism of the proposed method in comparison to existing approaches.

1 Introduction

The utilization of waste heat resources is a common method to enhance energy efficiency in various industries (Guo et al., 2013; Pan et al., 2020). It plays a crucial role in national strategies to reduce carbon emissions by reducing the reliance on high-carbon or polluting resources such as natural gas or coal-generated electricity (Mago et al., 2007; Brown and Valentina, 2021). Over the past decade, significant advancements and research have been made in waste heat recovery (WHR) technologies across different sectors (Brückner et al., 2015; Xia et al., 2019). For instance, Zhao et al. implemented distributed heat pump technology in district heating systems to regulate the heat in secondary substation networks, effectively reducing the return water temperature of the primary network (Zhao et al., 2017).

To maximize the benefits of WHR utilization, consumers require an optimal planning method that considers the characteristics of various potential utilization devices, the economic aspects of different energy quality utilization methods, and the operational implications of WHR utilization. To identify an appropriate planning approach, an extensive review of existing literature on optimal WHR planning methods was undertaken, revealing three typical categories of studies in this domain. The first type primarily focuses on predefined WHR physical utilization systems and aims to determine their optimal operation (Gu et al., 2010; Amin et al., 2017). For example, Dehghani et al. (Javad Dehghani and Chang, 2020) designed a system for WHR and biofuel extractability from effluents in the textile industry. The study optimized seven key parameters to determine the most efficient operational strategy, demonstrating the system’s high energetic and thermodynamic performance with a payback time of 5 years. Kim et al. (Kim and Nam, 2016) evaluated the heating and cooling coefficient of performance (COP) of a system by considering different groundwater levels, flow rates, groundwater temperatures, and heat exchanger (HE) characteristics. Similarly, Mohammadi et al. (Amin et al., 2017) proposed a hybrid power system consisting of a gas turbine, an Organic Rankine Cycle (ORC) unit, and an absorption refrigerator (AR), which resulted in an increased total system efficiency of 67.6%. The study evaluated several key parameters to identify further means of enhancing system performance. Gu et al. (Gu et al., 2010) pre-defined a cogeneration system, including a waste heat boiler, to achieve optimal system operation while considering the output of renewable energy. In summary, this type of research offers potential solutions for consumers who already possess WHR utilization systems but require optimization of their operations. However, these predefined systems do not provide an optimal solution for consumers who seek to upgrade their systems with additional utilization dimensions or install entirely new systems.

The second type of research involves providing multiple predefined WHR candidate installation solutions. The capacity of devices in each candidate solution is determined through physical analysis to maximize WHR utilization. A comparison is then performed among these solutions to identify the optimal candidate (Hassan, 2015; Pantaleo et al., 2018; Yu et al., 2018). For instance, Yu et al. (Yu et al., 2018) defined three scenarios for WHR utilization from exhaust gas in the aluminum industry and compared the exergy efficiency and energy output power of these schemes. Their findings demonstrated that two of these scenarios adequately met the local basic space-heating load. Similarly, Pantaleo et al. (Pantaleo et al., 2018) predefined three schemes for flue gas WHR utilization in a coffee roasting plant. They discovered that the optimal solution varied based on the production capacity and electricity price, sometimes resulting in unprofitable investments. Hajabdollahi (Hassan, 2015) predefined a Combined Cooling, Heating, and Power (CCHP) system and proposed a model to determine the optimum type and nominal power of prime movers for various cooling, heating, and electrical load demands. The results indicated that selecting the prime mover type according to the load condition yielded better economic benefits. However, this type of research may overlook optimal solutions as the practical candidates for WHR solutions often exceed those for predefined solutions. Additionally, an optimal solution may require different device capacity levels, which are often neglected in predefined capacity settings.

The third type of research involves a minimal number of predefined factors and in-stead constructs an optimization model that considers various potential WHR utilization methods. It allows an optimization algorithm to determine the device selection, installation capacity, and optimal operation. The results obtained through this type of research are generally more realistic due to their objectivity and a more comprehensive solution space that avoids unreliable transcendental knowledge. However, such models often face challenges in terms of modelling and solving algorithms, resulting in limited quantities of research in this area. For example, Wang et al. (Wang et al., 2018) proposed a detailed mixed-integer linear programming optimization model for WHR utilization in a district-scale microgrid. The model incorporated operation models of seven types of WHR utilization technologies and prioritized economic considerations as the optimization objective. The optimization algorithm automatically generated optimal solutions for WHR utilization in a district-scale microgrid.

While research in the third category holds substantial promise, it tends to overlook critical factors affecting WHR utilization. The first issue relates to the impact of WHR utilization on consumers’ regular manufacturing operations and the consequent increase in operational costs, a dimension unaddressed in existing studies of this type. For instance, the harnessing of waste heat from low-temperature flue gas in a steel factory necessitates the installation of a heat-exchange device within the flue gas pipeline. However, this device leads to heightened pressure loss in the pipeline, necessitating additional power from the air pump. Such augmented power consumption can significantly disrupt the optimal solution, particularly when electricity prices are elevated.

The second issue lies in the assumption prevalent in current research, where device capacity installation is treated as a continuous variable. This allows the model to install devices of any capacity within defined constraints. In practice, however, device capacity is discrete since device sellers offer only a limited range of product options. Consequently, models that permit continuous capacity allocation may grapple with difficulties in identifying practical devices.

Considering the aforementioned issues, this study introduces a Type 3 WHR utilization planning model specifically designed for steel manufacturing consumers. This model enables the optimization algorithm to select optimal WHR utilization devices, determine their capacity, and provide guidance for optimal operation. The proposed model makes three key contributions:

1. In addressing the concern of overlooking the impact of WHR utilization on regular manufacturing operations, the proposed model incorporates an assessment of the pressure loss in the flue gas pipeline resulting from WHR utilization. Furthermore, it takes into consideration the supplementary electricity costs associated with the operation of the air pump.

2. To tackle the challenge of discrete device capacity, the proposed model introduces a novel structural approach, which effectively represents discrete capacity. This innovation yields more practical and realistic outcomes when compared to models that only allow for continuous capacity allocations.

3. Building upon the two aforementioned contributions, this study introduces a comprehensive WHR utilization plan featuring a nested optimization model. Within this framework, device selection, capacity, and operational behaviors are seamlessly integrated as variables. Through a numerical study, it is demonstrated that this model has the capability to automatically account for environmental factors and device capabilities tailored to individual consumers, thereby generating adaptive optimal solutions customized for a steel factory.

The remainder of this paper is organized as follows: Section 2 describes the WHR planning structure. Furthermore, Section 3 presents the formulation of the proposed nested optimization model of WHR utilization. In Section 4, the results of the numerical analysis are presented. Finally, the conclusion is given in Section 5.

2 WHR planning structure

In the industrial sector, various fluids like flue gas, dry-hot air, steam, circulating cooling water, and process wastewater transport significant quantities of waste heat. Established recovery technologies such as AR, the Rankine Cycle, and heat pumps are capable of efficiently capturing waste heat from these fluids. Another approach involves the direct utilization of waste heat resources for heating hot water or air by employing a HE. It is important to note that the temperature and physical properties of different waste heat sources may vary, necessitating the use of different applicable recovery technologies. For example, the low temperature of circulating cooling water renders it unsuitable for utilization in the Rankine Cycle.

This study primarily focuses on optimizing low-temperature WHR utilization in steel factories based on four commonly used WHR technologies: AR (absorption refrigeration), ORC (organic Rankine cycle), EHP (electric heat pumps), and HE (heat exchangers). However, the framework can easily accommodate other technologies as well.

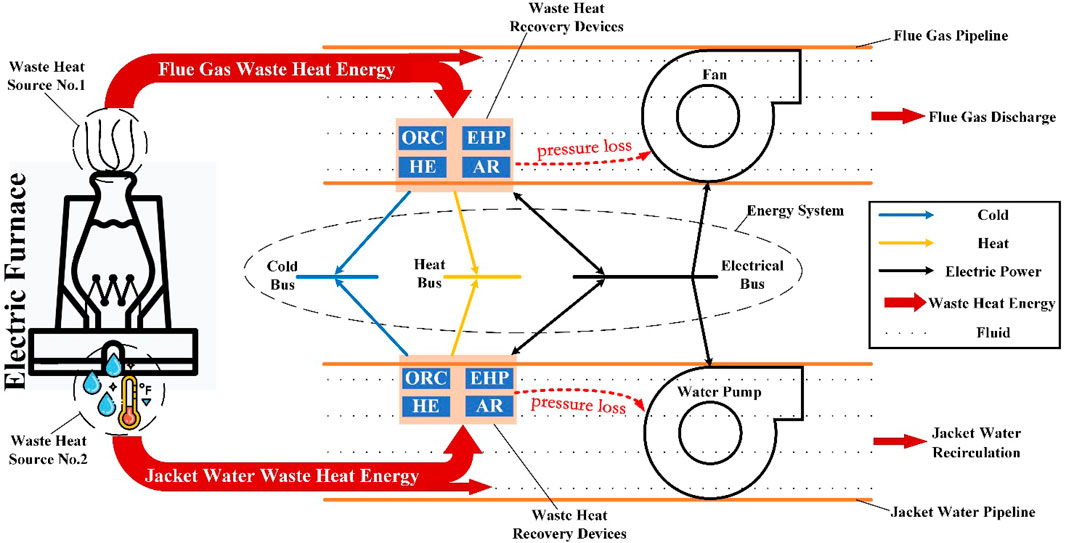
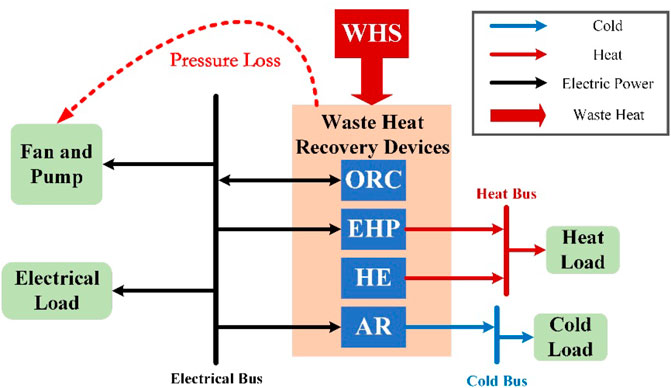
In WHR systems, there can be multiple types of WHS. Figure 1 illustrates the structure of a typical WHR system in a steel factory. The waste heat in electric furnace is continuously carried away by flue gases and circulating cooling water. Therefore, the flue gases and circulating cooling water, which are rich in waste heat energy, is regarded as WHS in this study. The flue gases and circulating cooling water are propelled through pipelines using fans or pumps. When these fluids flow through the heat exchange components of WHR devices, some of the waste heat is converted into energy in the form of electricity, heat or cold and output to the energy system to meet load demand. The remaining waste heat is discharged to the environment or recirculated with the fluid. The installment of WHR devices inevitably leads to fluid pressure loss. Without external intervention, the fluid flow velocity will decrease significantly. Fans and pumps must consume more power to ensure an acceptable flow velocity. This negative effect of WHR introduces additional operational costs for fans and pumps. This study considers this detrimental effect during both the planning and operation stages of WHR utilization.

FIGURE 1

FIGURE 1. Typical structure of a WHR system in the steel plant.

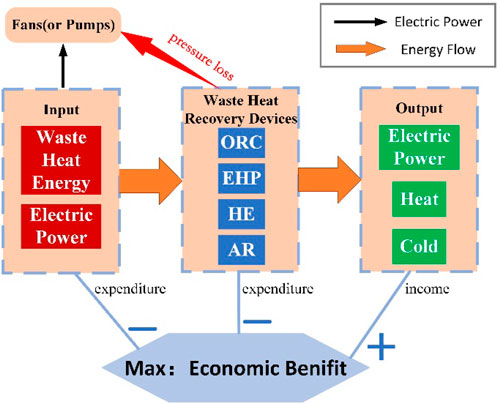
Figure 2 illustrates the economic benefits associated with WHR utilization, comprising three components: positive benefits from energy generation and negative benefits from energy consumption and device installation. To maximize overall benefits, the optimization process should focus on maximizing positive benefits while minimizing negative ones. WHR utilization technologies vary in terms of energy conversion efficiency, investment cost, and energy input-output ratios. Thus, an optimal selection of recovery technology, device capacity, and operational strategy is crucial. This study presents a novel nested optimization model for WHR utilization planning. The main optimization model considers the number of devices of each type as independent variables and incorporates device investment cost into the objective function. In the sub-optimization model, an operational model is developed for WHR devices, fans, and pumps, where the output power of the devices is treated as an independent variable. The objective function integrates energy costs and output benefits of the devices. The subsequent section provides detailed information on the proposed model.

FIGURE 2

FIGURE 2. Economic evaluation of the WHR system.

It is crucial to emphasize that the proposed model takes into consideration the operational characteristics of four specific WHR devices. However, the decision regarding which devices to invest in should be guided by the optimization solutions. The optimization process may indicate that investing in just one or two of these devices is the most cost-effective strategy. In situations where none of the devices demonstrate profitability, it might be prudent to refrain from investing in any WHR device at all.

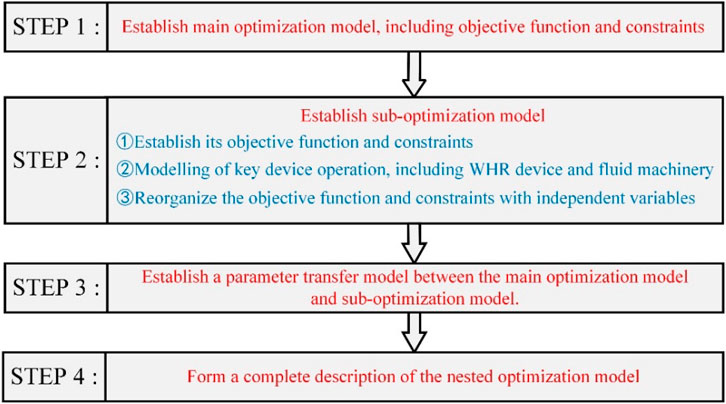
3 Nested optimization model for WHR system planning and operation

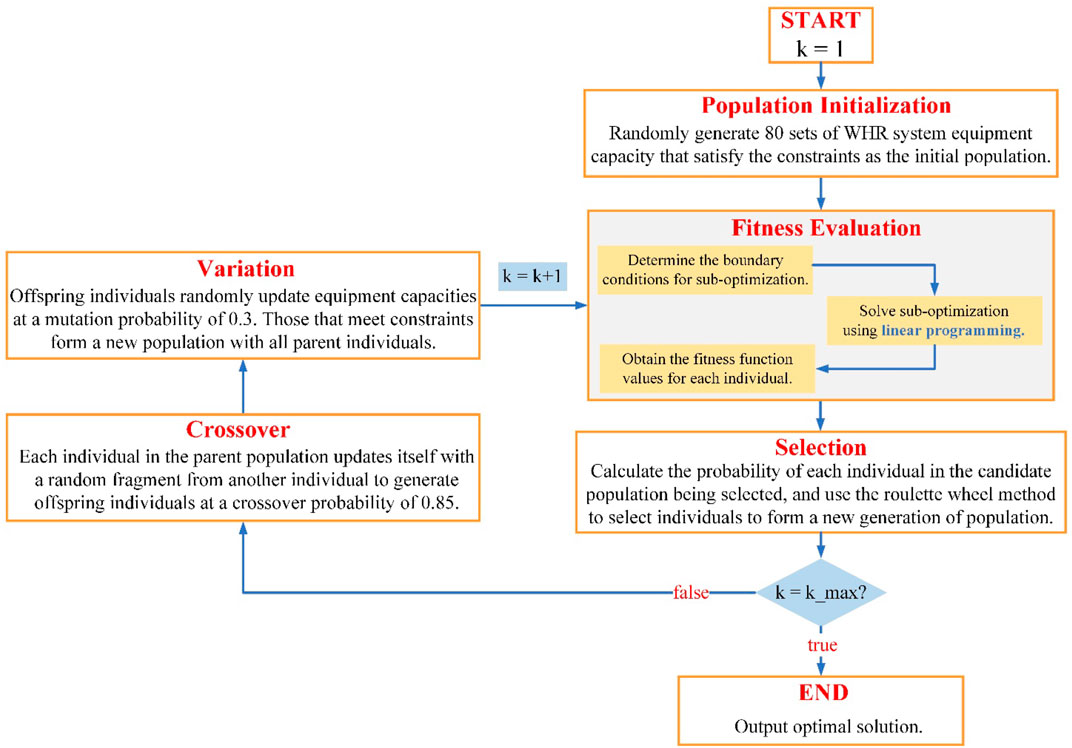
The system planning process is influenced by various scenarios, and it is closely linked to system operation. The outcomes of system planning serve as the boundary conditions for operation. Only when the system planning is determined can the optimal system operation be further solved. Taking into account the interplay between planning and operation in the optimization process, this study formulates the system optimization model as a nested optimization model. The flowchart of the overall modelling process is summarized in Figure 3. The nested optimization model effectively captures the solution space to obtain the most realistic and comprehensive solution, enabling simultaneous decision-making on recovery methods, device capacity planning, and optimal system operation. As mentioned earlier, the model considers four commonly used WHR devices, but it can be readily extended to incorporate additional devices.

FIGURE 3

FIGURE 3. Modelling process of the proposed nested optimization model.

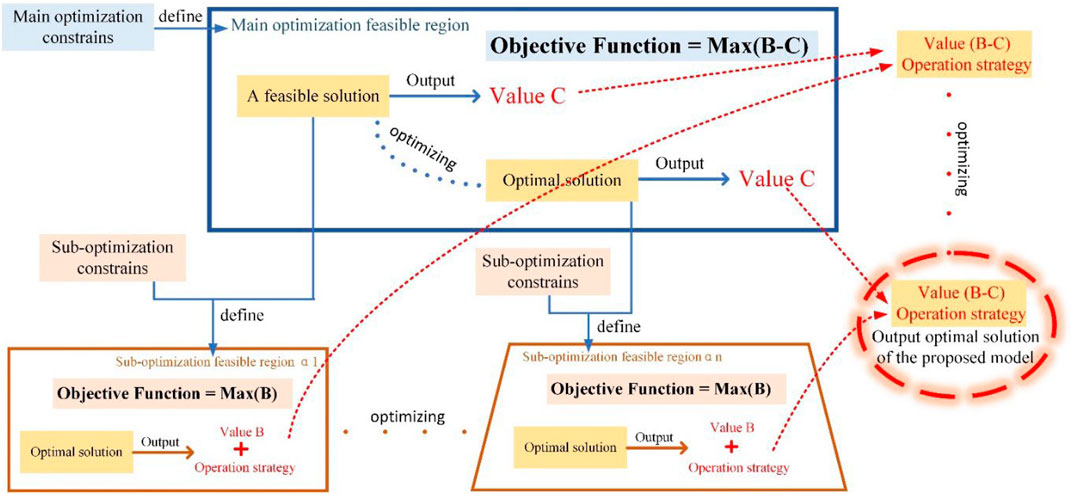
As depicted in Figure 4, within the feasible region of the main optimization model, each feasible solution can be linked to a unique sub-optimization problem. To determine the objective function value for a given feasible solution, it is imperative to solve its associated sub-optimization problem. Upon solving this sub-optimization, the daily operational economic benefits and the optimal operational strategy of the system are derived as output. Ultimately, the optimization algorithm is used to identify the solution set that maximizes the primary optimization objective function. The optimal operational strategy is then computed based on the sub-optimization problem corresponding to the optimal solution set.

FIGURE 4

FIGURE 4. The structure of the proposed nested optimization model.

3.1 Main optimization model

This model takes into account both the installation and operational costs associated with a WHR system. The overarching aim of the optimization is to maximize operational benefits while simultaneously minimizing the discounted present value of the installation costs. In a system comprising N WHS and offering a selection of 4 types of potential WHR devices, the objective function can be defined as the optimal operational benefits minus the discounted present value of the total installation cost for the specific system configuration. Within the main model, for every defined system, a dispatch optimization process is essential to compute the optimal operational benefits. This dispatch optimization ensures that the system operates at its most efficient capacity, contributing to the determination of the objective function’s value for each specific system setup. Eq. 3.2 reflects how the optimal operational benefits changes with the system components. Additionally, Eq. 3.3 describes the constraints on the independent variables, which ensures that a choice is made within the limited capacity of devices.

$\begin{array}{l}\mathit{Max}:Obj\_1\left(b_{i,j}\right)=Benefi{t}_{opt}-\mathrm{Cos}{t}_{con}\\ =Benefi{t}_{opt}-\alpha \cdot {\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^4}\left({\beta }_{i,j}\cdot {\lambda }_{i,j}\right)\\ =Benefi{t}_{opt}-\alpha \cdot {\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^4}\left(b_{i,j}\cdot {\mathrm{\Lambda }}_{i,j}\cdot {\lambda }_{i,j}\right)\end{array}(3.1)$

$Benefi{t}_{opt}=Of\left(b_{i,j},\mathrm{\Phi }\right)(3.2)$

$Const1.1:b_{i,j}\in \left\{\mathrm{0,1},\cdot \cdot \cdot ,b_{i,j,\max }\right\},\forall i\in \left[\mathrm{1,2},\cdot \cdot \cdot ,N\right]andj\in \left[1,\cdot \cdot \cdot ,4\right](3.3)$

The details of Eq. 3.1 are introduced in the next section. Eq. 3.2 is the optimization objective.

3.2 Sub-optimization model

3.2.1 Modelling of objective function and constraints

The model presented in this section provides a detailed explanation of how changes in device planning capacity impact the system’s operation.

Eq. 3.4 is the objective function indicating the operational economic benefits of a WHR system. It quantifies the net operating revenue of cold, heat, and electricity during the dispatch period. Constraint Eq. 3.5 denotes that the system must satisfy the total amount of waste heat energy recovered by WHR equipment.

$\mathit{Max}:Obj\_2={\mathrm{{\rm B}}}^{cold}+{\mathrm{{\rm B}}}^{heat}+{\mathrm{{\rm B}}}^{power}(3.4)$

$Const2.1:0\le Q_{i,AR,t}+Q_{i,EHP,t}+Q_{i,ORC,t}+Q_{i,HE,t}\le Q_{i,\max ,t},\forall i\in \left[\mathrm{1,2},\cdot \cdot \cdot ,N\right](3.5)$

3.2.2 Modelling of key devices operation

Operation models of typical WHR utilization technologies have been used in many other studies. Most of these studies regard the conversion efficiency of the devices as constant (Wang et al., 2010; Jin et al., 2017). The following describes the operation models of the four types of commonly used WHR devices in detail. In addition, models of the fluid machinery are included. It is used to calculate the extra energy cost brought about by WHR utilization in $P_t$, serving as the foundation for analyzing the impact of WHR utilization on normal manufacturing operations.

(1) Modelling of AR Operation

The AR is composed of a generator, condenser, evaporator, absorber, and working-fluid pump. It can convert the heat energy in the waste heat into cold energy, and the working medium pump consumes electric energy during its operation. The model can be expressed as (Wang et al., 2018):

$\left\{\begin{array}{l}{C}_{i,AR,t}=CO{P}_{i,AR}\cdot Q_{i,AR,t}\\ C_{i,AR,\min }\le C_{i,AR,t}\le C_{i,AR,\max }\\ P_{i,AR,t}=\frac{C_{i,AR,t}}{{\eta }_{i,AR}}\end{array}\right.(3.6)$

(2) Modelling of EHP Operation

An EHP can complete the transfer of heat energy by consuming a small amount of electricity. The COP of the electric heat pump can reach more than four, which means that the transfer of four units of heat energy consumes only one unit of electric energy, effectively reducing the use of conventional energy. Its model can be expressed as (Jin et al., 2017):

$\left\{\begin{array}{l}{H}_{i,EHP,t}=CO{P}_{i,EHP}\cdot P_{i,EHP,t}\\ H_{i,EHP,\min }\le H_{i,EHP,t}\le H_{i,EHP,\max }\end{array}\right.(3.7)$

According to the principle of energy conservation, the expression for the heat energy recovered from the waste heat by the EHP is as follows:

$Q_{i,EHP,t}=\left(1-\frac{1}{CO{P}_{i,EHP}}\right)\cdot H_{i,EHP,t}(3.8)$

(3) Modelling of ORC Power Generation Unit Operation

The ORC operates according to the principle of the Clausius-Rankine (C-R) cycle. It uses organic substances as the working fluid to generate electricity, which is suitable for heat recovery from low-temperature heat sources such as geothermal, biomass, and solar energy. The climbing rate of the device is considered in the model and can be expressed as (Wang et al., 2018):

$\left\{\begin{array}{l}{P}_{i,ORC,t}={\eta }_{i,ORC}\cdot Q_{i,ORC,t}\\ P_{i,ORC,\min }\le P_{i,ORC,t}\le P_{i,ORC,\max }\\ -\Delta P_{i,ORC,\max }\le P_{i,ORC,t+1}-P_{i,ORC,t}\le \Delta P_{i,ORC,\max }\end{array}\right.(3.9)$

(4) Modelling of HE Operation

HE is used to transfer heat from a hot fluid to a cold fluid and is the most direct and common device for WHR. There are many types of HE, and the general model can be expressed as (Wang et al., 2018):

$\left\{\begin{array}{l}{H}_{i,HE,t}={\eta }_{i,HE}\cdot Q_{i,HE,t}\\ H_{i,HE,\min }\le H_{i,HE,t}\le H_{i,HE,\max }\end{array}\right.(3.10)$

(5) Modelling of Fans and Pumps Operation

The fluids require fans and pumps to supply sufficient power. WHR utilization significantly increases the resistance of the pipeline. This resistance may result in 40% of the output energy of WHR devices that must be used to compensate for the extra energy consumption of fans and pumps, and it may even make WHR projects less profitable (Aranguren et al., 2018; Tian et al., 2022). This significantly affects the operational costs of the WHR system. However, many scholars have ignored this point when optimizing WHR utilization (Wang et al., 2018). Considering the influence of WHR devices on the power of the fans and pumps in the optimization model is one of the innovations of this study.

Calculating the pressure loss caused by the WHR devices is the premise for calculating the power increments of the fans and water pumps. In general, the flow of flue gas and water is considered a steady state-incompressible-three-dimensional flow (Yuan et al., 2019). Thermophysical parameters such as density ($\rho$), humidity, and specific heat capacity showed little difference between the flue gas and saturated moist air (Zhu et al., 2016). To facilitate this study, the density of the flue gas in the numerical analysis was taken as a fixed value of 0.6 kg/m³, and the actual measured value should be used in practical application (Tsilingiris, 2018). The additional pressure loss is related to the local resistance coefficient ($\zeta$) of the device, the velocity ($v$), and the density of the fluid. The specific mathematical relationship is shown in Eq. 3.11, (Filis et al., 2021; Dvořák and Tomáš, 2015). To obtain a more accurate $\zeta$, experiments are typically required to obtain accurate calculations.

$\Delta p_{i,t}={\zeta }_i\cdot \frac{{v_{i,t}}^2}{2}\cdot {\rho }_{i,t}(3.11)$

After the installation of WHR devices, the pressure loss in the pipeline increased significantly. Fans and pumps had to work harder to provide a higher pressure to the fluid in order to maintain its velocity. The power of fans and pumps is influenced by the efficiency (${\eta }_{dy}$), volume flow ($q$) of the fluid and pressure loss (Amiri Rad and Mohammadi, 2018; Dong et al., 2020). Therefore, after WHR utilization, the additional power consumption of the fans and pumps can be calculated as:

$P_{i,add,t}=\frac{q_{i,t}\cdot \Delta p_{i,t}}{3600\cdot {\eta }_{i,dy}}(3.12)$

3.2.3 Reorganize the objective function and constraints with independent variables

As shown in Figure 1 and 2, the energy consumed by the system includes the additional electric energy consumed by the fans and pumps. This study assumed that the resistance coefficient of the devices was proportional to their capacity. Therefore, the influence of WHR utilization on the power of the fans and pumps can be expressed using Eq. 3.13. Therefore, based on the model of key devices, the details of net output power, thermal energy and cold energy can be expressed by Eqs. 3.14–3.16.

$P_{i,add,t}=\frac{{\displaystyle \sum _{j=1}^4}\left(b_{i,j}\cdot {\mathrm{\Lambda }}_{i,j}\cdot {\zeta }_{i,j}\right)\cdot q_{i,t}\cdot \frac{{v_{i,t}}^2}{2}\cdot {\rho }_{i,t}}{3600\cdot {\eta }_{i,dy}}(3.13)$

$C_t={\displaystyle \sum _{i=1}^N}{C}_{i,AR,t}(3.14)$

$H_t={\displaystyle \sum _{i=1}^N}\left(H_{i,EHP,t}+H_{i,HE,t}\right)(3.15)$

$P_t={\displaystyle \sum _{i=1}^N}\left(P_{i,ORC,t}-\frac{C_{i,AR,t}}{{\epsilon }_{i,AR}}-\frac{H_{i,EHP,t}}{CO{P}_{i,EHP}}-P_{i,add,t}\right)(3.16)$

It can be observed from the operation model of the devices that there is a certain mathematical relationship between the input and output power of the devices. The system operation boundary shown in the constraint Eq. 3.5 can be described by the independent variables. Therefore, considering the operational constraints of the devices, the sub-optimization model can be reorganize using Eqs. 3.18–3.21. where, T is the number of time intervals in a typical day.

$\begin{array}{l}\mathit{Max}:Obj\_2\left(C_{i,AR,t},H_{i,EHP,t},P_{i,ORC,t},H_{i,HE,t}\right)={\mathrm{{\rm B}}}^{cold}+{\mathrm{{\rm B}}}^{heat}+{\mathrm{{\rm B}}}^{power}={\displaystyle \sum _{t=1}^T}\mathrm{Pr}{C}_t\cdot C_t\cdot \Delta t+{\displaystyle \sum _{t=1}^T}\mathrm{Pr}{H}_t\cdot H_t\cdot \Delta t+{\displaystyle \sum _{t=1}^T}\mathrm{Pr}{E}_t\cdot P_t\cdot \Delta t\end{array}(3.18)$

$Const2.1:0\le \frac{C_{i,AR,t}}{CO{P}_{i,AR}}+\left(1-\frac{1}{CO{P}_{i,EHP}}\right)\cdot H_{i,EHP,t}+\frac{P_{i,ORC,t}}{{\epsilon }_{i,ORC}}+\frac{H_{i,HE,t}}{{\eta }_{i,HE}}\le Q_{i,\max ,t},\forall i\in \left[\mathrm{1,2},\cdot \cdot \cdot ,N\right]and\forall t\in \left[\mathrm{1,2},\cdot \cdot \cdot ,T\right](3.19)$

$Const2.2:\left\{\begin{array}{l}{C}_{i,AR,\min }\le C_{i,AR,t}\le C_{i,AR,\max }\\ H_{i,EHP,\min }\le H_{i,EHP,t}\le H_{i,EHP,\max }\\ P_{i,ORC,\min }\le P_{i,ORC,t}\le P_{i,ORC,\max }\\ H_{i,HE,\min }\le H_{i,HE,t}\le H_{i,HE,\max }\end{array}\right.,\forall i\in \left[\mathrm{1,2},\cdot \cdot \cdot ,N\right](3.20)$

$Const2.3:-\Delta P_{i,ORC,\max }\le P_{i,ORC,t+1}-P_{i,ORC,t}\le \Delta P_{i,ORC,\max },\forall i\in \left[\mathrm{1,2},\cdot \cdot \cdot ,N\right](3.21)$

3.3 Parameter transfer model

The boundary conditions of the sub-optimization problem are related to the capacity of the WHR system, which is the independent variable of the main optimization. The parameter transfer model is the key to determining these two parts of the parameters, which enables the sub-optimization problem to be solved and returns the optimal solution. It can be expressed specifically in Eq. 3.22.

$\left\{\begin{array}{l}{C}_{i,AR,\max }=b_{i,AR}\cdot {\mathrm{\Lambda }}_{i,AR},C_{i,AR,\min }=k_{i,AR}\cdot b_{i,AR}\cdot {\mathrm{\Lambda }}_{i,AR}\\ H_{i,EHP,\max }=b_{i,EHP}\cdot {\mathrm{\Lambda }}_{i,EHP},H_{i,EHP,\min }=k_{i,EHP}\cdot b_{i,EHP}\cdot {\mathrm{\Lambda }}_{i,EHP}\\ P_{i,ORC,\max }=b_{i,ORC}\cdot {\mathrm{\Lambda }}_{i,ORC},P_{i,ORC,\min }=k_{i,ORC}\cdot b_{i,ORC}\cdot {\mathrm{\Lambda }}_{i,ORC}\\ H_{i,HE,\max }=b_{i,HE}\cdot {\mathrm{\Lambda }}_{i,HE},H_{i,HE,\min }=k_{i,HE}\cdot b_{i,HE}\cdot {\mathrm{\Lambda }}_{i,HE}\\ \Delta P_{i,ORC,\max }={\mu }_{i,ORC}\cdot b_{i,ORC}\cdot {\mathrm{\Lambda }}_{i,ORC}\end{array}\right.,\forall i\in \left[\mathrm{1,2},\cdot \cdot \cdot ,N\right](3.22)$

3.4 A complete description of the nested optimization model

Reviewing the sub-optimization model in this section, we can see that the function $Of\left(\right)$ in Eq. 3.2 is a sub-optimization of the main optimization problem, and Eq. 3.23 can review this logic. It means that the influencing path from the planning capacity of devices of the WHR system to final economic benefit is constructed by changing the boundary conditions of sub-optimization.

$\begin{array}{l}\left\{\begin{array}{l}Benefi{t}_{opt}=Of\left(b_{i,j},\mathrm{\Phi }\right)\\ Benefi{t}_{opt}=Obj\_2\left(\underset{C_{i,AR,t},H_{i,EHP,t},P_{i,ORC,t},H_{i,HE,t}}{\overset{Obj\_2}{\mathrm{argmin}}}\left(b_{i,j},\mathrm{\Phi }\right)\right)\end{array}\right.\\ \Rightarrow \left\{\begin{array}{l}\mathit{Max}:Obj\_1\left(b_{i,j}\right)=Obj\_2\left(\underset{C_{i,AR,t},H_{i,EHP,t},P_{i,ORC,t},H_{i,HE,t}}{\overset{Obj\_2}{\mathrm{argmin}}}\left(b_{i,j},\mathrm{\Phi }\right)\right)-\alpha \cdot {\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^4}\left(b_{i,j}\cdot {\mathrm{\Lambda }}_{i,j}\cdot {\lambda }_{i,j}\right)\\ Const1.1:b_{i,j}\in \left\{\mathrm{0,1},\cdot \cdot \cdot ,b_{i,j,\max }\right\},\forall i\in \left[\mathrm{1,2},\cdot \cdot \cdot ,N\right]andj\in \left[1,\cdot \cdot \cdot ,4\right]\end{array}\right.\end{array}(3.23)$

3.5 Solving algorithm

Calculating the objective function with the candidate parameters in Obj_1 must solve the sub-optimization problem. This mathematical structure is called nested optimization. The nested optimization model in this study was solved using a genetic algorithm that does not require the gradient of the optimization object to the parameters. Sub-optimization is a typical linear programming problem, and many effective solving tools are available. The basic idea of the optimization solution in this study was to use the capacity of each WHR device in the system as the individual gene, the total objective function Obj_1 (Eq. 3.2) as the individual fitness function, and to find the optimal solution through the evolution of the population. It must be stated that each time the fitness value of the individual is calculated, it is necessary to optimize the sub-optimization. The process of solving the model is shown in Figure 5.

FIGURE 5

FIGURE 5. Model’s solving process.

4 Numerical study and analysis

4.1 Background

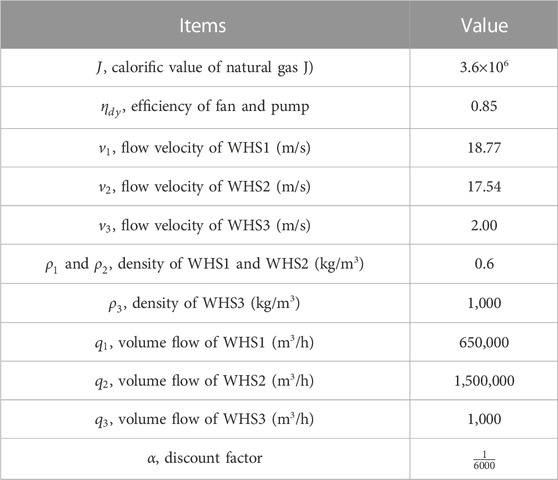
The numerical study was carried out in MATLAB (version R2019a) on a computer with an AMD Ryzen 71,700 Eight-Core Processor, 3.00 GHz, and 8.0 GB of RAM. For the numerical study, a representative steel factory was selected, which exhibited substantial waste heat in the form of flue gas and circulating cooling water. The factory had three WHS with potential for recovery, and their basic structures are depicted in Figure 6. Both waste heat source 1 (WHS1) and waste heat source 2 (WHS2) utilized flue gas as the medium, with temperatures ranging from 100°C to 220°C. Previous research has indicated that the waste heat energy from these two sources can primarily be recovered using AR, EHP, ORC, and HE. Waste heat source 3 (WHS3) employed circulating cooling water as the medium, with temperatures ranging from 30°C to 40°C. The waste heat energy in WHS3 can be mainly recovered using EHP. In the numerical study, it was assumed that the steel factory had sufficient demand for electricity, heat, and cold energy. The energy generated from WHR would be utilized for the production and operation of the factory.

FIGURE 6

FIGURE 6. The structure of WHR system in the steel factory.

Table 1 provides information on the maximum recoverable waste heat power from the three WHS and the corresponding local resistance coefficients. The factory operated continuously for 24 h, and it was assumed that the local resistance coefficients of the various WHR devices within the same WHS were consistent. Notably, the maximum available waste heat energy is definite and finite. The amount of waste heat energy recovered by a device depends on its conversion efficiency. Higher conversion efficiency results in lower consumption of waste heat energy to achieve the same output power.

TABLE 1

TABLE 1. Maximum waste heat power and local resistance coefficient of 1 kW device capacity for each WHS.

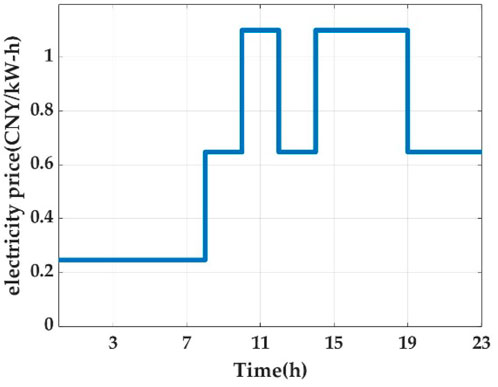
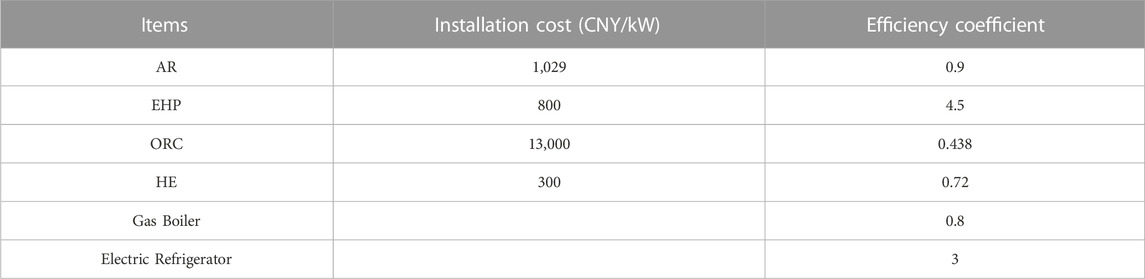
The time-of-use (TOU) tariff for a typical city in China was employed (DRC, 2021), as shown in Figure 7, with electricity prices set at 1.1008 CNY/(kW-h), 0.6475 CNY/(kW-h), and 0.2461 CNY/(kW-h) for different periods. The discrete capacity of the devices was set at 200 kW. The parameters utilized in this study are listed in Tables A1, A2 of the Appendix, which are based on typical conditions in China.

FIGURE 7

FIGURE 7. TOU tariff used in the numerical study.

This section encompasses four numerical studies. Numerical Study 1 examined the optimization results under different boundary conditions, demonstrating that the proposed model can automatically consider environmental and device capability factors specific to a steel factory and produce adaptive optimal solutions. Numerical Study 2 compared the optimization results with and without considering the pressure loss, illustrating the significance and necessity of incorporating pressure loss in the evaluation of the operational economy. Numerical Study 3 compared discrete device capacity with continuous device capacity, affirming the practicality of using discrete capacity. Throughout the experiments, strict control was maintained over the values of these parameters. Numerical Study 4 analyzed the impact of two uncertainties, the amount of waste heat energy that can be recovered and the probability of equipment failure, on the outcome at the system operation level. All parameters were held constant, except for the parameter being investigated for its effect.

4.2 Numerical study 1: sensitivity analysis of equipment parameters

This study demonstrates the effectiveness of the proposed model in providing optimal solutions for various device capability factors and consumer environments. Figure 2 illustrates the impact of three factors on the economic benefits of recovering 1 kW-h of waste heat energy from the WHS. Changes in these factors influence the optimal solutions. By successively examining the optimal solutions generated by the model with variations in device efficiency, resistance coefficient, and investment cost, the adjusted values of these parameters were compared and analyzed. Ultimately, the validity of the proposed model was established.

4.2.1 Influence of efficiency on optimal solutions

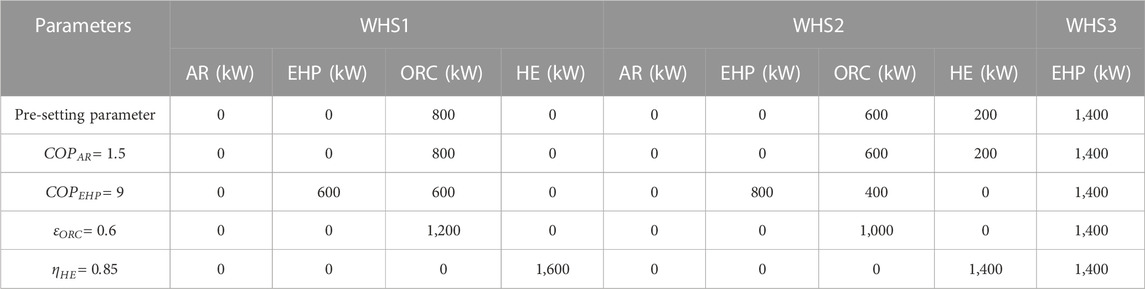
The efficiency coefficients of AR, ORC, EHP, and HE were increased from their preset values to 1.5, 0.6, 9, and 0.85, respectively, while keeping other parameters unchanged. The resulting optimal solutions for the model are presented in Table 2.

TABLE 2

TABLE 2. Optimal solution as the efficiency coefficient of the device changes.

Under the preset parameters, the economic benefit of recovering 1 kWh of waste heat energy from the WHS was approximately 0.187 CNY for the ORC unit, 0.052 CNY for AR, 0.124 CNY for EHP, and 0.176 CNY for HE. The ORC unit exhibited the highest economic benefit, followed by HE, while AR had the lowest economic benefit, less than half the value of the other three devices. When the efficiencies of the four devices increased, four dis-tinct scenarios emerged. Despite an increase in its efficiency coefficient, AR maintained the lowest economic benefit. Meanwhile, the economic benefit of the ORC unit remained the highest and the gap widened compared to other devices. The economic benefits of EHP and ORC were only slightly different but noticeably higher than those of the other two de-vice types when the efficiency coefficient of EHP increased. Finally, when the efficiency coefficient of HE increased, it yielded the highest economic benefit.

Table 2 reveals that an increase in the efficiency coefficient of AR did not alter its position of inferior economic benefit. The optimal solutions remained the same as those obtained with the preset parameters. On the other hand, an increase in the efficiency coefficients of EHP, ORC, and HE significantly impacted the optimization results. Firstly, the improvement in efficiency coefficients enhanced the utilization rate of waste heat, leading to improved output power and increased device capacity. Secondly, the device capacity was adjusted, allocating it to devices with substantial economic benefits. Based on the analysis above, it can be concluded that the proposed model and algorithm accurately perceive changes in the economic benefits of devices and provide optimal solutions. The device efficiency coefficient affects the optimization solutions, but under these conditions, the solutions consistently remain optimal.

4.2.2 Influence of resistance coefficient on optimal solutions

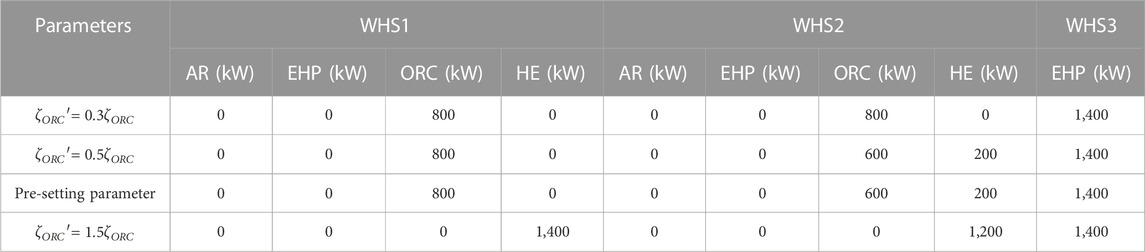
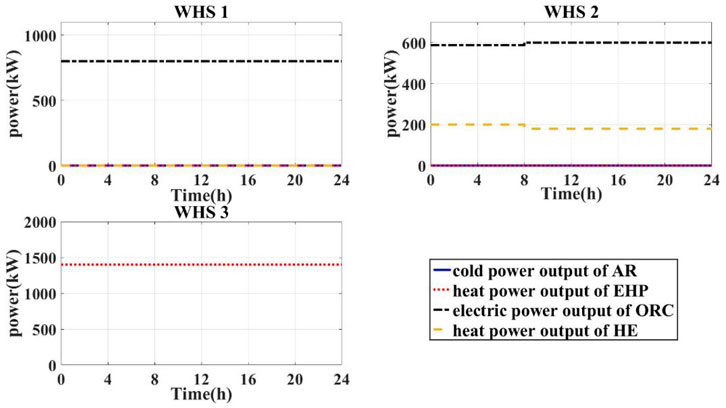
In addition to the device’s efficiency coefficient, the resistance coefficient also has a significant impact on its economic benefits. By increasing and decreasing the resistance coefficients of the ORC units, we observed changes in the economic benefits of these units. The optimal solutions for device capacity are presented in Table 3.

TABLE 3

TABLE 3. Optimal solution as the resistance coefficient of the ORC unit changes.

When the resistance coefficient of the ORC unit was increased by a factor of 1.5, its economic benefit became significantly lower than that of the HE unit. Under these conditions, the capacity of the ORC unit in WHS1 and WHS2 decreased to 0, while the capacity of the HE unit increased to 1,400 kW and 1,200 kW, respectively. With an ORC unit operating at its maximum power capacity of approximately 700 kW, the available waste heat energy from WHS2 can be fully utilized. Therefore, investing in an ORC unit with a capacity of 800 kW for WHS2 would result in approximately 100 kW of capacity redundancy. Such redundancy brings no economic benefits and only increases investment costs and pressure losses. In contrast, constructing an HE unit would be more cost-effective. Only when the resistance coefficient of the ORC unit is reduced to 0.3 times its pre-set value, does the model recommend building an 800 kW ORC unit for WHS2.

4.2.3 Influence of investment cost on optimal solutions

During the planning process, consumers encounter various environmental factors, including changes in device investment costs and rising energy prices. In this study, we examine the change in device investment costs, while the investigation of increasing natural gas prices is addressed in numerical study 3. We adjusted the investment cost of the ORC device from its pre-set value of 13,000 CNY/kW to 21,000 CNY/kW, while retaining the preset values for other parameters. The optimal solutions are listed in Table 4.

TABLE 4

TABLE 4. Optimal solution as the investment cost of the ORC unit changes.

Increasing the investment cost of the ORC unit leads to a decrease in its economic benefits. When the investment cost of the ORC unit reached 17,000 CNY/kW, the economic benefit of the HE unit surpassed that of the ORC unit. According to the results in Table 4, when the investment cost of the ORC unit exceeds 17,000 CNY/kW, the HE unit recovers most of the waste heat energy from WHS1 and WHS2. This change maximizes the economic benefits of WHR utilization.

Based on the aforementioned observations, it is evident that the proposed model can automatically determine the optimal solution when various key factors change. This reflects the effectiveness and feasibility of the proposed model.

4.3 Numerical study 2: sensitivity analysis of resistance coefficient

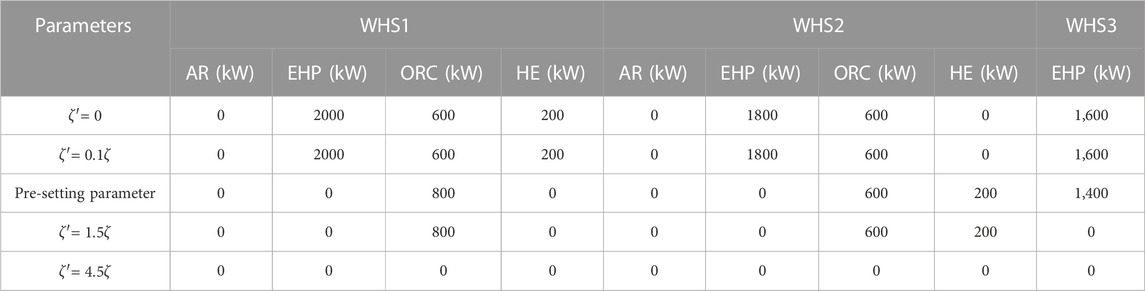
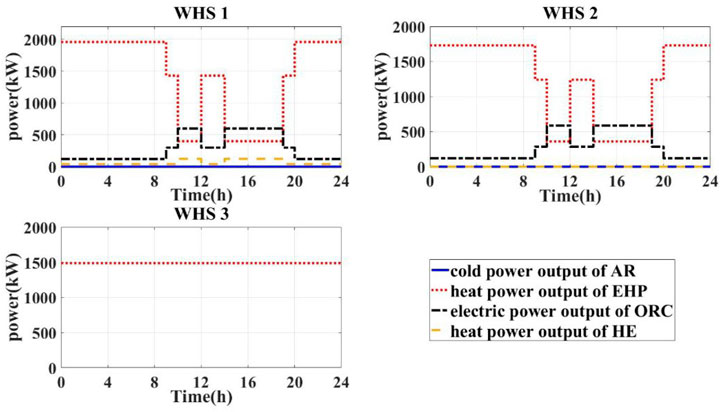
This study highlights the importance of considering the impact of WHR device installation on pressure loss in the normal steel manufacturing process. By gradually increasing the resistance coefficients of the devices, we obtained the optimal solutions from the model for different resistance coefficient values, as presented in Table 5. It is worth noting that a zero-resistance coefficient implies neglecting the additional pressure loss caused by WHR devices, which is the case in traditional WHR utilization methods.

TABLE 5

TABLE 5. Optimal solution as the resistance coefficient of the device changes.

When the values of ${\zeta }^{\prime }$ are low, the device capacities exhibit significant redundancy. This is due to the higher economic benefit of the EHP during the valley and flat periods of TOU pricing, while the ORC unit offers the highest economic benefit during peak periods. Figure 8 provides insight into this observation, where the EHP operates at high power during valley and flat periods, while the ORC unit operates at high power during peak periods. Constructing an excessive number of devices would lead to higher investment costs. However, this additional investment can be recovered through the devices’ flexible response to TOU tariff.

FIGURE 8

FIGURE 8. Optimal operating solution without considering the pressure loss caused by the device.

Conversely, when ${\zeta }^{\prime }$ is normal or higher, the situation changes significantly. The device capacity becomes precisely adequate for maximizing the utilization of waste heat energy. This is because the devices substantially increase the power of fans or pumps. Investing in redundant devices to respond to TOU pricing becomes uneconomical. During this time, the device power on a typical day remains stable and close to the maximum power capacity. Figure 9 displays the optimal operation solutions provided by the model for a typical day when ${\zeta }^{\prime }$ is set to its pre-determined value.

FIGURE 9

FIGURE 9. Optimal operating solution under pre-setting parameter.

4.4 Numerical study 3: contrast experiment on discrete and continuous device capacity

In this study, we conducted a comparison between discrete device capacity and continuous device capacity to establish the practicality of using discrete capacity. Complete data for WHR utilization are essential. When dealing with real-world scenarios, the data should reflect the actual performance of the candidate devices. These devices can be standardized or customized. Standardized devices are more prevalent, simpler, and widely adopted, while customization tends to be costlier and time-consuming. The WHR planning and operation optimization model proposed in (Wang et al., 2018) assumes continuous device capacity, making it applicable only to customized WHR devices. However, this approach lacks practicality as standardized devices are more commonly employed. A standardized device implies a discrete capacity. For instance, an EHP may have standardized devices available with output powers of 200 kW and 400 kW but finding a standardized device with an output power of 333 kW can be challenging.

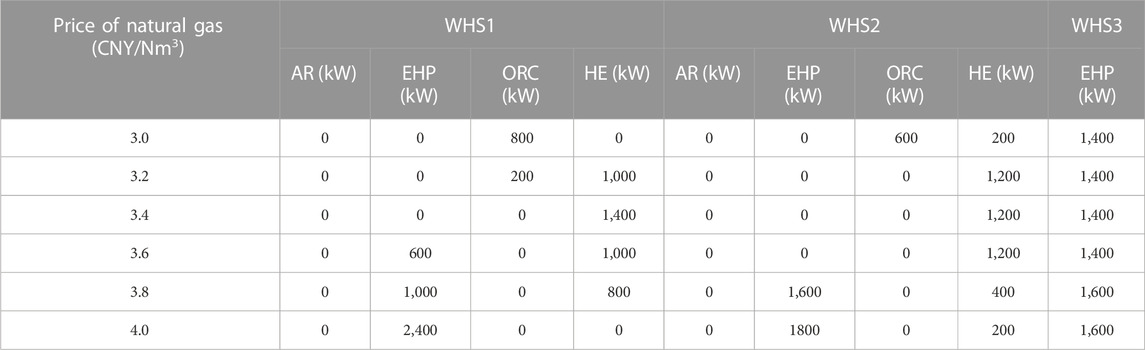
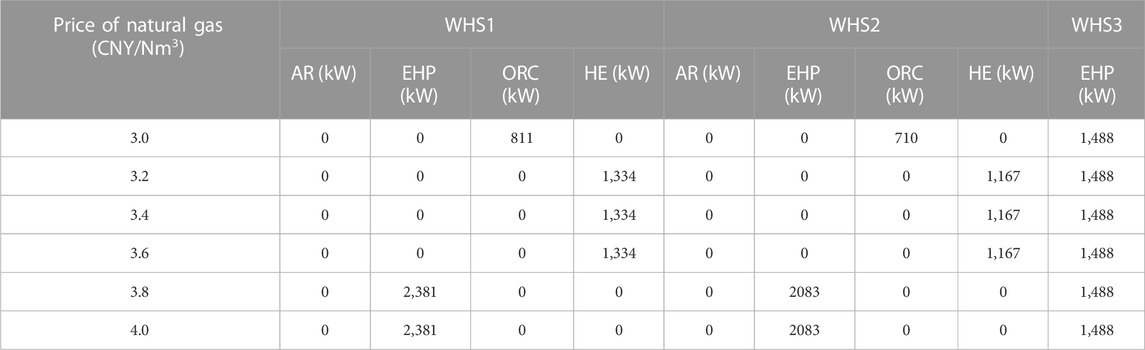
To compare the influences of discrete and continuous device capacities on the optimization results, we increased the price of natural gas from 3.0 CNY/Nm³ to 4.0 CNY/Nm³. The optimization results are presented in Tables 6, 7. With discrete device capacity, waste heat can be recovered using one or two different types of devices. As the natural gas price increases, the type of device with the highest capacity in WHS1 and WHS2 transitions from the ORC unit to the HE, and ultimately to the EHP. This trend aligns with the economic benefits of the devices.

TABLE 6

TABLE 6. Optimization solutions for a discrete device capacity.

TABLE 7

TABLE 7. Optimization solutions for a continuous device capacity.

When the device capacity is continuous, all three WHS utilize a single recovery device, with waste heat energy being recovered by the device offering the highest economic benefits. Initially, an ORC unit recovers the waste heat in WHS1 and WHS2. However, as the price of natural gas reaches 3.2 CNY/Nm³, the HE device recovers all waste heat. Furthermore, when the price of natural gas exceeds 3.8 CNY/Nm³, the EHP device becomes the sole means of WHR utilization. This pattern aligns with the observations made when the device capacity is discrete. Nevertheless, if the capacity of a standardized device is determined based on the optimization solutions provided in Table 7, it may result in reduced waste heat utilization or significant capacity redundancy. For instance, the optimal capacity suggested by the results is 710 kW, but if the available device capacities are only 600 kW or 800 kW, choosing either option leads to drawbacks. Opting for 600 kW decreases the waste heat utilization rate, while selecting 800 kW introduces unnecessary redundancy, both resulting in reduced economic efficiency.

The practicality of the proposed model is evidenced in two aspects. First, it is common practice to use standardized devices with discrete capacities for WHR utilization, emphasizing the importance of using discrete device capacity. Second, if the proposed model allows for small capacity intervals, it becomes suitable for cases involving customized devices. As a result, our model accommodates the planning of both standardized and customized devices simultaneously, thereby establishing its universal significance.

4.4 Numerical study 4: uncertainty analysis

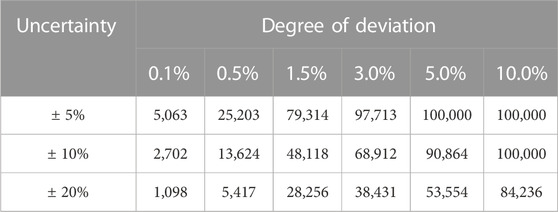
After the system is put into operation, uncertainty mainly comes from two aspects. On one hand, the fluctuations of fluid temperature and volume flow rate in the WHS will affect the quantity of recoverable waste heat energy and thus affect the operational profitability of the system. On the other hand, the uncertainty of equipment failure status will reduce the overall profitability of the system. Based on the optimal device planning capacity obtained from preset data, we have separately analyzed the impact of these two factors through a large number of repeated random experiments. The experiment was repeated 100,000 and 10,000 times respectively. Table 8 shows the optimal device planning capacity of numerical study. Table 9 shows the distribution of daily operational benefit under random fluctuations in the original baseline value of recoverable waste heat at uncertainties of 5%, 10%, and 20%.

TABLE 8

TABLE 8. The optimal device planning capacity of numerical study.

TABLE 9

TABLE 9. The distribution of daily operational benefit under recoverable waste heat uncertainties.

The relationship between the failure rate of conventional power equipment and the operating time in its life cycle can be known as the ‘‘bathtub curve’‘. In the situation of ignoring the influence of weather conditions (or other conditions) on failure rate and the debugging period. Set the failure probability ${\delta }_1$ of a single device to $0.015+0.0315\times {year}^{1.1}$ (Su et al., 2019). Equipment maintenance time is set to 1 week. Table 10 shows the distribution of accumulated system operational benefits during a 20-year device service life under conditions of device failure probabilities of ${\delta }_1$, ${2\times \delta }_1$, and $4\times {\delta }_1$.

TABLE 10

TABLE 10. The distribution of accumulated system operational benefits under different conditions of device failure probabilities.

Table 9 shows that when the amount of recoverable heat is fluctuating within a range of $\pm 5\%$ from the preset value, 97,713 experiments resulted in a degree of deviation of less than 3.0%. However, as the fluctuation range increases, this number will decrease. When the fluctuation range expands to $\pm 20\%$, the number will drop to 38,431. The number is only 84,236 even with a deviation value of 10%. Therefore, as the fluctuation range of the amount of recoverable heat increases, the result is more likely to significantly deviate. But even with a fluctuation range of $\pm 20\%$, there is still a high probability of up to 84% that the deviation of the result will not exceed 10%.

Table 10 shows that as the failure probabilities change, for a specific failure probability value, the range of deviations remains relatively constant. In these 10,000 repeated experiments, when the failure probability is ${\delta }_1$, the degree of deviation of the results falls within the range of 0%–0.8%. When the failure probability is $2\times {\delta }_1$, the results fall within the range of 0.4%–1.2%. Furthermore, as the failure probabilities increase, the degree of deviation will gradually increase. However, even under high failure probabilities $4\times {\delta }_1$ and a long maintenance cycle of 1 week, more than 99% of the experiments have deviations no greater than 1.8%.

5 Conclusion

Waste heat recovery (WHR) plays a critical role in enhancing energy efficiency and reducing carbon emissions. Unfortunately, prior studies often neglected the impact on regular manufacturing operations and assumed continuous device capacity, limiting their practicality and authenticity. In response, we’ve introduced an innovative WHR utilization planning method that factors in how WHR devices affect manufacturing processes. Additionally, we’ve incorporated a discrete capacity selection model for device selection, recognizing the constraints of limited product options.

Our numerical study underscores the importance of considering the influence of WHR utilization on regular manufacturing operations. Overlooking this aspect may lead to an excessive investment in redundant devices, especially in scenarios requiring demand-side response to time-of-use (TOU) tariffs. Such device selection can result in a significant increase in pressure loss, ultimately compromising the investment’s profitability.

Furthermore, our research suggests that continuous device capacity is preferable in customized scenarios where finding devices with precise capacities is challenging, and compromises are necessary. However, it is important to note that our proposed model is not confined to standardized devices but also adaptable to situations with customized devices, particularly when the capacity interval is small. Additionally, our uncertainty experiments reveal that the actual performance deviation from the model’s predictions remains relatively small, even under highly uncertain conditions. Consequently, our model holds broad applicability and can be tailored to diverse scenarios.

The proposed model optimizes device selection, capacity configuration, and operational behavior for WHR in steel factories. Our numerical study affirms its capacity to generate adaptive optimal solutions, considering consumer-specific environmental factors and device capabilities.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

RW: Investigation, Writing–original draft. WZ: Conceptualization, Formal Analysis, Writing–original draft. SY: Methodology, Software, Writing–original draft. ZZ: Resources, Visualization, Writing–original draft. SF: Data curation, Writing–review and editing. CL: Methodology, Writing–original draft.

Funding

The authors declare financial support was received for the research, authorship, and/or publication of this article. This work is in part by science and technology project of State Grid Zhejiang Electric Power Co., Ltd. entitled “Research on Energy Efficiency Enhancement Technologies in End-Use Energy” (5211LS220004).

Conflict of interest

Authors RW, WZ, SY, ZZ, and SF were employed by Lishui Power Supply Company of State Grid Zhejiang Electric Power Co., Ltd.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

The authors declare that this study received funding from Lishui Power Supply Company of State Grid Zhejiang Electric Power Co., Ltd. The funder had the following involvement in the study: Study design, data collection and analysis, modelling, simulations, decision to publish, and preparation of the manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Amin, M., Kasaeian, A., Pourfayaz, F., and Hossein Ahmadi, M. (2017). Thermodynamic analysis of a combined gas turbine, ORC cycle and absorption refrigeration for a CCHP system. Appl. Therm. Eng. 111, 397–406. doi:10.1016/j.applthermaleng.2016.09.098

CrossRef Full Text | Google Scholar

Amiri Rad, E., and Mohammadi, S. (2018). Energetic and exergetic optimized Rankine cycle for waste heat recovery in a cement factory. Appl. Therm. Eng. 132, 410–422. doi:10.1016/j.applthermaleng.2017.12.076

CrossRef Full Text | Google Scholar

Aranguren, P., Araiz, M., and Astrain, D. (2018). Auxiliary consumption: a necessary energy that affects thermoelectric generation. Appl. Therm. Eng. 141, 990–999. doi:10.1016/j.applthermaleng.2018.06.042

CrossRef Full Text | Google Scholar

Brown, M. A., and Valentina, S. H. (2021). Combined heat and power as a platform for clean energy systems. Appl. Energy 304, 117686. doi:10.1016/j.apenergy.2021.117686

CrossRef Full Text | Google Scholar

Brückner, S., Liu, S., Miró, L., Radspieler, M., Cabeza, L. F., and Lävemann, E. (2015). Industrial waste heat recovery technologies: an economic analysis of heat transformation technologies. Appl. Energy 151, 157–167. doi:10.1016/j.apenergy.2015.01.147

CrossRef Full Text | Google Scholar

Dong, H.-W., Kim, B.-J., Yoon, S.-Y., and Jeong, J.-W. (2020). Energy benefit of organic Rankine cycle in high-rise apartment building served by centralized liquid desiccant and evaporative cooling-assisted ventilation system. Sustain. Cities Soc. 60, 102280. doi:10.1016/j.scs.2020.102280

CrossRef Full Text | Google Scholar

Drc, (2021). Notice of guangdong provincial development and reform commission on further improving the policy of peak and valley TOU tariff in our province. Available: http://drc.gd.gov.cn/ywtz/content/post_3500421.html.

Google Scholar

Dvořák, V., and Tomáš, V. (2015). Numerical investigation of counter flow plate heat exchanger. Energy Procedia 83, 341–349. doi:10.1016/j.egypro.2015.12.188

CrossRef Full Text | Google Scholar

Filis, V., Kolarik, J., and Michael Smith, K. (2021). The impact of wind pressure and stack effect on the performance of room ventilation units with heat recovery. Energy Build. 234, 110689. doi:10.1016/j.enbuild.2020.110689

CrossRef Full Text | Google Scholar

Gu, W., Wu, Z., and Yuan, X. (2010). “Microgrid economic optimal operation of the combined heat and power system with renewable energy,” in Proceedings of the IEEE PES General Meeting, Minneapolis, MN, USA, July 2010. doi:10.1109/PES.2010.5590140

CrossRef Full Text | Google Scholar

Guo, Li, Liu, W., Cai, J., Hong, B., and Wang, C. (2013). A two-stage optimal planning and design method for combined cooling, heat and power microgrid system. Energy Convers. Manag. 74, 433–445. doi:10.1016/j.enconman.2013.06.051

CrossRef Full Text | Google Scholar

Hassan, H. (2015). Investigating the effects of load demands on selection of optimum CCHP-ORC plant. Appl. Therm. Eng. 87, 547–558. doi:10.1016/j.applthermaleng.2015.05.050

CrossRef Full Text | Google Scholar

Javad Dehghani, M., and Chang, K. (2020). Modeling and extensive analysis of the energy and economics of cooling, heat, and power trigeneration (CCHP) from textile wastewater for industrial low-grade heat recovery. Energy Convers. Manag. 205, 112451. doi:10.1016/j.enconman.2019.112451

CrossRef Full Text | Google Scholar

Jin, M., Feng, W., Liu, P., Marnay, C., and Spanos, C. (2017). MOD-DR: microgrid optimal dispatch with demand response. Appl. Energy 187, 758–776. doi:10.1016/j.apenergy.2016.11.093

CrossRef Full Text | Google Scholar

Kim, J., and Nam, Y. (2016). A numerical study on system performance of groundwater heat pumps. Energies 9, 4. doi:10.3390/en9010004

CrossRef Full Text | Google Scholar

Mago, P. J., Fumo, N., and Chamra, L. M. (2007). Methodology to perform a non-conventional evaluation of cooling, heating, and power systems. Proc. Institution Mech. Eng. (Part A J. Power Energy) 221 (8), 1075–1087. doi:10.1243/09576509JPE442

CrossRef Full Text | Google Scholar

Pan, G., Gu, W., Lu, Y., Qiu, H., Lu, S., and Yao, S. (2020). Optimal planning for electricity-hydrogen integrated energy system considering power to hydrogen and heat and seasonal storage. IEEE Trans. Sustain. Energy 11, 2662–2676. doi:10.1109/TSTE.2020.2970078

CrossRef Full Text | Google Scholar

Pantaleo, A. M., Fordham, J., Oyewunmi, O. A., De Palma, P., and Markides, C. N. (2018). Integrating cogeneration and intermittent waste-heat recovery in food processing: microturbines vs. ORC systems in the coffee roasting industry. Appl. Energy 225, 782–796. doi:10.1016/j.apenergy.2018.04.097

CrossRef Full Text | Google Scholar

Su, S., Hu, Y., He, L., Yamashita, K., and Wang, S. (2019). An assessment procedure of distribution network reliability considering photovoltaic power integration. IEEE Access 7, 60171–60185. doi:10.1109/ACCESS.2019.2911628

CrossRef Full Text | Google Scholar

Tian, M.-W., Abed, A. M., Anqi, A. E., Guo, W., Wae-hayee, M., Mohamed, F., et al. (2022). A simplified economic model and case study for recovery ventilation based on SPECO method. Case Stud. Therm. Eng. 40, 102567. doi:10.1016/j.csite.2022.102567

CrossRef Full Text | Google Scholar

Tsilingiris, P. T. (2018). Review and critical comparative evaluation of moist air thermophysical properties at the temperature range between 0 and 100 °C for Engineering Calculations. Renew. Sustain. Energy Rev. 83, 50–63. doi:10.1016/j.rser.2017.10.072

CrossRef Full Text | Google Scholar

Wang, J.-J., Zhang, C.-Fa, and You-Yin, J. (2010). Multi-criteria analysis of combined cooling, heating and power systems in different climate zones in China. Appl. Energy 87, 1247–1259. doi:10.1016/j.apenergy.2009.06.027

CrossRef Full Text | Google Scholar

Wang, X., Jin, M., Feng, W., Shu, G., Tian, H., and Liang, Y. (2018). Cascade energy optimization for waste heat recovery in distributed energy systems. Appl. Energy 230, 679–695. doi:10.1016/j.apenergy.2018.08.124

CrossRef Full Text | Google Scholar

Xia, Li, Liu, R., Zeng, Y., Zhou, P., Liu, J., Cao, X., et al. (2019). A review of low-temperature heat recovery technologies for industry processes. Chin. J. Chem. Eng. 27, 2227–2237. doi:10.1016/j.cjche.2018.11.012

CrossRef Full Text | Google Scholar

Yu, M., Gudjonsdottir, M. S., Valdimarsson, P., and Saevarsdottir, G. (2018). Waste heat recovery from aluminum production. Energy Technol., 165–178. doi:10.1007/978-3-319-72362-4_14

CrossRef Full Text | Google Scholar

Yuan, M., Ming, P., and Zhang, W. (2019). Numerical study of hydrodynamic and thermodynamic characteristics of a heat exchanger muffler. J. Mech. Sci. Technol. 33, 5515–5525. doi:10.1007/s12206-019-1045-z

CrossRef Full Text | Google Scholar

Zhao, X., Fu, L., Wang, X., Sun, T., Wang, J., and Zhang, S. (2017). Flue gas recovery system for natural gas combined heat and power plant with distributed peak-shaving heat pumps. Appl. Therm. Eng. 111, 599–607. doi:10.1016/j.applthermaleng.2016.09.130

CrossRef Full Text | Google Scholar

Zhu, X., Sui, X., Zhao, Y., Meng, J. 'an, and Li, Z. (2016). Experimental study of the flow and heat transfer of a gas–water mixture through a packed channel. Sci. Bull. 61, 406–415. doi:10.1007/s11434-016-1018-x

CrossRef Full Text | Google Scholar

Appendix

TABLE A1

TABLE A1. Equipment parameters.

TABLE A2

TABLE A2. Other key parameters.

Nomenclature