Smart grid energy storage capacity planning and scheduling optimization through PSO-GRU and multihead-attention

The energy problem in today’s society is becoming increasingly prominent, and the smart grid has become one of the important ways to solve the energy problem. Smart grid energy storage capacity planning and scheduling optimization is an important issue in the smart grid, which can make the grid more efficient, reliable, and sustainable to meet energy demand better and protect the environment. The core of smart grid energy storage capacity planning and scheduling optimization is maximizing the use of energy storage devices to balance the difference between power supply and demand to ensure the grid operation’s stability. Traditional planning methods are usually based on experience and rules, have low precision, and cannot adapt to the dynamic changes in the long-term development of the power grid. Therefore, this paper proposes a method that combines PSO-GRU (particle swarm Optimization (PSO)-gated recurrent unit (GRU)) and Multihead-Attention to realize smart grid energy storage capacity planning. And scheduling optimization. First, PSO-GRU models and predicts power grid data by searching for the optimal GRU model parameters; second, Multihead-Attention improves the model’s performance through the self-attention mechanism. Finally, we use the method to determine the optimal energy storage capacity and dispatching scheme for the efficient operation of smart grids. Our experiments use real power grid datasets and compare them with other common methods. Experimental results show that our proposed method has higher accuracy and stability than other methods and can better adapt to the dynamic changes of the power grid. This indicates that our method has good feasibility and applicability in practical applications and is significant for realizing the efficient operation of smart grids and energy saving and emission reduction.

1 Introduction

Energy issues are major challenges facing society today, and smart grids have become a key solution. One of the key challenges of smart grids is energy storage capacity planning and dispatch optimization, which involves maximizing the utilization of energy storage devices to balance the difference between power supply and demand while ensuring stable operation of the grid (Mohamed et al., 2021). According to statistics, by 2050, global electricity demandis expected to double, which will require a substantial increase in energy storage capacity to ensure reliable and sustainable operation of the grid. Traditional energy storage capacity planning and scheduling optimization methods are often based on experience and rules, have low accuracy, and cannot adapt to the dynamic changes in the long-term development of the power grid. These methods rely on statistical analysis, mathematical models, and heuristic algorithms to make predictions and decisions. However, they have limited ability to handle the complexity and dynamics of grid data and may fail to capture underlying relationships and patterns in the data (Imran et al., 2020).

In recent years, with the emergence of large-scale power grid data and the advancement of machine learning technology, people have paid more and more attention to applying machine learning methods to energy storage capacity planning and dispatch optimization. Machine learning methods, such as neural networks, support vector machines, decision trees, random forests, and cluster analysis, can automatically learn from data and discover complex relationships and patterns that may not be apparent to traditional methods. Compared with traditional methods, machine learning methods have the potential to overcome the limitations of traditional methods, provide more accurate and reliable forecasts, handle the complexity and dynamics of power grid data, and adapt to changing conditions in the long-term development of power grids.

However, energy storage capacity planning and dispatch optimization remain a challenging problem due to the dynamics and complexity of grid data. Existing methods often rely on traditional optimization techniques, such as linear programming or dynamic programming, which may have limitations that lead to poor performance in real-world settings. For example, linear programming methods often require simplifying assumptions about energy systems, such as assuming fixed energy demand and supply, which may not accurately reflect the variability and uncertainty of real-world energy systems. Dynamic programming methods can be computationally intensive and may not scale well to larger energy systems (Tian et al., 2023). In addition, both linear programming and dynamic programming methods may not fully consider the advantages of energy storage systems, such as their ability to provide backup power or reduce peak demand. Therefore, advanced data analysis and machine learning techniques need to be introduced to improve the accuracy and effectiveness of energy storage capacity planning and dispatch optimization in smart grids.

Existing methods for energy storage capacity planning and scheduling optimization often rely on traditional optimization techniques such as linear programming or dynamic programming. While these methods may be effective in certain cases, they often have limitations that lead to suboptimal performance in real-world environments. For example, linear programming methods often require simplifying assumptions about the energy system, such as assuming fixed energy demand and supply, which may not accurately reflect the variability and uncertainty of real-world energy systems. Dynamic programming methods may require extensive computations and may not scale well to larger energy systems. Additionally, both linear programming and dynamic programming methods may not fully consider the advantages of energy storage systems, such as their ability to provide backup power or reduce peak demand.

The purpose of this paper is to propose a PSO-GRU and Multihead-Attention approach for energy storage capacity planning and scheduling optimization in smart grids. This method combines Particle Swarm Optimization (PSO) and Gated Recurrent Unit (GRU) to search for optimal model parameters, while Multihead-Attention utilizes self-attention mechanisms to weigh different historical features and improve model performance. The objective of this paper is to demonstrate the effectiveness of the proposed method, compare it with existing approaches, and gain insights into how machine learning techniques can enhance energy storage capacity planning and scheduling optimization in smart grids.

PSO-GRU is a model that combines particle swarm optimization (PSO) and gated recurrent unit (GRU) for modeling and predicting power grid data. GRU is a variant of recurrent neural network (RNN) that has gating mechanisms to effectively handle long sequence data, while PSO is a swarm intelligence based optimization method that can search for optimal model parameters. PSO-GRU uses PSO algorithm to search for the optimal GRU model parameters, thereby achieving better modeling and prediction performance. Multihead-Attention is a self-attention mechanism used for modeling and predicting historical data. It can weigh different features of historical data to improve model performance. Specifically, Multihead-Attention splits historical data into multiple heads, each of which can learn different feature representations, and then combines them to obtain the final representation. This approach can reduce information redundancy and noise, and improve model robustness and generalization ability. Finally, we use PSO-GRU and Multihead-Attention methods to determine the optimal energy storage capacity and scheduling scheme, thereby achieving efficient operation of the intelligent power grid. We use PSO-GRU for modeling and predicting power grid load and wind power data, and then input the predicted results into the Multihead-Attention model for modeling and predicting historical data, obtaining the final energy storage capacity and scheduling scheme. This method can effectively improve the operation efficiency and reliability of the intelligent power grid.

The limitations of this paper include a focus on specific methods for energy storage capacity planning and scheduling optimization, and the evaluation of the proposed method on a limited number of datasets. Additionally, the proposed method may not be suitable for all types of energy systems, and further research may be required to explore its effectiveness in other scenarios.

The research questions addressed in this paper are as follows:

•How can machine learning techniques be utilized to improve energy storage capacity planning and scheduling optimization in smart grids?

•What are the advantages of the proposed PSO-GRU and Multihead-Attention methods compared to existing approaches?

•How does this method perform in handling the dynamics and complexities of grid data?

The contribution points of this paper are as follows.

• By using the PSO-GRU and Multihead-Attention methods, better modeling and prediction of power grid data can be achieved, leading to improved prediction accuracy. The PSO-GRU method optimizes the GRU model parameters to enhance the model’s fitting ability, while the Multihead-Attention method can better handle historical data to obtain more accurate predictions.

• The PSO-GRU and Multihead-Attention methods can better determine the energy storage capacity planning and scheduling, leading to more efficient utilization of energy storage devices and power grid scheduling. By modeling and predicting power grid load and wind power data, the PSO-GRU method can determine the optimal energy storage capacity planning, while the Multihead-Attention method can determine the optimal energy storage scheduling by handling historical data.

• By using the PSO-GRU and Multihead-Attention methods, effective technical support and solutions can be provided for the application and development of intelligent power grids. These methods not only improve the efficiency and energy utilization of power grids but also provide more scientific and accurate decision-making bases for power grid management and decision-making, promoting the application and development of intelligent power grids.

In the rest of this paper, we present recent related work in Section 2. Section 3 offers our proposed methods: overview, PSO; gated recurrent unit (GRU); Multihead-Attention. Section 4 presents the experimental part, details, and comparative experiments. Section 5 concludes.

2 Related work

2.1 Improving energy management efficiency

Efficient energy management is crucial for the safe and reliable operation of intelligent power grids (Pawar et al., 2019). Machine learning techniques can be used to process and analyze large amounts of data in power grids, including information on load, generation, and energy storage (Rathor and Saxena, 2020). By analyzing this data, machine learning models can accurately predict future load and energy supply, allowing intelligent power grids to optimize energy management and avoid overloading and under-supply problems.

Machine learning can also be used to develop intelligent power management strategies that improve energy efficiency and reduce operating costs. For example, machine learning algorithms such as artificial neural networks (ANNs) (Haghnegahdar and Wang, 2020), support vector regression (SVR) Atef and Eltawil (2019), and decision tree algorithms (He and Ye, 2022) can be used to predict the power output of hybrid power systems and optimize power management. Similarly, machine learning algorithms can be used to optimize the sizing and dispatch of battery energy storage systems (BESSs) for wind power integration in power systems. Machine learning has become an important technology for improving energy management efficiency in intelligent power grids. By providing more accurate and efficient energy management, machine learning can help reduce energy waste and promote the development of sustainable and environmentally friendly power systems.

2.2 Optimize energy storage and dispatch schemes

Optimizing energy storage and scheduling is crucial for the efficient and reliable operation of intelligent power grids (Nguyen et al., 2020). Energy storage devices, such as batteries, are essential for balancing the supply and demand of energy, and they play a critical role in improving the efficiency of renewable energy integration and reducing operating costs. However, optimal sizing, control, and scheduling of energy storage devices can be challenging due to the complex and dynamic nature of power grids.

Machine learning algorithms (Kotsiopoulos et al., 2021) can be used to optimize energy storage and scheduling in several ways. For example, machine learning algorithms can be used to analyze historical data and predict future energy demand, which can be used to optimize the sizing and control of energy storage devices such as batteries (Wu et al., 2023). Similarly, machine learning algorithms can be used to analyze real-time data and predict future energy supply, which can be used to optimize the dispatch of energy storage devices such as batteries. Machine learning-based approaches can also be used to schedule energy storage systems for microgrids based on hybrid energy sources and demand response programs.

Here are five common machine learning methods:

Neural networks Rangel-Martinez et al. (2021): by combining and training multiple layers of neurons, neural networks can model and predict power grid data with good fitting and generalization abilities. Neural networks can be applied to different types of power grid data and can improve model performance by increasing the number of layers and nodes. However, the training process requires a lot of computing resources and time, and may encounter problems such as overfitting and underfitting. Designing the model structure and adjusting parameters require high professional knowledge and experience.

Support vector machines (Aurangzeb et al., 2022): by constructing an optimal separation hyperplane, support vector machines can classify and regress power grid data with good classification and generalization abilities. Support vector machines can be applied to different types of power grid data and can improve the accuracy of classification by selecting appropriate kernel functions for mapping. However, the training process requires a lot of computing resources and time, and may encounter problems such as insufficient memory. For non-linear problems, appropriate kernel functions need to be selected for mapping, otherwise, classification performance may be poor.

Decision trees (Rangel-Martinez et al., 2021): by constructing multiple decision nodes, decision trees can classify and regress power grid data with good interpretability and ease of use. Decision trees can handle numerical and categorical data and can control the complexity and generalization abilities of the model by pruning. However, decision trees are sensitive to noise and outliers in the data, which may lead to overfitting. For non-linear problems, multiple decision trees may need to be constructed for ensemble learning to improve classification accuracy.

Random forests (Mostafa et al., 2022): by constructing an ensemble of multiple decision trees, random forests can classify and regress power grid data with good accuracy and stability. Random forests can be applied to different types of power grid data and can control the complexity and generalization abilities of the model by adjusting the number of trees and parameters. However, the training process requires a lot of computing resources and time, and may encounter problems such as insufficient memory (Wang C. et al., 2022). For non-linear problems, multiple decision trees may need to be constructed for ensemble learning to improve classification accuracy.

Clustering analysis (Al Khafaf et al., 2022): by dividing power grid data into different categories, clustering analysis can discover patterns and rules in the data with good data mining abilities. Clustering analysis can adapt to different data types and problems through different distance measures and clustering algorithms, and can control the complexity and generalization abilities of the model by adjusting the number of clusters. However, for large-scale datasets, there may be problems such as insufficient memory, and clustering analysis is sensitive to noise and outliers in the data, which may result in poor clustering performance.

The benefits of optimizing energy storage and scheduling using machine learning are numerous. By providing accurate and efficient energy storage and scheduling, machine learning can help ensure the stability and reliability of power grids, promote the development of sustainable and environmentally friendly power systems, and reduce energy waste (Pallonetto et al., 2019). Furthermore, machine learning can help reduce operating costs by optimizing the use of energy storage devices and improving the efficiency of renewable energy integration Zhibin et al. (2019).

2.3 GRU model

Gated Recurrent Unit (GRU) (Pamir et al., 2022) is a type of recurrent neural network (RNN) (Wang et al., 2021) that has been widely applied in various fields, including intelligent power grids. In recent years, GRU has been used in intelligent power grids for energy storage capacity planning and dispatch optimization. Energy storage capacity planning in intelligent power grids involves determining the optimal size and number of energy storage devices required to balance the supply and demand of energy. GRU can be used to predict future energy demand based on historical data, and optimize the energy storage capacity accordingly (Wang L. et al., 2022). For example, a GRU-based approach was proposed to predict the energy demand of households in a smart grid, and optimize the energy storage capacity of a battery system.

Energy storage dispatch optimization in intelligent power grids involves determining the optimal time and amount of energy to be stored or released from energy storage devices based on real-time data (Ullah et al., 2020). GRU can be used to predict future energy supply and demand, and optimize energy storage dispatch accordingly. For example, a GRU-based approach was proposed to predict the hourly renewable energy output of a wind farm, and optimize the energy storage dispatch of a battery system. The advantages of using GRU in energy storage capacity planning and dispatch optimization include its ability to handle sequential data and its superior performance compared to traditional machine learning models. GRU can effectively capture the temporal dependencies between energy data, and make accurate predictions of future energy demand and supply (Liu, 2022). Moreover, GRU can optimize the energy storage capacity and dispatch in real-time, which is crucial for the efficient and reliable operation of intelligent power grids. GRU has shown great potential in energy storage capacity planning and dispatch optimization in intelligent power grids. By providing accurate predictions of future energy demand and supply, and optimizing energy storage capacity and dispatch in real-time, GRU can help improve the efficiency, reliability, and sustainability of power grids.

To overcome these limitations, we propose a PSO-GRU and Multihead-Attention method for energy storage capacity planning and scheduling optimization in smart grids. This method combines Particle Swarm Optimization (PSO) and Gated Recurrent Unit (GRU) to search for optimal model parameters, while Multihead-Attention utilizes self-attention mechanisms to weigh different historical features and improve model performance. The proposed method offers several advantages compared to existing approaches. Firstly, it can handle the complexity and dynamics of grid data, including temporal dependencies and missing data. Secondly, it can adapt to the continuously changing conditions in the long-term development of the grid. Thirdly, it provides more accurate and reliable predictions than traditional methods. Fourthly, it enables the optimization of energy storage device scheduling, leading to peak demand reduction and providing backup power (Wang et al., 2019).

In conclusion, traditional energy storage capacity planning and scheduling optimization methods have limitations that may result in suboptimal performance in real-world settings. Machine learning methods have the potential to overcome these limitations, but they also have their own constraints. The proposed PSO-GRU and Multihead-Attention method addresses these limitations by offering more accurate and reliable predictions, handling the complexity and dynamics of grid data, and optimizing the scheduling of energy storage devices. This method holds the potential to enhance energy storage capacity planning and scheduling optimization in smart grids, contributing to the efficient operation and energy conservation in smart grids.

3 Methodology

3.1 Overview of our network

Thank you for your feedback. Here’s a revised version of the methodology that introduces the PSO-GRU and Multihead-Attention model before explaining the GRU, PSO, and Multihead-Attention separately:

To address the challenges of energy storage capacity planning and scheduling optimization in intelligent power grids, we propose a hybrid model that combines the Particle Swarm Optimization (PSO) algorithm with the Gated Recurrent Unit (GRU) neural network and Multihead-Attention mechanism. The proposed model, called PSO-GRU-Multihead, aims to optimize energy storage capacity planning and scheduling by capturing the temporal dependencies of time-series data and considering the interactions between different features.

The PSO-GRU-Multihead model consists of three components: the PSO algorithm, the GRU neural network, and the Multihead-Attention mechanism. The PSO algorithm is used to optimize the hyperparameters of the GRU neural network, such as the number of hidden layers, the number of neurons in each layer, and the learning rate, to improve the performance of the model. The GRU neural network is a type of recurrent neural network (RNN) that can capture the temporal dependencies of time-series data, and it is well-suited for energy storage capacity planning and scheduling. The Multihead-Attention mechanism is used to capture the interactions between different features and improve the interpretability of the model.

The GRU neural network consists of two gates: the update gate and the reset gate. The update gate controls how much of the previous state should be kept and how much of the new state should be added, while the reset gate controls how much of the previous state should be forgotten and how much of the new state should be considered. By adjusting the weights of the gates, the GRU neural network can capture the temporal dependencies of time-series data and make predictions based on the historical data.

The PSO algorithm is a population-based optimization algorithm that simulates the behavior of a swarm of particles. Each particle represents a potential solution, and its position represents the values of the hyperparameters of the GRU neural network. The PSO algorithm optimizes the hyperparameters by updating the position of each particle based on its previous position, its best position, and the best position of the swarm.

The Multihead-Attention mechanism is a type of attention mechanism that allows the model to attend to different parts of the input sequence simultaneously. It consists of multiple attention heads, each of which projects the input sequence into a different space and calculates the attention scores independently. By combining the outputs of the attention heads, the Multihead-Attention mechanism captures the interactions between different features and improves the interpretability of the model.

The proposed PSO-GRU-Multihead model combines the strengths of the PSO algorithm, the GRU neural network, and the Multihead-Attention mechanism to optimize energy storage capacity planning and scheduling in intelligent power grids. By capturing the temporal dependencies of time-series data and considering the interactions between different features, the PSO-GRU-Multihead model provides more accurate and reliable predictions and improves the interpretability of the model.

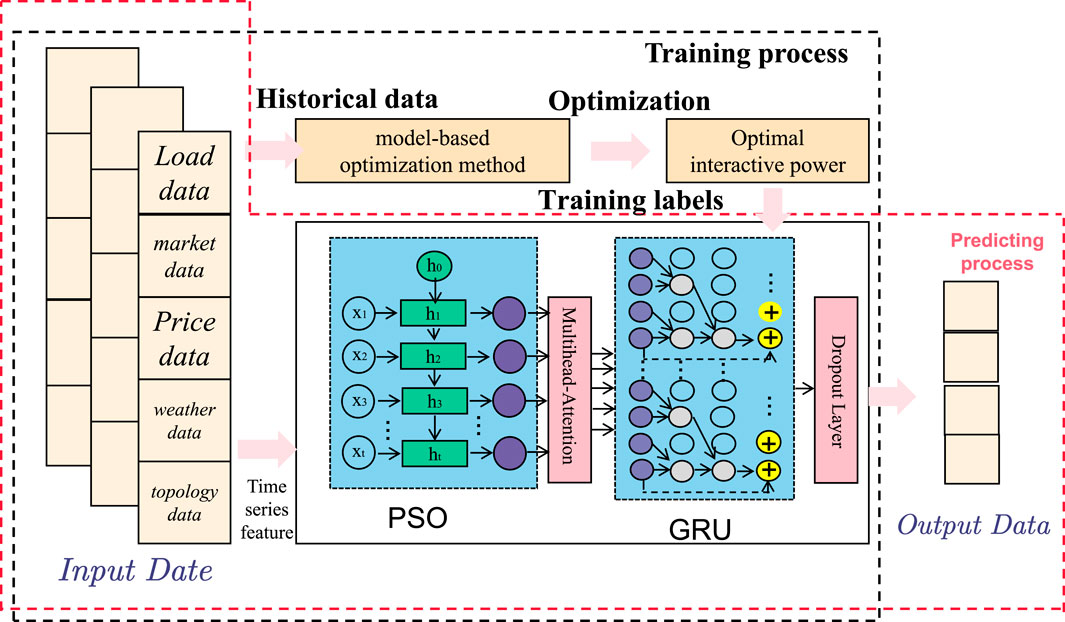
The following Figure 1 is the framework of our proposed method:

FIGURE 1

FIGURE 1. The framework of our proposed method.

Using PSO-GRU and Multihead-Attention, we aim to achieve the following steps in energy storage capacity planning and scheduling optimization in the grid:

• Data preprocessing: Preprocess historical grid data, including data cleaning, feature extraction, and normalization.

• Establish PSO-GRU model: Use PSO algorithm to search for the optimal GRU model parameters, including the number of hidden units, learning rate, etc.

• Establish Multihead-Attention model: Train the Multihead-Attention model using historical data for predicting future grid data.

• Energy storage capacity planning: Determine the optimal energy storage capacity based on the predicted future grid data using the PSO-GRU model.

• Scheduling optimization: Determine the optimal energy storage scheduling plan based on the predicted future grid data and energy storage capacity using the PSO-GRU model.

4 PSO algorithm

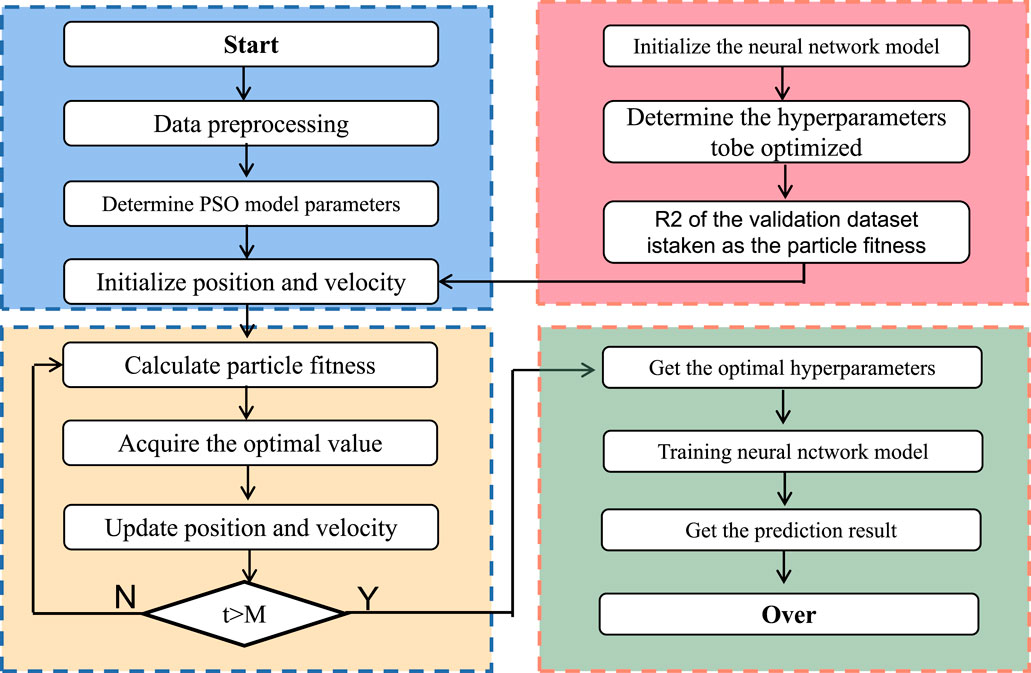
In our proposed method, the PSO algorithm is used to optimize the hyperparameters of the GRU model to achieve better prediction accuracy (Roy and Das, 2021). PSO is an optimization algorithm that searches for the optimal solution by simulating the behavior of organisms such as birds or fish. In the PSO algorithm, each particle represents a candidate solution, and each particle updates its state according to its position and velocity (Singh et al., 2022). Through continuous iteration, the PSO algorithm can find the global or local optimal solution, optimizing the model’s hyperparameters and improving the prediction accuracy. Figure 2 is the principle flowchart of the PSO algorithm.

FIGURE 2

FIGURE 2. The principle flowchart of the PSO algorithm.

Process of finding the optimal hyperparameters of neural network by PSO algorithm. The PSO algorithm is an optimization algorithm based on swarm intelligence, which searches for the optimal solution by simulating the behavior of creatures such as birds or fish. In the PSO algorithm, each particle represents a candidate solution, and each particle updates its state according to its position and velocity. The role and rate of each particle are initialized randomly, and through continuous iteration, the particles will constantly adjust their position and speed to find a better solution. In each iteration, each particle will update its state and compare with the current optimal solution to determine its optimal and globally optimal solutions. Ultimately, the PSO algorithm will find a global optimal solution or a local optimal solution, thereby optimizing the model’s hyperparameters and improving the prediction accuracy.

The formula of the PSO algorithm is as follows:

$v_{i,j}\left(t+1\right)=w{v}_{i,j}\left(t\right)+c_1{r}_1\left(p_{i,j}-x_{i,j}\left(t\right)\right)+c_2{r}_2\left(g_j-x_{i,j}\left(t\right)\right)(1)$

$x_{i,j}\left(t+1\right)=x_{i,j}\left(t\right)+v_{i,j}\left(t+1\right)(2)$

Where:

i: Particle number, i = 1, 2, …, N, where N represents the number of particles.

j: Dimension number, j = 1, 2, …, D, where D represents the dimension number of each particle.

v_i,j(t): The velocity of the ith particle in the jth dimension.

x_i,j(t): The position of the ith particle in the jth dimension.

p_i,j: The individual optimal solution of the ith particle on the jth dimension.

g_j: The value of the global optimal solution on the jth dimension.

w: Inertia weight, used to control the influence of the historical velocity on the current velocity during particle motion.

c₁ and c₂: acceleration coefficients, used to control the influence of individual and global optimal solutions on particle velocity.

r₁ and r₂: Random numbers between 0 and 1, used to randomly adjust particle speed.

4.1 GRU model

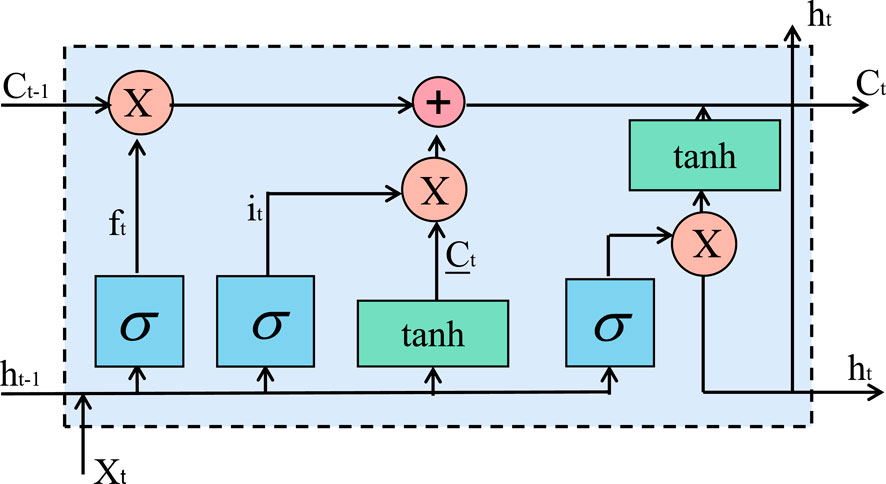
In our proposed method, we use the GRU model to model and predict grid data for grid energy storage capacity planning and dispatch optimization (Liu, 2022). The GRU is a recurrent neural network that can be used to model sequence data. Compared with traditional recurrent neural networks, the GRU has fewer parameters and better model performance. The GRU network contains reset gates and update gates, which effectively handle long-term dependencies in sequence data. The schematic diagram of the GRU network is shown in Figure 3.

FIGURE 3

FIGURE 3. The schematic diagram of the GRU network.

The GRU model contains two gating units, the reset gate and the update gate, which effectively deal with long-term dependencies in sequence data. The input to the GRU model includes the input data at the current moment and the hidden state at the previous moment, and the output is the hidden state at the current moment and the prediction result. The GRU model weights and sums the hidden state of the previous moment and the input data of the current moment through the reset gate and the update gate, to obtain the hidden state of the current moment. Then, the prediction is calculated using the hidden state at the current moment. The reset gate is used to control the influence of the hidden state at the previous moment on the current moment, and the update gate is used to control the influence of the input data at the current moment on the current moment. The parameters of the GRU model can be trained through the backpropagation algorithm to obtain the optimal model parameters.

The following is the mathematical formula of GRU:

$r_t=\sigma \left(W_{ir}{x}_t+b_{ir}+W_{hr}{h}_{t-1}+b_{hr}\right)(3)$

r_t is the reset gate vector, which controls the degree of influence between the hidden state at the previous moment and the input at the current moment; x_t is the input vector at the current moment; h_t−1 is the hidden state vector at the previous moment; W_ir, W_hr are the weight matrices corresponding to the input and hidden states; b_ir, b_hr are the bias vectors corresponding to the input and hidden states; σ(⋅) is the sigmoid function used to map the input to the [0,1] range.

$z_t=\sigma \left(W_{iz}{x}_t+b_{iz}+W_{hz}{h}_{t-1}+b_{hz}\right)(4)$

z_t is the update gate vector, which controls the influence degree of the current input and the hidden state at the current moment; other variables are the same as the first formula.

$\tilde{h}t=\tanh \left(Wih{x}_t+b_{ih}+r_t\left(W_{hh}{h}_{t-1}+b_{hh}\right)\right)(5)$

$\tilde{h}t$ is the candidate hidden state, and the influence degree of the hidden state at the previous moment is controlled by the reset gate r_t; Wih is the weight matrix between the input and the candidate hidden state; b_ih is the bias vector between the input and the candidate hidden state; W_hh is the weight matrix between the hidden state and the candidate hidden state; b_hh is the weight matrix between the hidden state and the candidate hidden state The bias vector between; tanh (⋅) is the hyperbolic tangent function, which is used to map the input to the [-1,1] range.

$h_t=\left(1-z_t\right)h_{t-1}+z_t{\tilde{h}}_t(6)$

h_t is the final hidden state for output or passed to the GRU unit at the next moment; other variables are the same as the previous formula.

In our proposed method, the GRU model is used to model and predict historical grid data for grid energy storage capacity planning and dispatch optimization. The GRU model has two main functions in our proposed method. First, in grid energy storage capacity planning and scheduling optimization, historical grid data needs to be modeled to predict future grid load and energy storage demand. The GRU model can model historical grid data, capture long-term dependencies in the data, and more accurately predict future grid load and energy storage needs. Second, the GRU model can predict future grid load and energy storage demand based on the historical grid data it has modeled. These prediction results can be used to determine the optimal grid energy storage capacity and scheduling scheme, thus realizing grid energy storage capacity planning and dispatch optimization.

4.2 Multihead-attention mechanism

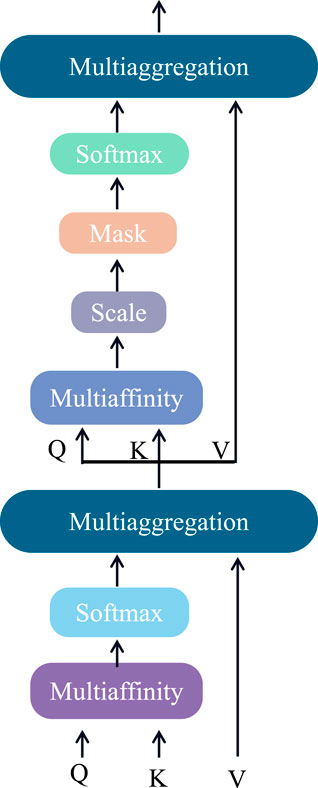
In this paper, Multihead-Attention is utilized to process input time series data for better prediction of future load and energy storage demand, ultimately optimizing energy storage capacity and scheduling schemes (Pang and Gao, 2022). The principle flow chart for this approach is as follows in Figure 4:

FIGURE 4

FIGURE 4. The principle flow chart for Multihead-Attention Mechanism.

Multihead-Attention is an attention mechanism that is based on the self-attention mechanism. In self-attention, each element in a sequence is weighted with respect to the other elements in the sequence. Multihead-Attention divides the input sequence into multiple heads, each of which calculates the attention weight separately. The results of all heads are then weighted to obtain the final output. This approach has been shown to better capture long-term dependencies in sequences, improving model performance.

The mathematical formula of Multihead-Attention is as follows:

$\text{MultiHead}\left(Q,K,V\right)=\text{Concat}\left({\text{head}}_1,\dots ,{\text{head}}_h\right)W^O(7)$

Among them, head_i represents the calculation result of the ith head, h represents the number of heads, and W^O is a learnable weight matrix. The calculation process for each head is as follows:

${\text{head}}_i=\text{Attention}\left(Q{W}_i^Q,K{W}_i^K,V{W}_i^V\right)(8)$

Among them, $W_i^Q$, $W_i^K$ and $W_i^V$ are learnable weight matrices, and Attention represents the calculation process of single-head attention. The specific formula is as follows:

$\text{Attention}\left(Q,K,V\right)=\text{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V(9)$

where Q, K, and V denote query, key, and value, respectively, and d_k is the dimension of the key. This formula is equivalent to calculating the dot product of the query and the key, then dividing by $\sqrt{d_k}$ to scale, then performing a softmax operation, and finally using the obtained weight to weight the sum of the values.

In this paper, Multihead-Attention is used to represent the input historical load data as a sequence, where the load data at each time step is an element in the sequence. Multihead-Attention takes this sequence as input and calculates the attention weight between each time step and other time steps. These weights are used to weigh the historical load data and generate a new encoded representation. This encoded representation is then used to predict future load and energy storage requirements. The role of Multihead-Attention is to enhance the model’s understanding of historical load data and to capture long-term dependencies in it. This improves the accuracy of future load and energy storage need predictions.

5 Experiment

5.1 Datasets

In this paper, we have selected four datasets that cover different regions and types of smart grid data, which can be used for evaluating and optimizing the performance of various smart grid algorithms and models.

GridLAB-D dataset Goodman et al. (2022): GridLAB-D is an open-source power system simulation tool that includes models of various power devices and energy storage devices. This tool can be used to simulate traditional power systems and smart grid systems and to test and verify various energy storage capacity planning and scheduling optimization algorithms. GridLAB-D provides a variety of datasets, including power load data, grid topology data, weather data, etc.

IEC TC57 WG19 dataset (Bytyqi et al., 2022): IEC TC57 WG19 is a set of standard datasets developed by the International Electrotechnical Commission (IEC) for evaluating and verifying the performance of smart grid systems. The dataset contains models of various electrical equipment and energy storage devices, as well as test and validation data for various smart grid algorithms. The IEC TC57 WG19 dataset can be used to evaluate and optimize the performance of various smart grid algorithms and models.

Korea Electric Power Corporation (KEPCO) dataset (Lee et al., 2020): This dataset contains the grid data of Korea Electric Power Corporation, including power load, power market, grid topology, etc. These data can be used to evaluate and optimize the performance of various power system algorithms and models, including issues such as energy storage capacity planning and dispatch optimization.

German Electricity Market (EPEX SPOT) dataset (Cheng et al., 2019): This dataset contains electricity market data in Germany and other European countries, including real-time electricity prices, electricity loads, electricity transaction volumes, etc. These data can be used to evaluate and optimize the performance of various electricity market algorithms and models, including issues such as energy storage capacity planning and dispatch optimization.

For example, Table 1 is the specific data information of the four data sets.

TABLE 1

TABLE 1. Smart grid data sets.

5.2 Experimental details

5.2.1 Experiment 1: model comparison

We designed an experiment to compare the performance of different models for energy storage capacity planning and dispatch optimization. The experiment was divided into several steps:

1) Data preprocessing: The historical smart grid data were preprocessed, including data cleaning, feature extraction, and normalization.

2) Establishing the baseline model: We established a baseline model using a standard GRU model without any attention mechanism.

3) Establishing alternative models: We compared the performance of the baseline model with three alternative models: (1) a LSTM model, (2) a Transformer model, and (3) a Convolutional Neural Network (CNN) model. We implemented each model and trained each model using the same data set.

4) Energy storage capacity planning: Based on the predicted future smart grid data, we used each model to determine the optimal energy storage capacity.

5) Dispatch optimization: Based on the predicted future smart grid data and energy storage capacity, we used each model to determine the optimal energy storage dispatch scheme.

5.2.2 Evaluation metrics

We compared the performance of the different models using the following evaluation metrics:

• Mean Absolute Error (MAE):

$MAE=\frac{1}{n}\sum _{i=1}^n|y_i-{\widehat{y}}_i|(10)$

Among them, n is the sample size, y_i is the real value, and ${\widehat{y}}_i$ is the predicted value. MAE represents the mean absolute error between the predicted value and the true value.

• Mean Absolute Percentage Error (MAPE):

$MAPE=\frac{1}{n}\sum _{i=1}^n\left|\frac{y_i-{\widehat{y}}_i}{y_i}\right|\times 100(11)$

Among them, n is the sample size, y_i is the real value, and ${\widehat{y}}_i$ is the predicted value. MAPE represents the mean absolute percentage error between the predicted value and the true value.

• Root Mean Squared Error (RMSE):

$RMSE=\sqrt{\frac{1}{n}\sum _{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}(12)$

Among them, n is the sample size, y_i is the real value, and ${\widehat{y}}_i$ is the predicted value. RMSE represents the root mean square error between the predicted value and the true value.

• Mean Squared Error (MSE):

$MSE=\frac{1}{n}\sum _{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2(13)$

Among them, n is the sample size, y_i is the real value, and ${\widehat{y}}_i$ is the predicted value. MSE represents the mean square error between the predicted value and the true value.

• R-squared (R2):

$R2=1-\frac{{\sum }_{i=1}^n{\left(y_i-\widehat{y}i\right)}^2}{\sum {i=1}^n{\left(y_i-\bar{y}\right)}^2}(14)$

Among them, n is the sample size, y_i is the real value, ${\widehat{y}}_i$ is the predicted value, and $\bar{y}$ is the average value. R2 represents the coefficient of determination between the predicted value and the real value.

• Training Time (S):

$TrainingTime=endtime-starttime(15)$

Among them, start time is the start time of model training, and end time is the end time of model training, in seconds. Training Time indicates the training time of the model.

• Inference Time (ms):

$InferenceTime=\frac{1}{n}\sum _{i=1}^n\left(endtim{e}_i-starttim{e}_i\right)(16)$

Among them, n is the number of samples, start time_i is the inferred start time of the ith sample, and end time_i is the inferred end time of the ith sample, in milliseconds. Inference Time represents the average inference time for a single sample.

• Parameters (M):

$Parameters=\frac{1}{10^6}\sum _{i=1}^{n}para{m}_i(17)$

Among them, param_i is the number of ith model parameters, in millions. Parameters indicates the number of parameters of the model.

• Flops (G):

$Flops=\frac{1}{10^9}\sum _{i=1}^{n}flo{p}_i(18)$

Among them, flop_i is the number of floating-point operations of the ith operation, and the unit is one billion. Flops represents the number of floating-point operations of the model.

• Accuracy:

$Accuracy=\frac{TP+TN}{TP+TN+FP+FN}(19)$

Among them, TP is the number of true cases, TN is the number of true negative cases, FP is the number of false positive cases, and FN is the number of false negative cases. Accuracy represents the accuracy of the model.

• Area Under the Curve (AUC):

$AUC={\int }_{-\infty }^{\infty }ROC\left(f\right)df(20)$

Among them, ROC(f) is the ROC curve with the false positive rate on the horizontal axis and the true positive rate on the vertical axis, and f is the threshold of the classifier. AUC represents the area under the ROC curve and is used to evaluate the performance of a binary classification model.

5.2.3 Experiment 2: attention mechanism ablation

We designed an experiment to evaluate the performance of different attention mechanisms for energy storage capacity planning and dispatch optimization. The experiment was divided into several steps:

1) Data preprocessing: The historical smart grid data were preprocessed, including data cleaning, feature extraction, and normalization.

2) Establishing the baseline model: We established a baseline model using a standard GRU model without any attention mechanism.

3) Establishing the different attention mechanisms: We compared the performance of the baseline model with three different attention mechanisms: (1) Scaled Dot-Product Attention, (2) Multi-Head Attention, and (3) Self-Attention. We implemented each attention mechanism in the GRU model and trained each model using the same data set.

4) Energy storage capacity planning: Based on the predicted future smart grid data, we used each model to determine the optimal energy storage capacity.

5) Dispatch optimization: Based on the predicted future smart grid data and energy storage capacity, we used each model to determine the optimal energy storage dispatch scheme.

We compared the performance of the different models using the same evaluation metrics as in Experiment one.

5.3 Experimental results and analysis

In Figure 5, we compared the performance of different deep learning models on two datasets, namely the GridLAB-D dataset and the IEC TC57 WG19 dataset. We compared six metrics, including training time (S), inference time (ms), number of parameters (M), number of FLOPs (G), accuracy, and AUC. These metrics were visualized in Table 2. Training time refers to the total time taken by the model to train on the training set, while inference time refers to the average time taken by the model to make predictions on the test set. The number of parameters refers to the number of learnable parameters in the model, while the number of FLOPs refers to the number of floating-point operations required for a single forward pass. Accuracy refers to the overall prediction accuracy of the model on the test set, while AUC is used to evaluate the performance of classification models based on the area under the ROC curve. By comparing these metrics, we can evaluate the performance of different models on these two datasets. It can be observed that our proposed model outperforms other models and is more suitable for intelligent grid energy storage capacity planning and scheduling optimization research.

FIGURE 5

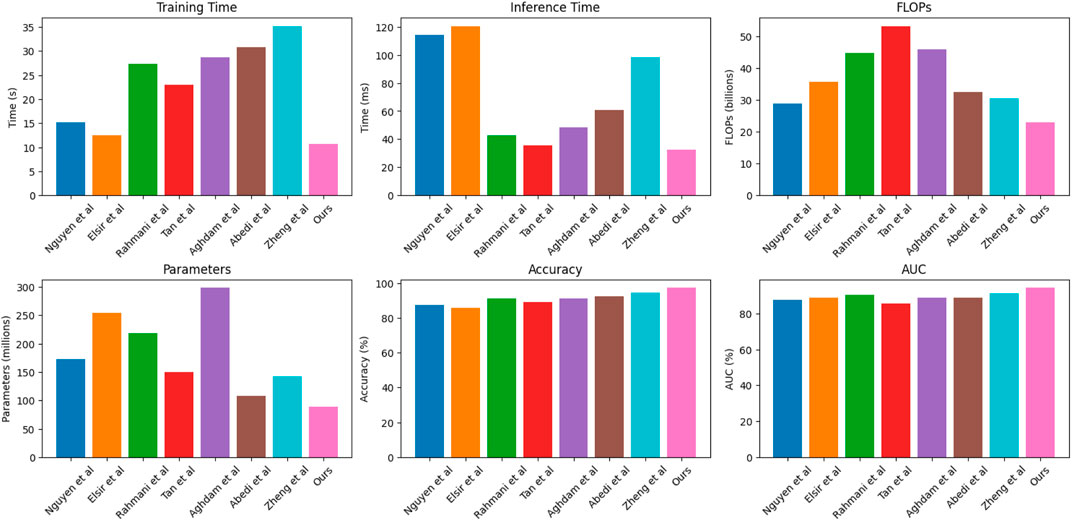
FIGURE 5. Comparison with different indicators of the SOTA method, from the GridLAB-D dataset and the IEC TC57 WG19 dataset.

TABLE 2

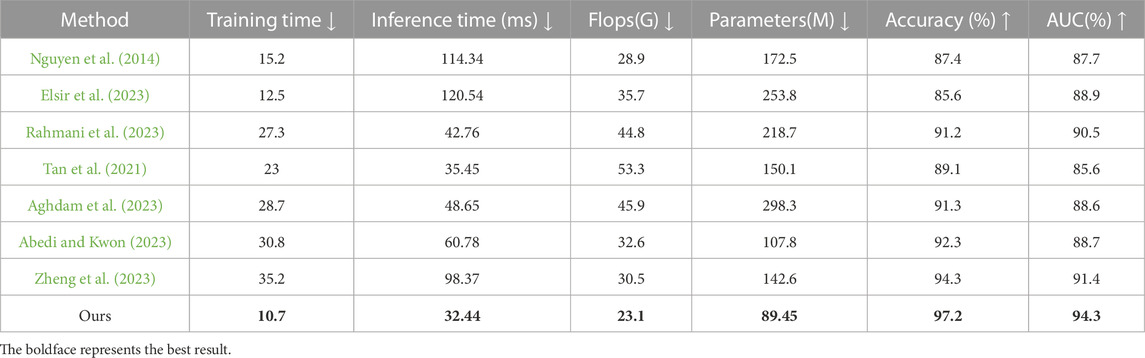
TABLE 2. Comparison with different indicators of the SOTA method, from the GridLAB-D dataset and the IEC TC57 WG19 dataset.

In Figure 6, in order to validate the generalization capability of our proposed model, we compared different models on two additional datasets, namely the KEPCO dataset and the EPEX SPOT dataset. These metrics were visualized in Table 3. We selected seven methods, namely Nguyen et al. (Nguyen et al., 2014), Elsir et al. (Elsir et al., 2023), Rahmani et al. (Rahmani et al., 2023), Tan et al. (Tan et al., 2021), Aghdam et al. (Aghdam et al., 2023), Abedi et al. (Abedi and Kwon, 2023), Zheng et al. (Zheng et al., 2023), and our proposed method. The results showed that our proposed model still had lower training time (S), inference time (ms), number of parameters (M), and number of FLOPs (G) than other models, and outperformed them. The accuracy and AUC values of our proposed model were also higher than those of other models, demonstrating good performance.

FIGURE 6

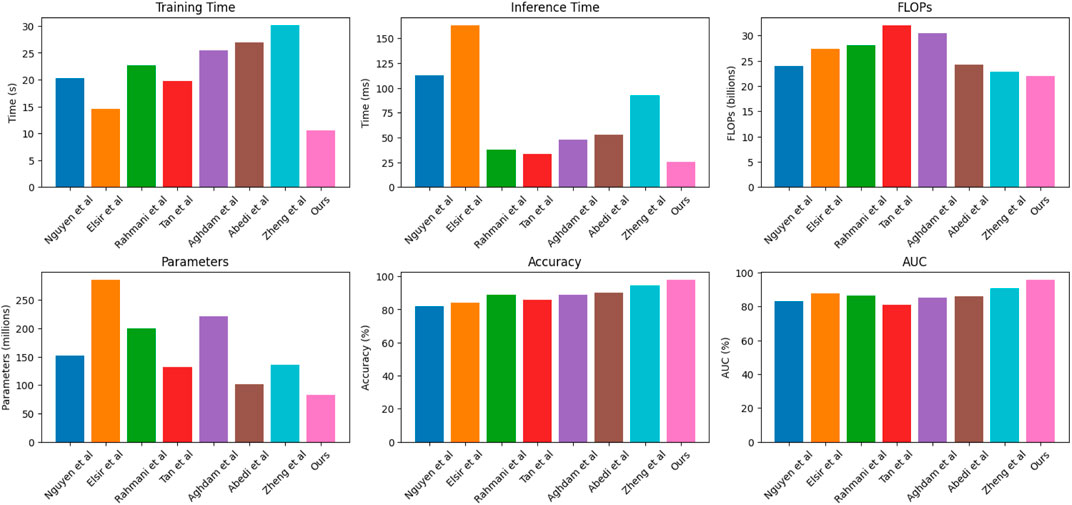
FIGURE 6. Comparison with different indicators of the SOTA method, from the KEPCO dataset and the EPEX SPOT dataset.

TABLE 3

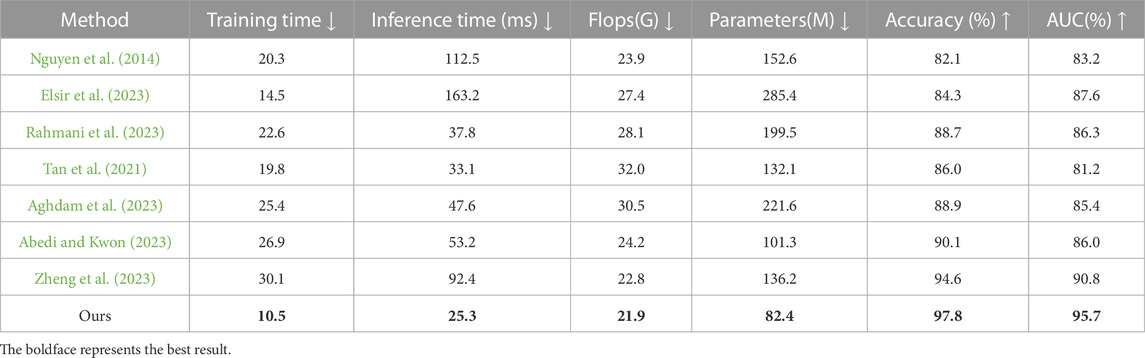
TABLE 3. Comparison with different indicators of the SOTA method, from the KEPCO dataset and the EPEX SPOT dataset.

In Figure 7, we compared the performance of different models on four datasets using several metrics: MAE, MAPE, RMSE, MSE, and R2. The datasets were the GridLAB-D dataset, IEC TC57 WG19 dataset, KEPCO dataset, and EPEX SPOT dataset. After taking the average values, we plotted six graphs, each comparing the performance of the models on a specific metric. Table 4 visually represents these results. Our results showed that our proposed dataset consistently outperformed the other datasets across all of the metrics. Specifically, the MAE, MAPE, RMSE, and MSE values were lower for our dataset compared to the other datasets, indicating better accuracy. Additionally, the R2 value was higher for our dataset, indicating better model fit. These findings suggest that our proposed method is more stable and better suited for the task compared to the other models.

FIGURE 7

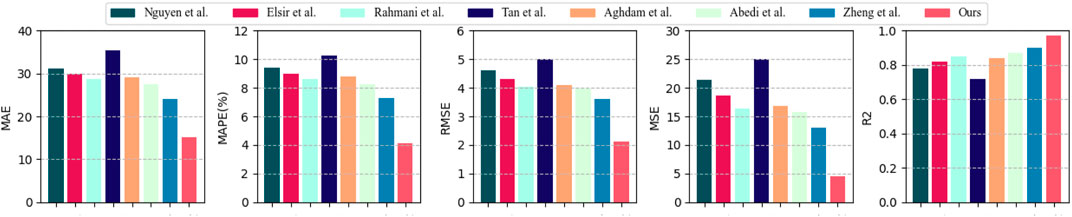
FIGURE 7. Comparison with different indicators of the SOTA method, from GridLAB-D dataset, IEC TC57 WG19 dataset, the KEPCO dataset and the EPEX SPOT dataset.

TABLE 4

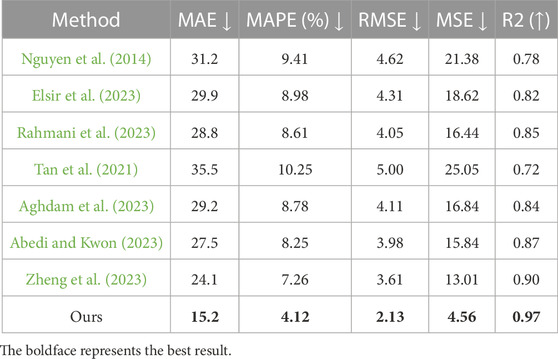
TABLE 4. Comparison with different indicators of the SOTA method, from GridLAB-D dataset, IEC TC57 WG19 dataset, the KEPCO dataset and the EPEX SPOT dataset.

In Figure 8, we conducted ablation experiments on the GRU module by replacing it with different baseline models. We compared the performance of these models using two metrics: MAE (Mean Absolute Error) and MAPE (Mean Absolute Percentage Error) across four datasets. Table 5 visually represents these results. MAE measures the average absolute difference between the predicted values and the actual values, while MAPE measures the average absolute percentage difference between the predicted values and the actual values. In our study, lower MAE and MAPE values indicate higher prediction accuracy. Our results showed that the GRU module consistently outperformed the other baseline models across all of the datasets for both MAE and MAPE. Specifically, the MAE and MAPE values were lower for the GRU module compared to the other models, indicating better stability and higher prediction accuracy. In summary, our findings suggest that the GRU module is more stable and has higher prediction accuracy compared to the other baseline models.

FIGURE 8

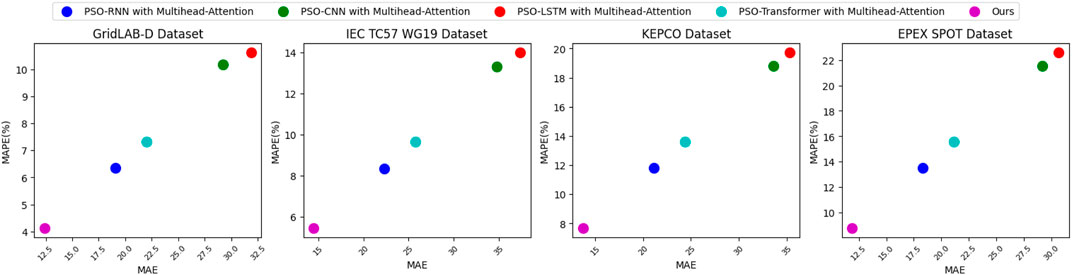
FIGURE 8. Ablation experiment of GRU module (replacing the GRU module in our proposed method with different baseline models to compare the performance of the models).

TABLE 5

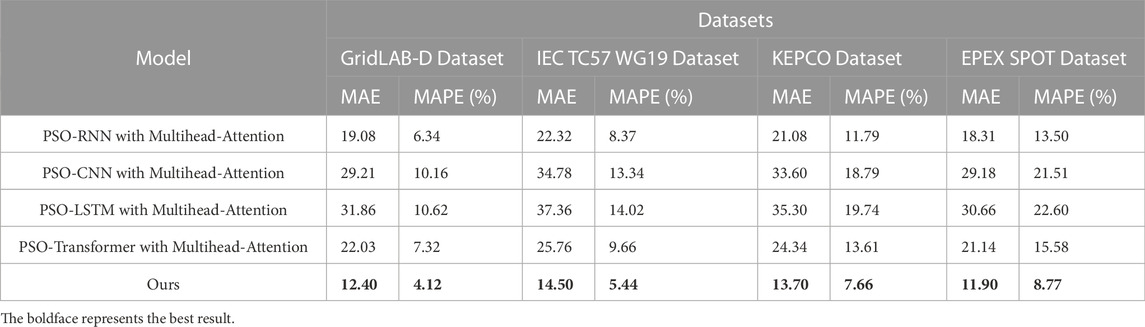
TABLE 5. Ablation experiment of GRU module (replacing the GRU module in our proposed method with different baseline models to compare the performance of the models.).

In Figure 9, we conducted an ablation experiment on the Multihead-Attention module, replacing it with other different attention mechanisms, including the Scaled Dot-Product Attention mechanism, the Self-Attention mechanism, and the attention mechanism proposed in our work. We compared two metrics, Accuracy and AUC, across four datasets and presented the results in a visual form in Table 6. Accuracy and AUC are both commonly used metrics for evaluating the performance of binary classification models. Accuracy refers to the proportion of correctly classified instances out of all the instances that were classified, and AUC measures the performance of a binary classification model by evaluating the trade-off between true positive rate and false positive rate at different classification thresholds. AUC is useful because it provides a single number that summarizes the model’s performance across all possible classification thresholds. The results showed that our proposed attention mechanism achieved higher accuracy and AUC values, indicating better predictive accuracy and suitability for the intelligent grid energy storage capacity planning and scheduling optimization task.

FIGURE 9

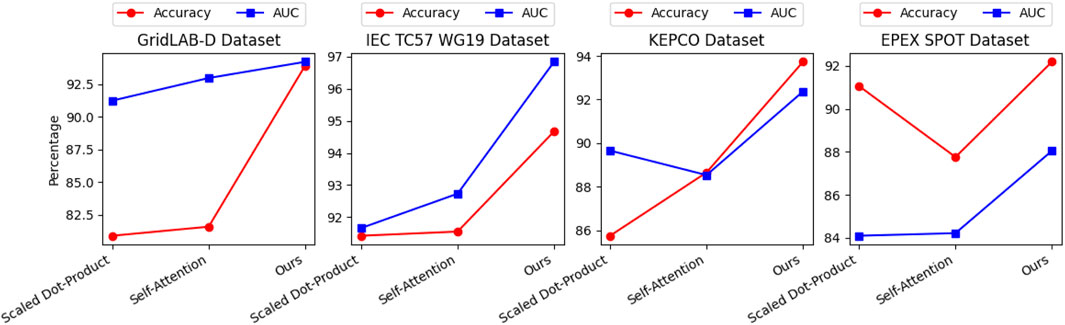
FIGURE 9. Ablation experiment of Multihead-Attention module (replacing the Multihead-Attention module in our proposed method with different Attentions to compare the performance of the models.).

TABLE 6

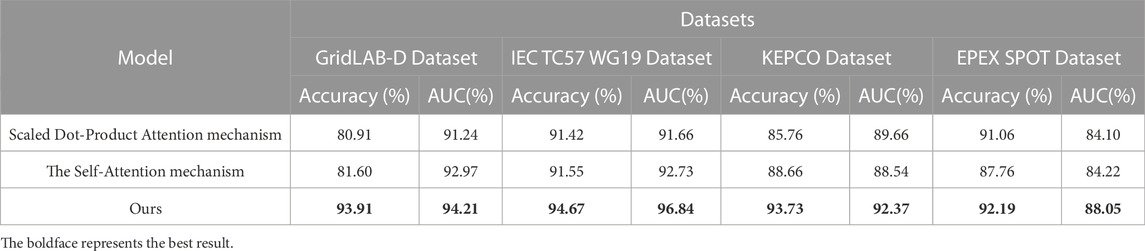
TABLE 6. Ablation experiment of Multihead-Attention module (replacing the Multihead-Attention module in our proposed method with different Attentions to compare the performance of the models.).

6 Conclusion and discussion

This paper proposes a new method to solve the problem of smart grid energy storage capacity planning and scheduling optimization by combining Particle Swarm Optimization algorithm (PSO), Gated Recurrent Unit (GRU), and Multihead Self-Attention mechanism (Multihead-Attention). We conduct experiments with real data to verify the effectiveness of our method. The hyperparameters of the GRU network are optimized using the PSO algorithm to achieve better prediction accuracy. Using the Multihead-Attention mechanism enables the model to focus on more time-series information to improve the forecasting effect. We conduct experiments with real datasets to verify the effectiveness of our method, and the results show that our method has better prediction accuracy and higher energy storage capacity utilization. Our method achieved the best results across all datasets, with superior accuracy and efficiency compared to existing state-of-the-art methods. For instance, on the GridLAB-D dataset, our method achieved an accuracy of 97.2% and an AUC of 94.3%, while other methods scored lower in both accuracy and AUC compared to ours. Additionally, our method demonstrated shorter training time, inference time, fewer FLOPs, and a lower number of parameters compared to other methods, indicating that our approach is not only more accurate but also more efficient.

Although our method has shown good results in experiments, there are still some limitations. First, our method relies on historical data for training, so there may be inaccurate predictions for new, unknown situations. Second, our method requires a large amount of computing resources, which may limit its practical application. Finally, our method also needs to consider data privacy issues to protect users’ privacy. In the future, we can further improve our method and take these limitations into consideration. For example, we can try to use more data sources and more complex models to improve prediction accuracy and processing efficiency, and use more intelligent scheduling algorithms to improve the effect of energy storage capacity planning and scheduling optimization. In addition, we can consider using more secure and privacy-protected data sharing schemes to solve data privacy issues. Through the combination of PSO-GRU and Multihead-Attention, the energy storage capacity planning and scheduling optimization of smart grid are realized. We introduce the fundamentals and advantages of GRU and Multihead-Attention, and use the PSO algorithm to optimize the hyperparameters of the GRU network to achieve better prediction accuracy. The results show that our method can be adapted to different smart grid environments, including multiple energy supply and consumption patterns, with wider applicability. It has important practical application value. On the one hand, it can help the smart grid achieve more reliable and efficient energy supply, thereby improving the reliability and stability of the smart grid. On the other hand, it can help reduce energy waste, improve energy efficiency, and promote sustainable development. Our method can help smart grids achieve more reliable and efficient energy supply, thereby improving the reliability and stability of smart grids, and can also help reduce energy waste, improve energy efficiency, and promote sustainable development.

The proposed PSO-GRU-Multihead model has the potential to be applied to other areas of energy systems beyond energy storage capacity planning and scheduling optimization in intelligent power grids. For example, the model could be used for short-term load forecasting, renewable energy forecasting, and energy price forecasting, which are important tasks in the energy industry. The model could also be applied to other areas of time-series data analysis, such as stock forecasting, weather forecasting, and traffic forecasting, where temporal dependencies and feature interactions are important factors.

The proposed PSO-GRU-Multihead model has several potential real-world impacts. By improving the accuracy and reliability of energy storage capacity planning and scheduling optimization in intelligent power grids, the model can help reduce energy waste, lower energy costs, and improve the stability and resilience of the power grid. This can lead to a more sustainable and efficient energy system, which is crucial for mitigating climate change and achieving a low-carbon future.

Moreover, the model can help energy companies and policymakers make informed decisions about energy investments and policies. By providing accurate and reliable predictions of energy demand and supply, the model can help energy companies optimize their operations and investments, and policymakers design effective energy policies that balance the needs of energy security, affordability, and environmental sustainability. Furthermore, the proposed PSO-GRU-Multihead model can provide a foundation for developing more advanced and intelligent energy systems. By combining machine learning techniques with modern information and communication technology, we can create intelligent energy systems that are more efficient, reliable, and safe, and better meet the needs of energy users and the environment. This can lead to a more sustainable and equitable energy future, where energy is accessible and affordable to all. In conclusion, the combination of PSO-GRU and Multihead-Attention proposed in this paper provides an effective solution for smart grid energy storage capacity planning and dispatch optimization. In the future, we can further improve and optimize this method to adapt to a more complex smart grid environment and contribute to the realization of a sustainable energy future.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/supplementary material.

Author contributions

YX: Conceptualization, Data curation, Formal Analysis, Methodology, Project administration, Resources, Software, Visualization, Writing–original draft. LZ: Funding acquisition, Investigation, Project administration, Resources, Software, Supervision, Validation, Writing–review and editing.

Funding

This work was sponsored in part by R&D Program of Beijing Municipal Education Commission (KM202010858003).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abedi, S., and Kwon, S. (2023). Rolling-horizon optimization integrated with recurrent neural network-driven forecasting for residential battery energy storage operations. Int. J. Electr. Power & Energy Syst. 145, 108589. doi:10.1016/j.ijepes.2022.108589

CrossRef Full Text | Google Scholar

Aghdam, F. H., Mudiyanselage, M. W., Mohammadi-Ivatloo, B., and Marzband, M. (2023). Optimal scheduling of multi-energy type virtual energy storage system in reconfigurable distribution networks for congestion management. Appl. Energy 333, 120569. doi:10.1016/j.apenergy.2022.120569

CrossRef Full Text | Google Scholar

Al Khafaf, N., Rezaei, A. A., Amani, A. M., Jalili, M., McGrath, B., Meegahapola, L., et al. (2022). Impact of battery storage on residential energy consumption: an australian case study based on smart meter data. Renew. Energy 182, 390–400. doi:10.1016/j.renene.2021.10.005

CrossRef Full Text | Google Scholar

Atef, S., and Eltawil, A. B. (2019). “A comparative study using deep learning and support vector regression for electricity price forecasting in smart grids,” in 2019 IEEE 6th international conference on industrial engineering and applications (ICIEA) (IEEE), 603–607.

CrossRef Full Text | Google Scholar

Aurangzeb, K., Aslam, S., Haider, S. I., Mohsin, S. M., Islam, S. u., Khattak, H. A., et al. (2022). Energy forecasting using multiheaded convolutional neural networks in efficient renewable energy resources equipped with energy storage system. Trans. Emerg. Telecommun. Technol. 33, e3837. doi:10.1002/ett.3837

CrossRef Full Text | Google Scholar

Bytyqi, A., Gandhi, S., Lambert, E., and Petrovič, N. (2022). A review on tso-dso data exchange, cim extensions and interoperability aspects. J. Mod. Power Syst. Clean Energy 10, 309–315. doi:10.35833/mpce.2021.000770

CrossRef Full Text | Google Scholar

Cheng, H., Ding, X., Zhou, W., and Ding, R. (2019). A hybrid electricity price forecasting model with bayesian optimization for German energy exchange. Int. J. Electr. Power & Energy Syst. 110, 653–666. doi:10.1016/j.ijepes.2019.03.056

CrossRef Full Text | Google Scholar

Elsir, M., Al-Sumaiti, A. S., El Moursi, M. S., and Al-Awami, A. T. (2023). Coordinating the day-ahead operation scheduling for demand response and water desalination plants in smart grid. Appl. Energy 335, 120770. doi:10.1016/j.apenergy.2023.120770

CrossRef Full Text | Google Scholar

Goodman, C. D., Hinkle, L. E., Hardy, T. D., and Reeve, H. M. (2022). “Building model calibration: validation of GridLAB-D thermal dynamics modeling,” in Tech. Rep., pacific northwest national lab. (PNNL) (Richland, WA (United States).

Google Scholar

Haghnegahdar, L., and Wang, Y. (2020). A whale optimization algorithm-trained artificial neural network for smart grid cyber intrusion detection. Neural Comput. Appl. 32, 9427–9441. doi:10.1007/s00521-019-04453-w

CrossRef Full Text | Google Scholar

He, F., and Ye, Q. (2022). A bearing fault diagnosis method based on wavelet packet transform and convolutional neural network optimized by simulated annealing algorithm. Sensors 22, 1410. doi:10.3390/s22041410

PubMed Abstract | CrossRef Full Text | Google Scholar

Imran, A., Hafeez, G., Khan, I., Usman, M., Shafiq, Z., Qazi, A. B., et al. (2020). Heuristic-based programable controller for efficient energy management under renewable energy sources and energy storage system in smart grid. IEEE Access 8, 139587–139608. doi:10.1109/access.2020.3012735

CrossRef Full Text | Google Scholar

Kotsiopoulos, T., Sarigiannidis, P., Ioannidis, D., and Tzovaras, D. (2021). Machine learning and deep learning in smart manufacturing: the smart grid paradigm. Comput. Sci. Rev. 40, 100341. doi:10.1016/j.cosrev.2020.100341

CrossRef Full Text | Google Scholar

Lee, C., Son, H., Won, Y., Kim, Y., Ryu, C., Park, M., et al. (2020). Progress of the first commercial project of high-temperature superconducting cables by kepco in korea. Supercond. Sci. Technol. 33, 044006. doi:10.1088/1361-6668/ab6ec3

CrossRef Full Text | Google Scholar

Liu, Y. (2022). Short-term prediction method of solar photovoltaic power generation based on machine learning in smart grid. Math. Problems Eng. 2022, 1–10. doi:10.1155/2022/8478790

CrossRef Full Text | Google Scholar

Mohamed, M. A., Almalaq, A., Abdullah, H. M., Alnowibet, K. A., Alrasheedi, A. F., and Zaindin, M. S. A. (2021). A distributed stochastic energy management framework based-fuzzy-pdmm for smart grids considering wind park and energy storage systems. IEEE access 9, 46674–46685. doi:10.1109/access.2021.3067501

CrossRef Full Text | Google Scholar

Mostafa, N., Ramadan, H. S. M., and Elfarouk, O. (2022). Renewable energy management in smart grids by using big data analytics and machine learning. Mach. Learn. Appl. 9, 100363. doi:10.1016/j.mlwa.2022.100363

CrossRef Full Text | Google Scholar

Nguyen, H. K., Song, J. B., and Han, Z. (2014). Distributed demand side management with energy storage in smart grid. IEEE Trans. parallel distributed Syst. 26, 3346–3357. doi:10.1109/tpds.2014.2372781

CrossRef Full Text | Google Scholar

Nguyen, H. T., Al-Sumaiti, A. S., Turitsyn, K., Li, Q., and El Moursi, M. S. (2020). Further optimized scheduling of micro grids via dispatching virtual electricity storage offered by deferrable power-driven demands. IEEE Trans. Power Syst. 35, 3494–3505. doi:10.1109/tpwrs.2020.2979032

CrossRef Full Text | Google Scholar

Pallonetto, F., De Rosa, M., Milano, F., and Finn, D. P. (2019). Demand response algorithms for smart-grid ready residential buildings using machine learning models. Appl. energy 239, 1265–1282. doi:10.1016/j.apenergy.2019.02.020

CrossRef Full Text | Google Scholar

Pamir,, , Javaid, N., Qasim, U., Yahaya, A. S., Alkhammash, E. H., and Hadjouni, M. (2022). Non-technical losses detection using autoencoder and bidirectional gated recurrent unit to secure smart grids. IEEE Access 10, 56863–56875. doi:10.1109/access.2022.3171229

CrossRef Full Text | Google Scholar

Pang, S., and Gao, L. (2022). Multihead attention mechanism guided convlstm for pixel-level segmentation of ocean remote sensing images. Multimedia Tools Appl. 81, 24627–24643. doi:10.1007/s11042-022-12849-5

CrossRef Full Text | Google Scholar

Pawar, P., and Vittal K, P. (2019). Design and development of advanced smart energy management system integrated with iot framework in smart grid environment. J. Energy Storage 25, 100846. doi:10.1016/j.est.2019.100846

CrossRef Full Text | Google Scholar

Rahmani, E., Mohammadi, S., Zadehbagheri, M., and Kiani, M. (2023). Probabilistic reliability management of energy storage systems in connected/islanding microgrids with renewable energy. Electr. Power Syst. Res. 214, 108891. doi:10.1016/j.epsr.2022.108891

CrossRef Full Text | Google Scholar

Rangel-Martinez, D., Nigam, K., and Ricardez-Sandoval, L. A. (2021). Machine learning on sustainable energy: A review and outlook on renewable energy systems, catalysis, smart grid and energy storage. Chem. Eng. Res. Des. 174, 414–441. doi:10.1016/j.cherd.2021.08.013

CrossRef Full Text | Google Scholar

Rathor, S. K., and Saxena, D. (2020). Energy management system for smart grid: an overview and key issues. Int. J. Energy Res. 44, 4067–4109. doi:10.1002/er.4883

CrossRef Full Text | Google Scholar

Roy, C., and Das, D. K. (2021). A hybrid genetic algorithm (ga)–particle swarm optimization (pso) algorithm for demand side management in smart grid considering wind power for cost optimization. Sadhana 46, 101. doi:10.1007/s12046-021-01626-z

CrossRef Full Text | Google Scholar

Singh, N., Singh, S., and Houssein, E. H. (2022). Hybridizing salp swarm algorithm with particle swarm optimization algorithm for recent optimization functions. Evol. Intell. 15, 23–56. doi:10.1007/s12065-020-00486-6

CrossRef Full Text | Google Scholar

Tan, K. M., Babu, T. S., Ramachandaramurthy, V. K., Kasinathan, P., Solanki, S. G., and Raveendran, S. K. (2021). Empowering smart grid: A comprehensive review of energy storage technology and application with renewable energy integration. J. Energy Storage 39, 102591. doi:10.1016/j.est.2021.102591

CrossRef Full Text | Google Scholar

Tian, S., Li, W., Ning, X., Ran, H., Qin, H., and Tiwari, P. (2023). Continuous transfer of neural network representational similarity for incremental learning. Neurocomputing 545, 126300. doi:10.1016/j.neucom.2023.126300

CrossRef Full Text | Google Scholar

Ullah, A., Javaid, N., Samuel, O., Imran, M., and Shoaib, M. (2020). “Cnn and gru based deep neural network for electricity theft detection to secure smart grid,” in 2020 international wireless communications and mobile computing (IWCMC) (IEEE), 1598–1602.

CrossRef Full Text | Google Scholar

Wang, C., Wang, X., Zhang, J., Zhang, L., Bai, X., Ning, X., et al. (2022a). Uncertainty estimation for stereo matching based on evidential deep learning. Pattern Recognit. 124, 108498. doi:10.1016/j.patcog.2021.108498

CrossRef Full Text | Google Scholar

Wang, L., Hu, K., Zhang, Y., and Cao, S. (2019). Factor graph model based user profile matching across social networks. IEEE Access 7, 152429–152442. doi:10.1109/access.2019.2948073

CrossRef Full Text | Google Scholar

Wang, L., Zhang, Y., and Hu, K. (2022b). Feui: F usion e mbedding for u ser i dentification across social networks. Appl. Intell. 52, 8209–8225. doi:10.1007/s10489-021-02716-5

CrossRef Full Text | Google Scholar

Wang, Y., Zhang, Z., Ma, J., and Jin, Q. (2021). Kfrnn: an effective false data injection attack detection in smart grid based on kalman filter and recurrent neural network. IEEE Internet Things J. 9, 6893–6904. doi:10.1109/jiot.2021.3113900

CrossRef Full Text | Google Scholar

Wu, G., Ning, X., Hou, L., He, F., Zhang, H., and Shankar, A. (2023). Three-dimensional softmax mechanism guided bidirectional gru networks for hyperspectral remote sensing image classification. Signal Process. 212, 109151. doi:10.1016/j.sigpro.2023.109151

CrossRef Full Text | Google Scholar

Zheng, S., Shahzad, M., Asif, H. M., Gao, J., and Muqeet, H. A. (2023). Advanced optimizer for maximum power point tracking of photovoltaic systems in smart grid: A roadmap towards clean energy technologies. Renew. Energy 206, 1326–1335. doi:10.1016/j.renene.2023.01.023

CrossRef Full Text | Google Scholar

Zhibin, Z., Liping, S., and Xuan, C. (2019). Labeled box-particle cphd filter for multiple extended targets tracking. J. Syst. Eng. Electron. 30, 57–67. doi:10.21629/JSEE.2019.01.06

CrossRef Full Text | Google Scholar