- 1Key Laboratory of Low-Grade Energy Utilization Technologies and Systems, Ministry of Education, Chongqing University, Chongqing, China
- 2Department of Nuclear Engineering and Technology, Chongqing University, Chongqing, China
- 3Postdoctoral Station of Power Engineering and Engineering Thermophysics, Chongqing University, Chongqing, China
- 4Nuclear Power Institute of China, Chengdu, China
In fusion reactors, many blanket concepts are designed with water as a coolant to transfer high-density heat from the fusion reaction out of the reactor core. The coolant temperature and pressure are maintained as the validated use in water-cooled fission reactors. However, the flow channel in a water-cooled blanket is independent of each other, and there is no flow mixing between coolant channels. Therefore, flow instability may occur in the independent parallel channels in a water-cooled blanket due to its unique structure and heat distribution, especially under the high heat flux caused by plasma rupture. In this study, the parametric analysis of density wave instability is performed using a thermal-hydraulic code developed for independent parallel channels based on the homogeneous model for the two-phase flow. The parallel-channel system in a water-cooled ceramic breeder (WCCB) blanket of the China Fusion Engineering Experimental Reactor (CFETR) is established for its first wall structure. A small disturbance is introduced into the system to determine if it is stable under different conditions. It is found that the channel number has no obvious influence on the prediction of the flow instability boundary. Therefore, the two-channel system is adopted to investigate the influence of different parameters, such as the pressure, resistance, flow rate, and inclination, on the flow instability boundary of the parallel-channel system in the CFETR WCCB blanket. The results show that flow instability occurs more easily in this study compared to the traditional instability analysis, especially under high-pressure conditions. In general, conditions of high pressure, large flow rate, and no inclination can stabilize the system, while the influence of resistance is quite different under different conditions of resistance and pressure. The research work indicates that more attention should be paid to the joint influence of different parameters for the water-cooled blanket during its design and operation.
1 Introduction
In a fusion reactor, a blanket is used for tritium breeding, heat extraction, and radiation shielding (Zhuang et al., 2019). Water is adopted as the main coolant for many blanket concepts during their design stage (Jiang et al., 2016; Pavel and Slavomir, 2019; Liu S. L. et al., 2022) due to its validated widespread use, especially in nuclear fission reactors. The coolant working condition is mostly maintained at the same conditions as in a pressurized water reactor (PWR), in which the pressure is 15.5 MPa and the temperature is 290°C/330°C. However, under certain circumstances, the coolant undergoes a two-phase flow due to insufficient heat transfer capability compared to the large heat load introduced by plasma rupture. Unlike the open channel in the reactor core of a PWR, there is no flow mixing in the parallel channel of a fusion blanket because the flow channel is independent of each other. Therefore, flow instability occurs more easily between these channels (Tian et al., 2020). Due to the existence of manifold isolating channels from the external system, the flow rate may oscillate between parallel channels even if the pressure drop in the adjacent manifolds does not change. It is difficult to detect the flow instability because there is no obvious signal out of the manifold, which is a potential danger for the blanket, especially for the first wall facing the extreme-temperature plasma. The water coolant in the unique U-shaped channel of the first wall is heated along all the channels. The geometry structure and the heating condition should be considered carefully during the flow instability analysis for the parallel-channel system in the blanket. Density wave instability is one of the most common types of two-phase instabilities (Ruspini et al., 2014). Therefore, it is necessary to investigate the influence of different parameters on the density wave instability in a water-cooled blanket to avoid potential damage.
Recently, the analysis of thermally induced instability in a water-cooled blanket has been performed by some researchers. It is found that flow excursion and flow oscillation may occur in the parallel-channel system in a blanket under different working conditions (Lian et al., 2019). However, compared to the BWR condition with a pressure of 7MPa, flow excursion could disappear for the PWR condition of 15.5 MPa. The two-phase flow instability after the loss of coolant accident (LOCA) is investigated for a water-cooled blanket (Wang et al., 2020). For the small-break LOCA, flow instability occurs, while there is no flow instability phenomenon under large-break LOCA because the system pressure decreases instantaneously. The influence of the opposite flow direction in adjacent channels on the instability of flow excursion and flow oscillation is investigated for the 4-channel system in a water-cooled blanket (Liu Z. H. et al., 2022). Flow excursion, in-phase density wave oscillation, and out-phase density wave oscillation are found to occur in the parallel channels. The relative stability with the condition of the opposite flow direction depends mainly on the operating point of the system. More stability analyses are carried out for fission reactor core channels. Experimental results of two-phase instability in parallel twin channels are compared to the calculation of RELAP5 under a low pressure of 1–3 MPa (Guo et al., 2010). The comparison shows that the non-homogeneous, non-equilibrium model is accurate to simulate the flow instability phenomenon in parallel channels. The code is also used to perform a parametric study of two-phase flow instabilities in 1–2–4–9 channels (Xia et al., 2012). The influences of various parameters are obtained by changing the simulation condition. The capability of RELAP5 to predict the density wave instability in parallel channels is also ascertained by the comparison with experimental results (Ambrosini and Ferreri, 2006; Colombo et al., 2012). However, RELAP5 may not be suitable for the analysis of narrow rectangular channels (Lian et al., 2018).
Although the homogeneous model is not suitable for predicting the bubble behavior in the two-phase flow (Papoulias et al., 2021), it is usually used to describe systematic phenomena, such as flow instability (Ruspini et al., 2014). The instability of the parallel-channel system in a water-cooled blanket is influenced by many factors. The parametric research in this study is performed to enrich the understanding of flow instability in a blanket. The first wall in a water-cooled ceramic breeder (WCCB) blanket of the China Fusion Engineering Experimental Reactor (CFETR) is chosen as the research object. The unique working condition of the geometry structure and heat distribution in a blanket is considered in the developed parallel-channel instability analysis model. The small-disturbance method is adopted to determine if the system is stable by the brief power increase introduced into one channel. After the validation of the analysis method, the two-channel system is adopted to investigate the influence of different parameters, such as the pressure, resistance, flow rate, and inclination, on the flow instability boundary of the parallel-channel system in the CFETR WCCB blanket. The results show that the joint influence of different factors of the water-cooled blanket requires further research.
2 Theoretical model
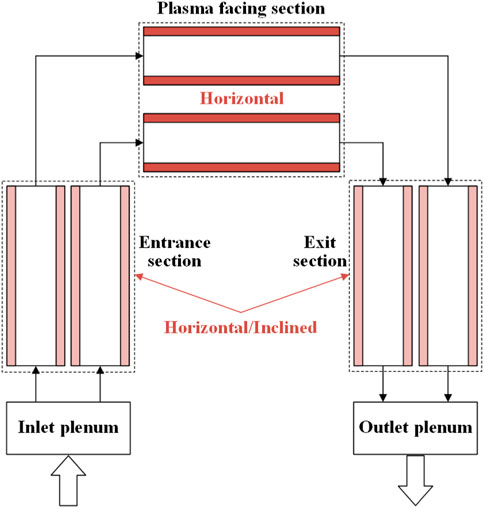
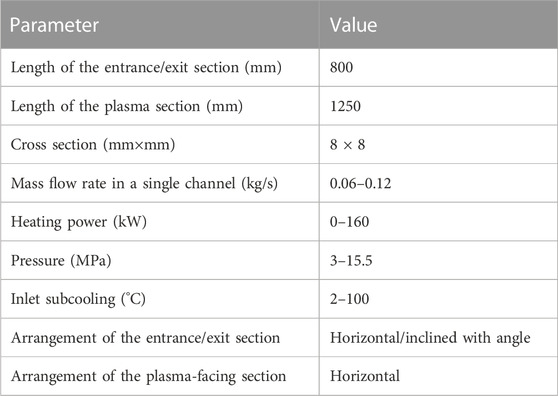
The local phenomenon, such as flow instability, could not be predicted in the systematic safety analysis of the blanket because many parallel channels are simulated as one pipe with the same hydraulic diameter (Lian et al., 2018) to improve the calculation efficiency. In order to investigate the flow instability, the coolant channel in the system should be modeled independently. The thermal-hydraulic model for the parallel channel in the first wall of the water-cooled blanket is shown in Figure 1. It is composed of the inlet plenum, parallel flow channel, and outlet plenum. The fluid is distributed and collected by inlet and outlet plenums, which represent flow manifolds in the blanket. The U-shaped flow channel in the first wall of the water-cooled blanket is heated along all the paths, which is the unique characteristic of the flow channel in the blanket. According to the heating condition of the first wall in the blanket, the U-shaped flow path is divided into an entrance section, a plasma-facing section, and an exit section to simulate the different heating conditions along the channel. The shaded parts in Figure 1 represent the heating condition of different sections. There is only nuclear heat deposition in the entrance and exit sections, while both nuclear heat deposition and high heat flux from plasma are imposed on the plasma-facing section. According to the updated design of the CFETR WCCB blanket, the plasma-facing section is kept horizontal in all blankets, while the entrance and exit sections have some inclined angles for different blanket arrangements. The inclination influence is also considered in this study. The heating power is given with reference to the heat distribution along the radial direction in the blanket (Jiang et al., 2016). It should be pointed out that a maximum of nine parallel-channel systems is investigated in the following study besides the two-channel system shown in Figure 2.
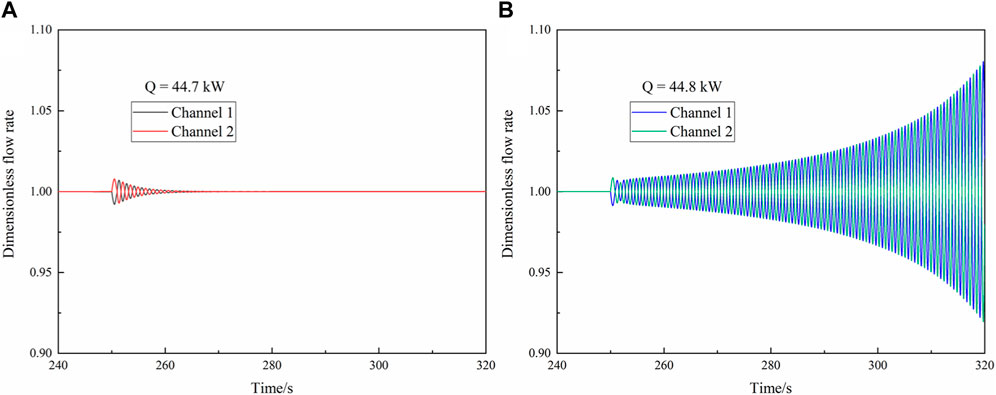
FIGURE 2. Schematic representation of the analysis method to detect (A) convergent and (B) divergent flow oscillations.
The thermal-hydraulic model of the parallel-channel system is established based on the following assumptions: (1) homogeneous two-phase flow; (2) one-dimensional flow; (3) compressible two-phase mixture; (4) thermodynamic equilibrium in two phases; (5) bulk boiling consideration. Then, the governing equation for the one-dimensional homogeneous flow can be derived as follows:
The local fluid density is dependent on the state of pressure and enthalpy:
Substituting the derivative of Eq. 4 into Eqs 1–3, the mass and energy conservation equations can be rearranged as follows:
2.1 Constitutive model
For parallel channels which share the same inlet and outlet plenums, the pressure drop in each channel should be identical:
Under the force flow condition with a constant flow rate, the sum of the flow rate change in each channel equals zero:
The void fraction is ascertained by a correlation proposed by Chexal and Lellouche, as shown in Eq. 9, which is also adopted by other validated codes, such as RELAP5 (U.S. NRC, 2001).
The drift velocity in Eq. 9 is expressed as follows:
where parameters
The single-phase frictional factor is calculated by the Blasius formula (White, 1974):
The two-phase frictional pressure drop is calculated by the Lockhart–Martinelli formula (Lockhart and Martinelli, 1949). The two-phase frictional multiplier is expressed as follows:
where
The local pressure drop caused by flow resistance is calculated by the Darcy correlation (Su et al., 2013):
The gravitational pressure drop in the inclined flow channel is considered by the effective force term in the momentum equation, and the gravitational acceleration along the inclined channel is changed to
where
2.2 Numerical method
The governing equations are discretized into differential equations. Based on the constitutive models introduced in Section 2.1, the ordinary differential equations are solved using the Gear multi-value solver (Gear, 1974), which is quite efficient, considering the stiffness of the equation system. The time step is set as 0.001, the precision is 0.0001, and the error bar is
3 Validation of the analysis method
Analysis of the multi-channel system shows that chaos phenomena may occur in the parallel-channel system (Guo et al., 2008), which means that the channel number could influence the thermal-hydraulic characteristics of the parallel-channel system. Such an effect should be ascertained before the parametric study. The first wall in the blanket faces the high-temperature plasma directly, and the thermal shock attacks the surface if the plasma disrupts. Therefore, the parallel channels in the first wall are chosen for the parametric study. The analysis method used in this work is introduced in detail, and the validation is carried out by comparison to the experimental results.
3.1 Analysis method
A system is recognized as stable if the operating point can be maintained even after a slight disturbance. In this study, a small power disturbance is introduced into the plasma-facing section shown in Figure 1 to find out the threshold of the flow instability. In the design of the CFETR WCCB blanket, one channel in the first wall is allocated with the corresponding heating power of 15–26 kW under the normal heat flux of 0.5 MW/m2 from the plasma (Liu et al., 2022). However, the heat flux will increase dramatically from 0.5 MW/m2 to 5 MW/m2 when plasma disruption happens, which is a conservative assumption in the safety analysis (Guo et al., 2008; Wang et al., 2020; Liu et al., 2022). In addition, even during the steady state, the heat flux from the plasma is not always a constant value. Therefore, the power disturbance on the plasma-facing section is a reasonable choice. After the original state is established with certain thermal-hydraulic parameters, a slight power disturbance of 1% operating power with a 1-s duration is introduced into the plasma-facing section of one channel. Then, the inlet flow of different channels oscillates. The oscillation is of a small amplitude compared to the nominal flow rate and would disappear to maintain the original operation state. Such a system is considered stable. However, the oscillation would be divergent if the system is unstable. The minimum resolution of the operating heating power is set as 0.1 kW. The typical convergent and divergent flow oscillations for the parallel twin-channel system are shown in Figure 2. The system is stable if the heating power is 44.7 kW, while it is unstable for the heating power of 44.8 kW. In this condition, 44.7 kw is considered the threshold heating power of the flow instability.
3.2 Validation
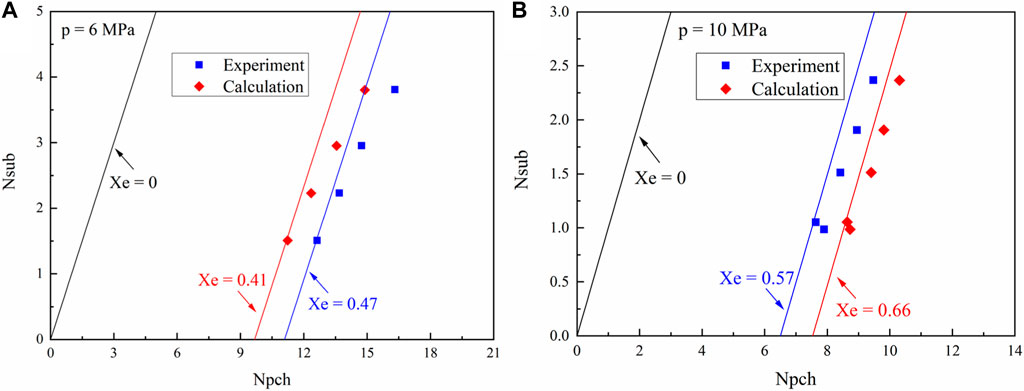
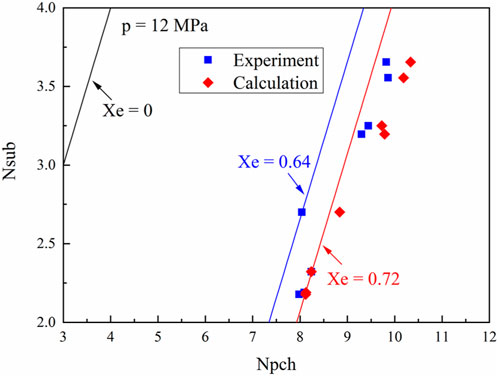
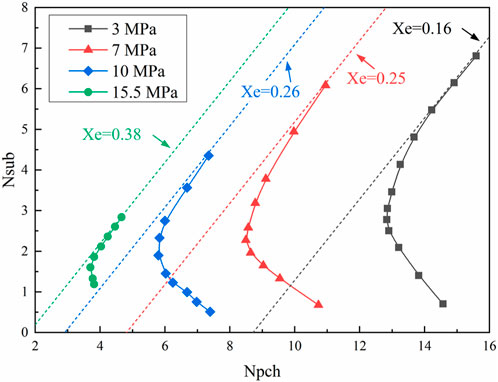
Usually, the validation of calculation should be performed based on the relative experiments. However, such a process is very difficult because there is almost no experimental result of flow instability in long channels for a water-cooled blanket. Therefore, a compromise is made that the analysis method in this study is validated by the comparison to experimental data obtained from vertical channels (Tian et al., 2020). The validation of the analysis method to predict flow instability under different pressures is shown in Figures 3, 4 using the experimental data from vertical channels. The density wave instability is mainly caused by the sufficient interaction and delayed feedback between the compressibility and the flow inertia in the heated channel. When the disturbance propagates along the channel, its speed in the two-phase mixture is much slower than that in the single-phase zone due to the smaller density in the two-phase zone, which leads to delayed feedback between the two zones. Combining the compressibility volume in the two-phase zone, the divergent oscillation between parallel channels can be triggered with sufficient heat input in the system. It can be concluded that in the simulation, the influence of different flow channels on the density wave instability is dominated by the thermal-hydraulic models adopted in the code. Therefore, the thermal-hydraulic model and numerical method described in Section 2 are validated by the experimental data obtained in the vertical channel system.
The calculation results and the experimental data are compared on the stability map represented by the phase change number
The characteristic equation and similarity parameters are derived by Ishii (Tian et al., 2020) to select the nondimensional numbers that could represent the typical stability in a thermal-hydraulic system.
Therefore, the constant quality equals to the slope of an inclined straight line in the stability map under the given pressure (
3.3 Qualification of the channel number
There are many parallel channels in the structure of the first wall. In order to simplify the parametric study of flow instability in the water-cooled blanket, the effect of the number of channels on the prediction of flow instability is also qualified under different pressures, as shown in Figure 5. For all conditions, the difference of threshold heating power between two-channel, four-channel, and nine-channel systems is no larger than 0.5 kW, which leads to the almost overlapped boundaries in the stability map. Such an effect is probably caused by the identical geometrical and thermal-hydraulic parameters in the numerical calculation for different channel numbers. Considering the calculation efficiency, the two-channel system is adopted in the following parametric analysis.
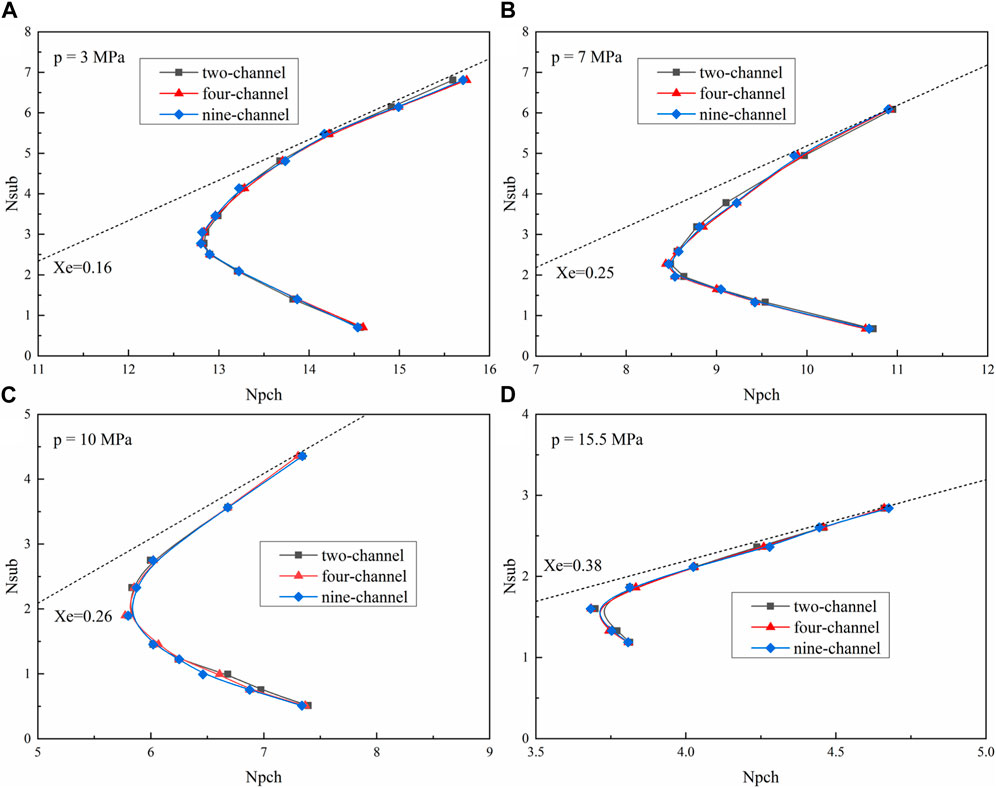
FIGURE 5. Effect of the number of channels on the prediction of flow instability under (A) 3 MPa, (B) 7 MPa, (C) 10 MPa, and (D) 15.5 MPa.
4 Parametric study
The two-channel system shown in Figure 1 is established. The geometrical and thermal-hydraulic parameters in the calculation are given in Table 1. The geometry of the channel is ascertained with reference to the design feature of the CFETR WCCB blanket. The parametric influence of the pressure, resistance, flow rate, and inclination on the flow instability is investigated using the control variable method.
4.1 Influence of pressure
The pressure influence is mainly on the physical properties of the water coolant. The higher the pressure, the larger the density. Then, the propagation of the disturbance is faster under high pressure, which leads to a smaller time lag between the single-phase zone and the two-phase mixture. Therefore, the system is more stable under higher pressure, which is also presented in Figure 6 by the constant quality line on the stability map under different pressures. As the pressure increases from 3 MPa to 15.5 MPa, the threshold quality increases from 0.16 to 0.38, which means that the system becomes more stable. It is noteworthy that the threshold quality under 15.5 MPa is quite lower than the value of 1.36, which was obtained in a similar instability analysis (Lian et al., 2019), where the heating power along the entrance and exit sections was not considered. The comparison shows that the heating power along all the flow paths has an obvious destabilizing effect on the parallel-channel system in the water-cooled blanket. Therefore, the heat distribution in the blanket should not be ignored in the flow instability analysis. Such an effect could also be observed for the threshold quality of 0.25 under 7 MPa compared to the value of 0.56 under the BWR condition of 7 MPa reported in Lian et al. (2019). The destabilizing effect is mainly caused by the distribution change of single-phase water and two-phase mixture. The longer two-phase zone in the blanket channel could enlarge the time lag effect, which results in the flow instability occurring earlier with a lower heating power.
4.2 Influence of inclination
The blankets along the poloidal direction in CFETR form a D-shaped chamber in which the plasma fusion produces energy. Although the plasma-facing section of the first wall is maintained horizontally in all blankets according to the design feature of the CFETR WCCB blanket (Liu et al., 2022), the entrance and exit sections incline with a certain angle based on the installation location of the blanket. The inclined angle in this study is assumed between −90° and +45° with reference to the blanket arrangement in CFETR.
Due to the structure of the water-cooled blanket, the entrance and exit sections are inclined, while the plasma-facing section is always horizontal. The influence of inclination in such a unique structure is quite different from that for the inclined channel in most research studies, in which the whole channel is inclined with some angle. The inclination of entrance and exit sections can influence the distribution of pressure drop in the single-phase zone and two-phase mixture. If the entrance and exit sections are all horizontal, the flow instability is dominated by the frictional pressure drop, which is usually out-phase with the inlet flow rate (Tian et al., 2020). On the other hand, if the entrance and exit sections are inclined, the gravitational pressure drop plays a more important role than that with the horizontal entrance and exit sections. In general, the relative magnitude of in-phase and out-phase pressure drop along all the channels, including the horizontal plasma-facing section, dominates the stability characteristics of the system with inclined entrance and exit sections. The detailed influence is shown in Figure 7 under different pressures. Under the relatively low pressure of 3 MPa and 7 MPa, the inclination of entrance and exit sections makes the parallel-channel system more unstable since the boundary in the stability map moves toward the left, which means that the flow instability occurs under lower quality. However, under the relatively high pressure of 10 MPa and 15.5 MPa, the influence of inclination is more complicated. In the high subcooling region, the inclination has a similar destabilizing effect on the system, while in the low subcooling region, some inclination conditions stabilize the system. From the point of view of the conservative estimate, the inclination could be considered a disadvantageous factor for the stability of the parallel-channel system in the water-cooled blanket. Under the designed operation condition with the pressure of 15.5 MPa, the threshold quality is reduced from 0.38 to 0.3 with the inclined angle of −90°, which validates that the joint influence of inclination and heating distribution along all the flow paths makes the system more unstable even under the high pressure of 15.5 MPa.
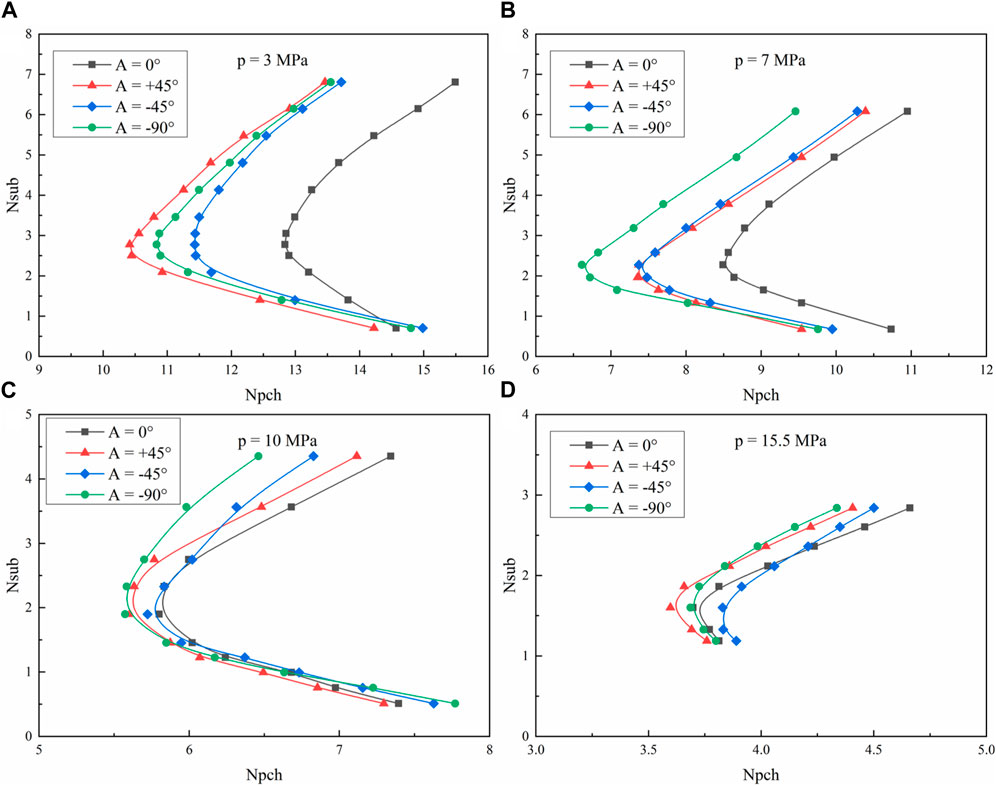
FIGURE 7. Influence of inclination on the flow instability boundary under (A) 3 MPa, (B) 7 MPa, (C) 10 MPa, and (D) 15.5 MPa.
4.3 Influence of resistance
For the design of the first wall of the CFETR WCCB blanket, approximately 95 channels are connected to the inlet and outlet manifolds. The flow area deference between the flow channel and manifolds is large enough to generate a concentrated form loss when the fluid flows through the junction. Since the inlet and outlet of the flow channel are almost the same, the inlet and outlet resistances are considered by changing the inlet and outlet resistance coefficients simultaneously. The resistance coefficients are assumed to be 0–40 to perform the parametric analysis of flow instability.
Due to the time lag of void propagation in the two-phase mixture, the inlet flow and outlet flow rates are not synchronous after the disturbance. It is widely accepted that the inlet resistance stabilizes the parallel-channel system, while the outlet resistance has the opposite function (Colombo et al., 2012; Xia et al., 2012; Lian et al., 2018). This is because the concentrated form pressure drop at the inlet is in-phase with the inlet flow rate, while the outlet form pressure drop is out-phase. The joint influence of inlet and outlet resistances is shown in Figure 8 under different pressures. For most conditions with a pressure of 7–15.5 MPa, the destabilizing effect of outlet resistance plays a dominant role in the stability characteristic of parallel channels in the water-cooled blanket. Under some particular conditions, such as high subcooling with a pressure of 10 MPa, the inlet stabilizing effect is more evident if the resistance coefficient is 5. For the condition with a low pressure of 3 MPa, the system is always more stable compared to that with no resistance at the inlet and outlet. For the nominal operating condition with a pressure of 15.5 MPa, the larger the coefficient, the more unstable the parallel-channel system is due to the destabilizing effect at the outlet. The threshold quality is reduced to 0.2 with the coefficient k = 40, which indicates that the flow instability occurs more easily with the unique geometry structure of the first wall in the WCCB blanket. The uneven resistance for the inlet and outlet is suggested during the design stage to obtain a more stable operating point for the blanket.
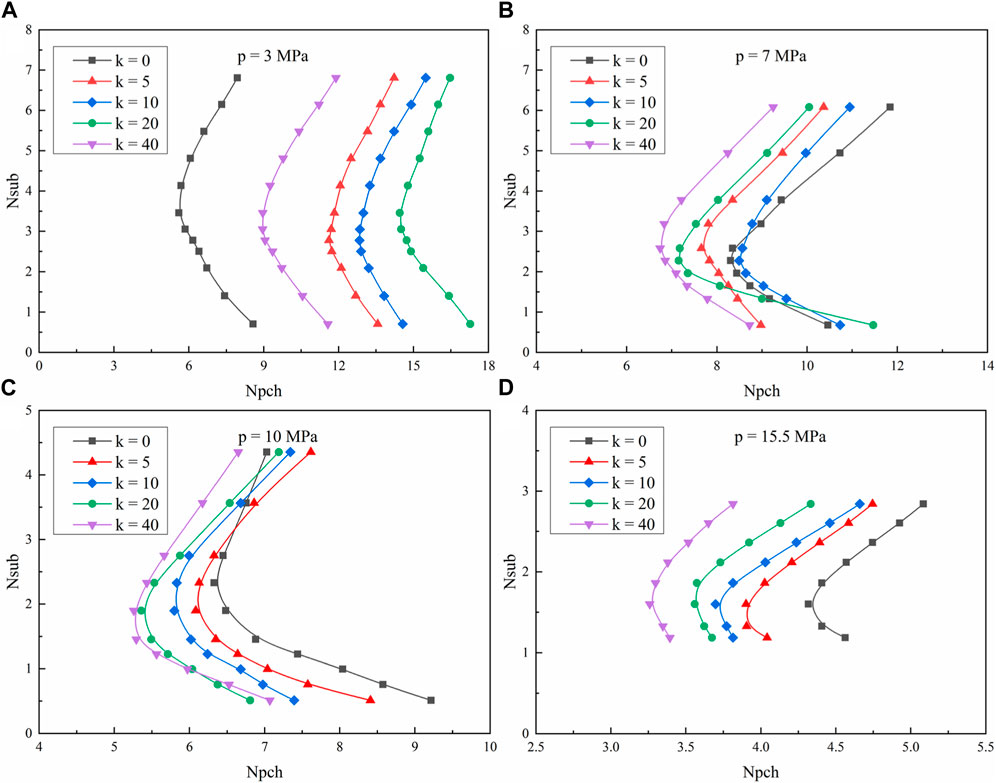
FIGURE 8. Influence of resistance on the flow instability boundary under (A) 3 MPa, (B) 7 MPa, (C) 10 MPa, and (D) 15.5 MPa.
4.4 Influence of the flow rate
CFETR is proposed to operate on different fusion power levels from 200 MW to 1.5 GW. Correspondingly, the flow rate in the first wall of the WCCB blanket is adjusted from 0.06 kg/s to 0.12 kg/s to cool down the first wall with the demand temperature of 285°C/325°C. The influence of the flow rate on the instability of the parallel-channel system is clear. The large flow rate means the relatively long single-phase region in the channel, and the time lag of void propagation in the two-phase zone reduces, which has a stabilizing effect on the system. The detailed influence of the flow rate is shown in Figure 9 under different pressures. It is found that under all the conditions, the system is the most stable with a flow rate of 0.12 kg/s in the channel, while its stability is the worst if the flow rate is 0.06 kg/s. It is believed that if the flow rate is large enough, there will be no two-phase flow instability in the parallel-channel system even with the high-density heating power on the plasma-facing section. The ratio of the two-phase region reduces, and the small effect of time lag could not trigger the flow instability. For the nominal operating condition with a pressure of 15.5 MPa, the threshold quality reduced to 0.24 with a flow rate of 0.06 kg/s in the channel. The destabilizing effect of a low flow rate could not be eliminated for the system, which is of practical interest for the operation of the blanket.
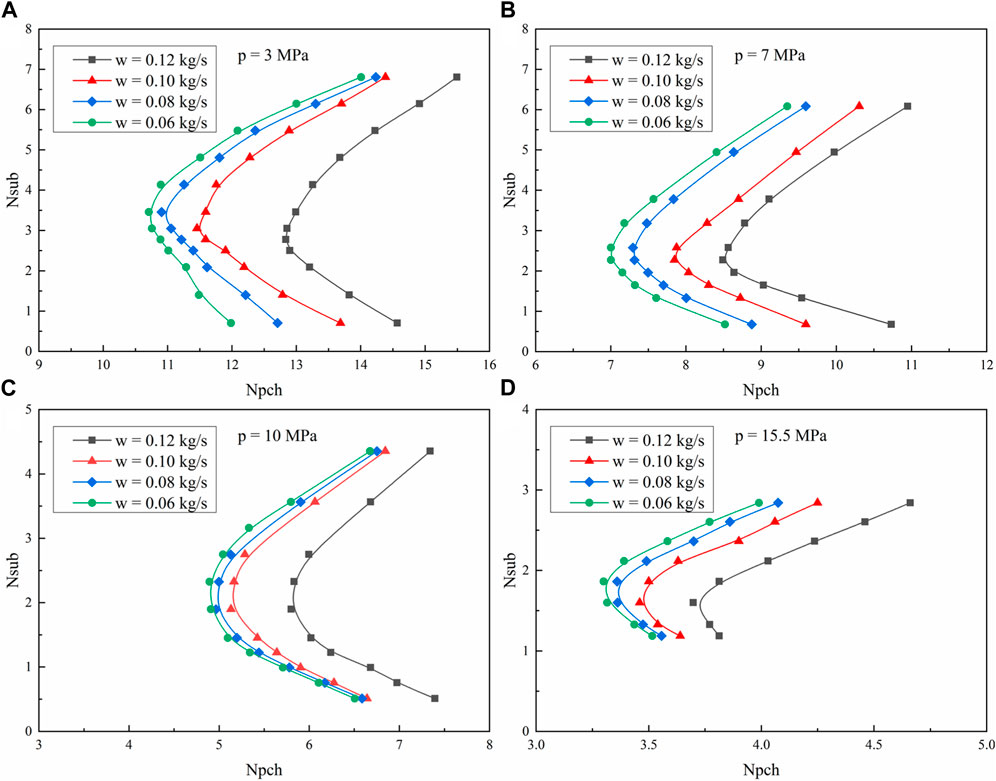
FIGURE 9. Influence of the flow rate on the flow instability boundary under (A) 3 MPa, (B) 7 MPa, (C) 10 MPa, and (D) 15.5 MPa.
5 Conclusion
In this study, the parametric influence of different factors on the density wave instability in a water-cooled blanket has been investigated using the thermal-hydraulic model developed for the parallel-channel system. The geometrical structure and operating conditions are ascertained with reference to the design feature of the CFETR WCCB blanket. The method of slight power disturbance on the plasma-facing section of the first wall is used to determine if the system could maintain its original operating point. The parametric study is performed for pressure, resistance, flow rate, and inclination. The main conclusions are summarized as follows:
(1) If the geometrical and thermal-hydraulic parameters in parallel channels are all identical in the calculation, the influence of the number of channels on the prediction of flow instability could be neglected for the high efficiency of calculation. The difference of threshold heating power between two-channel, four-channel, and nine-channel systems is no larger than 0.5 kW.
(2) Considering the unique geometry structure and heating distribution in a water-cooled blanket, the flow instability occurs more easily in parallel channels with heating power along all the flow paths compared to the analysis only considering the heating effect of the plasma-facing section. The destabilizing effect is caused by the enlarged ratio of the two-phase zone with an increase in time lag. Therefore, detailed modeling is more reliable, considering the unique characteristics of the water-cooled blanket structure.
(3) The influence of pressure and flow rate on the flow instability in the parallel-channel system of the water-cooled blanket is similar to that in the traditional vertical channel system. The system is more stable with the higher pressure and larger flow rate, which could reduce the time lag effect in the two-phase zone in the channel.
(4) The influence of the inclination of entrance and exit sections is quite complicated under different pressures. The changed pressure drop distribution dominates the stability characteristics of the system. In general, the inclination could be considered a disadvantageous factor for the system stability from the perspective of a conservative estimate.
(5) The joint influence of even resistance at the inlet and outlet of the flow channel should be evaluated specifically under different pressures. For a system with a pressure of 3 MPa, it has a stabilizing effect, while for conditions with other pressure values, the destabilizing effect is more evident. The uneven resistance for the inlet and outlet is suggested during the design stage of the water-cooled blanket.
The unified regularity of influence for different parameters on the flow instability in the water-cooled blanket could not be obtained. Therefore, the specific stability analysis should be carried out during the design of different modules of the water-cooled blanket. To design the blanket with enough margin to avoid the occurrence of flow instability, some blanket features need to be optimized, such as the inlet and outlet resistances. A detailed stability analysis should be performed for other structures of the water-cooled blanket besides the first wall. The influence of the transient process of rapid heat loading for plasma breakdown should be investigated in future works to avoid the potential danger for the blanket’s first wall from flow oscillation between the parallel channels.
Data availability statement
The datasets presented in this article are not readily available because the authors do not have permission to share data. Requests to access the datasets should be directed to bGlhbmdpYW5nMTIzNThAZm94bWFpbC5jb20=.
Author contributions
QL: validation, formal analysis, writing—original draft, and methodology. YL: validation. HL: validation. ST: writing—original draft. LZ: formal analysis and validation. ZM: formal analysis and validation. WS: formal analysis. All authors contributed to the article and approved the submitted version.
Funding
This work was supported by a grant from the China Postdoctoral Science Foundation (No. 2022M720563).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ambrosini, W., and Ferreri, J. C. “Analysis of basic phenomena in boiling channel instabilities with different flow models and numerical schemes,” in Proceedings of the 14th International Conference on Nuclear Engineering (ICONE 14), Miami, FL, USA, July 2006.
Chexal, B., Merilo, M., Maulbetsch, J., Horowitz, J., Harrison, J., Westacott, J., et al. (1997). Void fraction technology for design and analysis Tech. rep., Washington, DC, United States: Electric Power Research Institute.
Colombo, M., Cammi, A., Papini, D., and Ricotti, M. E. (2012). RELAP5/MOD3.3 study on density wave instabilities in single channel and two parallel channels. Progr. Nucl. Energy 52, 15–23. doi:10.1016/j.pnucene.2011.12.002
Gear, A. C. (1974). Ordinary differential equation system solver. Livermore, CA, United States: Lawrence Livermore Laboratory.
Guo, Y., Huang, J., Xia, G. L., and Zeng, H. (2010). Experiment investigation on two-phase flow instability in a parallel twin-channel system. Ann. Nucl. Energy 37, 1281–1289. doi:10.1016/j.anucene.2010.05.021
Guo, Y., Qiu, S. Z., Su, G. H., and Jia, D. (2008). Theoretical investigations on two-phase flow instability in parallel multichannel system. Ann. Nucl. Energy 35, 665–676. doi:10.1016/j.anucene.2007.08.006
Jiang, K. C., Ma, X. B., Cheng, X. M., Lin, S., Huang, K., and Liu, S. (2016). Thermal-hydraulic analysis on the whole module of water cooled ceramic breeder blanket for CFETR. Fusion Eng. Des. 112, 81–88. doi:10.1016/j.fusengdes.2016.07.027
Lian, Q., Tian, W. X., Gao, X. L., Qiu, S., and Su, G. (2019). Study of flow instability in parallel channel system for water cooled blanket. Fusion Eng. Des. 148, 111291. doi:10.1016/j.fusengdes.2019.111291
Lian, Q., Tian, W. X., Qiu, S. Z., and Su, G. (2018). Improvement of RELAP5 code for density wave instability analysis in parallel narrow rectangular channels. Ann. Nucl. Energy 122, 241–255. doi:10.1016/j.anucene.2018.08.049
Liu, S. L., Chen, L., Ma, X. B., Cheng, X., Lu, P., Lei, M., et al. (2022b). Design of the water-cooled ceramic breeder blanket for CFETR. Fusion Eng. Des. 177, 113059. doi:10.1016/j.fusengdes.2022.113059
Liu, Z. H., Bai, T. Z., Peng, C. H., Bao, H., and Lu, J. (2022a). Research of flow instabilities in parallel channels with opposite flow directions for WCCB blankets. Ann. Nucl. Energy 169, 108964. doi:10.1016/j.anucene.2021.108964
Lockhart, R. W., and Martinelli, R. C. (1949). Proposed correlation of data for isothermal two phase, two-component flow in pipes. Chem. Eng. Prog. 45, 39–48.
Papoulias, D., Vichansky, A., and Tandon, M. (2021). Multi-fluid modelling of bubbly channel flows with an adaptive multigroup population balance method. Exp. Comput. Multiph. Flow 3, 171–185. doi:10.1007/s42757-020-0084-5
Pavel, Z., and Slavomir, E. (2019). High heat flux limits of the fusion reactor water-cooled first wall. Nucl. Eng. Technol. 51, 1251–1260. doi:10.1016/j.net.2019.03.013
Ruspini, L. C., Marcel, C. P., and Clausse, A. (2014). Two-phase flow instabilities: A review. Int. J. Heat. Mass Transf. 71, 521–548. doi:10.1016/j.ijheatmasstransfer.2013.12.047
Su, G. H., Qiu, S. Z., and Tian, W. X. (2013). The thermal-hydraulic calculation method for nuclear power system. Beijing, China: Tsinghua University Press, 17–37.
Tian, W. X., Lian, Q., Qiu, S. Z., and Su, G. (2020). Research of two-phase density wave instability in reactor core channels with rolling motion. Int. J. Energy Res. 44, 7323–7341. doi:10.1002/er.5444
U.S. NRC (2001). Nuclear safety analysis division RELAP5/mod3.3 code manual. https://www.nrc.gov/docs/ML1103/ML110330252.pdf.
Wang, D. L., Peng, C. H., and Guo, Y. (2020). The flow instability phenomenon in the loss of coolant accident of the water cooled blanket. Fusion Eng. Des. 160, 111979. doi:10.1016/j.fusengdes.2020.111979
Xia, G. L., Peng, M. J., and Guo, Y. (2012). Research of two-phase flow instability in parallel narrow multi-channel system. Ann. Nucl. Energy 48, 1–16. doi:10.1016/j.anucene.2012.05.014
Zhuang, G., Li, G. Q., Li, J., Wan, Y., Liu, Y., Wang, X., et al. (2019). Progress of the CFETR design. Nucl. Fusion 59, 112010. doi:10.1088/1741-4326/ab0e27
Nomenclature
Keywords: flow instability, parallel channels, water-cooled blanket, fusion reactor, parametric analysis
Citation: Lian Q, Liang Y, Liao H, Tang S, Zhang L, Ma Z and Sun W (2023) Parametric study of density wave instability in parallel channels of a water-cooled blanket in a fusion reactor. Front. Energy Res. 11:1251233. doi: 10.3389/fenrg.2023.1251233
Received: 01 July 2023; Accepted: 18 August 2023;
Published: 05 September 2023.
Edited by:
Wei Ding, Helmholtz Association of German Research Centres (HZ), GermanyCopyright © 2023 Lian, Liang, Liao, Tang, Zhang, Ma and Sun. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qiang Lian, bGlhbnFAY3F1LmVkdS5jbg==
 Qiang Lian
Qiang Lian Yu Liang4
Yu Liang4