
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 25 September 2023
Sec. Smart Grids
Volume 11 - 2023 | https://doi.org/10.3389/fenrg.2023.1249782
The information monitoring of distribution networks usually relies on multiple measurement systems, and the placement and number of measurement configurations are also restricted by objective factors. It is highly likely that insufficient measurements will affect the parameter estimation of distribution lines. To deal with the aforementioned issue, this paper establishes the measurement equations for static parameters of distribution lines and proposes a method of parameter estimation based on the elitist searching approach. Aiming at different measurement conditions, the testability analysis method is introduced to distinguish clear parameters and uncertain parameters of distribution lines. For the constructed line parameter samples, the estimated values of line parameters are calculated with the consideration of multi-source effective measurement data at different time points. Moreover, the indices of relative errors between the sample values and the estimated values are used to judge the testability of static parameters of distribution lines. The case study on IEEE 33 bus distribution system analyzes the application scenarios with and without measurement errors. The simulation results show that the testability analysis method can effectively identify whether the parameters to be estimated are clear or not, and then the estimated values of clear parameters and the bounds of some disturbing uncertain parameters can be estimated accurately to provide certain decision support for engineering applications.
In recent years, the operation of distribution networks has turned into a more complex process. The integration of distributed power generations and controllable loads, like electric vehicles, into distribution networks has transformed traditional passive distribution networks into active networks (Lefebvre et al., 2014; Ma et al., 2022), which presents new challenges to the safety and reliability for the operation of distribution networks. The transition puts forward higher requirements for the advanced measurement system in distribution networks and advanced applications of the distribution management system such as state estimation (Deshmukh et al., 2014).
The accuracy of line parameters in a distribution network is the foundation of various analyses and calculations in the distribution management system (Deshmukh et al., 2014; Xue et al., 2019). However, reasons such as line aging or faults lead to a certain difference between the static parameters of distribution lines and the values of design parameters, which affects the credibility of online or offline calculations in the system. Therefore, it is necessary to estimate the line parameters of distribution networks according to the available measurement information. It is worth noting that although there are some relatively mature methods to obtain the parameters of high-voltage lines in transmission networks, including theoretical calculation, traditional live line measurement and online parameter estimation (Du and Liao, 2012; Rezaei et al., 2022). However, there exist few relevant research studies on the parameter identification of distribution lines because the real-time monitoring devices in distribution networks are less than those in transmission networks. As a result, the information monitoring system in distribution networks has gradually received considerable attention.
At present, various types of measurement devices have supplied key data information for the operation and control of the distribution network. The traditional method of information collection is to obtain measurement data using the supervisory control and data acquisition (SCADA) system (Gómez-Expósito et al., 2015). With the widespread application of the wide-area measurement system (WAMS), the data collection system, which takes synchronous phasor measurement units (PMUs) as the primary measurement units, can provide measurement data with accurate time scales and phase angles (Von Meier et al., 2017). However, a relatively small number of PMUs are configured in practical engineering applications because of multiple factors. Therefore, line monitoring and identification based on measurement information from the SCADA system and PMUs have become the mainstream of current research studies and applications. A number of achievements have been made in the accurate identification of lines under different measurement conditions (Pegoraro et al., 2019; Xue et al., 2019; Li et al., 2022), line aging assessment based on parameter estimation (Wu et al., 2022), and parameter estimation of three-phase imbalance lines (Das, 2011; Dutta et al., 2021). Xue et al. (2019) presented a three-phase π-type equivalent model based on the phase component description to identify impedance and admittance parameters of non-symmetrical operation lines by the voltage phasor and current phasor at both sides of distribution lines, and a median estimation-based robust method is selected to achieve robust identification of the lines. A weighted least square method considering the system measurement error was introduced in Pegoraro et al. (2019), which utilizes PMU measurement information to estimate multiple impedance parameters of multiple branches in the distribution network. In the absence of the measurement data of T-connection nodes, Li et al. (2022) made use of differential evolution algorithm to realize the accurate identification of distribution lines according to the measurement data from the SCADA system and micro-PMU (μPMU). Wu et al. (2022) achieved the topology verification and parameter estimation of the distribution system on account of the measured information of power and voltage amplitude and analyzed the deviation between the calculated line parameters and the theoretical values to quantify the severity of line aging. Without considering the phasor measurement information, an approach for identifying the resistance and reactance parameters of unbalanced three-phase feeder lines based on the measured data of node voltage and power was proposed in Das (2011). Dutta et al. (2021) improved the non-linear least squares method for parameter estimation of three-phase untransposed distribution lines under the condition that only voltage amplitude and power data were available from the remote terminal units (RTUs) which are connected to substations.
With the development of intelligent distribution networks, advanced metering infrastructure (AMI) has gradually become an important source of measurement data for distribution networks (Luan et al., 2015). AMI is an information network system that utilizes smart meters distributed in the distribution network to collect voltage, current, power, and other data from users. By measuring, summarizing, storing, calculating, and mining the power consumption information on the consumer’s side, the real-time or quasi real-time analysis of electricity demand characteristics can be achieved, and the demand-side management can be carried out. Xiong et al. (2022) established an impedance model of three-phase four-wire low-voltage distribution lines and calculated the impedance parameters of lines on the basis of the given topology and the finite scalar data, which are provided by smart meters of AMI. In view of the limited measurement data of smart meters, (Zhang et al. 2020) and (Liu et al. 2023) highlighted the method that can effectively identify network topology and line parameters when the measurement errors are taken into account. Srinivas and Wu (2022) obtained the measured data from smart meters and μPMU and proposed a novel approach to identify the network topology and line parameters using the unscented Kalman filter method and Newton–Raphson method. Moreover, the influence of measurement noise was analyzed to quantify the acceptable measurement errors.
Considering the technical and economic conditions in the actual operation of the distribution network, the type, quantity, and location of measurement devices are limited, and the obtained measurement information in the distribution network often comes from multiple measurement systems. It is highly likely that the measurement information of the distribution network will be insufficient due to objective reasons, which will result in the inability to uniquely determine all static parameters based on the obtained measurement data. Therefore, it is necessary to evaluate the testability of static parameters of distribution lines under given measurement conditions to effectively identify which line parameters can be uniquely determined and those cannot be (Liu et al., 2022a).
In view of the aforementioned discussion, this paper conducts a study on the static parameter estimation of distribution lines and its testability analysis based on multi-source measurement information. According to the voltage, current, and power data collected by distribution automation terminals in the SCADA system and the voltage phasor and current phasor collected by μPMUs configured at key nodes at different time points, the measurement equations of distribution lines are established, and the elitist searching approach is adopted to solve the value of line parameters. Considering the insufficient measurement information due to the lack of measurement devices in practical engineering applications, the testability analysis method based on Monte Carlo simulation is improved to achieve the automatic discrimination for clear and uncertain parameters of distribution lines. The values of clear parameters can be estimated as the foundation of advanced applications in the distribution management system. In addition, some line parameters are identified as uncertain parameters because of the measurement errors rather than measurement configuration, and thus the confidence interval of these disturbing uncertain parameters can be obtained, which is also meaningful in applications. The effectiveness of the proposed principle and method is demonstrated based on the IEEE 33 bus system, and the mean value and standard deviation of relative errors can be calculated and are used to identify clear line parameters. The distribution line parameters are solved accurately based on the elitist searching approach. Meanwhile, the bounds of some uncertain parameters are determined according to the calculation of the uncertainty degree.
The remainder of this paper is organized as follows: Section 2 analyzes the measurement equations for distribution lines, and then the elitist searching approach is adopted to solve the parameter estimation model to obtain the parameter values of distribution lines. In Section 3, the process of testability analysis of line parameters based on Monte Carlo simulation is described in detail to effectively identify whether the parameters to be estimated can be uniquely determined. The simulation results of the IEEE 33 bus system are presented and discussed in Section 4. Section 5 concludes the paper.
For the conventional parameter estimation of electric power lines, the resistance R, reactance X, and susceptance to ground B are usually considered independent parameter variables to be estimated. Furthermore, the traditional π-type equivalent model is used to establish measurement equations. The overhead lines in the medium-voltage distribution network, which are concerned in this paper, are usually short in length. In addition, the voltage level of distribution lines is much lower than that of transmission lines. The value of susceptance to ground of overhead lines is much lower than the value of impedance; that is, the impact of susceptance to ground can be ignored in actual engineering calculations. Therefore, the π-type model can be simplified as a straight equivalent model to reflect the impedance parameters of distribution lines, which is shown in Figure 1.
In Figure 1, subscripts 1 and 2 denote the node numbers at both sides of the line; P and Q denote the active power and reactive power, respectively;
During the actual operation of the distribution network, the SCADA system can collect the effective values of voltage and current as well as the active and reactive power data at the nodes of the substation’s medium-voltage outgoing switches, feeder section switches, and tie switches from different types of RTUs configured in the distribution network. The distribution transformer terminal units (TTUs) are also used to collect these data at the load nodes. μPMUs are generally installed at the root node of the 10 kV bus in the distribution network, tie switches, and some important nodes to collect the amplitude and phase angle of node voltage and current. The sampling frequency of μPMU is given in milliseconds, and the sampling interval of SCADA data is generally given in seconds. Then, the timestamp feature of μPMU can be utilized to add timestamps for SCADA data in the distribution network, and the measurement data from μPMUs and SCADA are integrated to establish measurement equations for the distribution lines.
For the distribution line shown in Figure 1, considering the measurement parameters at both sides of the line, supposing the phase angle of voltage at the end node is 0 and the phase angle of voltage at the start node is δ, so the phase angle difference of voltage at both sides of the line is δ, that is:
where U1 and U2 denote the voltage amplitude at both sides of the line.
The phase angle difference between the voltage and current phasors at both sides of the line can be calculated from the measured power data, which is shown in Eq. 2. Then, the current phasors can be expressed as shown in Eq. 3:
where θ1 and θ2 denote the phase angle difference between the voltage and current phasors and I1 and I2 denote the current amplitude.
Therefore, according to Kirchhoff’s law, the voltage and current at both sides of the line should obey the following equation:
Substituting Eqs 1–3 into Eq. 4, Eq. 5 can be calculated by separating the real and imaginary parts on both sides of the equal sign in the equation:
According to Eq. 1 and Eq. 5, the active and reactive power at the end node of the line can be calculated as shown in Eq. 6:
Thus, by combining Eq. 5 and Eq. 6, the measurement equations can be established as Eq. 7 using the measurement data at t time from μPMU and SCADA configured at Nodes 1 and 2, respectively:
where the state variables containing the subscript t denote the measured data at t time.
For the estimated static parameters based on the parameter estimation method, that is, the parameters g and b, the form of admittance can be converted into resistance and reactance for practical applications, which is expressed in Eq. 8:
where R and X denote the resistance and reactance parameters of the line, respectively.
Taking the aforementioned discussion on the measurement equations for distribution lines into account, the measurement equations for parameter estimation based on multi-source data fusion can be expressed as:
where z denotes the measurement information obtained by μPMU and SCADA; x∈RN×1 denotes the line parameters to be estimated; h(x) denotes the measurement function that reflects the relationship between the line parameters and measurement values; and v denotes the measurement errors. Therefore, an implicit residual function (f (x) = z-h(x)) can be established between the measurement information and the parameters to be estimated.
Considering the frequent interaction between supply and demand in the distribution network, the increase in redundancy of independent measurement equations can be achieved by collecting different measurement data at multiple time points for parameter estimation calculation. Moreover, the possible changes in line parameters can also be corrected when the operation state of the distribution network has changed. It can improve the testability of static parameters and fault tolerance for measurement errors. When the number of parameters to be estimated is constant, the unique solutions can be obtained for the parameters to be estimated by increasing the number of independent equations.
The establishment of measurement equations for measurement data at multiple time points from different measurement sources can be expressed as shown in Eq. 10:
where M denotes the number of measurement equations, and the selection of the value should meet the requirement M > N.
Thus, the objective function to minimize the residual sum of squares can be expressed as:
Given the physical significance of estimation values for the line parameters, the effectiveness constraints of the variables to be estimated should be considered as expressed in Eq. 12:
The traditional Newton–Raphson iteration-based least square method is easily affected by the initial value of the algorithm for parameter estimation. The iteration process is highly dependent on the Jacobian matrix of measurement equations, which leads to the unstable values of parameter estimation (Bian et al., 2008). For most parameter estimation problems, when the objective function reaches the minimum value, the corresponding parameter values are the estimated values of the parameters to be estimated. The process is exactly the solution procedure of an optimization problem. That is, the optimal solution of the objective function should be determined within the given constraint range of the control variables (Abo-Hammour et al., 2014). Considering that parameter estimation can be regarded as an optimization process of searching for the “best solution” to minimize the value of the objective function, a number of intelligent search algorithms are adopted in the calculation of parameter estimation. At present, the genetic algorithm (Abu Arqub and Abo-Hammour, 2014) and particle swarm optimization (Bian et al., 2008) have been widely used in many fields owing to their advantage of fast convergence speed, global optimization technique, and so on. Currently, some scholars also try to utilize these algorithms to solve the problem of parameter estimation. However, many algorithm parameters are artificially set in most popular intelligent algorithms. Furthermore, the algorithm process is too cumbersome to be conducive to practical engineering applications.
The elitist searching approach (Liu et al., 2022b), which is suitable for solving technical problems in engineering applications, is adopted to obtain the “elite solutions” of parameter estimation in this paper. A simple and effective process is used to calculate the values of static parameters for distribution lines.
The control variables of the parameter estimation problem are the values of static parameters to be estimated for distribution lines, which are the continuous variables within the constraint range based on Eq. 12. It means that the control variables are consistent with the requirement of infinite solutions in the elitist searching approach. The solution space for parameter estimation is composed of combinations of different parameter values, where the individuals are uniformly distributed. The flowchart of parameter estimation for distribution lines based on the elitist searching approach is shown in Figure 2. To calculate the values of line parameters, the main steps are as follows:
(1) First, the satisfaction 1-p% and the credibility 1-q% of the parameter estimation are set up, and the sampling number is initialized to 1 (n = 1). Then, the minimum sampling number Nmin, which is required by the algorithm, can be calculated according to Eq. 13:
where int( ) is the calculation of integer rounding.(2) The line parameters to be estimated are randomly selected within their constraints to obtain a solution in the solution space. If the solution is the same as the existing solution should be judged, the solution should be deleted and the line parameters are reselected to generate a new solution which is different from the existing solution.
(3) The generated solution is substituted into the measurement equations which are established by the measurement data collected at different time points, and then the value of the objective function shown in Eq. 11 can be calculated.
(4) Sampling operation and the aforementioned two steps are constantly repeated until the sampling number n reaches Nmin. Comparing the values of the objective function for all sampled solutions, the corresponding solution with the minimum value of objective function can be regarded as the elite solution.
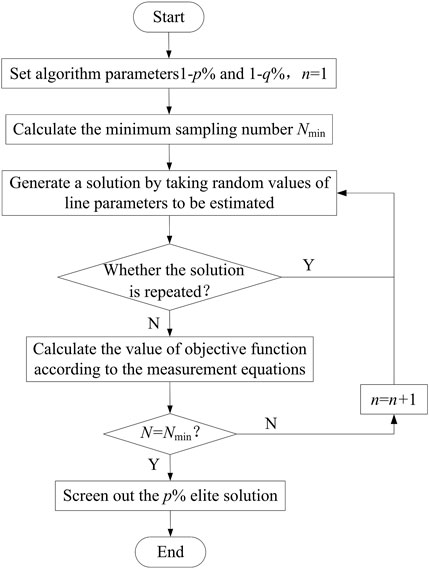
FIGURE 2. Flowchart of parameter estimation for distribution lines based on the elitist searching approach.
In order to ensure the accuracy of the algorithm in solving the parameters of distribution lines, multiple computations should be carried out and the computed results can be analyzed to determine whether the adequacy requirement of sampling is met. Specifically, with the increase in the sampling number, the parameter p% in the satisfaction value of the algorithm can be formed into an equally spaced sequence of parameters (p1%, p2%,…,pk%) according to Eq. 14, and pk% is the current value p% set in Step (1).
For a parameter pi% in the sequence, it is feasible to compute the values of the objective function for the first Nmin,i solutions which correspond to parameter pi%. The optimal value of the objective function (f1,i) and the value ranked hth (fh,i) are selected to calculate the change rate which reflects the change in the value of the objective function as pi% decreases. It can be expressed as shown in Eq. 15:
where d1,i and dh,i denote the change rate of the objective function value according to the decrease in the value of pi%.
If the calculated values of change rate for i = k-3∼k are within the predetermined threshold range, that is, Eq. 16 can be satisfied, then the parameter estimation based on the elitist searching approach with parameter pk% meets the adequacy requirement.
where εd denotes a previously set threshold value.
The relevant concepts of engineering testability for parameter estimation are given in Liu et al. (2022a). Measuring testability analysis reflects the influence of measurement schemes on parameter estimation without the regard to measurement errors. Based on measuring testability analysis, disturbing testability analysis is used to reflect the actual testable degree for parameters in engineering applications, in which the measurement errors should be fully taken into consideration.
In view of different measurement conditions, this paper adopts the analysis approach of parameter testability based on Monte Carlo simulation proposed in Liu et al. (2022a) to explicitly judge whether the static parameters of the distribution lines to be estimated are clear or uncertain. Moreover, the identification method is improved for clear and uncertain parameters, which is aimed at the threshold setting problem in the judgment standard. The process of parameter testability analysis is shown in Figure 3. The main steps are as follows:
(1) Initially, the sample mark is set at λ = 1, and the maximum number of samples is λmax. The initial values of the absolute value of average relative errors (μ<λ>) and the standard deviation of relative errors (σ<λ>) are all equal to 0. Two judgment thresholds are selected in advance: Λ1 is set as a smaller value and Λ2 is set as a larger value.
(2) For a given distribution network, within the reasonable range of the static parameters for each line, a set of values containing all the line impedance parameters to be estimated are randomly generated as a sample, which can be converted into the form of admittance
where xi denotes the value of the ith measurement parameter in MT,
(3) For different types of testability analysis, the measurement equations are established based on the corresponding measurement data, and the elitist searching approach is used to estimate the line parameters. The estimated results are expressed as
where
(4) Eq. 21 is used as a criterion, if the formula holds, then μ = μ<λ> and σ = σ<λ> to take the next step. Otherwise, making λ = λ+1 and returning to Step (2), a new sample of static parameters to be estimated is generated for calculation.
where
(5) It should be judged by the criterion of whether the maximum number of samples is reached. If λ<λmax, the action of making λ = λ+1 and returning to Step (2) is implemented. When the maximum number of samples is reached, the values of μ and σ of the parameters to be estimated can be regarded as horizontal or vertical coordinates, respectively, to generate a group of vertices on the two-dimensional plane.
(6) The Euclidean distance between two vertices can be calculated accordingly, and then the minimum spanning tree (MST) connecting all vertices is constructed on the basis of Prim algorithm. The Euclidean distance between each vertex and the origin of the two-dimensional plane formed by μ and σ should be calculated to identify the parameters. The parameters, which correspond to the vertices whose distance from the origin is less than the threshold Λ1, are identified as clear parameters. Meanwhile, the distance between some vertices and the origin is greater than the threshold Λ2, and the parameters corresponding to these vertices are identified as uncertain parameters.
(7) The two vertices that are the farthest from each other in the remaining part of MST are selected to calculate the Euclidean distance between the two vertices and the origin, and the smaller of the two values is regarded as Λ3. Therefore, the ith parameter to be estimated is identified as a clear parameter when its relevant parameters of relative errors meet Eq. 22; otherwise, it is an uncertain parameter. The ratio of the number of clear parameters to all parameters to be estimated is the testable degree of the entire distribution network lines.
For the disturbing testability analysis, some measuring clear parameters may be changed into disturbing uncertain parameters because of the influence of measurement errors. For the ith disturbing uncertain parameter, if the parameter is identified as a disturbing clear parameter when the threshold in the testability analysis is gradually increased to
In order to verify the feasibility of the proposed parameter estimation and the testability analysis method for distribution lines, an IEEE 33 bus distribution network is used for simulation analysis. The topology structure of the case system is shown in Figure 4. The measurement data of the network root node (Node 1) can be obtained by the configured μPMU and RTU, the μPMUs configured at branch nodes and partial switch nodes could collect phasor data, and the RTUs configured at some load nodes could also acquire relevant measurement data. For the simulation system, in order to ensure the time synchronization of measurement data, the same sampling pulse should be used to collect the data of RTUs. It means that the measurement data at different nodes is collected at the same time when conducting data collection at a certain moment. The simulation takes the fusion of multi-source measurement data at the database of the distribution automation system into account, aiming at different sampling frequencies of μPMU and RTU, and the timestamps of SCADA data can be added according to the feature of μPMU. The fused data at different time points are used to establish measurement equations.
According to the measurement configuration of the case system, the branches within the red box are selected as the object of parameter estimation. The type selection of the lines shown in Figure 4 is the LJ-120-type overhead line, with the parameter of unit resistance r0 = 0.27 Ω/km and the parameter of unit reactance x0 = 0.327 Ω/km (Fang, 2004). The line length of each branch is shown in Table 1.
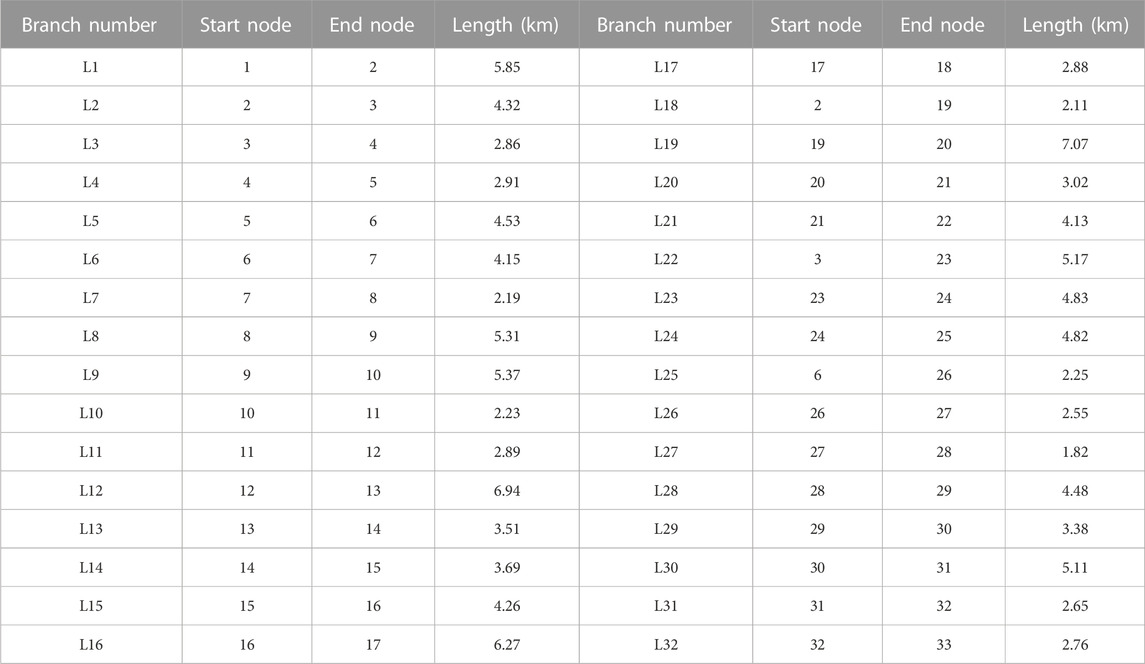
TABLE 1. Length of distribution lines shown in Figure 4.
Two thresholds are determined with Λ1 = 0.05 and Λ2 = 0.2, respectively, and the parameters of the elitist searching approach can be set at p% = 0.5% and q% = 1% for solving the values of line parameters. From Eq. 13, the minimum sampling number can be obtained, that is, Nmin = 919. The solution space for parameter estimation is composed of different value combinations of line parameters to be estimated. An individual value is obtained by taking values of parameters to be estimated in the presence of constraints. Moreover, the individual values are considered uniformly distributed in the solution space.
The measuring testability analysis is carried out to explore the testable degree of line parameters under the current measurement conditions based on the method described in Section 3. Following that, the comprehensive precision of measurement devices in the distribution network is defined as ±φ = ±0.5% (indication relative error), and the disturbing testability analysis is conducted considering the influence of measurement errors. The testability analysis results of static parameters for distribution lines are shown in Table 2, which is obtained from different measurement scenarios.
The area shown in the red box in Figure 4 contains a total of 18 branches, so there are 36 static parameters to be estimated. From Table 2, it can be seen that 22 clear parameters and 14 uncertain parameters are identified by the measuring testability analysis without measurement errors. Therefore, the testable degree is ET = 22/36 = 0.611 under the current measurement condition. By considering the measurement errors of 0.5%, the disturbing testability analysis identifies 20 disturbing uncertain parameters. With the exception of 14 measuring uncertain parameters, three clear branch parameters of the distribution network are transformed into uncertain parameters because of the influence of measurement errors. Therefore, the disturbing testable degree can be calculated as ED= (36–20)/36 = 0.444.
The elitist searching approach is employed three times to calculate the values of line parameters in the absence of measurement errors. To verify the adequacy of sampling, the relevant parameters in Section 2.3 are set at k = 10, i = 7∼10, h = 3, and εd = 0.1. Taking Branch L24 as an example, the sequences of d1,i and dh,i obtained by three calculations are shown in Table 3. Moreover, the calculation results are compared with the results according to the traditional non-linear least squares method, which are shown in Table 4.
It can be seen from Table 3 that the results of the three calculations are in accordance with the adequacy criterion shown in Eq. 16; that is, it is difficult to achieve a smaller value of the objective function by reducing the value of p%, indicating that the current sampling meets the adequacy requirement of the elitist searching approach. As shown in Table 4, the comparison among the three solutions and nominal values of the factory parameters for distribution lines indicates that the proposed method of parameter estimation can obtain elite solutions that meet the requirement of accuracy. Moreover, these elite solutions have relatively small differences compared to the results obtained by the least squares method. It reveals the superiority of the elitist searching approach, that is, the approach with simple optimizing principles does not require different parameter configurations for different problems and is not influenced by the initial values. As a consequence, the approach is appropriate for resolving engineering problems.
For the measuring clear parameters in Table 2, the average value of the relative errors shown in Eq. 19 is used as the performance evaluation criterion for the calculation of parameter estimation. The average relative errors obtained from multiple calculations are shown in Figure 5 on the basis of multiple groups of measurement data. The figure shows that the estimated values of measuring clear parameters, which are solved by using the elitist searching approach according to the measurement data from μPMU and SCADA at multiple time points, are all within the acceptable error scope. In addition, as can be seen from Figure 5, the estimation errors tend to be greater for distribution lines with smaller impedance.
Concerning the uncertain parameters that are derived from measuring clear parameters in the disturbing testability analysis considering measurement errors, the accuracy requirement for the estimation can be gradually relaxed by increasing the threshold Λ3 in Eq. 22 until the allowable accuracy that can transform the disturbing uncertain parameters into clear parameters can be obtained. Under this condition, the average value and standard deviation of the relative errors for line parameters are calculated in testability analysis so that the uncertainty degree and confidence interval of these parameters can be calculated as shown in Table 5 (taking the reactance parameters of branches as an example).
According to the aforementioned calculation results, although a portion of line parameters are transformed into disturbing uncertain parameters due to the influence of measurement errors, the calculation of the value ranges of these parameters remains practically valuable in engineering applications.
To address the issue of the parameter estimation of distribution lines without sufficient measurement information, this paper proposes an approach for the static parameter estimation and testability analysis of distribution lines based on multi-source measurement data, considering the practical application of multiple measurement systems in distribution networks. The elitist searching approach is adopted to solve the values of the constructed line parameters, and then the relevant standards for relative errors are used to determine the testability of line parameters. The simulation results verify that the proposed testability analysis method can effectively distinguish clear line parameters from uncertain line parameters. The testability is related to the configuration of measurement devices and the accuracy of measurement data. It has an important reference value for the practical engineering applications of the distribution network to acquire the values of clear line parameters and the bounds of some uncertain line parameters.
The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Authors JL and ZZ were employed by State Grid Shaanxi Electric Power Research Institute.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abo-Hammour, Z., Abu Arqub, O., Momani, S., and Shawagfeh, N. (2014). Optimization solution of Troesch’s and Bratu’s problems of ordinary type using novel continuous genetic algorithm. Discrete Dyn. Nat. Soc. 2014, 1–15. doi:10.1155/2014/401696
Abu Arqub, O., and Abo-Hammour, Z. (2014). Numerical solution of systems of second-order boundary value problems using continuous genetic algorithm. Inf. Sci. 279, 396–415. doi:10.1016/j.ins.2014.03.128
Bian, X., Qiu, J., and Xu, X. (2008). A heuristic method for static line parameter estimation in power systems. Proc. CSEE 28 (1), 41–46. (in Chinese). doi:10.13334/j.0258-8013.pcsee.2008.01.008
Das, B. (2011). Estimation of parameters of a three-phase distribution feeder. IEEE Trans. Power Deliv. 26 (4), 2267–2276. doi:10.1109/tpwrd.2011.2165858
Deshmukh, S., Natarajan, B., and Pahwa, A. (2014). State estimation and voltage/VAR control in distribution network with intermittent measurements. IEEE Trans. Smart Grid 5 (1), 200–209. doi:10.1109/tsg.2013.2288142
Du, Y., and Liao, Y. (2012). On-line estimation of transmission line parameters, temperature and sag using PMU measurements. Electr. Power Syst. Res. 93, 39–45. doi:10.1016/j.epsr.2012.07.007
Dutta, R., Patel, V. S., Chakrabarti, S., Sharma, A., Das, R. K., and Mondal, S. (2021). Parameter estimation of distribution lines using SCADA measurements. IEEE Trans. Instrum. Meas. 70, 9000411–11. doi:10.1109/tim.2020.3026116
Fang, D. (2004). Instant reference and calculation manual for power transmission and distribution. Beijing: China Water Power Press. (in Chinese).
Gómez-Expósito, A., Gómez-Quiles, C., and Džafi´c, I. (2015). State estimation in two time scales for smart distribution systems. IEEE Trans. Smart Grid 6 (1), 421–430. doi:10.1109/tsg.2014.2335611
Lefebvre, S., Prévost, J., and Lenoir, L. (2014). “Distribution state estimation: A necessary requirement for the smart grid,” in 2014 IEEE Power & Energy Society General Meeting, National Harbor, Mary land, July 27-31, 2014 (IEEE).
Li, X., Wang, S., and Lu, Z. (2022). Reverse identification method of line parameters in distribution network with multi-T nodes based on partial measurement data. Electr. Power Syst. Res. 204, 107691. doi:10.1016/j.epsr.2021.107691
Liu, J., Chen, L., Zhang, Z., and Wang, Y. (2022a). Testability analysis for engineering to explore the value of insufficient information. Distrib. & Utilization 39 (8), 81–84. (in Chinese). doi:10.19421/j.cnki.1006-6357.2022.08.010
Liu, J., Zhao, P., Zhang, Z., and Wang, Y. (2022b). An elitist searching approach to find the satisfied solutions. Distrib. & Utilization 39 (6), 2–5. (in Chinese). doi:10.19421/j.cnki.1006-6357.2022.06.001
Liu, Y., Wang, J., and Wang, P. (2023). Hybrid data-driven method for distribution network topology and line parameters joint estimation under small data sets. Int. J. Electr. Power Energy Syst. 145, 108685. doi:10.1016/j.ijepes.2022.108685
Luan, W., Peng, J., Maras, M., Lo, J., and Harapnuk, B. (2015). Smart meter data analytics for distribution network connectivity verification. IEEE Trans. Smart Grid 6 (4), 1964–1971. doi:10.1109/tsg.2015.2421304
Ma, Z., Zhang, H., Zhao, H., Wang, M., Sun, Y., and Sun, K. (2022). New mission and challenge of power distribution and consumption system under dual-carbon target. Proc. CSEE 42 (19), 6931–6944. (in Chinese). doi:10.13334/j.0258-8013.pcsee.213091
Pegoraro, P. A., Brady, K., Castello, P., Muscas, C., and Von Meier, A. (2019). Line impedance estimation based on synchrophasor measurements for power distribution systems. IEEE Trans. Instrum. Meas. 68 (4), 1002–1013. doi:10.1109/tim.2018.2861058
Rezaei, M. R., Hadian-amrei, S. R., and Miveh, M. R. (2022). Online identification of power transformer and transmission line parameters using synchronized voltage and current phasors. Electr. Power Syst. Res. 203, 107638. doi:10.1016/j.epsr.2021.107638
Srinivas, V. L., and Wu, J. (2022). Topology and parameter identification of distribution network using smart meter and µPMU measurements. IEEE Trans. Instrum. Meas. 71, 1–14. doi:10.1109/tim.2022.3175043
Von Meier, A., Stewart, E., McEachern, A., Andersen, M., and Mehrmanesh, L. (2017). Precision micro-synchrophasors for distribution systems: A summary of applications. IEEE Trans. Smart Grid 8 (6), 2926–2936. doi:10.1109/tsg.2017.2720543
Wu, Z., Long, H., and Chen, C. (2022). Line aging assessment in distribution network based on topology verification and parameter estimation. J. Mod. Power Syst. Clean Energy 10 (6), 1658–1668. doi:10.35833/mpce.2021.000165
Xiong, W., Song, G., Li, Y., Song, X., Huang, L., and Zhang, W. (2022). Parameter identification of three-phase four-wire distribution line using smart meter measurement data. Automation Electr. Power Syst. 46 (20), 155–166. (in Chinese). doi:10.7500/aeps20210728002
Xue, A., Xu, F., You, H., Xu, J., Martin, K. E., and Bi, T. (2019). Robust parameter identification of distribution line based on micro PMU. Electr. Power Autom. Equip. 39 (2), 1–7+43. (in Chinese). doi:10.16081/j.issn.1006-6047.2019.02.001
Keywords: distribution lines, parameter estimation, testability analysis, measurement data, elitist searching approach
Citation: Chen L, Liu J, Pan Z and Zhang Z (2023) Static parameter estimation and testability analysis of distribution lines based on multi-source measurement information. Front. Energy Res. 11:1249782. doi: 10.3389/fenrg.2023.1249782
Received: 29 June 2023; Accepted: 07 September 2023;
Published: 25 September 2023.
Edited by:
Haris M. Khalid, University of Dubai, United Arab EmiratesReviewed by:
Omar Abu Arqub, Al-Balqa Applied University, JordanCopyright © 2023 Chen, Liu, Pan and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lupeng Chen, Y2hlbmxwMDAyQDEyNi5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.