Weighted Minkowski distance-based differential protection for active distribution networks considering the uncertainty of frequency-domain characteristics

With the increasing use of DGs (distributed generators) in the power system, the distribution network is becoming more and more complicated. The rapid change of DG output power and the diversity of DG location make the computing calculation of relay protection difficult, bringing severe challenges to the current protection based on single-end electrical volume. Therefore, double-end-based protection is a good choice in view of the DG uncertainty and the network complexity. However, the power frequency offset after fault and the uncertainty of DG fault current result in uncertainty in the frequency-domain characteristics, which can also negatively affect the differential protection. In view of this, a new differential protection method based on the weighted Minkowski distance algorithm is proposed in this paper. First, the Minkowski distance algorithm is used to describe the similarity of both currents considering the uncertainty in the frequency-domain characteristics. Second, each current similarity including the phase current, the positive current, and the negative current is calculated separately to increase the protection sensitivity. Through the weighted algorithm distribution, the weight is assigned. Furthermore, a high-performance protection mechanism is designed to improve the protection sensitivity. This method is suitable for the active distribution network with different penetration rates of DGs and different types of DGs. The simulations show that the proposed method has good feasibility and high superiority.

1 Introduction

In September 2020, China set a clear target of achieving “peak carbon dioxide emissions” by 2030 and “carbon neutrality” by 2060 (Cao, 2023), which greatly promoted the development of the energy system in a clean and low-carbon direction. With the increasing proportion of distributed generators (DGs) in the new power system, the vigorous development of renewable energy generation has become an inevitable trend in the national energy and power layout (Xin, 2022). However, with the use of distributed generation and their power electronic devices (Bullich-Massagué et al., 2016; Yu et al., 2017; Tafti et al., 2019), the topology and tidal direction of the traditional distribution network have changed dramatically. At the same time, the new power system has more complex characteristics when faults occur, such as more non-fundamental low-order harmonics, frequency offset, and severe phase distortion (Jia et al., 2022). Many conventional protection methods have exposed defects such as rejection and misoperation to a certain extent. Therefore, it is of great significance to study a new protection method for the safe operation of the distribution network.

Differential protection has obvious advantages in complex distribution networks, but currently there are still problems of poor adaptability in some specific environments. Some scholars have analyzed this. Wei et al. found that the ratio of current differential protection is affected by the fault characteristics of phase angle distortion and amplitude limitation (Wei et al., 2014). The sensitivity of the conventional current differential protection method is not good when the new energy station is connected to a strong synchronization system. There is a risk of rejection of the traditional current differential protection when the new energy station is integrated into a weakly synchronized system. The fault current has the characteristics of phase distortion, frequency offset, and low proportion of the power frequency component after the new energy station is connected to a strong power grid (Kar and Subhransu Ranjan, 2020). The performance of conventional differential protection that relies on the comparison of phase amplitude and phase angle of industrial frequency has deteriorated. Just improving the conventional protection cannot solve the problem once and for all. Hao Liu et al. pointed out that under the influence of the harmonics of the inverter, errors occur in the measurement of the work frequency vector during faults, which leads to the risk of rejection and false activation of traditional protection (Liu et al., 2019).

In order to solve a series of problems caused by the increasing scale of the DG, many domestic and foreign scholars have put forward some schemes on how to improve the adaptability of the conventional differential protection. Ansari Salauddin and Gupta Om Hari used the power angle of positive sequence before and after a fault to identify the fault and send an action signal to the protection device (Salauddin and Hari, 2021). However, the steady-state positive-order component before the fault will be affected by the frequency offset, so the reliability of this method is not very high. Using the voltage and current at both ends of the line to calculate the line impedance as the criterion of differential protection is proposed in Bolandi et al. (2015). This method will reduce the accuracy of measuring the power frequency impedance due to the frequency shift of short-circuit current. A new differential protection scheme based on the equivalent traveling wave is proposed in Tang et al. (2017). Although the equivalent traveling wave theory achieves reduced communication traffic, the 250 kHz sampling frequency is still a challenge. In summary, on one hand, the improvement measures for conventional protection methods will make the protection device complicated and suffer from lack of economy. On the other hand, it is difficult to completely improve the adaptability of distribution network protection methods (Li et al., 2021).

In addition, many experts have studied the fault characteristics of distribution networks with a high proportion of distributed generation, and some new differential protection methods using the waveform similarity criterion are proposed. Distance is a commonly used measure of waveform similarity (Qing et al., 2021). K. Jia et al. used cosine similarity as the criterion for waveform similarity (Zheng et al., 2021; Zheng et al., 2022). However, when the sampling data at one end of the line are all 0, the calculation result of the criterion will be that the numerator and denominator of the result are infinitely close to 0. Obviously, this will make it impossible to get accurate results. Many scholars used the Pearson correlation coefficient and similarity distance to reflect the difference in current between the head and end (Jia et al., 2018; Jia et al., 2019). The related waveform similarity differential protection principle is proposed. However, the protection principle has poor performance when the new energy sources have almost no output power.

Jia et al. (2021) took Spearman’s rank correlation coefficient as the fault criterion. Zheng et al. (2020) used structural similarity and square error in statistics as the criteria. Weng et al. (2021) used the Bhattacharyya coefficient of current distribution histograms as the protection criterion. Ding et al. (2019); Weng et al. (2019) mainly used the Hausdorff distance to characterize the current waveform similarity of 50 Hz. The three aforementioned methods are all based on the protection of fundamental components, failing to fully utilize the positive and negative sequence data.

To sum up, the change of fault characteristics of the new distribution network makes the conventional differential protection have the problem of insufficient adaptability. In this paper, the Minkowski distance algorithm is studied and used to represent the waveform difference. Waveform similarity is used to describe the characteristics of fault current after DG access to the distribution network. We construct a criterion for differential protection based on the weighted Minkowski distance to identify faults. The characteristics of the algorithm for data processing are studied and discussed, and the weights are allocated reasonably. The working principle and concrete implementation method of the proposed protection method are analyzed. Finally, a simulation model based on MATLAB Simulink is established, and the reliability of the method is verified by simulation experiments. The dynamic performance of the protection is analyzed, and the adaptability of the protection method to severe frequency offset is also verified. The tolerance of the protection to transition resistance is also discussed.

2 Principle and characteristics of Minkowski distance

In China, the radial distribution network is usually equipped with traditional three-stage current protection. In practical applications, only two-stage protection is generally used, namely, instantaneous current quick-break protection and fixed-time overcurrent protection. Figure 1 is a typical topology diagram of the distribution network connected with DG. When the protection is short-circuited at the upstream (F₁), the fault point will flow through the reverse current provided by the DG, and this current is related to the DG output power P. When P increases to a certain extent, the reverse current may be greater than the setting value of the protection, resulting in protection misoperation, so it is necessary to install a directional element. However, due to the uncertainty of the output of the inverter-type photovoltaic DG and the potential possibility of frequency offset, the direction component criterion originally for the traditional bilateral power system is likely to be no longer applicable. When the fault occurs downstream (F₂) of the DG, the grid power supply and the distributed power supply simultaneously provide a short-circuit current to it, and the short-circuit current is related to the output power P of the DG. When P increases to a certain extent, the protection range may even be extended to the lower line, resulting in the fault current of the lower line exceeding its set value.

FIGURE 1

FIGURE 1. Three-stage protection defect.

Minkowski distance is a kind of distance quantity first proposed by Russian-born German mathematician Minkowski, which is widely used to characterize the similarity between two sets of data in the field of machine learning (Peerapong and Suebkul, 2022). It does not refer to a certain distance alone, but to the sum of a class of distances.

Let there be two sets of point sets in the space:

$A=\left\{a_1,a_2,a_3,\cdots ,a_n\right\};B=\left\{b_1,b_2,b_3,\cdots ,b_n\right\}.$

Then, the Minkowski distance can be calculated by Formula (1).

$\begin{array}{l}E={\left({\left|b_1-a_1\right|}^p+{\left|b_2-a_2\right|}^p+\cdots +{\left|b_n-a_n\right|}^p\right)}^{\frac{1}{p}}\\ ={\left({\displaystyle \sum _{i=1}^n}{\left|b_i-a_i\right|}^p\right)}^{\frac{1}{p}},\end{array}(1)$

where E is the Minkowski distance and p is the Minkowski distance parameter, which can be 1, 2, 3…

When p takes different values, the Minkowski distance has different meanings. For example, when p = 1, the Minkowski distance becomes the Manhattan distance, also known as absolute distance. It can be calculated by (2).

$E_1={\displaystyle \sum _{i=1}^n}\left|b_i-a_i\right|.(2)$

This formula shows that $E_1$ is calculated as the right-angle side distance between two points in two-dimensional space. This distance is as shown by the polyline α or γ in Figure 2.

FIGURE 2

FIGURE 2. Schematic diagram of distance calculation.

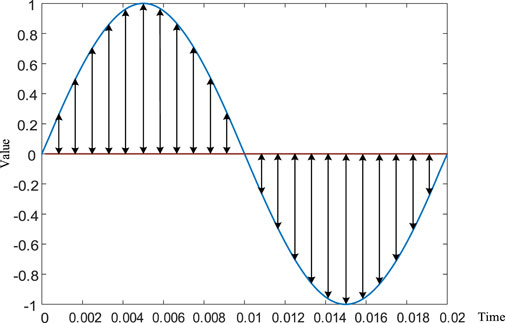
When p = 2, the Minkowski distance becomes the Euclidean distance, and its formula is as follows:

$E_2=\sqrt{{\displaystyle \sum _{i=1}^n}{\left(b_i-a_i\right)}^2}.(3)$

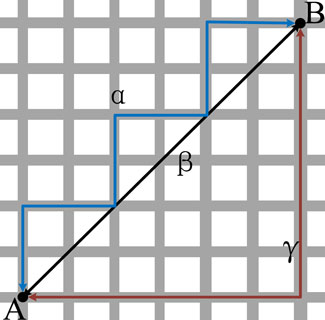
The Euclidean distance means the straight-line distance between two points, which is shown as β in Figure 2. When the Minkowski distance is used to describe the similarity of two groups of data, scholars usually do not only use a fixed p to calculate the distance because using different distance algorithms for different data waveforms has different effects and physical significance. In order to comprehensively use the Minkowski distance to describe the similarity, the author set p = 1, 2, 3, and assigned a weight to each p, named as $w_1$, $w_2$, and $w_3$. By assigning weights to the corresponding Minkowski distances when calculating the similarity of two data sets, a new distance metric formula is defined: weighted Minkowski distance. It can be calculated by (4).

$M_r=\frac{{\displaystyle \sum _{p=1}^3}{w}_p{M}_r^{\left(p\right)}}{n},(4)$

where n is the sampling number of current transformers and $w_p$ is the weight for each p. P = 1, 2, 3; r = 1, 2, 3; $M_1^{\left(p\right)}$ denotes the distance between the current data of one cycle sampling time window on both sides of the line. $M_2^{\left(p\right)}$ and $M_3^{\left(p\right)}$ are Minkowski distances of positive-order component and negative-order component of the three-phase current, respectively. The formula of $M_1^{\left(p\right)}$ is $M_1^{\left(p\right)}={({\displaystyle \sum _{i=1}^n}{\left|b_i-a_i\right|}^p)}^{\frac{1}{p}}$, which is similar to formula (2), and those of $M_2^{\left(p\right)}$ and $M_3^{\left(p\right)}$ are similar.

3 Differential protection based on weighted Minkowski distance

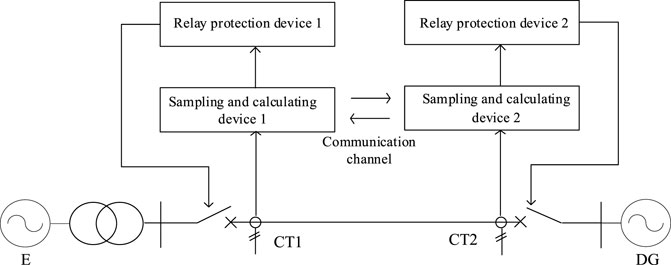
A typical model with power supply at both ends of the new distribution network is shown in Figure 3. The following describes the fault criterion and implementation method of line longitudinal protection based on the weighted Minkowski distance according to the model.

FIGURE 3

FIGURE 3. Schematic diagram of differential protection.

We take the measured data of one-phase current as an example to explain. The current transformers on both sides collect the current data at the same time, which are arranged in a time sequence. The point set $i_M=\left\{i_{M1},i_{M2},i_{M3}\cdots i_{Mk}\right\}$ is the current sampling data at different moments at the head of the line. The point set $i_N=\left\{i_{N1},i_{N2},i_{N3}\cdots i_{Nk}\right\}$ is the current sampling data at different moments at the end of the line. The weighted Minkowski distance is calculated by substituting the two sets of current data into Formula (4), which is called M₁. Similarly, the weighted Minkowski distances M₂ and M₃ of the positive and negative sequence components of the three-phase currents can be calculated.

If the difference between the two vectors is small, the similarity between the two sets of data will be high, and the Minkowski distance will be small irrespective of the value p equals. When the power grid is in normal operation or an external fault occurs, the similarity of current waveforms at both ends is high, while the similarity is low when an internal fault occurs. Therefore, the following differential protection criterion based on the weighted Minkowski distance is proposed:

When the power grid is operating normally or an external fault occurs, ignoring the capacitive current to the ground, it can be known from Kirchhoff’s current law that the current flowing into the line is equal to the current flowing out of the line. So, M₁, M₂, and M₃ will all be 0. However, in practice, due to the manufacturing error of the current transformer, the distributed capacitance, and so on, the weighted Minkowski distance is not completely 0. However, it is approximated as 0.

$\forall r\in \left\{\mathrm{1,2,3}\right\}{,M}_r\approx 0.(5)$

The high-frequency harmonic brought by the distributed generation will increase the difference of the current waveform currents from the two terminals. This will increase the value of M, thus improving the reliability of protection. When an internal fault occurs, the weighted distance of the fundamental wave obviously increases, and so do the weighted distances of positive-order and negative-order waves. If setting an appropriate threshold named M_r and fixing that when any of the calculated Minkowski distances is over its action threshold will cause a signal to be sent to the circuit breaker, then the fault can be cut off in time. The action criterion of the weighted Minkowski distance differential protection is as follows:

$\exists r\in \left\{\mathrm{1,2,3}\right\},M_r>{\epsilon }_r.(6)$

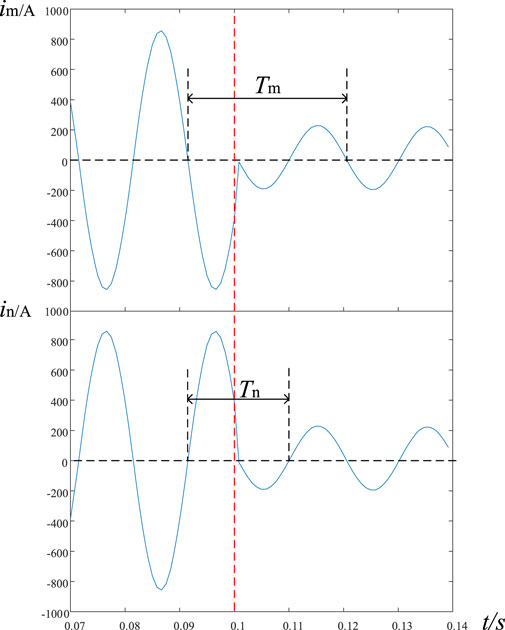
The specific implementation method is as follows: Install two protection devices at both ends of the line to independently measure the three-phase current data. Then, the current information of the local side can be sent to the opposite side through the communication channel. The data on both sides can be synchronized by using the fault information self-synchronization technology developed in Zhou et al. (2022). The specific waveform diagram is shown in Figure 4. For medium- and low-voltage distribution networks, the capacitance of the line is much larger than that of the transmission line. At the same time, the ground capacitance current of the distribution network line is very small and can be ignored. The current phase difference between the two ends of the protected line before fault occurrence is 180°. This means that the time interval between two adjacent zeros of the same trend is 20 ms. After the fault occurs, the current phase at both ends changes, and the time interval also changes: it is no longer 20 ms. The phase difference of the current at both ends after the fault occurrence can be calculated by using the variation of this time interval. The specific calculation formula is as follows:

$\varphi {}_{MN}=\pi -\frac{T_M-T_N}{T}2\pi .(7)$

FIGURE 4

FIGURE 4. Self-synchronization method diagram.

When the sampling frequency is high enough, the change trend of the data can be obtained by linear fitting of two positive and two negative numbers near the zero-crossing point. If the slope of the fitting line of the four continuous sampling points is positive, it is at the rising edge, and vice versa. After simulation, the error of this timing method was approximately 5 ms, which is enough to meet the requirements of the existing distribution network for protection speed.

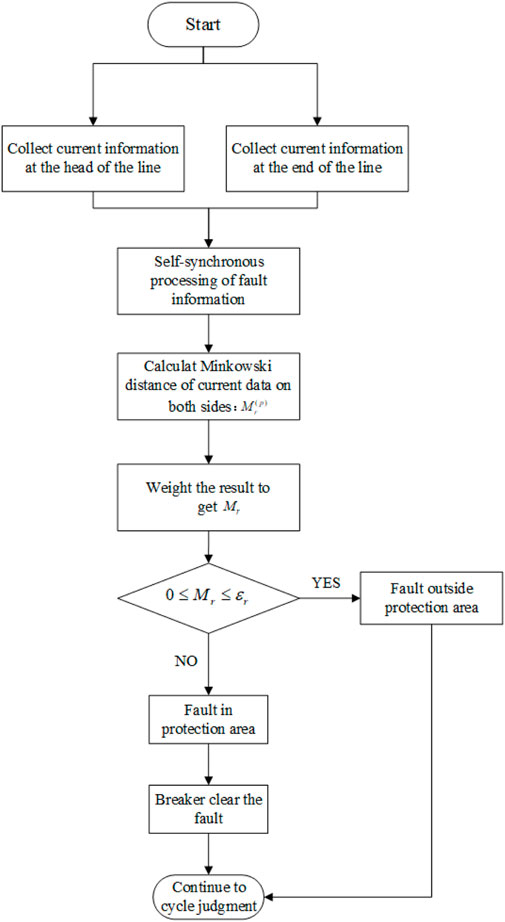
The two sets of devices calculate the weighted Minkowski distance of the initial and final currents and their positive and negative sequence components in the same period width of the 20 ms time window and then send a signal to the circuit breaker if any weighted Minkowski distance is over the action threshold. The workflow of the whole protection method is shown in Figure 5.

FIGURE 5

FIGURE 5. Flow chart of the protection method.

3.1 Selection of Minkowski’s weight

Different weights are used to make different types of weighted Minkowski distances that better adapt to different data. It is not difficult to see from the distance calculation formula that the weighted Minkowski distance has some characteristics:

(A) When the two groups of data are exactly the same, the value of p does not affect the result of distance calculation because every distance will be 0. It means that the starting benchmark of different distances to describe the degree of data difference is the same.

(B) From Figure 2 and a lot of simulation results shown as follows, it can be found that because the calculation of the weighted Minkowski distance includes the step of “finding the absolute value,” the calculated Manhattan distance ≥ Euclidean distance ≥ the distance when p = 3.

To sum up, these characteristics make the sensitivity of distance calculation results different with different p, and giving different weights to different data can make the Minkowski distance better adapt to the characteristics of the data. As the distributed power supply is connected to the power grid, the fault current will be doped with more serious harmonic components (Li et al., 2023). In the fault current, all harmonic components will be included, so its harmonic distortion rate will be the highest. However, in the positive-order component and negative-order component, only a part of harmonics is included. It should be pointed out that the negative-order component only appears when the fault is asymmetric, so the weighted Minkowski protection based on negative current has high sensitivity. In order to better portray the fault characteristics, for the Minkowski distance of the fundamental component $M_1^{\left(p\right)}$, $w_1$ is 1/2; $w_2$ is 1/4; $w_3$ is 1/4, which can improve the protection sensitivity. On the contrary, the weights can be set as $w_1$ is 1/4; $w_2$ is 1/2; $w_3$ is 1/4 for the Minkowski distance of the positive-order component and negative-order component.

3.2 Threshold setting of weighted Minkowski protection

The calculation result of the Minkowski distance of the three-phase current and its positive-order component and negative-order component is used to describe the waveform difference between both sides of the line, so the setting principle of protection is that the threshold value exceeds the weighted Minkowski distance of the protected line during normal operation and external fault. During the occurrence of a power grid fault, the line current increases rapidly, and the current transformers’ errors and other errors also increase proportionally. In order to ensure the reliability of protection, the author set the reliability coefficient named $K_{mr}$. $K_{m1}$, $K_{m2}$, and $K_{m3}$ are defined as the reliability coefficients of three-phase current, positive-order component, and negative-order component, respectively. The setting value formula of each weighted Minkowski distance is as follows:

${\epsilon }_r=K_{mr}\cdot \max \left\{i_M,i_N\right\}.(8)$

In the formula, $\max \left\{i_M,i_N\right\}$ means taking the maximum of the current at both protected line ends.

According to the experience and a large number of simulation data, the value of $K_{mr}$ can be set. $K_{m1}$ is generally approximately 0.15, $K_{m2}$ is 0.05, and $K_{m3}$ is 0.04. In view of the possible CT line-break, there are many perfect fast monitoring methods for the fault. If necessary, corresponding protection can be added to the weighted Minkowski distance differential protection to form a new operation logic.

3.3 Special characteristics of the fault in the active distribution network

When the distributed generation and a large number of power electronic devices are connected to the distribution network, the original fundamental frequency of 50 Hz will be shifted. The process of calculating the weighted Minkowski distance is different from that of some differential protection methods. The first step is always to subtract the sampled data which are at the same time point. The second step is to find the p power of the first result and then sum it. Then, the third step is to calculate the 1/p power of the sum result. The influence of the same frequency shift of the sampled data at both protected line ends is eliminated in the first step of the calculation, so it will not affect the subsequent operation and the final result.

Because not every protected line in the distribution network is involved in distributed power supply access, and the utilization of new energy is difficult at present, there are distributed power supplies that sometimes do not contribute to the situation. It is generally difficult to determine whether the protected line is in a single-power supply situation. When the sampled data on one side of the line are all 0, it can be known from Formula (4) that n, which is the denominator of the weighted Minkowski distance, is not equal to 0 because it is independent of the sampled data. It ensures the reliability of protection during single-terminal power supply. At the same time, the original weighted Minkowski formula is simplified as follows:

$M_r^{\left(p\right)}={\left({{\displaystyle \sum _{i=1}^n}\left|a_i\right|}^p\right)}^{\frac{1}{p}}.(9)$

The schematic diagram is shown in Figure 6. Such a large waveform difference can obviously make the protection act reliably.

FIGURE 6

FIGURE 6. Waveform diagram when a section of line data is 0.

3.4 Blind area of longitudinal differential protection

As a differential protection method, it is also necessary to consider the blind area of determining the fault only by the current data at both ends of the protected line. At present, the capacity of distributed generation is increasing, which can inevitably lead to the problem that the longitudinal differential protection may not be able to identify the fault after a fault occurs somewhere in the line. The specific schematic diagram is shown in Figure 7.

FIGURE 7

FIGURE 7. Schematic diagram of possible protection blind area.

In this situation, because the fault point is far away from the AC network side and close to the distributed generation, the difference between the fault currents measured at the two ends is not obvious, which may lead to the failure of Minkowski distance protection based on the phase current or even the positive sequence component proposed in this paper. However, the negative sequence current component only appears in asymmetric faults, and the weighted Minkowski protection that uses a negative sequence component still has high sensitivity, so this method can still effectively identify all kinds of asymmetric faults in this case. For symmetrical faults, the harmonic characteristics of the output current of the distributed power supply can be considered for screening. The protection proposed in this paper still has room for further improvement.

4 Simulation results

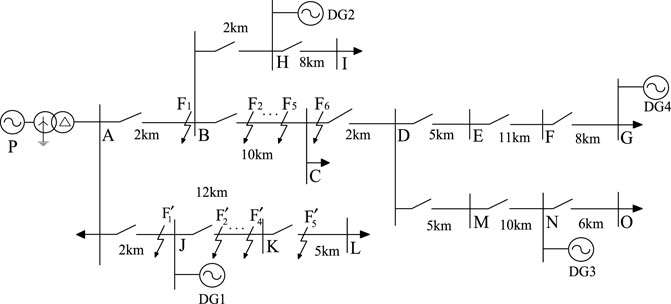
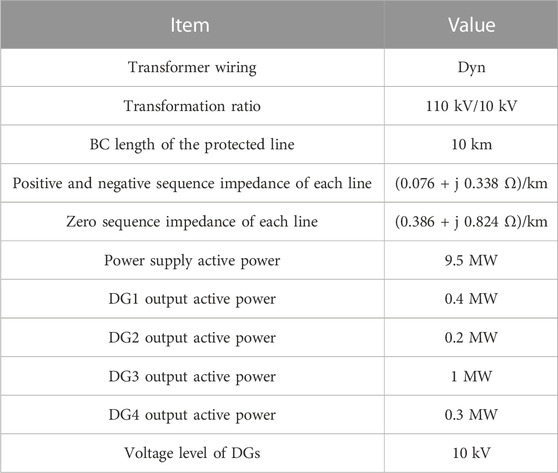
The simulation model of the active distribution network built in Simulink is shown in Figure 8. This model is similar to the IEEE typical 10 kV distribution network model which has 14 nodes. The specific model parameters are shown in Table 1.

FIGURE 8

FIGURE 8. Circuit structure of the simulation model.

TABLE 1

TABLE 1. Parameters of the vehicle model.

4.1 Protection performance of symmetric and asymmetric faults

On the basis of the distribution network structure in Figure 8, a set of six fault locations are set. Four of them are internal faults, which are set at 15%, 30%, 75%, and 90% away from the head of line BC. These four faults are recorded as $F_2$, $F_3$, $F_4$, and $F_5$, respectively. Two external faults are set on line AB and line CD, which are recorded as $F_1$ and $F_6$, respectively In order to cover all types of faults, the simulation validation is carried out by taking most types of faults, which are marked as AG (phase A to ground fault), ABG (phase A to phase B to ground fault), BC (phase B to phase C fault), and ABC (three-phase fault). The fault is set at 0.1 s after the simulation is started. The sampling frequency is 1.2 kHz, and the weights of the Minkowski distance of the three-phase current are taken as $w_1=1/2$, $w_2=1/4$, and $w_3=1/4$. For the Minkowski distance of positive-order component and negative-order component, the weights are taken as $w_1=1/4$, $w_2=1/2$, and $w_3=1/4$.

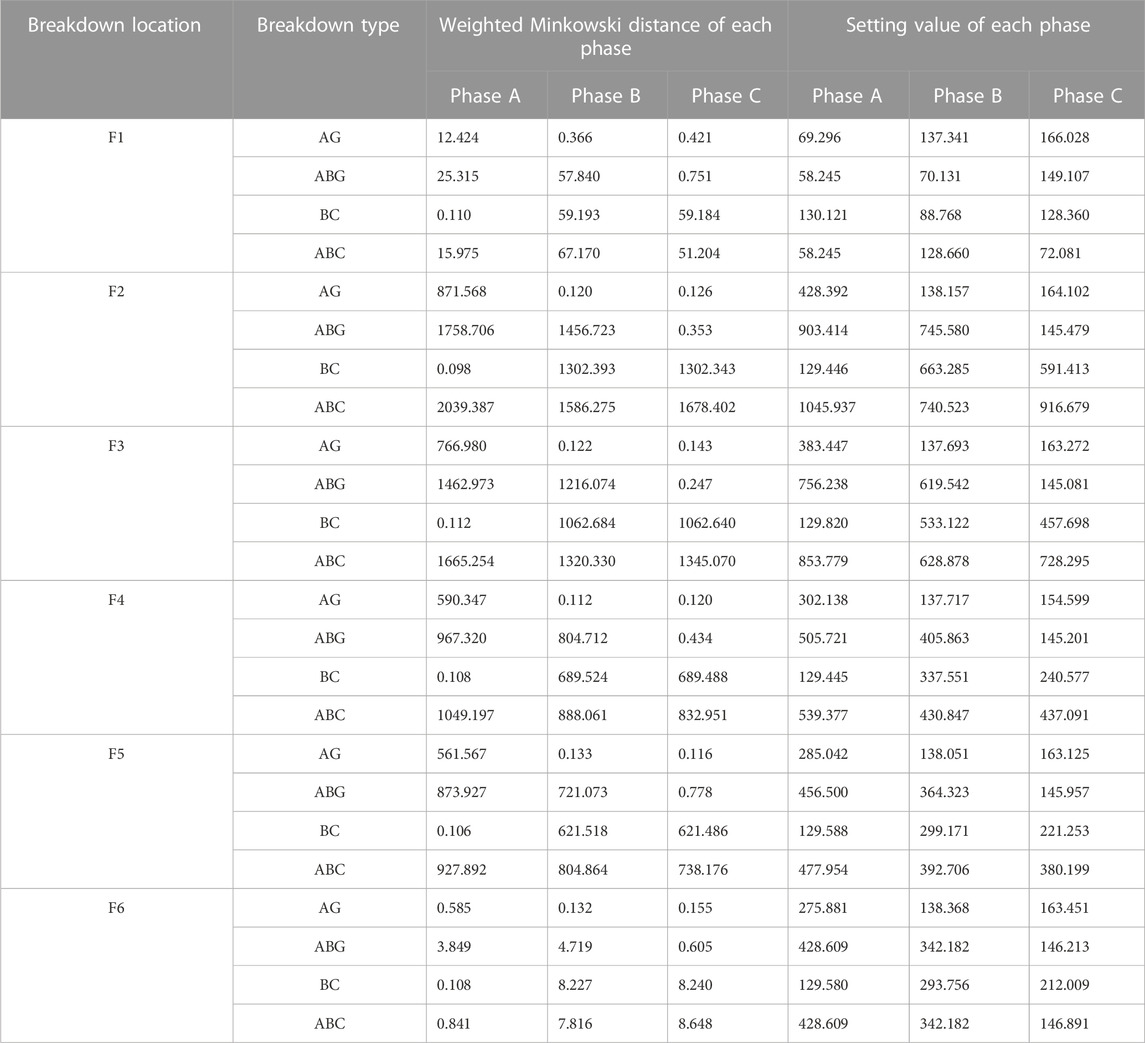
Run the simulation model under the aforementioned set conditions, and the data of 20 ms after the fault are used for calculation. Table 2 gives the weighted Minkowski distances of each phase current under different fault positions and fault types, and Table 3 gives the weighted Minkowski distances of positive and negative sequence components of three-phase current under different fault positions and fault types.

TABLE 2

TABLE 2. Calculation value and setting value of the weighted Minkowski distance of phase current.

TABLE 3

TABLE 3. Calculation value and setting value of weighted Minkowski distance of positive and negative sequence components of current.

When a fault occurs in the protected line, the power sources on both sides of the line provide current to the fault point at the same time. When the output fluctuation of DG is not considered, the current waveform at the head and end of the line can be obtained in the simulation. The two have different characteristics due to the different paths of the current at the two ends. As shown in Figure 9, the meaning of the shadow part is the current difference between the two ends of the line after the fault occurs. If these two sets of current data are substituted into Formula 4, the weighted Minkowski distance measurement value can be obtained. The threshold of this protection can be calculated by the same two sets of data according to Formula 8.

FIGURE 9

FIGURE 9. Current comparison diagram of the head and end of the line before and after the fault.

By comparing every weighted Minkowski distance under various faults, it can be found that the Minkowski distance under internal faults is significantly higher than that under external faults. It is consistent with the aforementioned analysis. This feature can be used to well-discriminate the difference between internal faults and external faults. The protection can cut off faults reliably insofar as any weighted Minkowski distance is over its threshold. These facts verify the feasibility of this protection method.

Taking all kinds of faults at $F_4$ as examples, the three-phase current weighted Minkowski distance and its threshold can be calculated with the data obtained by simulation. The comparison between the setting waveform and the calculated waveform is shown in Figure 7.

In Figure 10, the blue line represents the measured value, and the red line represents the threshold. As shown in Figure 10, the pre-fault weighted Minkowski distance is close to 0, and it increases rapidly after faults. This change means that the algorithm proposed in this article can accurately detect any type of fault on the line and act on the tripping circuit breaker. Therefore, the reliability of this protection has been verified.

FIGURE 10

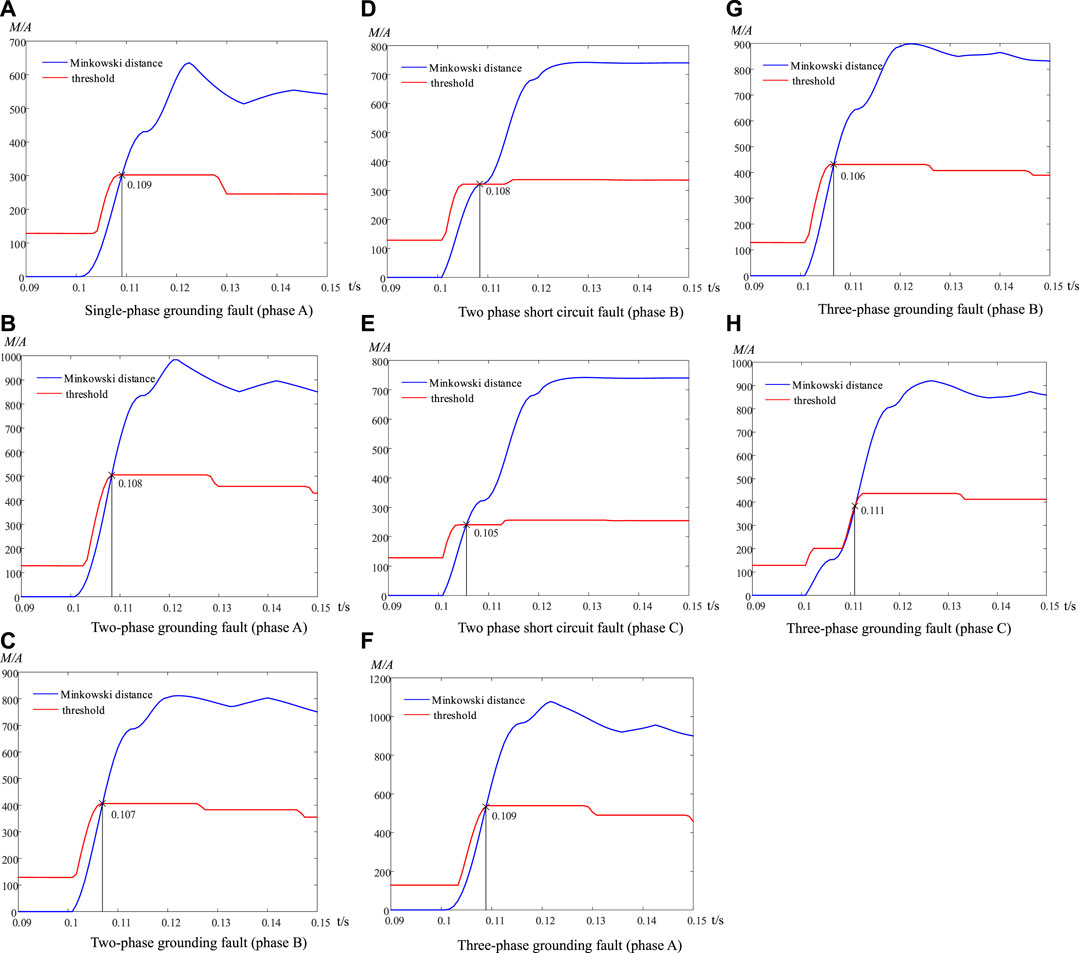
FIGURE 10. Calculation result and the set value of the distance before and after the fault of the fault phase.

Because of the fact that the protection proposed in this article is a differential protection and only the weighted Minkowski distance of the faulty line exceeds the threshold, the selectivity of this protection has been verified. Figures 10A–H show that Minkowski’s calculated value exceeded the threshold within approximately 0.01 s after the fault and then remained above the threshold. This means that the method proposed in this article can quickly identify faults, and the sensitivity of this protection has been verified.

At the same time, Figure 10 already includes both symmetric and asymmetric faults. This means that all types of faults can be accurately identified by using the weighted Minkowski algorithm. The simulation result verifies the aforementioned analysis and shows that the protection method can identify the fault quickly and accurately, so this protection has good dynamic performance.

4.2 Protection performance of a single-ended power supply line

The performance test of the weighted Minkowski distance differential protection is still carried out according to the simulation model in Section 4.1. The setting of the fault location is shown in Figure 8. However, the fault line in this simulation is line JK, which is a typical line with single-ended power supply. For such lines, when a metal grounding fault occurs in the system, the fault phase current at the end of the line decays rapidly. Especially, once the three-phase short-circuit fault occurs, the data measured by the current transformer at the end of the protected line will all become 0. This will lead to the risk of failure of differential protection methods proposed by some scholars in the past. In response to this problem, the weighted Minkowski distance algorithm can still work in such an environment.

Supplementary Table S4 can be found in the Supplementary Material. As can be seen from Supplementary Table S4, when only one end of the line with power supply has a short-circuit fault, the calculated value of the weighted Minkowski distance differential protection can still reliably exceed the threshold. At the same time, because the waveforms are very different, the calculated value of this method exceeds the threshold faster than that mentioned in Section 4.1, which shows the good fast-moving characteristics of this method.

4.3 Protection performance considering frequency offset

In order to investigate the performance of this protection principle under severe frequency instability of the distribution network, the simulation is still carried out in the 10 kV distribution network model mentioned in Section 4.1, with a total of five fault locations. Three of them are internal faults, which are set at 1.5 km, 5 km, and 8.5 km away from the head of line BC and recorded as $F_2$, $F_3$, and $F_4$, respectively. Two external faults are still set on line AB and line CD and recorded as $F_1$ and $F_5$. The setting of the fault location is shown in Figure 11. The fault types are the same as mentioned earlier. After the fault, the frequency of the distribution network changes to 40 hz or 60 hz, respectively.

FIGURE 11

FIGURE 11. Fault location diagram.

Supplementary Tables S5–S8 can be found in the Supplementary Material. The values of the weighted Minkowski distance are shown in Supplementary Tables S5–S8 under different fault locations and fault types. By comparing the data with the threshold, it can be known that the weighted Minkowski distance will have some change after the frequency shifting, but the change itself is not big enough to change the feature that the weighted Minkowski distance reliably exceeds the threshold, which verifies the ability of this method to resist the frequency shift. It means that even if the output frequency of the DG changes greatly after the fault occurs, this method can still accurately identify the fault.

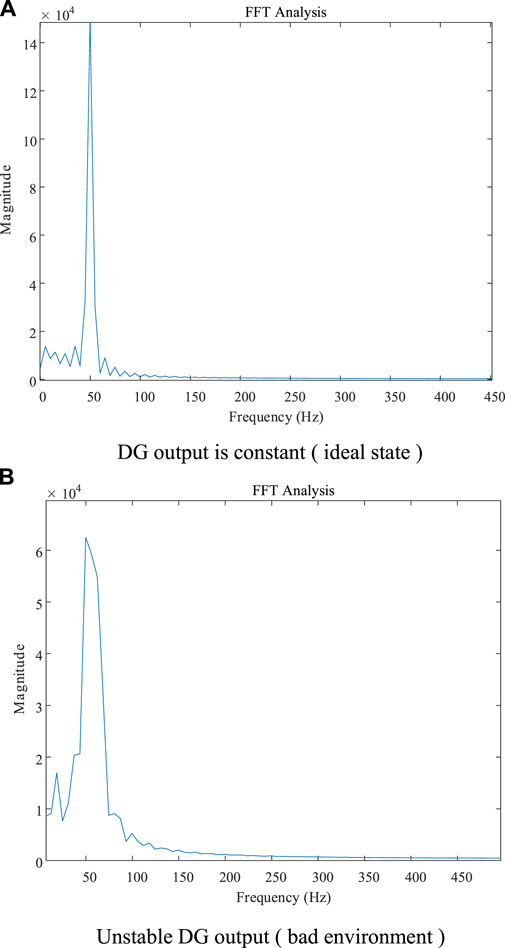
On the other hand, many of the current distribution network differential protection methods are based on the power frequency component of the measured data. For example, Salauddin and Hari (2021) used the positive sequence current phasor ratio before and after the fault to determine whether the fault is located upstream or downstream of the protection. (Bolandi et al., 2015) proposed using the voltage and current at both ends of the line to calculate the line impedance to form a differential protection. The first step of the calculation process of these methods is to extract the power frequency component from the electrical data at both ends of the line. However, once the frequency of the electrical quantity output by the DG changes due to light or wind, the proportion of the power frequency component in the fault current will decrease. In this case, the differential protection based on the power frequency component cannot obtain an effective signal, resulting in a decrease in the reliability of the protection. The fault current spectrum analysis of whether the DG output is stable is shown in Figure 12. Picture (A) is the current harmonic analysis of the line when the DG is in a constant output state under ideal conditions. Picture (B) is the current harmonic analysis of the line when the DG output is unstable. The waveforms analyzed in Figure 12 are based on the simulation results Supplementary Tables S6–S8.

FIGURE 12

FIGURE 12. Fault waveform spectrum analysis and comparison.

4.4 Protection performance affected by fault resistance

When a single-phase grounding fault occurs in a distribution network, it is usually accompanied by a high transition resistance. To verify the ability of this method, set the fault at the midpoint of the BC line in the aforementioned simulation model. The other parameters of simulation models remain unchanged. Then, continue the simulation experiment and still use the data within 20 ms after the fault to calculate the Minkowski distance. Only different fault resistances are set at the fault point to explore the tolerance of this protection principle to the high transition resistance fault.

Supplementary Tables S9, S10 can be found in the Supplementary Material. Supplementary Tables S9, S10 are the calculation results and the threshold values of weighted Minkowski distance with different transition resistances, respectively. By comparing the two tables, it can be found that with the continuous increase of transition resistance, the weighted Minkowski distance of A-phase current and its positive-order component cannot reach the threshold value, while the weighted Minkowski distance of the negative-order component can still effectively identify the fault. This case proves that the aforementioned principle of weight selection is right. In addition, any weighted Minkowski distance exceeding the threshold can assure precise action of protection, so this method still has good reliability under the condition that transition resistance is approximately 1700 Ω, which demonstrates that the method can correctly identify a fault even with very high fault resistance.

4.5 Comparison with other protection methods

Similarity and distance measures are two main methods for the measurement of waveform similarity. Cosine similarity and Pearson similarity are often used by scholars to characterize the similarity of data or waveforms (Jia et al., 2018; Zheng et al., 2021; Jarrahi et al., 2022). The model parameters in Figure 13 are consistent with those in Figure 8; Table 1. The most different part between Figure 8 and Figure 3 is that there are no DGs in Figure 13.

FIGURE 13

FIGURE 13. Single-ended power supply distribution network.

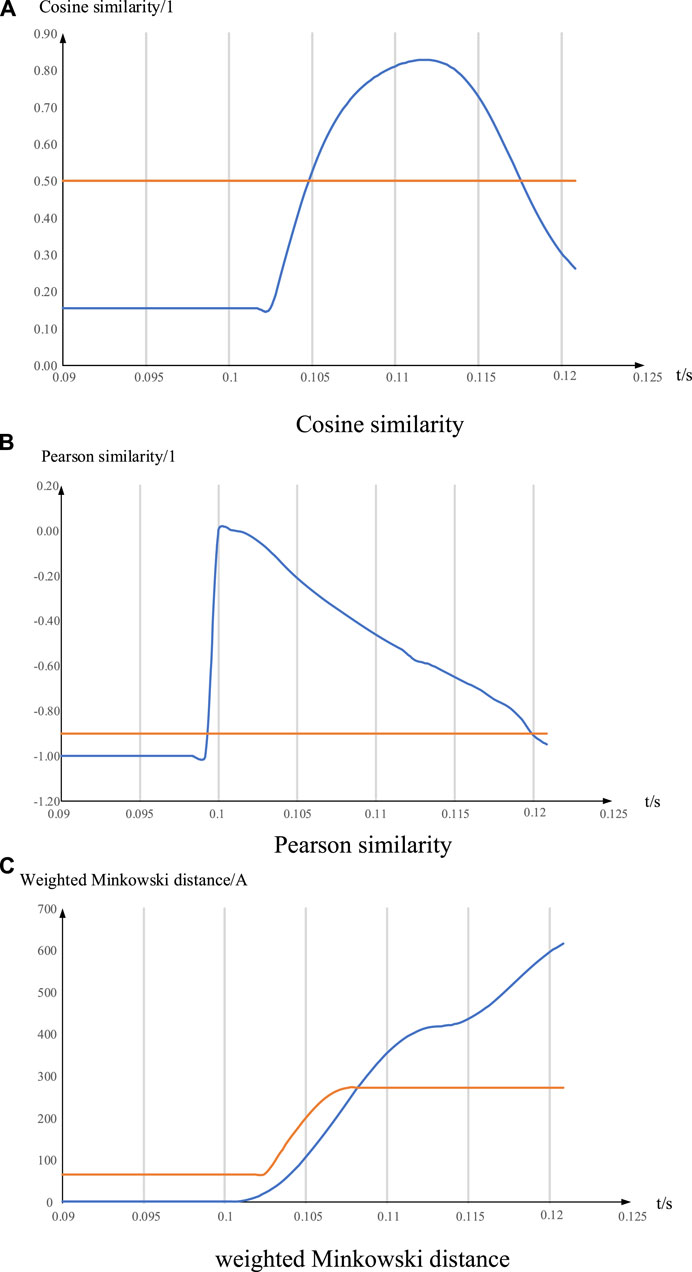
When simulated according to the single-ended power supply distribution network model in Figure 13, this method does not have the problem of protection failure. Otherwise, the other two methods cannot work correctly. This is because the algorithm formula of the method proposed in this paper has the advantage that when a set of data is 0, the molecules and denominators do not tend to zero together. The specific formulas for calculating cosine similarity and Pearson similarity are as follows:

$\cos \left(X,Y\right)=\frac{{\displaystyle \sum _{i=1}^n}\left(x_i\cdot y_i\right)}{\sqrt{{\displaystyle \sum _{i=1}^n}{x}_i^2}\sqrt{{\displaystyle \sum _{i=1}^n}{y}_i^2}}=\frac{{\displaystyle \sum _{i=1}^n}\left(0\cdot y_i\right)}{\sqrt{{\displaystyle \sum _{i=1}^n}{0}^2}\sqrt{{\displaystyle \sum _{i=1}^n}{y}_i^2}}=\frac{0}{0}.(10)$

$\begin{array}{ll}{P}_{pear}\left(X,Y\right)& =\frac{{\displaystyle \sum _{i=1}^n}\left(x_i-\frac{1}{n}{\displaystyle \sum _{j=1}^n}{x}_j\right)\left(y_i-\frac{1}{n}{\displaystyle \sum _{j=1}^n}{y}_j\right)}{\sqrt{{{\displaystyle \sum _{i=1}^n}\left(x_i-\frac{1}{n}{\displaystyle \sum _{j=1}^n}{x}_j\right)}^2}\sqrt{{{\displaystyle \sum _{i=1}^n}\left(y_i-\frac{1}{n}{\displaystyle \sum _{j=1}^n}{y}_j\right)}^2}}\\ =\frac{{\displaystyle \sum _{i=1}^n}\left(0-\frac{1}{n}\cdot 0\right)\left(y_i-\frac{1}{n}{\displaystyle \sum _{j=1}^n}{y}_j\right)}{\sqrt{{{\displaystyle \sum _{i=1}^n}\left(0-\frac{1}{n}\cdot 0\right)}^2}\sqrt{{{\displaystyle \sum _{i=1}^n}\left(y_i-\frac{1}{n}{\displaystyle \sum _{j=1}^n}{y}_j\right)}^2}}=\frac{0}{0}.\end{array}(11)$

When a single-phase ground fault occurs on the protected line, the calculation results and thresholds of these three methods are shown in Figure 14. The blue line in the figure represents the calculated value of the fault criterion, and the yellow line represents the corresponding threshold.

FIGURE 14

FIGURE 14. Comparison of different methods.

From the graph, it can be seen that all three methods can quickly detect the occurrence of faults. However, the calculated values of cosine similarity and Pearson similarity fell below the threshold again at 0.118 s and 0.12 s. Therefore, these two methods cannot accurately detect faults in the single-ended distribution network. This is because the calculated values of these two algorithms begin to change irregularly, as the data on one side of the line tend to 0 after the fault. The weighted Minkowski distance can consistently exceed the threshold, so this method can accurately detect faults.

In recent years, with the development of science and technology, new differentials based on waveform similarity have emerged in an endless stream, and most of them have good sensitivity. For example, a signed correlation index-based differential protection has been proposed by Saber et al. (2023). This method and the method proposed in this paper can reliably identify faults in the protection area. Comparing the two methods based on the speed of protection action, the sensitivity of the two methods is in the same order of magnitude. The signed correlation index-based differential protection operates in approximately 1 ms, and the differential protection based on the Minkowski distance operates in 5–9 ms.

However, the authors make it clear that signed correlation index-based differential protection is suitable for inverter-based islanded microgrids (IBIMGs). The fault current of an IBIMG is small, which is different from that of the distribution network. There is no evidence that this method is suitable for a distribution network whose DG has a large capacity. In China‘s current distribution network protection, three-stage current protection is widely used. The fastest action time of this protection is also in seconds. At the same time, a high-power DG will provide a large short-circuit current, which may cause the original three-stage current protection to malfunction. If the three-stage current protection is still set according to the original grid parameters, the DG may also cause the protection range of the line to change or even lose cooperation with the lower line. In this way, the protection scheme proposed in this paper can fully meet the needs of distribution network protection. The differential protection based on the weighted Minkowski distance can be used as both the main protection scheme and the reserve protection of the line.

5 Conclusion

With the increasing application of DGs in the distribution network, the fault current presents some characteristics, such as the increase of harmonic content, the decrease of the power frequency component, the frequency fluctuation, and the distortion of phase angle. In order to reverse the negative situation in which traditional protection methods can hardly recognize faults accurately in the distribution network with DGs, a differential protection method based on the difference of transient waveform characteristics between both ends of the line during internal faults is proposed. In addition, the weighted Minkowski distance is used to measure the difference of the transient waveform. The following conclusions are drawn:

(1) The proposed method can correctly identify the fault in this paper. It can adapt to strong changes in distributed generation output power and always obtains distinguishable calculation results.

(2) The Minkowski distance is used to measure current similarity to include more uncertain frequency components in fault current in this paper. In addition, the weighted algorithm based on sequence current is adopted to highlight fault characteristics and improve protection sensitivity.

(3) The proposed method can effectively resist the influence of severe frequency fluctuation of the fault current and identify the high transition resistance fault, which presents strong adaptability and feasibility.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

WJ wrote the vast majority of this paper and proposed an overall innovative approach, making him the core contributor. JL built relevant simulation models and conducted simulation verification. SZ wrote some of the content of the paper. Other participants made detailed revisions to each section of the paper. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the Fundamental Research Funds for the Central Universities (Grant Number: 2021QN1067).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2023.1242325/full#supplementary-material

References

Bolandi, T. G., Seyedi, H., Hashemi, S. M., and Nezhad, P. S. (2015). Impedance-differential protection: a new approach to transmission-line pilot protection. IEEE Trans. Power Deliv. 30 (6), 2510–2518. doi:10.1109/TPWRD.2014.2387689

CrossRef Full Text | Google Scholar

Bullich-Massagué, E., Ferrer-San-José, R., Aragüés-Peñalba, M., Serrano-Salamanca, L., Pacheco-Navas, C., and Gomis-Bellmunt, O. (2016). Power plant control in large-scale photovoltaic plants: design, implementation and validation in a 9.4 MW photovoltaic plant. IET Renew. Power Gener. 10, 50–62. doi:10.1049/iet-rpg.2015.0113

CrossRef Full Text | Google Scholar

Cao, H. (2023). The “dual carbon” strategy leads green transformation. Economic Daily. doi:10.28425/n.cnki.njjrb.2023.006978

CrossRef Full Text | Google Scholar

Ding, S., Lin, X., Zhang, Z., Li, Z., Chen, L., and Weng, H. (2019). A novel Hausdorff distance based restrain criterion for zero-sequence differential protection of converter transformer. Int. J. Electr. Power Energy Syst. 105, 753–764. doi:10.1016/j.ijepes.2018.08.046

CrossRef Full Text | Google Scholar

Jarrahi, M. A., Haidar, S., and Teymoor, G. (2022). Protection framework for microgrids with inverter-based DGs: a superimposed component and waveform similarity-based fault detection and classification scheme. IET Generation, Transm. Distribution 16, 11. doi:10.1049/GTD2.12438

CrossRef Full Text | Google Scholar

Jia, K., Li, Y., Fang, Y., Zheng, L., Bi, T., and Yang, Q. (2018). Transient current similarity based protection for wind farm transmission lines. Appl. Energy 225, 42–51. doi:10.1016/j.apenergy.2018.05.012

CrossRef Full Text | Google Scholar

Jia, K., Liu, Q., Yang, B., Zheng, L., Fang, Y., and Bi, T. (2022). Transient Fault current analysis of IIRESs considering controller saturation. IEEE Trans. Smart Grid 13 (1), 496–504. doi:10.1109/TSG.2021.3118680

CrossRef Full Text | Google Scholar

Jia, K., Wang, C., Bi, T., Zhu, R., and Xuan, Z. (2019). Transient current waveform similarity based protection for flexible DC distribution system. IEEE Trans. Industrial Electron. 66 (12), 9301–9311. doi:10.1109/TIE.2019.2891457

CrossRef Full Text | Google Scholar

Jia, K., Yang, Z., Zheng, L., Zhu, Z., and Bi, T. (2021). Spearman correlation-based pilot protection for transmission line connected to PMSGs and DFIGs. IEEE Trans. Industrial Inf. 17 (7), 4532–4544. doi:10.1109/TII.2020.3018499

CrossRef Full Text | Google Scholar

Kar, S., and Subhransu Ranjan, S. (2020). Impact of microgrid operation on the performance of overcurrent relay coordination and assessment of diffe rential relay coordination. Electr. Power Components Syst. 48 (9-10), 1049–1062. doi:10.1080/15325008.2020.1825550

CrossRef Full Text | Google Scholar

Li, H., Deng, C., Zhang, Z., Liang, Y., and Wang, G. (2021). An adaptive fault-component-based current differential protection scheme for distribution networks with inverter-based distributed generators. Int. J. Electr. Power Energy Syst. 128, 106719. doi:10.1016/J.IJEPES.2020.106719

CrossRef Full Text | Google Scholar

Li, Y., Sun, Y., Wang, Q., Sun, K., Li, K. J., and Zhang, Y. (2023). Probabilistic harmonic forecasting of the distribution system considering time-varying uncertainties of the distributed energy resources and electrical loads. Appl. Energy 329, 120298. doi:10.1016/J.APENERGY.2022.120298

CrossRef Full Text | Google Scholar

Liu, H., Li, J., Li, J., Tian, J., Bi, T., Martin, K. E., et al. (2019). Synchronised measurement devices for power systems with high penetration of inverter-based renewable power generators. IET Renew. Power Gener. 13, 40–48. doi:10.1049/iet-rpg.2018.5207

CrossRef Full Text | Google Scholar

Peerapong, S., and Suebkul, K. (2022). Applications of fuzzy soft sets over semigroups based on the Minkowski distance. J. Interdiscip. Math. 25, 8. doi:10.1080/09720502.2022.2083119

CrossRef Full Text | Google Scholar

Qing, H., Qin, L., Liu, K., Hooshyar, A., Ding, H., Gong, C., et al. (2021). A pilot line protection for MT-HVDC grids using similarity of traveling waveforms. Int. J. Electr. Power Energy Syst. 131, 107162. doi:10.1016/J.IJEPES.2021.107162

CrossRef Full Text | Google Scholar

Saber, A., Zeineldin, H., El-Fouly, T. H., and Al-Durra, A. (2023). A signed correlation index-based differential protection scheme for inverter-based islanded microgrids. Int. J. Electr. Power Energy Syst. 145, 108721. doi:10.1016/J.IJEPES.2022.108721

CrossRef Full Text | Google Scholar

Salauddin, A., and Hari, G. O. (2021). Differential positive sequence power angle-based microgrid feeder protection. Int. J. Emerg. Electr. Power Syst. 22, 5. doi:10.1515/IJEEPS-2021-0071

CrossRef Full Text | Google Scholar

Tafti, H. D., Townsend, C. D., Konstantinou, G., and Pou, J. (2019). A multi-mode flexible power point tracking algorithm for photovoltaic power plants. IEEE Trans. Power Electron. 34 (6), 5038–5042. doi:10.1109/TPEL.2018.2883320

CrossRef Full Text | Google Scholar

Tang, L., Dong, X., Luo, S., Shi, S., and Wang, B. (2017). A new differential protection of transmission line based on equivalent travelling wave. IEEE Trans. Power Deliv. 32 (3), 1359–1369. doi:10.1109/TPWRD.2016.2568206

CrossRef Full Text | Google Scholar

Wei, W., Zhang, L., Gao, B., Tang, Y., Chen, N., and Zhu, L. (2014). “Frequency inconsistency in DFIG-based wind farm during outgoing transmission line faults and its effect on longitudinal differential protection,” in The 4th Annual IEEE International Conference on Cyber Technology in Automation, Control and Intelligent, Hong Kong, China, 04-07 June 2014 (IEEE), 25–30. doi:10.1109/CYBER.2014.6917430

CrossRef Full Text | Google Scholar

Weng, H., Chen, H., Wu, L., Huang, J., and Li, Z. (2021). A novel pilot protection scheme for transmission lines based on current distribution histograms and their Bhattacharyya coefficient. Electr. Power Syst. Res. 194, 107056. doi:10.1016/J.EPSR.2021.107056

CrossRef Full Text | Google Scholar

Weng, H., Wang, S., Lin, X., Li, Z., and Huang, J. (2019). A novel criterion applicable to transformer differential protection based on waveform sinusoidal similarity identification. Int. J. Electr. Power Energy Syst. 105, 305–314. doi:10.1016/j.ijepes.2018.08.027

CrossRef Full Text | Google Scholar

Xin, B. (2022). Building a new development pattern by serving, striving to promote high-quality development and writing a new chapter in the great rejuvenation of the Chinese nation [N]. Beijing: The newspaper office of China Electric Power News. doi:10.28061/n.cnki.ncdlb.20011.100010001106

CrossRef Full Text | Google Scholar

Yu, Y., Konstantinou, G., Townsend, C. D., Aguilera, R. P., and Agelidis, V. G. (2017). Delta-connected cascaded H-bridge multilevel converters for large-scale photovoltaic grid integration. IEEE Trans. Industrial Electron. 64 (11), 8877–8886. doi:10.1109/TIE.2016.2645885

CrossRef Full Text | Google Scholar

Zheng, L., Jia, K., Bi, T., Fang, Y., and Yang, Z. (2021). Cosine similarity based line protection for large-scale wind farms. IEEE Trans. Industrial Electron. 68 (7), 5990–5999. doi:10.1109/TIE.2020.2998756

CrossRef Full Text | Google Scholar

Zheng, L., Jia, K., Bi, T., Yang, Z., and Fang, Y. (2020). A novel structural similarity based pilot protection for renewable power transmission line. IEEE Trans. Power Deliv. 35 (6), 2672–2681. doi:10.1109/TPWRD.2020.2973505

CrossRef Full Text | Google Scholar

Zheng, L., Jia, K., Wu, W., Liu, Q., Bi, T., and Yang, Q. (2022). Cosine similarity based line protection for large scale wind farms Part II—the industrial application. IEEE Trans. Industrial Electron. 69 (3), 2599–2609. doi:10.1109/TIE.2021.3069400

CrossRef Full Text | Google Scholar

Zhou, C., Zou, G., Du, X., and Zang, L. (2022). Adaptive current differential protection for active distribution network considering time synchronization error. Int. J. Electr. Power Energy Syst. 140, 108085. doi:10.1016/J.IJEPES.2022.108085

CrossRef Full Text | Google Scholar