Stability analysis of different control modes of grid-connected converters under different grid conditions

With the sustained popularity of renewable energy generation, high penetration of variable energies, e.g., wind and solar, is reshaping the form of power systems and weakening the strength of the grid. The stability mechanism of the grid-connected converter in a weak power network, however, has yet to be evaluated. This paper establishes impedance and transient models for Grid-Following (GFL) as well as Grid-Forming (GFM) converters through the impedance analysis method and equal area criterion analysis method. The stability of these two control methods is then comprehensively studied under small and large interference with different grid conditions. The analytical results show that the GFM control is more stable against small disturbances in a weak network. In contrast, it is prone to a significant disturbance stability problem in the strong grid due to the large grid impedance. The GFL control is more suitable for a vigorous power grid, whereas introducing oscillation in a weak power grid due to its negative damping. Simulation experiments have verified the accuracy of the analytical results.

1 Introduction

To render the electric power system more sustainable, replacing conventional fossil fuel-based power plants with Renewable Energy Sources (RESs) based on power electronic interfaces to the grid is an inevitable trend (Bikdeli et al., 2022), Currently, most RESs are connected to the grid using Grid-Following (GFL) control, which tracks the Point of Common Coupling (PCC) voltage phase and controls the current output in real time through a Phase-Locked Loop (PLL). These GFL RESs can be characterized as controllable current sources (Wen et al., 2015), which are suitable for connection to a strong power grid (Poolla et al., 2019; Chen et al., 2021). However, in a weak power grid, where the grid impedance is very high, it is difficult to guarantee the stability of GFL converters. To improve the system’s stability, RESs must actively form potential high points on the grid to provide voltage and frequency regulation. These control methods that can achieve the abovementioned functions are so-called Grid-Forming (GFM) control (Wu et al., 2016; Lasseter et al., 2019; Khan et al., 2022). Unlike GFL control, GFM RESs present controllable voltage source characteristics with respect to the grid (Chen et al., 2021), and can provide inertia and damping to the system (Chen et al., 2020; Orihara et al., 2021; Xiong et al., 2022), which can enhance the synchronization stability of grid-connected RESs in a weak grid (Anttila, et al., 2022).

Both control strategies (GFL and GFM) have stability problems in different conditions (Lourenço et al., 2021). Suppose we want to compare the stability of grid-connected converters with these control strategies comprehensively and profoundly. In this case, we need to start from two aspects: small disturbance stability and large disturbance stability (Xiong et al., 2020). The most popular analysis methods for assessing power systems’ small disturbance stability problem can be divided into time and frequency domain methods (Xiong et al., 2015; Wang et al., 2018; Wu et al., 2018; Chen and O’Donnell, 2019; Yu et al., 2021). Based on the frequency domain analysis of the impedance model, actual grid-connected converter and AC line impedance models are established. Then the stability criteria of impedance are used to evaluate the system stability. Zhang et al. (2019) and Zhang et al. (2017) state that the sequential impedance has a clear physical meaning compared to the dq-domain impedance and can be measured directly. Therefore, the sequential impedance is more suitable for large-scale RES analysis and practical engineering applications. Feng et al. (2022) investigates the stability of GFL inverters considering grid impedance and proposes several cases of small signal instability caused by positive and negative sequence components. A voltage-controlled and current-controlled VSG (Virtual Synchronous Generator) sequential impedance model is developed (Wu et al., 2018). It is pointed out that the volt-age-controlled type is more suitable for weak grids than the current-controlled VSG. The precise sequence impedance models are derived for the load virtual synchronous machine (LVSM), and the influence of grid impedance on its small disturbance stability is analyzed (Liu et al., 2020).

The new generation power system’s large disturbance stability analysis methods are evaluated: stepwise integration, direct, and linear (Gurrala et al., 2015; Pan et al., 2019). The linear method shows that the converter is stable when a stable equilibrium point exists for its operation after the disturbance (Gao et al., 2016). However, Göksu et al. (2014) presents a viewpoint against the linear approach, i.e., in some cases where a stable equilibrium point exists in the system, the grid-connected converter may also suffer from transient instability. Considering the nonlinear characteristics of the grid-connected converter, Tang et al. (2022) and Wu et al. (2019) propose a method to analyse the large-signal stability of the grid-connected converter using the equal-area criterion. Chen et al. (2019) and Chen et al. (2022) analyze the effect of capacity limitation and PLL frequency limiter on the stability of large disturbances in a GFL converter based on the equal-area criterion, respectively. Chen et al. (2020) proposes a high precision model for GFL converters to capture the effect of current transients on the stability of large disturbances. Based on the above literature, the studies on the stability of grid-connected converters of GFL and GFM types are at the early stage of separate discussions. As a result, few comparative studies on their stability are provided. There needs to be a more exhaustive comparison and discussion on the stability of small and large disturbances for these two control methods.

This paper presents the small interference impedance analysis method and the large interference equal-area criterion analysis method of GFL and GFM converters, aiming at comprehensively comparing the stability of these two converters. The main contributions of this paper are as follows:

(i) The positive sequence impedance models of the GFL and GFM converters are established to evaluate their small disturbance stability.

(ii) The transient models of the GFL and GFM converters are established to evaluate their large disturbance stability.

(iii) The stability of the two different control strategies under different grid conditions, especially the weak grid, is wholly and comprehensively compared and verified by combining the above analysis.

The topology and control strategies for GFL and GFM converter systems utilized in this work are presented in Section 2. Section 3 illustrates the impedance model along with its characteristic analysis. Section 4 analyses the large disturbance synchronous stability. Results and discussion for two control strategies in different network conditions are presented in Section 5. Conclusions are presented in Section 6.

2 Topology and control strategies for GFL and GFM converter systems

2.1 GFL converter

The topology of the GFL converter and its control strategy is shown in Figure 1, which consists of a dc bus, a two-level power electronic inverter, an LC filter, a grid impedance, and an ideal voltage source.

FIGURE 1

FIGURE 1. Control block diagram of the GFL converter.

Currently, the GFL converter uses a vector control strategy in dq frame. This control samples the output current i_abc and voltage u_gabc at the PCC and then convert them into dq components. Furthermore, the PLL gives the grid phase angle θ in the synchronous reference frame. The control of GFL converters usually uses a dual closed-loop control, where the external voltage loop aims to maintain the dc bus current constant. In contrast, the internal current loop converts the reference current into a voltage reference signal. Then the modulation module generates the modulating waveform m_abc. Finally, the Pulse Width Modulation (PWM) generator drives the converter switching circuit to realize the function of regulating the reactive power on the Alternating Current (AC) side and delivering the active power generated by the RES to the grid. For simplicity, the Direct Current (DC) bus voltage U_dc is assumed to be constant, and the outer loop is ignored for modeling processes in the following sections. The transfer functions of the sampling G_del(s), the inner-loop current controller H_c(s), and the PLL controller H_PLL(s) are given in Eqs 1–3, respectively.

${\mathit{G}}_{\mathit{d}\mathit{e}\mathit{l}}\left(\mathit{s}\right)=\frac{{\mathit{G}}_{\mathit{d}\mathit{e}\mathit{l}}}{\mathit{1}+\mathit{s}{\mathit{T}}_{\mathit{d}\mathit{e}\mathit{l}}}(1)$

${\mathit{H}}_{\mathit{c}}\left(\mathit{s}\right)={\mathit{K}}_{\mathit{p}-\mathit{c}}+\frac{{\mathit{K}}_{\mathit{i}-\mathit{c}}}{\mathit{s}}(2)$

${\mathit{H}}_{\mathit{P}\mathit{L}\mathit{L}}\left(\mathit{s}\right)=\left({\mathit{K}}_{\mathit{p}-\mathit{p}\mathit{l}\mathit{l}}+\frac{{\mathit{K}}_{\mathit{i}-\mathit{p}\mathit{l}\mathit{l}}}{\mathit{s}}\right)\times \frac{\mathit{1}}{\mathit{s}}(3)$

where G_del and T_del are the sampling gain and sampling delay, respectively; K_p-c and K_i-c are the Proportional-Integral (PI) control parameters in the current loop; and K_p-pll and K_i-pll are the PI control parameters in the PLL control loop.

2.2 GFM converter

Figure 2 shows the topology of the GFM converter and its control strategy. The GFM control actively forms the voltage output at the PCC point by simulating the synchronous machine power angle characteristics. At the same time, it controls the virtual turn angle according to the active power instead of collecting the voltage and phase at the PCC point through the PLL, and its modulation method is the same as that of the GFL type. The active power control loop of the GFM control simulates the swing equation of a conventional synchronous generator to provide virtual inertia and achieve primary frequency regulation. In contrast, its reactive power control simulates a conventional synchronous generator’s primary voltage regulation characteristics. The virtual rotor equation of motion of the GFM converter is shown below.

$\mathit{J}\frac{\mathit{d}\mathit{\omega }}{\mathit{d}\mathit{t}}={\mathit{P}}_{\mathit{ref}}-{\mathit{P}}_{\mathit{e}}-{\mathit{D}}_{\mathit{d}}\left(\mathit{\omega }-{\mathit{\omega }}_{\mathit{N}}\right)(4)$

$\mathit{\theta }=\frac{\mathbf{1}}{\mathit{S}}\mathit{\omega }(5)$

where J is the virtual inertia coefficient; D_d is the damping coefficient; ω_N and ω are the nominal and virtual angular frequencies, respectively; and θ is the phase angle generated by the active power control loop; P_ref and P_e are the reference active power and the actual active power output, respectively.

FIGURE 2

FIGURE 2. Control block diagram of the GFM converter system.

The excitation system of a synchronous generator is controlled by the excitation current, while the equivalent variable in the inverter control is the reference voltage. Therefore, by simulating a synchronous generator’s excitation current control method, the control equation for voltage regulation can be obtained as follows.

$\sqrt{\mathit{2}}\mathit{E}=\mathit{G}\left(\mathit{s}\right)\left(\sqrt{\mathit{2}}{\mathit{U}}_{\mathit{ref}}-\sqrt{\mathit{2}}{\mathit{U}}_{\mathit{m}}\right)(6)$

where G(s) is the voltage regulator. U_ref and U_m are the effective values of the reference and measured voltages, respectively.

The primary voltage regulation equation of the synchronous generator can be expressed as:

${\mathit{D}}_{\mathit{q}}=\frac{\Delta \mathit{Q}}{\Delta \mathit{V}}=\frac{{\mathit{Q}}_{\mathit{ref}}-{\mathit{Q}}_{\mathit{e}}}{\sqrt{\mathit{2}}{\mathit{U}}_{\mathit{ref}}-\sqrt{\mathit{2}}{\mathit{U}}_{\mathit{N}}}(7)$

where D_q denotes the reactive power regulation coefficient; Q_ref and Q_e are the reference reactive power and real-time reactive power, respectively; and U_N is the effective value of the rated voltage.

Combining Eqs 6, 7, the Q-V equation can be obtained as follows.

$\sqrt{\mathit{2}}\mathit{E}=\frac{\mathit{G}\left(\mathit{s}\right)}{{\mathit{D}}_{\mathit{q}}}\left[{\mathit{Q}}_{\mathit{ref}}-{\mathit{Q}}_{\mathit{e}}+\sqrt{\mathit{2}}{\mathit{D}}_{\mathit{q}}\left({\mathit{U}}_{\mathit{N}}-{\mathit{U}}_{\mathit{m}}\right)\right](8)$

Considering the consistency, the reactive power control loop can be rewritten similarly to the active power loop:

$\sqrt{\mathit{2}}\mathit{E}=\frac{\mathit{1}}{{\mathit{K}}_{\mathit{s}}}\left[{\mathit{Q}}_{\mathit{ref}}-{\mathit{Q}}_{\mathit{e}}+\sqrt{\mathit{2}}{\mathit{D}}_{\mathit{q}}\left({\mathit{U}}_{\mathit{N}}-{\mathit{U}}_{\mathit{m}}\right)\right](9)$

where $K_s$ is the equivalent inertia coefficient of the reactive power loop; E is the effective value of the internal voltage.

The power calculation module in Figure 2 is derived based on the instantaneous power theory. The instantaneous active power P_e and reactive power Q_e output of the GFM converter can be calculated as:

$\left\{\begin{array}{c}{\mathit{P}}_{\mathit{e}}=\frac{\mathit{3}}{\mathit{2}}\left({\mathit{v}}_{\mathit{\alpha }}{\mathit{i}}_{\mathit{\alpha }}+{\mathit{v}}_{\mathit{\beta }}{\mathit{i}}_{\mathit{\beta }}\right)\\ {\mathit{Q}}_{\mathit{e}}=\frac{\mathit{3}}{\mathit{2}}\left({\mathit{v}}_{\mathit{\beta }}{\mathit{i}}_{\mathit{\alpha }}-{\mathit{v}}_{\mathit{\alpha }}{\mathit{i}}_{\mathit{\beta }}\right)\end{array}\right.(10)$

where i_α, i_β and v_α, v_β are the currents and voltages measured in the αβ reference frame, respectively.

Then, the modulated waves of the grid-connected converter are generated from the active and reactive power control loops, which can be expressed as follows.

$\left\{\begin{array}{c}{\mathit{m}}_{\mathit{a}}==\sqrt{\mathit{2}}\mathit{E}\mathit{c}\mathit{o}\mathit{s}\mathit{\theta }\\ {\mathit{m}}_{\mathit{b}}=\sqrt{\mathit{2}}\mathit{E}\mathit{c}\mathit{o}\mathit{s}\left(\mathit{\theta }-\mathit{2}\mathit{\pi }/\mathit{3}\right)\\ {\mathit{m}}_{\mathit{c}}=\sqrt{\mathit{2}}\mathit{E}\mathit{c}\mathit{o}\mathit{s}\left(\mathit{\theta }+\mathit{2}\mathit{\pi }/\mathit{3}\right)\end{array}\right.(11)$

3 Impedance model and characteristic analysis

The grid-connected converter is controlled in a synchronous rotating frame and is stationary concerning the three-phase voltage vector. Considering the characteristics of different impedance modeling methods, sequence impedance modeling based on harmonic linearization applies to GFL and GFM converters. This section presents the small-signal positive sequence impedance modeling of the GFL and GFM control, and their characteristics are compared.

The basic concept of harmonic linearization is that the nonlinear output can be approximated by the first harmonic component under sinusoidal excitation when the target system satisfies certain conditions (Wu et al., 2018). Thus, the nonlinear system can be approximated as an equivalent linear system. By applying harmonic linearization, the positive sequence impedance of the GFL converter can be calculated as:

${\mathit{Z}}_{\mathit{G}\mathit{F}{\mathit{L}}_{-}\mathit{p}}\left(\mathit{s}\right)=\frac{{\mathit{V}}_{\mathit{G}\mathit{F}{\mathit{L}}_{-}\mathit{p}}\left(\mathit{s}\right)}{{\mathit{I}}_{\mathit{G}\mathit{F}{\mathit{L}}_{-}\mathit{p}}\left(\mathit{s}\right)}=\frac{{\mathit{K}}_{\mathit{m}}{\mathit{V}}_{\mathit{d}\mathit{c}}{\mathit{G}}_{\mathit{1}}\left(\mathit{s}\right){\mathit{G}}_{\mathit{del}}\left(\mathit{s}\right)+\mathit{s}{\mathit{L}}_{\mathit{f}}}{\mathit{1}-{\mathit{K}}_{\mathit{m}}{\mathit{V}}_{\mathit{d}\mathit{c}}{\mathit{G}}_{\mathit{del}}\left(\mathit{s}\right)\left[\mathit{1}+{\mathit{G}}_{\mathit{2}}\left(\mathit{s}\right)\right]}(12)$

$\left\{\begin{array}{c}{\mathit{G}}_{\mathit{1}}\left(\mathit{s}\right)={\mathit{H}}_{\mathit{c}}\left(\mathit{s}-\mathit{j}\mathit{2}\mathit{\pi }{\mathit{f}}_{\mathit{1}}\right)-\mathit{j}{\mathit{K}}_{\mathit{d}}\\ {\mathit{G}}_{\mathit{2}}\left(\mathit{s}\right)=\frac{{\mathit{T}}_{\mathit{PLL}}\left(\mathit{s}-\mathit{j}\mathit{2}\mathit{\pi }{\mathit{f}}_{\mathit{1}}\right)}{\mathit{2}{\mathit{V}}_{\mathit{d}}}\left[{\mathit{H}}_{\mathit{c}}\left(\mathit{s}-\mathit{j}\mathit{2}\mathit{\pi }{\mathit{f}}_{\mathit{1}}\right)\left({\mathit{I}}_{\mathit{d}\mathit{r}}+\mathit{j}{\mathit{I}}_{\mathit{q}\mathit{r}}\right)\right]\\ {\mathit{T}}_{\mathit{PLL}}\left(\mathit{s}\right)=\frac{{\mathit{V}}_{\mathit{d}}{\mathit{H}}_{\mathit{PLL}}\left(\mathit{s}\right)}{\mathit{1}+{\mathit{V}}_{\mathit{d}}{\mathit{H}}_{\mathit{PLL}}\left(\mathit{s}\right)}\end{array}\right.(13)$

where V_dc and V_d are the dc bus voltage and its steady-state value, respectively; L_f is the filter inductance value; f₁ is the grid frequency; K_m is the modulation gain; K_d is the current loop decoupling factor; I_dr and I_qr are the steady-state values of the d-axis and q-axis current references, respectively.

The positive sequence impedance of the grid-forming control can be calculated as:

${\mathit{Z}}_{GF{\mathit{M}}_{-}\mathit{p}}\left(\mathit{s}\right)=\frac{{\mathit{V}}_{GF{\mathit{M}}_{-}\mathit{p}}\left(\mathit{s}\right)}{{\mathit{I}}_{GF{\mathit{M}}_{-}\mathit{p}}\left(\mathit{s}\right)}=\frac{{\mathit{G}}_{\mathit{4}}\left(\mathit{s}\right){\mathit{e}}^{\mathit{j}{\mathit{\phi }}_{\mathrm{i}\mathrm{r}}}+\mathit{s}{\mathit{L}}_{\mathit{f}}}{\mathit{1}+{\mathit{G}}_{\mathit{4}}\left(\mathit{s}\right){\mathit{e}}^{\mathit{j}\left({\mathit{\phi }}_{vit}-{\mathit{\phi }}_{\mathit{i}\mathit{1}}\right)}}(14)$

$\left\{\begin{array}{c}{\mathit{G}}_{\mathit{3}}\left(\mathit{s}\right)=\frac{\mathit{1}}{\mathit{s}\left(Js+{\mathit{D}}_{\mathit{d}}\right)}\\ {\mathit{G}}_{\mathit{4}}\left(\mathit{s}\right)=\frac{\mathit{3}{\mathit{V}}_{\mathit{1}}}{\mathit{4}{\mathit{\omega }}_{\mathit{N}}}{\mathit{G}}_{\mathit{del}}\left(\mathit{s}\right){\mathit{G}}_{\mathit{3}}\left(\mathit{s}-\mathit{j}\mathit{2}\mathit{\pi }{\mathit{f}}_{\mathit{1}}\right)\end{array}\right.(15)$

where V₁ is the effective value of the voltage at PCC point; φ_vir = δ+π/2, δ is the virtual power angle; and φ_i1 is the fundamental current phase.

The system parameters of GFL control and GFM control evaluated in this paper are shown in Tables 1, 2. The control parameters ensure good dynamic performance and can be utilized to analyze their stability when connected to the weak grid.

TABLE 1

TABLE 1. GFM control parameters.

TABLE 2

TABLE 2. GFL control parameters.

The amplitude-frequency characteristic curves of the positive sequence impedance for GFM control and GFL control are shown in Figures 3, 4. In the figures, the blue and red lines indicate the positive sequence impedance model and the impedance Z_g(s) of the grid, respectively. Comparing Figures 3, 4, we can see that the impedance amplitude of the GFM control is smaller than that of the GFL control in the low and medium frequency bands due to the external characteristics of the GFM control are expressed as a voltage source with a small equivalent output impedance. In contrast, the external characteristics of the GFL control are expressed as a current source with a more significant equivalent output impedance. At the same time, the positive sequence impedance of the GFM control is inductive, which is consistent with the impedance characteristics under the weak grid. In comparison, the positive sequence impedance of the GFL control is capacitive in the middle frequency band, which leads to the oscillation problem of the GFL control interacting with the inductive grid.

FIGURE 3

FIGURE 3. GFM control positive sequence impedance.

FIGURE 4

FIGURE 4. GFL control positive sequence impedance.

4 Large disturbance synchronous stability analysis

4.1 GFM large disturbance stability

GFM converter controls its output voltage through the reactive control loop. Assuming that the voltage at the output is a constant value, the grid voltage is U_g∠0, and the grid resistance is ignored, the active power output of the GFM converter can be expressed as follows:

${\mathit{P}}_{\mathit{e}}=\left(\sqrt{\mathit{2}}\mathit{E}{\mathit{U}}_{\mathit{g}}/{\mathit{X}}_{\mathit{g}}\right)\mathit{sin}\mathit{\delta }(16)$

Eq. 16 shows that the active power output Pe is related to the grid impedance X_g, network side voltage, and virtual power angle. Merging Eqs 4, 16, the active power control loop for the GFM control is:

$\mathit{J}\ddot{\mathit{\delta }}={\mathit{P}}_{\mathit{ref}}-\frac{\sqrt{\mathit{2}}\mathit{E}{\mathit{U}}_{\mathit{g}}}{{\mathit{X}}_{\mathit{g}}}\mathit{sin}\left(\mathit{\delta }\right)-{\mathit{D}}_{\mathit{d}}\dot{\mathit{\delta }}(17)$

This equation leads to the GFM control transient model (see Figure 5). Eq. 16 determines the system recovery capability, while the deviation of the power reference value P_ref from the actual active power output drives the virtual rotor motion, the output angular frequency ω, and the angle δ.

FIGURE 5

FIGURE 5. GFM control transient model.

From Eq. 17 and the transient model shown in Figure 5, it is clear that the system restoring capability is related to the grid impedance. The Pe-δ curves of the GFM control with different grid strengths and voltage dips are given in Figure 6. The solid line corresponds to the strong grid with short-circuit ratio SCR = 4, while the dashed line corresponds to the weak grid with short-circuit ratio SCR = 2. When in the strong grid condition, assuming that the GFM control initially operates at the equilibrium point a, when the grid voltage drops from 1 pu to 0.6 pu, the power angle characteristic curve will change from the solid blue line to the solid red line. At that time, the acceleration power P_re-P_e is more significant than zero, and the output angular frequency increases. The drive δ red solid line moves to the equilibrium point b and reaches the maximum angular frequency at point b. After passing through point b, the acceleration power becomes negative, so the system output angular frequency decreases. As shown in Figure 6, the deceleration area is more prominent at this point, and δ can re-stabilize at equilibrium point b. However, if the deceleration area is too small so that the angular frequency is still greater than ω_N when passing through point c, the system will lose stability. Therefore, as seen in Figure 6, the weak grid condition indicated by the dashed line leads to a significant decrease in the P_e-δ curve due to the increase in grid impedance. In the same deep voltage dip case, the power angle curve changes from the blue dashed line to the red dashed line after the system contains almost no deceleration area, leading to system instability. The above analysis shows that the reduction in grid strength leads to a reduction in the stability of large disturbances in the GFM control.

FIGURE 6

FIGURE 6. Schematic diagram of large disturbance stability analysis of GFM control converters.

4.2 GFL large disturbance stability

GFL control relies on the PLL module to identify terminal voltage U_t to provide synchronous phase θ_pll for synchronous operation. The large disturbance stability of GFL control mainly depends on the closed-loop control composed of a PLL module and current control. The phase-locked loop dynamics can be represented in Figure 7. Under normal operating conditions, the output current vector I, the terminal voltage vector U_t, and the grid voltage vector U_g rotate at the output angular velocity ω_pll of the PLL in a GFL system.

FIGURE 7

FIGURE 7. Grid-following control phase locked loop dynamics.

Assuming that the dynamic performance of the GFM control meets the requirement that I is consistent with the reference value I_dqref In this case, there are:

$\mathit{I}=\left({\mathit{i}}_{\mathit{dref}}+\mathit{j}{\mathit{i}}_{\mathit{qref}}\right){\mathit{e}}^{\mathit{j}{\mathit{\theta }}_{\mathit{pll}}}(18)$

From Eq. 18, it can be seen that the actual output current I of GFL control is related to I_dqref and the PLL dynamics, and its terminal voltage can be expressed as:

${\mathit{U}}_{\mathit{t}}={\mathit{U}}_{\mathit{g}}+{\mathit{Z}}_{\mathit{g}}\left({\mathit{\omega }}_{\mathit{pll}}\right)\mathit{I}(19)$

where Z_g = R_g + jX_g represents the line impedance, and R_g is generally small in a large inductive power grid. According to Eqs 18, 19, the PLL dynamics further influence the terminal voltage by affecting the output current. The terminal voltage is added to the PLL module, which, in turn, affects its output phase.

According to the PLL model, the terminal voltage q-axis component can be expressed as:

${\mathit{u}}_{tq}={\mathit{R}}_{\mathit{g}}{\mathit{i}}_{\mathit{qref}}+{\mathit{\omega }}_{\mathit{0}}{\mathit{L}}_{\mathit{g}}{\mathit{i}}_{\mathit{dref}}+{\mathit{\omega }}_{\mathit{p}}{\mathit{L}}_{\mathit{g}}{\mathit{i}}_{\mathit{dref}}-{\mathit{U}}_{\mathit{g}}\mathit{sin}\left(\mathit{\delta }\right)(20)$

As can be seen from Eq. 20, u_tq is determined by grid impedance, grid-side voltage, current reference value, and PLL output phase. Combining Eq. 20 with the PLL dynamics, a transient model with grid control can be obtained (see Figure 8), where δ in the figure is the virtual power angle.

FIGURE 8

FIGURE 8. GFL control transient model.

The model in Figure 8 can be organized as:

${\mathit{u}}_{in}={\mathit{a}}_{\mathit{1}}\ddot{\mathit{\delta }}+{\mathit{a}}_{\mathit{2}}\dot{\mathit{\delta }}+{\mathit{U}}_{\mathit{g}}\mathit{sin}\left(\mathit{\delta }\right)(21)$

Where,

${\mathit{u}}_{in}={\mathit{R}}_{\mathit{g}}{\mathit{i}}_{\mathit{qref}}+{\mathit{\omega }}_{\mathit{0}}{\mathit{L}}_{\mathit{g}}{\mathit{i}}_{\mathit{dref}}(22)$

${\mathit{a}}_{\mathit{1}}=\left(\mathit{1}-{\mathit{k}}_{\mathit{p}-\mathit{pll}}{\mathit{L}}_{\mathit{g}}{\mathit{i}}_{\mathit{dref}}\right)/{\mathit{k}}_{\mathit{i}-\mathit{pll}}(23)$

${\mathit{a}}_{\mathit{2}}=-{\mathit{L}}_{\mathit{g}}{\mathit{i}}_{\mathit{dref}}+\left({\mathit{k}}_{\mathit{p}-\mathit{pll}}{\mathit{U}}_{\mathit{g}}\mathit{cos}\left(\mathit{\delta }\right)\right)/{\mathit{k}}_{\mathit{i}-\mathit{pll}}(24)$

According to the GFL control transient model and Eq. 21, the PI parameter (k_p-pll + k_i-pll/s) of PLL can be regarded as virtual inertia; L_gidref can be considered as system damping. The deviation between the input u_in and U_gsin(δ) drives the PLL action, and outputs angular frequency ω_pll and virtual power angle δ. Unlike the configuration control adjustable damping coefficient, there are:

$-{\mathit{L}}_{\mathit{g}}{\mathit{i}}_{\mathit{dref}}+\left({\mathit{k}}_{\mathit{p}-\mathit{pll}}{\mathit{U}}_{\mathit{g}}\mathit{cos}\left(\mathit{\delta }\right)\right)/{\mathit{k}}_{\mathit{i}-\mathit{pll}}>\mathit{0}(25)$

$\mathit{\delta }<\mathit{arccos}\left(\frac{{\mathit{L}}_{\mathit{g}}{\mathit{l}}_{\mathit{dref}}{\mathit{k}}_{\mathit{i}-\mathit{pll}}}{{\mathit{U}}_{\mathit{g}}{\mathit{k}}_{\mathit{p}-\mathit{pll}}}\right),\mathit{\delta }\mathit{\in }\left[\mathit{0},\mathit{\pi }\right](26)$

In other words, when Eqs 25, 26 are satisfied, there is positive damping with GFL control, which is conducive to the recovery of the converter in the transient process. Otherwise, GFL control will appear as negative damping and thus, destroying its large disturbance stability.

Figure 9 shows the u_tq-δ curve of GFL control under transient conditions. Assuming that the GFL control initially runs at the equilibrium point b, when the voltage input increases from u_ino to u_in, the accelerating voltage (u_in-u_tq) drives u_tq to point a. At this point, the accelerating voltage is zero, but the angular frequency ω_pll is still higher than the synchronous angular frequency ω_o, causing δ increase. When the δ is greater than δ_a, the accelerating voltage becomes negative, and the driving ω_pll decelerates to ω_o and reaches point c. However, since the accelerating voltage is still negative, the ω_pll continues to decelerate below ω_o while moving toward point a. If there is positive damping in GFL control, the δ will stabilize at the new equilibrium point. Under the condition of no damping or negative damping, the δ will constantly oscillate between point b and point c, or even away from the original equilibrium point. Since the damping coefficient is negatively correlated with L_g, a large L_g will cause negative damping of the system, resulting in system instability under a weak grid. In addition, increasing L_g will also increase u_in, thereby increasing the acceleration area in the transient process, which is not conducive to system stability.

FIGURE 9

FIGURE 9. Schematic diagram of large disturbance stability analysis of GFL control converters.

In summary, the impedance of the power grid affects both GFL control and GFM control. Strong grid conditions can improve the large disturbance stability of both controls. However, under a weak power grid, the damping coefficient of the GFM control converter is only determined by the control parameter D_d, which can easily maintain the positive damping effect. However, due to the damping coefficient of the GFL control converter, the parameter L_g is affected. When the grid impedance is high under the weak grid, the GFL control converter will show negative damping and reduce its large disturbance stability.

5 Simulation verification

In order to verify the correctness of the stability analysis of small disturbance and large disturbance proposed in this paper under weak power grid, a simulation model of electromagnetic transient of GFL control and GFM control is built in Matlab/Simulink. The control parameters are shown in Tables 1, 2 above and the grid reference voltage is 10 kV. The grid inductance l_g is set to 0.1062 H for a weak power grid and the short circuit ratio SCR = 2, while the l_g is set to 0.0531 H and the short circuit ratio SCR = 4 for a strong power grid.

5.1 Verification of small disturbance stability

In this section, different short-circuit ratios are used to simulate the power grid strength to verify the small disturbance stability of GFL and GFM control under the weak power grid. In the simulation experiment, these controls are first utilized in the strong grid condition (SCR = 4). The impedance switch between GFL and GFM control in 1.5 s, respectively, to make them work in the weak grid condition (SCR = 2). Figure 10 presents the results of the three-phase current simulation experiment under the simulated grid strength of GFL control under different short-circuit ratios and the analysis results of the Total Harmonic Distortion (THD). It can be seen that in a strong power grid, the GFL control can operate stably, and the harmonic components of the output current are nearly zero. The three-phase current remains balanced, but when switching to the weak grid for SCR = 2, the three-phase current waveform has equal amplitude oscillations and loses stability, THD is as high as 20%. In contrast, the three-phase current with GFM control in Figure 11 has amplitude reduction oscillations under the condition of a strong power grid. The oscillation frequency and amplitude comparison performance are smaller than that of the weak grid type and the THD of GFM control under strong power grid conditions is approximately 9%. At the same time, GFM control can operate stably under weak grid conditions, and the three-phase current will be balanced quickly, and THD is only 1%. The simulation results are consistent with the analysis results of the small disturbance stability of the two types of control in a weak power grid in this paper. The small disturbance stability of GFM control under the weak network is significantly better than that of GFL control.

FIGURE 10

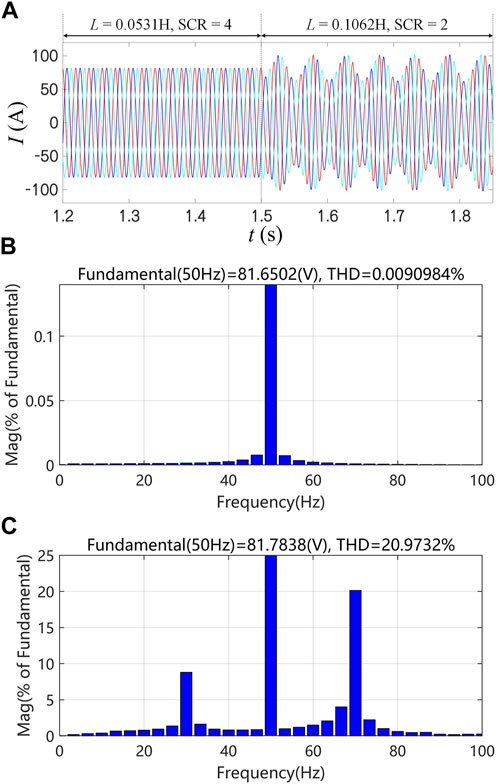
FIGURE 10. Simulation of three-phase currents with different short-circuit ratios for GFL control and its THD analysis results: (A) Simulation result; (B) THD analysis results for SCR = 4; (C) THD analysis results for SCR = 2.

FIGURE 11

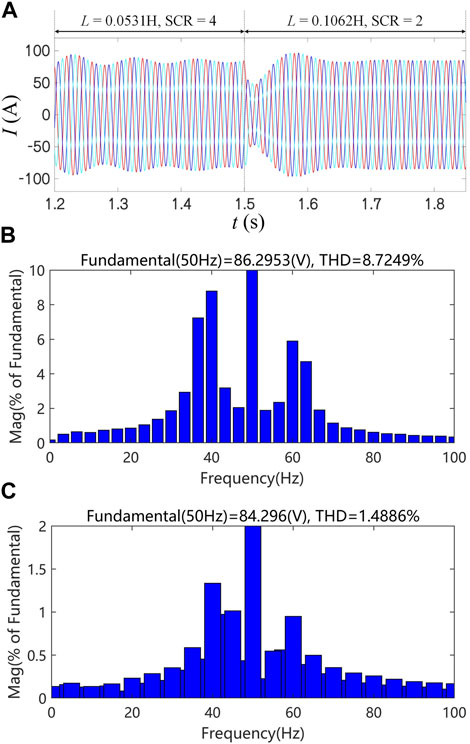
FIGURE 11. Simulation of three-phase currents with different short-circuit ratios for GFM control and its THD analysis results: (A) Simulation result; (B) THD analysis results for SCR = 4; (C) THD analysis results for SCR = 2.

5.2 Verification of large disturbance stability

In order to verify the large disturbance stability of GFL and GFM control, the grid voltage drop of different degrees is simulated for these controls based on different power grid strengths. The grid voltage is reduced for a small voltage drop from 1 pu to 0.8 pu at 2.5 s. Figures 12A, B are the three-phase current simulation results of GFM and GFL control under the strong grid condition with SCR = 4, respectively. It can be seen that under strong grid conditions when the voltage drops slightly, both controls can maintain stability after the voltage drops. GFM control in Figure 12A has enough deceleration area to remain stable after a voltage drop. However, its transient process is slightly longer than the GFL control, as shown in Figure 12B. The transient and steady-state currents after returning to stability are more significant than the GFL control. It can be seen that under a strong power grid condition, GFL control can stabilize faster than GFM control after a small voltage drop. The current amplitude of GFL control after stabilization is also lower than that of GFM control, which makes it difficult to exceed the current protection limit after the voltage drop.

FIGURE 12

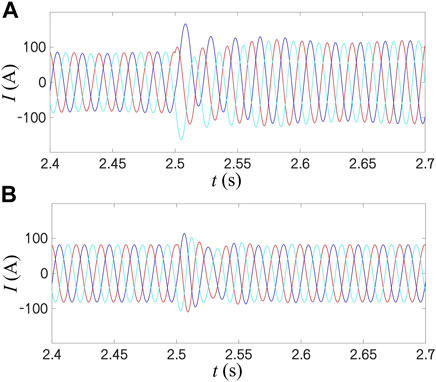
FIGURE 12. Simulation of three-phase currents for GFM and GFL control under strong grid: voltage dips to 0.8 pu: (A) GFM; (B) GFL.

Figures 13A, B are the three-phase current simulation results of the two controls under weak grid conditions with SCR = 2. Under weak grid conditions, although the increase of grid impedance reduces the power angle characteristic curve of GFM control due to the low voltage drop amplitude, GFM control still has a sufficient deceleration area (see Figure 13A). GFM control can remain stable, and the transient and steady-state currents are more substantial and lower in the power grid state. For GFL control shown in Figure 13B, the three-phase current waveform is unstable be-fore and after the voltage drop. The oscillation amplitude increases after the voltage drop because the voltage is initially unstable before and after. The weak grid makes GFL control appear negative damping; thus, the three-phase current waveform is un-stable before and after the voltage drop. The oscillation amplitude further increases after the voltage drop.

FIGURE 13

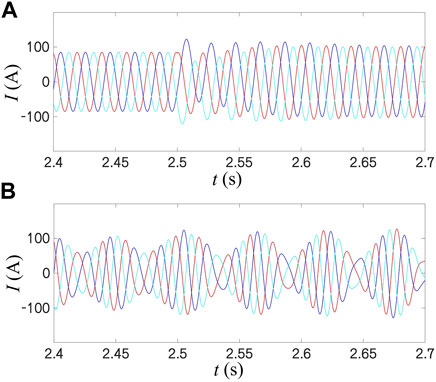
FIGURE 13. Simulation of three-phase currents for GFM and GFL control under weak grid: voltage dips to 0.8 pu: (A) GFM; (B) GFL.

Considering the significant voltage drop, we reduce the grid voltage from 1 pu to 0.6 pu at 2.5 s about these two controls. Figure 14A is the three-phase current simulation results of GFM control under the condition of a strong power grid. According to the analysis of Section 4.1, at this time, due to the acceleration area still tiny than the deceleration area, after a transient process for about 0.4 s, the GFM control under the strong grid is stable after the voltage drop and the three-phase cur-rent is balanced. However, the transient process is more extended, and the steady-state current is high. With the same condition, the GFL control shown in Figure 14B has significantly superior performance after voltage drop, the transient process is shorter, and the current amplitude is unchanged after stabilization, which can better avoid the over-current.

FIGURE 14

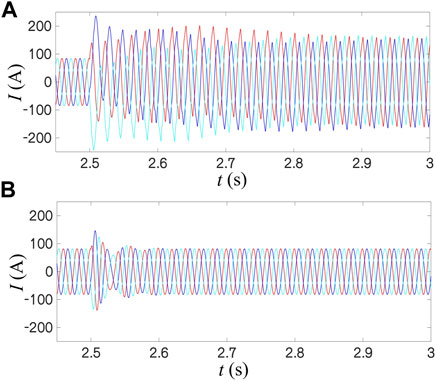
FIGURE 14. Simulation of three-phase currents for GFM and GFL control under strong grid: voltage dips to 0.6 pu: (A) GFM; (B) GFL.

In the case of a weak grid, the GFM control shown in Figure 15A becomes unstable after the voltage drop. According to the power angle characteristic curve of GFM control shown in Figure 6, due to the large impedance of the power grid, at this time, the power angle curve is significantly reduced. Moreover, the deceleration area is insufficient after the voltage drop, resulting in the instability of GFM control. For Grid-following control under the same condition, as shown in Figure 15B, the three-phase current waveform is similar to the case of a slight voltage drop. The more significant grid impedance makes GFL control unstable before the voltage drop. The voltage drop further aggravates the oscillation due to the negative damping effect. The above simulation results are consistent with the analysis of enormous disturbance stability in Section 4.

FIGURE 15

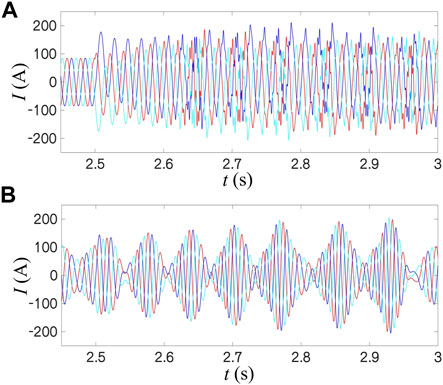
FIGURE 15. Simulation of three-phase currents for GFM and GFL control under weak grid: voltage dips to 0.6 pu: (A) GFM; (B) GFL.

In summary, according to the analysis of the stability of small disturbance and large disturbance of the GFL control and GFM control, as well as the simulation experiment results, the following conclusions can be further drawn: GFL control is more suitable for strong power grids with SCR >4, while instability is prone to occur under weak power grid conditions with SCR <2. On the other hand, for GFM control, under strong power grid conditions with SCR >4, its stability under small disturbances is worse than that of GFL control. However, as SCR decreases, indicating a decrease in grid strength, GFM control gradually outperforms GFL control in terms of stability. Under weak power grid conditions with SCR <2, significant large disturbance stability issues only exist when the grid voltage decreases significantly. In other cases, GFM control demonstrates significant advantages in stability compared to GFL control.

6 Conclusion

This paper first compared and analyzed the small disturbance stability of GFL and GFM control based on the impedance analysis method. And then, separately, the paper analyzed the influence of the power grid strength on the large disturbance stability of GFL and GFM control based on the equal area rule. The following conclusions can be drawn from the comparative analysis and simulation results of the two control methods.

(1) The equivalent impedance of the GFL control converter in the medium frequency band is large and capacitive, and it is easy to oscillate when interacting with an inductive power grid. In contrast, the equivalent impedance of the GFM control is small and inductive, which has better small interference stability under a weak power grid.

(2) In strong power grids, GFL control maintains a positive damping effect, whereas under weak grid conditions, GFL control exhibits negative damping, aggravates the oscillation and further deteriorating its significant interference stability. GFM control damping can be adjusted, and its enormous disturbance stability under the weak grid is better than GFL control. However, the large grid impedance will reduce the power angle characteristic curve, and it is easy to have a significant disturbance stability problem in the case of a deep voltage drop.

(3) GFL control is more suitable for application in strong power grid conditions with SCR >4. Under conditions where 2 < SCR < 4, the large disturbance stability and small disturbance stability of GFM control gradually surpass GFL control as the grid strength decreases. Under weak power grid conditions with SCR <2, GFL control exhibits poorer stability, while GFM control only experiences significant large disturbance stability issues when there is a deep voltage drop. Overall, GFM control is more suitable for application in weak power grids compared to GFL control.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, ZX; methodology, ZX and YQ; software, ZX; validation, ZL and CJ; resources, BZ; data curation, BZ; writing–original draft preparation, ZX; Table drawing, YQ; writing–review and editing, ZL and CJ; project administration, ZX; funding acquisition, ZX and XC; review comments reply and modify, XC. All authors contributed to the article and approved the submitted version.

Funding

This research was funded by the Technology Programme of State Grid Xinjiang and grant number 5230DK22000V.

Conflict of interest

Authors ZX, YQ, ZL, CJ, and BZ were employed by Xinjiang Electric Power Research Institute of State Grid Xinjiang Electric Power, Co., Ltd. Author XC was employed by State Grid Xinjiang Power Co., Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anttila, S., Döhler, J. S., Oliveira, J. G., and Boström, C. (2022). Grid forming inverters: a review of the state of the art of key elements for microgrid operation. Energies 15 (15), 5517. doi:10.3390/en15155517

CrossRef Full Text | Google Scholar

Bikdeli, E., Islam, M. R., Rahman, M. M., and Muttaqi, K. M. (2022). State of the art of the techniques for grid forming inverters to solve the challenges of renewable rich power grids. Energies 15 (5), 1879. doi:10.3390/en15051879

CrossRef Full Text | Google Scholar

Chen, J., Liu, M., Geng, H., O'Donnell, T., and Milano, F. (2022). Impact of PLL frequency limiter on synchronization stability of grid feeding converter. IEEE Trans. Power Syst. 37 (3), 2487–2490. doi:10.1109/TPWRS.2022.3145636

CrossRef Full Text | Google Scholar

Chen, J., Liu, M., Guo, R., Zhao, N., Milano, F., and O'Donnell, T. (2021b). Co-ordinated grid forming control of AC-side-connected energy storage systems for converter-interfaced generation. Int. J. Elec. Power 133, 107201. doi:10.1016/j.ijepes.2021.107201

CrossRef Full Text | Google Scholar

Chen, J., Liu, M., Milano, F., and O'Donnell, T. (2020a). Adaptive virtual synchronous generator considering converter and storage capacity limits. CSEE JPES 8 (2), 580–590. doi:10.17775/CSEEJPES.2019.03360

CrossRef Full Text | Google Scholar

Chen, J., Liu, M., O'Donnell, T., and Milano, F. (2020b). Impact of current transients on the synchronization stability assessment of grid-feeding converters. IEEE Trans. Power Syst. 35 (5), 4131–4134. doi:10.1109/TPWRS.2020.3009858

CrossRef Full Text | Google Scholar

Chen, J., Liu, M., O'Donnell, T., and Milano, F. (2021a). “On the synchronization stability of converters connected to weak resistive grids,” Proceedings of the 2021 IEEE Power & Energy Society General Meeting (PESGM), July 2021, Washington, DC, USA, 1–5. doi:10.1109/PESGM46819.2021.9638083

CrossRef Full Text | Google Scholar

Chen, J., Milano, F., and O'Donnell, T. (2019). Assessment of grid-feeding converter voltage stability. IEEE Trans. Power Syst. 34 (5), 3980–3982. doi:10.1109/TPWRS.2019.2920516

CrossRef Full Text | Google Scholar

Chen, J., and O'Donnell, T. (2019). Parameter constraints for virtual synchronous generator considering stability. IEEE Trans. Power Syst. 34 (3), 2479–2481. doi:10.1109/TPWRS.2019.2896853

CrossRef Full Text | Google Scholar

Feng, G., Ye, Z., Xia, Y., Huang, L., and Wang, Z. (2022). Impedance modeling and stability analysis of three-phase four-wire inverter with grid-connected operation. Energies 15 (8), 2754. doi:10.3390/en15082754

CrossRef Full Text | Google Scholar

Gao, F., Bozhko, S., Costabeber, A., Patel, C., Wheeler, P., Hill, C. I., et al. (2016). Comparative stability analysis of droop control approaches in voltage-source-converter-based DC microgrids. IEEE Trans. Power Electr. 32 (3), 2395–2415. doi:10.1109/TPEL.2016.2567780

CrossRef Full Text | Google Scholar

Göksu, Ö., Teodorescu, R., Bak, C. L., Iov, F., and Kjær, P. C. (2014). Instability of wind turbine converters during current injection to low voltage grid faults and PLL frequency based stability solution. IEEE Trans. Power Syst. 29 (4), 1683–1691. doi:10.1109/TPWRS.2013.2295261

CrossRef Full Text | Google Scholar

Gurrala, G., Dimitrovski, A., Pannala, S., Simunovic, S., and Starke, M. (2015). Parareal in time for fast power system dynamic simulations. IEEE Trans. Power Syst. 31 (3), 1820–1830. doi:10.1109/TPWRS.2015.2434833

CrossRef Full Text | Google Scholar

Khan, S. A., Wang, M., Su, W., Liu, G., and Chaturvedi, S. (2022). Grid-forming converters for stability issues in future power grids. Energies 15 (14), 4937. doi:10.3390/en15144937

CrossRef Full Text | Google Scholar

Lasseter, R. H., Chen, Z., and Pattabiraman, D. (2019). Grid-forming inverters: a critical asset for the power grid. IEEE J. Em. Sel. Top. P. 8 (2), 925–935. doi:10.1109/JESTPE.2019.2959271

CrossRef Full Text | Google Scholar

Liu, Y., Zhou, X., Yu, H., Hong, L., Xia, H., Yin, H., et al. (2020). Sequence impedance modeling and stability assessment for load converters in weak grids. IEEE Trans. Ind. Electr. 68 (5), 4056–4067. doi:10.1109/TIE.2020.2987257

CrossRef Full Text | Google Scholar

Lourenço, L. F., Perez, F., Iovine, A., Damm, G., Monaro, R. M., and Salles, M. B. (2021). Stability analysis of grid-forming MMC-HVDC transmission connected to legacy power systems. Energies 14 (23), 8017. doi:10.3390/en14238017

CrossRef Full Text | Google Scholar

Orihara, D., Kikusato, H., Hashimoto, J., Otani, K., Takamatsu, T., Oozeki, T., et al. (2021). Contribution of voltage support function to virtual inertia control performance of inverter-based resource in frequency stability. Energies 14 (14), 4220. doi:10.3390/en14144220

CrossRef Full Text | Google Scholar

Pan, D., Wang, X., Liu, F., and Shi, R. (2019). Transient stability of voltage-source converters with grid-forming control: a design-oriented study. IEEE J. Em. Sel. Top. P. 8 (2), 1019–1033. doi:10.1109/JESTPE.2019.2946310

CrossRef Full Text | Google Scholar

Poolla, B. K., Groß, D., and Dörfler, F. (2019). Placement and implementation of grid-forming and grid-following virtual inertia and fast frequency response. IEEE Trans. Power Syst. 34 (4), 3035–3046. doi:10.1109/TPWRS.2019.2892290

CrossRef Full Text | Google Scholar

Tang, Y., Tian, Z., Zha, X., Li, X., Huang, M., and Sun, J. (2022). An improved equal area criterion for transient stability analysis of converter-based microgrid considering nonlinear damping effect. IEEE Trans. Power Electr. 37 (9), 11272–11284. doi:10.1109/TPEL.2022.3164687

CrossRef Full Text | Google Scholar

Wang, X., and Blaabjerg, F. (2018). Harmonic stability in power electronic-based power systems: concept, modeling, and analysis. IEEE Trans. Smart Grid 10 (3), 2858–2870. doi:10.1109/tsg.2018.2812712

CrossRef Full Text | Google Scholar

Wen, B., Dong, D., Boroyevich, D., Burgos, R., Mattavelli, P., and Shen, Z. (2015). Impedance-based analysis of grid-synchronization stability for three-phase paralleled converters. IEEE Trans. Power Electr. 31 (1), 26–38. doi:10.1109/TPEL.2015.2419712

CrossRef Full Text | Google Scholar

Wu, H., Ruan, X., Yang, D., Chen, X., Zhao, W., Lv, Z., et al. (2016). Small-signal modeling and parameters design for virtual synchronous generators. IEEE Trans. Ind. Electron. 63 (7), 4292–4303. doi:10.1109/tie.2016.2543181

CrossRef Full Text | Google Scholar

Wu, H., and Wang, X. (2019). Design-oriented transient stability analysis of PLL-synchronized voltage-source converters. IEEE Trans. Power Electr. 35 (4), 3573–3589. doi:10.1109/TPEL.2019.2937942

CrossRef Full Text | Google Scholar

Wu, W., Chen, Y., Zhou, L., Luo, A., Zhou, X., He, Z., et al. (2018b). Sequence impedance modeling and stability comparative analysis of voltage-controlled VSGs and current-controlled VSGs. IEEE Trans. Ind. Electr. 66 (8), 6460–6472. doi:10.1109/TIE.2018.2873523

CrossRef Full Text | Google Scholar

Wu, W., Zhou, L., Chen, Y., Luo, A., Dong, Y., Zhou, X., et al. (2018a). Sequence-impedance-based stability comparison between VSGs and traditional grid-connected inverters. IEEE Trans. Power Electr. 34 (1), 46–52. doi:10.1109/TPEL.2018.2841371

CrossRef Full Text | Google Scholar

Xiong, L., Liu, X., Liu, H., and Liu, Y. (2022). Performance comparison of typical frequency response strategies for power systems with high penetration of renewable energy sources. IEEE J. Em Sel. Top. C 12 (1), 41–47. doi:10.1109/JETCAS.2022.3141691

CrossRef Full Text | Google Scholar

Xiong, L., Liu, X., Liu, Y., and Zhuo, F. (2020). Modeling and stability issues of voltage-source converter-dominated power systems: a review. CSEE JPES 8 (6), 1530–1549. doi:10.17775/CSEEJPES.2020.03590

CrossRef Full Text | Google Scholar

Xiong, L., Zhuo, F., Wang, F., Liu, X., Chen, Y., Zhu, M., et al. (2015). Static synchronous generator model: a new perspective to investigate dynamic characteristics and stability issues of grid-tied PWM inverter. IEEE Trans. Power Electr. 31 (9), 6264–6280. doi:10.1109/tpel.2015.2498933

CrossRef Full Text | Google Scholar

Yu, J., Qi, Y., Deng, H., Liu, X., and Tang, Y. (2021). Evaluating small-signal synchronization stability of grid-forming converter: a geometrical approach. IEEE Trans. Ind. Electron. 69 (9), 9087–9098. doi:10.1109/TIE.2021.3113000

CrossRef Full Text | Google Scholar

Zhang, C., Cai, X., Rygg, A., and Molinas, M. (2017). Sequence domain SISO equivalent models of a grid-tied voltage source converter system for small-signal stability analysis. IEEE Trans. Energy Conver. 33 (2), 741–749. doi:10.1109/TEC.2017.2766217

CrossRef Full Text | Google Scholar

Zhang, C., Molinas, M., Rygg, A., and Cai, X. (2019). Impedance-based analysis of interconnected power electronics systems: impedance network modeling and comparative studies of stability criteria. IEEE J. Em. Sel. Top. P. 8 (3), 2520–2533. doi:10.1109/JESTPE.2019.2914560

CrossRef Full Text | Google Scholar