Numerical study on density-driven convection of CO2-H2S mixture in fractured and sequential saline aquifers

Dissolution trapping stands as a critical mechanism for the geological carbon storage (GCS) and can be notably improved through density-driven convection. However, to the best of the author’s knowledge, the discussion on density-driven convection of CO₂-H₂S mixture has been limited to the exclusion of intersected fractures and lithology sequence effects. Therefore, this study aims to systematically investigate the impact of H₂S concentration, fractures, and lithology sequence on convective mixing. Four distinct mechanisms that influence convective mixing of CO₂-H₂S mixtures in the presence of fractures were identified: 1) accelerated downward solute transportation in fractures, 2) coalescence between plumes around fractures and primary down-swelling plumes, 3) high fracture conductivity inhibiting plume migration across fractures, and 4) upward flow in fractures facilitating the transport of high-concentration solute out of the system. Additionally, the effects of lithology sequence on the shape of CO₂ plumes and the curve shape of the total flux at the top boundary were described. The results demonstrated that density-driven convection is enhanced with decreasing H₂S concentration and increasing fracture interaction angle and fracture conductivity ratio. The magnitudes of density-driven convection, ranked from high to low, are fining downward, uniform, and fining upward lithology sequences. Furthermore, the H₂S concentration affects the flow direction within fractures and alters the relative magnitude of the dimensionless concentration in the noise sequences. The findings of this study on a small scale were proven to be applicable on a large scale.

1 Introduction

The substantial increase in CO₂ emissions resulting from the extensive utilization of fossil fuel-based energy sources has led to significant climate-related challenges since the advent of the industrial revolution (Kumar et al., 2020). As an effective strategy to mitigate net CO₂ emissions, the implementation of CO₂ capture and storage (CCS) technology has emerged as a promising solution (Zhao et al., 2023). Geological formations suitable for CO₂ storage include saline aquifers, depleted oil and gas reservoirs, and oil and gas reservoirs under CO₂-enhanced oil recovery (Hannis et al., 2017; Nguyen et al., 2018). Among these formations, saline aquifers have garnered particular interest due to their significant porosity and permeability, offering substantial storage capacity (Celia, 2017; Jia et al., 2023).

The injected CO₂ in the saline aquifer is supercritical because saline aquifers usually exist at depths greater than 800 m (Bachu and Adams, 2003). The supercritical CO₂ density varies between 266 and 766 kg/m³, while the water density is 945–1,230 kg/m³ (Adams and Bachu, 2010). Due to the buoyancy effect caused by the large density difference between Sc-CO₂ and water, the Sc-CO₂ rises upward until it reaches an impermeable caprock called structural trapping (Taku Ide et al., 2007). The structurally trapped Sc-CO₂ then dissolves into brine through molecular diffusion, causing an increase in brine density from 0.1% to 1% depending on reservoir conditions such as pressure, temperature, and salinity (Ennis-King and Paterson, 2003). The higher density of CO₂-saturated brine overlying fresh brine causes the instability of the system and finger-like CO₂ plumes to form (Amooie et al., 2018). This process is called density-driven convection, which improves the amount of CO₂ dissolved in brine by continuously replacing CO₂-saturated brine with fresh brine so that fresh brine can be in constant contact with Sc-CO₂ above (Farajzadeh et al., 2007; Hassanzadeh et al., 2007).

The co-injection of CO₂ mixtures into deep saline aquifers has been a promising way to achieve capital and energy savings because separating CO₂ from impure streams is an expensive and energy-consuming process (Knauss et al., 2005; Wang et al., 2011; Markewitz et al., 2012). Depending on whether the density of gas-saturated brine decreases or increases, co-injection of CO₂ mixtures may delay or accelerate convective dissolution. Li and Jiang (2014) investigated the effects of nitrogen and sulfur dioxide impurities on convective dissolution. They stated that the nitrogen impurity hindered while the sulfur dioxide impurity enhanced the convective mixing. Liu et al. (2017) found that H₂S had an inhibitive effect on convective mixing. However, the above studies ignored the double-diffusive effects on the onset of convection. Jafari Raad and Hassanzadeh (2016) first investigated double diffusive effects and stated that the diffusion contrast between CO₂ and impurities resulted in a non-monotonic density profile. Kim and Song (2017) indicated that double diffusive effects had positive or negative effects on system stability depending on the diffusivity ratio, buoyancy ratio, and impurity concentration. The effects of CO₂ mixtures on density-driven convection have been investigated through experimental studies. Mahmoodpour et al. (2020) conducted experiments under reservoir conditions, analyzing N₂ mole fractions of 0%, 10%, 20%, and 100% with varying brine salinities. Their findings highlighted that the presence of N₂ can either hinder or promote density-driven convection, depending on the mole fraction of N₂. Li et al. (2023) performed experiments in Hele-Shaw cells, examining the influence of O₂ and Ar as impurities. The results demonstrated that Ar impurities had the potential to enhance convective mixing, while O₂ impurities were found to weaken convective mixing.

Formation heterogeneity also plays an essential role in convective mixing. In terms of heterogeneous permeability, Farajzadeh et al. (2011) investigated different flow regimes of density-driven convection with different magnitudes of permeability variance. Aggelopoulos and Tsakiroglou (2012) investigated the micro-heterogeneous permeability and showed that the micro-heterogeneity strengthened the convective mixing. Soltanian et al. (2016) investigated the effect of the facies-based heterogeneity on convective mixing and upgraded it to three dimensions. Concerning fractures, the effects of fracture angle, fracture density, fracture permeability, fracture aperture, fracture surface roughness, fracture-matrix permeability ratio, and intersected fractures on the convective mixing were investigated (Kim et al., 2019; Rezk and Foroozesh, 2019; Shafabakhsh et al., 2021). Numerous experimental studies have also been conducted to explore the impact of heterogeneous porous media on CO₂ convective mixing. Agartan et al. (2015) conducted an experiment in heterogeneous media under atmospheric conditions, revealing that significant convective mixing may not exist in some formations, particularly in layered systems with low-permeability layers. Wang et al. (2021) observed that the sand layer initially affected by downward fingers plays a dominant role in finger evolution. Amarasinghe et al. (2020) conducted experiments under reservoir conditions (10 MPa and 50°C) and observed fingering in highly permeable porous media, whereas lower permeable porous media (500 mD) exhibited piston-like displacement.

Previous studies have separately examined the effects of impurity and heterogeneity on convective mixing. Nevertheless, it is imperative to consider the realistic scenario where CO₂ mixtures are injected into heterogeneous formations. Therefore, the present work focuses on the co-injection of CO₂-H₂S in fractured and sequential saline aquifers. The study aims to elucidate how fractures and lithology sequences impact plume shape and the subsequent convective mixing rate. Additionally, the study analyzes how the effects of H₂S concentration on convective mixing change in the presence of fractures and lithology sequences. The simulation model coupling the continuity equation, Darcy’s flow, and mass balance equation was developed based on COMSOL Multiphysics 5.6 (COMSOL, 2020).

This article is structured as follows. First, the governing equations and flash calculation process are detailed. Then, the model description and parameters are listed. The model is validated by the published results. Furthermore, the numerical results and discussion are provided, and the small-scale results are extended to the large scale. The main conclusions of the paper are presented at the end.

2 Methodology and model description

2.1 Governing equations

The governing equations for convective mixing include the continuity equation and the mass balance equation. The continuity equation in the porous medium is given by

$\frac{\partial \left({\varphi }_m\rho \right)}{\partial t}=-\nabla \bullet \left(\rho \mathit{u}\right)(1)$

Darcy’s velocity $\mathit{u}$ is calculated by Darcy’s law

$\mathit{u}=-\frac{{\mathbf{K}}_{\mathit{m}}}{\mu }\left(\nabla p-\rho \mathit{g}\nabla D\right)(2)$

Where $t$ is the time, ${\varphi }_m$ is the matrix porosity, $\rho$ is the mixture density, ${\mathbf{K}}_{\mathit{m}}$ is the matrix permeability, $\mu$ is the dynamic viscosity of the mixture, $p$ is the pressure and $\mathit{g}$ is the gravity term. The mass balance equation for the transport of dissolved CO₂ and H₂S is

$\frac{\partial \left({\varphi }_m{c}_i\right)}{\partial t}=\nabla \bullet \left({\varphi }_m{\mathbf{D}}_{\mathit{e}\mathit{i}}\nabla c_i-c_i\mathit{u}\right),i={\mathrm{C}\mathrm{O}}_2\mathrm{o}\mathrm{r}{\mathrm{H}}_2\mathrm{S}(3)$

Where $c_i$ is the component concentration and ${\mathbf{D}}_{\mathit{e}\mathit{i}}$ is the effective diffusion coefficient of the component. The Millington and Quirk model (Millington and Quirk, 1961) is used to calculate the effective diffusion coefficient given by

${\mathbf{D}}_{\mathit{e}\mathit{i}}={\varphi }_m^{4/3}{\mathit{D}}_{\mathit{i}}(4)$

Fluid density is a function of temperature, pressure, and component concentration. The density equation expressed by Diersch and Kolditz (2002) is used for simplicity.

$\rho ={\rho }_0\left[1+{\displaystyle \sum _{i=1}^n}{\beta }_i\left(c_i-c_{0,i}\right)\right](5)$

${\beta }_i=\frac{1}{{\rho }_0}{\left[\frac{\partial \rho }{\partial c_i}\right]}_T(6)$

Where ${\rho }_0$ is the density of CO₂-free water, ${\beta }_i$ is the densification coefficient.

To account for the presence of fractures within the porous medium, the “Fracture Flow” interface available in COMSOL Multiphysics 5.6 was utilized. This interface utilizes tangential derivatives to characterize the flow along the interior boundaries. The flow in the fracture is governed by the continuity equation and the mass balance equation, represented as (COMSOL, 2020).

$d_f\frac{\partial \left({\varphi }_f\rho \right)}{\partial t}=-{\nabla }_{\mathrm{T}}\left(\rho {\mathbf{q}}_{\mathit{f}}\right)(7)$

$d_f\frac{\partial \left({\varphi }_f{c}_i\right)}{\partial t}={\nabla }_{\mathrm{T}}\left({\varphi }_f{\mathbf{D}}_{\mathit{i}}\nabla c_i-c_i{\mathbf{q}}_{\mathit{f}}\right),i={\mathrm{C}\mathrm{O}}_2\mathrm{o}\mathrm{r}{H}_2\mathrm{S}(8)$

${\mathbf{q}}_{\mathit{f}}=-d_f\frac{{\mathbf{K}}_{\mathit{f}}}{\mu }\left({\nabla }_{\mathrm{T}}p-\rho \mathit{g}{\nabla }_{\mathrm{T}}D\right)(9)$

Where ${\mathbf{q}}_{\mathit{f}}$ is the volume flow rate per unit length in the fracture, $d_f$ denotes the fracture aperture, ${\varphi }_f$ is the fracture porosity, ${\mathrm{K}}_f$ represents the fracture permeability and ${\nabla }_{\mathrm{T}}$ is the tangential derivatives along the interior boundary representing fractures.

COMSOL Multiphysics’ flash calculation at the thermodynamic interface was used to obtain CO₂ and H₂S concentrations at the top boundary, assuming local thermodynamic equilibrium. The Rachford-Rice equation (Rachford and Rice, 1952) is used to obtain the partitioning of different components into two phases given as:

$f\left(nL\right)=\sum \frac{z_i\left(1-k_i\right)}{nL\left(1-k_i\right)+k_i}=0(10)$

Once the mole fraction of the liquid phase ($nL$) is solved, the mole fractions of components in both phases can be solved by:

$x_i=\frac{z_i}{nL\left(1-k_i\right)+k_i}(11)$

${\mathrm{y}}_{\mathrm{i}}={\mathrm{x}}_{\mathrm{i}}{\mathrm{k}}_{\mathrm{i}}(12)$

The dissolved H₂S and CO₂ compositions in the water phase are used as the top boundary conditions, as shown in Table 1. The average error between our results and the results from Li and Jiang (2020) is 1.3%, indicating that our results can be used in this study.

TABLE 1

TABLE 1. The dissolved gas compositions at 10 Mpa and 45$℃$. The units are mole fractions.

2.2 Boundary and initial conditions

The domain boundaries are characterized to govern the flow and concentration behaviors. For the left, right, and bottom boundaries, impermeability is assumed, resulting in the following conditions:

$u_x\left(0,z,t\right)=u_x\left(\mathrm{W},z,t\right)=u_z\left(\mathrm{x},H,t\right)=0(13)$

${\left(\frac{\partial c}{\partial x}\right)}_{x=0}={\left(\frac{\partial c}{\partial x}\right)}_{x=W}={\left(\frac{\partial c}{\partial z}\right)}_{z=H}=0(14)$

At the top boundary, a constant pressure condition is implemented to satisfy the continuity equation:

$P\left(\mathrm{x},0,t\right)=P_{top}(15)$

To account for perturbations caused by CO₂ injection or formation heterogeneity, a sine wave function is introduced. This function represents the concentrations of CO₂ and H₂S at the top boundary and is defined as

$c\left(x,0,t\right)=1+A_0\sin \left(2\pi x/{\lambda }_o\right)(16)$

Where $A_0$ is the dimensionless amplitude of the sine wave function and ${\lambda }_o$ denotes the wavelength.

Initially, the water phase contains no CO₂ or H₂S, and the pressure in the domain is equal to the pressure at the top boundary:

$c\left(x,z,0\right)=0(17)$

$P\left(\mathrm{x},z,0\right)=P_{top}(18)$

2.3 Model setup and simulation parameters

To investigate the density-driven convection, a two-dimensional domain below the gas-saturated brine layer was built using COMSOL Multiphysics 5.6, as shown in Figure 1A. Both the domain width and height were 1 m. The formation brine in the research domain was assumed to be pure water, and no gas was initially dissolved. All domain boundaries were assumed to be closed except the top boundary, which was assumed to be a constant concentration boundary. The CO₂ and H₂S concentrations are shown in Table 1. Other assumptions included the following: First, the top boundary was assumed to be sharp, and the two-phase transition zone caused by capillary pressure was ignored (Emami-Meybodi et al., 2015). Second, the free gas mixture above the top boundary was assumed to be abundant, so the pressure change due to the dissolution of the gas mixture was ignored, and the top boundary was kept gas-saturated (Li and Jiang, 2020). Third, the domain was assumed to be isothermal (Islam et al., 2014).

FIGURE 1

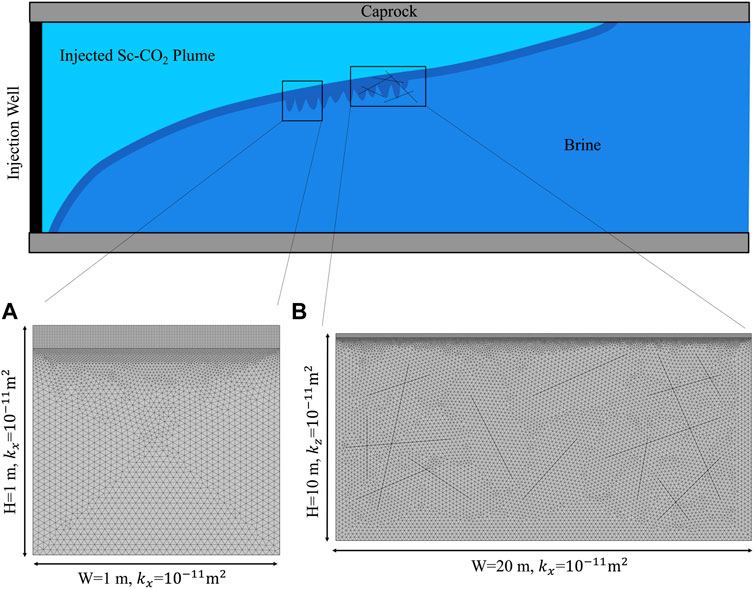
FIGURE 1. Schematic illustration of (A) small-scale domain, and (B) large-scale domain with intersected fractures.

To simulate the convective dissolution problem, the “Darcy’s flow” interface and the “transport of diluted species in porous media” interface were coupled. To accurately capture the diffusive behavior during the early stages, it is necessary to ensure that the grid size near the top boundary is smaller than the critical thickness of the diffusive boundary layer at the onset of convection. The critical thickness, denoted as L, can be calculated using the equation $L=3.6c_1\mu \varphi D/g∆\rho k_h$, where $c_1$ is a constant factor from linear stability results (Ennis-King et al., 2005). In this study, the calculated critical thickness is 0.0076 m. To meet this requirement, the grid block size near the top boundary was set to 0.0067 m. Away from the top boundary, the grid block size gradually increased to 0.028 m in order to improve computational efficiency. The time-stepping algorithm employed in this study is the strict backward differentiation formula (BDF), with a maximum BDF order set to 2 to ensure numerical stability. To enhance computational efficiency, a segregated solver with an automatic Newton-Raphson iteration method is utilized. For the solution of the linear system, the MUMPS solver is employed, utilizing preordering algorithms to effectively permute columns and minimize fill-in. The simulation parameters used in this study are shown in Table 2. The model is validated by the published model constructed by Kim et al. (2019) on the base case without H₂S and fractures, as shown in the Supplementary Appendix.

TABLE 2

TABLE 2. Simulation parameters.

2.4 Measurements of convective dissolution

Four measurable parameters were defined to study the dynamic behavior of convective dissolution. The first parameter is dimensionless spatial concentration, which quantifies the extent of CO₂ dissolved in water calculated by

$c_D=\frac{{\displaystyle \underset{0}{\overset{y}{\int }}}{\displaystyle \underset{0}{\overset{x}{\int }}}c\left(x,y\right)dxdy}{C_{top}{\displaystyle \underset{0}{\overset{H}{\int }}}{\displaystyle \underset{0}{\overset{L}{\int }}}dxdy}(19)$

This parameter is analyzed versus the dimensionless time represented by

$t_D=\frac{k_m\Delta \rho g}{{\varphi }_m\mu H}t(20)$

Where $k_m$ is matrix permeability, $\Delta \rho$ is the density difference between gas-saturated water and gas-free water, $g$ is the gravity term, ${\varphi }_m$ is the matrix porosity, $\mu$ is the mixture viscosity and $H$ is the domain height.

The second parameter is the total mass flux at the top boundary (${TF}_{top}$), which is analyzed versus dimensionless time to describe the temporal variation of flow magnitude at the top boundary.

The third parameter is the Rayleigh number (Ra), which measures the magnitude of convective flow to diffusive flow, represented by

$Ra=\frac{\Delta \rho g{k}_{m}H}{{\varphi }_m\mu D}(21)$

The fourth parameter is the Sherwood number (${Sh}_n$) which characterizes the relative contribution of convective to diffusive flux, defined as

${Sh}_n=\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{f}\mathrm{l}\mathrm{u}\mathrm{x}\mathrm{m}\mathrm{a}\mathrm{g}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}/\mathrm{D}\mathrm{i}\mathrm{f}\mathrm{f}\mathrm{u}\mathrm{s}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{f}\mathrm{l}\mathrm{u}\mathrm{x}\mathrm{m}\mathrm{a}\mathrm{g}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}(22)$

3 Results and discussion

3.1 Measurements of convective dissolution

To study the effects of H₂S concentration on convective mixing, three H₂S concentrations (0%, 10%, and 20%) were designed. The typical features of CO₂ plume development and curve are explained using the 0% H₂S case as an example. As Figures 2, 3 show, from ${\mathrm{t}}_{\mathrm{D}}$ = 0 to ${\mathrm{t}}_{\mathrm{D}}$ = 0.21, the small fingers at the top boundary exist due to the onset of convective mixing. In this period, the ${TF}_{top}$ keeps increasing and reaches its peak at ${\mathrm{t}}_{\mathrm{D}}$ = 0.21, called the flux-growth regime. From ${\mathrm{t}}_{\mathrm{D}}$ = 0.21 to ${\mathrm{t}}_{\mathrm{D}}$ = 1.41, convective fingers start merging because of the lateral movement called the merging regime. In this regime, the ${TF}_{top}$ decreases from its peak. From ${\mathrm{t}}_{\mathrm{D}}$ = 1.41 to ${\mathrm{t}}_{\mathrm{D}}$ = 6.64, the complex down-swelling fingers develop and introduce a stronger counter-current around them (the white arrows around the down-swelling fingers become visible), hindering the downward movement of small fingers and making small fingers at the top boundary disappear. In this period, the merged high-concentration fingers keep moving downward, and the ${TF}_{top}$ stays constant, called the constant-flux regime. From ${\mathrm{t}}_{\mathrm{D}}$ = 6.64 to ${\mathrm{t}}_{\mathrm{D}}$ = 9.98, the complex down-swelling fingers hit the boundary, and the domain begins to be saturated. These down-swelling fingers then begin to move upward, taking the high-concentration solute out of the domain (the map color of the upward flow zone changes from blue to yellow), leading to the decrease in the ${TF}_{top}$ called the shutdown regime. At ${\mathrm{t}}_{\mathrm{D}}$ = 9.98, the domain is nearly saturated. The temporal regimes observed in this study, including the flux-growth regime, merging regime, constant-flux regime, and shutdown regime, align with the typical temporal regimes for convective mixing, as described by Slim (2014). This alignment serves as validation for the accuracy of the constructed model.

FIGURE 2

FIGURE 2. The comparison of CO₂ plume development for three H₂S concentration cases.

FIGURE 3

FIGURE 3. The comparison of ${TF}_{top}$ curve for three H₂S concentration cases.

The density difference between gas-saturated and gas-free water, the Rayleigh number, the dimensionless CO₂ concentration at ${\mathrm{t}}_{\mathrm{D}}$ = 9.98, and the Sherwood number at ${\mathrm{t}}_{\mathrm{D}}$ = 9.98 of three H₂S concentrations are shown in Table 3. The density difference decreases with the increase in H₂S concentration. The lower density difference results in a lower convective mixing magnitude. As a result, the Rayleigh number, dimensionless CO₂ concentration, and Sherwood number all decrease as the H₂S concentration increases. The obtained results align with the conclusions drawn by Kim and Song (2017) in their linear stability analysis. They emphasized the substantial impact of impurity concentration on finger shape and growth history, with the presence of H₂S delaying the onset of convective mixing. Similarly, the results are consistent with the observations of Liu et al. (2017) in their direct numerical simulations, revealing the inhibitive influence of dissolved H₂S on convective mixing in the brine phase. The maximum Sherwood number is around 200 at ${\mathrm{t}}_{\mathrm{D}}$ = 9.98, indicating that the convective flow is 200 times greater than the diffusive flow, indicating that density-driven convection effectively enhances solubility trapping and significantly increases the amount of CO₂ sequestered. The lower convective mixing magnitude also delays the onset time of each flow regime shown in Figure 3. For example, the 20% H₂S case does not experience the shutdown regime at ${\mathrm{t}}_{\mathrm{D}}$ = 9.98, but the flux-growth regime is apparent.

TABLE 3

TABLE 3. Results for different H₂S concentration cases.

3.2 Effects of fracture intersection angle ($\theta$)

This section analyzed the effects of three fracture intersection angles (30$°$, 60$°$, and 90$°$) for three H₂S concentrations (0%, 10%, and 20%). Figure 4 compares CO₂ plume development for 10% H₂S concentration between cases with three fracture intersection angles and the case without fracture. There were two intersected fractures in the domain. One (fracture A) was horizontal and fixed. The other (fracture B) was changed to make intersection angles vary from 90$°$ to 30$°$. Figures 4, 5A show that different fracture intersection angles play different roles in CO₂ plume development, resulting in an increase or decrease in the dimensionless CO₂ concentration. For the case of $\theta$ = 90$°$ (10% H₂S), the presence of a highly conductive fracture B causes the plumes in the central region to merge. As a result, the merged plumes flow through fracture B and reach the bottom boundary before the plume in the left area, leading to accelerated convective mixing within the fractures. These findings are in agreement with the convective mixing analysis results for pure CO₂ presented by Kim et al. (2019). Concerning the case of $\theta$ = 60$°$ (10% H₂S), the merged central plume flows in the fracture and coalesces with the left plume before hitting the bottom boundary, which slows down the accelerated convective mixing in the central region. The dimensionless CO₂ concentrations of $\theta$ = 60$°$ and 90$°$ are higher than that of the case without fracture, indicating that intersected fractures have a positive effect. In comparison, for the case of $\theta$ = 30$°$ (10% H₂S), the fingers flowing in fracture B merge with the left plume so early that the merging effect delays the convective mixing. The dimensionless CO₂ concentration of $\theta$ = 30$°$ is lower than that of the case without fracture, indicating the negative effect of intersected fractures.

FIGURE 4

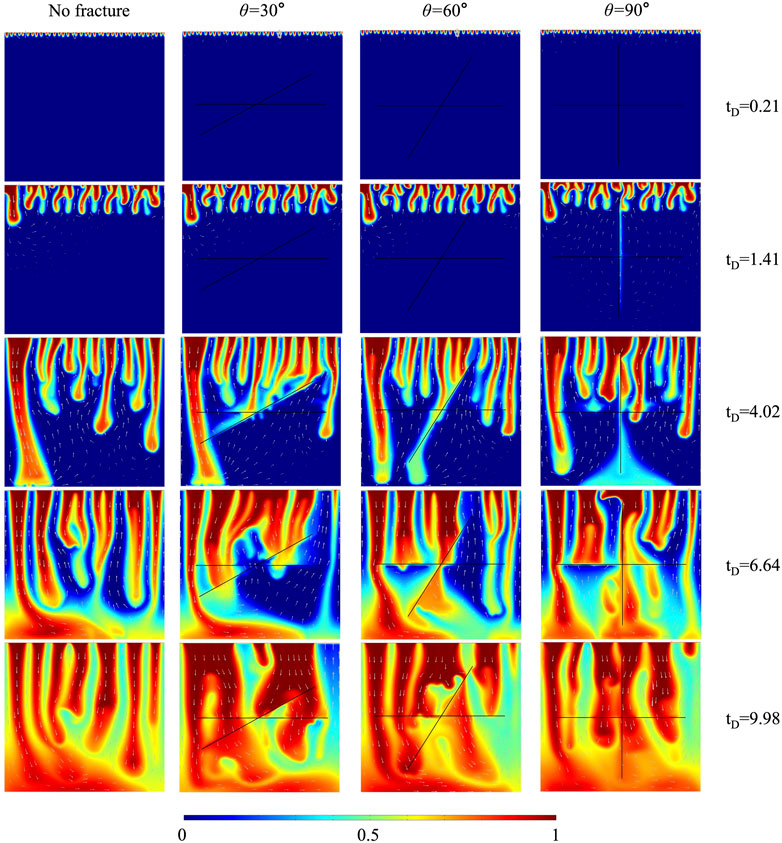
FIGURE 4. The comparison of CO₂ plume development between cases with three fracture intersection angles and case without fracture for 10% H₂S concentration.

FIGURE 5

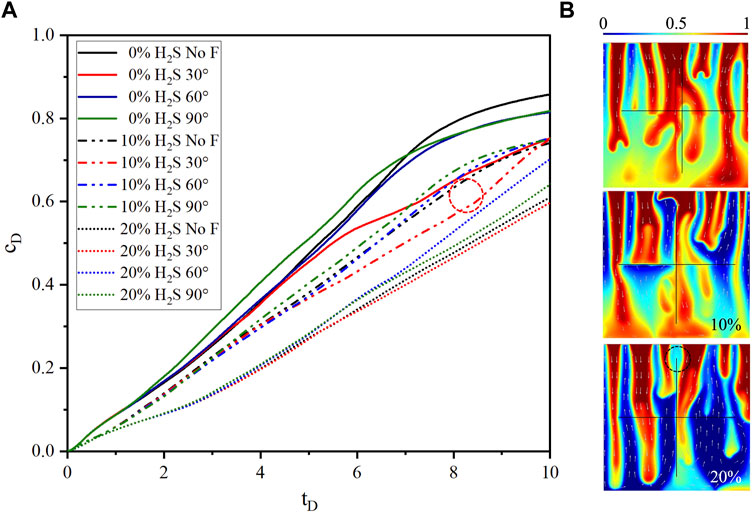
FIGURE 5. (A) The comparison of dimensionless CO₂ concentration between cases with three fracture intersection angles and case without fracture for 10% H₂S concentration. (B) CO₂ plume shapes of three H₂S concentrations at ${\mathrm{t}}_{\mathrm{D}}$ = 6.64 ($\theta$ = 90$°$).

The dimensionless CO₂ concentration difference between the case without fracture (10% H₂S) and the case of $\theta$ = 30$°$ (10% H₂S) is prominent in the early to mid-term, and this gap is narrowed after ${\mathrm{t}}_{\mathrm{D}}$ = 8 (marked by the circle in Figure 5A). This is because, in the case of $\theta$ = 30$°$ (10% H₂S) shown in Figure 4, the plumes in fractures flow horizontally instead of downward and merge with the left plume, which prevents the plumes from flowing across fractures in the central area in the early to mid-term. More plumes flow across fractures until convective mixing delays due to the boundary effect. Convective mixing is enhanced at this time. As shown in Figure 5A, the dimensionless CO₂ concentration of the case of $\theta$ = 60$°$ (20% H₂S) is higher than that of the case of $\theta$ = 90$°$ (20% H₂S), which is different from the normal trend that the dimensionless concentration of CO₂ increases with the increase of the intersection angle. This abnormal case is due to the upward flow in the fracture. Figure 5B presents the alteration of flow direction in response to changes in H₂S concentration. Notably, for the 20% H₂S concentration case, the solute exhibits an upward flow within the fracture, denoted by the black circle. Conversely, for other H₂S concentration cases, the solute flows downward. The upward flow within the fracture acts as a conduit for transporting high-concentration solute out of the domain, hindering convective mixing. Additionally, the H₂S concentration significantly impacts the onset time of flow regime in the presence of fractures. As illustrated in Figure 5A, the plume with 0% H₂S reaches the shutdown regime at ${\mathrm{t}}_{\mathrm{D}}$ = 8, while the plume with 20% H₂S remains in the constant-flux regime due to the decrease in density difference with increasing H₂S concentration, leading to a lower magnitude of convective mixing. The delayed onset time of each flow regime results in a decrease in the dimensionless CO₂ concentration.

In conclusion, four aspects of the influence mechanisms of intersected fractures on convective mixing are discussed. Fractures enhance convective mixing by accelerating downward solute transportation. The coalescence between merged plumes around fractures and main down-swelling plumes delays the convective mixing. The high fracture conductivity prevents plumes from flowing across fractures, hindering convective mixing. The upward flow in fractures delays convective mixing by transporting high-concentration solute out of the domain. These four mechanisms determine whether intersected fractures enhance or delay convective mixing.

3.3 Effects of fracture conductivity ratio (${RF}_{CD}$)

The fracture conductivity ratio (${RF}_{CD}$) refers to the ratio of vertical fracture conductivity to horizontal fracture conductivity. In this section, the vertical fracture permeability was set to ${10}^{-8}$, ${10}^{-9}$ and ${10}^{-10}{\mathrm{m}}^2$, and the fracture conductivity ratio was 0.1, 1, and 10.

The impact of fracture conductivity ratio on CO₂ plume development in 10% H₂S concentration cases is shown in Figure 6. The solute in the vertical fracture transports relatively slowly in the case of ${RF}_{CD}$ = 0.1 (10% H₂S). Part of the solute from the vertical fracture flows into the horizontal fracture and merges with the main plumes on the left and right sides of the horizontal fracture. As the fracture conductivity ratio increases to 1, the vertical fracture transports more solute downward instead of flowing into the horizontal fracture, which makes the plume along the vertical fracture hit the bottom boundary earlier than the plume on the left side of the fracture. However, the high conductivities of vertical and horizontal fractures make the solute flow into fractures and combine with the downward plumes. This merging effect prevents plumes from flowing across the horizontal fracture (marked by the rectangle). The vertical fracture takes most of the solute in the case of ${RF}_{CD}$ = 10 (10% H₂S), making the plumes merge around the vertical fracture and flow downward. In the meantime, the strong counter-current around the vertical fracture hinders the downward movement of other fingers. As a result, the plume along the vertical fracture is large.

FIGURE 6

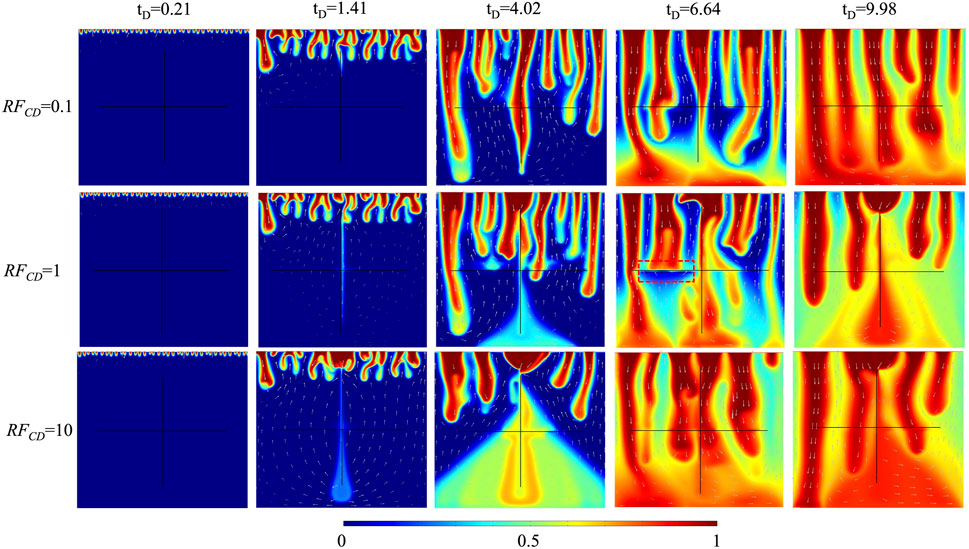
FIGURE 6. The comparison of CO₂ plume development of three fracture conductivity ratios for 10% H₂S concentration.

The comparison of dimensionless CO₂ concentrations and Sherwood numbers of three fracture conductivity ratios (${RF}_{CD}=0.1,110$) for all H₂S concentrations (0%, 10%, and 20%) is shown in Figures 7A, B. The dimensionless concentration before the shutdown regime increases with the rise in fracture conductivity ratio for all H₂S concentrations, which aligns with the conclusions of Rezk and Foroozesh (2019). Their study demonstrated that fractures cause fingers to deviate towards the high permeability path of the fracture, enhancing density-driven convection. The reason is that the high vertical fracture conductivity enhances the conductive mixing significantly, which can be supported by the high Sherwood number. The high magnitude of ${TF}_{top}$ shortens the duration of the constant-flux regime because the main plumes hit the bottom boundary earlier. Thus, the ultimate dimensionless CO₂ concentration might vary. Although an increase in fracture conductivity ratio enhances conductive mixing, it is noteworthy that the delayed onset time and reduced dimensionless CO₂ concentration resulting from an elevated H₂S concentration remain unaffected. This observation further emphasizes the crucial role of H₂S concentration in the density-driven convection problem.

FIGURE 7

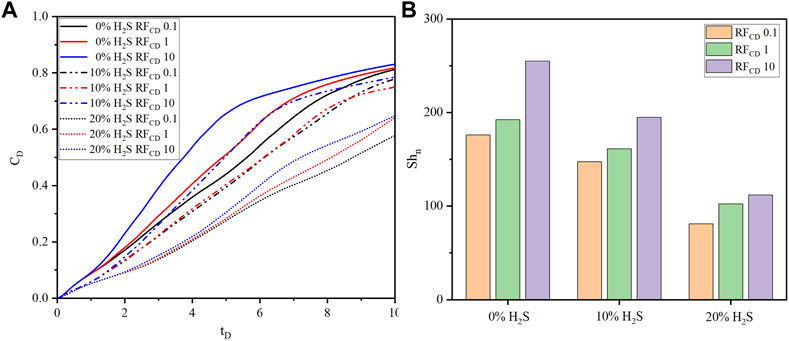
FIGURE 7. The comparison of (A) dimensionless CO₂ concentration, and (B) Sherwood number of three fracture conductivity ratios (${RF}_{CD}=0.1,1,$ and 10) for three H₂S concentrations (0%, 10%, and 20%).

3.4 Effects of lithology sequence

The grain size sequence controlled by hydrodynamic conditions results in sedimentary formation with spatial variation in permeability. Generally, stronger hydrodynamic conditions tend to induce the deposition of coarse grains and higher permeability formations (Jin et al., 2020). The typical lithology sequences include the uniform, fining upward, fining upward with noise, fining downward, and fining downward with noise, as described in Figure 8A. In this study, the permeability contrast was set to 3. The highest permeability was ${1.5\times 10}^{-11}{\mathrm{m}}^2$, and the lowest permeability was ${0.5\times 10}^{-11}{\mathrm{m}}^2$. The permeability variations of the modelled lithological sequences are shown in Figure 8B. To better study the effects of lithology sequences, the average domain permeabilities were the same.

FIGURE 8

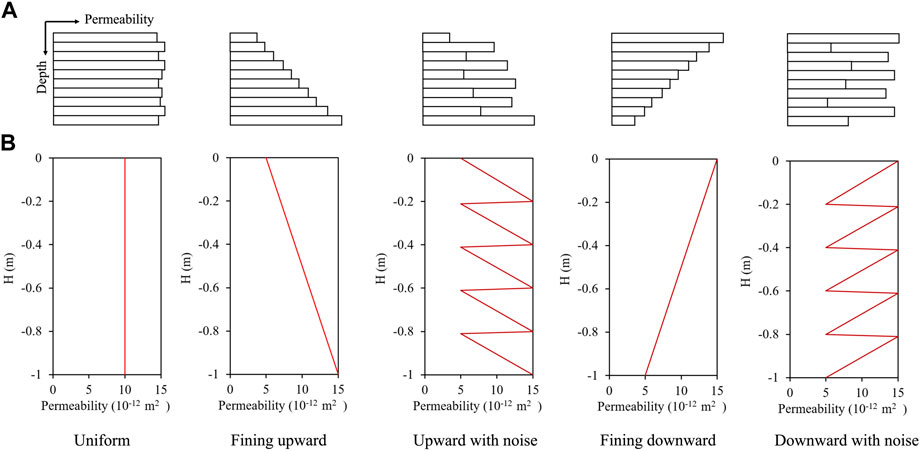
FIGURE 8. (A) The description of five typical lithology sequences, including the uniform, fining upward, fining upward with noise, fining downward and fining downward with noise sequences. (B) The permeability variations of five modelled lithology sequences.

Figure 9 shows the CO₂ plume developments of different lithology sequences for 10% H2S concentration. The plume shapes are different among uniform, fining upward, and fining downward cases. The plumes of fining upward sequence do not merge until the main plumes hit the bottom boundary, which creates many thin and long fingers. This is because the downward permeability is higher than the horizontal permeability, making plumes prefer to flow downward. The lower permeability near the top boundary limits convective mixing, which causes the dimensionless CO₂ concentration of fining upward sequence to be lower than that of uniform sequence. On the contrary, the plumes of fining downward sequence start merging earlier than the plumes of uniform sequence, and strong fingers are created. The reason is that plumes tend to flow horizontally because the downward permeability is lower than the horizontal permeability. The higher permeability near the top boundary facilitates the convective mixing and increases the dimensionless CO₂ concentration. The fining upward with noise sequence accelerates the merging compared to the fining upward sequence, while the fining downward with noise sequence delays the merging compared to the fining downward sequence, given that the increased number of noise layers results in a higher permeability change gradient near the top boundary. Besides, the layered structures of CO₂ plume developments are identified in the noise sequences.

FIGURE 9

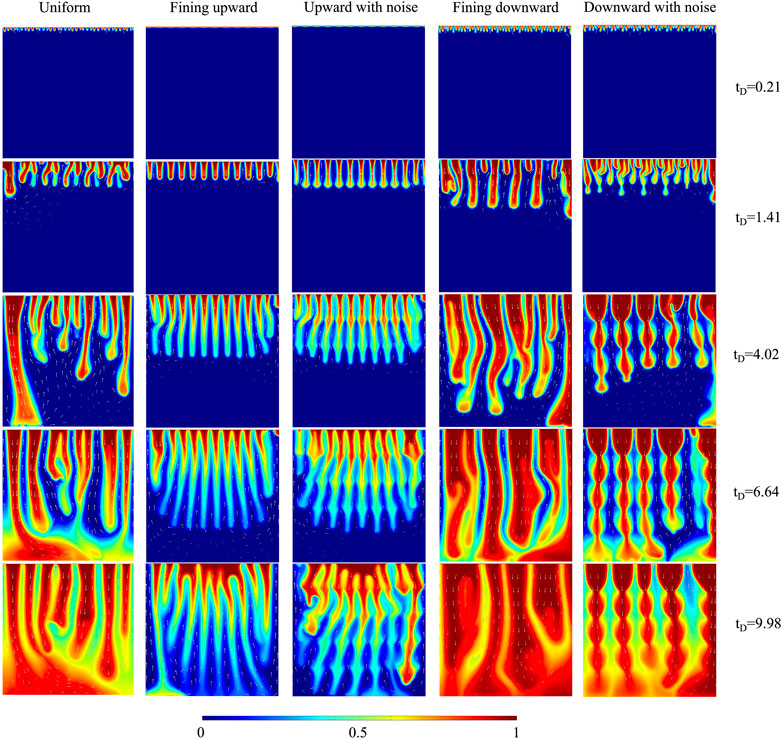
FIGURE 9. The comparison of CO₂ plume development of five lithology sequences for 10% H₂S concentration.

The magnitudes of dimensionless concentration, ranked from high to low, are fining downward, uniform, and fining upward lithology sequences, as shown in Figure 10A. The distinction between fining upward and upward with noise, as well as between fining downward and downward with noise, becomes more pronounced with an increase in H₂S concentration. This observation can be attributed to the interplay between density-driven convection and the effect of the noise sequence. When the H₂S concentration is low, density-driven convection is prominent, diminishing the impact of the noise sequence. Conversely, a high H₂S concentration leads to a delay in density-driven convection, amplifying the effect of the noise sequence. The curve shapes of ${TF}_{top}$ are different among different lithology sequences shown in Figure 10B. The curve shape of the fining upward sequence has a relatively flat peak, unlike the sharp peak in the uniform sequence. This is because the permeability increases downward, accelerating the convective mixing and extending the peak period. The curve shape of fining upward with noise sequence is basically the same as that of fining upward sequence except that the peak magnitude of fining upward with noise is higher due to the higher permeability change gradient at the top boundary. In comparison, the curve shapes of both fining downward sequence and fining downward with noise sequence have more than one peak because the formation of extra-large plumes accelerates the convective mixing. This positive effect exceeds the negative effect caused by the downward decrease in permeability.

FIGURE 10

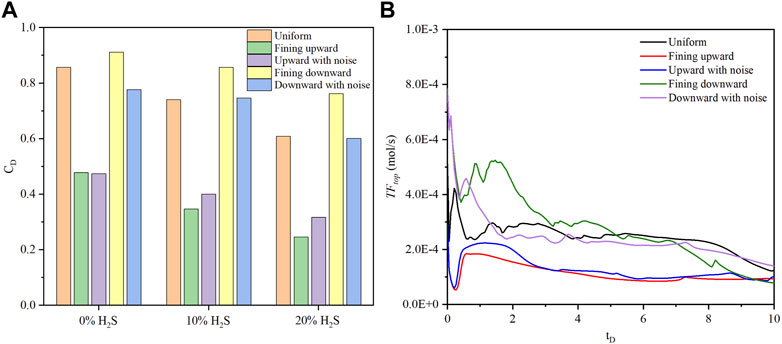
FIGURE 10. The comparison of (A) dimensionless CO₂ concentration of five lithology sequences for three H₂S concentrations (0%, 10%, and 20%) at ${\mathrm{t}}_{\mathrm{D}}$ = 9.98, and (B) ${TF}_{top}$ of five lithology sequences for 10% H₂S concentration.

3.5 Effects of domain scale

Six large-scale cases with 20 m in width and 10 m in height were run to investigate the scale effect on density-driven convection. The relative parameters are shown in Table 4. The matrix porosity and permeability were set to 0.2 and $1\times {10}^{-12}{\mathrm{m}}^2$, respectively. The fracture networks in cases C and E were identical, with 16 dead-end and intersected fractures. The fracture porosity and permeability were statistically generated following the normal distribution. The mean ($\mu )$ and standard deviation ($\sigma )$ of fracture porosity were 0.4 and 0.05, respectively. The mean and standard deviation of fracture permeability were ${10}^{-9}{\mathrm{m}}^2$ and $3\times {10}^{-10}{\mathrm{m}}^2$, respectively. The large-scale domain with a statistically generated fracture network is shown in Figure 1B. For fining upward sequence cases, the permeability increased from top ($0.5\times {10}^{-12}{\mathrm{m}}^2$) to bottom ($1.5\times {10}^{-12}{\mathrm{m}}^2$). Concerning fining downward sequence cases, the permeability decreased from top ($1.5\times {10}^{-12}{\mathrm{m}}^2$) to bottom ($0.5\times {10}^{-12}{\mathrm{m}}^2$). The average matrix permeabilities of large-scale cases were the same.

TABLE 4

TABLE 4. Parameters and results for six large scale cases.

The plume developments of cases B and C are shown in Figure 11. When case B is compared to the case with 10% H₂S concentration in Figure 2, the plume developments with dimensionless time are similar, demonstrating the applicability of small-scale results to large-scale. At ${\mathrm{t}}_{\mathrm{D}}$ = 0.21, the plumes in both cases become apparent, and complex plumes form at ${\mathrm{t}}_{\mathrm{D}}$ = 1.41. The complex swelling plumes move downward and hit the bottom boundary from ${\mathrm{t}}_{\mathrm{D}}$ = 1.41 to ${\mathrm{t}}_{\mathrm{D}}$ = 6.64 for small-scale and large-scale cases. At ${\mathrm{t}}_{\mathrm{D}}$ = 9.98, the domain is nearly saturated, and the upward flow takes the high-concentration solute out of the domain (the map color changes from blue to yellow). In the CO₂ plume developments of case C, four main influence mechanisms of fractures on a small scale, explained in Section 3.2, can be identified on a large scale. The downward solute transportation is accelerated by fractures, which enhances convective dissolution (zone A). The coalescence between plumes around fractures and main down-swelling plumes delays convective mixing (zone B). The high fracture conductivities prevent plumes from flowing across fractures, which makes the flux magnitude below fractures low and hinders convective mixing (zone C). The flow in fractures moves upward, and high-concentration solute is transported out of the domain, delaying convective mixing (zone D).

FIGURE 11

FIGURE 11. Temporal CO₂ plume developments of Case B and C.

The dimensionless CO₂ concentration and Sherwood number for six large-scale cases at ${\mathrm{t}}_{\mathrm{D}}$ = 9.98 are shown in Table 4. The dimensionless CO₂ concentration increases as the H₂S concentration decreases because of enhanced density-driven convection. Besides, the fining downward sequence has the highest dimensionless concentration, followed by uniform and fining upward sequences. Fractures accelerate the convective mixing in both the fining upward and uniform sequence due to the enhanced convective mixing by high conductivity fractures. The trends of Sherwood number are the same as the trends of dimensionless concentration. All trends on a large scale are the same as trends on a small scale, indicating the applicability of small-scale results to a large scale.

4 Conclusion

The effects of impurities on density-driven convection have been widely discussed without considering the effects of fracture and lithology sequence. This work addressed this gap through numerical simulations built on COMSOL Multiphysics. The effects of H₂S concentration, fracture interaction angle, fracture conductivity ratio, and lithology sequence on the density-driven convection were investigated. The following are the findings:

1. The increase in H₂S concentration delays the onset time of each flow regime and decreases the ${TF}_{top}$ magnitude, dimensionless CO₂ concentration, and Sherwood number. As the H₂S concentration increases, the density difference between gas-free water and gas-saturated water decreases, which hinders density-driven convection.

2. Four influence mechanisms of fractures on convective mixing are identified, including the accelerated downward solute transportation in fractures, which enhances convective mixing; the coalescence between plumes around fractures and the main down-swelling plumes, which delays convective mixing; the high fracture conductivity preventing plumes from flowing across fractures, which hinders convective mixing below fractures; and the upward flow in fractures transporting high-concentration solute out of the domain, which delays convective mixing.

3. The dimensionless CO₂ concentration increases with the fracture intersection angle due to the delayed coalescence between the merged central plume and left plume and increases with the fracture conductivity ratio because of the accelerated downward solute transportation. Besides, the H₂S concentration changes the effects of fractures because the flow direction in fractures changes with the H₂S concentration.

4. The CO₂ plume shapes and ${TF}_{top}$ curve shapes differ among different lithology sequences. The plumes of fining upward sequence do not merge until the main plumes hit the bottom boundary, resulting in thin and long fingers. The curve shape of fining upward sequence has a relatively flat peak, unlike the sharp peak of uniform sequence. In contrast, the plumes of fining downward sequence start merging around the top boundary, creating strong fingers, and its curve has more than one peak. The fining upward with noise sequence accelerates merging compared to the fining upward sequence, while the fining downward with noise sequence delays merging compared to the fining downward.

5. The magnitudes of dimensionless concentration, ranked from high to low, are fining downward, uniform, and fining upward lithology sequences. The distinction between fining upward and upward with noise, as well as between fining downward and downward with noise, becomes more pronounced with an increase in H₂S concentration.

6. Large-scale cases are designed to extend small-scale results to a large scale. Both the plume development with dimensionless time and the order of dimensionless concentration on a large scale are the same as those on a small scale. Besides, four influence mechanisms of fractures on convective mixing observed on a small scale are also identified on a large scale. Therefore, the deductions made on a small scale are applicable on a large scale.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: Datasets related to this article can be found at http://doi.org/10.5281/zenodo.6899947, an open-source online data repository hosted at Zenodo (Liu, 2022).

Author contributions

BL: Conceptualization, validation, methodology, software, investigation, and writing-original draft. JY: Writing-review and editing, supervision, project administration, funding acquisition. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Grant Number: 52034010).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2023.1241672/full#supplementary-material

References

Adams, J. J., and Bachu, S. (2010). Equations of state for basin geofluids: algorithm review and intercomparison for brines. Geofluids 2 (4), 257–271. doi:10.1046/j.1468-8123.2002.00041.x

CrossRef Full Text | Google Scholar

Agartan, E., Trevisan, L., Cihan, A., Birkholzer, J., Zhou, Q., and Illangasekare, T. H. (2015). Experimental study on effects of geologic heterogeneity in enhancing dissolution trapping of supercritical CO2. Water Resour. Res. 51 (3), 1635–1648. doi:10.1002/2014WR015778

CrossRef Full Text | Google Scholar

Aggelopoulos, C. A., and Tsakiroglou, C. D. (2012). Effects of micro-heterogeneity and hydrodynamic dispersion on the dissolution rate of carbon dioxide in water-saturated porous media. Int. J. Greenh. Gas Control 10, 341–350. doi:10.1016/j.ijggc.2012.06.012

CrossRef Full Text | Google Scholar

Amarasinghe, W., Fjelde, I., Rydland, J.-Å., and Guo, Y. (2020). Effects of permeability on CO2 dissolution and convection at reservoir temperature and pressure conditions: A visualization study. Int. J. Greenh. Gas Control 99, 103082. doi:10.1016/j.ijggc.2020.103082

CrossRef Full Text | Google Scholar

Amooie, M. A., Soltanian, M. R., and Moortgat, J. (2018). Solutal convection in porous media: comparison between boundary conditions of constant concentration and constant flux. Phys. Rev. E 98 (3), 033118. doi:10.1103/physreve.98.033118

CrossRef Full Text | Google Scholar

Bachu, S., and Adams, J. J. (2003). Sequestration of CO2 in geological media in response to climate change: capacity of deep saline aquifers to sequester CO2 in solution. Energy Convers. Manag. 44 (20), 3151–3175. doi:10.1016/s0196-8904(03)00101-8

CrossRef Full Text | Google Scholar

Celia, M. A. (2017). Geological storage of captured carbon dioxide as a large-scale carbon mitigation option. Water Resour. Res. 53 (5), 3527–3533. doi:10.1002/2017wr020841

CrossRef Full Text | Google Scholar

COMSOL (2020). Porous media flow module user's guide. COMSOL Multiphysics. 5.6.

Google Scholar

Diersch, H. J. G., and Kolditz, O. (2002). Variable-density flow and transport in porous media: approaches and challenges. Adv. Water Resour. 25 (8), 899–944. doi:10.1016/S0309-1708(02)00063-5

CrossRef Full Text | Google Scholar

Emami-Meybodi, H., Hassanzadeh, H., Green, C. P., and Ennis-King, J. (2015). Convective dissolution of CO2 in saline aquifers: progress in modeling and experiments. Int. J. Greenh. Gas Control 40, 238–266. doi:10.1016/j.ijggc.2015.04.003

CrossRef Full Text | Google Scholar

Ennis-King, J. P., and Paterson, L. (2003). Role of convective mixing in the long-term storage of carbon dioxide in deep saline formations. Spe J. 10 (03), 349–356. doi:10.2118/84344-pa

CrossRef Full Text | Google Scholar

Ennis-King, J., Preston, I., and Paterson, L. (2005). Onset of convection in anisotropic porous media subject to a rapid change in boundary conditions. Phys. Fluids 17, 084107. doi:10.1063/1.2033911

CrossRef Full Text | Google Scholar

Farajzadeh, R., Ranganathan, P., Zitha, P. L. J., and Bruining, J. (2011). The effect of heterogeneity on the character of density-driven natural convection of CO2 overlying a brine layer. Adv. Water Resour. 34 (3), 327–339. doi:10.1016/j.advwatres.2010.12.012

CrossRef Full Text | Google Scholar

Farajzadeh, R., Salimi, H., Zitha, P., and Bruining, J. (2007). Numerical simulation of density-driven natural convection in porous media with application for CO2 injection projects. Int. J. Heat Mass Transf. 50 (25-26), 5054–5064. doi:10.1016/j.ijheatmasstransfer.2007.08.019

CrossRef Full Text | Google Scholar

Hannis, S., Lu, J., Chadwick, A., Hovorka, S., Kirk, K., Romanak, K., et al. (2017). CO2 storage in depleted or depleting oil and gas fields: what can we learn from existing projects? Energy Procedia 114, 5680–5690. doi:10.1016/j.egypro.2017.03.1707

CrossRef Full Text | Google Scholar

Hassanzadeh, H., Pooladi-Darvish, M., and Keith, D. W. (2007). Scaling behavior of convective mixing, with application to geological storage of CO2. AIChE J. 53 (5), 1121–1131. doi:10.1002/aic.11157

CrossRef Full Text | Google Scholar

Islam, A., Korrani, A. K. N., Sepehrnoori, K., and Patzek, T. (2014). Effects of geochemical reaction on double diffusive natural convection of CO2 in brine saturated geothermal reservoir. Int. J. Heat Mass Transf. 77, 519–528. doi:10.1016/j.ijheatmasstransfer.2014.05.040

CrossRef Full Text | Google Scholar

Jafari Raad, S. M., and Hassanzadeh, H. (2016). Does impure CO2 impede or accelerate the onset of convective mixing in geological storage? Int. J. Greenh. Gas Control 54, 250–257. doi:10.1016/j.ijggc.2016.09.011

CrossRef Full Text | Google Scholar

Jia, C., Ren, B., Sepehrnoori, K., Delshad, M., Liu, B., Sun, H., et al. (2023). Numerical studies of hydrogen buoyant flow in storage aquifers. Fuel 349, 128755. doi:10.1016/j.fuel.2023.128755

CrossRef Full Text | Google Scholar

Jin, G., Liu, J., Liu, L., Zhai, H., Wu, D., and Xu, T. (2020). Effect of lithological rhythm on gas production performance via depressurization through a vertical well in a confined hydrate reservoir. Mar. Petroleum Geol. 122, 104696. doi:10.1016/j.marpetgeo.2020.104696

CrossRef Full Text | Google Scholar

Kim, M. C., and Song, K. H. (2017). Effect of impurities on the onset and growth of gravitational instabilities in a geological CO2 storage process: linear and nonlinear analyses. Chem. Eng. Sci. 174, 426–444. doi:10.1016/j.ces.2017.09.038

CrossRef Full Text | Google Scholar

Kim, M., Kim, K.-Y., Han, W. S., Oh, J., and Park, E. (2019). Density-driven convection in a fractured porous media: implications for geological CO2 storage. Water Resour. Res. 55 (7), 5852–5870. doi:10.1029/2019WR024822

CrossRef Full Text | Google Scholar

Knauss, K. G., Johnson, J. W., and Steefel, C. I. (2005). Evaluation of the impact of CO2, co-contaminant gas, aqueous fluid and reservoir rock interactions on the geologic sequestration of CO2. Chem. Geol. 217 (3), 339–350. doi:10.1016/j.chemgeo.2004.12.017

CrossRef Full Text | Google Scholar

Kumar, S., Foroozesh, J., Edlmann, K., Rezk, M. G., and Lim, C. Y. (2020). A comprehensive review of value-added CO2 sequestration in subsurface saline aquifers. J. Nat. Gas Sci. Eng. 81, 103437. doi:10.1016/j.jngse.2020.103437

CrossRef Full Text | Google Scholar

Li, D. D., Zhong, Y. H., and Jiang, X. (2023). Experimental study of impurity effects on convective mixing in Hele-Shaw cell with application to CO2 geological sequestration. Adv. Water Resour. 172, 104379. Article 104379. doi:10.1016/j.advwatres.2023.104379

CrossRef Full Text | Google Scholar

Li, D., and Jiang, X. (2014). A numerical study of the impurity effects of nitrogen and sulfur dioxide on the solubility trapping of carbon dioxide geological storage. Appl. Energy 128, 60–74. doi:10.1016/j.apenergy.2014.04.051

CrossRef Full Text | Google Scholar

Li, D., and Jiang, X. (2020). Numerical investigation of convective mixing in impure CO2 geological storage into deep saline aquifers. Int. J. Greenh. Gas Control 96, 103015. doi:10.1016/j.ijggc.2020.103015

CrossRef Full Text | Google Scholar

Liu, B. (2022). Effects of impurity on the density-driven convection of CO2 in fractured and rhythmic saline aquifers. doi:10.5281/zenodo.6899947

CrossRef Full Text | Google Scholar

Liu, Y., Ding, T., Yu, B., and Yang, Y. (2017). Convective dissolution analysis of long-term storage of acid gas in saline aquifers. Energy Procedia 114, 3417–3431. doi:10.1016/j.egypro.2017.03.1473

CrossRef Full Text | Google Scholar

Mahmoodpour, S., Amooie, M. A., Rostami, B., and Bahrami, F. (2020). Effect of gas impurity on the convective dissolution of CO2 in porous media. Energy 199, 117397. doi:10.1016/j.energy.2020.117397

CrossRef Full Text | Google Scholar

Mahmoodpour, S., Rostami, B., and Emami-Meybodi, H. (2018). Onset of convection controlled by N2 impurity during CO2 storage in saline aquifers. Int. J. Greenh. Gas Control 79, 234–247. doi:10.1016/j.ijggc.2018.10.012

CrossRef Full Text | Google Scholar

Markewitz, P., Kuckshinrichs, W., Leitner, W., Linssen, J., Zapp, P., Bongartz, R., et al. (2012). Worldwide innovations in the development of carbon capture technologies and the utilization of CO2. Energy Environ. Sci. 5, 7281–7305. doi:10.1039/c2ee03403d

CrossRef Full Text | Google Scholar

Millington, R. J., and Quirk, J. p. (1961). Permeability of porous solids. Trans. Faraday Soc. 57, 1200–1207. doi:10.1039/tf9615701200

CrossRef Full Text | Google Scholar

Nguyen, P., Carey, J. W., Viswanathan, H. S., and Porter, M. (2018). Effectiveness of supercritical-CO2 and N2 huff-and-puff methods of enhanced oil recovery in shale fracture networks using microfluidic experiments. Appl. Energy 230, 160–174. doi:10.1016/j.apenergy.2018.08.098

CrossRef Full Text | Google Scholar

Rachford, H. H., and Rice, J. D. (1952). Procedure for use of electronic digital computers in calculating flash vaporization hydrocarbon equilibrium. J. Petroleum Technol. 4 (10), 19–3. doi:10.2118/952327-g

CrossRef Full Text | Google Scholar

Rezk, M. G., and Foroozesh, J. (2019). Study of convective-diffusive flow during CO2 sequestration in fractured heterogeneous saline aquifers. J. Nat. Gas Sci. Eng. 69, 102926. doi:10.1016/j.jngse.2019.102926

CrossRef Full Text | Google Scholar

Shafabakhsh, P., Ataie-Ashtiani, B., Simmons, C. T., Younes, A., and Fahs, M. (2021). Convective-reactive transport of dissolved CO2 in fractured-geological formations. Int. J. Greenh. Gas Control 109, 103365. doi:10.1016/j.ijggc.2021.103365

CrossRef Full Text | Google Scholar

Slim, A. C. (2014). Solutal-convection regimes in a two-dimensional porous medium. J. Fluid Mech. 741, 461–491. doi:10.1017/jfm.2013.673

CrossRef Full Text | Google Scholar

Soltanian, M. R., Amooie, M. A., Dai, Z., Cole, D., and Moortgat, J. (2016). Critical dynamics of gravito-convective mixing in geological carbon sequestration. Sci. Rep. 6 (1), 35921. doi:10.1038/srep35921

PubMed Abstract | CrossRef Full Text | Google Scholar

Taku Ide, S., Jessen, K., and Orr, F. M. (2007). Storage of CO2 in saline aquifers: effects of gravity, viscous, and capillary forces on amount and timing of trapping. Int. J. Greenh. Gas Control 1 (4), 481–491. doi:10.1016/S1750-5836(07)00091-6

CrossRef Full Text | Google Scholar

Wang, J., Ryan, D., Anthony, E. J., Wildgust, N., and Aiken, T. (2011). Effects of impurities on CO2 transport, injection and storage. Energy Procedia 4, 3071–3078. doi:10.1016/j.egypro.2011.02.219

CrossRef Full Text | Google Scholar

Wang, S., Cheng, Z., Zhang, Y., Jiang, L., Liu, Y., and Song, Y. (2021). Unstable density-driven convection of CO2 in homogeneous and heterogeneous porous media with implications for deep saline aquifers. Water Resour. Res. 57 (3), e2020WR028132. doi:10.1029/2020WR028132

CrossRef Full Text | Google Scholar

Zhao, K., Jia, C., Li, Z., Du, X., Wang, Y., Li, J., et al. (2023). Recent advances and future perspectives in carbon capture, transportation, utilization, and storage (cctus) technologies: A comprehensive review. Fuel 351, 128913. doi:10.1016/j.fuel.2023.128913

CrossRef Full Text | Google Scholar

Zhao, Y., Wang, W., Guo, R., Wang, W., Zhu, Y., Wang, R., et al. (2021). Relation of heterogeneity and gas-bearing capacity of tight sandstone: A case study of the upper paleozoic tight gas sandstone reservoir in the southeast of the ordos basin. ACS Omega 6 (24), 15716–15726. doi:10.1021/acsomega.1c00965

PubMed Abstract | CrossRef Full Text | Google Scholar