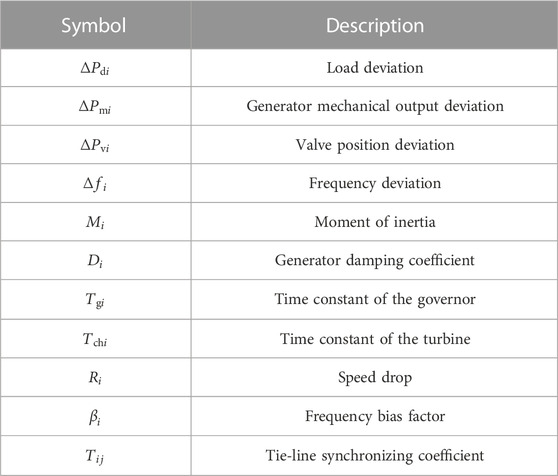
- School of Information Science and Engineering, Zhejiang Sci-Tech University, Hangzhou, China
Aiming at the impact of redundant information transmission on network resource utilization in current power systems, an improved event-triggered scheme based on particle swarm optimization and artificial fish swarm algorithm for power system load frequency control (LFC) with renewable energy is proposed. First of all, to keep the stability and security of power systems with renewable energy, the load frequency control scheme is investigated in this paper. Then, to relieve the communication burden and increase network utilization, an improved event-triggered scheme based on the particle swarm algorithm and artificial fish swarm algorithm is explored for the power system load frequency control. Then, by utilizing improved Lyapunov functional and the linear matrix inequality method, sufficient condition for the
1 Introduction
In the context of global clean energy and low-carbon development, environmental protection issues have gained increasing attention from numerous countries in recent years. Conventional power generation technologies’ defects in the economy and environmental protection have become more prominent (Liu et al., 2021). Meanwhile, several new problems affecting the stable operation of power systems have arisen due to the rapid development of clean energy generation technology. For instance, new energy power systems are often subject to interruptions or fluctuations in power supply (Gholamrezaie et al., 2018; Oubelaid et al., 2022a). Energy storage technology is then applied to solve the technical deficiencies of the system power supply and ease the instability of the new energy power system (Oubelaid et al., 2022b). Therefore, the power system combines with a growing number of renewable energy sources and battery storage (Choi et al., 2016; Mi et al., 2017; Pulazza et al., 2021; Oubelaid et al., 2022c). However, environmental variations can have a significant impact on the output of renewable energy sources, leading to fluctuations in the power system’s output power after the integration of renewable energy. Therefore, ensuring the maintenance of the load frequency within a safe range becomes particularly crucial after the integration of renewable energy sources into the power grid (Yan et al., 2022). Hence, the system needs a control strategy for regulation. As the core application of automatic power generation control in power systems, load frequency control (LFC) is also an essential tool for dealing with grid frequency matters resulting from load changes (Zhao et al., 2022; Sun et al., 2023). LFC mainly adjusts the grid frequency deviation and the exchange power value of the contact line to make the system frequency reach the rated value, while maintaining the tie-lines exchanged power at the normal value (Yang et al., 2020).
It is worth mentioning that traditional LFC technology usually uses a dedicated line communication method to transmit data (Wang et al., 2022), with the drawbacks of high maintenance costs and poor flexibility. The last few decades have witnessed a spurt of progress in communication, computer, and control technology. Thus, this traditional method of communication is gradually being replaced by open networks (Aluko et al., 2021). However, the application of open communication networks in power systems has brought new problems such as communication delays and limited network bandwidth constraints (Yuan et al., 2021). Therefore, how to improve the utilization of network resources has been the focus of investigation on the power system in the modern communication network environment. It is worth noting that event-trigger scheme can effectively relieve bandwidth pressure (Li M. et al., 2019; Zhang et al., 2020).
In an event-trigger scheme, the event generator will only release the data packet signal while the preset event-trigger conditions are satisfied. Therefore, the event-triggered scheme is adopted in modern power systems to achieve the expected goal of saving the occupancy of communication channels (Wen et al., 2016). Based on the event-triggered scheme, LFC has received considerable attention in the power system. In (Bu et al., 2022), an event-triggered data-driven LFC scheme via model-free adaptive control is proposed, which achieves better data-driven linear frequency regulation based on an event-triggered scheme and dynamic linearization technique. In (Hossain et al., 2022), a distributed event-trigger scheme has been applied, whose triggering conditions depend on output information for specific regions. It is noteworthy that the performance of the event-trigger scheme is related to the trigger threshold, however, In the design of the event-trigger scheme in the above research results, the performance of the trigger scheme has been limited since the trigger threshold is required to be preset in advance (Wu et al., 2018). In consideration of the above situation, various research scholars have applied adaptive event-trigger schemes (Chen et al., 2022) to the study of power systems. For example, an adaptive event-trigger scheme for multi-area power systems with communication bandwidth constraints is designed (Peng et al., 2018). Consequently, the system can adaptively adjust the threshold parameters based on current and past data; the dynamic event-trigger scheme and adaptive event-trigger scheme for networked power systems are investigated (Wu et al., 2020). The trigger parameters of the dynamic scheme are the upper limit of the trigger parameters of the adaptive scheme, both of which work together to balance the system control performance and the number of transmitted signals (Shangguan et al., 2022). Even though there have been many research results on the LFC event-triggered scheme, little research has been conducted on the optimal design of the event-trigger scheme.
Artificial fish swarm algorithm (AFSA) is a class of swarm intelligence optimization algorithms based on fish activity behavior (Tang et al., 2021). The algorithm has the ability of distributed processing as well as strong robustness of parameters and initial values (Lin et al., 2020; Yang et al., 2022). Particle swam optimization (PSO) is an algorithm inspired by the predatory behavior of birds and used to solve optimization problems (Tang et al., 2021; Belaid et al., 2022). The velocity of a particle is dynamically adjusted by its own and its companion’s flight experience, thus enabling the individual to search in the solvable space. It is rather remarkable that AFSA has a strong global search capability, but the algorithm converges slowly at a later stage (Zhu and Gao, 2020). In contrast, PSO has the capability of local fast convergence but tends to fall into the local optimum (Dashtdar et al., 2022). This paper presents a hybrid AFSA-PSO algorithm, to make the merits and demerits of the two algorithms complementary, thereby addressing the optimization problem better. AFSA uses an adaptive vision and step size which can dynamically regulate the operating speed of the algorithm. Additionally, the introduction of the compression factor and adaptive inertia weight to PSO ensures the convergence of the algorithm and removes the boundary restriction on the velocity, resulting in a more satisfactory solution.
Accordingly, to enhance the network bandwidth utilization, and reduce the transmission of redundant information for power system, this paper offers an improved event-triggered LFC based on a hybrid AFSA-PSO algorithm.
In consideration of the above discussions, this paper investigates a multi-area power system LFC based on the AFSA-PSO event-triggered scheme. The main contributions of this work are displayed below:
1) Since network communication is constrained by limited network bandwidth, this paper introduces an event-trigger scheme. The specific form of performance is to improve the utilization of network resources and ease the pressure on communication bandwidth by screening the measured output signal of the LFC power system. In the meantime, a hybrid AFSA-PSO algorithm is proposed to optimize the parameters that determine the threshold conditions in this paper, leading to the improved performance of the event-trigger scheme. AFSA is employed early in the method, and PSO has applied afterward, which makes the algorithm have high solution accuracy and convergence speed. In addition, this paper also optimizes and improves the AFSA and PSO respectively, to enable the algorithm to attain better performance.
2) The conservatism of the stability criterion design process is reduced under improved Lyapunov function. On the one hand, an improved Lyapunov function is constructed in the stability-proof process. On the other hand, the utilization of the double B-L inequality in the inequality scaling process decreases the conservatism of the resulting criterion.
2 Problem statement
2.1 Describe of LFC model
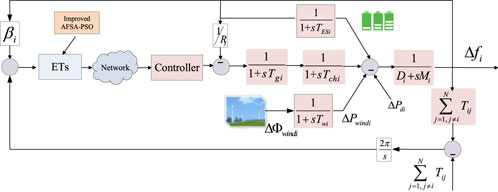
For multi-area power systems, the LFC system structure of the
The multi-area power system dynamics LFC model studied in this paper can be described as:
where:
The Area Control Error (ACE) for each control area can be expressed by:
2.2 Design of improved event-triggered scheme
To save network bandwidth resources, and improve information transmission efficiency, an event-triggered scheme based on the improved AFSA-PSO algorithm is proposed to increase the utilization of network resources in this study. When the transmitted signal meets the trigger scheme, it may be transmitted; otherwise, the sampling signal will not be transmitted, and the event-triggered conditions are designed as follows (Yue et al., 2013):
where,
The event trigger determines the transmission of the system state. Assuming that the data has been successfully transferred at time
Transmission delays are unavoidable due to the presence of communication networks. It is reflected in the trigger scheme as whether
(1) When
(2) When
where,
Thus,
where,
Therefore,
Remark 1. In this paper, a PSO with adaptive inertia weights (Li et al., 2019b) and compression factors (Zhou et al., 2019) are designed. This improved algorithm balances the local search and global search capability of PSO. Meanwhile, the boundary restriction on the conventional particle velocity is removed to ensure the convergence and accuracy of PSO. PSO can utilize the mechanism of sharing information among individuals in a group to make the whole solution process orderly. The core formula of the algorithm is given below:
Eq. 8 is the speed of the individual’s step
The algorithm is designed with adaptive inertia weights
Individual learning factor
In conclusion, the simultaneous introduction of adaptive inertia weights and compression factors can effectively improve the search capability and convergence accuracy of PSO, thus enhancing PSO performance.
Remark 2. In addition, an AFSA with an adaptive field of view and step size (Yuan and Yang, 2019) is designed in this paper. The algorithm can adaptively adjust the field of view and step length of the fish, which can enhance the global search ability in the early stage of the algorithm and accelerate the convergence speed in the late stage of the algorithm. The AFSA is a swarm intelligence stochastic optimization algorithm, in which the artificial fish self-renew by behavior such as prey, swarm, and follow, thus achieving the optimal search. However, the traditional AFSA involves the concept of the field of view in which the selection of viewpoints is random and the step length of movement is also random, which not only causes a lot of wasted computation time but also affects the search speed and accuracy. Given this, this paper presents the adaptive field of view factor
where,
Remark 3. It is worth noting that AFSA has a strong global search capability, but the algorithm converges slowly at a later stage; PSO has a local fast convergence capability and can obtain a more accurate solution by adjusting the parameters, but it is easy to fall into a local optimum. Even though the two algorithms have been optimized separately, the above mentioned defects are still difficult to eliminate, which allows the introduction of hybrid optimization algorithms (Veerasamy et al., 2020). The algorithm proposed in this paper combines AFSA and PSO, which can combine the good characteristics of the two basic algorithms (Tsai and Lin, 2011). AFSA is applied in the early stage of the algorithm to expand the search range of individual best position and group best position, and PSO is utilized in the later stage of the algorithm to achieve a fine step-by-step search. It is proved that the algorithm can improve the convergence speed and solution accuracy to a certain extent.
Remark 4. Using disturbance attenuation level
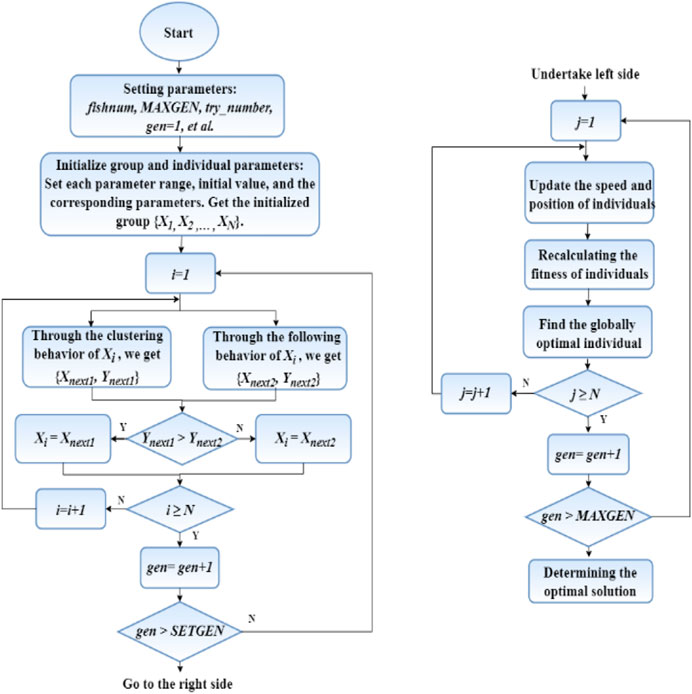
Step 1. Set parameters: such as fishnum(number of artificial fish),MAXGEN(maximum number of iterations), try_number(maximum number of tries), gen = 1(current number of iterations), etc.,; Initialize the population and individual parameters: set the range of each parameter, assign initial values to variables, form the population from the random array generated in the given range, set inertia weights, compression factors, control coefficients, etc.,;
Step 2. Start iteration, when the number of iterations is less than the preset value, the AFSA is used, otherwise the PSO is used;
Step 3. When the AFSA is used, the following operations are performed for each individual: set the adaptive field of view and step size, compare the fitness after performing following and swarming behaviors respectively, and keep the better fitness, then compare it with the individual optimum and population optimum, and update the fitness value;
Step 4. When the PSO is used, the following operations are performed for each individual: update the adaptive inertia weights, calculate the speed and position of the individual combined with the compression factor, recalculate the fitness value of the individual, find the global optimal individual, and update the optimal position of the individual and the group;
Step 5. Stop iteration when the maximum number of iterations is reached, and the obtained is the optimal solution.Figure 2 can show the implementation of the code.
3 Stability analysis of multi-area LFC
In this section, an improved Lyapunov function and the B-L inequality are applied to study the stability criteria for the multi-area LFC with the improved event-triggered scheme (Lv et al., 2020).
Lemma 1. (Peng and Zhang, 2016): For a given positive matrix
where:
The stability of the system (1) without disturbances will then be presented. The system (1) can be described as follows:
Theorem 1. For given positive
where:
Proof: Defining the Lyapunov function as:
where:
where:
Defining the following augmenting state variable:
Thus, the next inequality can be obtained:
where:
Applying the B-L inequality,
Applying Lemma 1, we obtain:
Therefore, if
LMI (17) can be verified if
Theorem 2. For given positive constant
where:
Proof: The proof of this theorem is based on Theorem 1. For the prescribed attenuation level
For
Considering the improved event-triggered scheme, if the following inequality hold,
Defining the augmenting state variable:
For
it yields:
Thus, Theorem 2 is proved. The stability with
4 Case studies and discussion
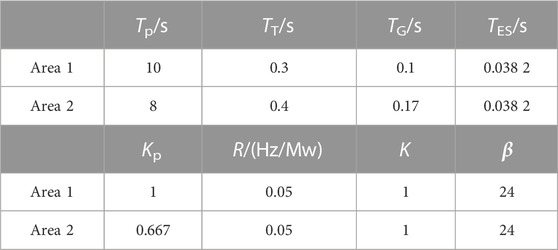
In this section, two simulation examples are carried out to verify the performance of the proposed event-triggered LFC based on an improved AFSA-PSO. In this section, the two-area LFC system model as well as the IEEE-39 node system model are built using Simulink. Among them, the parameters of the two-area system model are shown in Table 2.
4.1 Two-area LFC system simulation experiment
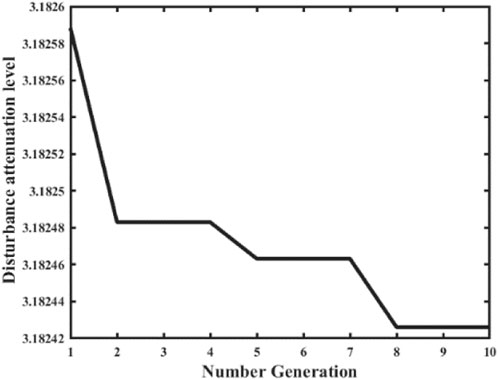
Since the thresholds of different event-triggered schemes in LFC systems can have an impact on the system’s performance. Therefore, this simulation experiment uses the hybrid AFSA-PSO to optimize the event-triggered scheme threshold with the system performance as the optimization objective. The process between the number of algorithm iterations and the optimized performance is shown in Figure 3. Meanwhile, this experiment takes the two-area LFC system as the object and adds
Based on the data presented in Figure 3, it is evident that the system’s target value converges to a constant value of 3.18243 after eight iterations of the algorithm. Consequently, selecting the trigger threshold
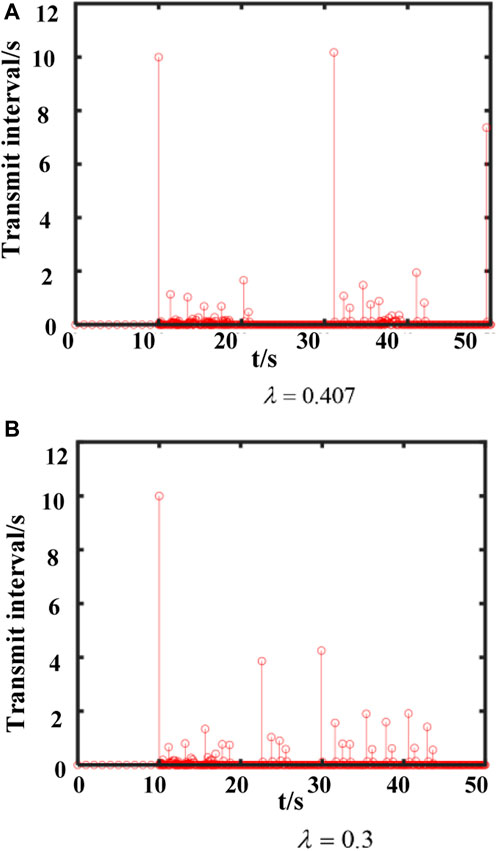
To assess the performance of the proposed event-triggered scheme, Figure 4B presents the release time and interval of data for the LFC system in two areas with the trigger threshold
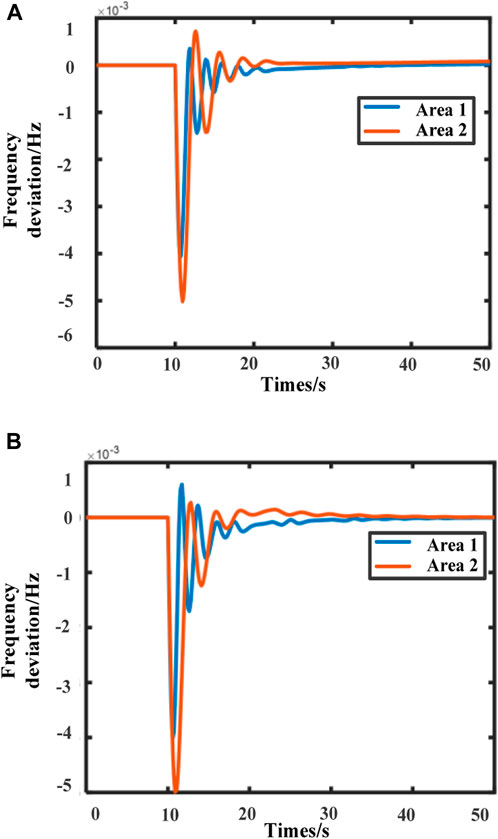
To verify the performance of the LFC under the designed event-triggered scheme, the frequency deviation response plots of the system under the two event-triggered schemes are given separately, as shown in Figure 5. Figures 5A, B show the system frequency deviation
4.2 IEEE-39 node system
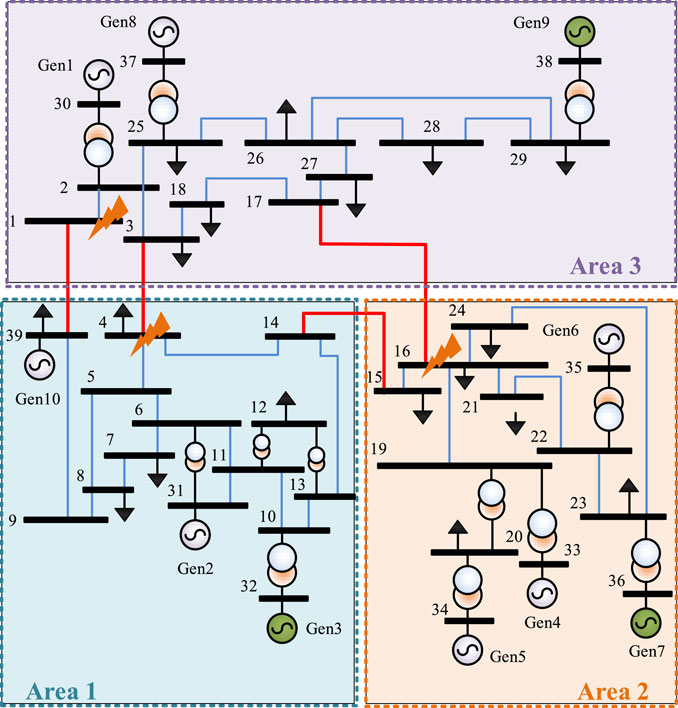
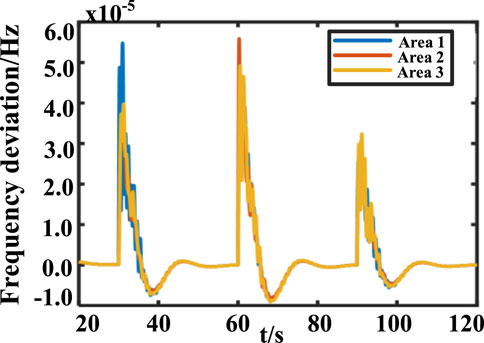
In this simulation experiment, an IEEE-39 node model is built using MATLAB/Simulink. The model contains 10 diesel generators along with 19 loads and 34 transmission lines (Shangguan et al., 2022). Also, to verify the performance of the proposed LFC based on the improved event-triggered scheme, the system is divided into three control areas, with Gen3 as the selected generator in Area 1, Gen7 as the selected generator in Area 2, and Gen9 as the selected generator in Area 3. Figure 6 shows the schematic diagram of the IEEE-39 bus test system and the division of the control area.
At
From Figure 7 and Figure 8, it can be seen that the frequency deviation
5 Conclusion
To save network communication resources and reduce the information transmission frequency of multi-area power systems, this paper proposes an improved event-triggered scheme based on a hybrid AFSA-PSO and investigates LFC based on this scheme. In this paper, an LFC model with wind power and battery storage is established based on Markov theory. Based on this model, the stability of this system is studied by an improved Lyapunov function. Moreover, the conservatism of the resulting stability criterion is reduced by utilizing the double B-L inequality in the inequality scaling process. Compared with the traditional event-triggered scheme, the hybrid AFSA-PSO can optimize the threshold value rapidly and efficiently. The algorithm adopts the improved AFSA in the first stage and applies the improved PSO in the later stage, which can take into account the global and local aspects of the search so that the algorithm has high solution accuracy and convergence speed. High performance event-triggered schemes obtained by optimizing event-triggered thresholds enable better frequency control while transmitting less information. In conclusion, this paper verifies the effectiveness of the improved event-triggered scheme in the two-area LFC system model as well as the IEEE-39 node system model.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
TH contributed to the conception of the study. The corresponding author XL is responsible for ensuring that the descriptions are accurate and agreed upon by all authors. All authors contributed to the article and approved the submitted version.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aluko, A. O., (2021). Robust State Estimation Method for Adaptive Load Frequency Control of Interconnected Power System in a Restructured Environment. IEEE Syst. J. 15 (4), 5046–5056. doi:10.1109/jsyst.2020.3005979
Belaid, S., (2022). Proposed Hybrid Power Optimization for Wind Turbine/Battery System. Periodica Polytech. Electr. Eng. Comput. Sci. 66 (1), 60–71. doi:10.3311/ppee.18758
Bu, X., (2022). Event-Triggered Data-Driven Load Frequency Control for Multiarea Power Systems. IEEE Trans. Ind. Inf. 18 (9), 5982–5991. doi:10.1109/tii.2021.3130415
Chen, P., (2022). Dynamic Event-Triggered Output Feedback Control for Load Frequency Control in Power Systems With Multiple Cyber Attacks. IEEE Trans. Syst. Man. Cybern. Syst. 52 (10), 6246–6258. doi:10.1109/tsmc.2022.3143903
Choi, J. W., Heo, S. Y., and Kim, M. K. (2016). Hybrid Operation Strategy of Wind Energy Storage System for Power Grid Frequency Regulation. IET Gener. Transm. Distrib. 10 (3), 736–749. doi:10.1049/iet-gtd.2015.0149
Dashtdar, M., (2022). Improving the Power Quality of Island Microgrid With Voltage and Frequency Control Based on a Hybrid Genetic Algorithm and PSO. IEEE Access 10, 105352–105365. doi:10.1109/access.2022.3201819
Gholamrezaie, V., (2018). An Optimal Frequency Control Method Through a Dynamic Load Frequency Control (LFC) Model Incorporating Wind Farm. IEEE Syst. J. 12 (1), 392–401. doi:10.1109/jsyst.2016.2563979
Hossain, M. M., (2022). Bandwidth Allocation-Based Distributed Event-Triggered LFC for Smart Grids Under Hybrid Attacks. IEEE Trans. Smart Grid 13 (1), 820–830. doi:10.1109/tsg.2021.3118801
Li, M., (2019a). An Improved Particle Swarm Optimization Algorithm With Adaptive Inertia Weights. Int. J. Inf. Technol. Decis. Mak. 18 (03), 833–866. doi:10.1142/s0219622019500147
Li, Y., (2019b). Event-Triggered-Based Distributed Cooperative Energy Management for Multienergy Systems. IEEE Trans. Ind. Inf. 15 (4), 2008–2022. doi:10.1109/tii.2018.2862436
Lin, L., (2020). Deep Reinforcement Learning for Economic Dispatch of Virtual Power Plant in Internet of Energy. IEEE Internet Things 7 (7), 6288–6301. doi:10.1109/jiot.2020.2966232
Liu, Y., (2021). Automatic Generation Control for Distributed Multi-Region Interconnected Power System With Function Approximation. Front. Energy Res. 9. doi:10.3389/fenrg.2021.700069
Lv, X., (2020). Event-Triggered Load Frequency Control for Multi-area Power Systems Based on Markov Model: A Global Sliding Mode Control Approach. IET Gener. Transm. Distrib. 14 (21), 4878–4887. doi:10.1049/iet-gtd.2020.0186
Mi, Y., (2017). Sliding Mode Load Frequency Control for Multi-area Time-delay Power System With Wind Power Integration. IET Gener. Transm. Distrib. 11 (18), 4644–4653. doi:10.1049/iet-gtd.2017.0600
Oubelaid, A., (2022a). Fuzzy-Energy-management-based Intelligent Direct Torque Control for A Battery—Supercapacitor Electric Vehicle. Sustainability 14 (14), 8407. doi:10.3390/su14148407
Oubelaid, A., (2022b). Secure Power Management Strategy for Direct Torque Controlled Fuel Cell/Supercapacitor Electric Vehicles. Front. Energy Res. 10. doi:10.3389/fenrg.2022.971357
Oubelaid, A., Taib, N., and Rekioua, T. (2022c). Novel Coordinated Power Sources Switching Strategy for Transient Performance Enhancement of Hybrid Electric Vehicles. COMPEL - Int. J. Comput. Math. Electr. Electron. Eng. 41 (5), 1880–1919. doi:10.1108/compel-10-2021-0399
Peng, C., and Zhang, J. (2016). Delay-Distribution-Dependent Load Frequency Control of Power Systems With Probabilistic Interval Delays. IEEE Trans. Power Syst. 31 (4), 3309–3317. doi:10.1109/tpwrs.2015.2485272
Peng, C., Zhang, J., and Yan, H. (2018). Adaptive Event-Triggering ${H}_{\infty }$ Load Frequency Control for Network-Based Power SystemsH∞Load Frequency Control for Network-Based Power Systems. IEEE Trans. Ind. Electron 65 (2), 1685–1694. doi:10.1109/tie.2017.2726965
Pulazza, G., (2021). Transmission Planning With Battery-Based Energy Storage Transportation For Power Systems With High Penetration of Renewable Energy. IEEE Trans. Power Syst. 36 (6), 4928–4940. doi:10.1109/tpwrs.2021.3069649
Shangguan, X.-C., (2022). Control Performance Standards-Oriented Event-Triggered Load Frequency Control for Power Systems Under Limited Communication Bandwidth. IEEE Trans. Control Syst. Technol. 30 (2), 860–868. doi:10.1109/tcst.2021.3070861
Sun, Y., (2023). Stability Analysis of Load Frequency Control for Power Systems With Interval Time-varying Delays. Front. Energy Res. 10. doi:10.3389/fenrg.2022.1008860
Tang, J., Liu, G., and Pan, Q. (2021). A Review on Representative Swarm Intelligence Algorithms for Solving Optimization Problems: Applications and Trends. IEEE/CAA J. Autom. Sinica 8 (10), 1627–1643. doi:10.1109/jas.2021.1004129
Tsai, H.-C., and Lin, Y.-H. (2011). Modification of the Fish Swarm Algorithm With Particle Swarm Optimization Formulation and Communication Behavior. Appl. Soft Comput. 11 (8), 5367–5374. doi:10.1016/j.asoc.2011.05.022
Veerasamy, V., (2020). A Hankel Matrix Based Reduced Order Model for Stability Analysis of Hybrid Power System Using PSO-GSA Optimized Cascade PI-PD Controller for Automatic Load Frequency Control. IEEE Access 8, 71422–71446. doi:10.1109/access.2020.2987387
Wang, X., (2022). A Data-Driven Uncertainty Quantification Method for Stochastic Economic Dispatch. IEEE Trans. Power Syst. 37 (1), 812–815. doi:10.1109/tpwrs.2021.3114083
Wen, S., (2016). Event-Triggering Load Frequency Control for Multiarea Power Systems With Communication Delays. IEEE Trans. Ind. Electron. 63 (2), 1308–1317. doi:10.1109/tie.2015.2399394
Wu, Z.-G., (2018). Event-Triggered Control for Consensus Problem in Multi-Agent Systems With Quantized Relative State Measurements and External Disturbance. IEEE Trans. Circuits Syst. I Regul. Pap. 65 (7), 2232–2242. doi:10.1109/tcsi.2017.2777504
Wu, Z., (2020). Adaptive Event-Triggered Observer-Based Output Feedback $\mathcal L_{\infty }$ Load Frequency Control for Networked Power SystemsL∞Load Frequency Control for Networked Power Systems. IEEE Trans. Ind. Inf. 16 (6), 3952–3962. doi:10.1109/tii.2019.2942637
Yan, C.-H., (2022). Stabilization of Load Frequency Control System via Event-Triggered Intermittent Control. IEEE Trans. Circuits Syst. II Express Briefs 69 (12), 4934–4938. doi:10.1109/tcsii.2022.3197460
Yang, D., (2020). Inertia - Adaptive Model Predictive Control-based Load Frequency Control for Interconnected Power Systems With Wind Power. IET Gener. Transm. Distrib. 14 (22), 5029–5036. doi:10.1049/iet-gtd.2020.0018
Yang, L., (2022). Indirect Multi-Energy Transactions of Energy Internet with Deep Reinforcement Learning Approach. IEEE Trans. Power Syst. 37 (5), 4067–4077. doi:10.1109/tpwrs.2022.3142969
Yuan, G., and Yang, W. (2019). Study on Optimization of Economic Dispatching of Electric Power System Based on Hybrid Intelligent Algorithms (PSO and AFSA). Energy 183, 926–935. doi:10.1016/j.energy.2019.07.008
Yuan, Z.-L., (2021). Delay-dependent Stability Analysis of Load Frequency Control for Power System With EV Aggregator. Front. Energy Res. 9. doi:10.3389/fenrg.2021.771465
Yue, D., Tian, E., and Han, Q.-L. (2013). A Delay System Method for Designing Event-Triggered Controllers of Networked Control Systems. IEEE Trans. Autom. Contr. 58 (2), 475–481. doi:10.1109/tac.2012.2206694
Zhang, H., Liu, J., and Xu, S. (2020). H-Infinity Load Frequency Control of Networked Power Systems via an Event-Triggered Scheme. IEEE Trans. Ind. Electron. 67 (8), 7104–7113. doi:10.1109/tie.2019.2939994
Zhao, X., (2022). Robust LFC of Power Systems With Wind Power Under Packet Losses and Communication Delays. IEEE J. Emerg. Sel. Top. Power Electron. 12 (1), 135–148. doi:10.1109/jetcas.2022.3141108
Zhou, Z., (2019). Application of Kriging Algorithm based on ACFPSO In Geomagnetic Data Interpolation. Math. Probl. Eng. 2019, 1–14. doi:10.1155/2019/1574918
Keywords: event-triggered scheme, LFC systems, particle swarm optimization, artificial fish swarm algorithm, IEEE-39 node simulation models
Citation: Huang T and Lv X (2023) Load frequency control of power system based on improved AFSA-PSO event-triggering scheme. Front. Energy Res. 11:1235467. doi: 10.3389/fenrg.2023.1235467
Received: 06 June 2023; Accepted: 19 July 2023;
Published: 04 August 2023.
Edited by:
Srete Nikolovski, Josip Juraj Strossmayer University of Osijek, CroatiaCopyright © 2023 Huang and Lv. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xinxin Lv, eGlueGlubHZoaHVjQDE2My5jb20=
 Tenghao Huang
Tenghao Huang Xinxin Lv
Xinxin Lv