Vector well pattern optimization of horizontal well in offshore edge water reservoirs

Abstract
The L30up reservoir is a strongly heterogeneous edge water reservoir with obvious provenance direction and channel direction. It is developed by horizontal wells, and the traditional well pattern adjustment is not suitable for tapping the remaining oil potential of this type of reservoirs, while vector well pattern adjustment is one of the important measures to enhance oil recovery. In this paper, aiming at maximizing the economic net present value, taking the characteristic parameter matrix of well pattern reconfiguration (well position, azimuth angle, horizontal section length) as variables, an optimization model of horizontal well pattern vector adjustment is established. Furthermore, the PSO-MADS algorithm is proposed to solve the above optimization model. Thus, a vector well pattern adjustment technology that can realize the distribution matching of reservoir heterogeneity and remaining oil has been formed. On the basis of the deployment strategy of vector well pattern in L30up reservoir, according to the direction of sediment source, reservoir heterogeneity, distribution of remaining oil, etc., we determined the best vector well pattern adjustment scheme, and applied the above optimization method to optimize the infill well locations. Through the optimal deployment of the vector well pattern, the oil recovery factor after the vector well pattern adjustment is 5.21% percentage points higher than the original well pattern conditions, which precisely matches the well pattern parameters and the geological vector parameters, such as sand body distribution, remaining oil distribution, and edge waters in L30up reservoir.

1 Introduction

Well pattern infill an important means of extracting residual oil and enhancing oil recovery (Han, 2010). Vector well pattern (Xiao and Liu, 2010; Yao, 2011) is a development adjustment scheme in high water cut period, which aims to match reservoir heterogeneity, permeability anisotropy and well pattern characteristics for the purpose of achieving balanced displacement. On the basis of the original injection-production well pattern, the matching relationship between the well pattern and reservoir parameters is adjusted by deploying the infill schemes, the flow field distribution is changed, so that the reservoir can achieve balanced and efficient displacement, so as to improve the recovery efficiency and development effect.

In recent years, well location optimization has become one of the research hotspots in reservoir development optimization (Bouzarkouna et al., 2011; Afshari et al., 2015; Bagherinezhad et al., 2017; Park et al., 2017; Ding et al., 2020; Mirzaei-Paiaman et al., 2022; Salehian and Morteza Haghighat Sefat Muradov, 2022). Based on optimization theory, this method obtains the location of infill wells by constructing objective functions, restricting constraints and solving for optimal values (Wang et al., 2016; Hamida et al., 2017; Semnani et al., 2021). The parameters characterizing the infill well location are taken as optimization variables, and combined with the given constraints, the optimization algorithm is used to solve the optimization problem. In order to obtain the best infill well location, further achieve the purpose of improving the reservoir development effect and enhancing oil recovery.

How to design a reasonable well pattern infill scheme suitable for the target reservoir, including vector well pattern scheme, many scholars have done a lot of research on the above work. Ariadji et al. (2014) introduced a fitness function based on reservoir parameters such as permeability, porosity, oil saturation, reservoir pressure and thickness, and optimized the infill well location by using a genetic algorithm. Jesmani et al. (2016a) studied the optimization of infill well location in oilfield development, and their research showed that practical constraints should be embedded in the construction of optimization models. These constraints are the prerequisites for better use of optimization methods in well location optimization problems, which can convert actual well location design constraints into mathematical models. Ding et al. (2016) a well location optimization model for irregular well patterns based on the characteristics of “few wells and high production” in deep-water reservoirs, and used an improved particle swarm optimization algorithm to solve the problem in combination with numerical simulation methods, realizing the auto-optimization of well locations of irregular well patterns. Park et al. (2017) changed the optimization strategy, and proposed a two-stage optimization method, which was first based on the preliminary judgment of dynamic flow characteristics, and then further optimized using a genetic algorithm. Compared with traditional methods, the main advantage of this method is that it can combine static reservoir properties with dynamic parameters such as sweep efficiency, which improves the calculation efficiency. Ding et al., 2020 proposed a well location optimization method combining particle swarm optimization (PSO) with efficient hybrid objective function (HOF), which used production potential value (PPV) in the early iterations of well location optimization to obtain potential well locations, and the traditional objective function cumulative oil production (COP) is used in subsequent iterations to obtain reservoir dynamics. Semnani et al. (2021) constructed a population-based meta-heuristic global optimization algorithm—teaching and learning optimization algorithm (TLBO), and on this basis, with the economic net present value (NPV) as the objective function, the well location optimization of a certain oil reservoir was carried out. To avoid the interwell interference problem, she proposes a method of constraining distances to any number of points in ordinary n-dimensional space. Nasir et al. (2022) developed and tested a new step-by-step solution strategy for large-scale optimization problems in oilfields. In the first stage, well locations are restricted to the scenario, optimization variables are reduced, and the scenario type and geometry (e.g., well spacing, orientation) are defined. Then, the solution obtained in the first stage is used as initialization variables in the second stage to obtain optimal well locations. Both stages were optimized using the particle swarm adaptive direct search (PSO-MADS) algorithm.

The L30up reservoir has complex geological characteristics, strong reservoir heterogeneity, and is driven by multi-directional edge water. Horizontal wells are used for production, but the well pattern is not perfect, which does not match the reservoir geology and development characteristics, and the synergy between injected water and edge water is poor, resulting in unbalanced well pattern reserve control and utilization. The well pattern development effect is poor, and the recovery rate is low, only 20.9%. It is necessary to carry out research on well pattern adjustment. However, in the study of well location optimization in water injection oilfields, the research object of infill well pattern is limited to vertical wells and there are few researches on infill well locations of horizontal wells. And well pattern design has not been carried out for edge water reservoir in current research. Therefore, according to the direction of sediment source, reservoir heterogeneity, distribution of remaining oil, etc., we proposed the deployment strategy of vector well pattern in L30up reservoir, and taking the well location, azimuth angle and horizontal section length as optimization variables, a vector well pattern reconstruction method for horizontal well development is established in this paper to optimize the infill well locations.

2 Construction of mathematics model

At present, the objective functions commonly used in infill well optimization mainly include cumulative oil production, recovery degree, economic net present value, etc (Wang et al., 2016; Hamida et al., 2017; Semnani et al., 2021). In this paper, the economic net present value (NPV) is used as the objective function, which can comprehensively measure the economic factors of reservoir production in the development process: production revenue, water injection cost, water treatment cost, and the impact of cost on development effect. In addition, NPV has been widely used in the optimization of oil and gas field development as an objective function (Jesmani et al., 2016a; Naderi and Khamehchi, 2017; Semnani et al., 2021). The objective function of well location optimization of horizontal well pattern can be expressed as:

$\max f={\displaystyle \sum _{t=1}^T}\left[\frac{1}{{\left(1+b\right)}^t}\cdot \left({\displaystyle \sum _{p=1}^{N_p}}{C}_{\mathrm{o}}{Q}_{\mathrm{o}}^{\left(t\right)}-{\displaystyle \sum _{p=1}^{N_p}}{C}_{\mathrm{w}}{Q}_{\mathrm{w}}^{\left(t\right)}-{\displaystyle \sum _{I=1}^{N_I}}{C}_I{Q}_I^{\left(t\right)}\right)\right]-N_{\inf }{C}_{\mathrm{d}}L(1)$

Here, T can be expressed as the total production time, year;t is the current time, year; C_o denotes the oil price,USD·m⁻³;C_w is the sewage treatment cost, USD·m⁻³;C_I denotes the cost of water injection, USD·m⁻³;C_d is the drilling and completion costs dependent on the length of the horizontal well, USD; Q_o is the oil production, m³·d⁻¹;Q_w is the water production, m³·d⁻¹;Q_I is the water injection rate, m³·d⁻¹;N_P and N_I refer to the number of production wells and injection wells, respectively; N_inf is number of infill wells; L denotes the length of the well, m; b is the interest rate (10.36% in this case).

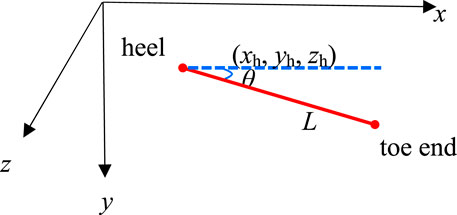
The variables of this optimization problem are the combination of characteristic parameters that characterizes the location of horizontal wells, and these parameters represent the location of the infill horizontal well, that is, five variables (x_h, y_h, z_h, L, θ) are required. Here, well location coordinates can be expressed by x_h, y_h, z_h, L represents the well length, and θ is the azimuth. As shown in Figure 1, it is a schematic diagram of specific horizontal well location parameters. Only by expressing the well position of the horizontal well in this way, that can reflect the structural parameters of the horizontal well such as horizon, wellbore length and azimuth angle.

FIGURE 1

FIGURE 1. Schematic diagram of horizontal well location optimization parameters.

In order to obtain infill well locations within a feasible range, constraints need to be considered in the optimization process, including infill range constraints, wellbore length constraints, azimuth constraints, and minimum well spacing constraints.

2.1 Infill constraint range

In this paper, constraints are introduced into the optimization of horizontal well locations, and the location of horizontal wells cannot exceed the feasible infill region. x_max, y_max, z_max and x_min, y_min, z_min represent the upper and lower limits of the position constraints in the three directions respectively. The constraints on the coordinates of starting point of horizontal wells can be expressed as follows:

$\begin{array}{l}{x}_{\min }\le x_h\le x_{\max }\\ y_{\min }\le y_h\le y_{\max }\\ z_{\min }\le z_h\le z_{\max }\end{array}(2)$

Similarly, the coordinates of the end point of horizontal wells should also be within the feasible region. Therefore, the following conditions should be satisfied:

$\begin{array}{l}{x}_{\min }\le x_t\le x_{\max }\\ y_{\min }\le y_t\le y_{\max }\\ z_{\min }\le z_t\le z_{\max }\end{array}(3)$

2.2 Well length constraint

On the other hand, there are some restrictions on the length of the well. L_min and L_max denote the minimum and maximum length of horizontal wells, which is a linear constraint and can be expressed as:

$L_{\min }\le L\le L_{\max }(4)$

2.3 Azimuth constraint

Since the optimized infill well is a horizontal well, its azimuth should be within the feasible range. θ_min can be expressed as the minimum azimuth angle, and θ_max is the maximum azimuth angle. It can be expressed as:

${\theta }_{\min }\le \theta \le {\theta }_{\max }(5)$

2.4 Minimum well spacing constraints

When the well spacing is too small, it will cause interference between wells. In order to avoid this situation, the influence of well spacing should be considered when optimizing the location of horizontal wells. In this case, i and j denote two wells, and M and N can be expressed as a point in well i and well j, respectively. Then, the distance between M and N can be expressed as D_i,j. Therefore, the minimum well spacing constraint can be expressed as:

$D_{i,j}\ge D_{\min },i,j\in N\left(i\ne j\right)(6)$

Then, with the NPV as the objective function, the well pattern parameters (well position, azimuth, horizontal length) as optimization variables, combined with the above constraints, a mathematical model for optimizing horizontal well location was established to realize the precise design of infill well location. It can be seen that the constraints of this optimization problem are very complex. In order to improve the solution speed and accuracy of the optimization algorithm, different processing methods should be adopted for different constraints. The following mainly introduces the constraint condition processing methods adopted in this paper.

Due to many types of constraints in the optimization solution, the optimization model is difficult to solve and to find a feasible solution. Therefore, linear constraints need to be preprocessed in the optimization problem, including the constraints of the starting point coordinates of the optimized horizontal well infill well position, the constraints of the wellbore length, and the constraints of the azimuth range. For the linear constraints, this paper adopts the truncation method to deal with them, so as to improve the automatic optimization ability. The specific processing steps of the truncation method are shown in Formula (7), and the solution that violates the constraint conditions is “dragged” into the feasible area, so that the infeasible solution is transformed into a feasible solution (Nwankwor et al., 2013; Chen and Reynolds, 2018).

$x_i=\left\{\begin{array}{l}{x}_{\min i}\mathrm{i}\mathrm{f}{x}_i\le x_{\min i}\\ x_{\max i}\mathrm{i}\mathrm{f}{x}_i\ge x_{\max i}\\ x_i\mathrm{i}\mathrm{f}{x}_{\min i}\le x_i\le x_{\max i}\end{array}\right.(7)$

Where, x_maxi is the maximum value of the ith parameter;x_mini is the minimum value of the ith parameter.

On the other hand, if the expression of the variables are nonlinear, these constraints are called nonlinear constraints, including constraints for optimizing the start-end coordinates of horizontal wells and the constraints for minimum well spacing. The following methods are mainly used to deal with the problem of nonlinear constraints. Among them, the adaptive penalty function method (Michalewicz, 1995) does not need to set the value of penalty factor in advance, but dynamically sets the penalty function factor according to the proportion of infeasible solutions during the search process, and thus more feasible solutions can be generated. The specific steps are as follows: the penalty factor is adjusted by making full use of the feedback value provided by the infeasible solutions during the search process in the penalty process. When there are more infeasible solutions in the search process, the penalty factor increases with the number of infeasible solutions; when there are fewer infeasible solutions in the search process, the penalty factor then decreases (Ben Hadj-Alouane and Bean, 1997; Li et al., 2009; Cai, 2015). The objective function expression of the adaptive penalty function method is as follows:

$eval\left(\mathbf{X}\right)=f\left(\mathbf{X}\right)-{10}^{{\alpha }_{\mathrm{a}\mathrm{d}\mathrm{a}}}{P}_{\mathrm{u}\mathrm{n}}{\displaystyle \sum _{\mathrm{c}\mathrm{o}\mathrm{n}=1}^{N_{\mathrm{c}\mathrm{o}\mathrm{n}}}}{f}_{\mathrm{c}\mathrm{o}\mathrm{n}}\left(\mathbf{X}\right)(8)$

Where, α_ada is an integer from 0 to 10; P_un is the ratio of infeasible solutions to all solutions.

In summary, the adaptive penalty method has certain advantages over other methods in that it can continuously adjust its own penalty strength in the search process, which increases the flexibility of handling constraints, therefore generating more feasible solutions and increasing the chance of convergence to the optimal solution. Due to the complexity of the constraints and solution process of horizontal well pattern optimization, the adaptive penalty method is chosen to handle the nonlinear constraints in order to accelerate the search speed and obtain the optimal solution. Therefore, the objective function of well location optimization of horizontal well pattern can be expressed as:

$eval\left(\mathbf{X}\right)=NPV\left(\mathbf{X}\right)-{10}^{{\alpha }_{\mathrm{a}\mathrm{d}\mathrm{a}}}{P}_{\mathrm{u}\mathrm{n}}{\displaystyle \sum _{\mathrm{c}\mathrm{o}\mathrm{n}=1}^{N_{\mathrm{c}\mathrm{o}\mathrm{n}}}}{f}_{\mathrm{c}\mathrm{o}\mathrm{n}}\left(\mathbf{X}\right)(9)$

3 Solution of mathematical model

3.1 Characteristic analysis of optimization problem

After a period of waterflood development, the reservoir physical properties such as permeability and porosity, and fluid properties such as oil saturation usually show heterogeneity. Within the feasible encryption range, reservoir development can vary depending on the well placement. Therefore, the optimization of horizontal well placement with vector well pattern is a complex optimization problem, which is associated with a variety of factors, such as reservoir heterogeneity, residual oil distribution, production dynamic parameters, etc.

3.1.1 Multiple optimization variables

According to the established mathematical model of horizontal well location optimization with vector well pattern encryption, it can be seen that optimizing a horizontal well involves 5 optimization variables. The number of wells that need to be optimized varies depending on the size of the reservoir, from a few wells to hundreds of wells in a real reservoir, and the number of optimization variables will increase accordingly. The dimensionality of optimization problem will increase with the increase of the number of optimization variables, which leads to the difficulty of solving the problem.

3.1.2 Nonlinearity of optimization problem

In the vector optimization problem of horizontal well pattern, different parameters such as oil saturation, injection-production well spacing and displacement pressure gradient under different infill well locations lead to different reservoir development effects, thus affecting the economic benefits generated during reservoir development. The economic benefits and optimization variables show a complex and highly nonlinear relationship, so it is difficult to obtain derivative information.

3.1.3 Many constraints of optimization problem

The established horizontal well vector adjustment optimization model corresponds to different constraints. The constraints of infill well location optimization include infill range constraint, well length constraint, azimuth constraint and minimum well distance constraint. These constraints include both linear and nonlinear constraints, and the above complex constraints need to be addressed in the solution to optimize feasible infill well parameters.

3.2 Analysis of solving algorithm characteristics

In view of the above analysis on the well location optimization problem of horizontal well vector pattern encryption, different types of intelligent optimization algorithms need to be optimized first in order to efficiently and accurately solve the optimization mathematical model. According to whether the optimization algorithm needs the gradient information of the objective function in the process of automatic optimization, it can be classified into gradient-free optimization algorithm and gradient optimization algorithm (Bukshtynov et al., 2015). Horizontal well location optimization problem with vector well pattern encryption is characterized by many optimization variables, many constraints and nonlinear optimization problems. In the process of objective function calculation, it is often difficult to derive or even non-derivable. The gradient optimization algorithm needs to use the derivative information of the objective function about the optimization variable in the optimization process, so it is not suitable for solving the optimization problem in this paper. The gradient-free optimization algorithm does not need the derivative information of the objective function, but only needs to calculate the value of the objective function NPV (Kolda et al., 2003; Sarma and Chen, 2008). Therefore, the gradient-free optimization algorithm is adopted to solve the problem.

Gradient-free optimization algorithm can be divided into local optimization algorithm and global optimization algorithm according to different optimization strategies. The search scope of the local optimization algorithm is around the selected initial solution to obtain the optimal solution of the objective function, so the local optimization has strong ability and high precision. However, the local search is performed. If it falls into the local extreme point, the optimization will stop. The optimization effect depends on the selection of the initial solution and cannot cover the global scope. Local optimization algorithms include mesh adaptive direct search algorithm (MADS), generalized scheme search method (GPS), etc. (Torczon, 1997; Liu, 2018)

Global optimization algorithm is a global optimization in the feasible domain, which can effectively avoid falling into the problem of local optimum, and then search the whole solution space, but can only find the general location of the global optimal solution with relatively low accuracy. Global optimization algorithms are mainly divided into the following types: genetic algorithm (GA), particle swarm optimization algorithm (PSO), differential evolution algorithm (DE), adaptive covariance matrix evolution algorithm (CMA-ES), etc. (Iruthayarajan and Baskar, 2010; Onwunalu and Durlofsky, 2010; Lyons and Nasrabadi, 2013; Yildiz, 2013).

In recent years, with the continuous in-depth study of various optimization algorithms, a variety of hybrid optimization algorithms have been derived, that is, by combining different types of optimization algorithms to complement each other’s advantages, so that global and local search capabilities can be taken into account.

The above analysis of the characteristics of optimization algorithms can be integrated to obtain better search performance by constructing a hybrid optimization algorithm that takes into account global and local search capabilities. PSO-MADS is a typical hybrid optimization algorithm that couples PSO with MADS, which belongs to a global-local stochastic search algorithm (Nasir et al., 2022). That is, on the basis of PSO for global search optimization, MADS is embedded for local search optimization.

The PSO-MADS algorithm starts with an initial particle swarm, including one or more custom initial values, and then applies PSO for iterations. If the global optimal position improves, the PSO search step is designated as successful, which means that a new global optimal position is generated whose objective function f is superior to the previous global optimal position, and the PSO continues to run. When the search step is unsuccessful (no improvement is provided), the MADS polling step is performed, centered on the best location of the cluster and then polling around the best solution found by PSO. As long as the polling step is successful, polling continues, that is, generating better feasible points about the objective function f. Run the MADS polling step until an unsuccessful iteration occurs, at which point the mesh size parameter decreases and the hybrid algorithm returns the PSO search. The PSO search continues around the best solution produced by the current MADS, repeating the above steps. This alternation between PSO and MADS continues until an optimal solution is found and terminated (Isebor et al., 2014; De Brito and Durlofsky, 2021).

4 Field application

The L30up reservoir has typical zoning characteristics in terms of source direction, tectonic orientation, and reserve abundance distribution. As shown in Figure 2A, the sand body configuration of the reservoir can be roughly divided into two directions: the west is mainly a northeast to southwest source direction, while the central and eastern are mainly a north to south source direction. According to the structural distribution of the reservoir, as shown in Figure 2B, the western structure is low in the west and high in the east; the central part is low in the north, high in the middle and low in the south; and the eastern part is low in the north and high in the south. According to the distribution of remaining oil reserves abundance, as shown in Figure 2C, it can be seen that the remaining oil reserves abundance is high in the central part, followed by the western part and poor in the eastern part. Therefore, considering source direction, structural strike and reservoir abundance distribution, L30up reservoir is divided into three typical areas, as shown in Figure 2D, namely, the central well area, the western edge water area and the eastern thin difference area.

FIGURE 2

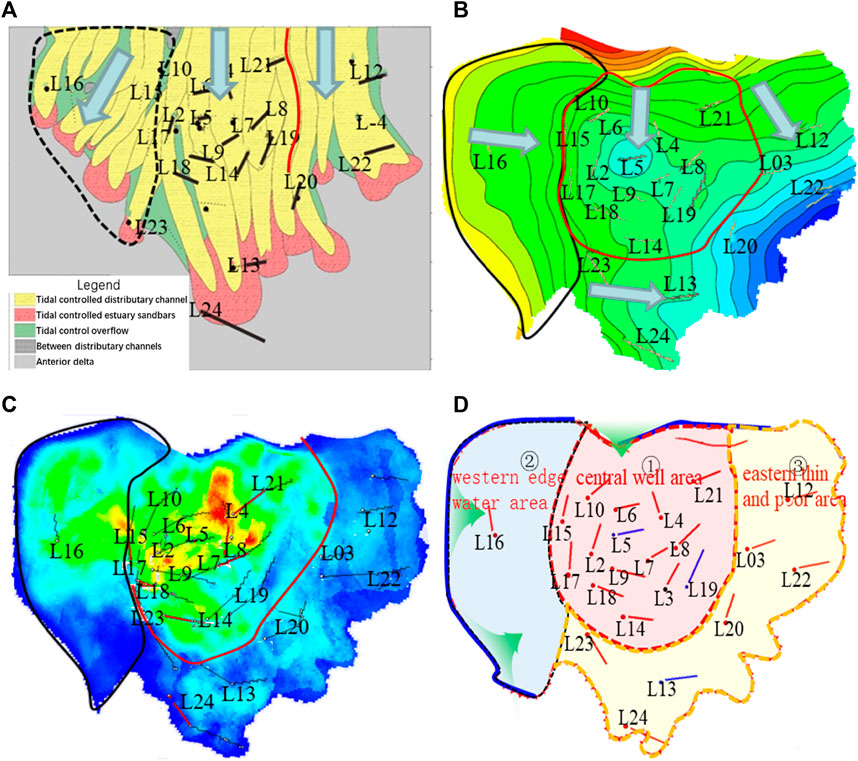
FIGURE 2. L30up reservoir zoning. (A) Sand body configuration distribution. (B) Reservoir structure distribution. (C) Reserve abundance distribution. (D) Partition diagram.

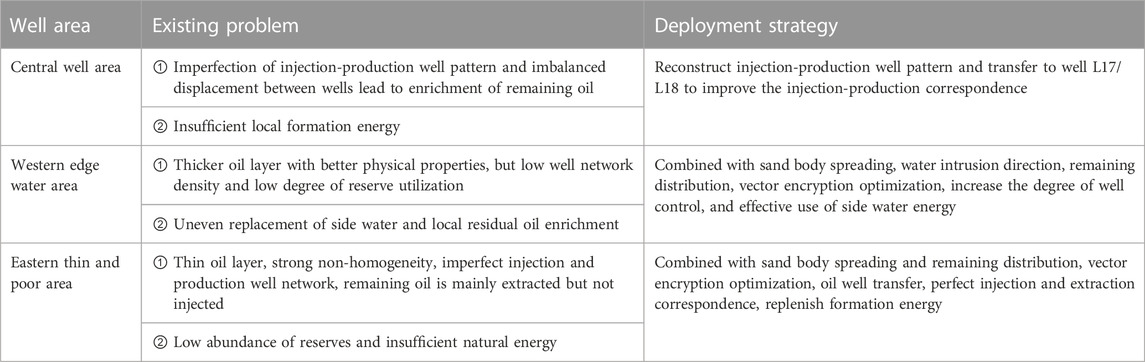
According to the characteristics and existing problems of L30up reservoir regions, vector well pattern deployment strategies are proposed, as shown in Table 1.

TABLE 1

TABLE 1. Deployment of vector horizontal well pattern in L30up reservoir.

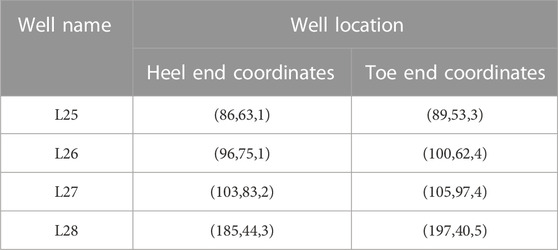
Based on reservoir engineering method, the reasonable well pattern density of horizontal wells in each region of L30up reservoir is calculated. The density of western edge water area is 0.38 wells per square kilometer, and three horizontal wells should be inserted; The central well area is 1.07 wells per square kilometer without encryption; The eastern thin difference zone is 0.61 wells per square kilometer, and one horizontal well should be encrypted. Combined with the vector well pattern deployment strategy, three horizontal wells are finally determined to be inserted in the tidal control overflow bank in the western edge water area, on both sides of the bay deposition between river channels, along the source direction. The strike of the horizontal section of the infill wells are almost perpendicular to the inflow direction of the edge water, so as to effectively utilize the edge water energy. For the central well area, L17 or L18 should be transferred into injection well to improve the injection and recovery correspondence, replenish the regional formation energy and effectively use the remaining oil in the original non-mainstream line area. In the eastern thin differential area, one horizontal well should be encrypted in the vertical source direction to form an injection and recovery correspondence with the surrounding wells, while considering that the line between the encrypted well and L12 is in the direction of the source and the physical properties between the well are better, the distance between the wells can be appropriately enlarged when deploying the encrypted wells. Therefore, the following eight vector well pattern adjustment schemes are designed comprehensively, as shown in Table 2. Figure 3 shows the deployment of each solution. Table 3 lists the coordinates of the encrypted well locations.

FIGURE 3

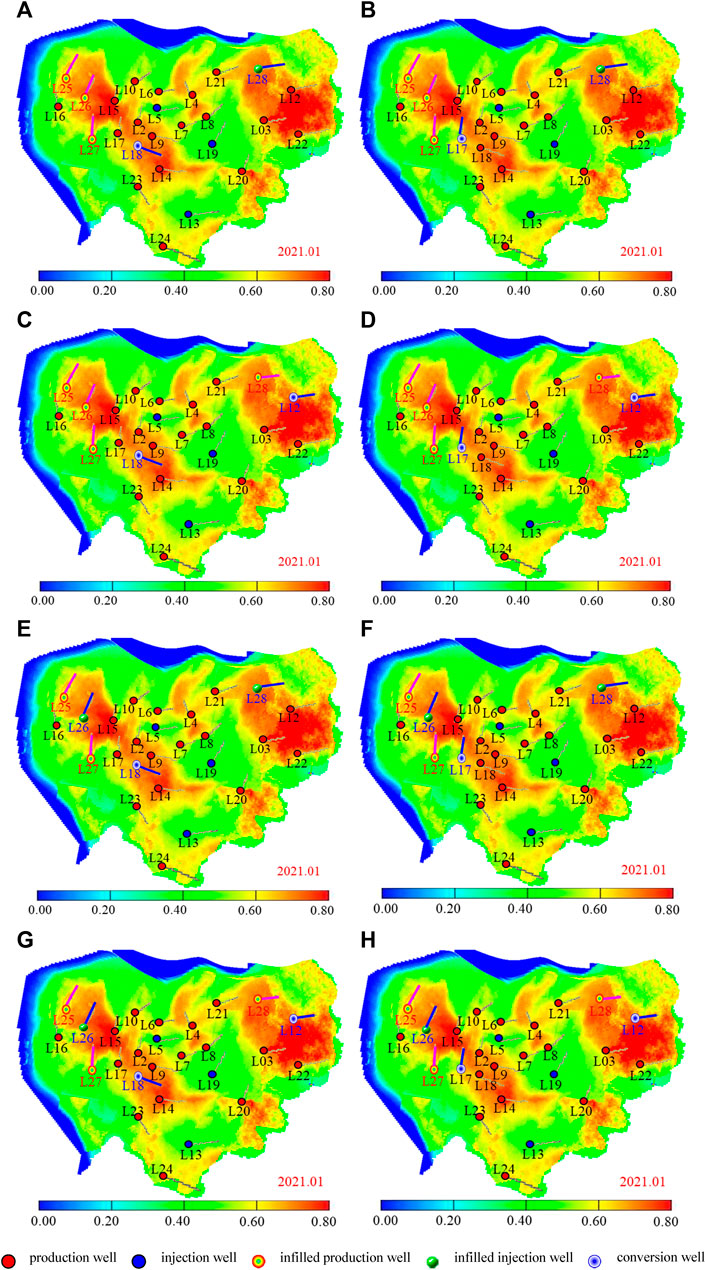
FIGURE 3. Schematic diagram of vector well pattern adjustment scheme. (A) Scheme one. (B) Scheme two. (C) Scheme three. (D) Scheme four. (E) Scheme five. (F) Scheme six. (G) Scheme seven. (H) Scheme eight.

TABLE 2

TABLE 2. Vector well pattern adjustment scheme of L30up reservoir.

TABLE 3

TABLE 3. Infill well coordinates of vector well pattern adjustment scheme in L30up reservoir.

Using numerical simulation software, predict the development indicators of the eight vector well network adjustment schemes mentioned above. The predicted termination conditions are that the daily oil production of a single well is less than 10 m³·d⁻¹, or the comprehensive water content is greater than 98%, and the maximum development period is set to October 2040.

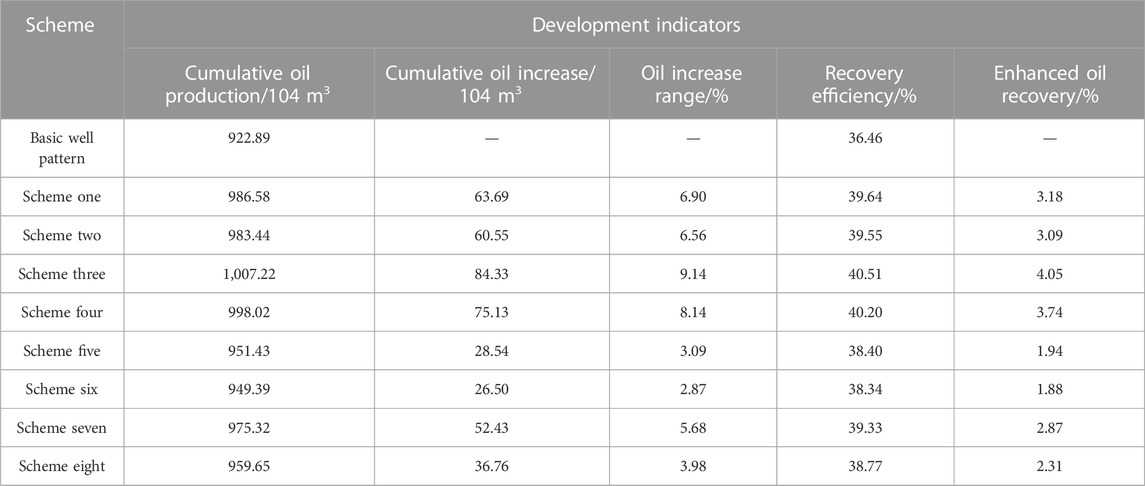
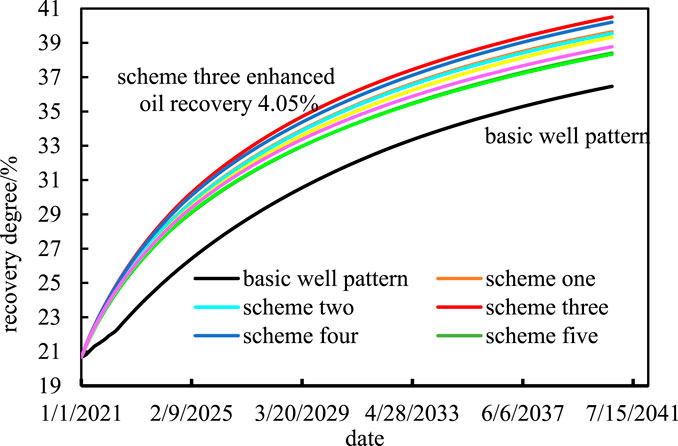
As shown in Table 4 and Figure 4, the predicted development indicators and recovery degree change curves for L30up reservoir under different vector well pattern adjustment schemes are presented. It can be seen that compared to the basic well pattern (without adjustment, simulated on the basis of the original well pattern until October 2040), the development effect of L30up reservoir has been significantly improved after vector well pattern adjustment. Among them, the vector well pattern adjustment scheme can improve oil recovery by 4.05% and increase oil production by 9.14% compared to the basic well pattern, with the best development effect. Therefore, the vector well pattern adjustment scheme three will be used as the basis for the subsequent optimization of L30up reservoir, which is to add three production wells in the western edge water area, transfer L18 well in the central well area to injection, and add one production well and transfer L12 well in the eastern thin and poor area, as shown in Figure 3C. The vector well pattern adjustment scheme three determines the primary position, injection production well type of the infill horizontal well, and injection production well type conversion measures of the existing wells in L30up reservoir. In the future, only the primary position of the infill horizontal well needs to be optimized to achieve precise design of the infill well position and further improve the reservoir development effect.

TABLE 4

TABLE 4. Comparison of development indicators under different vector well pattern adjustment.

FIGURE 4

FIGURE 4. Recovery degree curve under different vector well pattern adjustment schemes.

As shown in Figure 5, the remaining oil saturation of the whole L30up reservoir is compared respectively under the unadjusted basic well pattern and vector pattern adjustment scheme three. It can be seen that after infilling production wells L25, L26, and L27 in the western edge water area, the remaining oil has been significantly utilized. After the transfer of well L18, the remaining oil in the central well area is obviously utilized. After the infill production well L28 and the transfer of well L12 in the eastern thin poor area, the corresponding relationship between injection and production is formed, and the remaining oil is obviously used.

FIGURE 5

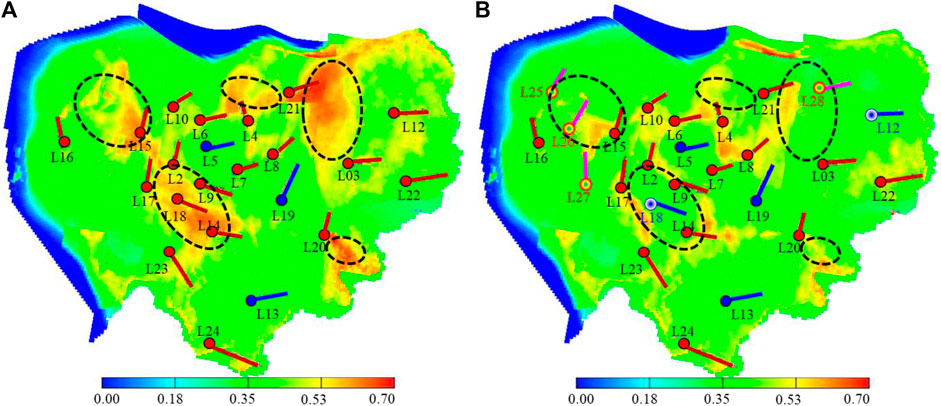
FIGURE 5. Remaining oil distribution of basic and vector well pattern adjustment scheme three. (A) Basic well pattern. (B) Vector pattern adjustment scheme three.

Based on the geological and development characteristics of L30up reservoir and on the basis of the vector well pattern adjustment scheme three, the infill well location optimization method of horizontal well vector pattern is used to optimize the infill well location of L30up reservoir. It can realize the precise determination of the infill well location. The initial optimization solution is the vector design well location in the vector well pattern adjustment scheme three. PSO-MADS is adopted as the solving algorithm. The population number is set as 50 and the iteration number is 200. Perform 10 independent optimizations.

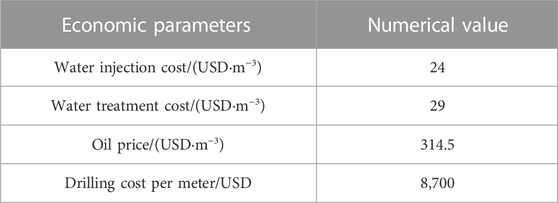
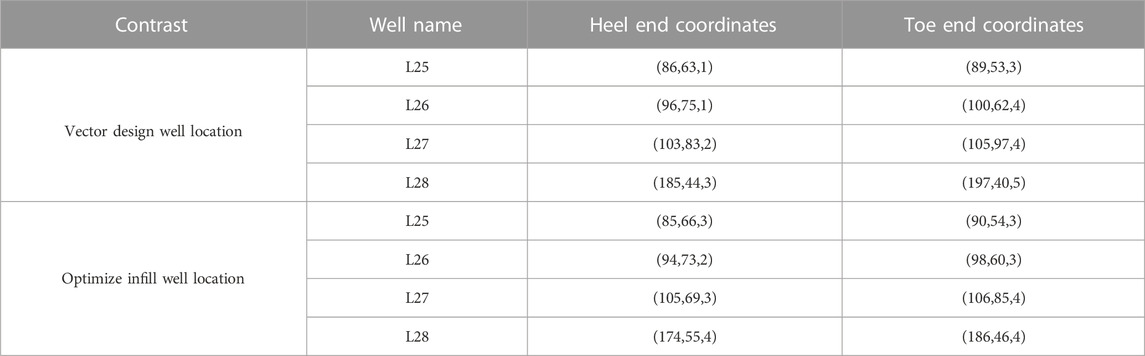
As shown in Table 5, the economic parameters related to L30up reservoir are set, including water injection cost, water treatment cost, oil price, and drilling cost per meter. According to the 10 optimization results, the optimization results of maximizing the economic net present value NPV are taken as the optimal infill well location of L30up reservoir, as shown in Table 6, which are the coordinates of infill well location before and after optimization. From Figure 6 and Table 7, it can be seen that compared to the vector well pattern adjustment scheme three, the infill well location optimization can further improve the matching degree between the infill wells and the reservoir development characteristics, increase the recovery rate by 1.16 percentage points, and significantly improve the economic benefits.

TABLE 5

TABLE 5. Relevant economic parameters setting.

TABLE 6

TABLE 6. Coordinate comparison before and after infilling in L30up reservoir.

TABLE 7

TABLE 7. Comparison of development indicators before and after infill well location optimization.

FIGURE 6

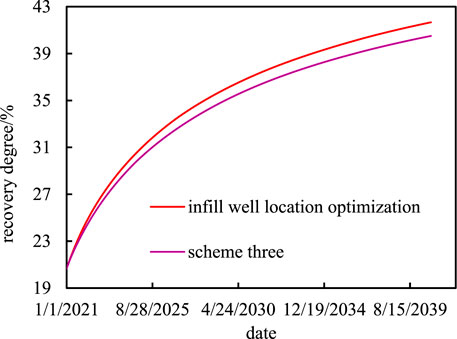
FIGURE 6. Recovery degree curve before and after infill well location optimization in L30up reservoir.

Figure 7 shows the distribution of remaining oil saturation before and after the optimization of infill well location in L30up reservoir by October 2040. As can be seen from the figure, the optimization of horizontal vector well pattern infill well location can further improve the development effect of L30up reservoir. It can also realize the optimal matching between well pattern and remaining oil distribution, sand body characteristics, edge water, etc., and effectively utilize the remaining oil in the block.

FIGURE 7

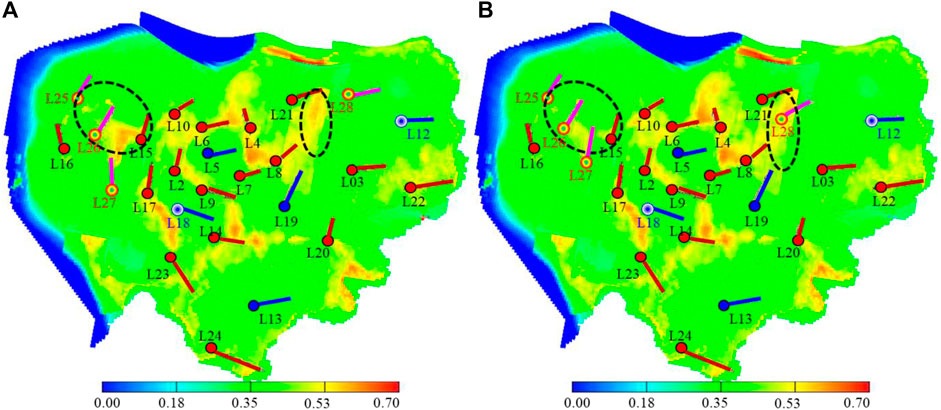
FIGURE 7. Distribution of remaining oil saturation before and after infill well location optimization. (A) Vector well pattern adjustment scheme three. (B) Infill well location optimization.

It can be seen from Table 8 that compared with the unadjusted basic well pattern, further optimizing the infill well location based on the vector well pattern adjustment scheme three can increase the ultimate oil recovery rate by 5.21% and effectively improve the reservoir development effect.

TABLE 8

TABLE 8. Coordinate comparison before and after infill well location optimization in L30up reservoir.

5 Conclusion

(1) Taking the maximization of economic net present value NPV as the objective function and well pattern characteristic parameter matrix (well location, azimuth angle, horizontal section length) as optimization variables, the vector well pattern optimization model of horizontal well was established, and the PSO-MADS algorithm is used to solve the optimized mathematical model.

(2) According to the vector characteristics of provenance direction, structural trend, channel distribution, edge water displacement direction, etc., combined with regional vector well pattern densification and injection-production well type conversion, a vector well pattern deployment strategy for L30up reservoir was proposed. On this basis, eight vector well pattern adjustment schemes were constructed. Through the comparison of the development effect predictions of different schemes, the vector well pattern adjustment scheme 3 was selected as the best vector well pattern deployment scheme for L30up reservoir. Compared with the basic well pattern, the optimum can increase the recovery rate by 4.05%.

(3) Based on the vector well pattern adjustment scheme 3, the precise position of infill wells in the scheme is optimized by using the established optimization method. The results show that, compared with the vector well pattern adjustment scheme 3, the precise optimization of the infill well position can further increase the recovery rate by 1.16%, and the economic net present value can increase by 94 million US dollars. This optimization method further improves the matching degree between the adjusted horizontal well pattern and the geological vector parameter distribution, so as to achieve a better reservoir development effect.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

C-HD: Methodology, software, programming, validation, formal analysis, investigation, writing-original draft, writing-review and editing, visualization.

Funding

This research was financially supported by the Major Science and Technology Project of CNOOC: Study on key technology of producing 20 million tons of oil in Eastern South China Sea. (grant number CNOOC-KJ 135 ZDXM 37 SZ 03 SZ).

Conflict of interest

Author C-HD was employed by CNOOC China Limited.

The authors declare that this study received funding from the Major Science and Technology Project of CNOOC. The funder had the following involvement in the study: study design, data collection, decision to publish.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Afshari, S., Aminshahidy, B., and Pishvaie, M. R. (2015). Well placement optimization using differential evolution algorithm[J]. Iran. J. Chem. Chem. Eng. 34 (2), 109–116.

Google Scholar

Ariadji, T., Haryadi, F., Rau, I. T., Aziz, P. A., and Dasilfa, R. (2014). A novel tool for designing well placements by combination of modified genetic algorithm and artificial neural network. J. Petroleum Sci. Eng. 122, 69–82. doi:10.1016/j.petrol.2014.05.018

CrossRef Full Text | Google Scholar

Bagherinezhad, A., Bozorgmehry, R. B., and Pishvaie, M. R. (2017). Multi-criterion based well placement and control in the water-flooding of naturally fractured reservoir. J. Petroleum Sci. Eng. 149 (4), 675–685. doi:10.1016/j.petrol.2016.11.013

CrossRef Full Text | Google Scholar

Ben Hadj-Alouane, A., and Bean, J. C. (1997). A genetic algorithm for the multiple-choice integer program. Operations Res. 45 (1), 92–101. doi:10.1287/opre.45.1.92

CrossRef Full Text | Google Scholar

Bouzarkouna, Z., Ding, D., and Auger, A. (2011). Well placement optimization with the covariance matrix adaptation evolution strategy and meta-models. Comput. Geosci. 16 (1), 75–92. doi:10.1007/s10596-011-9254-2

CrossRef Full Text | Google Scholar

Bukshtynov, V., Volkov, O., Durlofsky, L. J., and Aziz, K. (2015). Comprehensive framework for gradient-based optimization in closed-loop reservoir management. Comput. Geosci. 19 (4), 877–897. doi:10.1007/s10596-015-9496-5

CrossRef Full Text | Google Scholar

Cai, H. (2015). Research and application of penalty function method in constrained optimization problems[D]. Shanghai: East China Normal University.

Google Scholar

Chen, B., and Reynolds, A. C. (2018). CO2 water-alternating-gas injection for enhanced oil recovery: optimal well controls and half-cycle lengths. Comput. Chem. Eng. 113, 44–56. doi:10.1016/j.compchemeng.2018.03.006

CrossRef Full Text | Google Scholar

De Brito, D. U., and Durlofsky, L. J. (2021). Field development optimization using a sequence of surrogate treatments. Comput. Geosci. 25 (1), 35–65. doi:10.1007/s10596-020-09985-y

CrossRef Full Text | Google Scholar

Ding, S., Jiang, H., Zhou, D., et al. (2016). Automatic optimization of irregular well pattern based on modified particle swarm algorithm[J]. China Offshore Oil Gas 28 (01), 80–85.

Google Scholar

Ding, S., Lu, R., Xi, Y., et al. (2020). Efficient well placement optimization coupling hybrid objective function with particle swarm optimization algorithm[J]. Appl. Soft Comput. 95, 106–120.

CrossRef Full Text | Google Scholar

Hamida, Z., Azizi, F., and Saad, G. (2017). An efficient geometry-based optimization approach for well placement in oil fields. J. Petroleum Sci. Eng. 149, 383–392. doi:10.1016/j.petrol.2016.10.055

CrossRef Full Text | Google Scholar

Han, D. (2010). The current situation, challenges and technological development direction of China's oil and gas field development. Strategic Study CAE 12 (5), 51–57.

Google Scholar

Iruthayarajan, M. W., and Baskar, S. (2010). Covariance matrix adaptation evolution strategy based design of centralized PID controller. Expert Syst. Appl. 37 (8), 5775–5781. doi:10.1016/j.eswa.2010.02.031

CrossRef Full Text | Google Scholar

Isebor, O. J., Durlofsky, L. J., Ciaurri, D. E., et al. (2014). A derivative-free methodology with local and global search for the constrained joint optimization of well locations and controls. Comput. Geosci. 18 (3), 463–482. doi:10.1007/s10596-013-9383-x

CrossRef Full Text | Google Scholar

Jesmani, M., Bellout, M. C., Hanea, R., and Foss, B. (2016a). Well placement optimization subject to realistic field development constraints. Comput. Geosci. 20 (6), 1185–1209. doi:10.1007/s10596-016-9584-1

CrossRef Full Text | Google Scholar

Kolda, T. G., Lewis, R. M., and Torczon, V. (2003). Optimization by direct search: new perspectives on some classical and modern methods. SIAM Rev. 45 (3), 385–482. doi:10.1137/s003614450242889

CrossRef Full Text | Google Scholar

Li, H., Jing, Y., Ma, M., et al. (2009). Collaborative optimization algorithm based on dynamic penalty function method. J]. Control Decis. 56 (06), 911–915.

Google Scholar

Liu, M. (2018). Research on mesh adaptive direct search algorithm[D]. Xian: Xidian University.

Google Scholar

Lyons, J., and Nasrabadi, H. (2013). Well placement optimization under time-dependent uncertainty using an ensemble Kalman filter and a genetic algorithm. J. Petroleum Sci. Eng. 109, 70–79. doi:10.1016/j.petrol.2013.07.012

CrossRef Full Text | Google Scholar

Michalewicz, Z. (1995). A survey of constraint handling techniques in evolutionary computation methods[J]. Evol. Rogramming 36 (4), 135–155.

Google Scholar

Mirzaei-Paiaman, Abouzar, Santos, Susana M. G., and Schiozer, Denis J. (2022). Iterative sequential robust optimization of quantity and location of wells in field development under subsurface, operational and economic uncertainty. J. Petroleum Sci. Eng. 218, 111005. doi:10.1016/j.petrol.2022.111005

CrossRef Full Text | Google Scholar

Naderi, M., and Khamehchi, E. (2017). Well placement optimization using metaheuristic bat algorithm. J. Petroleum Sci. Eng. 150, 348–354. doi:10.1016/j.petrol.2016.12.028

CrossRef Full Text | Google Scholar

Nasir, Y., Volkov, O., and Durlofsky, L. J. (2022). A two-stage optimization strategy for large-scale oil field development. Optim. Eng. 23 (1), 361–395. doi:10.1007/s11081-020-09591-y

CrossRef Full Text | Google Scholar

Nwankwor, E., Nagar, A. K., and Reid, D. C. (2013). Hybrid differential evolution and particle swarm optimization for optimal well placement. Comput. Gcosciences 17 (2), 249–268. doi:10.1007/s10596-012-9328-9

CrossRef Full Text | Google Scholar

Onwunalu, J. E., and Durlofsky, L. J. (2010). Application of a particle swarm optimization algorithm for determining optimum well location and type. Comput. Geosci. 14 (1), 183–198. doi:10.1007/s10596-009-9142-1

CrossRef Full Text | Google Scholar

Park, H. Y., Yang, C., Al-Aruri, A. D., and Fjerstad, P. A. (2017). Improved decision making with new efficient workflows for well placement optimization. Joumnal Petroleum Sci. Eng. 152 (6), 81–90. doi:10.1016/j.petrol.2017.02.011

CrossRef Full Text | Google Scholar

Salehian, M, Morteza Haghighat Sefat, and Muradov, K (2022). Multi-solution well placement optimization using ensemble learning of surrogate models. J. Petroleum Sci. Eng. 210, 110076. doi:10.1016/j.petrol.2021.110076

CrossRef Full Text | Google Scholar

Sarma, P., and Chen, W. (2008). Efficient Well Placement Optimization with gradient-based algorithms and adjoint schemels. SPE-112257-MS. doi:10.2118/112257-MS

CrossRef Full Text | Google Scholar

Semnani, A., Ostadhassan, M., Xu, Y., et al. (2021). Joint optimization of constrained well placement and control parameters using teaching-learning based optimization and an inter-distance algorithm[J]. J. Petroleum Sci. Eng. 203, 108–122.

CrossRef Full Text | Google Scholar

Torczon, V. (1997). On the convergence of pattern search algorithms. SIAM J. Optim. 7 (1), 1–25. doi:10.1137/s1052623493250780

CrossRef Full Text | Google Scholar

Wang, X., Haynes, R. D., and Feng, Q. (2016). A multilevel coordinate search algorithm for well placement, control and joint optimization. Comput. Chem. Eng. 95, 75–96. doi:10.1016/j.compchemeng.2016.09.006

CrossRef Full Text | Google Scholar

Xiao, J., and Liu, D. (2010). Study on anisotropy multilayer sand reservoir with vectorization well pattern. J. Chongqing Univ. Sci. Technol. Sci. Ed. 12 (06), 38–40. doi:10.19406/j.cnki.cqkjxyxbzkb.2010.06.011

CrossRef Full Text | Google Scholar

Yao, T. (2011). The study of well pattern optimization method for deepwater oil field. Qingdao: China University Of Petroleum.

Google Scholar

Yildiz, A. R. (2013). Comparison of evolutionary-based optimization algorithms for structural design optimization. Eng. Appl. Artif. Intell. 26 (1), 327–333. doi:10.1016/j.engappai.2012.05.014

CrossRef Full Text | Google Scholar