
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 25 September 2023
Sec. Sustainable Energy Systems
Volume 11 - 2023 | https://doi.org/10.3389/fenrg.2023.1225416
This article is part of the Research Topic Energy-Efficient and Energy-Flexible Buildings Towards Net-Zero Carbon Emission View all 6 articles
 Nan Liang*
Nan Liang* Mengxuan Yu
Mengxuan YuIntroduction: The crucial transition toward carbon neutrality is developing and adopting low-carbon buildings and communities to achieve the recycling and reuse of resources and to minimize the damage to the natural environment by humans. Energy saving for residential buildings is essential for enhancing cost-effectiveness and redundant energy drain. Considering the increasing attention to energy conservation and the accessibility of sustainable energy sources, common energy-saving solutions expose inherent inadequacies limiting their effectiveness. The ineffectual use of traditional energy sources can result in waste, greater operating costs, and excessive energy consumption in residential structures.
Methods: Hence, a Multi-Objective Energy-Saving Optimization Method (MOESOM) has been proposed to optimize energy use and conservation in residential buildings in southern Anhui, China. The proposed approach examines lower operational costs and carbon emissions by using green energy sources and encouraging effective energy consumption habits. The suggested Multi-Objective Energy-Saving Optimization Method technique offers insight into energy saving by utilizing green energy sources and confining energy uses. The multi-objective turns around energy saving and resource usage for decreasing operational costs and averting carbon emissions. Thus, the suggested technique is verified utilizing the Osprey Optimization Algorithm (OOA); the detailed goal is recognized utilizing the multiple objectives described. Based on the progress of low-carbon emissions and energy saving, the number of iterations for augmenting Osprey agents is identified. This agent-based optimization is executed if the novel augmented agent fulfills any of the trailing progression. The emission control level and energy-saving factor are assessed considering the variance between new and old agent progression. This encourages the various objectives to be fulfilled under similar criteria balancing their outcomes.
Results and discussion: The output from different Osprey agents is induced for consecutive objectives and optimization factors. Then, the system ensures 8.97% energy savings and 8.04% high objectives compared to the other methods.
Residential structures are now more needed than ever for energy efficiency and conservation measures. The residential building’s shiftable load utilization at peak hours was managed using the load-shifting technique as a multi-objective optimization challenge (Ebrahimi and Abedini, 2022) that reduces peak load, energy losses, and expenses. The potential for energy savings and the viability of implementing active energy efficiency mechanisms (Mujeebu and Bano, 2022) on a detached residence in a warm, humid region were shown with the reduction in the energy performance index of conventional standards. Important energy-influencing elements in a conventional design were determined by green technologies (renovation) (Teng et al., 2021) and also to improve the energy-saving capabilities of residential buildings. One passive improvement technique for energy conservation used by (Ebrahimi-Moghadam et al., 2020) was light shelves that improved the indoor temperature of residential building occupants.
Low-carbon emission is an important feature used for energy saving in residential buildings (Liu et al., 2022). Low-carbon emissions have occurred using resources such as wind and solar power. Solar power is widely used in residential buildings, which emit low carbon into the environment (Luo et al., 2022).
Life cycle assessment was a useful method for assessing the impact of various factors and ensuring that carbon emission targets (Yang et al., 2021) are achieved from each of the five phases comprising manufacturing, distribution, building, operation, and demolishing stages. Low-carbon emissions increase the efficiency and viability of a wider range of energy-saving strategies. Energy-saving methods that expand the useful range of buildings also lower the greenhouse gas emissions (GHG) ratio. High-carbon emissions are mostly caused by population density, urbanization (Anser et al., 2020), and per capita Gross Domestic Product (GDP). The bottom-up method in (Zhang et al., 2022) permits municipalities to evaluate the environmental impact of the existing stock of urban buildings and urban planning initiatives, supporting the sustainable growth of cities.
An optimization algorithm is used in residential buildings to control the carbon emission and energy consumption level (Iqbal et al., 2020). The optimization algorithm identifies the exact tasks and produces relevant renewable resources to perform the task (Nikkhah et al., 2021). A controller technique is used to detect the control capability of energy management systems. A stochastic optimization model (Antoniadou-Plytaria et al., 2022) based on scenarios that can be used to decide the amount of power and flexibility should be distributed throughout a residential microgrid equipped with stationary battery systems and solar panels. The optimization model also minimizes the energy consumption ratio in residential buildings. Based on a second-order temperature network approach (Wang et al., 2022), an optimal precooling approach is suggested that accounts for the thermal state of the residence, authorized capacity for cooling, the environment, and energy rate structure. The optimization model increases the building’s energy efficiency (EE) level, which enhances the management systems’ significance range (Sheng et al., 2021). Multi-objective optimization is used for carbon emission control in residential buildings. The main aim of the optimization model is to provide beneficial resources to perform tasks in buildings and to calculate the decline in annual particular energy demand (Salata et al., 2020), the cost of building and installing new infrastructure, the cost of running energy annually, and the decline in greenhouse gas emissions. A cutting-edge algorithm for energy optimization is used for an existing commercial structure. The goal of this optimization is to lower energy use and improve the energy efficiency of the structure (Pirmohamadi et al., 2021). The optimization models minimize the energy consumption level in the computation process, which is used as an energy-saving technique. The multi-objective optimization model improves the feasibility range of residential buildings (Shen et al., 2022; Xue et al., 2022).
Contributions
1) Designing and discussing a multi-objective optimization method for energy saving in residential buildings and controlling carbon emissions in view of energy distribution.
2) Incorporating modifications in the conventional Osprey optimization for independent progression and difference estimation using agent augmentation.
3) Exploiting a dedicated data source for analyzing the eventual analysis of the modified optimization towards its objective satisfaction rate.
4) Accomplishing a comparative analysis for proving the proposed method’s efficiency compared to the existing methods.
Huang et al. (Huang et al., 2020) developed a hybrid optimization approach for residential energy management systems. The main aim of the approach is to solve the non-convex mixed-integer non-linear problems (H-MINLP) in management systems. MINLP consumes more energy ratio, which causes severe damage to the management systems. The developed approach increases the feasibility and functionality range of the systems.
Habib et al. (Hab et al., 2020) proposed a combined heat and power (CHP) unit for optimization in residential buildings. An artificial bee colony (ABC) algorithm is used here to identify the heat loads that are presented in the buildings. A cost–benefit analysis technique is also used in the system, which analyzes the beneficial level of energy consumption process. The CHP unit enhances the efficiency level of residential buildings.
Foroozandeh et al. (Foroozandeh et al., 2022) designed a goal programming (GP) approach for the energy management process in smart buildings. The designed GP approach predicts the exact necessity level of electricity, which reduces the complexity of the energy scheduling process. The GP approach also predicts the energy computational cost that produces optimal information for further processes. The designed GP approach minimizes the energy consumption level in smart buildings.
Nizami et al. (Nizami et al., 2019) introduced a multi-agent-based Transactive Energy Management Framework (TEMF) for residential buildings. The actual goal of the framework is to identify the optimization and grid overloading ratio of the buildings. The multi-agent architecture provides necessary services to the users, reducing the inconvenience level in performing tasks. The introduced framework increases the flexibility and effectiveness level of residential buildings.
Rezaei and Dagdougui (Rezaei and Dagdougui, 2020) proposed an efficient real-time optimization approach for residential buildings. The proposed approach uses a heating, ventilation, and air conditioning (HVAC) system that produces optimal control measures for the users. The proposed approach increases the accuracy in decision-making, which reduces the energy consumption level in computation. The proposed optimization approach improves the efficiency and performance range in multitasking.
Iturriaga et al. (Iturriaga et al.) developed a mixer-integer linear programming (MILP) optimization method for residential buildings in urban areas. The main aim of the method is to analyze the energy consumption ratio in buildings. MILP calculates the zero-energy district (ZED), which is presented in urban areas. The ZED produces relevant information for energy-saving measures. The developed MINP method enhances the significance and feasibility range of residential buildings.
Haider et al. (Haider et al., 2022) designed a new approach for multi-objective cost-peak optimization in smart buildings. The designed approach is mostly used for a multi-criteria decision-making process. It is also used to identify smart buildings’ peak energy consumption levels. The exact consumption ratio and task capacity are detected using an optimization scheme. The designed approach improves the overall performance and successful ratio in smart buildings. Table 1 summarizes the references from (Zhu et al., 2021) to (Du et al., 2022).
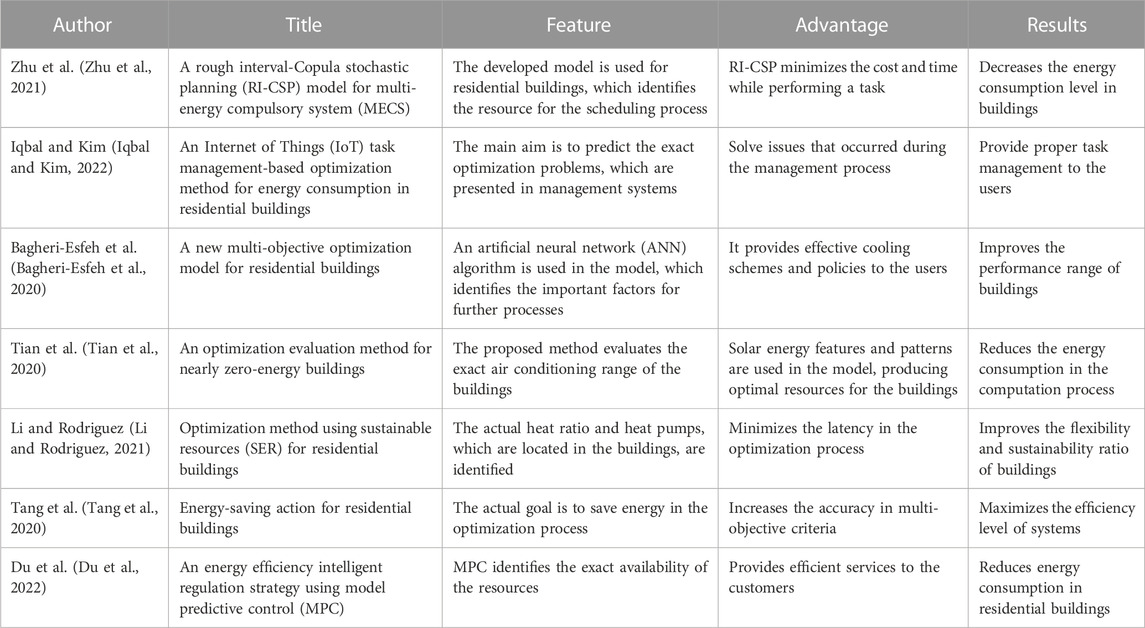
TABLE 1. Summary of references from (Zhu et al., 2021) to (Du et al., 2022).
Energy-saving optimization methods (Hab et al., 2020; Rezaei and Dagdougui, 2020; Rezaei and Dagdougui, 2020; Haider et al., 2022) are designed to improve the state of analysis and precise decisions for multiple constraints. The constraints are identified using the existing drawbacks identified from the previous outcomes. In the constraint mitigation process, multi-objective optimization is impeded in any spiking complex process. Therefore, constraint modification and optimization for differential problems are to be jointly addressed to prevent chained downfalls. This feature is best suited for energy saving and carbon control across different objectives for constraint mitigation. This feature is adapted in the proposed method for balancing energy saving and carbon emission control.
To enhance the remuneration of residential buildings and to eliminate the gratuitous energy impoverishment, energy saving is essential for the process. This energy saving can be enhanced by using the lower amount of carbon emissions power, which helps with the future optimization procedures in determining the objectives. The ideal energy-preserving methods are executed from the low-carbon-emitting origins and renewable energy origins. Contemplating these characteristics in this article, a Multi-Objective Energy-Saving Optimization Method (MOESOM) is introduced. This optimization method helps in the usage of less energy by fulfilling the requirements of the residential buildings with prompt needs. In this process, the Osprey Optimization algorithm is used for the progression identification operation. This is the meta-heuristic algorithm, which is widely used in the solvation of the optimization process. Here, the Osprey agents are helping in the optimization process, which aids in the adaption of the circumstances by producing effective outcomes in all kinds of problems and situations in residential buildings’ energy-saving processes. From the residential buildings, energy savings and low-carbon emissions are extracted for the optimization process. This method executes the perceptions into the energy-saving operation by using green energy resources and then circumscribing energy implementations. Now, the optimization process takes place with the help of Osprey agents. The vital objective of the optimization algorithm is determined by using the multiple objectives defined. The processes included in the proposed method are illustrated in Figure 1.
The progression and the difference are determined by using the Osprey agents in the optimization procedure, and then the objectives are identified. Based on the progression detection outcome of energy saving identified by the Osprey agents and low-carbon emission, the total number of repetitions for enlarging the Osprey agents is resolved. This progression checks whether there is consistency during the energy-saving procedure with renewable energy resources. Then, it verifies, depending on the progression, whether the objectives are satisfying the energy carbon and energy-saving operations. The difference is determined if there is a lack of progress during the energy-saving process, and then, based on the progression results, the agents are augmented for prompt progression for the determination of the objectives. The number of decreased progression results in the same number of differences during the optimization process. Based on the progression, the objectives are determined, and based on the different agents, the augmentation process takes place. It also checks whether the newly added agents help in the progression process for the estimation of the objectives. This Osprey agent-based optimization is accomplished if any of the lagging progression is satisfied by the newly added agent. Contemplating the difference between new and old agent progression, the carbon emission control level and energy-saving factors are calculated. This entire process helps in determining the different objectives that satisfy the given criteria with the prompt progression level and energy-saving factors.
The data from (Kaggle, 2023) are explored in this article for validating the energy-saving and carbon emission control factors. The data used for validation are represented in Figure 2.
The power is utilized, as is the energy drain from the outcome and saving. In this consideration, the unnecessary drain is optimized for energy saving and efficient utilization. The carbon emission is geared up from the final consumed for power generation that includes wastage and DF, as presented in the above data source. The OOA is allocated using the
The energy-saving resources are extracted from the residential buildings for the optimization process. Renewable resources are used for the elimination of unwanted energy loss and high-carbon emissions. It is necessary to save energy to protect the surroundings from the highly polluted carbon during the construction of residential buildings. Energy is also saved by using low-carbon powers, which help to keep the environment wholesome during residential building development. The process of energy saving from residential buildings is explained by Eq. 1:
Where
Where
The observed data are split based on
Along with the energy saving, low-carbon emissions are derived from the residential buildings to identify the progression and the difference by using the Osprey agents in the optimization algorithm. Where
Where
The
Now, the Osprey agents are helpful in the optimization process where the progression and the difference are determined. These Osprey agents are also used in the estimation of the wholesome low-carbon emission and the energy-saving process for the optimization algorithm. They help in the identification of the prompt objectives for the process of energy preservation. Due to the estimation of the energy saving and the low-carbon emission process, the optimization process takes place effectively, which aids in the objective determination operation. The outcome of the optimization in calculating the progression helps in augmenting the new agents for the satisfaction of the given conventionalities. The multiple objectives that are found are also helpful in making the optimization procedure efficacious for energy saving in the residential building operation. The process of Osprey agents in the optimization process is explained by Eq. 5:
Where
Where
The optimization process allocates
Where
Where
The conditional validation pursued by the OOA augments agents for reducing
Where
Different from the
The agent checks whether the objectives satisfy the energy carbon and the energy-saving procedures based on the progression. These objectives also help in the reduction of the differences that occurred in the progression by enhancing energy saving in residential buildings. The process of obtaining the objectives based on the progression is explained by Eqs. 11, 12:
Where
By contemplating the difference between the new agent and old agents’ progression, the emission control level and energy-saving characteristics are evaluated. The process of agent augmentation is explained by the equation given above, where
The conjoined points in the above representation are identified by satisfying
The expected (from the data source) and the optimized successive intervals are presented in Figure 9. The condition
The improvement in achieving Figure 9 and Figure 8 validations across 24-h time (operation) and weekdays is presented in Figure 10. The cumulative value of the buildings considered for 7 days of a week is analyzed. In the varying operation time, the successive intervals are by assigning different agents for
In this section, a few considered metrics of energy saving, objective attainment, progression estimation, control level, and optimization complexity are used for comparative analysis. The energy demand (100-1400 kWh) and the number of residential buildings (20–260) varied in this optimization verification process. The methods TEMF (Nizami et al., 2019), GFROA (Li and Rodriguez, 2021), and H-MINLP (Huang et al., 2020) from related works are used in this comparison. Experimental research has been performed when the system processes new data on varying energy demand levels with varying residential structures, as mentioned above. The research demonstrated the effectiveness of the data and produced useful findings.
Energy saving is efficacious in this method due to the use of an Osprey optimization algorithm with the Osprey agents. The energy saving and the low-carbon emission powers are extracted from the residential buildings for further optimization procedure. Renewable resources help save energy by reducing the unnecessary energy drain, and this also enhances the cost-effectiveness of the process. The Osprey agents in the optimization process help in the estimation of the energy saving and low-carbon emission in the residential building. Based on the energy-saving and low-carbon emission procedures, the progression and the difference are determined for the determination of the objectives and the agent augmentation process. Energy saving plays a vital role in estimating the progression and the difference in it. Furthermore, it aids in reducing the progression lags by adding new agents by enhancing the energy-saving process. The Osprey agents then determine the efficaciousness of the entire procedure after inducing the effective agents on behalf of the lagged progression (Figure 11).
The attainment of the objectives is efficacious from the results of the progression in the optimization process. Depending on the energy saving and the low-carbon emissions, the progression and the difference are determined for the estimation of the objectives. This objective checks whether it satisfies the energy carbon emission and energy-saving process, which is based on the determined progression. The difference in the progression is also identified along with the progression. To reduce the difference, new Osprey agents are added, and then the efficiency of the progression and energy-saving method is enhanced. It checks whether the newly added agents help in the progression, and then it is added whenever the progression is reduced during the energy-saving operation. The objectives help in the prompt saving of energy in residential buildings and enhance the low-carbon emission powers by eliminating the unnecessary energy drain during the procedure. By this, the objectives based on the progression obtained from the energy saving and the low-carbon emission are efficacious (Figure 12).
The estimation of the progression is better in this process by using the Osprey optimization algorithm. Depending on the energy saving and the low-carbon emission, the progression and the difference in the progression are estimated. The progression must be either in the energy-saving or low-carbon emission process. Here, it checks whether the progression is present in the energy-saving process or the low-carbon emission resource identification process. Along with the progression, the difference in the progression is also determined for the identification of the objectives for the energy-saving process. The difference in the progression is also enhanced by using the agent augmentation process. The progression lags are solved by adding the prompt new Osprey agents for the optimization process. This optimization process occurs with the help of the determined multiple objectives. The energy-saving and the low-carbon emission power detection processes help in the assumption of the progression level and to reduce the complexity of the multiple objective optimization operation (Figure 13).
The control level is effective in this method by contemplating the progression and difference of it in the optimization procedure. The energy saving and low carbon are estimated from the residential buildings for the further optimization process. Based on the progression detection outcome of energy saving identified by the Osprey agents and low-carbon emission, the total number of repetitions for enlarging the Osprey agents is resolved. This progression checks whether there is consistency during the energy-saving procedure with renewable energy resources. The objectives are satisfying the energy carbon emission powers, which depends on the progression obtained. The level of the progression lag control is effective by using the multiple objectives in the Osprey optimization progress. The differences are reduced by adding the new agents of the Osprey, which enhances the energy-saving process by eliminating the unwanted energy drains. By this, the control level is made efficacious by considering the results of progression and the difference in determination operations (Figure 14).
The complexity of the optimization is lesser in this process with the help of Osprey agents in the objective-based optimization algorithm. The outcomes of the energy-saving and then the low-carbon emission process are contemplated in the optimization process, which is determined through the Osprey agents. The multi-objective gyrates closely to the energy-saving and sources implementation for decreasing the costs of the utilization and countering the high-carbon emissions. These Osprey agents help in the identification of the prompt objectives for the process of energy preservation. Due to the estimation of the energy-saving and the low-carbon emission process, the optimization process takes place effectively, which aids in the objective determination operation. The outcome of the optimization in calculating the progression helps in augmenting the new agents for the satisfaction of the given conventionalities. Depending on the effective results of the progression and the agent augmentation process, the complexity of the optimization is lessened, and the energy-saving process is enhanced (Figure 15).
• The MOESOM is a solution to the challenges linked with the ineffective use of traditional energy sources, energy waste, greater operating costs, and extreme energy use in residential buildings.
• To aid environmental sustainability goals and economic viability, MOESOM utilizes green energy sources and endorses energy-efficient behaviors.
• The method uses a multi-objective framework concentrating on energy saving and efficient resource utilization, pointing to lower operational costs and decreased carbon emissions using optimization methods.
• By determining and modifying targets following predetermined criteria with the prompt progression level and energy-saving factors, the Osprey Optimization Algorithm (OOA) proves the effectiveness of MOESOM.
• To complete energy-saving and emission-controlling goals, MOESOM utilizes agent augmentation that is encouraged by progress thresholds and guarantees continual enhancement.
• By inspecting differences in agent progression, MOESOM computes emissions reduction levels and energy efficiency factors, resulting in an integrated method for attaining objectives.
• Regarding effective energy management, financial feasibility, and smaller environmental influences in residential structures, MOESOM appears to be a practical solution.
• Compared to competing methods, MOESOM’s real-world results demonstrate a significant 8.97% enhancement in energy consumption and an 8.04% rise in substantial objective accomplishment.
• In future studies, iterative multi-objective optimization should be improved with flexible recurring conditions, especially for changing energy requirements and handling scenarios, including peak energy demands and distribution difficulties.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
NL Writing–original draft, Methodology. MY Investigation, Writing–review and editing. All authors contributed to the article and approved the submitted version.
Key Research Project Fund of Humanities and Social Sciences in Anhui Universities: Expression of Traditional Design Vocabulary Based on Prefabricated Houses in Southern Anhui under the Background of Rural Revitalization, No. SK2020A0232.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Anser, M. K., Alharthi, M., Aziz, B., and Wasim, S. (2020). Impact of urbanization, economic growth, and population size on residential carbon emissions in the SAARC countries. Clean Technol. Environ. Policy 22, 923–936. doi:10.1007/s10098-020-01833-y
Antoniadou-Plytaria, K., Steen, D., Carlson, O., Mohandes, B., and Ghazvini, M. A. F. (2022). Scenario-based stochastic optimization for energy and flexibility dispatch of a microgrid. IEEE Trans. Smart Grid 13 (5), 3328–3341. doi:10.1109/TSG.2022.3175418
Bagheri-Esfeh, H., Safikhani, H., and Motahar, S. (2020). Multi-objective optimization of cooling and heating loads in residential buildings integrated with phase change materials using the artificial neural network and genetic algorithm. J. Energy Storage 32, 101772. doi:10.1016/j.est.2020.101772
Du, Y., Zhou, Z., and Zhao, J. (2022). Multi-regional building energy efficiency intelligent regulation strategy based on multi-objective optimization and model predictive control. J. Clean. Prod. 349, 131264. doi:10.1016/j.jclepro.2022.131264
Ebrahimi, J., and Abedini, M. (2022). A two-stage framework for demand-side management and energy savings of various buildings in multi smart grid using robust optimization algorithms. J. Build. Eng. 53, 104486. doi:10.1016/j.jobe.2022.104486
Ebrahimi-Moghadam, A., Ildarabadi, P., Aliakbari, K., Arabkoohsar, A., and Fadaee, F. (2020). Performance analysis of light shelves in providing visual and thermal comfort and energy savings in residential buildings. J. Braz. Soc. Mech. Sci. Eng. 42, 484–518. doi:10.1007/s40430-020-02565-2
Foroozandeh, Z., Ramos, S., Soares, J., and Vale, Z. (2022). Goal programming approach for energy management of smart building. IEEE Access 10, 25341–25348. doi:10.1109/ACCESS.2022.3153341
Habib, H. U. R., Wang, S., Waqar, A., Farhan, B. S., Kotb, K. M., and Kim, Y. S. (2020). Combined heat and power units sizing and energy cost optimization of a residential building by using an artificial bee colony algorithm. IEEE Access 8, 218289–218303. doi:10.1109/ACCESS.2020.3042173
Haider, H. T., Muhsen, D. H., Al-Nidawi, Y. M., Khatib, T., and See, O. H. (2022). A novel approach for multi-objective cost-peak optimization for demand response of a residential area in smart grids. Energy 254, 124360. doi:10.1016/j.energy.2022.124360
Huang, Y., Zhang, J., Mo, Y., Lu, S., and Ma, J. (2020). A hybrid optimization approach for residential energy management. IEEE Access 8, 225201–225209. doi:10.1109/ACCESS.2020.3044286
Iqbal, M. M., Zia, M. F., Beddiar, K., and Benbouzid, M. (2020). Optimal scheduling of grid transactive home demand responsive appliances using polar bear optimization algorithm. IEEE Access 8, 222285–222296. doi:10.1109/ACCESS.2020.3043639
Iqbal, N., and Kim, D. H. (2022). Iot task management mechanism based on predictive optimization for efficient energy consumption in smart residential buildings. Energy Build. 257, 111762. doi:10.1016/j.enbuild.2021.111762
Iturriaga, E., Campos-Celador, Á., Terés-Zubiaga, J., Aldasoro, U., and Álvarez-Sanz, M. (2021). A MILP optimization method for energy renovation of residential urban areas: towards zero energy districts. Sustain. Cities Soc. 68, 102787. doi:10.1016/j.scs.2021.102787
Kaggle, (2023). Buildings energy consumption. Available at: https://www.kaggle.com/datasets/arashnic/building-sites-power-consumption-dataset?resource=download (Accessed August 11, 2023).
Li, X., and Rodriguez, D. (2021). Optimization of a building energy performance by a multi-objective optimization, using sustainable energy combinations. Evol. Syst. 12, 949–963. doi:10.1007/s12530-020-09350-5
Liu, P., Alonso, M. J., Mathisen, H. M., and Halfvardsson, A. (2022). Development and optimization of highly efficient heat recoveries for low carbon residential buildings. Energy Build. 268, 112236. doi:10.1016/j.enbuild.2022.112236
Luo, X., Ren, M., Zhao, J., Wang, Z., Ge, J., and Gao, W. (2022). Life cycle assessment for carbon emission impact analysis for the renovation of old residential areas. J. Clean. Prod. 367, 132930. doi:10.1016/j.jclepro.2022.132930
Mujeebu, M. A., and Bano, F. (2022). Energy-saving potential and cost-effectiveness of active energy-efficiency measures for residential building in warm-humid climate. Energy Sustain. Dev. 67, 163–176. doi:10.1016/j.esd.2022.01.011
Nikkhah, S., Allahham, A., Royapoor, M., Bialek, J. W., and Giaouris, D. (2021). Optimising building-to-building and building-for-grid services under uncertainty: A robust rolling horizon approach. IEEE Trans. Smart Grid 13 (2), 1453–1467. doi:10.1109/TSG.2021.3135570
Nizami, M. S. H., Hossain, M. J., and Fernandez, E. (2019). Multiagent-based transactive energy management systems for residential buildings with distributed energy resources. IEEE Trans. Industrial Inf. 16 (3), 1836–1847. doi:10.1109/TII.2019.2932109
Pirmohamadi, A., Dastjerdi, S. M., Ziapour, B. M., Ahmadi, P., and Rosen, M. A. (2021). Integrated solar thermal systems in smart optimized zero energy buildings: energy, environment and economic assessments. Sustain. Energy Technol. Assessments 48, 101580. doi:10.1016/j.seta.2021.101580
Rezaei, E., and Dagdougui, H. (2020). Optimal real-time energy management in apartment building integrating microgrid with multizone HVAC control. IEEE Trans. Industrial Inf. 16 (11), 6848–6856. doi:10.1109/TII.2020.2972803
Salata, F., Ciancio, V., Dell'Olmo, J., Golasi, I., Palusci, O., and Coppi, M. (2020). Effects of local conditions on the multi-variable and multi-objective energy optimization of residential buildings using genetic algorithms. Appl. energy 260, 114289. doi:10.1016/j.apenergy.2019.114289
Shen, R., Zhong, S., Wen, X., An, Q., Zheng, R., Li, Y., et al. (2022). Multi-agent deep reinforcement learning optimization framework for building energy system with renewable energy. Appl. Energy 312, 118724. doi:10.1016/j.apenergy.2022.118724
Sheng, W., Kan, X., Wen, B., and Zhang, L. (2021). Design matters: new insights on optimizing energy consumption for residential buildings. Energy Build. 242, 110976. doi:10.1016/j.enbuild.2021.110976
Tang, F., Chen, J., Li, J., and Rodriguez, D. (2020). Energy saving actions toward NZEBs with multiple-criteria optimization in current residential buildings. Energy Rep. 6, 3008–3022. doi:10.1016/j.egyr.2020.10.069
Teng, J., Wang, P., Mu, X., and Wang, W. (2021). Energy-saving performance analysis of green technology implications for decision-makers of multi-story buildings. Environ. Dev. Sustain. 23, 15639–15665. doi:10.1007/s10668-021-01304-4
Tian, S., Su, X., Shao, X., and Wang, L. (2020). “Optimization and evaluation of a solar energy, heat pump and desiccant wheel hybrid system in a nearly zero energy building,” in Building simulation (Beijing, China: Tsinghua University Press). doi:10.1007/s12273-020-0627-0
Wang, J., Tang, C. Y., and Song, L. (2022). Analysis of precooling optimization for residential buildings. Appl. Energy 323, 119574. doi:10.1016/j.apenergy.2022.119574
Xue, Q., Wang, Z., and Chen, Q. (2022). “Multi-objective optimization of building design for life cycle cost and CO2 emissions: A case study of a low-energy residential building in a severe cold climate,” in Building simulation (Beijing, China: Tsinghua University Press). doi:10.1007/s12273-021-0796-5
Yang, X., Zhang, S., and Wang, K. (2021). Quantitative study of life cycle carbon emissions from 7 timber buildings in China. Int. J. Life Cycle Assess. 26 (9), 1721–1734. doi:10.1007/s11367-021-01960-8
Zhang, N., Luo, Z., Liu, Y., Feng, W., Zhou, N., and Yang, L. (2022). Towards low-carbon cities through building-stock-level carbon emission analysis: A calculating and mapping method. Sustain. Cities Soc. 78, 103633. doi:10.1016/j.scs.2021.103633
Zhu, Y., Yang, S., Bizhou, G. E., and Li, Y. (2021). Design optimization and uncertainty analysis of multi-energy complementary system for residential building in isolated area. Energy Convers. Manag. 241, 114310. doi:10.1016/j.enconman.2021.114310
Keywords: energy-saving, low-carbon emission, multi-objective, osprey optimization algorithm, residential buildings, green energy resources, resource utilization, agent-based optimization
Citation: Liang N and Yu M (2023) Low carbon and environmental preservation of residential buildings: MOESOM. Front. Energy Res. 11:1225416. doi: 10.3389/fenrg.2023.1225416
Received: 19 May 2023; Accepted: 01 September 2023;
Published: 25 September 2023.
Edited by:
Siamak Hoseinzadeh, Sapienza University of Rome, ItalyReviewed by:
Hassan Bazazzadeh, Poznań University of Technology, PolandCopyright © 2023 Liang and Yu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nan Liang, bGlhbmduYW4xODhAb3V0bG9vay5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.