Numerical investigation on the blade load distribution in a pump as turbine

Pump as turbine plays an important role in modern industrial process. One of the major goals of turbine design and optimization is to maximize its efficiency. Therefore, it is of great importance to connect force with work in the analysis process. In the present study, the three-dimensional flow field of the pump as a hydraulic turbine has been investigated in the steady-state mode. The load distribution along three captured streamlines (i.e., the shroud, hub and middle streamline) on both the pressure and the suction surface is observed, and the relationship between the load distribution and the working capability is systematically analyzed. The results show that the load distribution on the pressure surface of the hydraulic turbine blade gradually transitions from the reverse “S” shape to the “S” shape in the process of increasing flow rate, while the load distribution on the suction surface keeps increasing with a concave trend. The main work area of the fluid medium on the hydraulic turbine impeller is in the middle section of the blade. As the flow rate increases, the loads on the blade depict a linear decreasing trend from the inlet to the outlet. The net load acting on the blade is distributed in a concave parabola profile along the radial position of the blade. Focusing on the inlet and middle section of the blade profile in the design or optimization process of the hydraulic turbines will be more useful. This study provides a new analysis method for the design or optimization of hydraulic turbine impellers.

1 Introduction

The original purpose of the centrifugal pump is to transport liquid and convert the shaft power of the impeller into the energy of the fluid. The use of the centrifugal pump as turbine (PAT) reversely realizes the energy conversion of the centrifugal pump in the opposite direction, and transfers the energy (mechanical energy and internal energy) of the high-pressure liquid to the turbine impeller and outputs it as shaft work. When a pump is reversed, the outlet of the pump is the inlet of the turbine, and the inlet of the pump is the outlet of the turbine. The direction of rotation is opposite to that of the centrifugal pump. There are two main uses of pump reversal (Williams, 1996a; Van Antwerpen and Greyvenstein, 2005): one is as a low-cost turbine for power generation; the other is for energy recovery in pipelines. At present, the energy recovery efficiency of a hydraulic turbine is more than 80%. Comparing with the ordinary turbines and other turbine equipment, PAT is more flexible and simple to operate, and the efficiency of the turbine is similar to the pump’s working condition. Besides, the use of PAT has a lower cost.

Because of the convenient use of PAT, the change trend of the non-dimensional parameters were investigated (Sharma and Ahmad, 2008; Shahram et al., 2009; Zhou et al., 2010), such as flow rate and water head in two modes (pump mode and turbine mode) of centrifugal pumps with different specific speeds and off-design working conditions. Their study established the performance prediction relationship, the objective function of the impeller structure parameters, and optimized the impeller hydraulic model by gradient algorithm. Li (1993) made detailed discussion on various methods for the performance improvement of turbine, such as adding guide vanes, increasing the area of the impeller outlet, and trimming the head of blade. Williams (1996b) carried out experiments with 35 pumps of different shapes and sizes, compared the existing PAT performance prediction methods, and found that none of them can accurately predict the performance of PAT. Nautiyal et al. (2011) reviewed the previous performance prediction work of PAT, classified various methods and explained them in chronological order, and proposed a new method for predicting the performance of PAT by specific speed.

As is known, the performance of PAT (or pump) is closely related to its geometric parameters, including the diameter of impeller, inlet and outlet D, the blade placement angle β, the blade outlet width b, the number of blade z, the blade wrapping angle θ, etc. It is very useful to optimize PAT from above parameters. Yang et al. (2011) took a centrifugal pump with the specific speed of 72 as a turbine and studied the influence of blade wrapping angle. They found that with the increase of the blade wrapping angle, the flow head curve under pump conditions becomes steeper, and the shaft power gradually decreases; the head and shaft power under turbine conditions gradually increase, and the flow-head and flow-shaft power characteristic curves gradually increased. Yang and Wang (2011) investigated the influence of blade shape on the performance of hydraulic turbine using three PATs with different blade shapes. They found that there is an optimal combination of the blade inlet angle and wrapping angle, the turbine wheel is close to the blade inlet, there is an axial vortex near the pressure surface close to the inlet of the impeller blade. When the flow rate is greater than the design value, the larger the wrapping angle, the more obvious the decrease in turbine efficiency. Yang et al. (2013) conducted experimental research on a single-stage volute-type hydraulic turbine, and numerically studied the effect of the inlet placement angles. Their results show that the head and shaft power of the hydraulic turbine gradually increase with the increasing blade inlet angle. The efficiency of the hydraulic turbine decreases under small flow conditions, while increases under high flow conditions. The power loss inside the impeller is the main part of the turbine power loss. Researchers also investigated on the influence of blade outlet angles (Veselov, 1982; Yan, 1994; Li, 1999; Qu et al., 2005) and found that it is useful to improve the performance of PAT when the blade outlet angle increases to 90°–130°. However, further theoretical research is required to obtain the influence law of the blade outlet angle on the performance curve of PAT.

In addition, scholars have tried to using multi-objective optimization method for the design of the impeller to improve operating efficiency (Carlos et al., 2008; Kalyanmoy, 2009). Zhang et al. (2014) proposed an optimal design method of centrifugal pump impeller based on the adjoint method. This method directly uses the grid nodes on the impeller blade surface as the control variable, and establishes the objective function with the highest hydraulic efficiency of the pump at the designed operating point. Xiao and Wang (2006) used genetic algorithm (GA) global exploration, response surface approximate modeling, and sequential quadratic programming (SQP) local optimization strategy to obtain a full three-dimensional optimization strategy for hydraulic machinery. The design system realizes the fully automatic integration of the parametric design, meshing, calculation and post-processing of the blade. The genetic algorithm, neural network and gradient-based blade profile optimization algorithm were also adopted to optimize the blade profile of the pump turbine (Derakhshan et al., 2008; Derakhshan et al., 2009; Derakhshan et al., 2010). Some scholars further studied the optimal design of blades from the perspectives of numerical calculation, multiple operating conditions and three-dimensional design. Through theoretical analysis and experimental verification, the feasibility of the optimal design method is obtained (Zangeneh et al., 1996; Zangeneh et al., 1999; Kim and Park, 2000; Seo and Kim, 2004; Lehnhiuser and Scher, 2005).

The load distribution on the blade is closely related to the blade shape and the flow field in the impeller, and then affects the performance of the impeller (Shen, 1980; Otte, 1983). The basic idea of the “load method” is to use the momentum equation in the impeller to obtain the relationship between the load and the blade profile, and the twist of the blade can be obtained from this relationship (Wu and Bi, 1988). Therefore, the overall comprehensive analysis of the centrifugal pump can be carried out according to the load distribution on the blade profile and the performance of the impeller. Quan et al. (Quan et al., 2013) numerically studied the performance of screw centrifugal pump based on profile. The changes of speed, pressure, volume fraction and other parameters along the entire blade wrapping angle were explored, and the functional force of each segment of the screw centrifugal pump impeller was analyzed by introducing the concepts of centrifugal load, lift load and volume load coefficient. Lu and Wu (1987), Wu and Chen, 1988; Chen and Wu, 1989) studied the relationship between load distribution, relative speed distribution, blade outlet angle of centrifugal pump impeller and performance, and deduced the relationship between load and blade profile. Their study shown that as the maximum load moves to the exit direction, the blade wrapping angle becomes larger, the performance curve becomes steeper, and the high efficiency range becomes narrower. Zhu et al. (2004) studied the influence of the blade shape of the centrifugal solid-liquid two-phase flow pump on the hydrodynamic characteristics, and proposed a analyze method for the near wall centrifugal force to obtain a reasonable blade profile.

Although quite a few efforts have been made to investigate the performance and to improve the efficiency of the PAT, most of the studies on hydraulic turbine in terms of loads concentrate on the pressure pulsation (Ciocan et al., 2000; Zobeiri et al., 2006), axial force and radial force (Fernandez et al., 2004; Asuaje et al., 2005; Jain and Patel, 2014). However, there are few studies on the mechanism of energy conversion characteristics inside a pump as turbine, especially on the relationship between the load on blades and the blade profile and other geometric parameters of the impeller. With the gradual increase of energy requirement, researchers have tried different efforts to recover and use energy to its largest extent (Kariman et al., 2019; Kariman et al., 2020; Yargholi et al., 2020; Sohani et al., 2021; Nazarieh et al., 2023).

The present study investigates load distribution on the blade of a pump as turbine with the specific speed of 46. Connecting with the working capability, the law of load distribution on the shroud, the hub and the middle streamline has been systematically analyzed. Firstly, the three-dimensional flow field of the hydraulic turbine in the steady-state mode was studied with verified numerical model by experiment. Then the typical parameter reflecting the capability of working at the monitoring points were extracted by in the fluid domain, and the load distribution on both the pressure and the suction surface is observed. Finally, the relationship between the load distribution and the working capability is systematically analyzed. This study provides a new analysis method for the design or optimization of hydraulic turbine impeller. It is even useful to all of the fluid machineries by decomposing the load distribution on the blades and connecting them tightly with its working capability and efficiency.

2 Modeling

2.1 Physical model

Generally, reversal centrifugal pump with low specific speed (about 30–80) is used as hydraulic turbine. The specific speed n_s is defined by

$n_s=\frac{3.65n\sqrt{Q}}{H^{3/4}}$

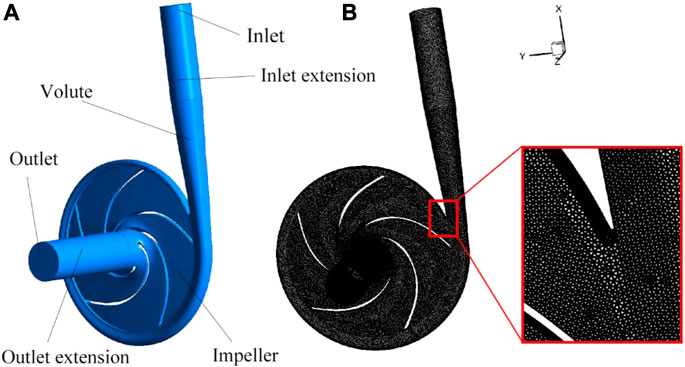
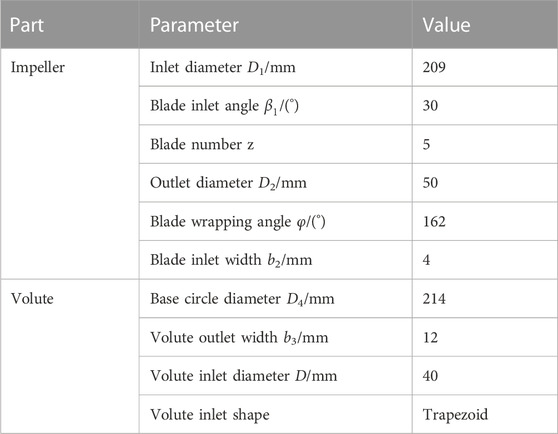
where n is the rotation speed of turbine, Q is the volume flux and H is the head. Considering low specific speed pumps are designed using the unary theory, in which the blades and impellers show similarities in terms of different geometric size. Without loss of generality, a widely used single stage PAT is adopted in the present study, as shown in Figure 1. The domain of the numerical simulation consists of the impeller, volute, and the inlet and outlet extension parts which are designed to obtain steady flow conditions. The design parameters of the hydraulic turbine are as follows: the flow rate is 24.75 m³/h, the head 51.06 m, the speed 2,900 r/min, and the specific speed 46.

FIGURE 1

FIGURE 1. Geometry (A) and mesh (B) of the hydraulic turbine.

The geometric parameters of this hydraulic turbine are shown in Table 1.

TABLE 1

TABLE 1. Geometrical parameters of the hydraulic turbine.

2.2 Mathematical model

According to the Bernoulli’s equation, the head of hydraulic machine H is described by

$H=\frac{p_1-p_2}{\rho g}+\frac{c_1^2-c_2^2}{2g}+\left(z_1-z_2\right),(1)$

where p is the static pressure, c the absolute velocity, z the position head, ρ the density of fluid and g the gravitational acceleration. The subscript 1 and 2 stands for the inlet and outlet of the turbine. When the hydraulic efficiency ${\eta }_h$ is considered, the theoretical head H_th is

$H_{th}=\frac{1}{g{\eta }_h}\left(u_1{c}_{u1}-u_2{c}_{u2}\right).(2)$

where u is the peripheral velocity.

In the present study, an incompressible steady flow field is considered due to the high incompressibility of the fluid media and the stable performance in the long run. Thus, the governing equations are as follows:

The continuity equation is

$\nabla \cdot \mathit{u}=0,(3)$

and the momentum equation is

$\frac{\mathit{\partial }\mathit{u}}{\mathit{\partial }t}+\mathit{u}·\nabla \mathit{u}=-\frac{1}{\rho }\nabla p+\nu {\nabla }^2\mathit{u},(4)$

where ν is the kinematic viscosity, m²/s, and $\mathit{u}$ is the velocity vector. Generally, the Reynolds number Re, defined by Re = ρud/μ, is of the order of 10⁶ in a turbine, which indicates the flow in the turbine remains turbulent state. Therefore, the widely used k-epsilon (k-ε) turbulent model is adopted to investigate the detailed flow field in a turbine. The governing equation of the k-ε model is

$\frac{\mathit{\partial }\left(\rho k\right)}{\mathit{\partial }t}+\frac{\mathit{\partial }\left(\rho k{u}_i\right)}{\mathit{\partial }{x}_i}=\frac{\mathit{\partial }}{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_k}\right)\frac{\mathit{\partial }k}{\mathit{\partial }{x}_j}\right]+G_k-\rho \epsilon ,(5)$

$\frac{\mathit{\partial }\left(\rho \epsilon \right)}{\mathit{\partial }t}+\frac{\mathit{\partial }\left(\rho \epsilon u_i\right)}{\mathit{\partial }{x}_i}=\frac{\mathit{\partial }}{\mathit{\partial }{x}_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_{\epsilon }}\right)\frac{\mathit{\partial }\epsilon }{\mathit{\partial }{x}_j}\right]+C_{1\epsilon }\frac{\epsilon }{k}{G}_k-C_{2\epsilon }\rho \frac{{\epsilon }^2}{k},(6)$

where μ is the dynamic viscosity, $\mu =\nu \rho$. The turbulent viscosity is

${\mu }_t=\rho C_{\mu }\frac{k^2}{\epsilon },(7)$

and the turbulent dissipation rate is originally defined by

$\epsilon =\frac{\mu }{\rho }\overline{\left(\frac{\mathit{\partial }{u}_i^{\prime }}{\mathit{\partial }{x}_k}\right)\left(\frac{\mathit{\partial }{u}_i^{\prime }}{\mathit{\partial }{x}_k}\right)}.(8)$

The coefficient $C_{1\epsilon }=1.44,C_{2\epsilon }=1.92,C_{\mu }=0.09$. The value of the turbulent Prandtl number ${\sigma }_k$ and ${\sigma }_{\epsilon }$, respectively for the kinetic energy k and the dissipation rate ε, are 1.0 and 1.3. The $G_k$, is defined by

$G_k={\mu }_t\left(\frac{\mathit{\partial }{u}_i}{\mathit{\partial }{x}_j}+\frac{\mathit{\partial }{u}_j}{\mathit{\partial }{x}_i}\right)\frac{\mathit{\partial }{u}_i}{\mathit{\partial }{x}_j}.(9)$

2.3 Initial and boundary conditions

(1) Inlet boundary condition. The inlet section of the turbine is calculated from the inlet of the volute. Due to the instability of flow, calculating the flow directly from the inlet of the volute in the calculation domain will cause a higher hydraulic loss as the fluid passing through the tapered section, and then will affect the accuracy of the numerical calculation. Therefore, an extension pipe with the length of 3–5 times the diameter of inlet was added, which is also in line with the actual situation. Considering the incompressibility of the fluid medium (water) in the present study, the velocity inlet condition is adopted based on the volume flow rate across the hydraulic turbine.

(2) Outlet boundary condition. Similar to the inlet boundary condition, the outlet is also extended. The outlet can be set as pressure, free outflow or pressure far field. Thinking of the fluid at the outlet of the turbine must have a certain residual pressure energy, it is suitable to set a pressure boundary condition for the outlet. The value of the outlet pressure is 500 kPa in the present study.

(3) Wall and interface boundary conditions. The wall among the hydraulic turbine includes the suction surface and pressure surface of the blade, the shroud and hub of the impeller, the surface of the volute and the extension section, etc. Among the above wall boundaries, the walls related to the impeller keep rotating relatively to the absolute coordinate system of the impeller, and the rest of the wall boundaries remain static. Based on the boundary layer flow theory, it is necessary to use the standard wall-function method to deal with the near-wall area. The wall surface roughness is set to 50 μm. Generally, The non-slip boundary condition is adopted in the simulation, which can be expressed by $\mathit{u}=0,\partial p/\partial n=0$, where n stands for the normal direction of the wall boundary.

2.4 Solving method

In the present study, the unstructured mesh which refined near the wall region was adopted for the entire fluid domain. The widely used SIMPLE algorithm was used to couple the velocity and pressure. Moreover, the standard k-ε model was carried out in the context of turbulent flow inside the hydraulic turbine. The fluid medium is clean water at room temperature (300 K). The dynamic (impeller) and static (volute) joints of the flow components were set as interface connection. During the steady numerical simulation, The spatial discretization is based on the least square cell. The second order upwind scheme was applied to the momentum and pressure calculation, with the converge standard of 10⁻⁴ relative error.

The numerical model was validated with the same scheme in (Shi et al., 2016), in which the external characteristics (head, power and efficiency vs. flow rate) of the pump as turbine with the specific speed of 46 was carried out experimentally. The compared results of numerical simulation and experiments indicated that the adopted numerical method was valid. The grid independence test was carried out for the PAT according to the external characteristic curve for different grid numbers 309812, 743564, 1492007 and 2798136. It was found that the difference of the selected variables between the grid number 1492007 and 2798136 less than 5%. Thus, the grid number 1492007 was adopted in the present study considering adequacy and efficiency of numerical calculation.

3 Result and discussion

3.1 External characteristics of the hydraulic turbine

The external characteristic parameters reflect the pros and cons of the operating performance the turbine. It is necessary to investigate the functions between external characteristics, (i.e., the head H, the efficiency η, and the power P) and the volume flow rate. Therefore, the numerical simulation of the selected turbine is carried out under the working condition of 0.6Q_d ∼ 2.2Q_d with the interval of 0.2Q_d, where Q_d is the designed volume flow rate of the pump working condition. The functions of turbine head H, the hydraulic efficiency of turbine η, and the output shaft power P over the flow rate are shown in Figure 2.

FIGURE 2

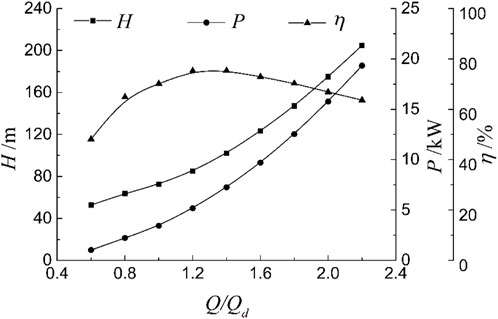
FIGURE 2. External characteristic curve of the hydraulic turbine. The curve stands for numerical results and the symbols stands for experimental results.

It can be seen that the turbine model adopted in this study reaches the highest efficiency η at 1.4 times the design flow rate (the design flow rate of the pump Q_d), to the value of 75.3%. At this time, the head H and power P are 102 m and 7.252 kW, respectively. With the gradual increase of the flow rate, the hydraulic efficiency of the turbine first increases and then decreases. Before the optimal operating point (with the highest hydraulic efficiency), the efficiency rises rapidly. After the optimal operating point, the efficiency declines more smoothly. The ratio of the rate of change is about 2, which also meets the requirement of keeping the flow rate above the design conditions during the actual operation of the turbine (Derakhshan and Nourbakhsh, 2008). When the flow rate is between 1.0Q_d and 1.8Q_d, the hydraulic efficiency of the turbine remains above 70%, which means the high efficiency zone of this model is relatively wide. The head H and the power P present a convex curve rising up monotonously with increasing flow rate, and the slope presents a gradually increasing trend. The slope of the power curve is larger than that of the head curve, indicating that the torque of the turbine impeller increases in the form of a high-order (higher than one) function as the flow rate gradually increases.

3.2 Blade load distribution and performance analysis

In a hydraulic turbine, the load on the impeller blade is the pressure that the fluid medium acts on the surface of the blade during the fluid flow through the channel of the impeller, with the unit of Pa or kPa. Here, firstly, the load data of the monitoring points were captured on the shroud, the hub and the middle streamline of the pressure and suction surface of the turbine impeller blade established by the method of Supplementary Appendix. The reason of selecting the three streamlines is that they are the basic profile lines of the blade. Then, the position of the monitoring point along the streamline was characterized by the radial distance, and normalization is performed to obtain the load distribution curve with the radial ratio under the corresponding working conditions for both the pressure surface and the suction surface. Among them, the monitoring point with the radial ratio of 1 is the monitoring point at the inlet position of the hydraulic turbine impeller, and the monitoring point with the radial ratio of 0 is the monitoring point at the outlet position of the impeller.

3.2.1 Load distribution on the pressure surface

Figure 3 shows the load distribution on the pressure surface under different working conditions. It can be seen that, as a whole, with increasing radial ratio, the load on the shroud, the middle and the hub streamline of the blade pressure surface (denoted as P₁, P₂, P₃, respectively) gradually increases, and the load increases faster in the context of large volume flow rate. When the hydraulic turbine runs at the optimal efficiency operating point 1.4Q_d, the loads P₁, P₂, and P₃ on the three streamlines increase linearly, and the load at the blade inlet position. The load of is approximately twice the load at the outlet, as shown in Figure 3D.

FIGURE 3

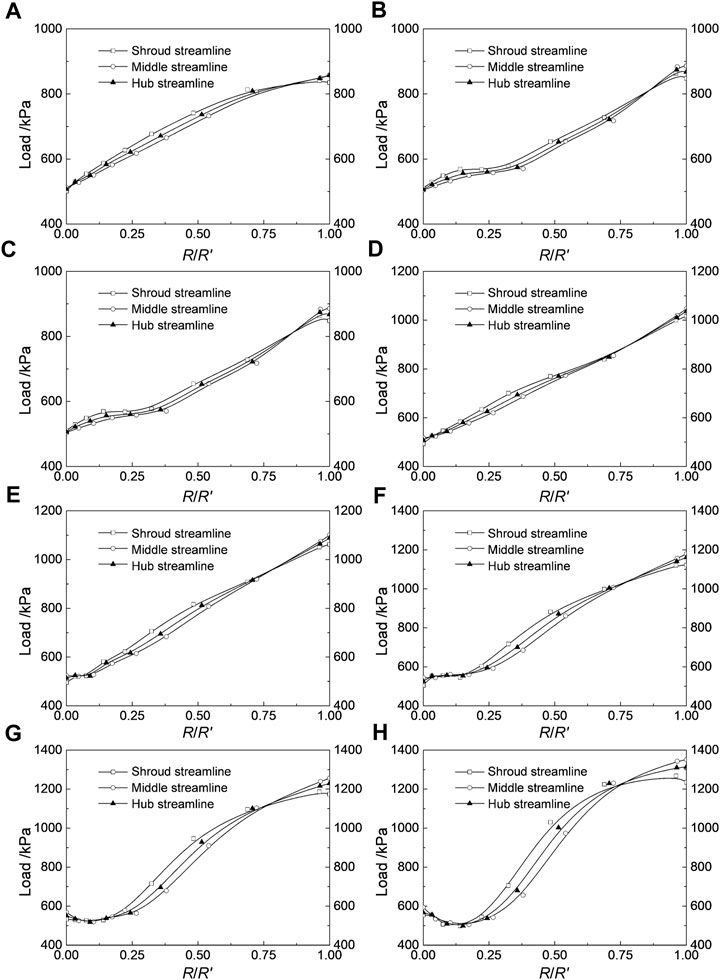
FIGURE 3. Load distribution on the pressure surface. The figures from (A–H) is for the volume flow rate of 0.6Q_d, 0.8Q_d, 1.0Q_d, 1.2Q_d, 1.4Q_d, 1.6Q_d, 1.8Q_d, 2.0Q_d.

When the volume flow rate is less than 1.4Q_d, the load curve gradually changes from concave to convex shape (reverse “S” shape), with the inflection point at 1/4 of the radial ratio. At the outlet of the turbine blade, the three load curves intersect for the first time $P_1\approx P_2\approx P_3$, namely, the load on the blade surface is nearly balanced from the shroud to the hub with uniform distribution. The three load curves intersect for the second time at the radial ratio of 7/8. At the inlet of the turbine blade, $P_2>P_3>P_1$. As the flow increases, the relative error between P₁, P₂, and P₃ first increases and then decreases, as shown in Table 2, where the $\Delta P_{\max }$ is the difference between the maximum and minimum of the three quantities $P_{1\max }$, $P_{2\max }$, $P_{3\max }$, and ${\overline{P}}_{\max }$ is the average of the three quantities. At the volume flow rate of 0.6Q_d (Figure 3A), the three load curves rise monotonously, which indicates that this case has a more uniform and stable flow state than 0.8Q_d (Figure 3 b)) and 1.0Q_d (Figure 3C).

TABLE 2

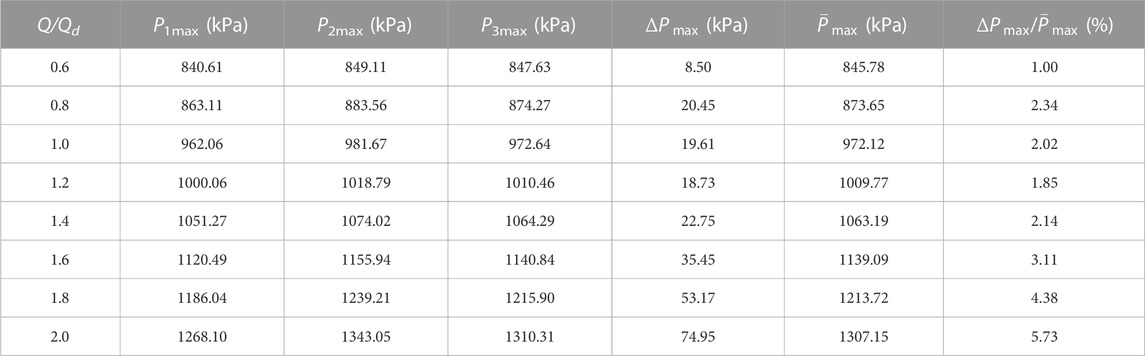
TABLE 2. The maximum load and relative load error on the shroud, hub and middle streamline of the pressure surface.

When the flow rate is greater than 1.4Q_d, the load curve gradually changes from convex to concave shape (“S" shape), and the inflection point is also at the 1/4 radial ratio. At the outlet of the turbine blade, $P_2>P_3>P_1$, however, the difference between them is small. The three load curves intersect for the first time at a radial ratio of 1/8. One the section from the outlet of blade to the first intersect point, the load on the blade has a slight monotonous reverse gradient from the middle streamline to the shroud and the hub which is opposite to the distribution of small volume flow rates. The three load curves intersect for the second time at 3/4 radial scale. At the inlet of the turbine blade, $P_2>P_3>P_1$, and the relative error between P₁, P₂, and P₃ gradually increases with the increasing volume flow rate. The relative error reaches 5.73% at 2.0Q_d (shown in Table 2), which is far more than the value of small volume flow state.

The parts between the two intersections of the three load distribution curves satisfy the relationship of $P_1>P_3>P_2$ for all the volume flow rates between 0.6Q_d and 2.0Q_d. With increasing volume flow rates, the discrepancy between P₁, P₂, and P₃ gradually increases. After the highest efficiency point of 1.4Q_d, the discrepancy increases significantly with increasing volume flow rate.

3.2.2 Load distribution on the suction surface

Figure 4 shows the load distribution on the suction surface of the blade under different working conditions. It can be seen that with increasing radial ratio, the load on the shroud, the middle and the hub streamline of the blade pressure surface (denoted as $P_1^{\prime }$, $P_2^{\prime }$, $P_3^{\prime }$, respectively) gradually increases. The three different load distribution curves are convex and parallel, which is different from the load distribution on the pressure surface (shown in Figure 3). And the curvature increases slightly with increasing volume flow rate. The load at the inlet of the hydraulic turbine is about twice the load at the outlet.

FIGURE 4

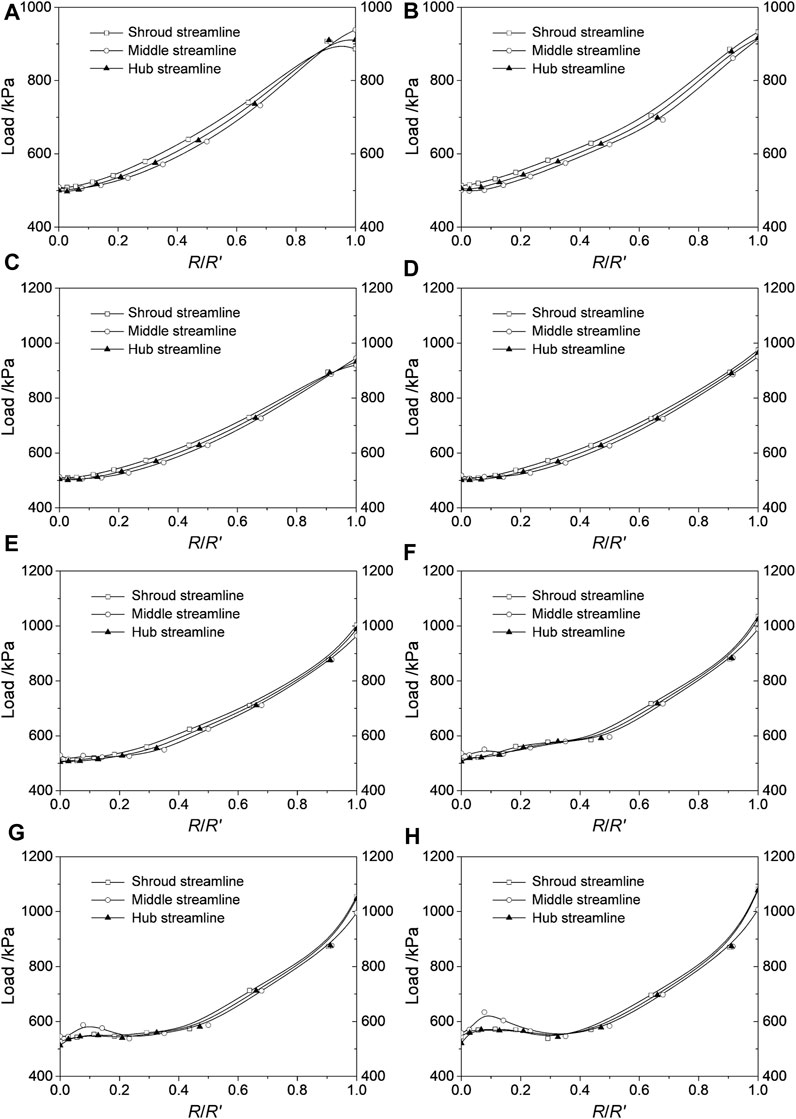
FIGURE 4. Load distribution on the suction surface. The figures from (A–H) is for the volume flow rate of 0.6Q_d, 0.8Q_d, 1.0Q_d, 1.2Q_d, 1.4Q_d, 1.6Q_d, 1.8Q_d, 2.0Q_d.

When the volume flow rate is less than 1.4Q_d, three of the load distribution curves present a smooth upward trend, and the load on the three streamlines at the blade outlet position is obviously more uniform than that at the inlet position. The relative error between $P_1^{\prime }$, $P_2^{\prime }$ and $P_3^{\prime }$ depicts the trend of increasing firstly and then decreasing with the increase of the volume flow rate (see Table 3), but the value of the relative error is smaller than that of the pressure surface. In the working conditions of 0.6Q_d (Figure 4A) and 1.0Q_d (Figure 4C), the three load distribution curves intersected at the position where the radial ratio of the blade is 0.9, and the load on the blade reaches a balanced state.

TABLE 3

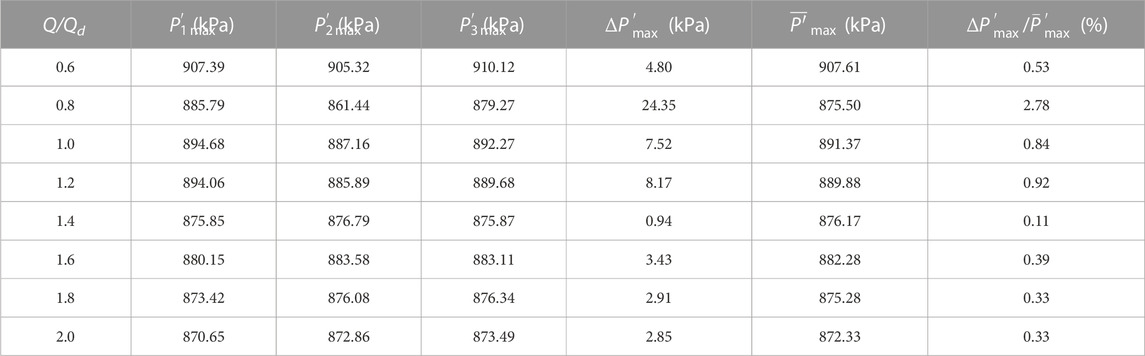
TABLE 3. The maximum load and relative load error on the shroud, hub and middle streamline of the suction surface.

When the volume flow rate is greater than 1.4Q_d, three of the load distribution curves appear to oscillate slightly at the blade outlet, especially for the load distribution on middle streamline at the radial ratio of 0.1, as shown in Figures 4G, H. After the radial ratio of 0.2, the three load distribution curves return to a consistent trend. The value of $P_1^{\prime }$ and $P_3^{\prime }$ at the position of the blade inlet tends to be the same, and is larger than $P_1^{\prime }$. The maximum relative error of the three load distribution gradually increases with increasing volume flow rate, as shown in Table 3. However, this error is less than 1/10 that of the pressure surface. Around the operating point 1.4Q_d, the maximum blade load for three streamlines remains nearly unchanged, however, when the operating point moves to smaller or larger volume flow rate, the discrepancies of the maximum load between the three streamlines are obvious (see Table 3). This trend is opposite to that of the pressure surface.

3.2.3 Net load distribution on the blade streamline

In order to investigate the power of the fluid medium on the hydraulic turbine blade, the net load distribution was calculated by the difference between the load on the pressure surface and the suction surface for the shroud, hub and middle streamline. Five typical operating conditions with the volume flow rate of 0.8Q_d, 1.0Q_d, 1.4Q_d, 1.6Q_d, and 2.0Q_d were selected, and the net load distribution on the blade are shown in Figure 5.

FIGURE 5

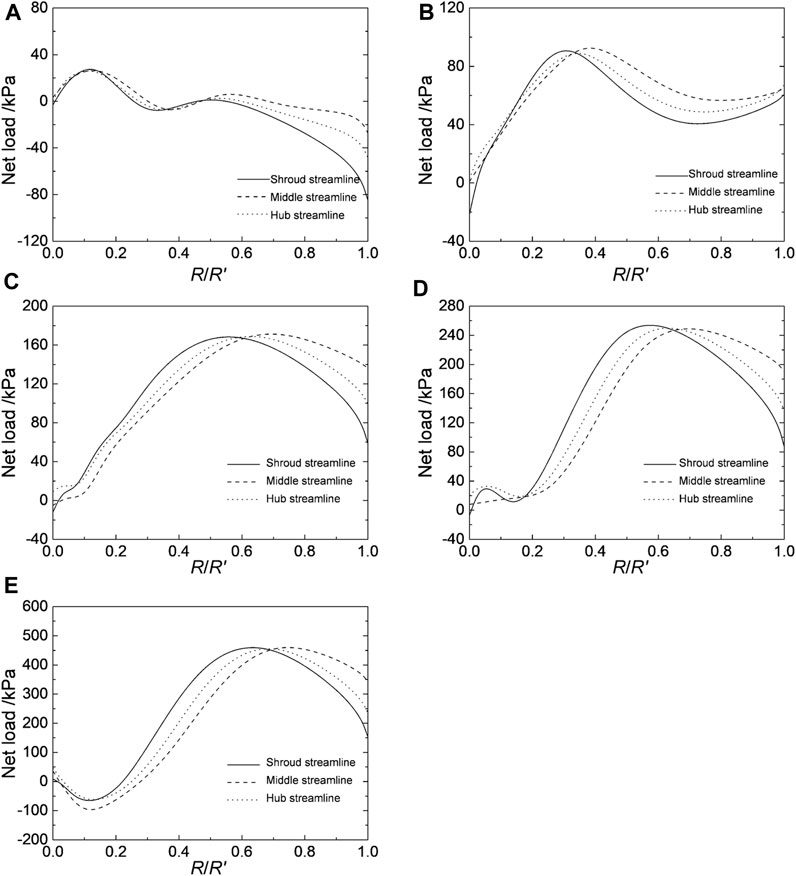
FIGURE 5. Net load distribution on the blade. The figures from (A–E) is for the volume flow rate of 0.8Q_d, 1.0Q_d, 1.4Q_d, 1.6Q_d, 2.0Q_d.

It can be seen from Figure 5A that the net load on the blade gradually decreases from the outlet to the inlet of the impeller. In the 0 ∼ 0.5 times radial ratio section, the net load on the shroud, the middle and the hub streamline of the blade (denoted as P_n1, P_n2, and P_n3 respectively) are almost greater than zero. The trend of the three net load distribution curves are consistent. When the radial ration is 0.1, the net load reaches its maximum value. In the range of 0.5 ∼ 1 times the radial ratio, P_n1, P_n2, and P_n3 begin to decline with increasing radial ratio, in which P_n1 declines the fastest, P_n2 declines the slowest. The three net load distribution curves are all below zero, which indicates that negative pressure is formed on this part of blade.

When the flow rate increases to 1.0Q_d, P_n1, P_n2, and P_n3 are all positive values in the entire blade flow path (see Figure 5B), indicating that the net load on the blade changes to positive pressure from the pressure surface to the suction surface. As the radial ratio increases, P_n1, P_n2, and P_n3 depicts concave increasing trends until reaching their maximum values at 0.3 ∼ 0.5 times the radial ratio position, and presents convex decreasing trend until reaching their minimum values at 0.7 ∼ 0.8 times the radial ratio.

As the volume flow rate continues to increase, the net load on the blade develops into a standard parabolic distribution, as shown in Figures 5C–E. The position of the maximum net load on the blade shifted from 0.5 to 0.7 times the radial ratio at 1.4Q_d to 0.6 ∼ 0.8 times the radial ratio at 2.0Q_d. When the flow rate is greater than the flow rate of 1.4Q_d, namely, the optimal efficiency operating point, there is a small fluctuation at the 0 ∼ 0.2 times radial ratio (i.e., near the blade outlet). This small fluctuation increases with increasing volume flow rate. However, the number of extreme points decrease with increasing volume flow rate, and the fluctuations finally develop into small upward convex curves at 2.0Q_d, with negative minimum load obtained at the position of 0.1 times the radial ratio. In the increasing part of the net load, P_n1>P_n2>P_n3, and in the decreasing part, P_n2>P_n3>P_n1.

Overall, the net load on the blade increases with increasing volume flow rate, which is consistent with the trend of the power changing with the volume flow rate in the external characteristic curve, as shown in Figure 2.

3.3 Discussion

The flow channel of the turbine impeller is a tapered and twisted three-dimensional flow channel. When the fluid medium flows from the inlet of the impeller through the flow channel of the impeller, it is accompanied by the mutual conversion between kinetic and potential energy and heat transfer (ignored here). The energy conversion satisfies the Bernoulli’s equation (Eq. 1). Since the fluid medium in the present study is clean water, $d\rho =0$, there must be a process in which the pressure potential energy is gradually transformed into kinetic energy in the tapered flow path, namely, the pressure gradually decreases and the total velocity energy gradually increases, as shown in Figure 6. This is consistent with the law of the aforementioned blade load distribution. At the same time, since there is a flow transition from the exit of the volute to the entrance of the turbine impeller, a series of vortices of different sizes are generated. Especially, large size reverse (counterclockwise) vortices occur at the entrance position back of the blade, which is affected strongly by the geometry of the blade, as shown in Figure 7. These vortices actually form obstruction to the fluid flow in the impeller channel to some extend. Low pressure region is formed in the center of the vortex, with the result of affecting the entire pressure distribution of the flow field. In the small volume flow rate condition, the load (pressure) on the suction surface of the blade presents a steady change (see Figure 4), however, the load on the pressure surface fluctuates from the middle position of the blade to the outlet due to the existence of the vortex. With increasing volume flow rate, the large-scale vortices gradually shift from the pressure surface to the suction surface of the blade, and gradually spreads from the inlet to the outlet of the blade, as shown in Figure 7. This is also the reason of the small rise of load on the suction surface near the 1/5 region of blade outlet for large volume flow rate cases. The vortices at the inlet of the pressure surface of the blade depicts a small scale in the context of large volume flow rates, as shown in Figure 7. Comparing with large-scale vortices at low volume flow rates, the effect on the mainstream velocity in the flow channel is reduced for the large volume flow rate cases, thus presenting a load distribution opposite to that of the small volume flow rate cases, as shown in Figure 3. Meanwhile, due to the influence of the axial vortex and the secondary flow (Gülich, 2008), the load on the pressure surface of the blade is distributed in the form of reverse “S” shape under the small volume flow rate, and transitions to the “S” shape under the large volume flow rate, as shown in Figure 3.

FIGURE 6

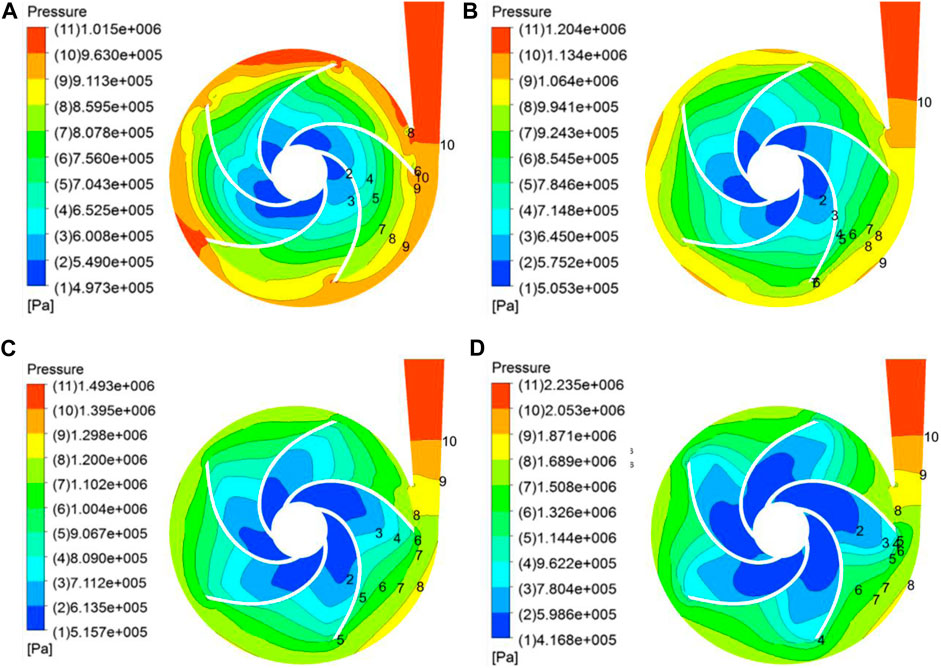
FIGURE 6. Pressure distribution at the middle section of the turbine. (A) 0.6Q_d, (B) 1.0Q_d, (C) 1.4Q_d, (D) 2.0Q_d.

FIGURE 7

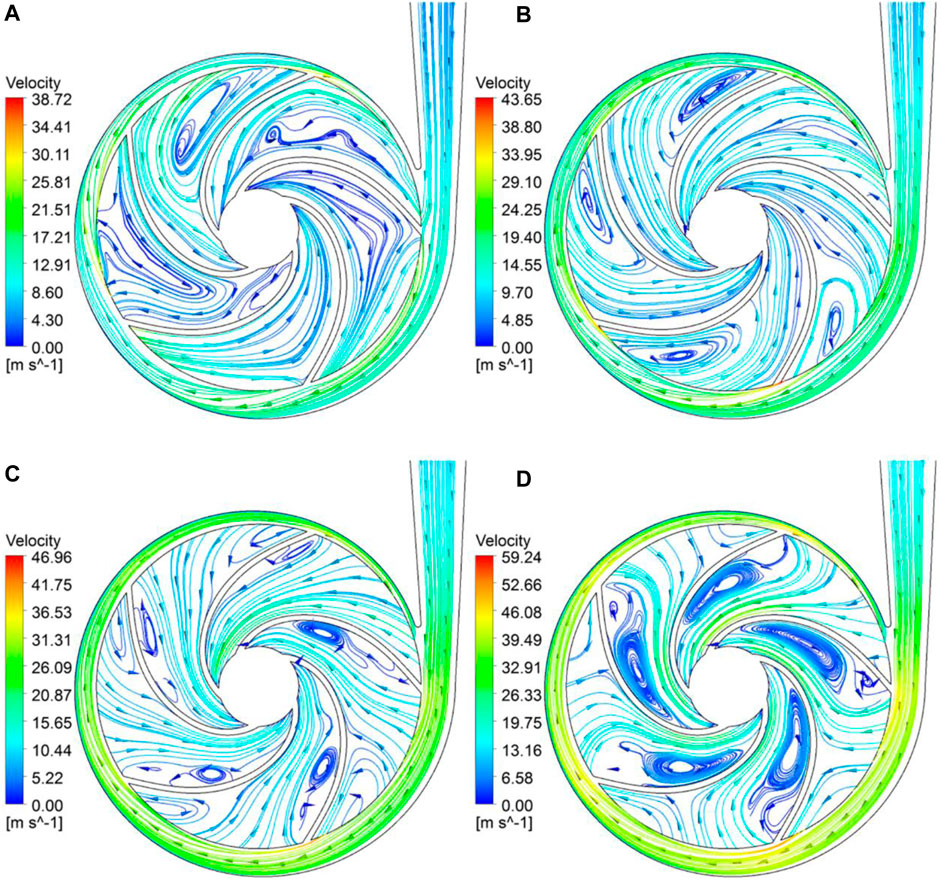
FIGURE 7. Streamline distribution at the middle section of the turbine. (A) 0.6Q_d, (B) 1.0 Q_d, (C) 1.4Q_d, (D) 2.0Q_d.

The load distributions on the shroud, the middle streamline and the hub streamline of the pressure and suction surface are generally in the relationship of $P_1>P_3>P_2$ and $P_1^{\prime }>P_3^{\prime }>P_2^{\prime }$. This is not only related to the vortices and velocity distributions in the flow field, but also related to the spatial geometric shapes of the blade. The highly twisted turbine blades ensure the stability of the flow, and also provide pressure gradient in the internal flow field towards the center of the impeller, which is able to reduce the friction loss of the disc between the shroud/hub and the fluid. Besides, the axial force is also reduced. Therefore, the efficiency of the hydraulic turbine is increased. At the same time, the existence of jet-wake structure (Shen, 1987) will also affect the distribution of the velocity field near the shroud and the hub of impeller, thereby changing the distribution of the pressure field. The load distribution with the “S” shape on the pressure surface presents two intersection near the inlet and the outlet position, which reflects that there is an alternate equilibrium state in the energy conversion process between the velocity field and the pressure field in the entire flow field. The blade part between the two intersections is the effective region where the turbine impeller really work.

The net load distribution curves are the result of superposition of the load between the pressure surface and the suction surface. Among them, the net load for the small volume flow rate (shown in Figure 5A) is negative, which is corresponding its relatively small power (see Figure 3), since the negative load prevents the fluid from working on the impeller. Although the power is increased for the large volume flow rate cases, the efficiency is decreased. As it can be seen in Figure 5, the design point 1.0Qd has wider and flatter positive net load distribution then the lager flow rate cases. This is why the efficiency of 1.0Qd is higher than other off-design operation points. Besides, the negative pressure in the small section of the outlet position also have small influence on the efficiency of the turbine. The physical mechanism of the differences of net loads and efficiencies is due to the increase of turbulence and dissipation in the flow field for larger flow rate cases. Thus, it is recommended to increase the net positive load distribution range to improve the efficiency of turbine.

This study mainly concentrates on the load distribution along the blade of turbine and analyzes the flow fields and physical mechanism. However, the energy conversion characteristics inside the turbine still need further investigation. Besides, some meaningful results maybe obtain by using large-eddy simulation (LES) considering the turbulent flows inside the turbine.

4 Conclusion

In the present study, the three-dimensional flow field of the pump as hydraulic turbine was numerically investigate in the steady-state mode. By extracting the typical parameter reflecting the capability of working at the monitoring points established in the fluid domain, the load distribution on both the pressure and the suction surface is observed, and the relationship between the load distribution and the working capability is systematically analyzed. The results show that the main work area of the fluid medium on the hydraulic turbine impeller is in the middle section of the blade. The inlet section does less work, while the outlet section almost does not work. As the flow rate increases, the load distribution on the pressure surface of the hydraulic turbine blade gradually transitions from the reverse “S” shape to the “S” shape in the process of increasing flow rate, while the load distribution on the suction surface keeps increasing with a concave trend. The loads on the shroud, the middle and the hub streamline depict linear decreasing trend from the inlet to the outlet of the blade. The net load acting on the blade is distributed in a concave parabola profile along the radial position of the blade. Therefore, it is more important to take the inlet and middle section of the blade profile into consideration when design or optimize a hydraulic turbine impeller. It is also recommended to increase the net positive load distribution range to enhance the efficiency of turbine in the optimal design process.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

XB, JY, and JL contributed to conception and design of the study. XB organized the database and wrote the first draft of the manuscript. JY, XW, and JL contributed to manuscript revision. All authors contributed to the article and approved the submitted version.

Funding

This study is supported by China Postdoctoral Science Foundation (No. 2022M712676) and Gansu Outstanding Youth Fund (No. 20JR10RA203).

Conflict of interest

Author XB was employed by the company Chongqing Pump Industry Co., Ltd. Author JL was employed by the company Naipu Min Machinery Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2023.1220395/full#supplementary-material

References

Asuaje, M., Bakir, F., Kouidri, S., Kenyery, F., and Rey, R. (2005). Numerical modelization of the flow in centrifugal pump: volute influence in velocity and pressure fields. Int. J. Rotating Mach. 2005 (3), 244–255. doi:10.1155/ijrm.2005.244

CrossRef Full Text | Google Scholar

Carlos, A. C., Lamont, G. B., and Van Veldhuizen, D. A. (2008). Evolutionary algorithms for solving multi-objective problems. second edition. London, England: Springer.

Google Scholar

Chen, S. L., and Wu, D. R. (1989). The drawing of a centrifugal impeller with computer AID. J. Xi’an Jiao Tong Univ. 23 (3), 99–108.

Google Scholar

Ciocan, G. D., Avellan, F., and Kueny, J. L. (2000). Optical measurement techniques for experimental analysis of hydraulic turbines rotor-stator interaction. Proc. ASME, 11–15.

Google Scholar

Derakhshan, S., Mohammadi, B., and Nourbakhsh, A. (2009). Efficiency improvement of centrifugal reverse pumps. J. fluids Eng. 131 (2), 204–209. doi:10.1115/1.3059700

CrossRef Full Text | Google Scholar

Derakhshan, S., Mohammadi, B., and Nourbakhsh, A. (2008). Incomplete sensitivities for 3D radial turbomachinery blade optimization. Comput. Fluids 37 (10), 1354–1363. doi:10.1016/j.compfluid.2008.01.002

CrossRef Full Text | Google Scholar

Derakhshan, S., Mohammadi, B., and Nourbakhsh, A. (2010). The comparison of incomplete sensitivi-ties and Genetic algorithms applications in 3D radial turbomachinery blade optimiza-tion. Comput. Fluids 39 (10), 2022–2029. doi:10.1016/j.compfluid.2010.07.003

CrossRef Full Text | Google Scholar

Derakhshan, S., and Nourbakhsh, A. (2008). Theoretical, numerical and experimental investigation of centrifugal pumps in reverse operation. Exp. Therm. Fluid Sci. 32 (8), 1620–1627. doi:10.1016/j.expthermflusci.2008.05.004

CrossRef Full Text | Google Scholar

Fernandez, J., Blanco, E., Parrondo, J., Stickland, M. T., and Scanlon, T. J. (2004). Performance of a centrifugal pump running in inverse mode. Proc. Institution Mech. Eng. Part A J. Power Energy 218 (4), 265–271. doi:10.1243/0957650041200632

CrossRef Full Text | Google Scholar

Gülich, J. F. (2008). Centrifugal pumps. Berlin, Germany: Springer.

Google Scholar

Jain, S. V., and Patel, R. N. (2014). Investigations on pump running in turbine mode: A review of the state-of-the-art. Renew. Sustain. Energy Rev. 30, 841–868. doi:10.1016/j.rser.2013.11.030

CrossRef Full Text | Google Scholar

Kalyanmoy, D. (2009). Multi-objective optimization using evolutionary algorithms. Canada: John Wiley & Sons.

Google Scholar

Kariman, H., Hoseinzadeh, S., and Heyns, P. S. (2019). Energetic and exergetic analysis of evaporation desalination system integrated with mechanical vapor recompression circulation. Case Stud. Therm. Eng. 16, 100548. doi:10.1016/j.csite.2019.100548

CrossRef Full Text | Google Scholar

Kariman, H., Hoseinzadeh, S., Shirkhani, A., Heyns, P. S., and Wannenburg, J. (2020). Energy and economic analysis of evaporative vacuum easy desalination system with brine tank. J. Therm. Analysis Calorim. 140, 1935–1944. doi:10.1007/s10973-019-08945-8

CrossRef Full Text | Google Scholar

Kim, J. S., and Park, W. G. (2000). Optimized inverse design method for pump impeller. Mechan-ics Res. Commun. 27 (4), 465–473. doi:10.1016/s0093-6413(00)00119-1

CrossRef Full Text | Google Scholar

Lehnhiuser, T., and Scher, M. (2005). A numerical approach for shape optimization of fluid flow domains. Comput. Methods Appl. Mech. Eng. 194 (50/51/52), 5221–5241. doi:10.1016/j.cma.2005.01.008

CrossRef Full Text | Google Scholar

Li, W. G. (1993). Design and amplification of industrial centrifugal pumps. Lanzhou, China: Fluid Machinery Lab of Lanzhou University of Technology, 236–240.

Google Scholar

Li, W. G. (1999). Flow measurements of water inside a centrifugal pump impeller with large blade discharge angle. Trans. Chin. Soc. Agric. Mach. 30 (2), 54–58.

Google Scholar

Lu, W. Z., and Wu, D. R. (1987). The influence of velocity distribution in centrifugal impellers and outlet blade angle on the performance of centrifugal pumps. Trans. Chin. Soc. Agric. Mach. (2), 25–32.

Google Scholar

Nautiyal, H., Varun, V., Kumar, A., and Yadav, S. Y. S. (2011). Experimental investigation of centrifugal pump working as turbine for small hydropower systems. Energy Sci. Technol. 1 (1), 79–86. doi:10.3968/j.est.1923847920110101.006

CrossRef Full Text | Google Scholar

Nazarieh, M., Kariman, H., and Hoseinzadeh, S. (2023). Numerical simulation of fluid dynamic performance of turbulent flow over Hunter turbine with variable angle of blades. Int. J. Numer. Methods Heat Fluid Flow 33 (1), 153–173. doi:10.1108/hff-12-2021-0774

CrossRef Full Text | Google Scholar

Otte, J. J. (1983). “Function of the aerodynamic blade loading as the criterion to the design of the centrifugal impeller,” in Proceedings of the seventh conference on fluid machinery (Budapest, Hungary: Akadémi Kiadó), 649.

Google Scholar

Qu, Y. P., Chen, S. Y., and Zhang, H. F. (2005). Experimental study on steady-state hydraulic performance of a centrifugal pump through changing outlet angle. Fluid Mach. 33 (10), 1–3.

Google Scholar

Quan, H., Li, R. N., Su, Q. M., Han, W., Li, Q. F., and Shen, Z. J. (2013). Research on work capacity of screw centrifugal pump impeller based on profile lines. J. Mech. Eng. 49 (10), 156–162. doi:10.3901/jme.2013.10.156

CrossRef Full Text | Google Scholar

Seo, S. J., and Kim, K. Y. “Design optimization of forward-curved blades centrifugal fan with response surface method,” in Proceedings of the ASME Heat Transfer, Fluids Engi-neering Summer Conference, Charlotte, North Carolina, USA, July 2004, 551–556.

Google Scholar

Shahram, D., Bijan, M., and Ahmad, N. (2009). Efficiency improvement of centrifugal reverse pumps. J. Fluids Eng. 131 (2), 204–209. doi:10.1115/1.3059700

CrossRef Full Text | Google Scholar

Sharma, D., and Ahmad, N. (2008). Experimental study of characteristic curves of centrifugal pumps working as turbines in different specific speeds. Exp. Therm. Fluid Sci. 32 (4), 800–807. doi:10.1016/j.expthermflusci.2007.10.004

CrossRef Full Text | Google Scholar

Shen, T. Y. (1980). A flow model and design method of the impeller of forward-swept blades. J. Tsinghua Univ. 20 (2), 37–50.

Google Scholar

Shen, T. Y. (1987). Fundamentals of centrifugal impeller internal flow theory. Hangzhou, China: Zhejiang University Press.

Google Scholar

Shi, G. T., Yang, J. H., Miao, S. C., and Wang, X. H. (2016). Unsteady calculation of pressure pulsations within hydraulic turbine under different entrance sections. J. Aerosp. Power 31 (3), 659–668. doi:10.13224/j.cnki.jasp.2016.03.017

CrossRef Full Text | Google Scholar

Sohani, A., Pedram, M. Z., Berenjkar, K., Sayyaadi, H., Hoseinzadeh, S., Kariman, H., et al. (2021). Techno-energy-enviro-economic multi-objective optimization to determine the best operating conditions for preparing toluene in an industrial setup. J. Clean. Prod. 313, 127887. doi:10.1016/j.jclepro.2021.127887

CrossRef Full Text | Google Scholar

Van Antwerpen, H. J., and Greyvenstein, G. P. (2005). Use of turbines for simultaneous pressure regulation and recovery in secondary cooling water systems in deep mines. Energy Convers. Manag. 46 (4), 563–575. doi:10.1016/j.enconman.2004.04.006

CrossRef Full Text | Google Scholar

Veselov, V. I. (1982). Effect of the outlet angle β₂ on the characteristics of low specific-speed centrifugal pumps. Power Technol. Eng. 16 (5), 267–273. doi:10.1007/bf01427809

CrossRef Full Text | Google Scholar

Williams, A. A. (1996a). Pumps as turbines for low cost micro hydropower. Renew. Energy An Int. J. 9 (1-4), 1227–1234. doi:10.1016/0960-1481(96)88498-9

CrossRef Full Text | Google Scholar

Williams, A. A. (1996b). Pumps as turbines for low cost micro hydropower. Renew. Energy An Int. J. 9 (1-4), 1227–1234. doi:10.1016/0960-1481(96)88498-9

CrossRef Full Text | Google Scholar

Wu, D. R., and Bi, Z. Y. (1988). Effect of load and relative velocity distribution on cavitation in centrifugal pump. Fluid Eng. (12), 5–10.

Google Scholar

Wu, D. R., and Chen, S. L. (1988). The relation between loading distribution and characteristics in impeller of centrifugal pump. Trans. Chin. Soc. Agric. Mach. (2), 58–65.

Google Scholar

Xiao, R. F., and Wang, Z. W. (2006). Centrifugal pump blade optimization based on a combined optimization strategy. J. Tsinghua Univ. Sci. Technol. 46 (5), 700–703. doi:10.3321/j.issn:1000-0054.2006.05.025

CrossRef Full Text | Google Scholar

Yan, J. (1994). Influence of impeller geometry parameters on the centrifugal pump capacity of different specific speeds. Pump. Technol. (4), 17–19.

Google Scholar

Yang, J. H., and Wang, X. H. (2011). Effect of vane profile on hydraulic energy recovery turbines performance. J. Drainage Irrigation Mach. Eng. 29 (4), 287–291. doi:10.3969/j.issn.1674-8530.2011.04.003

CrossRef Full Text | Google Scholar

Yang, S. S., Kun, F. Y., and Chen, B. (2011). Numerical research of blade wrap angle on the performance of reversible pump. Fluid Mach. 39 (6), 17–21. doi:10.3969/j.issn.1005-0329.2011.06.005

CrossRef Full Text | Google Scholar

Yang, S. S., Kun, F. Y., Chen, H., and Su, X. H. (2013). Effects of blade inlet angle on performance of pump as turbine. J. Central South Univ. Sci. Technol. 44 (1), 108–113.

Google Scholar

Yargholi, R., Kariman, H., Hoseinzadeh, S., Bidi, M., and Naseri, A. (2020). Modeling and advanced exergy analysis of integrated reverse osmosis desalination with geothermal energy. Water supply 20 (3), 984–996. doi:10.2166/ws.2020.021

CrossRef Full Text | Google Scholar

Zangeneh, M., Goto, A., and Harada, H. (1999). On the role of three-dimensional inverse design methods in turbomachinery shape optimization. J. Mech. Eng. 213 (1), 27–42. doi:10.1243/0954406991522167

CrossRef Full Text | Google Scholar

Zangeneh, M., Goto, A., and Takemura, T. (1996). Suppression of secondary flows in a mixed-flow pump impeller by application of three dimensional inverse design method Part 1: de-sign and numerical validation. J. Turbomach. 118 (7), 536–543. doi:10.1115/1.2836700

CrossRef Full Text | Google Scholar

Zhang, R. H., Guo, M., Yang, J. H., and Liu, Y. (2014). Blade shape optimization of centrifugal pump impeller with adjoint method. J. Drainage Irrigation Mach. Eng. 32 (11), 943–947. doi:10.3969/j.issn.1674-8530.14.0033

CrossRef Full Text | Google Scholar

Zhou, G. J., Yan, Z. Y., and Xu, S. X. (2011). Fluid mechanics. Beijing, China: High Education Press.

Google Scholar

Zhou, Y. F., Yan, J. C., and Fang, Y. (2010). Optimum design of the impellers of centrifugal pumps based on ANSYS. Chem. Eng. Mach. 37 (2), 165–169. doi:10.3969/j.issn.0254-6094.2010.02.009

CrossRef Full Text | Google Scholar

Zhu, Y. C., Wu, Y. L., Pan, A. X., Li, L., Qu, Y. G., Yu, J. N., et al. (2004). Influence of vane curve of solid liquid two-phase flow centrifugal pump on dynamic properties of fluid. J. Mech. Eng. 40 (8), 67–71. doi:10.3901/jme.2004.08.067

CrossRef Full Text | Google Scholar

Zobeiri, A., Kueny, J. L., Farhat, M., and Avellan, F. (2006). Pump-turbine rotor-stator interactions in gener-ating mode: pressure fluctuation in distributor channel. Proc. 23th IAHR symposium, 1–10.

Google Scholar