A fast linearized AC power flow-constrained robust unit commitment approach with customized redundant constraint identification method

The large-scale integration of renewable energy resources in the power system challenges its economic and secure operation. Particularly, the increasing penetration of renewable energy will result in insufficient system voltage regulation and reactive power support capabilities, and may cause high risks of nodal voltage and branch flow violations. Therefore, to hedge the operational risks under the worst realization of uncertainties of renewable energy sources, a two-stage robust unit commitment (UC) model is developed. Meanwhile, the convexified AC power flow model is incorporated in the robust UC model to more accurately characterize the real-time operating status of power systems. On this basis, an AC power flow-constrained robust unit commitment (ACRUC) model is formulated. A circular linearization method is then adopted to handle the quadratic constraints in the original AC power flow model, transforming them into tractable linear constraints. Furthermore, to reduce the computational complexity caused by the large-scale newly-added constraints after the linearization process, a customized redundant constraint identification (RCI) method is developed, in which two different modes (i.e., cold and warm start modes) are designed considering the difference in base case system operating condition for linearizing branch losses. Then, the redundant network security constraints could be identified by solving a series of relatively simple optimization subproblems. Numerical results on the modified NERL-118 test system indicate that the proposed model could accurately depict actual operation and scheduling conditions, and also verify that the proposed customized RCI method could effectively reduce the problem scale and improve the solution efficiency.

1 Introduction

The security-constrained unit commitment (SCUC) could ensure the economic and secure operation of power systems. With the integration of dispatchable sources, expansion of power grids, and interconnection between regional power grids, the traditional power system has sufficient flexibility to mitigate the operational risks (Han, X. et al., 2023). However, power systems now face increasing challenges caused by the uncertainty of renewable energy sources, resulting in high risks of nodal voltage (Wang R. et al., 2022) and branch flow limit violations (Wang S. et al., 2022). Moreover, the insufficient reactive power support capability of renewable energy resources further complicates power flow distribution (Nasri et al., 2015; Wang et al., 2021), making it challenging for system operators to decide their optimal strategies for complex system operations.

Robust optimization is well-recognized as an effective tool to cope with uncertainties of renewable energy resources. It focuses on the evaluation of system performance under the worst uncertainty realization (Ben-Tal and Nemirovski, 1998; Ben-Tal and Nemirovski, 1999; Ben-Tal and Nemirovski, 2000). Compared to deterministic optimization, robust optimization results are conservative but better able to deal with uncertainty caused by random factors. It has been widely used in the optimal operation problem of power systems with high renewable energy penetrations (Jiang et al., 2011; Ye et al., 2016; Cobos et al., 2018).

Most studies on the unit commitment (UC) problem have adopted the DC power flow model to formulate network constraints, rather than the more accurate AC power flow model (Wen et al., 2015; Chen et al., 2016). The DC power flow model is a simplified model used for approximate estimation of the active power distribution in a transmission network. Its main idea is to simplify the nonlinear flow problem into a linear problem by ignoring the influence of reactive power on the active power flow distribution (Wang et al., 2010). Traditional UC mainly focuses on the balance of active power supply and demand and energy transition within the system, and the DC power flow model can meet the modeling requirements for transmission security in traditional UC while ensuring computational efficiency (Wang et al., 2007; Wood et al., 2013; Yang et al., 2017a). However, this simplified DC power flow model may not be suitable for the UC problem with high renewable energy penetrations. This is mainly due to the fact that the DC flow model is unable to evaluate the sufficiency of the system’s voltage regulation and reactive power support ability, and accurately reflect the actual branches flow or transmission sections flow, and provide information related to network losses (Castillo et al., 2015). Therefore, it is necessary to introduce AC power flow models in the UC to comprehensively consider the impact of active and reactive components on the generation scheduling and transmission security.

However, introducing AC power flow models into the UC problem currently faces a major challenge. The traditional UC problem is an NP-hard problem (Lavaei and Low, 2011; Castillo et al., 2016). Adding AC power flow constraints introduces non-convexity into the model and makes the UC problem both a non-convex and an NP-hard problem, making it extremely difficult to solve (Lehmann et al., 2015). Some researchers focus on convex relaxation method to convexify the AC power flow model. Lorca and Sun. (2017) apply semidefinite programming and second-order cone programming to simplify the AC power flow model. However, the accuracy and convergence of convex relaxation methods cannot perform consistently well (Šepetanc and Pandzic., 2020). Several other works (Zhang et al., 2013; Yang et al., 2017b) have also convexified the AC power flow model using the Taylor series expansions technique and linearized losses. This approach reformulates the model into a tractable formulation. However, solving the convexified model remains considerably challenging for large-scale systems. One reason for this challenge is the existence of a substantial number of network constraints, which renders the model difficult to solve. Another factor contributing to the complexity is the quadratic form of the branch flow limit constraints, which transforms the model into a more intricate mixed-integer quadratically constrained programming problem.

In practice, power flows through non-critical branches may not generally reach their limits, and the flow through most critical branches may also not reach their limits for certain long time periods (Hua et al., 2013; Ardakani and Bouffard, 2014). This indicates that a certain proportion of network constraints will be redundant for power system operation problem in many cases, since they will not affect the feasible region of the UC problem and its optimal solution. However, these redundant constraints will cause the problem’s scale to become unnecessarily large and the solution efficiency to deteriorate (Zhai et al., 2010). Therefore, identifying and eliminating these redundant network constraints before solving the problem can greatly reduce the model’s complexity. In Zhai et al. (2010), sufficient conditions for quickly identifying redundant network security constraints are proposed, to reduce excessive relaxation and identify effective redundant constraints. A feasibility-based boundary tightening strategy is proposed in Ding et al. (2020) to deal with components whose output power fluctuation range varies over time. An improved redundant constraint identification (RCI) method is proposed in Yang et al. (2021), which is designed for long-term UC problem. However, the above studies are applied to DC flow-constrained UC model, which is different from AC flow-constrained UC models in mathematical properties. Therefore, these RCI methods based on DC flow-constrained UC model cannot be simply introduced to AC flow-constrained UC models. Therefore, its necessary to develop a customized RCI method based on AC network constraints by leveraging their special structures.

Based on the above literature review, this paper identifies the following research gaps:

(1) The majority of existing methods concentrate on the convexification of the UC problem with AC power flow constraints. However, the convexified model becomes a comparably intricate mixed-integer quadratically constrained programming problem due to the presence of quadratic branch flow constraints. Only a few methods address the linearization of these quadratic branch flow constraints.

(2) Although numerous studies propose RCI methods for the UC problem, these methods are primarily based on DC flow-constraints and cannot be directly applied to AC flow-constrained UC models. Therefore, a customized RCI method for the UC problem, considering AC network constraints, is currently lacking.

To address the above challenges, this paper proposes a robust unit commitment with customized RCI method under uncertainty of renewable energy sources. The main contributions of this paper are as follows:

(1) This paper presents an AC power flow-constrained robust unit commitment (ACRUC) model to characterize the security range of active and reactive power transmission in the transmission network. This model will enable coordinated optimization of active and reactive power generation scheduling.

(2) This paper also introduces a circular linearization method to fully linearize the quadratic branch flow constraints, transforming them into tractable linear constraints. The original circular feasible domain defined by quadratic constraints will thus be approximated by a polygonal feasible domain, whose approximation error is controllable by the number of linearization segments.

(3) To reduce the model scale, a customized RCI method is proposed, which includes two models (i.e., cold and warm start modes) based on different base case system operating condition for branch loss linearization. This method will remove redundant security constraints by solving a series of relatively simple optimization problems.

2 ACRUC formulation

In this section, in order to obtain actual branch flow and units’ output power accurately, the reactive power output of conventional units, the reactive power demand of loads, and the transmission characteristics of AC power transmission networks are considered. A completely linearized AC power flow model (Yang et al., 2017b) is introduced, which establishes the network constraints of a two-stage robust UC model (Li et al., 2015) are introduced. From the perspective of the entire model, the two-stage robust UC model adaptively adjusts to formulate power system unit commitment plans and generation scheduling plans with better robustness.

2.1 Two-stage robust UC problem formulation with DC flow

The two-stage robust UC model with DC flow constrained is established in this section. The first stage [constraints (4)–(5)] aims to optimize the UC decisions for conventional units, and the second stage [constraints (6)–(11)] optimizes the economic dispatch decisions of all units. From a physical perspective, the second stage explores all scenarios of renewable energy resources and obtains the decision results for the worst case. The first stage then adjusts the UC decisions based on the outcomes from the second stage.

The objective function (1) is the total cost, which includes the first-stage UC cost of conventional units and the second-stage dispatch cost under the worst-case scenario.

The first-stage cost (2) includes the startup cost and shutdown cost for conventional units. The relationship between binary variables is modeled in (4), which ensures the correctness of conventional units’ operation statuses during startup and shutdown periods (Zhang et al., 2017). Constraint (5) describes the minimum up and down time limits for each conventional unit (Yuan et al., 2022).

The second-stage cost (3) includes the dispatch costs of all units. The uncertain parameters in the robust solution are typically set at the upper or lower limits of their uncertainty range (Wu et al., 2008), and the uncertainty budget is commonly employed to mitigate conservative result. The uncertainty set and uncertainty budget are modeled in (6). Constraint (7) represents the maximum and minimum active power output limit for each conventional unit (Cao et al., 2021). Constraint (9) enforces the power output range for renewable units. Constraint (8) imposes ramping-up and ramping-down rate constraints for conventional units. System active power balance is ensured by (10). The nodal phase angle range is defined by (11).

2.1.1 Objective function

$\underset{{\xi }^f\in {\mathbb{F}}^f}{\mathit{min}}{C}^{UC}\left({\xi }^f\right)+\underset{{\stackrel{\sim }{P}}_{g,t}^{NE}\in \mathbb{U},}{\mathit{max}}\underset{{\xi }^s\in {\mathbb{F}}^s\left({\xi }^f,{\stackrel{\sim }{P}}_{g,t}^{NE}\right)}{\mathit{min}}{C}^{ED}\left({\xi }^s,{\stackrel{\sim }{P}}_{g,t}^{NE}\right)(1)$

$C^{UC}\left({\xi }^f\right)={{\displaystyle \sum }}_{g\in {\mathrm{\Omega }}_{TG}}{{\displaystyle \sum }}_{t\in \mathcal{T}}\left(S{U}_g^T{u}_{g,t}^T+S{D}_g^T{d}_{g,t}^T\right)(2)$

$\begin{array}{ll}\hfill C^{ED}\left({\xi }^s,{\stackrel{\sim }{P}}_{g,t}^{NE}\right)& ={{\displaystyle \sum }}_{g\in {\mathrm{\Omega }}_{TG}}{{\displaystyle \sum }}_{t\in \mathcal{T}}\left[C_g^{T,F}\left(p_{g,t}^T-P_g^T{x}_g^T\right)+C_g^{T,NL}{x}_g^T\right]\hfill \\ \hfill & +{{\displaystyle \sum }}_{g\in {\mathrm{\Omega }}_{NEG}}{{\displaystyle \sum }}_{t\in \mathcal{T}}{\beta }_g^{NE}\left({\stackrel{\sim }{P}}_{g,t}^{NE}-p_{g,t}^{NE}\right)\hfill \end{array}(3)$

2.1.2 Constraints of first stage

$\left\{\begin{array}{l}{x}_{g,t}^T-x_{g,t-1}^T=u_{g,t}^T-d_{g,t}^T\\ u_{g,t}^T+d_{g,t}^T⩽1\end{array}\right.(4)$

$\left\{\begin{array}{l}{\displaystyle {\sum }_{j=t}^{\mathit{min}\left\{t+M{U}_g^T-1,T\right\}}}{x}_{g,j}^T⩾\mathit{min}\left\{M{U}_g^T,T-t+1\right\}{u}_{g,t}^T\\ {\displaystyle {\sum }_{j=t}^{\mathit{min}\left\{t+M{D}_g^T-1,T\right\}}}\left(1-x_{g,t}^T\right)⩾\mathit{min}\left\{M{D}_g^T,T-t+1\right\}{d}_{g,t}^T\end{array}\right.(5)$

2.1.3 Conventional constraints of second stage

$\left\{\begin{array}{l}\begin{array}{c}{\stackrel{\sim }{P}}_{g,t}^{NE}=P_{g,t}^{NE,0}+\left({\overline{P}}_{g,t}^{NE}-P_{g,t}^{NE,0}\right)z_{g,t}^{NE+}\\ +\left(P_{g,t}^{NE,0}-P_{-g,t}^{NE}\right)z_{g,t}^{NE-}\end{array}\\ {{\displaystyle \sum }}_{t\in \mathcal{T}}\left(z_{g,t}^{NE+}+z_{g,t}^{NE-}\right)⩽{\Gamma }_g\\ z_{g,t}^{NE}=z_{g,t}^{NE+}+z_{g,t}^{NE-}\end{array}\right.;z_{g,t}^{NE}\in \left\{\mathrm{0,1}\right\}(6)$

$-P_{-g}^T{x}_{g,t}^T\le p_{g,t}^T\le {\overline{P}}_g^T{x}_{g,t}^T(7)$

$\left\{\begin{array}{c}-p_{g,t}^T+p_{g,t-1}^T+\left(P_g^T-R{U}_g^T\right)u_{g,t}^T⩾-R{U}_g^T\\ p_{g,t}^T-p_{g,t-1}^T+\left(P_g^T-R{D}_g^T\right)d_{g,t}^T⩾-R{D}_g^T\end{array}\right.(8)$

${\stackrel{\sim }{P}}_{g,t}^{NE}-p_{g,t}^{NE}⩾0(9)$

${{\displaystyle \sum }}_{g\in {\mathrm{\Omega }}_{TG\left(i\right)}}{p}_{g,t}^T+{{\displaystyle \sum }}_{g\in {\mathrm{\Omega }}_{NEG\left(i\right)}}{p}_{g,t}^{NE}-{{\displaystyle \sum }}_{\left(i,j\right)\in {\mathrm{\Omega }}_{L\left(i\right)}}{f}_{ij,t}^{P,A}={{\displaystyle \sum }}_{d\in {\mathrm{\Omega }}_{D\left(i\right)}}{p}_{d,t}^D(10)$

$\left\{\begin{array}{l}-\pi \le {\theta }_{i,t}\le \pi \\ {\theta }_{s,t}=0\end{array}\right.(11)$

2.2 AC network flow formulation and its convexification

1) Linearized branch flow model with $Q$ and $v$

The original nonlinear power flow equations are expressed as follows:

$\begin{array}{ll}\hfill f_{ij,t}^{\mathrm{\hspace{0.17em}P}}& =g_{ij}\left(v_{i,t}^2-v_{i,t}{v}_{j,t}{\mathit{cos}\theta }_{ij,t}\right)-b_{ij}{v}_{i,t}{v}_{j,t}{\mathit{sin}\theta }_{ij,t}\hfill \\ \hfill & :\forall l\in {\mathrm{\Omega }}_L,\left(i,j\right)=\left(B^{+}\left(l\right),B^{-}\left(l\right)\right),t\in \mathcal{T}\hfill \end{array}(12)$

$\begin{array}{ll}\hfill f_{ij,t}^{\mathrm{\hspace{0.17em}Q}}& =-b_{ij}\left(v_{i,t}^2-v_{i,t}{v}_{j,t}{\mathit{cos}\theta }_{ij,t}\right)-g_{ij}{v}_{i,t}{v}_{j,t}{\mathit{sin}\theta }_{ij,t}\hfill \\ \hfill & :\forall l\in {\mathrm{\Omega }}_L,\left(i,j\right)=\left(B^{+}\left(l\right),B^{-}\left(l\right)\right),t\in \mathcal{T}\hfill \end{array}(13)$

The phase angle ${\theta }_{i,t}$ and the square of the magnitude $v_{i,t}^2$ of the nodal voltage are chosen as independent variables to fully linearize the AC power flow model, where the auxiliary variable $v_{ij,t}^s$ is defined as follows:

$v_{ij,t}^s:={\left(v_{i,t}-v_{j,t}\right)}^2(14)$

A Taylor second-order expansion for the sine and cosine terms of ${\theta }_{ij,t}$, and an approximation and mathematical transformation for the nonlinear terms of $v_{i,t}$ are used (Yang et al., 2016):

$\left\{\begin{array}{l}{\mathit{sin}\theta }_{ij,t}\approx {\theta }_{ij,t}\\ {\mathit{cos}\theta }_{ij,t}\approx 1-\frac{{\theta }_{ij,t}^s}{2}\\ \begin{array}{l}{v}_{i,t}=v_{j,t}\approx 1\\ v_{i,t}^s-v_{i,t}{v}_{j,t}=\frac{v_{ij,t}^s}{2}+\frac{v_{i,t}^s-v_{j,t}^s}{2}\end{array}\end{array}\right.(15)$

After above analysis, the linearized AC power flow model can be obtained as follows:

$\begin{array}{l}\left\{\begin{array}{c}{f}_{ij,t}^{P,A}=g_{ij}\frac{v_{i,t}^s-v_{j,t}^s}{2}-b_{ij}{\theta }_{ij,t}+f_{l,t}^{P,L}\\ f_{ij,t}^{Q,A}=-b_{ij}\frac{v_{i,t}^s-v_{j,t}^s}{2}-g_{ij}{\theta }_{ij,t}+f_{l,t}^{Q,L}\end{array}\right.\\ :\forall l\in {\mathrm{\Omega }}_L,\left(i,j\right)=\left(B^{+}\left(l\right),B^{-}\left(l\right)\right),t\in \mathcal{T}\end{array}(16)$

The branch losses $f_{l,t}^{P,L}$ and $f_{l,t}^{Q,L}$ in (16) can be further linearized through an approximation process and a first-order Taylor expansion. The detailed derivation is provided in Yang et al. (2017b), and the final expression is as follows:

$\begin{array}{l}\left\{\begin{array}{l}{f}_{l,t}^{P,L}=g_{ij}{\theta }_{ij,t}^0{\theta }_{ij,t}+g_{ij}\frac{v_{i,t}^0-v_{j,t}^0}{v_{i,t}^0+v_{j,t}^0}\left(v_{i,t}^s-v_{j,t}^s\right)\\ -\frac{g_{ij}}{2}\left({\theta }_{ij,t}^{s,0}+v_{ij,t}^{s,0}\right)\\ \begin{array}{l}{f}_{l,t}^{Q,L}=-b_{ij}{\theta }_{ij,t}^0{\theta }_{ij,t}-b_{ij}\frac{v_{i,t}^0-v_{j,t}^0}{v_{i,t}^0+v_{j,t}^0}\left(v_{i,t}^s-v_{j,t}^s\right)\\ +\frac{b_{ij}}{2}\left({\theta }_{ij,t}^{s,0}+v_{ij,t}^{s,0}\right)\end{array}\end{array}\right.\\ :\forall l\in {\mathrm{\Omega }}_L,\left(i,j\right)=\left(B^{+}\left(l\right),B^{-}\left(l\right)\right),t\in \mathcal{T}\end{array}(17)$

2) Other network constraints with $Q$ and $v$ under AC power flow linearization

With the introduction of the linearized AC power flow model, the operational constraints of the second stage must also consider the reactive power output range of conventional units (18), the balance of system reactive power (19), nodal voltage magnitude range (20), and the limits of branch flow (21).

$-Q_g^T{x}_{g,t}^T\le q_{g,t}^T\le Q_g^T{x}_{g,t}^T;\forall g\in {\mathrm{\Omega }}_{TG},t\in \mathcal{T}(18)$

${{\displaystyle \sum }}_{g\in {\mathrm{\Omega }}_{TG\left(i\right)}}{q}_{g,t}^T-{{\displaystyle \sum }}_{\left(i,j\right)\in {\mathrm{\Omega }}_{L\left(i\right)}}{f}_{ij,t}^{Q,A}={{\displaystyle \sum }}_{d\in {\mathrm{\Omega }}_{D\left(i\right)}}{q}_{d,t}^D;\forall i\in {\mathrm{\Omega }}_B,t\in \mathcal{T}(19)$

${\left(v_i\right)}^2\le v_{i,t}^s\le {\left({\overline{v}}_i\right)}^2;\forall i\in {\mathrm{\Omega }}_B,t\in \mathcal{T}(20)$

${\left(f_{ij,t}^{P,A}\right)}^2+{\left(f_{ij,t}^{Q,A}\right)}^2⩽{\left({\overline{F}}_l\right)}^2;\forall l\in {\mathrm{\Omega }}_L,\left(i,j\right)=\left(B^{+}\left(l\right),B^{-}\left(l\right)\right),t\in \mathcal{T}(21)$

2.3 Two stage robust UC problem formulation with linearized AC flow

Further, the ACRUC model is formulated, with the objective function defined by Eqs 1–3. The constraints of the first stage include (4)–(11), while the constraints of the second stage include (16)–(17) and (18)–(21).

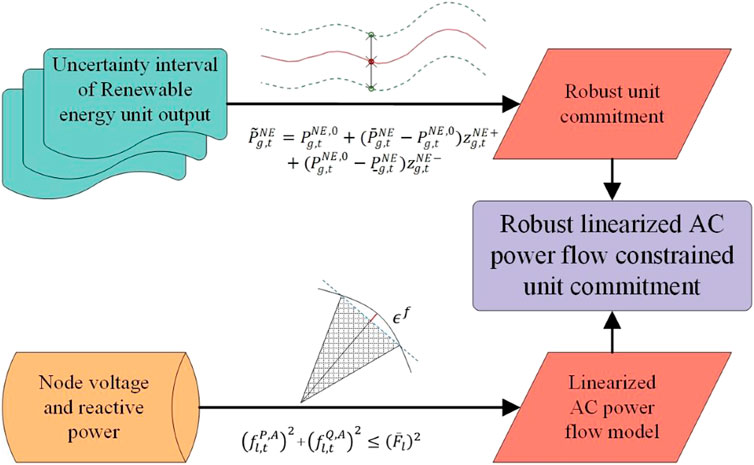
Figure 1 illustrates the proposed model architecture in this paper. Firstly, a robust UC model is employed to fully consider the output power uncertainty of renewable energy units. Then, a linearized AC power flow model is introduced to reflect the changes in nodal voltage and reactive power flow during the system operation. Based on the above, the ACRUC model is established.

FIGURE 1

FIGURE 1. Framework diagram of RACUC model and redundancy constraint identification algorithm.

However, direct solving of the ACRUC model is difficult due to the existence of stochastic variables. Therefore, this paper adopts the C&CG method (Zeng and Zhao, 2013) to transform the first stage into the master problem and the second stage into the feasibility subproblem under uncertain scenarios for iterative solving. The subproblem incorporates constraints and decision variables for worst-case scenarios into the master problem based on the results obtained from solving the master problem. In addition, the outer approximation method (Bertsimas et al., 2012) is used to handle the economic dispatch subproblem during the solving process.

3 Solution methodology

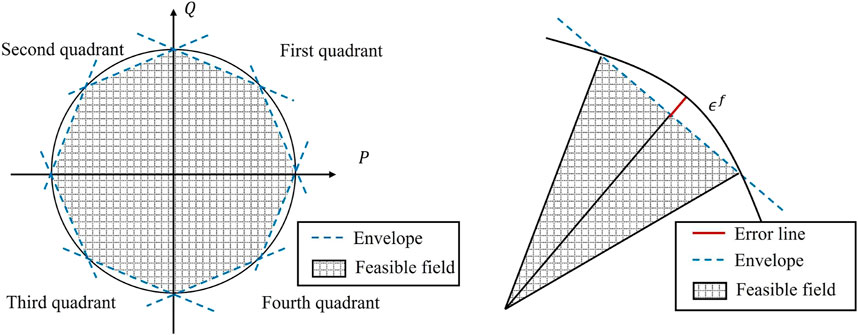
3.1 A circular linearization method for branch flow limits constraint

Note that the branch flow limits (21) is a quadratic constraint. Directly adding them to the UC model will make it a mixed-integer quadratic programming problem, that is, difficult to solve and yields poor scalability. However, it can be observed that these constraints essentially describe a security operating region of AC branches on the P-Q complex plane. Therefore, they can be approximated by circular linearization instead of quadratic constraints to obtain a fully linearized AC network constraint. Furthermore, the branch limits (21) can be approximated by a group of linear constraints as follows:

$\left\{\begin{array}{l}-K_{l,m}^f{f}_{ij,t}^{P,A}-f_{ij,t}^{Q,A}⩾B_{l,m}^f\\ K_{l,M^f+1-m}^f{f}_{ij,t}^{P,A}-f_{ij,t}^{Q,A}⩾B_{l,M^f+1-m}^f\\ K_{l,M^f+1-m}^f{f}_{ij,t}^{P,A}+f_{ij,t}^{Q,A}⩾B_{l,M^f+1-m}^f\\ -K_{l,m}^f{f}_{ij,t}^{P,A}+f_{ij,t}^{Q,A}⩾B_{l,m}^f\end{array}\right.(22)$

As shown in Figure 2, each quadrant is segmented into $M^f$ parts, and there exist errors when applying the circular linearization. The linearization error is quantified by calculating the ratio of the difference between the sector’s area and the triangle’s area to the sector’s area. According to error estimation in (23), increasing the number of linearization segments can effectively reduce the linearization error, making the linearized branch flow constraint a more exact approximation of the original one.

${ϵ}^f\approx 1-\mathit{cos}\frac{\pi }{4M^f}(23)$

FIGURE 2

FIGURE 2. Schematic diagram of AC network constraint linearization.

3.2 RCI method for removing redundant network constraints

Note that the scale of the network constraint Eq 21 is quite large, and it is necessary to add corresponding constraints to each branch at each time period in the scheduling horizon. After linearizing the AC power flow, the number of constraints will also double according to the number of linearization segments. For example, if $M$ linearization segments are required in one quadrant, a single branch at a single time period will have at least $4\times M$ branch flow limit constraints. In a UC model with about $N$ branches and a time scale of 24 h, there will be $96\times M\times N$ such constraints. This brings pressure to the solution efficiency of our problem and may cause the model to fall into the dilemma of exhausting computing resources or unacceptable solution time after several iterations. Furthermore, in the iterative solution process using the C&CG method, the scale of constraints added by sub-problems to the main problem will also increase sharply with the number of iterations.

Inspired by RCI technique under the DC power flow model (Zhai et al., 2010; Yang et al., 2021), this paper proposes a customized RCI method for the linearized AC power flow model. Its main idea is to estimate conservatively branch flow limits in actual operation under given load level, renewable energy prediction results, and uncertainty error by solving multiple relatively simple optimization subproblems. Hence, branch flow limits that will not be overloaded are eliminated.

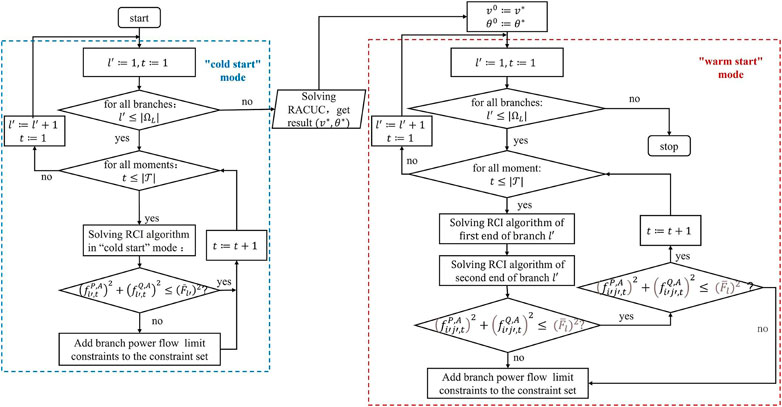
1) Identification method in “cold start” mode

The first step in the “cold start” mode is to identify network constraints to determine the power limits for each branch during each time period. To obtain the power loss for each branch, a Taylor expansion is used based on the base case system operating condition that in the “cold start” mode, in which nodal voltage magnitudes are 1 and nodal voltage phase angles are 0. In this case, the network power loss is zero and the first end branch flow is equal to the second end branch flow, so the two-end branch flow limits do not need to be considered separately. Based on this, the RCI model in “cold start” mode is established, which includes an objective function defined by Eq. 24 and constraints such as system power balance constraints (10) and (19), linearized AC branches flow model (25), branch flow limits (26), conventional units output range (7) and (18), renewable energy units output range (9), nodal voltage phase angle limit (11), and nodal voltage magnitude constraints (20).

$\mathit{max}{\left(f_{l^{\prime },t}^{P,A}\right)}^2+{\left(f_{l^{\prime },t}^{Q,A}\right)}^2(24)$

$\left\{\begin{array}{c}{f}_{l,t}^{P,A}=g_{ij}\frac{v_{i,t}^s-v_{j,t}^s}{2}-b_{ij}{\theta }_{ij,t}\\ f_{l,t}^{Q,A}=-b_{ij}\frac{v_{i,t}^s-v_{j,t}^s}{2}-g_{ij}{\theta }_{ij,t}\end{array}\right.(25)$

${\left(f_{l,t}^{P,A}\right)}^2+{\left(f_{l,t}^{Q,A}\right)}^2⩽{\left({\overline{F}}_l\right)}^2:\forall l\in {\mathrm{\Omega }}_L\backslash \left\{l^{\prime }\right\}(26)$

Since the constraints set of RCI model is a subset of the constraints set of the ACRUC model, its feasible region is greater than or equal to that of the ACRUC model. This ensures that the maximum value of the calculated branch flow is greater than or equal to the actual maximum value of the branch flow during operation. Therefore, if the RCI method finds that the constraint is not violated, then this constraint must be redundant in actual operation.

Assuming that $\left(f_{l^{\prime },t}^{P,A*},f_{l^{\prime },t}^{Q,A*}\right)$ is the optimal solution of the identification method problem under the “cold start” mode, if there is no feasible solution, no optimal solution, or the branch flow limit is exceeded, i.e., if ${\left(f_{l^{\prime },t}^{P,A*}\right)}^2+{\left(f_{l^{\prime },t}^{Q,A*}\right)}^2>{\left({\overline{F}}_{l^{\prime }}\right)}^2$, it is necessary to add a branch flow limit constraint for this branch at this time period. Otherwise, the constraint can be considered redundant and ignored without affecting the model solution.

2) Identification method in “warm start” mode

The identification model for the “warm start” mode is slightly different from that of the “cold start” mode. In the “warm start” mode, the base case system operating condition for branch power loss in the Taylor expansion is obtained from the nodal voltage magnitudes and voltage phase angles calculated by ACRUC with RCI method in the “cold start” mode. In this case, the network power loss on the branch cannot be ignored, resulting in different power flows at the first end and second end of the branch. Hence, the identification method must be carried out separately for the first end and second end of the branch. The objective function is expressed by Eq. 27 when identifying the first end branch flow, and by Eq. 28 when identifying the second end branch flow. The constraints for two-end of the branch flow include system power balance constraints (10) and (19), linearized AC branch flow model (16)–(17), conventional units output range (7) and (18), renewable energy units output range (9), nodal voltage phase angle range (11), and nodal voltage magnitude range (20). The branch flow limit constraint is expressed by Eqs. 29, 31 for the first end branch flow identification and Eqs. 29, 30 for the second end branch flow identification.

$\mathit{max}{\left(f_{i^{\prime }{j}^{\prime },t}^{P,A}\right)}^2+{\left(f_{i^{\prime }{j}^{\prime },t}^{Q,A}\right)}^2(27)$

$\mathit{max}{\left(f_{{j^{\prime }i}^{\prime },t}^{P,A}\right)}^2+{\left(f_{{j^{\prime }i}^{\prime },t}^{Q,A}\right)}^2(28)$

$\begin{array}{l}\left\{\begin{array}{c}{\left(f_{ij,t}^{P,A}\right)}^2+{\left(f_{ij,t}^{Q,A}\right)}^2⩽{\left({\overline{F}}_l\right)}^2\\ {\left(f_{ji,t}^{P,A}\right)}^2+{\left(f_{ji,t}^{Q,A}\right)}^2⩽{\left({\overline{F}}_l\right)}^2\end{array}\right.;\\ \forall l\in {\mathrm{\Omega }}_L⧵\left\{l^{\prime }\right\},\left(i,j\right)=\left(B^{+}\left(l\right),B^{-}\left(l\right)\right)\end{array}(29)$

${\left(f_{i^{\prime }{j}^{\prime },t}^{P,A}\right)}^2+{\left(f_{i^{\prime }{j}^{\prime },t}^{Q,A}\right)}^2⩽{\left({\overline{F}}_l\right)}^2;\left(i^{\prime }{,j}^{\prime }\right)=\left(B^{+}\left(l^{\prime }\right),B^{-}\left(l^{\prime }\right)\right)(30)$

${\left(f_{j^{\prime }{i}^{\prime },t}^{P,A}\right)}^2+{\left(f_{j^{\prime }{i}^{\prime },t}^{Q,A}\right)}^2⩽{\left({\overline{F}}_l\right)}^2;\left(i^{\prime }{,j}^{\prime }\right)=\left(B^{+}\left(l^{\prime }\right),B^{-}\left(l^{\prime }\right)\right)(31)$

Assuming that $\left(f_{i^{\prime }{j}^{\prime },t}^{P,A^{*}},f_{i^{\prime }{j}^{\prime },t}^{Q,A^{*}}\right)$ is the optimal solution for the RCI model of the first end branch flow, and $\left(f_{{j^{\prime }i}^{\prime },t}^{P,A^{*}},f_{{j^{\prime }i}^{\prime },t}^{Q,A^{*}}\right)$ is the optimal solution for the RCI model of the second end branch flow. If either of the RCI models for the two-end branch flows has no feasible solution, no optimal upper bound, or exceeds the branch flow limit, it is necessary to add a branch flow limit constraint for this branch at time period $t$. Otherwise, the constraint is considered as redundant and can be ignored without affecting the solution result of the model.

3) The process of proposed RCI method

The computational process of the RCI method under the linearized AC power flow model is shown in Figure 3. The linearized AC power flow network constraints on each branch at each time period are split into RCI sub-problems, and the calculations are completed using solvers separately. Then, the necessary branch flow limit constraints are added to the constraint set of the ACRUC model.

FIGURE 3

FIGURE 3. Framework diagram of RCI algorithm.

The RCI method based on linearized AC power flow can effectively reduce the scale of the constraints. In addition, since the models based on the RCI method for each branch and each time period are decoupled from each other, the solution can be independent and parallel. Therefore, the method has good potential for parallel computing and can fully utilize the computing resources of hardware devices.

4 Case study

In this section, the effectiveness of our proposed ACRUC model and customized RCI method is verified by a group of numerical experiments of modified NERL-118 test system. The parameters of elements are adopted from Pena et al. (2017), and detailed settings are introduced in IV-A. All calculations are performed by Gurobi 9.5.0 API for C++ on an Intel Core I5 8500 3 GHz processor.

4.1 The modified NERL-118 test case

The modified NERL-118 system includes 118 buses, 186 branches, and 54 thermal units. In addition, there are five different capacity wind farms located at bus 24, 27, 31, 82, and 100, and 14 different capacity photovoltaic plants located at bus 15, 18, 19, 32, 54, 55, 69, 76, 92, 100, 104, 105, 110, and 112. The case has large number of buses and branches, with renewable energy sources accounting for 38.52% of the total installed capacity. The complexity of the UC model is relatively high, which makes it difficult to solve. Therefore, to reduce the complexity of the robust UC model, the test system has merged the same type of renewable energy sources on same bus, treating them as equivalent renewable energy plants.

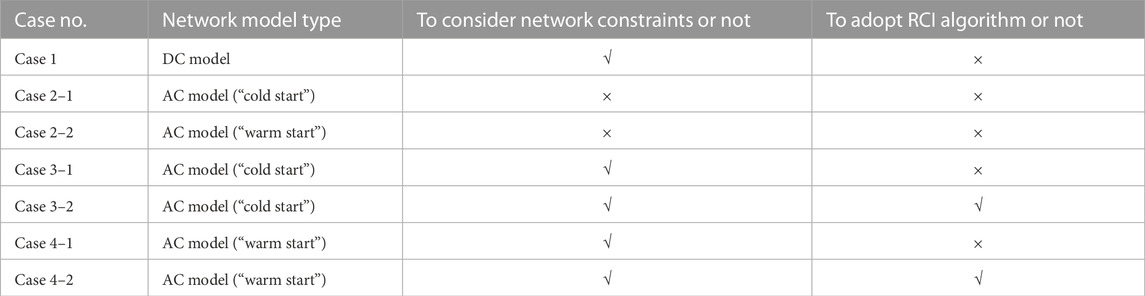
This paper presents case studies to analyze the rationality and effectiveness of linearized AC power flow network constraints by comparing the operation statuses of thermal units, the load conditions of overload branches, and the system operational cost. Additionally, the effectiveness of the proposed RCI method is verified by comparing the problem scale and solving efficiency with and without RCI method. The case study designed in this section is presented in Table 1.

TABLE 1

TABLE 1. Test system case scenario setting.

4.2 Analysis of the effectiveness of linearized AC power flow network constraints and RCI method

The number of segments used to linearize the network constraints is set to 6. The renewable energy forecasting error is assumed to be 30%, and the uncertainty budget for renewable energy units ${\Gamma }_g$ are 6, 12, and 24. The comparison results between Case 2–1 and Case 3–2, as well as between Case 2–2 and Case 4–2 (as shown in Table 2; Table 3), demonstrate that the proposed RCI method correctly selects redundant network constraints. In both “cold start” mode and “warm start” mode, constraints related to branches that may exceed the power transmission security limit during operation are retained, effectively limiting the transmission power of those branches within the security range.

TABLE 2

TABLE 2. Comparison of maximum load ratio of overloaded branches in “cold start” mode.

TABLE 3

TABLE 3. Comparison of maximum load ratio of overloaded lines in “warm start” mode.

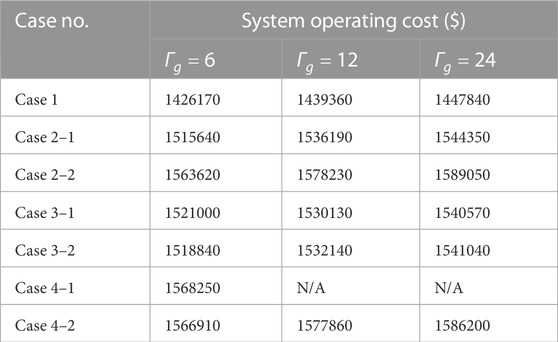
The comparison results of the system operating cost are shown in Table 4. Comparing Case 3–1 and Case 3–2, it can be observed that in the “cold start” mode, when ${\Gamma }_g$ is set to 6, 12, and 24, the relative errors of operating costs with and without RCI method are 0.14%, 0.13%, and 0.03%, respectively. Comparing Case 4–1 and Case 4–2, it can be observed that in the “warm start” mode, when ${\Gamma }_g$ is set to 6, the relative error of operating costs with and without RCI method is 0.09%. Therefore, the RCI has little effect on the optimal value of the objective function, ensuring its correctness.

TABLE 4

TABLE 4. Comparison of operating cost of thermal units.

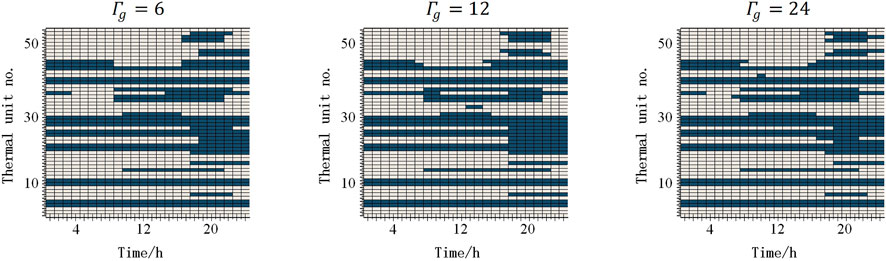
Figure 4 illustrate UC solutions of conventional units for Case 1 under different renewable energy uncertainty budgets (${\Gamma }_g$ is set to 6, 12, and 24). The comparison demonstrates that, as the level of renewable energy uncertainty increases, the unit commitment of conventional units become more frequent. This is mainly because that the generation scheduling is needed to ensure sufficient system flexibility to cope with high uncertainty.

FIGURE 4

FIGURE 4. Comparison of thermal units’ operation statuses of Case 1.

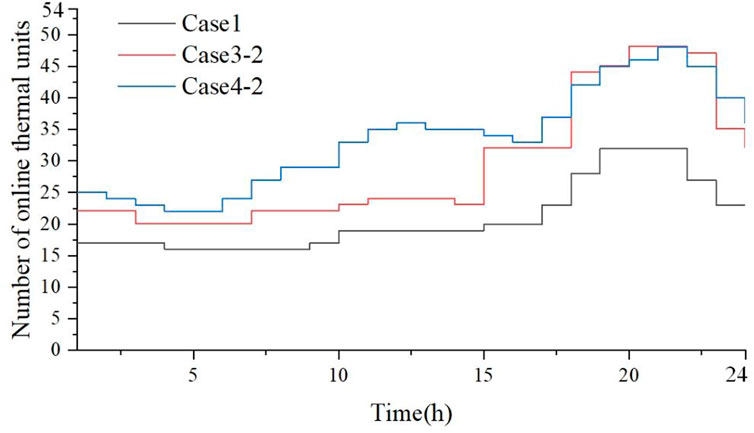
Figure 5 illustrates the number of online thermal units for Case 1, Case 3–2 and Case 4–2 under the same uncertainty budget of renewable energy (${\Gamma }_g$ is set to 6). The comparison reveals that, unlike Case 3–2 and Case 4–2, Case 1 uses a DC power flow model and fails to activate enough thermal units to mitigate the impact of reactive power flow and voltage changes. However, Case 4–2 considers both linearized AC power flow and network losses, requiring the activation of a larger number of thermal units and demanding a higher level of capacity adequacy for the dispatchable resources.

FIGURE 5

FIGURE 5. Number of online thermal units between different cases.

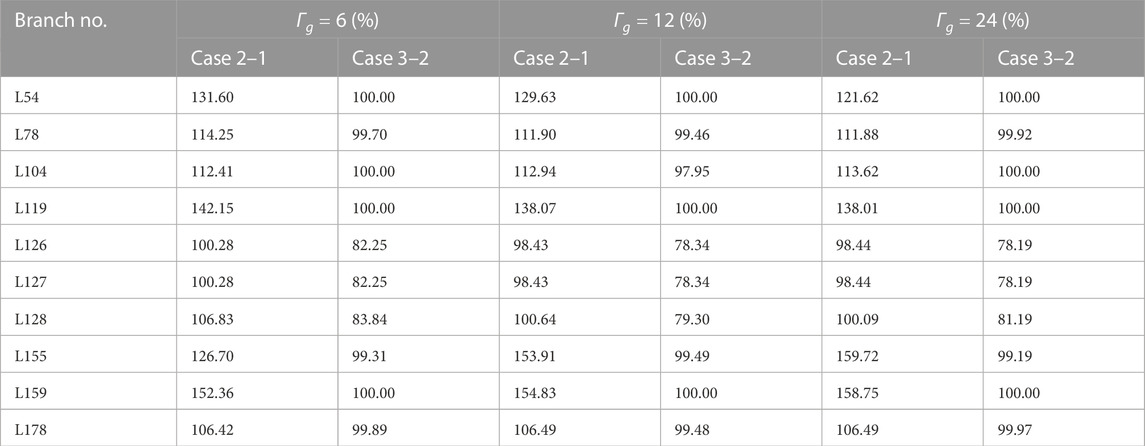
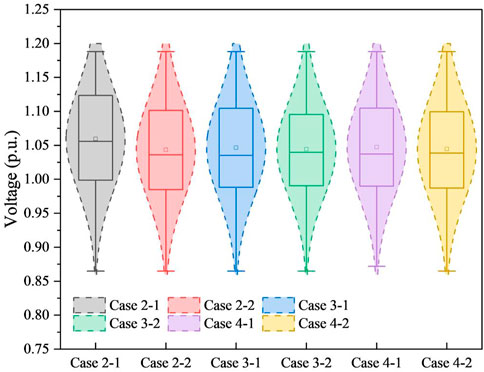
Figure 6 illustrates the distribution of voltage magnitude for Case 2–1, Case 2–2, Case 3–1, Case 3–2, Case 4–1, and Case 4–2. These cases all adopt the AC power flow model, which reflects the variation range and distribution of the system’s voltages. In contrast, the voltage is assumed to be constant in the DC power flow model. Therefore, the AC power flow model more accurately reflects the operational conditions of the system. Furthermore, by comparing Case 3–1 and Case 3–2, as well as Case 4–1 and Case 4–2 (${\Gamma }_g$ is set to 6), we observe that the voltage distributions obtained with and without considering RCI are very similar. This finding further validates the correctness of the RCI method.

FIGURE 6

FIGURE 6. System’s voltage magnitude distribution in the scheduling horizon of different cases.

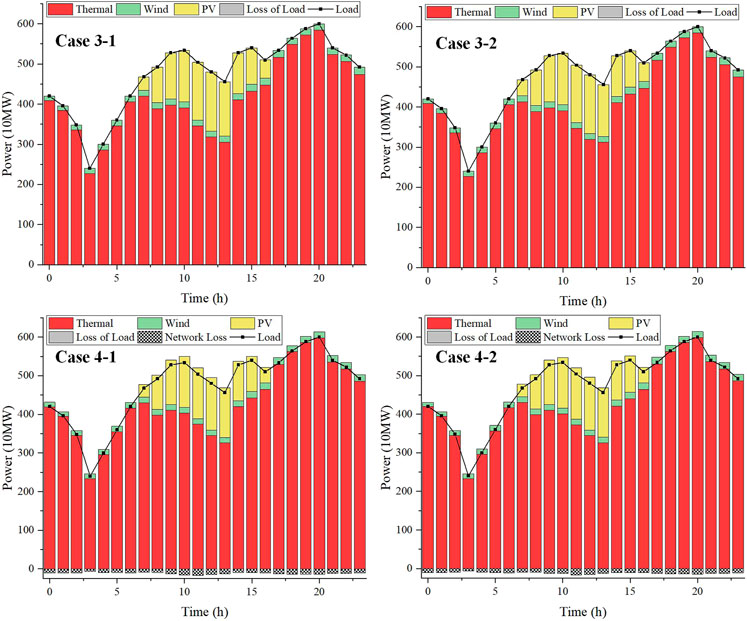
The dispatch results of all units for Case 3–1, Case 3–2, Case 4–1 and Case 4–2 (${\Gamma }_g$ is set to 6) are shown in Figure 7. By comparing Case 3–1 and Case 4–1, as well as Case 3–2 and Case 4–2, we observe that the warm-start AC model takes network losses into account. Therefore, the warm-start AC model provides a more accurate portrayal of the system’s operational conditions compared to the cold-start AC model.

FIGURE 7

FIGURE 7. Unit commitment decisions in the scheduling horizon of different cases.

4.3 Analysis of the efficiency of RCI method solution

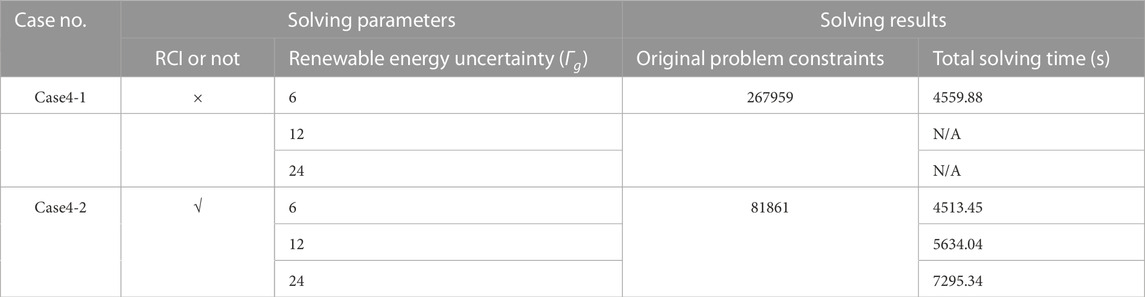
Table 5 and Table 6 demonstrate the improvement of the RCI method in both “cold start” and “warm start” modes. The term “original problem constraints” refers to the sum of the constraints in the robust model first stage and second stage. “Total solving time” refers to the total time spent on RCI and model solving. “N/A” indicates that the model was considered unsolvable due to excessive computational time in the solving environment described in the article. It can be seen that, under the premise of ensuring correctness, the identification method can effectively improve the efficiency of model solving.

TABLE 5

TABLE 5. Comparison of result with and without RCI in “cold start” mode.

TABLE 6

TABLE 6. Comparison of result with and without RCI in “warm start” mode.

As shown in Table 5, the “cold start” mode reduced the original problem constraints by 60.58% before and after using the RCI method. When the renewable energy uncertainty budgets ${\Gamma }_g$ are set to 6, 12, and 24, using the RCI method in the “cold start” mode can reduce the solving time by 70.54%, 38.1%, and 33.87%, respectively. This demonstrates that when the power system has a large network scale, the RCI method can significantly reduce the number of constraints and the original problem’s size, and improve the solving efficiency.

The effect of solution efficiency improvement is more significant in the “warm start” mode when the renewable energy uncertainty budgets ${\Gamma }_g$ is set to 6, as shown in Table 6, where the size of the original problem constraints is reduced by 69.45%, and there is also a corresponding improvement in the solving time.

5 Conclusion

To cope with the risks associated with a high proportion of renewable energy resources in power system operation, this paper analyzes the uncertainty factors and transmission security in system. A two-stage robust UC model and a convexified AC power flow model are used to develop an ACRUC model. In the ACRUC model, branch flow limit constraints are linearized using a circular linearization method. To overcome the difficulties in solving the large-scale branch flow limit constraints and the model, this paper proposes a customized RCI method for the linearized ACRUC model.

The computational results from the improved NERL-118 test system demonstrate that the AC power flow model imposes higher requirements for system reserve capacity and flexibility compared to the DC power flow network constraints. This is particularly significant in response to increasing renewable energy uncertainty. Additionally, the results show that the original problem constraints are reduced by 60.58% and 69.45% in the “cold start” and “warm start” modes, respectively. These reductions achieve the goal of reducing solving difficulty and improving efficiency.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

ZL contributed to the material organization and writing. HY contributed to the simulation. PW contributed to review and editing. CG contributed to the model and method. KW and YH offered financial support. All authors contributed to the article and approved the submitted version.

Funding

The authors declare that this study received funding from the Science and Technology Project of “Theory and method of coordinated provincial transmission and energy storage expansion planning conducive to low-carbon targets (520533220004)”, State Grid Shanxi Electric Power Company. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

Author PW, KW, and YH were employed by the company Economic and Technological Research Institute State Grid Shanxi Electric Power Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ardakani, A. J., and Bouffard, F. (2014). Acceleration of umbrella constraint discovery in generation scheduling problems. IEEE Trans. Power Syst. 30, 2100–2109. doi:10.1109/tpwrs.2014.2352318

CrossRef Full Text | Google Scholar

Ben-Tal, A., and Nemirovski, A. (1998). Robust convex optimization. Math. Oper. Res. 23, 769–805. doi:10.1287/moor.23.4.769

CrossRef Full Text | Google Scholar

Ben-Tal, A., and Nemirovski, A. (2000). Robust solutions of linear programming problems contaminated with uncertain data. Math. Program 88, 411–424. doi:10.1007/pl00011380

CrossRef Full Text | Google Scholar

Ben-Tal, A., and Nemirovski, A. (1999). Robust solutions of uncertain linear programs. Oper. Res. Lett. 25, 1–13. doi:10.1016/s0167-6377(99)00016-4

CrossRef Full Text | Google Scholar

Bertsimas, D., Litvinov, E., Sun, X. A., Zhao, J., and Zheng, T. (2012). Adaptive robust optimization for the security constrained unit commitment problem. IEEE Trans. Power Syst. 28, 52–63. doi:10.1109/tpwrs.2012.2205021

CrossRef Full Text | Google Scholar

Cao, X., Wang, J., and Zeng, B. (2021). A study on the strong duality of second-order conic relaxation of AC optimal power flow in radial networks. IEEE Trans. Power Syst. 37, 443–455. doi:10.1109/tpwrs.2021.3087639

CrossRef Full Text | Google Scholar

Castillo, A., Laird, C., Silva-Monroy, C. A., Watson, J. P., and O’Neill, R. P. (2016). The unit commitment problem with AC optimal power flow constraints. IEEE Trans. Power Syst. 31, 4853–4866. doi:10.1109/tpwrs.2015.2511010

CrossRef Full Text | Google Scholar

Castillo, A., Lipka, P., Watson, J. P., Oren, S. S., and O'Neill, R. P. (2015). A successive linear programming approach to solving the IV-ACOPF. IEEE Trans. Power Syst. 31, 2752–2763. doi:10.1109/tpwrs.2015.2487042

CrossRef Full Text | Google Scholar

Chen, Y., Casto, A., Wang, F., Wang, Q., Wang, X., and Wan, J. (2016). Improving large scale day-ahead security constrained unit commitment performance. IEEE Trans. Power Syst. 31, 4732–4743. doi:10.1109/tpwrs.2016.2530811

CrossRef Full Text | Google Scholar

Cobos, N. G., Arroyo, J. M., Alguacil, N., and Street, A. (2018). Robust energy and reserve scheduling under wind uncertainty considering fast-acting generators. IEEE Trans. Sustain Energy 10, 2142–2151. doi:10.1109/tste.2018.2880919

CrossRef Full Text | Google Scholar

Ding, T., Qu, M., Bai, J., Jia, W., Wu, J., He, Y., et al. (2020). Fast identifying redundant security constraints in SCUC in the presence of uncertainties. IET Gener. Transm. Distrib. 14, 2441–2449. doi:10.1049/iet-gtd.2019.1275

CrossRef Full Text | Google Scholar

Han, X., Li, Y., Nie, L., Huang, X., Deng, Y., Yan, J., et al. (2023). Comparative life cycle greenhouse gas emissions assessment of battery energy storage technologies for grid applications. J. Clean. Prod. 392, 136251. doi:10.1016/j.jclepro.2023.136251

CrossRef Full Text | Google Scholar

Hua, B., Bie, Z., Liu, C., Li, G., and Wang, X. (2013). Eliminating redundant line flow constraints in composite system reliability evaluation. IEEE Trans. Power Syst. 28, 3490–3498. doi:10.1109/tpwrs.2013.2248762

CrossRef Full Text | Google Scholar

Jiang, R., Wang, J., and Guan, Y. (2011). Robust unit commitment with wind power and pumped storage hydro. IEEE Trans. Power Syst. 27, 800–810. doi:10.1109/tpwrs.2011.2169817

CrossRef Full Text | Google Scholar

Lavaei, J., and Low, S. H. (2011). Zero duality gap in optimal power flow problem. IEEE Trans. Power Syst. 27, 92–107. doi:10.1109/tpwrs.2011.2160974

CrossRef Full Text | Google Scholar

Lehmann, K., Grastien, A., and Van Hentenryck, P. (2015). AC-feasibility on tree networks is NP-hard. IEEE Trans. Power Syst. 31, 798–801. doi:10.1109/tpwrs.2015.2407363

CrossRef Full Text | Google Scholar

Li, Z., Shahidehpour, M., Wu, W., Zeng, B., Zhang, B., and Zheng, W. (2015). Decentralized multiarea robust generation unit and tie-line scheduling under wind power uncertainty. IEEE Trans. Sustain Energy 6, 1377–1388. doi:10.1109/tste.2015.2437273

CrossRef Full Text | Google Scholar

Lorca, A., and Sun, X. A. (2017). The adaptive robust multi-period alternating current optimal power flow problem. IEEE Trans. Power Syst. 33, 1993–2003. doi:10.1109/tpwrs.2017.2743348

CrossRef Full Text | Google Scholar

Nasri, A., Kazempour, S. J., Conejo, A. J., and Ghandhari, M. (2015). Network-constrained AC unit commitment under uncertainty: A benders’ decomposition approach. IEEE Trans. Power Syst. 31, 412–422. doi:10.1109/tpwrs.2015.2409198

CrossRef Full Text | Google Scholar

Pena, I., Martinez-Anido, C. B., and Hodge, B. M. (2017). An extended IEEE 118-bus test system with high renewable penetration. IEEE Trans. Power Syst. 33, 281–289. doi:10.1109/tpwrs.2017.2695963

CrossRef Full Text | Google Scholar

Šepetanc, K., and Pandžić, H. (2020). Convex polar second-order taylor approximation of AC power flows: A unit commitment study. IEEE Trans. Power Syst. 36, 3585–3594. doi:10.1109/tpwrs.2020.3046970

CrossRef Full Text | Google Scholar

Wang, H., Murillo-Sanchez, C. E., Zimmerman, R. D., and Thomas, R. J. (2007). On computational issues of market-based optimal power flow. IEEE Trans. Power Syst. 22, 1185–1193. doi:10.1109/tpwrs.2007.901301

CrossRef Full Text | Google Scholar

Wang, R., Ma, D., Li, M. J., Sun, Q., Zhang, H., and Wang, P. (2022a). Accurate current sharing and voltage regulation in hybrid wind/solar systems: An adaptive dynamic programming approach. IEEE Trans. Consum. Electron. 68, 261–272. doi:10.1109/tce.2022.3181105

CrossRef Full Text | Google Scholar

Wang, R., Sun, Q., Sun, C., Zhang, H., Gui, Y., and Wang, P. (2021). Vehicle-vehicle energy interaction converter of electric vehicles: A disturbance observer based sliding mode control algorithm. IEEE Trans. Veh. Technol. 70, 9910–9921. doi:10.1109/tvt.2021.3105433

CrossRef Full Text | Google Scholar

Wang, S., Zhao, C., Fan, L., and Bo, R. (2022b). Distributionally robust unit commitment with flexible generation resources considering renewable energy uncertainty. IEEE Trans. Power Syst. 37, 4179–4190. doi:10.1109/tpwrs.2022.3149506

CrossRef Full Text | Google Scholar

Wang, X. F., Song, Y., and Irving, M. (2010). Modern power systems analysis. Berlin: Springer Science & Business Media.

Google Scholar

Wen, Y., Guo, C., Pandžić, H., and Kirschen, D. S. (2015). Enhanced security-constrained unit commitment with emerging utility-scale energy storage. IEEE Trans. Power Syst. 31, 652–662. doi:10.1109/tpwrs.2015.2407054

CrossRef Full Text | Google Scholar

Wood, A. J., Wollenberg, B. F., and Sheblé, G. B. (2013). Power generation, operation, and control. New Jersey: John Wiley & Sons.

Google Scholar

Wu, P., Cheng, H., and Xing, J. (2008). The interval minimum load cutting problem in the process of transmission network expansion planning considering uncertainty in demand. IEEE Trans. Power Syst. 23, 1497–1506. doi:10.1109/tpwrs.2008.922573

CrossRef Full Text | Google Scholar

Yang, Q., Wang, J., Yin, H., and Li, Q. (2021). A fast calculation method for long-term security-constrained unit commitment of large-scale power systems with renewable energy. J. Mod. Power Syst. Clean. Energy. 10, 1127–1137. doi:10.35833/mpce.2021.000155

CrossRef Full Text | Google Scholar

Yang, Z., Bose, A., Zhong, H., Zhang, N., Xia, Q., and Kang, C. (2016). Optimal reactive power dispatch with accurately modeled discrete control devices: A successive linear approximation approach. IEEE Trans. Power Syst. 32, 2435–2444. doi:10.1109/tpwrs.2016.2608178

CrossRef Full Text | Google Scholar

Yang, Z., Zhong, H., Bose, A., Zheng, T., Xia, Q., and Kang, C. (2017a). A linearized OPF model with reactive power and voltage magnitude: A pathway to improve the MW-only DC OPF. IEEE Trans. Power Syst. 33, 1734–1745. doi:10.1109/tpwrs.2017.2718551

CrossRef Full Text | Google Scholar

Yang, Z., Zhong, H., Xia, Q., and Kang, C. (2017b). A novel network model for optimal power flow with reactive power and network losses. Electr. Power Syst. Res. 144, 63–71. doi:10.1016/j.epsr.2016.11.009

CrossRef Full Text | Google Scholar

Ye, H., Wang, J., Ge, Y., Li, J., and Li, Z. (2016). Robust integration of high-level dispatchable renewables in power system operation. IEEE Trans. Sustain Energy 8, 826–835. doi:10.1109/tste.2016.2621136

CrossRef Full Text | Google Scholar

Yuan, Y., Zhang, Y., Wang, J., Liu, Z., and Chen, Z. (2022). Enhanced frequency-constrained unit commitment considering variable-droop frequency control from converter-based generator. IEEE Trans. Power Syst. 38, 1094–1110. doi:10.1109/tpwrs.2022.3170935

CrossRef Full Text | Google Scholar

Zeng, B., and Zhao, L. (2013). Solving two-stage robust optimization problems using a column-and-constraint generation method. Oper. Res. Lett. 41, 457–461. doi:10.1016/j.orl.2013.05.003

CrossRef Full Text | Google Scholar

Zhai, Q., Guan, X., Cheng, J., and Wu, H. (2010). Fast identification of inactive security constraints in SCUC problems. IEEE Trans. Power Syst. 25, 1946–1954. doi:10.1109/tpwrs.2010.2045161

CrossRef Full Text | Google Scholar

Zhang, H., Heydt, G. T., Vittal, V., and Quintero, J. (2013). An improved network model for transmission expansion planning considering reactive power and network losses. IEEE Trans. Power Syst. 28, 3471–3479. doi:10.1109/tpwrs.2013.2250318

CrossRef Full Text | Google Scholar

Zhang, Y., Wang, J., Zeng, B., and Hu, Z. (2017). Chance-constrained two-stage unit commitment under uncertain load and wind power output using bilinear benders decomposition. IEEE Trans. Power Syst. 32, 3637–3647. doi:10.1109/tpwrs.2017.2655078

CrossRef Full Text | Google Scholar

Nomenclature