DC voltage-based virtual synchronous generator scheme for eliminating circulating power of two-stage grid-tied converters

virtual synchronous generators (VSGs) powered by renewable energy sources prefer to have energy storage attached to the DC link with DC–DC converters, emulating the inertia and smoothing the intermittency of renewable generations. This paper proposes a new VSG method for a two-stage converter to eliminate the circulating power among inverters while having external characteristics identical to those of a traditional VSG. In particular, the proposed VSG method uses the inverter, energy storage converter, and DC capacitor together to implement the swing equation. Meanwhile, the method can still achieve strong similarities with synchronous generators in terms of physical structure, control, and mathematical model. Therefore, the stable operation of the proposed VSG is easy to evaluate by the well-developed traditional power system theory. Moreover, the method is developed to be capable of eliminating circulating power among paralleled VSGs. Simulation and experimental results have also verified the effectiveness of the proposed method.

1 Introduction

To solve environmental issues and energy crises, distributed generators (DGs) using renewable energy sources (RESs) have been developing in recent decades. The penetration of DGs/RESs has been growing rapidly, wherein wind, tidal, and photovoltaic energy are the most popular sources because of their cleanness, abundance, and low maintenance cost (Carrasco et al., 2006; Frede et al., 2006; Bevrani et al., 2014).

However, compared to conventional synchronous generators, DG/RES units have either very small or no rotating mass and damping effect, which are important properties of frequency dynamics and stability (Kundur, 1994; Zhong et al., 2011; Ulbig et al., 2014). With the growing penetration level of DGs/RESs, the impact of low inertia and damping on the grid dynamic and stability was even highlighted with the degradation of frequency regulation and stability maintenance, particularly with inverters working in the islanding mode, whose control is far more challenging due to the absence of the main grid as well as its sufficient inertia and damping effect from real synchronous generators (RSGs). In this sense, DGs are required to actively participate in the power regulation of the grid, playing the roles of RSGs. Along with this consideration, the idea of virtual synchronous generators (VSGs) (T. Shintai et al., 2014; Liu et al., 2016; Wu et al., 2016), or virtual synchronous machines (Alipoor et al., 2018), or synchronverters (Zhong et al., 2011; Bevrani et al., 2014), was proposed to mimic not only the damping characteristics of synchronous generators but also their inertia characteristics by applying the swing equation using the appropriate energy storage (ES). Synchronverters, proposed by Zhong et al. (2011), are realized based on the calculation of a detailed model of RSG and controlled to behave identically as an RSG, which inherits the exact characteristics of an RSG but complexes the algorithm, and thusn it requires a high-performance processor. The simpler methods in the work of Chen et al. (2011), Yang et al. (2011), Chen et al. (2012), Hirase et al. (2014), Shintai et al. (2014), Liu et al. (2016), and Wu et al. (2016) consider the essential properties of a RSG, such as swing equations and droop mechanisms, to control the inverters to mimic the external features of an RSG with lower costs. Moreover, Liu et al. (2016) proved that VSGs can be further simplified by a combination of droop control and a first-order lag unit, which provides useful insight into the VSG concept and parameter design (Wu et al., 2016). After all, present VSGs are based on controlling the inverters to inherit the advantages of conventional RSGs, connecting renewable DC sources to the grid like an RSG in terms of inertia and damping property, regardless of the topologies and operation of the DC side.

Several topologies have been proposed for VSG systems. The VSYNC research group implemented a VSG with an energy storage unit connected to a DC link and an inverter with an LCL output filter operating as a current source (K. Visscher et al., 2008; van Wesenbeeck et al., 2009; Vu Van et al., 2010). This method is designed for energy storage to behave as dedicated frequency regulators and is not suitable for RES integration. On the contrary, the Institute of Electrical Power Engineering (IEPE) (Hesse et al., 2009), the research team at Kawasaki Heavy Industries (KHI) (Hirase et al., 2012), and the ISE Laboratory (Sakimoto et al., 2012; Shintai et al., 2012), which are some of the most active research groups in the area, implement VSGs with RESs and ESs connected in parallel to the DC link, which is the widely accepted topology for RES integration in VSG systems.

A VSG with integrated renewable energy sources and an energy storage component is usually a two-stage converter (Bevrani et al., 2014; Shintai et al., 2014; Liu et al., 2016; Wu et al., 2016; Zhu et al., 2017), and the RESs and ESs are usually connected to the DC link through input converters. These controllers are controlled according to the energy sources and control objectives because of the good performance and flexibility of power electronics regulators. Most VSG researchers regard the DC side of primary energy as an ideal voltage source (Shintai et al., 2012; Bevrani et al., 2014), which is realized by controlling the energy storage converter to compensate the intermittency of RESs. Although the method is easy to implement without considering the operation of RESs and the inverter, it requires ESs to have sufficient capacity and operate stably; otherwise, the VSG will be out of order. In addition, two-stage converters have been widely employed for various applications (Carrasco et al., 2006; Frede et al., 2006; Vandoorn et al., 2011; Vandoorn et al., 2012; Elrayyah et al., 2015; Egwebe et al., 2016; Liu et al., 2016) with more control freedoms available for realizing the expected functions. Liu et al. (2016a) and Liu et al. (2016b) proposed an improved droop controller for two-stage converters with limited ESs using both DC-link voltage and generated power to achieve power sharing. Vandoorn et al. (2011) and Vandoorn et al. (2012) proposed the droop control technique to modify the grid voltage according to the DC voltage for exploiting the maximum power of RESs in the islanded mode. Meanwhile, the universal controller in Elrayyah et al. (2015) realized MPPT, droop control, and DC voltage regulation simultaneously. In addition, the stability issue and the operation of multiple VSGs have been extensively researched in recent years. Modeling of grid-forming and grid-following converters with DC capacitors/batteries was presented by Fang et al. (2023). Yang et al. (2021) placed a grid-forming converter to enhance the stability of a grid-following converter. Rosso et al. (2019) improved the stability performance of parallel VSGs in a weak grid. In addition, multiple parallel-connected VSGs can be analyzed by making all VSGs as one equivalent VSG (Cajigas et al., 2022) but without considering the possible circulating power among two-stage VSGs. So far, however, there are few literature records considering the characteristics of two-stage converters in VSG systems.

This paper, therefore, proposes a control method, DC voltage-based virtual synchronous generator (DCV-VSG) control, extending the research of two-stage inverters to VSG systems. In the proposed method, the AC frequency is determined by the DC-link voltage, and the ES converter and RES converter can be controlled accordingly. Compared with traditional virtual synchronous generators, the DCV-VSG can eliminate the circulating power among parallel VSGs. Moreover, the DCV-VSG provides a straightforward model like an RSG, and each component in the DCV-VSG can be regarded as a counterpart of an RSG, which provides useful insights into the VSG concept and the design, operation, monitoring, and maintenance problems that can be solved in a similar path to the well-developed conventional power systems theories.

The rest of the paper is organized as follows. First, the topology and control of two-stage traditional VSGs are reviewed with the problem of the circulating power analyzed in Section 2. Then, in Section 3, the operating principle of the DCV-VSG is presented with the analysis of circulating power elimination. In addition, the performance comparison and operational constraints are addressed in Section 4. Finally, the idea of the DCV-VSG was verified through both MATLAB simulation and experimental results.

2 Review and circulating power analysis of traditional VSGs

2.1 Topology and control of traditional VSGs

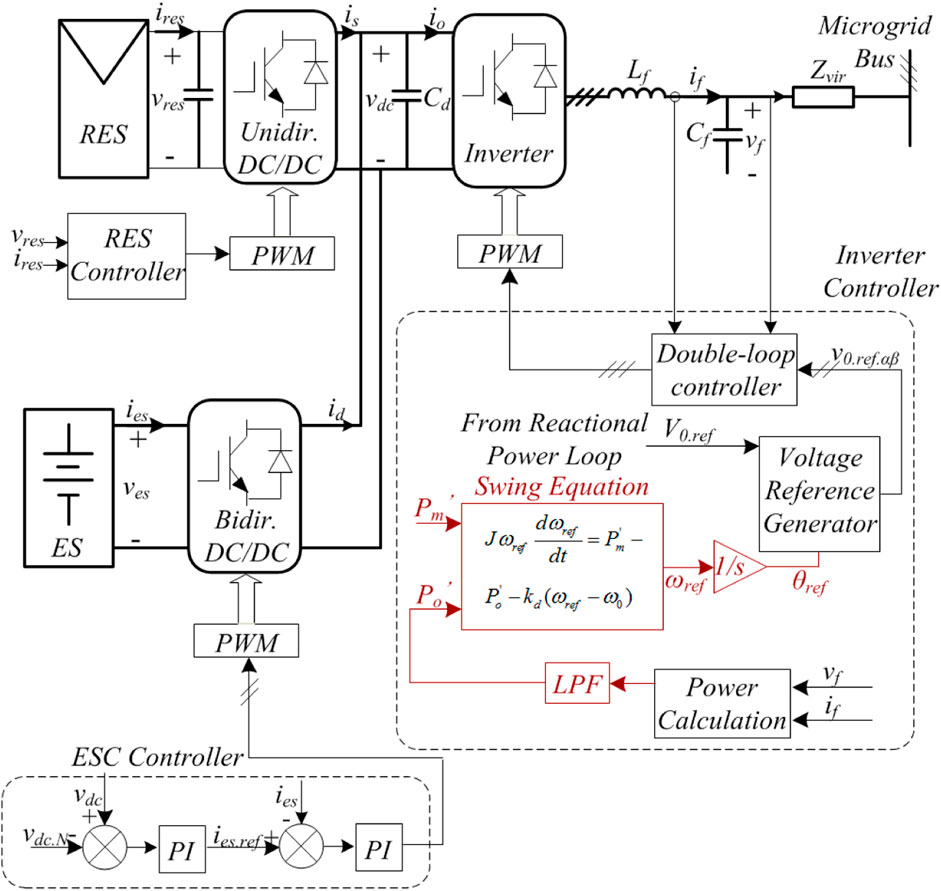
Ideally, a two-stage VSG designed for RESs should integrate ESs at the DC bus to emulate the VSG (Shintai et al., 2012). In specific, the topology of a two-stage VSG is shown in the upper part of Figure 1, where the ES is interfaced by a bidirectional DC/DC converter as it is required both to generate and absorb power.

FIGURE 1

FIGURE 1. Topology and real power control of a two-stage traditional VSG.

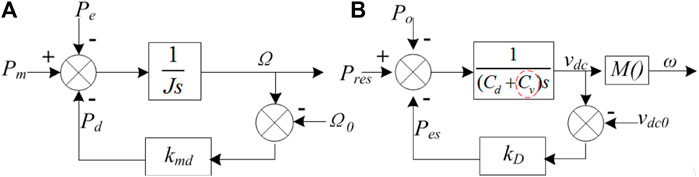
The control of a two-stage traditional VSG is illustrated in the lower part of Figure 1. The basic idea of a VSG is to reproduce the dynamic properties of an RSG; i.e., the swing equation is realized by the corresponding control algorithms for the power electronics-based DG/RES units. In this way, current traditional VSGs implement the dynamic in the data processor of inverters (Shintai et al., 2012; Bevrani et al., 2014) by measuring the power and solving the swing equation with numerical integration. The swing equation in a traditional VSG is expressed as follows:

${\mathit{J}}_{\mathit{v}}{\mathit{\omega }}_{\mathit{r}\mathit{e}\mathit{f}}\frac{\mathit{d}{\mathit{\omega }}_{\mathit{r}\mathit{e}\mathit{f}}}{\mathit{d}\mathit{t}}={\mathit{P}}_{\mathit{m}}^{\prime }-{\mathit{P}}_{\mathit{o}}^{\prime }-{\mathit{k}}_{\mathit{d}\mathit{v}}\left({\mathit{\omega }}_{\mathit{r}\mathit{e}\mathit{f}}-{\mathit{\omega }}_{\mathbf{0}}\right),(1)$

where ω_ref is the reference angular velocity of the inverter, whose nominal value is ω₀; k_dv is the virtual damping factor; J_v is the moment of inertia of the virtual rotor, P^’_o is the measured output power of the inverter filtered by a low-pass filter (LPF), and P^’_m is the virtual mechanical power, which is usually set as the rated power of the inverter (Bevrani et al., 2014; Liu et al., 2016). Meanwhile, the ES converter maintains DC voltage as a constant, and the RES converter harvests the energy determined by its control objective. The output of the ES converter can be determined as follows:

${\mathit{P}}_{\mathit{e}\mathit{s}}={\mathit{P}}_{\mathit{o}}-{\mathit{P}}_{\mathit{r}\mathit{e}\mathit{s}},(2)$

where P_o, P_res, and P_es are the actual output power of the inverter/RES/ES, respectively. Eq. 2 suggests that ES will cover the power gap between the RES power and inverter power.

According to (1), P^’_m is set before the operation, and P_o is determined merely by the grid loading, but P_res is affected by ambient conditions, such as the block effect or weather changes, resulting in random power fluctuations, which will introduce the problem of the ES converter circulating power among parallel VSGs, as analyzed in the following section.

2.2 Topology and control of paralleled traditional VSGs

An analysis of the circulating power can be performed by using the scale-down microgrid of two traditional VSG units connected in parallel, supplying a common load, as shown in Figure 2. The green lines represent the power flow generated by RESs. The blue lines show the power flow between the inverters. Suppose that the total converter power loading is P_LT, and the loading of each converter is P_Li (i = 1 or 2). The power flow within the microgrid satisfies the relationship as follows:

${\mathit{P}}_{\mathit{L}\mathbf{1}}+{\mathit{P}}_{\mathit{L}\mathbf{2}}={\mathit{P}}_{\mathit{L}\mathit{T}},(3)$

${\mathit{P}}_{\mathit{e}\mathit{s}\mathbf{1}}+{\mathit{P}}_{\mathit{r}\mathit{e}\mathit{s}\mathbf{1}}={\mathit{P}}_{\mathit{L}\mathbf{1}},(4)$

${\mathit{P}}_{\mathit{e}\mathit{s}\mathbf{2}}+{\mathit{P}}_{\mathit{r}\mathit{e}\mathit{s}\mathbf{2}}={\mathit{P}}_{\mathit{L}\mathbf{2}},(5)$

where P_resi is the output power of RES converter i and P_esi is the output power of ES converter i. As P_resi varies randomly, we consider a common situation where one of the RESs accidentally suffers from power deficiency while the other does not (probably due to local weather changes), i.e.,

${\mathit{P}}_{\mathit{r}\mathit{e}\mathit{s}\mathbf{1}}<{\mathit{P}}_{\mathit{L}\mathbf{1}},(6)$

${\mathit{P}}_{\mathit{r}\mathit{e}\mathit{s}\mathbf{2}}>{\mathit{P}}_{\mathit{L}\mathbf{2}}.(7)$

FIGURE 2

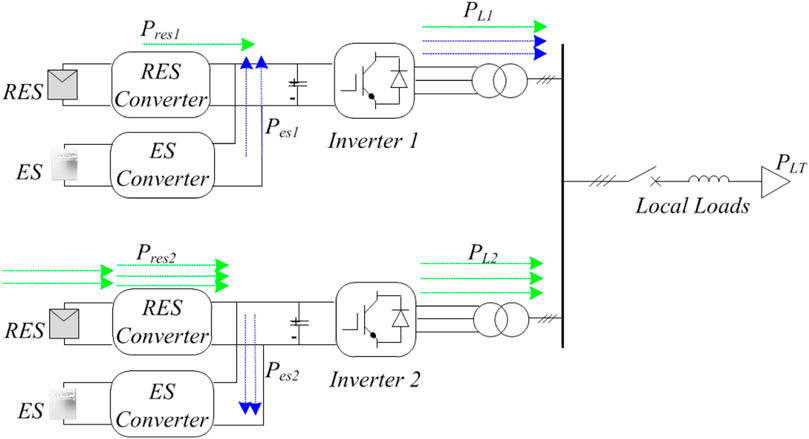
FIGURE 2. Power flow illustration within a simplified islanding microgrid with two traditional VSGs.

The output power of the ES unit of each VSG can be determined by the following equations:

${\mathit{P}}_{\mathit{e}\mathit{s}\mathbf{1}}={\mathit{P}}_{\mathit{L}\mathbf{1}}-{\mathit{P}}_{\mathit{r}\mathit{e}\mathit{s}\mathbf{1}}>\mathbf{0},(8)$

${\mathit{P}}_{\mathit{e}\mathit{s}\mathbf{2}}={\mathit{P}}_{\mathit{L}\mathbf{2}}-{\mathit{P}}_{\mathit{r}\mathit{e}\mathit{s}\mathbf{2}}<\mathbf{0}.(9)$

Clearly, there is part of power following from ES converter 2 to ES converter 1, which has no contribution to load sharing at the AC side but increases power losses by extra power conversion between DC converters. Hence, the circulating power P_C to quantify these extra conversions is presented by the following equation:

${\mathit{P}}_{\mathit{C}\mathbf{2}}=\frac{\mathbf{1}}{\mathbf{2}}\left(\left|{\mathit{P}}_{\mathit{e}\mathit{s}\mathbf{1}}\right|+\left|{\mathit{P}}_{\mathit{e}\mathit{s}\mathbf{2}}\right|-\left|{\mathit{P}}_{\mathit{e}\mathit{s}\mathbf{1}}+{\mathit{P}}_{\mathit{e}\mathit{s}\mathbf{2}}\right|\right).(10)$

Obviously, P_C2 serves as an indicator of the operation efficiency and should be made as small as possible. Now, we suppose that there are n VSGs parallel-connected together, and then, it can define the circulating power between n ES units as follows:

${\mathit{P}}_{\mathit{C}\mathbf{n}}=\frac{\mathbf{1}}{\mathbf{2}}\left({\displaystyle {\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}}}\left|{\mathit{P}}_{\mathit{e}\mathit{s}\mathbf{i}}\right|-\left|{\displaystyle {\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}}}{\mathit{P}}_{\mathit{e}\mathit{s}\mathbf{i}}\right|\right).(11)$

According to triangle inequality,

${\displaystyle {\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}}}\left|{\mathit{P}}_{\mathit{e}\mathit{s}\mathbf{i}}\right|\ge \left|{\displaystyle {\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}}}{\mathit{P}}_{\mathit{e}\mathit{s}\mathbf{i}}\right|.(12)$

It is noted that the circulating power is always non-negative and reaches zero if and only if the signs of P_esi are the same, i = 1, 2….n. Therefore, to eliminate the circulating power, the operation of the RES unit, the ES, and the inverter in the microgrid should be coordinated to balance the power both in the microgrid and among different ES converters. It is noted that the circulating power will not appear among parallel-connected single-stage VSGs, where the power source or energy storage component will directly connect to the DC link.

In addition, for a single RES unit, the aforementioned task can be performed to some extent by modifying the virtual mechanical power according to the measured RES output, but the method becomes inappropriate where multiple RESs are integrated or the ESs are located separately from the RESs. In such cases, high-bandwidth communication modules are needed to share information on power flow between each unit, which complicates the system and introduces potential failure points (Wang et al., 2008; Yang et al., 2011; Belvedere et al., 2012; Tan et al., 2013).

3 Proposed DC voltage-based VSG

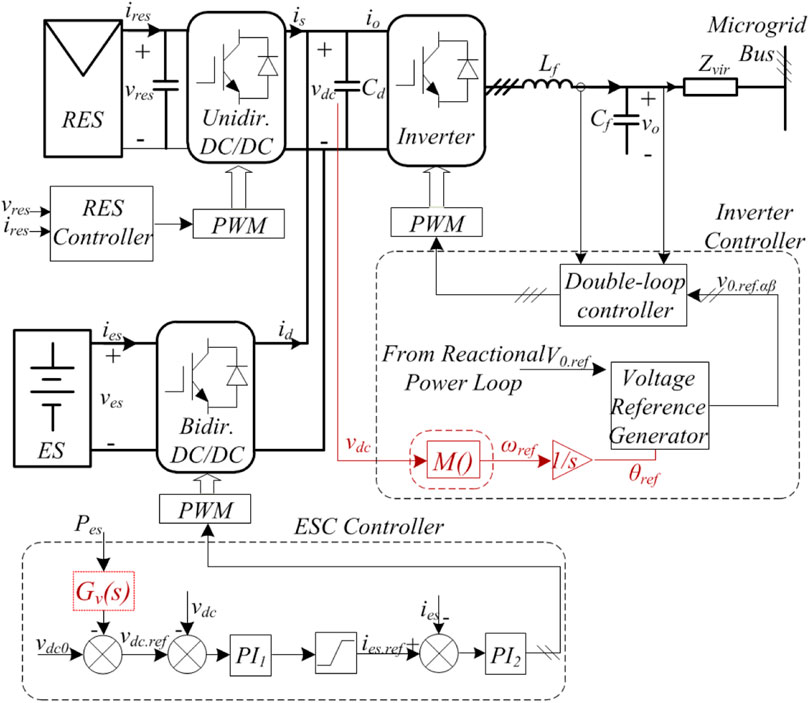
According to the analysis in Section 2, the generation mechanism of a traditional VSG’s circulating power lies in the swing Eq.1, which is realized purely by the digital processor based on power measurement and estimation. On the contrary, an RSG realizes the swing equation by the electromechanical/magnetic process (Kundur, 1994); i.e., the mechanical torque/power is dynamically balanced by the electrical torque/power, else the rotor speed sways and the mechanical torque/power is adjusted until a new equilibrium is met. Along this line of consideration, in this section, a DCV-VSG is proposed for two-stage inverters to realize the swing equation using the dynamic characteristic of a DC-link capacitor, by whose voltage the AC frequency and the ES converter output power are determined.

3.1 Control of a rear-end inverter

Assuming that the line impedance is inductive (if not, a virtual inductor can be introduced to be in series with the inverter through the control strategy, thus making the impedance to be inductive), the frequency is decoupled from the reactive power; therefore, the following analysis can be treated independently by active power distribution (Guerrero et al., 2005; He et al., 2011).

To utilize DC voltage to balance the power flow, the inverter should establish a relation between DC voltage and frequency. A mapping function can be defined to relate frequency reference with DC voltage as follows:

${\mathit{\omega }}_{\mathit{r}\mathit{e}\mathit{f}}=\mathit{M}\left({\mathit{v}}_{\mathit{d}\mathit{c}}\right),(13)$

where ω_ref is the angular frequency reference of the output voltage, M is a monotone increasing function defined to generate the frequency reference, whose physical meaning and selection will be explained in Section 4, and v_dc is the measured DC-link voltage. After obtaining the frequency reference, combined with the amplitude reference, the AC voltage reference can be generated, which is then sent into the double-loop controller to control the output voltage, as demonstrated in Figure 3.

FIGURE 3

FIGURE 3. Overall control strategy of the DCV-VSG.

3.2 Control of the energy storage converter

As v_dc must now vary slightly to indicate the power balance between each unit, the ES converter should work in the droop mode rather than the constant voltage mode. The voltage reference of the DC bus can be given as follows:

${\mathit{v}}_{\mathit{d}\mathit{c}.\mathit{r}\mathit{e}\mathit{f}}=-\frac{{\mathit{P}}_{\mathit{e}\mathit{s}}}{{\mathit{k}}_{\mathit{D}}}\frac{\mathbf{1}}{\mathbf{1}+{\mathit{T}}_{\mathit{v}\mathit{s}}}+{\mathit{v}}_{\mathit{d}\mathit{c}\mathbf{0}}=-{\mathit{P}}_{\mathit{e}\mathit{s}}{\mathit{G}}_{\mathit{v}}\left(\mathit{s}\right)+{\mathit{v}}_{\mathit{d}\mathit{c}\mathbf{0}},(14)$

where v_{dc. ref} is the DC voltage reference of the ES converter; v_dc0 is the nominal value of v_dc; k_D is the damping factor, and T_vs is the time constant of the low-pass filter (LPF), which will be explained in the next section. In addition, to avoid overload of the ES converter, a saturation component must be added after the current reference. Finally, the overall control scheme of the DCV-VSG is illustrated in Figure 3.

3.3 ES converter circulating power of paralleled DCV-VSGs

Supposing n DCV-VSGs are parallel-connected, under steady states, all DCV-VSGs share a unified frequency:

$\mathit{M}\left({\mathit{v}}_{\mathit{d}\mathit{c}\mathbf{1}}\right)=\mathit{M}\left({\mathit{v}}_{\mathit{d}\mathit{c}\mathbf{2}}\right)=\cdots =\mathit{M}\left({\mathit{v}}_{\mathit{d}\mathit{c}\mathbf{i}}\right)\cdots =\mathit{M}\left({\mathit{v}}_{\mathit{d}\mathit{c}\mathbf{n}}\right)=\mathit{\omega },(15)$

where v_dci is the DC-link voltage of inverter i. As M is monotone increasing, it is obtained as follows:

${\mathit{v}}_{\mathit{d}\mathit{c}\mathbf{1}}={\mathit{v}}_{\mathit{d}\mathit{c}\mathbf{2}}=\cdots ={\mathit{v}}_{\mathit{d}\mathit{c}\mathbf{i}}\cdots ={\mathit{v}}_{\mathit{d}\mathit{c}\mathbf{n}}={\mathit{M}}^{-\mathbf{1}}\left(\mathit{\omega }\right)\bullet {\mathit{V}}_{\mathit{d}\mathit{c}},(16)$

where M^-1 is the inverse function of M. It can be concluded all DCV-VSGs within the grid share the same DC voltage. According to (14), the output power of DCV-VSGs satisfies

$\frac{{\mathit{P}}_{\mathit{e}\mathit{s}\mathbf{1}}}{{\mathit{k}}_{\mathit{D}\mathbf{1}}}=\frac{{\mathit{P}}_{\mathit{e}\mathit{s}\mathbf{2}}}{{\mathit{k}}_{\mathit{D}\mathbf{2}}}=\cdots =\frac{{\mathit{P}}_{\mathit{e}\mathit{s}\mathbf{i}}}{{\mathit{k}}_{\mathit{D}\mathbf{i}}}\cdots =\frac{{\mathit{P}}_{\mathit{e}\mathit{s}\mathbf{n}}}{{\mathit{k}}_{\mathit{D}\mathbf{n}}}=-\left({\mathit{V}}_{\mathit{d}\mathit{c}}-{\mathit{v}}_{\mathit{d}\mathit{c}\mathbf{0}}\right),(17)$

where k_Di is the damping factor of ES converter i. Accordingly, the output power of the ES converter is proportional to its damping factor, which obviously has the same sign and satisfies (12). Hence, the circulating power is P_Cn = 0, which means that the circulating power is eliminated effectively.

4 Performance comparison and operational constraints

The reason why the DCV-VSG can achieve the same power allocation with higher efficiency is that the swing equation is implemented by an electromagnetic process like an RSG rather than the numerical operation of a traditional VSG. In this section, the physical process and mathematical models are compared between an RSG and a DCV-VSG to further clarify the concept of the DCV-VSG.

4.1 Physical features

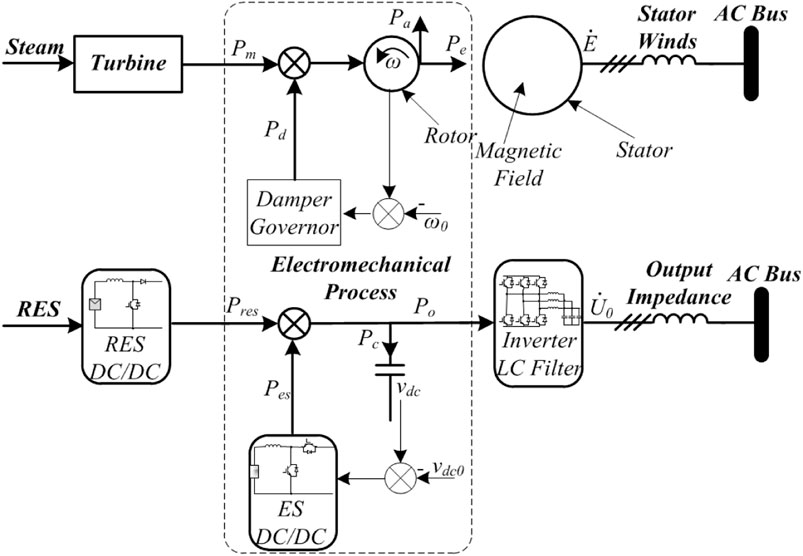
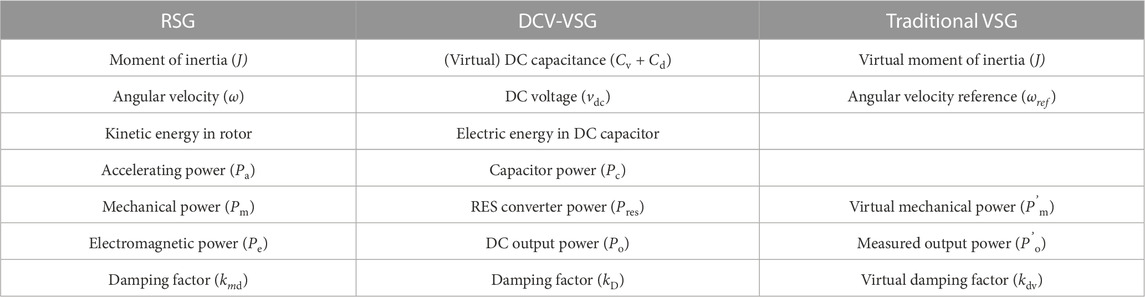
Figure 4 compares the power conversion process between an RSG and DCV-VSG. From the perspective of the energy flow path, it is apparent that there are analogies between these two systems. For an RSG, the primary components of active power control consist of a valve, turbine, governor, rotor, stator (winding), and damper (damping winding). The turbine is the prime mover, which converts primary energy into mechanical power P_m, driving the rotor at a certain angular frequency. At this frequency, the rotor, with its windings powered by direct current, produces a rotational magnetic field in the air gap to generate electromotive force in phase with a magnetic field in stator winding (Kundur, 1994). The governor and damper are critical for system stability, and they have similar functionality, i.e., adjusting mechanical power with damping power P_d to be inversely proportional to rotor speed error. It is worth noting that the main difference between the governor and damper lies in their response time to disturbances, but it is not a problem for power electronics devices, and their effect is considered as a whole. This feature contributes much to the damping of rotor oscillation and increases the stability margin in stability analysis (Kundur, 1994).

FIGURE 4

FIGURE 4. Power conversion comparison between a DCV-VSG and RSG.

The idea of a DCV-VSG is to inherit the dynamic power balancing feature of an RSG, as discussed in the previous section. In order to do so, components within the DCV-VSG have to be designed to mimic its counterpart in the RSG. In specific, the RES converter is to emulate the turbine of the RSG, which converts renewable energy into electric power (represented by P_res) determined by its own control objective. The ES converter is indispensable to simulate the damper and governor of an RSG to adjust the RES output according to the DC voltage error with output power P_es, since the output power of an RES is not as controllable as that of traditional sources. Under steady states, (14) suggests that P_es is inversely proportional to the DC voltage error, which is quite similar to the linear model of the damper and governor of an RSG [6]. Moreover, under normal operation with DC voltage around its rated value, the ES converters almost do not deliver or absorb any power.

The DC-link capacitor is correspondent to the rotor of the RSG, which is the core element to achieve dynamic power balancing and inertia response. In brief, when the input power is larger than the output power, the DC voltage becomes higher, resulting in a higher frequency of the inverter, which will increase the output power until a new equilibrium is reached, as indicated by Eqs 13–17.

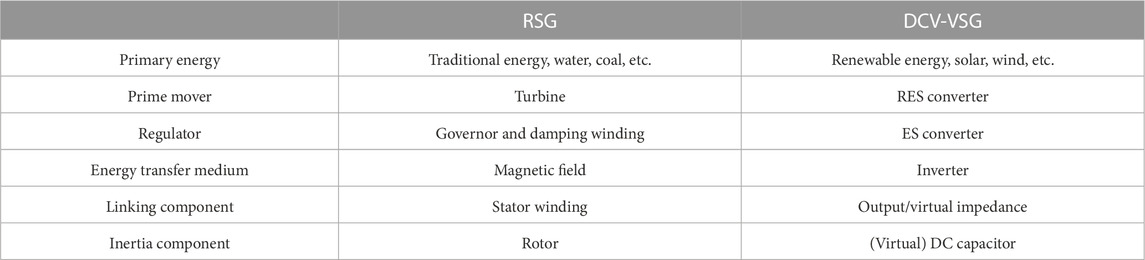
The inverter (with its LC filter) is controlled to emulate the magnetic field of the RSG, which produces AC voltage at the rotor frequency and transfers energy from the rotor to the stator, while the inverter generates AC voltage at a frequency determined by the mapping function of DC voltage from (13), and the energy will transfer from the DC capacitor to the AC output port. The word ‘synchronous’ is also utilized to describe the phenomenon where the rotors of all RSGs interconnected in parallel are synchronized to the same frequency, which coordinates with the conclusion that the paralleled DCV-VSGs share the same DC voltage demonstrated by (16). On the other hand, as shown in Figure 1, a traditional VSG does not inherent an electromechanical process, and thus, it is implemented with no physical process. To sum up, the correspondences of the physical process between a DCV-VSG and RSG are demonstrated in Table 1.

TABLE 1

TABLE 1. Comparison of an RSG and DCV-VSG in physical features.

4.2 Mathematical models and parameters

Based on the motion mechanic theory and circuit principles in Figure 4, the power characteristics of an RSG and DCV-VSG can be described by (18) and 19, respectively, (Kundur, 1994).

${\mathit{P}}_{\mathit{a}}={\mathit{P}}_{\mathit{m}}-{\mathit{P}}_{\mathit{e}}+{\mathit{P}}_{\mathit{d}},(18)$

${\mathit{P}}_{\mathit{c}}={\mathit{P}}_{\mathit{r}\mathit{e}\mathit{s}}-{\mathit{P}}_{\mathit{o}}+{\mathit{P}}_{\mathit{e}\mathit{s}},(19)$

where P_a, P_m, P_e, and P_d are the accelerating, mechanical, electromagnetic, and damping power of the rotor, respectively; P_c is the capacitor power.

Considering the dynamic process and damping characteristics of RSG, (18) can be further developed as follows:

$\mathit{J}\mathit{\Omega }\frac{\mathit{d}\mathit{\Omega }}{\mathit{d}\mathit{t}}={\mathit{P}}_{\mathit{m}}-{\mathit{P}}_{\mathit{e}}-{\mathit{k}}_{\mathit{m}\mathit{d}}\left(\mathit{\Omega }-{\mathit{\Omega }}_{\mathbf{0}}\right),(20)$

where J is the moment of inertia of the RSG rotor, Ω is the mechanical angular speed of the rotor whose rated value is Ω₀, and k_md refers to the mechanical damping factor considering the effect of the governor and damping windings together.

Meanwhile, substituting (14) into (19), we obtain

$\left({\mathit{C}}_{\mathit{d}}+{\mathit{k}}_{\mathit{D}}{\mathit{T}}_{\mathit{v}}\right){\mathit{v}}_{\mathit{d}\mathit{c}}\frac{\mathit{d}{\mathit{v}}_{\mathit{d}\mathit{c}}}{\mathit{d}\mathit{t}}={\mathit{P}}_{\mathit{r}\mathit{e}\mathit{s}}-{\mathit{P}}_{\mathit{o}}-{\mathit{k}}_{\mathit{D}}\left({\mathit{v}}_{\mathit{d}\mathit{c}}-{\mathit{v}}_{\mathit{d}\mathit{c}\mathbf{0}}\right),(21)$

where C_d is the DC-link capacitance of the DCV-VSG. A virtual capacitor determined by the LPF’s time constant of the ES converter can be defined as follows:

${\mathit{C}}_{\mathit{v}}={\mathit{k}}_{\mathit{D}}{\mathit{T}}_{\mathit{v}}.(22)$

According to (22), C_v also serves as the inertia of the DCV-VSG; thus, the variable inertia can be implemented easily by adjusting the LPF’s time constant of the ES converter.

Comparing (20) and (21), the mathematical models of an RSG and DCV-VSG have a unified form, which is illustrated in Figure 5, where when increasing k_D in Figure 5B, the energy storage converter will output or absorb more power and then minimize the variation of DC-link voltage and the variation of output frequency in consequence. Combining with (1), the correspondences of parameters are, thus, summarized in Table 2. It is noted that the DCV-VSG performs more like an RSG rather than a traditional VSG.

FIGURE 5

FIGURE 5. Mathematical models of (A) an RSG and (B) a DCV-VSG.

TABLE 2

TABLE 2. Correspondence in parameters of traditional VSG, RSG, and DCV-VSG models.

4.3 Implementation constraints

To implement a DCV-VSG in practice, some other constraints must be considered for stable operation under any condition. The mapping function M (v_dc) presented in Section 3 maps DC voltage to AC frequency, which is confined within a certain range by grid standards. Assuming the frequency is limited in the range from f_min to f_max, the mapping function must satisfy (23) in normal operation.

$\left\{\begin{array}{c}\mathit{M}\left({\mathit{v}}_{\mathit{d}\mathit{c}.\mathit{min}}\right)\ge \mathbf{2}\mathit{\pi }{\mathit{f}}_{\mathit{min}}\\ \mathit{M}\left({\mathit{v}}_{\mathit{d}\mathit{c}.\mathit{max}}\right)\le \mathbf{2}\mathit{\pi }{\mathit{f}}_{\mathit{max}},\end{array}\right.(23)$

where v_{dc. min} and v_{dc. max} are the lower and upper limits of the DC-link voltage, respectively.

In addition to the constraints on ES units for normal applications (SOC limits, etc.), power requirements should also be met for the expected performance. To prevent the DC voltage from exceeding the upper limit when the grid is lightly loaded, the ES should absorb all power generated by renewable energy sources when the DC voltage reaches its upper limit.

${\mathit{k}}_{\mathit{D}}\left({\mathit{v}}_{\mathit{d}\mathit{c}.\mathit{max}}-{\mathit{v}}_{\mathit{d}\mathit{c}\mathbf{0}}\right)\le {\mathit{P}}_{\mathit{r}\mathit{e}\mathit{s}\_\mathit{max}},(24)$

where P_{res. max} is the maximum output power of the RES under optimal circumstances.

At the same time, to support the DC voltage when the grid is heavily loaded, the ES should be capable of supplying maximum load when the DC voltage reaches its lower limit.

${\mathit{k}}_{\mathit{D}}\left|{\mathit{v}}_{\mathit{d}\mathit{c}.\mathit{min}}-{\mathit{v}}_{\mathit{d}\mathit{c}\mathbf{0}}\right|\ge {\mathit{P}}_{\mathit{L}.\mathit{max}},(25)$

where P_{L. max} is the maximum design load of a DCV-VSG.

5 Simulation and experimental verifications

Before the simulation and experimental verifications, the parameters in the control functions of (13) and 14 have to be specified. Considering the constraints in Table 3, (13) and (14) can be designed according to the discussion in Section 4.

TABLE 3

TABLE 3. Practical constraints for simulation and experiment.

To present a preliminary verification, we consider the simplest mapping function as a polynomial to take full advantage of the component capacity:

$\begin{array}{c}\mathit{M}\left({\mathit{v}}_{\mathit{d}\mathit{c}\mathbf{max}}\right)=\mathbf{2}\mathit{\pi }{\mathit{f}}_{\mathit{max}},\\ \mathit{M}\left({\mathit{v}}_{\mathit{d}\mathit{c}\mathbf{0}}\right)=\mathbf{2}\mathit{\pi }{\mathit{f}}_{\mathbf{0}},\\ \mathit{M}\left({\mathit{v}}_{\mathit{d}\mathit{c}\mathbf{min}}\right)=\mathbf{2}\mathit{\pi }{\mathit{f}}_{\mathit{min}}.\end{array}(26)$

By substituting the parameters in Table 3 to (26),

$\mathit{M}\left({\mathit{v}}_{\mathit{d}\mathit{c}}\right)=-\mathbf{0.0023}{\mathit{v}}_{\mathit{d}\mathit{c}}^{\mathbf{2}}+\mathbf{1.0524}{\mathit{v}}_{\mathit{d}\mathit{c}}+\mathbf{197.9203}.(27)$

On the other hand, substituting the parameters into Eqs 22, 23, 24, 25,

$\mathbf{27.5}\le {\mathit{k}}_{\mathit{D}}\le \mathbf{40}.(28)$

Here, it is better to choose k_D = 40 for its smaller frequency deviation.

5.1 Simulation verification

5.1.1 Circulating power elimination

To verify the performance of circulating power elimination of the DCV-VSG, MATLAB/Simulink was employed to model a microgrid of Figure 2 with two identical converters as DCV-VSG1 and DCV-VSG2, where power unbalances happen in RES sources. The main parameters are shown in Table 3, and the control parameters are the same as those in (27) and 28. The virtual inertia control is disabled here.

Two RES power sources, RES1 and RES2, both generate power of 200 W at the beginning of the simulation. At 1s, power imbalance happens when the generated power of RES1 decreases to 100 W, while that of RES2 increases to 300 W, as shown in Figure 6C, where the output power of DCV-VSG1 increases and that of DCV-VSG2 decreases, as shown in Figures 6A, B, which coordinates with the RES output deviation. In this sense, ESs of DCV-VSGs output little power before and after the unbalance happens except during the transient process, as shown in Figure 6E. It is obvious that the two DCV-VSGs have the same DC-link voltage after the transient process, as shown in Figure 6D, whose value slightly deviates from that before the imbalance happens as expected.

FIGURE 6

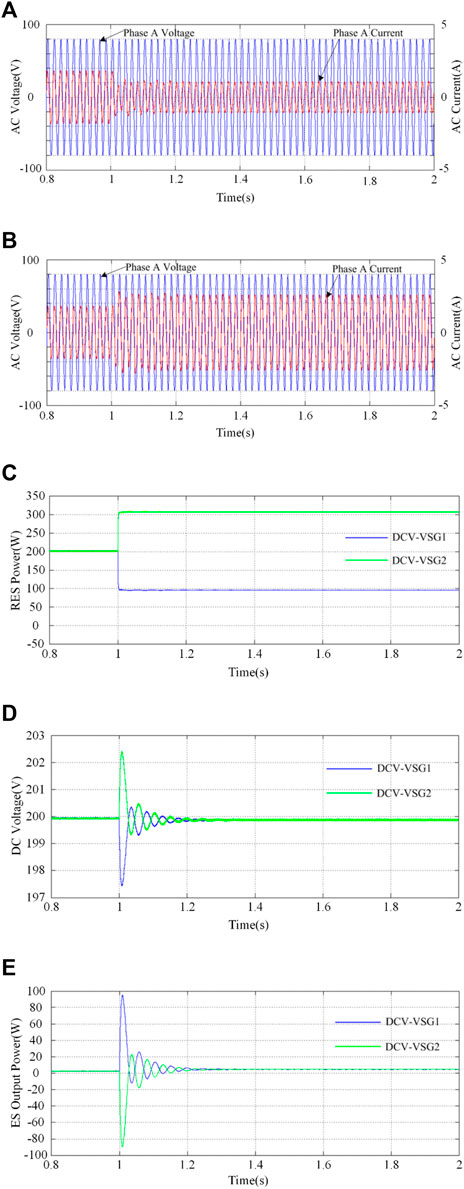
FIGURE 6. Simulation results of the DCV-VSG for circulating power eliminating with (A) DCV-VSG1, (B) DCV-VSG2 output voltage and current, (C) RESs output power, (D) DC voltage, and (E) ESs output power.

To make a comparison, the same simulation is repeated with traditional VSGs. The corresponding results are shown in Figure 7. The DC-link voltage is controlled to be constant before and after the power imbalance, as shown in Figure 7A. Meanwhile, ESs of traditional VSGs generate and absorb over 100 W at the same time, as illustrated in Figure 7B. In this sense, according to (10), the circulating power P_C2 = 100 W limits the efficiency of traditional VSGs.

FIGURE 7

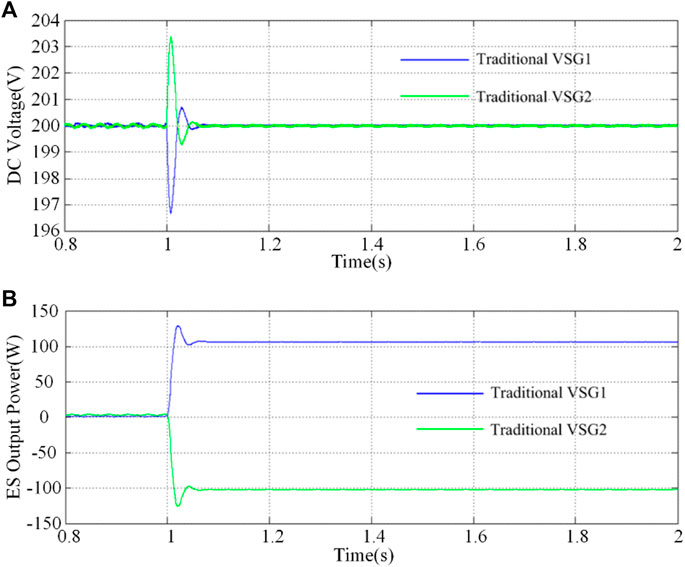
FIGURE 7. Simulation results of traditional VSGs when an RES power unbalance occurs with (A) DC voltage and (B) ES output power.

5.1.2 Virtual inertia performance

To verify the developed models and the performance of virtual inertia discussed in Section 4, the RES power is kept constant at 400 W, while another load of 400 W is added to the grid at 1s. The transient response of the AC voltage and frequency will be examined and compared. In Figure 8A, the DC voltage response of the DCV-VSG becomes smoother as C increases, which is coherent with the mathematical model developed in Section 4. In addition, the response with virtual inertia almost overlaps that with the same capacitance. Meanwhile, the frequency response is also smooth, proving the effectiveness of the DCV-VSG.

FIGURE 8

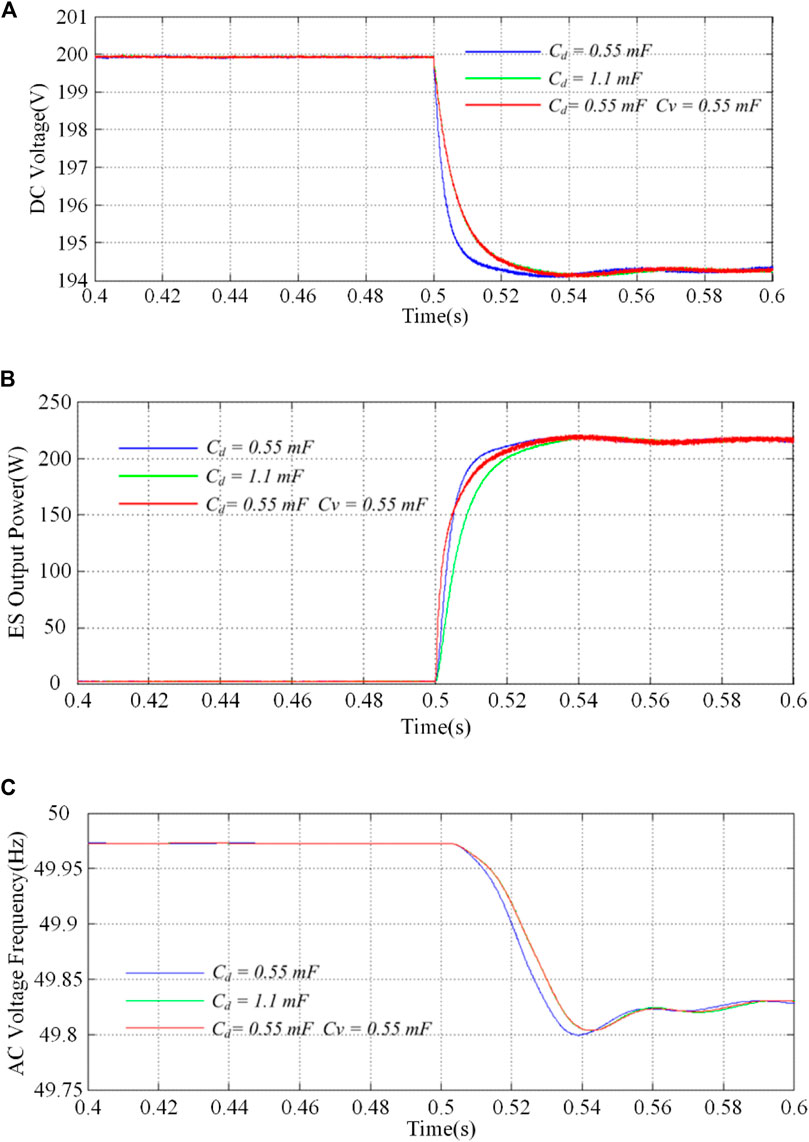
FIGURE 8. Simulation results when a load is added at 1s with (A) DC voltage response of DCV-VSGs, (B) ES output power of DCV-VSGs, and (C) voltage frequency.

5.2 Experimental results

To verify the practicality of the proposed scheme, a scaled-down AC microgrid was built in our laboratory, which comprises two VSG units with each powered by an independent PV string (V_MPP = 180 V, I_MPP = 3.1A at 800 W/m², 20°C) through the renewable energy source converter. Two Chroma DC programmable power supplies are used to emulate the energy storage units interfaced by the ES converter to the DC link of VSGs. All control algorithms are programmed in dSPACE DS1103.

5.2.1 Circulating power elimination

Typically, the power imbalance discussed in this paper occurs when PV strings powering different VSGs suffer a sudden change in the irradiance level. However, as the irradiance cannot be flexibly controlled for the rooftop-installed PV strings, this experimental microgrid can only examine the transient conditions where PV voltage references are changed suddenly and deliberately. The parameters for this experiment are also listed in Table 3.

Figure 9 shows the experimental results when the PV voltage reference suffers sudden change to verify the effect of the DCV-VSG on circulating power elimination. Before the change, the PV voltages are controlled by RES converters at 90 V, so the outputs of PV strings are identical. In this sense, two VSGs have equal load sharing of 207 W, as shown in Figure 9A, which are supplied by PVs with no power generated by ESs. Then, at t₁, the voltage references of PV strings change to 90 ± 40 V, respectively, to simulate the power imbalance between the VSGs. As the currents of PV strings remain constant at 2.3 A (because PVs are working in the constant current zone), the output powers of the PVs become 299 W and 115 W, respectively. By the proposed DCV-VSG, the inverters adjust their output automatically to adapt to the changes, with DCVVSG1 increasing and DCVVSG2 decreasing its power, as shown in Figure 9B. Because of this feature, the output of ES converters remains 0 W, as shown in Figure 9C, saving the extra operation introduced by the traditional VSG. As the total power of PVs remains constant, DC-link voltage v_dc1 and v_dc2 remain unchanged, as shown in Figure 9C; therefore, system frequency is not influenced by the RES power changes.

FIGURE 9

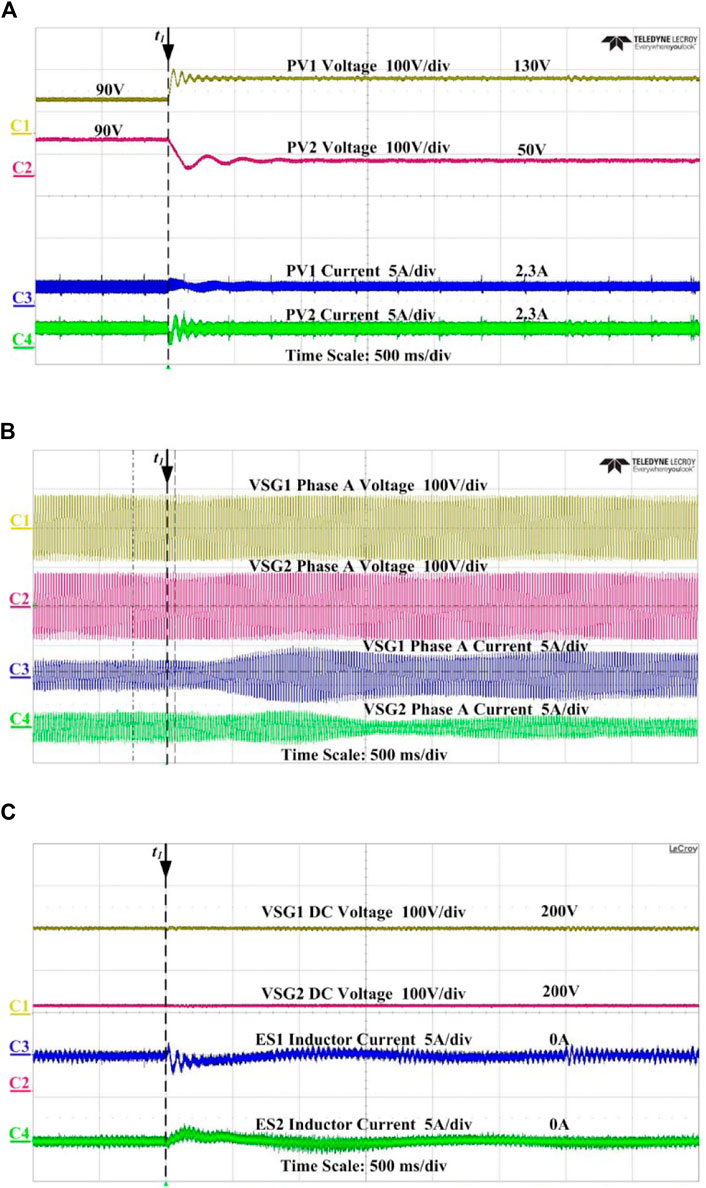
FIGURE 9. Experimental results using the DCV-VSG for circulating power elimination with (A) PVs input voltages and currents, (B) DCV-VSG output voltages and currents, and (C) DC voltages and ES output currents.

5.2.2 Virtual inertia verification

The developed model of the DCV-VSG in Section 4 suggests that the DC capacitance of the DCV-VSG is analogous to the moment of inertia of the RSG. This feature can be verified by an experimental comparison shown in Figures 10A, B. At first, DVG-VSGs supply a resistive load of 400 W powered almost all by PVs, with the DC voltage being 200 V and ESs output being 0 W. At t₁, another resistive load of 400 W is added to the AC bus, and the transient response of DC voltage and AC frequency around t₁ is our focus.

FIGURE 10

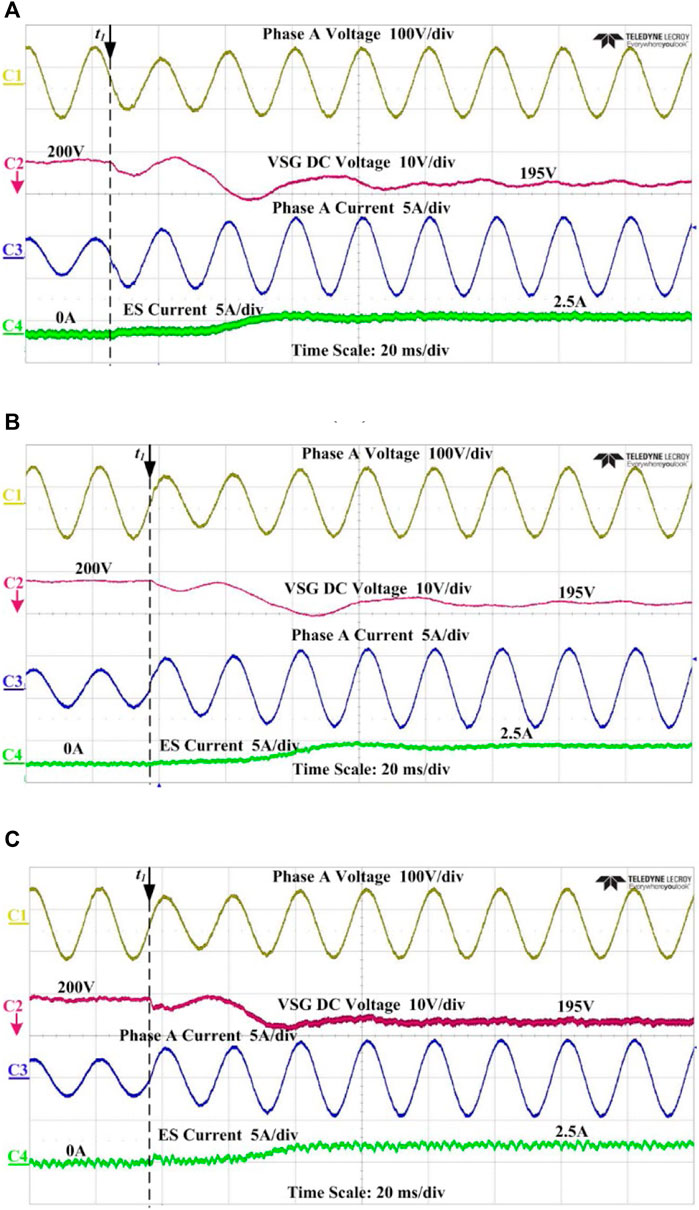
FIGURE 10. Experimental waveforms of the transient response of the DCV-VSG with different DC-link capacitances during a sudden load increase when (A) C = 0.55 mF, Cv = 0, (B) C = 1.1 mF, Cv = 0, and (C) C = 0.55 mF, Cv = 0.55 mF.

Figures 10A, B are plotted with C_v = 0 mF and C_d being 0.55 mF and 1.1 mF, respectively. After adding the load, the AC current instantly increases to supply the extra load. Therefore, the output power of the DC capacitor becomes larger than its input power, and then, the DC voltage decreases. Under steady states, DC voltages in both figures are finally 195 V, suggesting that the DC capacitance does not affect the steady-state performance. However, compared with Figure 10B, the DC voltage in Figure 10A swings more violently. This can be examined more clearly in Figure 11A, where the DC voltages of both scenarios are plotted in the same figure. Figure 11A indicates that the DC voltage response of the DCV-VSG to a certain disturbance becomes smoother as the DC capacitance increases, with a longer decreasing time and smaller overshoot. The observation suggests that a DCV-VSG with larger DC capacitance has greater inertia, coordinating with the conclusion drawn in Section 4.

FIGURE 11

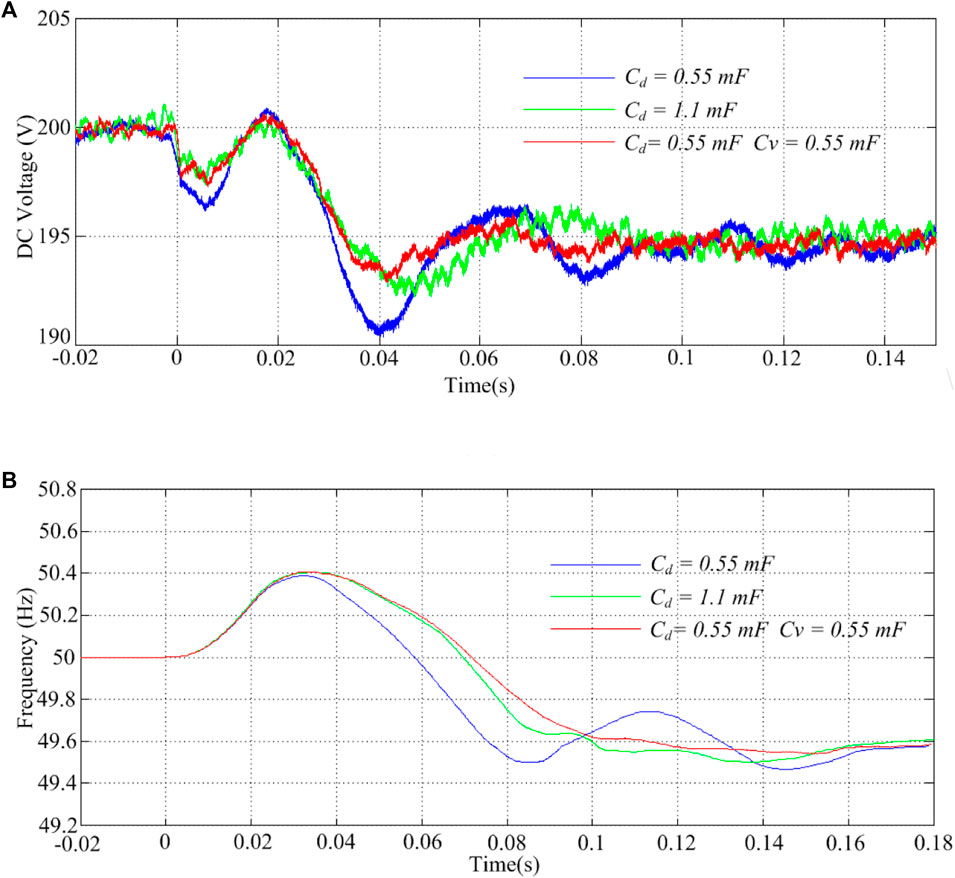
FIGURE 11. Experimental data of transient response of the DCV-VSG plotted by MATLAB with (A) DC voltage and (B) AC voltage frequency.

Furthermore, the same experiment was repeated with C_v = C_d = 0.55 mF, whose results are shown in Figures 10C, 11. Compared with Figure 10A, the DC voltage of the DCV-VSG with virtual inertia also has a smoother response to a disturbance. By a detailed observation of Figure 11A, the response of the DCV-VSG with the virtual capacitor almost overlaps that with the real capacitor, and with even a smaller overshoot. The same observation can be made in Figure 11B by the frequency curves using data of voltage of phase A in each case plotted by MATLAB. The frequency responses become less steep with smaller excursion as the DC capacitance increases, and the response with a virtual capacitor is quite close to that with a real one, which is coherent with the analysis in Section 4; therefore, it proves the effectiveness of virtual inertia.

6 Conclusion

This paper proposes a new DC voltage-based virtual synchronous generator method for two-stage converters. The method is identical to traditional VSGs in external characteristics, but can eliminate the circulating power among parallel VSGs. In this method, the swing equation is realized by the characteristic of the DC-link capacitor instead of solving the differential equation in the data processor, which is the way of traditional VSGs. The idea of the DCV-VSG is to take advantage of the similar physical structure between a two-stage converter and an RSG, making each component of the DCV-VSG mimic the corresponding component of the RSG. Additionally, the variable inertia of VSGs is emulated by the ES converter by introducing a virtual capacitor whose capacitance is determined by its LPF time constant. Based on the discussion in Section 4, the DCV-VSG resembles the RSG. The simulation and experimental results verified the performance of the proposed method.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, writing, and original draft preparation: TH; validation: FG; and writing—review and editing: JZ and XZ. All authors contributed to the article and approved the submitted version.

Conflict of interest

JZ was employed by China Southern Power Grid Foshan Electric Power Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alipoor, J., Miura, Y., and Ise, T. (2018). Stability assessment and optimization methods for microgrid with multiple VSG units. IEEE Trans. Smart Grid9 (2), 1462–1471. doi:10.1109/tsg.2016.2592508

CrossRef Full Text | Google Scholar

Belvedere, B., Bianchi, M., Borghetti, A., Nucci, C. A., Paolone, M., and Peretto, A. (2012). A microcontroller-based power management system for standalone microgrids with hybrid power supply. IEEE Trans. Sustain. Energy3 (3), 422–431. doi:10.1109/tste.2012.2188654

CrossRef Full Text | Google Scholar

Bevrani, H., Ise, T., and Miura, Y. (2014). Virtual synchronous generators: A survey and new perspectives. Int. J. Electr. Power & Energy Syst.54, 244–254. doi:10.1016/j.ijepes.2013.07.009

CrossRef Full Text | Google Scholar

Cajigas, A. G., Pérez, J. R., and Bueno, E. J. (2022). Design and analysis of parallel-connected grid-forming virtual synchronous machines for island and grid-connected applications. IEEE Trans. Power Electron.37 (5), 5107–5121. doi:10.1109/tpel.2021.3127463

CrossRef Full Text | Google Scholar

Carrasco, J. M., Franquelo, L., Bialasiewicz, J., Galvan, E., PortilloGuisado, R., Prats, M., et al. (2006). Power-electronic systems for the grid integration of renewable energy sources: A survey. IEEE Trans. Ind. Electron53 (4), 1002–1016. doi:10.1109/tie.2006.878356

CrossRef Full Text | Google Scholar

Chen, Y., Hesse, R., Turschner, D., and Beck, H.-P. (2012). “Comparison of methods for implementing virtual synchronous machine on inverters,” in International Conference on Renewable Energies and Power Quality, Santiago de Compostela, Spain, March 28-30, 2012, 1–6.

CrossRef Full Text | Google Scholar

Chen, Y., Hesse, R., Turschner, D., and Beck, H. -P. (2011). “Improving the grid power quality using virtual synchronous machines,” in Proceedings.2011 International Conference on Power Engineering, Energy and Electrical Drives, Malaga, Spain, May 11-13, 2011, 1–6.

CrossRef Full Text | Google Scholar

Egwebe, A. M., Fazeli, M., Igic, P., and Holland, P. M. (2016). Implementation and stability study of dynamic droop in islanded microgrids. IEEE Trans. Energy Convers.31 (3), 821–832. doi:10.1109/tec.2016.2540922

CrossRef Full Text | Google Scholar

Elrayyah, A., Sozer, Y., and Elbuluk, M. (2015). Microgrid-connected PV-based sources: A novel autonomous control method for maintaining maximum power. IEEE Ind. Appl. Mag.21 (2), 19–29. doi:10.1109/mias.2014.2345822

CrossRef Full Text | Google Scholar

Fang, J., Deng, H., Tashakor, N., Frede, B., and Goetz, S. M. (2023). State-space modeling and control of grid-tied power converters with capacitive/battery energy storage and grid-supportive services. IEEE J. Emerg. Sel. Top. Power Electron.11 (1), 234–250. doi:10.1109/jestpe.2021.3101527

CrossRef Full Text | Google Scholar

Frede, B., Teodorescu, R., Liserre, M., and Timbus, A. (2006). Overview of control and grid synchronization for distributed power generation systems. IEEE Trans. Ind. Electron.53 (5), 1398–1409. doi:10.1109/tie.2006.881997

CrossRef Full Text | Google Scholar

Guerrero, J. M., GarciadeVicuna, L., Matas, J., Castilla, M., and Miret, J. (2005). Output impedance design of parallel-connected UPS inverters with wireless load-sharing control. IEEE Trans. Ind. Electron52 (4), 1126–1135. doi:10.1109/tie.2005.851634

CrossRef Full Text | Google Scholar

He, J., and Li, Y. M. (2011). Analysis, design, and implementation of virtual impedance for power electronics interfaced distributed generation. IEEE Trans. Ind. Appl.47 (6), 2525–2538. doi:10.1109/tia.2011.2168592

CrossRef Full Text | Google Scholar

Hesse, R., Turschner, D., and Beck, H.-P. (2009). “Microgrid stabilization using the virtual synchronous machine (VISMA),” in Proceedings International Conference on Renewable Energies and Power Quality (ICREPQ’09), Valencia, Spain, April 15-17, 2009, 676–681.

CrossRef Full Text | Google Scholar

Hirase, Y., Abe, K., Sugimoto, K., and Shindo, Y. (2012). A grid connected inverter with virtual synchronous generator model of algebraic type. IEEJ Trans. Power Energy132 (4), 371–380. doi:10.1541/ieejpes.132.371

CrossRef Full Text | Google Scholar

Hirase, Y., Noro, O., Yoshimura, E., Nakagawa, H., Sakimoto, K., and Shindo, Y. (2014). “Virtual synchronous generator control with double decoupled synchronous reference frame for single-phase inverter,” in Proceedings 2014 International Power Electronics Conference (IPEC-Hiroshima 2014 - ECCE ASIA), Hiroshima, Japan, May 18-21, 2014, 1552–1559.

CrossRef Full Text | Google Scholar

Kundur, P., P. (1994). Power system stability and control. New York, NY: McGraw-Hill.

Google Scholar

Liu, H. P., Loh, P. C., Wang, X., Yang, Y., Wang, W., and Xu, D. (2016b). Droop control with improved disturbance adaption for a PV system with two power conversion stages. IEEE Trans. Ind. Electron63 (10), 6073–6085. doi:10.1109/tie.2016.2580525

CrossRef Full Text | Google Scholar

Liu, H. P., Yang, Y., Wang, X., Loh, P. C., Blaabjerg, F., Wang, W., et al. (2016a). An enhanced dual droop control scheme for resilient active power sharing among paralleled two-stage converters. IEEE Trans. Power Electron32 (8), 6091–6104. doi:10.1109/tpel.2016.2614324

CrossRef Full Text | Google Scholar

Liu, J., Miura, Y., and Ise, T. (2016). Comparison of dynamic characteristics between virtual synchronous generator and droop control in inverter-based distributed generators. IEEE Trans. Power Electron31 (5), 3600–3611. doi:10.1109/tpel.2015.2465852

CrossRef Full Text | Google Scholar

Rosso, R., Engelken, S., and Liserre, M. (2019). Robust stability analysis of synchronverters operating in parallel. IEEE Trans. Power Electron.34 (11), 11309–11319. doi:10.1109/tpel.2019.2896707

CrossRef Full Text | Google Scholar

Sakimoto, K., Miura, Y., and Ise, T. (2012). Stabilization of a power system including inverter type distributed generators by the virtual synchronous generator. IEEJ Trans. Power Energy132 (4), 341–349. doi:10.1541/ieejpes.132.341

CrossRef Full Text | Google Scholar

Shintai, T., Miura, Y., and Ise, T. (2014). Oscillation damping of a distributed generator using a virtual synchronous generator. IEEE Trans. Power Del.29 (2), 668–676. doi:10.1109/tpwrd.2013.2281359)

CrossRef Full Text | Google Scholar

Tan, K. T., So, P. L., Chu, Y. C., and Chen, M. Z. Q. (2013). Coordinated control and energy management of distributed generation inverters in a microgrid. IEEE Trans. Power Del.28 (2), 704–713. doi:10.1109/tpwrd.2013.2242495

CrossRef Full Text | Google Scholar

Shintai, T., Miura, Y., and Ise, T. (2012). ‘Reactive power control for load sharing with virtual synchronous generator control,’ in Proceedings of the 7th International Power Electronics and Motion Control Conference–ECCE Asia, Harbin, China, June 2-5, 2012, 846–853.

CrossRef Full Text | Google Scholar

Ulbig, A., Borsche, T. S., and Andersson, G. (2014). Impact of low rotational inertia on power system stability and operation. IFAC Proc. Vol.44 (3), 7290–7297. doi:10.3182/20140824-6-za-1003.02615

CrossRef Full Text | Google Scholar

van Wesenbeeck, M. P. N., de Haan, S. W. H., Varela, P., and Visscher, K. (2009). “Grid tied converter with virtual kinetic storage,” in Proceedings 2009 IEEE Bucharest PowerTech, Bucharest, Romania, June 28-July 2, 2009, 1–7.

CrossRef Full Text | Google Scholar

Vandoorn, T. L., Meersman, B., Degroote, L., Renders, B., and Vandevelde, L. (2011). A control strategy for islanded microgrids with DC-link voltage control. IEEE Trans. Power Del26 (2), 703–713. doi:10.1109/tpwrd.2010.2095044

CrossRef Full Text | Google Scholar

Vandoorn, T. L., Meersman, B., De Kooning, J. D. M., and Vandevelde, L. (2012). Analogy between conventional grid control and islanded microgrid control based on a global DC-link voltage droop. IEEE Trans. Power Del27 (3), 1405–1414. doi:10.1109/tpwrd.2012.2193904

CrossRef Full Text | Google Scholar

Visscher, K., and De Haan, S. W. H. (2008). “Virtual synchronous machines (VSG’s) for frequency stabilisation in future grids with a significant share of decentralized generation,” in Proceedings CIRED Seminar 2008: SmartGrids for Distribution, Frankfurt, June 23-24, 2008, 1–4.

Google Scholar

Vu Van, T., Visscher, K., Diaz, J., Karapanos, V., Woyte, A., Albu, M., et al. (2010). “Virtual synchronous generator: An element of future grids,” in Proceedings 2010 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT Europe), Gothenburg, Sweden, October 11-13, 2010, 1–7.

CrossRef Full Text | Google Scholar

Wang, C., and Nehrir, M. H. (2008). Power management of a stand-alone wind/photovoltaic/fuel cell energy system. IEEE Trans. Energy Convers.23 (3), 957–967. doi:10.1109/tec.2007.914200

CrossRef Full Text | Google Scholar

Wu, H., Ruan, X., Yang, D., Chen, X., Zhao, W., Lv, Z., et al. (2016). Small-Signal modeling and parameters design for virtual synchronous generators. IEEE Trans. Ind. Electron.63 (7), 4292–4303. doi:10.1109/tie.2016.2543181

CrossRef Full Text | Google Scholar

Yang, C., Huang, L., Xin, H., and Ju, P. (2021). Placing grid-forming converters to enhance small signal stability of PLL-integrated power systems. IEEE Trans. Power Syst.36 (4), 3563–3573. doi:10.1109/tpwrs.2020.3042741

CrossRef Full Text | Google Scholar

Yang, X. Y., Jian-hui, S., Ming, D., Jin-wei, L., and Yan, D. (2011). “Control strategy for virtual synchronous generator in microgrid,” in Proceedings 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Weihai, China, July 6-9, 2011, 1633–1637.

Google Scholar

Zhong, Q. C., and Weiss, G. (2011). Synchronverters: Inverters that mimic synchronous generators. IEEE Trans. Ind. Electron58 (4), 1259–1267. doi:10.1109/tie.2010.2048839

CrossRef Full Text | Google Scholar

Zhu, J., Gao, F., Liu, X., and Xiao, J. (2017). “A control method to mimic synchronous generator characteristics for two-stage converters,” in Proceedings 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, October 1-5, 2017, 2927–2933.

CrossRef Full Text | Google Scholar