Hierarchical transactive power exchange method on expressways for EV energy supplement

Electric vehicle (EV) users’ driving requirement is restricted by the long charging period and high cost. In this paper, a hierarchical transactive power exchange method on expressways is proposed to eliminate range anxiety faced by EV users and further reduce their cost. When EVs are driven on expressways, battery swapping is considered the suitable power exchange mode due to high efficiency and adjustability. EVs are scheduled to supplement energy in battery swapping stations (BSSs) according to the remaining energy and battery swapping cost. Then, the power exchange among batteries and the power grid in BSSs is optimized for reducing the operation cost. In the optimization process, battery-to-battery and battery-to-grid modes are considered for reducing the power cost in the high electric price period. Some EVs release battery energy in designated BSSs and supplement energy in other BSSs. It reduces fast charging power of the battery and operation costs in designated BSSs. Several case studies are presented to validate the effectiveness and economy of the proposed method.

1 Introduction

Electric vehicles (EVs) have gained significant attention due to their environmentally friendly characteristics (Liu et al., 2018; Ban et al., 2019; Fang et al., 2021). To promote EV development, the governments have implemented a series of relevant policies, such as driving restrictions and purchase subsidies (Haddadian et al., 2015). Consequently, it is expected that the number of EVs increases rapidly (Shao et al., 2017; Park et al., 2022). The proliferating number of EVs brings flexible resources to the power grid and provides promising solutions to improve power grid operation (Cao et al., 2022; Jozi et al., 2022). However, EV users’ driving requirement is restricted by the long charging period and high cost.

EV charging power is coordinated for satisfying users’ driving requirements. Liu et al. (2013) adaptively adjusted the charging power according to the battery’s state-of-charge (SOC) and EV plug-out time. This method satisfied various EV owners’ charging requirements and reduced the adverse impact of the massive charging loads integrated into the power grid. Luo et al. (2020) and Shen et al. (2021) coordinated the charging period of diverse EVs according to the plug-in period and load curve of the power grid. It reduced the power cost through peak-load shifting. López et al. (2015) dispatched the charging power in the load valley period. It improved the local consumption of renewable energy generation. The charging requirements of EV users were successfully satisfied in these methods by coordinating the charging power and periods. Meanwhile, the normal operation of the power grid was maintained.

In 1998, fast charging was proposed for supplementing energy in EVs within a short period (Kutkut et al., 1998). Duan et al. (2021) proposed a fast-charging method to improve EV users’ experience. Moradipari et al. (2020) stated that the real-time navigation guided EVs driving toward fast-charging stations to reduce the queuing time and improve the owners’ experience. These methods significantly reduced the charging period and expanded EVs’ driving range.

Zhang et al. (2020) integrated the interests of traffic networks into power distribution systems and the fast-charging station joint planning model. Through the information interaction, EV driving became more convenient. Gjelaj et al. (2020) proposed a stochastic planning method of the direct-current fast-charging stations that considered the EV driving route. The method significantly improved the user’s experience due to the short charging period. However, fast charging significantly accelerates the cycle aging of the battery. It results in an exorbitant battery degradation cost (BDC).

BSSs play a crucial role in promoting a sustainable EV ecosystem (Zulkarnain et al., 2014; Adepetu et al., 2016). The stations could reduce the BDC and EV charging period by extending the battery charging period and increasing the battery reserve (Ding et al., 2022; Kocer et al., 2022). Choi et al. (2020), Zhang et al. (2020), and Cui et al. (2023) stated that batteries in BSSs are centrally charged during the low electricity price period. It reduces BSSs’ operation cost and EV charging cost. Infante et al. (2018) proposed a two-level hierarchical BSS model, including the unit model and the station model. The unit model used a transition-based modeling technique, which allows the observation from a bottom-up approach on battery allocation. The station model acted as a system-view platform to evaluate operational strategies for BSS, considering BDC, users’ behavior, and supplementary grid services. Infante et al. (2020) proposed that the link between the electricity network and transport network provided opportunities for BSSs with a strategic optimization scheme. In these approaches, BSSs not only effectively satisfy users’ requirements but also improve the operation condition of the power grid.

In order to further reduce EV users’ cost and eliminate their range anxiety on the expressways, a hierarchical transactive power exchange method where EV supplements energy in a cost-effective manner is proposed in this paper. To satisfy users’ driving requirements, EVs driving on expressways are dispatched to BSSs at a lower level. In the process, the BSS energy storage situation, EV’s remaining energy, and moving energy consumption are considered. At the middle level, the power exchange among batteries and the power grid is optimized in each BSS. In this process, multiple power exchange modes, such as fast charging, battery-to-battery (B2B), and battery-to-grid (B2G), are coordinated. At the upper level, some EVs release energy in the BSSs at exorbitant costs. In the process, the fast-charging power in BSSs is reduced, and the parameters at lower and middle levels are changed.

The remainder of this paper is organized as follows: in Section 2, the system model is presented. The proposed hierarchical transactive power exchange method is presented in Section 3. In Section 4, the Hungarian assignment and particle swarm optimization algorithms are adopted to optimize the whole power exchange scheme. Extensive case studies are presented and discussed in Section 5. Conclusion is given in Section 6.

2 System model

2.1 Power exchange system

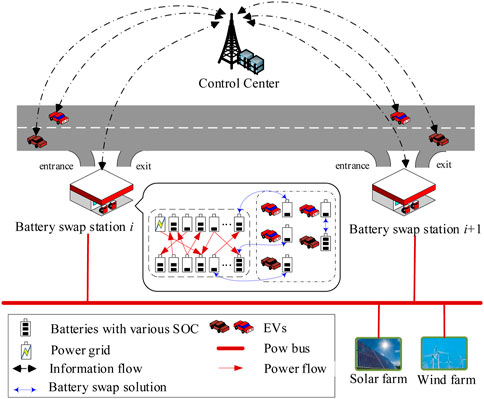
Figure 1 shows that the hierarchical transactive power exchange system on expressways includes the control center, the power grid, BSSs, and EVs. EVs are dispatched to BSSs according to the BSS energy storage situation, EV remaining energy, and moving energy consumption. In BSSs, the power exchange among the power grid and batteries is performed. When the BSS operates at an exorbitant cost, some EVs are encouraged to release energy in the BSS and supplement energy in other BSSs.

FIGURE 1

FIGURE 1. Framework of the proposed power exchange system.

The control center collects information from EVs, BSSs, and the power grid (e.g., SOC of batteries and forecast electricity price). According to the collected information, the power exchange schemes are optimized in the control center, and the results are sent to EVs and BSSs. When BSSs operate at prohibitive costs, EVs will be considered the energy prosumers in the optimized process.

The control center collects information from EVs. It increases the risk of privacy leakage. Privacy protection could be performed by increasing the difficulty and cost of privacy leakage. The following measures can be adopted:

1) Hidden EV user’s information. It increased the difficulty and the time cost of privacy leakage (Efthymiou et al., 2010; Su et al., 2019).

2) Entrust the third parties to manage the data. The parties could protect data professionally (Hur, 2013; Ruj et al., 2013).

3) Severe penalties for information disclosure should be imposed.

2.2 Power exchange model

To reduce BSSs’ operation and power costs, the process of EV supplementing energy is hierarchical. At the lower level, EVs are dispatched to BSSs for satisfying users’ driving requirements. For providing sufficient swappable batteries economically in each BSS, the power exchange among batteries and the power grid is performed at the middle level. At the upper level, some EVs release energy in the BSS which operates at exorbitant costs and supplement energy in other BSSs. It is worth noting that the power exchange scheme at the upper level will cause the updated schemes at lower and middle levels. The power exchange model is shown as follows (1):

${\mathit{C}}_{EV}={\mathit{P}}_{EV}^{up}\cdot \mathit{E}\mathit{P}{\mathit{P}}^{\omega }+{\mathit{C}}_{BD}-{\mathit{P}}_{EV}^{down}\cdot \mathit{E}\mathit{S}{\mathit{P}}^{\omega },(1)$

${\mathit{C}}_{EV}={\left[C_1,C_2,\cdots ,C_{N_L}\right]}^{\omega },{\mathit{C}}_{BD}={\left[C_{BD,1},C_{BD,2},\cdots ,C_{BD,N_L}\right]}^{\omega },(2)$

$\left\{\begin{array}{l}\mathit{E}\mathit{P}\mathit{P}={\left[a_{p,1},a_{p,2},\cdots ,a_{p,N_L}\right]}^{\omega },\mathit{E}\mathit{S}\mathit{P}={\left[a_{s,1},a_{s,2},\cdots ,a_{s,N_L}\right]}^{\omega },\\ {\mathit{P}}_{EV}^{up}=Q_{EV}\cdot {\left[\Delta SO{C}_1^{up},\Delta SO{C}_2^{up},\cdots ,\Delta SO{C}_{N_L}^{up}\right]}^{\omega },\\ {\mathit{P}}_{EV}^{down}=Q_{EV}\cdot {\left[\Delta SO{C}_1^{down},\Delta SO{C}_2^{down},\cdots ,\Delta SO{C}_{N_L}^{down}\right]}^{\omega },\end{array}\right.(3)$

where C_EV represents the cost matrix of EVs. ${\mathit{P}}_{EV}^{up}$ and ${\mathit{P}}_{EV}^{down}$ represent the supplement energy and the releasing energy matrixes of EVs, respectively. C_BD represents the BDC matrix of EVs. EPP^ω and ESP^ω represent the transposition of energy purchasing and selling price matrixes, respectively. a_p,l and a_s,l represent the electricity purchasing and selling prices, respectively. Q_EV represents the battery capacity. $\Delta SO{C}_1^{up}$ and $\Delta SO{C}_1^{down}$ represent the increasing and decreasing SOC of an EV battery, respectively. N_L represents the number of EVs at lower power exchange.

In (1), the cost matrix of EVs includes the power purchase cost and BDC. The power purchase cost and the power selling income depend on the real-time electricity prices and power cost. The cost at the middle level is reflected by electricity prices and the number of dispatched EVs.

3 Problem formulation of battery swapping

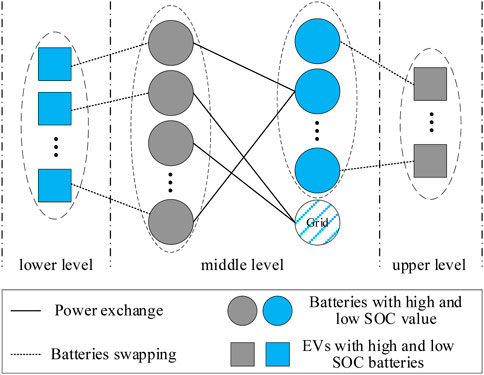
Figure 2 shows that EVs are dispatched to various BSSs for supplementing energy at a lower level. At the middle level, the power exchange among the batteries and the power grid is performed in each BSS. At the upper level, some EVs release energy in BSSs at exorbitant operation costs. It is worth noting that the power exchange at the upper level will change the power exchange scheme at other levels.

FIGURE 2

FIGURE 2. Proposed hierarchical power exchange method.

3.1 Battery swapping at the lower level

At the lower level, EVs are dispatched to various BSSs. The dispatching optimization model is established as follows:

$\mathit{min}\hspace{0.33em}{\displaystyle \sum _{l=1}^{N_L}}{C}_l={\displaystyle \sum _{l=1}^{N_L}}\left(a_{p,l}\cdot \Delta SO{C}_l^{up}\cdot Q_{EV}+C_{BD,l}\right),(4)$

$\mathrm{s}.\mathrm{t}.C_{BD,l}={\alpha }_1\left(P_l{\left(t\right)}^{{\beta }_1}+{\alpha }_2{\left(1-SO{C}_l\left(t\right)\right)}^{{\beta }_2}\right),(5)$

$\left\{\begin{array}{l}0<v_l\left(t\right)\le v_{\mathit{max}},\\ 0\le \Delta SO{C}_l^{up}\le \Delta SO{C}_{\mathit{max}},\\ \Delta {SOC}_{\mathit{max}}={SOC}_{\mathit{max}}-{SOC}_{\mathit{min}},\end{array}\right.\Rightarrow \left\{\begin{array}{l}0<P_l\left(t\right)\le v_{\mathit{max}}\cdot {\psi }_l,\\ {SOC}_{\mathit{min}}\le SO{C}_l\left(t\right)\le {SOC}_{\mathit{max}},\end{array}\right.(6)$

$a_{p,l}={\displaystyle \sum _{b=1}^{N_b}}{a}_{p,b}\cdot \Delta SO{C}_{l,b}^{up}\cdot Q_{EV}/{\displaystyle \sum _{b=1}^{N_b}}\Delta SO{C}_{l,b}^{up}\cdot Q_{EV},(7)$

$\left\{\begin{array}{l}{Q}_{EV}\cdot \left(SO{C}_l\left(t\right)-{SOC}_{\mathit{min}}\right)\ge D_{ad,l}\cdot {\psi }_l,\\ D_{ad,l}=\mathit{min}\left(D_{1,l},D_{2,l},\cdots ,D_{n,l},\cdots ,D_{N_B,l}\right)\ge 0,\end{array}\right.(8)$

where C_l represents the cost of the lth EV. C_BD,l represents the BDC of the lth EV battery. P_l represents the power consumption of the EV. α₁, α₂, β₁, and β₂ represent the battery degradation cost parameters. SOC_l represents the SOC value of the EV battery. v_l and v_max represent the speed and maximum speed of the moving EV, respectively. SOC_max and SOC_min represent the maximum and minimum SOC of the battery, respectively. D_n,l and D_ad,l represent the distance and minimum distance between the BSS and the lth EV, respectively. N_B represents the number of batteries in the BSS. ψ_l represents the unit moving energy cost of the EV.

In (4), the optimization object is the minimum EV cost. The number of EVs dispatched to each BSS is considered the decision variable. EV’s moving energy consumption accelerates the cycle aging of batteries, and the BDC is formulated as shown in (5). In (6), the real-time output power is constrained within the rational range, and the real-time SOC of batteries is constrained for preserving batteries from over-discharge. In BSSs, the energy price for EVs fluctuates, as shown in (7). The remaining energy of EV batteries is constrained, as shown in (8).

3.2 Power exchange at the middle level

At the middle level, the power exchange among batteries and the power grid is performed in each BSS. The optimization model is established as follows:

$\mathit{min}\hspace{0.33em}{C}_b=\left({\displaystyle \sum _{b=1}^{N_b}}{C}_{BD,b}+{\displaystyle \sum _{b=1}^{N_b-1+1}}{a}_{ch,b}\cdot P_b\right),(9)$

$\mathrm{s}.\mathrm{t}.a_{ch,b}=\frac{{\displaystyle \sum _{t_0}^{t_{end}}}{a}_{p,grid}\left(t\right)\cdot P_{b-grid}\left(t\right)+{\displaystyle \sum _{t_0}^{t_{end}}}{a}_{p,grid}\left(t\right)\cdot P_{b-b^{\prime }}\left(t\right)+C_{BD,b^{\prime }}}{{\displaystyle \sum _{t_0}^{t_{end}}}{P}_{b-grid}\left(t\right)+{\displaystyle \sum _{t_0}^{t_{end}}}{P}_{b-b^{\prime }}\left(t\right)},(10)$

$\left\{\begin{array}{c}{C}_{BD,b}={\displaystyle \sum _{t_0}^t}\left({\alpha }_1\left(P_b{\left(t\right)}^{{\beta }_1}+{\alpha }_2{\left(1-SO{C}_b\left(t\right)\right)}^{{\beta }_2}\right)\right),\\ P_b={\displaystyle \sum _{t_0}^t}{P}_b\left(t\right)={\displaystyle \sum _{t_0}^t}{\displaystyle \sum _{b^{\prime }=1}^{N_B-1+1}}{P}_{b-b^{\prime }}\left(t\right),t_0\le t\le t_{end},\end{array}\right.(11)$

$\begin{array}{ll}\hfill & \hfill \left\{\begin{array}{l}{P}_{b-b^{\prime }}\left(t\right)=\mathit{min}\left(P_{b,\mathrm{r}\mathrm{e}\mathrm{m}}\left(t\right),-P_{b^{\prime },rem}\left(t\right)\right),\\ P_{b,\mathrm{r}\mathrm{e}\mathrm{m}}\left(t\right)=P_b\left(t\right)-{\displaystyle \sum _{b^{\prime }=1}^{n_b}}{P}_{b-b^{\prime }}\left(t\right),P_{b^{\prime },rem}\left(t\right)=P_{b^{\prime }}\left(t\right)-{\displaystyle \sum _{b=1}^{n_b}}{P}_{b^{\prime }-b}\left(t\right)\\ P_{\mathrm{G}\mathrm{r}\mathrm{i}\mathrm{d}}\left(t\right)={\left.P_{b,\mathrm{r}\mathrm{e}\mathrm{m}}\left(t\right)\right|}_{n_b=N_b-1}+{\left.P_{b^{\prime },rem}\left(t\right)\right|}_{n_b=N_b-1},\end{array}\right.\\ \hfill & \Rightarrow \left\{\begin{array}{l}{P}_b\left(t\right)=P_{b-\mathrm{g}\mathrm{r}\mathrm{i}\mathrm{d}}\left(t\right)+{\displaystyle \sum _{b^{\prime }=1}^{N_b-1}}{P}_{b-b^{\prime }}\left(t\right),P_{b-\mathrm{g}\mathrm{r}\mathrm{i}\mathrm{d}}\left(t\right)\ge 0,\\ P_{b^{\prime }}\left(t\right)=P_{\mathrm{g}\mathrm{r}\mathrm{i}\mathrm{d}-b}\left(t\right)+{\displaystyle \sum _{b=1}^{N_b-1}}{P}_{b^{\prime }-b}\left(t\right),P_{\mathrm{g}\mathrm{r}\mathrm{i}\mathrm{d}-b^{\prime }}\left(t\right)\ge 0,\\ P_{\mathrm{G}\mathrm{r}\mathrm{i}\mathrm{d}}\left(t\right)={\displaystyle \sum _{b=1}^{N_b}}{P}_b\left(t\right)\ge \mathrm{0,0}\le P_b\left(t\right)\le P_{ch,\mathit{max}},-P_{dis,\mathit{max}}\le P_{b^{\prime }}\left(t\right)\le 0,\end{array}\right.\hfill \end{array}(12)$

$\left\{\begin{array}{l}SO{C}_b\left(t_{end}\right)\ge S{T}_b={SOC}_{\mathit{max}}-{SOC}_{dev},\\ {SOC}_{\mathit{min}}\le SO{C}_b\left(t\right)\le {SOC}_{\mathit{max}},\end{array}\right.(13)$

$\left(S{T}_b-SO{C}_b\left(t\right)\right)Q_{EV}\le {\displaystyle \sum _t^{t_{end}}}{P}_b\left(t\right)\le \left({SOC}_{\mathit{max}}-SO{C}_b\left(t\right)\right)Q_{EV},(14)$

$\left\{\begin{array}{c}SO{C}_{b^{\prime }}\left(t\right)\ge SO{C}_{\mathit{min}}\\ SO{C}_{b^{\prime }}\left(t\right)\le SO{C}_{\mathit{max}}\end{array}\right.\Rightarrow {\displaystyle \sum _t^{t_{end}}}{P}_{b^{\prime }}\left(t\right)\ge \left({SOC}_{\mathit{min}}-SO{C}_{b^{\prime }}\left(t\right)\right)Q_{EV},(15)$

$\left\{\begin{array}{l}SO{C}_b\left(t+\Delta t\right)=SO{C}_b\left(t\right)+\frac{P_b\left(t\right)}{Q_{EV}}\ge SO{C}_b\left(t\right),\\ SO{C}_{b^{\prime }}\left(t+\Delta t\right)=SO{C}_{b^{\prime }}\left(t\right)+\frac{P_{b^{\prime }}\left(t\right)}{Q_{EV}}\le SO{C}_{b^{\prime }}\left(t\right),\end{array}\right.(16)$

$\left\{\begin{array}{l}{N}_b\ge N_{b,l}\left(t\right)\Rightarrow {\displaystyle \sum _{b=1}^{N_B}}{N}_b\ge N_L\left(t\right),\\ n_b\left(t\right){|}_{SOC\ge \left({SOC}_{\mathit{max}}-{SOC}_{dev}\right)}\ge N_{b,l}\left(t\right),\end{array}\right.(17)$

where C_b represents the operation cost of the bth BSS. a_ch,b and a_p,grid represent the electricity prices of charging the battery and the power grid, respectively. P_b represents the charging power of the battery. P_Grid represents the output power of the power grid. P_b-grid represents the power that battery charges from the grid. P_b-b’ represents the B2B power. P_b,rem represents the battery’s unmatched optimization power. ST_b represents the desired SOC of the battery. SOC_dev represents the allowable SOC deviation of the battery. N_b,l represents the number of EVs dispatched to the lth BSS. N_B represents the number of BSSs. b and b' represent the indexes for the number of batteries and discharging batteries, respectively. P_ch,max and P_dis,max represent the maximum charging and discharging power of batteries, respectively. Δt represents the time interval. t₀ and t_end represent the initial and end of a certain period, respectively.

The power exchange performed in each BSS aims to reduce the operation cost, and the BSS’s minimum operation cost is the optimization object, as shown in (9). The total charging power of the BSS is considered the decision variable. In (10), the electricity price of BSSs is defined, and it depends on the power cost and BDC. The BDC is defined in (11). Each battery could match with multiple objects. In (12), the exchanged power is limited by the smaller power of matchable objects. The charging power and discharging power are both limited in the rational range. The SOC of the battery is constrained, as shown in (13) and (15). During the charging period, the real-time SOC of the charging batteries is constrained for preventing over-charging of the battery, and the battery’s power range is concluded as (14). During the discharging period, the real-time SOC of the battery is constrained for preventing over-discharging of the battery, and the battery’s power range is concluded as (15). The real-time SOC of the battery is updated and limited, as shown in (16). At the middle level, each BSS satisfies users’ driving requirements. Therefore, the number of batteries with the designated SOC value is constrained, as shown in (17).

3.3 Battery swapping at the upper level

At the upper level, some EVs release energy in BSSs, which operate at exorbitant operation costs, and supplement energy in other BSSs. The optimization model is established as follows:

$\mathit{max}\hspace{0.33em}{\displaystyle \sum _{u=1}^{N_u}}{R_u}^{\prime }=\lambda {\displaystyle \sum _{u=1}^{N_u}}{}_u=\lambda R_{BSS}>0,(18)$

$\mathrm{s}.\mathrm{t}.R_{BSS}=C_n{|}_{\mu -1}+C_{n+1}{|}_{\mu }+\cdots +C_{N_B}{|}_{\mu }-C_n{|}_{\mu },(19)$

$\Delta SO{C}_u^{up}+\Delta SO{C}_u^{down}-{\psi }_u\cdot D_{n,u}/Q_{EV}\ge 0,(20)$

$\left\{\begin{array}{c}{SOC}_{\mathit{min}}\le SO{C}_{m,u}\le {SOC}_{\mathit{max}},\\ {SOC}_{\mathit{min}}\le SO{C}_{m^{\prime },u}\le {SOC}_{\mathit{max}},\end{array}\right.(21)$

$SO{C}_{m^{\prime },u}-{SOC}_{\mathit{min}}\ge D_{ad,u}\cdot \frac{{\psi }_u}{Q_{EV}},(22)$

where R_u represents the decreasing cost of BSSs due to the uth EV releasing energy. R_u’ represents the income of the uth EV. R_BSS represents the decreasing cost of the BSS. C_n|_u represents the cost of the nth BSS that u EVs join in the upper power exchange. N_u represents the number of EVs at the upper power exchange. λ represents the operation cost ratio of BSSs.

In the optimization model, the maximum profit of users is the objective, and the number of EVs dispatched to BSSs is considered the decision variable. In (18), the users’ reward is dependent on the decreased cost of BSSs. The upper power exchange could avoid fast charging of some batteries and reduce BDC. When the electric price at the period is high, the upper power exchange could reduce the charging power and the power cost. The power cost and BDC in the BSS are decreased and slightly increased in other BSSs. This is because an acceptable number of EVs are dispatched to other BSSs. The fast-charging power in the BSS is decreased, and the charging power in other BSSs is slightly increased. Therefore, the total cost of BSSs is decreased. At the upper power exchange, the BSSs decreased the cost due to EVs releasing energy, and EVs’ extra cost due to supplementing energy in other BSSs is considered, as shown in (19). In (20), EV moving loss is considered, and the residual energy of EV batteries is constrained to ensure that EVs could drive to supplement energy. In (21) and (22), the SOC of batteries is limited in a reasonable range, and the residual energy of EVs is limited by the adjacent BSS’s distance.

4 Hierarchical power exchange algorithm

4.1 Lower power exchange

At the lower power exchange, EVs are dispatched to BSSs for supplementing energy. In this process, the number of EVs dispatched to each BSS is considered the decision variable, and the particle swarm optimization algorithm is applied. The optimization result will have an impact on the optimization process at the middle level.

4.2 Middle power exchange

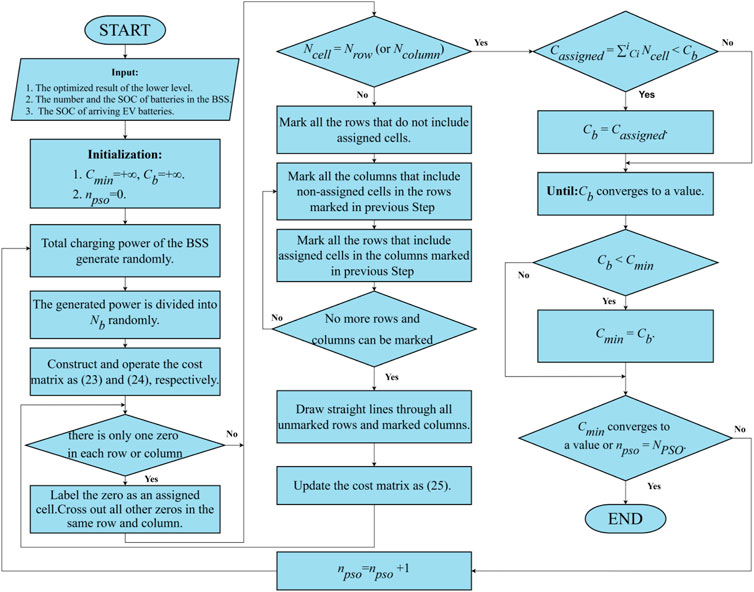
At the middle level, the power exchange among batteries and the power grid is performed in each BSS for reducing the operation cost. This process is considered a power assignment problem. The particle swarm optimization offers several advantages, including a fast rate of convergence, high precision, and simplicity in implementation. On the other hand, the Hungarian algorithm is a combinatorial optimization algorithm used to solve assignment problems efficiently within polynomial time. These algorithms are applied to solve the power assignment problem. The decision variable in this problem is the total charging power of the BSS, and the particle swarm optimization algorithm is employed to obtain the optimal solution. In the power assignment process, the Hungarian algorithm is applied to obtain the batteries’ optimal power exchange scheme at each particle (Zeng et al., 2020). The procedure of the designed algorithm is shown in Figure 3.

$C_{PSO}\left(t\right)=\left[\begin{array}{c}{c}_{11}\left(t\right),c_{12}\left(t\right)\dots c_{1\left(N_b\right)}\left(t\right)\\ c_{21}\left(t\right),c_{22}\left(t\right)\dots \hspace{0.33em}{c}_{2\left(N_b\right)}\left(t\right)\\ ⋮\\ c_{N_{b}1}\left(t\right),c_{N_{b}2}\left(t\right)\dots c_{N_b\left(N_b\right)}\left(t\right)\end{array}\right],(23)$

$\left\{\begin{array}{c}{c}_{ij}=c_{ij}-\mathit{min}\left\{c_{i1},c_{i2},\cdots ,c_{i{N}_b}\right\},i\in \left[\mathrm{1,2},\cdots ,N_b\right],\\ c_{ij}=c_{ij}-\mathit{min}\left\{c_{1j},c_{2j},\cdots ,c_{N_{b}j}\right\},j\in \left[\mathrm{1,2},\cdots ,N_b\right],\end{array}\right.(24)$

$\left\{\begin{array}{c}{c}_{ij}=c_{ij}-\mathit{min}{E}_{un},c_{ij}\in E_{un},\\ c_{ij}^{\prime }=c_{ij}^{\prime }+\mathit{min}{E}_{un},c_{ij}^{\prime }\in E_{co},\end{array}\right.(25)$

where E_un and E_co represent the uncovered elements and the elements covered by two lines, respectively. N_cell represents the number of assigned cells. N_row and N_column represent the row and column number of the matrix, respectively.

FIGURE 3

FIGURE 3. Designed middle power exchange algorithm.

In the optimization process, the operation cost matrix of the BSS is expressed as (23). In the matrix, the number of rows represents that of batteries. The number of columns represents that of the divided power. c_nn in the element represents the corresponding cost generated by the battery charging/discharging. In (24), the calculation rule ensures zero elements in each row and column. In (25), the calculation rule updates the cost matrix.

4.3 Upper power exchange

At the upper power exchange, EVs release energy in the BSS which operates at an exorbitant cost. In the optimization process, the number of EVs dispatched to the BSS is considered the decision variable, and the particle swarm optimization algorithm is applied. After EVs release energy, the number of EVs that supplement energy is changed, and the optimized schemes at the other two levels should be updated.

5 Simulation and discussion

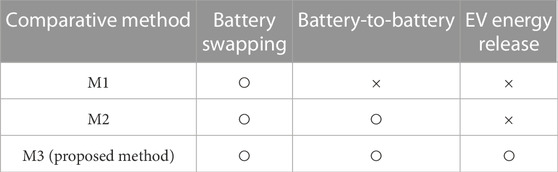
As shown in Table 1, three power exchange methods are employed for verifying the effectiveness of the proposed method.

TABLE 1

TABLE 1. Comparative method characteristics.

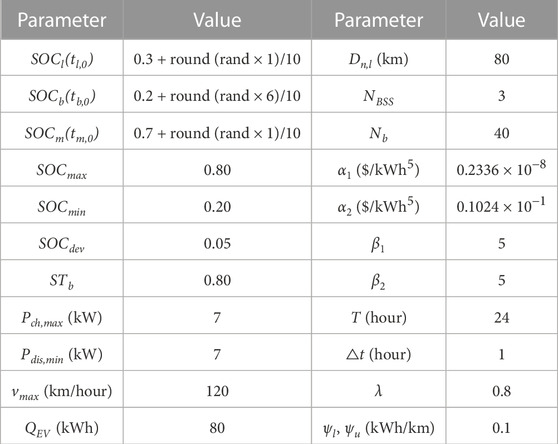
5.1 Simulation parameters

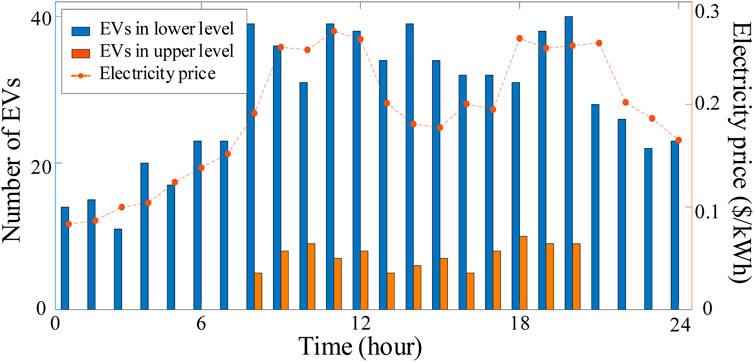
The simulation model parameters are presented in Table 2 (Song et al., 2017; Kim et al., 2018; Zhang et al., 2019). At the upper level, EVs release energy in the first BSS and supplement energy in other BSSs. For simplifying the computation, a_ch,b is assumed to be equal to a_p,l.

TABLE 2

TABLE 2. Simulation parameters.

The initial number of EVs that supplement energy and a_p,grid is dynamic, as shown in Figure 4 (Song et al., 2017). To simplify the simulation process, the BDC resulting from fast charging is assumed as shown in (26):

$C_{BD,b}=C_{BD,b}{|}_{P_b\left(t\right)=P_{ch,\mathit{max}}}\cdot \frac{\left(P_b\left(t\right)-P_{ch,\mathit{max}}\right)}{P_{ch,\mathit{max}}},if{P}_b\left(t\right)>P_{ch,\mathit{max}}.(26)$

FIGURE 4

FIGURE 4. Dynamic parameters in the simulation process.

5.2 Power exchange performance comparison

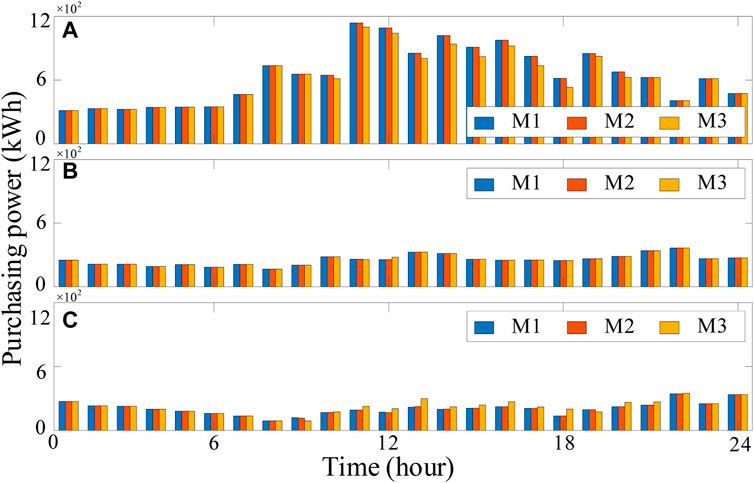
The purchasing power from the power grid using three different methods is shown in Figure 5. During some periods, such as the 01st–07th hours, P_Grid measured using three different methods is equal. Batteries in BSSs are charged from the power grid due to low electricity prices. The low operating cost of the BSS results in few EVs releasing energy. In the 09th hour, P_Grid using M2 is lesser than that using M1 in BSS3. This is because a_p,grid increases, and there is some B2B power in M2. Due to the increased number of dispatched EVs, almost all batteries are charged in BSS1. Therefore, there is less B2B power in BSS1, and P_Grid using M1 and M2 seems to be equal. In BSS2 and BSS3, the distinction between M1 and M2 is imperceptible due to the few dispatched EVs. P_Grid using M3 is significantly less than that using other methods in BSS1 and more than that using other methods in other BSSs. This is because some EVs release energy in BSS1, and the fast-charging power is decreased. However, this process increases the number of EVs that supplement energy in BSS2 and BSS3. EVs centralize supplement energy in BSS1 for reducing the BDC, resulting from EV moving.

FIGURE 5

FIGURE 5. Purchasing power using (A) M1, (B) M2, and (C) M3.

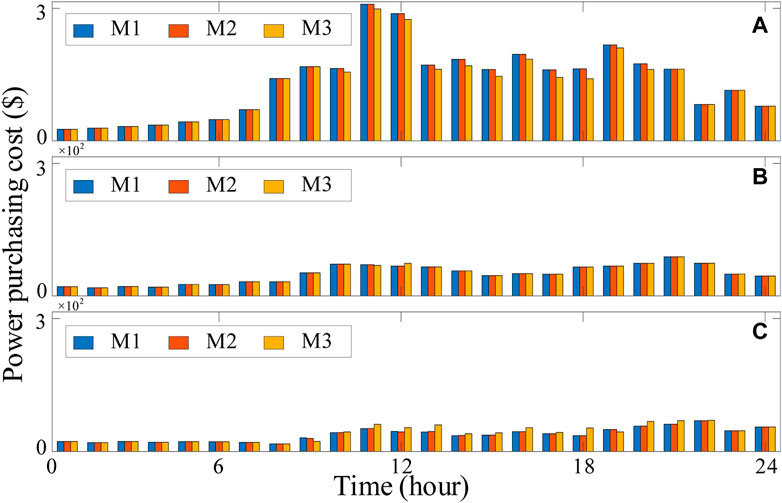
The power purchasing cost measured using three different methods is shown in Figure 6. The cost calculated using M1 and M2 is almost identical due to low electricity prices and less B2B power. The excessive EVs supplement energy in BSS1, resulting in few dischargeable batteries. Few EVs supplement energy in BSS2 and BSS3, resulting in low charging power and low power cost. In M3, the fast-charging power of BSS1 is reduced due to EVs releasing energy. It results in the decreased power cost in BSS1 and increased power cost in BSS2 and BSS3.

FIGURE 6

FIGURE 6. Purchasing power cost using (A) M1, (B) M2, and (C) M3.

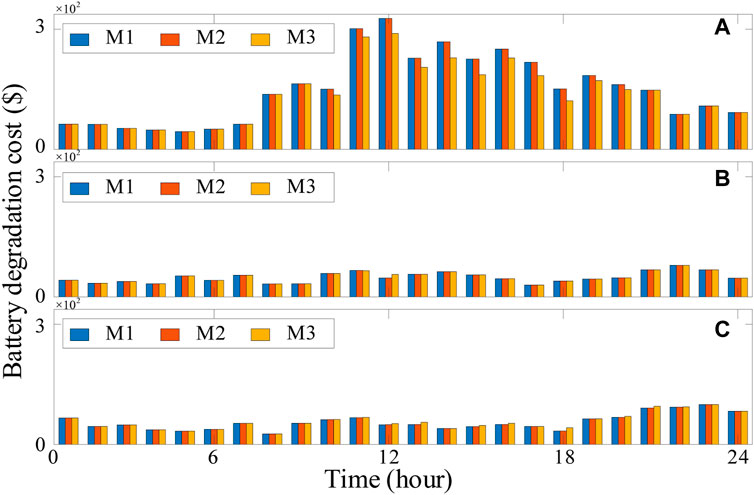
The power exchange schemes result in the inconsistent BDC, as shown in Figure 7. The BDC in BSS1 is more than that in BSS2 and BSS3. It is because EVs centralize supplement energy in BSS1 and fast charging in some batteries takes place. The BDC variance between M1 and M2 is not remarkable. This is because almost all batteries in BSS1 have to charge for excess EVs supplementing energy. With fewer EVs driving to BSS2 and BSS3, BSSs could schedule an economic and elastic charging scheme. The BDC using M3 in BSS1 is less than that using M1 and M2 by reducing the fast-charging power. Meanwhile, it increases the number of EVs that supplement energy in BSS2 and BSS3. The BDC using M3 is a little more than that using M1 and M2 due to an acceptable number of EVs being dispatched to BSS2 and BSS3.

FIGURE 7

FIGURE 7. Battery degradation cost using (A) M1, (B) M2, and (C) M3.

The detailed cost performance is presented in Table 3, and the power purchasing cost is referred to as PPC. According to the analysis shown in Figures 5–7, the power purchasing cost using M2 is less than that using M1 in BSS3 due to the slight B2B power. The BDC using M2 is only a little more than that using M1 in BSS3 due to few discharging batteries. The power purchasing cost using M3 in BSS1 is less than that using M1 and M2 and more in other BSSs. This is because the fast-charging power in BSS1 is decreased and the charging power in other BSSs is increased. The BDC using M3 in BSS1 is less than that using M1 and M2 and more in other BSSs. This is because the fast-charging power in BSS1 is reduced and the charging power in other BSSs is increased.

TABLE 3

TABLE 3. Cost comparison (×10²$).

Figure 8 shows the chosen battery location in each BSS. The charging power and SOC curve of the battery in the locations are presented with the three methods. In BSS1, due to some EVs releasing energy at the upper power exchange, the purchasing power using M3 is reduced significantly during the 14th–17th hours. In BSS2 and BSS3, the purchasing power using M3 increased remarkedly during the 12th–13th hours due to the additional EVs with low SOC batteries generated at the upper level. Batteries in BSS2 and BSS3 need more charging power for meeting owners’ driving requirements. In BSS3, during the 10th hour, the battery using M2 discharged because of the high electric price and idle batteries. The battery charging from other batteries could reduce the BSS’s operation cost. During the 11th hour, the purchasing power with M3 decreased relatively to that with M2. This is because the upper power exchange results in the varying number of EVs driving to BSS3 and the re-optimization for the lower and middle power exchange schemes.

FIGURE 8

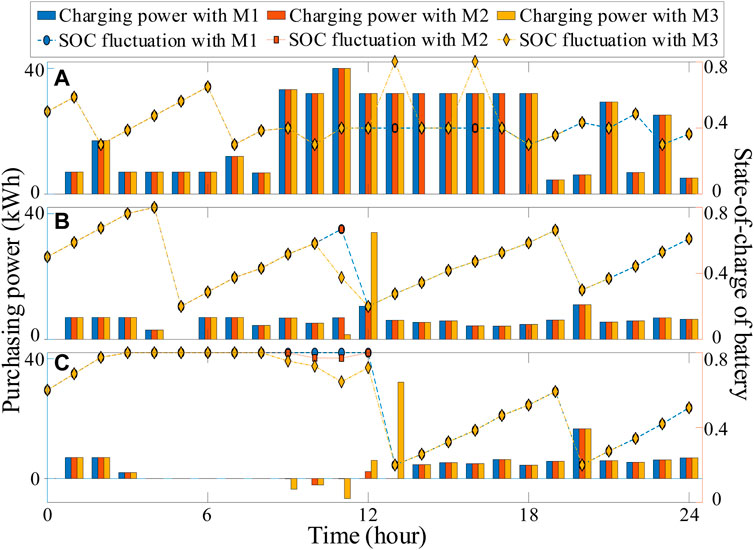
FIGURE 8. Power exchange of (A) location 16 in BSS1, (B) location 21 in BSS2, and (C) location 33 in BSS3.

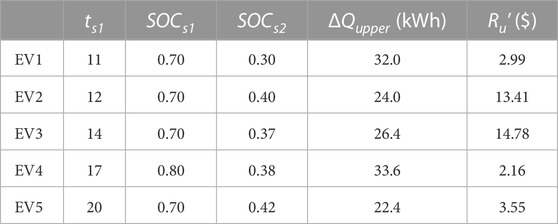
At the upper power exchange, the cost reduction of the randomly chosen EVs is shown in Table 4. EVs swap lower SOC batteries in BSS1 and supplement energy in BSS2 or BSS3. It can be seen from Table 4 that the initial SOC of the EV battery has little impact on the BSSs’ cost. The cost reduction of EV1 is approximately equal to that of EV4, and the cost reduction of EV3 is much more than that of EV4. The initial SOC of the EV1 battery is equal to that of the EV3 battery. This is because the cost reduction is dependent on the BSS’s operation conditions. When the BSS operates at an exorbitant cost, the responsive EVs at the upper power exchange will receive optimistic rewards. The BSS’s cost reduction is considered the user’s contribution, which directly affects their reward.

TABLE 4

TABLE 4. Cost reduction in the upper power exchange.

6 Conclusion

In this paper, a hierarchical transactive power exchange method is proposed to solve EV users’ range anxiety on expressways. At the lower level, EVs are dispatched to supplement energy in various BSSs. At the middle level, BSSs schedule the power exchange scheme that considered the power exchange modes, such as B2G and B2B. At the upper level, some EVs release battery energy in the BSS which operates at exorbitant costs and supplement energy in other BSSs.

The proposed method ensures that EVs supplement energy on expressways in a highly efficient, flexible, and cost-effective manner. To guarantee the normal operation of BSSs, EVs can gradually increase the SOC of batteries by multiple swapping batteries in BSSs. The subject requires additional investigation on how to schedule the rational and economic power exchange schemes.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

All the authors conceptualized and designed the study. LZ: project design, methodology, and writing—original draft preparation. S-ZC: investigation, idea, and supervision. CZ: investigation, idea, and supervision. TX: project administration and writing—review and editing. LT: project administration and writing—review and editing. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the project funded by the China Postdoctoral Science Foundation (2022M720833).

Conflict of interest

Author TX was employed by China Southern Power Grid Guangdong Zhuhai Power Supply Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adepetu, A., Keshav, S., and Arya, V. (2016). An agent-based electric vehicle ecosystem model: San Francisco case study. Transp. Policy46, 109–122. doi:10.1016/j.tranpol.2015.11.012

CrossRef Full Text | Google Scholar

Ban, M., Yu, J., Li, Z., Guo, D., and Ge, J. (2019). Battery swapping: An aggressive approach to transportation electrification. IEEE Electrification Mag.7 (3), 44–54. doi:10.1109/MELE.2019.2925762

CrossRef Full Text | Google Scholar

Cao, Y., Zhou, B., Chung, C. Y., Shuai, Z., Hua, Z., and Sun, Y. (2022). Dynamic modelling and mutual coordination of electricity and watershed networks for spatio-temporal operational flexibility enhancement under rainy climates. IEEE Trans. Smart Grid2022, 1. doi:10.1109/TSG.2022.3223877

CrossRef Full Text | Google Scholar

Choi, D. I., and Lim, D. E. (2020). Analysis of the state-dependent queueing model and its application to battery swapping and charging stations. Sustainability12 (6), 2343. doi:10.3390/su12062343

CrossRef Full Text | Google Scholar

Cui, D., Wang, Z., Liu, P., Wang, S., Dorrell, D. G., Li, X., et al. (2023). Operation optimization approaches of electric vehicle battery swapping and charging station: A literature review. Energy263, 126095. doi:10.1016/j.energy.2022.126095

CrossRef Full Text | Google Scholar

Ding, R., Liu, Z., Li, X., Hou, Y., Sun, W., Zhai, H., et al. (2022). Joint charging scheduling of electric vehicles with battery to grid technology in battery swapping station. Energy Rep.8, 872–882. doi:10.1016/j.egyr.2022.02.029

CrossRef Full Text | Google Scholar

Duan, X., Hu, Z., and Song, Y. (2021). Bidding strategies in energy and reserve markets for an aggregator of multiple ev fast charging stations with battery storage. IEEE Trans. Intelligent Transp. Syst.22 (1), 471–482. doi:10.1109/TITS.2020.3019608

CrossRef Full Text | Google Scholar

Eefthymiou, C., and Kalogridis, G. (2010). “Smart grid privacy via anonymization of smart metering data,” in Proceedings of the 2010 First IEEE International Conference on IEEE, Bangalore, India, August 2010, 238–243. doi:10.1109/SMARTGRID.2010.5622050

CrossRef Full Text | Google Scholar

Fang, B., Li, B., Li, X., Jia, Y., Xu, W., and Li, Y. (2021). Multi-objective comprehensive charging/discharging scheduling strategy for electric vehicles based on the improved particle swarm optimization algorithm. Front. Energy Res.9. doi:10.3389/fenrg.2021.811964

CrossRef Full Text | Google Scholar

Gjelaj, M., Hashemi, S., Andersen, P. B., and Traeholt, C. (2020). Optimal infrastructure planning for EV fast-charging stations based on prediction of user behaviour. IET Electr. Syst. Transp.10 (1), 1–12. doi:10.1049/iet-est.2018.5080

CrossRef Full Text | Google Scholar

Haddadian, G., Khodayar, M., and Shahidehpour, M. (2015). Accelerating the global adoption of electric vehicles – barriers and drivers. Electr. J.28 (10), 53–68. doi:10.1016/j.tej.2015.11.011

CrossRef Full Text | Google Scholar

Hur, J. (2013). Attribute-based secure data sharing with hidden policies in smart grid. IEEE Trans. Parallel & Distributed Syst.24 (11), 2171–2180. doi:10.1109/TPDS.2012.61

CrossRef Full Text | Google Scholar

Infante, W., Ma, J., Han, X., and Liebman, A. (2020). Optimal recourse strategy for battery swapping stations considering electric vehicle uncertainty. IEEE Trans. Intelligent Transp. Syst.21 (4), 1369–1379. doi:10.1109/TITS.2019.2905898

CrossRef Full Text | Google Scholar

Infante, W., Ma, J., and Liebman, A. (2018). Operational strategy analysis of electric vehicle battery swapping stations. IET Electr. Syst. Transp.8 (2), 130–135. doi:10.1049/iet-est.2017.0075

CrossRef Full Text | Google Scholar

Jozi, F., Abdali, A., Mazlumi, K., and Hosseini, S. H. (2022). Reliability improvement of the smart distribution grid incorporating EVs and BESS via optimal charging and discharging process scheduling. Front. Energy Res.10. doi:10.3389/fenrg.2022.920343

CrossRef Full Text | Google Scholar

Kim, J., Lee, J., Park, S., and Choi, J. K. (2018). Battery-wear-model-based energy trading in electric vehicles: A naive auction model and a market analysis. IEEE Trans. industrial Inf.15 (7), 4140–4151. doi:10.1109/TII.2018.2883655

CrossRef Full Text | Google Scholar

Kocer, M. C., Onen, A., Ustun, T. S., and Albayrak, S. (2022). Optimization of multiple battery swapping stations with mobile support for ancillary services. Front. Energy Res.10. doi:10.3389/fenrg.2022.945453

CrossRef Full Text | Google Scholar

Kutkut, N. H., Divan, D. M., Novotny, D., and Marion, R. (1998). Design considerations and topology selection for a 120-kW IGBT converter for EV fast charging. IEEE Trans. Power Electron13 (1), 169–178. doi:10.1109/63.654972

CrossRef Full Text | Google Scholar

Liu, H., Hu, Z., Song, Y., Wang, J., and Xie, X. (2013). Decentralized vehicle-to-grid control for primary frequency regulation considering charging demands. IEEE Trans. Power Syst.30 (3), 3480–3489. doi:10.1109/TPWRS.2013.2252029

CrossRef Full Text | Google Scholar

Liu, H., Huang, K., Yang, Y., Wei, H., and Ma, S. (2018). Real-time vehicle-to-grid control for frequency regulation with high frequency regulating signal. Prot. Control Mod. Power Syst.3 (1), 13. doi:10.1186/s41601-018-0085-1

CrossRef Full Text | Google Scholar

Lopez, M. A., Torre, S. D. L., Martin, S., and Aguado, J. A. (2015). Demand-side management in smart grid operation considering electric vehicles load shifting and vehicle-to-grid support. Int. J. Electr. Power & Energy Syst.64, 689–698. doi:10.1016/j.ijepes.2014.07.065

CrossRef Full Text | Google Scholar

Luo, Y., Feng, G., Wan, S., Zhang, S., Li, V., and Kong, W. (2020). Charging scheduling strategy for different electric vehicles with optimization for convenience of drivers, performance of transport system and distribution network. Energy, 194, 116807–116813. doi:10.1016/j.energy.2019.116807

CrossRef Full Text | Google Scholar

Moradipari, A., and Alizadeh, M. (2020). Pricing and routing mechanisms for differentiated services in an electric vehicle public charging station network. IEEE Trans. Smart Grid11 (2), 1489–1499. doi:10.1109/TSG.2019.2938960

CrossRef Full Text | Google Scholar

Park, K., and Moon, I. (2022). Multi-agent deep reinforcement learning approach for EV charging scheduling in a smart grid. Appl. Energy328, 120111. doi:10.1016/j.apenergy.2022.120111

CrossRef Full Text | Google Scholar

Ruj, S., and Nayak, A. (2013). A decentralized security framework for data aggregation and access control in smart grids. IEEE Trans. Smart Grid4 (1), 196–205. doi:10.1109/TSG.2012.2224389

CrossRef Full Text | Google Scholar

Shao, C., Wang, X., Wang, X., Du, C., and Wang, B. (2016). Hierarchical charge control of large populations of EVs. IEEE Trans. Smart Grid7 (2), 1147–1155. doi:10.1109/TSG.2015.2396952

CrossRef Full Text | Google Scholar

Shen, J., Wang, L., and Zhang, J. (2021). Integrated scheduling strategy for private electric vehicles and electric taxis. IEEE Trans. Industrial Inf.17 (3), 1637–1647. doi:10.1109/TII.2020.2993239

CrossRef Full Text | Google Scholar

Song, M., and Amelin, M. (2017). Purchase bidding strategy for a retailer with flexible demands in day-ahead electricity market. IEEE Trans. Power Syst.32 (3), 1839–1850. doi:10.1109/TPWRS.2016.2608762

CrossRef Full Text | Google Scholar

Su, X., Fan, K., and Shi, W. (2019). Privacy-preserving distributed data fusion based on attribute protection. IEEE Trans. industrial Inf.15 (10), 5765–5777. doi:10.1109/TII.2019.2912175

CrossRef Full Text | Google Scholar

Zeng, L., Li, C., Li, Z., Zhou, B., Liu, H., and Yang, H. (2020). Hierarchical dispatching method based on Hungarian algorithm for reducing the battery degradation cost of EVs participating in frequency regulation. IET Generation Transm. Distribution14 (23), 5617–5625. doi:10.1049/iet-gtd.2020.0754

CrossRef Full Text | Google Scholar

Zhang, Q., Zhu, Y., Wang, Z., Hu, Y., and Su, Y. (2020a). Siting and sizing of electric vehicle fast-charging station based on quasi-dynamic traffic flow. IET Renew. Power Gener.14 (19), 4204–4215. doi:10.1049/iet-rpg.2020.0439

CrossRef Full Text | Google Scholar

Zhang, R., Cheng, X., and Yang, L. (2019). Flexible energy management protocol for cooperative EV-to-EV charging. IEEE Trans. Intelligent Transp. Syst.20 (1), 172–184. doi:10.1109/TITS.2018.2807184

CrossRef Full Text | Google Scholar

Zhang, X., Peng, L., Cao, Y., Liu, S., Zhou, H., and Huang, K. (2020b). Towards holistic charging management for urban electric taxi via a hybrid deployment of battery charging and swap stations. Renew. Energy155, 703–716. doi:10.1016/j.renene.2020.03.093

CrossRef Full Text | Google Scholar

Zulkarnain, Z., Pekka, L., Tuomo, K., and Pekka, K. (2014). The electric vehicles ecosystem model: Construct, analysis and identification of key challenges. Manag. Glob. Transitions12 (3), 253–277. doi:10.1016/j.jtice.2013.12.012

CrossRef Full Text | Google Scholar