
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res., 06 June 2023
Sec. Energy Storage
Volume 11 - 2023 | https://doi.org/10.3389/fenrg.2023.1207194
This article is part of the Research TopicFull Lifecycle Management of Battery Energy Storage SystemsView all 6 articles
Accurate battery capacity estimation can contribute to safe and reliable operations of lithium-ion battery systems. The incremental capacity (IC) based techniques provide promising estimates of battery capacity. However, curve smoothing algorithms are usually required in the IC-based methods, which introduce additional errors and are computationally burdensome. To address this issue, this work proposes a novel approach using multi-voltage-interval IC peaks combined with a back-propagation neural network (BPNN) for battery capacity estimation. Multiple voltage intervals covering relatively narrow and wide values are applied for computing IC curves to enhance the estimation robustness. In particular, there is no need to employ smoothing algorithms. A BPNN is then applied to approximate the correlation between multi-voltage-interval IC peak and capacity. Besides, a five-point moving window technique is proposed to capture multi-voltage-interval IC peaks online effectively. Experimental results show capacity estimates with the majority of relative errors of ±1% and the maximum error of 2%.
With the advantages of high energy density, long cycle life, and no memory effects, lithium-ion battery is preferred as an energy storage device in renewable energy storage systems, smart grids, and electrified transportation (Shi et al., 2021; Su et al., 2022). An efficient battery management system (BMS) with accurate and robust state estimation techniques is indispensable to achieve safe and reliable battery operations. Among the core techniques of BMS, battery capacity estimation plays an essential role in estimating battery state of health (SOH), remaining useful life, and energy capability, but it still poses significant challenges. This is because lithium-ion batteries always demonstrate time-variable and highly nonlinear dynamics, which are involved in complicated electrochemical mechanisms (Deng et al., 2022; Sun et al., 2022).
A considerable amount of research about the techniques of battery capacity estimation and SOH estimation has been reported in the literature (Xiong et al., 2018; Severson et al., 2019; Sulzer et al., 2021; Zhao et al., 2023), in which the model-based methods outperform others in terms of their superior robustness against noise and erroneous initial states (Zheng et al., 2016). Observers with an equivalent circuit model or an electrochemical model are usually deployed in the scheme of the model-based methods for the co-estimation of battery capacity, states, and other parameters (Xiong et al., 2018). However, since cell divergence is ineluctable among battery cells, the model-based methods need to individually identify and update the model parameters for each cell (Feng et al., 2019; Yang et al., 2020). It requires high computational efforts and a high volume of memory in a microprocessor within the BMS, which heavily obstructs their applicability for practical applications.
In recent years, remarkable results have been achieved by applying incremental capacity analysis (ICA) not only for lithium-ion battery aging mechanism identification but also for battery capacity and SOH estimation. The ICA technique transforms a conventional voltage versus capacity curve into an incremental capacity (IC) curve. The shapes, positions, and intensities of IC peaks can be used to characterize the loss of active materials, increase of resistance or loss of lithium inventory (LLI) during battery aging processes. It has been reported that one of the leading causes of lithium-ion battery capacity degradation is the LLI (Liu et al., 2010; Dubarry et al., 2011; Han et al., 2014). For LiFePO4 cells, the LLI is mainly reflected in the IC peak located at the SOC range from about 60% to 90% (Weng et al., 2013; Riviere et al., 2015). Therefore, the IC curves and associated IC peaks can be indicators to estimate the actual capacity or SOH of batteries.
Data-driven methods have emerged as promising tools for predicting battery performance due to the rapid development of machine learning techniques (Zhu et al., 2023), and thus they are usually employed with the features of IC curves to establish a model for battery capacity or SOH estimation. (Li et al., 2020a) used Gaussian filter method to polish IC curves and then extracted features from partial IC curves, which served as the input of a Gaussian progress regression-based battery capacity degradation model for battery SOH estimation. (Li et al., 2019) combined the grey relational analysis and entropy weight methods to extract health performance indicators from IC curves to establish a battery degradation model for SOH estimation. She et al. proposed a radial basis function neural network-based model to depict the relationship between battery aging levels and its influencing factors in Ref. (She et al., 2019), wherein the IC peak indicates the battery aging level. (Zhang et al., 2022) combined voltage-capacity model-based ICA with support vector regression (SVR) for battery SOH estimation. (Tian et al., 2018) acquired the IC curves from battery open circuit voltage, which was identified by a fractional-order model, and the relationship between the IC peak and SOH was expressed as a linear function. (Jiang et al., 2020) developed an adaptive capacity estimation model based on three features of IC curves considering the influence of battery aging and charging conditions on the IC curves.
However, curve smoothing algorithms are required in the IC-based estimation methods to obtain a clear IC curve for easily identifying IC peaks (Tian et al., 2018; Li et al., 2019; She et al., 2019; Li et al., 2020a; Jiang et al., 2020; Zhang et al., 2022). These curve smoothing algorithms not only takes up high computational cost in embedded BMSs, but also introduce additional errors in data processing procedures (Zheng et al., 2018). The adjustable parameters of curve smoothing algorithms influence the result of IC curve fitting (Feng et al., 2020). Refs. (Li et al., 2020a; He et al., 2020). presented comparative results of IC curves by using different filters, and it is suggested that different parameters of filters have a significant influence on the intensities of IC peaks. Besides, the correlation between the IC peaks and cell capacities may change with the cell’s aging levels. In Ref. (Anseán et al., 2017), the authors presented the discontinuity of the IC peak area during battery aging, which grew linearly at its early aging stage and then reversed its tendency to follow a downward trend. In this case, it may lead to problematic results if the positive relation between IC peaks and capacity loss is directly employed for battery capacity estimation. Moreover, there are still some technical difficulties in implementing the ICA approach, such as the problem of selecting voltage intervals for yielding robust IC curves (Li et al., 2016). Accordingly, it is necessary to study the dependency of IC peaks on the voltage interval, and further develop the smoothing-free ICA technique for online battery capacity estimation.
This work aims at addressing the issues mentioned above and developing the ICA-based method for onboard implementation on battery capacity estimation. Multiple voltage intervals covering relatively narrow and wide values are first applied to figure out IC curves using numerical derivation. The voltage interval and cell aging dependencies of IC peaks are then experimentally analyzed, followed by proposing a novel method for battery capacity estimation using a back-propagation neural network (BPNN) with multi-voltage-interval IC peaks. A five-point moving window technique is then proposed to capture the multi-voltage-interval IC peaks for the estimation efficiently. The robustness and feasibility of the proposed methods are verified for different cells at various aging levels.
With the differential capacity, the method, known as ICA, transforms the voltage plateaus on a cell terminal voltage curve into clearly identifiable IC peaks on an IC curve. The IC curve is mathematically computed as the gradient of the charged/discharged capacity (Q) to the terminal voltage (V) using Eq. 1 (Pastor-Fernandez et al., 2016).
One of the significant technical difficulties in implementing the ICA approaches for onboard applications is the computation task for obtaining a precise IC curve (Weng et al., 2013; Riviere et al., 2015; Li et al., 2016; Weng et al., 2016). The numerical derivation is the most direct method to compute IC values from the original battery test data, but it is hard to determine a suitable voltage interval (ΔV) using this method. As reported in (Riviere et al., 2015; Li et al., 2020a), although the IC curve with a narrow voltage interval can well depict the peaks profile, it suffers from unavoidable measurement noise, thus leading to problems in accurately identifying the IC peaks. On the contrary, a wide voltage interval can smooth the IC curve, but it may have other issues, such as peak distortion and missing meaningful information.
Different curve smoothing algorithms are usually employed in data processing procedures to address the mentioned-above issue. But it inevitably results in introducing additional errors and adding computational efforts. Another problem is that no matter how smooth the IC curve is, one single voltage interval-based IC curve employed for estimating battery capacity does not have enough fault tolerance and may fail in some cases. For instance, although a smooth and robust IC curve can be obtained by applying the SVR-based smoothing algorithm in Ref. (Weng et al., 2013), there are still some outliers in the experimental results.
Accordingly, an effective approach to determine the voltage interval for enhancing the robustness of IC peaks and an efficient ICA-based capacity estimator for ease of implementation are highly required to cope with these technical difficulties.
To investigate the voltage interval and cell aging dependencies of IC peaks, three LiFePO4 cells with a rated capacity of 60 Ah were tested over 1800 aging cycles. The cycle test was conducted by a constant current (CC) and constant voltage (CV) charge scheme and a CC discharge scheme at room temperature (about 25°C). At each aging cycle, the battery cells were charged at a CC of 0.5 C until a cutoff voltage of 3.65 V was detected, followed by charging at a CV of 3.65 V until the loading current decreased to a cutoff current of 0.05 C. The cells’ charge data, including cell terminal voltage, loading current, and capacity, were exported from a host computer and then used for IC peak analysis.
A narrow voltage interval may result in a noisy IC curve, but a wide voltage interval may distort IC peaks. Therefore, one single voltage interval may not be able to achieve desirable results. In this paper, multiple voltage intervals covering narrow and wide values are proposed to simultaneously apply for obtaining various IC curves, which would have fault tolerance due to the distributed representation of the information of measurement noise and peak distortion. The IC peaks are then jointly used for capacity estimation, which is expected to merge the merits of both the narrow and wide voltage intervals.
Multiple voltage intervals, including 2 mV, 3 mV, 5 mV, and 8 mV, are employed for yielding different IC curves. Figure 1 shows the IC curves with various voltage intervals for Cell #1. With individual voltage intervals, three noticeable can be observed in the IC curves from Figure 1, consistent with the results presented in Refs. (Dubarry and Liaw, 2009; Weng et al., 2013; Han et al., 2014; Li et al., 2016). The staging process in the graphite negative electrode associated with these peaks was discussed in Refs. (Dubarry and Liaw, 2009; Dubarry et al., 2011; Han et al., 2014). In Figure 1, it can also be observed that the intensities of the second and the third IC peaks vary with different voltage intervals. It is worth mentioning that when the voltage interval is 2 mV, the IC curve is volatile at the range of SOC from about 10% to 30% and from 60% to 70% due to the inevitable measurement noise. However, when the voltage interval is 8 mV, there are very few IC points in the third IC peak, which may not truly reflect the entire IC peak. Therefore, the joint usage of the selected distribution of voltage intervals (i.e., 2 mV, 3 mV, 5 mV, and 8 mV) may incorporate the information on noise and peak distortion to some extent.
The third IC peak in the IC curve is typically employed for estimating battery available capacity. The IC peak in battery IC curves has been widely proven to be the highest correlation with battery available capacity using Pearson correlation analysis algorithm (Li et al., 2020a; Li et al., 2020b; Chang et al., 2021; Wen et al., 2022). The aging dependency of the third IC peak necessitates being investigated to achieve desirable estimates at different cell aging levels. To this end, the test data of three cells loaded over 1800 cycles are used for the following analysis. The intensities of the third IC peaks of the cells with the voltage interval of 2 mV, 3 mV, 5 mV, and 8 mV at different aging levels are depicted in Figure 2.
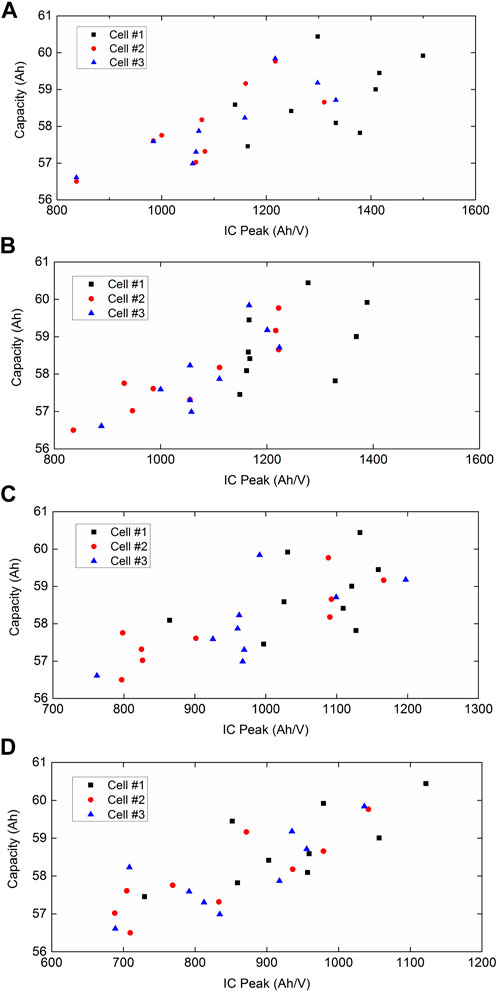
FIGURE 2. Intensities of the third IC peaks with multiple voltage intervals at various aging levels: (A) 2 mV, (B) 3 mV, (C) 5 mV, and (D) 8 mV.
As can be observed in Figure 2, the intensities of the third IC peak present a decreasing trend with the increasing cell aging, although some outliers exist. It is noted that the tendency is not as clear as the results reported in Refs. (Weng et al., 2013; Riviere et al., 2015). This is because the intensities of the third IC peaks depicted in Figure 2 were directly computed using numerical derivation with the measurement data, which are not polished by any curve smoothing algorithms in advance.
The intensities of the third IC peaks are related to the voltage intervals and battery aging levels. However, the relationship between the fading capacities and the third IC peak values with multiple voltage intervals are not explicitly explored. Thus, a back-propagation neural network (BPNN) is employed to establish the model of battery capacity estimation, which is elaborated in the following section.
Artificial neural networks (ANNs) are nonlinear learning mathematical models that always exhibit their feasibility in solving a wide variety of problems, such as nonlinear mapping, function approximation, and state prediction (Hu et al., 2014; Liu et al., 2014). ANNs have the ability to learn and approximate the relationship between the input variables and the output variables without being explicitly explored. One of the most commonly used ANNs, the BPNN, using the classical back propagation approach to update the weights between each layer (Hu et al., 2014), is employed in this work for approximating the relation between multi-voltage-interval IC peaks and battery capacities.
A typical three-layer BPNN depicted in Figure 3, consisting of an input layer, a hidden layer, and an output layer, is employed in the present study. The third IC peak values under multiple voltage intervals of 2 mV, 3 mV, 5 mV, and 8 mV serve as the input vector of the input layer. In the hidden layer, the number of neurons is set to 12 for equilibrating the network complexity and estimation accuracy. The estimated battery capacity is obtained from the output layer. In the hidden and output layers, the hyperbolic tangent sigmoid function is employed as the activation function, which is governed by
where u is the value of the neuron.
Each of the neurons in the hidden layer computes a weighted and biased sum of its input and transmits the sum through the activation function to the output layer. The mathematical expression of the hidden layer is determined by
where k denotes the index of the kth (k = 1, 2, 3, 4.) input node, i the index of the ith (I = 1, 2, … , 11, 12.) hidden node, xk the kth input IC peak value, wk,i the weight value connecting the kth input node and the ith hidden node, and bi the bias value of the ith hidden node.
Likewise, the mathematical equation of the output layer is expressed as
where wi,o and bo denote the weight value connecting the ith hidden node and the output node and the bias value of the output node, respectively, and o denotes the output value.
The proposed battery capacity estimator using a BPNN with multi-voltage-interval IC peaks has several apparent advantages.
a. One benefit of using multiple voltage intervals covering both narrow and wide values to obtain various IC peaks is that it has fault tolerance and enhances the robustness of the proposed method due to the distributed representation of measurement noise and peak distortion information.
b. The IC curves are computed directly by numerical derivation without pre-polishing by any curve smoothing algorithms and functions, thus efficiently reducing computational efforts and additional errors in the data preprocessing.
c. The main advantage of the BPNN is achieved by its ease of understanding and implementation, and therefore, the proposed method is promising to be applied in practice.
The method to accurately capture the multi-voltage-interval IC peaks is the prerequisite for effective estimation. In this section, a five-point moving window method is proposed for efficiently capturing the IC peaks.
During the battery charging process, the input information of BMSs, which includes cell voltage and loading current, changes with operating time. With the input data, a BMS should have the ability to compute IC values at each sampling voltage interval in its program. Figure 4 depicts the real-timely computed IC values (shown as the blue symbols) during the battery CC charging process, in which the voltage interval is 2 mV.
In Figure 4, a five-point moving window shown as the black dash window is proposed to capture the third IC peak during the battery charging process. The red arrows shown in the moving window indicate the changing trend of IC values for capturing the IC peak. If the IC values of the five points in the moving window satisfy the constraints of Eq. 5, Point (3) can be considered as the third IC peak. Otherwise, the first point will be released, and the moving window will move to add the next IC value to make a judgment again until it finds out the IC peak.
where Point (·) denotes the IC value of the point.
Figure 5 shows the capture processes of the IC peaks with different voltage intervals, where Point (3) represents the third IC peak value. By observing Figure 5, the captured IC peak values are consistent with the results shown in Figure 1. It suggests that the five-point moving window method has the ability to accurately identify the third IC peak, which provides a reliable foundation for subsequent validations.
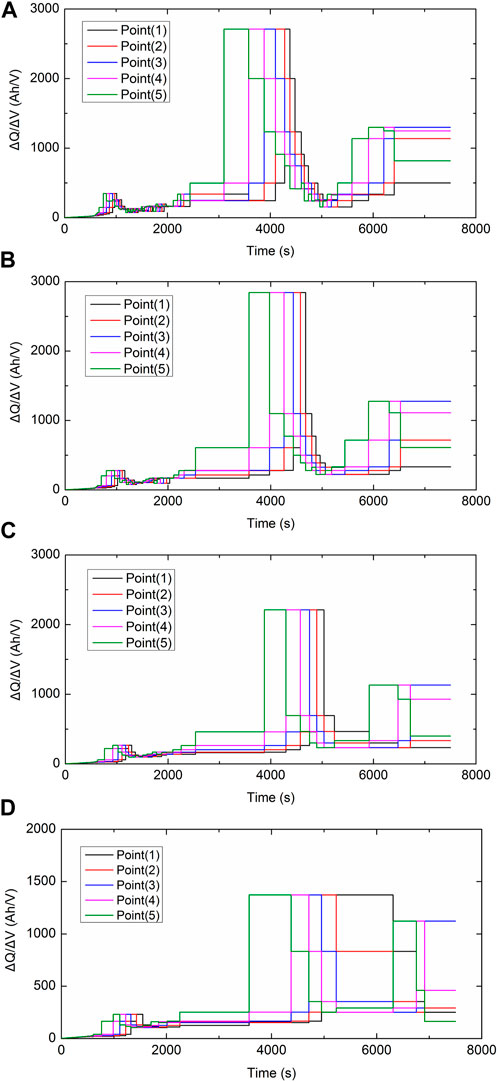
FIGURE 5. The capture processes of the third IC peaks with different voltage intervals: (A) 2 mV, (B) 3 mV, (C) 5 mV, and (D) 8 mV.
Based on the mentioned-above description, a block diagram of the entire proposed method is presented in Figure 6, which includes battery charge data collection, IC data calculation, IC peak capturing, and model training and testing.
It is important to adopt an efficient training algorithm to train the proposed BPNN model for accurate battery capacity estimation. The Levenberg-Marquardt backpropagation algorithm is considered as one of the most efficient training algorithms for small and medium sized patterns (Nawi et al., 2013). It is a derivative of the Newton method and able to achieve desirable network parameters identification. Therefore, the Levenberg-Marquardt backpropagation algorithm is employed as the training algorithm of the proposed BPNN model.
The BPNN model is trained using Matlab software. The Levenberg-Marquardt backpropagation algorithm (trainlm) is a network training function that updates weight and bias values according to Levenberg-Marquardt optimization. Trainlm is often the fastest backpropagation algorithm in the toolbox of Matlab, and is highly recommended as a first-choice supervised algorithm (MATLAB, 2023).
During the training process, the mean square error (MSE) measuring the average of the squares of the differences between the network output values and the target data, as given in Eq. 6, is applied as the performance function of the BPNN. The training process seeks to alter the network weights and biases to produce the correct output within a reasonable error margin (Lahiri and Ghanta, 2008). The training goal of trainlm is to find a set of weights and biases that minimize the MSE.
where EMSE denotes the MSE, N the number of the training data, Qi the ith target capacity value, and Qi* the ith estimated capacity value.
For the training stage, about two-thirds of the data sets of multi-voltage-interval IC peaks and battery capacities were selected randomly, which cover various cells and the whole range of aging cycles. The optimal parameters of the BPNN model, including the weights and biases of the hidden layer and output layer, can be obtained by the training stage. The BPNN model is then applied to the verifications of battery capacity estimation.
To investigate the feasibility and robustness of the battery capacity estimation approach, the battery charging data of three cells at different aging cycles are used for verification. Relative error measuring the deviation between the estimated capacity and the referenced value is used for evaluating the performance of the proposed method, which is determined by
where eRE denotes the capacity relative error, Q* the estimated capacity, and Q the referenced capacity. The referenced values are obtained from a host computer that records the battery operating data with high accuracy during battery charge/discharge processes, which are considered as the real cell capacities.
The capacity estimation results for three cells and their relative errors are depicted in Figures 7, 8, respectively. As can be observed in Figure 7, the referenced capacities present a downward trend with the growing aging levels. The estimated capacities can track with the referenced values for different cells at various aging cycles, except for two relatively large erroneous estimates, which place at the 1600th cycle of Cell #2 and the 1200th cycle of Cell #3.
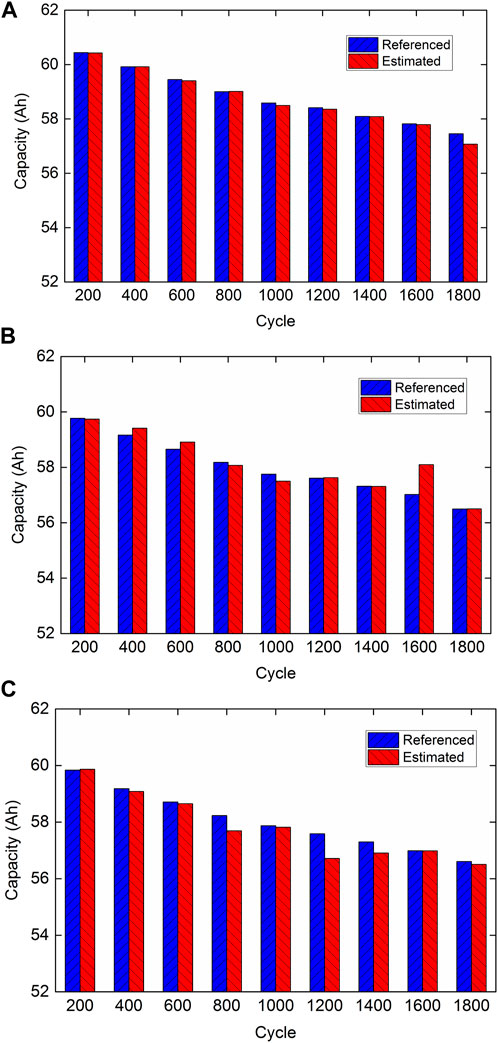
FIGURE 7. Capacity estimation results of three cells at different aging cycles: (A) Cell #1, (B) Cell #2, and (C) Cell #3.
Relative errors of the estimation results are computed and presented in Figure 8, where all relative errors are successfully confined into an error band of ±2%. It is noted that the relative errors of the two relatively large erroneous estimates stated above are 1.89% and −1.52%, respectively, and most of the relative errors can be limited in a narrow error band of ±1%, which suggests that the proposed method can handle various cells and aging levels quite well.
The proposed capacity estimation and IC peak capturing methods for LiFePO4 cells in this work are pretty general, and therefore are promising to provide valuable insight to the investigations of other types of batteries with various chemistries.
In this paper, a novel method using a back-propagation neural network (BPNN) with multi-voltage-interval incremental capacity (IC) peaks is proposed for on-board battery capacity estimation. A relatively reasonable distribution of voltage intervals covering both narrow and wide values (namely, 2 mV, 3 mV, 5 mV, and 8 mV) is first proposed for simultaneously yielding different IC curves, which has fault tolerance due to the representation of information of measurement noise and peak distortion. Note that there is no need to employ smoothing algorithms in numerical derivation, thus reducing computational efforts and avoiding introducing additional errors. For approximating the relation between multi-voltage-interval IC peaks and cell capacities, a three-layers BPNN is then employed in this work, and the network parameters are trained by using the Levenberg-Marquardt backpropagation algorithm. With the input vector of multi-voltage-interval IC peaks, the BPNN is applied for battery capacity estimation. Moreover, a five-point moving window technique is proposed to successfully capture the multi-voltage-interval IC peaks during the battery charging process for the estimation. The experimental results demonstrate that promising capacity estimates with relative errors within ±2% can be achieved, highlighting the feasibility and robustness of the proposed approach against different battery aging levels. However, this work has not considered the temperature influence on the IC peaks and the estimation. Since ambient temperature significantly impacts battery charging characteristics, the temperature dependency of IC peaks needs to be investigated in our future work to enhance the robustness of the estimation further.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Conceptualization: LZ and JX; methodology, data analysis, validation, writing—original journal draft: XG and BX; writing—review and editing: LZ and JX; Supervision, funding acquisition: LZ. All authors contributed to the article and approved the submitted version.
This work was supported by the National Natural Science Foundation of China (Grant No. 52102424), Zhuhai Basic and Applied Basic Research Foundation (Grant No. ZH22017003210051PWC), Guangzhou Basic and Applied Basic Research Foundation (Grant No. 202201010601), and Guangdong Basic and Applied Basic Research Foundation (Grant No. 2019A1515012210).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Anseán, D., Dubarry, M., Devie, A., Liaw, B. Y., García, V. M., Viera, J. C., et al. (2017). Operando lithium plating quantification and early detection of a commercial LiFePO4 cell cycled under dynamic driving schedule. J. Power Sources 356, 36–46. doi:10.1016/j.jpowsour.2017.04.072
Chang, C., Wang, Q., Jiang, J., and Wu, T. (2021). Lithium-ion battery state of health estimation using the incremental capacity and wavelet neural networks with genetic algorithm. J. Energy Storage 38, 102570. doi:10.1016/j.est.2021.102570
Deng, Z., Hu, X., Xie, Y., Xu, L., Li, P., Lin, X., et al. (2022). Battery health evaluation using a short random segment of constant current charging. Iscience 25 (5), 104260. doi:10.1016/j.isci.2022.104260
Dubarry, M., Liaw, B. Y., Chen, M-S., Chyan, S-S., Han, K-C., Sie, W-T., et al. (2011). Identifying battery aging mechanisms in large format Li ion cells. J. Power Sources 196 (7), 3420–3425. doi:10.1016/j.jpowsour.2010.07.029
Dubarry, M., and Liaw, B. Y. (2009). Identify capacity fading mechanism in a commercial LiFePO4 cell. J. Power Sources 194 (1), 541–549. doi:10.1016/j.jpowsour.2009.05.036
Feng, F., Hu, X., Hu, L., Hu, F., Li, Y., and Zhang, L. (2019). Propagation mechanisms and diagnosis of parameter inconsistency within Li-Ion battery packs. Renew. Sustain. Energy Rev. 112, 102–113. doi:10.1016/j.rser.2019.05.042
Feng, X., Merla, Y., Weng, C., Ouyang, M., He, X., Liaw, B. Y., et al. (2020). A reliable approach of differentiating discrete sampled-data for battery diagnosis. eTransportation 3, 100051. doi:10.1016/j.etran.2020.100051
Han, X., Ouyang, M., Lu, L., Li, J., Zheng, Y., and Li, Z. (2014). A comparative study of commercial lithium ion battery cycle life in electrical vehicle: Aging mechanism identification. J. Power Sources 251, 38–54. doi:10.1016/j.jpowsour.2013.11.029
He, J., Bian, X., Liu, L., Wei, Z., and Yan, F. (2020). Comparative study of curve determination methods for incremental capacity analysis and state of health estimation of lithium-ion battery. J. Energy Storage 29, 101400. doi:10.1016/j.est.2020.101400
Hu, J. N., Hu, J. J., Lin, H. B., Li, X. P., Jiang, C. L., Qiu, X. H., et al. (2014). State-of-charge estimation for battery management system using optimized support vector machine for regression. J. Power Sources 269, 682–693. doi:10.1016/j.jpowsour.2014.07.016
Jiang, B., Dai, H., and Wei, X. (2020). Incremental capacity analysis based adaptive capacity estimation for lithium-ion battery considering charging condition. Appl. Energy 269, 115074. doi:10.1016/j.apenergy.2020.115074
Lahiri, S. K., and Ghanta, K. C. (2008). Development of an artificial neural network correlation for prediction of hold-up of slurry transport in pipelines. Chem. Eng. Sci. 63 (6), 1497–1509. doi:10.1016/j.ces.2007.11.030
Li, X., Jiang, J., Chen, D., Zhang, Y., and Zhang, C. (2016). A capacity model based on charging process for state of health estimation of lithium ion batteries. Appl. Energy 177, 537–543. doi:10.1016/j.apenergy.2016.05.109
Li, X., Wang, Z., Zhang, L., Zou, C., and Dorrell, D. D. (2019). State-of-health estimation for Li-ion batteries by combing the incremental capacity analysis method with grey relational analysis. J. Power Sources 410, 106–114. doi:10.1016/j.jpowsour.2018.10.069
Li, X., Yuan, C., Li, X., and Wang, Z. (2020). State of health estimation for Li-Ion battery using incremental capacity analysis and Gaussian process regression. Energy 190, 116467. doi:10.1016/j.energy.2019.116467
Li, X., Yuan, C., and Wang, Z. (2020). State of health estimation for Li-ion battery via partial incremental capacity analysis based on support vector regression. Energy 203, 117852. doi:10.1016/j.energy.2020.117852
Liu, P., Wang, J., Hicks-Garner, J., Sherman, E., Soukiazian, S., Verbrugge, M., et al. (2010). Aging mechanisms of LiFePO[sub 4] batteries deduced by electrochemical and structural analyses. J. Electrochem. Soc. 157 (4), A499. doi:10.1149/1.3294790
Liu, X., Wu, J., Zhang, C., and Chen, Z. (2014). A method for state of energy estimation of lithium-ion batteries at dynamic currents and temperatures. J. Power Sources 270, 151–157. doi:10.1016/j.jpowsour.2014.07.107
MATLAB (2023). Matlab doc: Levenberg-Marquardt backpropagation - MATLAB trainlm. Available at: https://ww2.mathworks.cn/help/deeplearning/ref/trainlm.html.
Nawi, N. M., Khan, A., and Rehman, M. Z. (2013). A new Levenberg Marquardt based back propagation algorithm trained with cuckoo search. Procedia Technol. 11, 18–23. doi:10.1016/j.protcy.2013.12.157
Pastor-Fernandez, C., Widanage, W. D., Chouchelamane, G., and Marco, J. (2016). “A SoH diagnosis and prognosis method to identify and quantify degradation modes in Li-ion batteries using the IC/DV technique,” in Hybrid and Electric Vehicles Conference, London, UK, 02-03 November 2016 (IET).
Riviere, E., Venet, P., Sari, A., Meniere, F., and Bultel, Y. (2015). “LiFePO4 battery state of health online estimation using electric vehicle embedded incremental capacity analysis,” in 2015 IEEE Vehicle Power and Propulsion Conference (VPPC), Montreal, QC, Canada, 19-22 October 2015 (IEEE).
Severson, K. A., Attia, P. M., Jin, N., Perkins, N., Jiang, B., Yang, Z., et al. (2019). Data-driven prediction of battery cycle life before capacity degradation. Nat. Energy 4 (5), 383–391. doi:10.1038/s41560-019-0356-8
She, C., Wang, Z., Sun, F., Liu, P., and Zhang, L. (2019). Battery aging assessment for real-world electric buses based on incremental capacity analysis and radial basis function neural network. IEEE Trans. Industrial Inf. 16 (5), 3345–3354. doi:10.1109/tii.2019.2951843
Shi, G., Chen, S., Yuan, H., You, H., Wang, X., Dai, H., et al. (2021). Determination of optimal indicators based on statistical analysis for the state of health estimation of a Lithium-ion battery. Front. Energy Res. 9, 690266. doi:10.3389/fenrg.2021.690266
Su, X., Sun, B., Wang, J., Zhang, W., Ma, S., He, X., et al. (2022). Fast capacity estimation for lithium-ion battery based on online identification of low-frequency electrochemical impedance spectroscopy and Gaussian process regression. Appl. Energy 322, 119516. doi:10.1016/j.apenergy.2022.119516
Sulzer, V., Mohtat, P., Aitio, A., Lee, S., Yeh, Y. T., Steinbacher, F., et al. (2021). The challenge and opportunity of battery lifetime prediction from field data. Joule 5 (8), 1934–1955. doi:10.1016/j.joule.2021.06.005
Sun, X., Xu, N., Chen, Q., Yang, J., Zhu, J., Xu, J., et al. (2022). State of power capability prediction of lithium-ion battery from the perspective of electrochemical mechanisms considering temperature effect. IEEE Trans. Transp. Electrification 2022, 1. doi:10.1109/tte.2022.3206452
Tian, J., Xiong, R., and Yu, Q. (2018). Fractional-order model-based incremental capacity analysis for degradation state recognition of lithium-ion batteries. IEEE Trans. Industrial Electron. 66 (2), 1576–1584. doi:10.1109/tie.2018.2798606
Wen, J., Chen, X., Li, X., and Li, Y. (2022). SOH prediction of lithium battery based on IC curve feature and BP neural network. Energy 261, 125234. doi:10.1016/j.energy.2022.125234
Weng, C., Cui, Y., Sun, J., and Peng, H. (2013). On-board state of health monitoring of lithium-ion batteries using incremental capacity analysis with support vector regression. J. Power Sources 235, 36–44. doi:10.1016/j.jpowsour.2013.02.012
Weng, C., Feng, X., Sun, J., and Peng, H. (2016). State-of-health monitoring of lithium-ion battery modules and packs via incremental capacity peak tracking. Appl. Energy 180, 360–368. doi:10.1016/j.apenergy.2016.07.126
Xiong, R., Li, L., and Tian, J. (2018). Towards a smarter battery management system: A critical review on battery state of health monitoring methods. J. Power Sources 405, 18–29. doi:10.1016/j.jpowsour.2018.10.019
Yang, C., Wang, X., Fang, Q., Dai, H., Cao, Y., and Wei, X. (2020). An online SOC and capacity estimation method for aged lithium-ion battery pack considering cell inconsistency. J. Energy Storage 29, 101250. doi:10.1016/j.est.2020.101250
Zhang, Y., Liu, Y., Wang, J., and Zhang, T. (2022). State-of-health estimation for lithium-ion batteries by combining model-based incremental capacity analysis with support vector regression. Energy 239, 121986. doi:10.1016/j.energy.2021.121986
Zhao, J., Ling, H., Liu, J., Wang, J., Burke, A. F., and Lian, Y. (2023). Machine learning for predicting battery capacity for electric vehicles. eTransportation 15, 100214. doi:10.1016/j.etran.2022.100214
Zheng, L., Zhang, L., Zhu, J., Wang, G., and Jiang, J. (2016). Co-estimation of state-of-charge, capacity and resistance for lithium-ion batteries based on a high-fidelity electrochemical model. Appl. Energy 180, 424–434. doi:10.1016/j.apenergy.2016.08.016
Zheng, L., Zhu, J., Lu, D. D-C., Wang, G., and He, T. (2018). Incremental capacity analysis and differential voltage analysis based state of charge and capacity estimation for lithium-ion batteries. Energy 150, 759–769. doi:10.1016/j.energy.2018.03.023
Keywords: battery capacity estimation, incremental capacity peak, multiple voltage intervals, battery management system (BMS), back-propagation neural network (BPNN)
Citation: Guo X, Xu B, Zheng L and Xu J (2023) Robustness enhanced capacity estimation method for lithium-ion batteries based on multi-voltage-interval incremental capacity peaks. Front. Energy Res. 11:1207194. doi: 10.3389/fenrg.2023.1207194
Received: 17 April 2023; Accepted: 24 May 2023;
Published: 06 June 2023.
Edited by:
Haijun Ruan, Imperial College London, United KingdomReviewed by:
Kai Yang, University of Surrey, United KingdomCopyright © 2023 Guo, Xu, Zheng and Xu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Linfeng Zheng, bGZ6aGVuZ0BqbnUuZWR1LmNu; Jing Xu, eHUuamluZ0B6enUuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.