Research on force model and characteristics of large wind turbine pitch system based on SCADA data

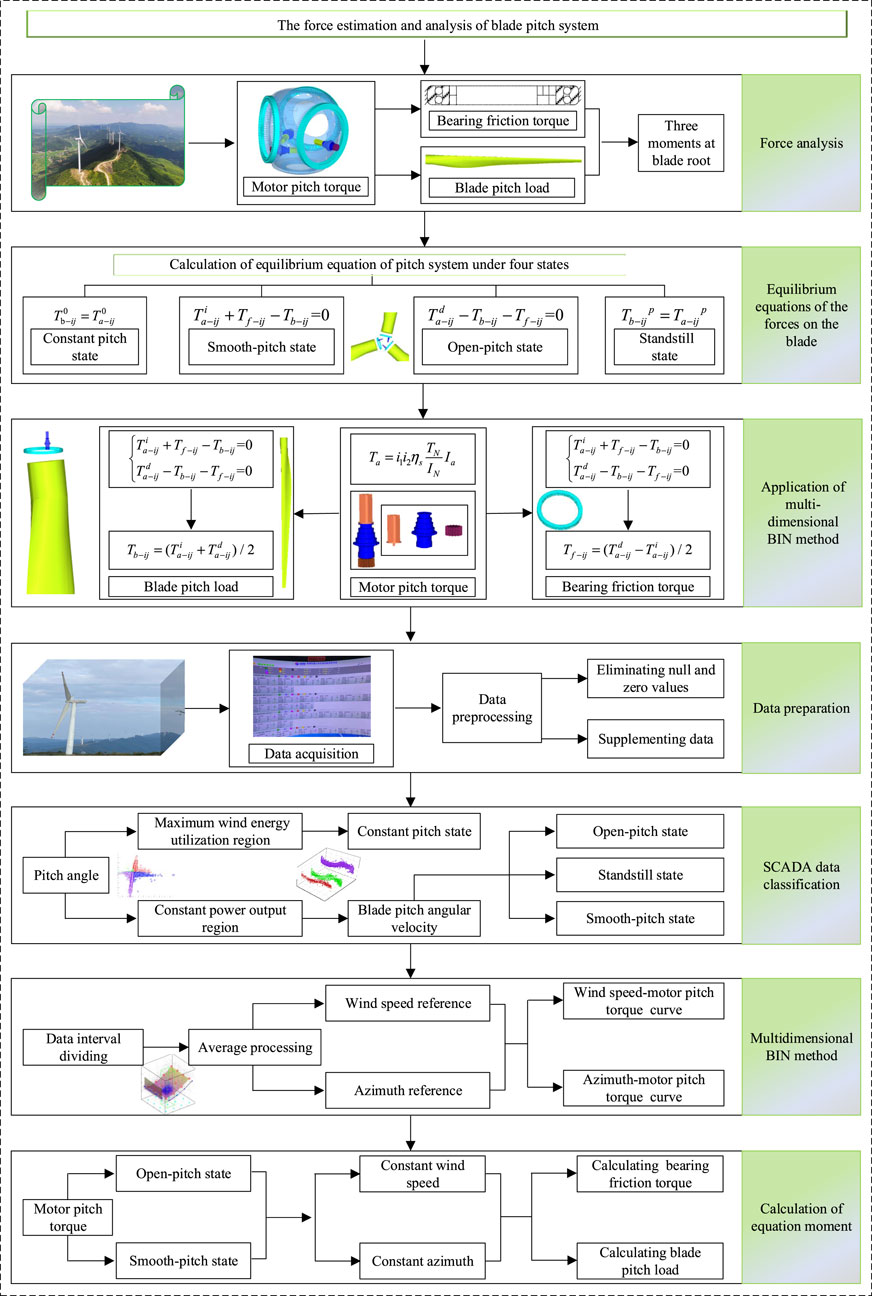
In large-scale wind turbines, the force state of the pitch system greatly influences safe operation and service life. This paper provides a novel method to estimate blade pitch load, bearing friction torque, and motor pitch torque. In this method, the force equilibrium equations are established by investigating the force of the pitch system under multiple operating conditions. The multidimensional BIN method is employed to classify the supervisory control and data acquisition (SCADA) data of wind turbines into several intervals. The multidimensional scatter data is processed in a single-valued way. Then, the estimating model of the pitch system forces is established by combining the obtained data and the equilibrium equations. Taking a 2 MW wind turbine as an example, the variation characteristics of blade pitch load, bearing friction torque, and motor pitch torque under multiple operating conditions are analyzed. Some interesting and valuable conclusions are obtained. For example, when the wind speed increases, the blade pitch load increases significantly in the maximum wind energy tracking region, but there is no obvious change in the observed constant power output region. The wind speed and azimuth have little effect on the bearing friction torque. The variation trend of motor pitch torque is consistent with that of blade pitch load in the maximum wind energy tracking region.

1 Introduction

Wind energy is renewable energy with the prospect of large-scale development. The research and development (R&D), installation, and operation of large wind turbines are booming all over the world. Optimizing the design and operation of large wind turbines has become a hot issue in the industry. The pitch system is one of the key components of large-scale wind turbines (Rosemeier et al., 2016). During the operation of wind turbines, the pitch system bears complex loads and has multiple working conditions, which causes frequent failures (Dai et al., 2022), for example, the pitch brake failure and the pitch bearing breakage (He et al., 2021; Li and Wang, 2021). Relevant statistical data show that the failures of pitch systems account for more than 40% of all wind turbine failures, resulting in more than 30% of wind turbine downtime (Bi et al., 2014). The failure of the pitch control system is closely related to its force state. However, in the process of wind turbine operation, the force state of the pitch system is very complex, and it is difficult to measure with sensors. Obtaining a clear understanding of the force state of the pitch system will be beneficial to the design, operation, and maintenance of wind turbines.

Recently, the force state of the pitch system has received considerable attention in academic and engineering circles. A lot of relevant theoretical research works have been carried out. Dai et al. deduced the blade pitch load expression considering the aerodynamics, centrifugal force, and gravity (Dai et al., 2010; Dai et al., 2011). Liu et al. applied the Fourier transform formula to calculate the gear meshing stress (Liu et al., 2019). There are also some studies to improve the force through control. Xu et al. used the improved fuzzy proportional control strategy to reduce the ultimate load at the blade root (Xu et al., 2020). Jiao et al. designed a novel adaptive pitch controller to predict the aerodynamic load of wind turbines (Jiao et al., 2018). Abdelbaky et al. established a nonlinear mathematical model to achieve optimal control based on the MPC (Abdelbaky et al., 2020). Yuan et al. adopted a robust multivariate pitch strategy to analyze periodic variations of blade load (Yuan et al., 2020). Some studies are also carried out through experiments and simulation (Wang and Chiang, 2016; Cheon et al., 2019; Wang et al., 2019). Despite these research works, the actual force state of the wind turbine pitch system has not been completely determined. This is because large wind turbines are installed and debugged on-site, and the actual performance can only be obtained after operation. The pitch system includes blade, pitch bearing, pitch gearbox, pitch drive motor, and other components. So, the blade pitch load, bearing friction torque, and motor pitch torque can only be obtained through the analysis of on-site operation data. At present, the on-site SCADA data of wind turbines are widely used, mainly for performance analysis, condition evaluation, and fault diagnosis (Chen et al., 2013). For example, Zeng et al. quantitatively described the oil tank temperature of wind turbine gearboxes based on SCADA data (Zeng et al., 2022). Astolfi conducted support vector regression analysis for power monitoring based on SCADA data (Astolfi, 2021). Wei et al. established a wind turbine aging evaluation model based on SCADA data by introducing four aging evaluation indicators (Wei et al., 2021). Neshat et al. estimated the power output of Swedish onshore wind turbines by optimizing the historical SCADA data (Neshat et al., 2021). Bhargava et al. analyzed the aerodynamic load of a 2.1 MW wind turbine based on blade element momentum (BEM) and SCADA data (Bhargava et al., 2020). Wei et al. detected faults in encoders and pitch motors based on an improved RVM neural network algorithm and SCADA data (Wei et al., 2020). McKinnon et al. used the isolated forest machine learning method to process SCADA data for pitch system fault predicting (McKinnon et al., 2021). Korkos et al. used ANFIS technology to analyze 10-year SCADA data and established a fault detection model for the pitch system (Korkos et al., 2022). Correa-Jullian et al. employed a quantum kernel classification method to detect faults in the pitch system (Correa-Jullian et al., 2022). Yin et al. detected high-temperature faults of the pitch motor by using the ensemble learning-based method (Yin et al., 2022).

In theory, the SCADA data includes wind speed, rotational speed, power, pitch angle, pitch motor current, and other information, covering various working conditions of wind turbines. Therefore, it is a new idea to reconstruct the pitch system load from SCADA data. How to establish a connection between SCADA data and pitch load is the key to solve this problem. A simple analysis of SCADA data is also not feasible, and it needs to be combined with the physical model of the pitch system. On the other hand, SCADA data contains a lot of noise data, so how to preprocess the data is also an important issue. Starting from these scenarios, this paper creatively proposes solutions, and the main contributions are as follows.

• All the blade pitch load, bearing friction torque, and motor pitch torque are investigated.

• The force equilibrium equations of the blade are established.

• The multidimensional BIN method is employed to preprocess SCADA data.

• The estimating model of the pitch system forces is established.

• The variation characteristics of pitch load under multiple operating conditions are analyzed.

The remaining part is organized as follows. In Section 2, the theoretical analysis of the forces acting on the pitch system is carried out, including the theoretical forces analysis of the pitch system and the force equilibrium equations. In Section 3, the force estimation model of the pitch system is established, including SCADA data preparation, use of the multidimensional BIN method, and force estimation model of the pitch system. The force characteristic investigation of the pitch system based on SCADA data is shown in Section 4. In this section, all the blade pitch load, bearing friction torque, and motor pitch torque are investigated. Finally, Section 5 ends the paper by summarizing the main achievements.

2 Theoretical analysis of forces acting on pitch system

2.1 Structure of pitch system

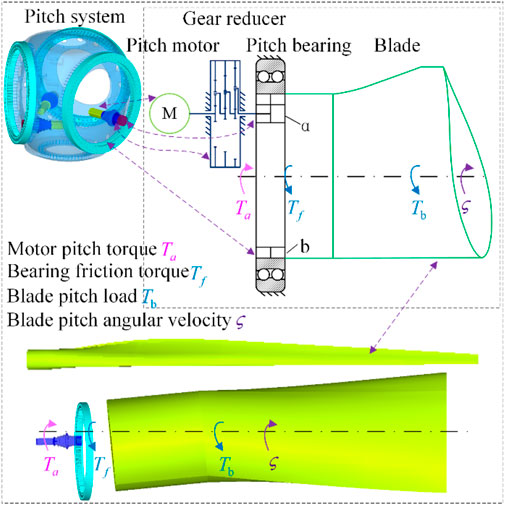
The pitch system structure of a 2 MW wind turbine is shown in Figure 1. A three-stage planetary reducer connects the pitch motor to the drive gear. The drive gear engages with the inner gear ring, and the blade is bolted onto the inner gear ring. When the pitch controller gives a pitch control command, the pitch motor will produce output torque. It passes through the transmission shaft and reduction mechanism and finally, through the drive gear $a$ to the inner gear ring $b$. The rotation of the inner gear ring will drive the blades connected to it to rotate together, thus changing the blade pitch angle.

FIGURE 1

FIGURE 1. Pitch system of wind turbines.

The forces acting on the pitch system are very complex. Here, three main forces that affect the behavior of the pitch system are discussed, namely, motor pitch torque ($T_a$), blade pitch load ($T_b$), and bearing friction torque ($T_f$). The blade pitch load plays a key role in the force distribution of the pitch system because its change will change other force states. Generally speaking, blade pitch load is affected by three aspects (Dai et al., 2010; Liu et al., 2021), namely, the gravity acting on the blade, the centrifugal force acting on the blade caused by the rotation of the wind rotor, and the aerodynamic force acting on the blade. More specifically, the gravity acting on the blade is determined by the mass distribution of the blade. The direction of gravity is always vertical and downward. It should be noted that the direction of gravity is different from the direction of blade pitch load caused by gravity. Here, the blade pitch load is analyzed from the angle of torque, which means that its direction is related to the position of the pitch axis. The centrifugal force is related to blade mass distribution and rotor speed, and its direction is the radial direction of the rotor. The aerodynamic force is related to wind speed, airfoil and size, blade pitch angle, etc. There are two main aspects of blade movement. One is synchronous rotation with the main shaft of the wind rotor, and the other is rotation around the pitch axis. When the blade rotates with the main shaft in space, the blade pitch load will also change with the space position.

In SCADA data, motor pitch torque, blade pitch load, and bearing friction torque are not directly recorded. However, the current of the pitch motor is collected and stored at all times. This provides the possibility for indirect calculation of motor pitch torque. Neglecting the motor’s empty torque $T_0$ and inertial torque, the motor pitch torque can be expressed as (Zhang et al., 2019)

$T_a=i_1{i}_2{\eta }_s{I}_a{T}_N/I_N(1)$

where, $T_a$ is motor pitch torque, $T_N$ is rated torque of pitch motor, $I_N$ is rated current of pitch motor, $I_a$ is pitch motor current, $i_1$ is the transmission ratio of the planetary gear reducer, $i_2$ the transmission ratio from the drive gear to the inner gear ring, and ${\eta }_s$ is the mechanical efficiency of the pitch transmission system. It can be seen that the current data extracted from the SCADA data can be effectively used to calculate the motor torque which drives the blade to rotate at the corresponding moment.

2.2 Force equilibrium equations

Maximum wind energy tracking region

When the wind speed is greater than the cut-in wind speed and less than the rated wind speed, wind turbines usually capture the wind energy to output electric energy under the condition of a constant pitch angle. In this region, wind turbines are expected to maximize the use of wind energy, which is called the maximum wind energy tracking region. Since the pitch angle is constant, the bearing friction torque is static friction torque. Then, motor pitch torque $T_a$, blade pitch load $T_b$ , and bearing friction torque $T_f$ act together to maintain the dynamic balance of the blade pitch system. In this scenario, the magnitude and direction of the bearing friction torque are time-varying and will change with the change of blade pitch load and motor pitch torque. The expression between the three can be written as

$T_a-T_{\mathrm{b}}\pm T_f=0(2)$

If the influence of bearing friction moment is ignored, the blade pitch load can be calculated from the motor pitch torque in the maximum wind energy tracking region.

Constant power output region

When the wind turbine runs in the constant power output region, the wind speed reaches or exceeds the rated wind speed, and the blade pitch angle is controlled by feedback. In this region, the wind speed may remain constant at some time, which means that the pitch angle is also constant. Then, the mechanical equilibrium equation is also written as

$T_a-T_{\mathrm{b}}\pm T_f=0(3)$

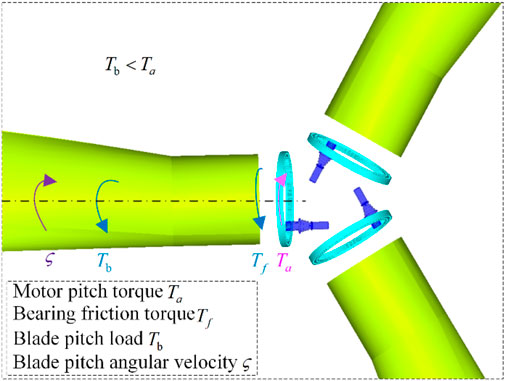
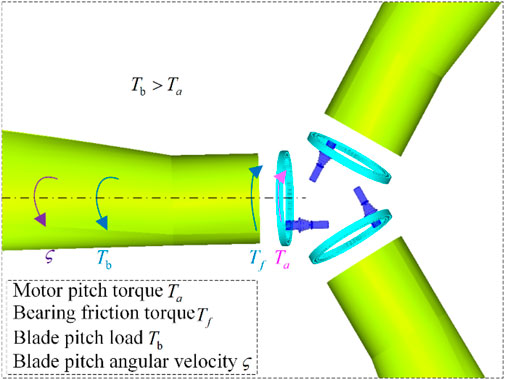
In the constant power output region, if the wind speed continues to decrease, the blade pitch angle will be driven to decrease to increase the windward area, which is called the open-pitch state, as shown in Figure 2. Motor pitch torque $T_a$ overcomes both blade pitch load $T_{\mathrm{b}}$ and bearing friction torque $T_f$, which makes the blade rotate, and blade forces can be described as

$T_a-T_{\mathrm{b}}-T_f=0(4)$

FIGURE 2

FIGURE 2. Open-pitch state of wind turbines.

When wind speed tends to increase, the blade pitch angle turns in the direction of becoming larger to reduce the windward area, which is called the smooth-pitch state, as shown in Figure 3. Blade pitch load $T_{\mathrm{b}}$ overcomes both motor pitch torque $T_a$ and bearing friction torque $T_f$, which makes the blade rotate, and blade forces can be described as

$T_{\mathrm{b}}-T_a-T_f=0(5)$

FIGURE 3

FIGURE 3. Smooth-pitch state of wind turbines.

When operating in the constant power output region, the blade rotation direction is different when the blade is in the open-pitch and smooth-pitch state, and the motor pitch torque is different. If the blades have the same windward surface and aerodynamic force, the blade pitch load and bearing friction moment are the same regardless of the rotation direction. Therefore, from Eqs 1, 3, it is easy to obtain blade pitch load when the pitch system is at a standstill state in the constant power output region. Combined with Eqs 4, 5 the blade pitch load and bearing friction torque can be obtained from the motor pitch torque when the blade is in the state of open-pitch and smooth-pitch. In other words, the blade pitch load and bearing friction torque can be calculated from the motor pitch torque in the constant power output region. It must be pointed out that in the process of blade movement, there is inertia force generated by acceleration start and deceleration stop. Considering that the blade is a large inertia body, in order to minimize the dynamic load of the pitch system, the blade angular acceleration is controlled below $0.01\mathrm{r}\mathrm{a}\mathrm{d}/s^2$. The resulting inertia moment is smaller than the motor pitch moment, so the influence of the blade rotational inertia moment is ignored in the force state analysis.

For a certain wind turbine, its rotor hub structure, blade geometry and its mass distribution, and blade aerodynamic characteristics are unchanged. If the influence of wind direction, yaw, and other factors is not considered, the blade pitch load depends on wind speed, rotor speed, blade azimuth, and pitch angle. When the wind turbine is in the maximum wind energy tracking region, the wind speed is lower than the rated wind speed, the blade will not be started to pitch, and the pitch angle remains unchanged. By controlling rotor speed $\omega ={\lambda }_{opt}v/R$, the blade tip speed ratio $\lambda$ is close to the optimum value so that the wind energy utilization coefficient (power coefficient) $C_p$ and the output power reach the maximum, that is, it is in the maximum wind energy tracking region. When the wind turbine is in the constant power output region, wind speed reaches or exceeds the rated wind speed, and rotor speed remains at the rated speed. At this time, to suppress the impact of wind speed changes on the output power, the control system will issue a pitch command, that is, by controlling the blade pitch angle $\beta$. When the wind speed increases, the pitch angle increases; when the wind speed decreases, the pitch angle decreases, which keeps the output power constant and obtains constant power output. Therefore, blade pitch load actually only depends on wind speed and blade azimuth.

3 Force estimation model of pitch system

3.1 Data preparation

In the raw SCADA data, even though it is standard operating state data, it will have both null and zero values because of the influence of external interference in the sensing test and the communication transmission process. The raw field data must be processed, including outlier elimination, null value supplement, etc. These works are collectively referred to as data preprocessing (Zhang et al., 2019).

After processing the raw SCADA data of wind turbines, wind speed, rotor speed, blade azimuth (hub angle), output power, pitch motor current, pitch angle, and other wind turbine state data are extracted. If the number of wind turbine state parameters is $n$, one sampling record constitutes a data sample, as follows

$X_i=\left(x_{i1},x_{i2},\cdots ,x_{ij},\cdots ,x_{in}\right)(6)$

Since the data is sampled and recorded at a fixed frequency, each time corresponds to a particular moment. If the sampling frequency is set to $f\left(\mathrm{H}\mathrm{z}\right)$, then the $i$ sample record is the moment $i/f$ after the start of sampling. If the total number of SCADA data samples extracted is $m$, the data can be expressed in matrix form.

$X={\left(X_1,X_2,\cdots ,X_i,\cdots ,X_m\right)}^{-1}=\left[\begin{array}{l}{x}_{11},x_{12},\dots ,x_{1j},\dots ,x_{1n}\\ ⋮\\ x_{i1},x_{i2},\dots ,x_{ij},\dots ,x_{in}\\ ⋮\\ x_{m1},x_{m2},\dots ,x_{mj},\dots ,x_{mn}\end{array}\right](7)$

For a specific parameter data, its corresponding data is a column of the matrix. Here, for the convenience of later discussion, the wind speed, rotor speed, blade azimuth angle, pitch angle, and pitch motor current parameters are listed as follows

$\left\{\begin{array}{l}v=\left(v_1,v_2,\cdots ,v_i,\cdots ,v_m\right);\\ \omega =\left({\omega }_1,{\omega }_2,\cdots ,{\omega }_i,\cdots ,{\omega }_m\right);\\ \alpha =\left({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_i,\cdots ,{\alpha }_m\right);\\ \beta =\left({\beta }_1,{\beta }_2,\cdots ,{\beta }_i,\cdots ,{\beta }_m\right);\\ I=\left(I_1,I_2,\cdots ,I_i,\cdots ,I_m\right);\\ P=\left(P_1,P_2,\cdots ,P_i,\cdots ,P_m\right);\end{array}\right.(8)$

The motor pitch torque $T_{\alpha }$ acting on the blade can be calculated by substituting the pitch motor current at each moment into Eq. 1

$T_{\alpha }=\left(T_1,T_2,\cdots ,T_i,\cdots ,T_m\right)(9)$

The average angular velocity and average acceleration of blade pitch can be calculated by using the pitch angle data of each moment as follows.

$\left\{\begin{array}{l}{\varsigma }_i=\frac{{\beta }_{i+1}-{\beta }_i}{\Delta t},i=1,\cdots ,m-1\\ {\zeta }_i=\frac{{\varsigma }_{i+1}-{\varsigma }_i}{\Delta t},i=1,\cdots ,m-2\end{array}\right.(10)$

where, $\Delta t=1/f$ is the data acquisition period.

3.2 Multidimensional BIN method

Due to many SCADA data samples, it is difficult to observe the relationship between parameters from the raw data scatter plots. Figure 4 shows a scatter plot of the relationship between motor pitch torque and wind speed obtained from SCADA raw data. It can be seen from the figure that the change in motor pitch torque is very complex, predominantly when the wind turbine operates in an area with high wind speed. Moreover, since the wind speed dimension of SCADA raw data is m/s, and one decimal place is reserved, it is inevitable that the same wind speed value corresponds to multiple motor pitch moments, as shown in the small figure. Therefore, in SCADA data analysis, the BIN method is usually used to simplify the processing, find out the relationship between parameters, and then put forward a mathematical model reflecting the relationship.

FIGURE 4

FIGURE 4. Effect of wind speed on motor pitch torque.

The BIN method is to divide a parameter range into the data set into several small intervals. Then, the relevant parameters of each small interval data sample are statistically analyzed, and the statistical average value of each parameter is taken as the relevant parameter value of the new sample (small interval). In this way, the relatively stable relationship between parameters can be more clearly observed and obtained by analyzing these new samples with a small number. In essence, the BIN method is a smoothing method to eliminate noise and average filtering to obtain a simpler and single-valued parameter relationship while ignoring the influence of parameter changes between small intervals.

Taking the relationship between wind speed and motor pitch torque as an example, wind speed is an independent variable, and motor pitch torque is a dependent variable. The wind speed distribution range or value range obtained from SCADA data is $\left[v_{\mathit{min}},v_{\mathit{max}}\right]$. By using the BIN method, the wind speed range is divided into m intervals, and the interval width is $\left(v_{\mathit{max}}-v_{\mathit{min}}\right)/\mathrm{m}$. The number of samples in the kth interval is $N_k$, and the samples in this range are counted to obtain the average value of wind speed and motor pitch torque, which is used as a new sample, namely,

$\left\{\begin{array}{l}{\overline{v}}_k=\frac{1}{N_k}{\displaystyle \sum _{i=1}^{N_k}}{v}_i\\ {\overline{T}}_k=\frac{1}{N_k}{\displaystyle \sum _{i=1}^{N_k}}{T}_i\end{array}\right.k=1,\dots ,m(11)$

To obtain more stable results, the abnormal samples can also be eliminated according to the PauTa criterion, and then the average value of the new sample parameters can be recalculated using Eq. 11. In fact, the SCADA data samples are very large, and some so-called abnormal samples have little impact on the statistical mean value. Generally, abnormal samples are not removed. Moreover, because the data sample is very large, it is assumed that the wind speed in each small interval is approximately uniformly distributed. Thus, Eq. 11 is simplified to

$\left\{\begin{array}{l}{\overline{v}}_k=\left(k-1/2\right)\frac{\left(v_{\max }-v_{\min }\right)}{m}\\ {\overline{T}}_k=\frac{1}{N_k}{\displaystyle \sum _{i=1}^{N_k}}{T}_i\end{array}\right.k=1,\dots ,m(12)$

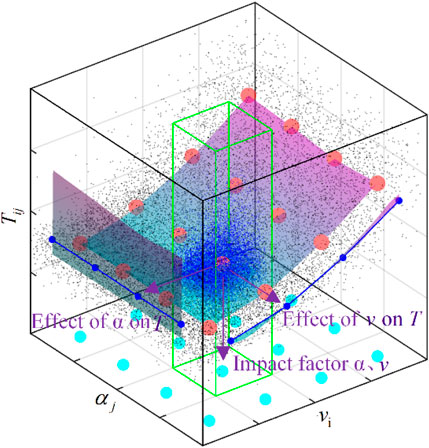
Subsequently, the BIN method used above to analyze the effects of a single parameter is extended to a multidimensional space. The multidimensional BIN method is applied to analyze problems with complex effects of multiple parameters. Firstly, these parameters are divided into small intervals within their value domain at certain intervals, ignoring parameter effects within each small interval. Then, the small interval BIN method is used for statistical analysis of the concerned parameters in their intervals. At this time, other parameters are within a fixed range, which means that other parameters remain unchanged. Finally, the small interval BIN method can be used for statistical analysis of all parameters in their intervals to obtain the influence rules of these parameters. To put it vividly, this is to mine a small multidimensional space from a large multidimensional data sample space composed of multiple parameters and carry out statistical analysis on the data samples existing in this small multidimensional space. Then, according to the research purpose, the BIN method can be carried out on the concerned parameters to obtain the influence and relationship of the concerned parameters, as shown in Figure 5. In the figure, wind speed $v_i$ is at its $m$ interval, and the azimuth $a_j$ is at its $n$ interval. $T_{ij}$ is the statistical average of the motor pitch torque for all samples in the region ${\mathrm{\Omega }}_{ij}$ consisting of wind speed $v_i$ and azimuth $a_j$.

FIGURE 5

FIGURE 5. Multidimensional BIN method visualization.

3.3 Force estimation model of pitch system

The generation process of wind turbines consists of two operating zones: the maximum wind energy tracking region and the constant power output region. Therefore, the pitch system has two stages: constant pitch and variable pitch. In addition, with the change of wind speed, the pitch stage has three states: smooth-pitch state, open-pitch state, and standstill state. Therefore, corresponding to the generation process of wind turbines, the pitch system exists in four different states: entire constant pitch state, smooth-pitch state, open-pitch state, and standstill state. As mentioned before, the force equilibrium equations of the blade are different for each state. Therefore, the force analysis of the pitch system based on field SCADA data should first obtain the data subset corresponding to the four states, that is, the SCADA data set should be decomposed.

The pitch system’s operating state is essentially the blade’s rotating state. According to the size and direction of the blade pitch angle, the running state of the pitch system can be determined. Because of the installation and test errors of wind turbines and the disturbance caused by the dynamic characteristics of wind energy and wind turbines, in the SCADA data, even when the wind speed is low, and the pitch system does not change, the pitch angle is not 0° but has a certain initial value of ${\beta }_{th}$. Thus, for convenience, ${\beta }_i\le {\beta }_{th}$ is defined as the constant pitch state and ${\beta }_i>{\beta }_{th}$ as the pitch state. Considering the pitch angle dynamic perturbation, the pitch speed threshold is set to ${\varsigma }_{th}$. From this scenario, the following are defined respectively: ${\varsigma }_i>{\varsigma }_{\mathrm{t}\mathrm{h}}$ is the smooth-pitch state, ${\varsigma }_i\le -{\varsigma }_{\mathrm{t}\mathrm{h}}$ is the open-pitch state, and $-{\varsigma }_{th}<{\varsigma }_i\le {\varsigma }_{th}$ is the standstill state.

Let $D_0$、 $D_i$、 $D_p$、 $D_d$ be the sample subsets of the wind turbine pitch system running in the four states of constant pitch state, smooth-pitch state, standstill state, and smooth-pitch state, namely,

$\left\{\begin{array}{l}{D}_0=\left({\beta }_i\le {\beta }_{th}\right)\\ D_i=\left({\beta }_i>{\beta }_{th}\right)\cap \left({\varsigma }_i>{\varsigma }_{th}\right)\\ D_p=\left({\beta }_i>{\beta }_{th}\right)\cap \left(-{\varsigma }_{th}<{\varsigma }_i\le {\varsigma }_{th}\right)\\ D_d=\left({\beta }_i>{\beta }_{th}\right)\cap \left({\varsigma }_i\le -{\varsigma }_{th}\right)\end{array}\right.(13)$

In this way, the data sample set is decomposed into four subsets of state data. According to the four state data subsets, the blade pitch load, bearing friction torque, and motor pitch torque of the four states of the variable pitch system can be obtained respectively by using the multidimensional BIN method and based on the previous force equilibrium equation.

In the constant pitch state, the corresponding wind turbine operation is in the maximum wind energy tracking region. According to the value range of wind speed and azimuth, it is divided into m and n intervals, and then the sample set $D_0$ is divided into mn subsets, namely,

$\left\{\begin{array}{l}{D}_0={\cup }_{i=1,m}^{j=1,n}{\mathrm{\Omega }}_{ij}\\ T_{a-ij}^0=\frac{1}{mn}{\displaystyle \sum }_{X_k\in {\mathrm{\Omega }}_{ij}}{T}_k\end{array}\right.(14)$

In this case, the corresponding is

$\left\{\begin{array}{l}{v}_i=\left(i-1/2\right)\Delta v/m\\ {\alpha }_j=\left(j-1/2\right)\Delta \alpha /n\end{array}\right.(15)$

According to the force equilibrium equation (Eq. 2) of the blade, the corresponding blade pitch load can be obtained from the motor pitch torque of Eq. 1 as

$T_{\mathrm{b}-ij}^0=T_{a-ij}^0(16)$

In the pitch state, the corresponding wind turbine operation is in the constant power output region. According to the value range of wind speed and azimuth, it is divided into m and n small intervals respectively, so that $D_i$, $D_p$, and $D_d$ are divided into mn subsets.

In the pitch system standstill state, from the data set $D_p$, according to the force equilibrium equation (Eq. 3) of the blade, the corresponding blade pitch load can be obtained from the motor pitch torque of Eq. 1 as

$\left\{\begin{array}{l}{D}_p={\cup }_{i=1,m}^{j=1,n}{\mathrm{\Omega }}_{ij}\\ T_{a-ij}^p=\frac{1}{mn}{\displaystyle \sum }_{X_k\in {\mathrm{\Omega }}_{ij}}{T}_k\end{array}\right.(17)$

$\left\{\begin{array}{l}{v}_i=\left(i-1/2\right)\Delta v/m\\ {\alpha }_j=\left(j-1/2\right)\Delta \alpha /n\end{array}\right.(18)$

${T_{b-ij}}^p={T_{a-ij}}^p(19)$

When the pitch system is in the smooth-pitch or open-pitch state, the blades are in the rotating phase, and the bearing friction torque could be considered. The pitch system force analysis shows that the motor pitch torque depends on the blade pitch load, bearing friction torque, and blade rotation direction. The blade pitch load and bearing friction torque depend on the wind speed and blade azimuth. When the wind speed and blade azimuth are the same, the blade pitch load and the bearing friction torque are the same in the smooth-pitch or open-pitch state. Therefore, from the data sets $D_i$ and $D_d$, the motor pitching torque can be obtained for the corresponding states.

$\left\{\begin{array}{l}{v}_i=\left(i-1/2\right)\Delta v/m\\ {\alpha }_j=\left(j-1/2\right)\Delta \alpha /n\end{array}\right.(20)$

$\left\{\begin{array}{l}{D}_i={\cup }_{i=1,m}^{j=1,n}{\mathrm{\Omega }}_{ij}\\ T_{a-ij}^i=\frac{1}{mn}{\displaystyle \sum }_{X_k\in {\mathrm{\Omega }}_{ij}}{T}_k\end{array}\right.(21)$

$\left\{\begin{array}{l}{D}_d={\cup }_{i=1,m}^{j=1,n}{\mathrm{\Omega }}_{ij}\\ T_{a-ij}^d=\frac{1}{mn}{\displaystyle \sum }_{X_k\in {\mathrm{\Omega }}_{ij}}{T}_k\end{array}\right.(22)$

Then, the corresponding blade pitch loads and bearing friction torque are obtained according to Eqs. 4, 5 as

$\left\{\begin{array}{l}{T}_{b-ij}=\left(T_{a-ij}^i+T_{a-ij}^d\right)/2\\ T_{f-ij}=\left(T_{a-ij}^d-T_{a-ij}^i\right)/2\end{array}\right.(23)$

In this way, the blade pitch load and bearing friction torque during wind turbine operation can be estimated from the motor pitch torque obtained in Eq. 1, which also facilitates the analysis of the effect of wind speed and blade azimuth on the motor pitch torque, blade pitch load, and bearing friction torque.

3.4 Analysis process of force estimation of pitch system

When estimating and analyzing the forces acting on the pitch system, first of all, it is necessary to clarify the research object and establish the force equilibrium equation of the wind turbine pitch system under various operating conditions. Then, the multidimensional BIN method is applied to estimate the blade pitch load, bearing friction torque, and motor pitch torque at the corresponding moment based on the field SCADA data. Finally, using wind speed and azimuth as influencing factors, the variation of blade pitch load, bearing friction torque, and motor pitch torque in four states, including constant pitch state in the maximum wind energy tracking region, and smooth-pitch, standstill and open-pitch state in the constant power output region, are analyzed. The specific analysis process is shown in Figure 6.

FIGURE 6

FIGURE 6. Flow chart of force estimation and analysis of pitch system.

4 Force characteristic investigation of the pitch system

4.1 Data observation and parameter setting

An entire year SCADA data of a 2 MW wind turbine are collected to conduct the research. The wind turbine locates at a mountainous wind farm in southern China. The technical performance parameters of the wind turbine and the pitch system are shown in Table 1 (Zhang et al., 2019). The SCADA system stores the operation parameters with an interval of 1 s (sampling frequency is 1 Hz). Table 2 shows the raw SCADA data form of the SCADA system. From the SCADA system, the operating parameters of the wind turbine are extracted for subsequent investigation, such as wind speed, rotor speed, blade azimuth, output power, pitch motor current, pitch motor power, and pitch angle. Considering the symmetry of the wind turbine, only one of the three blades is selected for analysis.

TABLE 1

TABLE 1. Main technical parameters of the 2 MW wind turbine.

TABLE 2

TABLE 2. Raw form of SCADA data.

The pitch angle of the extracted parameters is obtained by the angle sensor installed near the inside of the blade inner gear ring. The pitch angle data are divided into four typical periods to analyze the change with wind speed, as shown in Figure 7. When wind speed is lower than the rated value, the wind turbine operates in the maximum wind energy tracking region, and the blade does not pitch. However, the pitch angle is not zero due to installation, testing, and the pitch system’s dynamic characteristics. As shown in Figures 7A–E, when the wind speed is about $3\mathrm{m}/\mathrm{s}$ ∼ $6\mathrm{m}/\mathrm{s}$ and the pitch angle is roughly around 0.24°–0.28°. When the wind speed exceeds the rated value, the wind turbine operates in the constant output power region. During this period, the pitch system drives the blade to adjust the pitch angle increase or decrease to maintain the output power stable at the rated power, as shown in Figures 7F–O. It also can be seen from Figures 7F–O that when the wind speed is more significant than $8\mathrm{m}/\mathrm{s}$, the output power exceeds the rated power, and the pitch angle is greater than 4°, while the absolute pitch angle speed is more than 0.1 deg/s. It is important to note that pitch angle control is not based on wind speed but on the average power output. Considering the massive inertia of the wind wheel, the parameters such as wind speed, pitch angle, and output power do not correspond to each other at a specific time. When the wind turbine operates in the constant output power region and the wind speed is relatively stable, the pitch system does not drive the blade to pitch but stays on hold. At this time, the pitch angle changes slightly due to the interference of various factors. As can be seen in Figures 7P–T, the corresponding pitch angle speed distribution is between −0.02 deg/s and 0.02 deg/s.

FIGURE 7

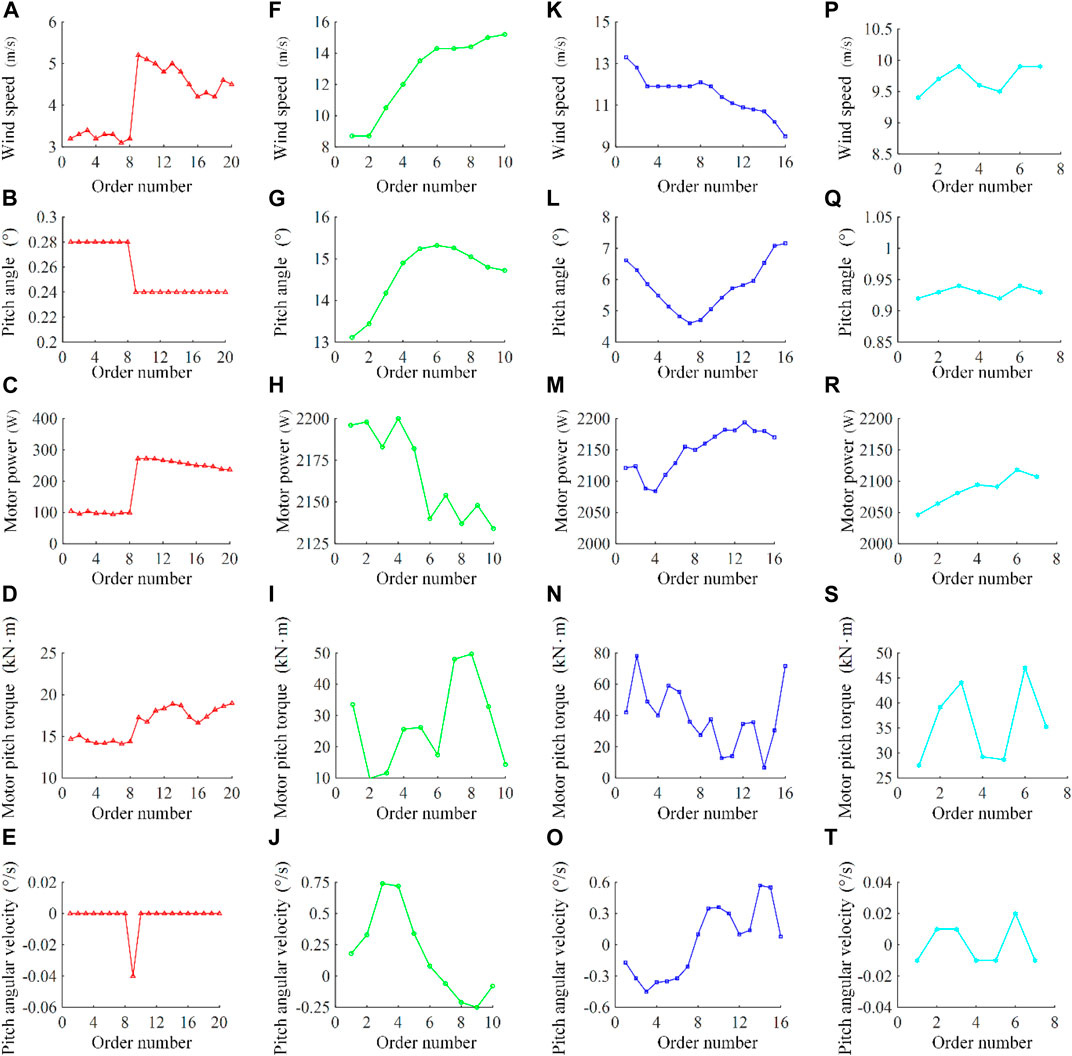
FIGURE 7. Four field data recording periods (A–E) the variation of wind speed, pitch angle, motor power, motor pitch torque and pitch angular velocity during low wind speed stage; (F–J) the variation of wind speed, pitch angle, motor power, motor pitch torque and pitch angular velocity during wind speed increases from low to high; (K–O) the variation of wind speed, pitch angle, motor power, motor pitch torque and pitch angular velocity during wind speed decreases from high to low; (P–T) the variation of wind speed, pitch angle, motor power, motor pitch torque and pitch angular velocity during minor changes in wind speed.

According to a comprehensive observation and analysis of SCADA data, the threshold of pitch angle value is selected as 0.5° (${\beta }_{\mathrm{t}\mathrm{h}}$ = 0.5°), and the threshold of pitch angle speed is selected as 0.03 deg/s ($\left|{\varsigma }_{\mathrm{t}\mathrm{h}}\right|$ = 0.03 deg/s). Taking into account the performance parameters of the wind turbine and the distribution of the SCADA data, the wind speed value domain is selected as [2.5 m/s, 8.5 m/s) in the non-pitch data set $D_0$, and [8.5 m/s, 13.5 m/s] in the pitch data complementary set $\complement D_0$. The blade azimuth variation range is [0°, 360°]. The wind speed interval is divided into 0.2 m/s, and the azimuth interval is divided into 4°.

4.2 Blade pitch load analysis

The combined action of aerodynamic forces generates the blade pitch load, centrifugal forces, and gravity. To conduct the analysis of the influence of wind speed and blade azimuth on the pitch load, the azimuths 0°, 90°, 180°, and 270° are selected to investigate the effect of wind speed, and the wind speed 4 m/s, 7 m/s, 9 m/s and 12 m/s are also selected to examine the impact of the blade azimuth. Then, the pitch load can be obtained for different wind speeds and azimuth angles by applying the proposed force estimation method of the pitch system, as shown in Figure 8.

FIGURE 8

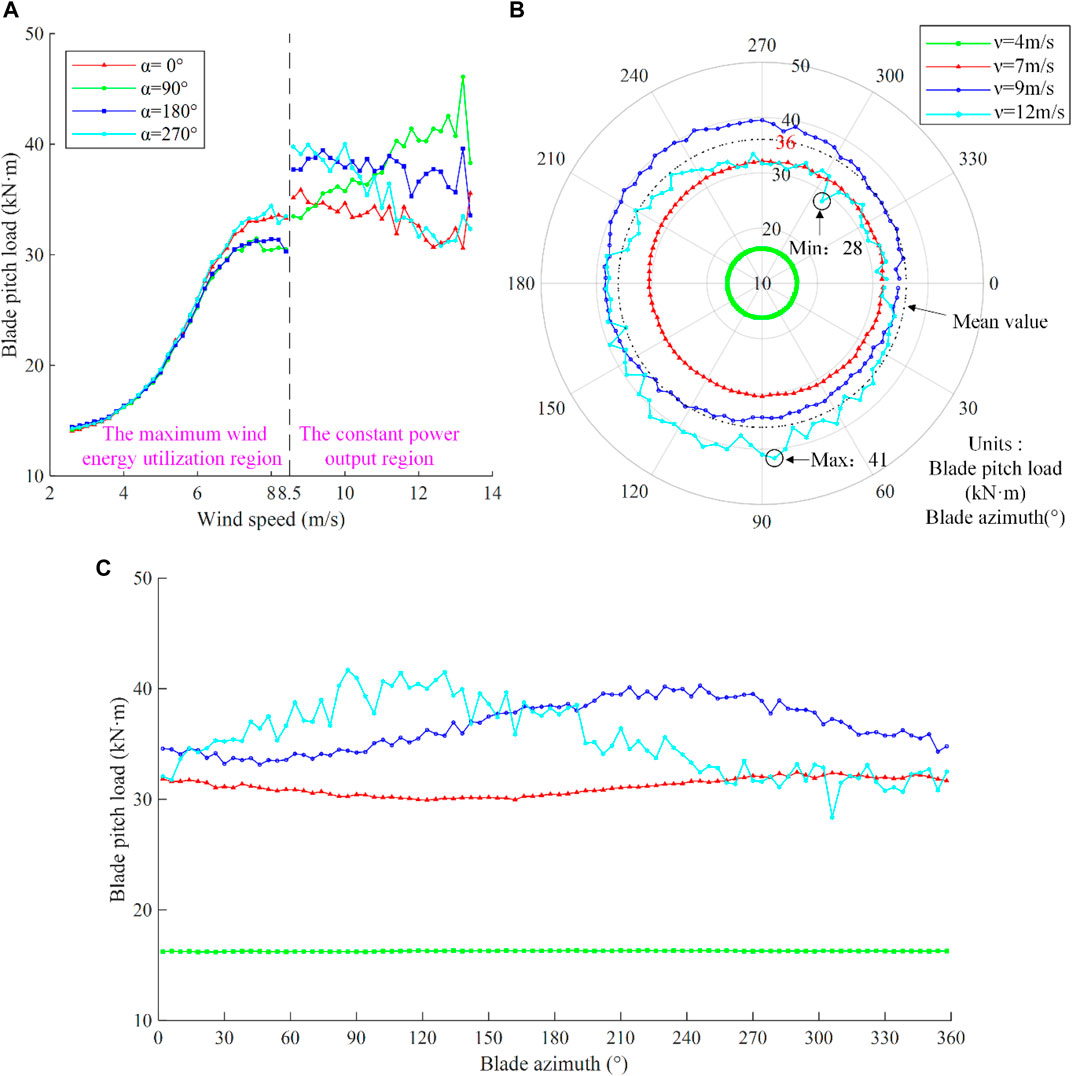
FIGURE 8. Relationship of blade pitch load with wind speed and azimuth angle (A) Influence of wind speed on blade pitch load; (B,C) Influence of azimuth on blade pitch load.

As shown in Figure 8, when the wind speed is relatively low, the blade pitch load first increases slowly with the wind speed and then rapidly increases with the wind speed. When the wind speed reaches about 7 m/s, the blade pitch load increases slowly with the wind speed or no longer increases until the wind speed reaches the rated wind speed. During this period, the wind turbine and its pitch system enter the state-switching phase, and the blade pitch load and wind speed undergo a very complex nonlinear jump change process. When the wind speed exceeds the rated speed, the blade pitch load does not change significantly with the wind speed. There is an interesting phenomenon, the blade pitch load first increases and then remains constant with wind speed. The reasons cause the phenomenon mainly has the following aspects. Firstly, when the wind turbine operates in the maximum wind energy tracking region, the blade does not pitch, the blade windward surface is the largest, and the aerodynamic force acting on the blade increases with wind speed. Meanwhile, the rotational speed of the wind wheel increases with wind speed; aerodynamic and centrifugal forces lead to an increase in blade pitch load. Secondly, when the wind turbine operates in the constant output power region, the rotational speed of the wind wheel is stable at the rated speed. At the same time, the centrifugal force remains unchanged. The blade pitch angle increases with wind speed which results in the decrease of the blade windward surface. Since the aerodynamic force acting on the blade depends on the wind pressure (wind speed) and the windward surface area, the two increase and decrease to cause the blade pitch load to remain unchanged. In general, the blade pitch control is designed to keep the output power constant and the blade pitch load from varying with wind speed.

It also can be seen from Figure 8 that the blade pitch load varies periodically with the blade azimuth., Taking the wind speed of 7 m/s as an example, when the azimuth changes from 0° to 90°, the pitch load decreases with azimuth. The pitch load is almost unchanged when the azimuth changes from 90° to 180°. When the azimuth changes from 180° to 270°, the pitch load increases with azimuth, and when the azimuth changes from 270° to 360° (0°), the pitch load first increases and then decreases. The wind wheel rotates in one circle, and the pitch load changes periodically. The periodicity of blade pitch load change with azimuth angle is closely related to wind speed. When the wind speed is relatively low $4\mathrm{m}/\mathrm{s}$, the pitch load is almost independent of the azimuth angle, and the periodicity is not reflected. When the wind speed exceeds $7\mathrm{m}/\mathrm{s}$, the pitch load varies periodically with azimuth. Comparing wind speeds of 7 m/s, 9 m/s and 12 m/s, it can be seen that the pitch load has a periodic change in amplitude. When the wind speed is 7 m/s, the amplitude of pitch load is about $30\sim 32\mathrm{k}\mathrm{N}\cdot \mathrm{m}$, with an amplitude ratio of $2\left(32-30\right)/\left(32+30\right)\approx 6.5\%$. When the wind speed is 9 m/s, the amplitude of pitch load is about $33\sim 40\mathrm{k}\mathrm{N}\cdot \mathrm{m}$. When the wind speed is 9 m/s, the amplitude of pitch load is about $28\sim 41\mathrm{k}\mathrm{N}\cdot \mathrm{m}$, with no significant increase in pitch load while the amplitude ratio increases to $2\left(41-28\right)/\left(41+28\right)\approx 38.3\%$ , which means the pitch load fluctuation increases with wind speed dramatically. It should be pointed out that the blade pitch load changes periodically with the azimuth angle, and the azimuth corresponding to the amplitude varies with the change in wind speed. When the wind speed is $7\mathrm{m}/\mathrm{s}$, the minimum pitch load corresponds to the azimuth of about 120°, and the maximum pitch load corresponds to the azimuth of about 300°. When the wind speed is 9 m/s, the minimum pitch load corresponds to the azimuth of about 60°, and the maximum pitch load corresponds to the azimuth of about 240°. When the wind speed is 12 m/s, the minimum value of blade pitch loading corresponds to the azimuth of about 300°, and the maximum pitch load corresponds to the azimuth of about 90°. When the wind turbine operates in the maximum wind energy tracking region, the pitch load varies periodically with the blade azimuth. The pitch load amplitude increases with the wind speed. However, the initial phase angle of the pitch load remains unchanged. When the wind turbine operates in the constant output power region, the initial phase angle of the pitch load decreases with the increase of the wind speed, while the amplitude of the pitch load remains the same. This is mainly due to the aerodynamic, centrifugal force, and gravity acting on the blade are all distributed forces. The resultant action point and direction are not only related to the blade shape and pitch angle but also to the blade azimuth angle, so the blade pitch load changes periodically with the rotation of the wind wheel and the change of azimuth angle. When the wind turbine operates in the maximum wind energy tracking region, the aerodynamic force acting on the blade increases with the wind speed, and the pitch load amplitude increases. However, the periodicity is not obvious at low wind speeds because the amplitude is relatively small, less than 10%. Since the pitch angle is unchanged, the initial phase angle of the pitch load remains unchanged, which is why the order of blade pitch load corresponding to the four azimuth angles in Figure 8 is not the same. When the wind turbine operates in the constant output power region, the pitch angle increases with the wind speed. Still, the blade windward surface decreases, keeping the blade pitch load and its change amplitude constant, and the amplitude ratio is nearly 20%. However, due to the change of pitch angle, the initial phase angle of pitch load at different wind speeds is different. That is, there is a phase difference.

4.3 Analysis of bearing friction torque

The bearing friction torque prevents the blade from rotating. When the blades are in the pitch state in the constant output power stage of the wind turbine, and the pitch system is in the state of smooth-pitch or open-pitch, the bearing friction torque can be estimated. The sample data near 0°, 90°, 180°, and 270° are extracted to investigate the relationship between bearing friction torque and wind speed. The sample data near wind speeds 4 m/s, 7 m/s, 9 m/s and $12\mathrm{m}/\mathrm{s}$ are also extracted to investigate the influence of blade azimuth in bearing friction torque. The estimated results are shown in Figure 9.

FIGURE 9

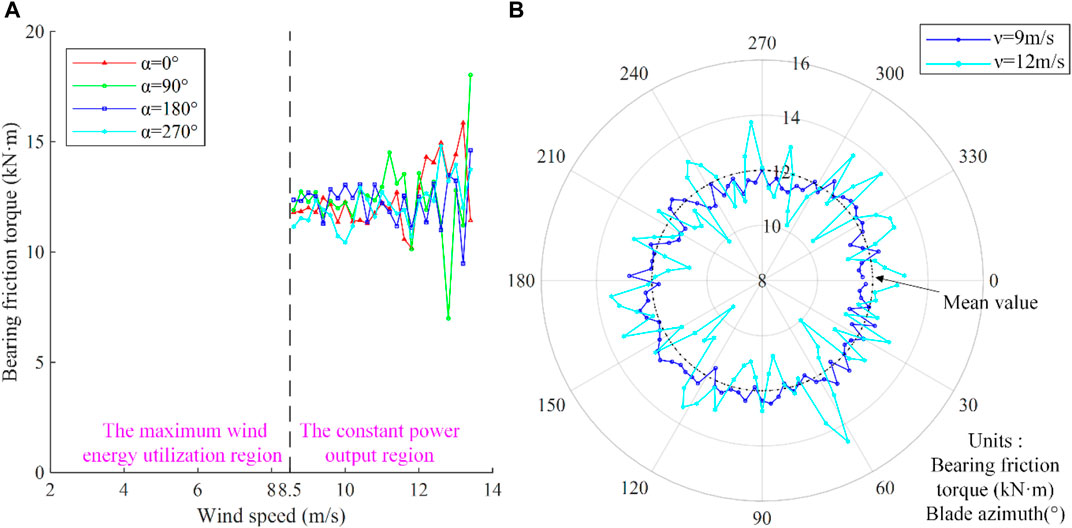
FIGURE 9. The relationship between bearing friction torque and wind speed and azimuth angle (A) Influence of wind speed on bearing friction torque; (B) Influence of azimuth on bearing friction torque.

It can be seen from Figure 9 that when the wind turbine operates in the constant output power region, the bearing friction torque fluctuates around 12 $\mathrm{k}\mathrm{N}\cdot \mathrm{m}$. The greater the wind speed, the greater the fluctuation of the friction torque. This is because the bearing friction torque depends on the load and friction coefficient of the bearing, while the friction coefficient is only related to the bearing type, the fit clearance, and the smoothness. Therefore, for a specific bearing, the bearing friction torque depends on the bearing load. The bearing load is generated by the aerodynamic force, centrifugal force, and gravity acting on the blade. The blade gravity is constant, and the wind wheel rotates at the rated speed during the constant output power output region, so the centrifugal force remains unchanged. As the pitch angle increases with the increase of wind speed, the windward surface area of the blade decreases to keep the aerodynamic force invariant. Therefore, the bearing load is the same, and the change in pitch angle only acts on different parts of the bearing. The bearing friction torque can be estimated from SCADA data. Once the friction coefficient is determined, the bearing load can also be calculated from the bearing friction torque. The pitch system bearing of the studied 2 MW wind turbine adopts a cylindrical roller negative clearance bearing with a diameter of 2110 mm. The friction coefficient of the bearing is close to the sliding friction, which is 0.01. In this way, the blade bearing of the wind turbine may suffer a load $1.14\times {10}^3\mathrm{N}$.

4.4 Analysis of motor pitch torque

The motor pitch torque is the main force driving the blade to rotate or keep the blade stationary. Its magnitude depends on the blade pitch load and bearing friction torque and is also related to the blade rotation direction. The sample data near azimuth of $0^{\circ }$, ${90}^{\circ }$, ${180}^{\circ }$ and ${270}^{\circ }$ are selected to investigate the relationship between the motor pitch torque and the wind speed. At the same time, the sample data near the wind speed of 4 m/s, 7 m/s, 9 m/s, and 12 m/s are selected to analyze the influence of azimuth angle on the motor pitch torque. The results are shown in Figure 10, Figure 11A refers to the constant state in the maximum wind energy tracking region, and Figure 10, Figures 11B–D refer to the smooth-pitch state, standstill state, and open-pitch state in the constant power output region of wind turbines.

FIGURE 10

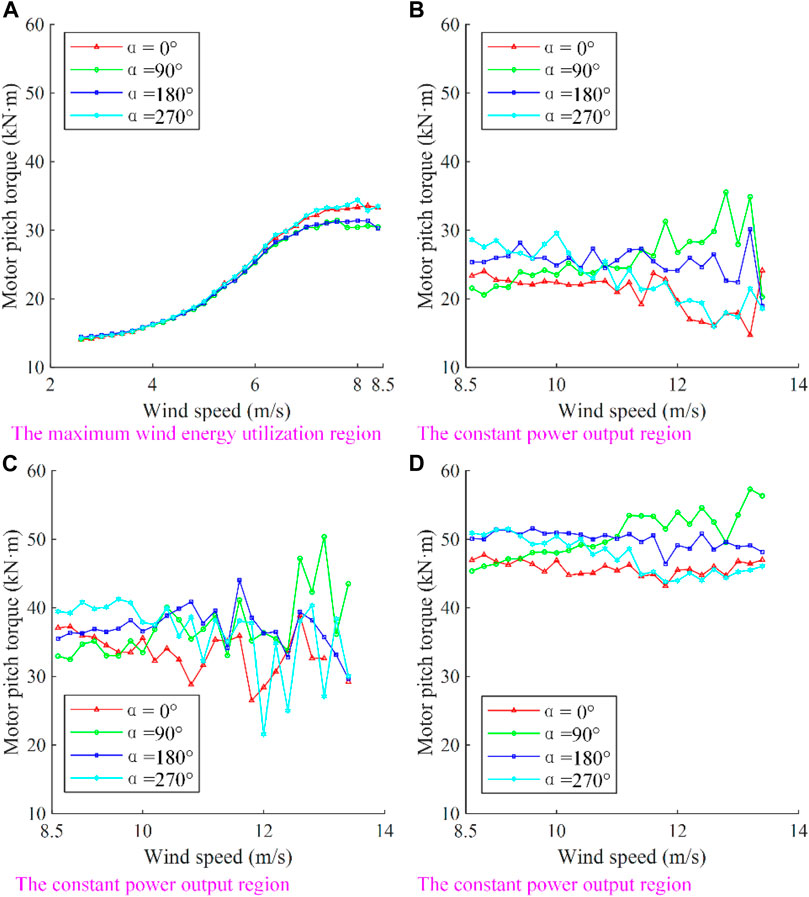
FIGURE 10. Relation between motor pitch torque and wind speed (A) The maximum wind energy utilization region; (B–D) The smooth-pitch state, standstill state, and open-pitch state in the constant power output region of wind turbines.

FIGURE 11

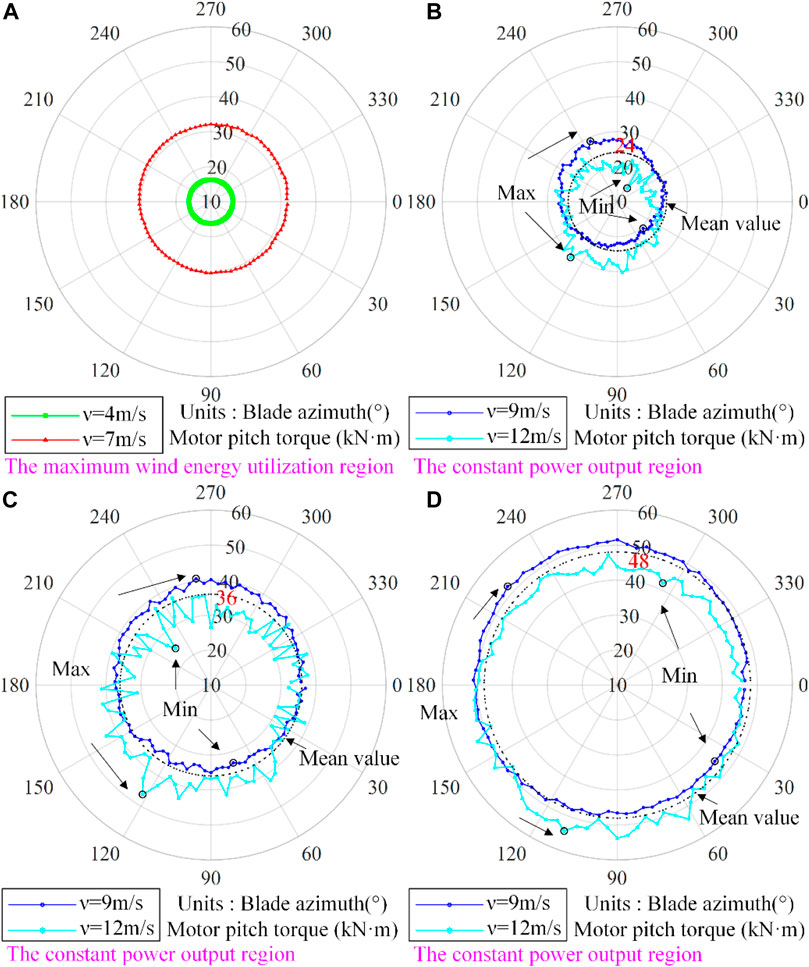
FIGURE 11. Relation between motor pitch torque and azimuth (A) The maximum wind energy utilization region; (B–D) The smooth-pitch state, standstill state, and open-pitch state in the constant power output region of wind turbines.

When wind turbines operate in the maximum wind energy utilization region, according to the force equilibrium equation mentioned above, if the friction torque is ignored, the motor pitch torque is equal to the blade pitch load. They all increase with the increase of wind speed and show periodic changes with the rotation of the wind rotor and the change of azimuth, as shown in Figure 10. Due to the constant pitch angle, the blade forces are relatively stable, and regression fitting can be performed as shown in Figure 12. The mathematical relationship is

$T_a=T_b=v^2\cdot \left(0.3529+0.0005917\cdot \sin \left(\alpha +0.3834\right)\right)+11.53,{\mathrm{R}}^2=0.94(25)$

FIGURE 12

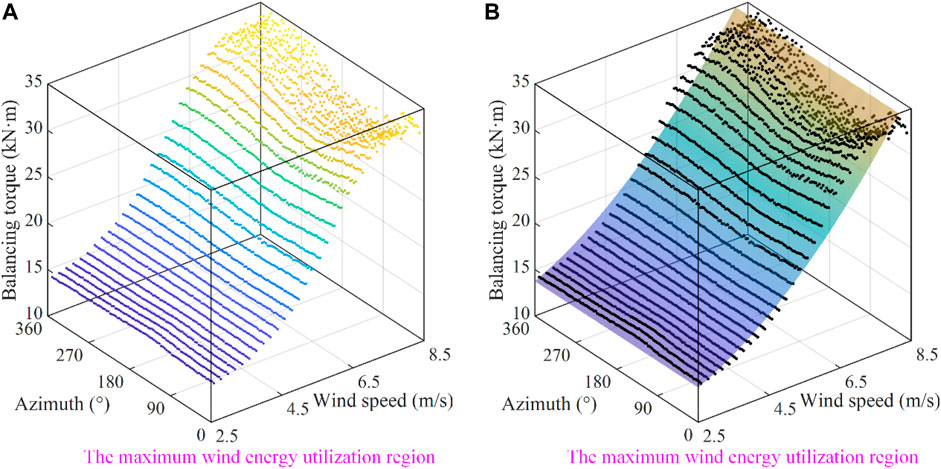
FIGURE 12. Regression fitting model of equilibrium torque in the maximum wind energy tracking region (A) Scatter plot of equilibrium torque; (B) Surface fitting of equilibrium torque.

From the model, if the influence of wind speed is not considered, that is, assuming that the wind speed is 0 and the blade pitch load is 11.53 $\mathrm{k}\mathrm{N}\cdot \mathrm{m}$, this can be considered as the blade pitch load generated by the blade gravity. The blade pitch load is proportional to the square of wind speed, which is consistent with the fact that the output power of the wind turbine is proportional to the cubic of wind speed. The proportion of the periodic function part is very small, so when the wind speed is low, the periodic change is not significant. The periodic variation of blade pitch load has an initial phase angle, which is related to the blade shape and its spatial position. When wind turbines operate in the constant power output region, the pitch system is in the variable pitch state, and the change of wind speed causes the corresponding change of blade pitch angle. This will not only achieve the basic stability of output power but also keep the blade pitch load, bearing friction torque, and motor pitch torque basically unchanged. However, the pitch angle causes nonlinear factors and torque fluctuations, which will become more and more severe with the increase of wind speed. According to the blade force equilibrium equation, when the pitch system is in the open-pitch state, the motor pitch torque is the sum of the blade pitch load and bearing friction torque, about 48 $\mathrm{k}\mathrm{N}\cdot \mathrm{m}$ (36 $\mathrm{k}\mathrm{N}\cdot \mathrm{m}$ +12 $\mathrm{k}\mathrm{N}\cdot \mathrm{m}$). When the pitch system is in the smooth-pitch state, the motor pitch torque is the blade pitch load minus the bearing friction torque, approximately 24 $\mathrm{k}\mathrm{N}\cdot \mathrm{m}$ (36 $\mathrm{k}\mathrm{N}\cdot \mathrm{m}$-12 $\mathrm{k}\mathrm{N}\cdot \mathrm{m}$). When the pitch system is in the standstill state, the motor pitch torque is considered to be equal to the blade pitch load, that is, about 36 $\mathrm{k}\mathrm{N}\cdot \mathrm{m}$. When wind turbines are in the three states of open-pitch, smooth-pitch, and standstill state, motor pitch torque changes periodically with the blade rotation and azimuth change, and the amplitude of change is different, as shown in Figure 11. It can be seen from the figure that in this operation region, the fluctuation of motor pitch torque increases with the increase of wind speed. When the wind speed is 9 m/s, the maximum fluctuation amplitude is about 8.3 $\mathrm{k}\mathrm{N}\cdot \mathrm{m}$; when the wind speed is 12 m/s, the maximum fluctuation amplitude is about 22 $\mathrm{k}\mathrm{N}\cdot \mathrm{m}$. It should be noted that these conclusions are based on the data after averaging.

In summary, for the investigated 2 MW wind turbine, when operating in a constant power output region, the blade pitch load is approximately 36 $\mathrm{k}\mathrm{N}\cdot \mathrm{m}$. Here, the blade pitch load caused by gravity is 11.53 $\mathrm{k}\mathrm{N}\cdot \mathrm{m}$, accounting for about 32%. During the rotation and azimuth change, the blade pitch load has a periodic change amplitude of 13 $\mathrm{k}\mathrm{N}\cdot \mathrm{m}$, accounting for about 36.1%. The bearing friction torque generated during blade rotation and pitch is approximately 12 $\mathrm{k}\mathrm{N}\cdot \mathrm{m}$. During the actual operation of wind turbines, the wind speed changes randomly, resulting in the change of blade pitch load and ultimately the change of motor pitch torque. The alternating characteristics of motor pitch torque come from three aspects. The first is the alternating nature of wind speed in the wind field, which depends on the characteristics of airflow variation and is naturally inevitable. The second is the alternation of blade pitch load when the wind rotor rotates. The azimuth changes from 0° to 360° and then returns to 0°. This will be affected by the spatial relationship between the two centerlines of the wind rotor rotation axis and the blade rotation axis, which exists throughout the entire process of wind turbine operation. The third is the switching of the smooth-pitch state and open-pitch state when the blade is pitching. The pitch angle increases from 0° and then decreases back to 0°, which is caused by the rotation of the blade in both positive and negative directions. The alternating nature of the motor pitch torque may be an important reason for affecting the fatigue failure of the components of the pitch system and causing the failure of the pitch system (Hameed et al., 2009; Bi et al., 2014).

5 Conclusion

In this paper, the blade pitch principle of a 2 MW direct-drive wind turbine is analyzed. By investigating the force of the pitch system under multiple operating conditions, the force equilibrium equations of the wind turbine blade are established. Based on SCADA data, a method for estimating the blade pitch load, bearing friction moment, and motor pitch torque is proposed by using the multidimensional BIN method. Many interesting phenomena have been observed. When the wind turbine operates in the maximum wind energy tracking region, the blade pitch load and motor pitch torque are proportional to the square of the wind speed and show periodic changes with the wind rotor rotation and azimuth changes. When the wind turbine operates in the constant power output region, the blade pitch load is about 36 $\mathrm{k}\mathrm{N}\cdot \mathrm{m}$, and the blade pitch load caused by gravity is 11.53 $\mathrm{k}\mathrm{N}\cdot \mathrm{m}$, accounting for about 32.1%. In the process of wind rotor rotation and azimuth change, the amplitude of periodic change is 13 $\mathrm{k}\mathrm{N}\cdot \mathrm{m}$, accounting for about 36.1%. The bearing friction torque fluctuates around 12 $\mathrm{k}\mathrm{N}\cdot \mathrm{m}$ during the pitching process, accounting for 33.3% of the pitching load, and the higher the wind speed, the more severe the fluctuation. The work of this paper is of great value to fully understand the load mechanism of pitch system, and can provide important knowledge support for the design, operation, and maintenance of large-scale wind turbine pitch system.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, JD and DL; data curation, ML and FZ; funding acquisition, JD and FZ; investigation, ML; software, ML and DL; validation, JD and DL; visualization, ML, DL, and JD; writing-original draft, ML; writing-review and editing, JD and DL. All authors contributed to the article and approved the submitted version.

Funding

This work is supported by the National Natural Science Foundation of People’s Republic of China (Grant Nos 52075164 and 52205098) and the science and technology innovation Program of Hunan Province (Grant No. 2021RC4038).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdelbaky, M. A., Liu, X., and Jiang, D. (2020). Design and implementation of partial offline fuzzy model-predictive pitch controller for large-scale wind-turbines. Renew. Energy 145, 981–996. doi:10.1016/j.renene.2019.05.074

CrossRef Full Text | Google Scholar

Astolfi, D. (2021). Wind turbine operation curves modelling techniques. Electronics 10 (3), 269. doi:10.3390/electronics10030269

CrossRef Full Text | Google Scholar

Bhargava, V., Kasuba, S., Maddula, S. P., Jagadish, D., Khan, M. A., Padhy, C. P., et al. (2020). A case study of wind turbine loads and performance using steady-state analysis of BEM. Int. J. Sustain. Energy 40 (1), 22–40. doi:10.1080/14786451.2020.1787411

CrossRef Full Text | Google Scholar

Bi, R., Qian, K., Zhou, C., Hepburn, D. M., and Rong, J. (2014). A survey of failures in wind turbine generator systems with focus on a wind farm in China. Int. J. Smart Grid Clean Energy 3, 373. doi:10.12720/sgce.3.4.366-373

CrossRef Full Text | Google Scholar

Chen, B., Matthews, P. C., and Tavner, P. J. (2013). Wind turbine pitch faults prognosis using a-priori knowledge-based ANFIS. Expert Syst. Appl. 40 (17), 6863–6876. doi:10.1016/j.eswa.2013.06.018

CrossRef Full Text | Google Scholar

Cheon, J., Kim, J., Lee, J., Lee, K., and Choi, Y. (2019). Development of hardware-in-the-loop-simulation testbed for pitch control system performance test. Energies 12 (10), 2031. doi:10.3390/en12102031

CrossRef Full Text | Google Scholar

Correa-Jullian, C., Cofre-Martel, S., San Martin, G., Lopez Droguett, E., de Novaes Pires Leite, G., and Costa, A. (2022). Exploring quantum machine learning and feature reduction techniques for wind turbine pitch fault detection. Energies 15 (8), 2792. doi:10.3390/en15082792

CrossRef Full Text | Google Scholar

Dai, J., Hu, Y., Liu, D., and Long, X. (2010). Calculation and characteristics analysis of blade pitch loads for large scale wind turbines. Sci. China Technol. Sci. 53 (5), 1356–1363. doi:10.1007/s11431-010-0058-8

CrossRef Full Text | Google Scholar

Dai, J., Li, M., Chen, H., He, T., and Zhang, F. (2022). Progress and challenges on blade load research of large-scale wind turbines. Renew. Energy 196, 482–496. doi:10.1016/j.renene.2022.07.017

CrossRef Full Text | Google Scholar

Dai, J. C., Hu, Y. P., Liu, D. S., and Long, X. (2011). Aerodynamic loads calculation and analysis for large scale wind turbine based on combining BEM modified theory with dynamic stall model. Renew. Energy 36 (3), 1095–1104. doi:10.1016/j.renene.2010.08.024

CrossRef Full Text | Google Scholar

Hameed, Z., Hong, Y. S., Cho, Y. M., Ahn, S. H., and Song, C. K. (2009). Condition monitoring and fault detection of wind turbines and related algorithms: A review. Renew. Sustain. Energy Rev. 13 (1), 1–39. doi:10.1016/j.rser.2007.05.008

CrossRef Full Text | Google Scholar

He, L., Hao, L., and Qiao, W. (2021). Remote monitoring and diagnostics of pitch-bearing defects in an MW-scale wind turbine using pitch symmetrical-component analysis. IEEE Trans. Industry Appl. 57 (4), 3252–3261. doi:10.1109/tia.2021.3079221

CrossRef Full Text | Google Scholar

Jiao, X., Meng, W., Yang, Q., Fu, L., and Chen, Q. (2018). Adaptive continuous neural pitch angle control for variable-speed wind turbines. Asian J. Control 21 (4), 1966–1979. doi:10.1002/asjc.1963

CrossRef Full Text | Google Scholar

Korkos, P., Linjama, M., Kleemola, J., and Lehtovaara, A. (2022). Data annotation and feature extraction in fault detection in a wind turbine hydraulic pitch system. Renew. Energy 185, 692–703. doi:10.1016/j.renene.2021.12.047

CrossRef Full Text | Google Scholar

Li, J., and Wang, S. (2021). Dual multivariable model-free adaptive individual pitch control for load reduction in wind turbines with actuator faults. Renew. Energy 174, 293–304. doi:10.1016/j.renene.2021.04.080

CrossRef Full Text | Google Scholar

Liu, D., Zhang, F., Dai, J., Xiao, X., and Wen, Z. (2021). Study of the pitch behaviour of large-scale wind turbines based on statistic evaluation. IET Renew. Power Gener. 15 (11), 2315–2324. doi:10.1049/rpg2.12166

CrossRef Full Text | Google Scholar

Liu, H., Liu, H., Zhu, C., Sun, Z., and Bai, H. (2019). Study on contact fatigue of a wind turbine gear pair considering surface roughness. Friction 8 (3), 553–567. doi:10.1007/s40544-019-0277-3

CrossRef Full Text | Google Scholar

McKinnon, C., Carroll, J., McDonald, A., Koukoura, S., and Plumley, C. (2021). Investigation of isolation forest for wind turbine pitch system condition monitoring using SCADA data. Energies 14 (20), 6601. doi:10.3390/en14206601

CrossRef Full Text | Google Scholar

Neshat, M., Nezhad, M. M., Abbasnejad, E., Mirjalili, S., Groppi, D., Heydari, A., et al. (2021). Wind turbine power output prediction using a new hybrid neuro-evolutionary method. Energy 229, 120617. doi:10.1016/j.energy.2021.120617

CrossRef Full Text | Google Scholar

Rosemeier, M., Berring, P., and Branner, K. (2016). Non-linear ultimate strength and stability limit state analysis of a wind turbine blade. Wind Energy 19 (5), 825–846. doi:10.1002/we.1868

CrossRef Full Text | Google Scholar

Wang, C-S., and Chiang, M-H. (2016). A novel pitch control system of a large wind turbine using two-degree-of-freedom motion control with feedback linearization control. Energies 9 (10), 791. doi:10.3390/en9100791

CrossRef Full Text | Google Scholar

Wang, W., Liu, H., Zhu, C., Tang, J., and Jiang, C. (2019). Evaluation of contact fatigue risk of a carburized gear considering gradients of mechanical properties. Friction 8 (6), 1039–1050. doi:10.1007/s40544-019-0317-z

CrossRef Full Text | Google Scholar

Wei, L., Qian, Z., and Zareipour, H. (2020). Wind turbine pitch system condition monitoring and fault detection based on optimized relevance vector machine regression. IEEE Trans. Sustain. Energy 11 (4), 2326–2336. doi:10.1109/tste.2019.2954834

CrossRef Full Text | Google Scholar

Wei, L., Qian, Z., Zareipour, H., and Zhang, F. (2021). Comprehensive aging assessment of pitch systems combining SCADA and failure data. IET Renew. Power Gener. 16 (1), 198–210. doi:10.1049/rpg2.12281

CrossRef Full Text | Google Scholar

Xu, B., Yuan, Y., Liu, H., Jiang, P., Gao, Z., Shen, X., et al. (2020). A pitch angle controller based on novel fuzzy-PI control for wind turbine load reduction. Energies 13 (22), 6086. doi:10.3390/en13226086

CrossRef Full Text | Google Scholar

Yin, X., Fan, Y., Qin, Y., Jiang, H., Jiang, H., and Ye, X. (2022). fault detection of wind turbine pitch motors based on ensemble learning approach. J. Phys. Conf. Ser. 2401 (1), 012086. doi:10.1088/1742-6596/2401/1/012086

CrossRef Full Text | Google Scholar

Yuan, Y., Chen, X., and Tang, J. (2020). Multivariable robust blade pitch control design to reject periodic loads on wind turbines. Renew. Energy 146, 329–341. doi:10.1016/j.renene.2019.06.136

CrossRef Full Text | Google Scholar

Zeng, H., Dai, J., Zuo, C., Chen, H., Li, M., and Zhang, F. (2022). Correlation investigation of wind turbine multiple operating parameters based on SCADA data. Energies 15 (14), 5280. doi:10.3390/en15145280

CrossRef Full Text | Google Scholar

Zhang, F., Dai, J., Liu, D., Li, L., and Long, X. (2019). Investigation of the pitch load of large-scale wind turbines using field SCADA data. Energies 12 (3), 509. doi:10.3390/en12030509

CrossRef Full Text | Google Scholar