Synchronous rectification of LLC resonant converters based on resonant inductor voltage

Synchronous rectification (SR) technology has been a critical technology for LLC converters to achieve high efficiency and power density. However, conventional SR driving methods face challenges in terms of light-load condition, module size, switching accuracy, and circuit complexity. This paper proposes an SR driving strategy based on resonant inductor voltage (RLV) to address those issues. This RLV-SR driving strategy does not require current sensors and is insensitive to rectifier parasitic parameters. In addition, the RLV-SR driving strategy can be applied in a relatively wide operating frequency range and load conditions. Experimental results based on a 100-W/24-V LLC converter are presented to verify the effectiveness of the proposed RLV-SR driving strategy. Furthermore, the error of turn-on time caused by stray inductance is significantly reduced compared with the conventional V_DS-ON sensing method, which improves the power converter’s efficiency.

1 Introduction

LLC converters are widely used in server power supply (Lee et al., 2016; Ahmed et al., 2019), light-emitting diode (LED) drivers (Wang Y. et al., 2016), electric vehicle charging (Wang X. et al., 2016; Lin et al., 2023), renewable energy systems (Tayebi et al., 2019), and solid-state transformers (Zhang et al., 2021) due to the high conversion efficiency brought by its soft-switching characteristics. The secondary side rectifier diode conduction loss is one of the major losses (Yang et al., 2013) through the analysis of the conventional LLC topology loss. Synchronous rectification (SR) has a pivotal role in improving the efficiency of LLC converters. SR technology is to use MOSFETs instead of rectifier diodes. The MOSFET is turned on when rectified current passes through, while the MOSFET is turned off the rest of the time. Since the MOSFET has a small on-resistance, the large loss of the on-resistance on the diode is significantly reduced. As a result, the conversion efficiency is improved. Recent years have seen a considerable increase in the literature concerning the SR driving strategies of LLC converters.

The reported SR driving strategies can be divided into the following four categories: current-driven method, sensorless model-based method, ${\mathrm{v}}_{\mathrm{D}\mathrm{S}}$ sensing method, and method for high voltage sensing. The basic principles and precautions of the four methods are illustrated in Figure 1.

FIGURE 1

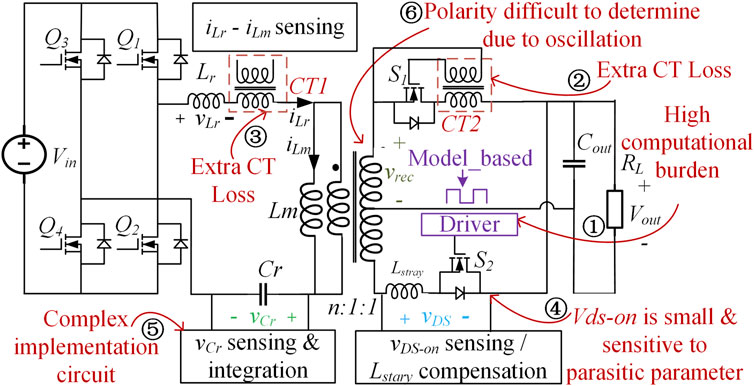
FIGURE 1. Conventional SR driving schemes: ① for sensorless model-based method, ②, ③for current sensing, ④ for V_DS-on sensing, and ⑤, ⑥ for high-voltage sensing.

The first category of SR driving strategies is the sensorless model-based method. Zhu et al. (2021) built a mathematical model to determine that the turn-on instant and conduction time are adjusted adaptively. Li et al. (2021) built mathematical models based on the LLC equivalent impedance to calculate the SR on-time in the forward and reverse modes. Li et al. (2022) built a mathematical model to calculate the SR conduction time online in the forward and reverse modes and to determine the SR turn off instant considering the switching frequency and load. These schemes can modulate the SR control signal with high accuracy in the steady state. These solutions can reduce the cost by eliminating additional sensors; however, the theoretical models of these schemes are complex, leading to a high computational burden on the controller.

The second category is based on detecting primary or secondary side currents. A method to directly drive the SR based on the secondary current is proposed in Xie et al. (2001). The advantage of the direct driving strategy its simplicity and accuracy, and the strategy can be used in different working modes without additional driving power. In Kim et al. (2012), an SR scheme based on the primary side current drive of the transformer is introduced. By generating an auxiliary current source, the magnetizing current ($i_{Lm}$) can be separated from the resonant current ($i_{Lr}$), which can be used to generate SR drive signals. The large current passed by the current sensor will lead to a sizeable primary loss of the sensor. In addition, considering the large volume of the sensor, it may not be suitable for cases requiring high power density. Since self-driven SR is needed, it may not be practical in light-load situations.

The third category of the existing technology is the $v_{DS}$ sensing methods. Since the voltage drop of the rectifier is different when the diode is turned on and the MOS is turned on, this difference can be used to generate SR signals. Due to the stray inductance of the MOS package, the $v_{DS}$ will reach the turn-off voltage faster, which results in the early turn-off of SR signals. To solve the problem of inaccurate turn-off time caused by stray inductance, the following two methods are adopted.

One method is to use an RC circuit to compensate for the stray inductance. Fu et al. (2009) used resistors, capacitors, and switches, and the conduction of the SR body diode was almost 0. A compensation circuit based on resistors, capacitors, and diodes was proposed by Wang et al. (2010) and Wang and Liu (2014), which can realize the compensation function more reliably and simply. However, this method needs to obtain an accurate SR parasitic inductance value to set the RC compensation circuit. At the same time, the compensation circuit may require a small switch MOS, which will increase the complexity of the system.

Another method is the use of an adaptive control strategy. The method was introduced by Qian et al. (2022) to improve reverse current. Moon et al. (2019) proposed an adaptive control method based on the last dead time measurement to realize the SR function. Measurement of dead time and a high-speed controller are also needed. The method proposed in Fei et al. (2018) is synchronized with the primary side, in which the switch-on point is at the primary side’s turn-on time, and the switch-off point is based on the automatic adjustment process. The main advantage of this method is that it reduces the controller requirements through ripple measurement. These methods may introduce system reliability issues, which may lead to shoot-through. MOS changes in on-time may also introduce loss.

The last category is the high-voltage sensing method. In Hsu et al. (2019), the synchronous rectification function is realized by integrating and comparing the resonant capacitor voltage ($v_{Cr}$). The resonant capacitor voltage is a large voltage signal and, therefore, insensitive to interference. But integrators and comparators complicate the converter. In Mohammadi and Ordonez (2019), the half-bridge mid-point voltage and the polarity of the transformer voltage are sampled and compared; when the rectifier voltage polarity is the same as the input voltage polarity, the SR should be turned on. However, due to the limitation of circuit parasitics, the oscillation of the rectified voltage will make it difficult to judge the polarity, especially at high frequencies.

To resolve the aforementioned challenges of LLC converters, an SR strategy for LLC resonant converters based on the resonant inductor voltage ($v_{Lr}$) is proposed, referred to as synchronous rectification based on the resonant inductor voltage (SR-RLV).

The principle of this method is shown in Figure 2. This method can judge the working stage of the LLC resonant converter by measuring the value of the resonant inductor voltage ($v_{Lr}$). The resonant inductor voltage ($v_{Lr}$) value and the jump direction are used to derive the working stage of the circuit. The SR strategy is established by judging the current stage and calculation stage duration, and the SR function of the LLC converter is realized.

FIGURE 2

FIGURE 2. Proposed RLV strategy senses large voltage signals.

The proposed RLV strategy can turn on the SR MOS accurately and quickly and improve the conversion efficiency of the LLC converter. The inductor voltage $v_{Lr}$ is large voltage amplitude, and the anti-interference performance is excellent. The strategy can work in the wide frequency range of the resonant converter. At the same time, the issues of bulky size and high cost caused by using a current transformer SR method are solved.

Section 2 describes the detailed steps of operations, which demonstrate that the RLV method covers a wide operating range of frequencies from below to above and loads from heavy to light. The realization of a driving strategy based on RLV-SR is also introduced in this section. In Section 3, experimental results are presented to verify the effectiveness of the proposed RLV method. The conclusion is provided in Section 4.

2 RLV-SR driving strategy

To illustrate this method, the LLC topology circuit is shown in Figure 2. A full-bridge structure is adopted for the inverter part, and the rectifier part is a half-bridge structure. The system inverter part Q1/Q4 is a group of identical signals, and Q2/Q3 is a group of identical signals, which are sent out by the controller as known signals.

The implementation of the proposed driving scheme is shown in Figure 3. The resonant inductor voltage $v_{Lr}$ and the output voltage $V_{\mathrm{o}\mathrm{u}\mathrm{t}}$ are input signals, which are input to the high-speed A/D converter through the signal conditioning circuit of the operational amplifier. The A/D conversion results are given to the FPGA module. The MOS drive signal on the primary side is also used as the input of the FPGA module.

FIGURE 3

FIGURE 3. Key implementation of the proposed driving scheme.

The FPGA module uses the RLV-SR strategy to determine the PON stage according to $v_{Lr}$ and $V_{\mathrm{o}\mathrm{u}\mathrm{t}}$ and the driving signals of the primary side. Simultaneously, the duration of the P stage ($t_{stage\_p}$) and the duration of the N stage ($t_{stage\_N}$) are measured. The on and off period of the SR signal is determined according to the RLV algorithm.

Before the SR drive signals are output, some output limits are set to avoid MOS shoot-through. When the upper and lower transistors of the SR signal are turned on, a dead time is set to prevent the MOS from being shoot-through. At the same time, when $V_{out}$ drops below the safe range, the DSP will turn off all MOS to avoid short-circuiting.

For LLC converters, according to the relationship between the current $i_{Lr}$ flowing in the resonant inductor and the current $i_{Lm}$ in the magnetizing inductance, the operating modes can be divided into three categories: P stage, N stage, and O stage. If $i_{Lr}>i_{Lm}$, the system is in the P stage, and the equivalent circuit is shown in Figure 4A, the upper half of the rectifier part is turned on, and the equivalent voltage is $\mathrm{n}{\mathrm{V}}_{\mathrm{o}\mathrm{u}\mathrm{t}}$.

FIGURE 4

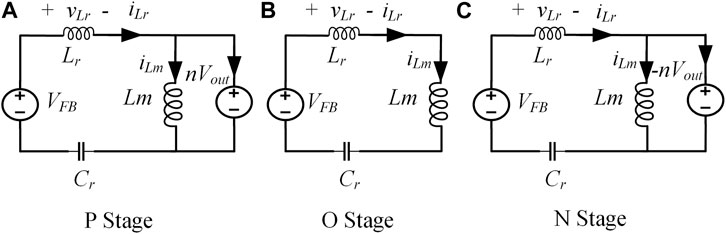
FIGURE 4. Three operation stages for the LLC resonant converter. (A) P stage. (B) N stage. (C) O stage.

If $i_{Lr}=i_{Lm}$, the system is in the O stage, and the equivalent circuit is shown in Figure 4B, the resonant inductor Lr and the magnetizing inductance Lm participate in the resonance together, no current flows in the rectifier part, and the voltage source on the right is 0.

If $i_{Lr}<i_{Lm}$, the system is in the N stage, and the equivalent circuit is shown in Figure 4C, the lower half of the rectifier part is turned on, and the equivalent voltage is reversed, which is $-n{V}_{out}$.

The RLV-based SR signal needs to be completed through the following steps.

Step 1:. Measure the resonant inductor Lr voltage $v_{Lr}$ of the LLC resonant converter and the system output voltage $V_{out}$ in real time.

Step 2:. Judge the working stage of the LLC converter according to the value of $v_{Lr}$ before or after the edge time of the primary-side control signals $V_{Q1}$ and $V_{Q2}$ and the value of $v_{Lr}$ at the jumping time. The specific working stage judgment method is described in detail later.

Step 3:. Measure the duration of the P stage ($t_{stage\_p}$) and the duration of the N stage ($t_{stage\_N}$) according to the circuit working stage.

Step 4:. Using the current working stage obtained in Step 2 and the duration of each stage measured in Step 3, under the condition that the system output voltage is stable and the system output frequency is stable, output the synchronous rectification signals $V_{S1}$ and $V_{S2}$.When the system enters the P state: $V_{S1}=1$, $V_{S2}=0$, when t = $t_{stage\_P}$, $V_{S1}=0$, $V_{S2}=0$.When the system enters the N state: $V_{S1}=0$, $V_{S2}=1$, when t = $t_{stage\_N}$, $V_{S1}=0$, $V_{S2}=0$.When the system is in the O state: $V_{S1}=0$, $V_{S2}=0$.If the system output voltage or system output frequency is unstable, waiting for stabilization is needed to output the SR signal.In Step 2, the current working stage of the resonant circuit needs to be judged, and the judgment method is different under different working frequencies. The RLV-SR strategy will be introduced from three aspects: the resonant converter works below the resonant frequency, above the resonant frequency, and under light-load conditions.

2.1 Below resonant frequency region

When the operating frequency ($f_s$) of the system is below the resonant frequency ($f_r$) of the LLC converter ($f_s<f_r$), as shown in Figure 5, the following method of using $v_{Lr}$ to judge the stage of the system is applied. From the time of the falling edge of $V_{Q2}$ to the time of the falling edge of $V_{Q1}$, including the time of $V_{Q1}$ = 1, it is the first half cycle of the system. The first half cycle is shown in the period from $t_0$ to $t_2$.

(1) The controller measures the resonant inductor v_Lr in real time, and the falling edge time of the control signal $V_{Q2}$ is recorded as $t_0$. The corresponding voltages of the resonant inductor Lr before and after the time $t_0$ are $v_{Lr,t0-}$ and $v_{Lr,t0+}$, respectively.

$\lambda \left|v_{Lr,t_0-}\right|>n{V}_o(1)$

FIGURE 5

FIGURE 5. Flow chart of the RLV-SR strategy algorithm for below resonance.

If the system meets condition (1) before $t_0$ arrives, the system will be in the P stage; otherwise, it will be in the O stage. Here, $\lambda =Lm/Lr$, and n represents the transformation ratio between the primary side and the secondary side.

(2) At the time of the rising edge of the control signal $V_{Q1}$, the voltage of $V_{FB}$ increases from $-V_{in}$ to $V_{in}$, and the resonant inductor voltage $v_{Lr}$ increases, which is recorded as the first time of the $v_{Lr}$ jump edge.

(3) Continue to judge condition (1), if $\mathrm{\lambda }\left|v_{Lr}\right|>n{V}_o$, the system changes to the P state; otherwise, the system continues to be in the O state.

(4) After the system enters the P state, by measuring the resonant inductor Lr voltage $v_{Lr}$, if the second increase occurs, this moment is recorded as $t_1$, and the system state will be converted to the O state or the N state. At the time $t_1$, the resonant capacitor Cr voltage is $v_{Cr,t1}:$

$v_{Cr,t_1-}=V_{in}-n{V}_o-v_{Lr,t1-}.(2)$

If it is converted from the P state to the O state, calculate the voltage $V_{Lm}$ of the magnetizing inductance Lm.

$\begin{array}{l}{v}_{Lm,t1+}=\frac{\lambda }{\lambda +1}\left(V_{in}-\left(V_{in}-n{V}_o-v_{Lr,t1-}\right)\right)\\ =\frac{\lambda }{\lambda +1}\left(n{V}_o+v_{Lr,t1-}\right)\end{array}(3)$

If the calculated value $\left|V_{Lm,t1+}\right|>n{V}_o$, the system enters the N state; otherwise, it enters the O state.

(5) If the system is at the O stage, the next stage will be the N stage. By measuring the resonant inductor Lr voltage $V_{Lr}$, calculate the current state magnetizing inductance Lm voltage $V_{Lm}$. If $\left|V_{Lm}\right|=\lambda V_{Lr}>n{V}_o$, the system enters the N state; otherwise, it remains in the O state until the end of the half cycle.

(6) If the system is converted to the N state, this state remains until the end of the first half cycle, and the end time is the control signal $V_{Q1}=0$, which is the falling edge of $V_{Q1}$.

(7) From the time of the falling edge of $V_{Q1}$ to the time of the falling edge of $V_{Q2}$, including the time of $V_{Q2}=1$, it is the second half cycle of the system. The second half cycle is shown as the period from $t_2$ to $t_4$.

As shown in Figure 6, the waveform of the lower half cycle of the LLC system is symmetrical with the upper half cycle about the time axis, and the O state is the same, while the P state and N state are opposite.

FIGURE 6

FIGURE 6. Key waveform of the RLV scheme for below resonance.

The specific algorithm flow chart of the RLV-SR strategy algorithm for below resonance is shown in Figure 5.

Since the real-time status of the system can be measured by the aforementioned method, the P stage and N stage duration time can be measured synchronously.

2.2 Above resonant frequency region

When $f_s>f_r$, as shown in Figure 7, the method of using $v_{Lr}$ to judge the stage of the system is as follows:

FIGURE 7

FIGURE 7. Key waveform of the RLV scheme for above resonance.

From the time of the falling edge of $V_{Q2}$ to the time of the falling edge of $V_{Q1}$, including the time of $V_{Q1}$ = 1, it is the first half cycle of the system. The first half cycle is shown as the period from $t_0$ to $t_2$.

(1) The controller measures the resonant inductor $v_{Lr}$ in real time, and the falling edge time of the control signal $V_{Q2}$ is recorded as $t_0$. The corresponding voltages of the resonant inductor Lr before and after the time $t_0$ are $v_{Lr,t0-}$ and $v_{Lr,t0+}$, respectively.

If the system meets condition (1) before $t_0$ arrives, the system will be in the N stage; otherwise, it will be in the O stage.

(2) At the time of the rising edge of the control signal $V_{Q1}$, the voltage of $V_{FB}$ jumps from $-V_{in}$ to $V_{in}$, and the resonant inductor voltage $V_{Lr}$ jumps, which is recorded as the first time of the $V_{Lr}$ jump edge.

(3) Continue to judge condition (1). If $\lambda \left|V_{Lr}\right|>n{V}_o$, the system changes to the N state; otherwise, the system continues to be in the O state.

(4) After the system enters the N state, by measuring the resonant inductor Lr voltage $V_{Lr}$, if the second increase occurs, this moment is recorded as $t_1$, and the system state will be converted to the O state or the P state. At the time $t_1$, the resonant capacitor Cr voltage $V_{Cr}$ can be calculated by Eq. 2.

If it is converted from the P state to the O state, calculate the voltage $V_{Lm}$ of the magnetizing inductance Lm with Eq. 3.

If the calculated value $\left|V_{Lm,t1+}\right|>n{V}_o$, the system enters the P state; otherwise, it enters the O state.

(5) If the system is at the O stage, the next stage will be the P stage. By measuring the resonant inductor Lr voltage $V_{Lr}$, calculate the current state magnetizing inductance Lm voltage $V_{Lm}$. If $\left|V_{Lm}\right|=\lambda V_{Lr}>n{V}_o$, the system enters the P state; otherwise, it remains in the O state until the end of the half cycle.

(6) If the system is converted to the P state, this state remains until the end of the first half cycle, and the end time is the control signal $V_{Q1}=0$, which is the falling edge of $V_{Q1}$.

(7) From the time of the falling edge of $V_{Q1}$ to the time of the falling edge of $V_{Q2}$, including the time of $V_{Q2}=1$, it is the second half cycle of the system. The second half cycle is shown as the period from $t_2$ to $t_4$.

The flow chart of the RLV-SR strategy algorithm for above resonance is similar to the one shown in Figure 5.

As shown in Figure 7, the waveform of the lower half cycle of the LLC system is symmetrical with the upper half cycle about the time axis, and the O state is the same, while the P state and N state are opposite. Since the real-time stage can be measured by the aforementioned method, the P stage and N stage duration time can be measured synchronously.

2.3 Light-load condition

When the system works in a light-load condition, it is divided into below and above resonant frequency zones, as shown in Figure 8.

FIGURE 8

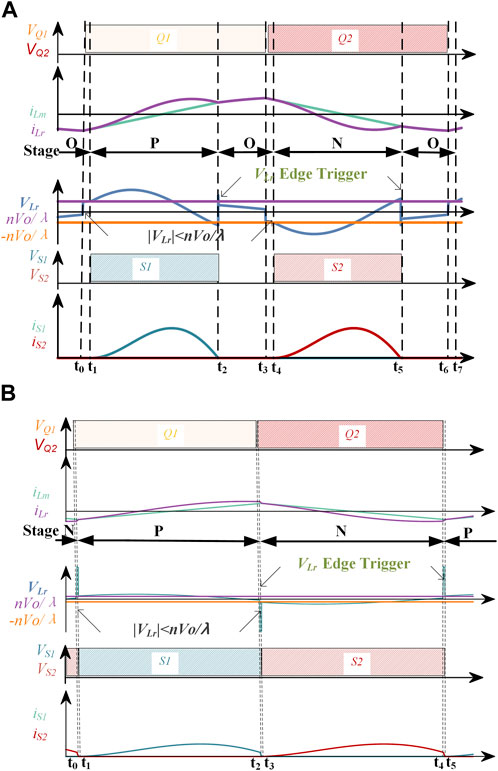
FIGURE 8. Key waveform of the RLV scheme for light-load condition: (A) below resonance and (B) above resonance.

The situation below the resonant frequency with light-load condition is shown in Figure 8A. At time $t_0$, the voltage of $V_{FB}$ increases from $-V_{in}$ to $V_{in}$. Since the system is in a light-load condition, the resonant capacitor voltage meets the requirements before the arrival of $t_0$, so the system stage is O.

During $t_0\sim t_1$, the system is in the O stage until $t_1$.At $t_1$, $\mathrm{\lambda }\left|v_{Lr}\right|>n{V}_o$, and the system enters the P stage.

During $t_1\sim t_2$, the resonant voltage $V_{Lr}$ jumps at time ${\mathrm{t}}_2$, and the system changes to O stage. During $t_2\sim t_3$, $\mathrm{\lambda }\left|v_{Lr}\right|<n{V}_o$ , the system remains in the O stage. At time $t_3$, $V_{FB}$ increases from $V_{in}$ to $-V_{in}$, and after the transition $\mathrm{\lambda }\left|v_{Lr}\right|<n{V}_o$, the system is in the O stage. The state of the system changes is OPO in the first half cycle.

During the second half cycle of $V_{FB}=-V_{in}$. The analysis method is similar to the aforementioned method during $t_3\sim t_7$, and the stage change in the first half cycle is ONO.

The situation above the resonant frequency with light load is shown in Figure 8B. During $t_0\sim t_1$, $V_{FB}$ increases from $-V_{in}$ to $V_{in}$ at time $t_0$. Since the system is in a light-load state and the resonant inductor voltage meets the requirements $\mathrm{\lambda }\left|v_{Lrt0-}\right|>V_o$ at $t_0$, the system will change to the N stage.

During $t_1\sim t_2$, the condition $\left|V_{Lmt1+}\right|>n{V}_o$ is satisfied at $t_1$, and then the system changes to the P state.

It can be seen from the aforementioned analysis that the state of the system changes from N to P in the first half cycle.

During the second half cycle of $V_{FB}=-V_{in}$, the analysis method for the time during ${\mathrm{t}}_2\sim {\mathrm{t}}_4$ is similar to the previously mentioned methods, and the state of change in the first half cycle is from P to N.

3 Experimental results

This section presents the experimental results of the proposed RLV strategy based on Table 1. This 100-W/24-V LLC converter is used to provide isolation for single-board power supplies. The RLV-SR strategy is compared with the conventional $V_{\mathrm{D}\mathrm{S}-\mathrm{o}\mathrm{n}}$ sensing scheme. The comparisons are carried out in the mode below the resonant frequency, above the resonant frequency, and in the light-load mode, respectively.

TABLE 1

TABLE 1. Parameters of the LLC resonant converter.

The experimental converter is shown in Figure 9. A full-bridge inverter on the primary side is controlled by the DSP controller. The RLV-SR control function is completed by the FPGA controller, and the driving signal of the SR is determined by collecting $v_{Lr}$, $V_{out}$, and the main switching signal of the primary side. The key components are shown in Table 2.

FIGURE 9

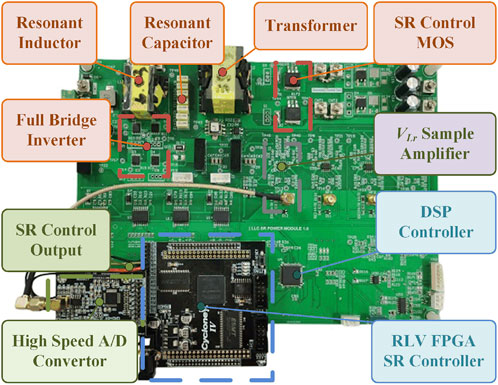
FIGURE 9. Experimental prototype: 100-W/24V resonant converter based on the RLV-SR control strategy.

TABLE 2

TABLE 2. Parameters of the SR controller.

Four voltage signals were given in the experimental result figures. While $V_{Q1}$ is the primary-side control signal, $V_{S1}$ is the synchronous rectification control signal of MOS S1, $V_{DS-S1}$ is the DS voltage signals of MOS S1, and $I_{S1}$ is the current signal of MOS S1.

In the below resonant frequency region, the converter operates at the same load and frequency, the results of the conventional $V_{\mathrm{D}\mathrm{S}-\mathrm{o}\mathrm{n}}$ method are shown in Figure 10A, and the proposed RLV strategy is shown in Figure 10B.

FIGURE 10

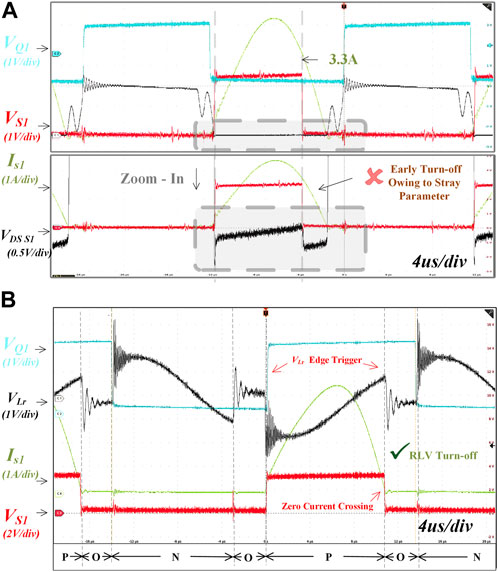
FIGURE 10. Experimental results below resonant frequency at the maximum power, 100 W/36 kHz. (A) V_DS-_ON measurement method shuts down the SR early since the $V_{DS}$ signal has reached the judgment threshold voltage when $I_{S1}$ is 3.3A, while (B) the RLV strategy effectively determines the zero-current crossing point by sensing the edge of large and stable Lr voltage signals.

As shown in the bottom part of Figure 10A, $V_{DS-S1}$ is zoomed. Due to stray inductance, the $V_{DS-S1}$ voltage leads $I_{S1}$ and reaches the voltage zero point before the rectified current is 0. At this time, the SR turn-off signal is triggered, and then the body diode of the MOSFET is on, which will cause premature turn-off of the system.

Unlike the conventional $V_{\mathrm{D}\mathrm{S}-\mathrm{o}\mathrm{n}}$ sensing method, the RLV-SR driving strategy does not use the $V_{DS}$. The RLV strategy is based on $v_{Lr}$ and $V_{out}$ is a large signal and cannot be disturbed. Therefore, as shown in Figure 10B, the work stage of the converter can be judged by the jumping edge of the ${\mathrm{v}}_{\mathrm{L}\mathrm{r}}$ signal and the output voltage signal $V_{out}$. Then, according to the state and the duration of this state, determine the timing of turning on and turning off the SR signals. $V_{S1}$ is the SR control signal and $I_{S1}$ is the current flowing in the rectifier MOS. $V_{S1}$ is turned on when the system enters the P state and turned off at the zero-crossing time of $I_{S1}$. The RLV-SR driving strategy can well-realize the function of SR function.

In the operating range above the resonant frequency, when the converter operates under the same load and frequency, the conventional $V_{\mathrm{D}\mathrm{S}-\mathrm{o}\mathrm{n}}$ sensing strategy and the proposed RLV strategy are compared. The key waveforms are shown in Figures 11AB.

FIGURE 11

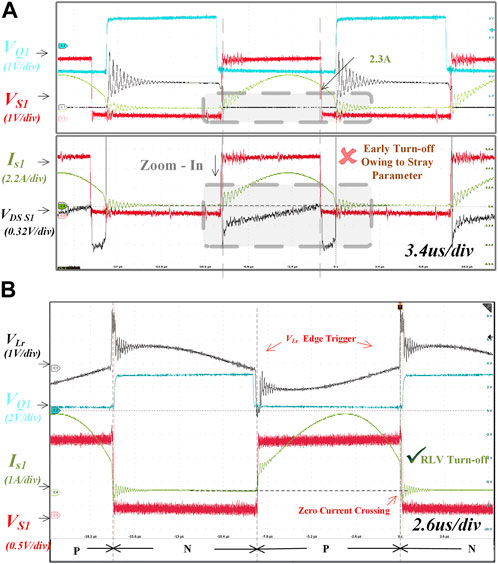
FIGURE 11. Experimental results of above resonant frequency at the maximum current, 3A/58 kHz. (A) The $V_{DS-on}$ measurement method turns off the SR MOSFET early due to stray inductance causing $V_{DS-S1}$ to reach the threshold voltage prematurely, while (B) the RLV strategy effectively determines the zero-current crossing point by detecting the jump edge of VLR and the operating state of the system.

When the operating frequency ($f_s$) of the system is nearby or above the resonant frequency ($f_r$) of the LLC converter ($f_s\ge f_r$), the proposed RLV-SR strategy generates the dead time between the two SR switches to avoid shoot-through. The inserted dead time (DT) should be long enough to ward off shoot-through of MOS. In the experimental results, 20 ns dead time (DT) is inserted, and this is 0.1% of the resonant period while $f_s$ = 50 kHz.

It can be seen in the upper part of Figure 11A that $V_{DS-S1}$ is close to 0 while $I_{S1}$ is greater than 0. The $V_{DS-S1}$ signal is amplified, as shown in the lower part of Figure 11A. The control signal $V_{S1}$ of the SR MOSFET S1 can be turned on when the current is greater than 0, but due to the existence of stray inductance, the $V_{DS-S1}$ signal reaches the threshold voltage in advance, while the current in the MOSFET is still 2.3 A at this time, which will reduce the conversion efficiency.

As shown in Figure 11B, when the converter operates in a mode above the resonant frequency, the RLV strategy effectively determines the zero-current crossing point by detecting the jump edge of ${\mathrm{V}}_{\mathrm{L}\mathrm{r}}$ and the operating state of the system.

When the load of the converter is light, the output power of the system is 20 W, and the system works at 36 kHz. The experiment results are shown in Figure 12. The traditional $V_{DS-on}$ sensing strategy and the RLV-based strategy are compared when the output is 20 W.

FIGURE 12

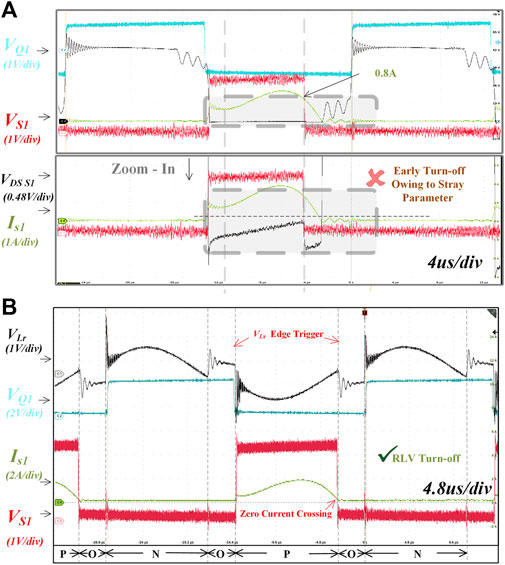
FIGURE 12. Experimental results at a light-load mode below resonant frequency, 20 W/36 kHz. (A) The $V_{DS-on}$ measurement method turns off the rectifier MOSFET prematurely because the parasitic inductance causes the threshold voltage to be reached, whereas (B) the RLV strategy can effectively identify the switching moment of SR MOSFETs by judging the system state with large and stable Lr voltage signals.

As shown in Figure 12A, the conventional $V_{DS-on}$ sensing strategy can turn on the $V_{S1}$ control signal when $I_{S1}$ just crosses the zero point. However, when it comes to $V_{S1}$ off time, due to the existence of stray inductance, premature off-time can be observed from the signal of $V_{DS-S1}$ zoomed in the lower part of Figure 12, which is ahead of the $I_{S1}$ signal. It is turned off when $I_{S1}$ is 0.8A, after which the MOSFET body diode is turned on. This will miss about 20% of the on-time, which is not conducive to the improvement of system efficiency.

On the contrary, with the RLV-based strategy, the system state can be accurately judged by the magnitude and jump edge of the $V_{Lr}$ voltage signal. As shown in Figure 12B, the on and off points of the SR signal $V_{S1}$ are synchronized with the timing when the $I_{S1}$ current is turned on and off.

The RLV-SR strategy tracks the actual rectifier current conduction time instantaneously under severe current dynamics. The input voltage of the experimental system is fixed. Therefore, the dynamic response results are shown while the load is changed dramatically. The results when the load condition steps up from 20 W to a load of 66 W are shown in Figure 13A. In the figure, I_S1 represents the output current, and V_S1 represents the driving signal of SR MOS. There are no spikes in the dynamic waveforms, which means the SRs can operate safely. To regulate the output voltage, the S1 peak current steps up from 3.8 A to 12 A. Figure 13B shows the load step-down response from 62 W to 20 W with a step-up increase in S1 peak current from 3.8 A to 12 A. The zoomed-in figure shows the waveforms after transients. It can be seen that the conducting time of SR can be tracked properly during the transients with the proposed driving scheme.

FIGURE 13

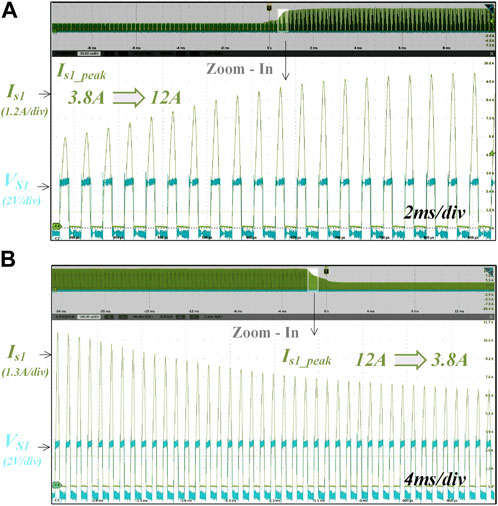
FIGURE 13. Dynamic test waveforms under a large load change: (A) I_{s1_peak} from 3.8 A to 12 A and (B) I_{s1_peak} from 12 A to 3.8 A.

The experimental results verify that the RLV-based synchronous rectification strategy can effectively cover the operating range from below to above the resonant frequency and can also cover the working scenarios from light load to heavy load. Compared with the conventional ${\mathrm{V}}_{\mathrm{D}\mathrm{S}-\mathrm{o}\mathrm{n}}$ sensing scheme, the conversion efficiency is improved by improving the accuracy of the MOSFET off time.

A comparison of the different schemes is shown in Table 3. The proposed RLV strategy does not require current sensors, which may introduce volume and cost issues. Although the proposed strategy contains one voltage sensor, it shows excellent performance in low extra power losses, low noise sensitivity, and low circuit, resulting in high SR accuracy and high efficiency. To summarize, the proposed SR scheme achieves better performance than most of the existing SR schemes of the LLC resonant converter to some extent.

TABLE 3

TABLE 3. Comparison of different driving schemes.

As shown in Figure 14, the converter achieves a peak efficiency of 92.45% with an improvement of 0.5% at 50 W compared to the conventional driving scheme because the current over zero point can be determined by detecting the jump edge of VLR and the operating state of the system.

FIGURE 14

FIGURE 14. Comparison of driving scheme efficiency.

4 Conclusion

In this paper, an RLV-SR strategy is proposed. This RLV-SR strategy does not use a current sensor, and the working stage of the LLC converter is judged by measuring the magnitude and jump time of the $v_{Lr}$ signal, which is used to output the corresponding SR signals. The function and effectiveness of this strategy are verified by the experiment with a 100W/24V LLC converter.

Compared with the conventional $V_{DS-on}$ sensing strategy, this strategy has better anti-interference performance. More importantly, the method can operate in various modes, including below and above the resonant frequency and in light-load mode. The RLV-SR driving strategy dramatically reduces the turn-on time error caused by the effect of stray inductance. So, the efficiency of the power converter is improved by 0.29% at full load.

Therefore, the RLV-SR strategy proposed in this paper is a simple and effective method to realize the synchronous rectification function of the LLC resonant converter.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

ZL: writing—original draft and review. ZW and XQ: conceptualization. XX, XD, and QH: formal analysis and revision.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmed, M. H., de Rooij, M. A., and Wang, J. (2019). High-power density, 900-W LLC converters for servers using GaN FETs: Toward greater efficiency and power density in 48 V to 6\/12 V converters. IEEE Power Electron. Mag. 6, 40–47. doi:10.1109/MPEL.2018.2886106

CrossRef Full Text | Google Scholar

Fei, C., Li, Q., and Lee, F. C. (2018). Digital implementation of adaptive synchronous rectifier (SR) driving scheme for high-frequency LLC converters with microcontroller. IEEE Trans. Power Electron. 33, 5351–5361. doi:10.1109/TPEL.2017.2731942

CrossRef Full Text | Google Scholar

Fu, D., Liu, Y., Lee, F. C., and Xu, M. (2009). A novel driving scheme for synchronous rectifiers in LLC resonant converters. IEEE Trans. Power Electron. 24, 1321–1329. doi:10.1109/TPEL.2009.2012500

CrossRef Full Text | Google Scholar

Hsu, J.-D., Ordonez, M., Eberle, W., Craciun, M., and Botting, C. (2019). LLC synchronous rectification using resonant capacitor voltage. IEEE Trans. Power Electron 34, 10970–10987. doi:10.1109/tpel.2019.2900459

CrossRef Full Text | Google Scholar

Kim, B.-C., Park, H.-S., Moon, S. C., Kim, Y.-D., Kim, D.-Y., and Moon, G.-W. (2012). “The novel synchronous rectifier driving method for LLC series resonant converter,” in Iecon 2012 - 38th annual conference on IEEE industrial electronics society (Montreal, QC, Canada), 810–813. doi:10.1109/IECON.2012.6388647

CrossRef Full Text | Google Scholar

Lee, J.-B., Kim, J.-K., Baek, J.-I., Kim, J.-H., and Moon, G.-W. (2016). Resonant Capacitor <sc&gt;O&lt;/sc&gt;n/<sc&gt;O&lt;/sc&gt;ff Control of Half-Bridge <italic&gt;LLC&lt;/italic&gt; Converter for High-Efficiency Server Power Supply. IEEE Trans. Ind. Electron. 63, 5410–5415. doi:10.1109/TIE.2016.2558481

CrossRef Full Text | Google Scholar

Li, H., Wang, S., Zhang, Z., Zhang, J., Li, M., Gu, Z., et al. (2021). Bidirectional synchronous rectification on-line calculation control for high voltage applications in SiC bidirectional LLC portable chargers. IEEE Trans. Power Electron. 36, 5557–5568. doi:10.1109/TPEL.2020.3027703

CrossRef Full Text | Google Scholar

Li, H., Wang, S., Zhang, Z., Zhang, J., Zhu, W., Ren, X., et al. (2022). An impedance-based digital synchronous rectifier driving scheme for bidirectional high-voltage SiC LLC converter. IEEE Trans. Ind. Electron. 69, 11314–11323. doi:10.1109/TIE.2021.3127037

CrossRef Full Text | Google Scholar

Lin, J.-Y., Yueh, H.-Y., Lin, Y.-F., and Liu, P.-H. (2023). Variable-frequency and phase-shift with synchronous rectification advance on-time hybrid control of LLC resonant converter for electric vehicles charger. IEEE J. Emerg. Sel. Top. Ind. Electron. 4, 348–356. doi:10.1109/JESTIE.2022.3176206

CrossRef Full Text | Google Scholar

Mohammadi, M., and Ordonez, M. (2019). Synchronous rectification of LLC resonant converters using homopolarity cycle modulation. IEEE Trans. Ind. Electron. 66, 1781–1790. doi:10.1109/tie.2018.2840493

CrossRef Full Text | Google Scholar

Moon, S. C., Chen, C., and Park, D. (2019). “Adaptive dead time synchronous rectification control for high efficiency LLC resonant converter,” in 2019 IEEE applied power electronics conference and exposition (APEC) (Anaheim, CA, USA: IEEE), 2939–2946. doi:10.1109/APEC.2019.8721896

CrossRef Full Text | Google Scholar

Qian, Q., Liu, Q., Zheng, M., Zhou, Z., Xu, S., and Sun, W. (2022). An improved adaptive synchronous rectification method with the enhanced capacity to eliminate reverse current. IEEE Trans. Power Electron. 37, 1–1410. doi:10.1109/TPEL.2021.3106477

CrossRef Full Text | Google Scholar

Tayebi, S. M., Hu, H., Abdel-Rahman, S., and Batarseh, I. (2019). Dual-input single-resonant tank LLC converter with phase shift control for PV applications. IEEE Trans. Ind. Appl. 55, 1729–1739. doi:10.1109/TIA.2018.2883015

CrossRef Full Text | Google Scholar

Wang, D., Jia, L., Fu, J., Liu, Y.-F., and Sen, P. C. (2010). “A new driving method for synchronous rectifiers of LLC resonant converter with zero-crossing noise filter,” in 2010 IEEE energy conversion congress and exposition (Atlanta, GA: IEEE), 249–255. doi:10.1109/ECCE.2010.5618032

CrossRef Full Text | Google Scholar

Wang, D., and Liu, Y.-F. (2014). A zero-crossing noise filter for driving synchronous rectifiers of LLC resonant converter. IEEE Trans. Power Electron. 29, 1953–1965. doi:10.1109/TPEL.2013.2264774

CrossRef Full Text | Google Scholar

Wang, X., Jiang, C., Lei, B., Teng, H., Bai, H. K., and Kirtley, J. L. (2016a). Power-loss analysis and efficiency maximization of a silicon-carbide MOSFET-based three-phase 10-kW bidirectional EV charger using variable-DC-bus control. IEEE J. Emerg. Sel. Top. Power Electron. 4, 880–892. doi:10.1109/JESTPE.2016.2575921

CrossRef Full Text | Google Scholar

Wang, Y., Gao, S., Guan, Y., Huang, J., Xu, D., and Wang, W. (2016b). A single-stage LED driver based on double LLC resonant tanks for automobile headlight with digital control. IEEE Trans. Transp. Electrification 2, 357–368. doi:10.1109/tte.2016.2571781

CrossRef Full Text | Google Scholar

Xie, X., Liu, J. C. P., Poon, F. N. K., and Pong, M. H. (2001). A novel high frequency current-driven synchronous rectifier applicable to most switching topologies. IEEE Trans. Power Electron. 16, 635–648. doi:10.1109/63.949496

CrossRef Full Text | Google Scholar

Yang, C.-H., Liang, T.-J., Chen, K.-H., Li, J.-S., and Lee, J.-S. (2013). “Loss analysis of half-bridge LLC resonant converter,” in 2013 1st international future energy electronics conference (IFEEC) (Tainan, Taiwan: IEEE), 155–160. doi:10.1109/IFEEC.2013.6687496

CrossRef Full Text | Google Scholar

Zhang, J., Shao, S., Li, Y., Zhang, J., and Sheng, K. (2021). A voltage balancing method for series-connected power devices in an LLC resonant converter. IEEE Trans. Power Electron. 36, 3628–3632. doi:10.1109/TPEL.2020.3025595

CrossRef Full Text | Google Scholar

Zhu, X., Li, H., Zhang, Z., Li, Z., Yang, Y., Gu, Z., et al. (2021). A sensorless model-based digital driving scheme for synchronous rectification in 1-kV input 1-MHz GaN LLC converters. Ieee Trans. Power Electron. 36, 8359–8369. doi:10.1109/tpel.2020.3042340

CrossRef Full Text | Google Scholar