- 1School of Civil Engineering and Architecture, Anhui University of Technology, Ma’anshan, China
- 2School of Civil Engineering and Architecture, Jiaxing University, Jiaxing, China
- 3Anhui MBO Intelligent Technology Co. Ltd., Wuhu, China
In order to improve the application possibility of CO2/R41 azeotropy mixture in the refrigeration industry, the optimum mass ratio of composition is defined and determined according to the thermodynamic properties and safety. On the basis of the first and second laws of thermodynamics, a model is proposed to evaluate the performance of CO2/R41 single-stage transcritical cycle (CO2/R41 cycle) in which a throttling valve is integrated and CO2/R41 azeotropy refrigerant is adopted. The performance of CO2/R41 cycle at the optimum mass ratio of CO2/R41 azeotropy mixture is then compared with that of a CO2 two-stage transcritical cycle with throttling valve (CO2 two-stage cycle) and that of a CO2 single-stage transcritical cycle with expander (CO2 expander cycle). The results show that the optimum mass ratio of CO2/R41 azeotropy mixture is 0.583/0.417. Compared with CO2 two-stage cycle and CO2 expander cycle, CO2/R41 cycle has the advantages of a simpler structure, lower optimum high pressure, appropriate discharge temperature of the compressor, and higher COP. Therefore, the CO2/R41 azeotropy mixture with the mass ratio of 0.583/0.417 is eco-friendly and can be considered as a good alternative refrigerant for application in the refrigeration industry. The simple CO2/R41 cycle shows great feasibility to replace the complex CO2 two-stage cycle and CO2 expander cycle.
1 Introduction
In line with the Kigali Amendment of the Montreal Protocol, a drastic phase-down of hydrofluorocarbons (HFCs) has been imposed from 2019 due to the high global warming potential (GWP) (Astrain et al., 2019; Wang et al., 2019). Because of this, one of the urgent tasks in the refrigeration industry is to search for alternative refrigerants with less influence on the environment (Zhao et al., 2019; Dai et al., 2023). Natural working fluid CO2 is considered to be a promising refrigerant because of its eco-friendly properties, such as having zero ozone depleting potential (ODP), low GWP, and high thermodynamic performance and being nonflammable, non-toxic, and cheap (Cecchinato et al., 2005; Dai et al., 2023). CO2 refrigeration systems have been widely applied in air conditioning and heat pumps (Wang et al., 2017). However, several defects (i.e., higher operating pressure, lower efficiency, and overheating of discharge refrigerant gas) existing in the CO2 systems should be solved to develop the application fields (Wang et al., 2017; Nemati et al., 2018; Wang et al., 2020). Three approaches are frequently employed to improve the comprehensive performance of CO2 systems: adopting two-stage compression with inter-cooling between the stages (Srinivasan, 2011), using an expander to replace throttling valve (Joneydi Shariatzadeh et al., 2016), and using mixture refrigerant instead of pure refrigerant (Wang et al., 2017). However, the two-stage compression system and the single compression system with an expander are complex. Moreover, it is difficult to design a satisfactory CO2 expander at present. Therefore, there is an obvious need to develop CO2-based blends as a refrigerant. In recent years, several CO2-based zeotropic refrigerants, such as CO2/R290, CO2/R600, and CO2/R32, have been studied and applied (Sugiyama et al., 2011; Dai et al., 2014). However, the high temperature glide and mass transfer resistance in nucleate boiling of zeotropic mixture cause a lower heat transfer coefficient compared with pure refrigerant and azeotropy mixture (Kundu et al., 2014). In addition, it is difficult to overcome the inherent problem of composition shift arising in the leaking or recharging processes in application aspects of zeotropic mixture (Morrison and McLinden, 1993). So, the azeotropy mixtures have been attracting increasing attention and are preferred as refrigerants among different types of mixtures, because the azeotropy mixtures have good performance similar to the pure fluids (Aslam and Sunol, 2004; Zhao et al., 2019). Moreover, the systems with azeotropy refrigerants would have higher coefficient of performance (COP), higher refrigeration capacity, and lower energy consumption than those with zeotropic refrigerants (Zhao et al., 2016).
Up to now, only two CO2-based azeotropy refrigerants (CO2/R170 and CO2/R41) have been reported and analyzed in the published literature. In our previous study, the performance of a heat pump water heater with CO2/R170 azeotropy refrigerant was studied, and a lower discharge temperature was observed for the system with CO2/R170 azeotropy refrigerant compared with the system with pure CO2 and R134a, indicating that the lifetime of a compressor can be significantly prolonged (Wang et al., 2019; Wang et al., 2020). Under supercritical conditions, Kravanja et al. (2018) measured the heat transfer coefficient of CO2, R170, and CO2/R170 azeotropy mixture in a double-pipe and countercurrent flow tube. The experimental results indicated that the heat transfer coefficient value of CO2/R170 mixture fell between that of pure CO2 and R170 near the critical point. Then, the COP of a simple system with pure CO2 and CO2/R170 mixture as a refrigerant was evaluated by a thermodynamic model. The comparison data showed that the COP values of CO2/R170 cycle were more than 50% higher than those of the pure CO2 cycle when the evaporation temperature was above 0°C, which could help to reduce the operational cost by a significant amount. For CO2/R41 azeotropy mixture, as a refrigerant, the performance of the refrigerated cabinet and heat pump water heater was analyzed under various working conditions in our previous study (Wang et al., 2017). The results showed that the comprehensive performance of CO2/R41 cycle was significantly better than that of CO2 cycle. Dai et al. (2015) developed a thermodynamic model to evaluate the performance of a heat pump water heater with ten CO2-based mixtures as a refrigerant. They found that the CO2/R41 mixture could be recommended as a suitable candidate to replace the pure CO2. Yu et al. (2019) conducted an experiment to comprehensively study the overall performance of CO2/R41 used in automobile air conditioning and heat pump systems. The experimental results demonstrated that the performance of the CO2/R41 system could be significantly improved with the increase of R41 mass fraction (from 0% to 100%). Under the condition of optimum charge, the COP of pure R41 system was 14.5% and 25.7% higher than that of pure CO2 system in the heating and cooling modes, respectively. Meanwhile, the operation pressure of the pure R41system significantly decreased with the increase of R41 mass fraction (from 0% to 100%) under the same gas cooler outlet temperature.
As was shown in the above-mentioned studies, both CO2/R41 and CO2/R170 can be used in refrigeration and heat pump systems as a refrigerant because of the higher COP and lower discharge temperature. However, CO2/R170 azeotropy refrigerant has an unfavorable effect in the operating pressure of systems (Wang et al., 2019). The results were compared with those obtained from references (Wang et al., 2019) and (Wang et al., 2017); it was found that the low/high pressures of the studied air-source heat pump water heater system using CO2/R170 azeotropy mixture are higher than those using pure CO2 refrigerant. In contrast, the CO2/R41 system has an obviously lower operating pressure than the CO2 system under the same conditions. So, the CO2/R41 azeotropy refrigerant is preferable and needs to be studied in further detail.
The mass fraction of CO2/R41 azeotropy refrigerant has a significant effect on the comprehensive performance of the system. It is important to identify an optimum mass ratio of CO2/R41 azeotropy refrigerant for its practical application in the refrigeration industry. In general, the optimum mass ratio is defined as the mass ratio of mixture composition corresponding to the maximum COP of the system. From the above literature analysis, it is observed that the thermodynamic performance of CO2/R41 system is improved continuously with an increasing R41 mass fraction. Hence, the COP of the system cannot be the only parameter to determine the optimum mass ratio in CO2/R41 azeotropy mixture.
For a refrigerant, the issues of safety and its thermodynamic properties must be considered. R41 can improve the COP of a refrigerating system with pure CO2, although it can also reduce the safety due to its flammability. Therefore, pure R41 cannot be directly recommended to replace CO2 in refrigeration systems.
In order to promote the industrial application of CO2/R41 mixture, the optimum mass ratio of composition should be determined. Under the premise of safety, the CO2/R41 systems should have an optimal thermodynamic performance when the mixture composition reaches an optimum mass ratio. So, the optimum mass ratio of CO2/R41 mixture is defined as the maximum R41 mass fraction corresponding to the A1 security level in this paper. In this situation, the mixture can be assured to be a non-combustible gas and correspond to the maximum COP of the system.
In this study, the optimum mass ratio of CO2/R41 mixture is firstly calculated and determined. On the basis of the first and second laws of thermodynamics, a model is proposed to evaluate the performance of three different cycles, namely, a single-stage compression transcritical cycle with a throttling valve when CO2/R41 mixture with the optimum mass ratio is used (i.e., CO2/R41 cycle), a single-stage compression transcritical cycle with an expander when pure CO2 is used (i.e., CO2 expander cycle), and a two-stage compression transcritical cycle with a throttling valve when pure CO2 is used (i.e., CO2 two-stage cycle). Finally, the feasibility of using simple CO2/R41 cycle to replace complex CO2 two-stage cycle and/or CO2 expander cycle is comprehensively evaluated in terms of COP, optimum high pressure, and discharge temperature.
2 Calculation of the optimum mass ratio
The CO2/R41 mixture is non-toxic; the safety issues stem from its flammability. For pure R41, the flammability limit is 6.8%/20.3% (volume fraction). The lower flammability limit (volume fraction, LFLV) and the upper flammability limit (volume fraction, UFLV) of CO2/R41 mixture can be calculated with the following expression (Niu, 2006).
Where CCO2/R41 and CR41 are the flammability limit of CO2/R41 and pure R41 respectively and BCO2 is the volume fraction of CO2 in the CO2/R41 mixture.
3 System modeling
3.1 System description
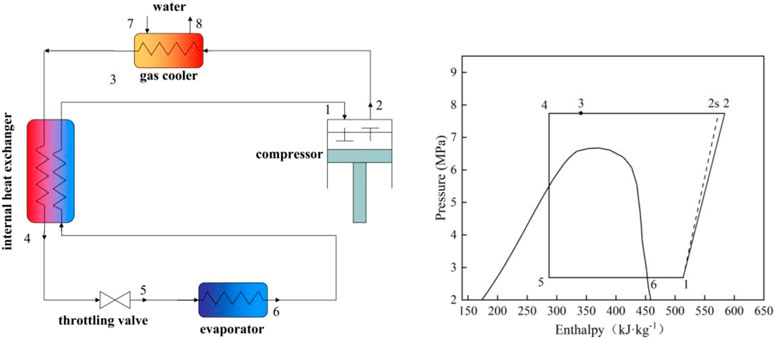
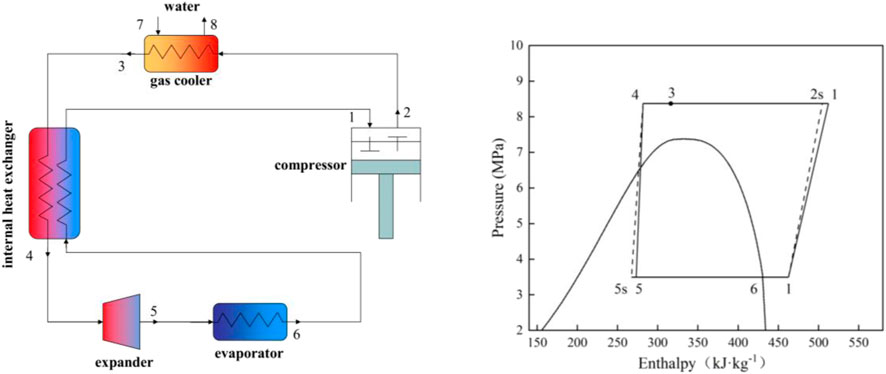
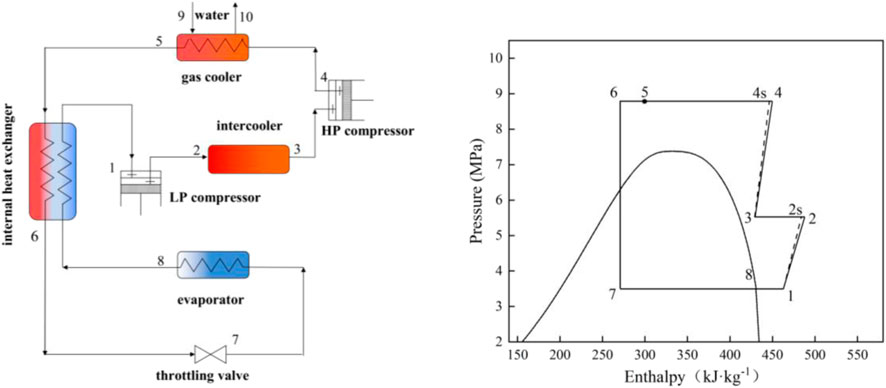
Three transcritical cycles are studied based on an air-source heat pump water heater (ASHPWH) system with optimal control strategy in the paper. Schematics and corresponding pressure-enthalpy diagrams of the systems with the three cycles analyzed in this study are shown in Figures 1–3.
The isentropic and actual compression processes are respectively illustrated by the dashed line ′′1–2s′′ (and ′′3–4s′′ in Figure 3) and the solid line ′′1–2′′ (and ′′3–4″ in Figure 3) in the pressure-enthalpy diagrams. Similarly, the lines ′′4–5s′′ and ′′4–5″ express isentropic and actual expansion processes respectively in Figure 3. On the basis of the first and second laws of thermodynamics, a model is proposed to evaluate and compare the performance of the three cycles carefully. The studied ASHPWH systems are assumed to operate based on optimal control strategy during simulation.
3.2 Assumptions for the model
The thermodynamic model is conducted based on the following assumptions:
(1) The three studied cycles are all operated under steady conditions.
(2) The heat loss and pressure drop of refrigerant flowing inside the heat exchangers and connecting pipes are ignored.
(3) The compression and expansion processes are adiabatic.
(4) The compression and expansion processes are non-isentropic.
(5) The refrigerant is in a saturated state at the evaporator outlet.
(6) The lubricant oil does not flow with the refrigerant.
3.3 Establishment of the thermodynamic model
The parameters of external conditions have a significant effect on the system performance. The external environment temperature and hot water inlet/outlet temperature of the studied ASHPWH systems in this paper are specified based on the Chinese standards GB/T 21362-2008 (GB/T 21362-2008, 2008) and GB/T 23137-2008 (GB/T 23137-2008, 2008), which are shown in Table 1.
(1) Isentropic efficiency of the compressor (Sarkar et al., 2004):
(2) Energy balance in the internal heat exchanger:
(3) The effectiveness of the internal heat exchanger is given by Eq. 4, as 0.6 (Sarkar et al., 2004):
(4) The effectiveness of the intercooler is given by the following expression, as 0.8 (Yari and Sirousazar, 2008):
(5) The inter-stage pressure is given by the following expression (Nemati et al., 2018):
(6) The isentropic efficiency of the expander is given by the following expression (Wang et al., 2020):
(7) The compression ratio of the cycle is given by:
(8) COP is given by:
(9) The irreversible loss of the adiabatic component is given by:
(10) The irreversible loss of the component exchanging heat with the external fluid is given by:
(11) The exergy efficiency for the overall system is given by:
4 Research steps
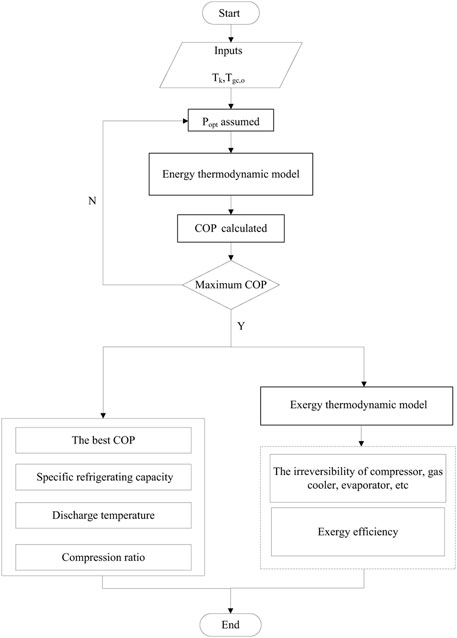
The research steps are provided in Figure 4. For a transcritical cycle, the outlet temperature of gas cooler (Tgc,o) and the evaporation temperature (Tk) are critical parameters effecting the cycle performance (Hu et al., 2018), and they are set to initial conditions in the present model. It is widely known that the system applying the transcritical cycle has an optimum high pressure (popt) that yields the best COP under the specific operation conditions. However, there is no existing correlation that can be used in the case of the three studied transcritical cycles. In the present thermodynamic model, the ever-increasing high operating pressure (1 kPa step) is assumed to calculate the performance of the analyzed system until the maximum COP is reached. Then, the optimum high pressure and the corresponding performance indicators can be obtained.
5 Results and discussion
5.1 Security level analysis of CO2/R41 azeotropy mixture
In order to overcome the shortcomings discussed in the literature and improve the application possibility of CO2/R41 azeotropy mixture in the refrigeration industry, the optimum mass ratio of composition is defined and determined in this study.
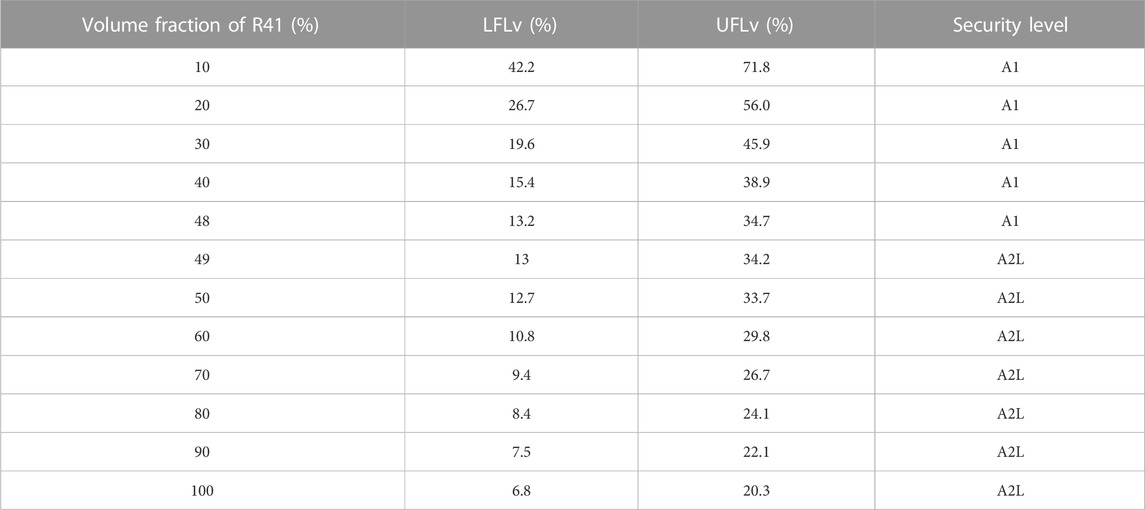
According to the Standard of the U. S. Department of Transportation DOT 173 .115 (Wang et al., 2002), working fluid with the LFLv higher than 13% or the difference between UFLv and LFLv less than 12% can be identified as non-flammable fluid (i.e., A1 security level). Table 2 shows the UFLv and LFLv of the CO2/R41 mixture with various volume fractions of composition. It is obvious that the increase of volume fraction of R41 can decrease the UFLv and LFLv and their difference. Under the condition of A1 security level, the maximum volume fraction of R41 is 48% in a CO2/R41 mixture. As can be observed from the existing literature, the thermodynamic performance of a refrigeration/heat pump system with CO2/R41 refrigerant can be improved continuously by increasing the fraction of R41. Therefore, when the safety and thermodynamic property are considered comprehensively, the optimum volume ratio of CO2/R41 azeotropy refrigerant is identified to be 0.52/0.48, which can be converted into the optimum mass ratio, i.e., the optimum mass ratio is 0.583/0.417.
The main thermo-physical properties of the CO2/R41 mixture with the optimum ratio can be obtained, as shown in Table 3. Therefore, the CO2/R41 mixture (0.583/0.417, mass ratio) is eco-friendly and particularly strong for a transcritical cycle because of its low critical temperature (i.e., 37.67°C).
5.2 Verification of the model accuracy
It is well known that the COP of a refrigeration/heat pump system can be directly affected by the high pressure. So, the optimum high pressure (popt) should be accurately determined to ensure the accuracy of the simulation results from the proposed thermodynamic model. For a single-stage transcritical cycle with a throttling valve when pure CO2 refrigerant is used, there are several correlations that can be employed to obtain the optimum high pressure with enough accuracy. However, relevant correlations are scarce for calculating the optimum high pressure in a CO2/R41 cycle, CO2 two-stage cycle, and CO2 expander cycle. In our present work, one iterative method is proposed to calculate the optimum high pressure of the above cycles. Equation 13 provided in (Hu et al., 2018) is a classic correlation to obtain the optimum high pressure of a single-stage transcritical CO2 cycle and is therefore used to verify the accuracy of the proposed iterative method.
where popt is the optimum high pressure, in Mpa; Tk is the evaporation temperature, in °C; and Tgc,o is the outlet temperature of the gas cooler, in °C.
Table 4 shows the values of the optimum high pressure that are obtained by Eq. 13 and the proposed iterative method. It is noted that the calculation results of the optimum high pressure using Eq. 13 and the iterative method are respectively marked as popt,equ and popt,ite. It can be seen that the maximum error between Eq. 13 and the iterative method is less than 1.2%, which indicates that the proposed iterative method in this study has enough accuracy, i.e., the established thermodynamic model is reasonable.
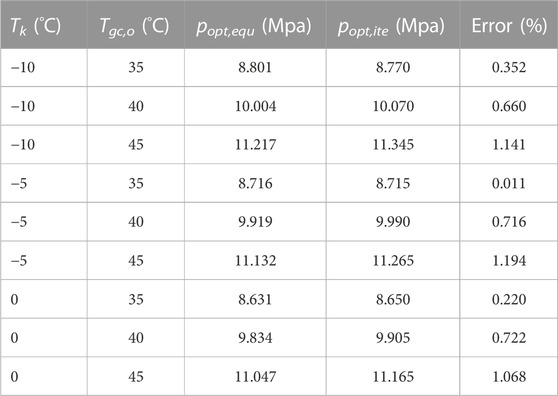
TABLE 4. The results of the optimum high pressure using Eq. 13 and the proposed iterative method.
5.3 The analysis of system thermodynamic performance
In this study, the optimum ratio of the CO2/R41 mixture is calculated and then the performance of three different cycles (i.e., CO2/R41 cycle, CO2 two-stage cycle, and CO2 expander cycle) are evaluated and compared under the same conditions, i.e., −10°C ≤ Tk ≤ 0°C, 35°C ≤ Tgc,o ≤ 45°C.
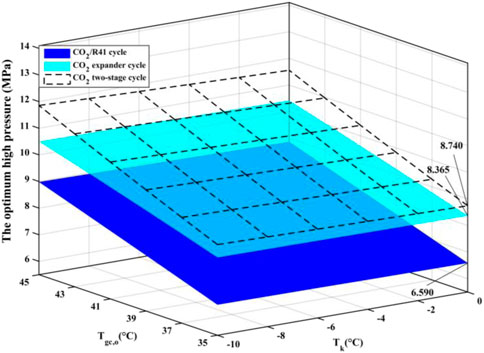
Figure 5 shows the optimum high pressure (popt) of the three studied cycles with various parameters of the evaporation temperature (Tk) and the outlet temperature of the gas cooler (Tgc,o). It is observed that the optimum high pressure of the CO2/R41 cycle is more than 26.9% lower than that of CO2 expander cycle under the same condition. In addition, the optimum high pressure of CO2/R41 cycle is more than 32.6% lower than that of CO2 two-stage cycles under the same condition. The decrease in operating pressure can help to improve the tightness and safety of a refrigeration system. Meanwhile, the tube thickness of the heat exchanger and connecting tubes can be appropriately reduced so as to lower the manufacturing cost of the device.
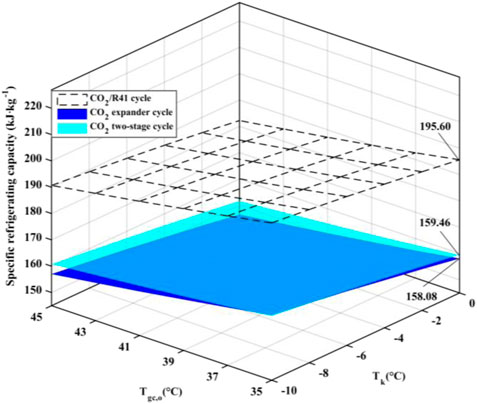
Figure 6 exhibits the effect of the evaporation temperature (Tk) and the outlet temperature of the gas cooler (Tgc,o) on the specific refrigerating capacity of the three studied cycles. It is observed that the CO2/R41 cycle has a higher specific refrigerating capacity than the other two cycles. Take the specific condition (Tk = 0°C and Tgc,o = 35°C) as an example: the difference of specific refrigerating capacity between CO2/R41 cycle and CO2 expander cycle can reach 23.73%, while it can reach 22.66% for the specific refrigerating capacity between CO2/R41 cycle and CO2 two-stage cycle.
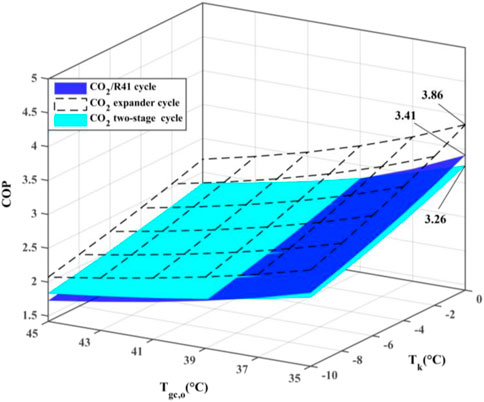
Figure 7 depicts the maximum COP of the three studied cycles with various evaporation temperatures (Tk) and the outlet temperature of the gas cooler (Tgc,o). The expander can recover a portion of the expansion work for driving the compressor, which leads to a significantly higher COP of a CO2 expander cycle. Moreover, the CO2/R41 cycle is observed to have a higher COP compared with the CO2 two-stage cycle when the outlet temperature of the gas cooler is less than 39°C. For instance, when Tk = 0°C and Tgc,o = 35°C, the maximum COP of the CO2/R41 cycle is about 4.6% higher than that of CO2 two-stage cycle.
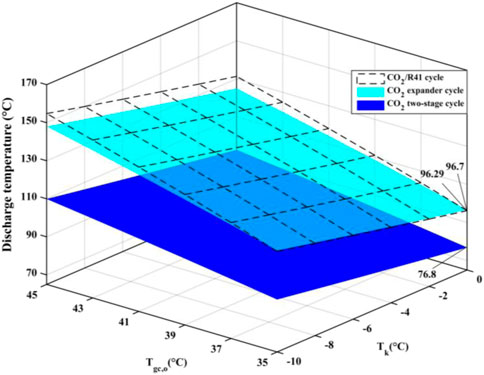
Excess discharge temperature is a serious problem in CO2 compressors, because the superheated refrigerant vapor may reduce the viscosity of lubricating oil, which affects the reliability and safety of the compressor. It is universally acknowledged that the most significant advantage of a two-stage cycle is its ability to reduce the discharge temperature of a compressor, as shown in Figure 8. It can be found that the difference in discharge temperature between the CO2/R41 cycle and CO2 expander cycle is negligible and is reduced with the decrease of Tgc,o. Under the specific condition of Tk = 0°C and Tgc,o = 35°C, the discharge temperature of CO2/R41 cycle is even lower than that of CO2 expander cycle, by about 0.4°C. Therefore, the CO2/R41 cycle is competitive with the CO2 expander cycle in terms of exhaust temperature, especially at a lower Tgc,o.
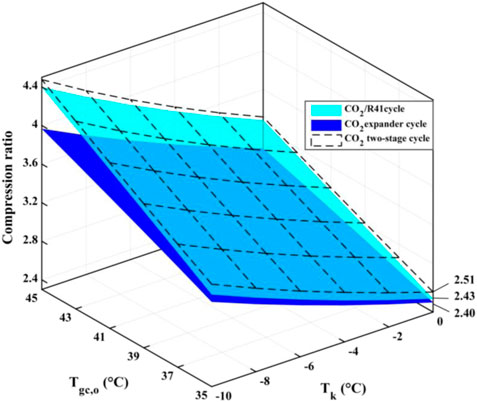
Since the compression ratio has a significant influence on wear and how leakproof the equipment is during the operation, it can affect the reliability and safety of the equipment. Therefore, it is an important performance index for a compressor. Figure 9 depicts the compression ratio of the compressor in the three studied cycles under various conditions. It is observed that for a low Tgc,o, the differences of the compression ratio among the three studied cycles are very small, while the compression ratio of the CO2 expander cycle is obviously lower than that of both CO2/R41 cycle and CO2 two-stage cycle for a high Tgc,o. For example, the differences in the compression ratio between CO2/R41 cycle and CO2 expander cycle is less than 1.24% when Tgc,o is 35°C and is about 10% when Tgc,o is 45°C.
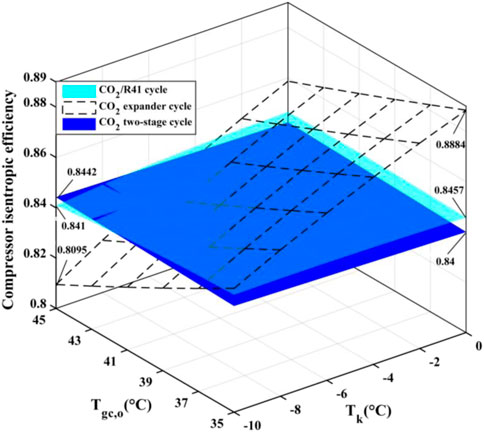
For a compressor, isentropic efficiency is an important parameter affecting the comprehensive performance of a vapor compression refrigeration/heat pump cycle. It expresses the power consumption ratio between the isentropic compression process and the actual compression process. Figure 10 shows the isentropic efficiencies of the compressor in the three studied cycles under various conditions. In the CO2 two-stage cycle, the inter-stage pressure can be given from the geometric mean value of low and high pressures. According to Eqs 2, 6, it can be seen that the isentropic efficiency of the high-pressure compressor (HP) is equal to that of the low-pressure compressor (LP). It is noted that the value of compressor isentropic efficiency in the CO2 two-stage cycle represents that of a single compressor (i.e., HP or LP) in Figure 10. In CO2 two-stage cycle and CO2/R41 cycle, the isentropic efficiency of the compressor varies little with the change of Tk and Tgc,o, especially for CO2 two-stage cycle. Meanwhile, it can be seen that the differences in the compressor isentropic efficiency between the CO2/R41 cycle and CO2 two-stage cycle are very small (i.e., less than 0.0057) under the studied conditions. In contrast, the operation condition has an obvious effect on the isentropic efficiencies of a compressor in the CO2 expander cycle.
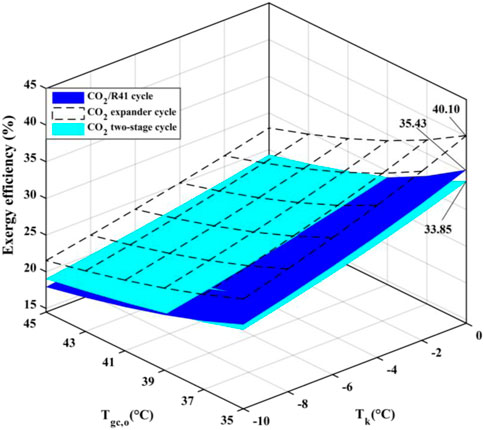
It is well known that the transcritical cycle is suitable for application in heat pump water heater systems. Since the temperature glide of the refrigerant in gas coolers can be perfectly coupled to that of the heated water, the three studied transcritical cycles are used in an ASHPWH system in the present work. In order to identify and quantify the thermodynamic losses, the exergy efficiency of an ASHPWH system under three transcritical cycles are analyzed in detail on the basis of the second law of thermodynamics. Figure 11 delineates the variation of exergy efficiency of the ASHPWH system under three transcritical cycles for various parameters of Tgc,o and Tk. It can be seen that the system exergy efficiency under the CO2/R41 cycle is higher than that under CO2 two-stage cycle when the outlet temperature of the gas cooler is less than 39°C (i.e., Tgc,o ≤ 39°C).
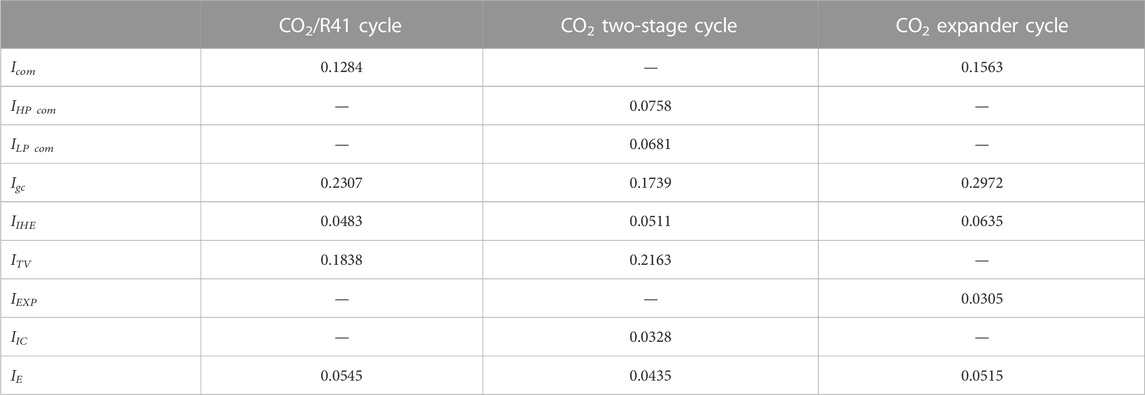
Table 5 shows the irreversible loss of each component in the studied systems under a specific condition (i.e., Tk = 0°C and Tgc,o = 35°C). It can be found that the gas cooler and throttling valve are the two main components in terms of irreversible loss in the studied systems. Due to the large pressure drop, the throttle valve produces a large irreversible loss in a refrigeration/heat pump system, which leads to low exergy efficiency for the system, as shown in Figure 11. However, the throttling valve is still usually used as a component in a CO2 refrigeration/heat pump system, because it has been difficult to design and manufacture an expander which can be satisfactorily used in a high-pressure CO2 refrigeration/heat pump system.
6 Conclusion
In this paper, the optimum mass ratio of CO2/R41 azeotropy mixture was defined and calculated based on the comprehensive consideration of thermodynamic properties and safety. A thermodynamic model was proposed to evaluate and compare the performance of three developed cycles. The main conclusions are listed as follows:
(1) The optimum mass ratio of CO2/R41 azeotropy mixture is 0.583/0.417 (i.e., volume ratio is 0.52/0.48).
(2) The CO2/R41 azeotropy refrigerant with optimum mass ratio is eco-friendly and particularly strong for the transcritical cycles because of its low critical temperature (37.67°C).
(3) It may be feasible to use a simple CO2/R41 cycle to replace the complex CO2 two-stage cycle and CO2 expander cycle because of the following reasons:
• The optimum high pressure of the CO2/R41 cycle is more than 26.9% lower than that of CO2 expander cycle and is more than 32.6% lower than that of CO2 two-stage cycle under the same conditions, which can help to improve the tightness and safety of the system.
• The CO2/R41 cycle has a higher specific refrigerating capacity than the other two cycles.
• Under a low outlet temperature of the gas cooler, CO2/R41 cycle is highly competitive with CO2 two-stage cycle in terms of COP and exergy efficiency.
• The compression ratio and discharge temperature of the compressor in CO2/R41 cycle are similar to those of CO2 expander cycle.
(4) For a refrigeration/heat pump system with CO2/R41 transcritical cycle, the outlet temperature of the gas cooler is required to be less than 39°C to obtain a more competitive performance for the system.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
DW: Data curation, Writing- original draft preparation. ML: writing- reviewing and editing. ZG: conceptualization, methodology, Software. SM: conceptualization, methodology, Software. SD: conceptualization, writing- reviewing and editing. All authors contributed to the article and approved the submitted version.
Acknowledgments
The authors would like to acknowledge the continuous support offered by Anhui MBO Intelligent Technology Co., LTD for this research. The research presented in this article has also been conducted by the Key University Science Research Project of Anhui Province (KJ2017A055).
Conflict of interest
Author FY was employed by the company Anhui MBO Intelligent Technology Co. Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aslam, N., and Sunol, A. K. (2004). Computing all the azeotropes in refrigerant mixtures through equations of state. Fluid Phase Equilib. 224, 97–109. doi:10.1016/j.fluid.2004.03.014
Astrain, D., Merino, A., Catalán, L., Aranguren, P., Araiz, M., Sánchez, D., et al. (2019). Improvements in the cooling capacity and the COP of a transcritical CO2 refrigeration plant operating with a thermoelectric subcooling system. Appl. Therm. Eng. 155, 110–122. doi:10.1016/j.applthermaleng.2019.03.123
Cecchinato, L., Corradi, M., Fornasieri, E., and Zamboni, L. (2005). Carbon dioxide as refrigerant for tap water heat pumps: A comparison with the traditional solution. Int. J. Refrig 28 (8), 1250–1258. doi:10.1016/j.ijrefrig.2005.05.019
Dai, B., Li, M., Chen, L., Liu, S., Wang, D., Wang, Q., et al. (2023). Life cycle techno-enviro-economic assessment of dual-temperature evaporation transcritical CO2high-temperature heat pump systems for industrial waste heat recovery. Appl. Therm. Eng. 219, 119570. doi:10.1016/j.applthermaleng.2022.119570
Dai, B. M., Dang, C. B., Li, M. X., Tian, H., and Ma, Y. T. (2015). Thermodynamic performance assessment of carbon dioxide blends with low-global warming potential (GWP) working fluids for a heat pump water heater. Int. J. Refrig 56 (7), 1–14. doi:10.1016/j.ijrefrig.2014.11.009
Dai, B. M., Li, M. X., and Ma, Y. T. (2014). Thermodynamic analysis of carbon dioxide blends with low GWP (global warming potential) working fluids-based transcritical Rankine cycles for low-grade heat energy recovery. Energy 64, 942–952. doi:10.1016/j.energy.2013.11.019
GB/T 21362-2008 (2008). “Heat pump water heater for commercial & industrial and similar application,” in General administration of quality supervision, inspection and quarantine of thePeople's Republic of China (Beijing, China: Standardization Administration of the People's Republic of China).
GB/T 23137-2008 (2008). “Heat pump water heat for household and similar application,” in General administration of quality supervision, inspection and quarantine of the people's Republic of China (Beijing, China: Standardization Administration of the People's Republic of China).
Hu, B., Li, Y. Y., Wang, R. Z., Cao, F., and Xing, Z. W. (2018). Real-time minimization of power consumption for air-source transcritical CO2 heat pump water heater system. Int. J. Refrig 85, 395–408. doi:10.1016/j.ijrefrig.2017.10.016
Joneydi Shariatzadeh, O., Abolhassani, S. S., Rahmani, M., and Ziaee Nejad, M. (2016). Comparison of transcritical CO2 refrigeration cycle with expander and throttling valve including/excluding internal heat exchanger: Exergy and energy points of view. Appl. Therm. Eng. 93, 779–787. doi:10.1016/j.applthermaleng.2015.09.017
Kravanja, G., Zajc, G., Ž, K., Škerget, M., Marčič, S., and Knez, M. (2018). Heat transfer performance of CO2, ethane and their azeotropic mixture under supercritical conditions. Energy 152, 190–201. doi:10.1016/j.energy.2018.03.146
Kundu, A., Kumar, R., and Gupta, A. (2014). Performance comparison of zeotropic and azeotropic refrigerants in evaporation through inclined tubes. Procedia Eng. 90, 452–458. doi:10.1016/j.proeng.2014.11.755
Morrison, G., and McLinden, M. O. (1993). Azeotropy in refrigerant mixtures: Azéotropie dans les mélanges de frigorigènes. Int. J. Refrig 16, 129–138. doi:10.1016/0140-7007(93)90069-k
Nemati, A., Mohseni, R., and Yari, M. (2018). A comprehensive comparison between CO2 and ethane as a refrigerant in a two-stage ejector-expansion transcritical refrig-eration cycle integrated with an organic Rankine cycle (ORC). J. Supercrit. Fluid 133, 494–502. doi:10.1016/j.supflu.2017.11.024
Niu, B. (2006). “Theory and experiment of natural refrigerant mixture used in low temperature circuit of cascade refrigeration,”. Doctoral Thesis (Tianjin, China: Tianjin University).
Sarkar, J., Bhattacharyya, S., and Gopal, M. R. (2004). Optimization of a transcritical CO2 heat pump cycle for simultaneous cooling and heating applications. Int. J. Refrig 27, 830–838. doi:10.1016/j.ijrefrig.2004.03.006
Srinivasan, K. (2011). Identification of optimum inter-stage pressure for two-stage transcritical carbon dioxide refrigeration cycles. J. Supercrit. Fluid 58, 26–30. doi:10.1016/j.supflu.2011.04.015
Sugiyama, T., Orita, S., and Miyamoto, H. (2011). (p,ρ,T,x) properties for CO2/n-butane binary mixtures at T=(280 to 440) K and (3 to 200) MPax) properties for CO2/n-butane binary mixtures at T= (280 to 440) K and (3 to 200) MPa. J. Chem. Thermodyn. 43, 645–650. doi:10.1016/j.jct.2010.11.012
Wang, D., Chen, Z., Gu, Z., Liu, Y., Kou, Z., and Tao, L. (2020). Performance analysis and comprehensive comparison between CO2 and CO2/ethane azeotropy mixture as a refrigerant used in single-stage and two-stage vapor compression transcritical cycles. Int. J. Refrig 115, 39–47. doi:10.1016/j.ijrefrig.2020.03.003
Wang, D., Liu, Y., Kou, Z., Yao, L., Lu, Y., Tao, L., et al. (2019). Energy and exergy analysis of an air-source heat pump water heater system using CO2/R170 mixture as an azeotropy refrigerant for sustainable development. Int. J. Refrig 106, 628–638. doi:10.1016/j.ijrefrig.2019.03.007
Wang, D., Lu, Y., and Tao, L. (2017). Thermodynamic analysis of CO2 blends with R41 as an azeotropy refrigerant applied in small refrigerated cabinet and heat pump water heater. Appl. Therm. Eng. 125, 1490–1500. doi:10.1016/j.applthermaleng.2017.07.009
Wang, X., Shi, L., and Zhu, M. (2002). Current status and research subjects of safety evaluation of refrigerant alternatives. HV&AC 32 (2), 38–42.
Yari, M., and Sirousazar, M. (2008). Cycle improvements to ejector-expansion transcritical CO2 two-stage refrigeration cycle. Int. J. Energ Res. 32, 677–687. doi:10.1002/er.1385
Yu, B., Yang, J., Wang, D., Shi, J., Guo, Z., and Chen, J. (2019). Experimental energetic analysis of CO2/R41 blends in automobile airconditioning and heat pump systems. Appl. Energy 239, 1142–1153. doi:10.1016/j.apenergy.2019.02.028
Zhao, Y., Gong, M., Dong, X., Zhang, H., Guo, H., and Wu, J. (2016). Prediction of ternary azeotropic refrigerants with a simple method. Fluid Phase Equilib. 425, 72–83. doi:10.1016/j.fluid.2016.05.010
Zhao, Y., Li, Z., Zhang, X., Wang, X., Dong, X., Gao, B., et al. (2019). Azeotropic refrigerants and its application in vapor compression refrigeration cycle. Int. J. Refrig 108, 1–13. doi:10.1016/j.ijrefrig.2019.08.024
Nomenclature
Keywords: CO2/R41, azeotropy, optimum mass ratio, heat pump water heater, thermodynamic analysis
Citation: Wang D, Li M, Gu Z, Mei S, Deng S, Lu Y and Yu F (2023) Thermodynamic performance assessment and application feasibility analysis of small heat pump water heater using CO2/R41 azeotropy mixture as refrigerant for sustainable development. Front. Energy Res. 11:1192145. doi: 10.3389/fenrg.2023.1192145
Received: 23 March 2023; Accepted: 20 June 2023;
Published: 29 June 2023.
Edited by:
Baomin Dai, Tianjin University of Commerce, ChinaReviewed by:
Chao Dang, Beijing Jiaotong University, ChinaKun Wang, Hebei University of Technology, China
Copyright © 2023 Wang, Li, Gu, Mei, Deng, Lu and Yu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dong Wang, d2FuZ2RvbmcyMjQ1NDVAMTYzLmNvbQ==
 Dong Wang
Dong Wang Mengxue Li1
Mengxue Li1