
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Energy Res. , 25 August 2023
Sec. Process and Energy Systems Engineering
Volume 11 - 2023 | https://doi.org/10.3389/fenrg.2023.1178169
Modern Electrical Vehicles (EV) and Electric Traction rely heavily on electrical drives. Every day, electric vehicles are being improved and expanded to include commercial vehicles such as passenger vehicles, goods delivery vehicles, and agricultural vehicles. Today, researchers are concentrating on multi-phase electrical drives to improve EV technology. This article provides a comprehensive analysis of the Five-Phase Induction Motor (FPIM) drive. The proposed study investigates the FPIM drive in terms of mathematical modeling and design, the different topologies of a Five-Phase Voltage Source Inverter (FPVSI) (Two-Level, Multi-Level, Matrix), the methodologies utilised to generate the pulse for FPVSI (Carrier-Based Pulse Width Modulation (CBPWM), Space Vector Pulse Width Modulation (SVPWM)), and the control of FPIM. This study evaluates the many strategies available in the literature for controlling the FPIM in order to assist researchers and industrial Research and Development (R&D) engineers in selecting the most suitable tool for their applications.
Nikola Tesla designed an induction motor in 1892 based on the advantages of the Alternating Current (AC) supply system and as a supplement for continuous current or Direct Current (DC) motors, prior to the widespread usage of electrical machine drives in engineering. The electromotive force (EMF) phenomena of the armature are studied. The single-phase induction motor is not independently turning. Hence, the number of stages increases from one to two. Observing the experimental findings, a two-phase distribution system was eventually created. A standard induction motor has a commutator for switching the rotor. Its complexity is replaced by a slip ring, and a three-phase induction motor is constructed Neidhöfer (2007).
Historically, direct-current series motors have dominated traction. It is more costly than AC motors. The primary disadvantage of the AC motor is that it consumes wattless electricity with no load and produces less torque. To address this, two induction motors with various pole configurations are electrically coupled in series to create three variable working speeds. This method was successfully and affordably used in traction Danielson (1902). The robust design of an induction motor encourages its usage in several applications. Changing design characteristics, such as resistance, reactance, and air gap distance, satisfy the needs of applications Reist and Maxwell (1909).
The primary need for the applications is speed adjustment. During operation, theinternal parameters of an induction motor cannot change. Nevertheless, the supply voltage, frequency, and pole have been altered to achieve a new speed range. Early on, the variable series resistance is linked to the input terminals to modify the voltage, while the alternator and DC motors are utilized to control the frequency Wickerham (1945). Subsequently, the introduction of semiconductor devices eased speed control. It has the capacity to regulate internal parameters, including flow and torque. For closed-loop speed control, Field Oriented Control (FOC), Direct Torque Control (DTC), and Sensorless Control are developed Gabriel et al. (1980); Bordry et al. (1980); Dickson and McClain (1982); Sathiakumar et al. (1986).
As part of the study of the continuous performance of a three-phase induction motor, DC link and rotor current harmonics are lowered and torque pulsation is made better. A five-phase induction motor can overcome this problem. In addition, the phase voltage and current values are significantly lower than those of three-phase induction motors with the same power rating, resulting in a higher fault tolerance. Electric vehicles (EV) and electric hybrid vehicles (EHV), aerospace, and ship propulsion are among the contemporary areas where FPIM is implemented due to its characteristics Kubota and Matsuse (1994); Ward and Härer (1969); Pavithran et al. (1988).
The articles Singh (2002) and Levi et al. (2007) discuss multiphase machines in terms of their harmonic components, mathematical modeling, carrier-based PWM approach, vector control, direct torque control, and fault analysis. In addition, this paper discusses harmonic injection in the mathematical modeling of FPIM, harmonic components provided in an FPIM stator winding interconnection, multilevel five-phase inverters, five-phase matrix inverters, model-predictive control, and sensorless control approaches.
This study contributes to the broad FPIM examination. The mathematical modelling of the FPIM, the topologies of the Five-Phase Voltage Source Inverter (FPVSI), the strategies used to generate the pulse for FPVSI (CBPWM, FHI, and SVPWM), the control of FPIM (FOC, DTC, and sensorless control), and fault tolerance were all examined. The outline of survey is illustrated in Figure 1. More than a hundred publications were analysed. The publications include topics that span many categories, and their promoter has classified them accordingly. This article is divided into nine sections. Start with an introduction, then describe the state-of-the-art, mathematical modeling, FPVSI topology, production of pulses for FPVSI, control techniques, fault-tolerant design, and evaluate the justification before concluding with a summary.
These days, high-torque applications are where FPIM drives are most frequently employed. Compared to three-phase induction motor drives, the FPIM drives can deliver high torque with less pulsation, a reduced DC link, and fewer rotor current harmonics. Compared to conventional, it has lower ratings for per-phase voltage and current. With several developments in numerous configurations, including design parameters, input supply, control techniques, and fault tolerance, it has blossomed during the past 50 years. A single or combination of FPIM control techniques can meet a wide variety of application requirements. The history of technological advancements and the current state of FPIM are both covered in detail in this chapter.
Solid-state drives are flexible and mature enough that they need to be made into a five-phase system. To quantitatively assess FPIM performance, a mathematical model was created. It was really put into practice, and Woodson and Herbert (1959); Abdel-Khalik et al. (2016b); Duran et al. (2008) showed the performance outcomes.
Magnetic saturation and harmonic injection were taken into consideration when developing the mathematical model. The prototype was tested, and the enhanced performance outcomes are shown in Fan et al. (2022). The articles look into the many structural links between pentagons, stars, and octaves. Moreover, the advancement in FPIM performance under various circumstances is detailed in the papers Perin et al. (2021), which detail several methods for calculating FPIM’s internal parameters and optimizing them. In the works Rizzoli et al. (2022); Sun et al. (2022), the dynamic and steady-state analyses were completed. For various limits, the Bode plot, Nyquist plot, and root locus were obtained. Comparisons are made between the outcomes and traditional three-phase induction motor drives. In Abdelwanis et al. (2021); Zaskalicky (2018); Muteba and Nicolae (2017); Hussain and Toliyat (2012); Levi (2008), an application-focused study of FPIM is provided.
The FPIM drives are controlled by changing the voltage and frequency of the input, and this is where research on the Five Phase Voltage Source Inverter (FPVSI) went in a different direction. A five-phase supply is created by inverting a three-phase supply into a DC supply. The topologies created in FPVSI, including matrix converters and two-, three-, four-, and five-level topologies, are shown in Chikondra et al. (2020); Liliang Gao and Fletcher (2010); Dordevic et al. (2013); Payami et al. (2015); Vancini et al. (2022); Panda and Pandey (2018); Ahmed et al. (2011); Wang et al. (2017); Rahman et al. (2017); Tran and Lee (2018). By changing the pulses sent to the switches in the FPVSI, the voltage and frequency sent to the FPIM can be controlled. For dependable control, the pulse generation steadily enhanced. The various CBPWM strategies are covered in Vancini et al. (2021); Yepes and Doval-Gandoy (2022).
A number of studies about SVPWM have been published.The switching states and voltage space vector values differ between the “dq” and “xy” reference frames. In works de Silva (2004); Ryu et al. (2005); Iqbal et al. (2010); Iqbal and Levi (2006); Renukadevi and Rajambal (2014); Durán et al. (2013); Ahmed et al. (2015); Elgenedy et al. (2016); Nguyen and Lee (2016); Abduallah et al. (2018); Bu et al. (2019); Rakesh et al. (2022); Ramasamy and Krishnasamy (2020), it was discussed how to estimate vectors, optimize the SVPWM pulse, and generate space vectors for effective FPIM control. It is done to compare CBPWM with SVPWM. Moreover, discussions of inverter and reduction systems bearing and shaft currents may be found between papers Prieto et al. (2011); Tan et al. (2016); Medina-Sánchez et al. (2023); Kumar et al. (2023).
The FPIM speed control feature is required while approaching various applications. Any change in voltage, frequency, or the voltage/frequency ratio results in open-loop control. To achieve the proper torque required by the application, the closed-loop control must monitor and maintain the stator current and rotor flux. The field-oriented control (FOC) and indirect field-oriented control (IFOC) are presented in the publications El-Barbary (2012); Rahman et al. (2022). The prediction and optimization of instantaneous processes are required by the process unit application. In articles Mayne et al. (2000); Cortes et al. (2008); Arahal et al. (2009); Kouro et al. (2009); Barrero et al. (2009); Duran et al. (2012); Lim et al. (2014); Xue et al. (2018); Bhowate et al. (2021a), the Model-Based Predictive Controllers (MBPC) are described.
The flux affects the motor’s speed. With traditional speed control, torque is managed by adjusting speed. The flux and torque are immediately within the DTC’s control. The different advances in DTC were presented in the publications Huangsheng Xu et al. (2002); Riveros et al. (2013); Payami and Behera (2017); Tatte and Aware (2017); Tatte et al. (2018); Naganathan and Srinivas (2020); Mavila and Rajeevan (2022); Chikondra et al. (2021); Barik and Jaladi (2016); Chikondra et al. (2022); Muduli et al. (2022b); Reddy and Devabhaktuni (2022); Kulandaivel et al. (2022). The development of DTC leads to sensorless control. The papers Zheng et al. (2011); Sathiakumar et al. (1986); Bhowate et al. (2021b); Liu et al. (2021) provide a study of numerous sensorless growth mechanisms.
The motor performs strangely if the VSI leg or stator phase winding fail. The articles Fu and Lipo (1994); Toliyat (1998); Levi et al. (2012); Morsy et al. (2014); Abdel-Khalik et al. (2015); Guzman et al. (2015); Abdel-Khalik et al. (2016c); Darijevic et al. (2016); Abdel-Khalik et al. (2016a); Bermudez et al. (2017); Gonzalez-Prieto et al. (2018); Mossa and Echeikh (2021); Sala et al. (2021) describe research that explains an essential FPIM drive feature that influences stability under fault circumstances. Under one, two, and three phases of failure, the fault-tolerant research was achieved. Control mechanisms play a significant role in ensuring that the FPIM rotates continuously. With these advances, the FPIM drive can react to nonlinear loads and faults.
The mathematical model of FPIM was developed in 1959. The five-phase voltage can be transformed into a four-phase “dqxy” reference frame. The working mechanism has been manipulated and transformed into a five-phase reference frame. It drives the output currents, speed, and torque Woodson and Herbert (1959). The five-phase ‘abcde’ is transformed into the four-phase ‘dqxy’. The transformation matrix is written by:
Where, ‘c’ represents cos, ‘s’ represents sin, D represents Decoupling transformation matrix and α represents
The first row of the matrix in Eq. 1 represents the ‘d’-axis component, the second row represents the ‘q’-axis component, the third and fourth rows represent the ‘xy’ axis, and the last row represents the zero sequence component. Figure 9 has been changed to show the “dqxy” axis in a voltage vector phasor.The ‘dqxy’ voltages are written as,
Where, v0 is the zero-sequence voltage, vd, vq, vx, vy are voltage at dqxy reference frame, v0 is voltage at zero-sequence, and va, vb, vc, vd, ve are voltage at natural reference frame.
The flux produced in the stator and rotor can be derived by, Stator,
Where, Ψds, Ψqs, Ψxs, Ψys are Stator flux linkage at dqxy reference frame, ids, iqs, ixs, iys are Stator current at dqxy reference frame, Rs, Rr are Stator and Rotor resistance, ωa is Arbitrary rotating speed of d-axis common reference frame, ω is Electrical rotating speed of Rotor, ωref is reference speed, and ωact is Actual speed of the Motor. Rotor,
Where, Ψdr, Ψqr, Ψxr, Ψyr are Rotor flux linkage at dqxy reference frame, and idr, iqr, ixr, iyr are Rotor current at natural reference frame. The current value of four-phase ‘dqxy’ in both stator and rotor is given by,
Stator,
Where, L1s, L1r are Inductance of the stator and rotor, Lm Magnetising inductance, and M is Co-efficient of mutual inductance.
Rotor,
These four-phase currents are transformed into five-phase currents. The inverse transformation is written by,
The mechanical torque developed in the FPIM is derived as,
Where,Te is electromechanical torque and P is Number of poles.
In 1969, the first FPIM was designed and experimented. It results in one-third of the torque pulsation that can be reduced over three-phase induction motors. The main advantages are,
• Refined torque pulsation
• Lesser voltage and current value per phase for the same power
• Refined torque pulsation
• Oppressed DC-link current harmonics and rotor harmonic currents
• Elevated fault tolerance.
Figure 2 represents the mathematical model of FPIM. The overall performance was obtained in MATLAB/Simulink and verified with hardware results. A 220 V, five-phase voltage has been generated with a phase displacement of It is converted into a DC supply and fed to a mathematical model of FPIM. The model’s five-phase voltage has transformed into a “dqxy” component. Continuously computing the electrical and mechanical parameters. Again, parameters are transformed into “abcde” components.
The refined mathematical model has taken into account third harmonic injection, magnetic saturation, and harmonics in the air gap Abdel-Khalik et al. (2016b).This change suggests improved torque pulsation and increased roughness. Running time and execution speed are significantly lower than in the previous model. According to the harmonics study, the model produces total harmonic distortion (THD) of less than 5.5% when combined with magnetic saturation Duran et al. (2008). The FPIM has a squirrel cage rotor and five sets of stator windings. The stator’s winding’s star, pentagon, and pentacle connections are made possible by the winding connection’s freedom.
The mathematical model is made for the star, pentagon, and pentacle windings of the stator. In an open-and-closed loop, the experimental set-up is used to test how well the dynamic performance works. According to the results, the pentagon connection generates more torque and power than the star connection. When something goes wrong, the pentacle connection can keep up a profile of high torque and low efficiency. When a rectangular voltage waveform is applied to an FPIM pentacle stator winding, one harmonic component stays the same even when the load changes. There are five harmonic components in total. The results of the harmonics investigation, which was performed on all connections, are shown in Table 1. Less voltage and current harmonics are produced by the pentacle connections Abdel-Khalik et al. (2016b); Duran et al. (2008).
A 120-way transposition is possible in all configurations. In this, 20 transpositions are used for forwarding and reverse motoring under normal operating conditions, and other transpositions are used in areas with unstable conditions. The conventional double-layer three-phase induction motor is rewound for five-phase and performs with a good working profile Fan et al. (2022). The offline estimation of design parameters was done accurately Perin et al. (2021); Rizzoli et al. (2022). The Particle Swarm Optimization (PSO) algorithm and the Non-dominated Sorting Genetic Algorithm (NSGA) optimize the design parameters of FPIM Sun et al. (2022); Abdelwanis et al. (2021). Performing the maximization and minimization of the constraints, such as total cost and conductor material in the stator and rotor, More than 25% of global error is reduced in an optimized design. The torque ripples or torque pulsations arise from the air-gap field flux behavior. The torque pulsation in an FPIM is less than that in a three-phase induction motor, and it can be measured by
The initial component of the current wave has harmonics with a higher number of times due to the strong torque pulsation. A stator’s winding can be organised into numerous layers with varied coil pitches or spans to further enhance this. According to the research, torque ripple has been examined in all interconnections, including a star, pentagon, and pentacle of the stator winding. The initial component of the present waveform has extremely few harmonics as a result of the pentacle link.
In a paper Zaskalicky (2018); Muteba and Nicolae (2017), the torque pulsation seen with single- and double-layer stator windings with varying coil pitch factors is demonstrated. The stator winding layout with a combination of double and triple-layer with a coil pitch of 19/20 produces an 8.7% torque ripple and a proper no-load average torque of 1.109 N-M as opposed to a combination of double and triple-layer winding with a coil pitch of 9/10. The winding configuration DTLS-13/15 produces 6.42% torque ripple.
Incorrect current waves may result from a bearing failure, and vice versa. If the current THD falls below 10.6%, a new switching pattern is used in the source to produce the lowest possible bearing current and current THD. FPIM’s stability was evaluated in a variety of imbalanced situations. They enable the computation of air gap induction, torque, voltage, current, and pulsating torque. The findings suggest that the FPIM has greater durability than traditional three-phase induction motors. When two five-phase induction motors are linked in series with a single supply, stability is improved. Hence, the extrusion pump, electric ship propulsion, electric traction, electric vehicle (EV), hybrid electric vehicle (HEV), fuel cell vehicle propulsion, electric power steering, and compressors may all be implemented using FPIM thanks to its dynamic, steady-state, and stability analyses. Hussain and Toliyat (2012); Levi (2008). Figure 3 depicts the thorough literature research on the modelling and design of FPIM.
Real-time implementation of the five-phase alternator is still pending. Through the connection of converters, a three-phase supply is changed into a five-phase supply. A three-phase supply is changed into a DC supply by a three-phase rectifier. To lessen voltage waveform ripple, DC bus filters are connected. The DC supply is inverted into a five-phase supply by the FPVSI.
The ability to shape the quality of the supply to the FPIM depends on the topology of the FPVSI. The performance of the FPIM can be enhanced because the FPVSI revolution is narrowly focused on sinusoidal output voltage. The FPVSI was first set up with two tiers. The inverter has five legs with two switches each in this architecture. A leg has two switches that are operated complementarily Pavithran et al. (1988). In Figure 4, the circuit connection is displayed.
Carrier-Based Pulse Width Modulation (CBPWM) and Space Vector Pulse Width Modulation (SVPWM) were utilised to create the pulse for multilayer FPVSI. The modulation index used for the performance testing ranged from 0.45 to 0.95. Less than 0.8% and 0.4%, respectively, are present in the third and seventh harmonics. By clamping the neutral point, the circuit was enhanced. By employing vectors selectively in SVPWM, the common-mode voltage and vibration are decreased. CBPWM outperforms SVPWM when using a multilayer inverter Liliang Gao and Fletcher (2010); Dordevic et al. (2013); Payami et al. (2015); Vancini et al. (2022); Panda and Pandey (2018).
The third harmonic contributes to the input voltage, which causes the current wave to be more chaotic. By selecting the switching patterns, pulse width modulation (PWM) may get rid of third harmonics. Two switches being modified as opposed to one suggests a higher fault tolerance than a three-phase induction motor.
A five-phase full-bridge can be used in place of a five-leg inverter to get the same results Chikondra et al. (2020). The configuration of FPVSI presently consists of three, four, and five levels. According to level, the number of switches is increased for each leg. The three-level FPVSI are shown in Figure 5.
The use of DC bus voltage is undergoing a fresh revolution owing to the five-level, 20-switch topology. One five-leg connects to one end of the stator in this circuit, while a second five-leg is connected to the opposite end of the stator winding. It produces an rms voltage of 140 V for a 200 V DC bus voltage, which is 40% more than the two-level inverter design. With this configuration, you can have a higher RMS voltage at the output end with a lot less DC bus voltage Mavila and Rajeevan (2022). For a number of FPIM driving applications, Neutral Point Clamp (NPC) inverter topologies have recently been employed. The five-level NPC converters can be used with a range of space voltage vectors and level operating modes. The voltage THD is decreased to less than 10% and the utilization of the DC bus voltage is increased thanks to the approximately 51-fold increase in the number of space vectors Jayakumar et al. (2022a); Acosta-Cambranis et al. (2023); Li et al. (2023).
For a number of FPIM driving applications, Neutral Point Clamp (NPC) inverter topologies have recently been employed. The five-level NPC converters can be used with a range of space voltage vectors and level operating modes. The voltage THD is decreased to less than 10% and the utilization of the DC bus voltage is increased thanks to the approximately 51-fold increase in the number of space vectors Jayakumar et al. (2022a); Acosta-Cambranis et al. (2023); Li et al. (2023).
With a matrix converter, a three-phase supply can be changed into a five-phase supply right away. Figure 6 shows the schematic for a five-phase matrix converter. The matrix converters are used with the CBPWM and SVPWM. The waveforms of the voltage and current are acquired. A five-phase supply is created from a three-phase voltage of more than 50% Ahmed et al. (2011). Seventy-eight percent of the three-phase supply was changed to a five-phase supply using the Direct Transfer Function Approach (DTFA). Moreover, it offers a THD of less than 7.9% even with fluctuating loads. For matrix converters, optimization is also carried out. SVPWM’s 243 switching states make it simple to cut the bearing current. Less than 18% of the common-mode voltage is suppressed from the nonlinear to the linear area. Simulation is used to simulate and validate the 3 × 5 multilevel matrix converter. That works effectively. mimics only the research done Wang et al. (2017); Rahman et al. (2017); Tran and Lee (2018) in large part.
According to research from articles Singh (2002), Chikondra et al. (2020); Liliang Gao and Fletcher (2010), a two-level FPVSI architecture is recommended for the inexpensive and effective regulation of FPIM. Hence, for dependable performance in closed-loop and secure operations under fault situations, the majority of research uses two-level FPVSI.
A high-quality inverter output is produced by multilevel and matrix converters, but more pulses are needed to operate more switches. The ability to really operate CBPWM pulse approaches is constrained by the SVPWM technique’s complexity for the multilevel and matrix converter. Researchers created CBPWM, SVPWM, and specialised pulse production techniques to provide the pulses needed for two-level FPVSI. Figure 7 illustrates the Summary of the FPVSI literature review.
This section reviews in detail the various approaches used to produce the pulse for FPVSI. The Pulse Width Modulation (PWM) approach prepares the pulses for controlling inverter switches by comparing a modulating waveform, also known as a basic waveform, with a carrier waveform. The solid-state switching components associated with the FPIM drive and FPIM behavior are what cause the harmonics to be produced. Integer multiples of the fundamental wave show harmonics in a voltage and current waveform. The major goal of the modified pulse generation techniques and pulse with modulation used in speed control is to minimize the harmonics and increase FPIM performance. The switching sequence is increasingly being optimized by researchers in order to provide sinusoidal output voltage with lower THD.
A carrier waveform with five phases, as opposed to triangles or sawtooths, which only have three phases. The duty cycle can be changed by changing the strength or frequency of the carrier signal [45]. The modulating signal is the sum of the fundamental and third harmonics, which is used to figure out the exact duty cycle. To get practical results in the duty cycle, a fifth harmonic waveform is subtracted from the fundamental waveform. In Figure 8, the signal comparison is displayed.
The switches on a single leg must function complementarily. Dead time plays a big part in controlling the output waveform and preventing short circuits. It generates compressed lower-order harmonics Vancini et al. (2021); Yepes and Doval-Gandoy (2022) and sinusoidal output. The optimization recommends several operating conductance modes, including 180o, 144o, 153o, and 171o. For each conduction mode, the THD value is calculated and examined. Effective results of the 144o conduction mode are 43.2% adjacent voltage THD, 24.12% non-adjacent THD, and 199 V of amplitude. The ripple in the voltage and current waveforms is looked at, and LC and Pi filters can be used to smooth them out. The THD value was reduced by less than 17.35%. The bearing and shaft current produced by the inverter voltage is reduced by the optimum selection of duty cycle de Silva (2004) in CBPWM. The Field Programmable Gate Array (FPGA) is used to write the CBPWM program in Verilog Hardware Description Language (VHDL). Multilevel inverters and matrix inverters are the most commonly used CBPWM techniques. This FPGA makes it easy to perform a duty cycle for complex circuits. The advancement of CBPWM poses the challenge of developing the five-phase rectifier for future utilization.
The utilization of DC bus voltage is exceptionally low in the CSPWM. It implies a need for a better system to improve. The phasor of a five-phase system has a pentagon structure. The phasor represents various levels of voltage. That can be sectionalized into ten. Each represents a vector of voltage levels. The FPVSI has five legs for five phases: a, b, c, d, and e. The 25 = 32 possibilities of switching states occupying voltage vector phases in a five-phase phasor. These vectors are called space vectors, and the method of generation of pulses for voltage vectors is called SVPWM de Silva (2004).
The structure of space vectors in the dq, and ‘xy’ planes is shown in Figure 9. It represents a 32-voltage vector position. Of the 32 vectors, 2 are called zero vectors, and the others are called live vectors.
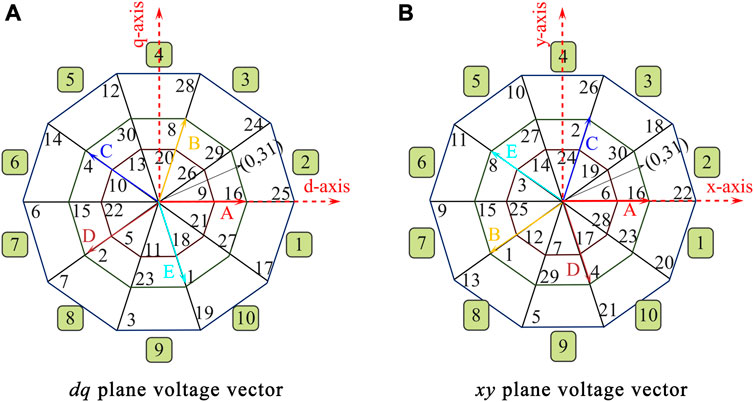
FIGURE 9. Phase voltage vectors associated with FPVSI. (A) dq plane voltage vector, (B) xy plane voltage vector
Most research takes ‘dq’ plane space vectors as a reference for modulation. Depending on the voltage vector length, the vectors are classified as low, medium, or large. The voltage vector lengths of the small, medium, and large vectors are 0.2472 Vdc, 0.4Vdc, and 0.6472 Vdc, respectively Ryu et al. (2005). At first, a triangular carrier wave and a modified modulating wave are compared to find the SVPWM.The minimum and maximum values from the fundamental five-phase sinusoidal wave are separated and added to generate a modified modulating signal.
The SVPWM is implemented in a lookup table and written as an algorithm. It leads to using the small, medium, and large vectors individually or combined. The large vectors are only used separately. Both medium and large vectors are used for the generation of the pulse. Mostly, the small vectors are not used due to high harmonics and low voltage levels. The phase voltage and THD values are presented in Table 2. It represents that large vectors are producing less THD and higher phase voltage.
To keep a dead band, the zero vectors are used over and over in every duty cycle. In both continuous and discontinuous SVPWM, a dead band is maintained to produce an output shape similar to a sine wave. The SVPWM maintains a voltage distortion of less than 2.7%. A small third harmonic component only presents 1.4% of the fundamental Iqbal et al. (2010); Iqbal and Levi (2006).
A DTC with an EG’s voltage vector sequence is altering a hysteresis band and smoothly switching patterns. From 0% load to 125% of the rated Current of a 1 HP FPIM drive, the current THD of load current is less than 2% over the whole loading range. A dynamic load modification responds in under 36 milliseconds Kulandaivel et al. (2022); Jayakumar et al. (2022b). With a programming language, the Digital Signal Processor (DSP) and FPGA make it easy to make an SVPWM pulse.The pulses for multilevel and matrix converters are done through controllers. A customized voltage vector pattern is created to reduce harmonics and ripples in the current waveform. The SVPWM patterns significantly minimize bearing and shaft current Renukadevi and Rajambal (2014); Bu et al. (2019); Rakesh et al. (2022); Ramasamy and Krishnasamy (2020).
A comparison of the different methods Prieto et al. (2011); Tan et al. (2016) of CBPWM and SVPWM was made. The SVPWM is the most effective in a two- and three-level FPVSI. It produces less THD and ripple. The harmonic injection in CBPWM and SVPWM has been studied. The third, fifth, seventh, and ninth harmonics are injected in VSI. The fifth harmonic injunction increases output voltage by 5.5% more than other injunctions.
Most of the research focuses on a reduction of losses combined with improving the performance of FPIM. The selection of materials for the stator and rotor core has saturated the hysteresis and eddy current losses. However, the copper and mechanical losses are considered areas for improvement. Various switching patterns were developed to minimize the harmonics in the current waveforms involved in the suppression of copper loss. The bearing current is the significance of increasing the temperature of an FPIM Medina-Sánchez et al. (2023); Kumar et al. (2023). The techniques are incorporated to reduce the mechanical losses of FPIM. A comprehensive literature review on the different pulse generation techniques is presented in Figure 10.
In this section, we look at the control techniques that are used to get the speed changes that applications need. Different technologies that improve the performance of FPIM are briefly explained.
Changes to the voltage, frequency, or the ratio of voltage to frequency can be used to control the speed of FPIM in an open loop. In a closed loop, the components of the stator current and rotor flux are kept strong to get a high torque El-Barbary (2012). The FOC method of speed control is illustrated in Figure 11.
The three-phase supply is converted into a DC supply and connected to a filter. FPVSI is connected between the DC bus and FPIM. The gate pulse of FPVSI is connected to the PWM generator circuit. The five-phase load currents and speeds are taken as feedback. The reference speed and flux are compared with the real value, and the error signal is sent to the ‘dqxy’ to ‘abcde’ transformation. Again, the current reference values are compared with the actual and error values sent to the controller through the hysteresis band. The PWM generator or controller generates a pulse for the inverter switch to obtain the required speed and torque. The CBPWM or SVPWM are used in FOC.
In IFOC, an additional sensor is connected to measure the magnetic flux in the air gap. So, this method is called indirect control. The closed-loop tests are obtained under different loading conditions. The output torque increases by 10% in FOC over conventional. The IFOC leads to less steady-state error. The fuzzy logic algorithm is used for FOC with SVPWM and results in effectiveness and robustness El-Barbary (2012); Rahman et al. (2022). The real-time process control applications there are in need of optimization for every process. The MBPC is used in process control industries Mayne et al. (2000); Cortes et al. (2008); Arahal et al. (2009).
The variables of load are taken as feedback. The predictive model selects the variables according to the required speed and torque. Optimization techniques such as Predictive Torque Control (PTC) and Successive Cost Function Predictive Torque Control (SCF-PTC) were applied and minimized the current THD to 2.98% and average torque ripple to 0.2562. The effective section of the switching region, CBPWM or SVPWM, makes the motor operate efficiently. This control technology creates reliable torque and speed control with minimum cost Kouro et al. (2009); Barrero et al. (2009); Duran et al. (2012); Lim et al. (2014); Xue et al. (2018); Bhowate et al. (2021a).
The DTC plays a vital role in the speed control of the FPIM. The torque and flux are taken as references and controlled directly Huangsheng Xu et al. (2002); Riveros et al. (2013); Payami and Behera (2017). The circuit connection of the DTC of the FPIM is shown in Figure 12. The supply system is the same in FOC. The speed, flux, and torque are taken as feedback. Speed is taken as a reference for torque. Torque and flux are compared to the reference value and are estimated. The SVPWM pulses are generated per the torque and flux estimated in the hysteresis band. It results in more reliable and precise torque and flux control Tatte and Aware (2017); Tatte et al. (2018). Optimal utilization of SVPWM pulses reduced the ripple current and bearing current. The torque pulsation can be reduced below 1.2% by selecting a switching pattern Naganathan and Srinivas (2020); Mavila and Rajeevan (2022); Chikondra et al. (2021); Barik and Jaladi (2016); Chikondra et al. (2022); Muduli et al. (2022b); Reddy and Devabhaktuni (2022); Kulandaivel et al. (2022).
In the DTC, speed control is necessary to take the speed of the FPIM to estimate the torque reference. A circuit is improved with sensorless control of DTC. In these techniques, there is no sensor for measuring the speed. Only the five-phase load currents are taken as feedback. The five currents taken from the load are transformed into alpha-beta components. Adaptive variable structure estimates the current and flux. These values are compared with reference and error values sent to the hysteresis band. The hysteresis band commands the lookup table to optimize pulse generation for FPVSI. The current THD is reduced by 2.5%, and the torque ripple is reduced by 50% compared to conventional DTC control Zheng et al. (2011); Khadar et al. (2021); Bhowate et al. (2021b); Liu et al. (2021).
Recently, sensorless control has been used in electric propulsion systems. A sensorless control FPIM drive uses a development of several observers. Response time to a significant dynamic loading is less than 3 s using a combination of sliding mode observers and the model reference adaptive system (MARS) Khadar et al. (2021); Abdelwanis et al. (2021); Chikondra et al. (2023). For closed-loop control of the FPIM in the past, sensors, A/D converters, D/A converters, and PROMs were employed Pavithran et al. (1988). The number of hardware components having built-in A/D and D/A converters has decreased with the development of DSP processors. The 16-bit data bus of the controller makes it simple to interface external sensors, and the internal memory is utilised to store temporary values for arithmetic and logical operations. For FOC, DTC, and Sensorless control of FPIM, the processor DSP/TI//TMS320C3x series is utilised. It can conduct logical operations with a speed range of 27–60 MHz, 8 KB of inbuilt SRAM, and 32-bit wide memory access, and it reacts to input changes very quickly El-Barbary (2012). The 64-bit memory of the TI C2000, C5000, C6000, and C7000 series processors allows for the direct conversion of MATLAB Simulink into programming code for processing Medina-Sánchez et al. (2023); Muduli et al. (2022a). This Spartan-6 XC6SLX25 series FPGA controller features a maximum of 484 packages, an integrated Internet Protocol (IP) address, an integrated memory controller, a maximum of 147,000 logic cells, and 4,800 kilobytes of memory. It includes capabilities for interacting with the simulation tools in MATLAB. This processor has primarily been utilized lately for industrial machine drive applications Kulandaivel et al. (2022); Jayakumar et al. (2022a). A comprehensive survey of different control techniques is illustrated in Figure 13.
Closed-loop control of the FPIM drive performs perfectly with linear and nonlinear loads. However, necessary to analyze an FPIM drive under unsymmetrical faults to understand the behavior. The failure of the FPVSI leg or stator winding may cause an open-circuit fault. The sudden failure of the phase makes the motor undergo abnormality Fu and Lipo (1994); Toliyat (1998); Levi et al. (2012); Morsy et al. (2014). Figure 14 represents the circuit connection of the FPIM drive when the two phases ‘a’ and ‘b’ are open.
The signal measured from the motor is observed by the digital controller and determines the failure of several phases in an FPIM or the failure of the inverter leg. The controller estimates and generates the pulses for the FPVSI switches to balance the supply in the healthy phases, making the FPIM rotate continuously. The mature control techniques and switching sequences allow it to run continuously with failure in one, two, and three phases. The controller maintains the rotation of FPIM till three phases of failure Abdel-Khalik et al. (2015); Guzman et al. (2015). In normal conditions, the five-phase currents are balanced and displaced with 72o.
The Magnetomotive Force (MMF) establishing a five-phase rotating magnetic field in each phase is expressed by.
The failure of one phase ‘a’ makes unbalance but the rotating magnetic field is maintained by other four-phase currents,
and.
In case of failure of two phases and b, the other three-phase currents are establishing a rotating magnetic field. The currents are given by,
The failure of three phases is compensated by the remaining two phases and one dc mid-point connected to neutral. The expression of healthy two phases and neutral current is,
and
Where, ias, ibs, ics, ids, ies are Stator current of FPIM, MMFas, MMFbs, MMFcs, MMFds, MMFes are Magneto Motive Force at five phases, Ns is Number of stator turns per phase,
These solutions are possible by regulating pulse generation for FPVSI and controller. In FOC, DTC, and sensorless control, the 32 switching states are optimized to control the failure of phases. Digital processors and FPGA quickly result in solutions for unsymmetrical faults. Multilevel inverters have more fault-tolerant properties. The steady-state and dynamic performances are improved with this fault-tolerant Abdel-Khalik et al. (2016c); Darijevic et al. (2016); Abdel-Khalik et al. (2016a); Bermudez et al. (2017); Gonzalez-Prieto et al. (2018); Mossa and Echeikh (2021); Sala et al. (2021).
Exist study of 95 papers related to FPIM. The mathematical model and its improvements and design of FPIM were analyzed. A different topology of FPVSI, viz., two-level, multilevel, and matrix converters, are studied. The various techniques used to generate a pulse for FPVSI and multiple techniques to control the speed of FPIM were examined. The fault-tolerant property of the FPIM drive has been studied.
• A FPIM performs with a particularly good torque profile when the model is developed, considering third harmonics in the airgap and magnetic saturation.
• Out of two-level, multilevel, and matrix converters, the two-level is mostly reliable for all switching techniques.
• For multilevel and matrix converters, CBPWM is the most suitable.
• SVPWM techniques optimize switching to control speed and compensate for unsymmetrical faults.
• Sensorless control responds quickly to varying loads in the closed-loop control of FPIM.
The thermal analysis at the stator, rotor, bearings, and yoke of FPIM, the Fundamental concept of the MMF generation in FPIM, and Power quality issues are to be solved.A comprehensive review of FPIM has been illustrated to provide a clear outlook on various features to the researchers and industrial R&D engineers working on multiphase induction motor drives for EV and Electric Traction. The conventional three-phase induction motor experiences a high-torque pulsation. The property of FPIM is that it can improve the torque range to greater than 1.5% and the pulsation to less than 0.2562. I surveyed the various topologies of FPVSI and methods of generating pulses for switches at varying voltage and frequency to obtain speed control. Improved control techniques reduce the current harmonics to 1.4% and produce less bearing current. The current review reviews the various control techniques that involve an efficient closed-loop and the handling of FPIM when the stator winding or inverter leg fails. In the future, the research will be concentrated on varied factors merged into the power quality issues in FPIM drives and the fundamental concept of the five-phase MMF.
Conceptualization, Methodology, Formal analysis, Writing, Investigation, and Writing—Original Draft GK, Editing, Supervision, ES, Resources, SC, resources and drafting revision, MG. All authors contributed to the article and approved the submitted version.
This work is supported by Coimbatore Institute of Technology, Coimbatore-641014, Tamil Nadu, India.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abdel-Khalik, A. S., Ahmed, S., Elserougi, A. A., and Massoud, A. M. (2015). Effect of stator winding connection of five-phase induction machines on torque ripples under open line condition. IEEE/ASME Trans. Mechatronics 20, 580–593. doi:10.1109/TMECH.2014.2303254
Abdel-Khalik, A., Ahmed, S., and Massoud, A. (2016a). Steady-state equivalent circuit of five-phase induction machines with different stator connections under open line conditions. IEEE Trans. Industrial Electron. 63, 1. doi:10.1109/TIE.2016.2550001
Abdel-Khalik, A. S., Ahmed, S., and Massoud, A. M. (2016b). Steady-state mathematical modeling of a five-phase induction machine with a combined star/pentagon stator winding connection. IEEE Trans. Industrial Electron. 63, 1331–1343. doi:10.1109/TIE.2015.2493151
Abdel-Khalik, A. S., Elgenedy, M. A., Ahmed, S., and Massoud, A. M. (2016c). An improved fault-tolerant five-phase induction machine using a combined star/pentagon single layer stator winding connection. IEEE Trans. Industrial Electron. 63, 618–628. doi:10.1109/TIE.2015.2426672
Abdelwanis, M. I., Sehiemy, R. A., and Hamida, M. A. (2021). Hybrid optimization algorithm for parameter estimation of poly-phase induction motors with experimental verification. Energy AI 5, 100083. doi:10.1016/j.egyai.2021.100083
Abduallah, A. A., Meraj, M., Al-Hitmi, M., and Iqbal, A. (2018). Space vector pulse width modulation control techniques for a five-phase quasi-impedance source inverter. IET Electr. Power Appl. 12, 379–387. doi:10.1049/iet-epa.2017.0340
Acosta-Cambranis, F., Zaragoza, J., Berbel, N., Capella, G. J., and Romeral, L. (2023). Constant common-mode voltage strategies using sigma–delta modulators in five-phase vsi. IEEE Trans. Industrial Electron. 70, 2189–2198. doi:10.1109/TIE.2022.3170617
Ahmed, S. K. M., Iqbal, A., Abu-Rub, H., and Cortes, P. (2011). “Model predictive control of a three-to-five phase matrix converter,” in Proceeding of the 2011 Workshop on Predictive Control of Electrical Drives and Power Electronics, Munich, Germany, October 2011 (IEEE), 36–39. doi:10.1109/PRECEDE.2011.6078685
Ahmed, S. M., Abu-Rub, H., and Salam, Z. (2015). Common-mode voltage elimination in a three-to-five-phase dual matrix converter feeding a five-phase open-end drive using space-vector modulation technique. IEEE Trans. Industrial Electron. 62, 6051–6063. doi:10.1109/TIE.2015.2420038
Arahal, M., Barrero, F., Toral, S., Duran, M., and Gregor, R. (2009). Multi-phase current control using finite-state model-predictive control. Control Eng. Pract. 17, 579–587. doi:10.1016/j.conengprac.2008.10.005
Barik, S. K., and Jaladi, K. K. (2016). Five-phase induction motor dtc-svm scheme with pi controller and ann controller. Procedia Technol. 25, 816–823. 1st Global Colloquium on Recent Advancements and Effectual Researches in Engineering, Science and Technology - RAEREST 2016 on April 22nd 23rd April 2016. doi:10.1016/j.protcy.2016.08.184
Barrero, F., Arahal, M., Gregor, R., Toral, S., and Duran, M. (2009). A proof of concept study of predictive current control for VSI-driven asymmetrical dual three-phase AC machines. IEEE Trans. Industrial Electron. 56, 1937–1954. doi:10.1109/TIE.2008.2011604
Bermudez, M., Gonzalez-Prieto, I., Barrero, F., Guzman, H., Duran, M. J., and Kestelyn, X. (2017). Open-phase fault-tolerant direct torque control technique for five-phase induction motor drives. IEEE Trans. Industrial Electron. 64, 902–911. doi:10.1109/TIE.2016.2610941
Bhowate, A., Aware, M. V., and Sharma, S. (2021a). Predictive torque control of five-phase induction motor drive using successive cost functions for cmv elimination. IEEE Trans. Power Electron. 36, 14133–14141. doi:10.1109/TPEL.2021.3089741
Bhowate, A., Aware, M. V., and Sharma, S. (2021b). Speed sensor-less predictive torque control for five-phase induction motor drive using synthetic voltage vectors. IEEE J. Emerg. Sel. Top. Power Electron. 9, 2698–2709. doi:10.1109/JESTPE.2020.3016335
Bordry, F., de Fornel, B., and Trannoy, B. (1980). Flux and speed numerical control of a voltage-fed asynchronous induction machine. IEE Proc. B Electr. Power Appl. 127, 91. doi:10.1049/ip-b.1980.0011
Bu, F., Pu, T., Huang, W., and Zhu, L. (2019). Performance and evaluation of five-phase dual random SVPWM strategy with optimized probability density function. IEEE Trans. Industrial Electron. 66, 3323–3332. doi:10.1109/TIE.2018.2854570
Chikondra, B., Muduli, U. R., and Behera, R. K. (2020). Performance comparison of five-phase three-level NPC to five-phase two-level VSI. IEEE Trans. Industry Appl. 56, 1. doi:10.1109/TIA.2020.2988014
Chikondra, B., Muduli, U. R., and Behera, R. K. (2021). An improved open-phase fault-tolerant dtc technique for five-phase induction motor drive based on virtual vectors assessment. IEEE Trans. Industrial Electron. 68, 4598–4609. doi:10.1109/TIE.2020.2992018
Chikondra, B., Muduli, U. R., and Behera, R. K. (2022). Improved dtc technique for thl-npc vsi fed five-phase induction motor drive based on vvs assessment over a wide speed range. IEEE Trans. Power Electron. 37, 1–1981. doi:10.1109/TPEL.2021.3102963
Chikondra, B., Yepes, A. G., Al Zaabi, O., Al Hosani, K., Doval Gandoy, J., and Behera, R. K. (2023). Open-phase fault-tolerant DTC technique for three-level NPC VSI-fed five-phase induction motor drives. IEEE J. Emerg. Sel. Top. Power Electron. 11, 2114–2125. doi:10.1109/JESTPE.2022.3224529
Cortes, P., Kazmierkowski, M., Kennel, R., Quevedo, D., and Rodriguez, J. (2008). Predictive control in power Electronics and drives. IEEE Trans. Industrial Electron. 55, 4312–4324. doi:10.1109/TIE.2008.2007480
Danielson, E. (1902). A novel combination of polyphase motors, for traction purposes. Trans. Am. Inst. Electr. Eng. XIX, 527–539. doi:10.1109/T-AIEE.1902.4764001
Darijevic, M., Jones, M., and Levi, E. (2016). An open-end winding four-level five-phase drive. IEEE Trans. Industrial Electron. 63, 538–549. doi:10.1109/TIE.2015.2418741
de Silva, P. (2004). “Development of space vector modulation strategies for five phase voltage source inverters,” in Proceeding of the Second IEE International Conference on Power Electronics, Machines and Drives, Edinburgh, UK, November 2004 (IEEE). v2–650–v2–650. doi:10.1049/cp:200403652004
Dickson, W. D., and McClain, J. E. (1982). Microcomputer control of variable frequency drives using the submersible motor as an instrument. IEEE Trans. Industry Appl. IA-18, 373–381. doi:10.1109/TIA.1982.4504096
Dordevic, O., Jones, M., and Levi, E. (2013). A comparison of carrier-based and space vector PWM techniques for three-level five-phase voltage source inverters. IEEE Trans. Industrial Inf. 9, 609–619. doi:10.1109/TII.2012.2220553
Duran, M., Salas, F., and Arahal, M. (2008). Bifurcation analysis of five-phase induction motor drives with third harmonic injection. IEEE Trans. Industrial Electron. 55, 2006–2014. doi:10.1109/TIE.2008.918470
Duran, M. J., Riveros, J. A., Barrero, F., Guzman, H., and Prieto, J. (2012). Reduction of common-mode voltage in five-phase induction motor drives using predictive control techniques. IEEE Trans. Industry Appl. 48, 2059–2067. doi:10.1109/TIA.2012.2226221
Durán, M. J., Prieto, J., and Barrero, F. (2013). Space vector PWM with reduced common-mode voltage for five-phase induction motor drives operating in overmodulation zone. IEEE Trans. Power Electron. 28, 4030–4040. doi:10.1109/TPEL.2012.2229394
El-Barbary, Z. (2012). Fuzzy logic based controller for five-phase induction motor drive system. Alexandria Eng. J. 51, 263–268. doi:10.1016/j.aej.2012.10.005
Elgenedy, M. A., Elserougi, A. A., Abdel-Khalik, A. S., Massoud, A. M., and Ahmed, S. (2016). A space vector PWM scheme for five-phase current-source converters. IEEE Trans. Industrial Electron. 63, 562–573. doi:10.1109/TIE.2015.2493514
Fan, S., Meng, D., and Ai, M. (2022). Efficiency analytical of five-phase induction motors with different stator connections for fracturing pump drives. Energy Rep. 8, 405–413. doi:10.1016/j.egyr.2021.11.240
Fu, J.-R., and Lipo, T. (1994). Disturbance-free operation of a multiphase current-regulated motor drive with an opened phase. IEEE Trans. Industry Appl. 30, 1267–1274. doi:10.1109/28.315238
Gabriel, R., Leonhard, W., and Nordby, C. J. (1980). Field-oriented control of a standard AC motor using microprocessors. IEEE Trans. Industry Appl. IA-16, 186–192. doi:10.1109/TIA.1980.4503770
Gao, Liliang, and Fletcher, J. E. (2010). A space vector switching strategy for three-level five-phase inverter drives. IEEE Trans. Industrial Electron. 57, 2332–2343. doi:10.1109/TIE.2009.2033087
Gonzalez-Prieto, I., Duran, M. J., Rios-Garcia, N., Barrero, F., and Martin, C. (2018). Open-switch fault detection in five-phase induction motor drives using model predictive control. IEEE Trans. Industrial Electron. 65, 3045–3055. doi:10.1109/TIE.2017.2748052
Guzman, H., Barrero, F., and Duran, M. J. (2015). IGBT-gating failure effect on a fault-tolerant predictive current-controlled five-phase induction motor drive. IEEE Trans. Industrial Electron. 62, 15–20. doi:10.1109/TIE.2014.2331019
Hussain, H. A., and Toliyat, H. A. (2012). “Reduction of shaft voltages and bearing currents in five-phase induction motors,” in Proceeding of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, November 2012 (IEEE), 3309–3316. doi:10.1109/ECCE.2012.6342337
Iqbal, A., and Levi, E. (2006). Space vector PWM techniques for sinusoidal output voltage generation with a five-phase voltage source inverter. Electr. Power Components Syst. 34, 119–140. doi:10.1080/15325000500244427
Iqbal, A., Moinuddin, S., Khan, M. R., Ahmed, S. M., and Abu-Rub, H. (2010). A novel three-phase to five-phase transformation using a special transformer connection. IEEE Trans. Power Deliv. 25, 1637–1644. doi:10.1109/TPWRD.2010.2042307
Jayakumar, V., Chokkalingam, B., and Munda, J. L. (2022a). Performance analysis of multi-carrier pwm and space vector modulation techniques for five-phase three-level neutral point clamped inverter. IEEE Access 10, 34883–34906. doi:10.1109/ACCESS.2022.3162616
Jayakumar, V., Chokkalingam, B., and Munda, J. L. (2022b). A twenty five switch inverter topology for controlling two independent five-phase load. IEEE Access 10, 81722–81740. doi:10.1109/ACCESS.2022.3195897
Khadar, S., Abu-Rub, H., and Kouzou, A. (2021). Sensorless field-oriented control for open-end winding five-phase induction motor with parameters estimation. IEEE Open J. Industrial Electron. Soc. 2, 266–279. doi:10.1109/OJIES.2021.3072232
Kouro, S., Cortes, P., Vargas, R., Ammann, U., and Rodriguez, J. (2009). Model predictive control—a simple and powerful method to control power converters. IEEE Trans. Industrial Electron. 56, 1826–1838. doi:10.1109/TIE.2008.2008349
Kubota, H., and Matsuse, K. (1994). Speed sensorless field-oriented control of induction motor with rotor resistance adaptation. IEEE Trans. Industry Appl. 30, 1219–1224. doi:10.1109/28.315232
Kulandaivel, G., Sundaram, E., Padmanaban, S., Khan, B., and Kamwa, I. (2022). Fpga-based control strategy of five-phase induction motor drives. J. Eng. 2022, 1173–1189. doi:10.1049/tje2.12197
Kumar, R., Singh, B., and Kant, P. (2023). Assessment of multi-phase conversion and modified pwm strategy for power converters of medium-voltage induction motors drive. IEEE Trans. Industry Appl. 59, 3458–3469. doi:10.1109/TIA.2023.3238003
Levi, E., Bojoi, R., Profumo, F., Toliyat, H., and Williamson, S. (2007). Multiphase induction motor drives – A technology status review. IET Electr. Power Appl. 1, 489. doi:10.1049/iet-epa:20060342
Levi, E., Satiawan, I. N. W., Bodo, N., and Jones, M. (2012). A space-vector modulation scheme for multilevel open-end winding five-phase drives. IEEE Trans. Energy Convers. 27, 1–10. doi:10.1109/TEC.2011.2178074
Levi, E. (2008). Multiphase electric machines for variable-speed applications. IEEE Trans. Industrial Electron. 55, 1893–1909. doi:10.1109/TIE.2008.918488
Li, Z., Du, Y., Zhao, W., Tao, T., and Tian, W. (2023). Zero-sequence current suppression strategy for five-phase OW-pmsm with reduced common-mode voltage and inverter losses. IEEE Trans. Power Electron. 38, 10116–10127. doi:10.1109/TPEL.2023.3278317
Lim, C. S., Levi, E., Jones, M., Rahim, N. A., and Hew, W. P. (2014). FCS-MPC-Based current control of a five-phase induction motor and its comparison with PI-PWM control. IEEE Trans. Industrial Electron. 61, 149–163. doi:10.1109/TIE.2013.2248334
Liu, H., Wang, D., Yi, X., and Meng, F. (2021). Torque ripple suppression under open-phase fault conditions in a five-phase induction motor with harmonic injection. IEEE J. Emerg. Sel. Top. Power Electron. 9, 274–288. doi:10.1109/JESTPE.2019.2952374
Mavila, P. C., and Rajeevan, P. P. (2022). A five-level torque controller based dtc scheme for open-end winding five-phase im drives with single dc source and auxiliary plane harmonic elimination. IEEE Trans. Industry Appl. 58, 2063–2074. doi:10.1109/TIA.2022.3140361
Mayne, D. Q., Rawlings, J. B., Rao, C. V., and Scokaert, P. O. M. (2000). Constrained model predictive control: Stability and optimality, 26.
Medina-Sánchez, M., Yepes, A. G., López, O., and Doval-Gandoy, J. (2023). Assessment and exploitation of the minimum current harmonic distortion under overmodulation in five-phase induction motor drives. IEEE Trans. Power Electron. 38, 4289–4305. doi:10.1109/TPEL.2022.3231138
Morsy, A. S., Abdelkhalik, A. S., Ahmed, S., and Massoud, A. M. (2014). Sensorless speed control of a five-phase induction machine under open-phase condition. J. Eng. 2014, 201–209. doi:10.1049/joe.2014.0050
Mossa, M. A., and Echeikh, H. (2021). A novel fault tolerant control approach based on backstepping controller for a five phase induction motor drive: experimental investigation. ISA Trans. 112, 373–385. doi:10.1016/j.isatra.2020.11.031
Muduli, U. R., Behera, R. K., Al Hosani, K., and Moursi, M. S. E. (2022a). Direct torque control with constant switching frequency for three-to-five phase direct matrix converter fed five-phase induction motor drive. IEEE Trans. Power Electron. 37, 11019–11033. doi:10.1109/TPEL.2022.3167477
Muduli, U. R., Chikondra, B., and Behera, R. K. (2022b). Space vector pwm based dtc scheme with reduced common mode voltage for five-phase induction motor drive. IEEE Trans. Power Electron. 37, 114–124. doi:10.1109/TPEL.2021.3092259
Muteba, M., and Nicolae, D. V. (2017). Influence of mixed winding arrangements on torque ripples of five-phase induction machines. Electr. Power Syst. Res. 151, 154–165. doi:10.1016/j.epsr.2017.05.027
Naganathan, P., and Srinivas, S. (2020). Direct torque control techniques of three-level H-bridge inverter fed induction motor for torque ripple reduction at low speed operations. IEEE Trans. Industrial Electron. 67, 8262–8270. doi:10.1109/TIE.2019.2950840
Neidhöfer, G. (2007). Early three-phase power winner in the development of polyphase ac. IEEE Power Energy Mag. 5, 88–100. doi:10.1109/MPE.2007.904752
Nguyen, T. D., and Lee, H.-H. (2016). Development of a three-to-five-phase indirect matrix converter with carrier-based PWM based on space-vector modulation analysis. IEEE Trans. Industrial Electron. 63, 13–24. doi:10.1109/TIE.2015.2472359
Panda, A. K., and Pandey, R. (2018). “A simplified carrier based PWM method for five-level inverter fed five-phase induction motor,” in Proceeding of the 2018 IEEMA Engineer Infinite Conference (eTechNxT), New Delhi, March 2018 (IEEE), 1–6. doi:10.1109/ETECHNXT.2018.8385307
Pavithran, K., Parimelalagan, R., and Krishnamurthy, M. (1988). Studies on inverter-fed five-phase induction motor drive. IEEE Trans. Power Electron. 3, 224–235. doi:10.1109/63.4353
Payami, S., and Behera, R. K. (2017). An improved DTC technique for low-speed operation of a five-phase induction motor. IEEE Trans. Industrial Electron. 64, 3513–3523. doi:10.1109/TIE.2017.2652397
Payami, S., Behera, R. K., Iqbal, A., and Al-Ammari, R. (2015). Common-mode voltage and vibration mitigation of a five-phase three-level NPC inverter-fed induction motor drive system. IEEE J. Emerg. Sel. Top. Power Electron. 3, 349–361. doi:10.1109/JESTPE.2014.2313153
Perin, M., Pereira, L. A., Pereira, L. F. A., and Nicol, G. (2021). Estimation of parameters of five-phase induction motors using step voltage at standstill. IEEE Trans. Energy Convers. 36, 3491–3501. doi:10.1109/TEC.2021.3085221
Prieto, J., Jones, M., Barrero, F., Levi, E., and Toral, S. (2011). Comparative analysis of discontinuous and continuous PWM techniques in VSI-fed five-phase induction motor. IEEE Trans. Industrial Electron. 58, 5324–5335. doi:10.1109/TIE.2011.2126540
Rahman, K., Iqbal, A., Al-Emadi, N., and Ben-Brahim, L. (2017). Common mode voltage reduction in a three-to-five phase matrix converter fed induction motor drive. IET Power Electron. 10, 817–825. doi:10.1049/iet-pel.2016.0661
Rahman, K., Rahman, S., Bhaskar, M. S., Iqbal, A., Khandakar, A., Tariq, M., et al. (2022). Field-oriented control of five-phase induction motor fed from space vector modulated matrix converter. IEEE Access 10, 17996–18007. doi:10.1109/ACCESS.2022.3142014
Rakesh, R., Majumder, M. G., Dewani, R., Gopakumar, K., Loganathan, U., Jarzyna, W., et al. (2022). A very high resolution 30-sided space vector generation from a single dc-link for induction motor drives. IEEE Trans. Industrial Electron. 69, 160–168. doi:10.1109/TIE.2021.3053884
Ramasamy, P., and Krishnasamy, V. (2020). Svpwm control strategy for a three phase five level dual inverter fed open-end winding induction motor. ISA Trans. 102, 105–116. doi:10.1016/j.isatra.2020.02.034
Reddy, V. S., and Devabhaktuni, S. (2022). Enhanced low-speed characteristics with constant switching torque controller-based dtc technique of five-phase induction motor drive with fopi control. IEEE Trans. Industrial Electron. 70–10. doi:10.1109/TIE.2022.3227275
Reist, H. G., and Maxwell, H. (1909). Multispeed induction motors. Trans. Am. Inst. Electr. Eng. XXVIII, 601–609. doi:10.1109/T-AIEE.1909.4768189
Renukadevi, G., and Rajambal, K. (2014). Field programmable gate array implementation of space-vector pulse-width modulation technique for five-phase voltage source inverter. IET Power Electron. 7, 376–389. doi:10.1049/iet-pel.2013.0078
Riveros, J. A., Barrero, F., Levi, E., Duran, M. J., Toral, S., and Jones, M. (2013). Variable-speed five-phase induction motor drive based on predictive torque control. IEEE Trans. Industrial Electron. 60, 2957–2968. doi:10.1109/TIE.2012.2198034
Rizzoli, G., Mengoni, M., Sala, G., Vancini, L., Zarri, L., Tani, A., et al. (2022). Exploitation of the power capability in a five-phase doubly fed induction motor drive for contact-less energy transfer. IEEE Trans. Industrial Electron. 69, 7596–7606. doi:10.1109/TIE.2021.3109507
Ryu, H.-M., Kim, J.-H., and Sul, S.-K. (2005). Analysis of multiphase space vector pulse-width modulation based on multiple d-q spaces concept. IEEE Trans. Power Electron. 20, 1364–1371. doi:10.1109/TPEL.2005.857551
Sala, G., Mengoni, M., Rizzoli, G., Degano, M., Zarri, L., and Tani, A. (2021). Impact of star connection layouts on the control of multiphase induction motor drives under open-phase fault. IEEE Trans. Power Electron. 36, 3717–3726. doi:10.1109/TPEL.2020.3024205
Sathiakumar, S., Biswas, S. K., and Vithayathil, J. (1986). Microprocessor-based field-oriented control of A CSI-fed induction motor drive. IEEE Trans. Industrial Electron. IE-33, 39–43. doi:10.1109/TIE.1986.351703
Singh, G. (2002). Multi-phase induction machine drive research—A survey. Electr. Power Syst. Res. 61, 139–147. doi:10.1016/S0378-7796(02)00007-X
Sun, J., Li, C., Zheng, Z., Wang, K., and Li, Y. (2022). Online estimation of per-phase stator resistance based on dc-signal injection for condition monitoring in multiphase drives. IEEE Trans. Industrial Electron. 69, 2227–2239. doi:10.1109/TIE.2021.3066935
Tan, C., Xiao, D., Fletcher, J. E., and Rahman, M. F. (2016). Analytical and experimental comparison of carrier-based PWM methods for the five-phase coupled-inductor inverter. IEEE Trans. Industrial Electron. 63, 7328–7338. doi:10.1109/TIE.2016.2592860
Tatte, Y. N., and Aware, M. V. (2017). Torque ripple and harmonic current reduction in a three-level inverter-fed direct-torque-controlled five-phase induction motor. IEEE Trans. Industrial Electron. 64, 5265–5275. doi:10.1109/TIE.2017.2677346
Tatte, Y. N., Aware, M. V., Pandit, J. K., and Nemade, R. (2018). Performance improvement of three-level five-phase inverter-fed DTC-controlled five-phase induction motor during low-speed operation. IEEE Trans. Industry Appl. 54, 2349–2357. doi:10.1109/TIA.2018.2798593
Toliyat, H. (1998). Analysis and simulation of five-phase variable-speed induction motor drives under asymmetrical connections. IEEE Trans. Power Electron. 13, 748–756. doi:10.1109/63.704150
Tran, Q.-H., and Lee, H.-H. (2018). An advanced modulation strategy for three-to-five-phase indirect matrix converters to reduce common-mode voltage with enhanced output performance. IEEE Trans. Industrial Electron. 65, 5282–5291. doi:10.1109/TIE.2017.2782242
Vancini, L., Mengoni, M., Rizzoli, G., Sala, G., Zarri, L., and Tani, A. (2021). Carrier-based pwm overmodulation strategies for five-phase inverters. IEEE Trans. Power Electron. 36, 6988–6999. doi:10.1109/TPEL.2020.3034170
Vancini, L., Mengoni, M., Rizzoli, G., Zarri, L., and Tani, A. (2022). Voltage balancing of the dc-link capacitors in three-level t-type multiphase inverters. IEEE Trans. Power Electron. 37, 6450–6461. doi:10.1109/TPEL.2021.3137083
Wang, R., Wang, W., Liu, R., Zhang, J., and Mu, X. (2017). Carrier-based pulse-width modulation control strategy of five-phase six-bridge indirect matrix converter under unbalanced load. IET Power Electron. 10, 1932–1942. doi:10.1049/iet-pel.2017.0323
Ward, E., and Härer, H. (1969). Preliminary investigation of an invertor-fed 5-phase induction motor. Proc. Institution Electr. Eng. 116, 980. doi:10.1049/piee.1969.0182
Wickerham, W. R. (1945). Variable-unbalanced-voltage control. Trans. Am. Inst. Electr. Eng. 64, 98–102. doi:10.1109/T-AIEE.1945.5059097
Xu, H., Toliyat, H., and Petersen, L. (2002). Five-phase induction motor drives with DSP-based control system. IEEE Trans. Power Electron. 17, 524–533. doi:10.1109/TPEL.2002.800983
Xue, C., Song, W., Wu, X., and Feng, X. (2018). A constant switching frequency finite-control-set predictive current control scheme of a five-phase inverter with duty-ratio optimization. IEEE Trans. Power Electron. 33, 3583–3594. doi:10.1109/TPEL.2017.2707440
Yepes, A. G., and Doval-Gandoy, J. (2022). Overmodulation method with adaptive x-y current limitation for five-phase induction motor drives. IEEE Trans. Industrial Electron. 69, 2240–2251. doi:10.1109/TIE.2021.3068687
Zaskalicky, P. (2018). “Electromagnetic torque ripple calculation of a pentacle connected five-phase IM supplied by a rectangular voltage,” in Proceeding of the 2018 ELEKTRO, Mikulov, May 2018 (IEEE), 1–5. doi:10.1109/ELEKTRO.2018.8398264
Keywords: direct torque control, fault tolerance, five-phase induction motor, voltage source inverter, sensorless control, space vector pulse width modulation
Citation: Kulandaivel G, Sundaram E, Gunasekaran M and Chenniappan S (2023) Five-phase induction motor drive-A comprehensive review. Front. Energy Res. 11:1178169. doi: 10.3389/fenrg.2023.1178169
Received: 02 March 2023; Accepted: 02 August 2023;
Published: 25 August 2023.
Edited by:
Manickam Minakshi, Murdoch University, AustraliaReviewed by:
Udit Mohanty, Halliburton Inc, United StatesCopyright © 2023 Kulandaivel, Sundaram, Gunasekaran and Chenniappan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gobikannan Kulandaivel, Z29iaWthbm5hbi5rQGdtYWlsLmNvbQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.