Finite element modeling of biomass hopper flow

Hoppers are widely used biomass handling devices that channel bulk biomass from storage to subsequent handling equipment. Jenike’s longstanding approach, based on the Mohr-Coulomb model, has been successfully used to design hoppers handling cohesionless granular materials such as grains and other agricultural produces. However, designing a hopper to ensure reliable biomass flow is found to be challenging due to cohesion, irregular particle shape, and bulk material elastoplasticity. This study aims to address the biomass handling engineering challenge with alternative constitutive material models concerning the flow behavior of bulk solids. Finite element modeling is an approach that allows for implementation of different material models, whose underlying constitutive theories assist in investigating the origin and manifestation of bulk mechanical behavior of granular materials. This study focuses on the incipient gravity hopper flow of two types of biomass feedstocks, i.e., ground corn stover and Douglas fir wood. Three widely used constitutive material models, i.e., Mohr-Coulomb model, modified Cam-Clay model, and Drucker-Prager/Cap model, are implemented. Using the flow pattern represented by the volume of biomass exhibiting more than 7% of axial strain (Kamath and Puri, 1999), the finite element model predicts that the bulk corn stover particulate material forms an arch, which represents a hampered transition from the static state to the dynamic flow-state out of the hopper, whereas bulk Douglas fir wood particulate material develops a reliable mass flow pattern. A laboratory scale hopper was used to experimentally determine the biomass flow conditions, which were subsequently compared with the predicted onset of flow by a finite element model (FEM). The developed FEM was found to correctly predict the initiation of mass flow for the milled Douglas fir wood, whereas corn stover was predicted to establish a strong core flow suggesting an unreliable handling characteristic. This observation aligns with the reported poor handling of milled corn stover.

Introduction

Reliable biomass handling is an essential and urgent prerequisite in using biomass as a significant part of renewable energy and material resources (Paulrud et al., 2002; Jensen et al., 2004; Miccio et al., 2009; Hinterreiter et al., 2012; Gil et al., 2013a; Gil et al., 2013b; Kenney et al., 2013; Miccio et al., 2013; Tannous et al., 2013; Westover et al., 2015; Williams et al., 2016; Gejdoš et al., 2018; Salehi et al., 2019). Unfortunately, the current knowledge and understanding of biomass flow behavior is inadequate to resolve biomass handling issues originating from the unique and cohesive flow behavior of biomass feedstocks.

As a step toward a first principle-based approach in engineering biomass handling systems, there have been efforts to quantify the biomass flowability (Miccio et al., 2009; Gil et al., 2013a; Salehi et al., 2019; Cheng et al., 2021; Lu et al., 2021). The term ‘biomass flowability’ suggests a quantitative metric representing the ability of biomass to flow. In reality, the flowability of bulk solid cannot be expressed with a single parameter because ‘flowability’ is the result of interactions between the physical and mechanical properties of bulk biomass and the handling equipment (Prescott and Barnum, 2000; Ganesan et al., 2008; Krantz et al., 2009; Blackwood, 2019). Therefore, in order to analyze and predict the flow behavior of biomass accurately, the use of a biomass flow model should include the interaction between biomass and biomass handling equipment.

In the procedure of calibrating a chosen constitutive model, a robust characterization protocol for determining material properties is crucial. To that end, the need for bulk mechanical property characterization free of confounding effects from the measurement device is apparent (Schwedes, 2003; Shao et al., 2017; Janssen and Verwijs, 2007; Ittershagen et al., 2011; Shi et al., 2018; Wang et al., 2018).

For the material properties relevant to the handling of biomass, the strength of the bulk biomass and the flow function are often used. Flow function is defined as the ratio between the yield strength of a consolidated material and unconfined yield strength (Jenike, 1961). Usually, yield strength is determined with a shear-cell type device. However, material properties determined with a shear-cell type device inherently include the interactions between the test specimen and rigid die wall, both materially and structurally. The states of a consolidation and shear plane are induced with implicit effects of such interactions, i.e., the calibrated parameters are confounded by the test device configuration.

For example, the shear test that is most widely used in the field relies on the framework of Jenike’s flow factor that uses unconfined yield stress of bulk material, which is defined as the major principal stress at which an unconfined bulk material yields in shear. Therefore, the determination of the unconfined yield stress of biomass is a critical step in shear tests. However, the definition of the yield does not always indicate the material failure, therefore, the determined value may or may not indicate the conditions indicating biomass flow.

In addition, a typical shear tester uses a rigid wall, which confines the sample and confounds the yield stress especially at low consolidation stress levels, which is critical in determining the unconfined yield stress. Further, a typical shear tester induces a forced failure plane, which can lead to measurements deviating from native yield condition. Therefore, it is important to use an experimental protocol that can impose stress conditions close to the first principle of given constitutive models, which enables the first-principle-based engineering.

For the determination of mechanical properties with minimal confounding effect, a triaxial tester is desired (Janssen and Verwijs, 2007; Yi et al., 2022). A conventional triaxial tester employs a cylindrical test specimen, allowing independent stress directions and modes of deformation in only two directions (Desai and Siriwardane, 1984). Yi et al. (Yi et al., 2022) reports an improved truly cubical triaxial tester (CTT) with a sample size appropriate for milled biomass, i.e., biomass scale CTT. Yi et al. (Yi et al., 2022) also demonstrate that such a fundamental characterization device and protocol allows for the application of stress and the measurement of corresponding strain in principal directions with minimal interferences of the device. The properties determined with the Forest Concepts biomass Cubical Triaxial Tester (fcCTT) (Forest Concepts Analytics Model CTT250-A01-100, Forest Concepts, LLC, Auburn, WA) are free of die-wall effects owing to flexible pressure application and sample holding membranes. Yi et al. (Yi et al., 2022) suggest that the bulk mechanical properties of biomass determined with the fcCTT represent truer material properties than available from cylindrical triaxial tester or a shear cell. Further, the stress application and measurement of corresponding strain are maintained in the principal axes, which makes the calibration of material parameters of constitutive models unambiguous.

The contribution of biomass handling equipment characteristics to flowability is equally important but not as systematically studied. Such a contribution can be described in a structural model in a finite element (FE) analysis. Important aspects of the structural model include the geometry of specific handling and storing equipment, as well as the interaction between biomass particles and the wall of biomass handling equipment (Jin et al., 2020a). From the perspective of FE biomass flow modeling, the biomass particle and wall interaction is implemented as a boundary condition.

Widely used Jenike’s flow function and hopper opening design implicitly combines the granular material properties of a bulk particulate biomass and a structural model of a hopper. The combination of the limits of the material model calibration using a shear-cell and the deficient structural model of biomass handling devices is thought to be responsible for unresolved engineering challenges in reliable biomass handling (Prescott and Barnum, 2000; Westover, 2014; Gejdoš et al., 2018). To that end, a computational approach is a proposed to be a more capable tool by enabling the modeling of holistic “biomass flowability.”

Recently, the discrete element model (DEM) has been actively studied in biomass flow and is the most widely used particle-based model owing to the advancement of computing capability. The major limit of the DEM as an engineering tool in designing biomass handling devices is that the model parameters calibration lacks direct experimental protocol on biomass particles. Rather, the calibration of parameters is achieved with optimization of fitting simulation results with a set of empirical tests, such as angle of repose or bulk density (Geldart et al., 2006; Coetzee, 2016; Elskamp et al., 2017; Pachón-Morales et al., 2020; Hoshishima et al., 2021; Soltanbeigi et al., 2021; Fang et al., 2022). In addition, accurate modeling of anisotropic biomass particles having high aspect ratios requires complex multi-sphere elements or irregular geometry description that greatly increase computing time and limits the utility of the DEM for day-to-day engineering practices. On the other hand, a coupled-Euler-Lagrangian scheme was shown to be able to simulate established biomass flow using a hypoplasticity model (Lu et al., 2021). While these approaches focus on the transient and steady-state biomass flow aiming to predict the discharge rate, the initiation of biomass flow remains one of the major challenges in bioenergy industry.

Therefore, this research aims to model and predict the onset of the gravity flow of biomass stored in a hopper using a FE model based on bulk properties rather than particle-level properties. In this study, the biomass flow model comprises a material model describing bulk biomass behavior and a structural model describing a gravity hopper. For material models, elasto-plasticity models (Drucker and Prager, 1952; Jenike, 1961; Jenike, 1964a; Jenike, 1964b; Jenike, 1967; Luis and Martin John, 1985; Han et al., 2008; Jiang and Wu, 2012; Jin et al., 2020b) and critical state model (Schofield and Wroth, 1968; Szalwinski, 2017) are considered. These models are more straightforward to calibrate with triaxial tests compared to the complex governing equations used in Lu et al. (Lu et al., 2022), therefore easier to adopt in existing engineering practices. Specifically, we calibrated Mohr-Coulomb (MC), modified Drucker-Prager/Cap (mDPC), and modified Cam-Clay (mCC) models, to compare and identify an outperforming analytical biomass flow model. The parameters of these models for milled corn stover and Douglas fir wood were determined using the fcCTT as reported in (Yi et al., 2022).

This study used corn stover and woody biomass samples. Corn stover is a crop residue that is a potential source of alternative biorenewable material. Corn stover was estimated to be more than three-fourths of primary crop residues profitable to collect (Perlack et al., 2011). However, difficulties in handling have obstructed establishing corn stover as a profitable and reliable biomass feedstock. Therefore, it is important to quantitatively examine its flow behavior to engineer the storage and handling. Douglas fir is a common softwood in Northwest U.S. with better handling characteristics than corn stover for similar (milling method and geometric mean particle size) bulk particulate materials. Current forest harvest practices leave considerable residue, which are considered to be a significant biomass resource.

This study assumes that the incipient flow pattern indicates the flowability of biomass (Kamath and Puri, 1999). Using the flow pattern represented by the volume of biomass exhibiting larger than a specific magnitude of axial strain, i.e., 7% (Kamath and Puri, 1999), the FE model predicts that the corn stover forms an arch, which predicts a hampered transition from the static storage state to the dynamic flow state out of the hopper, whereas Douglas fir develops a consistent mass flow pattern.

A laboratory scale hopper was used to experimentally observe the biomass flow, which was subsequently compared with the predicted onset of flow by a FE model. The developed FE biomass flow model was found to correctly predict the initiation of mass flow for the milled Douglas fir, whereas corn stover was predicted to establish a strong core flow suggesting an unreliable handling characteristic. This observation aligns with the reported poor handling of milled corn stover (Bioenergy Technologies Office, 2016; Westover et al., 2018) and demonstrates the potential of first principle-based approach in engineering design for biomass handling systems.

Materials and methods

Materials

Corn stover samples were collected from bales that were detangled by hand prior to milling at as-baled moisture content. Corn stover was comminuted to a 2 mm nominal particle size using a Forest Concepts model M24 rotary shear and model 2448 orbital screen system. (Forest Concepts LLC.) Fuel-grade Douglas fir chips were comminuted to a 1 mm nominal particle size using a Forest Concepts model M24 rotary shear and model 2448 orbital screen system and then dehydrated to less than 20% wet basis moisture content. (Forest Concepts LLC.) All materials were stored at ambient conditions after milling and prior to use in experiments, and the moisture content of corn stover 2 mm and Douglas fir 1 mm are 7.3% ± 0.3% and 10.3% ± 0.5%, respectively (n = 9 for each material). The material sizes were selected from those commonly requested by Forest Concepts’ customers for the respective materials at the time of experiment design.

Experimental study of hopper flow

This study aimed to model and to simulate the biomass flow out of the hopper using the FE analysis. For experimental verification of the FE biomass flow model, a hopper was designed and constructed with a transparent acrylic panel to allow visual observation of the flow pattern (Figure 1).

FIGURE 1

FIGURE 1. Hopper with a variable wall angle.

The sidewalls of the hopper were designed and constructed to have varying angles between 15° and 90°. This hopper has an opening of 20 cm $\times$ 20 cm that could be closed to fill and opened to initiate a discharge at the bottom. The hopper was filled with a consistent height of 20 cm for both milled corn stover 2 mm bulk biomass and Douglas fir 1 mm bulk biomass with the angle of the hopper wall of 45°. The gravity discharge of the biomass was measured with the Ohaus AS8201 precision balance (±0.01 g with 8.2 kg maximum load), and the flow pattern was observed and recorded with a Sony NEX-VG10 video camera.

Finite element model: Geometric model

A finite element biomass hopper geometric model was constructed with the same geometry as the experimental setup, i.e., 20 cm height with the side walls with the angles of 45°. The biomass volume was meshed with Gmsh v4.1.0 (Geuzaine and Remacle, 2009) using three-dimensional tetrahedrons seeded with two-dimensional Delaunay triangulation. The size of the mesh was determined through the mesh sensitivity test of the simulation result corresponding to the precision of the fcCTT, which was 0.1 kPa and was used in the calibration of the constitutive model parameters.

Material model parameters of finite element biomass flow model

A finite element biomass flow model reflecting the experimental hopper geometry was built using Abaqus (Dassault Systèmes, 2017) V.2020. Respective parameters of the material models were determined to implement biomass flow material models. As mentioned previously, constitutive biomass material models implemented in this study included Mohr-Coulomb model (Jenike, 1961; Dimaggio and Sandler, 1971; Heyman, 1997), Drucker-Prager/Cap model (Drucker and Prager, 1952; Menetrey and Willam, 1995), and modified Cam-Clay model (Schofield and Wroth, 1968; Tripodi et al., 1994; Kamath and Puri, 1997).

Shear cell type instruments had been widely used in determining biomass flow properties, specifically, cohesion coefficient ($c$) and angle of internal friction ($\varphi$) for Mohr-Coulomb (MC) Model. A shear cell could also produce experimental data to determine $d$ and $\beta$ for modified Drucker-Prager/Cap (mDPC) Model, and critical state line slope ($M$) and shear modulus ($G$) for modified Cam-Clay (mCC) model. However, other elastic properties involving the volumetric strain, such as bulk modulus ($K$) or Poisson’s ratio ($\nu$) for MC and mDPC models, or elasto-plasticity compression index ($\lambda$) or spring-back index ($\kappa$) for mCC model were not straight forward to determine with a conventional shear cell. Therefore, the calibration of these constitutive models was done by determining parameters of each model with the combination of hydrostatic triaxial compression test and conventional triaxial compression test using fcCTT.

Triaxial tests using a cubical triaxial tester, e.g., fcCTT, generated a set of data that could be used in populating the material properties for an analytic biomass flow models in a straightforward way (Desai and Siriwardane, 1984; Fang et al., 2022; Kamath and Puri, 1997; Donaghe et al., 1988). This was because the triaxial tester was a fundamental mechanical tester capable of applying and measuring stress in principal directions. It was shown that the properties measured with the biomass-scaled fcCTT can be used in determining above mentioned constitutive models in an unambiguous way (Yi et al., 2022).

The calibrated material parameters of the above-mentioned biomass flow models are listed in Tables 1, 2. The details of the calibration of these constitutive models can be found in Yi et al. (Yi et al., 2022).

TABLE 1

TABLE 1. Material parameters of selected constitutive models determined with Hydrostatic Triaxial Compression Test using the Forest Concept CTT using the calibration procedure of (Yi et al., 2022). The range is the standard deviation value.

TABLE 2

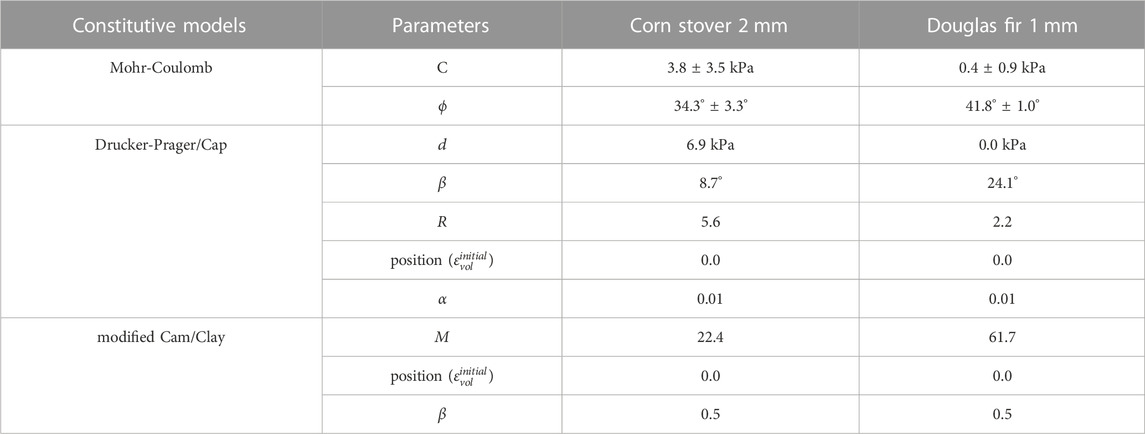
TABLE 2. Material parameters of selected constitutive models determined with Conventional Triaxial Compression Test using the Forest Concept CTT using the calibration procedure of Yi et al. (Yi et al., 2022). The range is the standard deviation value.

Results and discussion

Hopper flow patterns

The weight of milled biomass discharged from the hopper was measured as listed in Table 3. While the total discharge represented the tendency of the hopper flow in its entirety, the static nature of the finite element hopper flow model was limited to calculating the onset of flow rather than a fully developed steady flow state. Therefore, it was appropriate to use additional discharge metrics that can be related to the incipient hopper flow. In this study, the flow rate was chosen under the assumption that it was maintained throughout the discharge once a flow is established.

TABLE 3

TABLE 3. Experimental biomass discharge from the PSU hopper. The range is the standard deviation value.

Experimentally, the flow rate was determined using the measured weight of completed hopper discharge of respective biomass and the duration of discharge determined with the video recording. Computationally, the discharge rate is determined using the amount of volume, which exhibits the axial strain larger than the flow criterion, and the time duration determined from experiments, i.e., the duration from the opening of the bottom hopper gate to the initiation of the flow out of the hopper using the video recording of each test.

From the experiment, corn stover was found to have a tendency of developing core flow resulting in a rat-hole (Figure 2 A and B). On the contrary, Douglas fir tended to develop mass flow, where the entire mass flowed smoothly out of the hopper (Figure 2 C).

FIGURE 2

FIGURE 2. A hopper flow experiment of (A) a core flow pattern of corn stover 2 mm, (B) a rat-hole development of corn stover 2 mm, and (C) mass flow of Douglas fir 1 mm.

Finite element model predictions

Using predetermined parameters of MC, mDPC, and mCC models, hopper flow of corn stover 2 mm and Douglas Fir 1 mm bulk particulate materials were simulated and compared with experimental results. The axial deformation in the direction of gravity indicates the inclination of bulk biomass to establish the onset of flow. Figure 3 illustrates the region of corn stover and Douglas fir exhibiting different levels of axial deformation. For both corn stover and Douglas fir, the region with higher axial strain develops around the center. Qualitatively, Douglas fir was predicted to develop the deformation in the gravity direction throughout the cross-section, whereas corn stover was predicted to develop the gravity direction deformation near the core region for all three material models, i.e., MC, mDPC, and mCC models. This observation indicated a strong core flow pattern for corn stover leading to handling issues such as a rat-hole, whereas a mass flow was predicted for Douglas fir.

FIGURE 3

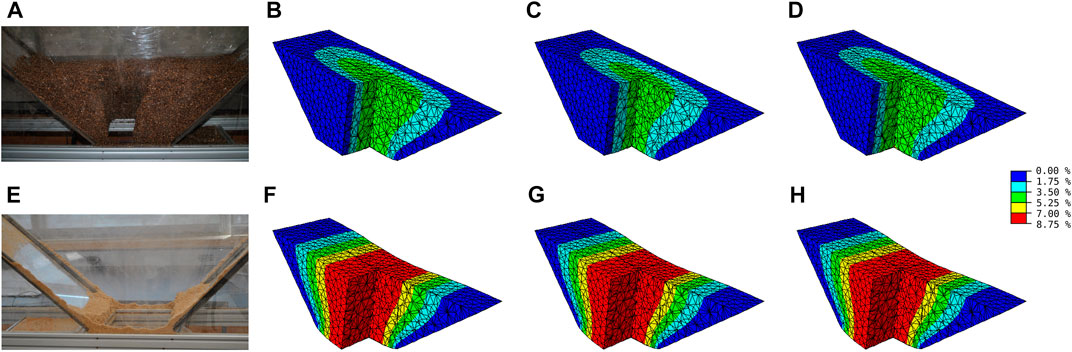
FIGURE 3. Comparison between incipient biomass flow simulation and experiment: (A) Experimental corn stover 1 mm hopper discharge. (B–D) FE prediction of corn stover 2 mm hopper discharge with Mohr-Coulomb, modified Drucker-Prager/Cap, and modified Cam-Clay models, respectively. (E) Experimental Douglas fir 1 mm hopper discharge. (F–H) FE prediction of Douglas fir 1 mm hopper discharge with Mohr-Coulomb, modified Drucker-Prager/Cap, and modified Cam-Clay models, respectively. The color bar represents axial strain levels in the gravity direction.

Quantitatively, corn stover was predicted to have a smaller magnitude of axial deformation than Douglas fir, which conformed with the experimental results. It was notable that the region exceeding the 7% of axial strain, which indicated an incipient flow, was established for Douglas fir, but it did not for corn stover.

This observation suggested that the 7% axial strain at the onset of flow might be a conservative criterion considering the experimental hopper discharge results showing discharges for both biomass feedstocks. In FE biomass hopper flow model, the core region of corn stover simulation showed larger than 3.5% of axial strain. Therefore, smaller axial deformation levels than 7% were investigated as alternative flow criteria.

To make a quantitative comparison, the total volume that deforms in the gravity direction enough to initiate the flow at different strain levels, i.e., 3%, 5%, and 7%, was calculated and compared to the experimental results. It should be noted that the predicted incipient flow volume was not a direct predictor of the eventual total discharge, although the predicted volume at the onset of flow was thought to be related to the eventual total discharge. To complement this comparison, the discharge rate is estimated and compared to the experimental results.

The computational predictions of the biomass volume that establish large enough axial deformation to be considered at the onset of the flow are also shown in Figure 4. The 7% axial strain criterion results in underestimated flow volume for both corn stover and Douglas fir. Especially for corn stover, no volume deformed as much as 7% axially in any of the three biomass flow models. When 5% of axial strain was used as the incipient flow criterion, the amount of volume at the incipient flow increased, but they remained as underestimations compared to the experimental results. However, Axial strain values of 3.5% resulted in much closer predictions for both corn stover 2 mm and Douglas fir 1 mm. This result suggests that biomass consolidated under self-weight may fail at a smaller axial strain under a tensile shear than the recommended value in the (Donaghe et al., 1988; ASTM Standard D4767, 2011; ASTM Standard D7181, 2020) or previously reported cohesive granular material (Kamath and Puri, 1997). This result also suggests that different biomass feedstocks may exhibit the onset of tensile failure at a different axial strain value.

FIGURE 4

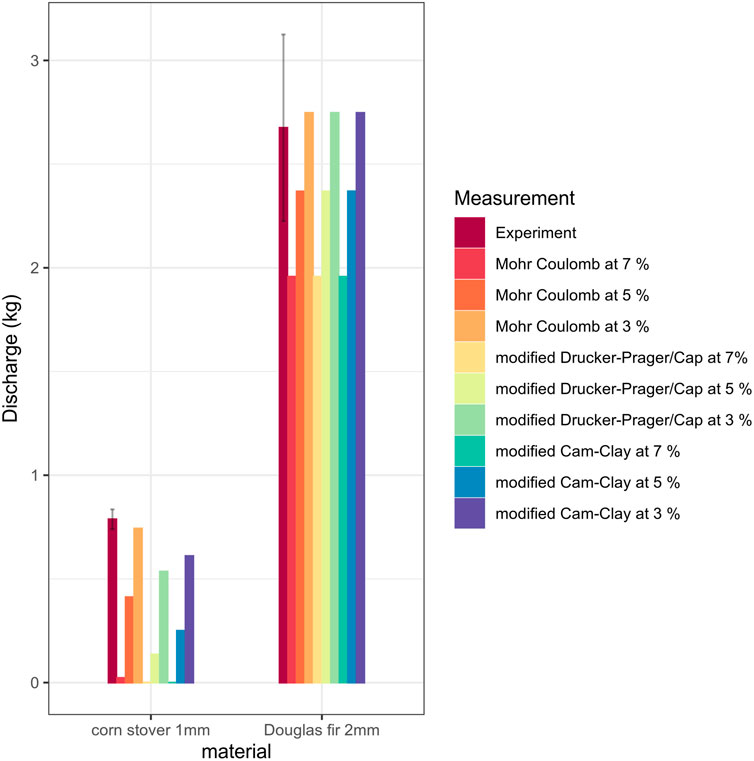
FIGURE 4. Comparison between experimental and predicted hopper discharge. Error bars of the experimental result represent standard deviations.

For corn stover, MC model resulted in the closest to the experimental observation, and mDPC model predicted the least amount of volume to be at the onset of flow. For Douglas fir, there were virtually no differences in the prediction between the three material models. This was thought to be because of the cohesionless flow characteristics of Douglas fir.

When comparing the prediction power of the finite element model, all material models and incipient flow criteria correctly predicted the cohesionless and mass flow of Douglas fir (c = 0, d = 0), and the cohesive and core flow of corn stover (c = 3.8 ± 3.5 kPa and d = 6.9 kPa). This observation suggests that the incipient flow prediction of a finite element hopper discharge model can be used as a tool for estimating the flow pattern of a gravity hopper.

From the comparison between experimental total discharge and predicted incipient flow volume of corn stover 2 mm and Douglas fir 1 mm, it is found that the incipient flow volume is a good predictor of the total discharge (correlation coefficient = 0.96). Considering the limited sample size of the experimental hopper flow (n = 3), the discharge rate was examined as an alternative metric.

Figure 4 shows the comparisons between the experimental observation and finite element model predictions of the total discharge of the biomass out of the hopper. Finite element model predictions were based on three criteria of the incipient flow, i.e., 3%, 5%, and 7% of axial deformation in the direction of gravity. The total discharge of Douglas fir was found to be significantly greater than the corn stover (p < 0.01, Wilcoxon test, n = 4).

Discharge rate

Discharge rate was experimentally measured with the hopper discharge experiments that were recorded with a time-stamped video recording. The weight of the total discharge of each test was divided by the duration of the total discharge time obtained from a video recording. For the computational modeling, the time required to reach the incipient flow was also obtained from the video recording by taking the timestamp of the first frame of visible biomass discharge. This duration was estimated to be the time interval between the start of the hopper gate opening and the onset of the biomass discharge. The experimental observation and computational predictions of the biomass discharge rates were compared (Figure 5).

FIGURE 5

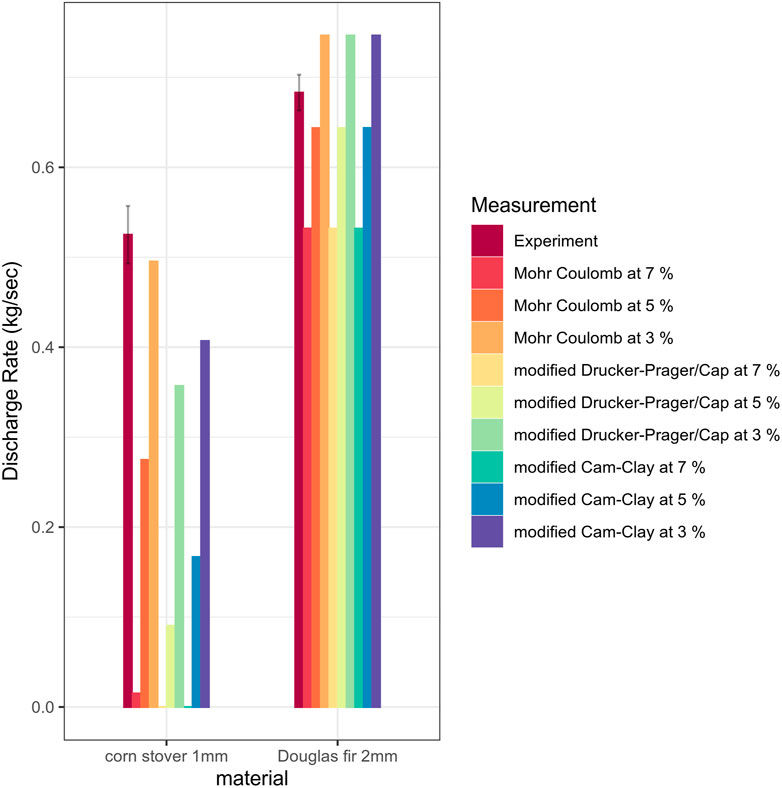
FIGURE 5. The comparison between experimental and predicted hopper discharge rate. Error bars of the experimental result represent standard deviations.

Similarly the total hopper discharge of biomass, the discharge rate of the corn stover 2 mm was found to be significantly less than Douglas fir 1 mm (p < 0.01, Wilcoxon test, n = 3). The discharge rate predicted with the 7% of axial strain was significantly smaller than the experimental results for all material models. At the same time, a relaxed axial strain criterion of 3.5% resulted in predictions closer to the experimental observation.

The discharge rate was slightly overestimated for Douglas fir when 3.5% was used as the criterion and slightly underestimated for corn stover when 5% was used as the criterion. This trend was consistent with all three material models with no noticeable differences for Douglas fir, whereas mDPC model resulted in the most conservative prediction and MC model resulted in the least conservative prediction for corn stover. The discharge rate of corn stover was underestimated by all three material models. Similar to the total discharge comparison, it was hypothesized that the difference in the discharge rate arose due to the material properties and the interaction between biomass and the handling device as further discussed in the ‘other discussions’ section.

Variability of bulk biomass flow prediction reflecting the variances of the parameters

It is well known that the large variability in mechanical properties of the milled biomass contributes significantly to unreliable handling operation. To engineer the biomass handling system, the magnitude of such a variability should be quantified. Descriptive statistics of the properties of milled biomass is a crucial starting point for this purpose. At the same time, the implication of the quantified variability in the biomass properties on the biomass handling operation should be also examined. Such an insight can be achieved via inferring the parameters of constitutive biomass flow models as discussed below.

For the three biomass flow models considered in this study, the Lamè parameters are commonly involved reflecting an isotropic elastic behavior before the deformation becomes plastic. Table 1 above lists the average and standard deviation of bulk modulus ($K$) and Poisson ratio ($\nu$) representing a Lamè parameter pair.

At the same time, the predicted hopper discharge fluctuated when the variation of bulk mechanical properties was considered. Tables 4, 5 list altered predictions of hopper discharge when the standard deviation of bulk modulus values was considered. When bulk modulus (K) increases from 463 kPa to 834 kPa, the predicted biomass discharge decreases from 0.208 kg to 0.006 kg for corn stover and from 0.602 to 0.0 with Mohr-Coulomb model. FE biomass flow model predictions with modified Drucker-Prager model and modified Cam-Clay model show the same trend for both corn stover and Douglas. This observation suggests that consideration of the variation will change the design target of biomass handling systems. For example, the upper bound value of bulk modulus (K + standard deviation) results in a smaller discharge prediction than a discharge predicted with a mean bulk modulus value (Table 4). When a hopper is designed with the upper bound of bulk modulus value, the actual discharge is expected to be larger and more reliable hopper performance. On the other hand, when a hopper is designed with the lower bound of bulk modulus value, the predicted discharge is an overestimation and the actual discharge will be smaller than expected, leading to an inadequate hopper performance.

TABLE 4

TABLE 4. Predicted corn stover 2 mm discharge in kg at different Elastic modulus at 3.5% axial strain as a failure criterion.

TABLE 5

TABLE 5. Predicted Douglas fir 1 mm discharge in kg at different Elastic modulus at 3.5% axial strain as a failure criterion.

Investigating the effect of the variability in the measurement of mechanical properties in this way can be expanded to other biomass flow material model parameters. In other words, by comparing calibrated model parameters, one can predict the flow characteristics of bulk biomass, such as MC model parameters (coefficient of cohesion and internal angle of friction). For mDPC and mCC model parameters, a chosen confidence intervals of respective regression analysis can be used for this purpose.

Parameters relevant to the quantitative flowability

As discussed before, the flowability of biomass should be quantified in conjunction with the geometry of and interaction between biomass and the handling equipment. Therefore, referring only to the properties of materials to describe the flowability is an incomplete description. Nonetheless, a relative flow tendency of a material is a useful information at an early stage of biomass handling system design.

Some of the intrinsic bulk mechanical properties of biomass can be inferred from parameters of constitutive biomass flow models. For MC model, the angle of internal friction ($\varphi$) represents the hardening tendency of biomass under the hydrostatic pressure or self-weight. A higher value for internal friction is associated with harder materials while a lower angle is associated with softer materials when they are subjected to a same magnitude of consolidation pressure. The $\varphi$ values of corn stover and Douglas fir were determined to be 34.3° ± 3.3° and 41.8° ± 1.0° with the fcCTT, respectively. The difference is significant ($p<0.01$, Wilcoxon test), i.e., this observation suggests that the hardening of bulk biomass can be an indicator of flowability.

The cohesion coefficient ($c$) represent the intrinsic cohesiveness of the bulk biomass and is related to the unconfined yield stress. The $c$ values of corn stover 2 mm and Douglas fir 1 mm were determined to be 3.8 ± 3.5 kPa and 0.4 ± 0.9 kPa with the fcCTT, respectively. The difference is significant ($p<0.01$, Wilcoxon test), and this observation also suggests that the cohesiveness of bulk biomass can be an indicator of flowability. It should be noted that the $c$ values of Douglas fir were found to be close to zero, and it suggests that Douglas fir will flow as a cohesionless material. Although cohesion coefficients represent the cohesion between biomass particles, it is also possible that Douglas fir may exhibit low friction between the bulk biomass and the wall of the hopper. Considering that the internal angle of friction ($\varphi$) of Douglas fir is larger than $\varphi$ of corn stover, it is reasonable to predict that Douglas fir will stiffen faster when compressed than corn stover, which will make it more difficult to flow. This reasoning leads to a hypothesis that the cohesion coefficient ($c$) rather than the internal angle of friction ($\varphi$) may control the initiation of the biomass flow.

For parameters of mDPC and mCC models determined with regression analysis using pooled data, i.e., $d,\beta ,\mathrm{a}\mathrm{n}\mathrm{d}M$, statistical test. Thus, there is no straightforward way to conduct statistical tests. However, some of mCC model parameters, including the compression index and elastic moduli, i.e., bulk modulus ($K$) and Poisson’s ratio ($\nu$), were determined directly from each triaxial test. Therefore, these parameters can be statistically tested. More specifically, the bulk modulus ($K$) can be determined with HTC data, and the shear modulus ($G$) can be determined with CTC data. Using these two values, the Lamè parameters, i.e., Young’s modulus ($E$) and Poisson’s ratio ($\nu$), can be determined.

For corn, stover, and Douglas fir, the bulk modulus ($K$) and shear modulus ($G$) were significantly different ($p<0.01$, Wilcoxon test), respectively. However, the compression index ($\lambda$) was not significantly different ($p=0.05$, Wilcoxon test). It is notable that both bulk modulus ($K$) and shear modulus ($G$) involve the shear resistance of the bulk material, whereas the compression index concerns the change in void spaces only. This observation implies that the different flow behavior of corn stover when it is compared to Douglas fir originates from the shear behavior.

On the other hand, the spring-back index ($\kappa$) of corn stover was significantly greater than Douglas fir ($p<0.01$, Wilcoxon test). Spring-back index also concerns the change in void spaces within the bulk material, but it measures the volumetric expansion upon the release of hydrostatic stress inside the biomass. This observation suggests that the volumetric expansion during the initiation of discharge out of a gravity hopper is more detrimental to reliable flow than the compression of stored biomass during the storage. This observation also explains the development of a core flow for the stover, in which the subsidiary region of the biomass volume establishing the onset of flow simultaneously develops a resistance to flow because of the larger degree of the volumetric expansion.

Other discussion

In the classical plasticity constitutive models employed in this study, the yield stress of bulk material is thought to indicate the onset of flow. However, milled biomass deformation becomes plastic as soon as a load is applied, even in hydrostatic compression. This observation indicates that milled biomass exhibits very low compressive yield stress. It is thought to behave so because the milled biomass under a slow loading condition behaves viscoelastically and the bulk modulus and strength of milled biomass keeps evolving due to continued creep and stress relaxation arising from the rearrangement and viscoelastic deformation of biomass particles. Therefore, the duration of triaxial tests is not long enough to capture the delayed consolidation and suggests a need to investigate time-dependent responses of biomass.

This behavior does not conform with the premises of constitutive models considered in this study because the yield of milled biomass is not solely due to the deviatoric stress. In other words, the onset of flow does not coincide with the compressive yield shear stress determined with a conventional triaxial compression test, in which the steady-state shear strain is measured in response to a compressive shear stress. Such a stress path does not allow determining compressive yield and tensile (extensive) shear failure. It is expected that a conventional ring shear test will aggravate such a discrepancy with confounding effect stemming from the unaccounted changes in the principal stress directions (Saraber et al., 1991). This observation suggests that the determination of shear failure represent the onset of a gravity flow requires different stress paths, such as reduced triaxial extension or conventional triaxial extension test (Desai and Siriwardane, 1984), which can be conducted with Forest Concept’s new Model CTT250-A01-100 biomass cubical triaxial tester (fcCTT).

It should also be noted that no distinct shear failure was observed for either corn stover 2 mm or Douglas fir 1 mm. ASTM standard and literature (Donaghe et al., 1988; ASTM Standard D7181, 2020) recommend the axial strain of 15% as an alternative axial strain when a test does not exhibit a distinct failure. However, it was observed that the excessive consolidation of bulk biomass induces a very large amount of volumetric compression leading to a limited dimension of the biomass sample not allowing the axial strain of 15%. This study found that the axial strain value should be smaller than 15% or previously reported 7% (Kamath and Puri, 1997). The corresponding values were used in determining model parameters as in Table 1 following Yi et al. (Yi et al., 2022). The examination of the finite element hopper flow model suggests that the axial strains of the onset of flow of corn stover and Douglas fir are as small as 3.5%. This finding calls for a further examination of the relationship between the magnitude of the axial strain of consolidated bulk biomass and the unconfined yield stress.

In addition, the hydrostatic compression test results suggest a significant anisotropic compression as well as nonlinear responses. However, most of the widely used biomass flow models, including the ones used in this study, assume an isotropic behavior. This discrepancy is thought to be a confounding factor of the reported study. The combination of the anisotropic and nonlinear behavior may induce the observed underestimation of the strength of biomass and thus leading to the overestimation of the biomass flow.

Conclusion

Biomass flowability is the result of interactions between the physical properties of bulk biomass and the handling equipment. Finite element analysis is a desirable modeling tool that can utilize a wide range of continuum bulk biomass flow models and incorporate diverse biomass handling equipment geometries.

For the calibration of biomass flow material models, Forest Concept’s new Model CTT250-A01-100 biomass cubical triaxial tester (fcCTT) was used to conduct fundamental triaxial tests to determine coefficients to use in continuum biomass flow models, i.e., Mohr-Coulomb (MC), modified Drucker-Prager/Cap (mDPC), and modified Cam-Clay models (mCC).

To enable testing of the effect of hopper geometry of the biomass handling device, a hopper with 45° wall angle with a 20 cm square opening was built and gravity hopper flow experiments were conducted using corn stover 2 mm and Douglas fir 1 mm at air-dried moisture contents. The onset of flow predicted by the finite element model was compared to the experimental hopper discharge of corn stover 2 mm and Douglas fir 1 mm with 3, 5, and 7% axial strain values as the incipient flow criteria. Both the total discharge and discharge rate indicate that 3% of axial strain is a more accurate predictor of the hopper flow. It is hypothesized that the observed small axial strain is enough to initiate the gravity hopper flow because of the high compressibility of bulk biomass. Also, it was discussed that the angle of internal friction and coefficient of cohesion of MC model, bulk modulus ($K$), shear modulus ($G$), and Spring-back index ($\kappa$) are significantly different at the of 95% confidence level for corn stover 2 mm and Douglas fir 1 mm bulk materials. These observations suggest that some of the fundamental mechanical properties of constitutive models can be used as relative flowability indicators.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

HY, CL, JD, and VP contributed to the conception and design of the study. CL and JD supervised material processing and triaxial tests. CL conducted the first stage triaxial test data processing. HY conducted the second stage triaxial test data process and determined parameters of the constitutive models of biomass flow. HY and VP contributed to experimental study and finite element modelling of gravity hopper flow. HY wrote the first draft of the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the Department of Energy under Grant DE-EE0008254 and partially supported by the USDA National Institute of Food and Agriculture Federal Appropriations under Project PEN04671 and Accession number 1017582.

Conflict of interest

Authors CL and JD were employed by the company Forest Concepts LLC.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2023.1162627/full#supplementary-material

References

ASTM Standard D4767 (2011). Test method for consolidated undrained triaxial compression test for cohesive soils. West Conshohocken, PA: ASTM International.

Google Scholar

ASTM Standard D7181 (2020). Test method for consolidated drained triaxial compression test for soils. West Conshohocken, PA: ASTM International.

Google Scholar

Bioenergy Technologies Office (2016). Biorefinery optimization workshop summary report. Chicago, IL: Department of Energy.

Google Scholar

Blackwood, T. (2019). Is particle science on solid ground? Available at:https://www.chemicalprocessing.com/articles/2020/is-particle-science-on-solid-ground/(Accessed December 12, 2019).

Google Scholar

Cheng, Z., Leal, J. H., Hartford, C. E., Carson, J. W., Donohoe, B. S., Craig, D. A., et al. (2021). Flow behavior characterization of biomass Feedstocks. Powder Technol. 387, 156–180. doi:10.1016/j.powtec.2021.04.004

CrossRef Full Text | Google Scholar

Coetzee, C. J. (2016). Calibration of the discrete element method and the effect of particle shape. Powder Technol. 297, 50–70. doi:10.1016/j.powtec.2016.04.003

CrossRef Full Text | Google Scholar

Dassault Systèmes (2017). AbaqusProvidence, RI: Dassault Systemes.

Google Scholar

Desai, C. S., and Siriwardane, H. J. (1984). Constitutive laws for engineering materials, with emphasis on geologic materials. Englewood Cliffs, N.J. Prentice-Hall.

Google Scholar

Dimaggio, F. L., and Sandler, I. S. (1971). Material model for granular soils. J. Eng. Mech. 97, 935–950. doi:10.1061/jmcea3.0001427

CrossRef Full Text | Google Scholar

Donaghe, R. T., Chaney, R. C., and Silver, M. L. (1988). “ASTM committee D-18 on soil and rock,” in Advanced triaxial testing of soil and rock, ASTM international, 100 barr harbor drive (West Conshohocken, PA: ASTM International).

Google Scholar

Drucker, D. C., and Prager, W. (1952). Soil mechanics and plastic analysis or limit design. Q. Appl. Math. 10, 157–165. doi:10.1090/qam/48291

CrossRef Full Text | Google Scholar

Elskamp, F., Kruggel-Emden, H., Hennig, M., and Teipel, U. (2017). A strategy to determine DEM parameters for spherical and non-spherical particles. Granul. Matter 19, 46. doi:10.1007/s10035-017-0710-0

CrossRef Full Text | Google Scholar

Fang, M., Yu, Z., Zhang, W., Cao, J., and Liu, W. (2022). Friction coefficient calibration of corn stalk particle mixtures using Plackett-Burman design and response surface methodology. Powder Technol. 396, 731–742. doi:10.1016/j.powtec.2021.10.040

CrossRef Full Text | Google Scholar

Ganesan, V., Rosentrater, K. A., and Muthukumarappan, K. (2008). Flowability and handling characteristics of bulk solids and powders – A review with implications for DDGS. Biosyst. Eng. 101, 425–435. doi:10.1016/j.biosystemseng.2008.09.008

CrossRef Full Text | Google Scholar

Gejdoš, M., Gergeľ, T., Jeřábek, K., and Hřebíček, Z. (2018). Optimization of transport logistics for forest biomass. Nase More 65, 246–249. doi:10.17818/NM/2018/4SI.15

CrossRef Full Text | Google Scholar

Geldart, D., Abdullah, E. C., Hassanpour, A., Nwoke, L. C., and Wouters, I. (2006). Characterization of powder flowability using measurement of angle of repose. China Particuology 4, 104–107. doi:10.1016/S1672-2515(07)60247-4

CrossRef Full Text | Google Scholar

Geuzaine, C., and Remacle, J.-F., (2009). Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities: The gmsh paper. Int. J. Numer. Methods Eng. 79, 1309–1331. doi:10.1002/nme.2579

CrossRef Full Text | Google Scholar

Gil, M., Arauzo, I., and Teruel, E. (2013). Influence of input biomass conditions and operational parameters on comminution of short-rotation forestry poplar and corn stover using neural networks. Energy fuels 27, 2649–2659. doi:10.1021/ef4000787

CrossRef Full Text | Google Scholar

Gil, M., Schott, D., Arauzo, I., and Teruel, E. (2013). Handling behavior of two milled biomass: SRF poplar and corn stover. Fuel Process. Technol. 112, 76–85. doi:10.1016/j.fuproc.2013.02.024

CrossRef Full Text | Google Scholar

Han, L. H., Elliott, J. A., Bentham, A. C., Mills, A., Amidon, G. E., and Hancock, B. C. (2008). A modified Drucker-Prager Cap model for die compaction simulation of pharmaceutical powders. Int. J. Solids Struct. 45, 3088–3106. doi:10.1016/j.ijsolstr.2008.01.024

CrossRef Full Text | Google Scholar

Heyman, J. (1997). Coulomb’s memoir on statics: An essay in the history of civil engineering. London, UK: University of Cambridge.

Google Scholar

Hinterreiter, S., Hartmann, H., and Turowski, P. (2012). Method for determining bridging properties of biomass fuels—Experimental and model approach. Biomass Conv. bioref. 2, 109–121. doi:10.1007/s13399-012-0033-7

CrossRef Full Text | Google Scholar

Hoshishima, C., Ohsaki, S., Nakamura, H., and Watano, S. (2021). Parameter calibration of discrete element method modelling for cohesive and non-spherical particles of powder. Powder Technol. 386, 199–208. doi:10.1016/j.powtec.2021.03.044

CrossRef Full Text | Google Scholar

Ittershagen, T., Schwedes, J., and Kwade, A. (2011). A new powder tester to investigate the anisotropic consolidation behaviour. Powder Technol. 211, 85–89. doi:10.1016/j.powtec.2011.03.038

CrossRef Full Text | Google Scholar

Janssen, R., and Verwijs, M. (2007). Why does the world need a true triaxial tester? Part. Part. Syst. Charact. 24, 108–112. doi:10.1002/ppsc.200601050

CrossRef Full Text | Google Scholar

Jenike, A. W. (1961). Gravity flow of bulk solids. Utah: Bulletin of the University of Utah, 322.

Google Scholar

Jenike, A. W. (1967). Quantitative design of mass-flow bins. Powder Technol. 1, 237–244. doi:10.1016/0032-5910(67)80042-1

CrossRef Full Text | Google Scholar

Jenike, A. W. (1964). Steady gravity flow of frictional-cohesive solids in converging channels. J. Appl. Mech. 31, 5–11. doi:10.1115/1.3629571

CrossRef Full Text | Google Scholar

Jenike, A. W. (1964). Storage and flow of solids. Utah: Bulletin of the University of Utah, 198.

Google Scholar

Jensen, P. D., Mattsson, J. E., Kofman, P. D., and Klausner, A. (2004). Tendency of wood fuels from whole trees, logging residues and roundwood to bridge over openings. Biomass Bioenergy 26, 107–113. doi:10.1016/s0961-9534(03)00101-6

CrossRef Full Text | Google Scholar

Jiang, J.-F., and Wu, Y.-F. (2012). Identification of material parameters for Drucker-Prager plasticity model for FRP confined circular concrete columns. Int. J. Solids Struct. 49, 445–456. doi:10.1016/j.ijsolstr.2011.10.002

CrossRef Full Text | Google Scholar

Jin, W., Klinger, J. L., Westover, T. L., and Huang, H. (2020). A density dependent Drucker-Prager/Cap model for ring shear simulation of ground loblolly pine. Powder Technol. 368, 45–58. doi:10.1016/j.powtec.2020.04.038

CrossRef Full Text | Google Scholar

Jin, W., Stickel, J. J., Xia, Y., and Klinger, J. (2020). A review of computational models for the flow of milled biomass Part II: Continuum-mechanics models. ACS Sustain. Chem. Eng. 8, 6157–6172. doi:10.1021/acssuschemeng.0c00412

CrossRef Full Text | Google Scholar

Kamath, S., and Puri, V. M. (1999). Finite element model development and validation for incipient flow analysis of cohesive powders from hopper bins. Powder Technol. 102, 184–193. doi:10.1016/S0032-5910(98)00192-2

CrossRef Full Text | Google Scholar

Kamath, S., and Puri, V. M. (1997). Measurement of powder flow constitutive model parameters using a cubical triaxial tester. Powder Technol. 90, 59–70. doi:10.1016/s0032-5910(96)03200-7

CrossRef Full Text | Google Scholar

Kenney, K. L., Smith, W. A., Gresham, G. L., and Westover, T. L. (2013). Understanding biomass feedstock variability. Biofuels 4, 111–127. doi:10.4155/bfs.12.83

CrossRef Full Text | Google Scholar

Krantz, M., Zhang, H., and Zhu, J. (2009). Characterization of powder flow: Static and dynamic testing. Powder Technol. 194, 239–245. doi:10.1016/j.powtec.2009.05.001

CrossRef Full Text | Google Scholar

Lu, Y., Jin, W., Klinger, J., Westover, T. L., and Dai, S. (2021). Flow characterization of compressible biomass particles using multiscale experiments and a hypoplastic model. Powder Technol. 383, 396–409. doi:10.1016/j.powtec.2021.01.027

CrossRef Full Text | Google Scholar

Lu, Y., Jin, W., Saha, N., Klinger, J. L., Xia, Y., and Dai, S. (2022). Wedge-shaped hopper design for milled woody biomass flow. ACS Sustain. Chem. Eng. 10, 16803–16813. doi:10.1021/acssuschemeng.2c05284

CrossRef Full Text | Google Scholar

Luis, R., and Martin John, B. (1985). Formulation of drucker-prager cap model. J. Eng. Mech. 111, 855–881. doi:10.1061/(asce)0733-9399(1985)111:7(855)

CrossRef Full Text | Google Scholar

Menetrey, Ph., and Willam, K. J. (1995). Triaxial failure criterion for concrete and its generalization. ACI Struct. J. 92. doi:10.14359/1132

CrossRef Full Text | Google Scholar

Miccio, F., Barletta, D., and Poletto, M. (2013). Flow properties and arching behavior of biomass particulate solids. Powder Technol. 235, 312–321. doi:10.1016/j.powtec.2012.10.047

CrossRef Full Text | Google Scholar

Miccio, F., Landi, A., Barletta, D., and Poletto, M. (2009). Preliminary assessment of a simple method for evaluating the flow properties of solid recovered fuels. Part. Sci. Technol. 27, 139–151. doi:10.1080/02726350902775988

CrossRef Full Text | Google Scholar

Pachón-Morales, J., Perré, P., Casalinho, J., Do, H., Schott, D., Puel, F., et al. (2020). Potential of DEM for investigation of non-consolidated flow of cohesive and elongated biomass particles. Adv. Powder Technol. 31, 1500–1515. doi:10.1016/j.apt.2020.01.023

CrossRef Full Text | Google Scholar

Paulrud, S., Mattsson, J. E., and Nilsson, C. (2002). Particle and handling characteristics of wood fuel powder: Effects of different mills. Fuel Process. Technol. 76, 23–39. doi:10.1016/S0378-3820(02)00008-5

CrossRef Full Text | Google Scholar

Perlack, R. D., Eaton, L. M., Turhollow, A. F., Langholtz, M. H., Brandt, C. C., Downing, M. E., et al. (2011). US billion-ton update: Biomass supply for a bioenergy and bioproducts industry. Available at: https://works.bepress.com/douglas_karlen/47/(Accessed July 3, 2016).

CrossRef Full Text | Google Scholar

Prescott, J. K., and Barnum, R. A. (2000). On powder flowability, Pharmaceutical Technology. Cleveland 24, 60–82.

Google Scholar

Salehi, H., Poletto, M., Barletta, D., and Larsson, S. H. (2019). Predicting the silo discharge behavior of wood chips - a choice of method. Biomass Bioenergy 120, 211–218. doi:10.1016/j.biombioe.2018.11.023

CrossRef Full Text | Google Scholar

Saraber, F., Enstad, G. G., and Haaker, G. (1991). Investigations on the anisotropic yield behaviour of a cohesive bulk solid. Powder Technol. 64, 183–190. doi:10.1016/0032-5910(91)80132-3

CrossRef Full Text | Google Scholar

Schofield, A., and Wroth, P. (1968). Critical state soil mechanics. London, UK: McGraw-Hill.

Google Scholar

Schwedes, J. (2003). Review on testers for measuring flow properties of bulk solids. Granul. Matter 5, 1–43. doi:10.1007/s10035-002-0124-4

CrossRef Full Text | Google Scholar

Shao, S., Wang, Q., Luo, A., and Shao, S. (2017). True triaxial apparatus with rigid-flexible-flexible boundary and remolded loess testing. J. Test. Eval. 45, 20150177. doi:10.1520/JTE20150177

CrossRef Full Text | Google Scholar

Shi, H., Mohanty, R., Chakravarty, S., Cabiscol, R., Morgeneyer, M., Zetzener, H., et al. (2018). Effect of particle size and cohesion on powder yielding and flow. KONA Powder Part. J. 35, 226–250. doi:10.14356/kona.2018014

CrossRef Full Text | Google Scholar

Soltanbeigi, B., Podlozhnyuk, A., Kloss, C., Pirker, S., Ooi, J. Y., and Papanicolopulos, S.-A. (2021). Influence of various DEM shape representation methods on packing and shearing of granular assemblies. Granul. Matter 23, 26. doi:10.1007/s10035-020-01078-y

CrossRef Full Text | Google Scholar

Szalwinski, C. M. (2017). On critical states, rupture states and interlocking strength of granular materials. Materials 10, 865. doi:10.3390/ma10080865

PubMed Abstract | CrossRef Full Text | Google Scholar

Tannous, K., Lam, P. S., Sokhansanj, S., and Grace, J. R. (2013). Physical properties for flow characterization of ground biomass from Douglas fir wood. Part. Sci. Technol. 31, 291–300. doi:10.1080/02726351.2012.732676

CrossRef Full Text | Google Scholar

Tripodi, M. A., Puri, V. M., Manbeck, H. B., and Messing, G. L. (1994). Triaxial testing of dry, cohesive powder and its application to a modified Cam-clay constitutive model. Powder Technol. 80, 35–43. doi:10.1016/0032-5910(94)02843-5

CrossRef Full Text | Google Scholar

Wang, Y., Yu, Y., Wu, Y., Zhang, B., Lv, H., and Sun, X. (2018). Development and application of a large-scale static and dynamic true triaxial apparatus for gravel. Int. J. Geomechanics 18, 04018004. doi:10.1061/(ASCE)GM.1943-5622.0001096

CrossRef Full Text | Google Scholar

Westover, T. L. (2014). FY14-Q1 1.2.1.3.ML.1 INL biomass feeding survey report. Idaho Falls: Idaho National Laboratory INL.

Google Scholar

Westover, T. L., and Hartley, D. S. (2018). “Biomass handling and feeding,” in Advances in Biofuels and bioenergy. Editors M. Nageswara-Rao, and J. R. Soneji (London, UK: InTech).

CrossRef Full Text | Google Scholar

Westover, T. L., Phanphanich, M., and Ryan, J. C. (2015). Comprehensive rheological characterization of chopped and ground switchgrass. Biofuels 6, 249–260. doi:10.1080/17597269.2015.1091189

CrossRef Full Text | Google Scholar

Williams, C. L., Westover, T. L., Emerson, R. M., Tumuluru, J. S., and Li, C. (2016). Sources of biomass feedstock variability and the potential impact on Biofuels production. Bioenergy Res. 9, 1–14. doi:10.1007/s12155-015-9694-y

CrossRef Full Text | Google Scholar

Yi, H., Lanning, C. J., Slosson, J. C., Wamsley, M. J., Puri, V. M., and Dooley, J. H. (2022). Determination of fundamental mechanical properties of biomass using the cubical triaxial tester to model biomass flow. Biofuels 0, 1–12. doi:10.1080/17597269.2022.2037816

CrossRef Full Text | Google Scholar