Multiple game trading strategy of multiple virtual power plants considering carbon trading

The large-scale access of distributed energy resources has a certain impact on the power grid, so distributed energy resources cannot participate in the power market transactions alone. The concept of the virtual power plant (VPP) has thus emerged, which can aggregate distributed power sources and controllable loads in a region for coordinated regulation. The trading of VPPs should not only consider the economy but also its degree of low carbon. Therefore, this paper constructs a unified bidding strategy for multi-VPPs that considers carbon–electricity integration trading. We design a multi-game trading strategy among multi-VPPs to achieve unified trading, after each VPP determines its internal trading strategy. Finally, through simulation, we verify that the multiple game strategy between multi-VPPs that considers carbon trading here proposed can effectively improve the efficiency and trading income of VPPs and promote the consumption of new energy.

1 Introduction

Due to the fluctuating power output and high uncertainty of each distributed energy source, direct participation in grid dispatch and power trading is not possible (Huang et al., 2019). VPP can aggregate generation and consumption units in the region to form a “self-generating and self-consuming” whole (Liu et al., 1109) which can be self-sufficient and conduct two-way power trading with external interests (Wang et al., 2022a). It can conduct direct trading between VPPs or choose to trade with the grid, reducing power supply pressure on the main network and ensuring that renewable energy can be consumed locally (Shayegan-Rad et al., 2017).

At present, research on the trading of individual VPP is relatively mature (Feng et al., 2018). Improving the uncertainty that the system will face in ensuring that VPPs can participate in the medium and long-term electricity market can improve its robustness. In the current electricity market environment, the number of subjects that can participate in electricity trading is gradually increasing, and the competition is more diversified. Therefore, the influence of the bidding strategies of other competitors amongst multi-VPPs must be considered (Zhi et al., 2021). Aggregated electric vehicles with dual characteristics of energy storage and load use market clearing to characterize the relationship between other VPPs and their own strategies and use non-cooperative game method to conduct day-ahead transactions.

Existing trading models for VPPs tend to focus only on economic benefits and ignore the additional environmental costs incurred in the generation of electricity by the internal units of VPPs, and on the process of purchasing electricity, which can inhibit the carbon reducing potential of VPPs. Some literature has also studied the low-carbon operation of VPPs (Chu et al., 2023). Some has considered the coordination and optimization of the environment and economy in a single VPP trading model and reducing pollution caused by VPP operations (Zhao et al., 2020). Other literature has considered the uncertainty faced by the power system and the impact of carbon emissions on the conservatism of VPP bidding, building a low-risk VPP bidding model to analyze the impact of carbon emissions (Liu et al., 2023). A VPP low-carbon economic dispatch has been proposed that accounts for the user electricity consumption behavior considering carbon trading (Huang et al., 2022). The impact of carbon consumption constraints on VPP participation in electricity market bidding has been considered; the results demonstrate that carbon emission constraints can change the bidding strategies of VPPs.

Considering these problems and challenges, this paper will limit the carbon utilization in VPP operations based on stepped carbon trading so as to improve renewable energy consumption. First, it establishes a multi-VPPs model consisting of wind turbines (WTs), photovoltaic power generation (PV), energy storage systems (ESSs), micro-turbines (MTs), and controllable loads (CL) to study how they participate in integrated carbon–electricity trading. In the trading process, each VPP should consider not only its own trading strategy but also the impact of other participants’ trading strategies on itself. This paper designs a multiple game mechanism for multi-VPPs and uses a distributed solution method to determine the final game equilibrium solution. Finally, by setting different scenarios, the accuracy and rationality of the proposed method are verified. The following principal contributions we make are:

1) A stepped carbon trading mechanism is introduced into the power trading system of VPPs to form integrated carbon–electricity trading of multi-VPPs, thus reducing the system’s carbon emissions. At the same time, the introduction of a ladder-type carbon emission transaction strategy can improve the level of clean energy consumption.

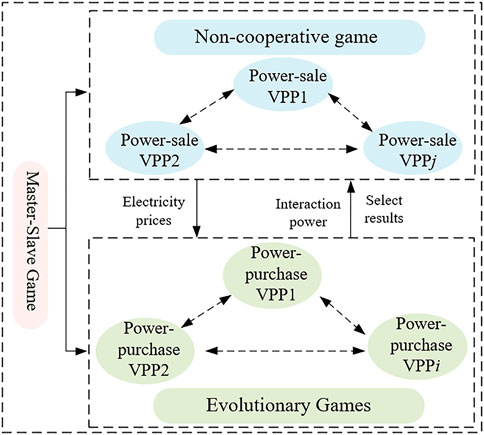
2) We propose a multiple game trading mechanism among multi-VPPs which no longer uses a one-game approach with unstable game equilibrium points, as in previous studies. Non-cooperative and evolutionary games are introduced in the framework of a master–slave game.

3) For coordinated optimization problems between multiple regions, the use of distributed solution algorithms can greatly accelerate the iteration speed and improve the solution’s efficiency.

This article is organized thus: Section 2 focuses on the integrated carbon–electricity trading market for VPPs; Section 3 introduces a proposed multiple game model; Section 4 is the solution method; Section 5 performs the simulation analysis; Section 6 draws conclusions.

2 Integrated carbon–electricity trading model

2.1 Virtual power plant operation structure analysis

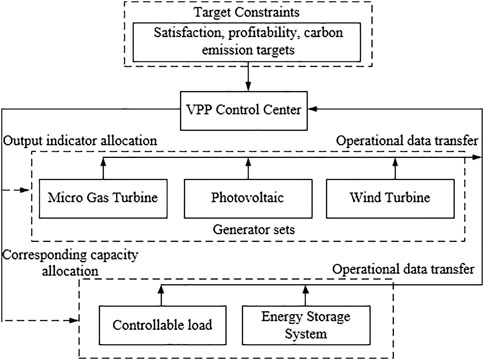
In traditional power systems, wind power, photovoltaic, and various types of loads participate independently in the market, and the grid lacks real-time awareness of each unit’s operating status (Li et al., 2020). The system cannot come to a unified dispatch and trading method due to distributed power resources, the power characteristics of differentiated loads, and the carbon emission level of each unit (Wang et al., 2022b). Building an integrated carbon–electricity market needs to rely on VPP to aggregate distributed energy, load, and energy storage systems in a certain region (Zhu et al., 2022). The structure of VPP operation is shown in Figure 1.

FIGURE 1

FIGURE 1. Operation structure of typical VPP.

At the data level, each unit in a VPP needs to report internal data to the VPP control center (Dou et al., 2022), which then allocates the output and load of each generator unit and the response capacity of ESS according to the constraints of current user satisfaction, income, carbon emissions, and other objectives.

2.2 Characterization of integrated carbon–electricity trading market

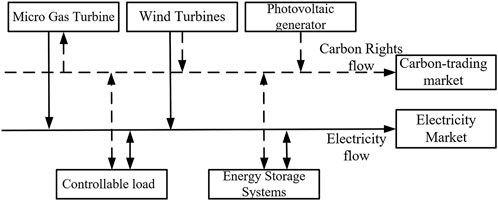
Carbon trading is the trading of carbon credits as commodities. It is crucial to measure and count the carbon credits and also to monitor their non-reuse. Carbon credits flow together with electricity trading, and the credits and corresponding benefits are transferred together with the electricity (Zhang et al., 2017). The flow of an integrated carbon–electricity transaction in a VPP is shown in Figure 2.

FIGURE 2

FIGURE 2. Integrated carbon–electricity trading volume.

The trading features are.

1) No carbon emission is generated while WT and PV operate, and the VPP centralized control center can allocate the corresponding carbon emission to MT or sell them to obtain additional economic benefits (Liu et al., 2021);

2) If VPP invokes CL for demand response in the dispatch, it needs to give corresponding carbon credits to users as economic compensation.

2.3 Calculation of VPP stepped carbon trading cost

Regulatory authorities will first allocate a certain amount of free carbon emissions to each carbon emission source and ensure that total amounts decrease annually (Liu, 2022). Each VPP will formulate and adjust the scheduling and bidding plan according to the allocated amount. Therefore, there are two situations in the process of carbon trading by VPPs (Chen et al., 2021b): the first is that the actual amount of carbon emissions generated in the VPP scheduling is more than the free quota allocated by the regulatory authority, so the VPP needs to pay for the excess in the market; in the second case, when the actual amount of carbon emissions generated in the VPP scheduling is less than the given free quota, the manufacturer can sell the remaining quota on the carbon trading market and obtain the corresponding income according to the current carbon trading price (Zhang et al., 2020).

Unlike the traditional carbon trading approach, a stepped carbon trading mechanism further motivates power producers to reduce emissions by linearizing the carbon price in segments. The cost of carbon emissions exceeding a certain amount of carbon quotas will be penalized according to the amount exceeded, thus prompting them to adjust their power generation strategies or introduce low-carbon technologies. The stepped carbon trading mentioned in this study principally comprises three parts: initial carbon emission quota, actual carbon emissions of operators, and carbon trading costs.

2.3.1 Initial carbon emission quota model

Generally speaking, the electricity purchased by a VPP from the external network comes from thermal units (Guotao et al., 2021). This makes two major sources of carbon emissions in the operation of VPP: MT and the electricity purchased from the external network. At present, China’s carbon trading policy is mainly based on the free quota of the actual power generation of the manufacturer, so the determination by the regulatory authority of the carbon emission quota of the VPP operator by two sources is expressed thus:

$\begin{array}{c}{\mathit{E}}_{\mathit{F}}={\mathit{\delta }}_{\mathbf{3}}{\displaystyle \sum _{\mathit{t}=\mathbf{1}}^{\mathit{T}}}\left({\mathit{P}}_{\mathit{t}}^{\mathit{P}\mathit{V}}∆\mathit{t}+{\mathit{P}}_{\mathit{t}}^{\mathit{W}\mathit{T}}∆\mathit{t}+{\mathit{P}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}\mathit{s}}∆\mathit{t}+{\mathit{P}}_{\mathit{t}}^{\mathit{M}\mathit{T}}∆\mathit{t}\right)\end{array}.(1)$

Here, T is the dispatch period; ${\mathit{P}}_{\mathit{t}}^{\mathit{P}\mathit{V}}$, ${\mathit{P}}_{\mathit{t}}^{\mathit{W}\mathit{T}}$, and ${\mathit{P}}_{\mathit{t}}^{\mathit{M}\mathit{T}}$ are the power output of the corresponding unit at time t; ${\mathit{E}}_{\mathit{F}}$ is the free carbon emission allowances for VPP operators set by the regulator; ${\mathit{\delta }}_{\mathbf{3}}$ is the carbon emission allowances of the production of per unit electricity; and ${\mathit{P}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}\mathit{s}}$ is the purchased power by the VPP from the main network at time t.

2.3.2 Actual carbon emissions model

According to the power network carbon emission calculation method, the actual carbon emissions generated by a VPP during the dispatch process are determined as

$\begin{array}{c}{\mathit{E}}_{\mathit{A}}={\displaystyle \sum _{\mathit{t}=\mathbf{1}}^{\mathit{T}}}{\mathit{\delta }}_{\mathbf{1}}{\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}\mathit{s}}+{\displaystyle \sum _{\mathit{t}=\mathbf{1}}^{\mathit{T}}}{\mathit{\delta }}_{\mathbf{2}}{\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{M}\mathit{T}}.\end{array}(2)$

Here, ${\mathit{E}}_{\mathit{A}}$ is the amout of actual carbon emission by the VPP; ${\mathit{\delta }}_{\mathbf{1}}$ and ${\mathit{\delta }}_{\mathbf{2}}$ are the carbon emission factor of per unit active output of thermal power units and MT, respectively.

2.3.3 Stepped carbon trading cost model

Compared with the traditional unified pricing mechanism, this paper adopts a stepped carbon trading pricing model to achieve further control carbon emission reduction. Under this mechanism, carbon emissions are divided into multiple intervals (Liu et al., 2022). For intervals with higher carbon emissions, the unit carbon emission price and the carbon compensation cost will be higher. The specific calculation formula is as follows:

$\begin{array}{c}{\mathit{C}}_{\mathit{T}}=\left\{\begin{array}{l}\mathit{\mu }\left({\mathit{E}}_{\mathit{A}}-{\mathit{E}}_{\mathit{F}}\right),{\mathit{E}}_{\mathit{A}}\le {\mathit{E}}_{\mathit{F}}+\mathit{l}\\ \mathit{\mu }\mathit{l}+\left(\mathbf{1}+\mathit{\alpha }\right)\mathit{\mu }\left({\mathit{E}}_{\mathit{A}}-{\mathit{E}}_{\mathit{F}}-\mathit{l}\right),{\mathit{E}}_{\mathit{F}}+\mathit{l}\le {\mathit{E}}_{\mathit{A}}\le {\mathit{E}}_{\mathit{F}}+\mathbf{2}\mathit{l}\\ \left(\mathbf{2}+\mathit{\alpha }\right)\mathit{\mu }\mathit{l}+\left(\mathbf{1}+\mathbf{2}\mathit{\alpha }\right)\mathit{\mu }\left({\mathit{E}}_{\mathit{A}}-{\mathit{E}}_{\mathit{F}}-\mathbf{2}\mathit{l}\right),{\mathit{E}}_{\mathit{F}}+\mathbf{2}\mathit{l}\le {\mathit{E}}_{\mathit{A}}\le {\mathit{E}}_{\mathit{F}}+\mathbf{3}\mathit{l}\\ \left(\mathbf{3}+\mathbf{3}\mathit{\alpha }\right)\mathit{\mu }\mathit{l}+\left(\mathbf{1}+\mathbf{3}\mathit{\alpha }\right)\mathit{\mu }\left({\mathit{E}}_{\mathit{A}}-{\mathit{E}}_{\mathit{F}}-\mathbf{3}\mathit{l}\right),{\mathit{E}}_{\mathit{F}}+\mathbf{3}\mathit{l}\le {\mathit{E}}_{\mathit{A}}\le {\mathit{E}}_{\mathit{F}}+\mathbf{4}\mathit{l}\\ \left(\mathbf{4}+\mathbf{6}\mathit{\alpha }\right)\mathit{\mu }\mathit{l}+\left(\mathbf{1}+\mathbf{4}\mathit{\alpha }\right)\mathit{\mu }\left({\mathit{E}}_{\mathit{A}}-{\mathit{E}}_{\mathit{F}}-\mathbf{4}\mathit{l}\right),{\mathit{E}}_{\mathit{A}}\ge {\mathit{E}}_{\mathit{F}}+\mathbf{4}\mathit{l}.\end{array}\right.\end{array}(3)$

Here, ${\mathit{C}}_{\mathit{T}}$ is the carbon trading cost to be paid by VPPs; $\mathit{\mu }$ is the market benchmark price of carbon emissions; l is the interval length of each carbon emission interval; and $\mathbf{\alpha }$ is the growth rate of the stepped carbon trading price.

2.4 Objective function

Costs include two items: VPP operating costs ${\mathit{f}}_{\mathit{k}}$ and carbon trading costs ${\mathit{C}}_{\mathit{T}}$.

$\begin{array}{c}{\mathit{F}}_{\mathit{k}}=\mathbf{min}\left({\mathit{f}}_{\mathit{k}}+{\mathit{C}}_{\mathit{T}}\right),\end{array}(4)$

$\begin{array}{c}{\mathit{f}}_{\mathit{k}}={\mathit{C}}_{\mathit{k}}^{\mathit{W}\mathit{T}}+{\mathit{C}}_{\mathit{k}}^{\mathit{P}\mathit{V}}+{\mathit{C}}_{\mathit{k}}^{\mathit{E}\mathit{S}\mathit{S}}+{\mathit{C}}_{\mathit{k}}^{\mathit{l}\mathit{d}}+{\mathit{C}}_{\mathit{k}}^{\mathit{M}\mathit{T}}+{\mathit{C}}_{\mathit{k}}^{\mathit{V}\mathit{P}\mathit{P}}+{\mathit{C}}_{\mathit{k}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}.\end{array}(5)$

Here, ${\mathit{C}}_{\mathit{k}}^{\mathit{W}\mathit{T}},{\mathit{C}}_{\mathit{k}}^{\mathit{P}\mathit{V}},{\mathit{C}}_{\mathit{k}}^{\mathit{E}\mathit{S}\mathit{S}},{\mathit{C}}_{\mathit{k}}^{\mathit{M}\mathit{T}}$, respectively, denote the operating costs of WT, PV, ESS, and MT in VPPk; ${\mathit{C}}_{\mathit{k}}^{\mathit{V}\mathit{P}\mathit{P}},{\mathit{C}}_{\mathit{k}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}}$ denote the direct power trading costs between VPPk and other VPPs, and between VPPk and the main grid; and ${\mathit{C}}_{\mathit{k}}^{\mathit{l}\mathit{d}}$ denotes the compensation cost of VPPk calling CL. Among these, the operation cost function of each unit is the same as that in the traditional way and will not be repeated.

2.5 Constraint condition

2.5.1 Power balance constraint

$\begin{array}{c}{\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{l}\mathit{d}}+{\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}\mathit{p}}={\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{W}\mathit{T}}+{\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{P}\mathit{V}}+{\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{E}\mathit{S}\mathit{S}}+{\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{M}\mathit{T}}{+\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}\mathit{s}}.\end{array}(6)$

Here, ${\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{l}\mathit{d}}$ is the load after VPPk scheduling optimization at moment t; ${\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{E}\mathit{S}\mathit{S}}$ is positive when the energy storage system is charging and negative when it is discharging; and ${\mathit{P}}_{\mathit{t}}^{\mathit{g}\mathit{r}\mathit{i}\mathit{d}\mathit{p}}$ is the power sold by VPP to the main network at time t.

2.5.2 Renewable energy output constraints

$\begin{array}{c}\left\{\begin{array}{l}{\mathbf{0}\le \mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{W}\mathit{T}}\le {\mathit{P}}_{\mathit{k}}^{\mathit{W}\mathit{T},\mathit{max}},\\ {\mathbf{0}\le \mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{P}\mathit{V}}\le {\mathit{P}}_{\mathit{k}}^{\mathit{P}\mathit{V},\mathit{max}}.\end{array}\right.\end{array}(7)$

Here, ${\mathit{P}}_{\mathit{k}}^{\mathit{W}\mathit{T},\mathit{max}}$ and ${\mathit{P}}_{\mathit{k}}^{\mathit{P}\mathit{V},\mathit{max}}$ are the upper limits of WT and PV output of VPPk, respectively.

2.5.3 Energy storage system constraints

For the ESS, its first priority is to meet the charging and discharging power without exceeding the limit:

$\begin{array}{c}{{\mathit{P}}_{\mathit{k}}^{\mathit{E}\mathit{S}\mathit{S},\mathit{min}}\le \mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{E}\mathit{S}\mathit{S}}\le {\mathit{P}}_{\mathit{k}}^{\mathit{E}\mathit{S}\mathit{S},\mathit{max}}.\end{array}(8)$

Here, ${\mathit{P}}_{\mathit{k}}^{\mathit{E}\mathit{S}\mathit{S},\mathit{min}}$ and ${\mathit{P}}_{\mathit{k}}^{\mathit{E}\mathit{S}\mathit{S},\mathit{max}}$ are the lower limit and upper limits of ESS power of VPPk, respectively.

The internal storage power of ESSk is

$\begin{array}{c}{{\mathit{S}\mathit{O}\mathit{C}}_{\mathit{k},\mathit{t}}={\mathit{S}\mathit{O}\mathit{C}}_{\mathit{k},\mathit{t}-\mathbf{1}}+{\mathit{\omega }}_{\mathit{c}}\left(\mathbf{1}-\mathit{b}\right)\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{E}\mathit{S}\mathit{S}}∆\mathit{t}+\frac{\mathbf{1}}{{\mathit{\omega }}_{\mathit{d}}}\mathit{b}{\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{E}\mathit{S}\mathit{S}}∆\mathit{t}.\end{array}(9)$

At the same time, its state of charge must also meet certain constraints:

$\begin{array}{c}\left\{\begin{array}{l}{\mathit{S}\mathit{O}\mathit{C}}_{\mathit{k},\mathbf{0}}={\mathit{S}\mathit{O}\mathit{C}}_{\mathit{k},\mathit{T}}\\ {{\mathit{S}\mathit{O}\mathit{C}}_{\mathit{k}}^{\mathit{min}}<\mathit{S}\mathit{O}\mathit{C}}_{\mathit{k},\mathit{t}}^{\mathit{E}\mathit{S}\mathit{S}}\le {\mathit{S}\mathit{O}\mathit{C}}_{\mathit{k}}^{\mathit{max}}.\end{array}\right.\end{array}(10)$

Here, ${\mathit{\omega }}_{\mathit{c}}$ and ${\mathit{\omega }}_{\mathit{d}}$ denote the charging and discharging efficiency of the ESS, respectively; b denotes charging and discharging state: 0 when charging, 1 when discharging; and ${\mathit{S}\mathit{O}\mathit{C}}_{\mathit{k},\mathbf{0}}\mathit{a}\mathit{n}\mathit{d}{\mathit{S}\mathit{O}\mathit{C}}_{\mathit{k},\mathit{T}}$ denote the initial and termination power of the ESS in one dispatching cycle, respectively.

2.5.4 Interaction power constraint

This equation includes direct interactive power constraints between VPPs and interactive power constraints between VPPs and the grid:

$\begin{array}{c}\left\{\begin{array}{l}{-{\mathbf{P}}_{\mathbf{k}}^{\mathbf{V}\mathbf{P}\mathbf{P},\mathbf{max}}\le \mathbf{P}}_{\mathbf{k},\mathbf{t}}^{\mathbf{V}\mathbf{P}\mathbf{P}}\le {\mathbf{P}}_{\mathbf{k}}^{\mathbf{V}\mathbf{P}\mathbf{P},\mathbf{max}}\\ {\mathbf{0}\le \mathbf{P}}_{\mathbf{k},\mathbf{t}}^{\mathbf{g}\mathbf{r}\mathbf{i}\mathbf{d}\mathbf{p}}\le {\mathbf{P}}_{\mathbf{max}}^{\mathbf{g}\mathbf{r}\mathbf{i}\mathbf{d}}\\ {\mathbf{0}\le \mathbf{P}}_{\mathbf{k},\mathbf{t}}^{\mathbf{g}\mathbf{r}\mathbf{i}\mathbf{d}\mathbf{s}}\le {\mathbf{P}}_{\mathbf{max}}^{\mathbf{g}\mathbf{r}\mathbf{i}\mathbf{d}\mathbf{s}}.\end{array}\right.\end{array}(11)$

2.5.5 MT output and climbing constraint

$\begin{array}{c}\mathbf{0}\le {\mathit{e}}_{\mathit{M}\mathit{T}}^{\mathit{t}}\le {\mathit{P}}_{\mathit{M}\mathit{T}}^{\mathit{max}},\end{array}(12)$

$\begin{array}{c}{\mathit{P}}_{\mathit{M}\mathit{T}}^{\mathit{d}\mathit{o}\mathit{w}\mathit{n}}\le \left|{\mathit{e}}_{\mathit{M}\mathit{T}}^{\mathit{t}}-{\mathit{e}}_{\mathit{M}\mathit{T}}^{\mathit{t}-\mathbf{1}}\right|\le {\mathit{P}}_{\mathit{M}\mathit{T}}^{\mathit{u}\mathit{p}}.\end{array}(13)$

Here, ${\mathit{P}}_{\mathit{M}\mathit{T}}^{\mathit{max}}$, ${\mathit{P}}_{\mathit{M}\mathit{T}}^{\mathit{min}}$ are the upper and lower limits of MT unit output, respectively; ${\mathit{P}}_{\mathit{M}\mathit{T}}^{\mathit{d}\mathit{o}\mathit{w}\mathit{n}}$, ${\mathit{P}}_{\mathit{M}\mathit{T}}^{\mathit{d}\mathit{o}\mathit{w}\mathit{n}}$ are the downward and upward climbing power of the MT unit, respectively.

3 Multi-game model for multi-VPPs

Based on the optimal results of each VPP in the first stage, the supply–demand ratio (SDR) coefficient is introduced to distinguish between power-sale VPP and power-purchase VPP.

$\begin{array}{c}{\mathit{S}\mathit{D}\mathit{R}}_{\mathit{k},\mathit{t}}=\frac{{\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{S}}}{{\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{D}}},\end{array}(14)$

$\begin{array}{c}{\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{S}}={\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{G}}+{\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{E}\mathit{S}\mathit{S}}+{\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{M}\mathit{T}}.\end{array}(15)$

Here, ${\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{S}}$ is the electricity supply of VPPk in time period t; ${\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{D}}$ is the whole electricity demand of VPPk in time period t; and ${\mathit{P}}_{\mathit{k},\mathit{t}}^{\mathit{G}}$ is the renewable energy output of VPPk in time period t; during period t: if ${\mathit{S}\mathit{D}\mathit{R}}_{\mathit{k},\mathit{t}}<\mathbf{1}$, define the VPPk as power-purchase VPP, if ${\mathit{S}\mathit{D}\mathit{R}}_{\mathit{k},\mathit{t}}>\mathbf{1}$, define the VPPk as power-sale VPP.

3.1 VPP utility function

3.1.1 Power-sale VPP utility function

The power-sale VPP obtains economic benefits by selling excess power to the load side and the power-purchase VPP, whose utility function can be expressed as

$\begin{array}{c}{\mathit{U}}_{\mathit{j},\mathit{t}}^{\mathit{s}}={\mathit{\alpha }}_{\mathit{j},\mathit{t}}{\mathit{P}}_{\mathit{j},\mathit{t}}^{\mathit{l}\mathit{d}}-\frac{{\mathit{\beta }}_{\mathit{t}}}{\mathbf{2}}{\left({\mathit{P}}_{\mathit{j},\mathit{t}}^{\mathit{l}\mathit{d}}\right)}^{\mathbf{2}}+{\mathit{\gamma }}_{\mathit{j},\mathit{t}}{\mathit{P}}_{\mathit{j},\mathit{t}}^{\mathit{V}\mathit{P}\mathit{P}}.\end{array}(16)$

Here, ${\mathit{\alpha }}_{\mathit{j},\mathit{t}}$ is the satisfaction coefficient of the demand side of the power-sale VPP; ${\mathit{\gamma }}_{\mathit{j},\mathit{t}}$ is the power trading strategy of the power-sale VPP—electricity price in t period; and ${\mathit{P}}_{\mathit{j},\mathit{t}}^{\mathit{V}\mathit{P}\mathit{P}}$ is the interactive electricity of VPPj participating in VPP direct trading.

3.1.2 Power-purchase VPP utility function

The internal power supply of the power-purchase VPP is insufficient to meet its own internal demand, so it needs to purchase the corresponding demand from the power-sale VPP. The utility function of the power-purchase VPPi choosing the power-sale VPPj to purchase power at time t can be expressed as

$\begin{array}{c}{\mathit{U}}_{\mathit{i}\mathit{j},\mathit{t}}^{\mathit{s}}={\mathit{\alpha }}_{\mathit{i},\mathit{t}}{\mathit{P}}_{\mathit{i},\mathit{t}}^{\mathit{l}\mathit{d}}-\frac{{\mathit{\beta }}_{\mathit{t}}}{\mathbf{2}}{\left({\mathit{P}}_{\mathit{i},\mathit{t}}^{\mathit{l}\mathit{d}}\right)}^{\mathbf{2}}-{\mathit{\gamma }}_{\mathit{j},\mathit{t}}{\mathit{P}}_{\mathit{i},\mathit{t}}^{\mathit{V}\mathit{P}\mathit{P}}.\end{array}(17)$

Here, ${\mathit{\alpha }}_{\mathit{i},\mathit{t}}$ is the satisfaction coefficient on the demand side of the power-purchase VPP.

3.2 The evolutionary game between power-purchase VPP

After comprehensive evaluation of its electricity price information, the power-purchase VPP selects the best source for electricity trading. Power-purchase VPPs must constantly adjust their selection strategies to form an evolutionary game, which takes the following form.

The selection strategy of a power-purchase VPP at the time of power purchase can be expressed by the probability ${\mathit{r}}_{\mathit{j},\mathit{t}}\left(\mathbf{0}{\le \mathit{r}}_{\mathit{j},\mathit{t}}\le \mathbf{1},{\displaystyle \sum _{\mathit{j}=\mathbf{1}}^{\mathit{J}}}{\mathit{r}}_{\mathit{j},\mathit{t}}=\mathbf{1}\right)$ of power-purchase VPPi choosing power-sale VPPj to purchase power at time t. The ultimate goal is to maximize the utility function of power-purchase VPPi.

In the evolution process, a correction factor ${\mathit{\nu }}_{\mathit{m},\mathit{j}}\left({\mathit{U}}_{\mathit{i},\mathit{t}}^{\mathit{P}}\right)$ is introduced to denote the proportion of power-purchase VPPi shifted from the selection of power-sale VPPm to power-sale VPPj in time period t. The modified protocol of the dynamic evolutionary game can be formulated as

$\begin{array}{c}{\mathit{\nu }}_{\mathit{m},\mathit{j}}\left({\mathit{U}}_{\mathit{i},\mathit{t}}^{\mathit{P}}\right)=\frac{\mathit{exp}\left({\mathit{U}}_{\mathit{i},\mathit{j},\mathit{t}}^{\mathit{P}}\right)}{{\displaystyle \sum _{\mathit{m}=\mathbf{1}}^{\mathit{J}}}\mathit{exp}\left({\mathit{U}}_{\mathit{i},\mathit{m},\mathit{t}}^{\mathit{P}}\right)}.\end{array}(18)$

The dynamic evolution equation of power-purchase VPP is

$\begin{array}{c}\frac{\partial {\mathit{r}}_{\mathit{j},\mathit{t}}}{\partial \mathit{t}}=\frac{\mathit{exp}\left({\mathit{U}}_{\mathit{i},\mathit{j},\mathit{t}}^{\mathit{P}}\right)}{{\displaystyle \sum _{\mathit{m}=\mathbf{1}}^{\mathit{J}}}\mathit{exp}\left({\mathit{U}}_{\mathit{i},\mathit{m},\mathit{t}}^{\mathit{P}}\right)}-{\mathit{r}}_{\mathit{j},\mathit{t}}={\mathit{\nu }}_{\mathit{m},\mathit{j}}\left({\mathit{U}}_{\mathit{i},\mathit{t}}^{\mathit{P}}\right)-{\mathit{r}}_{\mathit{j},\mathit{t}}.\end{array}(19)$

The power-purchase VPP group reaches evolutionary equilibrium when $\frac{\partial {\mathit{r}}_{\mathit{j},\mathit{t}}}{\partial \mathit{t}}=\mathbf{0}$; that is, ${\mathit{\nu }}_{\mathit{m},\mathit{j}}\left({\mathit{U}}_{\mathit{i},\mathit{t}}^{\mathit{P}}\right)-{\mathit{r}}_{\mathit{j},\mathit{t}}=0$.

3.3 The non-cooperative game among power-sale VPPs

When the trading between the power-sale VPP and the power-purchasing VPP begins, the utility of each power-sale VPP depends not only on its own reported trading strategy and the power-purchasing VPP’s selection strategy but also on the published electricity prices of other power-sale VPPs—the process of publishing electricity selling prices by the power-sale VPP can be described by the non-cooperative game model.

The power-sale VPP chooses the power sales price ${\mathit{\gamma }}_{\mathit{j},\mathit{t}}$ at time t as its game strategy when playing the power sales game, with the final goal of optimizing the utility function of the power-sale VPPj. From Eq. 17, the optimal purchased electricity for power-purchase VPPi in time period t is

$\begin{array}{c}{\mathit{P}}_{\mathit{i}\mathit{j},\mathit{t}}=\frac{{\mathit{\alpha }}_{\mathit{i},\mathit{t}}-{\mathit{\gamma }}_{\mathit{i},\mathit{t}}}{{\mathit{\beta }}_{\mathit{t}}}.\end{array}(20)$

The total amount of electricity purchased by power-purchase VPPi from power-sale VPPj in time period t is

$\begin{array}{c}{\mathit{Q}}_{\mathit{j},\mathit{t}}={\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{I}}}{\mathit{r}}_{\mathit{j},\mathit{t}}{\mathit{P}}_{\mathit{i}\mathit{j},\mathit{t}}.\end{array}(21)$

Therefore, the utility function of the power-sale VPP can be expressed as

$\begin{array}{c}{\mathit{U}}_{\mathit{j},\mathit{t}}^{\mathit{s}}=\left\{\begin{array}{l}{\mathit{\alpha }}_{\mathit{i},\mathit{t}}{\mathit{P}}_{\mathit{j},\mathit{t}}^{\mathit{s}\mathit{l}\mathit{d}}-\frac{{\mathit{\beta }}_{\mathit{t}}}{\mathbf{2}}{\left({\mathit{P}}_{\mathit{j},\mathit{t}}^{\mathit{s}\mathit{l}\mathit{d}}\right)}^{\mathbf{2}}+{\mathit{\gamma }}_{\mathit{j},\mathit{t}}{\mathit{P}}_{\mathit{i}\mathit{j},\mathit{t}},{\mathit{P}}_{\mathit{i}\mathit{j},\mathit{t}}\le {\mathit{Q}}_{\mathit{j},\mathit{t}},\\ {\mathit{\alpha }}_{\mathit{i},\mathit{t}}{\mathit{P}}_{\mathit{j},\mathit{t}}^{\mathit{s}\mathit{l}\mathit{d}}-\frac{{\mathit{\beta }}_{\mathit{t}}}{\mathbf{2}}{\left({\mathit{P}}_{\mathit{j},\mathit{t}}^{\mathit{s}\mathit{l}\mathit{d}}\right)}^{\mathbf{2}}+{\mathit{\gamma }}_{\mathit{j},\mathit{t}}{\mathit{r}}_{\mathit{j},\mathit{t}}{\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{I}}}\frac{{\mathit{\alpha }}_{\mathit{i},\mathit{t}}-{\mathit{\gamma }}_{\mathit{i},\mathit{t}}}{{\mathit{\beta }}_{\mathit{t}}},{\mathit{P}}_{\mathit{i}\mathit{j},\mathit{t}}>{\mathit{Q}}_{\mathit{j},\mathit{t}.}\end{array}\right.\end{array}(22)$

In the process of the game, each VPP changes its pricing strategy according to the aforementioned utility function until the utility is optimal; the game reaches equilibrium when all power-sale VPPs cannot benefit from changing their strategies.

3.4 The master–slave game between power-sale VPP and power-purchase VPP

Figure 3 shows the overall game framework for multi-VPPs. The power-sale VPP changes its pricing according to the market situation, so as to guide the power-purchase VPP to make trading choices and feed them back to the power-sale VPP, which updates its pricing according to its latest utility function and the power-purchasing VPP’s strategy, thus ultimately maximizing the benefits of both parties. In this case, there is a certain sequence of participants in the electricity market when making corresponding decisions, and this behavior can be described by a follower–leader game model, with the power-sale VPP as the leader and the power-purchase VPP as the follower.

FIGURE 3

FIGURE 3. Game structure diagram of multi-VPP system.

Both the power-purchase VPP and the power-sale VPP need to participate in the follower–leader game, and the strategy sets of both are still the power sale price of the power sale-VPP and the power purchase choice state of the power-purchase VPP. The objective of the game is still to optimize the utility function of both players.

The strategy set of the leader power-sale VPP can be expressed as

$\begin{array}{c}{\mathit{\gamma }}_{\mathit{j}}=\left[{\mathit{\gamma }}_{\mathit{j},\mathbf{1}},{\mathit{\gamma }}_{\mathit{j},\mathbf{2}},\dots ,{\mathit{\gamma }}_{\mathit{j},\mathit{t}},\dots ,{\mathit{\gamma }}_{\mathit{j},\mathit{T}}\right].\end{array}(23)$

Here, ${\mathit{\gamma }}_{\mathit{j}}$ is the vector of electricity price strategies published by the power-sale VPPj.

The strategy set of the follower power-purchase VPP can be expressed as

$\begin{array}{c}{\mathit{r}}_{\mathit{i}}=\left[{\mathit{r}}_{\mathit{j},\mathbf{1}},{\mathit{r}}_{\mathit{j},\mathbf{2}},\dots ,{\mathit{r}}_{\mathit{j},\mathit{t}},\dots ,{\mathit{r}}_{\mathit{j},\mathit{T}}\right].\end{array}(24)$

Here, ${\mathit{r}}_{\mathit{i}}$ is the probability vector that power-purchase VPPi chooses power-sale VPPj.

The objective of the master–slave game model is to optimize the utility of both the power-sale VPP and the power-purchase VPP. After the power-sale VPP releases selling price information ${\mathit{\gamma }}_{\mathit{j}}$, the power-purchase VPP can find an equilibrium strategy to optimize its own utility, which is expressed by ${\mathit{r}}_{\mathit{i}}^{*}$, and feed it back to the power-sale VPP. The power-sale VPP determines its optimal electricity price strategy set ${\mathit{\gamma }}_{\mathit{j}}^{*}$ according to its own utility function and the optimal response strategy of the power-purchase VPP, so the Nash equilibrium solution of this master–slave game can be expressed by (${\mathit{\gamma }}_{\mathit{j}}^{*},{\mathit{r}}_{\mathit{i}}^{*}$).

4 Multiple game solving process

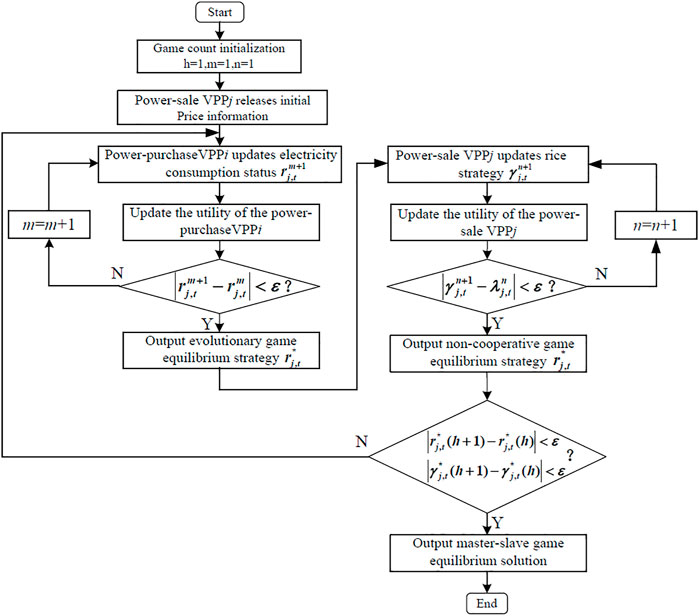
For the proposed multiple game model, this paper adopts a parallel distributed solution method; the solution process is shown in Figure 4.

FIGURE 4

FIGURE 4. Flowchart of multiple game solution.

Step 1. As the leader of the master–slave game, the power-sale VPP first transmits initial price information to the follower power-purchase VPP.

Step 2. The power-purchase VPP makes decisions on its own power purchasing selection status according to the leader’s strategy and continuously updates it until the evolutionary game reaches equilibrium to obtain its optimal utility. The evolutionary game equilibrium solution is solved as follows:

1) Power-purchase VPPi selects a power-sale VPP according to the leader’s strategy and calculates the optimal power purchase and power consumption utility of the power-purchase VPP according to Eq. 20 and Eq. 17, respectively.

2) Discretize Eq. 19 as follows:

$\begin{array}{c}{\mathit{r}}_{\mathit{j},\mathit{t}}^{\mathit{m}+\mathbf{1}}={\mathit{r}}_{\mathit{j},\mathit{t}}^{\mathit{m}}+{\mathit{\tau }}_{\mathbf{1}}\left[{\mathit{\nu }}_{\mathit{m},\mathit{j}}\left({\mathit{U}}_{\mathit{i},\mathit{t}}^{\mathit{P}}\right)-{\mathit{r}}_{\mathit{j},\mathit{t}}^{\mathit{m}}\right].\end{array}(25)$

Here, m is the number of iterations of the evolutionary game; ${\mathit{\tau }}_{\mathbf{1}}$ is the iteration step size.The power-purchase VPP updates the power purchase status by Eq. 25;3) Judge whether the power purchase strategy reaches the evolutionary equilibrium. If it reaches equilibrium state, go to Step 3, otherwise return to 1); Step 3: According to the results of Step 2, each power-sale VPP obtains the optimal power selling price through a non-cooperative game. The non-cooperative game solving process is as follows:

1) Calculate the total amount of power purchased by power-purchase VPPi from power-sale VPPj and the own utility of power-sale VPPj in time period t according to Eqs 21, 22.

2) The power-sale VPPj updates its own price strategy through Eq. 26.

$\begin{array}{c}{\mathit{\gamma }}_{\mathit{j},\mathit{t}}^{\mathit{n}+\mathbf{1}}={\mathit{\gamma }}_{\mathit{j},\mathit{t}}^{\mathit{n}}+{\mathit{\tau }}_{\mathbf{2}}\left({\mathit{Q}}_{\mathit{j},\mathit{t}}^{\mathit{n}}-{\mathit{P}}_{\mathit{i}\mathit{j},\mathit{t}}\right)\end{array}.(26)$

Here, n is the number of iterations of the non-cooperative game; ${\mathit{\tau }}_{\mathbf{2}}$ is the iteration step size.3) Judge whether the power-sale VPP strategy reaches equilibrium. If it reaches equilibrium state, go to Step 4, otherwise return to 1); Step 4: Judge whether the system master–slave game reaches equilibrium. If so, stop the iterative solution and output the result, otherwise return to Step 2.

5 Case studies

5.1 Basic data

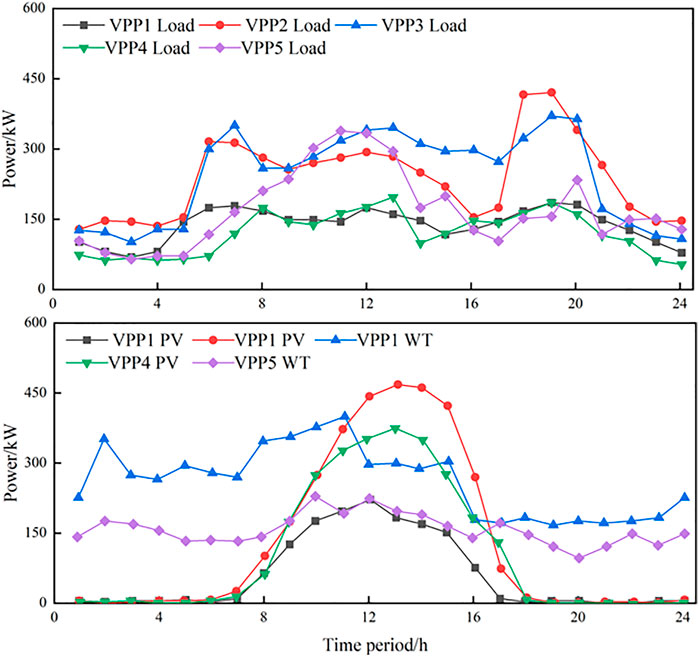
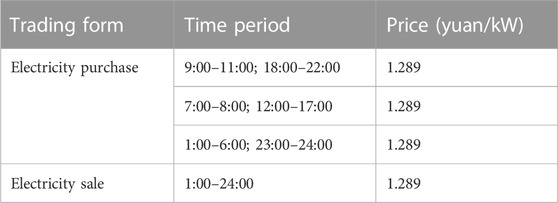
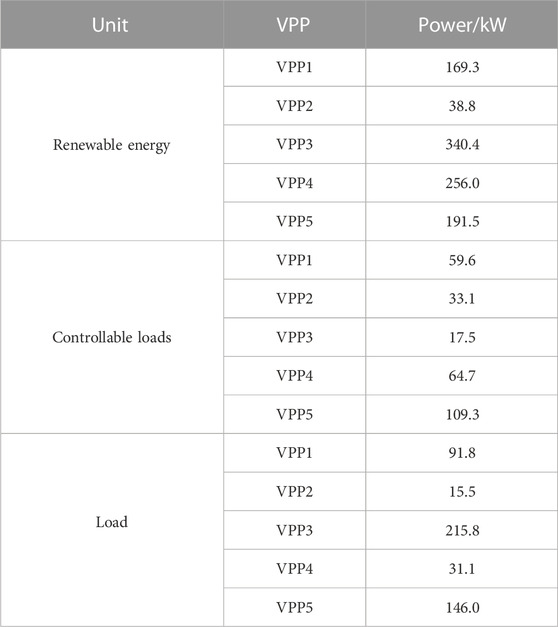
In this paper, we established a multi-VPPs system consisting of five VPPs. The total output of WT and PV in each VPP, load situation, and the unit purchase price of electricity from the VPP to the main network is shown in Figure 5. The price range of VPP electricity sales specified by the electricity sales market is [0.3,1.2]; the price of electricity trading from VPP to main grid is shown in Table 1. In the stepped carbon trading model, μ is set at 280 yuan/t, l is set at 2t, and α is set at 25%.

FIGURE 5

FIGURE 5. Forecasting curves of renewable energy output and load demand.

TABLE 1

TABLE 1. Electricity purchase and sale price from VPP to main network.

5.2 Model simulation results

In order to verify the effectiveness of the stepped-type carbon trading model designed in this paper in the operation of VPP, we set up four different models. Model 1 is the traditional carbon trading model in which the carbon trading range is not divided, and the CO₂ exceeding the carbon emission quota is directly settled at the initial carbon trading price. Model 2 is still the traditional carbon trading model, but the benchmark price is set at 320 yuan/t. Model 3 is a stepped carbon trading model without considering the carbon emission cost. In the objective function, only the operating costs and power purchase costs of each unit in the VPP are considered. Model 4 comprehensively considers the stepped carbon emission cost and VPP operation cost for economic and low-carbon enhancement. Taking VPP1 as an example, the operation results of these four scenarios are shown in Table 2.

TABLE 2

TABLE 2. Operation results of these four scenarios of VPP1.

Model 1 has the lowest total cost among the four models because it adopts the traditional carbon trading mechanism with a uniform benchmark price for carbon emissions; however, its energy saving and emission reduction potential is not fully exploited, and there is a certain amount of new energy output within the VPP that cannot be absorbed. In Model 2, since the benchmark price is no longer used for carbon emissions, the total cost of the VPP increases significantly. Although the unit operation cost of Model 3 is the lowest of the four models, huge amounts of CO₂ are emitted because carbon transaction costs are not considered in the scheduling process which require VPP operators to pay high carbon emission costs. After Model 4 divides the carbon emission range, the carbon emission of VPP is significantly reduced compared with the traditional model.

According to the operational comparison of models 1 and 4 in Table 2, the carbon emission cost increases after adopting the stepped carbon trading scheduling strategy, but the carbon emission decreases by 1,206.7 kg. This is because the carbon emission interval is strictly divided after adopting the stepped carbon trading model. With the gradual increase in carbon emissions, the carbon emission price faced by VPP operators will increase exponentially, greatly limiting the call of carbon sources. Although the total cost is slightly higher for VPP operators, it promotes the absorption of internal “abandoned wind and light” and generally achieves the goal of low-carbon economic operation.

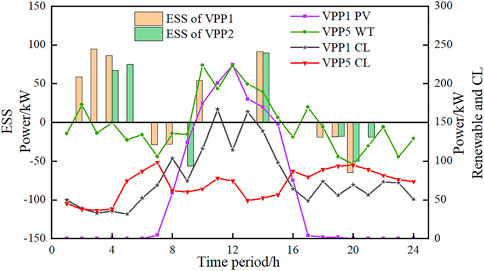
We can take VPP1 (PV) and VPP5 (WT) as examples to draw the day-ahead resource scheduling curve as shown in Figure 6. From the internal supply and demand relationship of each VPP in each period, the required external interactive power can be obtained, thus introducing the trading strategy proposed in this paper.

FIGURE 6

FIGURE 6. Day-ahead dispatching results.

In Figure 6, the PV output of VPP1 shows a peak trend during the time of high light intensity (7–17), and the demand response call is less then; VPP5, which is dominated by wind power output, charges during the time of low load demand and peak wind power output at night, and its energy storage system charges for three periods in 24 h per day. Thus, the VPP energy storage system, while meeting its own load demand through charging, sells excess power to other VPPs to promote the balance between the supply and demand of the system and improve the system's overall economic effectiveness.

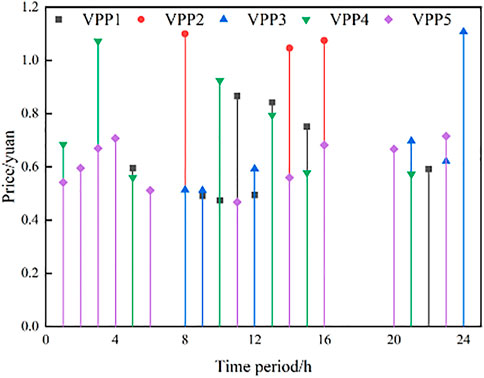
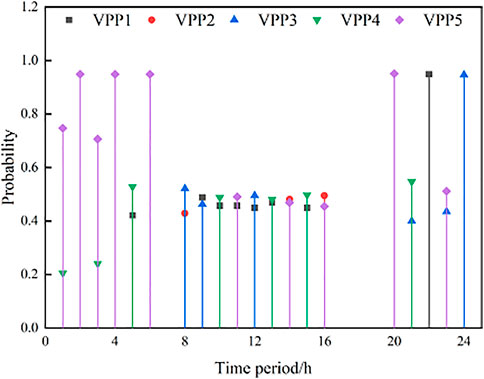
In each dispatching time period, the five VPPs are divided into power-sale VPP and power-purchase VPP according to the SDR of each VPP. When the multiple games reach the equilibrium state, each VPP will decide different power sales prices for each time period, and the probability that the power-purchase VPP selects the power-sale VPP is also different. Figures 7, 8 show the sale prices of the power sales VPPs at time t and the probability distribution of each power-sale VPP being selected by the power-purchase VPPs, respectively.

FIGURE 7

FIGURE 7. Electricity sale price of power-sale VPPs in t period.

FIGURE 8

FIGURE 8. Probability of power-sale VPPs to be chosen to purchase electricity in t period.

Taking time periods t = 2, t = 12, and t = 18 as examples, it can be seen from Figure 7 that only VPP5 is a power-sale VPP in time period 2, and VPP5 delivers power to the remaining four VPPs while satisfying its own load. The power-sale VPPs in time period 12 are VPP1 and VPP3; at t = 18, all five VPPs are in the state of power purchase. During this period, there is no power interaction between VPPs, and only power is purchased from the main network. It can be seen that, in 24 time periods of a day, each VPP can present different states, and its internal available power can be consumed by interacting with other VPPs when there is a surplus state.

From Figures 7, 8, it can be seen that the power-purchase VPPs prefer a power-sale VPP with low power selling prices, but it can be observed that the probability of the power-purchase VPPs choosing the power-sale VPP with the lowest price at t = 10, t = 12, t = 14, and t = 16 is not the highest.

Taking t = 10 as an example, it can be seen from Tables 3, 4 that the optimal electricity price issued by VPP1 is lower than that of VPP4, but the probability of the power-purchase VPPs choosing VPP1 is 0.4819, which is lower than the probability of choosing VPP4 by 0.5181. It can be seen that, during the dispatching process of the system, the electricity price is not the only factor to be considered by the power-purchase VPP when choosing the power sales VPP but also the influence of the controllable load call and its own load demand on the strategy.

TABLE 3

TABLE 3. Resource allocation of each VPP in t = 10 period.

TABLE 4

TABLE 4. Selection strategy of power-purchase VPP in t = 10 period.

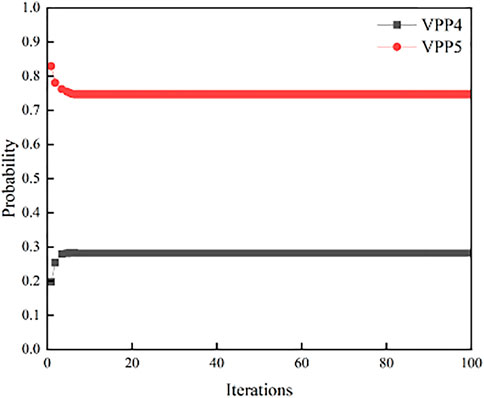
When t = 3, the convergence process of the probability of each power-sale VPP being selected when the power-purchase VPP purchases electricity is shown in Figure 9. It can be seen that the probability of each power-sale VPP being selected can converge to the equilibrium value quickly; that is, the dynamic selection behavior of the power-purchase VPP can reach the evolutionary equilibrium state in a short time.

FIGURE 9

FIGURE 9. Probability convergence process of selecting power-sale VPP to purchase electricity.

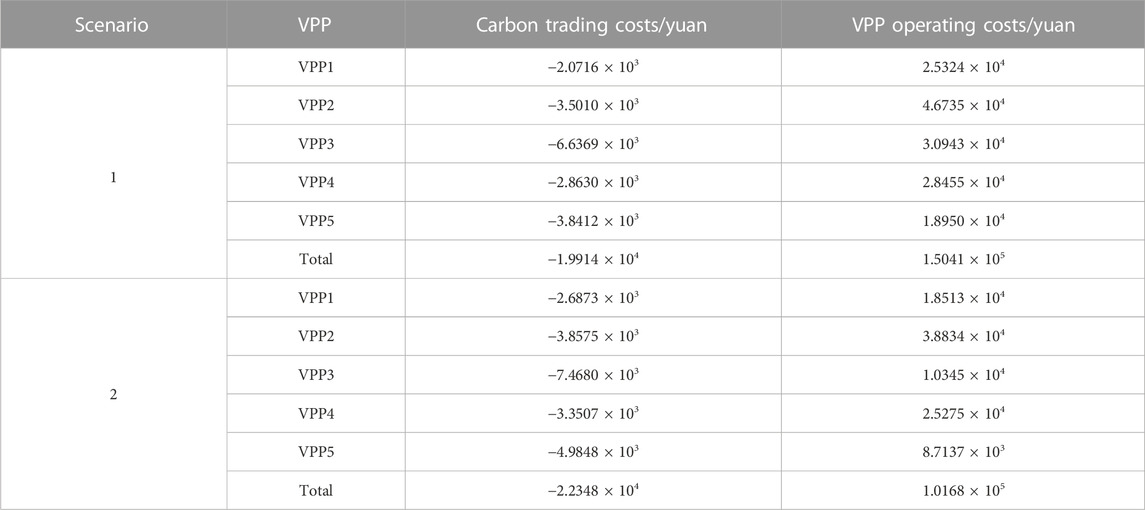
In order to verify the rationality of the proposed multiple game trading strategy for multi-VPPs considering carbon trading model, two different operation scenarios were set to analyze the multi-VPPs trading cost results.

Scenario 1: the multi-VPPs trading model with carbon trading market described in this paper, while the trading between multi-VPPs is based on the traditional method.

Scenario 2: the multi-VPPs trading model with stepped carbon trading market described in this paper and multiple game strategies among multi-VPPs are constructed.

By comparing Scenario 2 (considering multiple game strategy) with Scenario 1 (conventional game strategy) in Table 5, the total cost of carbon trading and multi-VPP system operation are reduced by 2,434 yuan and 4.873×10⁴ yuan, respectively. Therefore, if there is no electric energy interaction among the VPPs, as soon as the power in the VPP cannot meet its own internal electricity demand, only purchasing power from the main network increases the operating cost of VPP system, which makes the main network face the huge pressure of electricity supply. this shows that, when the resource allocation among the subjects in the multi-VPPs is carried out through the game idea, the resource utilization rate of VPP can be improved, and the carbon transaction cost of the system can be reduced to promote the economic operation of the system.

TABLE 5

TABLE 5. VPP scheduling cost in different scenarios.

6 Conclusion

In this paper, we analyzed a multi-VPPs unified trading strategy considering integrated carbon–electricity trading and proposed a new multiple game strategy among multi-VPPs, in which a non-cooperative game between power-sale VPPs is prioritized to determine the power sales price, and then an evolutionary game is played among power-purchase VPPs to make the choice of power purchase objects according to the power price strategy at this time. This will reduce pollution levels from VPP operations while increasing the benefits of VPP operations. After the corresponding case analysis, the following results are obtained.

1) Under the carbon trading mechanism, the multi-VPP system trading model with wind and photovoltaic is considered, which effectively promotes the consumption of renewable energy and achieves the goal of system economic operation.

2) From the perspective of multiple power-sale VPPs and multiple power-purchase VPPs, a multiple game trading strategy is adopted to improve the safe and stable operation of the system, which in turn has a positive effect on the coordinated distribution of benefits among the various entities in the system.

3) For multi-VPPs unified trading in multiple regions, a parallel distributed solution strategy is chosen in this paper, which can greatly accelerate the solution speed and avoid large amounts of computation.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

TC conceived the idea for the manuscript and XA, YZ, XW, and LD wrote it. All authors have read and agreed to its published version.

Funding

This work is supported by the Science and Technology Project of Electric Power Research Institute of State Grid Liaoning Electric Power Supply Co., Ltd.—Research on Power Transaction and Multi regional Energy Coordination Optimization Technology of Virtual Power Plants Based on Blockchain (2022YF-78).

Conflict of interest

Authors TC, YZ and XW were employed by the company State Grid Liaoning Electric Power Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer editor BZ declared a shared affiliation with authors TC, WA, and LD at the time of the review.

The authors declare that this study received funding from the Science and Technology Project of Electric Power Research Institute of State Grid Liaoning Electric Power Supply Co., Ltd. The funder had the following involvement in the study: Research on Power Transaction and Multi regional Energy Coordination Optimization Technology of Virtual Power Plants Based on Blockchain (2022YF-78).

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, J., Hu, Z., Chen, J., Chen, Y., Gao, M., and Lin, M. (2021). Optimal scheduling of integrated energy systems considering stepped carbon trading and flexible dual response of supply and demand. High. Volt. Tech. 47 (09), 3094–3106. doi:10.13336/j.1003-6520.hve.20211094

CrossRef Full Text | Google Scholar

Chu, T., An, X., Zhang, W., Lu, Y., and Tian, J. (2023). Multiple virtual power plants transaction matching strategy based on alliance blockchain. Sustainability 15 (8), 6939. doi:10.3390/su15086939

CrossRef Full Text | Google Scholar

Dou, Yangming, Ming, Chi, Liu, Zhi-Wei, Wen, Guanghui, and Sun, Qihai (2022). Distributed secondary control for voltage regulation and optimal power sharing in DC microgrids. IEEE Trans. Control Syst. Technol. 30, 2561–2572. doi:10.1109/TCST.2022.3156391

CrossRef Full Text | Google Scholar

Feng, C., Hua, H., Yong, W., Jianfeng, H., and Mian, G. (2018). A virtual power plant bidding model considering uncertainty. Appl. Sci. Technol. 45 (05), 62–66.

Google Scholar

Guotao, Z., Quan, D., Junhua, F., Guoming, Q., Ying, C., and Chao, H. (2021). Research on the low-carbon path of regional energy systems based on multi market linkage. Electr. Power Constr. 42 (03), 19–26.

Google Scholar

Huang, B., Zheng, S., Wang, R., Wang, H., Xiao, J., and Wang, P. (2022). Distributed optimal control of DC microgrid considering balance of charge state. IEEE Trans. Energy Convers. 37 (3), 2162–2174. doi:10.1109/TEC.2022.3169462

CrossRef Full Text | Google Scholar

Huang, Bonan, Liu, Lining, Zhang, Huaguang, Li, Yushuai, and Sun, Qiuye (2019). Distributed optimal economic dispatch for microgrids considering communication delays. IEEE Trans. Syst. Man, Cybern. Syst. 49 (8), 1634–1642. doi:10.1109/tsmc.2019.2900722

CrossRef Full Text | Google Scholar

Li, Y., Gao, D. W., Gao, W., Zhang, H., and Zhou, J. (2020). Double-mode energy management for multi-energy system via distributed dynamic event-triggered Newton-raphson algorithm. IEEE Trans. Smart Grid 11 (6), 5339–5356. doi:10.1109/tsg.2020.3005179

CrossRef Full Text | Google Scholar

Liu, Xiaoou (2022). Research on optimal dispatch method of virtual power plant considering various energy complementary and energy low carbonization. Int. J. Electr. Power and Energy Syst. 136, 107670. doi:10.1016/j.ijepes.2021.107670

CrossRef Full Text | Google Scholar

Liu, Z., Huang, B., Hu, X., Du, P., and Sun, Q. (2023). Blockchain-based renewable energy trading using information entropy theory. IEEE Trans. Netw. Sci. Eng., 1–12. doi:10.1109/TNSE.2023.3238110

CrossRef Full Text | Google Scholar

Liu, Z., Liu, R., Liang, N., and Liu, X. (2021). A multi microgrid energy trading method based on game theory. Power Grid. Technol. 45 (02), 587–595. doi:10.13335/j.1000-3673.pst.2020.0175

CrossRef Full Text | Google Scholar

Liu, Z., Xu, Y., Zhang, C., Elahi, H., and Zhou, X. (2022). A blockchain-based trustworthy collaborative power trading scheme for 5G-enabled social internet of vehicles. Digital Commun. Netw. 8 (6), 976–983. doi:10.1016/j.dcan.2022.10.014

CrossRef Full Text | Google Scholar

Liu, Zhi-Wei, Shi, Yu-Lun, Yan, Huaicheng, Han, Bing-Xin, and Guan, Zhi-Hong. Secure consensus of multi-agent systems via impulsive control subject to deception attacks. IEEE Trans. Circuits Syst. II Express Briefs 170, 166–170. doi:10.1109/TCSII.2022.3196042

CrossRef Full Text | Google Scholar

Shayegan-Rad, A., Badri, A., and Zanganeh, A. (2017). Day-ahead scheduling of virtual power plant in joint energy and regulation reserve markets under uncertainties. Energy 121 (2), 114–125. doi:10.1016/j.energy.2017.01.006

CrossRef Full Text | Google Scholar

Wang, R., Li, W., Sun, Q., Li, Y., Gui, Y., and Wang, P. (2022). Fully distributed dynamic edge-event-triggered current sharing control strategy for multi-bus DC microgrids with power coupling. IEEE Trans. Industrial Inf. 19, 5667–5678. doi:10.1109/TII.2022.3188352

CrossRef Full Text | Google Scholar

Wang, R., Ma, D., Li, M. -J., Sun, Q., Zhang, H., and Wang, P. (2022). Accurate current sharing and voltage regulation in hybrid wind/solar systems: An adaptive dynamic programming approach. IEEE Trans. Consumer Electron. 68 (3), 261–272. doi:10.1109/tce.2022.3181105

CrossRef Full Text | Google Scholar

Zhang, H., Li, Y., Gao, D. W., and Zhou, J. (2017). Distributed optimal energy management for energy internet. IEEE Trans. Industrial Inf. 13 (6), 3081–3097. doi:10.1109/tii.2017.2714199

CrossRef Full Text | Google Scholar

Zhang, X., Liu, X., and Zhong, J. (2020). Comprehensive energy system planning considering the uncertainty of reward and punishment for tiered carbon trading and electricity heat transfer load. Proc. CSEE 40 (19), 6132–6142. doi:10.13334/j.0258-8013.pcsee.191302

CrossRef Full Text | Google Scholar

Zhao, Haotian, Wang, Bin, Wang, Xuanyuan, Pan, Z., Sun, H., Liu, Z., et al. (2020). Active dynamic aggregation model for distributed integrated energy system as virtual power plant. J. Mod. Power Syst. Clean Energy 8 (5), 831–840. doi:10.35833/mpce.2020.000202

CrossRef Full Text | Google Scholar

Zhi, C., Zhijian, H., Changhong, W., and Tiange, L. (2021). Multi stage planning of a comprehensive energy system in a park based on a tiered carbon trading mechanism. Power Autom. Equip. 41 (09), 148–155. doi:10.16081/j.epae.202109012

CrossRef Full Text | Google Scholar

Zhu, Y. S., Nie, C. J., Chen, B., Li, Q. Y., Yang, Z. T., and Yang, J. L. (2022). Research on multiple game cooperative scheduling of microgrid cluster systems under mixed time scales. Power Grid Technol., 1–12. doi:10.13335/j.1000-3673.pst.2022.0611

CrossRef Full Text | Google Scholar