
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 08 March 2023
Sec. Electrochemical Energy Storage
Volume 11 - 2023 | https://doi.org/10.3389/fenrg.2023.1147113
Oil-immersion transformer plays an important role in the operation of power system, and its reliable operation is the basis of the safe and economic operation of power system. Transformer internal failure will not only cause the transformer to stop, but also damage, affecting the proper operation of the power system. The transformer is often in a high-temperature and high-pressure environment during its operation, so it is difficult to effectively and accurately protect the transformer from failure in the harsh working environment. Because the existing methods can not detect and protect the faults of transformer equipment sensitively and accurately, based on this, this paper carried out the research on the detection and protection of oil immersed transformer. By analyzing the calculation results, the relationship between the temperature rise of the transformer structure and the ambient temperature is discussed. It is found that the higher the ambient temperature of the transformer, the greater the harm to the equipment. High temperature area is mainly concentrated at the pull plate of transformer. This provides a reference for making the starting strategies of transformers in different environments, and helps to avoid mechanical structure damage and insulation aging damage caused by temperature.
The energy storage industry plays an increasingly important role in the development of power technology (Guo et al., 2022a; Li et al., 2022; Sun et al., 2022; Zhang et al., 2023a). Power transformers play an important role in energy conversion and transmission in power system. It is an indispensable and expensive equipment in power systems. From the perspective of power supply reliability, whether the power transformer can operate safely and reliably determines whether the power grid can reliably supply power to power users. If the transformer is damaged, it will directly lead to large-scale power outages. In terms of economy, the economic loss caused by large area power failure due to transformer damage is also huge (Guo et al., 2022b). Therefore, the safe, reliable and economical operation of transformers is crucial to the whole power grid (Lin et al., 2020).
The proper monitoring system of power transformer can help to reduce the failure rate and improve the system reliability and economic efficiency. Yang et al. (2022) proposed a new type of double stack automatic encoder (DSAE), which is mainly used to quickly and accurately judge the health of power transformers with unbalanced data structure. Due to the adaptability of the conventional model structure, the performance of the diagnosis model is difficult to improve under theoretical support. In order to fill this gap, Qi et al. (2020) proposed a new power transformer self-diagnosis model. The existing transformer fault diagnosis methods need to locate specific components, so correct modeling is of great significance for transformer fault diagnosis.
The oil flow velocity is low in oil-immersed transformer, and the influence of oil flow and heat transfer is very complicated. In order to improve the cooling performance of oil-immersed transformers (Susa et al., 2005; Ahmadi et al., 2022). It is very important to study the internal heat transfer process, oil flow characteristics, temperature rise and temperature rise of reverse winding (Li et al., 2016; Liu et al., 2022). The hot spot temperature of the transformer determines the load capacity of the transformer and the thermal aging of the insulation materials (Singh and Bandyopadhyay, 2010). The hot spot temperature is too high, the internal insulation aging is accelerated, and the operating life is shortened. The low temperature of the hot spot will not make full use of the transformer capacity, which will seriously affect the efficiency and economy of transformer operation (Wang et al., 2017; Zhang et al., 2020; Wang et al., 2023). Therefore, it is of great practical significance to accurately obtain the hot spot temperature of the transformer to extend the service life of the transformer and improve the capacity utilization ratio of the transformer (Perise et al., 2020; Cui et al., 2022a; Cui et al., 2022b; Zhang et al., 2023b).
In this paper, the oil immersed power transformer is modeled in three dimensions, simplified reasonably according to the requirements of electromagnetic field calculation, and the thermal field of transformer is simulated. The temperature variation law of the maximum structure of transformer under different ambient temperatures is analyzed.
Because the temperature of different positions of objects is different, it can lead to the spread of heat. From the actual observation experience, we can draw a conclusion that every point in the space position of an object has only one unique temperature value. The temperature values of all points on the object constitute the temperature field or temperature distribution (Faiz et al., 2008).
The temperature field can be described as a function of space coordinates and time:
The primary objective of thermal process analysis is to determine the temperature field of an object in the process of heat transfer. It is classified according to the relationship between temperature field and time.
Stable temperature field means that the temperature field is independent of time, which is accurately expressed as the change of temperature relative to time and space is small enough to be negligible. In this case, the heat transfer system is stable, and the mathematical expression of the temperature field can be expressed as follows:
The thermal module in Simcenter MagNet can be used to solve for the steady-state and time-varying temperature distributions caused by time-varying heat sources, in the presence of the mally conducting materials and convective/radiative boundary losses. It handles heat transfer through conduction, convection, and radiation. The equations to be solved are as follows:
where
Boundary conditions are specified temperature T or specified heat flux:
Where
where
Based on the size of oil-immersed transformer, the three-dimensional model can completely simulate the actual situation of the transformer operation. The model includes the structure and oil tank composed of iron core, coil, magnetic permeability and conductive materials on the leakage path, and the related insulating materials that affect the heating and cooling of the structure when the temperature field is coupled. Establish a complete model including pulling plate, electromagnetic shield, oil tank, iron core, coil and lead-out.
The MagNet electromagnetic field simulation results are coupled to the ThermNet thermal field, the heat dissipation boundary is established, and the magnetic thermal coupling simulation is carried out to obtain the temperature field distribution of the structural parts. The quality and quantity of mesh generation have a great influence on the calculation results. High quality and large quantity can improve the accuracy of calculation (Szczepaniak and Klosinski, 2012; Zhao et al., 2018). However, the calculation speed will be greatly affected by the quantity, so it should be controlled reasonably when setting the type and size of grid elements. The grid is manually set according to the experience of electromagnetic simulation, and the whole model has about 4.8 million tetrahedrons. Because the magnetic field and the thermal field use the same grid, the thermal field does not set a separate grid, but uses the grid established by the magnetic field. Because the magnetic field model and grid are used, only the components that affect the transformer leakage magnetic field are considered in the modeling. It mainly includes the iron core, coil, lead wire and metal structure of transformer, as well as the electromagnetic shielding system involved in electromagnetism. The modeling for transformer is shown in Figure 1.
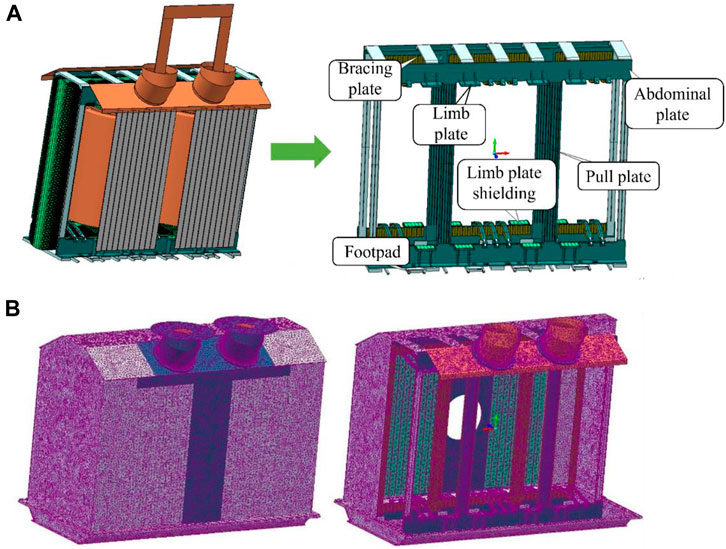
FIGURE 1. Model of oil-immersed transformer (A) Main structure of transformer (B) Grid of transformer field thermal model.
ThermNet heat sources are all replaced by magnetic field MagNet. The parameter settings of magneto-thermal coupling field are shown in Table 1. After the heat sources under work conditions 1 (5% rated capacity) and 2 (85% rated capacity) are replaced respectively. Different temperature distribution nephograms have detailed differences in temperature appreciation, which are two orders of magnitude different in value. The heat source distribution clouds are shown in Figure 2.

FIGURE 2. Cloud map of electromagnetic heat source density distribution of transformer structure under working condition of (A) 5% capacity (B) 85% capacity.
The transient process of transformer at 0°C and capacity of 5% and 85% is simulated. The temperature field results are shown in Figure 3.
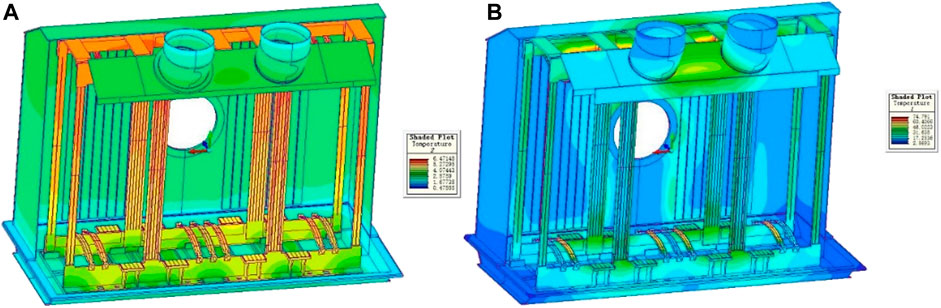
FIGURE 3. Cloud Map of Temperature Field Distribution in Oil Tank with Coupled Thermal Field at 0°C (A) 5% capacity (B) 85% capacity.
As can be seen from Figure 3, the temperature rise of the transformer is not high at ambient temperature of 0°C. From the temperature distribution of the windings and cores, the flow of transformer oil contributes to the heat loss of the windings and cores. At 5% capacity, the maximum structure temperature of transformer is 6.5°C. the maximum structure temperature rise is 6.5K. At 85% capacity, the maximum structure temperature of transformer is 74.8°C. the maximum structure temperature rise is 74.8K.
The transient process of transformer with 5% and 85% capacity at room temperature of 20°C is simulated. The temperature field results are shown in Figure 4.
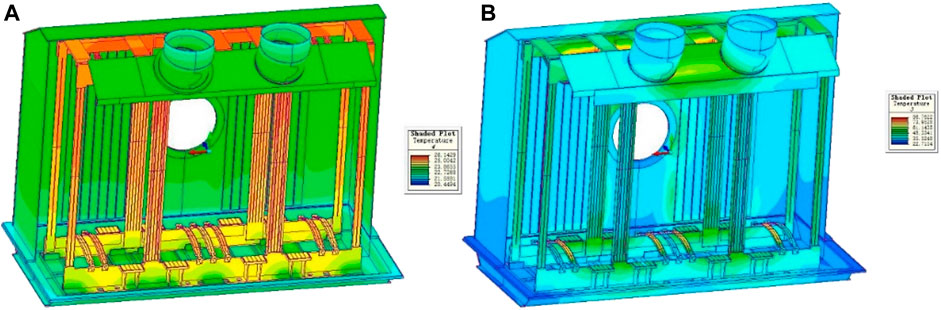
FIGURE 4. Cloud Map of Temperature Field Distribution in Oil Tank with Coupled Thermal Field at 20°C (A) 5% capacity (B) 85% capacity.
The temperature of upper winding of transformer is higher than that of lower winding from the distribution of core temperature and hot spot of winding at 20°C. The flow of transformer oil is conducive to heat dissipation. At 5% capacity, the maximum temperature of transformer structural parts is 26.1°C. the maximum temperature rise of structural parts is 6.1K. At 85% capacity, the maximum temperature of transformer structural parts is 86.8 °C. the maximum temperature rise of structural parts is 66.8K.
The transient process of transformer with 5% and 85% capacity at room temperature of 30°C is simulated. The temperature field results are shown in Figure 5.
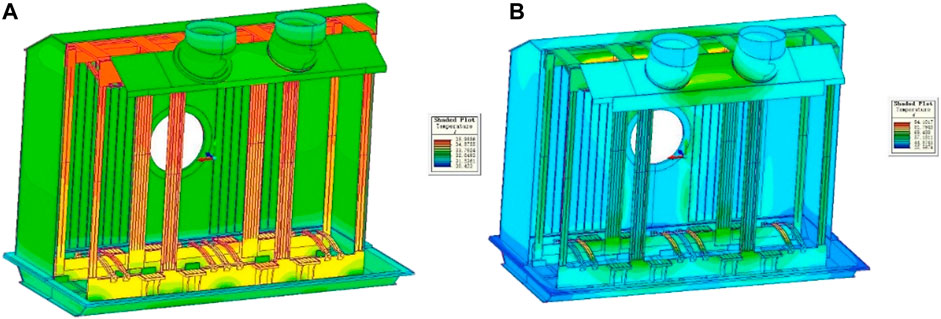
FIGURE 5. Cloud Map of Temperature Field Distribution in Oil Tank with Coupled Thermal Field at 30°C (A) 5% capacity (B) 85% capacity.
As shown in Figure 5, the temperature of transformer is symmetrically distributed at 30°C, and the flow property of oil is not obvious. At 5% capacity, the maximum temperature of transformer structural parts is 36.0°C. the maximum temperature rise of structural parts is 6.0K. At 85% capacity, the maximum temperature of transformer structural parts is 94.1°C. the maximum temperature rise of structural parts is 64.1K.
The transient process of transformer with 5% and 85% capacity at room temperature of 40°C is simulated. The temperature field results are shown in Figure 6.
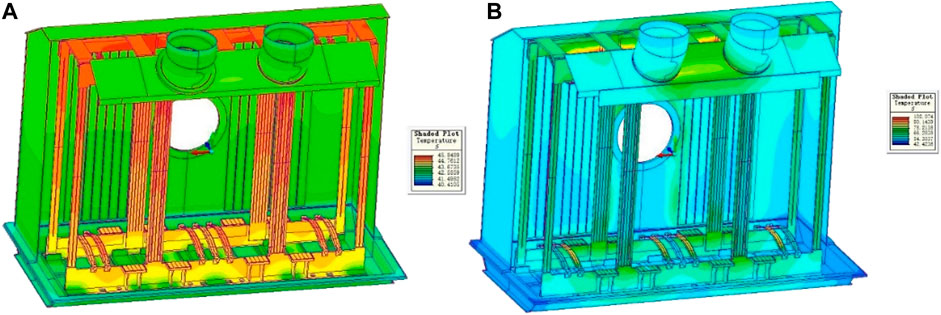
FIGURE 6. Cloud Map of Temperature Field Distribution in Oil Tank with Coupled Thermal Field at 40 °C (A) 5% capacity (B) 85% capacity.
As shown in Figure 6, the temperature rise of transformer oil surface is about 5.3K at 40°C. The temperature distribution of transformer is symmetrical and the flow of oil is not obvious. At 5% capacity, the maximum temperature of transformer structural parts is 45.8°C. the maximum temperature rise of structural parts is 5.8K. At 85% capacity, the maximum temperature of transformer structural parts is 102.0°C, the maximum temperature rise of structural parts is 62.0 K.
The analysis of simulation results in the previous section shows that transformers exhibit different temperature characteristics under different temperature conditions. Through many simulation calculations, the temperature rise of transformer structure at different ambient temperatures is obtained. When the transformer is directly, the relationship between the temperature rise of hot spot and the ambient temperature is shown in Figure 7.
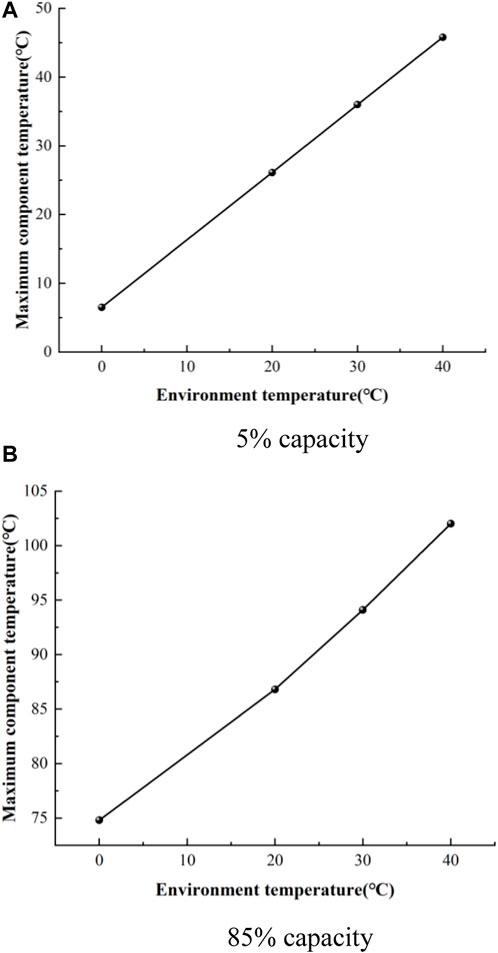
FIGURE 7. Relationship between transformer structure temperature and environment temperature under different capacities.
As shown in Figure 7. Because the ambient temperature is between 0°C and 40 °C, which is the normal working temperature of the transformer, the temperature of the transformer components changes little with the increase of the ambient temperature. It has a linear relationship with it. At 5% of the capacity, the high temperature area of the transformer is mainly concentrated at the pull plate and support plate. At 85% of the capacity, it is only concentrated at the pull plate.
Abnormal operating temperature accounts for a considerable proportion of all kinds of transformer faults. Due to the variety of fault location and performance, it is difficult to diagnose the fault. Abnormal temperature is a vicious cycle process, which not only increases the loss of transformer, causes unnecessary waste of energy, but also damages the internal insulation, resulting in more serious faults. In this paper, a calculation model for temperature field of oil-immersed power transformer is established, and the temperature field of transformer is calculated at 0, 20, 30°C and 40 °C. The relationship between temperature of each component of the transformer and the ambient temperature is obtained, and the curve of their relationship is drawn. The higher the ambient temperature, the higher the maximum construction temperature, and the greater the natural harm to the equipment. By comparing the two capacities, it can be found that proper increase of transformer capacity can achieve certain protection effect. The model and method presented in this paper can be extended to the calculation of internal fault pressure of various transformers, which has some reference value for setting the setting value of pressure protection relay.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Conceptualization, ZY and KW; methodology, YF and KW; software, LH; validation, EG, CG, and ZY; formal analysis, ZY and KW; investigation, CG; resources, CG; data curation, CG and KW; writing—original draft preparation, YF and KW; writing—review and editing, ZY and KW; visualization, LH; supervision, EG, and KW; project administration, EG; All authors have read and agreed to the published version of the manuscript.
CG, YF, and EG were employed by China Nuclear Power Operations Co., Ltd. LH and ZY were employed by Suzhou Nuclear Power Research Institute Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Ahmadi, S. A., Sanaye-Pasand, M., Abedini, M., and Samimi, M. H. (2022). Online sensitive turn-to-turn Fault detection in power transformers. IEEE Trans. Industrial Electron. 69 (12), 13555–13564. doi:10.1109/tie.2022.3140504
Cui, Z., Kang, L., Li, L., Wang, L., and Wang, K. (2022). A combined state-of-charge estimation method for lithium-ion battery using an improved BGRU network and UKF. Energy 259, 124933. doi:10.1016/j.energy.2022.124933
Cui, Z., Kang, L., Li, L., Wang, L., and Wang, K. (2022). A hybrid neural network model with improved input for state of charge estimation of lithium-ion battery at low temperatures. Renew. Energy 198, 1328–1340. doi:10.1016/j.renene.2022.08.123
Faiz, J., Sharifian, M. B. B., and Fakhri, A. (2008). Two-dimensional finite element thermal modeling of an oil-immersed transformer. Eur. Trans. Electr. Power 18 (6), 577–594. doi:10.1002/etep.193
Guo, Y., Yang, D., Zhang, Y., Wang, L., and Wang, K. (2022). Online estimation of SOH for lithium-ion battery based on SSA-Elman neural network. Prot. Control Mod. Power Syst. 7, 40. doi:10.1186/s41601-022-00261-y
Guo, Y., Yu, P., Zhu, C., Zhao, K., Wang, L., and Wang, K. (2022). A state-of-health estimation method considering capacity recovery of lithium batteries. Int. J. Energy Res. 46 (15), 23730–23745. doi:10.1002/er.8671
Li, D., Yang, D., Li, L., Wang, L., and Wang, K. (2022). Electrochemical impedance spectroscopy based on the state of health estimation for lithium-ion batteries. Energies 15 (18), 6665. doi:10.3390/en15186665
Li, J. Z., Zhang, Q. G., Wang, K., Wang, J. Y., Zhou, T. C., and Zhang, Y. Y. (2016). Optimal dissolved gas ratios selected by genetic algorithm for power transformer fault diagnosis based on support vector machine. IEEE Trans. Dielectr. Electr. Insulation 23 (2), 1198–1206. doi:10.1109/tdei.2015.005277
Lin, M. J., Chen, L. B., and Yu, C. T. (2020). A methodology for diagnosing faults in oil-immersed power transformers based on minimizing the maintenance cost. IEEE Access 8, 209570–209578. doi:10.1109/access.2020.3038827
Liu, C., Li, D., Wang, L., Li, L., and Wang, K. (2022). Strong robustness and high accuracy in predicting remaining useful life of supercapacitors. Apl. Mater. 10 (6), 061106. doi:10.1063/5.0092074
Perise, J. S., Bakkar, M., and Rodriguez, S. B. (2020). Open-circuit fault diagnosis and maintenance in multi-pulse parallel and series TRU topologies. IEEE Trans. Power Electron. 35 (10), 10906–10916. doi:10.1109/tpel.2020.2976895
Qi, B., Wang, Y. M., Zhang, P., Li, C. R., Wang, H. B., and Chen, J. X. (2020). A novel self-decision fault diagnosis model based on state-oriented correction for power transformer. IEEE Trans. Dielectr. Electr. Insulation 27 (6), 1778–1786. doi:10.1109/tdei.2019.008423
Singh, S., and Bandyopadhyay, M. N. (2010). Dissolved gas analysis technique for incipient fault diagnosis in power transformers: A bibliographic survey. IEEE Electr. Insul. Mag. 26 (6), 41–46. doi:10.1109/mei.2010.5599978
Sun, H., Yang, D., Wang, L., and Wang, K. (2022). A method for estimating the aging state of lithium-ion batteries based on a multi-linear integrated model. Int. J. Energy Res. 46 (15), 24091–24104. doi:10.1002/er.8709
Susa, D., Lehtonen, M., and Nordman, H. (2005). Dynamic thermal modelling of power transformers. IEEE Trans. Power Deliv. 20 (1), 197–204. doi:10.1109/tpwrd.2004.835255
Szczepaniak, P. S., and Klosinski, M. (2012). Maximal margin classifiers applied to DGA-based diagnosis of power transformers. Przeglad Elektrotechniczny 88 (2), 100–104.
Wang, L., Xie, L., Yang, Y., Zhang, Y., Wang, K., and Cheng, S. j. (2023). Distributed online voltage control with fast PV power fluctuations and imperfect communication. IEEE Trans. Smart Grid 2023, 1. doi:10.1109/TSG.2023.3236724
Wang, L., Zhou, L., Tang, H., Tang, H., Wang, D., Cui, Y., et al. (2017). Numerical and experimental validation of variation of power transformers’ thermal time constants with load factor. Appl. Therm. Eng. 126, 939–948. doi:10.1016/j.applthermaleng.2017.07.167
Yang, D. S., Qin, J., Pang, Y. H., and Huang, T. W. (2022). A novel double-stacked autoencoder for power transformers DGA signals with an imbalanced data structure. IEEE Trans. Industrial Electron. 69 (2), 1977–1987. doi:10.1109/tie.2021.3059543
Zhang, M., Liu, Y., Li, D., Cui, X., Wang, L., Li, L., et al. (2023). Electrochemical impedance spectroscopy: A new chapter in the fast and accurate estimation of the state of health for lithium-ion batteries. Energies 16, 1599. doi:10.3390/en16041599
Zhang, M., Wang, K., and Zhou, Y. T. (2020). Online state of charge estimation of lithium-ion cells using particle filter-based hybrid filtering approach. Complexity 2020, 1–10. doi:10.1155/2020/8231243
Zhang, M., Wang, W., Xia, G., Wang, L., and Wang, K. (2023). Self-powered electronic skin for remote human-machine synchronization. ACS Appl. Electron. Mater. 5 (1), 498–508. doi:10.1021/acsaelm.2c01476
Keywords: oil-immersed transformer, power system, mechanics, fault detection, thermal field modeling
Citation: Gao C, Huang L, Feng Y, Gao E, Yang Z and Wang K (2023) Thermal field modeling and characteristic analysis based on oil immersed transformer. Front. Energy Res. 11:1147113. doi: 10.3389/fenrg.2023.1147113
Received: 18 January 2023; Accepted: 23 February 2023;
Published: 08 March 2023.
Edited by:
Mohd Faizul Mohd Sabri, University of Malaya, MalaysiaReviewed by:
Navid Aslfattahi, Czech Technical University in Prague, CzechiaCopyright © 2023 Gao, Huang, Feng, Gao, Yang and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kai Wang, d2FuZ2thaUBxZHUuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.