- 1SCK CEN, Belgian Nuclear Research Center, Mol, Belgium
- 2NEMO Group, Dipartimento Energia, Politecnico di Torino, Torino, Italy
Nuclear data uncertainty analysis on the spent nuclear fuel inventory was performed on the Takahama-3 NT3G23 assembly, where the sample SF95-4 was irradiated up to a burnup of approximately 36
1 Introduction
Spent nuclear fuel (SNF) characterization is of key importance for many research and technological applications of the back end of the fuel cycle. Several observables (Žerovnik et al., 2018) have been identified to be of interest for SNF applications. This is because many nuclides present in the fuel at discharge pose risks and technological issues due to their decay. The relevance of the contribution of different nuclides to these observables varies in time because of their different half-lives.
Experimental assessment of SNF observables is often expensive and time-consuming (Ilas and Liljenfeldt, 2017), so numerical computer codes are a key tool in this field. SNF observables and SNF nuclide concentration are tightly linked; this means that all the observables can be computed from the nuclide inventory (Žerovnik et al., 2018). The SNF nuclide concentration is often predicted using computer codes for burnup analysis, which couple the solution of neutron transport and of the Bateman equation. Validation of dedicated codes and input parameters used in this field involves the simulation of benchmark cases (Michel-Sendis et al., 2017) with experimental evaluation of the SNF nuclide composition, which is performed by comparing the best estimate model results with the experimentally assessed sample composition. The quality of the best estimate results is much dependent on the model assumptions and on the quality of the assay and nuclear data. Nuclear data are provided in the form of libraries by international evaluation projects, such as ENDF/B-VIII.0 (Brown et al., 2018), JEFF-3.3 (Plompen et al., 2020), and JENDL-4.0u (Shibata et al., 2011). Nuclear data are stored in computer-readable files (Herman and Trkov, 2010) containing best estimate and covariance/uncertainty evaluations.
In this context, several international programs are aiming at developing knowledge on SNF inventories and uncertainty. Among them, EURAD (Rochman et al., 2022) proposes several benchmark case studies, two of which will be of interest for this work: Takahama-3 sample SF95-4 and Calvert Cliffs-1 MKP109 sample P. A model of the former is described in the following study, while the results presented in Grimaldi et al. (2022a) were considered for the latter. In both cases, the nuclear data-evaluated uncertainty was propagated to the SNF inventory. Nuclear data libraries later than in other studies found in the literature (Fiorito et al., 2015; Rochman et al., 2017) were considered. This is to assess the state of the recent library releases, with particular attention to covariance evaluation for the cross-sections. This aspect has been included in the evaluation in the last decades, and covariance evaluations for a progressively increasing number of nuclides have been provided. The effort in this sense is not finalized yet, resulting in incomplete datasets allowing for partial uncertainty quantification only. The aim of this study is also to identify which nuclides relevant for the uncertainty propagation to the SNF composition are lacking in the uncertainty evaluation and the difference originating by the use of the three considered nuclear data libraries.
This work focuses on the propagation of the evaluated uncertainties through the Monte Carlo model of sample SF95-4 (Nakahara et al., 2002a) irradiated in Takahama-3 pressurized water reactor (PWR), developed with the Serpent code (Leppänen et al., 2015). The results of the best estimate simulation were then validated against the results of the radiochemical analysis reported in the SFCOMPO database (Michel-Sendis et al., 2017). The uncertainty given in the form of covariance matrices evaluated by ENDF/B-VIII.0, JEFF-3.3, and JENDL-4.0u was then propagated through the model to SNF composition with the SANDY code (Fiorito et al., 2017), where a stochastic sampling scheme is implemented. This work follows the approach considered in the literature for nuclear data uncertainty propagation to SNF composition (Rochman et al., 2014b; Williams et al., 2014; Díez et al., 2015; Fiorito et al., 2015; Leray et al., 2016; Ilas and Liljenfeldt, 2017; Rochman et al., 2017; Wemple and Zwermann, 2017; Ebiwonjumi et al., 2021; Fiorito et al., 2021; Grimaldi et al., 2022a). The concentration uncertainty results are then thoroughly compared with those reported in Grimaldi et al. (2022a).
Aiming to better describe the phenomena through which the uncertainty propagates from the nuclear data to the SNF nuclide inventory, the uncertainty analysis was performed at different burnups. The change of relevance in the uncertainty contributions with the burnup accumulation was then assessed, complementing what was carried out in Fiorito et al. (2021). When comparing the SNF inventory uncertainty results obtained in this work with the ones reported in Grimaldi et al. (2022a), relevant similarities were found both at discharge and during sample irradiation. This was found despite numerous differences in the two models. The degree of mutual representativity of the two systems was therefore assessed following what was reported in Blaise et al. (2021) for a number of nuclides.
A preliminary analysis of the concentration uncertainty results carried out hereby was presented in Grimaldi et al. (2022b); Grimaldi (2022).
2 Materials and methods
2.1 Description of the assembly models
The SF95-4 sample was irradiated in Takahama unit 3 PWR for two cycles. Assembly NT3G23, where the sample was located, is a 17 × 17 fuel assembly (FA), and the initial enrichment of the sample was 4.1 wt% in 235U. Of the 289 rods in the FA, 24 were guide tubes; one was used to host the in-core instrumentation; 16 were enriched with gadolinium, 2.63 wt% 235U enrichment and 6 wt% gadolinium enrichment; and the others were made of UO2 fuel enriched as the fuel sample. SF95-4 was not enriched in gadolinium.
Being the sample irradiated close to the core mid-plane, a 2D Serpent model of the assembly NT3G23 was designed according to the specifications given in the SFCOMPO database and in Nakahara et al. (2002a). With 105 neutron histories per batch, 25 inactive and 250 active batches were used. Reflective boundary conditions were adopted for this model since the assembly was located in the axial midplane of the fuel column. To take into account spatial self-shielding, a pin-by-pin depletion was performed, with an equi-volume radial division in 10 rings for the sample, fuel, and Gd-bearing pins. Effective average temperatures of 900 K for the sample, fuel, and Gd pins were taken, while the other materials were simulated at 600 K. The water density was calculated at the sample axial level from the given pressure and temperature. ENDF/B-VII.1 cross-sections, energy-dependent branching ratios, fission yields, and decay data were used. The irradiation history was simulated as given in the SFCOMPO database, where the average burnup steps of approximately 1
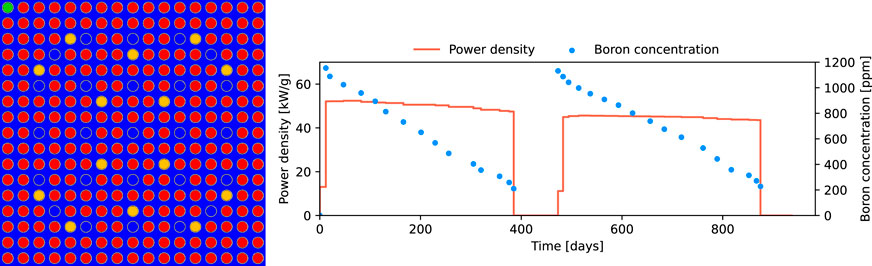
FIGURE 1. Two-dimensional lattice of the assembly NT3G23 Takahama SF95-4 (left) and sample power density and boron concentration time evolution (right).
The material temperatures were taken from Nakahara et al. (2002b). The flux was normalized to the sample burnup of 36.69
The modeled sample power history and boron concentration taken from SFCOMPO are reported in Figure 1.
The computational burden of statistical sampling uncertainty propagation through the Monte Carlo models has been reported by many scientific publications (Rochman et al., 2014a; Fiorito et al., 2015; Rochman et al., 2017). A second model, simplified, was therefore designed to reduce the computational time of the uncertainty propagation procedure. These included the following:
• reduction by a factor of 10 of the number of particle histories per transport calculation;
• use of cycle-averaged boron concentration values;
• reduction of the number of depletion zones, resulting in the fuel sample, the fuel rods adjacent to the sample, and the remaining fuel rods.
To validate the simplified model, the concentration results were compared with those of the accurate model and are reported in Section 2.2. A more detailed discussion on the bias introduced by the simplifying assumptions is out of the scope of this work.
2.2 Validation of the models
In this section, the computational results (C) of the accurate FA model are compared against the experimentally assessed nuclide concentrations (E) in the form of C/E−1 in Figure 2. The impact of model simplifications for the uncertainty analysis was assessed by comparing the accurate prediction of the concentrations against their accurate estimates, as given in Figure 3. All the compared results were computed using nuclear data from ENDF/B-VII.1 (Chadwick et al., 2011).
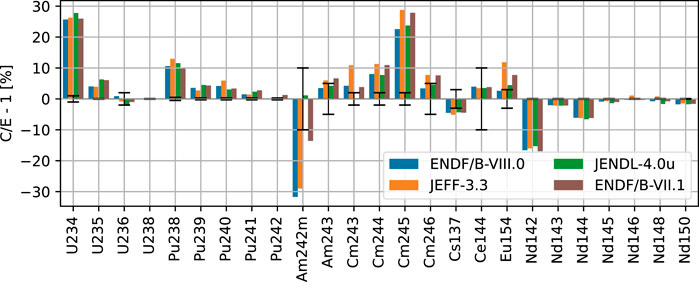
FIGURE 2. Deviation (in percent) between the calculated (C) and experimentally measured (E) concentrations given as C/E−1. The error bar represents the experimental error as one standard deviation.
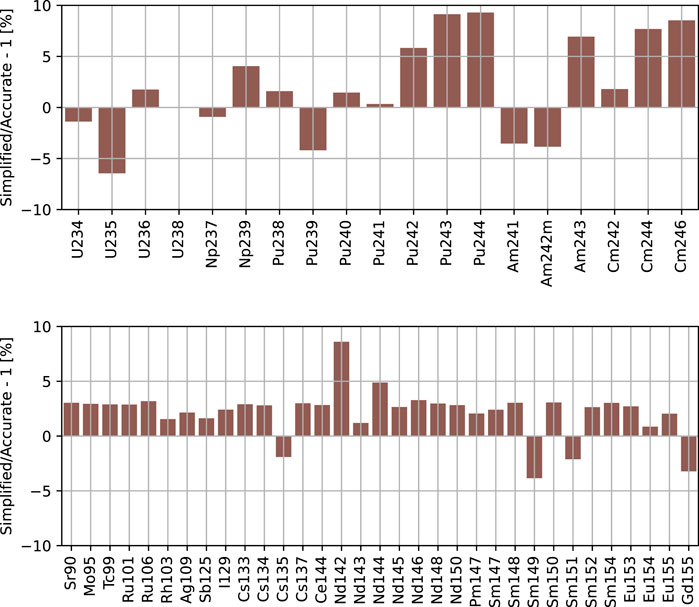
FIGURE 3. Deviations (in percent) on nuclide concentrations (also called C/C-1) introduced by the Serpent model simplifications. The ratio denominators are the results of the accurate model.
The experimental campaign on the SF95-4 sample was performed at the JAERI. The results of those experimental assessments were reported to the sample discharge date (Ilas et al., 2010). The estimated experimental uncertainties range from 0.1% for the concentration of uranium isotopes to 10% for the concentrations of minor actinides and of some fission products, measured through α and γ spectroscopy.
The comparison with experimental results (Figure 2) gives an overall quite good agreement, with discrepancies often below or in the range of 10%. The experimental uncertainty is reported in the form of one-standard-deviation error bars. A number of outliers were excluded from the plot, its discrepancy being larger than 30%, namely, 241Am, 242Cm, 106Ru, and 125Sb. The disagreement in the plutonium isotopes might originate from the vicinity of the sample to the assembly boundaries, which makes its concentration results more affected by the assumption of reflective boundary conditions. The reported information in Figure 2 is consistent to that found in the literature (Radulescu et al., 2010; Fiorito et al., 2015).
The results of the simplified model are compared to those of the accurate model, as shown in Figure 3. A very good matching of the results of the two simulations was found, with discrepancies lower than 10% and in many cases lower than 5%. The reduction in the number of depletion zones might explain the larger discrepancies found in the concentrations of the minor actinides. Those nuclides are produced via neutron captures in the plutonium isotopes building up in the periphery of the fuel pin, which is described with less precision when the in-pin spatial discretization is removed. The impact of the use of cycle-averaged boron concentration is expected to be negligible according to Nea Nuclear Science Committee (2016).
In Figure 3, a discrepancy on the concentrations of 235U and 239Pu indicates a burnup-matching problem, which reflects on the concentration of the neodymium isotopes. This originates from the fact that Serpent imposes power normalization in the transport calculation PT as proportional to the neutron flux phi and to the macroscopic fission cross-section Σf:
while using one-group-averaged fluxes and cross-section—denoted with 1G subscript—in the depletion calculation. The depletion power results in
The Serpent output power is the batch1-wise average, denoted as
which holds as long as ϕ and Σf are not correlated. The better the statistics, the closer the reproduced correlation is to 0—i.e., the correlation will be larger in the simplified model, resulting in sample burnup discrepancy. The sample burnup discrepancy amounts to about 3% and is consistent with that reported in Grimaldi et al. (2022a).
3 Results
3.1 Discharge concentration uncertainty results
The uncertainties originated from the nuclear data of the SNF concentration at discharge were evaluated. The SANDY code was used to produce samples from multivariate normal distributions considering the covariance matrices given in ENDF/B-VIII.0, JEFF-3.3, and JENDL-4.0u. The standard deviation of the concentrations resulting from the simulations with perturbed inputs is, here, reported as the concentration uncertainty. In the analysis, only the evaluated uncertainty on the cross-section was propagated. Other nuclear data uncertainties were not propagated in this work; this assumption is discussed with more detail in Fiorito et al. (2015); Leray et al. (2016); Rochman et al. (2021). The most relevant effect of this is expected to be on the underestimation of the concentration uncertainty of fission products, with the evaluated uncertainty on the fission yields being often quite large.
For each of the considered nuclear data libraries, sets of 200 and 100 perturbed cross-section data were produced for the actinides and for the fission products, respectively. Among the main observables, 244Cm concentration uncertainty was found to be slower converging. Figure 4 reports the convergence of its concentration standard deviation (std.) predicted by increasing the number of actinide cross-section samples.
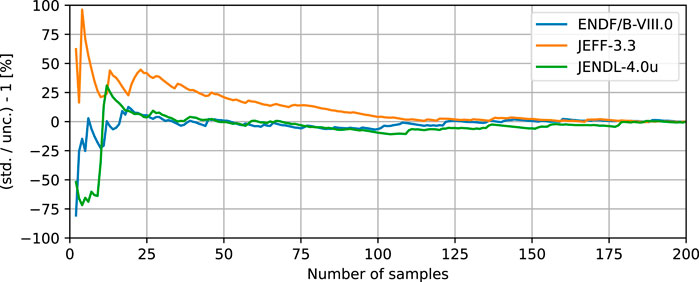
FIGURE 4. Convergence of the standard deviation (std.) of the discharge concentration of 244Cm with the number of cross-section samples for the actinides. The values are normalized over the best prediction of the concentration uncertainty of 244Cm (unc.), i.e., the standard deviation computed with 200 cross-section samples.
Each datum was processed with NJOY (Macfarlane et al., 2017). All available cross-section uncertainties were propagated for the actinides—U, Np, Pu, Am, and Cm—and for the fission products—charge number from 33 to 65. Exceptions to this are the JEFF-3.3 uncertainty evaluations for the cross-sections of 241Am, which would require further processing2 for the sampling with SANDY, and of 103Rh, where an error occurred. These data and the ones for which no covariance evaluation was provided were excluded from the analysis. A detailed list of the perturbed cross-sections is reported in Tables 1, 3.
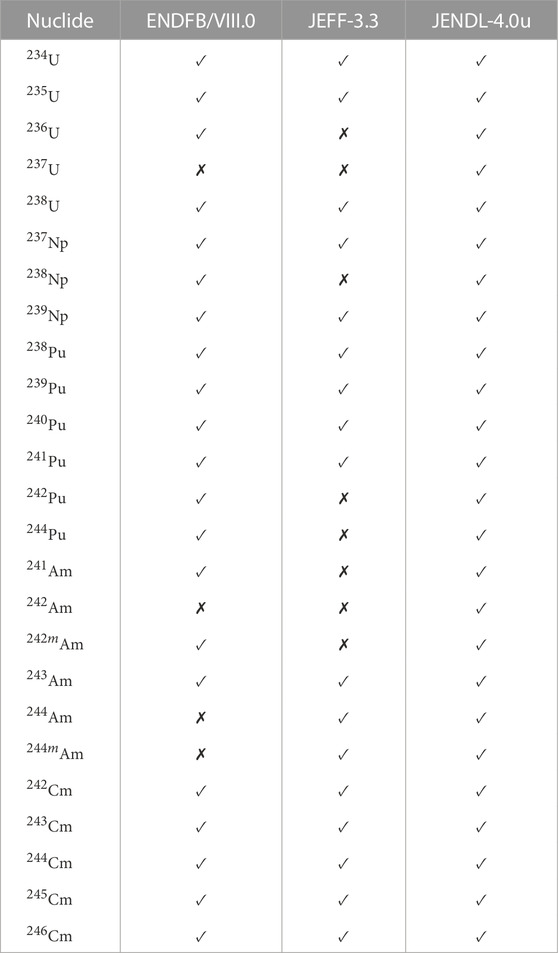
TABLE 1. Actinides whose cross-section covariance matrices were considered in the uncertainty propagation study.
The magnitude of the statistical error inherent to the Monte Carlo simulations is increased by the simplifying assumption of reduced particle histories. This contribution to the uncertainty was evaluated by running 100 simulations with varying seeds. For each ith component of the SNF array, the one-standard-deviation concentration uncertainty was then computed as follows:
where the uncertainties are considered as standard deviations, originating from the nuclear data uND and from the counting statistics uSTAT. This approach assumes that all the calculations run with different sets of perturbed nuclear data have the same statistical error. The uncertainties were propagated separately from the cross-sections of the actinides and of the fission products. Summing the two contributions assumes model linearity and no correlation between them. This is further investigated in Rochman and Bauge (2021).
No covariance evaluation on the cross-section of fission products is provided in JENDL-4.0u. For this reason, the concentration uncertainty results of the fission products will be reported for ENDF/B-VIII.0 and JEFF-3.3 only.
3.1.1 Concentration uncertainty of the actinides
The uncertainty propagated from the cross-sections to the actinides’ concentration at discharge of assembly NT3G23 is reported in Figure 5. The uncertainty analysis highlighted the overall negligible uncertainty originating from the counting statistics and from the fission products’ cross-sections.
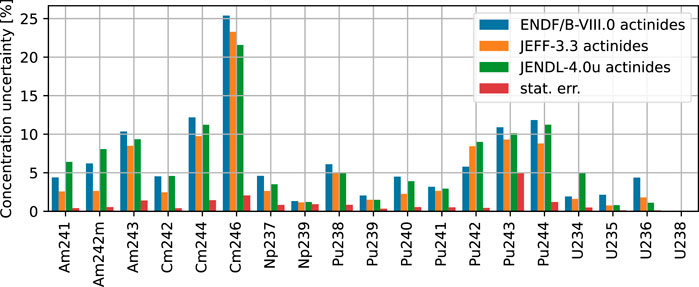
FIGURE 5. Nuclear data uncertainty on actinide composition and comparison with the propagated statistical error inherent to the Monte Carlo method.
Uncertainties below 0.05% were found for the concentration of 238U. This is a consequence of the low evaluated uncertainty—about 1%—on its captured cross-section (see Table 2 too) and of the low sensitivity of its concentration to the reactions happening in the fuel (Fiorito et al., 2021). The latter is explained by the large quantity of 238U in the fuel, which also justifies the negligible—below 0.005%—statistical error on its concentration. Uncertainties below 5% on the concentration of 235U and 236U were found. Those are even of the order of 2% when propagated from JEFF-3.3 and from JENDL-4.0u, as the evaluated cross-section uncertainties for those nuclides are lower in those libraries. The uncertainty builds via neutron capture from 235U to 236U. Such an uncertainty rise is also visible when the uncertainty is propagated from JEFF-3.3, where no covariance evaluation for the cross-section of 236U is given. The concentration uncertainty of 236U, therefore, seems to be mainly attributable to the neutron capture cross-section of 235U. The larger uncertainty propagated to the concentration uncertainty of 235U—and then to the one of 236U—from ENDF/B-VIII.0 is also related to the uncertainties on other fissioning isotopes’ cross-section uncertainties—e.g., 239Pu—, which are larger in ENDF/B-VIII.0 evaluations. The fissioning nuclides are correlated by flux normalization. The same uncertainty evaluation is reported in ENDF/B-VIII.0 and in JEFF-3.3 for the neutron capture cross-section of 234U, of the order of 2%, whereas the one evaluated by JENDL-4.0u is of the order of 10%. This is likely to explain the uncertainty prediction differences on the concentration of 234U.
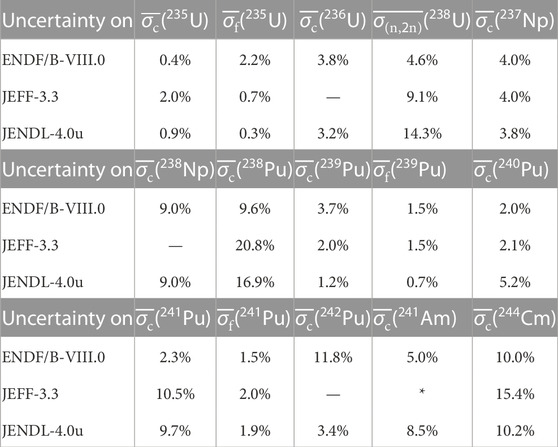
TABLE 2. Uncertainty of a number of one-group reactions. For readability, the reactions are reported in the columns (c: capture, f: fission (n, 2n) (n, 2n) reaction; —missing covariance evaluation, *: covariance matrix not processed).Uncertainties ranging from 1.0%—JEFF-3.3 and ENDF/B-VIII.0—to 1.2%—JENDL-4.0u—were found for the one-group capture cross-section of 238U.
The uncertainty on the concentration of 238Pu is consistent and of the order of 5%. Similar considerations hold for 239Pu, whose concentration uncertainty is about 2%. The concentration uncertainties of 240Pu and 241Pu are below 5%. The 240Pu neutron capture cross-section uncertainty evaluated in JEFF-3.3 is about twice lesser than in the other libraries. This reflects on its concentration uncertainty. The uncertainty evaluation for the concentration of 241Am ranges from 3 to 6%. The effect of not having propagated the cross-section uncertainty of 241Am from JEFF-3.3 is visible in Figure 5. Consistent uncertainty results of about 10% were also found for the concentration uncertainty of 244Cm. This was noticed despite that JEFF-3.3 lacks in the covariance evaluation for the cross-section of 242Pu, involved in the production of 244Cm (Fiorito et al., 2021). The concentration uncertainty of 246Cm exceeds 20%.
3.1.2 Concentration uncertainty of the fission products
The uncertainty was propagated from the fission product capture cross-sections. The contribution to this of the uncertainties on the cross-sections of the actinides is negligible with respect to the one propagated from the fission product ones. As reported in Table 3, JENDL-4.0u is excluded from this analysis as no covariance evaluation for the cross-section of fission products is reported there.
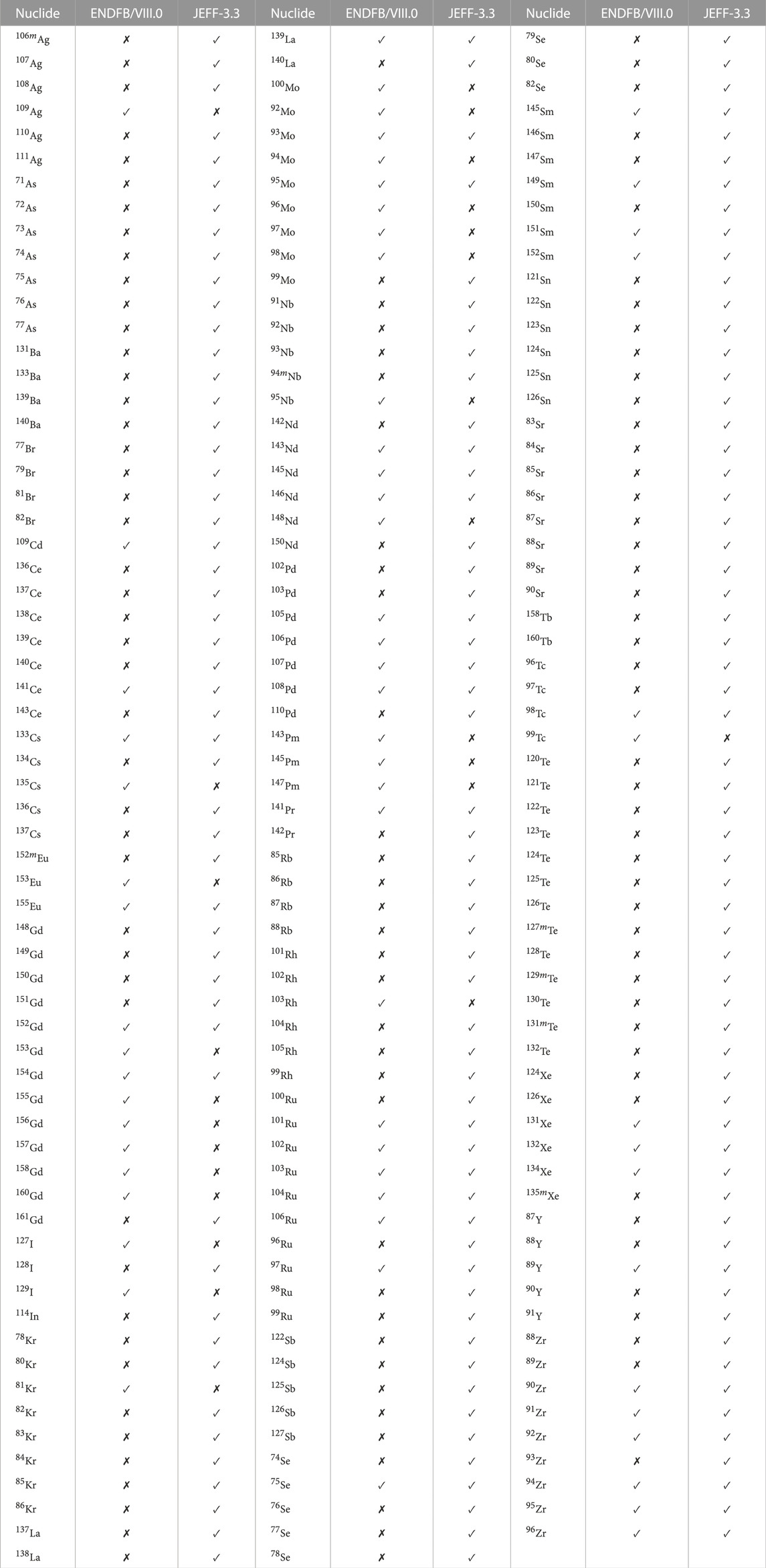
TABLE 3. Fission products whose cross-section covariance matrices were considered in the uncertainty propagation study.
This analysis gives larger concentration uncertainty predictions for 134Cs, produced by captures in 133Cs, than for many fission products with less neutron captures involved in their production. An underestimation of the uncertainty on the concentration of fission products predicted in this work is to be expected, the fission yields being excluded from the uncertainty propagation and because of a number of missing covariance evaluations for fission products. Overall, the statistical error was found to be negligible with respect to the nuclear data uncertainty. In general, the contribution of the actinides’ cross-section uncertainty to the concentration uncertainty of fission products is negligible.
Figure 6 reports uncertainties of the order of 25% or larger on the concentration of 155Eu and 155Gd. The uncertainty on the concentration of 155Eu is comparable with the evaluated uncertainty in ENDF/B-VIII.0 and in JEFF-3.3. The larger uncertainty prediction given by ENDF/B-VIII.0 builds from the preceding europium isotopes, more relevant than the one coming from the larger evaluation given from the neutron capture cross-section of 155Eu for energies below 0.5 eV. This trend differs from the one identified in Grimaldi et al. (2022a) because of the harder spectrum in the Takahama sample derived from the gadolinium-enriched pins. The main contribution to the concentration uncertainty of 155Gd comes from the neutron capture cross-section uncertainty shared evaluation of the two libraries, which comes from ENDF/B-VII.1. The missing covariance evaluation for the neutron capture cross-section of 155Gd in JEFF-3.3 explains the lower concentration uncertainty predicted using this dataset.
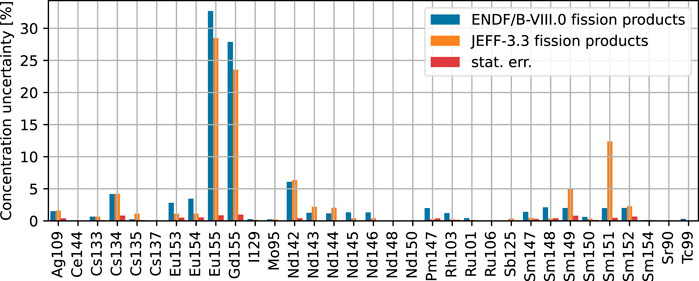
FIGURE 6. Nuclear data uncertainty on fission product composition and comparison with the propagated statistical error inherent to the Monte Carlo method.
The concentration uncertainties of the neodymium isotopes are of the order of 5% or lower. The concentrations of 148Nd and 137Cs are strictly correlated to the sample burnup at the extent that those nuclides are often used as burnup indicators. Because the simulations are normalized to the power generation in the sample and given this correlation, the concentration uncertainties on 148Nd and 137Cs are null. ENDF/B-VIII.0 and JEFF-3.3 share the same evaluation for the cross-section uncertainty of 133Cs, which reflects on the concentration uncertainty of 133Cs and 134Cs, of the order of 1% and 4%, respectively. JEFF-3.3 does not provide uncertainty evaluation for the capture cross-section of 153Eu, which reflects on the concentration uncertainty results of 153Eu and 154Eu. The largest discrepancy among the concentration uncertainty propagated from ENDF/B-VIII.0 and JEFF-3.3 was found on 151Sm, for which capture cross-section evaluated uncertainty is about double that in JEFF-3.3. Overall, the concentration uncertainty results on the isotopes of samarium predicted by ENDF/B-VIII.0 might be compromised in their reliability because of the non-physical uncertainty evaluation on the capture cross-section of 145Pm, involved in their production.
3.2 Uncertainty evolution with burnup
The presented results are pretty much in line with that reported in Grimaldi et al. (2022a) for a model of sample MKP109 irradiated in Calvert Cliffs. A study of the concentration uncertainty buildup in the two benchmarks (Calvert Cliffs MKP109 and Takahama SF95-4) was performed to better understand how the uncertainty propagation mechanisms change during irradiation, modifying the relevance of different uncertainty sources—the cross-sections of different nuclides in this study. The analysis is performed considering the results until 36.69
The uncertainty propagation mechanisms are tightly linked with the production and removal phenomena, consisting in neutron-induced reactions and decay for the considered nuclides. While 235U is mainly already present in the fuel, the production of other actinides allows one to consider many of the most relevant transmutation chains starting from the uranium isotopes. The considered production paths are as follows (Oizumi et al., 2015; Fiorito et al., 2021):
1) 235U
2) 238U
3) 238U
4) 238U
The evaluated reaction uncertainties were also propagated to the most relevant one-group cross-section, computed as
where the integrals are computed over the energy domain E and σj(i) refers to the cross-section σ of nuclide i for reaction j. The spectrum computed in the simplified model of Takahama SF95-4 using ENDF/B-VII.1 data was used for the calculation and 200 cross-section samples were taken. The results are reported in Table 2, which were rather consistent with the ones computed with the PWR spectrum tabulated in NJOY as the “mid-life PWR spectrum” (card IWT = 5 in the GROUPR module). When referring to the uncertainties reported in Table 2, one should bear in mind that the results are only indicative of the relevance of the evaluated cross-section uncertainties. Moreover, the concentration uncertainty results from the convolution of uncertainties and sensitivities, making Table 2 not exhaustive as a tool.
When the concentration of actinides is considered, one should bear in mind that the production/removal mechanisms tend to accumulate with burnup. For this reason, it is often convenient to refer to the relative relevance of the uncertainty sources. Moreover, this means that the phenomena identified until a certain burnup keep existing later, still contributing to the total uncertainty, just possibly with lower relative relevance.
3.2.1 238Pu concentration uncertainty
The production of 238Pu through captures in 241Am is not relevant for the considered burnup (Fiorito et al., 2021); therefore, production path 3 from the previous section is excluded from the analysis. Production path 1 is also reported to be more relevant than production path 2. The concentration uncertainty evolution of 238Pu is reported in Figure 7.
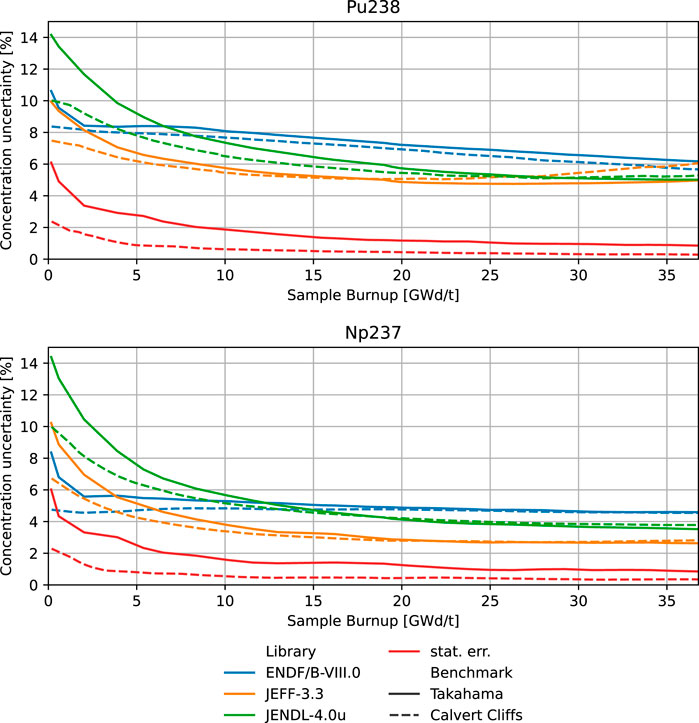
FIGURE 7. Concentration uncertainty evolution with burnup for nuclides 238Pu (top) and 237Np (bottom).
3.2.1.1 Until 5.
The production of 238Pu happens earlier in the sample irradiated in Calvert Cliffs as a consequence of the initial 236U concentration included in this model only. Therefore, the larger concentration of 236U results in lower relative relevance of other reactions, such as the ones in 235U and 237U.
Being the only library with a covariance evaluation for the capture cross-section of 237U, JENDL-4.0u gives a larger estimation of the 238Pu concentration uncertainty and a larger discrepancy when comparing the two benchmarks. No uncertainty evaluation is given in JEFF-3.3 for the capture in 236U, which is likely to explain the lower 238Pu concentration uncertainty prediction.
When comparing the concentration uncertainty of 238Pu with the one of 237Np (Figure 7), one can note quite relevant similarities, resulting from the common uncertainty sources. The concentration uncertainty predicted by JEFF-3.3 is similar for both nuclides (even equal at beginning of irradiation, 10%). This is an effect of the missing uncertainty evaluation on the capture cross-section of 238Np, nuclide linking the 238Pu production to 237Np. Such an evaluation is instead the same in ENDF/B-VIII.0 and JENDL-4.0u (Table 2). This results in the larger concentration uncertainty prediction by ENDF/B-VIII.0 for 238Pu than for 237Np, reported in Figure 7. Such an effect is not visible when it comes to JENDL-4.0u because of its lower relative relevance.
3.2.1.2 Until 20.
The production path starting from (n, 2n) reaction in 238U gains relevance, but no clear effect of this reaction evaluated uncertainty was found. Overall, the consistency of the 238Pu concentration uncertainty results predicted by each library for the two benchmarks appears to be larger in this phase where 236U concentration builds up. The larger discrepancy in the predictions given by JENDL-4.0u is attributable to the larger 236U content in the Calvert Cliffs sample, shading the effect of 237U cross-section uncertainties.
With the buildup of 236U, the relative relevance of the reactions in 235U and 237U decreases. This explains the decreasing trend of 238Pu concentration uncertainty predicted by JEFF-3.3 and JENDL-4.0u. This is more pronounced in the prediction given by JENDL-4.0u as an effect of the uncertainty evaluation for the cross-section of 237U, present only there. In the concentration uncertainty prediction given by JEFF-3.3, this effect and the missing covariance evaluation for the 236U reactions are partially compensated by the larger uncertainty evaluation on the 238Pu reactions, increasing in relative relevance with the progressive buildup of this nuclide. The 238Pu concentration uncertainty prediction given by ENDF/B-VIII.0 is quite steady around 7.5%. This is an effect of the larger cross-section uncertainty evaluation given in ENDF/B-VIII.0 for the neutron capture in 236U.
3.2.1.3 Until 36.
Among the considered nuclear data libraries, JEFF-3.3 predicts the lowest 238Pu concentration uncertainty until a burnup of approximately 20
3.2.2 241Am concentration uncertainty
The uncertainty on the concentration of 241Am mainly comes from the isotopes of plutonium that contribute to its creation. Their concentration increases progressively with burnup, resulting in a progressive increase of relevance of the reactions in the later plutonium isotopes in determining the concentration uncertainty of 241Am.
3.2.2.1 Until 10.
A larger uncertainty prediction for the concentration of 240Pu and 241Am given by ENDF/B-VIII.0 is visible in Figure 8. This is related to the uncertainty evaluation on the capture cross-section of 239Pu, reported in its one-group average in Table 2. The contribution given by the uncertainty on the fission cross-section of 239Pu to the concentration uncertainty of 240Pu and 241Am is less relevant, and the evaluated fission cross section uncertainties are less discrepant, as reported in Table 2.
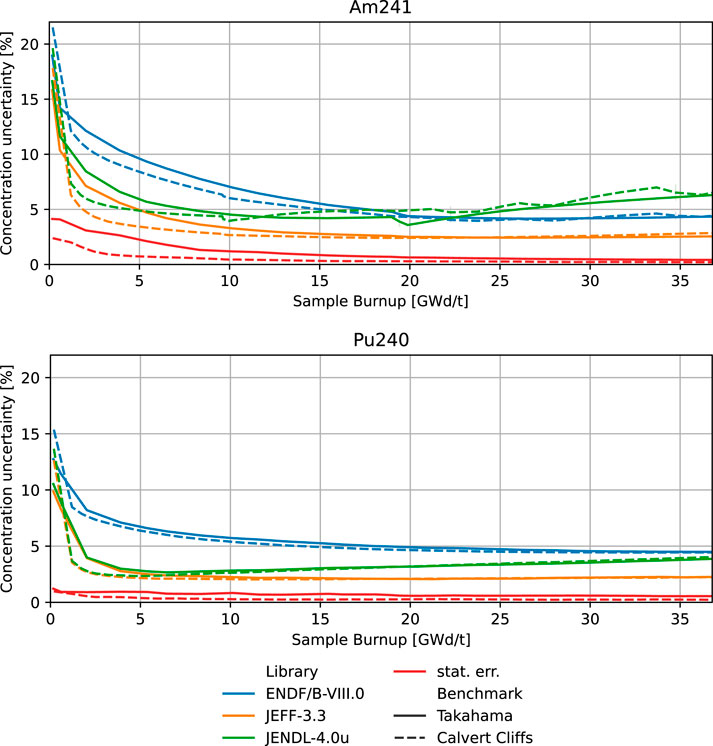
FIGURE 8. Concentration uncertainty evolution with burnup for nuclides 241Am (top) and 240Pu (bottom).
3.2.2.2 Until 36.
The increase in the concentration uncertainty of 241Am results from the increased sensitivity to 240Pu capture cross-section. Table 2 reports the larger one-group uncertainty evaluated by JENDL-4.0u for such a reaction. A similar phenomenon happens previously for the concentration uncertainty of 240Pu. This highlights a certain propagation time of these effects, as the concentration 240Pu will be more sensitive to 240Pu data before such a sensitivity develops for the concentration of 241Am.
Similarly, 241Am builds up and the contribution of its cross-section uncertainty becomes more relevant to its concentration uncertainty. This effect overlaps to the one induced by the sensitivity to captures in 240Pu and 241Pu, with JENDL-4.0u giving a larger uncertainty evaluation for the cross-sections of those nuclides as well (Table 2).
In Figure 8, the effect of refueling is visible not only in the form of jumps mainly in the concentration uncertainty prediction given by JENDL-4.0u but also in the one given by ENDF/B-VIII.0 at a lower extent. During the decay, there is no sensitivity to the cross-sections anymore and part of the 240Pu concentration decays to 241Am. The concentration of 240Pu that decays has a lower uncertainty than that of the 241Am that is present in the sample. This results in a lowering effect of the concentration of 241Am. Overall, the 241Am concentration uncertainty predicted by JEFF-3.3 is affected by the non-propagation of the 241Am capture cross-section uncertainty evaluation.
3.2.3 244Cm concentration uncertainty
The evaluated uncertainty on 239Pu capture cross-section is reflected on the concentration uncertainty of 244Cm in the early stages of irradiation. As reported for 241Am in Figure 8, this results in larger concentration uncertainty predicted by ENDF/B-VIII.0 for 244Cm, reported in Figure 9. With burnup, this gets compensated by the increasing sensitivity to the reactions in the other plutonium isotopes, for which capture cross-sections lower uncertainty evaluations are given in ENDF/B-VIII.0 than in JENDL-4.0u. This results in the decreasing trend of the concentration uncertainty predicted by ENDF/B-VIII.0. A similar and even stronger effect was visible previously on the concentration uncertainty of 242Pu. Both nuclides show high sensitivity to the capture cross-section of 240Pu and 241Pu. The missing covariance evaluation for the capture cross-section of 242Pu in JEFF-3.3 reflects the lower prediction of the concentration uncertainty of 244Cm given by this library.
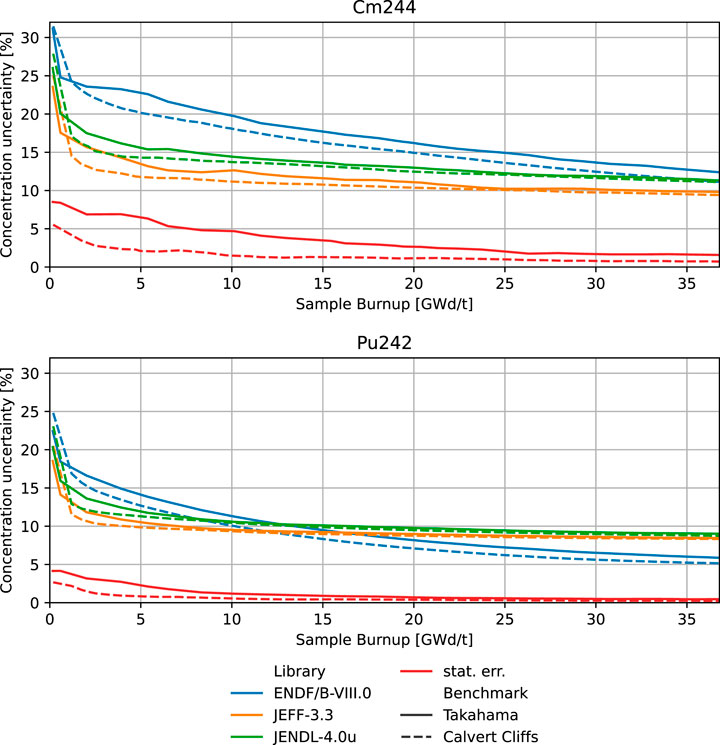
FIGURE 9. Concentration uncertainty evolution with burnup for nuclides 244Cm (top) and 242Pu (bottom).
3.2.4 235U concentration uncertainty
The results on the concentration uncertainty of 235U reported in Figure 10 are the most reflective of the difference in the initial sample enrichment. This follows from the power P normalization over the sample volume V implemented in the two models, which entails a correlation of the concentration of 235U to the nuclear data of other fissioning nuclides, such as 239Pu. The power normalization can be expressed as follows:
where RR is the fission reaction rate and Q is the energy release per fission. Eq. 2 clarifies the analogy of the power normalization to a normalization of the total number of fissions.
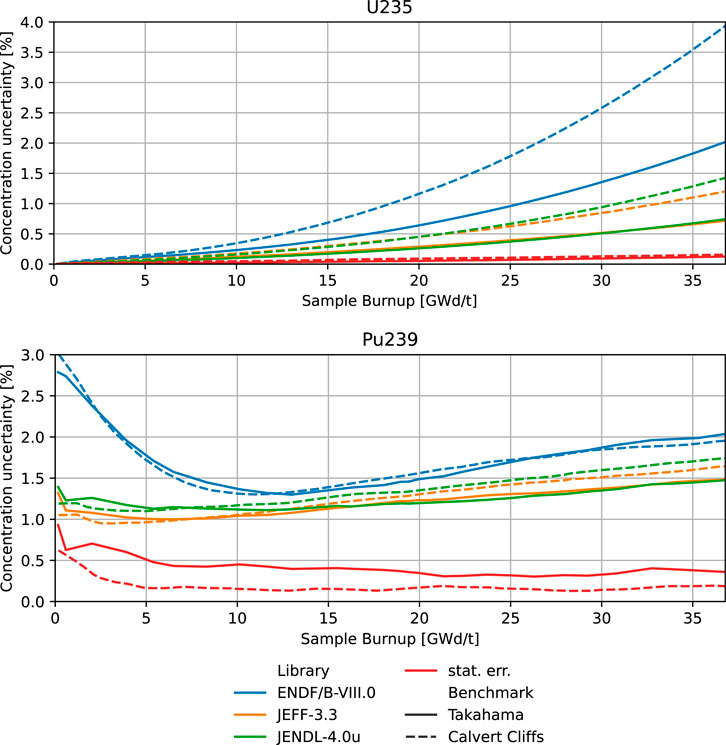
FIGURE 10. Concentration uncertainty evolution with burnup for nuclides 235U (top) and 239Pu (bottom).
This results in a correlation of the concentration of 235U to the nuclear data of 239Pu and to the nuclear data impacting on their concentration (and in principle to those of all other fissioning systems). The 235U results are then correlated to a number of plutonium isotope data and production chain. This correlation is then made stronger in the Calvert Cliffs sample, where the relative number of 239Pu fissions is more relevant because of its lower enrichment. The increasing concentration uncertainty trend with burnup, reported in Figure 10, is explained by the gain in relevance of non-235U fissioning systems. Relevant contributions to the concentration uncertainty of 235U also come from the uncertainty on its own reactions and to the captures in 238U, as reported in Fiorito et al. (2021).
The effect of uncertainty evaluated for the reactions of 235U on its concentration uncertainty proves to be increasing over time. As a matter of fact, a simplified model can be defined for the consumption of 235U. Assuming negligible production of such a nuclide and constant reaction rate RR, the concentration of 235U
The sensitivity S of
Assuming no other uncertainty source, the uncertainty on
increasing in time. The non-linear trend in Figure 10 is explained by the non-linearity of other phenomena, such as the correlation to the nuclear data of 239Pu and 238U.
The capture cross-section of 239Pu relevantly contributes to the concentration uncertainty of 235U, the uncertainty evaluations being similar in the three nuclear data libraries for the capture cross-sections of 235U and 238U and for the fission cross-sections of 235U and 239Pu. This also reflects on the concentration uncertainty of 239Pu, reported in Figure 10, explaining the larger concentration uncertainty predicted by ENDF/B-VIII.0 until 20
3.3 Representativity study
Relevant similarities were found in the concentration uncertainty results obtained for 238Pu, 241Am, 244Cm, and 235U, comparing them at discharge and considering their evolution with burnup. This was the case despite many significant differences in the models, such as the different initial enrichment. This section performs a quantitative assessment of this similarity, reporting the representativity of one model to the other at a sample burnup of approximately 36
Several measures of model similarity were found in the literature. To consider the effect of the nuclear data uncertainties, the representativity coefficient r is defined as in Blaise et al. (2021):
where S is the sensitivity vector of the observable to the nuclear data, Σnd is the nuclear data covariance matrix and subscripts, and T and C indicate the samples obtained from Takahama and Calvert Cliffs, respectively. As reported in Blaise et al. (2021), this equals the correlation between the concentrations predicted by the two models, being the numerator the covariance of the two model responses and the denominator a re-normalization to the response uncertainty computed with the two models. Computing the representativity coefficient r using the sensitivity profiles requires extra computational effort. Therefore, an approximation
Very high levels of representativity were found, implying the similarity brought by the capture-decay scheme, from which the nuclide concentration builds up, is more relevant than the differences in the simulation parameters. Further analyses on the topic will be performed in the future based on these results.
4 Discussion
The concentration uncertainty results predicted for 238Pu (Section 3.2.1) highlight the need for discriminating among the uncertainty sources. The consistent uncertainty prediction of about 5% given by the three nuclear data libraries at discharge is not reflective of a similar concentration uncertainty evolution during irradiation. This can partly be due to the differences in the uncertainty evaluations given by the libraries and the effect of missing evaluations, which can be hidden by compensation. As an example, the large uncertainty evaluation given in JEFF-3.3 for the capture cross-section of 238Pu compensates the effect of the missing covariance evaluation for the cross-section of 236U. This study stresses the need of having complete uncertainty information in the nuclear data libraries to allow for multi-purpose analyses and complete uncertainty propagation. Moreover, it points out that the consistency found among the concentration uncertainties predicted by the nuclear data libraries can be a consequence of the specific sample burnup considered rather than an indication of actual uncertainty evaluation consistency.
The concentration uncertainty results computed for 241Am (Section 3.2.2) highlight the importance of considering both time and burnup in the analysis. This emerges from the considerations on the inventory decay during refueling. Moreover, a time-shift in the concentration uncertainty results was identified when comparing the predictions for 240Pu and 241Am. Similar phenomena, even correlated, explain the uncertainty trend of the two actinides. Yet, these effects appear later on the concentration uncertainty of 241Am than on the one of 240Pu. This is because of the slower production of 241Am and of the slower propagation of the 240Pu cross-section uncertainty to the concentration of 241Am.
The concentration uncertainty results predicted for 235U (Section 3.2.4) stress the need of considering model-induced correlations in the uncertainty quantification and in discrimination of the different uncertainty sources. In the case of fissioning nuclides, mutual correlations are of key importance in the interpretation of the concentration uncertainty results. These correlations are not only to the nuclear data of the other fissioning nuclides but also to their concentrations and therefore to all the nuclear data involved in their production. These correlations can be quite hidden in the results, and detailed understanding of the model behavior (power normalization in this case) is crucial for their identification.
5 Conclusion
Assembly NT3G23 irradiated in Takahama unit 3 PWR was modeled in Serpent, predicting the nuclide concentration in sample SF95-4 and its uncertainty. The model was validated against experimental results, and the obtained C/E values were compared with those of a similar analysis found in the literature. Nuclear data from ENDF/B-VIII.0, JEFF-3.3, and JENDL-4.0u were considered in the analysis.
For uncertainty propagation, the samples of the reaction cross-sections were taken with the SANDY code, according to a multivariate Gaussian distribution defined by the evaluated best estimates and covariance matrices stored in those libraries. In the fuel sample irradiated in Takahama, discharge concentration uncertainties of the order of 2% are predicted by all the considered nuclear data libraries for 235U and 239Pu. The concentration uncertainty predicted at discharge for most of the uranium, neptunium, and plutonium isotopes relevant for SNF applications is of the order of 5%. Larger uncertainties were predicted for the discharge concentration of 244Cm, up to 12%, and 246Cm, up to 25%. Overall, the predicted concentration uncertainties already explain most of the C/E discrepancies, despite only having propagated cross-section uncertainties.
Concentration uncertainty evolution with fuel sample burnup was analyzed comparing the results of the two PWR spent fuel benchmarks. This analysis was performed considering the concentration uncertainty results found in the literature for the fuel sample MKP109-P irradiated in the Calvert Cliffs PWR reactor and the ones computed for SF95-4. The effect of different initial enrichment is visible in the concentration uncertainty of 235U, resulting in a doubled concentration uncertainty as a consequence of a 1% initial enrichment difference. At low burnup, the cross-sections of 239Pu and 240Pu and their evaluated uncertainties were found to play a major role in determining the uncertainty concentration of both 241Am and 244Cm. At higher burnup, the concentration uncertainty results of minor actinides were found to be increasingly sensitive to the quality of their nuclear data uncertainty evaluation. Overall, for the minor actinides, the concentration uncertainty was found to be lower at discharge than at the beginning of irradiation. During the irradiation, JEFF-3.3 predicts lower concentration uncertainties than the other nuclear data libraries. This is likely to be related to the missing uncertainty evaluations in this library, such as the one for 236U cross-sections.
A study of representativity of the two PWR assembly models was performed at discharge. Despite the differences, correlations larger than 95% were found. This hints the predominance of the PWR irradiation environment over a case-dependent assembly setup. This result needs to be complemented with further studies, extending the analysis to a broader set of observables and to more different irradiation conditions and environments. Moreover, studies on the evolution of representativity with burnup could also be considered. Yet, if confirmed, this result could open the ground for relevant simplifications of uncertainty quantification of the SNF inventory.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
FG: Conceptualization, methodology, investigation, and writing—original draft; PR: investigation, methodology, and writing—review and editing; LF: investigation, software, and writing—review and editing; EB: investigation and writing—review and editing; CB: writing—review and editing; SD: writing—review and editing.
Funding
The authors acknowledge that the work presented herein was financially supported by the Euratom Research and Training Program under grant agreement no. 847593 (EURAD project).
Acknowledgments
The authors would like to acknowledge the team of researchers and students who contributed to the development of SANDY through the years for their support and helpful discussion.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1The term batch refers to a number of particles simulated simultaneously. A Monte Carlo simulation is composed of several batches of particles successively simulated.
2Cross-section uncertainties—MF33—data were processed in this work, while only uncertainties on the resonance parameters—MF32—are given on the JEFF-3.3 241Am evaluation.
References
Blaise, P., Fougeras, P., and Cathalau, S. (2021). An application of sensitivity and representativity approach for the design of a 100%mox bwr experimental program in zpr. Ann. Nucl. Energy 163, 108566. doi:10.1016/j.anucene.2021.108566
Brown, D., Chadwick, M., Capote, R., Kahler, A., Trkov, A., Herman, M., et al. (2018). ENDF/B-VIII.0: The 8 th major release of the nuclear reaction data library with CIELO-project cross sections, new standards and thermal scattering data. Nucl. Data Sheets 148, 1–142. doi:10.1016/j.nds.2018.02.001
Chadwick, M., Herman, M., Obložinský, P., Dunn, M., Danon, Y., Kahler, A., et al. (2011). ENDF/B-VII.1 nuclear data for science and Technology: Cross sections, covariances, fission product yields and decay data. Nucl. Data Sheets 112, 2887–2996. doi:10.1016/j.nds.2011.11.002
Díez, C., Buss, O., Hoefer, A., Porsch, D., and Cabellos, O. (2015). Comparison of nuclear data uncertainty propagation methodologies for PWR burn-up simulations. Ann. Nucl. Energy 77, 101–114. doi:10.1016/j.anucene.2014.10.022
Ebiwonjumi, B., Kong, C., Zhang, P., Cherezov, A., and Lee, D. (2021). Uncertainty quantification of PWR spent fuel due to nuclear data and modeling parameters. Nucl. Eng. Technol. 53, 715–731. doi:10.1016/j.net.2020.07.012
Fiorito, L., Piedra, D., Cabellos, O., and Diez, C. (2015). Inventory calculation and nuclear data uncertainty propagation on light water reactor fuel using ALEPH-2 and SCALE 6.2. Ann. Nucl. Energy 83, 137–146. doi:10.1016/j.anucene.2015.03.046
Fiorito, L., Romojaro, P., Cabellos, O., García-Hormigos, M., Hernandez-Solis, A., Sánchez-Fernández, S., et al. (2021). On the use of criticality and depletion benchmarks for verification of nuclear data. Ann. Nucl. Energy 161, 108415. doi:10.1016/j.anucene.2021.108415
Fiorito, L., Žerovnik, G., Stankovskiy, A., Van den Eynde, G., and Labeau, P. (2017). Nuclear data uncertainty propagation to integral responses using SANDY. Ann. Nucl. Energy 101, 359–366. doi:10.1016/j.anucene.2016.11.026
Grimaldi, F., Fiorito, L., Romojaro, P., and Hernandez-Solis, A. (2022a). “Nuclear data uncertainty quantification for the nuclide inventory of a Calvert Cliffs spent fuel sample,” in International conference on physics of reactors 2022. PHYSOR 2022).
Grimaldi, F., Fiorito, L., Romojaro, P., and Žerovnik, G. (2022b). Burnup-dependence of the fuel composition uncertainty. Presented at the 31st AMPHOS spent fuel workshop.
Grimaldi, F. (2022). Nuclear data uncertainty quantification in fuel depletion calculations. Master’s thesis defended at Politecnico di Torino.
Herman, M., and Trkov, A. (2010). ENDF-6 formats manual. NY: National Nuclear Data Center Brookhaven National Laboratory Upton. Tech. rep.
Ilas, G., Gauld, I. C., Difilippo, F. C., and Emmett, M. B. (2010). Analysis of experimental data for high burnup PWR spent fuel isotopic validation -Calvert Cliffs, Takahama, and three mile island reactors. Tech. rep.
Ilas, G., and Liljenfeldt, H. (2017). Decay heat uncertainty for bwr used fuel due to modeling and nuclear data uncertainties. Nucl. Eng. Des. 319, 176–184. doi:10.1016/j.nucengdes.2017.05.009
Leppänen, J., Pusa, M., Viitanen, T., Valtavirta, V., and Kaltiaisenaho, T. (2015). The Serpent Monte Carlo code: Status, development and applications in 2013. Ann. Nucl. Energy 82, 142–150. doi:10.1016/j.anucene.2014.08.024
Leray, O., Rochman, D., Grimm, P., Ferroukhi, H., Vasiliev, A., Hursin, M., et al. (2016). Nuclear data uncertainty propagation on spent fuel nuclide compositions. Ann. Nucl. Energy 94, 603–611. doi:10.1016/j.anucene.2016.03.023
Macfarlane, R., Muir, D. W., Boicourt, R. M., Kahler, A. C., and Conlin, J. L. (2017). The NJOY nuclear data processing system. Version 2016. Los Alamos, NM (United States): Los Alamos National Laboratory (LANL. Tech. rep. doi:10.2172/1338791
Michel-Sendis, F., Gauld, I., Martinez, J., Alejano, C., Bossant, M., Boulanger, D., et al. (2017). SFCOMPO-2.0: An OECD NEA database of spent nuclear fuel isotopic assays, reactor design specifications, and operating data. Ann. Nucl. Energy 110, 779–788. doi:10.1016/j.anucene.2017.07.022
Nakahara, Y., Inagawa, J. U. N., Nagaishi, R., Kurosawa, S., Kohno, N., Onuki, M., et al. (2002a). Nuclide composition benchmark data set for verifying burnup codes on spent light water reactor fuels. Nucl. Technol. 137, 111–126. doi:10.13182/nt02-2
Nakahara, Y., Suyama, K., and Suzaki, T. (2002b). Technical development on burn-up credit for spent LWR fuels (translation). Tech. Rep. January.
Nea Nuclear Science Committee (2016). Evaluation guide for the evaluated spent nuclear fuel assay database (sfcompo).
Oizumi, A., Jin, T., Ishikawa, M., and Kugo, T. (2015). Physical mechanism analysis of burnup actinide composition in light water reactor MOX fuel and its application to uncertainty evaluation. Ann. Nucl. Energy 81, 117–124. doi:10.1016/J.ANUCENE.2015.03.033
Plompen, A. J. M., Cabellos, O., De Saint Jean, C., Fleming, M., Algora, A., Angelone, M., et al. (2020). The joint evaluated fission and fusion nuclear data library, JEFF-3.3. Eur. Phys. J. A 56, 181. doi:10.1140/epja/s10050-020-00141-9
Radulescu, G., Gauld, I. C., and Ilas, G. (2010). SCALE 5.1 predictions of PWR spent nuclear fuel isotopic compositions. Oak Ridge, TN (United States): Oak Ridge National Laboratory (ORNL. Tech. rep. doi:10.2172/983556
Rochman, D. A., and Bauge, E. (2021). Fission yields and cross sections: Correlated or not? EPJ Nucl. Sci. Technol. 7, 5. doi:10.1051/epjn/2021005
Rochman, D., Alvarez-Velarde, F., Dagan, R., Fiorito, L., Hakkinen, S., Kromar, M., et al. (2022). On the estimation of nuclide inventory and decay heat: A review from the EURAD European project. EPJ Nucl. Sci. Technol. 9, 14. doi:10.1051/epjn/2022055
Rochman, D., Hursin, M., Vasiliev, A., and Ferroukhi, H. (2021). Impact of H in H2O thermal scattering data on depletion calculation: k∞, nuclide inventory and decay heat. EPJ Nucl. Sci. Technol. 7, 24. doi:10.1051/epjn/2021027
Rochman, D., Leray, O., Hursin, M., Ferroukhi, H., Vasiliev, A., Aures, A., et al. (2017). Nuclear data uncertainties for typical LWR fuel assemblies and a simple reactor core. Nucl. Data Sheets 139, 1–76. doi:10.1016/j.nds.2017.01.001
Rochman, D., van der Marck, S., Koning, A., Sjöstrand, H., and Zwermann, W. (2014a). Uncertainty propagation with fast Monte Carlo techniques. Nucl. Data Sheets 118, 367–369. doi:10.1016/j.nds.2014.04.082
Rochman, D., Zwermann, W., van der Marck, S. C., Koning, A. J., Sjöstrand, H., Helgesson, P., et al. (2014b). Efficient use of Monte Carlo: Uncertainty propagation. Nucl. Sci. Eng. 177, 337–349. doi:10.13182/NSE13-32
Shibata, K., Iwamoto, O., Nakagawa, T., Iwamoto, N., Ichihara, A., Kunieda, S., et al. (2011). JENDL-4.0: A new library for nuclear science and engineering. J. Nucl. Sci. Technol. 48, 1–30. doi:10.1080/18811248.2011.9711675
Wemple, C., and Zwermann, W. (2017). Nuclear data uncertainty propagation by the XSUSA method in the HELIOS2 lattice code. EPJ Web Conf. 146, 02020. doi:10.1051/epjconf/201714602020
Williams, M. L., Ilas, G., Marshall, W. J., and Rearden, B. T. (2014). Applications of nuclear data covariances to criticality safety and spent fuel characterization. Nucl. Data Sheets 118, 341–345. doi:10.1016/j.nds.2014.04.075
Keywords: burnup, spent nuclear fuel, nuclide inventory, uncertainty analysis, nuclear data, SANDY, model comparison
Citation: Grimaldi F, Romojaro P, Fiorito L, Belfiore E, Bruggeman C and Dulla S (2023) Nuclear data uncertainty quantification on PWR spent nuclear fuel as a function of burnup. Front. Energy Res. 11:1146598. doi: 10.3389/fenrg.2023.1146598
Received: 17 January 2023; Accepted: 03 April 2023;
Published: 18 April 2023.
Edited by:
Jingang Liang, Tsinghua University, ChinaReviewed by:
Oscar Cabellos, Universidad Politécnica de Madrid, SpainJiankai Yu, Massachusetts Institute of Technology, United States
Copyright © 2023 Grimaldi, Romojaro, Fiorito, Belfiore, Bruggeman and Dulla. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Federico Grimaldi, ZmVkZXJpY28uZ3JpbWFsZGlAc2NrY2VuLmJl
 Federico Grimaldi
Federico Grimaldi Pablo Romojaro
Pablo Romojaro Luca Fiorito
Luca Fiorito Enrica Belfiore
Enrica Belfiore Christophe Bruggeman
Christophe Bruggeman Sandra Dulla2
Sandra Dulla2