Applications of machine learning approaches in aerodynamic aspects of axial flow compressors: A review

A compressor is one of the key components of a gas turbine engine and its performance and characteristics significantly affect the overall performance of the engine. Axial flow compressors are one of the most conventional types of compressors and are widely used in turbine engines for large-scale power generation. Intelligent techniques are useful for numerical simulation, characterization of axial compressors, and predicting their performance. The present work reviews studies applying different intelligent methods for performance forecasting and modeling different aerodynamic aspects of axial compressors. Corresponding to the outcomes of the considered research works, it can be expressed that by using these methods, axial compressors can be characterized properly with acceptable exactness. In addition, these techniques are useful for performance prediction of the compressors. The accuracy and performance of these methods is impacted by several elements, specifically the employed method and applied input variables. Finally, some suggestions are made for future studies in the field.

1 Introduction

Gas turbines are used around the world for power generation, with different capacities achievable by using different fuels (Bothien et al., 2019; Kurata et al., 2019). One of the main components of a gas turbine engine is the compressor. Compressors used in gas turbine engines for power generation are classified into two main groups: axial flow and centrifugal flow types. Centrifugal compressors are used in cases where a low mass flow rate and medium pressure are required while the axial flow types are used for high mass flow rates and low pressure. Regarding the ability of axial flow compressors to provide higher mass flow rates with increased pressure, these kinds are mainly used in turbines for large-scale power generation. In axial flow compressors, the operating fluid, mainly air, is compressed by accelerating it in the first step and then diffusing it in order to have higher pressures. The acceleration of the fluid is done by a row of blades that rotate, known as the rotor, while the diffusion is done by a row of stationary blades, known as the stator. It should be noted that increases in the pressure are obtained by diffusion in the stator that converts increased velocity, obtained in the rotor, to pressure increases (Boyce, 2012a).

Several studies have focused on the characteristics of various axial compressors and the elements influencing their performance (Huang et al., 2022; Babin et al., 2023). For instance, Blinov and Zubkov (2020) investigated the effect of blade row defects on the performance of a compressor. It was found that defects in the blade row, depending on the features of the defects such as its location, affect the characteristics of the airfoils of the compressor and consequently the performance. Hu et al. (2019) applied a combined flow control method, based in a vortex generator and blade slot usable for decrement in flow loss and enhancement of flow stability, in a single-stage transonic compressor. They concluded that by using this approach it is possible to enhance the mean pressure ratio by 1.82 and improve isentropic efficiency by 0.88%; this was attributed to the significant decrease in separations. Dong et al. (2014) proposed a model to forecast variations of the compressors tip clearance in various working conditions and used it for simulation of an 11-stage axial compressor. It was found that variations of tip clearance cause 1% and 0.5% impacts on the determined efficiency and mass flow rate, respectively. Sun et al. (2011) applied Computational Fluid Dynamics (CFD) to investigate the impact of wet compression on the separation in an axial compressor. It was found that wet compression makes it possible to decrease and eliminate the separation of flow. Suder et al. (1995) assessed the impact of adding roughness on the characterizations of a transonic axial compressor. They concluded that roughness addition at the blade’s leading edge leads to increment in the thickness of the blade boundary layer. In another work (Syverud and Bakken, 2006), roughness effect was considered and it was noticed that the most remarkable impact on increment in the roughness is the flow coefficient variation.

According to the literature review, different aspects of axial compressors have been investigated by scholars in recent decades, and mainly experimental and numerical simulations have been applied for these purposes. Despite the advantages of these approaches, they are costly and time-consuming. In this regard, utilization of intelligent techniques can be attractive alternatives. Intelligent methods such as Artificial Neural Networks (ANNs) have demonstrated great performance in modeling numerous engineering problems and systems (Alhuyi Nazari et al., 2021; Komeili Birjandi et al., 2022; Rashidi et al., 2022). These techniques are applicable for different turbomachines and the related systems (Liu and Karimi, 2020). For instance, Li et al. (2001) compared the accuracy of a regression model and ANN in estimation of the turbine power curve and found that ANN outperforms the regression. In anotherr study (Lazzaretto and Toffolo, 2001), ANN was applied for design and off-design simulation of a gas turbine and it was observed that the model has significant exactness. Barad et al. (2012) applied ANN for monitoring the performance and health of a gas turbine engine. Lin et al. (2002) used ANN to create the flowfield models and predict flow performance of fan. The output of their model was used for optimization of the system. Kim et al. (2009) employed a radial basis neural network to obtain optimal design of the impeller of a centrifugal compressor; the isentropic efficiency was improved by 1%. Nikiforov et al. (2019) used ANN for gas-dynamic characteristics of a centrifugal compressor vane diffuser. Liu and Karimi (2020) employed ANN for performance prediction of a gas turbine engine. The proposed model had the ability of capturing working characteristics with a mean error of less than 1%.

Thus far, no review paper on the applications of intelligent techniques for axial compressors has been published. According to the mentioned references, it can be seen that intelligent techniques can be used for modeling various aspects of turbomachines and optimizing their performance, geometry, and operating conditions (Joly et al., 2019). This article focuses on the applications of these methods for aerodynamic aspects of axial flow compressors.

2 Intelligent methods

Intelligent approaches are useful for regression, classification, and clustering. In this section, six of the most used intelligent methods for the analysis of axial flow compressors are explained.

2.1 Multilayer perceptron artificial neural network

One of the most conventional kind of ANNs used for regression is the Multilayer Perceptron (MLP), which is constructed by coupling the intelligent approaches usable for computation and biological principles; in Figure 1, a simple architecture of this type of ANN is illustrated (Ramezanizadeh et al., 2019a; Ramezanizadeh et al., 2019b).

FIGURE 1

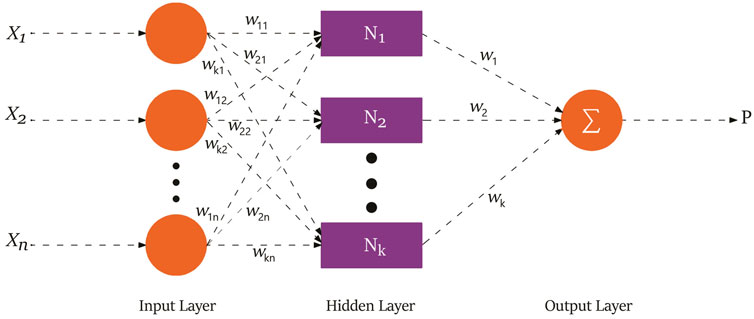
FIGURE 1. Structure of MLP-ANN (Ramezanizadeh et al., 2019a).

In this network, there are several nodes in some layers. In its simplest form, with three layers, there is a hidden layer besides the input and output layers, while in networks with a higher degree of complexity, the number of hidden layers can be higher. In each network node, a weight vector is employed to link it to the upcoming layer. The summation of the nodes is the input of the next layer. By assumption of the input vector as X, n_j is the jth node’s input that is in the following layer which is determined by using Eq. (1) as follows (Zendehboudi and Li, 2017):

$\begin{array}{cc}{n}_j={\displaystyle \sum _{i=1}^n}{\omega }_{ji}{x}_i+{\theta }_{\mathrm{j}}& j=\mathrm{1,2},\dots .,K\end{array}(1)$

In Eq. (1), ${\theta }_{\mathrm{j}}$_, ${\omega }_{ji}$, and K are the threshold, weight, and number of nodes, respectively. Thereafter, a transfer function is used to determine the inputs of the next layer as provided in Eq. (2).

$y_j=f\left(n_j\right)=f({\displaystyle \sum _{i=1}^n}{\omega }_{ji}{x}_i+{\theta }_j)j=\mathrm{1,2},\dots ,K(2)$

There are different transfer functions applicable in the abovementioned equation. Multiplying the connecting weight and the hidden layer output will determine the output of the node. It should be noted that there is no specific rule to define the size of the hidden layer and its number. The number of this layer depends on the complexity of the problems, noise of data, etc. (Du and Swamy, 2006). In the process of training the network for regression, values of bias and weights are regulated. The backpropagation algorithm is among the most applied training approaches.

2.2 GA-KM-radial basis function

A standard Radial Basis Function (RBF) neural network is able to project linear data with low dimensions into non-linear data with high dimensions. This network is applied to estimate non-linear functions and set up mappings between the input and output parameters. Standard RBF forward-propagation is as follows (Tang and Liu, 2021):

$F\left(x\right)={\displaystyle \sum _{i=1}^n}{w}_{i}G\left(x,O_i\right)(3)$

In Eq. 3, n is the training samples number, i.e., the hidden nodes number, and $w_i$ is the coefficients of weights. $G\left(x,O_i\right)$ is presented as follows (Tang and Liu, 2021):

$G\left(x,O_i\right)=\exp \left(-\frac{1}{2{\sigma }^2}{‖x-O_i‖}^2\right)(4)$

In Eq. 4, $O_i$ refers to the hidden nodes’ values and $\sigma$ is the mean expansion constant. On the basis of the Galerkin method, F(x) can be replaced with $\stackrel{\sim }{F}\left(x\right)$ as follows (Tang and Liu, 2021):

$\stackrel{\sim }{F}\left(x\right)={\sum }_{i=1}^m{w}_{i}G\left(x,t_i\right)={\sum }_{i=1}^m{w}_i.\exp \left(-\frac{1}{2{\sigma }^2}{‖x-t_i‖}^2\right)(5)$

In this equation, $t_i$ refers to the clustering centers’ means values. By minimizing the cost function, $\epsilon \left(\stackrel{\sim }{F}\right)={‖Y-\stackrel{\sim }{F}‖}^2,$ that means the minimization of forecasting error, a set of coefficients of weights could be calculated as follows (Tang and Liu, 2021):

$\min \left\{\epsilon \left(\stackrel{\sim }{F}\right)\right\}=\min \left\{{\displaystyle {\sum }_{i=1}^n}{\left[y_i-{\displaystyle {\sum }_{j=1}^{m1}}{w}_{j}G\left(x_{i,}{t}_j\right)\right]}^2+\lambda {‖D\stackrel{\sim }{F}‖}^2\right\}=\min \left\{{\displaystyle {\sum }_{i=1}^n}{\left[y_i-{\displaystyle \sum _{j=1}^{m1}}{w}_j.\exp (-\frac{1}{2{\sigma }^2}{‖x_i-t_j‖}^2\right]}^2+\lambda {‖D\stackrel{\sim }{F}‖}^2\right\}(6)$

where $\lambda$ is the coefficient of regularization, $y_i$ refers to the ith training sample real fitness value, and D is the neural network output stability factor. The first term of Eq. 6 can be rewritten as $‖Y-GW‖$ where

$\begin{array}{c}Y={\left[y_1,y_2,\dots ,y_n\right]}^T\\ G=\left[\begin{array}{c}\begin{array}{cc}\begin{array}{cc}G\left(x_1,t_1\right)& G\left(x_1,t_2\right)\\ G\left(x_2,t_1\right)& G\left(x_2,t_2\right)\end{array}& \begin{array}{cc}\dots & G\left(x_1,t_{m1}\right)\\ \dots & G(x_2,t_{m1}\end{array}\end{array}\\ \begin{array}{cc}\begin{array}{cc}⋮& ⋮\\ G\left(x_n,t_1\right)& G\left(x_n,t_2\right)\end{array}& \begin{array}{cc}\ddots & ⋮\\ \dots & G\left(x_1,t_{m1}\right)\end{array}\end{array}\end{array}\right]\\ W={\left[w_1,w_2,\dots ,w_{m1}\right]}^T\end{array}(7)$

In addition, ${‖D\stackrel{\sim }{F}‖}^2$ can be rewritten as follows (Tang and Liu, 2021):

${‖D\stackrel{\sim }{F}‖}^2=〈D\stackrel{\sim }{F},D\stackrel{\sim }{F}〉=\left[{\sum }_{i=1}^{m1}{w}_{i}G\left(x,t_i\right),\stackrel{\sim }{D}D{\sum }_{i=1}^{m1}{w}_{i}G\left(x,t_i\right)\right]=\left[{\sum }_{i=1}^{m1}{w}_{i}G\left(x,t_i\right),{\sum }_{i=1}^{m1}{w}_i{\delta }_{ti}\right]={\sum }_{i=1}^{m1}{\sum }_{j=1}^{m1}{w}_j{w}_{i}G\left(t_i,t_j\right)=W^T{G}_{0}W(8)$

In Eq. 8, $\stackrel{\sim }{D}$ refers to the adjoint operator of D as the linear differential operator and ${\delta }_{ti}$ denotes the Dirac Delta function at point x = ti. By combining Eq. 8, Eq. 6 would be equivalent to Eq. 9 for the matrix of weight as follows (Tang and Liu, 2021):

$\left(G^{T}G+\lambda G_0\right)W=G^{T}Y(9)$

Susbequently, the weight matrix could be directly solved by using Eq. 10 as follows (Tang and Liu, 2021):

$W={\left(G^{T}G+\lambda G_0\right)}^{-1}{G}^{T}d(10)$

Corresponding to the above theorem, coefficients of weight could be calculated. In standard RBF, the hidden nodes number is equal to the samples of the training number; consequently, a long convergence time and overfitting is typical when there is too large a number of training samples. When there are a small number of training data, mapping relation cannot be captured. To restrict the number of hidden nodes in standard RBF and enhance its performance, a combination scheme has been presented: GA-KM-RBF. A clustering algorithm of K-Means++ (KM) is employed in order to calculate the hidden nodes’ number. Subsequently, the Genetic Algorithm is utilized for optimization of network hyperparameters that further decreases the empirical coefficient dependence (Tang and Liu, 2021).

2.3 Adaptive neuro-fuzzy inference system

Adaptive neuro-fuzzy inference system (ANFIS) is another intelligent technique applicable for regression and proposing predictive models. The architecture of this method in its simplest form, in the case of a single output and two inputs, is illustrated in Figure 2. The first layer of this structure is used to convert input variables to fuzzy sets and project them based on fuzzy membership in span of 0 and 1. The inputs’ signals are created in the following layer and the weights are checked. Afterwards, normalized firing strength is determined in the 3rd layer. Subsequently, in the 4th layer, the obtained values are converted into defuzzy sets. In the last layer of this architecture, inputs from the previous part are summed up and the output is determined.

FIGURE 2

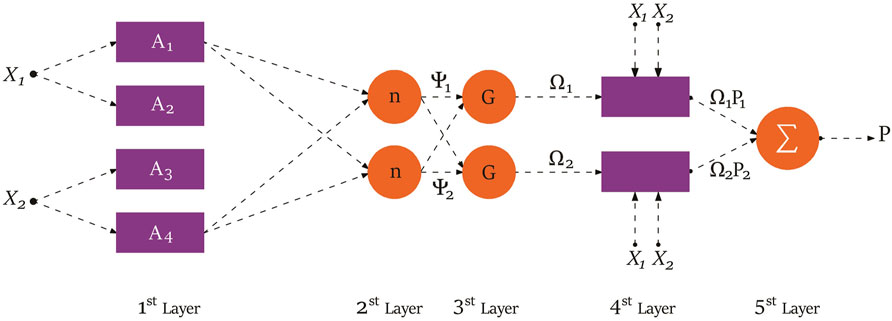
FIGURE 2. Structure of the ANFIS model (Ramezanizadeh et al., 2019a).

2.4 Least square support vector machine (LS-SVM)

SVM is another intelligent method utilizable for regression and training (Sreedhara et al., 2019); however, this approach is not usable for solving overfitting problems. In order to resolve this issue, LS-SVM is applied, which will be introduced here. In general, Eq. (11) is applied as the non-linear function of this method (Suykens and Vandewalle, 2000; van Gestel et al., 2004; Ahmadi and Mahmoudi, 2016):

$f\left(x\right)=w^t\phi \left(x\right)+b(11)$

In Eq. (11), f denotes the association between the input and output and w and b are weight vector and value of bias, respectively. $\phi$ is employed in order to convert inputs into the characteristics’ vector (Ahmadi and Mahmoudi, 2016; Ramezanizadeh et al., 2019a).

A fitting error function is applied to be minimized in order to have the highest accuracy. This function is obtained by using Eq. (12) as follows (Ahmadi and Mahmoudi, 2016; Ramezanizadeh et al., 2019a):

$\mathrm{Min}\mathrm{J}\left(w,e\right)=\frac{1}{2}{w}^{T}w+\gamma {\displaystyle \sum _{k=1}^m}{e_k}^2(12)$

In this regard, a limitation equation is defined as follows (Ahmadi and Mahmoudi, 2016; Ramezanizadeh et al., 2019a):

$y_k=w^T\phi \left(x_k\right)+b+e_k,\mathrm{k}=\mathrm{1,2},\cdots ,\mathrm{m}(13)$

where e_k and γ and are loose variables of kth x and margin parameter, respectively (Ahmadi and Mahmoudi, 2016; Ramezanizadeh et al., 2019a).

Lagrange multipliers are used in order to calculate the optimization process solution. The multiplier is defined as follows (Ahmadi and Mahmoudi, 2016; Ramezanizadeh et al., 2019a):

$L\left(w,b,e,\alpha \right)=J\left(w,e\right)-{\displaystyle \sum _{k=1}^m}{\alpha }_i\left\{w^T\varnothing \left(x_k\right)+b+e_k-Y_k\right\}(14)$

By implementing partial derivatives of Eq. (14) based on the variables, as provided in Eq. (15), it is possible to determine the optimal state.

$\left\{\begin{array}{c}w={\displaystyle \sum _{k=1}^m}{\alpha }_i\varnothing \left(x_i\right)\\ {\displaystyle \sum _{k=1}^m}{\alpha }_i=0\\ \begin{array}{c}{\alpha }_i=\gamma e_i\\ w^T\varnothing \left(x_i\right)+b+e_i-Y_i=0\end{array}\end{array}\right\}(15)$

The linear form of the abovementioned equation is as follows (Ahmadi and Mahmoudi, 2016; Ramezanizadeh et al., 2019a):

$\left[\begin{array}{cc}0& {-Y}^T\\ Y& Z{Z}^T+1/\gamma \end{array}\right]\left[\begin{array}{c}b\\ \alpha \end{array}\right]=\left[\begin{array}{c}0\\ 1\end{array}\right](16)$

Where α, Y, and Z are assumed as: α = [α₁,…,α₁], {Y = Y₁;. . .; Y_ym }, and Z = φ(_X1)^TY_i,…, φ(_Xm)^TY_m, respectively. Applying kernel function of K (X,X_k) = φ(X)^Tφ(X_k), i = 1,2,…,m, the regression is as follows (Ahmadi and Mahmoudi, 2016; Ramezanizadeh et al., 2019a):

$f\left(x\right)={\displaystyle \sum _{k=1}^n}{\alpha }_{k}K\left(x,x_k\right)+b(17)$

There are several functions such as RBF that can be used as a kernel in regression errors, as in Eq. (17). In regression models, radial basis function is a regular kernel (Ahmadi and Mahmoudi, 2016; Ramezanizadeh et al., 2019a). In the process of optimization, to obtain the parameter of kernel function, mean squared error (MSE) is considered as the objective function to be minimized (Fazeli et al., 2013; Ahmadi and Ebadi, 2014; Ahmadi et al., 2014).

2.5 Group method of data handling (GMDH)

In this approach, a Volterra series is used for defining the relationship between the inputs and output. This series is similar to Kolmogorov discerete polynomial functions. In GMDH, the total estimator models are replaced by the incrementing iterative algorithm. In this method, polynomial neurons are generated and combined with each other in order to create a complex system with proper performance. GMDH is composed of a number of neurons with binomial transfer function that arise from the linking between various pairs of variables via the 2nd order Kolmogorov relation according to Eq. (18) (Moosavi et al., 2019).

$y=c_0+{\sum }_{i=1}^m{c}_i{x}_i+{\sum }_{i=1}^m{\sum }_{j=1}^m{c}_{ij}{x}_i{x}_j(18)$

where $x=\left[x_1,x_2,\dots ,x_m\right]$ is the input vector and $c={\left[c_1,c_2,\dots ,c\right]}^T$ is the weight vector which is obtained by the least-squares approach. Similar to MLP, GMDH is a multilayer feed forward network and the outputs of the previous layer are utilized as the inputs of the current layer. In this method, the architecture of the model and number of neurons and layers is determined in the process of training. In general, a large number of basic models are created in GMDH and some of them are selected to be combined amd utilized for reconstruction of other functions. Selection and generation steps are repeated till the best model is obtained (Moosavi et al., 2019).

2.6 Support vector data description (SVDD)

In addition to modeling and regression, intelligent methods are applicable for clustering and classification. SVDD is a one-class classification approach. The principle idea of this method is finding a hypersphere with a small radius and as many as possible points in this. Support vectors are the points on the hypersphere surface. Eq. (19) is applied for the definition of the structure error function as follows:

$\begin{array}{c}F\left(R,a\right)=R^2\\ s.t.{‖x_i-a‖}^2\le R^2,\forall i\end{array}(19)$

where R is the radius and a is the center. The distance from $x_i$ point to centre could not be strictly less than R in order to allow the training set to have outliers induced by noise or other parameters. A relaxation factor is introduced to punish the outliers. Consequently, the minimization error can be written as follows:

$\begin{array}{c}F\left(R,a\right)=R^2+C{\sum }_i{\xi }_i\\ s.t.{‖x_i-a‖}^2\le R^2+{\xi }_i,{\xi }_i\ge 0\forall i\end{array}(20)$

In this equation, C is applied for controlling the compromise between the false treated points number and hypersphere radius. To solve this problem, Lagrange multipliers are used as follows:

$L\left(R,a,{\alpha }_i,{\gamma }_i,{\xi }_i\right)=R^2+C{\sum }_i{\xi }_i-{\displaystyle \sum }_i{\alpha }_i\left\{R^2+{\xi }_i-\left({‖x_i‖}^2-2a.x_i\right)\right\}-{\sum }_i{{\gamma }_i\xi }_i(21)$

where ${\alpha }_i\ge 0$ and ${\gamma }_i\ge 0$ refer to Lagrange multipliers. By applying partial derivative to L, we obtain the following equations:

$\frac{\partial L}{\partial R}=0,\to {\sum }_i{\alpha }_i=1(22)$

$\frac{\partial L}{\partial a}=0,\to a={\sum }_i{\alpha }_i{x}_i(23)$

$\frac{\partial L}{\partial {\xi }_i}=0\to C-{\alpha }_i-{\xi }_i=0(24)$

Therefore, Eq. (25) can be written as follows:

$\begin{array}{c}L={\displaystyle \sum }_i{\alpha }_i\left(x_i.x_i\right)-{\sum }_{i,j}{\alpha }_i{\alpha }_j\left(x_i.x_i\right)\\ 0\le {\alpha }_i\le C\end{array}(25)$

When the description of the data set by the hypersphere in the original space is not sufficient, the data set could be mapped from the space with a low dimension to a high-dimension one. In order to substitute the interproduct, kernel function K ($x_i.x_j)$ is applied as follows:

$L={\sum }_i{\alpha }_{i}K\left(x_i.x_i\right)-{\sum }_{i,j}{\alpha }_i{\alpha }_{j}K\left(x_i.x_j\right)(26)$

The definition of distinguish function is as follows:

$I\left(A\right)=I({‖z-a‖}^2\le R^2=\left\{\begin{array}{cc}1& Aistrue\\ 0& Aisfalse\end{array}\right.(27)$

3 Applications of intelligent techniques for axial compressors

Intelligent approaches are employable for modeling various aspects of compressors. In the following subsections, research works on each aspect are represented and reviewed.

3.1 Characteristics of axial compressor

As previously stated, intelligent methods can be applied for different turbomachines in order to model their behavior, predict the output, and design control systems (Javadi Moghaddam et al., 2011; Zhang et al., 2021). Different aspects of axial compressors, as the main components of gas turbine engines, have been modeled by using these approaches (Yu et al., 2007). In a study by Benini and Toffolo (2002), cascade performance was modeled by using ANN under generalized conditions. In this regard, quasi 3D CFD simulations were applied to prepare a database for the training network. As the model knew the characteristics of the geometry, including the effects of IGV depending on the mass flow rate and speed of rotation, it could directly determine the operating point of a compressor. In another work (Fei et al., 2016), three different intelligent techniques, namely, Back Propagation Neural Network (BPNN), SVM, and Gaussian kernel function Back Propagation Neural Network (GBPNN), were employed to estimate the performance of an axial compressor. They found that increments in the number of training datasets leads to enhancement in the exactness of the generated models by all of the applied approaches. Furthermore, it was demonstrated that making use of GBPNN provides the highest accuracy, followed by the SVM and BPNN. In another work, Sohail et al. (2021) focused on the forecasting tool of transonic compressor instability. In this regard, they utilized a dataset obtained from CFD for supervised learning of an ANN. The input variables and outputs of their model are shown in Figure 3. Obtained results from the deep learning ANN revealed that it is a promising method to forecast the performance of the compressor and rotor blade parameters.

FIGURE 3

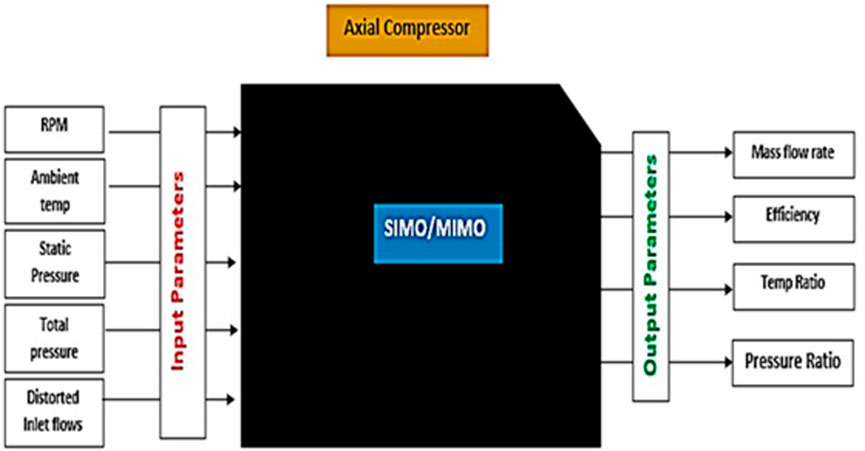
FIGURE 3. Inputs and outputs of the developed model for the compressor with distorted flow by Sohail et al. (2021).

Yue et al. (2022) generated a model for spanwise loss of a compressor stator. In order to construct the model, a significant number of numerical simulations were implemented to provide a database. Afterwards, intensity of secondary flow was introduced as the independent variable in order to implement feature engineering. The proposed model contained a selector that was obtained by using Support Vector Machine (SVM) regression in addition to estimators that were obtained on the basis of K-nearest neighbor regression. The proposed model reflected proper exactness for mid-span position loss coefficient with R² value of 0.97; however, its precision was lower for all spans. Intelligent methods are usable for modeling more than one output. For instance, in a work (Wu et al., 2019), two methods, Gaussian Process Regression (GPR) and Support Vector Regression (SVR), were applied to model adiabatic efficiency and total pressure ratio. In the case of applying SVR, the predicted error of the empirical model was reduced by 62.2% and 48.4% for the total pressure ratio and adiabatic efficiency, respectively. These values, in the case of employing GPR, were 55.2% and 50.1% for the denoted parameters, respectively. Gholamrezaei and Ghorbanian (2010) made use of ANN and rig data to generate compressor map. Two models were proposed in their research applicable for the prediction of mass flow rate and pressure ratio. In the first model, compressor pressure ratio was formulated based on the function of corrected mass flow rate for constant speed lines, while in the second model, the corrected mass flow rate was formulated as a function of pressure ratio for constant speed lines. It was observed that the first model is more precise for cases of relatively low speed lines while the second model showed higher robustness for cases of higher speed lines.

The performance of intelligent methods is dependent on several parameters, namely, the applied algorithm and the function (Ghorbanian and Gholamrezaei, 2007). Their performance could be enhanced by applying some modifications. A work was done to consider different Neural Networks (NNs) including General Regression NN (GRNN), Radial Basis Function (RBF), Multilayer Perceptron (MLP), and modified approach based on GRNN, called Rotated GRNN (RGRNN) (Ghorbanian and Gholamrezaei, 2009), to model compressor pressure ratio and mass flow rate by using two models. It was observed that making use of RGRNN leads to the highest accuracy; however, it is just applicable for representing characteristic curves for cases where experimental data is provided. The superior performance of RGRNN compared with GRNN in performance prediction of axial compressors has been observed in some other studies (Ghorbanian and Gholamrezaei, 2007). Integration of various intelligent techniques can determine outputs with better accuracy. For instance, Gholamrezaei and Ghorbanian (2015) assessed the performance of ANN and Fuzzy Inference System (FIS)+ANN for map generation of a compressor. The success rates in cases of using the mentioned approaches were 88% and 94%, respectively. In some studies, different functions and architectures are applied to find the optimal model in terms of accuracy. For instance, Yazar et al. (2014) applied various types of FIS structures and utilized different numbers of membership function. They found that number of membership function can affect the model exactness. Integration of optimization algorithm with intelligent techniques, used for modeling and regression, to tune the hyper parameters is another approach for modification of precision. Tang and Liu (2021) coupled Genetic Algorithm (GA) and generalized RBF. In their work, deviation angle and total pressure loss coefficient were predicted in the first step by applying surrogate model. Afterwards, these variables linked the model with throughflow theory. Efficiency and pressure ratio were predicted in the next stage and compared with the actual values determined in the experiments. In comparison with the traditional models and spanwise mixing model, the proposed approach provided much better performance.

3.2 Surge and stall

There is a useful range for operation of axial compressors, as shown in Figure 4. At high mass flow rates, chocking occurs and sonic velocity is reached in some units. One the other hand, at low mass flow rate, there is possibility for the occurrence of stall and surge that causes instabilities in the fluid flow and performance of axial compressors. Stall is a type of instability caused by the disturbance of the circumferential flow (Gravdahl and Egeland, 1999; Wang et al., 2022). In terms of aerodynamics, there are two types of stall: individual blade stall and rotating stall. The first one happens when all of the blades around the annulus of the compressor simultaneously stall without propagation of stall. The second type, rotating stall, happens when there are large zones of stall that cover various passages of the blade and there is propagation in the rotation direction and at relative rotor speed (Boyce, 2012b). Surge refers to the flow axisymmtrical oscillation in the compressors and is featured by a limit cycle in the characteristics of these machines (Gravdahl and Egeland, 1999). This phenomenon is the flow reversal and continuous steady flow complete break down via the compressor. This phenomenon, surge, is the reversal of flow and complete break down of continuous flow in the compressor. Surge induces mechanical problems due to the high fluctuations of flow that causes changes in the direction of thrust force in the rotor section (Boyce, 2012b; Zhao et al., 2023).

FIGURE 4

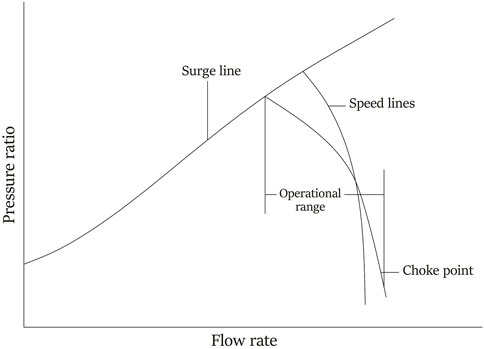
FIGURE 4. Map of axial flow compressor (Gravdahl and Egeland, 1999).

In addition to performance prediction and the characteristics of fluid flow, intelligent methods are useful for other purposes in different energy-related systems (Hipple et al., 2020). For instance, Changzheng and Yong (Li and Lei, 2012) applied Support Vector Data Description (SVDD), developed on the basis of the SVM theory, to detect compressor surge. In their work, total pressure at the outlet was used as the characteristic signal and ten spectral lines were utilized in order to create vectors of the feature. For the applied technique, 400 vectors were determined to provide a training dataset. The outcomes of the training were applied to distinguish surge of the compressor. It was shown that the applied technique can provide a warning signal 50 ms prior to the surge point. In another work, Amanifard et al. (2008) proposed a model based on evolved Group Method of Data Handling (GMDH) by using experimental data to model multiple short-length-scale stall cells. Flow rate coefficient, pressure coefficient, and rotor rotational speed were the inputs of the generated model. Exactness of the model in prediction was acceptable with R² and Mean Absolute Percentage Error (MAPE) of around 0.86268 and 0.00065, respectively. In addition to modeling surge, it is possible to apply ANN to provide backstepping active control for axial compressor surge. In a study by Sheng et al. (2020), a closed coupled valve was used as the actuator in order to generate a compression system second order Moore-Greitzer surge model. The controller was designed on the basis of a wavelet neural network. They found that by using the proposed method, the compressor is allowed to stably work with high efficiency and pressure ratio beyond the boundary of surge. In another work, Methling et al. (2004) used wall static pressure signals to train a network to indicate when instability was being neared. They found that the provided monitoring system based on the ANN has the ability to cover the whole working range of the compressor to provide adequate training datasets.

3.3 Design and optimization

Aerodynamic design of modern compressors is challenging because of the higher gradient of adverse pressure and increment in the interaction blade rows that induce internal turbulent flow. In this regard, it is beneficial to develop new approaches and algorithms for design and optimization of axial flow compressors (Ning et al., 2016). There is significant potential for applying intelligent methods for these intentions. In this condition, outputs of the models, e.g., characteristics of the compressor such as pressure ratio and mass flow rate, could be used for design or optimization in a faster process since these methods can generate databases for the mentioned intentions based on their prediction ability. As an example, Ghalandari et al. (2019) utilized a hybrid machine learning model composed of ANN, genetic algorithm, and design of experiment to optimize an aeromechanical aspect of compressor first row. In their work, ANN was trained by employing the results of 3D CFD simulation that was generated by design of experiment. The procedure of the optimization was initiated with values of approximated function by the ANN and the optimization algorithm (GA) was applied to reach the optimized point of the function; it was validated by the results of the simulation in order to update the model based on ANN. By using this process, the behavior of the blade and aerodynamic performance was increased by around 5.7%. Ju and Zhang (2011) applied a method consisting of Design of Experiment (DOE), GA, and ANN to optimize cascades of axial compressors. In their work, ANN was trained by using a back propagation algorithm and GA where the training sets were gathered by means of DOE approach and analyzed by CFD. The model based on ANN and GA was created to be used as a rapid flow solver to forecast aerodynamic performance. Multi-objective GA was employed in order to search a series of Pareto-optimum solutions. It was found that, depending on the incidence angle, the pressure loss coefficient can significantly decrease by employing the proposed approach.

Uelschen and Lawerenz (2000) applied ANN and GA for design of compressor airfoils. In their study, ANN was employed to map coherence between aerodynamics and geometry. In comparison with flow calculations, which are very time-consuming processes, much lower computational effort is required for the assessment of the trained network; consequently, the optimization and design is accelerated. Giassi et al. (2003) applied ANN for optimization of aerodynamic aspects of axial compressors and inverse design problem resolution. Their approach was based on the integration of ANN and a classical optimizer. Flow solver, on the basis of Navier-stokes, was applied for precise determination of the objective function. The trained network in the first stage, by using the primary datasets, was applied to reach a new design point. It was determined by the solver to update datasets used for training for more iterative steps. The proposed method showed significantly lower computational effort in comparison with the classical optimization approaches. In another work by Pakatchian et al. (2019), optimization of blade shape was implemented by making use of ANN. In their study, ANN was employed to develop datasets for 2D sections. Subsequently, trained ANNs were employed for optimization of 3D shapes along with the stacking line parametrization. This algorithm was applied for the first four stages. Utilization of the optimization process led to 1.5% increment in the isentropic efficiency of first four stages of a 16-stage axial compressor.

In Table 1, studies related to the employment of machine learning techniques in axial flow compressors are summarized.

TABLE 1

TABLE 1. Summaries of the studies on the use of machine learning approaches for axial compressors.

4 Recommendations for future

The previous section focused on reviewing the scientific works performed on the usage of machine learning methods in axial flow compressors. Despite the significance of the studies on the utilization of these methods for aerodynamic aspects of axial flow compressors, there are some issues and potential for enhancement. For instance, the comprehensiveness of the proposed models for different purposes such as determination of characteristics, design, and surge or stall prediction is not sufficient. Furthermore, some ideas can be developed to achieve more precise models with higher exactness. According to the knowledge of the authors, some recommendations are presented here for upcoming studies. Corresponding to the influence of model characteristics and type on the precision of the predictions (Maleki et al., 2021), it is strongly suggested to apply more types of intelligent techniques such as SVMs with various functions for different intentions like prediction of pressure ratio, mass flow rate, efficiency, surge, and stall. In addition, regarding the potential of improvement by using optimization, it is beneficial to couple several novel optimization algorithms with intelligent approaches applied for characteristics determination of compressors to enhance the precision (Ramezanizadeh et al., 2019c); moreover, the performance of the models coupled with optimization algorithms can be compared by consideration of different criteria such as time and computational costs and exactness. Furthermore, owing to the relatively remarkable influence of functions and structure of models on the performance of intelligent approaches in some cases, it is suggested to the scholars to apply different networks by changing the mentioned factors that would enable them to find the model with more exactness. In addition, it is highly recommended to develop more comprehensive models with usability for different axial compressors with various features. These models are achievable by considering more inputs for the models. In this regard, additional inputs such as the number of stages and geometrical parameters such as dimensions of hub, tip, chord and cambers, and blade profile type, such as NACA series (Amin et al., 2021) and C4 (Chhugani et al., 2023), can be used.

In addition to the mentioned suggestions, mainly on the characteristics of the applied approaches, there are some recommendations for the applications of these techniques with focus on the axial compressors. Some studies have applied intelligent methods for flow field modeling and prediction. For instance, Santos et al. (2020) made use of a convolutional neural network to forecast flow field via porous media. It was reported that the information obtained by the proposed model was adequate to reach accurate forecasting of flow field in less than a second without any requirement for numerical simulation. In another work, Sekar et al. (2019) approximated flow field over an airfoil as a function of angle of attack, Reynolds number, and geometry of air by utilizing deep neural network without solving Navier-Stokes equations. In the first step, a convolutional neural network was applied for extracting the geometrical parameters from the shape of airfoil. Afterwards, these parameters in addition to the other inputs were used in MLP ANN to determine an approximation model for flow field prediction. Similar procedures can be employed for axial flow compressors to obtain their flow field characteristics. The obtained data related to flow field is usable for prediction of more phenomena such as flow separation, causing some problems such as blockage of passage that limits the static pressure and loading increment reachable by the compressor (Gbadebo et al., 2005). In this condition, proper inputs must be employed to reach acceptable outputs. For instance, in the case of predicting hub corner separation, consideration of secondary flow, and adverse pressure gradient, as applied in a study (Lei, 2006), intelligent approaches can be useful to develop a model based on intelligent techniques. Casing treatment and applying slots (Lu et al., 2023), grooves (Wu et al., 2021), or both of them on the casing (Li et al., 2019), is one of the techniques used by the scholars to modify the stability of compressors. It is can be helpful to develop intelligent models for the modified compressors, e.g., the compressors with casing treatment (Vuong and Kim, 2021). In these cases, specifications of the applied modifications such as the dimensions of the grooves and slots should be employed as additional inputs. Moreover, regarding the applicability of intelligent techniques for clustering and classification, utilization of these methods in axial compressors can be developed for these purposes.

5 Conclusion

Regarding the time-consuming process of numerical 3D simulation, it is essential to develop novel, efficient, and fast methods for the modeling and forecasting characteristics of axial compressors. Intelligent techniques are suitable alternatives for 3D numerical simulations. In this article, studies on this field are reviewed. The key findings of the considered research works are as follows.

• Using intelligent techniques makes it possible to properly determine the operating point of axial compressors.

• Different characteristics of axial compressors such as pressure ratio, mass flow rate, and pressure loss can be predicted by intelligent methods with acceptable exactness.

• Modification on the intelligent techniques such as applying optimization approaches for tuning the hyperparameters can further enhance the exactness.

• Outputs of intelligent methods could be usable for providing databases to optimize the performance and other characteristics of axial compressors.

• Prediction of surge and stall is possible by utilization of different intelligent methods such as GMDH and SVDD.

• Similar to optimization, intelligent methods are attractive alternatives for generating databases for the design of compressors.

• Specification of the intelligent methods such as architecture, applied functions, and formulation influence the exactness.

• Some recommendations such as utilization of intelligent methods for flow field analysis of axial flow compressors have been suggested for forthcoming works.

Author contributions

The MP and AZ authors were involved in writing, search, edition. The MN author was responsible for design of study, supervision and edition.

Conflict of interest

MP, AZ and MN were employed by MAPNA Group.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

ANFIS, Adaptive Neuro Fuzzy Inference System; ANN, Artificial Neural Network; GA-KM, Genetic Algorithm K-Means++; GMDH, Group Method of Data Handling; LS-SVM, Least Square Support Vector Machine; MLP, Multilayer Perceptron; MSE, Mean Squared Error; RBF, Radial Basis Function; SVDD, Support Vector Data Description; Parameters and Operators $c$, Coefficient; $D$, Linear Differential Operator; $\stackrel{\sim }{D}$, Adjoint Operator of D; $X$, Input Vector; $K$, Number of Nodes; $Y$, Output Vector; $\alpha$, Lagrange Multiplier; $\delta$, Dirac Delta Function; $\gamma$, Coefficient of Regularization; $\epsilon \left(\stackrel{\sim }{F}\right)$, Cost Function; $\theta$, Threshold; $\lambda$, Coefficient of Regularization; $\omega$, Weight.

References

Ahmadi, M. A., and Ebadi, M. (2014). Evolving smart approach for determination dew point pressure through condensate gas reservoirs. Fuel 117, 1074–1084. doi:10.1016/J.FUEL.2013.10.010

CrossRef Full Text | Google Scholar

Ahmadi, M. A., Ebadi, M., Marghmaleki, P. S., and Fouladi, M. M. (2014). Evolving predictive model to determine condensate-to-gas ratio in retrograded condensate gas reservoirs. Fuel 124, 241–257. doi:10.1016/J.FUEL.2014.01.073

CrossRef Full Text | Google Scholar

Ahmadi, M. A., and Mahmoudi, B. (2016). Development of robust model to estimate gas–oil interfacial tension using least square support vector machine: Experimental and modeling study. J. Supercrit. Fluids 107, 122–128. doi:10.1016/J.SUPFLU.2015.08.012

CrossRef Full Text | Google Scholar

Alhuyi Nazari, M., Salem, M., Mahariq, I., Younes, K., and Maqableh, B. B. (2021). Utilization of data-driven methods in solar desalination systems: A comprehensive review. Front. Energy Res. 9, 541. doi:10.3389/FENRG.2021.742615

CrossRef Full Text | Google Scholar

Amanifard, N., Nariman-Zadeh, N., Farahani, M. H., and Khalkhali, A. (2008). Modelling of multiple short-length-scale stall cells in an axial compressor using evolved GMDH neural networks. Energy Convers. Manag. 49, 2588–2594. doi:10.1016/j.enconman.2008.05.025

CrossRef Full Text | Google Scholar

Amin, G. A., Salunkhe, P. B., and Kini, C. R. (2021). “A parametric study on the effect of casing treatment slots on performance enhancement of a single stage axial flow compressor,” in Proc. ASME 2021 gas turbine India conf. GTINDIA 2021 (American Society of Mechanical Engineers ASME). doi:10.1115/GTINDIA2021-76007

CrossRef Full Text | Google Scholar

Babin, C., Ottavy, X., and Fontaneto, F. (2023). Leakage flow impact on shrouded stator cavity flow topology and associated high-speed axial compressor stage performance. J. Turbomach. 145, 1–32. doi:10.1115/1.4056698

CrossRef Full Text | Google Scholar

Barad, S. G., Ramaiah, P. V., Giridhar, R. K., and Krishnaiah, G. (2012). Neural network approach for a combined performance and mechanical health monitoring of a gas turbine engine. Mech. Syst. Signal Process 27, 729–742. doi:10.1016/j.ymssp.2011.09.011

CrossRef Full Text | Google Scholar

Benini, E., and Toffolo, A. (2002). Axial-flow compressor model based on a cascade stacking technique and neural networks. Am. Soc. Mech. Eng. Int. Gas. Turbine Inst. Turbo Expo. IGTI 5, 793–801. doi:10.1115/GT2002-30443

CrossRef Full Text | Google Scholar

Blinov, V. L., and Zubkov, I. S. (2020). Influence of the axial compressor blade row defects on the industrial gas turbine performance. J. Phys. Conf. Ser. 1683, 042049. doi:10.1088/1742-6596/1683/4/042049

CrossRef Full Text | Google Scholar

Bothien, M. R., Ciani, A., Wood, J. P., and Fruechtel, G. (2019). Toward decarbonized power generation with gas turbines by using sequential combustion for burning hydrogen. J. Eng. Gas. Turbines Power 141. doi:10.1115/1.4045256

CrossRef Full Text | Google Scholar

Boyce, M. P. (2012). “An overview of gas turbines,” in Gas turbine eng. Handb. (Elsevier), 3–88. doi:10.1016/b978-0-12-383842-1.00001-9

CrossRef Full Text | Google Scholar

Boyce, M. P. (2012). Axial-flow compressors. Gas turbine eng. Handb. Elsevier, 303–355. doi:10.1016/B978-0-12-383842-1.00007-X

CrossRef Full Text | Google Scholar

Chhugani, H. T., Kumar, A., and Pradeep, A. M. (2023). Effects of radial distortion on low-speed tandem stage axial compressor. Lect. Notes Mech. Eng., 55–77. Springer Science and Business Media Deutschland GmbH. doi:10.1007/978-981-19-2378-4_4

CrossRef Full Text | Google Scholar

Dong, Y., Xinqian, Z., and Qiushi, L. (2014). An 11-stage axial compressor performance simulation considering the change of tip clearance in different operating conditions. Proc. Inst. Mech. Eng. Part A J. Power Energy 228, 614–625. doi:10.1177/0957650914535389

CrossRef Full Text | Google Scholar

Du, K., and Swamy, M. (2006). Neural networks in a softcomputing framework. Springer.

Google Scholar

Fazeli, H., Soleimani, R., Ahmadi, M-A., Badrnezhad, R., and Mohammadi, A. H. (2013). Experimental study and modeling of ultrafiltration of refinery effluents using a hybrid intelligent approach. Energy and Fuels 27, 3523–3537. doi:10.1021/ef400179b

CrossRef Full Text | Google Scholar

Fei, J., Zhao, N., Shi, Y., Feng, Y., and Wang, Z. (2016). Compressor performance prediction using a novel feed-forward neural network based on Gaussian kernel function. Adv. Mech. Eng. 8, 168781401662839. doi:10.1177/1687814016628396

CrossRef Full Text | Google Scholar

Gbadebo, S. A., Cumpsty, N. A., and Hynes, T. P. (2005). Three-dimensional separations in axial compressors. J. Turbomach. 127, 331–339. doi:10.1115/1.1811093

CrossRef Full Text | Google Scholar

Ghalandari, M., Ziamolki, A., Mosavi, A., Shamshirband, S., Chau, K-W., and Bornassi, S. (2019). Aeromechanical optimization of first row compressor test stand blades using a hybrid machine learning model of genetic algorithm, artificial neural networks and design of experiments. Eng. Appl. Comput. Fluid Mech. 13, 892–904. doi:10.1080/19942060.2019.1649196

CrossRef Full Text | Google Scholar

Gholamrezaei, M., and Ghorbanian, K. (2015). Application of integrated fuzzy logic and neural networks to the performance prediction of axial compressors. Proc. Inst. Mech. Eng. Part A J. Power Energy 229, 928–947. doi:10.1177/0957650915596877

CrossRef Full Text | Google Scholar

Gholamrezaei, M., and Ghorbanian, K. (2010). Compressor map generation using a feed-forward neural network and rig data. Proc. Inst. Mech. Eng. Part A J. Power Energy 224, 97–108. doi:10.1243/09576509JPE792

CrossRef Full Text | Google Scholar

Ghorbanian, K., and Gholamrezaei, M. (2009). An artificial neural network approach to compressor performance prediction. Appl. Energy 86, 1210–1221. doi:10.1016/j.apenergy.2008.06.006

CrossRef Full Text | Google Scholar

Ghorbanian, K., and Gholamrezaei, M. (2007). “Axial compressor performance map prediction using artificial neural network,” in Proc. ASME turbo expo (American Society of Mechanical Engineers Digital Collection), 6, 1199–1208. PART B. doi:10.1115/GT2007-27165

CrossRef Full Text | Google Scholar

Giassi, A., Pediroda, V., Poloni, C., and Clarich, A. (2003). Three-dimensional inverse design of axial compressor stator blade using neural-networks and direct Navier–Stokes solver. Inverse Probl. Eng. 11, 457–470. doi:10.1080/1068276031000147545

CrossRef Full Text | Google Scholar

Gravdahl, J. T., and Egeland, O. (1999). Compressor surge and stall: An introduction. London: Springer, 1–62. doi:10.1007/978-1-4471-0827-6_1

CrossRef Full Text | Google Scholar

Hipple, S. M., Bonilla-Alvarado, H., Pezzini, P., Shadle, L., and Bryden, K. M. (2020). Using machine learning tools to predict compressor Stall. J. Energy Resour. Technol. Trans. ASME 142, 142. doi:10.1115/1.4046458

CrossRef Full Text | Google Scholar

Hu, J., Wang, R., and Huang, D. (2019). Improvements of performance and stability of a single-stage transonic axial compressor using a combined flow control approach. Aerosp. Sci. Technol. 86, 283–295. doi:10.1016/j.ast.2018.12.033

CrossRef Full Text | Google Scholar

Huang, J., Lv, Y., Xia, A., Zhang, S., Tuo, W., Xue, H., et al. (2022). Improved body force model for estimating off-design axial compressor performance. Energies 15, 4389. doi:10.3390/en15124389

CrossRef Full Text | Google Scholar

Javadi Moghaddam, J., Farahani, M. H., and Amanifard, N. (2011). A neural network-based sliding-mode control for rotating stall and surge in axial compressors. Appl. Soft Comput. J. 11, 1036–1043. doi:10.1016/j.asoc.2010.02.002

CrossRef Full Text | Google Scholar

Joly, M., Sarkar, S., and Mehta, D. (2019). Machine learning enabled adaptive optimization of a transonic compressor rotor with precompression. J. Turbomach. 141. doi:10.1115/1.4041808

CrossRef Full Text | Google Scholar

Ju, Y. P., and Zhang, C. H. (2011). Multi-point and multi-objective optimization design method for industrial axial compressor cascades. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 225, 1481–1493. doi:10.1177/0954406210395878

CrossRef Full Text | Google Scholar

Kim, J. H., Choi, J. H., and Kim, K. Y. (2009). “Design optimization of a centrifugal compressor impeller using radial basis neural network method,” in Proc. ASME turbo expo (American Society of Mechanical Engineers Digital Collection), 7, 443–451. doi:10.1115/GT2009-59666

CrossRef Full Text | Google Scholar

Komeili Birjandi, A., Fahim Alavi, M., Salem, M., Assad, M. E. H., and Prabaharan, N. (2022). Modeling carbon dioxide emission of countries in southeast of Asia by applying artificial neural network. Int. J. Low-Carbon Technol. 17, 321–326. doi:10.1093/ijlct/ctac002

CrossRef Full Text | Google Scholar

Kurata, O., Iki, N., Inoue, T., Matsunuma, T., Tsujimura, T., Furutani, H., et al. (2019). Development of a wide range-operable, rich-lean low-NOx combustor for NH 3 fuel gas-turbine power generation. Proc. Combust. Inst. 37, 4587–4595. doi:10.1016/j.proci.2018.09.012

CrossRef Full Text | Google Scholar

Lazzaretto, A., and Toffolo, A. (2001). Analytical and neural network models for gas turbine design and off-design simulation. Int. J. Thermodyn. 4. doi:10.5541/ijot.78

CrossRef Full Text | Google Scholar

Lei, V. M. (2006). A simple criterion for three-dimensional flow separation in axial compressors. Doctoral dissertation, Massachusetts Institute of Technology.

Google Scholar

Li, C., and Lei, Y. (2012). Compressor surge detection based on support vector data description. Appl. Mech. Mater. 152–154, 1545–1549. doi:10.4028/www.scientific.net/AMM.152-154.1545

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Du, J., Li, F., Zhang, Q., and Zhang, H. (2019). Stability enhancement using a new hybrid casing treatment in an axial flow compressor. Aerosp. Sci. Technol. 85, 305–319. doi:10.1016/j.ast.2018.12.018

CrossRef Full Text | Google Scholar

Li, S., Wunsch, D. C., O’Hair, E., and Giesselmann, M. G. (2001). Comparative analysis of regression and artificial neural network models for wind turbine power curve estimation. J. Sol. Energy Eng. Trans. ASME 123, 327–332. doi:10.1115/1.1413216

CrossRef Full Text | Google Scholar

Lin, B-J., Hung, C-I., and Tang, E-J. (2002). An optimal design of axial-flow fan blades by the machining method and an artificial neural network. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 216, 367–376. doi:10.1243/0954406021524954

CrossRef Full Text | Google Scholar

Liu, Z., and Karimi, I. A. (2020). Gas turbine performance prediction via machine learning. Energy 192, 116627. doi:10.1016/j.energy.2019.116627

CrossRef Full Text | Google Scholar

Lu, B., Teng, J., Zhu, M., and Qiang, X. (2023). Design optimization of a transonic compressor blade with sweep and lean integrated with axial slot casing treatment. Aerosp. Sci. Technol. 136, 108225. doi:10.1016/j.ast.2023.108225

CrossRef Full Text | Google Scholar

Maleki, A., Haghighi, A., and Mahariq, I. (2021). Machine learning-based approaches for modeling thermophysical properties of hybrid nanofluids: A comprehensive review. J. Mol. Liq. 322, 114843. doi:10.1016/j.molliq.2020.114843

CrossRef Full Text | Google Scholar

Methling, F-O., Stoff, H., and Grauer, F. (2004). The pre-stall behavior of a 4-stage transonic compressor and stall monitoring based on artificial neural networks. Int. J. Rotating Mach. 10, 387–399. doi:10.1155/s1023621x04000399

CrossRef Full Text | Google Scholar

Moosavi, M., Firoozi Rad, K., and Daneshvar, A. (2019). A comparative study in the prediction of thermal conductivity enhancement of nanofluids using ANN-MLP, ANN-RBF, ANFIS, and GMDH methods. J. Iran. Chem. Soc. 16, 2629–2637. doi:10.1007/s13738-019-01725-z

CrossRef Full Text | Google Scholar

Nikiforov, A., Kuchumov, A., Terentev, S., Petukhov, E., and Kabalyk, K. (2019). Simulation of gas-dynamic characteristics of a centrifugal compressor vane diffuser using neural networks. E3S Web Conf. 140, 05003. doi:10.1051/e3sconf/201914005003

CrossRef Full Text | Google Scholar

Ning, T., Gu, C-W., Ni, W-D., Li, X-T., and Liu, T-Q. (2016). Aerodynamic analysis and three-dimensional redesign of a multi-stage axial flow compressor. Energies 9, 296. doi:10.3390/en9040296

CrossRef Full Text | Google Scholar

Pakatchian, M. R., Saeidi, H., and Ziamolki, A. (2019). CFD-based blade shape optimization of MGT-70(3)axial flow compressor. Int. J. Numer. Methods Heat. Fluid Flow. 30, 3307–3321. HFF-10-2018-0603. doi:10.1108/HFF-10-2018-0603

CrossRef Full Text | Google Scholar

Ramezanizadeh, M., Ahmadi, M. A., Ahmadi, M. H., and Alhuyi Nazari, M. (2019). Rigorous smart model for predicting dynamic viscosity of Al₂O₃/water nanofluid. J. Therm. Anal. Calorim. 137, 307–316. doi:10.1007/s10973-018-7916-1

CrossRef Full Text | Google Scholar

Ramezanizadeh, M., Ahmadi, M. H., Nazari, M. A., Sadeghzadeh, M., and Chen, L. (2019). A review on the utilized machine learning approaches for modeling the dynamic viscosity of nanofluids. Renew. Sustain Energy Rev. 114, 109345. doi:10.1016/J.RSER.2019.109345

CrossRef Full Text | Google Scholar

Ramezanizadeh, M., Alhuyi Nazari, M., Ahmadi, M. H., Lorenzini, G., and Pop, I. (2019). A review on the applications of intelligence methods in predicting thermal conductivity of nanofluids. J. Therm. Anal. Calorim., 1–17. doi:10.1007/s10973-019-08154-3

CrossRef Full Text | Google Scholar

Rashidi, M. M., Alhuyi Nazari, M., Mahariq, I., and Ali, N. (2022). Modeling and sensitivity analysis of thermal conductivity of ethylene glycol-water based nanofluids with alumina nanoparticles. Exp. Tech. 47, 83–90. doi:10.1007/S40799-022-00567-4

CrossRef Full Text | Google Scholar

Santos, J. E., Xu, D., Jo, H., Landry, C. J., Prodanović, M., and Pyrcz, M. J. (2020). PoreFlow-net: A 3D convolutional neural network to predict fluid flow through porous media. Adv. Water Resour. 138, 103539. doi:10.1016/j.advwatres.2020.103539

CrossRef Full Text | Google Scholar

Sekar, V., Jiang, Q., Shu, C., and Khoo, B. C. (2019). Fast flow field prediction over airfoils using deep learning approach. Phys. Fluids 31, 057103. doi:10.1063/1.5094943

CrossRef Full Text | Google Scholar

Sheng, H., Chen, Q., Li, J., Li, Z., Wang, Z., and Zhang, T. (2020). Robust adaptive backstepping active control of compressor surge based on wavelet neural network. Aerosp. Sci. Technol. 106, 106139. doi:10.1016/j.ast.2020.106139

CrossRef Full Text | Google Scholar

Sohail, M. U., Hamdani, H. R., Islam, A., Parvez, K., Khan, A. M., Allauddin, U., et al. (2021). Prediction of non-uniform distorted flows, effects on transonic compressor using CFD, regression analysis and artificial neural networks. Appl. Sci. 11, 3706. doi:10.3390/app11083706

CrossRef Full Text | Google Scholar

Sreedhara, B. M., Rao, M., and Mandal, S. (2019). Application of an evolutionary technique (PSO–SVM) and ANFIS in clear-water scour depth prediction around bridge piers. Neural Comput. Appl. 31, 7335–7349. doi:10.1007/s00521-018-3570-6

CrossRef Full Text | Google Scholar

Suder, K. L., Chima, R. V., Strazisar, A. J., and Roberts, W. B. (1995). The effect of adding roughness and thickness to a transonic axial compressor rotor. J. Turbomach. 117, 491–505. doi:10.1115/1.2836561

CrossRef Full Text | Google Scholar

Sun, L., Zheng, Q., Li, Y., and Bhargava, R. (2011). Understanding effects of wet compression on separated flow behavior in an axial compressor stage using CFD analysis. J. Turbomach. 133. doi:10.1115/1.4003003

CrossRef Full Text | Google Scholar

Suykens, J. A. K., and Vandewalle, J. (2000). Recurrent least squares support vector machines. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 47, 1109–1114. doi:10.1109/81.855471

CrossRef Full Text | Google Scholar

Syverud, E., and Bakken, L. E. (2006). “The impact of surface roughness on axial compressor performance deterioration,” in Proc. ASME turbo expo (American Society of Mechanical Engineers Digital Collection), 5, 491–501. PART A. doi:10.1115/GT2006-90004

CrossRef Full Text | Google Scholar

Tang, T., and Liu, B. (2021). The genetic algorithm-radial basis function neural network to quickly predict aerodynamic performance of compressors. Proc. Inst. Mech. Eng. Part G. J. Aerosp. Eng. 235, 537–552. doi:10.1177/0954410020948977

CrossRef Full Text | Google Scholar

Uelschen, M., and Lawerenz, M. (2000). “Design of axial compressor airfoils with artificial neural networks and genetic algorithms,” in Fluids 2000 conf. Exhib. (American Institute of Aeronautics and Astronautics Inc.). doi:10.2514/6.2000-2546

CrossRef Full Text | Google Scholar

van Gestel, T., Suykens, J. A. K., Baesens, B., Viaene, S., Vanthienen, J., Dedene, G., et al. (2004). Benchmarking least squares support vector machine classifiers. Mach. Learn 54, 5–32. doi:10.1023/B:MACH.0000008082.80494.e0

CrossRef Full Text | Google Scholar

Vuong, T-D., and Kim, K-Y. (2021). Stability enhancement of a single-stage transonic axial compressor using inclined oblique slots. Energies 14, 2346. doi:10.3390/en14092346

CrossRef Full Text | Google Scholar

Wang, Y., Song, M., Xin, J., and Yang, B. (2022). Analysis of the flow field at the tip of an axial flow compressor during rotating stall process based on the POD method. Processes 11, 69. doi:10.3390/pr11010069

CrossRef Full Text | Google Scholar

Wu, X., Liu, B., Ricks, N., and Ghorbaniasl, G. (2019). Surrogate models for performance prediction of axial compressors using through-flow approach. Energies 13, 169. doi:10.3390/en13010169

CrossRef Full Text | Google Scholar

Wu, X., Liu, B., Zhang, B., and Mao, X. (2021). Effect of circumferential single casing groove location on the flow stability under tip-clearance effect in a transonic axial flow compressor rotor. Energies 14, 6143. doi:10.3390/en14196143

CrossRef Full Text | Google Scholar

Yazar, I., Kiyak, E., and Yavuz, H. S. (2014). Modelling and comparison of compressor performance parameters by using ANFIS. Adv. Mater. Res. 1016, 710–715. doi:10.4028/www.scientific.net/AMR.1016.710

CrossRef Full Text | Google Scholar

Yu, Y., Chen, L., Sun, F., and Wu, C. (2007). Neural-network based analysis and prediction of a compressor’s characteristic performance map. Appl. Energy 84, 48–55. doi:10.1016/j.apenergy.2006.04.005

CrossRef Full Text | Google Scholar

Yue, Z., Zhou, C., Jin, D., and Gui, X. (2022). A spanwise loss model for axial compressor stator based on machine learning. Chin. J. Aeronaut. 35, 74–84. doi:10.1016/j.cja.2022.05.013

CrossRef Full Text | Google Scholar

Zendehboudi, A., and Li, X. (2017). Robust predictive models for estimating frost deposition on horizontal and parallel surfaces. Int. J. Refrig 80, 225–237. doi:10.1016/J.IJREFRIG.2017.05.013

CrossRef Full Text | Google Scholar

Zhang, M., Hao, S., and Hou, A. (2021). Study on the intelligent modeling of the blade aerodynamic force in compressors based on machine learning. Mathematics 9, 476. doi:10.3390/math9050476

CrossRef Full Text | Google Scholar

Zhao, H., Du, J., Zhang, W., Zhang, H., and Nie, C. (2023). A review on theoretical and numerical research of axial compressor surge. J. Therm. Sci. 32, 254–263. doi:10.1007/s11630-022-1682-x

CrossRef Full Text | Google Scholar