- Department of Electrical Engineering, National Institute of Technology Srinagar, Hazratbal, Srinagar, India
This paper proposes a new method for assigning distribution system (DS) losses to consumers and distributed generations in the framework of a liberalized energy market. The architecture of the proposed method is based on a synthesis of electrical network analytical theory and cooperative game theory (CGT). Weighted shapely value (WSV) is a solution idea that is regarded to be efficient in CGT for n-player games with characteristic function form. By retaining the notion of electrical networks, the axioms of game theory will be preserved while employing the WSV in loss allocation theory. To allocate system losses, the proposed method estimates the average marginal contribution of each participant to all conceivable coalitions and also determines the weight of the marginal contribution of each participant based on its power rating. Rather than a sequential branch-oriented approach, the proposed methodology is node-oriented. Additionally, a majority rule game is used to constrain the population of a coalition without jeopardizing the efficacy of the solutions to achieve a fair allocation of losses. The results of the proposed method are presented and contrasted with those obtained using the conventional pro-rata method and the well-known Shapley value solution concept in CGT.
1 Introduction
Since the introduction of the deregulation and liberalization of the electricity market in the power system, the traditional operations of generation, transmission, and distribution networks, as well as their commercial practices, have changed (Raikar and Jagtap, 2018). Additionally, as a result of technological advancements in small scale generators, referred to as distributed generators (DGs) and the establishment of competition among retail market participants, distribution systems (DSs) have garnered significant attention in the energy market. However, distribution service providers are currently confronted with several substantial operational challenges, including protection against bidirectional power flow and identifying the appropriate economic signal for the contributions of participants to system performance.
Costs associated with DS services must be assigned using suitable technology aspects capable of distinguishing between economic signals generated by numerous users/participants (including DGs). Due to the fact that DSs have a higher resistance to reactance ratio than transmission systems, they are therefore considered to be lossy networks. Thus, the cost of system losses accounts for a significant portion of service charges, and in order to preserve economic efficiency, it should be allocated fairly among consumers and DGs through a mechanism that takes into account the interaction of participants and their contributions to system losses (Amaris et al., 2018).
System losses are also a component of the active and reactive power flows that are lost in distribution lines during a distribution event, and thus fall into the same category as unit energy consumption expenses. Thus, the distribution of losses is entirely economic in nature. Allocating system losses, on the other hand, is not as straightforward because of two critical factors: first, system losses are a non-linear consequence of active and reactive power flows; and second, there is mutual interaction or interdependency among participants involved in the distribution activities (Amaris et al., 2018; Shafeeque Ahmed and Prabhakar Karthikeyan, 2018). On the other hand, a group of DGs adds complexity by requiring compensation for their contributions to minimizing system losses and improving system voltage profiles through optimum power injection.
Researchers attempt to address the problem of loss allocation in a variety of ways in the existing scientific literature. However, in order to reduce volatility and maximize efficiency, techniques must follow and adhere to the axioms specifically stated for loss allocation algorithms (Digs and Chen, 2020). Salgado, Moyano and Medeiros. (2004) discussed a variety of approaches, including the use of participation factors derived from power flow solutions, the direct application of sensitivity relationships between transmission losses and bus power injections, and the integration of sensitivity relationships between participation factor and bus power injection. Conejo et al. (2002) provided theoretical and mathematical overviews of several allocation approaches, including pro-rata (Savier and Das, 2012), marginal allocation (Mutale et al., 2000; Galiana et al., 2002), unsubsidized marginal allocation (Mutale et al., 2000; Galiana et al., 2002), and proportional sharing (Bialek, 1996). The methods described in (Conejo et al., 2002) are well-established and often quoted in the literature. Proportional sharing is based on the idea of proportionality, marginal allocation is based on the incremental transmission loss coefficient, and proportional sharing is based on a linear proportional power tracing algorithm.
Kumar et al. (2019) presented circuit theory-based branch-oriented approach for active power loss allocation by decomposing the cross-terms among load points. Hota, Mishra and Mishra. (2021) discussed various types of DGs technology and assigned system losses to them along with different load points using bifurcating the cross-term. Sindi, H. et al. (2021) presented convolutional neural network architecture uses the Z-bus matrix as input is 1D for system loss allocation in distribution systems. With characterization of unbalanced distribution networks as multilayered radial graphs, Nikolaidis et al. (2019) proposed a graph-based loss allocation method for dispersed market settings that harmonizes the physical characteristics of the distribution grid with the underlying financial transactions. Moret, F. et al. (2021) studied market behavior by taking into consideration the various system operators and retailers. The distribution of operational costs in those decentralized markets was also discussed. Authors examined loss allocation rules and their effects on pricing in order to prevent market outcomes that prejudice agents based on their locations. Usman, M. et al. (2019) introduced a multi-phase loss allocation methodology that explicitly disclosed losses allocated to the neutral as well as fairly separated losses associated with cross-terms of phase-currents. Branch-oriented approaches are specifically designed to address the problem of loss allocation in radial DSs. All branch-oriented approaches developed are classified into two categories: current-based approaches as described (Savier and Das, 2012; Kumar et al., 2018; Shafeeque Ahmed and Prabhakar Karthikeyan, 2018; Usman, Coppo et al., 2019) and power-based approaches as described in (Atanasovski and Taleski, 2012; Ghofrani-Jahromi, Mahmoodzadeh and Ehsan, 2014; Jagtap and Khatod, 2015).
Cooperative game theory (CGT) and artificial intelligence have also been proposed in the previous decade as strategic and interactive solution approaches for the non-linear problem of loss allocation in power DSs. Amaris et al. (2018) introduced a game theory-based Aumann-Shapley solution idea in which unitary participation coefficients for each network user were determined based on the currents demanded/injected by each user and the network structure. Dev Choudhury and Goswami. (2011) sought to address the loss allocation problem using an artificial neural network (ANN) trained using Levenberg–Marquardt back propagation and Bayesian regularization back propagation. Molina, Prada and Saavedra. (2010) presented the Aumann-Shapley solution approach for calculating the contribution of generators and consumers to overall system losses in CGT. Dev Choudhury and Goswami. (2012) combined ANN with Shapley value CGT to solve a given non-linear issue. Pourahmadi and Dehghanian. (2018) presented the Shapley Value, a cooperative game-theory concept for loss allocation in power distribution networks. The proposed method was a generic strategy that could be applied to both radial and meshed distribution systems, as well as those networks which have integration of significant penetration of renewables and DG units. Shaloudegi et al. (2012) introduced the Shapley value for allocating reduced system losses gained by adding DGs and rewarding them using the locational marginal pricing approach. Yu et al. (2018) provided a strategy for allocating losses and emission reductions based on the minimal cost-remaining savings and the Aumann-Shapley value methods.
1.1 Author contribution and novelty of the work
In light of the preceding research, this paper proposes a new scheme for allocating DS losses to network participants in the deregulated energy market. The proposed method is based on a synthesis of electrical circuit theory and weighted Shapley values - a new notion in CGT.
To allocate the losses, existing techniques that cited in the given literature, take into account either the steady-state power rating of loads and DGs or their in-cooperative contribution w.r.t. to their location in the network. This led to bias and unfair solutions to passive participants who are connected away from the substations. However, on the other hand, in comparison to techniques cited in the given literature, the key contribution of this work is that the proposed method considers the average marginal contribution of each load and DG, as well as their weights, as a coefficient for sharing system losses. This not only benefits the loads but also grant maximum incentives to DGs for their contribution to loss reduction.
The management and handling of coalitions associated with CGT are the most tedious and time-consuming tasks. Coalitions can further grow to be very large in size depending on the number of participants in the system. To alleviate the stress associated with coalition computation, the paper proposes an algorithm named as majority rule game strategy for reducing the population of coalitions without jeopardizing the CGT axioms or the solution’s effectiveness. Novelty of this work is stated that proposed method can manage and reduce the number of coalitions effectively without compromission in fairness of loss sharing so that it may apply for any practical distribution systems which have thousands of nodes and participants.
The highlight of this paper exhibits that the proposed method produces efficient results by determining the significant contributions of consumers and DGs to overall system losses (including loss saving). The impacts of different market participants and their mutual contribution on system power losses are also considered. The proposed method fairly and rationally assigns system losses, and the allocation results are unaffected by the reduced number of coalitions constituted. Based on cooperative game theory, a weighted Shapley value-based power loss allocation approach is proposed and thoroughly compared with the Shapley value-based allocation method and the pro-rata method.
The remainder of the paper is structured as follows: The second section introduces the terminology and axioms of CGT; it also discusses the Weighted Shapley value, Shapley value, and majority rule game in CGT; the third section derives mathematical expressions for the proposed method; the fourth section discusses the obtained results; and the fifth section concludes the work.
2 Cooperative game theory
Game theory is a mathematical framework for describing and analyzing social interactions in which two or more individuals make decisions that affect the payoff of the other. The formal definition of CGT is as follows: let
Axiom 1: (Monotonicity) Let
Axiom 2: (Positivity) Let
Axiom 3: (Individual rationality) Let
Axiom 4: (Coalitional rationality) Let
Axiom 5: (Efficiency) Let
2.1 Weighted shapley value
For any transferable utility game
Let
Such that
2.2 Shapley value
For any transferable utility game
Where, the term
2.3 Majority rule game
Any transferable utility game
or
3 Proposed mathematical formulation
The CGT model is used in this paper to tackle a non-linear problem of loss allocation. As a result, this section first discusses the generalized model of system power flow that follows the idea of an electrical network, and the problem of loss allocation in the context of CGT value is modelled in the next subsection.
3.1 Model of system power flow
Losses in distribution networks are caused by both consumer and DG. Therefore, responsibility for losses must be allocated among them based on their contributions.
This paper uses node and branch indexing techniques, as well as the power flow algorithm described in (Savier and Das, 2012). Following the execution of the power flow, system losses are calculated. The phasor value of current drawn by load (consumer current) at bus i, i.e., load i, may be calculated as follows:
where,
Similarly, the generator current phasor value may be represented as:
Where,
Assumption for power sign convention of participants as follows: consumers draw power from the network, so their power and current are both assumed to be positive, whereas DGs inject power into the network, so their power and current are both assumed to be negative.
In the case where both the consumer and the DG are connected to a common bus i the resultant value of current at bus i is given by:
where,
The sign of
The structural design of the DS is radial, and the resultant power will flow unidirectional, i.e., from the reference/root node to the end nodes. Thus, in this paper, current flowing through any branch is calculated using the bus injection to branch current (BIBC) matrix and is stated as:
Where, n is the total number of buses in the system;
Elements in the row matrix are defined as:
Eij=
Eq. 14 can be expressed in its canonical form as:
where, BIBC is the bus injection to branch current matrix whose dimension is
Bus 1 serves as the root node/reference bus, and it is presumed that no load is connected to it, hence it is excluded from the BIBC matrix.
From (14), the equation for current in any branch i may be expressed as,
The real power loss of the system is stated as:
where,
Using (16) and (17), the real power loss of the system can also be expressed as,
3.2 Application of CGT in loss allocation problem
To yield maximum advantage to DGs in terms of their contributions in loss saving without affecting the economic efficiency of the system, or in other words, to eliminate consumer cross-subsidies, this article uniquely distinguishes the changes in losses caused by consumers and DGs separately. Hence, following Subsection 3.2.1 describes the allocation of system losses to load (i.e., base case or without DG), and thus (12) can be modified
3.2.1 Loss allocation to load
The proposed approach tries to ascertain the contribution of each consumer to the system power losses produced by them all. Assume
Characteristic function of a grand coalition, i.e.,
Coalition S is defined as a subset of N, or in other words, as the set of all conceivable consumer combinations that do not repeat. However, the overall number of coalitions in the game
Consider a coalition
Where,
In the CGT model, the contribution of any consumer i to system losses may be determined by the marginal contribution of that customer to all conceivable coalitions. However, this paper uses majority rule games in which only coalitions with consumers greater than 50% of total consumers participated; or in other words, due to the large number of participants, system losses offered by only those coalitions are clearly greater than 50%–80% of total system losses, as expressed as:
For given game
The marginal contribution of the Harsanyi dividend to any coalition S is determined by its coefficients which are the probability of apparent power rating of the consumer in that coalition, referred to as the weight of consumer.
In given DS, weight of any consumer i is defined as:
The probability of the customer i having a certain weight in a coalition S is represented as follows:
Finally, the contribution of consumers to system losses as measured by the weighted shapely value
3.2.2 Loss saving allocation to DG
The base case for DSs is modified by incorporating DGs optimally, and as a consequence, system losses are reduced relative to the base case scenario. As a result of DG integration, the resultant current at the node where both load and DG are coupled is denoted by
Loss savings are stated as a grand coalition and are defined as the difference between system losses with and without DG, as follows:
where,
Generators are a component of coalition S. As a result, the characteristic function of each coalition S is defined as follows:
In this section, the majority rule game may not be used since the game involves a smaller number of generators. As a result, the number of coalitions in the game is likewise lower, which may be managed without using the majority rule game.
For given game
Finally, the contribution of DG to loss reduction as shown by the weighted shapely value
Eqs 26–30 denote the weighted Shapley value of the consumer and DG who contributed to system losses, respectively.
4 Result and discussion
The proposed technique has been evaluated on three different test systems, namely,: 4-bus, 33-bus, and 69-bus radial DSs. Two distinct scenarios have been evaluated for each of the test systems, namely, the system without DGs, referred to as the base case, and the system with DGs. To eliminate cross-subsidies and ensure consistency in economic signals, the proposed technique examines system power flow individually for each scenario. In the base case, system losses have been allocated to all consumers, while loss reduction has been awarded to DGs. To validate the proposed method, the results have been compared to those obtained using the Shapley value and pro-rata methods. The Shapley value approach allocates losses based on the average marginal contribution of participants, whereas the pro-rata approach allocates losses based on the proportionality principle.
4.1 Test system 1: 4-Bus distribution system
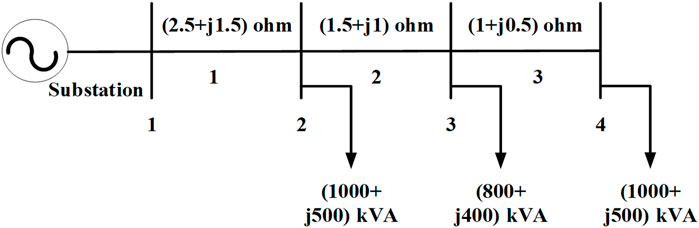
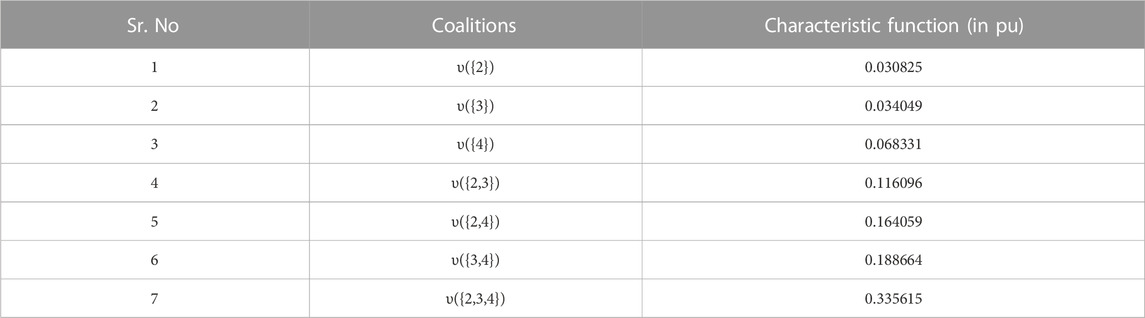
A hypothetical 4-bus DS is used to illustrate the CGT model for system loss allocation and to evaluate the proposed method. The circuit diagram of the test system is depicted in Figure 1, and its actual line and load data are given in figure. As shown in Figure 1, bus 1 acts as a substation and it is assumed that no load is connected on it and voltage is regulated at specified value, whereas loads are connected to buses 2, 3, and 4. To analyze and comprehend the proposed mechanism, allocation of system losses using base case has been considered. The number of coalitions that participated in establishing a fair allocation of losses is 7, and they are shown in Table 1. Due to a smaller number of coalitions, it may be managed without incurring a computational execution burden. So, for the given network, no need to use the majority rule game for allocation.
Base values of test system are 11 kV and 1 MVA. After execution of power flow, voltages on system buses are V1=(1 + j0) pu; V2=(0.91533-j0.00572) pu; V3=(0.88127-j0.0096) pu; and V4=(0.86939-j0.00947) pu. The total real losses in the system are 0.335621 pu. The first stage in determining the participation of consumer to system losses is to ascertain the coalitions and their worth. Table 1 illustrates the coalitions that have been formed, and worth corresponding to each coalition.
Similarly, for each coalition, compute the Harsanyi dividend based on the worth of the characteristic function. Thus,
Now, the share of losses of consumers connected to bus 2 is determined as
After estimating the shares of consumers in system losses, it is required to determine whether or not they are fairly allocated by establishing axioms.
The losses shared by the proposed method fulfil all of the key axioms for fair game as specified in Section 2, as follows: By following axiom 1, the proposed method has penalized the consumers for the cause of system losses of a given DS in the game
From the preceding results, it is clear that no consumer is expected to agree to receive less than the consumer obtained acting alone, as indicated by individual rationality, and additionally, the payoff vector of the total system losses received by the consumer, with the understanding that consumer i must receive
Because coalitional rationality is not a criterion for defining the weighted Shapley value, the solution produced using the proposed method does not necessarily belong to the core. However, depending on the network architecture, the number of consumers, and the manner in which power is distributed, the solution of the proposed method may belong to the core.
Table 2 depicts the allocated losses (in kW) by the proposed method compared to those of the other two methods. Because the power consumption of buses 2 and 4 is identical, the pro-rata method assigns identical losses. However, the proposed method and the Shapley value method differentiate consumers based on their marginal contributions to coalitions and thus assign different losses than the pro-rata method does. However, in addition to marginal contribution, the proposed method takes the weight of the consumer into account, and hence the resulting value differs from the Shapley value. Thus, as shown in Table 2, neither a consumer located far from the substation nor a consumer located close to the substation experiences economic overload as a result of the proposed method.
As a result of the aforementioned analysis, it is clear that the proposed method fulfils the agreement on unbiased system loss allocation. Additionally, while the proposed method satisfies all of the axioms necessary for equitable allocation, it may not fulfil coalition rationality for specific networks. Apart from this, the proposed method has an advantage over the Shapley value method in that it bases loss allocation on the marginal contribution of consumers to system losses as well as the probability of the consumer drawing power in coalitions of their marginal contributions.
4.2 Test systems 2: 33-Bus and 69-bus distribution systems
In this test system, 33-bus and 69-bus DSs have been considered. Line and load data of 33-bus and 69-bus DSs were obtained from (Atanasovski and Taleski, 2012) and (Savier and Das, 2012), respectively. To reduce the system losses and improve the voltage profile, DGs are optimally located and sized in a 33-bus test system at bus numbers 7,17 and 32 with power injection of
Table 3 depicts the loss allocated to consumers and the loss saving to DGs of a 33-bus DS using all three methods. In the CGT model, the total number of coalitions required for a 33-bus (excluding bus-1) DS is
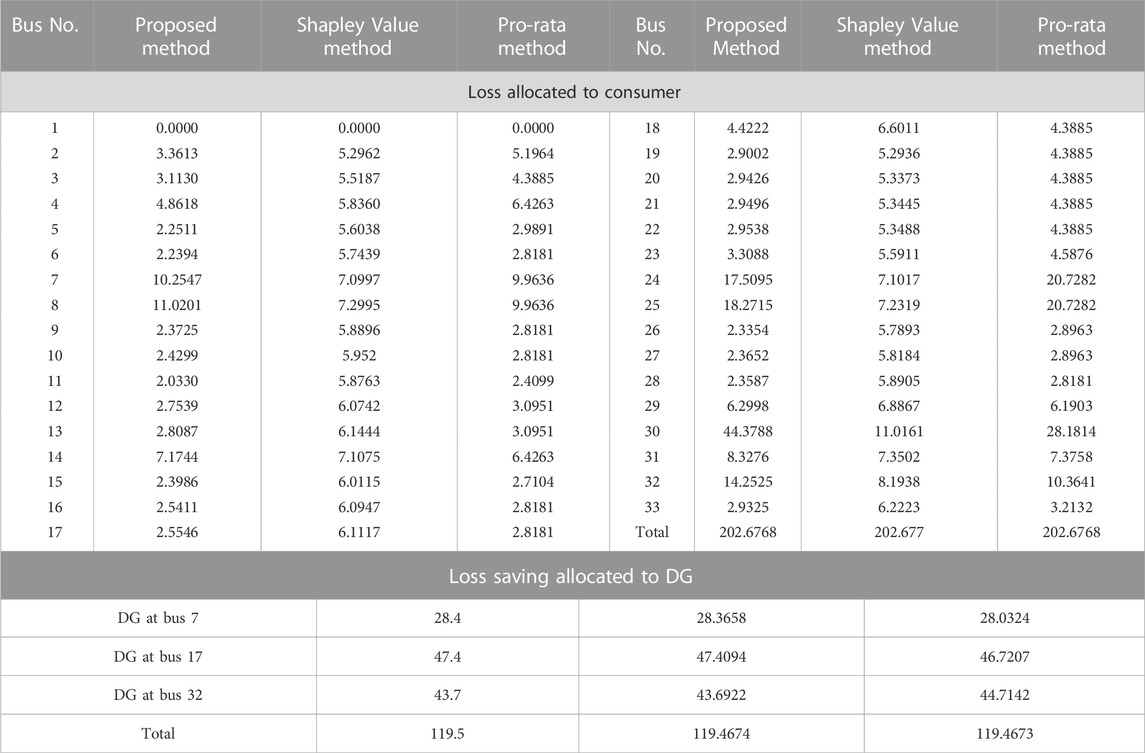
TABLE 3. Comparison of allocated losses (in kW) and loss saving (in kW) to load and DG, respectively, of 33-bus DS by all three given methods.
As shown in Table 3, the proposed method did not assign the higher losses to the consumers with the large power rating nor did it assign equal losses to consumers with the same power rating in various buses. Additionally, Table 3 details the allocation of loss savings to DGs. Loss savings are used to reward DGs for their contributions to system performance improvement. Each of the three techniques assigned nearly identical loss savings to all connected DGs.
Table 4 shows the loss allocated to consumers and loss saving allocated to DGs of a 69-bus DS using all three methods. The total number of coalitions required for 69-bus DS is 2.951

TABLE 4. Comparison of allocated losses (in kW) and loss saving (in kW) to load and DG, respectively, of 69-bus DS by all three given methods.
As a result of the foregoing test systems and discussion, it is concluded that the proposed method may be used to any size of realistic DSs without jeopardizing the consistency and fairness of loss allocation.
5 Conclusion
This paper has proposed a new, simple, and effective technique for allocating losses in radial DSs with DGs. The proposed method has allocated system losses using a node-oriented approach. It has employed weighted shapely value in CGT for the allocation of system losses. It has developed by integrating the fundamental principles of the electrical network with the CGT model. The results obtained using the proposed method satisfy the axioms of fairness in the sharing of system losses. It combines the characteristics of both the Shapley value and pro-rata methods. Hence, it distributes system losses more fairly to consumers and DGs than either of these two methods. From results of 33 and 69 bus test systems, it is observed that when the number of participants increases, the proposed method has offered a great deal of flexibility and adaptability through the majority rule game. Therefore, the proposed method is applicable and produce efficient results for practical DSs which contain thousands of nodes and participants. The proposed technique has the advantage of being applicable to modern DSs without imposing an undue economic burden on consumers irrespective of their power ratings. Additionally, it has prompted DGs to infuse power into local DSs by giving a desirable economic gain in exchange for their system performance improvements.
Distribution system gets modernized by incorporating non-linear loads and green energy technology which adversely affects the system power flow and therefore losses. Furthermore, majority of the time, DS is in imbalanced mode. In such environment, allocation of system losses to various participants is challenged and offer future scope for this work.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Al-Digs, A., and Chen, Y. C. (2020). Power system loss divider. IEEE Trans. Power Syst. 35 (6), 3286–3289. doi:10.1109/TPWRS.2020.2989632
Amaris, H., Molina, Y. P., Alonso, M., and Luyo, J. E. (2018). Loss allocation in distribution networks based on aumann-shapley. IEEE Trans. Power Syst. 33 (6), 6655–6666. doi:10.1109/TPWRS.2018.2844740
Atanasovski, M., and Taleski, R. (2012). Energy summation method for loss allocation in radial distribution networks with DG. IEEE Trans. Power Syst. 27 (3), 1433–1440. doi:10.1109/TPWRS.2011.2182663
Bialek, J. (1996). Tracing the flow of electricity. IEE Proc. Generation, Transm. Distribution 143 (4), 313–320. doi:10.1049/ip-gtd:19960461
Conejo, A. J., Arroyo, J. M., Alguacil, N., and Guijarro, A. L. (2002). Transmission loss allocation: A comparison of different practical algorithms. IEEE Power Eng. Rev. 22 (5), 66. doi:10.1109/MPER.2002.4312201
Dev Choudhury, N. B., and Goswami, S. K. (2011). Artificial intelligence solution to transmission loss allocation problem. Expert Syst. Appl. 38 (4), 3757–3764. doi:10.1016/j.eswa.2010.09.035
Dev Choudhury, N. B., and Goswami, S. K. (2012). Transmission loss allocation using combined game theory and artificial neural network. Int. J. Electr. Power Energy Syst. 43 (1), 554–561. doi:10.1016/j.ijepes.2012.05.017
Galiana, F. D., Conejo, A., and Kockar, I. (2002). Incremental transmission loss allocation under pool dispatch. Power 17 (1), 26–33. doi:10.1109/59.982189
Ghofrani-Jahromi, Z., Mahmoodzadeh, Z., and Ehsan, M. (2014). Distribution loss allocation for radial systems including DGs. IEEE Trans. Power Deliv. 29 (1), 72–80. doi:10.1109/TPWRD.2013.2277717
Gilles, R. P. (2010a). “The cooperative game theory of networks & hierarchies,” in Recherche (Berlin, Heidelberg: Springer (Theory and Decision Library C)), 44. doi:10.1007/978-3-642-05282-8
Gilles, R. P. (2010b). THEORY and decision library general Editors: W. Leinfellner, and G. Eberlein (Munich) Series A: Philosophy and methodology of the social sciences series B: Mathematical and statistical methods series C: Game theory, Mathematical Programming and Op. Heidelberg, Germany: Springer.
Hota, A. P., Mishra, S., and Mishra, D. P. (2021). Active power loss allocation in radial distribution networks with different load models and DGs. Electr. Power Syst. Res. 205, 107764–764. doi:10.1016/j.epsr.2021.107764
Jagtap, K. M., and Khatod, D. K. (2015). Loss allocation in distribution network with distributed generations. IET Generation, Transm. Distribution 9 (13), 1628–1641. doi:10.1049/iet-gtd.2014.0923
Kalai, E., and Samet, D. (1987). On weighted Shapley values. Int. J. Game Theory 16 (3), 205–222. doi:10.1007/BF01756292
Kumar, P., Gupta, N., Niazi, K. R., and Swarnkar, A. (2019). A circuit theory-based loss allocation method for active distribution systems. IEEE Trans. Smart Grid 10 (1), 1005–1012. doi:10.1109/TSG.2017.2757059
Kumar, P., Gupta, N., Niazi, K., and Swarnkar, A. (2018) ‘Branch current decomposition method for loss allocation in contemporary distribution systems’, Int. J. Electr. Power Energy Syst., 99(2017), pp. 134–145. doi:10.1016/j.ijepes.2018.01.004
Molina, Y. P., Prada, R. B., and Saavedra, O. R. (2010). Complex losses allocation to generators and loads based on circuit theory and aumann-shapley method. IEEE Trans. Power Syst. 25 (4), 1928–1936. doi:10.1109/TPWRS.2010.2044425
Moret, F., Tosatto, A., Baroche, T., and Pinson, P. (2021). Loss allocation in joint transmission and distribution peer-to-peer markets. IEEE Trans. Power Syst. 36 (3), 1833–1842. doi:10.1109/TPWRS.2020.3025391
Mutale, J., Strbac, G., Curcic, S., and Jenkins, N. (2000). Allocation of losses in distribution systems with embedded generation. IEE Proc. Generation, Transm. Distribution 147 (1), 7–14. doi:10.1049/ip-gtd:20000003
Nikolaidis, A. I., Charalambous, C. A., and Mancarella, P. (2019). A graph-based loss allocation framework for transactive energy markets in unbalanced radial distribution networks. IEEE Trans. Power Syst. 34 (5), 4109–4118. doi:10.1109/TPWRS.2018.2832164
Nowak, A. S., and Radzik, T. (1995). On axiomatizations of the weighted shapley values. Games Econ. Behav. 8 (2), 389–405. doi:10.1016/S0899-8256(05)80008-9
Pourahmadi, F., and Dehghanian, P. (2018). A Game-theoretic loss allocation approach in power distribution systems with high penetration of distributed generations. Mathematics 6 (9), 158. doi:10.3390/math6090158
Raikar, S. B., and Jagtap, K. M. (2018) ‘Role of deregulation in power sector and its status in India’, 2018 National Power Engineering Conference, NPEC , Bhubaneswar, India, pp. 1–6. doi:10.1109/NPEC.2018.8476714
Salgado, R. S., Moyano, C. F., and Medeiros, A. D. R. (2004). Reviewing strategies for active power transmission loss allocation in power pools. Int. J. Electr. Power Energy Syst. 26 (2), 81–90. doi:10.1016/j.ijepes.2003.07.001
Savier, J. S., and Das, D. (2012). An exact method for loss allocation in radial distribution systems. Int. J. Electr. Power Energy Syst. 36 (1), 100–106. doi:10.1016/j.ijepes.2011.10.030
Shafeeque Ahmed, K., and Prabhakar Karthikeyan, S. (2018). Modified penalized quoted cost method for transmission loss allocation including reactive power demand in deregulated electricity market. Elsevier Ltd. 16, 370–379. doi:10.1016/j.segan.2018.10.004
Shaloudegi, K., Madinehi, N., Hosseinian, S. H., and Abyaneh, H. A. (2012). A novel policy for locational marginal price calculation in distribution systems based on loss reduction allocation using game theory. IEEE Trans. Power Syst. 27 (2), 811–820. doi:10.1109/TPWRS.2011.2175254
Sindi, H., Nour, M., Rawa, M., Ozturk, S., and Polat, K. (2021). Random fully connected layered 1D CNN for solving the Z-bus loss allocation problem. Measurement 171, 108794. doi:10.1016/j.measurement.2020.108794
Usman, M., Coppo, M., Bignucolo, F., Turri, R., and Cerretti, A. (2019). A novel methodology for the management of distribution network based on neutral losses allocation factors. Int. J. Electr. Power Energy Syst. 110, 613–622. doi:10.1016/j.ijepes.2019.03.051
Usman, M., Coppo, M., Bignucolo, F., Turri, R., and Cerretti, A. (2019). Multi-phase losses allocation method for active distribution networks based on branch current decomposition. IEEE Trans. Power Syst. 34 (5), 3605–3615. doi:10.1109/TPWRS.2019.2908075
Keywords: cooperative game theory, distributed generations, distribution systems, shapley value, weighted shapley value
Citation: Singh VP, Ahmad A and Jagtap KM (2023) Weighted shapley value: A cooperative game theory for loss allocation in distribution systems. Front. Energy Res. 11:1129846. doi: 10.3389/fenrg.2023.1129846
Received: 22 December 2022; Accepted: 28 February 2023;
Published: 22 March 2023.
Edited by:
Bhavnesh Kumar, Netaji Subhas University of Technology, IndiaReviewed by:
Dinesh Kumar Singh, Shambhunath Institute of Engineering and Technology, IndiaNavneet Kumar Singh, Motilal Nehru National Institute of Technology Allahabad, India
Sumedha Sharma, University of Calgary, Canada
Copyright © 2023 Singh, Ahmad and Jagtap. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kushal Manoharrao Jagtap, amFndGFwa3VzaGFsQG5pdHNyaS5hYy5pbg==
 Vijay Pal Singh
Vijay Pal Singh Aijaz Ahmad
Aijaz Ahmad