Transient stability enhancement using optimized PI tuning of static synchronous series compensator in wind power conversion system

Power systems are expanding comprehensively with the increase in load demand from both residential and industrial usage. Renewable energy is penetrating the power system to satisfy the power needs of the load demand. With its potential to generate power and compensate for a large portion of the load demand, wind generators make a major renewable power contribution. Power oscillations inherent in wind generator integration with the grid are a power quality issue to be addressed. Oscillation damping using flexible AC transmission system (FACTS) devices is a relevant solution for the power quality issue. There are multiple reasons for power oscillation. Mainly, power systems encounter fault conditions. The faults can be cleared, and the power system tries to retain stability. Sometimes, the system fails due to a longer settling time. A series-connected FACTS device utilized as a series compensator is referred to as a static synchronous series compensator (SSSC). Controlling the flow of electricity over a transmission line using this method is incredibly efficient. The capacity to switch between a capacitive and an inductive reactance characteristic is necessary. The SSSC regulates the flow of power in transmission lines to which it is linked by adjusting both the magnitude of the injected voltage and the phase angle of the injected voltage in series with the transmission line. This allows the SSSC to manage the power flow in the transmission lines. It does it by inserting a voltage that can be controlled into a transmission line in series with the fundamental frequency. This paper develops the optimally tuned SSSC in the wind-integrated grid system to dampen the oscillation. Teacher–learner-based optimization (TLBO) and gray wolf optimization (GWO) algorithms are used to tune the PI controller to improve the damping response. The obtained results show that the damping performance of the proposed controller is better than that of the other traditional controllers.

Introduction

The generation of electricity has been almost entirely dependent on fossil fuels, which are a contributing factor to climate change. Many attempts are being made to incorporate renewable energy sources (RES) into the power system to supplant the traditional fuels that are currently used for generation of electricity (Poultangari et al., 2012). One of these renewable energy sources is wind energy, which, compared to fossil fuels, is both abundant and affordable (Osman et al., 2015). Controlling the pitch angle is one of the control strategies used in wind turbines. It is utilized to achieve the goals of controlling the output power and lowering the loading on the wind turbine components. The PI controller, hydraulic or servo motor, and rate limiter comprise the bulk of its constituent parts. Recent years have seen the implementation of several controllers, including the fuzzy logic controller (FLC), the programmable logic controller (PLC), the maximum point power tracker (MPPT), and the adaptive controller (Burakov and Shishlakov, 2017; Yang et al., 2017). In contrast to the PI controllers, however, these controllers are not only difficult to use but are also expensive. Consequently, PI controllers continue to have a variety of uses in the wind power industry. Finding the gains that are best suited for the PI controller is a challenge. In Civelek et al. (2016), an improved genetic algorithm (IGA) was used to fine-tune the gains of a proportional integral derivative (PID) controller. Compared to the Zeigler and GA tuning methods, the outcome produced by the IGA tuning method is superior.

The gains of the PID controller in the blade pitch angle control were optimized with the help of the PSO algorithm, which increased the amount of power that the variable speed wind turbine was able to produce. Consequently, a larger quantity of power was produced. A considerable performance improvement was observed by switching from the GA tuning strategy to the PSO tuning method. Due to the low efficiency and also the challenges in managing the generator speed of the fixed-speed wind turbines, the variable-speed wind turbines were studied as an alternative to the fixed-speed wind turbines. Regulation of the pitch angle fuzzy is explained in Civelek (2019). Employing PSO to achieve better pitch control is reported in Zahra et al. (2017). The optimization of the PMSG wind turbine grid control is accomplished with the assistance of gray wolf optimizers (Qais et al., 2018) and whale optimization described in Mohamed A and Haridy (2019). Soued et al. (2017) discussed many different metaheuristic optimizers.

Variable-speed wind turbines are more durable, straightforward in construction, and have lower maintenance costs. The PSO tuning approach offers the benefit of rapid convergence, but the GA tuning method is well-accepted due to its high level of accuracy. Nevertheless, the PSO has the potential to converge on a local optimum solution. Additionally, the tuning of the GA can converge too soon, leading to local optimality.

The following is a brief overview of some of the most recent papers written about wind turbines. Choi et al. (2016) made a few suggestions for hybrid power generation. The technical document is beneficial in gaining a grasp of the operation of the wind turbine (Wwd- and Wwd, 2019). A review of hybrid wind–solar energy systems is presented in Sinha and Chandel (2015), which makes use of several optimization strategies. Syahputra et al. (2014) suggested the idea of harnessing wind energy for power generation on the distribution side of the system. A discussion of the Simulink model can be found in Costea et al. (2015). Naik and Gupta (2016) and Ou et al. (2017) provided additional information about the fluctuation of power and the transient study analysis. Bektache and Boukhezzar (2018) discussed optimal power capture, and Naresh and Tripathi (2018) discussed optimal power capture as a hardware solution that uses FPGA. A Java algorithm is utilized in Annamraju and Nandiraju (2019), a fuzzy logic controller is utilized in Duong et al. (2015), an electro-search optimizer is utilized in Dahab et al. (2020), a social search algorithm is utilized in Mohapatra et al. (2019), whale optimization is utilized in Khadanga et al. (2019), gray wolf optimization is utilized in Padhy and Panda (2021), and TLBO is utilized in Pahadasingh (2021) to study stability. However, these algorithms are not widely used in the generation of wind power utilizing doubly fed induction generators (DFIGs) and for power oscillation damping, which is the most important issue.

The integration of wind power generation into the electricity system is done to enhance the power available on the distribution side of the system. The power is disrupted due to wind turbulence. One of the effective series flexible AC transmission systems (FACTS) for increasing the stability of the power system is the static synchronous compensator (SSSC). When managing the injected voltage, the SSSC makes use of the PI controller. Due to the size of the system, PI controller tuning is not a task that can be performed by SSSC controllers. Therefore, the meta-heuristic approach is utilized to modify the PI controller. In this present study, the tuning of the PI controller, which is intended to increase the response, uses the teacher and learner (TLBO) and gray wolf optimization (GWO) algorithms.

Methodology

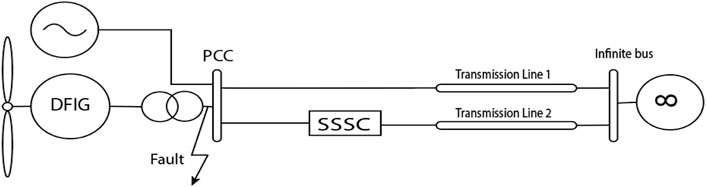
Figure 1 depicts the planned organizational structure of the proposed system in terms of blocks. In this configuration, the step-up transformer is connected to the DFIG wind generator and the point of common connection (PCC), which is then coupled to the PCC. Then it is wired to the grid using two transmission lines. DFIG causes more oscillations because of the fault in the transmission line system, and eventually, it settles down. The proposed SSSC and associated control will need to dampen these oscillations to be effective.

FIGURE 1

FIGURE 1. Block diagram of the proposed system.

SSSC modeling

The components of the series injected voltage for the aforementioned two components are expressed by the following equations:

$V_{dse}=n_c{K}_{inv}{V}_{d{c}_{sssc}}\mathit{cos}{\alpha }_{se},(1)$

$V_{qse}=n_c{K}_{inv}{V}_{d{c}_{sssc}}\mathit{sin}{\alpha }_{se},(2)$

where

$n_c$—ratio of the coupling transformer

${V_{dc}}_{sssc}$—Dclink voltage

${\alpha }_{se}$—Series-injected phase angle

$K_{inv}$—Is a constant to convert the DC to AC using an inverter.

The real (P) and reactive (Q) flows are given as follows:

$P=\frac{V_s{V}_r}{X_L}\sin \left({\delta }_s-{\delta }_r\right)=\frac{V^2}{X_L}\sin \delta ,(3)$

$Q=\frac{V_s{V}_r}{X_L}\left(1-\cos \left({\delta }_s-{\delta }_r\right)\right)=\frac{V^2}{X_L}\sin \delta ,(4)$

where $V_S$ and $V_r$ are the magnitudes, and ${\delta }_s$ and ${\delta }_r$ are the phase angles of the voltage sources $V_S$ and $V_r$, respectively. For simplicity, the voltage magnitudes are chosen such that $V_s=V_r=V$, and the difference between the phase angle is ${\delta }_s={\delta }_r=\delta$.

$P_q=\frac{V^2}{X_{eff}}\sin \delta =\frac{V^2}{X_l\left(1-\frac{X_q}{X_l}\right)}\mathit{sin}\delta .(5)$

$Q=\frac{V^2}{X_{eff}}\left(1-\cos \left(\delta \right)\right)=\left\{\frac{V^2}{X_l\left(1-\frac{X_q}{X_l}\right)}\right\}\sin \delta .(6)$

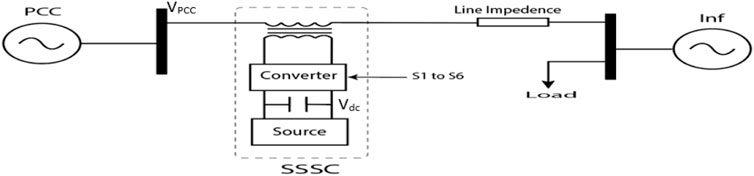
Figure 2 shows the details of the SSSC system. It has capacitors as a storage element, and a converter used is the inverter. The transformer is connected in series. The DC link is connected to the converter, and the three-phase end of the converter is connected to the transformer end. The S1 to S6 switches in the converter are controlled as shown in Figure 3.

FIGURE 2

FIGURE 2. Detailed system model of an SSSC without a control.

FIGURE 3

FIGURE 3. Detailed SSSC control system.

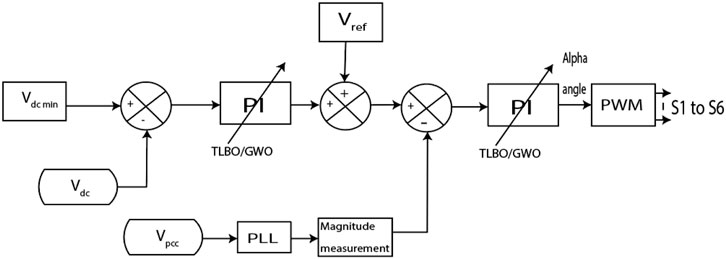
Figure 3 shows the control system of the SSSC. The minimum voltage requirement at the DC link ($V_{dc\mathit{min}}$) is compared to the DC voltage ($V_{dc})$ that is measured. This error generated is connected to the PI controller. The PI controller is tuned with TLBO/GWO. This PI controller output is connected to another comparator. Then, the output is compared with the reference voltage ($V_{ref})$. This output is again connected to another comparator. The point of common coupling voltage $\left(V_{pcc}\right)$ magnitude is compared with this error, and the desired converter alpha angle is determined. This alpha angle is sent to the pulse width modulation (PWM) system. S1 to S6 are the PWM signals, which are connected to the SSSC block as shown in Figure 2.

Objective function

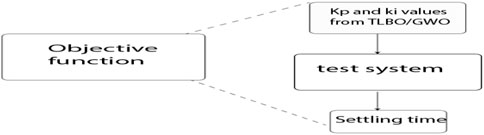
As shown in Figure 3, the PI controller must be tuned using an objective function. This objective function (Figure 4) must be minimized by selecting optimal kp and ki parameters. Eq. 7 is the objective function. Eqs 8, 9 are constraints.

FIGURE 4

FIGURE 4. Operational diagram for tuning the controller.

Minimizing voltage settling time

${\displaystyle \sum }_{i=1}^{n}Ts.(7)$

With respect to constraints

$K_{p\mathit{min}}\le K_p\le K_{p\mathit{max}.}(8)$

$K_{i\mathit{min}}\le K_i\le K_{i\mathit{max}.}(9)$

where Ts—settling time,

$K_{p\mathit{min}}$—minimum proportional gain

$K_{p\mathit{max}}$—maximum proportional gain

$K_{i\mathit{min}}$—minimum integral gain

$K_{i\mathit{max}}$—maximum integral gain

The values are obtained by experience while using the PI controller. The problem is formulated using the aforementioned objectives and constraints.

Teacher-learner-based optimization (TLBO)

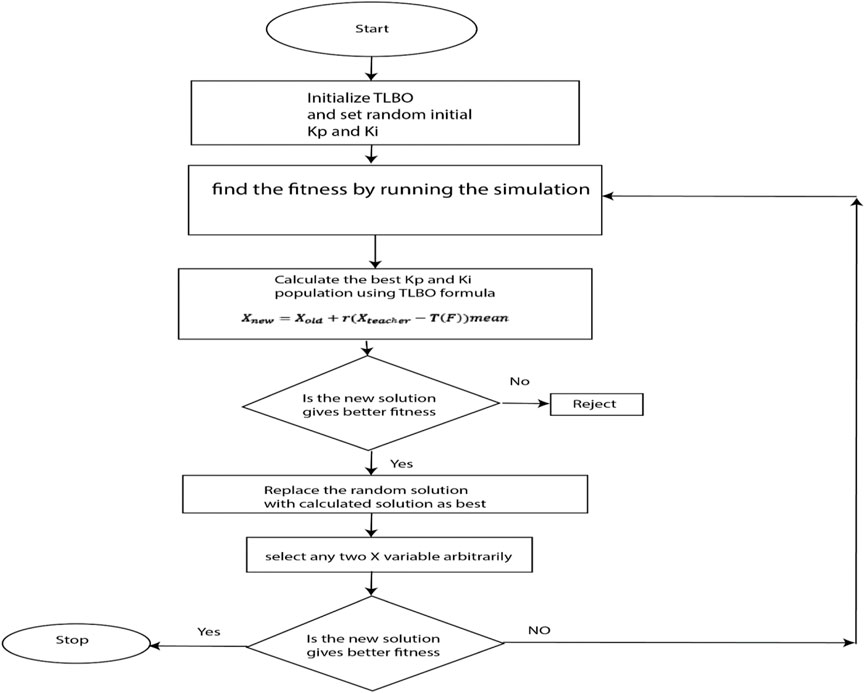
The optimization techniques used in the present research work are based on the TLBO algorithm, and the steps are presented along with the flow chart (Figure 5).

FIGURE 5

FIGURE 5. Proposed TLBO-based tuning procedure.

Step 1: The TLBO algorithm is initialized with the random values of the initial group of Kp and Ki values

Step 2: The Kp and Ki from Step 1 are used in the simulation, and the fitness function is identified.

Step 3: In the group of Kp and Ki values, the values that give lesser fitness are selected.

Step 4: The new Kp and Ki values are calculated using the formula given in the TLBO algorithm, and the fitness is found for new Kp and Ki values.

Step 5: If the new Kp and Ki values give lesser fitness, then replace the best values with the new Kp and Ki values.

Step 6: Else, reject the new Kp and Ki values, go to Step 2, and repeat till the end of the final iteration.

The TLBO algorithm is inspired by the process of teaching and learning in a classroom. The algorithm outlines the two fundamental ways that learning might occur: Through instruction from an instructor, which is called the teaching phase, and through collaboration with other students, which is called learning. The procedure and the flow chart are explained previously.

Gray wolf optimization (GWO)

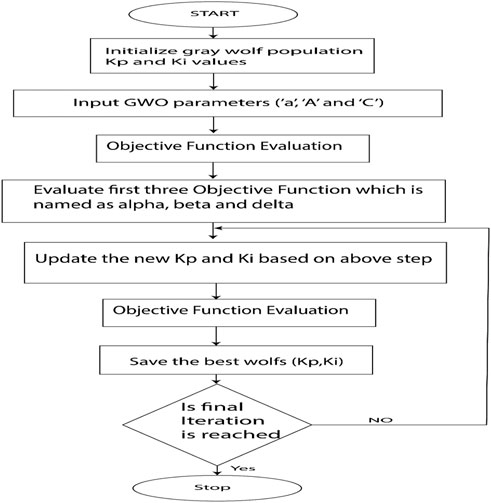
The second optimization technique used is GWO. The steps involved in the implementation are shown as a flowchart (Figure 6) with a brief description in this section. Here, the wolf is the Kp and Ki values. “Position” means in which the position of the array vector within the group of wolves the Kp and Ki values are placed.

FIGURE 6

FIGURE 6. Proposed GWO-based tuning procedure flow chart.

Step 1: Randomly initialize the gray wolf Kp and Ki values for N wolves Yi (i = 1, 2, …, n)

Step 2: Find the fit value to reduce the settling time for each individual.

Sort the wolves based on fitness. The three best solutions are named alpha_wolf, beta_wolf, and gamma_wolf.

Alpha_wolf—least fit wolf.

Beta_wolf—second least fit wolf.

Gamma_wolf—third least fit wolf.

Step 3: Do for maximum iteration:

Find the wolf constant “a:”

$a=2\ast \left(1-\frac{Iter}{ma{x}_{iter}}\right).$

Do for each wolf till N:

ACalculate the wolf constants Aa1, Aa2, Aa3, Bb1, Bb2, and Bb3, such that

Aa1 = a*(2*r1 − 1).

Aa2 = a*(2*r2 − 1).

Aa3 = a*(2*r3 − 1).

Bb1 = 2*r1.

Bb2 = 2*r2.

Bb3 = 2*r.

BCalculate Xx1, Xx2, and Xx3, such that

Xx1 = Aa1*abs (Bb1* position of alpha_wolf—ith position of wolf).

Xx2 = Aa2*abs (Bb2*position of beta_wolf—ith position of wolf).

Xx3 = Aa3*abs (C3*position of gamma_wolf—ith wolf position).

CCompute a new solution and its fitness:

Xnew = (Xx1 + Xx2 + Xx3)/3

Fitnew = fitness (Xnew).

D Update the ith wolf greedily:

if the fitnew is less than the ith fitness,

ith wolf position = Xxnew

ith wolf fitness = fitnew

End-for

Find the new values of alpha_wolf, beta_wolf, and gamma_wolf.

Based on the fit value, sort the wolves.

Update with the new value.

Alpha_wolf—least fit wolf.

Beta_wolf—second least fit wolf.

Gamma_wolf—third least fit wolf.

End the for loop.

Step 4: Send the final best wolf.

Results and discussion

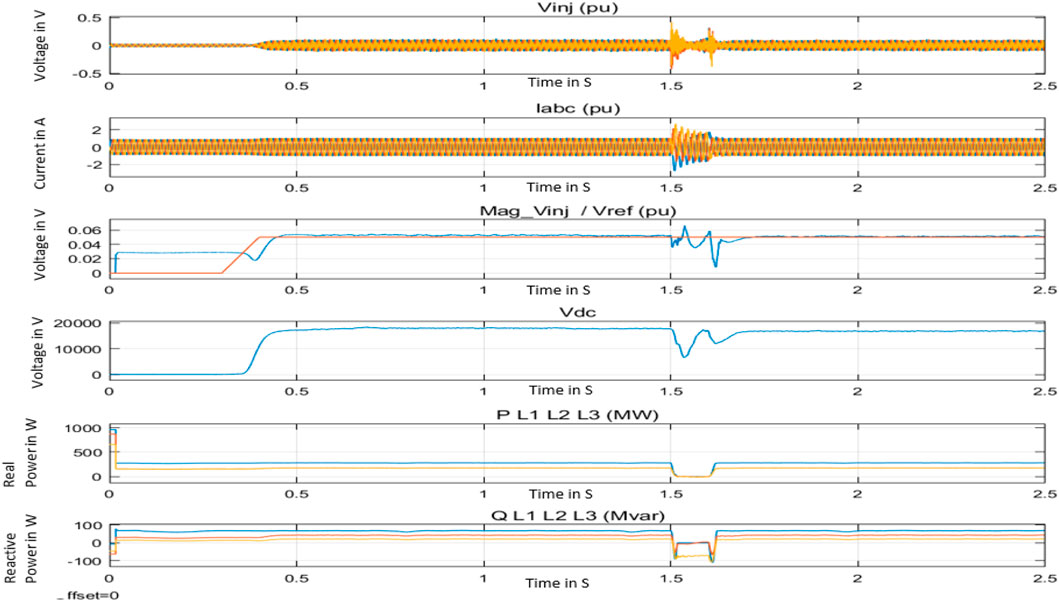
The SSSC is connected according to the proposed block diagram shown in Figure 1. The fault is created at the time 1.5 s and released at 1.6 s. The SSSC is connected in the circuit at 0.3 s.

Here, three cases are studied.

Case 1. With the PI controller

Case 2. With TLBO-PI

Case 3. With GWO-PI

Case 1 uses the PI controller in place of the SSSC control. The Case 2 Kp and Ki parameters are tuned using the TLBO algorithm. Then in Case 3, the GWO algorithm is used to tune the PI controller.

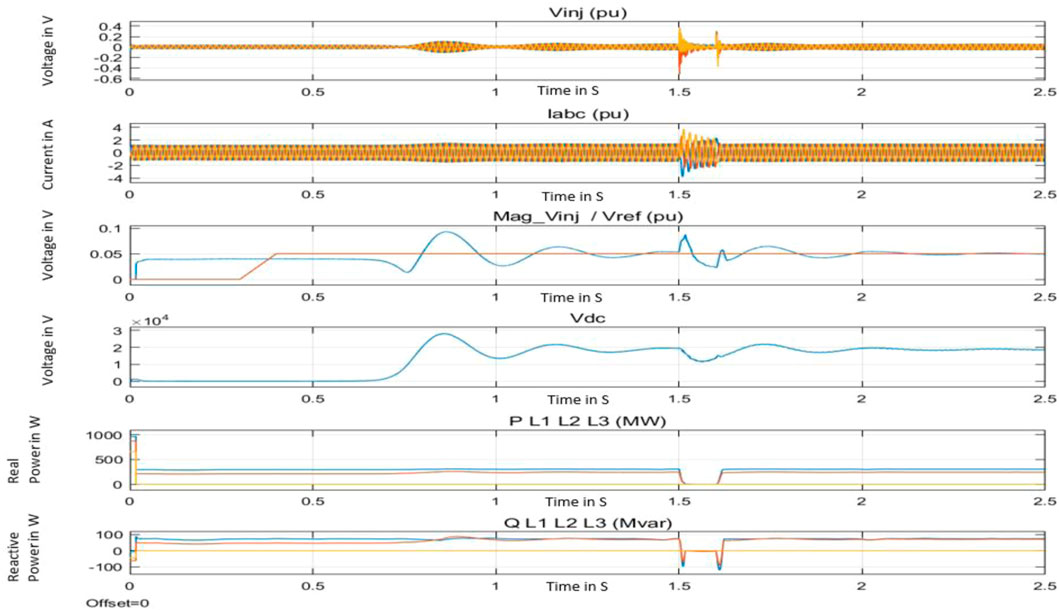
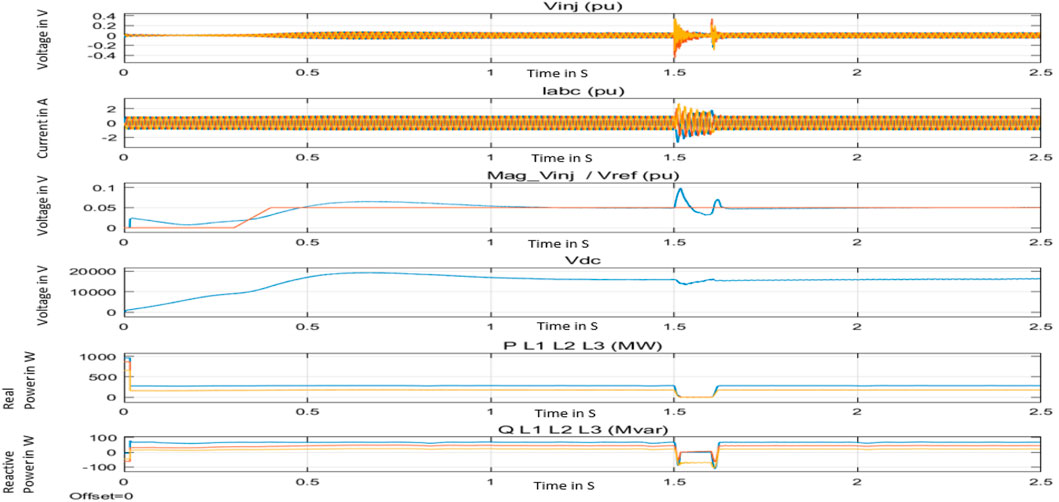
The setup and the system are common for all three cases. The results of voltage injection from SSSC (Vinj), the current through the SSSC (Iabc), the reference voltage of SSSC (Vref) and the injected voltage (Mag_inj), the DC voltage measured at the DC link (Vdc), the real power flow and reactive power flow of the power (P L1 L2 L3 and Q L1 L2 L3) are depicted as results for each case. Vinj is the voltage that must be injected when the SSSC is connected at 0.3 s. The current through the SSSC has a phase variation from the voltage of the power system. The magnitude of the Vinj is measured separately and shown as Mag_inj. Then, the SSSC has the DC link as the capacitor voltage. This voltage should be maintained to get compensation from the SSSC. There are three lines of real and reactive power available in the system labeled P_L1 and Q_L1, P_ L2 and Q_L2, and P_L3 and Q_L1.

The SSSC is designed for 10% of injection voltage. The set point of the voltage of SSSC of 0.05 pu is set as the DC link voltage reference. Figure 7 shows the results of PI, Figure 8 shows the results of TLBO-PI, and Figure 9 shows the results of GWO-PI. It can be seen that the Mag_inj takes a very long time to respond, and the oscillations are more in the waveform. This oscillation is also reflected in the other waveforms.

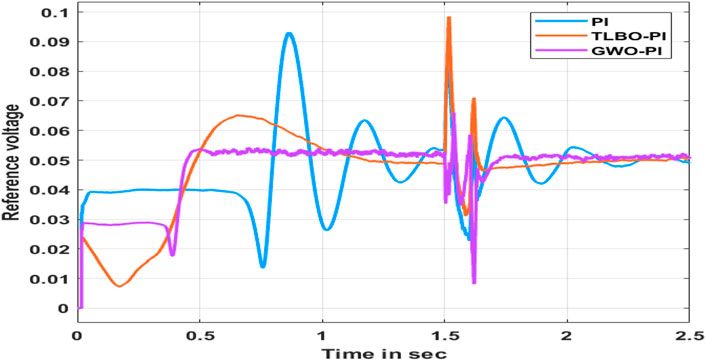
All three methods follow the reference voltage set. However, PI is more oscillatory than TLBO-PI and GWO-PI. The final results show that the settling time is better when using TLBO and GWO than when using PI, while the overshoot is less in GWO than in TLBO. The improvements result in faster stability in the power system, as shown in Figure 10.

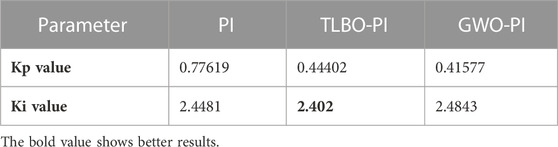
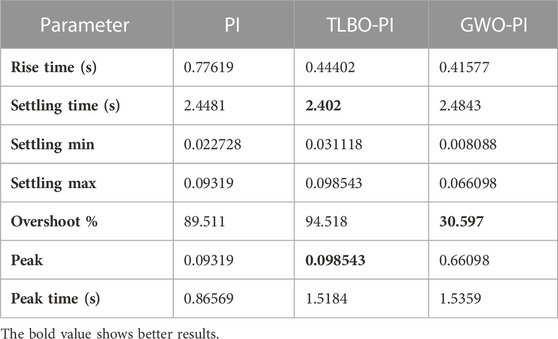
Table 1 shows the Kp and Ki values. Here, Table 2 shows the rise time, settling time, minimum and maximum values of settling time, percentage of overshoot, peak value, and the time taken to reach the peak values. The settling time shows that TLBO-PI has a smaller value of 2.402 s, while the PI and GWO-PI take longer to settle. The overshoot value shows 30.597%, which is less than PI and GWO-PI. The peak value of the error is smaller in the PI controller, where the TLBO-PI is slightly higher than the PI and very high in GWO-PI. The research objective is to minimize the settling time, which improves the stability of the system considered. The settling time is less when using the TLBO-PI controller than in other cases. The tendency to reach a peak value is also smaller. However, the percentage of overshoot is less in GWO-PI. Therefore, the TLBO-PI performs better in this study. In addition, the oscillations are smaller, as depicted in Figure 10.

FIGURE 7

FIGURE 7. PI controller results after connecting the SSSC.

FIGURE 8

FIGURE 8. TLBO-PI controller results after connecting the SSSC.

FIGURE 9

FIGURE 9. GWO-PI controller results after connecting the SSSC.

FIGURE 10

FIGURE 10. Comparison of the measured voltage amplitude of the SSSC injected voltage.

TABLE 1

TABLE 1. Kp and Ki values.

TABLE 2

TABLE 2. Comparative study of waveform properties while using PI, TLBO-PI, and GWO-PI.

Conclusion

To increase power on the system’s distribution side, wind power generation is connected to the power grid. The power is disrupted by this wind’s increased disruptions. One of the successful series FACTS for enhancing power system stability is the static synchronous compensator (SSSC). The injected voltage is controlled by the SSSC using a PI controller. Due to the size of the system, SSSC controllers cannot handle this PI controller setting. Therefore, the PI controller is tuned using a meta-heuristic method. This study uses the TLBO and GWO algorithms to tune the PI controller. Improved PI-controller tuning results are shown with the TLBO and GWO. TLBO reduces the settling time by 1.88%, along with a reduction in the peak value of voltage set by the SSSC. The validity of tuning the PI controller and the oscillations is established.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Annamraju, A., and Nandiraju, S. (2019). Coordinated control of conventional power sources and PHEVs using Jaya algorithm optimized PID controller for frequency control of a renewable penetrated power system. Prot. Control Mod. Power Syst. 4, 28. doi:10.1186/s41601-019-0144-2

CrossRef Full Text | Google Scholar

Bektache, A., and Boukhezzar, B. (2018). Nonlinear predictive control of a DFIG-based wind turbine for power capture optimization. Int. J. Electr. Power Energy Syst. 101, 92–102. doi:10.1016/j.ijepes.2018.03.012

CrossRef Full Text | Google Scholar

Burakov, M., and Shishlakov, V. (2017). Genetic algorithm optimization for pitch angle control of variable speed wind turbine. MATEC Web Conf. 113, 1–6.

CrossRef Full Text | Google Scholar

Choi, J. W., Heo, S. Y., and Kim, M. K. (2016). Hybrid operation strategy of wind energy storage system for power grid frequency regulation. IET Gener. Transm. Distrib. 10 (3), 736–749. doi:10.1049/iet-gtd.2015.0149

CrossRef Full Text | Google Scholar

Civelek, Z., Çam, E., Lüy, M., and Mamur, H. (2016). Proportional–integral–derivative parameter optimisation of blade pitch controller in wind turbines by a new intelligent genetic algorithm. Renew. Power Gener. 10 (8), 1220–1228. doi:10.1049/iet-rpg.2016.0029

CrossRef Full Text | Google Scholar

Civelek, Z. (2019). Optimization of fuzzy logic (Takagi-Sugeno) blade pitch angle controller in wind turbines by genetic algorithm. Sci. Technol. Int. J. 23 (1), 1–9. doi:10.1016/j.jestch.2019.04.010

CrossRef Full Text | Google Scholar

Costea, M., Vladu, E., and Károly, T. (2015). Wind turbine modelling in matlab Simulink. Romania: SSRN, 113–120.

Google Scholar

Dahab, Y. A., Abubkar, H., and Tarek Hassan, M. (2020). Adaptive load frequency control of power systems using electro-search optimization supported by balloon effect. IEEE ACCESS. 8. 7408–7422. doi:10.1109/ACCESS.2020.2964104

CrossRef Full Text | Google Scholar

Duong, M. Q., Grimaccia, F., Leva, S., Mussetta, M., Le, K. H., and District, L. (2015). Improving transient stability in a grid-connected squirrel cage induction generator wind turbine system using a fuzzy logic controller. energies 8, 6328–6349.

CrossRef Full Text | Google Scholar

Khadanga, R. K., Kumar, A., and Panda, S. (2019). A novel modified whale optimization algorithm for load frequency controller design of a two-area power system composing of PV grid and thermal generator”, Neural computing and application. doi:10.1007/s00521-019-04321-7

CrossRef Full Text | Google Scholar

Mohamed A, H. A. M., and Haridy, A. L. (2019). “The Whale Optimization Algorithm based controller for PMSG wind energy generation system,” in 2019 International Conference on Innovative Trends in Computer Engineering (ITCE), no. February, 438–443.

CrossRef Full Text | Google Scholar

Mohapatra, T. K., Dey, A. K., and Sahu, B. K. (2019). Implementation of SSA based two degrees of freedom fractional order PID controller for AGC with diverse source of generation. Int. J. Recent Technol. Eng. 7, 346–356.

Google Scholar

Naik, K. A., and Gupta, C. P. (2016). Improved fluctuation behaviour of SCIG based wind energy system using hybrid pitch angle controller. IEEE Uttar Pradesh Sect. Int. Conf. Electr. Comput. Electron. Eng. UPCON 1, 508–514., no.

Google Scholar

Naresh, M., and Tripathi, R. K. (2018). “Operation and control of doubly fed induction generator based wind energy system using FPGA,” in 2017 14th IEEE India Council International Conference (INDICON, 1–6.

Google Scholar

Osman, P. A. A., El-wakeel, A. S., and Seoudy, H. M. (2015). Optimal tuning of PI controllers for doubly-fed induction generator-based wind energy conversion system using grey wolf optimizer” J. Eng. Res. Appl. 5 (11), 81–87.

Google Scholar

Ou, T., Lu, K., and Huang, C. (2017). Improvement of transient stability in a hybrid power multi-system using a designed NIDC. energies Artic. 10 (4), 1–16.

CrossRef Full Text | Google Scholar

Padhy, S., and Panda, S. (2021). Application of a simplified Grey Wolf optimization technique for adaptive fuzzy PID controller design for frequency regulation of a distributed power generation system. Prot. Control Mod. Power Syst. 6, 2. doi:10.1186/s41601-021-00180-4

CrossRef Full Text | Google Scholar

Pahadasingh, S. (2021). “TLBO based CC-PID-TID controller for load frequency control of multi area power system”,” in Odisha International Conference on Electrical Power Engineering, Communication and Computing Technology, 1–7. doi:10.1109/ODICON50556.2021.9429022

CrossRef Full Text | Google Scholar

Poultangari, I., Shahnazi, R., and Sheikhan, M. (2012). RBF neural network based PI pitch controller for a class of 5-MW wind turbines using particle swarm optimization algorithm. algorithm” ISA Trans. 51 (5), 641–648. doi:10.1016/j.isatra.2012.06.001

CrossRef Full Text | Google Scholar

Qais, M. H., Hasanien, H. M., and Alghuwainem, S. (2018). A grey wolf optimizer for optimum parameters of multiple PI controllers of a grid-connected PMSG driven by variable speed wind turbine. IEEE Access 6, 44120–44128. doi:10.1109/access.2018.2864303

CrossRef Full Text | Google Scholar

Sinha, S., and Chandel, S. S. (2015). Review of recent trends in optimization techniques for solar photovoltaic–wind based hybrid energy systems. Sustain. Energy Rev. 50, 755–769. doi:10.1016/j.rser.2015.05.040

CrossRef Full Text | Google Scholar

Soued, S., Ebrahim, M. A., Ramadan, H. S., and Becherif, M. (2017). Optimal blade pitch control for enhancing the dynamic performance of wind power plants via metaheuristic optimisers. IET Electr. Power Appl. 11 (8), 1432–1440. doi:10.1049/iet-epa.2017.0214

CrossRef Full Text | Google Scholar

Syahputra, R., Robandi, I., and Ashari, M. (2014). Performance analysis of wind turbine as a distributed generation unit in distribution system. J. Comput. Sci. Inf. Technol. 6 (3), 39–56. doi:10.5121/ijcsit.2014.6303

CrossRef Full Text | Google Scholar

Wwd-, D., and Wwd, D. T. (2019). WWD-3 3 MW wind turbine detailed technical-specification,” document WWD-1003. Available at: https://pdf4pro.com/view/wwd-3-3-mw-wind-turbine-ecosource-energy-dc2b5.html.

Google Scholar

Yang, B., Zhang, X., Yu, T., Shu, H., and Fang, Z. (2017). Grouped grey wolf optimizer for maximum power point tracking of doubly-fed induction generator based wind turbine. Convers. Manag. 133, 427–443. doi:10.1016/j.enconman.2016.10.062

CrossRef Full Text | Google Scholar

Zahra, B., Salhi, H., and Mellit, A. (2017). “Wind turbine performance enhancement by control of pitch angle using PID controller and particle swarm optimization,” in 2017 5th International Conference on Electrical Engineering - Boumerdes (Boumerdes, Algeria: ICEE-B), 1–5.

CrossRef Full Text | Google Scholar